Skip to main content

Advertisement

SpringerLink
Log in

Single species growth consuming inorganic carbon with internal storage in a poorly mixed habitat

  • Published:
Journal of Mathematical Biology Aims and scope Submit manuscript

Abstract

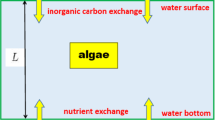
This paper presents a PDE system modeling the growth of a single species population consuming inorganic carbon that is stored internally in a poorly mixed habitat. Inorganic carbon takes the forms of “CO2” (dissolved CO2 and carbonic acid) and “CARB” (bicarbonate and carbonate ions), which are substitutable in their effects on algal growth. We first establish a threshold type result on the extinction/persistence of the species in terms of the sign of a principal eigenvalue associated with a nonlinear eigenvalue problem. If the habitat is the unstirred chemostat, we add biologically relevant assumptions on the uptake functions and prove the uniqueness and global attractivity of the positive steady state when the species persists.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Amann H, López-Gómez J (1998) A priori bounds and multiple solutions for superlinear indefinite elliptic problems. J Differ Equ 146:336–374

    Article  MathSciNet  MATH  Google Scholar 

  • Ballyk M, Dung LE, Jones DA, Smith HL (1998) Effects of random motility on microbial growth and competition in a flow reactor. SIAM J Appl Math 59:573–596

    Article  MathSciNet  MATH  Google Scholar 

  • Baxley JV, Robinson SB (1998) Coexistence in the unstirred chemostat. Appl Math Comput 89:41–65

    MathSciNet  MATH  Google Scholar 

  • Cunningham A, Nisbet RM (1980) Time lag and co-operativity in the transient growth dynamics of microalgae. J Theor Biol 84:189–203

    Article  Google Scholar 

  • Cunningham A, Nisbet RM (1983) Transient and oscillation in continuous culture. In: Bazin MJ (ed) Mathematics in microbiology. Academic, New York, pp 77–103

    Google Scholar 

  • Diekmann O, Metz JAJ (1986) The dynamics of physiologically structured populations. Lecture Notes in Biomath, vol 68. Springer, Berlin

  • Diekmann O, Heijmans HJAM, Thieme HR (1984) On the stability of the cell size distribution. J Math Biol 19:227–248

    Article  MathSciNet  MATH  Google Scholar 

  • Droop M (1968) Vitamin B12 and marine ecology. IV. The kinetics of uptake, growth and inhibition in Monochrysis lutheri. J Mar Biol Assoc UK 48:689–733

    Article  Google Scholar 

  • Droop M (1973) Some thoughts on nutrient limitation in algae. J Phycol 9:264–272

    Google Scholar 

  • Droop M (1974) The nutrient status of algal cells in continuous culture. J Mar Biol Assoc UK 54:825–855

    Article  Google Scholar 

  • Du Y, Hsu S-B (2010) On a nonlocal reaction–diffusion problem arising from the modeling of phytoplankton growth. SIAM J Math Anal 42:1305–1333

    Article  MathSciNet  MATH  Google Scholar 

  • Freedman HI, Zhao X-Q (1997) Global asymptotics in some quasimonotone reaction–diffusion systems with delays. J Differ Equ 137:340–362

    Article  MathSciNet  MATH  Google Scholar 

  • Friedman A (1964) Partial differential equations of parabolic type. Prentice-Hall Inc., Englewood Cliffs

    MATH  Google Scholar 

  • Grover JP (1992) Constant- and variable-yield models of population growth: responses to environmental variability and implications for competition. J Theor Biol 158:409–428

    Article  Google Scholar 

  • Grover JP (2009) Is storage an adaptation to spatial variation in resource availability? Am Nat 173:E 44–E 61

    Article  Google Scholar 

  • Grover JP (2011) Resource storage and competition with spatial and temporal variation in resource availability. Am Nat 178:E 124–E 148

    Article  Google Scholar 

  • Grover JP, Hsu S-B, Wang F-B (2009) Competition and coexistence in flowing habitats with a hydraulic storage zone. Math Biosci 222:42–52

    Article  MathSciNet  MATH  Google Scholar 

  • Grover JP, Hsu S-B, Wang F-B (2012) Competition between microorganisms for a single limiting resource with cell quota structure and spatial variation. J Math Biol 64:713–743

    Article  MathSciNet  MATH  Google Scholar 

  • Henry D (1981) Geometric theory of semilinear parabolic equations. Lecture Notes in Math, vol 840. Springer, Berlin

  • Hirsch WM, Smith HL, Zhao X-Q (2001) Chain transitivity, attractivity, and strong repellers for semidynamical systems. J Dyn Differ Equ 13:107–131

    Article  MATH  Google Scholar 

  • Hsu S-B, Lou Y (2010) Single phytoplankton species growth with light and advection in a water column. SIAM J Appl Math 70:2942–2974

    Article  MathSciNet  MATH  Google Scholar 

  • Hsu S-B, Waltman P (1993) On a system of reaction–diffusion equations arising from competition in an unstirred chemostat. SIAM J Appl Math 53:1026–1044

    Article  MathSciNet  MATH  Google Scholar 

  • Hsu S-B, Jiang J, Wang F-B (2010) On a system of reaction–diffusion equations arising from competition with internal storage in an unstirred chemostat. J Differ Equ 248:2470–2496

    Article  MathSciNet  MATH  Google Scholar 

  • Hsu S-B, Shi J, Wang F-B (2014) Further studies of a reaction–diffusion system for an unstirred chemostat with internal storage. Discrete Contin Dyn Syst Ser B 19:3169–3189

    Article  MathSciNet  MATH  Google Scholar 

  • Huisman J, van Oostveen P, Weissing FJ (1999) Species dynamics in phytoplankton blooms: Incomplete mixing and competition for light. Am Nat 154:46–67

    Article  Google Scholar 

  • Jiang J (1994) On the global stability of cooperative systems. Bull Lond Math Soc 26:455–458

    Article  MathSciNet  MATH  Google Scholar 

  • Jin W, Thieme HR (2014) Persistence and extinction of diffusing populations with two sexes and short reproductive season. Discrete Contin Dyn Syst Ser B 19:3209–3218

    Article  MathSciNet  MATH  Google Scholar 

  • Jin W, Smith HL, Thieme HR (2016) Persistence and critical domain size for diffusing populations with two sexes and short reproductive season. J Dyn Differ Equ 28:689–705

    Article  MathSciNet  MATH  Google Scholar 

  • Klausmeier CA, Litchman E (2001) Algal games: The vertical distribution of phytoplankton in poorly mixed water columns. Limnol Oceanogr 46:1998–2007

    Article  Google Scholar 

  • De Leenheer P, Levin SA, Sontag ED, Klausmeier CA (2006) Global stability in a chemostat with multiple nutrients. J Math Biol 52:419–438

  • Lieberman G (1996) Second order parabolic differential equations. World Scientific Publishing Co., Inc., River Edge

    Book  MATH  Google Scholar 

  • Li B, Smith HL (2007) Global dynamics of microbial competition for two resources with internal storage. J Math Biol 55:481–515

    Article  MathSciNet  MATH  Google Scholar 

  • Magal P, Zhao X-Q (2005) Global attractors and steady states for uniformly persistent dynamical systems. SIAM J Math Anal 37:251–275

    Article  MathSciNet  MATH  Google Scholar 

  • Mallet-Paret J, Nussbaum RD (2002) Eigenvalues for a class of homogeneous cone maps arising from max-plus operators. Discrete Contin Dyn Syst 8:519–562

    Article  MathSciNet  MATH  Google Scholar 

  • Mallet-Paret J, Nussbaum RD (2010) Generalizing the Krein–Rutman theorem, measures of noncompactness and the fixed point index. J Fixed Point Theor Appl 7:103–143

    Article  MathSciNet  MATH  Google Scholar 

  • Mei L, Hsu S-B, Wang F-B (2016) Growth of single phytoplankton species with internal storage in a water column. Discrete Contin Dyn Syst Ser B 21:607–620

    Article  MathSciNet  MATH  Google Scholar 

  • Nie H, Hsu S-B, Grover JP (2016) Algal Competition in a water column with excessive dioxide in the atmosphere. J Math Biol 72:1845–1892

    Article  MathSciNet  MATH  Google Scholar 

  • Protter MH, Weinberger HF (1984) Maximum principles in differential equations. Springer, Berlin

    Book  MATH  Google Scholar 

  • Smith HL (1995) Monotone dynamical systems: an introduction to the theory of competitive and cooperative systems. Math. Surveys Monogr, vol 41. American Mathematical Society, Providence

  • Smith HL, Thieme HR (2011) Dynamical systems and population persistence, Graduate Studies in Mathematics, vol 118. American Mathematical Society, Providence

  • Smith HL, Waltman PE (1995) The theory of the chemostat. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  • Smith HL, Zhao X-Q (2001) Robust persistence for semidynamical systems. Nonlinear Anal 47:6169–6179

    Article  MathSciNet  MATH  Google Scholar 

  • Thieme HR (1992) Convergence results and a Poincare–Bendixson trichotomy for asymptotically autonomous differential equations. J Math Biol 30:755–763

    Article  MathSciNet  MATH  Google Scholar 

  • Thieme HR (2016) Spectral radii and Collatz–Wielandt numbers for homogeneous order-preserving maps and the monotone companion norm. In: de Jeu M, de Pagter B, van Gaans O, Veraar M (eds) Ordered structures and applications. Birkhäuser, Basel, pp 415–467

    Chapter  Google Scholar 

  • Van de Waal DB, Verspagen JMH, Finke JF, Vournazou V, Immers AK, Kardinaal W, Edwin A, Tonk L, Becker S, Van Donk E, Visser PM, Huisman J (2011) Reversal in competitive dominance of a toxic versus non-toxic cyanobacterium in response to rising CO2, I.S.M.E. J. 5 (2011), pp 1438–1450

  • Woods JD (2005) The Lagrangian ensemble metamodel for simulating plankton ecosystems. Prog Oceanogr 67:84–159

    Article  Google Scholar 

  • Yoshiyama K, Mellard JP, Litchman E, Klausmeier CA (2009) Phytoplankton competition for nutrients and light in a stratified water column. Am Nat 174:190–203

    Article  MATH  Google Scholar 

  • Zhao X-Q (2003) Dynamical systems in population biology. Springer, New York

    Book  MATH  Google Scholar 

Download references

Acknowledgements

We are grateful to three anonymous referees for their careful reading and helpful suggestions which led to improvements of our original manuscript. We also express our thanks to Prof. H. R. Thieme for suggesting us the key reference Mallet-Paret and Nussbaum (2010) in this paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Tsing Hua University, Hsinchu, 300, Taiwan

    Sze-Bi Hsu

  2. Department of Mathematics, The Ohio State University, Columbus, OH, USA

    King-Yeung Lam

  3. Department of Natural Science in the Center for General Education, Chang Gung University, Guishan, Taoyuan, 333, Taiwan

    Feng-Bin Wang

  4. Community Medicine Research Center, Chang Gung Memorial Hospital, Keelung, Keelung, 204, Taiwan

    Feng-Bin Wang

Authors
  1. Sze-Bi Hsu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. King-Yeung Lam
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Feng-Bin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Feng-Bin Wang.

Additional information

Sze-Bi Hsu: Research supported in part by Ministry of Science and Technology, Taiwan.

King-Yeung Lam: Research partially supported by NSF Grant DMS-1411476.

Feng-Bin Wang: Research supported in part by Ministry of Science and Technology, Taiwan; and National Center for Theoretical Sciences (NCTS), National Taiwan University; and Chang Gung Memorial Hospital (BMRPD18 and NMRPD5F0541).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hsu, SB., Lam, KY. & Wang, FB. Single species growth consuming inorganic carbon with internal storage in a poorly mixed habitat. J. Math. Biol. 75, 1775–1825 (2017). https://doi.org/10.1007/s00285-017-1134-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00285-017-1134-5

Keywords

Mathematics Subject Classification

Search

Navigation