Mathematical assessment of the role of temperature and rainfall on mosquito population dynamics

Abstract

A new stage-structured model for the population dynamics of the mosquito (a major vector for numerous vector-borne diseases), which takes the form of a deterministic system of non-autonomous nonlinear differential equations, is designed and used to study the effect of variability in temperature and rainfall on mosquito abundance in a community. Two functional forms of eggs oviposition rate, namely the Verhulst-Pearl logistic and Maynard-Smith-Slatkin functions, are used. Rigorous analysis of the autonomous version of the model shows that, for any of the oviposition functions considered, the trivial equilibrium of the model is locally- and globally-asymptotically stable if a certain vectorial threshold quantity is less than unity. Conditions for the existence and global asymptotic stability of the non-trivial equilibrium solutions of the model are also derived. The model is shown to undergo a Hopf bifurcation under certain conditions (and that increased density-dependent competition in larval mortality reduces the likelihood of such bifurcation). The analyses reveal that the Maynard-Smith-Slatkin oviposition function sustains more oscillations than the Verhulst-Pearl logistic function (hence, it is more suited, from ecological viewpoint, for modeling the egg oviposition process). The non-autonomous model is shown to have a globally-asymptotically stable trivial periodic solution, for each of the oviposition functions, when the associated reproduction threshold is less than unity. Furthermore, this model, in the absence of density-dependent mortality rate for larvae, has a unique and globally-asymptotically stable periodic solution under certain conditions. Numerical simulations of the non-autonomous model, using mosquito surveillance and weather data from the Peel region of Ontario, Canada, show a peak mosquito abundance for temperature and rainfall values in the range $[20{-}25]\,^\circ$C and [15–35] mm, respectively. These ranges are recorded in the Peel region between July and August (hence, this study suggests that anti-mosquito control effects should be intensified during this period).

1 Introduction

Mosquito is the major vector for numerous vector-borne diseases, such as malaria, dengue and West Nile virus (WNv) (Cailly et al. 2012; Chitnis 2005; Esteva and Vargas 2000; Juliano 2007; Lewis et al. 2006; Mordecai et al. 2012; Wan and Zhu 2010; Wu et al. 2009). There are approximately 3500 mosquito species in the world, of which 200 species cause diseases in humans (WHO 2014). These (mosquito-borne) diseases cause significant public health burden in endemic areas. For instance, more than $55\%$ ($50\%$) of the world’s population live in areas at risk of dengue (malaria), which is transmitted by female Aedes aegypti (Anopheles) mosquitoes, with over 50 (300) million people infected and 20,000 (800,000) deaths annually (WHO 2014). Aedes aegypti causes numerous diseases, including Chikungunya, dengue and Zika virus (Yakob and Walker 2016). Currently, Chikungunya has been identified in over 60 countries in Asia, Africa, Europe and the Americas (WHO 2014) (outbreaks of Zika virus are also currently ongoing in some parts of the Americas (Yakob and Walker 2016). Moreover, culex mosquito, which is the primary vector for WNv in North America transmits pathogens responsible for important zoonotic diseases (Abdelrazec et al. 2014).

Owing to the significant burden inflicted by mosquitoes on human and animal health, mosquitoes have become the target of medical, veterinary and conservation research since the nineteenth century (Shaman and Day 2007). Hence, understanding the population dynamics of mosquitoes, and the relationship between mosquitoes and the environment, is fundamental to the study of the epidemiology of mosquito-borne diseases (Shaman and Day 2007). Mosquito abundance is a key determining factor that affects the persistence or resurgence of mosquito-borne diseases in populations (Wang et al. 2011) (it also affects the risk index of mosquito-borne diseases in a given region WHO 2014). Hence, it is crucial to study the dynamics of mosquitoes, and devise effective and realistic methods for controlling mosquito population in communities.

Climate variables, such as temperature, humidity, rainfall and wind, significantly affect the life-cycle and, consequently, the abundance of mosquitoes in populations (Agusto et al. 2015; Cailly et al. 2012; Mordecai et al. 2012; Shaman and Day 2007; Wu et al. 2009). Numerous mathematical models have been designed and used to assess the impact of climate change and seasonality on the transmission dynamics of mosquito-borne diseases, such as malaria (Agusto et al. 2015; Ebi et al. 2005; Jaenisch and Patz 2002; Mordecai et al. 2012; Paaijmans et al. 2009), dengue (Chen et al. 2010; Hales et al. 2002; Pham et al. 2011; Wu et al. 2009; Yang et al. 2011), chikungunya (Fischer et al. 2013; Meason and Paterson 2014) and WNv (Abdelrazec et al. 2015; Wang et al. 2011). For instance, such models allow for the determination of parameters, or variables, that influences the life-cycle of the mosquitoes (Ahumada et al. 2004; Cailly et al. 2012; Tran et al. 2013). The spatio-temporal dynamics of mosquito populations (in urban areas) have been studied in Cummins et al. (2012) and Oluwagbemi et al. (2013). Furthermore, several models have been developed to predict the temporal dynamics of mosquito abundance, in the presence of climate change, using either statistical (Wang et al. 2011), stochastic (Otero et al. 2006) or deterministic formulations (Lutambi et al. 2013). However, most of the existing models of mosquito population dynamics were built for a specific mosquito species, within a specific geographic context (e.g., Anopheles gambiae in the Sahel (Yamana and Eltahir 2013); Anopheles arabiensis in Zambia (Oluwagbemi et al. 2013) and culex in Canada (Wang et al. 2011)) and may not be applied to other mosquito species or areas. A model for the dynamics of general species of mosquitoes is developed in Cailly et al. (2012).

The purpose of the current study is to qualitatively assess the impact of temperature and rainfall on the population dynamics of female mosquitoes in a certain region. To achieve this objective, a new compartmental mathematical model, which incorporates variability in temperature and rainfall, will be designed and used to study the dynamics of the aquatic and adult stages of female mosquitoes in the given region (the resulting model, which takes the form of a non-autonomous deterministic system of nonlinear differential equations, can be applied to several mosquito species and different areas). Mosquito surveillance and weather data from the Peel region of Ontario, Canada will be used to parametrize the model. The model is formulated in Sect. 2, and its autonomous equivalent is rigorously analysed in Sect. 3. The full non-autonomous model is analysed in Sect. 4. Numerical simulations are reported in Sect. 5.

2 Model formulation

The complete metamorphosis of the mosquito entails going through four distinct stages of development, namely egg, larva, pupa, and adult mosquito stages (Chitnis et al. 2008). Mosquito-borne diseases are spread to humans following an effective bite from an infected female mosquito (in quest of blood meal, needed for egg development) (Hilker and Westerhoff 2007). Hatching of eggs (into larvae) may occur either within a few days or may be delayed for several months, depending on the species and the period of the year when the eggs are laid (Clements 1999). Larvae molt four times as they grow. After the fourth molt, they become pupae, from which adult mosquitoes emerge on the surface of the water (Hilker and Westerhoff 2007).

Table 1 Description of variables and parameters of the model (2.1)

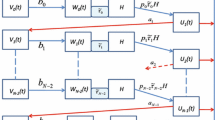
The model to be designed, which splits the total (immature and adult) mosquito population at time t into mutually exclusive compartments of eggs (E(t)), larvae (L(t)), pupae (P(t)) and female adult mosquitoes (M(t)),  is given by the following deterministic, non-autonomous system of nonlinear differential equations (the parameters of the model are defined in Table 1):

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{dE}{dt} = M B(M) - \left[ F_{E}(T,R)+\mu _{E}(T,R)\right] E, \\ \displaystyle \frac{dL}{dt} = F_{E}(T,R)E-\left[ F_{L}(T,R)+\mu _{L}(T,R) + \delta _L L \right] L, \\ \displaystyle \frac{dP}{dt} =F_{L}(T,R) L - \left[ F_{P}(T,R)+ \mu _{P}(T,R) \right] P, \\ \displaystyle \frac{dM}{dt} = \sigma F_{P} (T,R) P - \mu _M(T) M, \end{array} \right. \end{aligned}$$

(2.1)

where $T=T(t)$ and $R=R(t)$ represent temperature and rainfall, respectively. It is assumed that T and R are non-negative, continuous and bounded periodic functions. Furthermore, the parameters $F_E(T,R), F_L(T,R), F_P(T,R), \mu _E(T,R), \mu _L(T,R), \mu _P(T,R)$ and $\mu _M(T)$ are non-negative, bounded, periodic and continuous functions defined on $[0,\infty )$. The term $\delta _L L,$ which captures the density-dependent mortality rate of larvae, is non-negative. It is also assumed that ambience and water temperature are approximately equal (near the surface of the water) (Kothandaraman 1972). In (2.1), B(M) is the general form of the eggs oviposition function. It is assumed that B(M) is a strictly non-negative and continuously-differentiable function (Cooke et al. 1999), with

$$\begin{aligned} B(M): [0,\infty ) \rightarrow [0,\infty ). \end{aligned}$$

The following two functional forms of B(M) are considered in this study (Ngwa et al. 2010):

$$\begin{aligned} \begin{aligned}&\displaystyle B_L: \ \ \ B(M) = b(T,R) \left( 1-\frac{M}{K} \right) , \ \ \ M \in [0,K); \\&\displaystyle B_S: \ \ \ B(M)=\frac{b(T,R)}{1+\left( \frac{M}{K}\right) ^n}, \ \ \ n>0, \end{aligned} \end{aligned}$$

(2.2)

where b(T, R) is the rate at which eggs are laid by adult female mosquitoes per oviposition (which is assumed to be non-negative, bounded, periodic and continuous functions defined on $[0,\infty )$] and $K > 0$ is the environmental carrying capacity of female adult mosquitoes (which is related to the availability of host to take blood meals from). The forms $MB_L$ and $MB_S$ are the Verhulst-Pearl logistic (Abdelrazec et al. 2014; Ngwa 2005) and Maynard-Smith-Slatkin (Brannstrom and Sumpter 2005) oviposition functions, respectively. It should be mentioned that, in the form $B_L,$ the non-negativity condition on B(M) will only hold if $M<K$ (hence, K is assumed to be greater than M).

One of the main objectives of this study is to use the model (2.1) to provide realistic estimate of mosquito abundance, subject to variability in temperature and rainfall. In order to achieve this objective, realistic functional forms of the temperature- and rainfall-dependent parameters of the model will be derived. The model (2.1) is an extension of the autonomous mosquito population biology model in Ngwa et al. (2010), by adding: $(\mathrm{i})$ the effect of temperature and rainfall, $(\mathrm{ii})$ the aquatic stages of the mosquito and $(\mathrm{iii})$ density-dependent larval mortality rate. It also extends the non-autonomous mosquito dynamics model in Cailly et al. (2012) by giving a novel and realistic formulation of the temperature- and rainfall-dependent parameters of the model, as described below.

2.1 Temperature-and rainfall-dependent parameters

The main climate drivers that affect the dynamics of mosquitoes are temperature and rainfall (see, for instance, Mordecai et al. 2012). It is, first of all, assumed (for mathematical convenience) that temperature and rainfall act independently. The effect of temperature depends upon the stage of development of the mosquito. Statistical study by Hilker and Westerhoff (2007) showed that hatching of the culex mosquito eggs varies during the year; being low in the winter (whenever the temperature is less than $10\,^\circ$C) and high in the summer (whenever the temperature is in the range $(22{-}30)\,^\circ$C). Rainfall can induce positive (where rainfall increases the availability of breeding sites for female culex mosquitoes to lay their eggs) or negative (excessive rainfall increases the mortality of immature mosquitoes) effect on culex dynamics (Turell and Dohm 2005).

The parameter b(T, R),  for the rate of eggs laid per oviposition, is defined as

$$\begin{aligned} b(T,R) = \alpha _b u_b(T) v_b(R), \end{aligned}$$

(2.3)

where $u_b(T)$ and $v_b(R)$ account for the effect of temperature and rainfall on the daily survival probability of eggs laid. The parameter $\alpha _b$ represents the maximum rate of eggs laid per oviposition. Similarly, the transition rates $F_j(T,R)$ are defined as

$$\begin{aligned} F_j(T,R) =\alpha _j g_j(T)h_j(R); \quad j=\{E,L,P\}, \end{aligned}$$

(2.4)

where $g_j(T)$ and $h_j(R)$ account for the effect of temperature and rainfall, respectively, on the transition rates $F_j(T,R).$ Furthermore, $\alpha _j$ represents the maximum rate of transition between the aquatic stages. The mortality rate for the three aquatic stages of the mosquito are defined as

$$\begin{aligned} \mu _j(T,R) = p_j(T) q_j(R); \quad j=\{E,L,P,\}, \end{aligned}$$

where $p_j(T)$ and $q_j(R)$ account for the effect of temperature and rainfall, respectively, on the mortality rate for each aquatic stage. The temperature-dependent functions $u_b(T), \mu _M(T),$ $g_j(T)$ and $p_j(T)$ are defined, respectively, as

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle u_b(T) = e^{-a_b(T-T_b)^2}, \\ \displaystyle \mu _M(T) = c_M(T-T^*_M)^2+d_M, \\ \displaystyle g_j(T)= e^{-a_j(T-T_j)^2}, \\ \displaystyle p_j(T) =c_j(T-T^*_j)^2+d_j, \end{array} \right. \end{aligned}$$

(2.5)

where the parameters $a_b, c_M,$ $a_j$ and $c_j$ specify the amplitude of the functions $u_b(T), \mu _M(T),$ $g_j(T)$ and $p_j(T),$ respectively (these parameters can be determined using mosquito surveillance and weather data). Moreover, $d_M$ and $d_j$ ($\ j=\{E,L,P\}$) are the minimum values of the functions $\mu _M(T)$ and $p_j(T),$ respectively. Furthermore, $T_b$ and $T_j$ ($T^*_M$ and $T^*_j$) are the temperature values that correspond to the maximum (minimum) value of $u_b(T)$ and $g_j(T),$ respectively ($\mu _M(T)$ and $p_j(T),$ respectively).

Table 2 Description of the temperature- and rainfall-dependent functions and parameters given in Eqs. (2.5) and (2.6)

Fig. 1

Plot of some temperature- and rainfall-dependent functions of the model (2.1)

To capture the effects of rainfall as described above, the following functional forms for $v_b(R),$ $h_j(R)$ and $q_j(R)$ are derived:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle v_b(R) = \frac{(1+s_b)e^ {-r_b(R-R_b)^2}}{ e^ {-r_b(R-R_b)^2}+ s_b}, \\ \displaystyle h_j(R)=\frac{(1+s_j)e^ {-r_j(R-R_j)^2}}{ e^ {-r_j(R-R_j)^2}+ s_j}, \\ \displaystyle q_j(R)= 1+\frac{e_jR}{1+R}, \end{array} \right. \end{aligned}$$

(2.6)

where $c_b, s_b$ $r_j, s_j$ and $e_j$ are parameters that specify the amplitude of the functions $v_b(R),$ $h_j(R)$ and $q_j(R),$ respectively. Furthermore, $R_j$ is the rainfall value that corresponds to the maximum value of $h_j(R).$ The parameters described in this section are tabulated in Table 2. Furthermore, the functions given by Eqs. (2.5) and (2.6) are depicted in Fig. 1.

2.2 Basic properties

It is convenient to define, for each parameter Q(t),  the quantities:

$$\begin{aligned} \begin{array}{lll} \displaystyle Q^*=\sup _{t \ge 0} Q(t), \quad \displaystyle Q_{*}=\inf _{t \ge 0} h(t), \quad \displaystyle \overline{Q} = \frac{1}{w} \int ^w_0 Q(t)dt. \end{array} \end{aligned}$$

(2.7)

Lemma 2.1

Consider the non-autonomous linear initial-value problem (IVP)

$$\begin{aligned} \dfrac{dz}{dt} = a(t)-b(t)z; \quad z(0)=z_0, \ \ a(t)> 0, \ \ b(t) > 0, \ \ \forall \ \ t \ge 0. \end{aligned}$$

(2.8)

Then,

• (1) All solutions z(t) with initial conditions $z_0\ge 0$ are non-negative for all $t \ge 0.$

• (2) Each fixed solution z(t) (with $z_0 \ge 0$ and a(t), b(t) bounded and continuous functions) is bounded.

• (3) There exist $m_1, m_2$ such that $m_1<\lim \nolimits _{t\longmapsto \infty } \inf z(t)< \lim \nolimits _{t\longmapsto \infty } \sup z(t) < m_2.$

• (4) There exists $d \ge 0$ such that if z(t) is a solution of (2.8) and Z(t) is a solution of $\dfrac{dZ}{dt} = a(t)-b(t)Z + f(t)$ with f bounded and $Z(0)=z_0,$ then

  $$\begin{aligned} \sup |Z(t)-z(t)| \le d \sup |f(t)|. \end{aligned}$$

The proof of Lemma 2.1 is given in Appendix A. Lemma 2.1 will be used to prove the boundedness of the model (2.1).

The basic properties of the non-autonomous model (2.1) will now be studied. Since the system (2.1) monitors populations in each stage of mosquito development (and recalling that all parameters of the model (Table 1) are positive), the analysis of the model will be carried out in the following invariant region

$$\begin{aligned} \gamma = \left\{ (E,L,P,M) \in {{\mathcal {R}}}^4 : E(t), L(t), P(t), M(t) \ge 0 \right\} , \end{aligned}$$

where the model is mathematically and ecologically well-posed. That is, all solutions of the system (2.1) with non-negative initial data will remain non-negative in the feasible region $\gamma$ for all time $t \ge 0$. It is convenient to define $N(t)=E(t)\,+\,L(t)\,+\,P(t)\,+\,M(t).$ It follows, by adding the right-hand sides of the equations in (2.1), that (in $\gamma$)

$$\begin{aligned} \dfrac{dN(t)}{dt} \le MB(M)-\mu _m N(t), \end{aligned}$$

where $\mu _m= \min (\mu _M, \mu _E, \mu _L, \mu _P).$ Thus, $\frac{dN}{dt} \le Kb(t)-\mu _m N(t)$ for each of the functional forms $B(M)=B_L$ or $B_S.$ The result below can be proved (using, for instance, a comparison theorem (Smith and Waltman 1995) and Lemma 2.1; and is not given here).

Theorem 2.2

The system (2.1), with $B(M)=B_L$ or $B_S,$ has a unique and bounded solution with initial values in the region $\gamma .$ Furthernore, the compact set

$$\begin{aligned} \Gamma = \left\{ (E,L,P,M) \in \gamma : N(t) \le \left[ \left( \int _0^t Kb(s) e^{\mu _m s} ds \right) + N_0 \right] e^{- \mu _m t } = m \right\} , \end{aligned}$$

is positively-invariant and attracts all positive orbits in $\gamma$.

Before analysing the qualitative dynamics of the non-autonomous model (2.1), it is instructive to analyse its autonomous equivalent (where all parameters of the model (2.1) are independent of temperature and rainfall), with the aim of determining whether or not the non-autonomous model and the autonomous equivalent have differing qualitative dynamics (with respect to the existence and asymptotic stability of associated steady-state solutions).

3 Analysis of autonomous model

Consider the autonomous version of the model (2.1), obtained by setting $b(T,R)=b,$ $\mu _E(T,R)=\mu _E, F_E(T,R)=F_E, \mu _L(T,R)=\mu _L, F_L(T,R)=F_L, \mu _P(T,R)=\mu _P, F_P(T,R)=F_P$ and $\mu _M(T)=\mu _M,$ given by (denoted as the “autonomous model”)

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{dE}{dt} = M B(M) - \left( F_{E} + \mu _{E} \right) E, \\ \displaystyle \frac{dL}{dt} = F_{E}E-\left( F_{L}+\mu _{L} + \delta _L L \right) L, \\ \displaystyle \frac{dP}{dt} =F_{L}L - \left( F_{P} +\mu _{P} \right) P, \\ \displaystyle \frac{dM}{dt} = \sigma F_{P} P - \mu _M M. \end{array} \right. \end{aligned}$$

(3.1)

Since the state variables of the autonomous model (3.1) are non-negative for all time t (and all its parameters are positive), the model (3.1) can be studied in the invariant region:

$$\begin{aligned} {{\mathcal {D}}}=\left\{ (E,L,P,M) \in {{\mathcal {R}}}^4 : E,L,P,M\ge 0 \right\} , \end{aligned}$$

where the model is mathematically and ecologically well-posed.

3.1 Existence and stability of equilibria

3.1.1 Trivial equilibrium point

The model (3.1) has a mosquito-free equilibrium (trivial equilibrium), denoted by

$$\begin{aligned} P_0 =(E_*, L_*, P_*, M_*) =(0,0,0,0). \end{aligned}$$

It is convenient to define

$$\begin{aligned} {{\mathbb {R}}}_{0} = \frac{b \sigma F_E F_L F_P}{\mu _1 \mu _2 \mu _3 \mu _M}, \end{aligned}$$

(3.2)

where $\mu _1 = \mu _E + F_E, \mu _2 = \mu _L + F_L$ and $\mu _3 =\mu _P+F_P.$ The threshold quantity, ${{\mathbb {R}}}_{0}$, is the vectorial reproduction number. It measures the average expected number of new adult female offsprings produced by a single female mosquito during its life time. It can be ecologically interpreted as the product of the fraction of eggs that survived and hatched into larvae $\left( \frac{bF_E}{\mu _{1}}\right)$, the fraction of larvae that survived and progressed into pupae $\left( \frac{F_L}{\mu _{2}}\right)$, the fraction of pupae that survived to become adult female mosquitoes $\left( \frac{\sigma F_P}{\mu _{3}}\right)$ and the average lifespan of female adult mosquitoes $\left( \frac{1}{\mu _M}\right)$.

Theorem 3.1

Consider the model (3.1), subject to the two forms of B(M) given in (2.2). The mosquito-free equilibrium, $P_0,$ is locally-asymptotically stable (LAS), whenever ${{\mathbb {R}}}_{0}<1,$ and unstable if ${{\mathbb {R}}}_{0} > 1.$

Proof

Evaluating the Jacobian of the system (3.1) at $P_0$ gives, for each of the two forms of B(M),

$$\begin{aligned} J(P_0) = \left( \begin{array}{cccccc} -\mu _1 &{}\quad 0 &{}\quad 0 &{}\quad b \\ F_E &{}\quad -\mu _2 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad F_L &{}\quad -\mu _3 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad F_P \sigma &{}\quad -\mu _M \end{array} \right) , \end{aligned}$$

with eigenvalues satisfying the following characteristic Equation:

$$\begin{aligned} \lambda ^4 + a_3 \lambda ^3 + a_2 \lambda ^2 + a_1 \lambda + a_0 = 0, \end{aligned}$$

(3.3)

where,

$$\begin{aligned} \left\{ \begin{array}{lll} a_3 = \mu _1 + \mu _2 + \mu _3 + \mu _M, \\ a_2 =\mu _1 \mu _2 + \mu _1 \mu _3 + \mu _1 \mu _M + \mu _2 \mu _3 + \mu _2 \mu _M + \mu _3 \mu _M, \\ a_1 = \mu _1 \mu _2 \mu _3 + \mu _1 \mu _2 \mu _M + \mu _1 \mu _3 \mu _M + \mu _2 \mu _3 \mu _M, \\ a_0 = \mu _1 \mu _2 \mu _3 \mu _M (1-{{\mathbb {R}}}_{0}). \end{array} \right. \end{aligned}$$

(3.4)

The local stability of $P_0$ is investigated by applying the Routh-Hurwitz criterion on (3.3). The relevant Routh-Hurwitz determinants (for a quartic) are:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta _{1}=a_{3}>0, \\ \Delta _{2}=a_{3}a_{2}-a_{1}>0, \\ \Delta _{3}=a_{1} \Delta _{2}-a_{3}^{2}a_{0}>0, \\ \Delta _{4}=a_{0} \Delta _{3} >0. \end{array} \right. \end{aligned}$$

(3.5)

Let,

$$\begin{aligned} \alpha = (\mu _1+\mu _2)(\mu _1+\mu _3) ( \mu _2+\mu _3)(\mu _M+\mu _1)( \mu _M+\mu _2)(\mu _M+\mu _3) > 0, \end{aligned}$$

and,

$$\begin{aligned} \beta = \mu _1 \mu _2 \mu _3 \mu _M > 0. \end{aligned}$$

Since all the parameters of the model (3.1) are positive, it follows that $\Delta _{1}>0.$ Furthermore, it can be seen that $\Delta _{2} >0.$ Hence, $a_1\Delta _{2} = \alpha + a^2_3 \beta > 0.$ To show that $\Delta _{3} > 0$, it is convenient to re-write $a_0$ (in (3.4)) and $\Delta _{3} > 0$ (in (3.5)) as

$$\begin{aligned} a_0= \beta \left( 1 - {{\mathbb {R}}}_0 \right) \ \ \ \text {and} \ \ \ \Delta _3 = \alpha + a^2_3 \beta {{\mathbb {R}}}_{0} > 0, \end{aligned}$$

respectively. The following conclusions can be drawn:

• If ${{\mathbb {R}}}_{0}<1,$ then $a_0 >0$. Moreover, $\Delta _3 > 0.$ Hence, all roots of the characteristic Eq. (3.3) are negative. Thus, $P_0$ is LAS.

• If ${{\mathbb {R}}}_{0}>1,$ then $a_0 <0.$ Hence, there exists at least one positive root for the characteristic Eq. (3.3). Thus, $P_0$ is unstable. $\square$

The ecological implication of Theorem 3.1 is that if the initial sub-populations of the model (3.1) are in the basin of attraction of the trivial equilibrium $P_0$, then the mosquito population can be effectively controlled if ${{\mathbb {R}}}_{0}<1.$ To ensure that the effective control of the mosquito population is independent of the initial size of the mosquito populations, a global asymptotic stability result must be established for the trivial equilibrium. This is done below.

Theorem 3.2

Consider the system (3.1), subject to the two forms of B(M) in (2.2). The trivial equilibrium, $P_{0}$, is globally-asymptotically stable (GAS) in ${{\mathcal {D}}}$ whenever ${{\mathbb {R}}}_0 < 1$.

Proof

Consider the Lyapunov function

$$\begin{aligned} V=\sigma F_LF_P [F_E E(t) + \mu _1 L(t)] + \mu _1 \mu _2 [\sigma F_P P(t) + \mu _3 M(t)], \end{aligned}$$

with Lyapunov derivative,

$$\begin{aligned} \frac{dV}{dt}= & {} \sigma F_LF_P \left( F_E \frac{dE}{dt} + \mu _1 \frac{dL}{dt}\right) + \mu _1 \mu _2 \left( \sigma F_P \frac{dP}{dt} + \mu _3 \frac{dM}{dt}\right) , \\= & {} \sigma F_LF_P [F_E (M B(M) - \mu _{1}E)+\mu _1(F_E E - \mu _2 L -\delta _L L^2)] \\&\quad +\, \mu _1 \mu _2 [\sigma F_P (F_L L- \mu _3 P) + \mu _3(\sigma F_P P-\mu _M M)],\\= & {} \sigma F_LF_P [F_E M B(M) - \mu _1 \mu _2 L - \mu _1\delta _L L^2] + \mu _1 \mu _2 [\sigma F_P F_L L-\mu _3\mu _M M], \\= & {} - \left( M [\mu _M \mu _1 \mu _2 \mu _3 - \sigma F_L F_E F_P B(M)] + \sigma \mu _1\delta _LF_LF_P L^2 \right) , \\\le & {} - M [\mu _M \mu _1 \mu _2 \mu _3 - \sigma F_L F_E F_P B(M)], \end{aligned}$$

which, using (3.2), can be re-written as

$$\begin{aligned} \frac{dV}{dt}\le - \mu _M \mu _1 \mu _2 \mu _3 M(t) \left[ 1-\frac{{{\mathbb {R}}}_{0} }{b}B(M)\right] . \end{aligned}$$

Since $max_M B(M)\le b$ for each of the cases of B(M) given in (2.2), it follows, for ${{\mathbb {R}}}_0 < 1,$ that the quantity $\frac{{{\mathbb {R}}}_{0} }{b}B(M) < 1$ (for all $M(t) \in {{\mathcal {D}}}$ ). Hence, $\frac{dV}{dt} \le 0.$ The Lyapunov-LaSalle theorem (Kolmanovskii and Shaikhet 2002) implies that the solutions approach (asymptomatically) $M=0,$ the largest compact invariant subset of the set $\frac{dV}{dt}=0$. Furthermore, all solutions on the plane $M=0$ approach the equilibrium, $P_{0},$ asymptotically. Thus, for the two forms of B(M) given in (2.2), the trivial equilibrium, $P_{0},$ is GAS in ${{\mathcal {D}}}$ whenever ${{\mathbb {R}}}_0 < 1$. $\square$

The above result shows that, for the autonomous model (3.1), a vector control strategy that brings (and maintains) the threshold quantity, ${{\mathbb {R}}}_0,$ to a value less than unity will lead to the effective control (or elimination) of mosquitoes from the community. In other words, the requirement ${{\mathbb {R}}}_0 <1$ is necessary and sufficient for the effective control (or elimination) of mosquitoes in the community.

3.1.2 Non-trivial equilibrium point

The system (3.1) has a non-trivial equilibrium, denoted by $P_1 = (E^*,L^*,P^*,M^*),$ where

$$\begin{aligned} \left\{ \begin{array}{lll} E^*=\dfrac{\mu _2 + \delta _L L^* }{F_E } L^*, \\ P^*= \dfrac{F_L}{\mu _3}L^*, \\ M^*= \dfrac{F_LF_P \sigma }{\mu _3 \mu _M}L^*, \end{array} \right. \end{aligned}$$

(3.6)

with $L^*$ satisfying the equation

$$\begin{aligned} \frac{F_E F_LF_P \sigma }{\mu _3 \mu _M} B\left( M^*\right) - \mu _1(\mu _2 + \delta _L L^*) = 0. \end{aligned}$$

(3.7)

Consider, using (2.2), (3.6) and (3.7), the following cases for the existence of the non-trivial equilibrium of the autonomous model (3.1).

• Case 1: $B(M)=B_L.$ Here, $L^*$ can be determined by re-writing (3.7) as

  $$\begin{aligned} L^*= \frac{1}{Q}\left( 1-\frac{1}{{{\mathbb {R}}}_0}\right) , \ \ \ \text {with} \ \ \ Q = \frac{\mu _1 \mu _3 \mu _M \delta _L}{F_E F_L F_P \sigma } + \frac{F_L F_P \sigma }{\mu _3 \mu _M K}, \end{aligned}$$

  (3.8)

  from which it follows that $P_1$ exists only if ${{\mathbb {R}}}_{0} > 1.$

• Case 2: $B(M)=B_S.$ In this case, $L^*$ can be obtained by finding the roots of $(n+1)$-degree polynomial

  $$\begin{aligned} \nu \delta _L \left( L^{*}\right) ^{(n+1)} + \nu \mu _2 \left( L^{*}\right) ^{n} +\delta _L L^* + \mu _2 \left( 1-{{\mathbb {R}}}_0 \right) = 0, \end{aligned}$$

  (3.9)

  where $\nu = \left( \frac{F_L F_P \sigma }{\mu _3 \mu _M K}\right) ^n.$ It follows, using Descartes’ Rule of Signs, that the polynomial (3.9) has a unique positive non-trivial root ($P_1$) whenever ${{\mathbb {R}}}_{0} > 1,$ and no positive root whenever ${{\mathbb {R}}}_{0} \le 1.$ It should be noted that, for the special case where $\delta _L =0,$ the quantity $L^*$ can easily be computed from (3.9) (and is given by $L^*=\frac{\mu _3 \mu _M K}{F_L F_P \sigma } \left( {{\mathbb {R}}}_0 -1\right) ^{-n}$).

It is convenient to define $\delta ^*_L = \frac{F_E F_L^2 F_P^2}{K \mu _1 \mu _3^2 \mu _M^2}$ and $\delta ^{**}_L = \frac{\nu \mu _2}{1-\nu }$ (and recall that $a=\frac{\delta _L}{\nu (\delta _L+\mu _2)}$).

Theorem 3.3

Consider the autonomous system (3.1).

• 1. If $B(M)=B_L,$ then $P_1$ exists only if ${{\mathbb {R}}}_{0} > 1.$ Furthermore,

  • (a) if $\delta _L \ge \delta ^*_L,$ then $P_1$ is LAS whenever ${{\mathbb {R}}}_{0} >1,$

  • (b) if $\delta _L < \delta ^*_L$ and $1< {{\mathbb {R}}}_{0} < 2+ \frac{1-C}{2C-1} + \chi ,$ with $\chi = \frac{\alpha (1 + 2\delta _L^2)}{a_3^2 \beta (1+\delta _L)}> 0$ and $\frac{1}{2} \le C = \frac{F_E F_L^2 F_P^2}{K\mu _1 \mu _3^2 \mu _M^2 \delta _L + F_E F_L^2 F_P^2} < 1,$ then $P_1$ is LAS and unstable otherwise.

• 2. If $B(M)=B_S,$ then $P_1$ exists only if ${{\mathbb {R}}}_{0} > 1,$ and if $n=1,$ then $P_1$ is LAS whenever ${{\mathbb {R}}}_{0} > 1.$ Furthermore,

  • (a) if $\delta _L \ge \delta ^{**}_L,$ with $n > 1$ then $P_1$ is LAS for all ${{\mathbb {R}}}_{0} >1,$

  • (b) if $\delta _L < \delta ^{**}_L,$ then $P_1$ is LAS if and only if

    $$\begin{aligned} 1<&{{\mathbb {R}}}_{0} < 1+ \frac{\beta a_3^2 \left( 1+ a\right) }{\left( 1+a \right) \beta a^2_3 \left[ n\left( 1-a \right) - 1\right] -\alpha }, \ \ \ \text {with}\\ n> & {} 1+ \frac{a}{1-a} + \frac{\alpha }{\beta a^2_3 \left( 1-a^2\right) }, \end{aligned}$$

    and unstable otherwise.

Proof

Consider the model (3.1) with the two forms of B(M) given in (2.2). Evaluating the Jacobian of the system (3.1) at $P_1$ gives

$$\begin{aligned} J (P_1)= \left( \begin{array}{cccccc} -\mu _1 &{} 0 &{} 0 &{} B(M^*)+M^*\frac{dB(M^*)}{dM} \\ F_E &{} -\mu _2-2\delta _L L^* &{} 0 &{} 0\\ 0 &{} F_L &{} -\mu _3 &{} 0\\ 0 &{} 0 &{} \sigma F_P &{} -\mu _M \end{array} \right) , \end{aligned}$$

where $M^*$ is obtained from (3.6), and $L^*$ is obtained from (3.7). The eigenvalues of $J(P_1)$ satisfy the polynomial

$$\begin{aligned} \lambda ^4 + A_3 \lambda ^3 + A_2 \lambda ^2 + A_1 \lambda + A_0 = 0, \end{aligned}$$

(3.10)

with,

(3.11)

Here, too, the local stability of $P_1$ can be established using the Routh-Hurwitz criterion. Let,

$$\begin{aligned} \alpha ^*= (\mu _1+\mu _2 + 2\delta _L L^*)(\mu _1+\mu _3) (\mu _2 + 2\delta _L L^*+\mu _3)(\mu _M+\mu _1)( \mu _M+ \mu _2+2\delta _L L^*)(\mu _M+\mu _3), \end{aligned}$$

and,

$$\begin{aligned} \beta ^*= \mu _1 \left( \mu _2 + 2\delta _L L^*\right) \mu _3 \mu _M. \end{aligned}$$

Since all parameters of the model (3.1) are positive, it follows that $\alpha ^* > 0,$ $\beta ^* > 0,$ $\Delta _{1}>0$ and $\Delta _{2} >0$ whenever ${{\mathbb {R}}}_0 >1.$ Furthermore, using (3.5), $\Delta _3$ can be re-written as

$$\begin{aligned} \Delta _3 = \alpha ^* + A^2_3 \beta \frac{{{\mathbb {R}}}_{0}}{b} \left[ B(M^*)+M^*\frac{dB(M^*)}{dM} \right] . \end{aligned}$$

(3.12)

It is convenient to use the following notation: $\Delta ^L_3 = \Delta _3$ for $B(M)=B_L$ and $\Delta ^S_3 = \Delta _3$ for $B(M)=B_S.$ Consider the following two cases:

• 1. If $B(M)=B_L,$ then

  $$\begin{aligned} A_0= & {} \mu _1 \mu _2 \mu _3 \mu _M - \sigma b F_E F_L F_P \left[ 1 - \frac{2M^*}{K}\right] + 2\delta _L L^* \mu _1 \mu _3 \mu _M \\= & {} \beta \left( \frac{\sigma F_L F_P }{\mu _3 \mu _M K Q} \right) \left( {{\mathbb {R}}}_0 - 1 \right) + 2\delta _L L^* \mu _1 \mu _3 \mu _M. \end{aligned}$$

  Since $P_1$ exists only when ${{\mathbb {R}}}_{0}>1,$ then $A_0 >0.$ Furthermore,

  $$\begin{aligned} \Delta ^L_3 = \alpha - a^2_3 \beta \left[ (2C -1){{\mathbb {R}}}_{0} - 2C\right] , \end{aligned}$$

  (3.13)

  where $C = \frac{F_E F_L^2 F_P^2}{K\mu _1 \mu _3^2 \mu _M^2 \delta _L + F_E F_L^2 F_P^2}<1.$ Hence, we have two cases:

  • (a) If $\delta _L \ge \delta ^*_L,$ then $2C-1 \le 0$ (noting that $\delta ^*_L = \frac{F_E F_L^2 F_P^2}{K \mu _1 \mu _3^2 \mu _M^2}$). In this case, $\Delta ^L_3 > 0.$ Thus, $P_1$ is LAS for all ${{\mathbb {R}}}_{0} >1.$

  • (b) If $\delta _L < \delta ^*_L,$ then $2C-1>0.$ In this case, $\Delta ^L_3 > 0$ if and only if

    $$\begin{aligned} 1< {{\mathbb {R}}}_{0} < 2+ \frac{1-C}{2C-1} + \chi , \end{aligned}$$

    (3.14)

    where $\chi = \frac{\alpha (1 + 2\delta _L^2)}{a_3^2 \beta (1+\delta _L)}> 0.$

  It should be noted that for the special case of the model with $\delta _L =0,$ the quantity C reduces to $C=1.$ Hence, in this case, $\Delta ^L_3 = \alpha - a^2_3 \beta \left( {{\mathbb {R}}}_{0} - 2\right) .$ Thus, for the special case of the autonomous model with $\delta _L=0$, the non-trivial equilibrium $P_1$ is LAS whenever $1< {{\mathbb {R}}}_{0} < 2 + \frac{\alpha }{a^2_3 \beta },$ and unstable if ${{\mathbb {R}}}_{0} > 2 + \frac{\alpha }{a^2_3 \beta }$.

• 2. If $B(M)=B_S,$ then

  $$\begin{aligned} A_0= & {} \beta \left( 1 - {{\mathbb {R}}}_{0} \left[ \frac{1+(1-n)\left( \frac{M^*}{K} \right) ^n }{ \left( 1+\left( \frac{M^*}{K} \right) ^n\right) ^2} \right] \right) + 2\delta _L L^* \mu _1 \mu _3 \mu _M, \\= & {} \beta \left[ 1+ \frac{2\delta _L}{\mu _2} L^* - \frac{1}{{{\mathbb {R}}}_{0} }\left( 1+ \frac{\delta _L}{\mu _2} L^*\right) \left( (1-n){{\mathbb {R}}}_{0} + n \left( 1+ \frac{\delta _L}{\mu _2} L^* \right) \right) \right] , \\= & {} \beta n\left[ 1+ \frac{n+1}{n} {{\mathbb {R}}}_{0} \frac{\delta _L}{\mu _2} L^* - \frac{1}{{{\mathbb {R}}}_{0}} \left( 1+ \frac{\delta _L}{\mu _2} L^* \right) ^2\right] , \\= & {} \beta n\left[ 1 - \frac{1}{{{\mathbb {R}}}_{0}}+ \frac{\delta _L}{\mu _2} L^* \left( \frac{n-1}{n} {{\mathbb {R}}}_{0} + \delta _L (L^*)^{n} + \nu (L^*)^{(n+1)} \right) \right] . \end{aligned}$$

  Since $P_1$ exists only when ${{\mathbb {R}}}_{0}>1$ (and $n>1)$, then $A_0 >0.$ Furthermore,

  $$\begin{aligned} \Delta ^S_3= & {} \alpha ^* + A^2_3 \beta {{\mathbb {R}}}_{0} \left( \frac{(1-n) \left( \frac{M^*}{K}\right) ^n + 1}{\left[ \left( \frac{M^*}{K}\right) ^n + 1 \right] ^2}\right) , \\= & {} \alpha - a^2_3 \beta n \left( 1+ \frac{\delta _L}{\nu (\delta _L+\mu _2)} \right) \left( \frac{n-1}{n} - \frac{\delta _L}{\nu (\delta _L+\mu _2)} - \frac{1}{{{\mathbb {R}}}_{0}} \left[ 1- \frac{\delta _L}{\nu (\delta _L+\mu _2)}\right] \right) . \end{aligned}$$

  Since $P_1$ exists only when ${{\mathbb {R}}}_{0}>1,$ it can be shown, in this case, that if $n = 1$ then $\Delta ^S_3 > 0$ for all ${{\mathbb {R}}}_{0}>1.$ In this case, $P_1$ is LAS whenever ${{\mathbb {R}}}_{0}>1$. For all $n > 1$, we have the following two cases:

  • (a) If $\delta _L \ge \delta ^{**}_L,$ with $\delta ^{**}_L = \frac{\nu \mu _2}{1-\nu }$ and $\nu = \left( \frac{\sigma F_L F_P }{\mu _3 \mu _M K}\right) ^n < 1,$ then $\Delta ^L_3 > 0.$ Thus, $P_1$ is LAS whenever ${{\mathbb {R}}}_{0} >1.$

  • (b) If $\delta _L < \delta ^{**}_L,$ then $\Delta ^L_3 > 0$ if and only if

    $$\begin{aligned} 1<&{{\mathbb {R}}}_{0} < 1+ \frac{\beta a_3^2 \left( 1+ a\right) }{\left( 1+a \right) \beta a^2_3 \left[ n\left( 1-a \right) - 1\right] -\alpha }; \quad \nonumber \\ n> & {} 1+ \frac{a}{1-a} +\frac{\alpha }{\beta a^2_3 \left( 1-a^2\right) }, \end{aligned}$$

    (3.15)

    and unstable otherwise, where $a=\frac{\delta _L}{\nu (\delta _L+\mu _2)}.$

  For the special case of the model with $\delta _L =0,$ then $a=0.$ Hence, in this case, it follows that

  $$\begin{aligned} \Delta ^S_3 = \alpha - a^2_3 \beta n \left( \frac{n-1}{n} -\frac{1}{{{\mathbb {R}}}_{0}} \right) . \end{aligned}$$

  Thus, $\Delta ^S_3>0$ if and only if

  $$\begin{aligned} {{\mathbb {R}}}_{0} < 1 + \frac{\alpha + a^2_3 \beta }{(n-1)a^2_3 \beta - \alpha } \ \ \ \text {with} \ \ \ n> 1 + \frac{\alpha }{a^2_3 \beta }. \end{aligned}$$

$\square$

The global asymptotic property of the non-trivial equilibrium ($P_1$) will now be explored. Consider the following region (for $t \ge 0$):

$$\begin{aligned} {{\mathcal {D}}}^*=\left\{ (E,L,P,M) \in {{\mathcal {D}}} : 0< E(t) \le E^*, 0< L(t) \le L^*, 0< P(t) \le P^*, 0 < M(t) \le M^* \right\} . \end{aligned}$$

Since ${{\mathcal {D}}}^* \subset {{\mathcal {D}}},$ it follows that ${{\mathcal {D}}}^*$ is positively-invariant with respect to the model (3.1).

Theorem 3.4

Consider the autonomous model (3.1).

• (a) If $B(M)=B_L$ and $1 < {{\mathbb {R}}}_{0} \le 2,$ then the non-trivial equilibrium, $P_1,$ is GAS in ${{\mathcal {D}}}^*.$

• (b) If $B(M)=B_S$ and $1 < {{\mathbb {R}}}_{0} \le 1+\frac{1}{n-1}$ (for all $n>1$), then $P_1$ is GAS in ${{\mathcal {D}}}^*.$

Proof

Consider the model (3.1) for the case ${{\mathbb {R}}}_{0} > 1.$ Furthermore, consider the following Lyapunov function

$$\begin{aligned} V_1=\frac{1}{2}(S - S^*)^2, \end{aligned}$$

where,

$$\begin{aligned} S=\frac{\sigma F_L F_P}{\mu _1 \mu _2 \mu _3} [F_E E(t) + \mu _{1} L(t)] + \frac{1}{\mu _3} [\sigma F_P P(t) + \mu _{3} M(t)], \end{aligned}$$

and,

$$\begin{aligned} S^*=\left( \frac{\mu _M}{\mu _1}+ \frac{\mu _M}{\mu _2} + \frac{\mu _M}{\mu _3} + 1 \right) M^*. \end{aligned}$$

Thus,

$$\begin{aligned} \frac{dS}{dt}= & {} \frac{\sigma F_L F_P}{\mu _1 \mu _2 \mu _3} \left( F_E \frac{dE}{dt} + \mu _{1} \frac{dL}{dt}\right) + \frac{1}{\mu _3} \left( \sigma F_P \frac{dP}{dt} + \mu _{3} \frac{dM}{dt}\right) , \\= & {} \frac{\sigma F_L F_P}{\mu _1 \mu _2 \mu _3} [ F_E M B(M) - \mu _1 \mu _2 L - \mu _1 \delta _L L^2 ] + \frac{1}{\mu _3} [\sigma F_P F_L L(t) - \mu _3 \mu _M M],\\\le & {} \mu _M M(t) \left[ \frac{\sigma F_E F_L F_P}{\mu _1 \mu _2 \mu _3 \mu _M } B(M) - 1\right] . \end{aligned}$$

The Lyapunov derivative is

$$\begin{aligned} \frac{dV_1}{dt} = (S-S^*) \frac{dS}{dt}. \end{aligned}$$

(3.16)

Consider, next, the following two cases.

• (a) $B(M)=B_L.$ In this case, $\frac{dS}{dt}$ can be re-written as

  $$\begin{aligned} \frac{dS}{dt} \le \mu _M M(t) \left[ {{\mathbb {R}}}_{0} \left( 1-\dfrac{M}{K}\right) -1 \right] = \mu _M M(t) {{\mathbb {R}}}_{0} \left( 1- \frac{1}{{{\mathbb {R}}}_{0}}-\dfrac{M}{K}\right) , \end{aligned}$$

so that,

$$\begin{aligned} \frac{dS}{dt} \le \frac{\mu _M M(t) {{\mathbb {R}}}_{0} }{K}[M^* - M(t)]. \end{aligned}$$

(3.17)

Similarly, $(S-S^*)$ can be re-written as

$$\begin{aligned} S-S^*= & {} \frac{\mu _M}{\mu _1} \left[ \frac{\sigma F_E F_L F_P}{\mu _2 \mu _3 \mu _M} E(t) - M^*\right] + \frac{\mu _M}{\mu _2} \left[ \frac{\sigma F_L F_P }{\mu _3 \mu _M} L(t) - M^*\right] \\&\quad + \frac{\mu _M}{\mu _3} \left[ \frac{\sigma F_P}{\mu _M} P(t) - M^*\right] + M(t)-M^*. \end{aligned}$$

Since $E \le \frac{b}{\mu _1}M(1-\frac{M}{K}),$ $L \le \frac{F_E}{\mu _2} E \le \frac{bF_E}{\mu _1 \mu _2}M(1-\frac{M}{K})$ and $P\le \frac{F_L }{\mu _3} L \le \frac{bF_E F_L}{\mu _1 \mu _2 \mu _3}M(1-\frac{M}{K})$ in ${{\mathcal {D}}}^*,$ it follows that

$$\begin{aligned} S-S^*\le & {} \left( \frac{\mu _M}{\mu _1} + \frac{\mu _M}{\mu _2} + \frac{\mu _M}{\mu _3}\right) \left[ {{\mathbb {R}}}_{0} M(t)(1-\dfrac{M(t)}{K}) - M^*\right] + M(t)-M^*, \\\le & {} \left( \frac{\mu _M}{\mu _1} + \frac{\mu _M}{\mu _2} + \frac{\mu _M}{\mu _3}\right) \left[ {{\mathbb {R}}}_{0} M(t)(1-\dfrac{M(t)}{K})-M(t) + (M(t)- M^*)\right] \\&+ M(t)-M^*, \\\le & {} \left[ M^* - M(t)\right] \left[ \left( \frac{\mu _M}{\mu _1} + \frac{\mu _M}{\mu _2} + \frac{\mu _M}{\mu _3}\right) {{\mathbb {R}}}_{0} \frac{M^*}{K} - \left( \frac{\mu _M}{\mu _1} + \frac{\mu _M}{\mu _2} + \frac{\mu _M}{\mu _3} + 1\right) \right] . \end{aligned}$$

Hence,

$$\begin{aligned} S-S^* \le \mu _M [M^*- M(t)] \left( {{\mathbb {R}}}_{0} - 2 \right) . \end{aligned}$$

(3.18)

Thus, using (3.17) and (3.18), it follows from (3.16) that the Lyapunov derivative $\frac{dV_1}{dt}$ can be re-written as

$$\begin{aligned} \frac{dV_1}{dt} \le - K \mu _M^{2}M(t) {{\mathbb {R}}}_{0} \left[ \frac{M^*}{K} - \frac{M(t)}{K} \right] ^2 \left( 2 - {{\mathbb {R}}}_{0}\right) . \end{aligned}$$

Hence, $\frac{dV_1}{dt} <0$ if and only if $1 < {{\mathbb {R}}}_{0} \le 2.$ The proof is concluded as in the proof of Theorem 3.2.

• (b) $B(M)=B_S.$ For this case, $\frac{dS}{dt}$ and $(S-S^*)$ can be, respectively, re-written as

  $$\begin{aligned} \frac{dS}{dt} \le \mu _M M(t) \left[ \frac{{{\mathbb {R}}}_{0}}{1+ \left( \frac{M}{K} \right) ^n} -1 \right] = \frac{\mu _M M(t)}{1+ \left( \frac{M}{K} \right) ^n} \left[ \left( \frac{M^*}{K}\right) ^n - \left( \frac{M(t)}{K} \right) ^n \right] ,\nonumber \\ \end{aligned}$$

  (3.19)

and,

$$\begin{aligned} S-S^*= & {} \frac{\mu _M}{\mu _1} \left[ \frac{\sigma F_E F_L F_P}{\mu _2 \mu _3 \mu _M} E(t) - M^*\right] + \frac{\mu _M}{\mu _2} \left[ \frac{\sigma F_L F_P }{\mu _3 \mu _M} L(t) - M^*\right] \\&\quad +&\frac{\mu _M}{\mu _3} \left[ \frac{\sigma F_P}{\mu _M} P(t) - M^*\right] + M(t)-M^*,\\\le & {} \left( \frac{\mu _M}{\mu _1} + \frac{\mu _M}{\mu _2} + \frac{\mu _M}{\mu _3}\right) \left[ \frac{{{\mathbb {R}}}_{0} M(t)}{1+ \left( \frac{M}{K} \right) ^n} - M^*\right] + M(t)-M^*, \\\le & {} \left( \frac{\mu _M}{\mu _1} + \frac{\mu _M}{\mu _2} + \frac{\mu _M}{\mu _3}\right) \left[ \frac{{{\mathbb {R}}}_{0} M(t)}{1+ \left( \frac{M}{K} \right) ^n}-M(t) + M(t)- M^*\right] + M(t)-M^*,\\\le & {} K \frac{\left[ \frac{M^*}{K} - \frac{M(t)}{K} \right] }{1+ \left( \frac{M}{K} \right) ^n} \left[ \left( \frac{\mu _M}{\mu _1} + \frac{\mu _M}{\mu _2} + \frac{\mu _M}{\mu _3}\right) (n-1) {{\mathbb {R}}}_{0} \frac{M^*}{K}\right. \\&\left. - n\left( \frac{\mu _M}{\mu _1} + \frac{\mu _M}{\mu _2} + \frac{\mu _M}{\mu _3} + 1\right) \right] . \end{aligned}$$

Thus,

$$\begin{aligned} S-S^* \le K \mu _M \frac{\left[ \frac{M^*}{K} - \frac{M(t)}{K} \right] }{1+ \left( \frac{M}{K} \right) ^n} \left[ (n-1){{\mathbb {R}}}_{0} - n \right] . \end{aligned}$$

(3.20)

Hence, using (3.19) and (3.20), it follows from (3.16) that the Lyapunov derivative $\frac{dV_1}{dt}$ can be written as

$$\begin{aligned} \frac{dV_1}{dt} \le - (n-1)^2 K \mu _M^{2}M(t) {{\mathbb {R}}}_{0} \frac{\left( \frac{M^*}{K} - \frac{M(t)}{K} \right) ^2}{\left[ 1+ \left( \frac{M}{K} \right) ^n \right] ^2 } \left( \frac{n}{n-1} - {{\mathbb {R}}}_{0} \right) , \end{aligned}$$

so that, $\frac{dV_1}{dt} <0$ if and only if $1 < {{\mathbb {R}}}_{0} \le 1+\frac{1}{n-1}$ (with $n>1$). Thus, for $B(M)=B_S,$ the non-trivial equilibrium, $P_{1},$ is GAS in ${{\mathcal {D}}}^*$ whenever $1 < {{\mathbb {R}}}_0 \le 1+\frac{1}{n-1}$ (for $n>1$). $\square$

Fig. 2

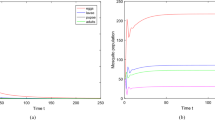
Simulations of the autonomous model (3.1), showing the time series of the state variables of the model for two forms of B(M). Parameter values used are: $\mu _M=0.05; \mu _E =0.36; \mu _L=0.34; \mu _P=0.17; F_L=0.14; F_E=0.4; F_P=0.3$ and $K=10^6$. a $B(M) = B_L,$ with $b=10.7$ (so that, ${{\mathbb {R}}}_{0}=7.01$) and in case $\delta _L =0.01 > \delta ^*_L=0.000157$. b $B(M) = B_S,$ with $b=10.7$ and $n=10$ (so that, ${{\mathbb {R}}}_{0}=7.01$) and $\delta _L =0.01 > \delta ^{**}_L=0.000012$

The ecological implication of Theorem 3.3 is that, for each of the two eggs laying functions ($B_L$ and $B_S$), mosquitoes will persist in the community whenever the associated conditions for the global asymptotic stability of $P_1$ (given in Theorem 3.3) are satisfied. The results of Theorem 3.3 are illustrated numerically, by simulating the autonomous model (3.1) using appropriate parameter values, for both the Verhulst-Pearl logistic (Fig. 2a) and the Maynard-Smith–Slatkin oviposition function (Fig. 2b). These simulation results show convergence of the solutions to $P_1$ for each of the oviposition functions $B_L$ or $B_S$ (in line with Theorem 3.3).

3.2 Hopf bifurcation analysis

Hopf bifurcation can occur, when the Jacobian of the system, evaluated at $P_1,$ has a pair of pure imaginary eigenvalues. The possability of Hopf bifurcation from the non-trivial equilibrium $P_1$ is investgated for the case of the model (3.1) with $B(M)=B_L$ and $B_S.$ Generally, it has been shown that oscillations about the non-trivial equilibrium $(P_1)$ can occur when the sign of $\Delta _3$ changes (it should be noted, from Routh Hurwitz criteria, that if $\Delta _3 = 0,$ then the polynomial (3.10) has complex conjugate roots). To prove the existence of Hopf bifurcation, it suffices to verify the transversality condition (Chow et al. 1994). This is done below.

Theorem 3.5

Consider the autonomous system (3.1), with $B(M)=B_L$ or $B_S.$ A Hopf bifurcation occurs

• (i) for $B(M)=B_L,$ if $\delta _L < \delta ^*_L$ and

  $$\begin{aligned} b = b^* = \dfrac{2C\beta a^2_3 + \alpha }{ F_E F_L F_P \sigma a^2_3 (2C-1)}. \end{aligned}$$

  (3.21)

• (ii) for $B(M) = B_S,$ if $\delta _L < \delta ^{**}_L$ and

  $$\begin{aligned} b = b^{**} =\frac{na^2_3 \beta ^2 \left( 1- a^2\right) }{\sigma F_E F_L F_P \left[ (n-1)a^2_3 \beta (1-a^2)-\alpha \right] }, \end{aligned}$$

  (3.22)

  with $n > 1+ \frac{a}{1-a} + \frac{\alpha }{\beta a^2_3 \left( 1-a^2\right) }$,

Proof

Part (i): Consider the model (3.1) with $B(M)=B_L.$ Using (3.2), the term $\Delta ^L_3$ [in Eq. (3.13)] can be re-written as

$$\begin{aligned} \Delta ^L_3 = \alpha - a^2_3 \left[ b\sigma F_E F_L F_P (2C-1)- 2 \beta C \right] . \end{aligned}$$

Let $b=b^*$ be a bifurcation parameter (and all other parameters of the model (3.1) are fixed). Hence, $\Delta ^L_3 (b)= 0$ if and only if $b=b^*.$ Furthermore, if $\delta _L < \delta ^*_L$ then $2C-1 > 0.$ Thus,

$$\begin{aligned} \frac{d \Delta ^L_3(b)}{d b}\Big |_{b=b^{*}} = - a^2_3 \sigma F_E F_L F_P (2C-1) < 0. \end{aligned}$$

Similarly, let $\mu _M$ be a bifurcation parameter (and all other parameters of the model (3.1) are fixed). Then,

$$\begin{aligned} \frac{d \Delta ^L_3(\mu _M)}{d \mu _M}\Big |_{\mu _M=\mu _M^{*}} = \frac{d \alpha (\mu _M)}{d \mu _M}\Big |_{\mu _M=\mu _M^{*}} +\frac{2C}{a_3(\mu _M^{*})} [(\mu _1\mu _2\mu _3) a^{3}_3(\mu _M^{*}) - \alpha (\mu _M^{*})], \end{aligned}$$

for all $\Delta ^L_3 (\mu _M^*)= 0.$ It can be verified that $\frac{d \Delta ^L_3(\mu _M)}{d \mu _M}\Big |_{\mu _M=\mu _M^{*}} > 0.$

Part (ii): In the case $B(M)=B_S,$ it can be shown, using (3.2), that

$$\begin{aligned} \Delta ^S_3 = \alpha - a^2_3 \beta n\left( 1+ a \right) \left[ \frac{(n-1)}{n} - a -\frac{ \beta }{b\sigma F_E F_L F_P} \right] . \end{aligned}$$

Let $b=b^{**}$ be a bifurcation parameter, and all other parameters of the model (3.1) are fixed. Then, $\Delta ^S_3 (b)= 0$ if and only if $b=b^{**}.$ Furthermore, $\frac{d \Delta ^S_3(b)}{d b}\Big |_{b=b^{**}} < 0.$ Similarly, it can be shown that $\frac{d \Delta ^S_3(\mu _M)}{d \mu _M}\Big |_{\mu _M=\mu _M^{*}} > 0,$ for $n > 1+ \frac{a}{1-a} + \frac{\alpha }{\beta a^2_3 \left( 1-a^2\right) }.$

$\square$

Theorem 3.5 shows that sustained oscillations are possible using any of the two oviposition functions ($B_L$ or $B_S$). The results of Theorem 3.5 are illustrated in Fig. 3, from which it follows that the plot for the case with $B(M)=B_S$ has higher amplitude than that for the case of $B(M)=B_L$ (in other words, the functional form $B(M)=B_S$ leads to higher sustained oscillations in the total adult female mosquito population, in comparison to the case when $B(M)=B_L$ is used). This result is consistent with the study by Ngwa et al. (2010) (which establishes the existence of a Hopf bifurcation for an autonomous model for the population dynamics of mosquitoes subject to Verhulst-Pearl logistic and Maynard-Smith-Slatkin birth functions of adult mosquitoes). Furthermore, Theorem 3.5 shows that increased competition in the larval stages (i.e., $\delta _L$ large in comparison to $\delta _L^*$ or $\delta _L^{**}$) reduces the likelihood of Hopf bifurcation (sustained oscillations) in the population biology of the mosquitoes.

It is worth mentioning that, in the proof of Theorem 3.5, two bifurcation parameters (b and $\mu _M$) are considered. The reason is that the transversality condition may fail at some points if only one parameter is used (Chow et al. 1994; Yu 2005). The nature of the Hopf bifurcation property of the model (3.1) is investigated numerically. The results obtained, depicted in Fig. 4, show convergence of the solutions to a stable limit cycle (arising via a supercritical Hopf bifurcation) (Ngwa et al. 2010).

Fig. 3

Simulations of the autonomous model (3.1), showing the total number of female adult mosquitoes (M(t)) as a function of time using two forms of B(M). Parameter values used are: $\mu _M=0.05; \mu _E =0.36; \mu _L=0.34; \mu _P=0.17; F_L=0.14; F_E=0.4; F_P=0.3$ and $K=10^6.$ a $B(M) = B_L,$ with $b=b^*=34.2$ (so that, ${{\mathbb {R}}}_{0}=13.05$) and $\delta _L =0.00001 < \delta ^{*}_L$. b $B(M) = B_S$, with $b=b^{**}=39.2$ and $n=25$ (so that, ${{\mathbb {R}}}_{0}=14.01$) and $\delta _L =0.00001 < \delta ^{**}_L$

Fig. 4

Phase portraits of the autonomous model (3.1), using two forms of B(M). a $B(M)=B_L.$ b $B(M)=B_S.$ Parameter values used are as given in the simulations for Fig. 3

Fig. 5

Bifurcation curves in $\mu _M-b$ plane for the autonomous model (3.1)

3.2.1 Bifurcation diagram

In this section, a bifurcation diagram of the model (3.1) will be generated in the $\mu _M-b$ plane as follows.

• (i) Solving for b from $\mathbb {R}_0 = 1$ gives the following line (denoted by l,  depicted in Fig. 5):

  $$\begin{aligned} l : \ \ \ b=b^l =\frac{\mu _1 \mu _2 \mu _3}{\sigma F_E F_L F_P} \mu _M. \end{aligned}$$

• (ii) Solving for b from $\Delta _3 = 0,$ with $\delta _L < \delta ^*_L$ and $\delta _L <\delta ^{**}_L$ (fixing all parameters of the model (using their values as in Fig. 3), except the bifurcation parameters, $\mu _M$ and b) gives the following curves (denoted by $H_L,$ in the case of $B(M)=B_L,$ and $H_S,$ in the case of $B(M)=B_S;$ the latter curve drawn for $n=10$):

  $$\begin{aligned} H_L : \ \ \ b= & {} b^*= \dfrac{2C(\mu _M)\beta (\mu _M) a^2_3(\mu _M) + \alpha (\mu _M) }{(2C(\mu _M)-1)\sigma F_E F_L F_P a^2_3(\mu _M)}, \\ H_S : \ \ \ b= & {} b^{**} =\frac{10a^2_3(\mu _M) \beta ^2(\mu _M) (1-a^2(\mu _M))}{\sigma F_E F_L F_P [9a^2_3(\mu _M) \beta (\mu _M) (1-a^2(\mu _M))- \alpha (\mu _M)]}. \end{aligned}$$

The curves l,  $H_L$ and $H_S,$ depicted in Fig. 5, divide the $\mu _M-b$ plane into four distinct regions, namely ${{\mathcal {D}}}_1, {{\mathcal {D}}}_2, {{\mathcal {D}}}_3$ and ${{\mathcal {D}}}_4,$ given by:

$$\begin{aligned} \begin{array}{lll} \displaystyle {{\mathcal {D}}}_1=\{(\mu _M,b) \ \ \ | 0<b< b^l; \ \mu _M> 0 \}, \\ \displaystyle {{\mathcal {D}}}_2=\{(\mu _M,b) \ \ \ | b^l<b<b^{**}; \ \mu _M> 0 \}, \\ \displaystyle {{\mathcal {D}}}_3=\{(\mu _M,b) \ \ \ | b^{**}<b<b^{*}; \ \mu _M> 0 \}, \\ \displaystyle {{\mathcal {D}}}_4=\{(\mu _M,b) \ \ \ | b>b^*; \ \mu _M>0 \}. \end{array} \end{aligned}$$

The regions can be described (using Theorems 3.2 and 3.3) as follows:

• (i) ${{\mathbf {Region}}~{\mathcal {D}}_1}$. In this region, $\mathbb {R}_0 < 1.$ Hence, the model (3.1) has a GAS trivial equilibrium ($P_0$) for each of the two forms of B(M).

• (ii) ${{\mathbf {Region}}~{\mathcal {D}}_2}$. Here, $1< {{\mathbb {R}}}_{0} < 1+ \frac{\beta a_3^2 \left( 1+ a\right) }{\left( 1+a \right) \beta a^2_3 \left[ n\left( 1-a \right) - 1\right] -\alpha }.$ For the cases $B(M)=B_L$ or $B_S,$ the model has two equilibria, namely the unstable trivial equilibrium ($P_0$) and the LAS non-trivial equilibrium ($P_1$). In this region, and for $B(M)=B_S,$ the model undergoes a Hopf bifurcation at all points on the line $b=b^{**}.$

• (iii) ${{\mathbf {Region}}~{{{\mathcal {D}}}}_3}$. In this region, $1+ \frac{\beta a_3^2 \left( 1+ a\right) }{\left( 1+a \right) \beta a^2_3 \left[ n\left( 1-a \right) - 1\right] -\alpha }<{{\mathbb {R}}}_{0} < 2+ \frac{1-C}{2C-1} + \chi .$ For the case with $B(M)=B_L,$ the model has two equilibria, the unstable trivial equilibrium ($P_0$) and the LAS non-trivial equilibrium ($P_1$). Furthermore, in this case, the model undergoes a Hopf bifurcation at all points on the line $b=b^{*}.$ Similarly, for the case $B(M)=B_S,$ the model has two equilibria, the unstable trivial equilibrium ($P_0$) and the unstable non-trivial equilibrium ($P_1$).

• (iv) ${\mathbf {Region}~{{\mathcal {D}}}_4}$. Here, ${{\mathbb {R}}}_{0} > 2+ \frac{1-C}{2C-1} + \chi .$ In the case of $B(M)=B_L$ or $B_S,$ the model has two equilibria, namely the unstable trivial equilibrium ($P_0$) and unstable non-trivial equilibrium ($P_1$).

The region of stability of the non-trivial solution ($P_1$) will now be compared for the cases where the Verhulst-Pearl logistic ($B(M)=B_L$) or Maynard-Smith-Slatkin oviposition function ($B(M)=B_S)$ is used. Consider, now, the model (3.1) with $B(M)=B_S$ and $\delta _L < \delta _L^{**}.$ Solving for n from the right-hand side of (3.15) gives $n= \left[ 1 + \frac{a}{1-a} + \frac{\alpha }{a^2_3 \beta (1-a^2)}\right] .$ Substituting $n=m \left[ 1 + \frac{a}{1-a} + \frac{\alpha }{a^2_3 \beta (1-a^2)}\right]$, with $m > 1$, in the inequality (3.15) gives (the stability condition for the non-trivial equilibrium ($P_1$) of the autonomous model with $B(M)= B_S$):

$$\begin{aligned} 1< {{\mathbb {R}}}_{0}< 1+ \dfrac{1}{m-1}< 2< 2 + \frac{1-C}{2C-1} + \chi , \ \ \ m>1. \end{aligned}$$

(3.23)

By comparing the inequalities (3.14) and (3.23), it can be concluded that, for large values of n, the size of the stability interval for $P_1$ is larger for the case when the Verhulst-Pearl logistic oviposition function ($B_L$) is used than for the case when the Maynard-Smith-Slatkin function ($B(M)=B_S$) is used. Thus, owing to its smaller stability region (hence, higher region of instability, which corresponds to higher likelihood of Hopf bifurcation), the Maynard-Smith-Slatkin functional form ($B(M)=B_S$) induces more sustained oscillations than the Verhulst-Pearl logistic oviposition function ($B(M)=B_L.$) In other words, this study shows that the Maynard-Smith-Slatkin function is more suitable (from ecological point of view) for modeling mosquito oviposition than the Verhulst-Pearl logistic function (since, ecologically-speaking, higher sustained oscillations ensures the preservation of the mosquito population). These results are summarized in Table 3 (in terms of ${{\mathbb {R}}}_{0}$). Furthermore, the results are illustrated numerically in Fig. 5, from which it is evident that the region (${{\mathcal {D}}}_2$) for the asymptotic stability of the non-trivial equilibrium ($P_1$) is smaller in the case where the functional form $B(M)=B_S$ is used, in comparison to the corresponding region (${{\mathcal {D}}}_2 \cup {{\mathcal {D}}}_3$) when the form $B(M)=B_L$ is used (this result supports the finding in Ngwa et al. (2010) that the Maynard-Smith-Slatkin function is more suitable to model the birth rate of adult mosquitoes, in comparison to the Verhulst-Pearl logistic birth function).

Table 3 The stability properties of the solutions of the autonomous model (3.1) “DNE” denotes “does not exist”

3.3 Sensitivity analysis of ${{\mathbb {R}}}_{0}$

Sensitivity analysis determines the effects of parameters on model outcomes (Cariboni et al. 2007). A highly sensitive parameter should be carefully estimated, because a small variation in that parameter will lead to large quantitative changes. A parameter that is not sensitive, on the other hand, does not require as much effort to estimate (since a small variation in that parameter will not produce large changes to the quantity of interest). To study the local sensitivity analysis, we find the partial derivative of the output variables with respect to the input parameters to compute the sensitivity index (Cariboni et al. 2007). In this study the threshold quantity (${{\mathbb {R}}}_{0}$) is taken as the model outcome. The normalized sensitivity index of ${{\mathbb {R}}}_{0}$ with respect to a parameter x, denoted by $\Phi ^{{{\mathbb {R}}}_{0}}_{x}$, is given by (Cariboni et al. 2007):

$$\begin{aligned} \Phi ^{{{\mathbb {R}}}_{0}}_{x} = \frac{\partial {{\mathbb {R}}}_{0}}{\partial x} \frac{x}{{{\mathbb {R}}}_{0}}. \end{aligned}$$

(3.24)

Given the expression (3.2) for the vectorial reproduction number $({{\mathbb {R}}}_{0})$ of the autonomous model (3.1), an analytical expression for the sensitivity of ${{\mathbb {R}}}_{0},$ with respect to each parameter in the expression for ${{\mathbb {R}}}_{0}$, are given in Table 4. It should be noted that the sensitivity index may be a constant or a parameter (Cariboni et al. 2007) (as in Table 4). It follows from Table 4 that the three parameters that most affect the dynamics of the autonomous model (3.1), with respect to the response function (${{\mathbb {R}}}_{0}$), are the rate of eggs laid per oviposition (b), the mosquito sex ratio ($\sigma$) and the natural death rate of adult mosquitoes ($\mu _M$). Since the parameters b and $\sigma$ are positvely-correlated, and the parameter $\mu _M$ is negatively-correlated (with respect to ${{\mathbb {R}}}_{0}$), this study suggests that a control strategy that reduces b and $\sigma$, while increasing $\mu _M$, can significantly minimize mosquito abundance in the community. In other words, the use of adulticiding (reduces b and increases $\mu _M$) and any other mechanism (perhaps biological) which reduces the production of new female offsprings (reduce $\sigma$) can lead to effective reduction of the adult mosquito population in the community.

Table 4 Sensitivity indices of the parameters of the model (3.1)

4 Analysis of non-autonomous model

In this section, the dynamical properties of the non-autonomous model (2.1) will be explored. It is convenient to define [recall the definitions for $Q^*$ and $Q_*$ in (2.7)]:

$$\begin{aligned} {{\mathbb {R}}}^{*}_{0} = \frac{\sigma b^{*} F^{*}_{E} F^{*}_{L} F^{*}_{P}}{ \mu _{1*} \mu _{2*} \mu _{3*} \mu _{*}} \ \ \ \text {and} \quad {{\mathbb {R}}}_{0*} = \frac{\sigma b_* F_{E*} F_{L*} F_{P*}}{\mu _1^* \mu _2^* \mu _3^* \mu ^*}. \end{aligned}$$

4.1 Trivial solution

The non-autonomous model (2.1) also has a unique trivial solution, $P_0,$ for each of the forms of the oviposition functions given in (2.2). The vectorial reproduction ratio of the non-autonomous model (2.1), denoted by ${{\mathbb {R}}}^t_{0},$ can be computed using the technique in Bacaer (2009, (2007), Bacaer and Guernaoui (2006), Bacaer and Abdurahman (2008), Bacaer et al. (2011) and Wang and Zhao (2008). Using the notation in Bacaer and Guernaoui (2006), Bacaer and Ouifki (2007) and Wang and Zhao (2008), let $z(t)=(E(t),L(t),P(t),M(t))^{tr}.$ The model (2.1) is linearized at $P_0$ to obtain

$$\begin{aligned} \displaystyle \frac{dz}{dt}=[F(T,R)-V(T,R)]z(t), \end{aligned}$$

where,

$$\begin{aligned} F(T,R)= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{}0&{}0&{} B(M) \\ 0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0 \end{array} \right) , \end{aligned}$$

and,

$$\begin{aligned} V(T,R)= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \mu _1(T,R)&{}0&{}0&{}0\\ -F_E(T,R)&{}\mu _2(T,R) + \delta _L L&{} 0&{}0\\ 0&{} -F_L(T,R)&{} \mu _3(T,R)&{}0\\ 0&{}0&{}-\sigma F_P(T,R)&{} \mu _M(T) \end{array} \right) . \end{aligned}$$

Let $Y(t,s), t \ge s$ be the evolution operator of the linear periodic system $\displaystyle \frac{dy}{dt}=-Vy(t)$ Wang and Zhao (2008). For each $s \in {{\mathcal {R}}},$ the matrix Y(t, s) satisfies Wang and Zhao (2008)

$$\begin{aligned} \displaystyle \frac{dY(t,s)}{dt}=-VY(t,s), \ \ \ Y(s,s)=I, \ \ \ t \ge s, \end{aligned}$$

where I is the identity matrix of order 4. Let $C_{\omega }$ be the Banach space of all $\omega$-periodic functions equipped with the maximum norm (Wang and Zhao 2008). Suppose $F(s)\Phi (s) \in C_{\omega }$ is the rate of generation (hatching) of new eggs in the breeding habitats at time s in a compartment individuals in this periodic environment at time s. Thus,

$$\begin{aligned} \Psi (t)=\int ^{t}_{-\infty } Y(t,s)F(s)\Phi (s) ds = \int ^{\infty }_{0} Y(t,t-a)F(t-a)\Phi (t-a) da, \end{aligned}$$

is the distribution of new eggs at time t,  hatched by all female adult mosquitoes $\Phi (s)$ introduced at the previous time (Wang and Zhao 2008). Define the linear operator $L : C_{\omega } \longrightarrow C_{\omega }$ by Wang and Zhao (2008)

$$\begin{aligned} (L\Phi )(t) = \int ^{\infty }_{0} Y(t,t-a)F(t-a)\Phi (t-a) da \ \ \ \forall t \in {{\mathcal {R}}}, \ \ \ \Phi \in C_{\omega }. \end{aligned}$$

Following Wang and Zhao (2008), let ${{\mathbb {R}}}^t_{0}=\rho (L)$ (the spectral radius of L). Furthermore, let $W(t,\lambda )$ be the monodromy matrix of the linear $\omega$-periodic system:

$$\begin{aligned} \displaystyle \frac{du}{dt}=[-V+\frac{1}{\lambda }F(t)]u, \end{aligned}$$

with parameter $\lambda \in (0,\infty ).$ It can be verified that the system (2.1) satisfies Assumptions (A1)-(A7) in Wang and Zhao (2008). Thus, it follows from Bacaer and Guernaoui (2006) and Wang and Zhao (2008) that:

• ${{\mathbb {R}}}^t_{0}=1$ if and only if $\rho (\Phi _{F-V}(\omega ))=1.$

• ${{\mathbb {R}}}^t_{0}<1$ if and only if $\rho (\Phi _{F-V}(\omega ))<1.$

• ${{\mathbb {R}}}^t_{0}>1$ if and only if $\rho (\Phi _{F-V}(\omega ))>1.$

These results are summarized below.

Theorem 4.1

Consider the non-autonomous model (2.1), subject to the two functions of B(M) given in (2.2). The mosquito-free equilibrium, $P_0,$ is LAS whenever ${{\mathbb {R}}}^t_{0}<1,$ and unstable if ${{\mathbb {R}}}_{0}^t>1$.

We claim the following result.

Theorem 4.2

Consider the non-autonomous model (2.1), subject to the two functions of B(M) given in (2.2). The trivial equilibrium, $P_{0}$ is GAS in $\Gamma$ whenever ${{\mathbb {R}}}^t_0 < 1$.

Proof

Consider the non-autonomous model (2.1) with ${{\mathbb {R}}}^*_0 < 1.$ Furthermore, consider the Lyapunov function,

$$\begin{aligned} V_2=F^{*}_LF^{*}_P \sigma (F^{*}_E E + \mu _{1*} L) + \mu _{1*} \mu _{2*} (F^{*}_P \sigma P + \mu _{3*} M ), \end{aligned}$$

with Lyapunov derivative,

$$\begin{aligned} \frac{dV_2}{dt}= & {} - \{ E [ F^{*}_L F^{*}_P F^{*}_E \mu _1(T,R) - F^{*}_LF^{*}_P F_E(T,R) \mu _{1*} ]\\&\quad + L [ F^{*}_LF^{*}_P \mu _{1*} \mu _{2}(T,R) - F^{*}_L F_P(T,R)\mu _{1*} \mu _{2*} ] \\&\quad + P [ F^{*}_P \mu _{1*} \mu _{2*}\mu _3(T,R) - F_P(T,R) \mu _{1*} \mu _{2*} \mu _{3*} ]\\&\quad + M [ \mu _M(T) \mu _{1*} \mu _{2*} \mu _{3} - F^{*}_LF^{*}_P F^{*}_E B(M) ] \} \\&\quad - F^{*}_L F^{*}_P \sigma \mu _{1*} \delta _L L^2 . \end{aligned}$$

Since for any parameter h,  $h^* > h(t)$ and $h_*<h(t),$ then $\frac{dV_2}{dt}$ can be re-written as

$$\begin{aligned} \frac{dV_2}{dt} \le - \mu _{1*} \mu _{2*} \mu _{3*} \mu _M(T) M(t) [1-\frac{{{\mathbb {R}}}^*_{0} }{b^*}B(M)]. \end{aligned}$$

Furthermore, since $max_M B(M)\le b^*$ for all cases of B(M) in (2.2), it follows, for all ${{\mathbb {R}}}^*_{0} < 1,$ that $\frac{{{\mathbb {R}}}^*_{0} }{b^*}B(M) < 1$ in $\Gamma .$ Hence, $\frac{dV_2}{dt} \le 0.$ The proof is concluded as in the proof of Theorem 3.2. Thus, $P_{0}$ is GAS in $\Gamma ,$ for all cases of B(M) given in (2.2), whenever ${{\mathbb {R}}}^t_0< {{\mathbb {R}}}^*_0 < 1.$ $\square$

The results in Theorems 3.2 and 4.2 show that the non-autonomous and autonomous models, (2.1) and (3.1), have the same qualitative dynamics with respect to the local and global asymptotic stability of the trivial equilibrium ($P_0$). In other words, relaxing the temperature and rainfall dependence of the parameters of the non-autonomous model (2.1) does not alter its asymptotic stability property with respect to the trivial equilibrium $(P_0)$.

4.2 Non-trivial periodic solutions: special case

Consider the special case of the autonomous model (2.1) in the absence of density-dependent mortality rate for larvae (i.e., $\delta _L =0$). This assumption is needed for mathematical tractability.

4.2.1 Existence

The proof for the existence of non-trivial periodic solution of the model (2.1) is based on using the following result (from Gaines and Mawhin (1977)).

Lemma 4.3

[Gaines and Mawhin (1977)] Let Y and Z be Banach spaces and $N_1 : Dom(N_1) \subset Y \rightarrow Z$ be a linear mapping and $N_2 : Y \rightarrow Z$ is continuous. We say the mapping $N_1$ is Fredholm of index zero if $dim(Ker (N_1)) = codim(Im (N_1)) < \infty$ and the image of $N_1$ is closed. If the mapping $N_1$ is Fredholm of index zero and if there exist continuous projectors $Q_1 : S \rightarrow S$ and $Q_2 : T \rightarrow T$ such that $Im(Q_1) = Ker(L)$ and $Ker(Q_2) = Im(L) = Im(I - Q_2),$ then the mapping $L : (I - Q_1)S \rightarrow Im(L)$ will be invertible and we denote the inverse by $K_p.$ Let $\Omega \subsetneq Y$ be a open bounded set and let $N_1$ be a Fredholm mapping of index zero and the mapping $N_2$ is $N_1$-compact. Assume that

• 1. for each $\lambda \in (0,1)$, $x \notin \partial \Omega$, $N_1x = \lambda N_2x,$

• 2. for each $x \in \partial \Omega \cap Ker(N_1)$, $Q_2N_2x \ne 0,$

• 3. $deg (JQ_2N_2, Q_2 \cap Ker(N_1), 0) \ne 0$

then the equation $N_1x = N_2x$ has at least one periodic solution.

We claim the following.

Theorem 4.4

The non-autonomous model (2.1), with $\delta _L =0$ and the oviposition function $B(M)=B_L,$ has at least one positive periodic solution, whenevr ${{\mathbb {R}}}_{0*} \ge 1.$

Proof

The proof, based on using the approach in Gaines and Mawhin (1977), is given in Appendix B. $\square$

Similarly, the following result can be proved for the oviposition form $B(M)=B_S.$

Theorem 4.5

The non-autonomous model (2.1), subject to the oviposition function $B(M)=B_S$ and $\delta _L =0,$ has at least one positive $w-$periodic solution, whenevr ${{\mathbb {R}}}_{0*} \ge 1,$ for $n \ge 1.$

4.2.2 Uniqueness

The uniqueness property of a periodic solution of the non-autonomous model (2.1) will now be explored.

Theorem 4.6

Consider the non-autonomous model (2.1), with $\delta _L =0$.

• (a) If $B(M)=B_L$ and ${{\mathbb {R}}}_{0*} > 2,$ then the positive w-periodic solution of the model (2.1) is unique.

• (b) If $B(M)=B_S$ and ${{\mathbb {R}}}_{0*} > 1+\frac{1}{n-1}$ $(n>1),$ then the positive w-periodic solution of the model (2.1) is unique.

Proof

The proof is based on using the approach in Gaines and Mawhin (1977). Define the invariant region below (the stable manifold of $P_0$):

$$\begin{aligned} \gamma _0=\left\{ (E,L,P,M) \in \gamma : E = L = P = M = 0 \right\} . \end{aligned}$$

Pick any two arbitrary positive periodic solutions $x_1=(E_1,L_1,P_1,M_1)$ and $x_2=(E_2,L_2,P_2,M_2)$ in $\gamma \backslash \gamma _0.$ Consider the following function

$$\begin{aligned} V_3=|E_1(t)-E_2(t)| + |L_1(t)-L_2(t)| + |P_1(t)-P_2(t)| + |M_1(t)-M_2(t)|. \end{aligned}$$

(a) The upper right derivative of $V_3$, denoted by $D^+ V_3(t)$ (in case of $B(M)=B_L$), is given by

$$\begin{aligned}&D^+ V_3(t) \le - \mu _E(T,R) |E_1(t)-E_2(t)| - \mu _L(T,R)|L_1(t)-L_2(t)| - \mu _P(T,R) |P_1(t)-P_2(t)|\\&\qquad - b(T,R)\left( \frac{M_1(t) + M_2(t)}{K} - 1 \right) |M_1(t)-M_2(t)| - \mu _M(T) |M_1(t)-M_2(t)|,\\&\quad \le - \mu _E(T,R) |E_1(t)-E_2(t)| - \mu _L(T,R)|L_1(t)-L_2(t)| - \mu _P(T,R) |P_1(t)-P_2(t)| \\&\qquad - b(T,R) \left( \frac{M_1(s_4) + M_2(s_4)}{K} - 1 \right) |M_1(t)-M_2(t)| - \mu _M(T) |M_1(t)-M_2(t)|,\\&\quad \le - \mu _E(T,R) |E_1(t)-E_2(t)| - \mu _L(T,R)|L_1(t)-L_2(t)| - \mu _P(T,R) |P_1(t)-P_2(t)| \\&\qquad - b(T,R) \left( 2(1-\frac{1}{{{\mathbb {R}}}_{0*}}) - 1 \right) |M_1(t)-M_2(t)| - \mu _M(T) |M_1(t)-M_2(t)|,\\&\quad \le - \mu _{E*} |E_1(t)-E_2(t)| - \mu _{L*}|L_1(t)-L_2(t)| - \mu _{P*} |P_1(t)-P_2(t)| \\&\qquad - b_*\left( 1-\frac{2}{{{\mathbb {R}}}_{0*}} \right) |M_1(t)-M_2(t)|- \mu _{M*} |M_1(t)-M_2(t)|. \end{aligned}$$

It follows that $D^+ V_3(t) < 0$ if and only if ${{\mathbb {R}}}_{0*}>2.$ Thus, $V_3(t) \rightarrow 0$ as $t \rightarrow +\infty$. Furthermore, integrating the last inequality above, from 0 to t,  gives

$$\begin{aligned}&V_3(t) + \mu _{E*} \int _{0}^{t} |E_1(s)-E_2(s)| ds + \mu _{L*} \int _{0}^{t} |L_1(s)-L_2(s)| ds - \mu _{P*} \int _{0}^{t} |P_1(s)\\&\quad -P_2(s)| ds + \left[ b_*\left( 1-\frac{2}{{{\mathbb {R}}}_{0*}}\right) + \mu _{M*}\right] \int _{0}^{t} |M_1(s)-M_2(s)| ds< V_3(0) < \infty . \end{aligned}$$

Thus, $\lim \nolimits _{t \rightarrow +\infty } |x_1(t)-x_2(t)| = 0$ if and only if ${{\mathbb {R}}}_{0*} >2.$

(b) Similarly, the upper right derivative of $V_3$ (in case of $B(M)=B_S$) is given by

$$\begin{aligned}&D^+ V_3(t) \le - \mu _E(T,R) |E_1(t)-E_2(t)| - \mu _L(T,R)|L_1(t)-L_2(t)| - \mu _P(T,R) |P_1(t)-P_2(t)|\\&\qquad - b(T,R)\left[ \frac{M_1^{n-1}(t)M_2(t)+M_1^{n-2}(t)M_2^{2}(t)+{\cdots }+M_1(t)M_2^{n-1}(t) }{K^n} - 1 \right] |M_1(t)-M_2(t)| \\&\qquad -\mu _M(T) |M_1(t)-M_2(t)|,\\&\quad \le - \mu _E(T,R) |E_1(t)-E_2(t)| - \mu _L(T,R)|L_1(t)-L_2(t)| - \mu _P(T,R) |P_1(t)-P_2(t)|\\&\qquad - b(T,R)\left[ \frac{M_1^{n-1}(s_4)M_2(s_4)+M_1^{n-2}(s_4)M_2^{2}(s_4)+{\cdots }+M_1(s_4)M_2^{n-1}(s_4) }{K^n} - 1 \right] \\&\qquad \times \,|M_1(t)-M_2(t)|-\mu _M(T) |M_1(t)-M_2(t)|,\\&\quad \le - \mu _{E*} |E_1(t)-E_2(t)| - \mu _{L*}|L_1(t)-L_2(t)| - \mu _{P*} |P_1(t)-P_2(t)|\\&\qquad - b_*\left[ (n-1)({{\mathbb {R}}}_{0*} -1) - 1 \right] |M_1(t)-M_2(t)| -\mu _{M*} |M_1(t)-M_2(t)|. \end{aligned}$$

It follows that $D^+ V_3(t) < 0$ if and only if ${{\mathbb {R}}}_{0*}>1+\frac{1}{n-1},$ for all $n>1.$ Thus, $V_3(t) \rightarrow 0$ as $t \rightarrow +\infty$. Furthermore, integrating the last inequality from 0 to t,  gives

$$\begin{aligned}&V_3(t) + \mu _{E*} \int _{0}^{t} |E_1(s)-E_2(s)| ds\\&\quad + \mu _{L*} \int _{0}^{t} |L_1(s)-L_2(s)| ds - \mu _{P*} \int _{0}^{t} |P_1(s)-P_2(s)| ds \\&\quad + \left( b_* ((n-1)({{\mathbb {R}}}_{0*}-1)-1)+\mu _{M*}\right) \int _{0}^{t} |M_1(s)-M_2(s)| ds< V_3(0) < \infty . \end{aligned}$$

Hence, $\lim \nolimits _{t \rightarrow +\infty } |x_1(t)-x_2(t)| = 0$ if and only if ${{\mathbb {R}}}_{0*} >1+\frac{1}{n-1}.$ $\square$

4.2.3 Stability

It is instructive to determine whether or not the unique periodic solution of the model (2.1), guaranteed by Theorem 4.4 is asymptotically stable. This is explored below. Let $P_w= (E_w(t),L_w(t),P_w(t),M_w(t))$ represents the unique $w-$periodic solution of the model (2.1). Define the invariant region ($\gamma _1 \subset \Gamma$).

$$\begin{aligned} \gamma _1= & {} \left\{ (E,L,P,M) \in \gamma : 0<E(t) \le E_w(t), 0<L(t)\right. \\&\left. \le L_w(t), 0< P(t) \le P_w(t), 0<M(t)\le M_w(t) \right\} . \end{aligned}$$

Theorem 4.7

Consider the non-autonomous model (2.1), with $\delta _L =0$.

• (a) If $B(M)=B_L$ and ${{\mathbb {R}}}_{0*} > 2,$ then the unique positive w-periodic solution of the model (2.1) is GAS in $\gamma _1.$

• (b) If $B(M)=B_S$ and ${{\mathbb {R}}}_{0*} > 1+\frac{1}{n-1}$ $(n>1),$ then the unique positive w-periodic solution of the model (2.1) is GAS in $\gamma _1.$

Proof

Let ${{\mathbb {R}}}_{0*} > 2$ (so that $P_w$ exists, by Theroem 4.6). Consider the following Lyapunov function

$$\begin{aligned} V_4 =\frac{1}{2} [S_w(t)]^2, \end{aligned}$$

such that,

$$\begin{aligned} S_w(t)= [E(t)-E_w(t)] + [L(t)-L_w(t)] + [P(t)-P_w(t)] + [M(t)-M_w(t)] . \end{aligned}$$

The Lyapunov derivative is

$$\begin{aligned} \frac{dV_4}{dt} = S_w \frac{dS_w}{dt}, \end{aligned}$$

where,

$$\begin{aligned} \frac{dS_w}{dt} = \left[ \frac{dE}{dt} + \frac{dL}{dt} + \frac{dP}{dt} +\frac{dM}{dt} \right] - \left[ \frac{dE_w}{dt} + \frac{dL_w}{dt} +\frac{dP_w}{dt} +\frac{dM_w}{dt}\right] . \end{aligned}$$

(a) $B(M)=B_L.$ For this case, the derivative of $S_w$ is given by

$$\begin{aligned} \frac{dS_w}{dt}= & {} - \mu _E(T,R) |E(t)-E_w(t)| - \mu _L(T,R)|L(t)-L_w(t)| - \mu _P(T,R) |P(t)-P_w(t)|\\&\quad - b(T,R)\left( \frac{M(t) + M_w(t)}{K} - 1 \right) |M(t)-M_w(t)| - \mu _M(T) |M(t)-M_w(t)|. \end{aligned}$$

It should be recalled from Theorem 4.6 that $M(s_4)$ and $M_w(s_4)$ are the minimum values of M(t) and $M_w(t),$ respectively. Furthermore, $M(s_4) \ge K \left( 1-\frac{1}{{{\mathbb {R}}}_{0*}}\right)$ and $M_w(s_4) \ge K (1-\frac{1}{{{\mathbb {R}}}_{0*}}).$ Hence,

$$\begin{aligned}&\frac{dS_w}{dt} \le - \mu _E(T,R) |E(t)-E_w(t)| - \mu _L(T,R)|L(t)-L_w(t)| - \mu _P(T,R) |P(t)-P_w(t)| \\&\qquad - b(T,R) \left( \frac{M(s_4) + M_w(s_4)}{K} - 1 \right) |M(t)-M_w(t)| - \mu _M(T) |M(t)-M_w(t)|, \\&\quad \le - \mu _E(T,R) |E(t)-E_w(t)| - \mu _L(T,R)|L(t)-L_w(t)| - \mu _P(T,R) |P(t)-P_w(t)| \\&\quad - b(T,R) \left( 2(1-\frac{1}{{{\mathbb {R}}}_{0*}}) - 1 \right) |M(t)-M_w(t)| - \mu _M(T) |M(t)-M_w(t)|,\\&\quad \le - \mu _{E*} |E(t)-E_w(t)| - \mu _{L*}|L(t)-L_w(t)| - \mu _{P*} |P(t)-P_w(t)| \\&\qquad - b_*\left( 1-\frac{2}{{{\mathbb {R}}}_{0*}} \right) |M(t)-M_w(t)|- \mu _{M*} |M(t)-M_w(t)|. \end{aligned}$$

It follows that $\frac{dV_4}{dt} < 0$ in $\gamma _1$ if and only if ${{\mathbb {R}}}_{0*}>2.$

(b) Similarly, the derivative of $S_w$ (in case of $B(M)=B_S$) is given by

$$\begin{aligned}&\frac{dS_w}{dt} = - \mu _E(T,R) |E(t)-E_w(t)| - \mu _L(T,R)|L(t)-L_w(t)| - \mu _P(T,R) |P(t)-P_w(t)|\\&\quad - b(T,R)\left[ \frac{M^{n-1}(t)M_w(t)+M^{n-2}(t)M_w^{2}(t)+{\cdots }+M(t)M_w^{n-1}(t) }{K^n} - 1 \right] |M(t)-M_w(t)| \\&\quad -\mu _M(T) |M(t)-M_w(t)|, \\&\le - \mu _E(T,R) |E(t)-E_w(t)| - \mu _L(T,R)|L(t)-L_w(t)| - \mu _P(T,R) |P(t)-P_w(t)|\\&\quad - b(T,R)\left[ \frac{M^{n-1}(s_4)M_w(s_4)+M^{n-2}(s_4)M_w^{2}(s_4)+{\cdots }+M(s_4)M_w^{n-1}(s_4) }{K^n} - 1 \right] |M(t)-M_w(t)| \\&\quad -\mu _M(T) |M(t)-M_w(t)|, \\&\le - \mu _{E*} |E(t)-E_w(t)| - \mu _{L*}|L(t)-L_w(t)| - \mu _{P*} |P(t)-P_w(t)|\\&\quad - b_*\left[ (n-1)({{\mathbb {R}}}_{0*} -1) - 1 \right] |M(t)-M_w(t)| -\mu _{M*} |M(t)-M_w(t)|. \end{aligned}$$

Hence, $\frac{dV_4}{dt} < 0$ in the region $\gamma _1$ whenever ${{\mathbb {R}}}_{0*}>1+\frac{1}{n-1}.$ The proof is completed as in the proof of Theorem 3.2. $\square$

This result shows that the periodic solution of the non-autonomous model (2.1) is globally-asymptotically stable, for the cases when $B(M)=B_L$ or $B_S,$ under certain conditions (specified in Theorem 4.7). Thus, under these conditions, the non-autonomous system (2.1) will undergo sustained oscillations.

5 Numerical simulations

The non-autonomous model (2.1), will now be simulated using relevant (mosquito surveillance and weather) data to assess the impact of temperature and rainfall on the population dynamics of mosquitoes in the Peel region of Ontario, Canada. The study area, and associated mosquito species, in the chosen study area, are described below.

5.1 Study area and mosquito species

The Peel region is a municipality in the southern Ontario province of Canada, extending from latitude $43.35^\circ$N to $43.52^\circ$N and from longitude $79.37^\circ$W to $80.00^\circ$W (Wang et al. 2011). The total annual rainfall recorded in this region is around 793 mm (DeGaetano 2005). The mean temperatures vary by season ($[5-10]\,^\circ$C in the spring; $[22-32]\,^\circ$C in the summer; $[(-2) - 6]\,^\circ$C during the fall and snowy winter with mean temperature $[(-20) - (-5)]$) (Wang et al. 2011). Numerous outbreaks of WNv, a mosquito-borne zoonotic arbovirus caused by female culex mosquito, have been recorded in the Peel region since 2001 (Abdelrazec et al. 2015; Peel Public Health 2013). The disease remains a major public health problem in North America, since its inception in 1999 (for instance, in 2012, WNv causes 5,387 human cases and 300 mortality; Abdelrazec et al. (2014)).

Prior studies have established a strong positive correlation between culex abundance and WNv activity in the Peel region (Wang et al. 2011). Hence, the current study, which focuses on the qualitative and quantitative assessment of the role of temperature and rainfall on the estimate of culex abundance, will implicitly contribute in predicting the risk of WNv outbreaks in the Peel region. Culex pipiens L.-culex restuans theobald mosquitoes are the two primary WNv vectors in North America. The two species, which prefer water habitats with high organic content for their development cycle (Hilker and Westerhoff 2007; Turell and Dohm 2005), are morphologically the same (DeGaetano 2005). Owing to such similarity, the mosquito surveillance data for the Peel region lumps the two species together (it should be recalled that the model developed in the current study does not also distinguish between the two culex species).

Fig. 6

Map of the Peel region of Ontario, Canada, showing the location of mosquito traps and weather station Peel Public Health (2013)

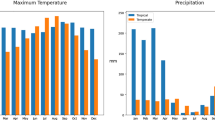
Trap data is collected in the Peel region weekly, during the period between mid-June to early October (usually Weeks 24-39 of the year), using light traps to attract host-seeking adult female mosquitoes (the collected mosquitoes are then separated based on species) (Wang et al. 2011). Figure 6 depicts a map of the Peel region showing the locations of 30 mosquito traps (distributed across the region) and a weather station. The number of mosquitoes collected in this region, for the period 2008–2012, is tabulated in Table S1 of the Supplementary Material. Furthermore, data for mean daily temperature and daily mean rainfall over the same time period is depicted in Fig. 7 (see also Table S2 of the Supplementary Material).

Fig. 7

Observed daily mean temperature (a) and rainfall (b) for in Peel region for the period 2008 to 2012. Data recorded by Canada’s National Climate Archive (http://www.climate.weatherofce.gc.ca)

Table 5 Values of the parameters defined in Eqs. (2.5) and (2.6) (for culex mosquito). $^*$ These parameters are estimated using the surveillance data given in Peel Public Health (2013)

5.2 Effect of temperature and rainfall in Culex abundance

The model (2.1) will now be simulated using the parameter values tabulated in Table 5. These parameter values were obtained (or adapted) from the literature. For instance, the maximum rate of eggs laid per oviposition is taken to be $\alpha _b = 300$ (recorded at $27\,^\circ$C; (Clements 1999)). Furthermore, the maximum values for the rates of eggs hatching, maturation from larvae to pupae and maturation from pupae to adult mosquitoes are taken to be $\alpha _E =0.5, \alpha _L =0.35$ and $\alpha _P = 0.5,$ respectively Clements (1999). Finally, while the peak survival rates of maturation of mosquitoes are recorded at $20\,^\circ$C (Turell and Dohm 2005), that of mature (adult) mosquitoes occur at $28\,^\circ$C Turell and Dohm (2005). Hence, we set $T^*_E=T^*_L=T^*_P=20\,^\circ$C, and $T^*_M=28\,^\circ$C. Simulations were started near the trivial equilibrium (January 1, corresponding to $t=1$ day) and ran until the end of the year (see attached Matlab code in Appendix C).

Fig. 8

Simulations of the model (2.1), showing the effect of temperature (T) and rainfall (R) on the dynamics of culex mosquitoes. All parameter values used are as given in Table 5

Figure 8 depicts the distribution of the total female adult culex mosquitoes (for the Peel region) as a function of temperature and rainfall. This figure shows that a peak mosquito abundance is recorded for temperatures in the range [20–25]$\,^\circ$C and rainfall in the range [15–35] mm. In other words, this study shows that culex mosquito abundance is maximized in the Peel region between July and August. It is worth recalling that the aforementioned suitable temperature range for culex development ([20–25]$\,^\circ$C) lie within the range reported in the statistical study by Hilker and Westerhoff (2007) (but the temperature range in the current study is narrower). Hence, this study suggests that the Peel region should intesify anti-WNv control effort during the months of July and August, when the temperature and rainfall values lie in the aforementioned ranges. It should be mentioned that only larviciding is implemented in the Peel region, typically for a period of 3 weeks (Peel Public Health 2013) (hence, this study suggests that larviciding should be implemented for a 3-week period between July and August, when the temperature and rainfall are in the ranges described above).

Figure 9 shows the correlation between culex abundance values and human mortality due to WNv in the Peel region, for the period 2008 to 2012 (the culex abundance data was generated using the model (2.1), and the WNv human mortality, superimposed to the culex abundance data, is obtained from Peel region (Peel Public Health 2013)). This figure shows a strong positive correlation between culex abundance and WNv mortality in humans. In particular, this figure shows a peak culex abundance in 2012 [which is consistent with the finding in the annual report on WNv published by the Peel region (Peel Public Health 2013)]. Table 6 depicts the mean average temperature and rainfall values recorded in the Peel region for the period 2008–2012, from which it follows that the values recorded for the year 2012 ([10–28]$\,^\circ$C and [10–30] mm) lie within the suitable range for mosquito development (described above).

Fig. 9

Simulations of the model (2.1), showing the total number of adult female culex mosquitoes (M) super-imposed with data for human mortality due to WNv for the Peel region between 2008 and 2012. WNv mortality data collected from Peel Public Health (2013)

Table 6 Mean averge temperature and rainfall in the Peel region (during mosquito season) from 2008 to 2012

6 Conclusions

A new non-autonomous model is designed and used to assess the impact of temperature and rainfall on the abundance of adult female mosquitoes. The model, which incorporates the dynamics of both the immature and female adult mosquitoes, was rigorously analysed, subject to forms of the egg oviposition function (namely, Verhulst-Pearl logistic and Maynard-Smith-Slatkin functions) to gain insight into its qualitative features. The main results obtained are as follows.

• (i) The trivial solution of the autonomous version of the model (with no temperature or rainfall effects) is locally- and globally-asymptotically stable whenever a certain threshold quantitative (${{\mathbb {R}}}_0$) is less than unity, for each of the two eggs oviposition functions used. The autonomous model with the two oviposition functions (Verhulst-Pearl logistic and Maynard-Smith-Slatkin), has a unique stable non-trivial solution whenever ${{\mathbb {R}}}_0 > 1.$ Furthermore, the autonomous model subject to the Verhulst-Pearl logistic and Maynard-Smith-Slatkin oviposition functions, can have a stable limit cycle (via a Hopf bifurcation) under certain conditions.

• (ii) The autonomous model with Maynard-Smith-Slatkin oviposition function sustains more oscillations than the case with the Verhulst-Pearl logistic oviposition function (hence, this study suggested that the Maynard-Smith-Slatkin function is more suitable to model the population biology of mosquitoes).

• (iii) Increase competition in the larval stages reduces the likelihood of sustained oscillator (Hopf bifurcation) in the population biology of the mosquitoes.

• (iv) For the non-autonomous model (with temperature and rainfall effects), it is shown that its local and global asymptotic dynamics, with respect to the trivial solution, matches that of the associated autonomous model (with a different, but similar, threshold condition). Conditions for the existence, uniqueness and global asymptotic stability of the nontrivial periodic solution of the model (in the absence of density-dependent mortality rate for larvae) are derived, for the case of the model subject to the Verhulst-Pearl logistic and Maynard-Smith-Slatkin oviposition functions.

• (v) Using mosquito surveillance and weather data for the Peel region of Ontario, Canada, for the period 2008–2012, numerical simulations of the non-autonomous model (using the Maynard-Smith-Slatkin oviposition functions) show that the ranges of temperature and rainfall suitable for the growth of adult female culex mosquitoes are [20–25]$\,^\circ$C and [15–35] mm. These ranges are recorded, in the Peel region, during the period between mid-July and August (hence, this study shows that anti-WNv control strategies should be intensified during these periods). The model matches the observed data for mosquito abundance during the period 2008–2012.

Appendices

Appendix A: Proof of Lemma 2.1

1. The solution of the IVP (2.8) is given by

$$\begin{aligned} z(t)=e^{-\int _0^t b(s)ds} z_0 + \int _0^t e^{-\int _n^t b(s)ds} a(n)dn, \end{aligned}$$

(5.1)

from which it follows that $z(t) \ge 0$ for all $t\ge 0, a(t)\ge 0$ and $z_0 \ge 0.$

2. Since a(t) and b(t) are non-negative, bounded and continuous functions, it follows from (5.1) that z(t) is bounded.

3. Let $z_1(t)$ be the solution of the IVP (2.8) with $z_1(0)=z_0.$ It can then be shown that $|z(t) - z_1(t)| \longmapsto 0$ as $t \longmapsto \infty .$ Furthermore, for all $t>0$ sufficiently large, there exists $a_* > 0$ such that

$$\begin{aligned} z_1(t) = e^{-\int _{t-w}^t b(s)ds} z_0 + \int _{t-w}^t e^{-\int _n^t b(s)ds} a(n)dn \ge a_* e^{-b_* d w}. \end{aligned}$$

Hence, it follows, from the boundedness of $z_*(t),$ that $z_1(t)\le \frac{a^* e^{b^*}}{b_*}.$ Thus, $m_1<\lim \nolimits _{t\longmapsto \infty } \inf z(t)< \lim \limits _{t\longmapsto \infty } \sup z(t) < m_2,$ for $m_1 = a_* e^{-b_* d w}$ and $m_2 = \frac{a^* e^{b^*}}{b_*}$.

4. Let $w(t)=Z(t)-z(t).$ Then, it follows from (2.8) that $\dfrac{dw}{dt} = -b(t)w + f(t),$ with $w(0)=0$ (this takes the form of the IVP (2.8) with $f(t) = a(t)$). Hence, $\sup |Z(t)-z(t)| \le d \sup |f(t)|$ for $d=\frac{e^{b^*}}{b_*}.$

Appendix B: Proof of Theorem 4.4

Consider the model (2.1) with $B(M)=B_L.$ Let ${{\mathbb {R}}}_{0*} \ge 1.$ Furthermore, let $E=e^{x_1}$, $L=e^{x_2}$, $P=e^{x_3}$ and $M=e^{x_4}.$ Then, the model (2.1) can be re-written as

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{dx_1}{dt} =b(T,R)e^{x_4 - x_1} \left( 1-\frac{e^{x_4}}{K}\right) - \mu _{1}(T,R), \\ \displaystyle \frac{dx_2}{dt} = F_{E}(T,R) e^{x_1 - x_2}-\mu _{2}(T,R), \\ \displaystyle \frac{dx_3}{dt} =F_{L}(T,R) e^{x_2 - x_3} - \mu _{3}(T,R), \\ \displaystyle \frac{dx_4}{dt} = F_{P}(T,R)\sigma e^{x_3 - x_4} - \mu _M(T), \end{array} \right. \end{aligned}$$

(5.2)

with the initial values, $x_1(0) = ln[E(0)], x_2(0)=ln[L(0)], x_3(0)=ln[P(0)]$ and $x_4(0)=ln[M(0)].$ It follows (Theroem 4 in Krasnoselskii 1968) that if the system (5.2) has one $w-$periodic solution, then the system (2.1) will also have one $w-$periodic solution. Furthermore, following Krasnoselskii (1968), let

$$\begin{aligned} Y= & {} \lbrace x=(x_1,x_2,x_3,x_4)^{tr} \in C^1[{{\mathcal {R}}},{{\mathcal {R}}}^4] : x_i(t+w)=x(t) ,i=1,2,3,4, t \in \mathcal {R_+} \rbrace ,\\ Z= & {} \lbrace x=(x_1,x_2,x_3,x_4)^{tr}\in C[\mathcal {R_+},\mathcal {R_+}^4] : x_i(t+w)=x(t) ,i=1,2,3,4, t \in \mathcal {R_+} \rbrace . \end{aligned}$$

Hence, Y and Z are Banach spaces with the supremum norm Krasnoselskii (1968). Define (Gaines and Mawhin 1977) $N_1 : Dom(N_1) \subset Y \rightarrow Z$ such that $N_1[x(t)] = \frac{dx(t)}{dt}$ and $N_2 : Y \rightarrow Z$ such that $N_2[x(t)] = f(t,x),$ where f(t, x) as the right-hand side functions for the system (5.2). Thus, it follows from (5.2) that

$$\begin{aligned} N_1 [x(t)] = N_2[x(t)], \ \ \ x \in Y. \end{aligned}$$

Furthermore, $Dom(N_1) = Y$ and

$$\begin{aligned} Ker(N_1)=\left\{ x \in Y : N_1(x) = 0 \right\} \subseteq {{\mathcal {R}}}^4,\\ Im(N_1) = \left\{ z \in Z : \int ^w_0 z(t) = 0 \right\} , \end{aligned}$$

are closed in Z,  and,

$$\begin{aligned} dim(Ker(N_1))= codim(Im(N_1))=4. \end{aligned}$$

It follows then that $N_1$ is a Fredholm mapping of index zero (Gaines and Mawhin 1977). Following Gaines and Mawhin (1977), define, $Q_1 : Y \rightarrow Y$ and $Q_2 : Z \rightarrow Z$ be the projectors given by $Q_1 (x)= \frac{1}{w} \int ^w_0 x(t)dt, x \in Y$ and $Q_2 (z)= \frac{1}{w} \int ^w_0 z(t)dt, z \in Z.$ Moreover, $Q_1,$ and $Q_2$ are continuous operators such that (Gaines and Mawhin 1977)

$$\begin{aligned} Im(Q_1) = Ker(N_1) = {{\mathcal {R}}}^4, \ \ \ Ker(Q_2) = Im(N_1) = Im(I-Q_2), \end{aligned}$$

Furthermore, the generalized inverse (to $N_1$) $K_{Q_1} : Im(N_1) \rightarrow Ker(Q_1) \bigcap Dom (N_1)$ exists, and is given by Gaines and Mawhin (1977)

$$\begin{aligned} K_{Q_1}(x) = \int ^t_0 x(s)ds - \dfrac{1}{w} \int ^w_0 \int ^t_0 x(s) ds dt. \end{aligned}$$

Then, $Q_2N_2 : Y \rightarrow Z$ and $K_{Q_1}(I-Q_2)N_2 : Y \rightarrow Y.$ Furthermore,, $Q_2N_2$ and $K_{Q_1}(I-Q_2)N_2$ are continuous (by the Lebesgue dominated convergence theorem; Bartle 1995). Since Y is a finite-dimensional Banach space, it follows, using the Ascoli-Arzela theorem (Gaines and Mawhin 1977), that for any open bounded set $\Omega \subset Y,$ $Q_2N_2(\overline{\Omega })$ is bounded and $\overline{K_{Q_1}(I-Q_2)N_2(\overline{\Omega })}$ is compact (Gaines and Mawhin 1977). Thus, $N_2$ is $N_1$-compact on $\overline{\Omega }.$

The next task is to find an appropriate open and bounded subset $\Omega$ (needed for the application of the continuation theorem (Bartle 1995). Using to the operator equation $N_1 x = \lambda N_2x,$ with $\lambda \in (0,1),$ the model (2.1) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{dx_1}{dt} =\lambda \left[ b(T,R)e^{x_4 - x_1} \left( 1-\frac{e^{x_4}}{K}\right) - \mu _{1}(T,R)\right] , \\ \displaystyle \frac{dx_2}{dt} =\lambda \left[ F_{E}(T,R) e^{x_1 - x_2} -\mu _{2}(T,R) \right] , \\ \displaystyle \frac{dx_3}{dt} =\lambda \left[ F_{L}(T,R) e^{x_2 - x_3} - \mu _{3}(T,R) \right] , \\ \displaystyle \frac{dx_4}{dt} =\lambda \left[ F_{P}(T,R)\sigma e^{x_3 - x_4} - \mu _M(T) \right] . \end{array} \right. \end{aligned}$$

(5.3)

Suppose that $x=(x_1,x_2,x_3,x_4)^{tr}$ is a periodic solution of the system (5.3) for some $\lambda .$ Then, there exist $t_i, s_i \in [0,w]$ such that $x_i(t_i) = max_{t \in [0,w]} x_i(t)$ (Bartle 1995). Using the bounds of the parameters $b,F_E,F_L,F_P,\mu _M,\mu _i, (i=1,2,3),$ and from the model (5.3), we get

$$\begin{aligned} b^*e^{x_4(t_4)-x_1(t_1)} \left( 1-\frac{e^{x_4(s_4)}}{K}\right) \ge b e^{x_4(t_1)-x_1(t_1)} \left( 1-\frac{e^{x_4(t_1)}}{K}\right) = \mu _1 \ge \mu _{1*} \end{aligned}$$

and,

$$\begin{aligned} b_*e^{x_4(s_4)-x_1(s_1)} \left( 1-\frac{e^{x_4(t_4)}}{K}\right) \le b e^{x_4(s_1)-x_1(s_1)} \left( 1-\frac{e^{x_4(s_1)}}{K}\right) = \mu _1 \le \mu ^*_{1}, \end{aligned}$$

with,

$$\begin{aligned} \left\{ \begin{array}{lll} x_1(t_1) \le ln\frac{b^* }{\mu _{1*}}+ x_4(t_4), \\ x_2(t_2) \le ln\frac{b^* F^{*}_{E}}{\mu _{1*} \mu _{2*}} + x_4(t_4), \\ x_3(t_3) \le ln \frac{b^* F^{*}_{E} F^{*}_{L}}{\mu _{1*} \mu _{2*}\mu _{3*}}+x_4(t_4), \end{array} \right. \end{aligned}$$

for $x_4(t_4) < ln K.$ Similarly,

$$\begin{aligned} \left\{ \begin{array}{lll} x_4(s_4) \ge x_1(s_1) + ln \frac{ F_{E*} F_{L*} F_{P*}}{\mu _M^* \mu ^*_{2}\mu ^*_{3}}, \\ x_3(s_3) \ge ln\frac{ F_{E*} F_{L*}}{\mu ^*_{2} \mu ^*_{3}} + x_1(s_1), \\ x_2(s_2) \ge ln\frac{ F_{E*}}{\mu ^*_{2}} + x_1(s_1). \end{array} \right. \end{aligned}$$

Hence, it can be concluded that $ln K(1-\frac{1}{{{\mathbb {R}}}^*_{0}})> x_4(s_4) > ln K(1-\frac{1}{{{\mathbb {R}}}_{0*}}).$ Thus, ${{\mathbb {R}}}_{0*} \ge 1.$ Furthermore, define $\Omega = \{ (x_1,x_2,x_3,x_4)^{tr} \in Y : \Vert (x_1,x_2,x_3,x_4)\Vert \le m \}.$ Then, it can be seen that $\Omega$ is an open, bounded set in Y (this satisfies the first two requirements of Lemma 4.3).

In order to prove the third condition of Lemma 4.3, we construct a homotopy family (Bartle 1995)

$$\begin{aligned} \varPsi (x,k) = f_k, \end{aligned}$$

for all $f_k =\left( \tilde{b} e^{x_4 - x_1} \left( 1-\frac{e^{x_4}}{K} \right) - \tilde{\mu _{1}}, \tilde{F_E} e^{x_1 - x_2}-\tilde{\mu _{2}},\tilde{F_L} e^{x_2 - x_3} - \tilde{\mu _{3}}, \tilde{F_P}\sigma e^{x_3 - x_4} - \tilde{\mu _M}) \right) ^{tr},$ and $\tilde{h}= (1-k)\overline{h} +k h(t)$ with $k \in [0,1]$ is a parameter. It can be seen that for $x \in \partial \Omega \cap N_1,$ we have $\varPsi (x,k) \ne 0.$ Let J be the identity mapping. Thus, it follows from the property of coincidence degree theory (Bartle 1995) that

$$\begin{aligned}&deg(JQ_2N_2x; \Omega \cap KerN_1;(0,0,0,0)^{tr})\\&\quad = deg(\varPsi (x,1)^{tr};\Omega \cap KerN_1;(0,0,0,0)^{tr}), \\&\quad = deg(\varPsi (x,0)^{tr};\Omega \cap KerN_1;(0,0,0,0)^{tr}), \\&\quad = sign \left[ det A \right] \ne 0, \end{aligned}$$

where,

$$\begin{aligned} A= \left( \begin{array}{cccc} -\overline{b}e^{x_4 - x_1}(1-\frac{e^{x_4}}{K}) &{} 0 &{} 0 &{} \overline{b} (e^{x_4 - x_1}(1-\frac{e^{x_4}}{K})-\frac{e^{2x_4-x_1}}{K}) \\ \overline{F_E}e^{x_1 - x_2}&{} - \overline{F_E}e^{x_1 - x_2} &{} 0 &{} 0\\ 0 &{} \overline{F_L}e^{x_2 - x_3} &{}- \overline{F_L}e^{x_2 - x_3} &{} 0 \\ 0 &{} 0 &{} \overline{F_P}e^{x_3 - x_4} &{} - \overline{F_P}e^{x_3 - x_4}\\ \end{array} \right) . \end{aligned}$$

In summary, it has been shown that $\Omega$ satisfies all the assumptions in Lemma 4.3. Hence, the non-autonomous model (2.1), with $B(M)=B_L,$ has at least one positive periodic solution when ${{\mathbb {R}}}_{0*} \ge 1.$

Appendix C: Matlab code for generating Figs. 8 and 9