Transmission dynamics of West Nile virus in mosquitoes and corvids and non-corvids

Abstract

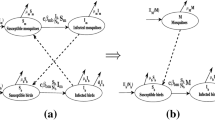
There are more than 300 avian species that can transmit West Nile virus (WNv). In general, the corvid and non-corvid families of birds have different responses to the virus, with corvids suffering a higher disease-induced mortality rate. By taking both corvids and non-corvids as the primary reservoir hosts and mosquitoes as vectors; we formulate and study a system of ordinary differential equations to model a single season of the transmission dynamics of WNv in the mosquito–bird cycle. We calculate the basic reproduction number and analyze the existence and stability of the equilibria. The existence of a backward bifurcation gives a further sub-threshold condition beyond the basic reproduction number for the spread of the virus. We also discuss the role of corvids and non-corvids in spreading the virus. We conclude that knowledge of the relative abundance of corvid bird species and other mammals assist us in accurate estimation of the epidemic of WNv.

Appendix

In this Appendix, the proof of Theorem 4.1 is given. It employs Theorem 6.1 (demonstrated below), which is adopted from Castillo-Chavez and Song (2004) that is, in turn, based on the use of the center manifold theory (Carr 1981; Guckenheimer and Holmes 1983).

Theorem 6.1

(Castillo-Chavez and Song 2004) Consider the following general system of ordinary differential equations with a parameter

$$\begin{aligned} \frac{dx}{dt} = f(x,\phi ), \ \ \ f:R^{n} \longrightarrow R, \ \ \ and \ \ \ f \in C^{2}(R \times R). \end{aligned}$$

(6.1)

Without loss of generality, it is assumed that $0$ is an equilibrium for system (6.1) for all values of the parameter $\phi ,$ (that is $f(0,\phi ) = 0 \ \ \ \forall \phi$). Assume

• 1. $B= D_{x}f(0,0) = \left( \frac{\partial f_{j}}{\partial x_{i}},0,0\right)$ is the linearized matrix of system (6.1) around the equilibrium $0$ with $\phi$ evaluated at $0$. Zero is a simple eigenvalue of $B$ and all other eigenvalues of $B$ have negative real parts;

• 2. Matrix $B$ has a right eigenvector $w$ and a left eigenvector $v$ corresponding to the zero eigenvalue. Let $f_{k}$ be the $k{th}$ component of $f$ and

  $$\begin{aligned} a&= \sum ^{8}_{k,i,j} v_{k}w_{i}w_{j} \frac{\partial ^{2}f_{k}}{\partial x_{i} \partial x_{j}} (0,0)\\ b&= \sum ^{8}_{k,i} v_{k}w_{i} \frac{\partial ^{2}f_{k}}{\partial x_{i} \partial \phi } (0,0). \end{aligned}$$

  The local dynamics of system (6.1) around $0$ are totally determined by $a$ and $b$.

  • (a) In the case where $a > 0; b > 0,$ we have that when $\phi < 0$ with $\left| \phi \right|$ close to zero, $0$ is locally asymptotically stable and there exists a positive unstable equilibrium; when $0<\phi << 1,$ $0$ is unstable and there exists a negative and locally asymptotically stable equilibrium.

  • (b) In the case where $a < 0; b < 0,$ we have that when $\phi < 0$ with $\left| \phi \right|$ close to zero, $0$ is unstable; when $0<\phi << 1,$ 0 is locally asymptotically stable, and there exists a positive unstable equilibrium;

  • (c) In the case where $a > 0; b < 0,$ we have that when $\phi < 0$ with $\left| \phi \right|$ close to zero, 0 is unstable and there exists a locally asymptotically stable negative equilibrium; when $0<\phi << 1,$ $0$ is stable and a positive unstable equilibrium appears

  • (d) In the case where $a < 0; b > 0,$ we have that when $\phi$ changes from negative to positive, $0$ changes its stability from stable to unstable. Correspondingly, a negative unstable equilibrium becomes positive and locally asymptotically stable.

To apply Theorem (6.1), the following simplification and change of variables are made on the system (2.1). First of all, let $x_{1}=M_{s}, x_{2}=M_{i}, x_{3}=B_{1s}, x_{4}=B_{1i}, x_{5}=B_{1r}, x_{6}=B_{2s}, x_{7}=B_{2i}, x_{8}=B_{2r}.$ Further, by using the vector notation $X=(x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7},x_{8})^{T},$ the system (2.1) can be written in the form of $\frac{dX}{dt} = F(x),$ with $F=(f_{1},f_{2},f_{3},f_{4},f_{5},f_{6},f_{7},f_{8})^{T},$ such that

$$\begin{aligned} \left\{ \begin{array}{lcl} \displaystyle \frac{dx_{1}}{dt} &{}=&{} \left( r_{m}x_{1}+(1-q)r_{m}x_{2}\right) \left( 1-\frac{x_{1}+x_{2}}{K_{m}}\right) -d_{m}x_{1} - \beta _{m}b_{m}\frac{x_{4}+x_{7}}{\sum ^{8}_{j=3}x_{j}+A}x_{1}, \\ \displaystyle \frac{dx_{2}}{dt}&{}=&{} qr_{m}x_{2}\left( 1-\frac{x_{1}+x_{2}}{K_{m}}\right) - d_{m}x_{2}+\beta _{m}b_{m}\frac{x_{4}+x_{7}}{\sum ^{8}_{j=3}x_{j}+A}x_{1}, \\ \displaystyle \frac{dx_{3}}{dt}&{}=&{} \gamma _{b1}-d_{b}x_{3}-\beta _{b}b_{m}\frac{x_{3}}{\sum ^{8}_{j=3}x_{j}+A}x_{2},\\ \displaystyle \frac{dx_{4}}{dt}&{}=&{} -\delta _{1}x_{4}+\beta _{b}b_{m}\frac{x_{3}}{\sum ^{8}_{j=3}x_{j}+A}x_{2},\\ \displaystyle \frac{dx_{5}}{dt}&{}=&{} -d_{b}x_{5}+\nu _{1}x_{4},\\ \displaystyle \frac{dx_{6}}{dt}&{}=&{} \gamma _{b2}-d_{b}x_{6}-\beta _{b}b_{m}\frac{x_{6}}{\sum ^{8}_{j=3}x_{j}+A}x_{2},\\ \displaystyle \frac{dx_{7}}{dt}&{}=&{} -\delta _{2}x_{7}+\beta _{b}b_{m}\frac{x_{6}}{\sum ^{8}_{j=3}x_{j}+A}x_{2},\\ \displaystyle \frac{dx_{8}}{dt}&{}=&{} -d_{b}x_{8}+\nu _{2}x_{7}. \end{array} \right. \end{aligned}$$

(6.2)

Assume that $(1-q)d_{m}\mu _{2}-\beta _{m}b_{m}d_{b} > 0.$ Choose $(\delta _{1},\delta _{2})$ as a bifurcation parameters. As a result of solving $R_{0}=1,$ backward bifurcation occurs at any point on the curve defined at Eq. (4.1) (see Sect. 4).

The Jacobian matrix of the system (2.1) at $E_{1}$ (with $(\delta _{1},\delta _{2})$ satisfying Eq. (4.1)) is given by

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -(r_{m}-d_{m})&{}d_{m}(1-q)+(d_{m}-r_{m})&{}0&{}-\beta _{m}b_{m} \frac{\tilde{M}}{\tilde{B}}&{}0&{}0&{}-\beta _{m}b_{m}\frac{\tilde{M}}{\tilde{B}}&{}0 \\ 0&{} -(1-q)d_{m}&{}0&{}\beta _{m}b_{m}\frac{\tilde{M}}{\tilde{B}}&{}0&{}0&{} \beta _{m}b_{m}\frac{\tilde{M}}{\tilde{B}}&{}0 \\ 0&{}-\beta _{b}b_{m}\frac{\tilde{B_{1}}}{\tilde{B}}&{}-d_{b}&{}0&{}0&{}0&{}0&{}0 \\ 0&{}\beta _{b}b_{m}\frac{\tilde{B_{1}}}{\tilde{B}}&{}0&{}-\delta _{1}&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}\nu _{1}&{}-d_{b}&{}0&{}0&{}0 \\ 0&{}-\beta _{b}b_{m}\frac{\tilde{B_{2}}}{\tilde{B}}&{}0&{}0&{}0&{}-d_{b}&{}0&{}0 \\ 0&{}\beta _{b}b_{m}\frac{\tilde{B_{2}}}{\tilde{B}}&{}0&{}0&{}0&{}0&{}-\delta _{2}&{}0 \\ 0&{} 0&{}0&{}0&{}0&{}0&{}\nu _{2}&{}-d_{b}. \end{array} \right) \!, \end{aligned}$$

The eigenvalues of the Jacobian matrix can be obtained by the following equation:

$$\begin{aligned} \chi (\lambda )=\lambda (\lambda +d_{b})^{4}(\lambda + (r_{m}-d_{m}))(\lambda ^{2} + a_{2} \lambda + a_{1}), \end{aligned}$$

where $a_{2} = \delta _{1}+\delta _{2}+(1-q)d_{m}$ and $a_{1}=\delta _{2}(\delta _{1}+(1-q)d_{m}).$

Thus, the Jacobian matrix has a simple zero eigenvalue and all the other eigenvalues have negative real parts for all $r_{m}>d_{m}$. Hence, Theorem (6.1) can be used to analyze the dynamics of the system (2.1).

When $R_{0}=1$, it can be shown that the Jacobian matrix has a right eigenvector (associated to the zero eigenvalue), given by $w=(w_{1},w_{2},w_{3},w_{4},w_{5},w_{6},w_{7},w_{8})^{T},$ where $w_{1}=-w_{2},\, w_{2}=w_{2},\,w_{3}=-\beta _{b}b_{m}\frac{\tilde{B_{1}}}{d_{b} \tilde{B}} w_{2},\,w_{4}=\beta _{b}b_{m}\frac{\tilde{B_{1}}}{\delta _{1} \tilde{B}} w_{2},\,w_{5}=\beta _{b}b_{m}\frac{\nu _{1} \tilde{B_{1}}}{\delta _{1} d_{b} \tilde{B}} w_{2},\,w_{6}=-\beta _{b}b_{m}\frac{\tilde{B_{2}}}{d_{b} \tilde{B}} w_{2},\,w_{7}=\beta _{b}b_{m}\frac{\tilde{B_{2}}}{\delta _{2} \tilde{B}} w_{2},\,w_{8}=\beta _{b}b_{m}\frac{\nu _{2} \tilde{B_{2}}}{\delta _{2} d_{b} \tilde{B}} w_{2}.$

Similarly, the components of the left eigenvector of Jacobian matrix (corresponding to the zero eigenvalue), denoted by $v=(v_{1},v_{2},v_{3},v_{4},v_{5},v_{6},v_{7},v_{8})^{T},$ are given by $v_{1}=0, v_{2}=v_{2},v_{3}=0,v_{4}=\beta _{m}b_{m}\frac{\tilde{M}}{\tilde{B}}v_{2}, v_{5}=0, v_{6}=0, v_{7}=\beta _{m}b_{m}\frac{\tilde{M}}{\tilde{B}}v_{2}, v_{8}=0.$

Let $a$ and $b$ be the coefficients defined in Theorem (6.1). We can calculate $a$ as follows: for the transformed system (6.2), the associated non-zero partial derivatives of $f$ (evaluated at the DFE $E_{1}$) are given by

$$\begin{aligned} \dfrac{\partial ^{2}f_{2}}{\partial x_{1} \partial x_{2}}&= -\dfrac{qr_{m}}{K_{m}}, \quad \quad \quad \dfrac{\partial ^{2}f_{2}}{\partial x_{1} \partial x_{j}} =\dfrac{\beta _{m}b_{m}}{ \tilde{B}}, \quad (j=4, 7),\\ \dfrac{\partial ^{2}f_{2}}{\partial x_{2} \partial x_{2}}&= -2\dfrac{qr_{m}}{K_{m}}, \quad \quad \dfrac{\partial ^{2}f_{2}}{\partial x_{i} \partial x_{j}} = - \beta _{m}b_{m} \dfrac{\tilde{M}}{\tilde{B}^{2}},\quad (i=3, 4, 5, 6, 7, 8; j=4, 7), \\ \dfrac{\partial ^{2}f_{4}}{\partial x_{2} \partial x_{j}}&= - \beta _{b}b_{m} \dfrac{\tilde{B_{1}}}{\tilde{B}^{2}},\qquad (j=4, 5, 6, 7, 8),\\ \dfrac{\partial ^{2}f_{4}}{\partial x_{2} \partial x_{3}}&= \beta _{b}b_{m} \frac{\tilde{B} -\tilde{B_{1}}}{\tilde{B}^{2}},\quad \dfrac{\partial ^{2}f_{7}}{\partial x_{2} \partial x_{j}} = - \beta _{b}b_{m} \frac{\tilde{B_{2}}}{\tilde{B}^{2}},\quad (j=3, 4, 5, 7, 8),\\ \frac{\partial ^{2}f_{7}}{\partial x_{2} \partial x_{6}}&= \beta _{b}b_{m} \frac{\tilde{B} -\tilde{B_{2}}}{\tilde{B}^{2}}. \end{aligned}$$

Then,

$$\begin{aligned} \begin{array}{lcl} a &{}=&{}\displaystyle \sum ^{8}_{k,i,j} v_{k}w_{i}w_{j} \frac{\partial ^{2}f_{k}}{\partial x_{i} \partial x_{j}} (0,0)\\ &{}=&{}\displaystyle \frac{2\beta _{m}\beta _{b}^{2}b^{3}_{m}}{d_{b}}\frac{\tilde{M}}{\tilde{B}^{4}} v_{2}w^{2}_{2} (\tilde{B_{1}} + \tilde{B_{1}}) \left( \tilde{B_{1}}\left( \frac{\nu _{1}+d_{b}}{\delta _{1}}-1\right) + \tilde{B_{2}}\left( \frac{\nu _{2}+d_{b}}{\delta _{2}}-1\right) \right) \\ &{}&{}\displaystyle +\frac{2\beta _{m}\beta _{b}^{2}b^{3}_{m}}{d_{b}}\frac{\tilde{M}}{\tilde{B}^{4}} v_{2}w^{2}_{2} (\tilde{B_{1}} \!+\! \tilde{B_{1}})\left( A \!+\! \tilde{B_{1}}\left( 1\!-\!\frac{\mu _{1}}{\delta _{1}}\right) \!+\! \tilde{B_{2}}\left( 1\!-\!\frac{\mu _{2}}{\delta _{2}}\right) \!+\! \frac{\beta _{m}b_{m}d_{b}}{(1\!-\!q)d_{m}} \left( \frac{\tilde{B_{1}}}{\delta _{1} } \!+\! \frac{\tilde{B_{2}}}{\delta _{2} } \right) \right) \\ &{}=&{}\displaystyle \frac{2\beta _{m}\beta _{b}^{2}b^{3}_{m}}{d_{b}}\frac{\tilde{M} (\tilde{B_{1}} + \tilde{B_{2}})}{\tilde{B}^{4}}v_{2}w^{2}_{2} \left( A- \left( \mu _{1}- \nu _{1} - d_{b}-\frac{d_{b}\beta _{m}b_{m}}{(1-q)d_{m}}\right) \frac{\tilde{B_{1}}}{\delta _{1}}\right. \\ &{}&{} \displaystyle -\left. \left( \mu _{2}- \nu _{2} - d_{b}-\frac{d_{b}\beta _{m}b_{m}}{(1-q)d_{m}}\right) \frac{\tilde{B_{2}}}{\delta _{2}}\right) . \end{array} \end{aligned}$$

Then, from the above equation we can conclude that $a$ is negative if and only if $A$ satisfies the Eq. (4.4).

From Eq. (4.1) we can see that $\delta _{1} \ge \frac{\alpha \tilde{B_{1}}\delta _{2}}{\delta _{2} -\alpha \tilde{B_{2}}},$ if and only if $R_{0}\le 1.$ Using the same notation as in Castillo-Chavez and Song (2004), $\phi =\frac{\alpha \tilde{B_{1}}\delta _{2}}{\delta _{2}-\alpha \tilde{B_{2}}} - \delta _{1},$ then $\phi \ge 0$ if and only if $R_{0}\ge 1,$ and $\phi < 0$ if and only if $R_{0}<1.$

We can calculate $b$ by substituting the vectors $v$ and $w$ and the respective partial derivatives (evaluated at the DFE $E_{1}$) into the expression

$$\begin{aligned} b =\sum ^{8}_{k,i} v_{k}w_{i} \frac{\partial ^{2}f_{k}}{\partial x_{i} \partial \phi } (0,0), \end{aligned}$$

which implies

$$\begin{aligned} b =\frac{2\beta _{m}\beta _{b}b^{2}_{m}}{d_{b}}\frac{\tilde{M} \tilde{B_{1}}}{\tilde{B}^{2}}v_{2}w_{2} >0. \end{aligned}$$

Since coefficient $b$ is always positive, it follows that the system (2.1) will undergo backward bifurcation if the coefficient $a$ is negative.