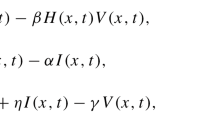Abstract
A general mathematical model of viral infections inside a spherical organ is presented. Transported quantities are used to represent external cells or viral particles that penetrate the organ surface to either promote or combat the infection. A diffusion mechanism is considered for the migration of transported quantities to the organ inner tissue. Cases that include the effect of penetration, diffusion and proliferation of immune system cells, the generation of latently infected cells and the delivery of antiviral treatment are analyzed. Different antiviral mechanisms are modeled in the context of spatial variation. Equilibrium conditions are also calculated to determine the radial profile after the infection progresses and antiviral therapy is delivered for a long period of time. The dynamic and equilibrium solutions obtained in this paper provide insight into the temporal and spatial evolution of viral infections.










Similar content being viewed by others
References
Andrew SM, Baker CTH, Bocharov GA (2007) Rival approaches to mathematical modelling in immunology. J Comput Appl Math 205(2):669–686
Beauchemin C (2006) Probing the effects of the well-mixed assumption on viral infection dynamics. J Theor Biol 242(2):464–477
Beauchemin C, Dixit NM, Perelson AS (2007) Characterizing T cell movement within lymph nodes in the absence of antigen. J Immunol 178(9):5505–5512
Berencsi K, Rani P, Zhang T, Gross L, Mastrangelo M, Meropol NJ, Herlyn D, Somasundaram R (2011) In vitro migration of cytotoxic T lymphocyte derived from a colon carcinoma patient is dependent on CCL2 and CCR2. J Transl Med 9:33
Bonhoeffer S, May R, Shaw GM, Nowak MA (1997) Virus dynamics and drug therapy. Proc Natl Acad Sci USA 94:6971–6976
Callaway D, Perelson A (2002) HIV-1 infection and low steady state viral loads. Bull Math Biol 64(1):29–64
Chou TC (1976) Derivation and properties of MichaelisMenten type and Hill type equations for reference ligands. J Theor Biol 59:253–276
Ferguson N, Fraser C, Anderson R (2001) Viral dynamics and anti-viral pharmacodynamics: rethinking in vitro measures of drug potency. Trends Pharmacol Sci 22:97–100
Friedman A, Tian JP, Fulci G, Chiocca EA, Wang J (2006) Glioma virotherapy: effects of innate immune suppression and increase viral replication capacity. Cancer Res 66(4):2314–2319
Funk G, Jansen V, Bonhoeffer S, Killingback T (2005) Spatial models of virus-immune dynamics. J Theor Biol 233:221–236
Funk G, Gosert R, Hirsch H (2007) Viral dynamics in transplant patients: implications for disease. Lancet Infect Dis 7:460–472
Hakre S, Chavez L, Shirakawa K, Verdin E (2012) HIV latency: experimental systems and molecular models. FEMS Microbiol Rev 36:706–716
Heffernan J, Smith R, Wahl L (2005) Perspectives on the basic reproductive ratio. J R Soc Interface 0042 (online)
Hernandez JO, Norstrom J, Wysock G (2009) Acyclovir-induced renal failure in an obese patient. Am J Health Syst Pharm 66(14):1288–1291
Herzmann C, Karcher H (2004) Nevirapine plus Zidovudine to prevent mother-to-child transmission of HIV. New Engl J Med 351:2013–2016
Jacobson IM, Cacoub P, Dal Maso L, Harrison SA, Younossi ZM (2010) Manifestations of chronic Hepatitis C virus infection beyond the liver. Clin Gastroenterol Hepatol 8(12):1017–1029
Kepler G, Nguyen H, Webster-Cyriaque J, Banks H (2007) A dynamic model for induced reactivation of latent virus. J Theor Biol 244:451–462
Komarova N, Wodarz D (2010) ODE models for oncolytic virus dynamics. J Theor Biol 263:530–543
Lequan M, Yu Z, Yongmei S (2009) Study of dynamics of dimensionless basic virus infection model and prediction for long term therapy efficacy. FBIE, pp 496–500
Leroy V, Viho I, Blanche S, Rouzioux C, Dabis F, Rouet F, Sakarovitch C, Msellati P, Elenga N (2003) Pediatric viral human immunodeficiency virus type 1 RNA levels, timing of infection, and disease progression in African HIV-1-infected children. Pediatrics 112(4):289–297
Lopez CB, Fernandez-Sesma A, Czelusniak SM, Schulman JL, Moran TM (2000) A mouse model for immunization with ex vivo virus-infected dendritic cells. Cell Immunol 206:107–115
Miller MJ, Wei SH, Parker I, Cahalan MD (2002) Two-photon imaging of lymphocyte motility and antigen response in intact lymph node. Science 296(5574):1869–1873
Nowak M, Bangham C (1996) Population dynamics of immune responses to persistent viruses. Science 272(5258):74–79
Nowak M, Bonhoeffer S, Shaw GM, May R (1997) Anti-viral drug treatment: dynamics of resistance in free virus and infected cell populations. J Theor Biol 184:203–217
Nowak MA, May R (2000) Virus dynamics. Oxford University Press, London
Regoes RR, Barber DL, Ahmed R, Antia R (2007) Estimation of the rate of killing by cytotoxic T lymphocytes in vivo. Proc Natl Acad Sci USA 104(5):1599–1603
Rong L, Gilchrist M, Feng Z, Perelson A (2007) Modeling within-host HIV-1 dynamics and the evolution of drug resistance: trade-offs between viral enzyme function and drug susceptibility. J Theor Biol 247:804–818
Segovia-Juarez JL, Ganguli S, Kirschner D (2004) Identifying control mechanisms of granuloma formation during M. tuberculosis infection using an agent-based model. J Theor Biol 231:357–376
Shen L, Rabi SA, Siliciano RF (2009) A novel method for determining the inhibitory potential of anti-HIV drugs. Trends Pharmacol Sci 30(12):610–616
Shi X, Zhou X, Song X (2010) Dynamical behavior of a delay virus dynamics model with CTL immune response. Nonlinear Anal Real World Appl 11:1795–1809
Stengel R (2008) Mutation and control of the human immunodeficiency virus. Math Biosci 213:93–102
Stilianakis N, Boucher C, DeJong M, VanLeeuwen R, Schuurman R, DeBoer R (1997) Clinical data sets of human immunodeficiency virus type 1 reverse transcriptase-resistant mutants explained by a mathematical model. J Virol 71(1):161–168
Strain M, Richman D, Wong J, Levine H (2002) Spatiotemporal dynamics of HIV propagation. J Theor Biol 218:85–96
Tao Y, Guo Q (2005) The competitive dynamics between tumor cells, a replication-competent virus and an immune response. J Math Biol 51:37–74
Tramontano A (2006) The role of molecular modelling in biomedical research. FEBS Lett 580:2928–2934
Wang K, Wang W (2007) Propagation of HBV with spatial dependence. Math Biosci 210(1):78–95
Wang K, Wang W, Song S (2008) Dynamics of an HBV model with diffusion and delay. J Theor Biol 253(1):36–44
Wilkinson PC (1990) Relation between locomotion, chemotaxis and clustering of immune cells. Immunology 69:127–133
Wodarz D (2003) Hepatitis C virus dynamics and pathology: the role of CTL and antibody responses. J Gen Virol 84:1743–1750
Wodarz D (2005) Mathematical models of immune effector responses to viral infections: virus control versus the development of pathology. J Comput Appl Math 184:301–319
Wodarz D, Levy DN (2011) Effect of different modes of viral spread on the dynamics of multiply infected cells in human immunodeficiency virus infection. J R Soc Interface 8(55):289–300
Xu R, Ma Z (2009) An HBV model with diffusion and time delay. J Theor Biol 257(3):499–509
Yu J, Min L, Ye Y (2010) Global analysis of a viral infection model with application to HBV infection. J Biol Syst 18:325–337
Acknowledgments
The authors acknowledge the suggestions made by the reviewers and the guidance provided by Dr. Marisol Fernandez from the infectious disease staff at Dell Children’s Hospital in Austin, Texas.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Model parameters and variables
The uninfected host cells \(X\) proliferate at a rate of \(\lambda \), and are infected at a rate of \(\beta \). The calculation of \(\beta \) considers that 70 % of the virion successfully infect host cells. A productive infected cell lives five times less than a latently infected cell. For convenience, the expectancy life time of a latently infected cell is made equivalent to the uninfected cell, \(a_L = d\). Therefore, an uninfected cell is expected to live 10 days, which makes 2 days the life of a productive infected cell. The lifetime of an immune cell is around 5 days. Immune cells are stimulated by infected cells and the production of immune cells is a function of the infected cells concentration. In the case immune cell production is assumed inside the infected organ, the generation term \(c Y Z\) is included in \(\mathbf{G}\). Nevertheless, infected cells at the organ surface may trigger the generation of immune cells at the surface and their penetration, measured by \(p_{ZY}\), to the infected organ. Table 1 shows these parameters and literature sources.
Appendix B: Numerical solution approach
A numerical solution for the system defined by Eqs. (2, 3) is obtained by the discretization of the spherical organ into \(n\) equal volume shells. This discretization originates \(n+1\) nodes at radial locations defined by \(\eta _i\), where \(i = 0, 1, \ldots , n-1, n\). The center and surface nodes are given by \(\eta _0 = 0\) and \(\eta _n = 1\), respectively. The following recursive expression is used to calculate the nodes locations for an equal volume shell configuration,
Two contiguous shell elements, which are equivalent to three consecutive nodes, are used to approximate the diffusion terms inside the spherical organ. This approximation consists of making \(T(\eta ,t)\) a piecewise quadratic function. The expression for the quadratic transported function defined by three consecutive nodes \(i-1\), \(i\) and \(i+1\) is given by,
where \(\varDelta _j = \eta _j - \eta _{j-1}\), \(\delta _j = \eta - \eta _j\), and the node \(i\) is chosen such that \(\eta \in [\eta _{i-1} \quad \eta _{i+1}]\). Notice that \(T_{i} \equiv T(\eta _i, t)\). The partial derivative with respect to \(\eta \) for the quadratic approximation in Eq. (15) is given by,
Note that the two boundary conditions at \(\eta _0\) and \(\eta _n\) can be substituted in the previous equation to obtain the correspondent expressions for \(T_{-1}\) and \(T_{n+1}\) necessary for the calculation of \(T(\eta , t)\) in Eq. (15) when \(\eta < \eta _{1}\) and \(\eta > \eta _{n-1}\), respectively. The second derivative of the quadratic approximation in Eq. (15) is used in the calculation of the diffusion term,
Substitution of Eqs. (16, 17) in the diffusion term of any transported quantity gives:
where the coefficients are a function of \(\eta \),
It is important to determine a minimum number of nodes \(n+1\) to reliably approximate the diffusion term. This condition can be estimated by comparing the numerical approximation solution for different number of nodes at equilibrium condition.
Figure 11 illustrates de effect of the number of shell elements for the equilibrium solution of the basic virus model. The continuous line represents the solution provided by the Runge–Kutta 23 solver with variable step size. The solution provided by 25 shell elements shows acceptable as it seems to lie very close to the Runge–Kutta 23 solution profile.
Rights and permissions
About this article
Cite this article
Dunia, R., Bonnecaze, R. Mathematical modeling of viral infection dynamics in spherical organs. J. Math. Biol. 67, 1425–1455 (2013). https://doi.org/10.1007/s00285-012-0593-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-012-0593-y