Abstract
Purpose
The main purpose of this study is to establish which of two methods is more reliable in glenoid assessment for instability in pre-operative planning. Accordingly, we have studied the intra- and inter-observer reliability of glenoid parameters with the use of two-dimensional (2D) and three-dimensional (3D) reconstructed computed tomography (CT) images.
Methods
One hundred glenoids were measured with the use of 2D-CT and 3D-CT (in 3D orientation) by two independent observers (one experienced and one inexperienced). Measurements were repeated after one week for 30 randomly selected glenoids.
Results
The intra-class correlation coefficient (ICC) for inter-observer reliability was significantly greater for 3D-CT (0.811 to 0.915) than for 2D-CT (0.523 to 0.925). All intra-observer reliability values for 3D-CT were near perfect (0.835 to 0.997), while those for 2D-CT were less reliable (0.704 to 0.960). A dependent t-test showed that, for both observers, almost all glenoid parameters (except R and d) differed significantly (p < 0.05) between 2D and 3D measurement methods.
Conclusions
Therefore, it can be concluded that 3D glenoid reconstructions are more reliable for glenoid bone loss assessment than 2D-CT. The results suggest that quantifying a glenoid defect with the use of 2D image only—even if performed by an experienced orthopaedic surgeon—is prone to errors. Differences in measurements between and within observers can be explained by plane setting and identifying glenoid rim in 2D-CT. Accordingly, we recommend that glenoid measurements should be performed in 3D orientation using 3D reconstruction obtained from CT images for pre-operative assessments, which are crucial for surgical planning.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
Accurate assessment of glenoid bone loss is important in pre-operative decision making and planning. Significant glenoid defects lead to increased risk of recurrence following arthroscopic shoulder stabilisation techniques [1, 2]. The choice of operative procedure for shoulder instability is predominantly based on the calculation of glenoid bone loss [3–5]. The bone loss might also affect the selection of the treatment method in other circumstances (posterior instability, osteoarthritis) [6–8]. Accurate measurement of glenoid parameters is challenging, and thus of great interest in clinical research [7]. The first studies which focus on intra- and inter-reliability have shown unsatisfactory precision of measurement of radiographic parameters used to quantify a glenoid retroversion [9, 10]. The low reproducibility of X-ray evaluation results from great variation in scapular positioning, which affects identification of homological points on this bone [11, 12]. Nevertheless, radiographic imaging is still widely used in shoulder instability to assess the presence or absence of bony abnormalities, fractures, Hill-Sachs lesion or any other pathologic changes in the joint [13–16]. Additionally, roentgenographic examination is used in the following: post-operative assessment of changes in the implant position after total shoulder arthroplasty (TSA) [7, 17, 18], measuring glenoid version [19], detection of scapular fractures [20], or evaluation of reverse shoulder arthroplasty (RSA) [21]. However, due to certain limitations of this method several research projects focus on comparing the reliability of radiographic imaging, two-dimensional (2D) and three-dimensional (3D) computed tomography (CT).
Recent technological advancements allow for obtaining better quality CT images, thus making it possible to receive high-resolution three-dimensional reconstruction of the bone which accurately reflects the anatomy of the glenoid [22]. Therefore, 3D reconstruction of the scapula allows accurate prediction of the physiologic glenoid version [23]. According to Hirschmann et al. [24] intra- and inter-observer reliability of knee measurements were the lowest for radiographs, slightly better for 2D-CT and highest for 3D-reconstructed images. In turn, the study by Budge et al. [25] showed that 2D-CT and 3D-CT methods are characterised by a high degree of intra- and inter-observer reliability. Nevertheless, correcting 2D measurements by the 3D model of the bone might give better accuracy of glenoid version assessment [12]. Additionally, recent data have shown that 3D reconstruction could provide reliable assessment of component position after TSA [7], reliable measurement of glenoid version [26] or adequately quantified erosion in type B glenoids [27].
So far, research which quantified glenoid osseous defects in patients with anterior instability has usually used 2D measurement on 2D-CT, 3D-CT, MRI or photographs of the fresh frozen scapulae [28–31]. However, using 2D measurement on 2D-CT or 3D-CT poses certain limitations. According to researchers, modern population display a diversity in glenoid size and shape [32–35]. Moreover, flatness of the glenoid is associated with increased retroversion [36, 37]; thus, 2D images of the articular surface may vary among patients with different levels of shoulder instability. Additionally, setting the scapula in en face plain might be problematic due to the orientation of the glenoid fossa that might be variable and difficult to assess [6, 27]. Even slight discrepancies in plane setting can lead to different linear measurements [38].
These limitations might be solved by the 3D measurement method, but only a few studies have used it to assess the size of a glenoid defect so far [39–41] and only one of these assessed the reliability of the new method [40]. Moreover, in all of these studies reproducibility of the parameters was compared to the 2D measurement method. Thus, the main purpose of the research is to compare the reliability of 2D with 3D-CT measurements commonly used to assess the size of glenoid defect. We have hypothesised that for glenoid bone loss diagnosis 3D measurements are more reliable than 2D measurements. To test this hypothesis, we have computed intra- and inter-observer errors for each method and compared them with each other.
Material and methods
The analysed material consisted of CT images of the shoulder of 100 patients (39 females and 61 males), ranging in age between 20 and 85 (mean age 43.4, SD 16.4). The study was approved by the ethical committee of the University of Medical Sciences (number of permission: 437/13). In order to ensure the anonymity of the patients, all personal information was removed from CT imaging and each patient received their individual number.
From 2009 to 2011, a retrospective study was conducted. Computed-tomography scans of the shoulders of 100 patients were randomly selected and included in the study by an experienced orthopaedic surgeon who was not involved in further analysis of the reliability of the two compared methods. Subsequently, the diagnosis of each patient, consisting of three stages, was carried out by the same experienced researcher.
The first was a physical examination in order to identify deformities, rotator cuff atrophy, scapular dyskinesia or fractures. Next, a basic radiographic view was obtained. However, since radiographs may fail to detect and quantify glenoid bone loss, a 3D CT scan was used [5]. According to these three stages, each patient was diagnosed as having or not having traumatic shoulder instability. Therefore 63 out of 100 examined shoulders displayed signs of traumatic shoulder instability. The remaining shoulders (37 out of 100) came from patients without glenoid bone loss but with traumatic fractures of the upper thorax (e.g. clavicle, first rib, humeral head).
This was a retrospective case–control because all CT images came from the database of the patients with shoulder CT performed in the radiology department of our university hospital. All CT images were taken with the use of 32-slice CT (Siemens Somatom Sensation) with the same standard chest protocol by the same technician (slice thickness: 0.6 mm; kV: 120, mAS/ref: 114/150, TIL 1.0, cSL: 0.6). The CT images.
2D measurement method
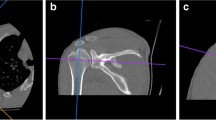
All the collected CT images were analysed using OsiriX MD v. 6.5 64-bit software (Pixmeo). Before measuring, each glenoid was set in transverse, sagittal and coronal plane, as shown in Fig. 1. Then, various parameters of glenoid fossa were measured using the following methods: Gerber and Nyffeler [39], Griffith et al. [29], Sugaya et al. [41], Barchilon et al. [28], Magarelli et al. [42] (for description and visualisation of measurements see Table 1 and Fig. 2). All of the measurements were independently performed by two independent observers. One observer was an orthopaedic surgeon experienced in shoulder surgery, whereas the other had no such experience and was a medical student in training. In order to demonstrate reproducibility of the measurements, the observers repeated the same measurement parameters for 30 randomly selected glenoids after one week. The observers were unaware of each other’s results.
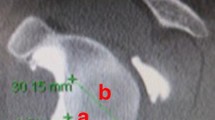
a three-dimensional reconstruction of the scapula without glenoid bone loss, b three-dimensional reconstruction of the scapula with glenoid bone loss. Description of the following measurements: A – area of the glenoid, B – superior-inferior height, C – anterior-posterior width, D – perpendicular line from the anterior edge to the centre of the circle, E – the radius of the glenoid circle, F – eroded area, G – erosion edge
3D measurement method
All the scapulae were reconstructed in 3D using 3D Slicer software (version 4.4). 3D bone reconstruction was conducted by one observer. To avoid any errors associated with 3D reconstruction, 30 randomly selected CT images were again reconstructed with a week’s interval. Therefore, the average distance between two reconstructed scapulae was computed using GOM Inspect software (version V8). In each pair, one scapula was chosen to be a reference model, thus was transformed to CAD file. Then, the other scapula from each pair was transformed to a Mesh file and compared to the CAD file. None of the average distances within pairs was greater than 0.15 mm. Thus, 3D bone reconstruction of CT images was reliable.
Next, the same measurements as in 2D reconstruction were performed with the use of GOM Inspect software (V8). This software enables rotation of the object during the measuring process and acquisition of 3D measurements in order to achieve better localisation of points in the glenoid cavity. All 3D bone reconstructions were assessed by the same two independent observers. After one week both raters repeated the measurements for the same 30 randomly selected scapulae as in 2D measurement.
Statistical analysis
Statistical analyses were performed using SPSS software (version: 22.0.0.1) and Microsoft Office Excel. In order to show which two measurement methods (2D and 3D) were characterised by better reliability, inter-observer error was calculated for 100 glenoid by means of Intra-class Correlation Coefficient (ICC). Intra-observer reliability was assessed using ICC for the 30 glenoids selected for repeat examination.
Values of ICC can range from 0 to 1, where 1 indicates perfect reliability. The strength of the agreement was classified according to Walter et al. [43]: very good (ICC > 0.81), good (0.61 < ICC < 0.80), moderate (0.41 < ICC < 0.60) and poor (ICC < 0.40). In order to compare ICC-values between 2D and 3D measurement methods Fisher’s z-values were calculated. The dependent t-test was also carried out to analyse whether glenoid cavity measurements carried out by two observers significantly differed between 2D and 3D methods. The level of significance for ICC, Fisher’s test and dependent t-test was accepted as p < 0.05.
Results
Inter-observer error for the 2D and 3D measurement methods
Table 2 shows the values of inter-observer reliability for the 2D and 3D measurement methods. The coefficient value of ICC for the 2D measurement method was significant (p < 0.05) for all glenoid parameters except eroded area and erosion edge, whereas all ICC values obtained for the 3D measurement method were significant (p < 0.05). ICC values for repeated measurements between two observers were very good (circle area, AP width, SI height), good (R, d) and moderate (eroded area, erosion edge) for the 2D measurement method, whereas all obtained inter-observer reliability values for the 3D measurement method were very good and significant (p < 0.05). Fisher’s test showed that the 3D measurement method is significantly (p < 0.05) more reliable for eroded area, erosion edge, R and d, but less reliable for AP width.
Intra-observer error for the 2D and 3D measurement methods
Table 3 shows the results for ICC and Fisher’s test for an experienced observer using the 2D and 3D measurement methods. All ICC values obtained for both methods are significant (p < 0.05). Intra-observer ICC values for the 2D method were near perfect for the following measurements: circle area, eroded area, erosion edge and d. For parameters such as AP width, SI height and R, ICC values were good. All coefficients for an experienced observer using the 3D method were near perfect, attaining acceptable levels. Fisher’s test showed that almost all glenoid parameters were more reliable when measured using the 3D rather than the 2D method.
Table 4 shows the results for ICC and Fisher’s test comparing the accuracy of the 2D and 3D measurement methods for an inexperienced rater. ICC values for repeated measurements by the second observer using the 2D method were very good for circle area, eroded area, AP width and SI height and good for erosion edge, R and d, whereas all intra-observer ICC values for the 3D method were very good and significant (p < 0.05). Fisher’s test showed that, for an inexperienced rater, almost all 3D-CT measurements showed significantly (p < 0.05) higher intra-observer reliability than 2D-CT measurements.
Differences in glenoid measurements between 2D and 3D methods
Table 5 shows the average values for glenoid measurements and results of the dependent t-test for 2D and 3D methods. The dependent t-test showed that for both raters (experienced and inexperienced) almost all glenoid parameters significantly differed (p < 0.05) between 2D and 3D measurement methods. Only two glenoid parameters (R and d) showed no significant differences between the two analysed methods.
Discussion
3D bone reconstruction from CT images is becoming widely used in pre- and post-operative assessment [24–27, 40, 44]. However, of all research focussing on assessing glenoid bone loss (see a scoping review in [12]), only one study analysed 3D-CT in 3D orientation [45], in which the object could be freely rotated during the measuring process. Thus, rotation of the glenoid cavity may enable more accurate localisation of the borders of the articular surface.
Given the above mentioned advantages of 3D measurements, the main purpose of this study was to investigate inter- and intra-observer reliability of two different measurement methods (2D-CT and 3D-CT) used for glenoid bone loss evaluation. However, it should be taken into account that in this research 3D-CT was analysed in 3D orientation. Due to our focus on methods of assessing potential bone loss, 63 of 100 examined glenoids displayed signs of shoulder instability. ICC values for inter-observer reliability for the 3D measurement method were superior to those obtained for the 2D measurement method. For the 3D measurement method all ICC values were near perfect whereas in the 2D measurement method only three glenoid parameters (circle area, AP width and SI height) reached an acceptable level. All the remaining measurements in 2D-CT were good (R, d) or moderate (eroded area, erosion edge). Slightly better results were obtained for intra-observer reliability in the 2D measurement method. For the experienced and the inexperienced rater four glenoid parameters were highly reliable (experienced observer: circle area, eroded area, erosion edge, d; inexperienced observer: circle area, eroded area, AP width, SI height) and three were good (experienced observer: AP width, SI height, R and inexperienced observer: erosion edge, R, d). In turn, much better ICC values for intra-observer reliability were obtained for the 3D measurement method, where all ICC values were very good for the experienced and the inexperienced rater. The results of Fisher’s test showed that ICC values for 3D-CT were higher than for 2D-CT but not all differences were significant.
The dependent t-test showed that, for both observers, almost all glenoid parameters (except measurements R and d) differed significantly between 2D and 3D measurement methods. Other studies [22, 24, 46] showed that improvements in computer performance enable the acquisition of very detailed 3D models. Thus, differences in glenoid cavity parameters do not result from inaccurate 3D reconstruction, since R and d measurements showed no significant differences between the two methods (2D and 3D).
Sugaya et al. [41] quantified glenoid osseous defects in patients with anterior instability based on two glenoid parameters (circle area and eroded area) measured in the sagittal view of the 2D-CT and 3D-CT glenoid reconstructions. The same glenoid parameters were used in Magarelli et al.'s [42] research. They analysed inter- and intra-observer reliability of the method used for anterior gleno-humeral instability assessment based only on 2D-CT images. Magarelli et al. [42] showed that measurement of glenoid bone defect in anterior shoulder instability could be assessed based on 2D-CT images, with a very good intra-observer and inter-observer reliability. In turn, Sugaya and co-workers [41] concluded that 2D-CT is not adequate for quantification and surgical planning because it did not show details of the glenoid rim. This conclusion was not confirmed by inter- and intra-observer reliability of the created method; however, our study has validated their statement.
Huijsmans with co-workers [30] tested only the Sugaya et al. [41] method, and suggested that glenoid defect could be assessed using 3D-CT as well as 2D-MRI. In turn, our inter- and intra-observer reliability of two measurements (circle area and eroded area) show that for glenoid defect assessment the 3D measurement method is much more reliable than the 2D one. These discrepancies might be associated with the limitations of the research by Huijsmans et al. [30]. They used the 2D measurement instead of the 3D measurement on the 3D glenoid reconstruction. Flatness of the glenoid varies among patients with different levels of shoulder instability [36, 37]. Moreover, different orientation of the glenoid fossa changes the object’s shape and leads to discrepancies in linear measurement [38]. Thus, 2D measurement may vary from 3D measurement on the 3D reconstruction.
Another method for quantitative assessment of the missing glenoid area has been created by Griffith et al. [29] who used glenoid measurements (AP width, SI height and erosion edge) on 2D CT images. They concluded that the best parameter for glenoid defect assessment was the width of the glenoid and the width to length ratio. The authors did not compute the reliability of the method; however, our results show that measuring the width and length on 2D-CT is not reliable because it is difficult to determine the exact top of the glenoid. Similar parameters (AP width and erosion edge) were analysed by Gerber and Nyffeler [39], but the main aim of this study was to create a classification of glenohumeral joint instability and not to analyse the reliability of the created method.
In turn, the method created by Barchilon et al. [28], used for glenoid bone loss diagnosis parameters (R, d, erosion edge), measured on 2D-CT and 3D-CT. The best parameter to calculate the amount of missing bone was depth to radius ratio obtained from the 3D reconstruction combined with femoral head gauge. The authors did not compute and compare the reliability of the measurements, nevertheless, our findings confirmed that the 3D measurements better reflect the true anatomy of the glenoid.
The described 3D measurement method has two weaknesses. Measuring the 3D glenoid reconstruction is more time consuming than quantifying a glenoid defect using 2D-CT because the CT reconstruction needs to be cleaned from other bones and structures. Moreover, the number of the details of the 3D bone reconstructions depends on the slice thickness of the CT images [46]. According to Ford and Decker [46] slice thickness should not be greater than 1.25 mm in order to obtain representative anatomy. Nevertheless, measuring 2D-CT is associated with the orientation of the glenoid fossa in three planes (transverse, sagittal, coronal), which may be difficult to assess—especially in patients with increased retroversion [6, 27]. These limitations of 2D-CT cause different linear measurement [38].
Our study shows that methods based on 3D measurements used for glenoid bone loss diagnosis are more reliable between and within observers than 2D ones. Based on our findings we recommend using 3D scapula reconstruction for quantifying a glenoid defect because 2D-CT does not show detailed information about the glenoid rim. This method provides reliable and accurate glenoid assessment by both an experienced and inexperienced surgeon, which may be helpful in the reconstruction of the native glenoid plane and improve the planning and the choice of the operative technique.
References
Burkhart SS, De Beer JF (2000) Traumatic glenohumeral bone defects and their relationship to failure of arthroscopic Bankart repairs: significance of the inverted-pear glenoid and the humeral engaging Hill-Sachs lesion. Arthroscopy 16:677–694
Itoi E, Lee SB, Berglund LJ et al (2000) The effect of a glenoid defect on anteroinferior stability of the shoulder after Bankart repair: a cadaveric study. J Bone Joint Surg Am 82:35–46. doi:10.1002/sim.5330
Boileau P, Villalba M, Héry J-Y et al (2006) Risk factors for recurrence of shoulder instability after arthroscopic Bankart repair. J Bone Joint Surg 88:1755–1763. doi:10.2106/JBJS.E.00817
Inui H, Sugamoto K, Miyamoto T et al (2002) Glenoid shape in atraumatic posterior instability of the shoulder. Clin Orthop Relat Res 403:87–92
Piasecki DP, Verma NN, Romeo AA et al (2009) Glenoid bone deficiency in recurrent anterior shoulder instability: diagnosis and management. J Am Acad Orthop Surg 17:482–493
Churchill RS, Brems JJ, Kotschi H (2001) Glenoid size, inclination, and version: an anatomic study. J Shoulder Elb Surg 10:327–332. doi:10.1067/mse.2001.115269
Iannotti JP, Ricchetti ET, Rodriguez EJ, Bryan JA (2013) Development and validation of a new method of 3-dimensional assessment of glenoid and humeral component position after total shoulder arthroplasty. J Shoulder Elb Surg 22:1413–1422. doi:10.1016/j.jse.2013.01.005
Weishaupt D, Zanetti M, Nyffeler RW et al (2000) Posterior glenoid rim deficiency in recurrent (atraumatic) posterior shoulder instability. Skelet Radiol 29:204–210
Nyffeler RW, Jost B, Pfirrmann CWA, Gerber C (2003) Measurement of glenoid version: conventional radiographs versus computed tomography scans. J Shoulder Elb Surg 12:493–496. doi:10.1016/S1058274603001812
Rozing PM, Obermann WR (1999) Osteometry of the glenohumeral joint. J Shoulder Elb Surg 8:438–442
Sullivan DO, Bokor DJ, Hazan J (1999) Variability computed of measurement of glenoid tomography scan version on. J Shoulder Elb Surg 8:595–598. doi:10.1016/S1058-2746(99)90096-4
Saliken DJ, Bornes TD, Bouliane MJ et al (2015) Imaging methods for quantifying glenoid and Hill-Sachs bone loss in traumatic instability of the shoulder: a scoping review. BMC Musculoskelet Disord 18:164. doi:10.1186/s12891-015-0607-1
Bishop JY, Jones GL, Rerko MA, Donaldson C (2013) 3-D CT is the most reliable imaging modality when quantifying glenoid bone loss shoulder. Clin Orthop Relat Res 471:1251–1256. doi:10.1007/s11999-012-2607-x
Engebretsen L, Craig E (1993) Radiologic features of shoulder instability. Clin Orthop Relat Res 291:29–44
Rerko MA, Pan X, Donaldson C et al (2013) Comparison of various imaging techniques to quantify glenoid bone loss in shoulder instability. J Shoulder Elb Surg 22:528–534. doi:10.1016/j.jse.2012.05.034
Paladini P, Singla R, Merolla G, Porcellini G (2016) Latarjet procedure: is the coracoid enough to restore the glenoid surface? Int Orthop. doi:10.1007/s00264-015-3093-z
Gregory T, Hansen U, Khanna M et al (2014) A CT scan protocol for the detection of radiographic loosening of the glenoid component after total shoulder arthroplasty. Acta Orthop 85:91–96. doi:10.3109/17453674.2013.869653
Lubiatowski P, Olczak I, Lisiewicz E et al (2013) Clinical and functional evaluation of patients after total elbow arthroplasty. Polish Orthop Traumatol 78:53–58
Andrin J, Macaron C, Pottecher P et al (2015) Determination of a new computed tomography method for measuring the glenoid version and comparing with a reference method. Radio-anatomical and retrospective study. Int Orthop 40:525–529. doi:10.1007/s00264-015-2867-7
Otto RJ, Virani NA, Levy JC et al (2013) Scapular fractures after reverse shoulder arthroplasty: evaluation of risk factors and the reliability of a proposed classification. J Shoulder Elb Surg 22:1514–1521. doi:10.1016/j.jse.2013.02.007
Castricini R, Gasparini G, Di Luggo F et al (2013) Health-related quality of life and functionality after reverse shoulder arthroplasty. J Shoulder Elb Surg 22:1639–1649. doi:10.1016/j.jse.2013.01.020
Kwon YW, Powell KA, Yum JK et al (2005) Use of three-dimensional computed tomography for the analysis of the glenoid anatomy. J Shoulder Elb Surg 14:85–90. doi:10.1016/j.jse.2004.04.011
Scalise JJ, Codsi MJ, Bryan J, Iannotti JP (2008) The three-dimensional glenoid vault model can estimate normal glenoid version in osteoarthritis. J Shoulder Elb Surg 17:487–491. doi:10.1016/j.jse.2007.09.006
Hirschmann MT, Konala P, Amsler F et al (2011) The position and orientation of total knee replacement components: a comparison of conventional radiographs, transverse 2D-CT slices and 3D-CT reconstruction. J Bone Joint Surg (Br) 93:629–633. doi:10.1302/0301-620X.93B5.25893
Budge MD, Lewis GS, Schaefer E et al (2011) Comparison of standard two-dimensional and three-dimensional corrected glenoid version measurements. J Shoulder Elb Surg 20:577–583. doi:10.1016/j.jse.2010.11.003
Hoenecke HR, Hermida JC, Flores-Hernandez C, D’Lima DD (2010) Accuracy of CT-based measurements of glenoid version for total shoulder arthroplasty. J Shoulder Elb Surg 19:166–171. doi:10.1016/j.jse.2009.08.009
Beuckelaers E, Jacxsens M, Van Tongel A, De Wilde LF (2014) Three-dimensional computed tomography scan evaluation of the pattern of erosion in type B glenoids. J Shoulder Elb Surg 23:109–116. doi:10.1016/j.jse.2013.04.009
Barchilon VS, Kotz E, Barchilon B et al (2008) A simple method for quantitative evaluation of the missing area of the anterior glenoid in anterior instability of the glenohumeral joint. Skelet Radiol 37:731–736. doi:10.1007/s00256-008-0506-8
Griffith JF, Antonio GE, Tong CWC, Ming CK (2003) Anterior shoulder dislocation: quantification of glenoid bone loss with CT. Am J Roentgenol 180:1423–1430. doi:10.2214/ajr.180.5.1801423
Huijsmans PE, Haen PS, Kidd M et al (2007) Quantification of a glenoid defect with three-dimensional computed tomography and magnetic resonance imaging: a cadaveric study. J Shoulder Elb Surg 16:803–809. doi:10.1016/j.jse.2007.02.115
De Filippo M, Saba L, Negrini G et al (2015) Inter-observer agreement of CT measurement of the glenoid bone surface by the CT Pico method: comparison with laser in a cadaveric model. Skelet Radiol 44:1491–1497. doi:10.1007/s00256-015-2199-0
Prescher A, Klümpen T (1995) Does the area of the glenoid cavity of the scapula show sexual dimorphism? J Anat 186:223–226
Dabbs GR, Moore-Jansen PH (2010) A method for estimating sex using metric analysis of the scapula. J Forensic Sci 55:149–152. doi:10.1111/j.1556-4029.2009.01232.x
Papaioannou V, Kranioti EF, Joveneaux P et al (2012) Sexual dimorphism of the scapula and the clavicle in a contemporary Greek population: applications in forensic identification. Forensic Sci Int 217:231.e1–231.e7. doi:10.1016/j.forsciint.2011.11.010
Bockmann B, Soschynski S, Lechler P et al (2016) Age-dependent variation of glenohumeral anatomy: a radiological study. Int Orthop 40:87–93. doi:10.1007/s00264-015-2863-y
Couteau B, Mansat P, Darmana R et al (2000) Morphological and mechanical analysis of the glenoid by 3D geometric reconstruction using computed tomography. Clin Biomech (Bristol, Avon) 15(Suppl 1):S8–S12
Graichen H, Koydl P, Zichner L (1999) Effectiveness of glenoid osteotomy in atraumatic posterior instability of the shoulder associated with excessive retroversion and flatness of the glenoid. Int Orthop 23:95–99. doi:10.1007/s002640050316
Zeldith ML, Świderski DL, Sheets HD, Fink WL (2004) Geometric morphometrics for biologists: a primer. Elsevier, New York
Gerber C, Nyffeler RW (2002) Classification of glenohumeral joint instability. Clin Orthop Relat Res 400:65–76
Moineau G, Levigne C, Boileau P et al (2012) Three-dimensional measurement method of arthritic glenoid cavity morphology: feasibility and reproducibility. Orthop Traumatol Surg Res 98:S139–S145. doi:10.1016/j.otsr.2012.06.007
Sugaya H, Moriishi J, Dohi M et al (2003) Glenoid rim morphology in recurrent anterior glenohumeral instability. J Bone Joint Surg Am 85:878–884
Magarelli N, Milano G, Sergio P et al (2009) Intra-observer and interobserver reliability of the “Pico” computed tomography method for quantification of glenoid bone defect in anterior shoulder instability. Skelet Radiol 38:1071–1075. doi:10.1007/s00256-009-0719-5
Walter SD, Eliasziw M, Donner A (1998) Sample size and optimal designs for reliability studies. Stat Med 17:101–110
Parr WCH, Chamoli U, Jones A et al (2013) Finite element micro-modelling of a human ankle bone reveals the importance of the trabecular network to mechanical performance: new methods for the generation and comparison of 3D models. J Biomech 46:200–205. doi:10.1016/j.jbiomech.2012.11.011
Diederichs G, Seim H, Meyer H et al (2008) CT-based patient-specific modeling of glenoid rim defects: a feasibility study. Am J Roentgenol 191:1406–1411. doi:10.2214/AJR.08.1091
Ford JM, Decker SJ (2015) Computed tomography slice thickness and its effects on three-dimensional reconstruction of anatomical structures. J Forensic Radiol Imaging. doi:10.1016/j.jofri.2015.10.004
Acknowledgments
We thank anonymous referees for careful reading of the manuscript and useful comments. Anna Maria Kubicka was supported by the European Social Fund (grant numbers PO KL 8.2.2/30-310-13/14).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Funding
This study was funded by European Social Fund (PO KL 8.2.2/30-310-13/14).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kubicka, A.M., Stefaniak, J., Lubiatowski, P. et al. Reliability of measurements performed on two dimensional and three dimensional computed tomography in glenoid assessment for instability. International Orthopaedics (SICOT) 40, 2581–2588 (2016). https://doi.org/10.1007/s00264-016-3253-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00264-016-3253-9