Abstract
Purpose
Compartmental modelling of 3′-deoxy-3′-[18F]-fluorothymidine (18F-FLT) PET-derived kinetics provides a method for noninvasive assessment of the proliferation rate of gliomas. Such analyses, however, require an input function generally derived by serial blood sampling and counting. In the current study, 18F-FLT kinetic parameters obtained from image-derived input functions were compared with those from input functions derived from arterialized blood samples.
Methods
Based on the analysis of 11 patients with glioma (WHO grade II–IV) a procedure for the automated extraction of an input function from 18F-FLT brain PET data was derived. The time–activity curve of the volume of interest with the maximum difference in 18F-FLT uptake during the first 5 min after injection and the period from 60 to 90 min was corrected for partial-volume effects and in vivo metabolism of 18F-FLT. For each patient a two-compartment kinetic model was applied to the tumour tissue using the image-derived input function. The resulting kinetic rate constants K1 (transport across the blood–brain barrier) and Ki (metabolic rate constant or net influx constant) were compared with those obtained from the same data using the input function derived from blood samples. Additionally, the metabolic rate constant was correlated with the frequency of tumour cells stained with Ki-67, a widely used immunohistochemical marker of cell proliferation.
Results
The rate constants from kinetic modelling were comparable when the blood sample-derived input functions were replaced by the image-derived functions (K1,img and K1,sample, r = 0.95, p < 10−5; Ki,img and Ki,sample, r = 0.86, p < 0.001). A paired t-test showed no significant differences in the parameters derived with the two methods (K1,img and K1,sample, p = 0.20; Ki,img and Ki,sample, p = 0.92). Furthermore, a significant correlation between Ki,img and the percentage of Ki-67-positive cells was observed (r = 0.73, p = 0.01).
Conclusion
Kinetic modelling of 18F-FLT brain PET data using image-derived input functions extracted from human brain PET data with the practical procedure described here provides information about the proliferative activity of brain tumours which might have clinical relevance especially for monitoring of therapy response in future clinical trials.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Positron emission tomography (PET) is a powerful method for the noninvasive measurement of metabolic processes in vivo. Such measurements are performed by kinetic analysis, which requires, in addition to the tissue time–activity curve (TAC), the arterial input function (IF; the amount of tracer in blood plasma as a function of time). While the TAC is easily obtained from the PET data by dividing the scan time into several time frames, the arterial IF is commonly determined from blood samples taken during the PET scan. The direct determination of the IF via blood samples is laborious, introduces a potential source of errors, and quantification of PET data acquired without simultaneous blood sampling is not possible. Noninvasive methods have been developed for the extraction of IFs from PET data, for example by placing a region of interest on vascular structures within the field of view (FOV) such as the left ventricle of the heart or the aorta [1–8]. It has been shown that the image-derived IF act as a good substitute for the arterial IF and kinetic constants can be reproduced. However, in human brain PET images these large vascular structures are outside the FOV and smaller vessels have to be taken into account. An alternative approach consists of the estimation of an IF from a population-based arterial IF [9, 10]. These methods are minimally invasive since they require at least one blood sample for scaling. Recently, another minimally invasive method consisting of a cluster analysis of TACs and requiring three venous blood samples for the determination of an IF for [18F]-2-deoxy-2-fluoro-d-glucose (18F-FDG) human brain PET was presented [11]. Factor analysis of PET-derived time–activity data has also been used for extraction of the IF and quantification of pertinent kinetic parameters [12].
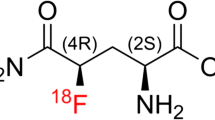
Thymidine is the only nucleoside that is incorporated exclusively into DNA but not into RNA and is therefore a good candidate for measuring cellular proliferation. Its phosphorylation occurs by two pathways: the salvage pathway via thymidine kinase (TK1) and the de novo pathway via thymidylate synthase (TS) [13]. For a number of tumour cell lines it has been shown that TK1 activity exceeds TS activity by a factor of at least 16 [14]. 3′-Deoxy-3′-[18F]-fluorothymidine (18F-FLT), an analogue of thymidine, is a selective substrate for TK1, that is for the salvage pathway. TK1 catalyses the phosphorylation of 18F-FLT to 18F-FLT-monophosphate, which is further phosphorylated to 18F-FLT-diphosphate and 18F-FLT-triphosphate. TK1 activity is proportional to the rates of DNA replication and cell proliferation in tumour [15–18]. Therefore, cellular proliferation can be assessed by 18F-FLT although 18F-FLT, in contrast to thymidine, is effectively not incorporated into DNA [19, 20]. The kinetics of 18F-FLT are qualitatively similar to those of 18F-FDG, with a two-tissue compartment model applicable to both tracers. Like phosphorylated 18F-FDG, 18F-FLT is trapped within the cell. i.e. the rate constant for dephosphorylation, k4, is small compared to the other rate constants, but not negligible in the model [21, 22].
We present a simple and practical method for extracting IFs from 18F-FLT PET data in the human brain. The rate constants resulting from kinetic modelling of 18F-FLT PET data from patients with high-grade glioma using the image-derived IFs are compared with those derived using IFs from arterialized blood samples. Our results are further validated by correlation of the metabolic rate constant with the percentage of cells positive in Ki-67 immunostaining of tumour tissue.
Materials and methods
PET scan, patients, samples
We used the same dataset as used in our previous study in order to investigate the potential of the image-derived IF to reproduce the results obtained with IFs from blood samples (cf. [20]). Two patients from the previous study were excluded from this analysis because they lacked Ki-67 staining.
In brief, 11 patients with newly diagnosed high-grade glioma were investigated with 18F-FLT PET. PET imaging was performed on an ECAT EXACT scanner (CTI, Siemens; one patient) or an ECAT EXACT HR scanner (CTI, Siemens; ten patients). After a 10-min transmission scan with a 68Ge/68Ga source, emission data were acquired for 90 min. The tracer was injected at the beginning of the emission scan. Arterialized blood samples were taken from the heated dorsal hand vein [23, 24]. Oxygen saturation was not measured in patients 1, 2, 3, and 10. In the other patients it was above 80% (minimum 82%, maximum 95%, mean 89%). The PET scan time was divided into time frames of 6 × 10 s, 3 × 20 s, 2 × 30 s, 2 × 60 s, 2 × 150 s, and 16 × 300 s. For the kinetic analysis of the data, a TAC was taken from an 8-mm diameter circular region of interest placed over the tumour region with the maximum tracer accumulation during the 90-min scan time.
Histology
PET-guided tumour tissue probes at the location of maximum tracer accumulation were taken by stereotactic biopsy (seven patients) or by resection (four patients). Staining was performed with MIB-1 (Ki-67) antibody using the avidin-biotin-peroxidase complex (ABC) method and the DCS detection kit with DAB and H2O2 (DCS, Hamburg, Germany). All cells with nuclear staining of any intensity were regarded as positive. Proliferative activity was defined as the percentage of nuclei stained with MIB-1 per total number of nuclei in the biopsy. The percentage of Ki-67-positive cells was determined in the four microscopic high-power fields (0.16 mm2) with the maximum fraction of labelled cells.
The metabolic rate constants derived from kinetic analysis of 18F-FLT PET were compared with proliferation rates determined via Ki-67 staining of tumour tissue. The IFs for the kinetic analysis were obtained from blood samples taken during the PET scan. For a detailed description of the methods see Ullrich et al. [20].
Extraction of the IF from PET data
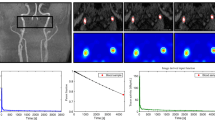
Compared to a usual TAC an IF resulting from a bolus injection has special characteristics, namely a distinct peak in the first minute after injection (this is when the bolus is transported through the vascular system) and a low slowly decreasing activity at late scan times. Based on these characteristic features, an automated algorithm was developed for extracting the 18F-FLT IF from the dynamic PET: the location of a suitable blood TAC was defined by the volume of interest (VOI, 6.6 × 6.6 × 9.3 mm3) with the maximum difference between the mean activity during the first 5 min after injection and the mean activity from 60 to 90 min. Since the volume of the VOI was larger than the spatial resolution of the PET scanners used, the parameters for partial volume correction were independent of the scanner type. As shown in Fig. 1a, the ‘raw’ IFs thus obtained had the characteristic appearance of a typical IF.
a Input functions: example IF from blood samples (sample IF), the corresponding raw image-derived IF (raw image derived IF) and the partial-volume effect- and metabolite-corrected IF (corrected image derived IF). b Correlation between sample-derived and corrected image-derived IF. Data points show the time integrals (AUC) and standard deviations of the image-derived and the sample-derived IFs at 0.3, 0.5, 1, 2, 5, 10, 25, 50, 75 and 90 min after injection normalized by the time integral of the sample-derived IF over the entire scanning time of 90 min. The error bars for the sample-derived AUCs show the variation of the sample-derived IFs; for example, at 25 min the mean AUC was 0.56 (±0.03)
Corrections of the raw IF
Simplified partial-volume correction
In order to correct the raw IF for partial-volume effects a simplified correction was applied. The VOI, from which the IF was extracted, was only partially covered by a blood vessel and partially by surrounding tissue. Furthermore, in the PET data the difference between the vessel and surrounding tissue decreased over time, i.e. the amount of activity in the blood vessel decreased due to the distribution of the tracer in the compartments while the surrounding activity increased to amounts that could not be explained by vascular structures. In order to take into account this observation we assumed that there was transport from vessel to surrounding tissue by passive diffusion. If av is the fractional volume of the vessel and k is the constant for the transport to the surrounding tissue, the background concentration Cbg is given by Cbg(t) = (1 − exp(−kt)) Creal(t) and the measured concentration is Cm(t) = av Creal(t) + (1−av) Cbg(t). The real intravascular concentration Creal can then be obtained from the measured concentration Cm by:
In this case the partial-volume correction is 1/av at the beginning of the scan time while it decreases to 1 at late times when the activity in the vessel is similar to the background activity of the surrounding tissue.
Equation 1 was applied to the data using a transport rate k of 0.01, 0.1 and 1.0 min−1 and a partial volume of the vessel av of 1 (this is equivalent to no partial-volume effect), 0.8 and 0.6 in order to test the sensitivity of the kinetic parameters as response to the partial-volume correction.
Glucuronidation
When 18F-FLT is circulating through the organism it is glucuronidated in the liver [25]. This radioactive metabolite is not transported from plasma into brain tissue. Shields et al. reported a contribution of 18F-FLT to the total plasma activity of 82% at 30 min and 74% at 60 min after injection [26]. A similar fraction has been reported by Visvikis et al. (69% at 60 min after injection) [25]. Assuming a monoexponential decrease in nonmetabolized 18F-FLT in plasma, this corresponds to an average time scale of Tgluc <170 min for this process. After the partial-volume correction described above the fraction of activity attributable to 18F-FLT was obtained by multiplying by the factor exp(−t/Tgluc) where t is the time after injection (in minutes).
Timing
In the ideal case the bolus of the tracer is injected simultaneously with the start of the PET scan. The accuracy of this procedure depends on several factors such as the injector, the patient, correct synchronization of clocks, etc. In order to correct for potential timing differences the blood curve obtained from the PET data was extrapolated to determine the offset of the true injection time with respect to the start time of the PET scan. Note that there was no time offset between the image-derived blood curve and the TACs because they originated from the same data. But the injection time point is important for the application of the corrections for partial-volume effect and for blood levels of the glucuronidation metabolite. The time in Eq. 1 is then relative to the injection time, i.e. t = tPET − tinj (tPET is the time relative to the start of the PET scan, and tinj is the time of injection relative to the start of the PET scan). Assuming a linear increase in the IF immediately after injection, tinj is given by the intercept of the line fitted to the first data points of the image-derived raw IF with the time axis.
Kinetic modelling
The kinetics of 18F-FLT in tumour tissue are best described by a two-compartment model corresponding to free and phosphorylated tracer, respectively, with the blood-borne activity accounted for by the IF [21]. The model includes five free parameters: the transport parameters K1 (transport from blood across the blood–brain barrier into the tissue), k2 (transport from tissue to blood), k3 (phosphorylation by Tk1), k4 (dephosphorylation), and vB (the fraction of blood volume in the tissue). In analogy to 18F-FLT, the salvage pathway of thymidine is characterized by the rate constants KTh1 … kTh4. Since thymidine—in contrast to 18F-FLT—is incorporated into DNA, there is an additional rate constant for thymidine describing its incorporation into DNA, kDNA. Proliferation is proportional to the rate of incorporation of thymidine into DNA and can be expressed as:
where ThB is the thymidine concentration in blood plasma.
In tumour tissue the dephosphorylation rate is small compared to the rate of incorporation of thymidine into DNA , kTh4<<kDNA. In this case the term in parentheses in the denominator of Eq. 2 reduces to 1 and the expression for the proliferation rate becomes independent of kDNA. Thus, the proliferation rate constant can be expressed in terms of the rate constants of 18F-FLT, although 18F-FLT in contrast to thymidine is not incorporated into DNA. Proliferation is then proportional to Ki = K1 × k3/(k2 + k3) [20]. The parameters were calculated using the commercial software PMOD (PMOD Technologies, version 2.85).
Results
Location of IF in PET images
In all cases the automatic procedure for finding the region suitable for extraction of a blood curve provided raw IFs, which showed the characteristic patterns of an IF (Fig. 1a). Visual inspection of the PET images and coregistered Gd-enhanced T1-weighted MR images revealed that the regions were localized within venous blood vessels. In 2 of the 11 subjects the procedure selected the confluens sinuum while in the remaining 9 subjects the sinus cavernosus was selected. Although the carotid artery could also be identified in the PET image with the help of the coregistered MR image (Fig. 2), the venous blood pools better fulfilled the criteria of an “ideal” IF (see Discussion).
Partial-volume correction
In order to determine the best set of parameters for a simplified partial-volume correction, different sets of parameters were applied to Eq. 1. From these corrected IFs the kinetic parameters of the tumour tissue were calculated; Table 1 shows the results. A fractional vessel volume av of 0.8 and a transport constant k of 0.1 min−1 provided the best correlation with the in vitro proliferation marker Ki-67 (r = 0.73, p = 0.01). All tested combinations of parameters displayed in the Table 1 showed significant correlations (p < 0.05).
Correlation of image- and sample-derived IFs
In order to compare the image- and the sample-derived IFs we calculated the time integrals (AUC) of the IFs at different time points and normalized them in relation to the time integral over the entire scan time (90 min) of the sample-derived IF (Fig. 1b). The mean normalized AUC of the image-derived IFs at 90 min was 1.02 (±0.28).
Modelling results
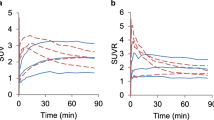
Kinetic modelling provides the kinetic parameters of 18F-FLT (Table 2). The most relevant of them are: the transport of tracer (and of its endogenous analogue thymidine) across the blood–brain barrier represented by the constant K1 and the metabolic rate constant of 18F-FLT (Ki) reflecting cellular proliferation. In the following the parameters obtained with the IF from blood samples are labelled with sample and those using the image-derived IFs are labelled with img. In order to investigate the effect of replacing the IFs measured from blood samples by the image-derived IFs obtained with the method described here on the modelling results we calculated three correlations: (1) between K1,img and K1,sample (r = 0.95, p < 10−5), (2) between Ki,img and Ki,sample (r = 0.86, p < 0.001), and (3) between Ki,img and the percentage of Ki-67-positive cells (r = 0.73, p = 0.01). The correlation between Ki,sample and Ki-67 immunostaining was r = 0.79, p = 0.004 [20]. The values are plotted in Fig. 3. The FLT standardized uptake value (SUV) was not significantly correlated with the percentage of Ki-67-positive cells (r = 0.57, p = 0.07) [20].
A paired t-test showed no significant differences in the parameters derived by the two methods (K1,img and K1,sample, p = 0.20; Ki,img and Ki,sample, p = 0.92).
Discussion
In this study we demonstrated that the rate constants provided by kinetic analysis of 18F-FLT brain PET data in high-grade glioma using an IF derived from blood samples measured during the PET scan can be reproduced if the measured IF is replaced by an IF extracted from the PET data. The respective values of the physiologically important rate constants, K1 and Ki, were comparable for these two different approaches to measurement of the IFs. The calculated metabolic rate constant, Ki,img, was correlated significantly with the percentage of Ki-67-positive cells, a standard immunohistochemical marker of cell proliferation.
The described procedure for the extraction of the IF from PET data involved three steps: (1) extraction of the raw IF, (2) simplified correction for partial-volume effect, and (3) correction for in vivo metabolism of 18F-FLT (glucuronidation). The processes were quite simple and can therefore be easily implemented in the routine clinical setting. Even if the step of partial-volume correction was omitted, the resulting Ki,img was still correlated significantly with the in vitro proliferation marker Ki-67 (r = 0.69, p = 0.02, see Table 1), indicating that partial-volume correction is not a critical issue here.
The coregistered MR images revealed that the raw-IF region was localized within the venous blood pool (confluens sinuum or sinus cavernosus) rather than within the arterial blood pool. Actually the arterial blood pool should provide a more accurate IF. In order to examine the difference we manually extracted the TACs from the carotid artery. Presumably due to the small size of the artery and therefore its greater sensitivity for patient motion, these raw IFs were very noisy and most of them could not be used for kinetic modelling. Thus, we conclude that, although preferred from a theoretical point of view, the intracranial cerebral arteries are not a suitable source in human brain PET data for the extraction of the IF.
Comparison of the peak time in the TACs from the artery with the peak time of the image-derived IFs from the described venous blood pool showed good agreement. The differences were below the temporal resolution of the early dynamic PET data, i.e. <10 s. In order to get the correct peak time for the IF from arterialized blood samples, a manual correction has to be applied. Arterialized blood samples are usually taken from the hand and the arrival time of the bolus in the hand differs from the arrival time in the brain by about 7 s [27]. The manual correction by a mean delay time introduces a potential source of error because this time difference is variable. Comparison of the peak location in image-derived IFs and the sample-derived IFs revealed a time delay that is even higher than the reported one and had a large standard deviation (24±16 s). Nevertheless, taking blood samples directly from the artery is invasive, painful and laborious and therefore the use of arterialized blood samples as surrogate for arterial blood samples has become part of clinical routine.
In comparison to a sample-derived IF an image-derived IF has important advantages: it is noninvasive, and it does not require any additional handling and measurements apart from the PET scan itself. Since all the data are acquired within the same system there is no cross-calibration needed (e.g. between the PET scanner and well counter), eliminating this possible source of error. Also no time offset needs to be determined since the only relevant reference time is that of the PET scan. The time of injection can be extracted from the PET data (see Materials and methods section).
Conclusion
Image-derived IFs represent an accurate, clinically practical, and convenient surrogate for blood sample-derived IFs for kinetic modelling of 18F-FLT data in patients with brain tumours. Whether our findings can be substantiated in a larger patient series has to be demonstrated in future trials.
References
de Geus-Oei LF, Visser EP, Krabbe PF, van Hoorn BA, Koenders EB, Willemsen AT, et al. Comparison of image-derived and arterial input functions for estimating the rate of glucose metabolism in therapy-monitoring 18F-FDG PET studies. J Nucl Med 2006;47:945–9.
Gambhir SS, Schwaiger M, Huang SC, Krivokapich J, Schelbert HR, Nienaber CA, et al. Simple noninvasive quantification method for measuring myocardial glucose utilization in humans employing positron emission tomography and fluorine-18 deoxyglucose. J Nucl Med 1989;30:359–66.
Germano G, Chen BC, Huang SC, Gambhir SS, Hoffman EJ, Phelps ME. Use of the abdominal aorta for arterial input function determination in hepatic and renal PET studies. J Nucl Med 1992;33:613–20.
Green LA, Gambhir SS, Srinivasan A, Banerjee PK, Hoh CK, Cherry SR, et al. Noninvasive methods for quantitating blood time-activity curves from mouse PET images obtained with fluorine-18-fluorodeoxyglucose. J Nucl Med 1998;39:729–34.
Kreissl MC, Wu HM, Stout DB, Ladno W, Schindler TH, Zhang X, et al. Noninvasive measurement of cardiovascular function in mice with high-temporal-resolution small-animal PET. J Nucl Med 2006;47:974–80.
Wahl LM, Asselin MC, Nahmias C. Regions of interest in the venous sinuses as input functions for quantitative PET. J Nucl Med 1999;40:1666–75.
Weinberg IN, Huang SC, Hoffman EJ, Araujo L, Nienaber C, Grover-McKay M, et al. Validation of PET-acquired input functions for cardiac studies. J Nucl Med 1988;29:241–7.
Yee SH, Jerabek PA, Fox PT. Non-invasive quantification of cerebral blood flow for rats by microPET imaging of 15O labelled water: the application of a cardiac time-activity curve for the tracer arterial input function. Nucl Med Commun 2005;26:903–11.
Meyer PT, Circiumaru V, Cardi CA, Thomas DH, Bal H, Acton PD. Simplified quantification of small animal [18F]FDG PET studies using a standard arterial input function. Eur J Nucl Med Mol Imaging 2006;33:948–54.
Takikawa S, Dhawan V, Spetsieris P, Robeson W, Chaly T, Dahl R, et al. Noninvasive quantitative fluorodeoxyglucose PET studies with an estimated input function derived from a population-based arterial blood curve. Radiology 1993;188:131–6.
Guo H, Renaut RA, Chen K. An input function estimation method for FDG-PET human brain studies. Nucl Med Biol 2007;34:483–92.
Schiepers C, Chen W, Dahlbom M, Cloughesy T, Hoh CK, Huang SC. 18F-fluorothymidine kinetics of malignant brain tumors. Eur J Nucl Med Mol Imaging 2007;34:1003–11.
Grierson JR, Schwartz JL, Muzi M, Jordan R, Krohn KA. Metabolism of 3′-deoxy-3′-[F-18]fluorothymidine in proliferating A549 cells: validations for positron emission tomography. Nucl Med Biol 2004;31:829–37.
Weber G, Nagai M, Natsumeda Y, Ichikawa S, Nakamura H, Eble JN, et al. Regulation of de novo and salvage pathways in chemotherapy. Adv Enzyme Regul 1991;31:45–67.
Barthel H, Cleij MC, Collingridge DR, Hutchinson OC, Osman S, He Q, et al. 3′-deoxy-3′-[18F]fluorothymidine as a new marker for monitoring tumor response to antiproliferative therapy in vivo with positron emission tomography. Cancer Res 2003;63:3791–8.
Jacobs AH, Thomas A, Kracht LW, Li H, Dittmar C, Garlip G, et al. 18F-fluoro-L-thymidine and 11C-methylmethionine as markers of increased transport and proliferation in brain tumors. J Nucl Med 2005;46:1948–58.
Shields AF, Grierson JR, Dohmen BM, Machulla HJ, Stayanoff JC, Lawhorn-Crews JM, et al. Imaging proliferation in vivo with [F-18]FLT and positron emission tomography. Nat Med 1998;4:1334-6.
Buck AK, Schirrmeister H, Hetzel M, Von Der Heide M, Halter G, Glatting G, et al. 3-deoxy-3-[(18)F]fluorothymidine-positron emission tomography for noninvasive assessment of proliferation in pulmonary nodules. Cancer Res 2002;62:3331–4.
Krohn KA, Mankoff DA, Muzi M, Link JM, Spence AM. True tracers: comparing FDG with glucose and FLT with thymidine. Nucl Med Biol 2005;32:663–71.
Ullrich R, Backes H, Li H, Kracht L, Miletic H, Kesper K, et al. Glioma proliferation as assessed by 3′-fluoro-3′-deoxy-L-thymidine positron emission tomography in patients with newly diagnosed high-grade glioma. Clin Cancer Res 2008;14:2049–55.
Muzi M, Mankoff DA, Grierson JR, Wells JM, Vesselle H, Krohn KA. Kinetic modeling of 3′-deoxy-3′-fluorothymidine in somatic tumors: mathematical studies. J Nucl Med 2005;46:371–80.
Muzi M, Vesselle H, Grierson JR, Mankoff DA, Schmidt RA, Peterson L, et al. Kinetic analysis of 3′-deoxy-3′-fluorothymidine PET studies: validation studies in patients with lung cancer. J Nucl Med 2005;46:274–82.
McGuire EA, Helderman JH, Tobin JD, Andres R, Berman M. Effects of arterial versus venous sampling on analysis of glucose kinetics in man. J Appl Physiol 1976;41:565–73.
Abumrad NN, Rabin D, Diamond MP, Lacy WW. Use of a heated superficial hand vein as an alternative site for the measurement of amino acid concentrations and for the study of glucose and alanine kinetics in man. Metabolism 1981;30:936–40.
Visvikis D, Francis D, Mulligan R, Costa DC, Croasdale I, Luthra SK, et al. Comparison of methodologies for the in vivo assessment of 18FLT utilisation in colorectal cancer. Eur J Nucl Med Mol Imaging 2004;31:169–78.
Shields AF, Briston DA, Chandupatla S, Douglas KA, Lawhorn-Crews J, Collins JM, et al. A simplified analysis of [18F]3′-deoxy-3′-fluorothymidine metabolism and retention. Eur J Nucl Med Mol Imaging 2005;32:1269–75.
Herholz K, Rudolf J, Heiss WD. FDG transport and phosphorylation in human gliomas measured with dynamic PET. J Neurooncol 1992;12:159–65.
Acknowledgments
This work was supported in part by Deutsche Forschungsgemeinschaft (DFG-Ja98/1-2) and the 6th FW EU grant EMIL (LSHC-CT-2004-503569).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Backes, H., Ullrich, R., Neumaier, B. et al. Noninvasive quantification of 18F-FLT human brain PET for the assessment of tumour proliferation in patients with high-grade glioma. Eur J Nucl Med Mol Imaging 36, 1960–1967 (2009). https://doi.org/10.1007/s00259-009-1244-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00259-009-1244-4