1 Introduction

Stochastic flows appear in a range of applications from fluid dynamics [1, 2] where small scale, turbulent dynamics can be modelled stochastically to shape modelling [3] where the shape of human organs or changes of animal morphology through evolution can be modelled as stochastic flows. We consider Brownian flows of diffeomorphisms in the sense of Kunita [4] given by stochastic differential equations of the form

$$\begin{aligned} d\varphi _t = u_t(\varphi _t) \, dt + \sum _{r=1}^J \sigma _{r,t}(\varphi _t) \circ dW^r,\quad \varphi _0=\varphi . \end{aligned}$$
(1)

Here \(u_t\), \(\sigma _{1,t}\), \(\dots \), \(\sigma _{J,t}\) are time-dependent vector fields on an open domain M in \(\mathbb {R}^d\), which are smooth in both the time and the space variable. Assume now that we are given a diffeomorphic transformation \(\psi \) of M. We can consider this a realization of the flow at some positive time \(T>0\), and we wish to find the most probable way for a diffeomorphism \(\varphi _0=\varphi \) to transform such that \(\varphi _T=\psi \). While being an infinite dimensional problem, we show how the most probable transformations can be identified by using a Riemannian metric on M originating from the noise fields \(\sigma _{r,t}\). We use this to identify evolution equations for most probable trajectories point-wise. This in turn gives equations for most probable flows between \(\varphi \) and \(\psi \).

1.1 Background

Most probable paths for Euclidean Brownian motions were identified by Onsager and Machlup [5, 6] and described by the Onsager–Machlup functional \(\gamma \mapsto \int _0^T H(\gamma (t),\dot{\gamma }(t)) dt=\frac{1}{2} \int _0^T \Vert \dot{\gamma }(t)\Vert ^2 \, dt\) that measures the probability that realizations of a Brownian motion \(W_t\) sojourn around smooth paths in the sense of staying in \(\varepsilon >0\) diameter cylinders. If instead \(\gamma \) is a curve on a finite dimensional Riemannian manifold, the Onsager–Machlup functional changes so that the integral is now over \(H(\gamma (t),\dot{\gamma }(t))=\left( \frac{1}{2}\Vert \dot{\gamma }(t)\Vert _g^2-\frac{1}{12}S(\gamma (t))\right) \) where S is the scalar curvature. Most probable paths on manifolds thus minimize a functional that in addition to the path energy includes the integral of the scalar curvature along the path.

The situation for stochastic processes on infinite dimensional spaces remains largely unexplored. In this paper, we consider Kunita flows of diffeomorphisms of the domain \(M\subseteq {\mathbb {R}}^d\). For a stochastic flow \(\varphi _t\in {{\,\textrm{Diff}\,}}(M)\), we ask what is the most probable single realization \(\hat{\varphi }_t\) that bridges \(\varphi _0\) to a fixed transform \(\psi \in {{\,\textrm{Diff}\,}}(M)\). We achieve this by equipping M with a Riemannian metric originating from the noise fields \(\sigma _{i,t}\). We then invoke the Onsager–Machlup result [7] for elliptic time-dependent diffusion operators on M to give a point-wise result. The resulting second-order ODE on M gives the most probable flow \(\hat{\varphi }_t\).

Onsager–Machlup functionals for infinite dimensional systems have been studied in the literature [8,9,10] for specific Hilbert-space valued SDEs. However, these are not available when considering smooth diffeomorphisms, which form a Lie–Fréchet group, see e.g. [11]. While the idea of encoding properties of the diffusion in a Riemannian metric has been used in the finite dimensional setting [12, 13], the main new idea of the paper is to use such a metric for infinite dimensional Kunita SDEs.

Particular examples of flows to which our result apply are perturbations of geodesic flows for right-invariant metrics on \({{\,\textrm{Diff}\,}}(M)\). These geodesics appear both in fluid dynamics describing e.g. the incompressible Euler equations [14] and in shape analysis in the Large deformation diffeomorphic metric mapping (LDDMM) framework [15, 16]. The stochastically perturbed flows have recently been applied in fluid dynamics to couple small-scale stochastic fluctuations and coarse scale deterministic dynamics [1, 17] and in shape analysis to model human organ shape changes or animal shapes changes through evolution [3]. By identifying the most probable paths for such processes, we are able to give one summary statistic of a fluid system or provide a most probable evolution of a given species shape through time. Shapes can here be interpreted generally as objects on which \({{\,\textrm{Diff}\,}}(M)\) act, e.g. on transformation landmark configurations \(x=(x_1,\ldots ,x_n)\) where they act by \(\varphi .x=(\varphi (x_1),\ldots ,\varphi (x_n))\) or on images \(I:M\rightarrow {\mathbb {R}}\) with action \(\varphi .I=I\circ \varphi ^{-1}\).

1.2 Outline

We start by a brief outline of Kunita type stochastic flows, stochastic flows in fluid dynamics and shape analysis, and most probable path theory. We then develop the general construction for retrieving Onsager–Machlup results of flows from the corresponding theory of manifold-valued diffusion processes. We discuss various instances of stochastic models with application in e.g. shape analysis and investigate the case of evolutions of finite sets of landmarks under stochastic shape models together with numerical visualization of the different types of evolutions.

2 Stochastic Flows and Measures on Path Space

2.1 Stochastic Flows

Given a probability space \((\Omega ,\mathscr {F},P)\), let \(\varphi _{s,t}\) denote s, t parametrized maps from \(M\times \Omega \) to M. A Brownian flow of homeomorphism in the sense of Kunita is a stochastic process \(\varphi _{s,t}\) such that \(\varphi _{s,t}(x,\cdot )\) is continuous in s, t, x in probability and \(\varphi _{s,t}(x,\omega )\) is continuous in t almost surely (a.s.); \(\varphi _{s,s}={{\,\textrm{id}\,}}_M\) for each s a.s.; \(\varphi _{s,t}=\varphi _{r,t}\circ \varphi _{s,r}\); and \(\varphi _{s,t}\) has independent increments [4]. Particular examples of Brownian flows are solutions \(\varphi _t=\varphi _{0,t}\) to the Itô SDE

$$\begin{aligned} d\varphi _t = {\hat{u}}_t(\varphi _t) \, dt + \sum _{r=1}^J \sigma _{r,t}(\varphi _t) dW^r\end{aligned}$$
(2)

for time-dependent vector fields \({\hat{u}}_t,\sigma _{1,t},\ldots ,\sigma _{J,t}:M\rightarrow {\mathbb {R}}^d\). \({\hat{u}}\) and \(a_t=\sum _{r=1}^J\sigma _{r,t}\sigma _{r,t}^T\) defines the local characteristics of the flow. If the local characteristics are \(C^1\) with bounded derivatives and if the derivatives of a are Lipschitz, the Itô to Stratonovich conversion applies giving the equivalent Stratonovich form (1), [4, 18].

2.2 Path Probability and Onsager–Machlup Functionals

Let \(\gamma \in C([0,T],{\mathbb {R}}^d)\) be a path in \({\mathbb {R}}^d\) and \(W_t\) a Brownian motion on \({\mathbb {R}}^d\). The probability that \(W_t\) sojourns in an \(\varepsilon \)-neighborhood around \(\gamma \) for all \(t\in [0,T]\) is defined by

$$\begin{aligned} \mu _\varepsilon (\gamma ) = P(\Vert W_t-\gamma (t)\Vert <\varepsilon \ \forall t\in [0,T]) . \end{aligned}$$
(3)

In [19], it was shown that, when \(\gamma \) is differentiable, \(\log \mu _\varepsilon (\gamma )\) tends to \(c_1+c_2/\varepsilon ^2- \int _0^T H(\gamma (t),\dot{\gamma }(t))\, dt\) for constants \(c_1,c_2\) as \(\varepsilon \rightarrow 0\) and with \(H(\gamma (t),\dot{\gamma }(t))=\frac{1}{2} \Vert \dot{\gamma }(t)\Vert ^2\). The function \(\gamma \mapsto \int _0^T H(\gamma (t),\dot{\gamma }(t))\, dt\) is called the Onsager–Machlup functional. Paths between two points minimizing this functional are denoted most probable, and, because of the equivalence to the standard Euclidean energy of a curve, the most probable paths will be straight lines. If \(\gamma \) is a curve on a finite dimensional Riemannian manifold, the Onsager–Machlup functional is the integral of \(H(\gamma (t),\dot{\gamma }(t)) = \frac{1}{2} \Vert \dot{\gamma }(t)\Vert _g^2-\frac{1}{12}S(\gamma (t)) \, dt\) with S the scalar curvature.

The functional has been explored in the literature after the original work by Onsager and Machlup. Encoding properties of the diffusion processes in a Riemannian metric has been used in works including [12, 13]. Particularly relevant here is the Onsager–Machlup functionals for time-dependent elliptic operators treated in [7]. Also related to the presented approach is the application of the Onsager–Machlup theory for semi-martingales on manifolds that are represented as development of Euclidean semi-martingales, see e.g. [20, 21] where the Onsager–Machlup functional is applied on anti-developments to determine most probable paths for semi-martingales on manifolds.

3 Most Probable Flows

The stochastic process in (1) has infinitesimal generator

$$\begin{aligned} L_t = \frac{1}{2} \sum _{r=1}^J \sigma _{r,t}^2 + u_t, \end{aligned}$$

see [4, Sect. 4.2] for details. We assume that \(L_t\) is a elliptic operator which is equivalent to assuming that \({{\,\textrm{span}\,}}\{ \sigma _r\}_{r=1}^J = \mathbb {R}^d\) at any point. Define a cometric

$$\begin{aligned} g^*_t = \sum _{r=1}^J \sigma _{r,t} \otimes \sigma _{r,t}, \end{aligned}$$

which will be a Riemannian cometric by our assumptions. Write \(\Delta _{g_t}\) for the Laplace–Beltrami operator of the corresponding Riemannian metric \(g_t\) and define a vector field \(z_t\) such that

$$\begin{aligned} L_t = \frac{1}{2}\Delta _{g_t} + z_t. \end{aligned}$$
(4)

For details around the stochastic flow \(\varphi _t\), see Remark 2. The result of [7] then tells us that the Onsager–Machlup functional is of the form \(\int _0^T H(t,\gamma (t),\dot{\gamma }(t)) \, dt\) with

$$\begin{aligned} H(t, \gamma , \dot{\gamma })&= \frac{1}{2} \Vert \dot{\gamma }_t - z_t (\gamma _t)\Vert _{g_t}^2 + \frac{1}{2} ({{\,\textrm{div}\,}}_{g_t} z_t)(\gamma _t) - \frac{1}{12} S_t(\gamma _t) + \frac{1}{4} {{\,\textrm{tr}\,}}_{g_t} \dot{g}_t|_{\dot{\gamma }_t} \nonumber \\&=: \frac{1}{2} \Vert \dot{\gamma }_t - z_t(\gamma _t) \Vert ^2_{g_t} + f_t(\gamma _t). \end{aligned}$$
(5)

Here, \(S_t\) is the scalar curvature of \(g_t\). We now have the following result.

Theorem 1

(Most probable flows) Let \(\nabla ^t\) be the Levi-Civita connection of \(g_t\) and let \(z_t\) be the vector field in (4). With slight abuse of notation, we define adjoint operators \(\dot{g}_t^*, (\nabla ^t \xi )^*: TM \rightarrow TM\) by

$$\begin{aligned} \left\langle \dot{g}_t^* \xi _1, \xi _2 \right\rangle _{g_t} = \dot{g}_t(\xi _1, \xi _2), \quad \left\langle (\nabla ^t \xi )^* \xi _1, \xi _2 \right\rangle _{g_t} =\left\langle \nabla _{\xi _2} \xi , \xi _1 \right\rangle _{g_t},\end{aligned}$$
(6)

for vector fields \(\xi \), \(\xi _1\), \(\xi _2\). Then \(\varphi _t\) is a most probable flow if and only if it solves the equation

$$\begin{aligned} \dot{\varphi }_t = (w_t+z_t)(\varphi _t), \end{aligned}$$

with \(w_t\) satisfying

$$\begin{aligned} \dot{w}_t + \nabla _{w_t+z_t}^t w_t + \dot{g}_t^* w_t + (\nabla ^t z_t)^* w_t =\nabla ^t f_t. \end{aligned}$$
(7)

We emphasize that \(\dot{g}_t^*\) denotes the metric adjoint of \(\dot{g}_t\) and not the time-derivative of the cometric. We remark that the above result was computed in [7] for the special case of \(g_t\) being given by the Ricci flow and \(z_t = 0\). Theorem 1 follows from defining \(\gamma _t = \varphi _t(x)\) for an arbitrary x and applying the lemma below. Write \(\frac{D^t}{dt}\) for the covariant derivative along the curve \(\gamma _t\) with respect to \(\nabla ^t\). Note that \(\frac{D^t}{dt} w_t(\gamma _t) = (\dot{w}_t)(\gamma _t) + (\nabla _{\dot{\gamma }_t}^t w_t)(\gamma _t)\) for the restriction of a time-dependent vector field along a curve.

Lemma 1

For two given fixed points, let \(\gamma \) be a minimizing curve of the functional H in (5) connecting these end points. Then \(\gamma _t\) is a solution of

$$\begin{aligned} \frac{D^t}{dt} \dot{\gamma }_t + \dot{g}_t^* \dot{\gamma }_t + \left( \nabla ^t z_t\right) ^* \dot{\gamma }_t = \dot{z}_t + \nabla _{\dot{\gamma }_t}^t z_t + \dot{g}_t^* z+t+ \left( \nabla ^t z_t\right) ^* z_t +\nabla ^t f_t. \end{aligned}$$
(8)

Proof

Let \(\gamma _t^s\) be a variation of \(\gamma _t\) with fixed end points. We recall that \(\frac{D^t}{ds} \dot{\gamma }_t^s = \frac{D^t}{dt} \partial _s \gamma _t^s \). We emphasize that \(\frac{D^t}{ds}\) is a derivative with respect to s, and that the dependence on t is through taking the covariant derivative with respect to \(\nabla ^t\). We introduce notation \(\partial _s \gamma _t^s|_{s=0} = v_t\) and \(\dot{\gamma }(t) = a_t+z_t(\gamma _t)\). Differentiating (5), we compute

$$\begin{aligned}&\frac{d}{ds}\int _0^T H(t,\gamma ^s,\dot{\gamma }^s)|_{s=0} \, dt |_{s=0} \\ {}&= \int _0^T \left( \left\langle a_t , \frac{D^t}{ds} (\dot{\gamma }_t^s - z_t) |_{s=0} \right\rangle _{g_t} + \left\langle \nabla ^t f, \partial _s \gamma _t^s |_{s=0} \right\rangle _{g_t} \right) dt \\ {}&= \int _0^T \left( \left\langle a_t , \frac{D^t}{dt} v_t \right\rangle _{g_t} - \left\langle a_t , \nabla _{v_t}^t z_t \right\rangle _{g_t} + \left\langle \nabla ^t f, v_t \right\rangle _{g_t} \right) dt. \end{aligned}$$

Using that

$$\begin{aligned} \frac{d}{dt} \left\langle a_t , v_t \right\rangle _{g_t}= \langle \dot{g}_t^* a_t, v_t \rangle _{g_t} + \left\langle \frac{D^t}{dt} a_t , v_t \right\rangle _{g_t} + \left\langle a_t , \frac{D^t}{dt} v_t \right\rangle _{g_t}, \end{aligned}$$

we get

$$\begin{aligned} \frac{d}{ds} \int _0^T H(t,\gamma ^s,\dot{\gamma }^s)|_{s=0} \, dt&= \int _0^T \left\langle v_t, - \frac{D^t}{dt} a_t - \dot{g}_t^* a_t - (\nabla ^t z_t)^* a_t +\nabla ^t f_t \right\rangle _{g_t} \, dt. \end{aligned}$$

We see that for this expression to vanish for any variational vector field \(v_t\) we must have

$$\begin{aligned} 0&= \frac{D^t}{dt} a_t + \dot{g}_t^* a_t + (\nabla ^t z_t)^* a_t -\nabla ^t f_t. \end{aligned}$$
(9)

The result follows. \(\square \)

Remark 1

Alternatively, the equations \(\dot{\gamma }= a_t + z_t(\gamma _t)\) and (9) can be used to find the flow lines of the most probable flow.

Remark 2

Up until now, we have not gone into details about the Kunita flow itself. For our classes of vector fields and for a fixed x, we can always find a unique maximal solution \(\varphi _t(x)\) of (1) with initial condition \(\varphi _0(x) = x\) up to its explosion time, see, e.g., [4, Theorem 3.4.5]. We need to be more careful when it comes to concluding that the flow \(x \mapsto \varphi _t(x)\) is a true diffeomorphism of M. For the time-homogeneous case when the vector fields \(\sigma _r = \sigma _{r,t}\) and \(u = u_t\) have no dependence on t, then \(\varphi _t\) is almost surely a diffeomorphism if the diffusion does not explode in finite time, see [22, 23, Theorem 5.1.1]. Sufficient conditions for non-explosions is completeness and lower-bound for the Ricci curvature, or that it in general does not decay too fast when approaching infinity, see [24, 25, Theorem 5.1.1] for details. For the time-inhomogeneous case, a sufficient condition for the solution to be a diffeomorphism is for any [0, T], there exists an \(L^1\) function \(C_t\) such that all of the vector fields \(\sigma _{1,t}, \dots , \sigma _{J,t}, u_t\) have all spacial derivatives bounded by \(C_t\), and furthermore, the vector fields themselves are bounded by \(C_t(1+|x|)\), see [4, Theorem 4.6.5].

3.1 Local Coordinate Representations for Numerical Implementation

We will below give explicit formulas for computing the most probable flow from the Eq. (1) that can be implemented numerically. We consider M as a \(\mathbb {R}^d\) with coordinates \(x = (x^1, \dots , x^d)\). In what follows, all terms will depend on t, but we will suppress this dependence to simplify notation. Write \(u = \sum _{k=1}^d u^k \partial _k\) and \(\sigma _{r} = \sum _{i=1}^d \sigma ^i_{r} \partial _i\).

  1. 1.

    The cometric \(g^* = \sum _{i,j=1}^d g^{ij} \partial _i \otimes \partial _j\) is given by \(g^{ij} = \sum _{r=1}^J \sigma _{r}^i \sigma _{r}^j\). The corresponding Laplacian is given by

    $$\begin{aligned} \Delta _{g} = \sum _{i,j=1}^d g^{ij} \partial _i \partial _j + \sum _{i,j=1}^d \frac{1}{\sqrt{|g|}} \partial _i (\sqrt{|g|} g^{ij}) \partial _j. \end{aligned}$$

    Since

    $$\begin{aligned} \sum _{r=1}^J \sigma _{r}^2&= \sum _{r=1}^J \sum _{i,j=1}^d \sigma _{r}^i \sigma _{r}^j \partial _{i} \partial _j + \sum _{r=1}^J \sum _{i,j=1}^d (\sigma _{r}^i \partial _i \sigma _{r}^j) \partial _j \\&= \Delta _{g} + \sum _{i,j=1}^d \left( \sum _{r=1}^J \sigma _{r}^j \partial _i \sigma _{r}^i - \frac{1}{2} g^{ij} \partial _i \log |g| - \partial _i g^{ij} \right) \partial _j , \end{aligned}$$

    we have that \(z = \sum _{j=1}^d z^j \partial _j\) equals

    $$\begin{aligned} z^j = u^j + \frac{1}{2} \sum _{i,j=1}^d \left( \sum _{r=1}^J \sigma _{r}^j \partial _i \sigma _{r}^i - \frac{1}{2} g^{ij} \partial _i \log |g| - \partial _i g^{ij} \right) \partial _j. \end{aligned}$$
  2. 2.

    As usual, the Christoffel symbols of the Levi–Civita connection is given by \(\Gamma _{ij}^k = \frac{1}{2} \sum _{l=1}^d g^{kl} \left( \partial _j g_{li} + \partial _i g_{lj} - \partial _l g_{ij} \right) \), with the scalar curvature expressed as

    $$\begin{aligned} S = \sum _{i,j,k=1}^d g^{ij} \left( \partial _k \Gamma _{ij}^k - \partial _j \Gamma _{ik}^k + \sum _{l=1}^d \left( \Gamma _{ij}^l \Gamma _{kl}^k - \Gamma _{ik}^l \Gamma _{jl}^k\right) \right) . \end{aligned}$$
  3. 3.

    For the maps introduced in (6), we have local expression

    $$\begin{aligned} \dot{g}^* \partial _j&= \sum _{k=1}^d \dot{g}_{jk} g^{ik} \partial _i, \\ (\nabla z)^* \partial _j&= \sum _{i,l=1}^d g_{lj} g^{ik} \left( \partial _k z^l + \sum _{m=1}^d z^m \Gamma _{km}^l\right) \partial _i. \end{aligned}$$
  4. 4.

    Finally, \(f = f_t\) is given by

    $$\begin{aligned} f = \frac{1}{2} \sum _{l,m=1}^d g^{lm} \left( \frac{1}{2} \dot{g}_{lm} +\partial _l z^m + \sum _{k=1}^d z^k\Gamma ^m_{lk}\right) - \frac{1}{12} S. \end{aligned}$$

For the global equation, we can write (7) as

$$\begin{aligned} 0&= \dot{w}^i + \sum _{j=1}^d (w^j +z^j) \partial _j w^i + \sum _{j,k=1}^d (w^k + z^k) w^j \Gamma _{kj}^i + \sum _{j,k=1}^d \dot{g}_{jk} g^{ik} w^j \\ {}&\quad + \sum _{j,k,l=1}^d g_{jl} g^{ik} w^j \left( \partial _k z^l + \sum _{m=1}^d z^m \Gamma _{km}^l \right) - \sum _{j=1}^d g^{ij} \partial _j f \end{aligned}$$

while the solution of (8) is

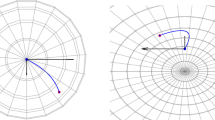
$$\begin{aligned} 0&= \ddot{x}^i - \dot{z}^i + \sum _{j,k=1}^d \dot{x}^k \dot{x}_t^j \Gamma _{t,kj}^i - \sum _{k=1}^d \dot{x}^k \left( \partial _k z_t^i + \sum _{j=1}^d \Gamma _{kj}^i z^j \right) + \sum _{j,k=1}^d \dot{g}_{jk} g^{ik} (\dot{x}^j- z^j) \\ {}&\quad + \sum _{j,k,l=1}^d g_{lj} g^{ik} \left( \partial _k z^l + \sum _{,=1}^d z^m \Gamma _{km}^i \right) (\dot{x}^j - z^j) - \sum _{k=1}^d g^{ij} \partial _j f . \end{aligned}$$

Figure 1 visualizes numerical realizations of most probable flows acting on landmarks with \(u = u_t\) solving the Euler–Poincaré equations (13).

Example 1

(Brownian background noise) Assume that we have that \(J=d\) and \(\sigma _r = \partial _r\). Then g is the Euclidean metric and \(S=0\). Furthermore \(\sum _{r=1}^d \sigma _r^2 = \Delta _g\), so \(z_t = u_t\) and \(f_t =\frac{1}{2} \sum _{r=1}^d \partial _r u_t^r\). We will let \(\bar{\nabla }\) denote the flat connection on \(\mathbb {R}^d\), that is, \(\bar{\nabla }_u w = (Dw)u\) where Dw is the Jacobi matrix of w. The equation for the most probable flow is then \(\dot{\varphi }_t = (w_t+ u_t)(\varphi _t)\) with \(w_t\) being a solution of

$$\begin{aligned} \dot{w}_t + \bar{\nabla }_{w_t+u_t} w_t + (\bar{\nabla } u_t)^* w_t =\frac{1}{2} \bar{\nabla } {{\,\textrm{div}\,}}u_t, \end{aligned}$$

or

$$\begin{aligned} \dot{w}_t^i + \sum _{j=1}^d \left( (w_t^j + u_t^j) \partial _j w^i_t + w_t^j \partial _i u_t^j - \frac{1}{2} \partial _i \partial _j u_t^j \right) =0, \end{aligned}$$

A most probable path is a solution

$$\begin{aligned} \ddot{x}_t^i + \sum _{j=1}^d \dot{x}_t^j \partial _i u_t^j(x_t) = \frac{1}{2} \partial _i (\Vert u_t\Vert ^2 + {{\,\textrm{div}\,}}(u_t))(x_t)=0. \end{aligned}$$

4 Perturbed Right-Invariant Geodesic Flows

We now focus on specific examples of Kunita SDEs, mainly arising from geometric mechanics and shape analysis. Right-invariant metrics on the diffeomorphism group \({{\,\textrm{Diff}\,}}(M)\) determine the drift field \(u_t\) as derivative of geodesic equations in the group. These are in turn described by the EPDiff equations (Euler–Poincaré on diffeomorphisms) and used extensively for example in the Large Deformation Diffeomorphic Metric Mapping (LDDMM) shape matching framework, see [15, 26]. Stochastic extensions of the EPDiff equations include the stochastic EPDiff equations [1] and the stochastic EPDiff perturbations [2]. In the former scheme, the minimization of a stochastic variational principle implies that the drift becomes stochastic and the flow thus non-Brownian. In the later, taking expected energy results in deterministic drift and thus Brownian flows. Below, we will outline these schemes and relate to most probable paths both theoretically and numerically.

4.1 Reduction and EPDiff Equations

Let M be a domain in \(\mathbb {R}^d\) and let \({{\,\textrm{Diff}\,}}(M)\) be its group of diffeomorphisms. We consider \({{\,\textrm{Diff}\,}}(M)\) as a Lie group with Lie algebra given by vector fields \(\mathcal {X}(M)\). With this formalism, \({{\,\textrm{ad}\,}}(u)v = -[u,v]\) is the negative of the usual Lie algebra for \(u,v \in \mathcal {X}(M)\), while for \(\varphi \in {{\,\textrm{Diff}\,}}(M)\), we have \({{\,\textrm{Ad}\,}}(\varphi )u (x) = \varphi _{*} u(\varphi ^{-1}(x))\). If \(\varphi _t\) a curve in \({{\,\textrm{Diff}\,}}(M)\), then \(\varphi _t\) has right logarithmic derivative

$$\begin{aligned} \delta ^r \varphi _t =: \dot{\varphi }_t \cdot \varphi _t^{-1} =u_t \in \mathcal {X}(M) \text { if } \dot{\varphi }(x) = u_t(\varphi _t(x)). \end{aligned}$$
(10)

Let A be a positive, self-adjoint operator on \(\mathcal {X}(M)\). Define

$$\begin{aligned} \langle u, u \rangle _{\mathcal {X}(M)}= \Vert u \Vert _{\mathcal {X}(M)}^2 = \int _M \langle Au, u \rangle dx, \quad u\in \mathcal {X}(M). \end{aligned}$$
(11)

This can be used to measure the energy of a curve \(\varphi _t\) by

$$\begin{aligned} E(\varphi _t) = \frac{1}{2} \int _0^T \Vert \delta ^r \varphi _t \Vert ^2_{\mathcal {X}(M)} dt.\end{aligned}$$
(12)

With \(\varphi _t\) satisfying (10), a first-order condition for \(\varphi _t\) to minimize the energy between an initial state \(\varphi _0\) and a final state \(\varphi _T\) is that it satisfies the Euler–Poincaré equation

$$\begin{aligned} \dot{u}_t + {{\,\textrm{ad}\,}}(u_t)^* u_t =0, \end{aligned}$$
(13)

where \({{\,\textrm{ad}\,}}(u_t)^*\) here is the adjoint of \({{\,\textrm{ad}\,}}(u_t)w_t = - [u_t, w_t]\) with respect to the inner product \(\langle \cdot , \cdot \rangle _{\mathcal {X}(M)}\). Explicitly,

$$\begin{aligned} \dot{m}_t + (Dm_t) u_t + ({{\,\textrm{div}\,}}u_t) m_t + (Du_t)^Tm_t =0, \quad m_t = Au_t. \end{aligned}$$

See e.g. [27] for more details.

The inner product \(\left<u,v\right>_{\mathcal X(M)}=\left<Au,v\right>_{L^2}\) used in (11) defines a right-invariant Riemannian metric on the subgroup \(G=\{\phi _T|\phi _0={{\,\textrm{id}\,}},\ \Vert u\Vert <\infty \}\) of end points \(\phi _T\) of finite energy paths satisfying the flow Eq. (10) by setting

$$\begin{aligned} \left<v,u\right>_{T_\phi G} = \left<v\circ \phi ^{-1},u\circ \phi ^{-1}\right>_{{\mathcal {X}}(M)} . \end{aligned}$$

The Euler–Poincaré equations are geodesic equations for this metric [14, 28].

4.2 Stochastic Euler–Poincaré Flows

A stochastic version of the EPDiff equations can be obtained by perturbing the reconstruction Eq. (10) to obtain

$$\begin{aligned} d\varphi _t(x) = u_t(\varphi _t(x))dt + \sum _{r=1}^J \sigma _r(\varphi _t(x)) \circ dW^r \end{aligned}$$
(14)

for J vector fields \(\sigma _r\in {\mathcal {X}}(M)\) are deterministic, but we allow \(u_t\) to be random. This results in the stochastic flows introduced in [1] for fluids and subsequently in [3] for shapes. Because the stochastics is added to the right logarithmic derivative, much of the right-invariant geometric structure is preserved, for example the momentum map. This implies that critical flows for the energy (12) with the relation between \(u_t\) and \(\phi _t\) given by (14) can identified with a reduction principle analogous to the deterministic case. Specifically, one has the following stochastic extension of the Euler–Poincaré Eq. (13).

Theorem 2

([1, 3]) With the stochastic perturbed (14), critical flows for (12) take the form

$$\begin{aligned} \dot{m}_t + {{\,\textrm{ad}\,}}(u_t)^* m_t + \sum _{r=1}^J{{\,\textrm{ad}\,}}(\sigma _r)^* m_t \circ dW_t^r =0, \end{aligned}$$
(15)

with momentum \(m_t=Au_t\) and with \(W_t\) an \({\mathbb {R}}^J\)-valued Wiener process.

Note that \(u_t\) satisfying the system (15) will be stochastic, and the stochastic EPDiff flows are therefore inherently different from the most probable flows, while both arise from a variational principle.

4.3 Energy Minimizing Flows

An alternative approach has been presented [2] for the setting of Riemannian manifolds, which we consider here in the flat case. Consider a semi-martingale \(\varphi _t\) in our open subset M of \(\mathbb {R}^d\) with induced filtration \(\mathscr {F}_t\), and let \(w_t = \int _0^t d\varphi _t \circ \varphi _t\) be its anti-development with respect to the flat connection, which is also a semi-martingale. We introduce a stochastic analogue of the left logarithmic derivative in (10),

$$\begin{aligned} \textstyle \delta ^r \varphi _t = \lim _{\varepsilon \downarrow 0} \mathbb {E}\left[ \frac{w_{t+\varepsilon } -w_t}{\varepsilon } |\mathscr {F}_t \right] . \end{aligned}$$

We use this definition to introduce the expected energy

$$\begin{aligned} \textstyle E[\varphi _{\cdot }] = \frac{1}{2} \mathbb {E} \left[ \int _0^T \Vert \delta ^r \varphi _t \Vert _{\mathcal {X}(M)} dt \right] , \end{aligned}$$
(16)

with the expectation taken with respect to the measure induced by \(\varphi _{[0,T]}\) on continuous paths from [0, T] into M. Furthermore, for any non-random vector field \(v_t\) with \(v_0 = v_T =0\), we define \(\psi _{t}^s\) as the solution of \(\psi _0^s = {{\,\textrm{id}\,}}\), \(\delta ^r \psi ^s_t = s \dot{v}_t\). We say that \(\varphi _t\) is a critical point of the expected energy E if \(\frac{d}{ds} \mathbb {E}[\psi ^s_{\cdot } \circ \varphi _{\cdot } ]|_{s=0}=0\) for any such vector field \(v_t\).

Consider now the case when \(\varphi _t\) is the solution of (1), giving us that \(w_t = \int _0^t (u_t dt + \sum _{r=1}^J \sigma _{r,t} \circ dW^r)\) and that

$$\begin{aligned} \delta ^r \varphi _t = \lim _{\varepsilon \downarrow 0} \mathbb {E}\left[ \frac{w_{t+\varepsilon } -w_t}{\varepsilon } |\mathscr {F}_t \right] = u_t + \frac{1}{2} \sum _{r=1}^J \bar{\nabla }_{\sigma _{r,t}}\sigma _{r,t}=: {\hat{u}}_t, \end{aligned}$$
(17)

is deterministic. We then have the following result.

Theorem 3

For the flat connection \(\bar{\nabla }\) on \(\mathcal {X}(M)\), define its Hessian by \(\bar{\nabla }^2_{u,v} w = \bar{\nabla }_u \bar{\nabla }_v w - \bar{\nabla }_{\bar{\nabla }_u v} w\). Introduce a second order operator on vector fields by

$$\begin{aligned} \Box ^\sigma _t = \sum _{r=1}^J \bar{\nabla }^2_{\sigma _{r,t}\sigma _{r,t}}. \end{aligned}$$

Then \(\varphi _t\) is critical if and only if \({\hat{u}}_t = u_t + \frac{1}{2}\sum _{r=1}^J \bar{\nabla }_{\sigma _{r,t}}^2 \sigma _{r,t}\) satisfies

$$\begin{aligned} \dot{{\hat{u}}}_t+ \frac{1}{2} \Box ^\sigma _t {\hat{u}}_t + {{\,\textrm{ad}\,}}({\hat{u}}_t)^* {{\hat{u}}}_t = 0 \end{aligned}$$
(18)

where \({{\,\textrm{ad}\,}}({\hat{u}}_t)^*\) is the dual with respect to \(\langle \cdot , \cdot \rangle _{\mathcal {X}(M)}\).

We remark that if we reformulate the Stratonovich SDE to the Itô SDE (2), then \({\hat{u}}_t\) in Theorem 3 is exactly the drift term in the Itô SDE. Furthermore, if we consider \(\Box ^\sigma _t\) acting on each component, then \(\Box ^\sigma _t v = \sum _{i=1}^d \sum _{j=1}^J (\sigma _{j,t}^2 - \bar{\nabla }_{\sigma _{j,t}} \sigma _{j,t}) v_j \partial _{j}\) and \(\sum _{j=1}^J (\sigma _{j,t}^2 - \bar{\nabla }_{\sigma _{j,t}} \sigma _{j,t})\) is the generator of the drift term in (2).

The proof of Theorem 3 can be deduced from that of [2, Theorems 3.2 and 3.4], but we include it here for the sake of completeness.

Proof

Before we begin the proof, let us consider the following property of the flat connection \(\bar{\nabla }\). Recall that the Hessian is the operator \(\bar{\nabla }^2_{u,v} = \bar{\nabla }_{u} \bar{\nabla }_v - \bar{\nabla }_{\bar{\nabla }_u v}\). Since \(\bar{\nabla }\) is flat and torsion free, its Hessian \(\bar{\nabla }^2\) is symmetric. We then see that

$$\begin{aligned}&[u, \bar{\nabla }_v w] - \bar{\nabla }_{[u,v]} w - \bar{\nabla }_{v} [u,w] \\ {}&= \bar{\nabla }_u \bar{\nabla }_v w - \bar{\nabla }_{\bar{\nabla }_v w} u - \bar{\nabla }_{\bar{\nabla }_u v} w + \bar{\nabla }_{\bar{\nabla }_v u} w - \bar{\nabla }_v \bar{\nabla }_u w + \bar{\nabla }_v \bar{\nabla }_w u \\ {}&= \bar{\nabla }^2_{u,v} w - \bar{\nabla }_{v,u}^2 w + \bar{\nabla }_{v,w}^2 u = \bar{\nabla }_{v,w}^2 u. \end{aligned}$$

Write \(\varphi ^s_t = \psi _t^s \circ \varphi _t\). By the chain rule for Stratonovich differentials,

$$\begin{aligned} d \varphi _t^s&= \dot{\psi }_t^s(\varphi _t) + \psi _{t,*}^s \circ dw_t(\varphi _t) = \dot{\psi }_t^s((\psi _t^s)^{-1} \circ \varphi _t^s) + \psi _{t,*}^s \circ dw_t(( \psi _t^s)^{-1} \circ \varphi _t) \\ {}&= s \dot{v}_t (\varphi _t^s) + {{\,\textrm{Ad}\,}}(\psi _t^s)u_t (\varphi _t^s) dt + \sum _{r=1}^J ({{\,\textrm{Ad}\,}}(\psi _t^s)\sigma _{r,t})(\varphi _{t}^s) \circ dW^r, \end{aligned}$$

and so by (17),

$$\begin{aligned} \delta ^r \varphi _t^s = s\dot{v}_t + {{\,\textrm{Ad}\,}}(\varphi _t^s) u_t + \frac{1}{2} \sum _{r=1}^J \bar{\nabla }_{{{\,\textrm{Ad}\,}}(\psi _t^s)\sigma _{r,t}}{{\,\textrm{Ad}\,}}(\psi _t^s) \sigma _{r,t}, \end{aligned}$$

Furthermore,

$$\begin{aligned} \tfrac{d}{ds}\delta ^r \varphi _t^s |_{s=0} = \dot{v}_t + {{\,\textrm{ad}\,}}(v_t) u_t + \frac{1}{2} \sum _{r=1}^J \bar{\nabla }_{{{\,\textrm{ad}\,}}(v_t) \sigma _{r,t}}\sigma _{r,t} + \frac{1}{2} \sum _{r=1}^J \bar{\nabla }_{ \sigma _{r,t}} {{\,\textrm{ad}\,}}(v_t)\sigma _{r,t}. \end{aligned}$$

Using our observation for \(\bar{\nabla }\), we have

$$\begin{aligned} \tfrac{d}{ds}\delta ^r \varphi _t^s |_{s=0}&= \dot{v}_t + {{\,\textrm{ad}\,}}(v_t) {\hat{u}}_t - \frac{1}{2} \sum _{r=1}^J \bar{\nabla }_{\sigma _{r,t}, \sigma _{r,t}}^2 v_t \\ {}&= \dot{v}_t - ({{\,\textrm{ad}\,}}({\hat{u}}_t) + \frac{1}{2} \Box ^\sigma _t) v_t . \end{aligned}$$

We then see that

$$\begin{aligned} \frac{d}{ds}E[\varphi _t^s]|_{s=0}&= \int _0^T \left\langle {\hat{u}}_t , \dot{v}_t - ({{\,\textrm{ad}\,}}({\hat{u}}_t) + \frac{1}{2} \Box ^\sigma _t) v_t \right\rangle _{\mathcal {X}(M)} dt \end{aligned}$$

and using that \(\Box ^\sigma _t\) is a symmetric operator with respect to \(\langle \cdot , \cdot \rangle _{\mathcal {X}(M)}\), the result follows. \(\square \)

Remark 3

For context of how we used the properties of the flat connection in the proof of Theorem 3, observe that for a general connection \(\nabla \) with curvature R and torsion T,

$$\begin{aligned}&[u, \nabla _v w] - \nabla _{[u,v]} w - \nabla _{v} [u,w] \\ {}&= \nabla _{v,w}^2 + R(u,v)w + u+ (\nabla _v T)(u, w) + T(\nabla _v u, w). \end{aligned}$$

4.4 Most Probable Flows

Let \(\phi _t\) and \(u_t=\delta ^r\phi _t\) satisfy the Euler–Poincaré equations (13). We can add noise to the system with the stochastic reconstruction (14) and obtain the stochastic system (15). Alternatively, we can consider the energy minimizing flows (18) to recover a deterministic flow. The most probable flow equations of Sect. 3 provide a second way to recover a deterministic flow as being most probable instead of energy minimizing, by solving (7).

Fig. 1
figure 1

Red curves: deterministic flow (zero noise) with \(u_t\) solving (18); blue curves: MPP trajectories; green curves: stochastic trajectories. Left column: flow field \(u_t\) at \(t=0\) with noise centers (green points); center left column: forward integration of MPP equations for 40 landmarks evenly distributed at horizontal \(y=-0.5\) line; center right column: initial value problem solved for each landmark between the end points of the deterministic landmark trajectories; right column: stochastic EPDiff sample path (noise amplitude downscaled for visualization). Top row: a single noise field at (0, 0); middle row: two noise fields at \((-0.5,0)\) and (0.5, 0); bottom row: grid of \(7^2\) noise fields

Full size image

4.5 Visualization of Perturbed Flows

We now numerically compare examples of solutions to the Euler–Poincaré equations, to the stochastic Euler–Poincaré equations, and most probable flows.Footnote 1 Figure 1 shows forward flows of the unperturbed system satisfying the Euler–Poincaré equations. We then add noise in three different configurations (1, 2, and \(7^2\) Gaussian noise fields) and compute forward MPP equations, and solve the boundary value problem of most probable paths between the start and end points of the deterministic flow. The effect of the noise and resulting deviation of the most probable paths from the unperturbed trajectories is clearly visible in both cases. Lastly, we plot sample paths from the stochastic Euler–Poincaré equations. The landmark trajectories are highly correlated because of the spatial regularity of the noise fields, and the noise clearly perturbs the large scale dynamics of the system.