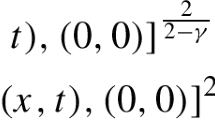Abstract
In this paper, we study three-dimensional Kirchhoff equations with critical growth and singular nonlinearity. We are concerned with the qualitative analysis of solutions to the following nonlocal problem
where \(\Omega \subset {\mathbb {R}}^3\) is a bounded domain with smooth boundary, \(0<\gamma <1\), and \(a,\,b,\,\lambda \) are positive constants. By combining variational methods with some delicate decomposition techniques, we obtain the existence of two positive solutions in the case of low perturbations of the singular nonlinearity, namely for small values of the parameter \(\lambda \).
Similar content being viewed by others
References
Ambrosetti, A., Rabinowitz, P.H.: Dual variational methods in critical point theory and applications. J. Funct. Anal. 14, 349–381 (1973)
Autuori, G., Fiscella, A., Pucci, P.: Stationary Kirchhoff problems involving a fractional elliptic operator and a critical nonlinearity. Nonlinear Anal. 125, 699–714 (2015)
Azzollini, A.: The elliptic Kirchhoff equation in \({\mathbb{R} }^N\) perturbed by a local nonlinearity. Differ. Integr. Equ. 25, 543–554 (2012)
Brézis, H., Nirenberg, L.: Positive solutions of nonlinear elliptic equations involving critical Sobolev exponent. Commun. Pure Appl. Math. 36, 437–477 (1983)
Canino, A., Degiovanni, M.: Nonsmooth critical point theory and quasilinear elliptic equations, in Topological Methods in Differential Equations and Inclusions (Montréal, 1994), In: NATO ASI series, C, Vol. 472, Kluwer, Dordrecht, 1–50 (1995)
Chen, C., Kuo, Y., Wu, T.: The Nehari manifold for a Kirchhoff type problem involving sign-changing weight functions. J. Differ. Equ. 250, 1876–1908 (2011)
Chen, S., Zhang, B., Tang, X.: Existence and non-existence results for Kirchhoff-type problems with convolution nonlinearity. Adv. Nonlinear Anal. 9(1), 148–167 (2020)
Crandall, M.G., Rabinowitz, P.H., Tartar, L.: On a Dirichlet problem with a singular nonlinearity. Commun. Partial Differ. Equ. 2, 193–222 (1977)
Deng, Y., Peng, S., Shuai, W.: Existence and asymptotic behavior of nodal solutions for the Kirchhoff-type problems in \({\mathbb{R} }^3\). J. Funct. Anal. 269, 3500–3527 (2015)
Díaz, J.I.: Nonlinear Partial Differential Equations and Free Boundaries. Vol. I. Elliptic equations, Research Notes in Mathematics, 106, Pitman, Londres (1985)
Ekeland, I.: On the variational principle. J. Math. Anal. Appl. 47, 324–353 (1974)
Fulks, W., Maybee, J.S.: A singular nonlinear equation. Osaka Math. J. 12, 1–19 (1960)
Figueiredo, G.M.: Existence of a positive for a Kirchhoff problem type with critical growth via truncation argument. J. Math. Anal. Appl. 401, 706–713 (2013)
He, X., Zou, W.: Existence and concentration of positive solutions for a Kirchhoff equation in \({\mathbb{R} }^3\). J. Differ. Equ. 252, 1813–1834 (2012)
Huang, Y.S., Liu, Z., Wu, Y.: On Kirchhoff type equations with critical Sobolev exponent. J. Math. Anal. Appl. 462, 483–504 (2018)
Hirano, N., Saccon, C., Shioji, N.: Existence of multiple positive solutions for singular elliptic problems with concave and convex nonlinearities. Adv. Differ. Equ. 9, 197–220 (2004)
Ioffe, A., Schwartzman, E.: Metric critical point theory I, Morse regularity and homotopic stability of a minimum. J. Math. Pures Appl. 75, 125–153 (1996)
Júnior, J.R.S., Siciliano, G.: Positive solutions for a Kirchhoff problem with vanishing nonlocal term. J. Differ. Equ. 265, 2034–2043 (2018)
Katriel, G.: Mountain pass theorems and global homeomorphism theorems. Ann. Inst. H. Poincaré, Anal. Non Linéaire 11, 73–100 (1994)
Kirchhoff, G.: Mechanik. Tübner, Leipzig (1883)
Lei, C.Y., Liao, J.F., Tang, C.L.: Multiple positive solutions for Kirchhoff type of problem with singularity and critical exponents. J. Math. Anal. Appl. 421, 521–538 (2015)
Li, Y.H., Li, F.Y., Shi, J.P.: Existence of a positive solution to Kirchhoff type problems without compactness conditions. J. Differ. Equ. 253, 2285–2294 (2012)
Li, Y.Y., Zhu, M.: Uniqueness theorem through the method of moving spheres. Duke Math. J. 80, 383–417 (1995)
Liu, J.Q., Guo, Y.X.: Critical point theory for nonsmooth functions. Nonlinear Anal. 66, 2731–2741 (2007)
Molica Bisci, G., Rădulescu, V.D., Servadei, R.: Variational Methods for Nonlocal Fractional Problems, Encyclopedia of Mathematics and its Applications, vol. 162. Cambridge University Press, Cambridge (2016)
Mukherjee, T., Pucci, P., Xiang, M.: Combined effects of singular and exponential nonlinearities in fractional Kirchhoff problems. Discrete Contin. Dyn. Syst. 42, 163–187 (2022)
Nachman, A., Callegari, A.: A nonlinear singular boundary value problem in the theory of pseudo plastic fluids. SIAM J. Appl. Math. 38, 275–281 (1980)
Naimen, D.: The critical problem of Kirchhoff type elliptic equations in dimension four. J. Differ. Equ. 257, 1168–1193 (2014)
Perera, K., Zhang, Z.T.: Nontrivial solutions of Kirchhoff-type problems via the Yang index. J. Differ. Equ. 221, 246–255 (2006)
Sacks, J., Uhlenbeck, K.: The existence of minimal immersions of 2-spheres. Ann. Math. 113, 1–24 (1981)
Shi, S.Z.: Ekeland’s variational principle and the mountain pass lemma. Acta Math. Sinica 1, 348–355 (1985)
Taliaferro, S.D.: A nonlinear singular boundary value problem. Nonlinear Anal. 3, 897–904 (1979)
Tintarev, K., Fieseler, K.H.: Concentration Compactness: Functional-Analytic Grounds and Applications. Imperial College Press, London (2007)
Wang, L., Xie, K., Zhang, B.L.: Existence and multiplicity of solutions for critical Kirchhoff-type \(p\)-Laplacian problems. J. Math. Anal. Appl. 458, 361–378 (2018)
Wang, L., Cheng, K., Zhang, B.: A uniqueness result for strong singular Kirchhoff-type fractional Laplacian problems. Appl. Math. Optim. 83, 1859–1875 (2021)
Yamabe, H.: On a deformation of Riemannian structures on compact manifold. Osaka Math. J. 12, 21–37 (1960)
Acknowledgements
The authors would like to express sincere gratitude to the anonymous referees and editors for their valuable comments. Chunyu Lei is supported by Science and Technology Foundation of Guizhou Province (No. KJ[2019]1163). The research of Vicenţiu D. Rădulescu was supported by a grant of the Romanian Ministry of Research, Innovation and Digitization, CNCS/CCCDI–UEFISCDI, project number PCE 137/2021, within PNCDI III. Binlin Zhang was supported by the National Natural Science Foundation of China (No. 11871199), the Heilongjiang Province Postdoctoral Startup Foundation, PR China (LBH-Q18109), and the Cultivation Project of Young and Innovative Talents in Universities of Shandong Province.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
This appendix contains two lemmas. In Lemma \(A_1\), we give the proof of Lemma 3.6, which is an application of the Ekeland’s variational principle, and adapted from [31]. In Lemma \(A_2\), we show that the functional \(I_\lambda \) fails to satisfy the concrete Palais-Smale condition at the level \(\mu _1\), by finding a sequence \(\{u_n\}\) of \(I_\lambda \) such that \(I_\lambda (u_n)\rightarrow \mu _1\), \(|dI_\lambda |(u_n)\rightarrow 0\), but \(\{u_n\}\) possesses no convergent subsequence in \(H_0^1(\Omega )\). Consequently, \(\mu _1\) is exactly the threshold value for \(I_\lambda \), since we have proved in Proposition 3.4 that below \(\mu _1\), the functional \(I_\lambda \) satisfies the concrete Palais-Smale condition.
Lemma
\(A_1\). Let \(c_1^*\) be the Mountain Pass value as defined in (3.29). Then there exists a concrete Palais-Smale sequence of \(I_\lambda \) at the level \(c_1^*\), that is a sequence \(\{u_n\}\) such that \(I_\lambda (u_n)\rightarrow c_1^*\) and \(|dI_\lambda |(u_n)\rightarrow 0\) as \(n\rightarrow \infty \).
Proof
We first recall (3.30) as follows:
As a closed subset of C([0, 1], P), \(\Gamma \) is a complete metric space. For \(g\in \Gamma \), define
Then F is continuous in \(\Gamma \). By relation (3.26), we have
Therefore, F(g) is bounded from below.
Given \(\varepsilon >0\), by Ekeland’s variational principle, there exists \(g\in \Gamma \) such that
Denote
Then
We claim that there exists \(t_\varepsilon \in {\widetilde{M}}(g)\) such that \(|dI_\lambda |(g(t_\varepsilon ))\le \varepsilon \), which completes the proof. Otherwise, for all \(t\in {\widetilde{M}}(g)\), \(|dI_\lambda |(g(t_\varepsilon ))>\varepsilon \). By the definition, for \(t\in {\widetilde{M}}(g)\), there exists \(v(t)\in P\) such that
By the Fatou lemma, in a neighborhood \(B_{\delta (t)}(t)\) of t in [0, 1], it holds that
for \(s\in B_{\delta (t)}(t)\).
We may assume \(B_{\delta (t)}(t)\cap \{0,1\}=\emptyset \), since \(I_\lambda (g(0))<0\), \(I_\lambda (g(1))<0\), \(\{B_{\delta (t)}(t)|t\in {\widetilde{M}}(g)\}\) is an open covering of \({\widetilde{M}}(g)\). There exists a finite covering \(B_i=B_{\delta (t_i)}(t_i)\), \(i=1,2,...,n\). Let
\(\varphi _0(t)=0\) for \(t\in {\widetilde{M}}(g)\) and \(\varphi _i(0)=\varphi _i(1)=0\) for \(i=1,2,...,n\). Also define
For \(t\in {\widetilde{M}}(g)\), by (4.1) we have
Hence \(\omega (t)\ne 0\) for \(t\in {\widetilde{M}}(g)\). There exists \(\delta >0\) such that \(\Vert \omega (t)\Vert \ge \delta \) for \(t\in {\widetilde{M}}(g)\). Let \(\varphi (t)=\min \left\{ 1, \frac{\delta }{\Vert \omega (t)\Vert }\right\} \), \(t\in [0,1]\), then \(\varphi \in C([0,1], {\mathbb {R}}^+)\). Define
Since \(h(0)=h(1)=0\), for \(\tau \) small enough, \(g+\tau h\in \Gamma \), we have
Choose \(t=t(\tau )\in {\widetilde{M}}(g+\tau h)\), one has
Let \(\tau _n\rightarrow 0^+\), \(t_n=t(\tau _n)\rightarrow t_\varepsilon \), we have
Thus, \(t_\varepsilon \in {\widetilde{M}}(g)\). It follows from (4.2) that
Taking the limit \(n\rightarrow \infty \) in (4.3), by the Fatou’s lemma we obtain
which is a contradiction. Hence, the proof is completed. \(\square \)
Here we use the notations \(U, U_\varepsilon , \eta , \varphi _\varepsilon =\eta U_\varepsilon \) and \(t_0\) as in Lemma 3.7. In particular, \(U, t_0\) satisfy the equation (3.33), and let u be the local minimizer of \(I_1\) obtained in Lemma 3.3.
Lemma
\(A_2\). Let \(u_\varepsilon =u+t_0\varphi _\varepsilon \). Then \(I_\lambda (u_\varepsilon )\rightarrow \mu _1\), \(|dI_\lambda |(u_\varepsilon )\rightarrow 0\), \(u_\varepsilon \rightharpoonup u\), but \(\int _{\Omega }|\nabla u_\varepsilon |^2dx=\int _{\Omega }|\nabla u|^2dx+t_0^2\int _{{\mathbb {R}}^3}|\nabla U|^2dx+o(1)\). Hence \(u_\varepsilon \) (\(\varepsilon \rightarrow 0\)) is a concrete Palais-Smale sequence of \(I_\lambda \) at the level \(\mu _1\), but possesses no convergent subsequence in \(H_0^1(\Omega )\).
Proof
Using the estimate for the integrals involving \(\varphi _\varepsilon \), we have
Hence we deduce as \(\varepsilon \rightarrow 0\)
For \(v\in P\), denote
By estimating, we show
which means
Note that \(u_\varepsilon =u+t\varphi _\varepsilon \) and \(\varphi _\varepsilon =\eta U_\varepsilon \). Then we have
In the above we assume \(\eta (x)=1\) for \(|x|\le \delta \). Moreover, we also have
and
Since \(u, U_\varepsilon \) solve the system:
where \(A=\int _{\Omega }|\nabla u|^2dx+{\mathcal {F}}_1(\int _{\Omega }|\nabla u|^2dx)\), the estimates (4.4) and (4.5) follow from (4.6). The proof is thus complete. \(\square \)
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Lei, C., Rădulescu, V.D. & Zhang, B. Low Perturbations and Combined Effects of Critical and Singular Nonlinearities in Kirchhoff Problems. Appl Math Optim 87, 9 (2023). https://doi.org/10.1007/s00245-022-09913-9
Accepted:
Published:
DOI: https://doi.org/10.1007/s00245-022-09913-9
Keywords
- Kirchhoff equation
- Critical growth
- Singular nonlinearity
- Multiple positive solutions
- Ekeland’s variational principle