Abstract
In this paper we deal with the inverse problem of determining cavities and inclusions embedded in a linear elastic isotropic medium from boundary displacement’s measurements. For, we consider a constrained minimization problem involving a boundary quadratic misfit functional with a regularization term that penalizes the perimeter of the cavity or inclusion to be identified. Then using a phase field approach we derive a robust algorithm for the reconstruction of elastic inclusions and of cavities modelled as inclusions with a very small elasticity tensor.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The focus of this paper is the reconstruction of cavities and inclusions embedded in an elastic isotropic medium by means of boundary tractions and displacements. Identification of defects from boundary measurements plays an important role in non-destructive testing for damage assessment of mechanical specimens, which are possibly defective due to the presence of interior voids or cavities appearing during the manufacturing process, see, for instance, [33, 47, 55, 63] for possible applications to 3D-printing and additive manufacturing. This kind of inverse problems has application also in medical imaging and in particular in elastography, a modality mapping the elastic properties and stiffness of soft tissue, [6,7,8, 31, 59, 60, 64] (to cite a few), and in reflection seismology [20, 62], a non invasive technique used by the oil and gas industry to map petroleum deposits in the Earth’s upper crust and based on seismic data from land acquisition, see for example [61]. We also mention some applications in volcanology, see for example [9, 10, 58] and references therein.
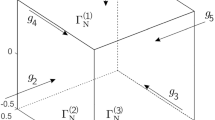
The underlying mathematical model is the following: Consider a bounded domain \(\Omega \subset \mathbb {R}^d\), with \(d=2,3\), representing the region occupied by an elastic isotropic medium and let \(\partial \Omega =\Sigma _D \cup \Sigma _N\), with \(\Sigma _D\) closed. Let the displacement field u be solution to the following mixed boundary value problem for the Lamé system of linearized elasticity:
where \(C\Subset \Omega \) is a cavity with Lipschitz boundary, and \(\widehat{\nabla }u\) is the strain tensor. \(\mathbb {C}_0\) is a fourth-order isotropic elastic tensor, uniformly bounded and strongly convex, and n and \(\nu \) are the outer unit normal vector to \(\partial C\) and \(\Sigma _N\), respectively. The Neumann boundary datum g is assumed to be in \(L^2(\Sigma _N)\).
The forward problem consists in finding the elastic displacement u in the elastic body occupying the region \(\Omega \) induced by the tractions on \(\Sigma _N\), given the cavity C. The inverse problem concerns the determination of the cavity C from partial observations of u on the boundary. More precisely, given measurements of the displacement, i.e. \(u_{meas}\in L^2(\Sigma _N)\), find C contained in \(\Omega \), such that \(u\lfloor _{\Sigma _N}=u_{meas}\), where \(u\in H^1_{\Sigma _D}(\Omega \setminus C)\) is the solution to the forward problem.
It is well known that this problem is severely ill-posed and only a very weak logarithmic conditional stability holds, assuming a-priori \(C^{1,\alpha }\) regularity of the unknown cavities [53]. A similar weak stability result holds also in the case of the determination of elastic inclusions, see for example [54]. Hence, in general, the reconstruction of cavities and inclusions turns out to be a challenging issue.
To solve the problem we follow a similar strategy as in [14, 30] and the one in [13] for the reconstruction of conductivity inclusions and cavities respectively. Specifically, we consider the problem of minimizing the functional
over a suitable set of cavities of finite perimeter and where u(C) is the solution of (1.1) for a given cavity C, \(\text {Per}(C)\) indicates the perimeter of C, and \(\alpha \) is a positive regularization parameter.
We first investigate the continuity of solutions to (1.1) with respect to perturbations of the cavity C in the Hausdorff distance topology and prove it using the Mosco convergence, see [21, 22, 37]. Similarly as in [13], continuity then allows us to prove existence of minima of the functional J(C), stability with respect to noisy data and convergence of the minimizers as \(\alpha \rightarrow 0\) to the solution of the inverse problem.
In the second part of the paper, we use a suitable phase-field relaxation of the functional J in order to overcome issues arising from non-convexity and non-differentiability. To be more precise, we employ an idea adopted by Bourdin and Chambolle, [18] in the context of topology optimization which consists in filling the cavity with a fictitious elastic material described by an elastic tensor \(\mathbb {C}_1:=\delta \mathbb {C}_0\), where \(\delta \) is a small positive parameter and \(\mathbb {C}_0\) has been extended to the whole domain \(\Omega \). In this way, we transform the original inverse problem in the one of reconstructing an elastic inclusion. Then, since the identification of sharp interfaces is in general difficult to be treated numerically, we use a phase-field approach. Instead of binary (i.e., either 0 or 1) phase parameter v describing sharp interfaces between regions with two different materials we use a phase parameter v as a \(H^1\) scalar field, taking values in the interval [0, 1]. Then, we approximate the functional J in (1.2) by means of a Ginzburg-Landau type functional (cf. [52])
where \(\varepsilon \) is a small positive parameter, \(\frac{4}{\pi }\) is a rescaled parameter in the Modica–Mortola relaxation of the perimeter, \(u_\delta (v)\) denotes the solution of the modified boundary value problem:
where
Here \(\mathbb {C}_0\) and \(\mathbb {C}_1\) are the elasticity tensors in \(\Omega \setminus C\) and C, respectively. Ideally, the optimal phase variable v should be close to an ideal binary field. In fact, when \(\varepsilon \) is small the potential term (\(\int _{\Omega }\frac{1}{\varepsilon }v(1-v)\, dx\)) prevails and the minimum is attained by a phase-field variable which takes mainly values close to 0 and 1 and the transition occurs in a thin layer of thickness of order \(\varepsilon \).
The phase-field approach to structural optimization problems has been successfully used by different authors (cf., e.g., [12, 15, 25, 36]), the main advantage being the fact that it allows to handle topology changes as well as nucleation of new holes.
To implement our algorithm in Sect. 3.2 we provide first order necessary optimality conditions for the minimization problem associated to \(J_{\delta ,\varepsilon }\) whose discretized version is then employed in Sect. 4 in order to develop the reconstruction algorithm. Minima of the functional \(J_{\delta ,\varepsilon }\) exist and the numerical experiments of Sect. 5 indicate that they are accurate approximations of minima of J, for \(\varepsilon \) and \(\delta \) sufficiently small. This fact could be rigorously justified proving that the \(\Gamma \)-convergence, as \(\varepsilon \) and \(\delta \) tend to 0, to the functional J holds, but this is still an open issue and will be the subject of a future research. Some attempts along this direction have been done in the scalar case for example in [13, 56, 57].
The literature on reconstruction algorithms for identification of inclusions and cavities in elastostatic, viscoelastic and elastic waves systems is very rich and of big impact. In the case of small elastic inclusions or cavities, asymptotic expansions of the perturbed displacement have been used to detect position, size and shape from boundary measurements, see for example [45] and [8]. The method followed in [5] is based on a shape derivative approach, both for elastic and thermoelastic problems. A topological gradient method has been applied in [24], for the detection of an elastic scatterer, and in [50], for identification of a cavity in time-harmonic wave elastic systems. Ikehata and Itou use the so-called enclosure method for the reconstruction of polygonal cavities in an elastostatic setting [42] and of a general cavity in a homogeneous isotropic viscoelastic body [43]. More recently, Doubova and Fernández–Cara proposed an augmented Lagrangian method to identify rigid inclusions in a elastic waves system [31]. Eberle and Harrach applied the monotonicity method for the reconstruction of elastic inclusions using the monotonicity property of the Neumann-to-Dirichlet map [32], and in [46] the authors used the method of fundamental solutions for the reconstruction of elastic cavities. For other reconstruction approaches we refer to the review paper [17] and references therein. Identification of cavities and elastic inclusions could be interpreted as a special case of the determination of Lamé parameters from boundary measurements, see for example [7, 41] and [61].
The plan of the paper is the following. In Sect. 2 we investigate the continuity of the solution to the direct problem with respect to perturbations of the cavity in the Haussdorff topology and then derive the major properties of the misfit functional J(C). In Sect. 3 we consider the approximation of the cavity with an inclusion of small elasticity tensor, the corresponding misfit functional and its properties. We then introduce its phase-field relaxation and analyze its differentiability and derive necessary optimality conditions related to the phase-field minimization problem. In Sect. 4 we propose an iterative reconstruction algorithm allowing for the numerical approximation of the solution and prove its convergence properties. Finally, in Sect. 5 we present some numerical results showing the efficiency and robustness of the proposed reconstruction algorithm.
1.1 Notation and Geometrical Setting
We introduce the principal notation used in the paper.
Notation We denote scalar quantities, points, and vectors in italics, e.g. x, y and u, v, and fourth-order tensors in blackboard face, e.g. \(\mathbb {A}, \mathbb {B}\).
The symmetric part of a second-order tensor A is denoted by \(\widehat{{A}}:=\tfrac{1}{2}\left( {A}+{A}^T\right) \), where \({A}^T\) is the transpose matrix. In particular, \(\widehat{\nabla } u\) represents the deformation tensor. We utilize standard notation for inner products, that is, \({u}\cdot {v}=\sum _{i} u_{i} v_{i}\), and \({A}: {B}=\sum _{i,j}a_{ij} b_{ij}\) (B is a second-order tensor). |A| denotes the norm induced by the inner product on matrices:
Domains. To represent locally a boundary as a graph of function, we adopt the notation: \(\forall \, x\in \mathbb {R}^d\), we set \(x=(x',x_d)\), where \(x'\in \mathbb {R}^{d-1}\), \(x_d\in \mathbb {R}\), with \(d=2,3\). Given \(r>0\), we denote by \(B_{r}({x})\subset \mathbb {R}^d\) the set \(B_{r}({x}):=\{(x',x_d)/\ |x'|^2+x_d^2<r^2\}\) and by \(B'_{r}({x'})\subset \mathbb {R}^{d-1}\) the set \(B'_{r}({x'}):=\{x'\in \mathbb {R}^{d-1}/\, |x'|^2<r^2\}\).
Definition 1.1
(\(C^{0,1}\) regularity) Let \(\Omega \) be a bounded domain in \(\mathbb {R}^d\). We say that a portion \(\Sigma \) of \(\partial \Omega \) is of Lipschitz class with constants \(r_0\), \(L_0\), if for any \({p}\in \Sigma \) there exists a rigid transformation of coordinates under which we have that p is mapped to the origin and
where \({\psi }\) is a \(C^{0,1}\) function on \(B'_{r_0}({0})\subset \mathbb {R}^{d-1}\), such that
The Hausdorff distance between two sets \(\Omega _1\) and \(\Omega _2\) is defined by
Functional setting: Let \(\Omega \) be a bounded domain. We set
where
is the total variation of v. The BV space is endowed with the natural norm \(\Vert {v}\Vert _{BV(\Omega )} = \Vert {v}\Vert _{L^1(\Omega )} + TV(v)\). We recall that the perimeter of \(\Omega \) is defined as
where \(\chi _{\Omega }\) is the characteristic function of the set \(\Omega \).
Setting \(H^1_{\partial \Omega }(\Omega ):=\{\upsilon \in H^1(\Omega ): \upsilon \lfloor _{\partial \Omega }=0\}\), we recall the following inequalities.
Proposition 1.1
Let \(\Omega \) be a bounded Lipschitz domain. For every \(\upsilon \in H^1_{\partial \Omega }(\Omega )\), there exists a positive constant \(\overline{c}=\overline{c}(\Omega )\) such that
Estimates (1.9) and (1.10) hold also in the case where \(\upsilon \) is zero, in the trace sense, only on a portion of \(\partial \Omega \).
2 Elastic Problem—Detection of a Cavity
The focus of this work is the reconstruction of a cavity in an elastic body from boundary measurements using a phase-field approach. We assume that \(\Omega \) is a bounded domain and that \(\partial \Omega :=\Sigma _N\cup \Sigma _D\), with \(|\Sigma _N| >0\), \(|\Sigma _D|>0\), \(\Sigma _D\) closed, where \(\partial \Omega \) is of Lipschitz class with constants \(r_0\) and \(L_0\). Denoting by C the cavity, we consider the mixed boundary value problem
where \(n,\nu \) are the outer unit normal vector to \(\partial C\) and \(\partial \Omega \), respectively.
We make the following assumptions.
Assumption 2.1
\(\mathbb {C}_0=\mathbb {C}_0(x)\) is a fourth-order tensor such that
Moreover, \(\mathbb {C}_0\) is assumed to be uniformly bounded and uniformly strongly convex, that is, \(\mathbb {C}_0\) defines a positive-definite quadratic form on symmetric matrices:
for \(\xi _0>0\).
Remark 2.1
We require that \(\mathbb {C}_0\) is defined in \(\Omega \), and not only in \(\Omega \setminus C\), because we employ, in the second part of the paper, a reconstruction algorithm based on the strategy of filling the cavity with a fictitious elastic material.
Assumption 2.2
We assume Lipschitz regularity of the cavity (see Definition 1.1), which is a typical requirement to prove uniqueness of the solution to the inverse problem, see [53]. More precisely, we make the following assumption.
Assumption 2.3
Let
We define
For the class of admissible sets \(\mathcal {C}\), the following result holds.
Remark 2.2
\(\mathcal {C}\) is compact with respect to the Hausdorff topology [29, 51].
Remark 2.3
From now on, we will denote with c any constant possibly depending on \(\Omega \), \(r_0\), \(L_0\), d, \(\xi _0\), \(d_0\), \(\overline{c}\), and on the uniform bounds of the elasticity tensor.
Well-posedness of (2.1) in \(H^1_{\Sigma _D}(\Omega \setminus C)\) follows from an application of the Lax-Milgram theorem to the weak formulation of Problem (2.1):
(see for example [28]). Moreover, it holds
Choosing \(\varphi =u\) in (2.4), the last inequality follows from the strong convexity of the elasticity tensor \(\mathbb {C}_0\) (see Assumption 2.1), from an application of the Korn and Poincaré inequality to the left-hand side of (2.4) (see Proposition 1.1), and from the use of a Cauchy–Schwarz inequality to the right-hand side. In fact,
and
and so estimate (2.5) follows by (2.6) and (2.7).
Our aim is to tackle the following inverse problem:
Problem 2.1
Under Assumptions 2.1, 2.2, and 2.3, given \(\displaystyle u_{meas} \in L^2(\Sigma _N)\), find \(C \in \mathcal {C}\) such that \(u\lfloor _{\Sigma _N} = u_{meas}\), where \(u\in H^1_{\Sigma _D}(\Omega \setminus C)\) solves (2.1).
It has been proved in [53] (see also [11]) that Problem 2.1 has a unique solution when \(\partial C\) is of Lipschitz class. Logarithmic stability estimates have been proved under the assumption of \(C^{1,\sigma }\) regularity, \(0<\sigma \le 1\), on the cavity C, cf. [53].
For the reconstruction of the solution to the inverse problem we consider a standard approach based on the minimization of a quadratic misfit functional, with a Tikhonov regularization penalizing the perimeter of C. More precisely, let
where \(\alpha >0\) represents a regularization parameter, \(\text {Per}(C)\) the perimeter of the set C, see (1.8), and \(u(C)\in H^1_{\Sigma _D}(\Omega \setminus C)\) the solution to (2.4).
2.1 Continuity Property of Solutions with Respect to C
Adapting to our case some known results in literature, see for example [21, 23, 26, 37, 49] and references therein, in this section we will show the continuity of the boundary term in (2.8) with respect to perturbations of the cavity C in the Hausdorff distance.
To this purpose, we recall the definition of Mosco convergence and some of its properties (see [21, 22, 37, 51]). Let X be a reflexive Banach space, and \(G_n\) a sequence of closed subspaces of X. We define
and
\(G',G''\) are called the weak-limsup and the strong-liminf of the sequence \(G_n\) in the sense of Mosco.
Definition 2.1
The sequence \(G_n\) converges in the sense of Mosco if \(G'=G''=G\). G is called the Mosco limit of \(G_n\).
In other words, \(G_n\) converges in the sense of Mosco to G when the following two conditions hold:
Given \(\Omega \) and \(\Omega \setminus C\), we can identify the Sobolev space \(H^1_{\Sigma _D}(\Omega \setminus C)\) with a closed subspace of \(L^2(\Omega ,\mathbb {R}^{d+d^2})\) through the map
with the convention of extending u and \(\nabla u\) to zero in C. The same identification holds for \(\Omega \setminus C_n\), extending \(u_n\) and \(\nabla u_n\) to zero in \(C_n\).
Since we are considering the case of uniform Lipschitz domains, we have the following result, which is an adaptation of Theorem 7.2.7 in [21].
Theorem 2.4
Let us assume that \(C_n, C\subset \Omega \) belong to the class \(\mathcal {C}\). If \(C_n\rightarrow C\) in the Hausdorff metric, then \(H^1_{\Sigma _D}(\Omega \setminus C_n)\) converges to \(H^1_{\Sigma _D}(\Omega \setminus C)\) in the sense of Mosco.
We can now prove the following continuity result.
Theorem 2.5
Let \(C_n\in \mathcal {C}\) be a sequence of sets converging to C in the Hausdorff metric (cf. Remark 2.2), and let \(u(C_n)=:u_n\in H^1_{\Sigma _D}(\Omega \setminus C_n)\), \(u(C)=:u\in H^1_{\Sigma _D}(\Omega \setminus C)\) be solutions of (2.4) in \(\Omega \setminus C_n\), \(\Omega \setminus C\), respectively. Then
Proof
Thanks to the uniform Lipschitz regularity of \(\partial (\Omega \setminus C_n)\) (and \(\partial (\Omega \setminus C)\)), we have that the Korn and Poincaré inequalities are uniform with respect to n in \(H^1_{\Sigma _D}(\Omega \setminus C_n)\), since they depend only on the Lipschitz constants of the domain \(\partial (\Omega \setminus C_n)\), see [2, 27]. Therefore, from (2.4) and (2.5), we have that
where c is independent of n.
Hence, from the identification (2.13), we get that \(\Vert u_n\Vert _{L^2(\Omega ,\mathbb {R}^{d+d^2})}\) is uniformly bounded. Up to subsequences, there exists \(u^*\in L^2(\Omega ,\mathbb {R}^{d+d^2})\) such that
Thanks to Theorem 2.4 and from the first condition of the Mosco convergence applied to \(G_n=H^1_{\Sigma _D}(\Omega \setminus C_n)\), \(G=H^1_{\Sigma _D}(\Omega \setminus C)\), and \(X=L^2(\Omega ,\mathbb {R}^{d+d^2})\), see (2.11), we have that \(u^*\in H^1_{\Sigma _D}(\Omega \setminus C)\).
Moreover, taking \(\varphi \in H^1_{\Sigma _D}(\Omega \setminus C)\), there exists \(\varphi _n\in H^1_{\Sigma _D}(\Omega \setminus C_n)\) by (2.12) such that
Considering the weak formulation for \(u_n\) (see (2.4) specialized to the case with \(C=C_n\) and \(\varphi =\varphi _n\))
and since \(\varphi _n\in H^1_{\Sigma _D}(\Omega \setminus C_n)\) and \(\varphi \in H^1_{\Sigma _D}(\Omega \setminus C)\), it holds
Hence, thanks to Assumption 2.3 and (2.16), we have
as \(n\rightarrow +\infty \), where \(\Omega ^{d_0/2}\) is defined as in (2.3). Therefore,
The term on the left-hand side of (2.17) is equal to
Then, by (2.15) and (2.16), it follows
as \(n\rightarrow +\infty \). Analogously, for the second integral on the right-hand side of (2.19), using the symmetries of the elasticity tensor, we get
as \(n\rightarrow +\infty \). Consequently, using (2.20) and (2.21) in (2.19), we get
Therefore, we find that
where the last equality comes from the weak formulation (2.4). Therefore,
so that \(u^*=u\). This conclusion comes from the choice \(\varphi =u^*-u\), and the use of Assumption 2.1 and Korn and Poincarè inequalities (see Proposition 1.1).
Next, we prove that \(u_n\rightarrow u\) in \(L^2(\Sigma _N)\) by showing strong convergence of \(u_n\) to u in \(H^1\)-norm in a neighborhood of the boundary of \(\Omega \). Consider the weak formulations
Now, we define \(\Phi =(u_n-u)\chi ^2\), where \(\chi \) is a smooth cut-off function, \(\chi \in [0,1]\) in \(\Omega \), such that
Then, we choose \(\varphi _1=\varphi _2=\Phi \) in (2.23) and (2.24), that is
Subtracting the last two equations, we find
that is,

On the second integral, we apply the Young’s inequality with a suitable parameter \(\kappa >0\), that is

Hence, using this last inequality in (2.25), we get

The right-hand side integral goes to zero, noticing that

The left-hand side can be estimated using the fact that
and, then, by means of the Korn inequality
From (2.27) and (2.26), and recalling that \(u_n\) is converging strongly in \(L^2\)-norm to u from the previous results, we find that
Finally, by the continuity of the trace theorem the proof is concluded. \(\square \)
Remark 2.6
In the previous result, \(u_n\rightarrow u\) in \(L^2(\Sigma _N)\) can be also proved using the following arguments: note that the trace operator is a linear continuous operator from \(H^1_{\Sigma _D}(\Omega \setminus C_n)\) to \(H^{\frac{1}{2}}(\Sigma _N)\) (and, analogously, from \(H^1_{\Sigma _D}(\Omega \setminus C)\) to \(H^{\frac{1}{2}}(\Sigma _N)\)), hence is also continuous in the weak topology, see [19]. Moreover, since \(H^{\frac{1}{2}}(\Sigma _N) \hookrightarrow L^2(\Sigma _N)\) is compact, we find that \(u_n\rightarrow u\) in \(L^2(\Sigma _N)\).
As a consequence of the continuity of the boundary functional, some properties of the functional J(C) defined in (2.8) follow.
Proposition 2.7
For every \(\alpha >0\) there exists at least one solution of the minimization problem (2.8).
Proof
Let \(\{C_n\}_{n\ge 0}\in \mathcal {C}\) be a minimizing sequence. Then there exists a positive constant M such that
hence
By compactness (see Thereom 3.39 in [4]), there exists a set of finite perimeter \(C_0\) such that, possibly up to a subsequence,
where \(C_n\triangle C_0\) is the symmetric difference of the two sets. Moreover, thanks to the compactness and equiboundedness of the sets \(C_n\) and the fact that \(C_n\in \mathcal {C}\), there exists a further subsequence which converges in the Hausdorff metric to \(C_0\in \mathcal {C}\), thanks to [39, Theorem 2.4.10]. Moreover, by the lower semicontinuity of the perimeter functional (see Section 5.2.1, Theorem 1, in [34]) it follows that
Using the continuity of the boundary functional, see (2.14), we also have
In conclusion, we find that
and the claim follows. \(\square \)
We also prove stability with respect to the measured data.
Proposition 2.8
Solutions of (2.8) are stable with respect to perturbations of the data \(u_{meas}\), i.e., if \(u_n\rightarrow u_{meas}\) in \(L^2(\Sigma _N)\) as \(n\rightarrow \infty \) then the solutions \(C_n\) of (2.8) with datum \(u_n\) are such that, up to subsequences,
where \(\widetilde{C}\in \mathcal {C}\) is a solution of (2.8), with datum \(u_{meas}\).
Proof
Using (2.8), we have that, for any n, \(C_n\) satisfies
for all \(C\in \mathcal {C}\). Therefore, \(\text {Per}(C_n)\le M\) and hence, possibly up to subsequences,
for some \(\widetilde{C}\in \mathcal {C}\), and
Moreover, by the continuity of the solution of (2.4) with respect to C, see Theorem 2.5, we get
for all \(C\in \mathcal {C}\). Summarizing, \(\widetilde{C}\in \mathcal {C}\) and it is a minimizer of the functional, hence the assertion follows. \(\square \)
Finally, we can prove that the solution of the minimization problem (2.8) converges to the unique solution of the inverse problem when the regularization parameter tends to zero.
Proposition 2.9
Let us assume that there exists a solution \(C^{\sharp }\in \mathcal {C}\) of the inverse problem corresponding to datum \(u_{meas}\). Moreover, for any \(\eta >0\) let \((\alpha (\eta ))_{\eta >0}\) be such that \(\alpha (\eta )=o(1)\) and \(\frac{\eta ^2}{\alpha (\eta )}\) is bounded as \(\eta \rightarrow 0\).
Furthermore, let \(C_{\eta }\) be a solution to the minimization problem (2.8) with \(\alpha =\alpha (\eta )\) and datum \(u_{\eta }\in L^2(\Sigma _N)\) satisfying \(\Vert u_{meas}-u_{\eta }\Vert _{L^2(\Sigma _N)}\le \eta \). Then
in the Hausdorff metric, as \(\eta \rightarrow 0\).
Proof
From the definition of \(C_{\eta }\), it immediately follows that
Straightforwardly, we find that
Hence, up to subsequences, arguing as in Proposition 2.8, we get
for some \(C_0\in \mathcal {C}\). From (2.30) and (2.31), as \(\eta \rightarrow 0\), we find
hence, also
By the continuity result in Theorem 2.5 and using the last relation, we find that
Therefore, thanks to the uniqueness result of the inverse problem in Lipschitz domains (cf. [53]) we get \(C_0=C^{\sharp }\). \(\square \)
3 Reconstruction of Cavities—Filling the Void
From the numerical point of view, the minimization of the functional (2.8) is complicated due to its non-differentiability. A typical approach to overcome this issue is to consider a further regularization of the functional, where the perimeter is approximated by a Ginzburg-Landau type functional, see for example [18]. This approach is well-known in the literature and it has been applied in different contexts, see for example [3, 12, 14,15,16, 18, 25, 30, 35, 44, 48].
First, we note that Problem (2.8) is equivalent to the following formulation
where \(X_{0,1}:=\{v\in BV(\Omega )\,:\, v=\chi _{C} \, \hbox { a.e. in }\Omega , \,C\in {{\mathcal {C}}}\}\), TV(v) is defined in (1.7), and \(\chi _C\) is the indicator function of C. Note that the space \(X_{0,1}\) is endowed with the norm \(\Vert {v}\Vert _{BV(\Omega )} = \Vert {v}\Vert _{L^1(\Omega )} + TV(v)\).
Remark 3.1
By compactness properties of \(BV(\Omega )\) (see, e.g., [4], Theorem 3.23), any uniformly bounded sequence in \(X_{0,1}\) admits a subsequence converging in \(L^1(\Omega )\) to an element in \(X_{0,1}\). In fact, let \(v_n\) a sequence uniformly bounded in \(X_{0,1}\), there exists, possibly up to a subsequence, \(v\in BV(\Omega )\) such that
Since \(v_n\) attains values 0 and 1 only, it follows that \(v\in X_{0,1}\).
Following the approach proposed in [18], we fill the cavity with a fictitious material with elastic properties that are different from the background. Specifically, we take an elasticity tensor \(\mathbb {C}_1:=\delta \mathbb {C}_0\), where \(\delta >0\) is sufficiently small. Therefore, the boundary value problem (2.1) is modified into
where
Here \(\mathbb {C}_0\) and \(\mathbb {C}_1\) are the elasticity tensors in \(\Omega \setminus C\) and C, respectively.
Remark 3.2
Thanks to Assumption 2.1, the fact that \(\delta >0\), and by (3.3), the elasticity tensor \(\mathbb {C}_{\delta }(v)\) is strongly convex.
Remark 3.3
The following analysis can be generalized to the case of a generic fourth-order elasticity tensor \(\mathbb {C}_1\) which is strongly convex and uniformly bounded with the further hypothesis that
Remark 3.4
When dealing with sequences, we will often use the simplified notation \(u_n:= u_{\delta }(v_n), \, u := u_{\delta }(v), \, \mathbb {C}_n := \mathbb {C}_{\delta }(v_n), \,\mathbb {C} := \mathbb {C}_{\delta }(v)\).
The elastic problem (3.2) has the following weak formulation:
Well-posedness of Problem (3.2) in \(H^1_{\Sigma _D}(\Omega )\) follows in the same way as for Problem (2.1), and, in addition
We now approximate Problem (3.1) with the following one
where \(u_{\delta }(v)\in H^1_{\Sigma _D}(\Omega )\) is the solution of Problem (3.2).
We prove the existence of minima of \(J_{\delta }(v)\) in \(X_{0,1}\), on account of the ideas contained in [14]. The proof is a consequence of the following property.
Proposition 3.5
Let \(\{v_n\} \subset X_{0,1}\) be strongly convergent in \(L^1(\Omega )\) to \(v \in X_{0,1}\). Then \(\{u_{\delta }(v_n)\lfloor _{\Sigma _N}\}\) strongly converges in \(L^2(\Sigma _N)\) to \(u_{\delta }(v)\lfloor _{\Sigma _N}\), i.e., the map \(F : v \rightarrow u_{\delta }(v)\lfloor _{\Sigma _N}\) is continuous from \(X_{0,1}\) to \(L^2(\Sigma _N)\) in the \(L^1\) topology.
Proof
Consider the weak formulation (3.4) associated to v and \(v_n\), respectively,
Subtracting the two equations and setting \(u_n:= u_{\delta }(v_n), \, u := u_{\delta }(v), \, \mathbb {C}_n := \mathbb {C}_{\delta }(v_n), \,\mathbb {C} := \mathbb {C}_{\delta }(v)\), we get
Thus, making the choice \(\varphi = u_n - u\) and proceeding similarly as in (2.5) to get \(H^1\)-estimates, we find
and then, by \(\mathbb {C}_n - \mathbb {C} = (\mathbb {C}_1 - \mathbb {C}_0)(v_n - v)\) and the uniform bound on the elasticity tensor, see Assumption 2.1, we derive
Observe now that \(v_n - v \rightarrow 0\) in \(L^1(\Omega )\) as \(n\rightarrow +\infty \) so that, possibly up to a subsequence, \(v_n -v \rightarrow 0\), a.e. in \(\Omega \). Moreover, recalling that \(v_n\) and v are bounded and \(u \in H^1(\Omega )\), we deduce, by dominated convergence theorem, that
Finally, the trace theorem implies
\(\square \)
Proposition 3.6
\(J_{\delta }(v)\) admits a minimum \(v \in X_{0,1}\).
Proof
Observe that \(J_{\delta }(v)\) is bounded from below, by definition. Moreover, \(J_{\delta }(v) \ne + \infty \), for \(v\in X_{0,1}\). So, let \(\{v_n\} \subset X_{0,1}\) be a minimizing sequence of \(J_{\delta }(v)\), that is
Then
Hence, there exists a positive constant c, independent on n, such that
This implies that \(v_n\) is uniformly bounded in \(X_{0,1}\). Therefore, thanks to Remark 3.1, there exists \(v \in X_{0,1}\) such that \(v_n\rightarrow v\) in \(L^1(\Omega )\). Due to the lower semicontinuity of TV(v) with respect to the \(L^1\)-convergence, we have
and, using Proposition 3.5, we get
\(\square \)
3.1 Phase-Field Relaxation
Proceeding as in [14, 30], we now consider a phase-field relaxation of the optimization problem (3.5). More precisely, we define a minimization problem for a differentiable cost functional defined on a convex subspace of \(H^1(\Omega )\), namely on the set
where \(\Omega ^{d_0/2}\) has been defined in (2.3), and, for every \(\varepsilon >0\), we replace the total variation term with the following Modica–Mortola functional.
Problem 3.1
Given \(u_{meas} \in L^2(\Sigma _N)\), and \(\varepsilon ,\delta >0\), find
\(u_{\delta }(v)\in H^1_{\Sigma _D}(\Omega )\) being the solution to (3.2), for \(v\in \mathcal {K}\), and \(\widetilde{\alpha }=\frac{4}{\pi }\alpha \), where \(4/\pi =(2\int _0^1 \sqrt{v(1-v)}\, dv)^{-1}\) is a rescaling parameter, see [1].
Remark 3.7
We expect \(\Gamma \)-convergence of the functional \(J_{\delta ,\varepsilon }\) to J, given in (3.1). However, this analysis is involved in the elastic context and is still an open issue that needs a specific accurate study.
The following result holds
Proposition 3.8
For any \(\delta ,\varepsilon >0\), Problem (3.8) admits a solution \(v=v_{\delta ,\varepsilon } \in \mathcal{K}\).
Proof
Let us fix \(\delta ,\varepsilon > 0\) and consider a minimizing sequence \(\{ v_n \} \subset \mathcal {K}\) for \(J_{\delta ,\varepsilon }(v)\) (we omit the dependence of \(v_n\) on \(\delta \) and \(\varepsilon \)). We have
Hence, by definition of minimizing sequence, \(0\le J_{\delta ,\varepsilon }(v_n) \le 2M\) independently of n, which implies that also \(\Vert {\nabla v_n}\Vert _{L^2(\Omega )}^2\) is bounded. Moreover, recalling that \(v_n \in \mathcal {K}\) and \(0\le v_n (x)\le 1\) a.e. in \(\Omega \), we deduce that \(\Vert {v_n}\Vert _{L^2(\Omega )}\le M_1\), with \(M_1\) independent of n and hence \(\Vert {v_n}\Vert _{H^1(\Omega )}\le M_2\), with \(M_2\) independent of n. Due to the weak compactness of \(H^1(\Omega )\), there exists \(v \in H^1(\Omega )\) such that, possibly up to a subsequence, \( v_n \rightharpoonup v\) in \(H^1(\Omega )\). Hence, \(v_n \rightarrow v\) strongly in \(L^2(\Omega )\) and \(v_n \rightarrow v\) a.e. in \(\Omega \). Since \(v_n(1-v_n)\le 1/4\), by means of the Lebesgue’s dominated convergence theorem, we get
Moreover, by the lower semicontinuity of the \(H^1(\Omega )\) norm with respect to the weak convergence, we obtain
By the last inequality and the convergence of \(v_n\) to v a.e., by the use of Proposition 3.5 and the fact that \(v_n\) is a minimizing sequence, we have
Finally, by pointwise convergence, we know that \(0 \le v \le 1\) a.e. in \(\Omega \) and \(v = 1\) a.e. in \(\Omega ^{d_0/2}\). Hence, v is a minimum of \(J_{\delta ,\varepsilon }\) in \(\mathcal {K}\). \(\square \)
3.2 Necessary Optimality Conditions
In this section we provide an expression for the first order necessary optimality condition associated with the minimization problem (3.8), formulated as a variational inequality involving the Fréchet derivative of \(J_{\delta ,\varepsilon }\).
Proposition 3.9
Define the map \(F:\mathcal {K} \rightarrow H^1(\Omega ), \, F(v) = u_{\delta }(v)\), \(u_{\delta }(v)\) solution to (3.2). Then the operators F and \(J_{\delta ,\varepsilon }\) (for every \(\delta , \varepsilon >0\)) are Fréchet-differentiable on \(\mathcal {K} \subset L^{\infty }(\Omega ) \cap H^1(\Omega )\).
Moreover, any minimizer \(v_{\delta ,\varepsilon }\) of \(J_{\delta ,\varepsilon }\) satisfies the variational inequality
where
Here \(\vartheta \in \mathcal {K}-v=\{z \ s.t. \ z+v \in \mathcal {K}\}\) and \(p_{\delta }\in H_{\Sigma _D}^1(\Omega )\) is the solution to the adjoint problem
Proof
First we prove that F is Fréchet differentiable in \(L^{\infty }(\Omega )\). More precisely,
where \(u^{\sharp }(v)\) is the solution in \(H_{\Sigma _D}^1(\Omega )\) of
namely,
To this aim, we first show that
Indeed, the difference \(u_{\delta }(v+\vartheta )-u_{\delta }(v)\) satisfies
Taking \(\varphi = u_{\delta }(v+\vartheta )-u_{\delta }(v)\) and recalling that \(\mathbb {C}_{\delta }(v + \vartheta ) - \mathbb {C}_{\delta }(v) = (\mathbb {C}_1 - \mathbb {C}_0)\vartheta \), we obtain
Hence, by using the assumptions on the elasticity tensors, Korn and Poincaré inequalities, and the fact that \(v + \vartheta \in \mathcal {K}\), we obtain
We now estimate \(u_{\delta }(v+\vartheta )-u_{\delta }(v) - u^{\sharp }(v)\). Subtracting (3.12) from (3.14) and setting \(\omega = u_{\delta }(v+\vartheta )-u_{\delta }(v)\), then it holds
from which
Choosing now \(\varphi = \omega - u^{\sharp }(v)\), we get
and again by the boundedness of the elasticity tensors and the use of Korn and Poincaré inequalities it follows
so that \(F^\prime (v)[\theta ] = u^{\sharp }(v)\).
We now prove that \(J_{\delta ,\varepsilon }\) is Fréchet differentiable. By means of the chain rule and the Frechét differentiability of F, we compute the expression of \(J'_{\delta ,\varepsilon }(v)\), i.e.,
where, with abuse of notation, F(v) and \(F'(v)[\vartheta ]\) denote the trace of F(v) and \(F'(v)[\vartheta ]\) on \(\Sigma _N\), respectively. By the definition of the adjoint problem and of \(u^{\sharp }(v)\), we get
and hence
Finally, by standard arguments, since \(J_{\delta ,\varepsilon }\) is a continuous and Frechét differentiable functional on a convex subset \(\mathcal {K}\) of the Banach space \(H^1(\Omega )\), the optimality conditions for the optimization problem (3.8) are expressed in terms of the variational inequality (3.9). \(\square \)
4 Discretization and Reconstruction Algorithm
4.1 Convergence Analysis
Here, we assume that \(\Omega \) is a polygonal (\(d=2\)) or polyhedral (\(d=3\)) domain. Again, for simplifying the notation, we denote by \(u:=u_{\delta }\) and \(p:=p_{\delta }\).
Let \((\mathcal {T}_h)_{0<h\le h_0}\) be a regular triangulation of \(\Omega \) and define
where \(\mathcal {P}_1(\mathcal {T})\) is the set of polynomials of first degree on \(\mathcal {T}\), and
For every \(h>0\), we set \(u_h:=(u_{\delta })_h:\mathcal {K}\rightarrow \mathcal {V}_{h,\Sigma _D}\) where \(u_h\) is solution to
Here \(g_h\) is a piecewise linear, continuous approximation of g such that \(g_h\rightarrow g\) in \(L^2(\Sigma _N)\) as \(h\rightarrow 0\).
As in [30], one can show that for every \(v\in \mathcal {K}\) there exists a sequence \(v_h\in \mathcal {K}_h\) such that \(v_h \rightarrow v\) in \(H^1(\Omega )\). Most of the following results are an adaptation of those presented in [30] for a scalar equation to the case of the elasticity system, hence we do not provide the proofs for some of them.
The following lemma is a consequence of the continuity and coercivity of the bilinear form on the left-hand side of (4.3) and Céa’s Lemma (see, e.g., [14]).
Lemma 4.1
Let \(g\in L^2(\Sigma _N)\). Then, \(\forall \, v\in \mathcal {K}\), \(u_h(v) \rightarrow u(v)\) strongly in \(H^1(\Omega )\) as \(h\rightarrow 0\).
Next we state a result concerning the continuity of \(u_h\) in the space \(\mathcal {V}_{h,\Sigma _D}\).
Proposition 4.2
Let \(h_k\), \(v_{h_k}\) be two sequences such that \(\lim \limits _{k\rightarrow +\infty } h_k=0\) and \(v_{h_k}\in \mathcal {K}_{h_k}\) with \(v_{h_k}\rightarrow v\) in \(L^1(\Omega )\). Then \(u_{h_k}(v_{h_k})\rightarrow u(v)\) in \(H^1_{\Sigma _D}(\Omega )\) for \(k\rightarrow +\infty \).
Proof
The proof can be obtained reasoning similarly as in Lemma 3.1 of [30]. \(\square \)
Let \(J_{\delta ,\varepsilon ,h}:\mathcal {K}_h\rightarrow \mathbb {R}\) be the approximation to \(J_{\delta ,\varepsilon }\) defined as follows
where we assume that \(u_{meas,h}\rightarrow u_{meas}\), as \(h\rightarrow 0\). Similarly as in Theorem 3.2 of [30], we can show the following result.
Theorem 4.3
There exists \(v_h\in \mathcal {K}_h\) such that \(J_{\delta ,\varepsilon ,h}(v_h)=\min _{\eta _h\in \mathcal {K}_h} J_{\delta ,\varepsilon ,h}(\eta _h)\). Moreover, let \(h_k\) be such that \(\lim _{k\rightarrow +\infty } h_k=0\). Then every sequence \(v_{h_k}\) has a subsequence converging strongly in \(H^1(\Omega )\) and a.e. in \(\Omega \) to a minimum of \(J_{\delta ,\varepsilon }\).
In our numerical algorithm we approximately solve (3.8) and so we look for an admissible point \(v_h\in \mathcal {K}_h\) that satisfies the first order necessary condition
rather than trying to locate a global minimum of \(J_{\delta ,\varepsilon ,h}\). To this aim, we consider the discrete adjoint problem: find \(p_h:=(p_{\delta })_h\in \mathcal {V}_{h,\Sigma _D}\) such that
Then using \(v_h\in \mathcal {K}_h\), we can prove the discrete version of Proposition 3.9, where the discrete variational inequality reads as:
Then, we can prove the following theorem:
Theorem 4.4
Let \(h_k\) be such that \(\lim _{k\rightarrow +\infty } h_k=0\) and \(v_{h_k}\) be a sequence satisfying (4.5). Then there exists a subsequence of \(v_{h_k}\) that converges strongly in \(H^1(\Omega )\) and a.e. in \(\Omega \) to a solution v of (3.9).
Proof
We set \(v_k:=v_{h_k}\), \(u_k:=u_{h_k}(v_{h_k})\) and \(p_k:=p_{h_k}(v_{h_k})\). Testing (4.6) with \(\psi _h=p_k\) we get
which yields, arguing as in (2.5) to get \(H^1\)-estimates,
As the problem for \(u_k\) is well-posed with \(u_k\in H^1_{\Sigma _D}(\Omega )\) and \(u_{meas,k}\rightarrow u_{meas}\) (implying that \(\Vert u_{meas,k}\Vert _{L^2(\Sigma _N)}\) is uniformly bounded with respect to k), we get
A similar result holds for \(\Vert u_k\Vert _{H^1(\Omega )}\). Therefore
From (4.7), employing \((1-2v_k)(w_k-v_k)\le w_k + 2v_k^2\) and testing with \(w_k=0\in \mathcal {K}_h\), we get
where we used (4.8). Therefore, \(v_k\) is bounded in \(H^1(\Omega )\), hence there exists a subsequence (still denoted by \(v_k\)) and \(v\in \mathcal {K}\) such that
Thanks to Proposition 4.2 we have
Now, let \(p\in H^1_{\Sigma _D}(\Omega )\) be the solution of the continuous adjoint problem and let \(\hat{p}_k\in \mathcal {V}_{h_k,\Sigma _D}\) be such that \(\hat{p}_k\rightarrow p\) in \(H^{1}_{\Sigma _D}(\Omega )\). Taking the difference of the problems solved by p and \(p_k\), after some standard manipulation we get
for all \(\psi \in \mathcal {V}_{h_k,\Sigma _D}\). Taking \(\psi =p_k-\hat{p}_k\), we get
By hypothesis, we have \( \Vert u_{meas}-u_{meas,k}\Vert _{L^2(\Sigma _N)}\rightarrow 0\) and \(\Vert p-\hat{p}_k\Vert _{H^1(\Omega )}\rightarrow 0\) for \(k\rightarrow +\infty \). Hence, invoking Proposition 4.2 and observing that \( \int _{\Omega } \vert v-v_k\vert ^2 \vert \widehat{\nabla }p\vert ^2 \rightarrow 0\) for \(k\rightarrow +\infty \), we deduce \(p_k\rightarrow p\) in \(H^1(\Omega )\).
Next, we have to show that v satisfies the variational inequality (3.9). Given \(\omega \in \mathcal {K}\), there exists a sequence \(\hat{\omega }_k\in \mathcal {K}_{h_k}\) such that \(\hat{\omega }_k\rightarrow \omega \) in \(H^1(\Omega )\) and a.e. in \(\Omega \). Then, from the discrete variational inequality (4.7) we have for \(v_k\) that
Now, observe that
The first integral on the right hand side converges to zero by (4.10) and \(p_k\rightarrow p\) in \(H^1(\Omega )\). To show that also the second integral converges to zero, we invoke the dominated convergence theorem. Hence, from (4.13), we obtain
as \(k\rightarrow +\infty \). Then, utilizing (4.14) into (4.12), together with the fact that \(v_k \rightharpoonup v\) in \(H^1(\Omega )\), and the lower semicontinuity of the norm, we find
Morover, noticing that \(\int _\Omega v_k \hat{\omega }_k\rightarrow \int _\Omega v \omega \) for \(k\rightarrow +\infty \), we get
Finally, it remains to show that \(v_k\rightarrow v\) strongly in \(H^1(\Omega )\). We choose a sequence \(\hat{v}_k\in \mathcal {K}_{h_k}\) such that \(\hat{v}_k\rightarrow v\) in \(H^1(\Omega )\) and using the discrete variational inequality (4.7) with \(\omega _{h_k}=\hat{v}_k\), we easily get \(\nabla v_k\rightarrow \nabla v\) in \(L^2(\Omega )\), implying the result. \(\square \)
4.2 Reconstruction Algorithm
In order to solve the discrete optimization problem we follow the method used in [14] and [30]. The method is based on solving the following parabolic obstacle problem. For \(\delta ,\varepsilon >0\) fixed, let v be the solution to
An easy computation shows that the value of the objective functional decreases in time. Hence, we expect that if the limit as \(t\rightarrow +\infty \) of its solution \(v(\cdot ,t)\) exists and it is equal to the asymptotic state \(v_\infty \), then this should satisfy the continuous optimality conditions (3.9).
We now discretize the above problem by using a semi-implicit time discretization scheme. We denote by \(\{ v_h^n\}_{n\in \mathbb {N}}\subset \mathcal {K}_h\) the sequence of approximations \(v_h^n\simeq v(\cdot ,t^n)\) obtained as follows:
where \(\tau _n\) is the time step, and \(u_h^n\), \(p_h^n\in \mathcal {V}_{h,\Sigma _D}\) are the discrete solutions of the forward problem (4.3) and adjoint problem (4.6), respectively, for \(v_h=v_h^n\). We now prove a monotonicity property of the method.
Lemma 4.5
For each \(n \in \mathbb {N}\), there exists a constant \(c^n>0\) such that, if \(\tau _n\le (1+c^n)^{-1}\), then
where \(c^n=c^n(\Omega ,\delta ,\xi _0,h,\Vert \mathbb {C}_0 - \mathbb {C}_1\Vert _{L^\infty (\Omega )}, \Vert p_h^n\Vert _{W^{1,\infty }(\Omega )}, \Vert u_h^n\Vert _{W^{1,\infty }(\Omega )}).\)
Proof
Choosing \(\omega _h=v_h^n\) in (4.16), after some simple manipulations we obtain
Adding and subtracting \(\frac{1}{2}\Vert {u_h^{n+1} - u_{meas,h}}\Vert _{{L^2(\Sigma _N)}}^2 \) and \(\frac{1}{2}\Vert {u_h^n- u_{meas,h}}\Vert _{{L^2(\Sigma _N)}}^2 \), we get
which implies
where in the last step we employed
It is easy to verify that it holds
where the last step follows from the definition of the discrete adjoint problem.
Then, using the Cauchy–Schwarz inequality, the trace theorem and the fact that in finite dimensional spaces all norms are equivalent, we have
where \(c_0^n=c_0^n(\Omega , h)\), \(c_1^n=c^n_1(\Vert \mathbb {C}_1 - \mathbb {C}_0\Vert _{L^\infty (\Omega )}, \Vert \widehat{\nabla }p_h^n\Vert _{L^\infty (\Omega )}, \Omega ,h)\) and \(c_2^n\) is the constant in the trace theorem.
In the sequel we bound \(\Vert u_h^{n+1} - u_h^n\Vert _{H^1(\Omega )}\) by means of the term \(\Vert v_h^n - v_h^{n+1}\Vert _{L^2(\Omega )}\). To this aim, we subtract the equations for \(u_h^{n+1}\) and \(u_h^n\) (cf. (4.3)) and employ \(\varphi =u_h^{n+1}- u_h^n\) as a test function. A standard manipulation yields
with \(c_3^n=c^n_3(\Omega ,\delta ,\xi _0,h,\Vert \mathbb {C}_1 - \mathbb {C}_0\Vert _{L^\infty (\Omega )}, \Vert \widehat{\nabla }p_h^n\Vert _{L^\infty (\Omega )})\). Employing (4.20) into (4.19), we obtain
where \(c_4^n=c^n_4(\Omega ,\delta ,\xi _0,h,\Vert (\mathbb {C}_1 - \mathbb {C}_0\Vert _{L^\infty (\Omega )}, \Vert \widehat{\nabla }p_h^n\Vert _{L^\infty (\Omega )},c_2^n)\).
Using (4.21) into (4.18), we deduce
Now, since
we get
Finally, choosing \(\tau _n \le \frac{1}{1+c_4^n}\), the assertion of the lemma follows, just setting \(c^n:=c^n_4\). \(\square \)
We are now ready to state a convergence result for our numerical scheme.
Theorem 4.6
Let \(v_h^0\in \mathcal {K}_h\) be an initial guess. Then there exists a collection of timesteps \(\tau _n\) such that \(0< \gamma \le \tau _n \le (1+c^n)^{-1} \), \(\forall n>0\), where \(c^n\) is the constant appearing in Lemma 4.5, and \(\gamma \) depends on the data and possibly on h. The corresponding sequence \(v_h^n\) generated by (4.16) has a convergence subsequence (still denoted by \(v_h^n\)) in \(W^{1,\infty }\) such that
where \(v_h\in \mathcal {K}_h\) satisfies the discrete optimality condition
Proof
Consider a collection of timesteps bounded by \((1+c^n)^{-1}\), for all \(n>0\). Employing Lemma 4.5, we have
Hence, the sequence \(v_h^n\) is bounded in \(H^1_0(\Omega )\) and it holds
From the weak formulation of the forward and adjoint problems, the previous relations give that \(u_h^n\) and \(p_h^n\) are bounded in \(H^1(\Omega )\), hence in \(W^{1,\infty }(\Omega )\) as we are in finite dimensional spaces. Therefore, thanks to the definition of the constant \(c^n\), reported in the last part of the proof of Lemma 4.5, this gives that there exists a constant \(M>0\) such that \(c^n<M\), and equivalently there exists a positive constant \(\gamma >0\), independent of n, such that \(\gamma \le (1+c^n)^{-1}\). Hence, there exists a subsequence of \((v_h^n,u_h^n,p_h^n)\) (still denoted by the same symbol) such that
and in particular
Hence, \(u_h\) is the solution of the discrete forward problem and \(p_h\) is the solution of the discrete adjoint problem. Finally, from (4.16) and \(\tau _n \ge \gamma \) we get
From (4.27) and recalling that \(v_h^n\rightarrow v_h\), we deduce that \(v_h\) satisfies the discrete optimality condition (4.5). \(\square \)
5 Numerical Examples
In this section we show the numerical results which are obtained from an application of the Primal Dual Active Set Method (PDASM) to the variational inequality (4.16). This method has been presented in [40] and later applied for the detection of conductivity inclusions in [30] and [14] for a linear and a semilinear elliptic equation, respectively. Primal dual active set methods represent a very good choice in engineering applications due to their effectiveness and robustness (cf., e.g., [38]). Here, we show that choosing the parameter \(\delta \) sufficiently small we are able to reconstruct elastic cavities of different shapes. Given a tolerance \(\text {tol}>0\), the reconstruction algorithm is based on the following steps.

In the implementation of Algorithm 1, the numerical experiments are performed for \(d=2\) in the domain \(\Omega =(-1,1)^2\), using a triangular tessellation \(\mathcal {T}_h\) of \(\Omega \). As boundary measurements, we use synthetic data. They are generated by solving via the Finite Element method the forward problem (2.1), with boundary conditions prescribed as in Fig. 2a on the square, with one or more cavities of given geometries. We use a tessellation \(\mathcal {T}^{ref}_h\) which is more refined than \(\mathcal {T}_h\) on the common part outside the cavities (see Fig. 1 for an example of the two tessellations) in order not to commit inverse crime. Once extracting the values of the solution of the forward problem on the boundary of the domain \(\Omega \) obtained by the mesh \(\mathcal {T}^{ref}_h\), we interpolate these values on the mesh \(\mathcal {T}_h\).
Therefore, by \(u_{meas}\) we denote the resulting boundary datum on the mesh \(\mathcal {T}_h\). We also mention that the triangular mesh is adaptively refined during the reconstruction procedure using the values of \(\nabla v_h\) after an a-priori fixed number of iterations which depend on the specific numerical example. See, as example, Fig. 2b related to the reconstruction of a circular cavity.
In the reconstruction procedure, i.e. for the implementation of the Algorithm 1, we assume to know two different boundary measurements. In fact, in the context of inverse boundary value problems of this kind, it is reasonable to use \(N_g>1\) different boundary measurements \(u^{i}_{meas}\), for \(i=1,\ldots ,N_g\) which clearly improve the numerical reconstruction results. Thus, we consider a slight modification of the original optimization problem (3.8), assuming the knowledge of \(N_g\) different Neumann boundary data \(g^i\), for \(i=1,\ldots ,N_g\) and hence considering
where \(u^{i}_{\delta }(v)\in H^1_{\Sigma _D}(\Omega )\) is the solution to (3.2) with \(g=g^{i}\) and for \(v\in \mathcal {K}\). The necessary optimality condition related to (5.1) can be equivalently obtained reasoning similarly as we did to derive (3.10).
In Table 1, we collect some of the parameters utilized in most numerical tests. Possible changes in these values are highlighted in the text related to each specific experiment.
Finally, all the numerical experiments are performed choosing, as initial guess, the phase-field variable \(v_0=0\).
5.1 Numerical Experiments with \(N_g=2\) and Without Noise in the Measurements
Test 1: reconstruction of a circular cavity The elastic medium is described by the Lamé parameters \(\mu =0.2\) and \(\lambda =1\). The Neumann boundary conditions are \(g^1(x,y)=(0, \frac{1}{10}-\frac{3}{10}y)\) and \(g^2(x,y)=(-\frac{1}{2}x^2, y^2)\). We set the parameter \(\varepsilon =\frac{1}{16\pi }\). The mesh is refined with respect to the gradient of the phase-field variable every 1000 iterations. The algorithm stops after \(n=3544\) iterations. In Fig. 3 we show the numerical results at three different time steps.
Test 2: reconstruction of a circular cavity—changing boundary conditions and Lamé parameters We propose the same numerical experiments of Test 1, showing how the results change using different Neumann boundary conditions and Lamé parameters. We report in the captions of Fig. 4 the selected parameters, data, and also the number of time steps needed for reaching the tolerance. Note that the three experiments consider different values for the Poisson coefficient \(\nu :=\frac{\lambda }{2(\lambda +\mu )}\), that is \(\nu =\frac{1}{4}\), \(\nu =\frac{1}{3}\), and \(\nu =-\frac{1}{18}\), respectively. In the three numerical examples of Fig. 4, the refinement of the mesh happens every 1500, 1000, 2000 iterations, respectively.
Test 3: reconstruction of a Lipschitz domain This experiment aims at reconstructing a square-shaped cavity. We show several numerical tests, choosing different values for \(\varepsilon \), different boundary conditions and different values of the number of iterations for the refinement of the mesh. We have already shown results based on different choices for the values of the Lamé parameters in the previous numerical tests, so we fix the values of Lamé coefficients to be \(\mu =0.5\) and \(\lambda =1\). In fact, recalling that the range of the Poisson coefficient is \(-1<\nu <\frac{1}{2}\) (\(\nu =\frac{1}{2}\) represents the incompressible case), we have considered four relevant cases for the Poisson coefficient: one test on an elastic material close to incompressible case (\(\nu =\frac{5}{12}\) in Fig. 3e), two tests on elastic coefficients of common materials (\(\nu =\frac{1}{4}\) and \(\nu =\frac{1}{3}\) in Fig. 4a, b, respectively), and one test on auxetic materials, that is materials with negative Poisson ratio (\(\nu =-\frac{1}{18}\) in Fig. 4c). In the results of Fig. 5, the refinement of the mesh happens every 6000 for the first two experiments and every 3000 iterations for the last one. The second numerical result, see Fig. 5b, has the same parameters of the numerical example of Fig. 5a except \(\widetilde{\alpha }\) which is chosen \(\widetilde{\alpha }=5\times 10^{-2}\).
Test 4: reconstruction of two cavities This test provides results when the two cavities to be reconstructed are a square and a circle. Neumann boundary conditions are given by \(g^1(x,y)=(x,y)\) and \(g^2(x,y)=(-y,-x)\). We propose two numerical reconstruction procedures, see Fig. 6. In Fig. 6a, we report the results obtained by the standard algorithm, while in Fig. 6b we use a variant of the Algorithm 1 where the parameter \(\varepsilon \) is initially set \(\varepsilon =\frac{1}{4\pi }\) but after a fixed and a-priori chosen number of iterations (8000 iterations) is updated and set \(\varepsilon =\varepsilon /4\). In both cases the mesh is refined after 5000 iterations. It is worth noting that the variant of Algorithm 1 does not produce the visible oscillations of the test in Fig. 6a.
Note that we also change a little bit the value of \(\delta \). We have observed that \(\delta \) cannot be chosen too small otherwise numerical instability can appear. Numerically we have seen that, in order to overcome this issue, \(\tau _n\) has to be chosen always smaller than \(\delta \). However, choosing \(\tau \) too small increases the number of necessary iterations to satisfy the stopping criterium.
Test 5: reconstruction of a non-convex domain We finally propose the reconstruction of a cavity which is not convex, see Fig. 7. We use \(g^1(x,y)=(x,y)\) and \(g^2(x,y)=(-y,-x)\) as Neumann boundary conditions and \(\mu =0.5\) and \(\lambda =1\). Parameters have the following values: \(\varepsilon =\frac{1}{16\pi }\), and \(\tau _n=5\times 10^{-4}\). Mesh is refined every 5000 iterations. The stopping criterium is satisfied after \(n=6825\) iterations.
5.2 Numerical Experiments with \(N_g=2\) and Noise in the Measurements
Test 6: reconstruction of cavities of different shapes using noisy measurements Here we run some of the numerical tests showed in the previous section, adding to the boundary measurements a normal distributed noise with zero mean and variance equal to one. We choose two different noise levels: \(2\%\) and \(5\%\). The results are reported in Fig. 8.
For the the test in Fig. 8a, b, we use values of parameters as in Test 1 and refine the mesh every 2000 and 2500 iterations, respectively. The reconstruction of a square-shaped cavity, that is Fig. 8c, d, are obtained by means of parameters of Test 3—Fig. 5c, refining the mesh every 3000 and 10000 iterations. Lastly, to get the results in Fig. 8e, f we use the same parameters of Test 4—Fig. 6b. The mesh is refined every 5000 and 8000 iterations, while the value of the parameter \(\varepsilon \) is adapted after 8000 and 10000 iterations, respectively. In the captions of the single figures, we specify the values that are changed with respect to the ones proposed in the Tests 1, 3, and 4.
References
Alberti, G.: Variational models for phase transitions, an approach via \(\Gamma \)-convergence. In: Calculus of variations and partial differential equations (Pisa, 1996), pp. 95–114. Springer, Berlin (2000)
Alessandrini, G., Morassi, A., Rosset, E.: The linear constraints in Poincaré and Korn type inequalities. Forum Math. 20(3), 557–569 (2008)
Almi, S., Stefanelli, U.: Topology optimization for incremental elastoplasticity: a phase-field approach. SIAM J. Control. Optim. 59(1), 339–364 (2021)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and free Discontinuity Problems. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York (2000)
Ameur, H.B., Burger, M., Hackl, B.: Cavity identification in linear elasticity and thermoelasticity. Math. Methods Appl. Sci. 30(6), 625–647 (2007)
Ammari, H.: An Introduction to Mathematics of Emerging Biomedical Imaging. Mathématiques & Applications, vol. 62. Springer, Berlin (2008)
Ammari, H., Bretin, E., Garnier, J., Kang, H., Lee, H., Wahab, A.: Mathematical Methods in Elasticity Imaging. Princeton Series in Applied Mathematics. Princeton University Press, Princeton, NJ (2015)
Ammari, H., Kang, H., Nakamura, G., Tanuma, K.: Complete asymptotic expansions of solutions of the system of elastostatics in the presence of an inclusion of small diameter and detection of an inclusion. J. Elast. 67(2), 97–129 (2003)
Aspri, A.: An Elastic Model for Volcanology. Lecture Notes in Geosystems Mathematics and Computing. Birkhäuser/Springer, Cham (2019)
Aspri, A., Beretta, E., Mascia, C.: Analysis of a Mogi-type model describing surface deformations induced by a magma chamber embedded in an elastic half-space. J. Éc. polytech. Math. 4, 223–255 (2017)
Aspri, A., Beretta, E., Rosset, E.: On an elastic model arising from volcanology: an analysis of the direct and inverse problem. J. Differ. Equ. 265(12), 6400–6423 (2018)
Auricchio, F., Bonetti, E., Carraturo, M., Hömberg, D., Reali, A., Rocca, E.: A phase-field-based graded-material topology optimization with stress constraint. Math. Models Methods Appl. Sci. 30(8), 1461–1483 (2020)
Beretta, E., Cerutti, M.C., Pierotti, D.: Detection of cavities in a nonlinear model arising from cardiac electrophysiology via \(\gamma \)-convergence. arXiv:2106.04213 (2021)
Beretta, E., Ratti, L., Verani, M.: Detection of conductivity inclusions in a semilinear elliptic problem arising from cardiac electrophysiology. Commun. Math. Sci. 16(7), 1975–2002 (2018)
Blank, L., Garcke, H., Farshbaf-Shaker, M.H., Styles, V.: Relating phase field and sharp interface approaches to structural topology optimization. ESAIM Control Optim. Calc. Var. 20(4), 1025–1058 (2014)
Blank, L., Garcke, H., Hecht, C., Rupprecht, C.: Sharp interface limit for a phase field model in structural optimization. SIAM J. Control. Optim. 54(3), 1558–1584 (2016)
Bonnet, M., Constantinescu, A.: Inverse problems in elasticity. Inverse Prob. 21(2), R1–R50 (2005)
Bourdin, B., Chambolle, A.: Design-dependent loads in topology optimization. ESAIM Control Optim. Calc. Var. 9, 19–48 (2003)
Brezis, H.: Analyse fonctionnelle. Collection Mathématiques Appliquées pour la Maîtrise. [Collection of Applied Mathematics for the Master’s Degree]. Masson, Paris, 1983. Théorie et applications. [Theory and applications]
Brown, B.M., Jais, M., Knowles, I.W.: A variational approach to an elastic inverse problem. Inverse Prob. 21(6), 1953–1973 (2005)
Bucur, D., Buttazzo, G.: Variational Methods in Shape Optimization Problems. Progress in Nonlinear Differential Equations and their Applications, vol. 65. Birkhäuser Boston Inc, Boston, MA (2005)
Bucur, D., Henrot, A., Sokołowski, J., Żochowski, A.: Continuity of the elasticity system solutions with respect to the geometrical domain variations. Adv. Math. Sci. Appl. 11(1), 57–73 (2001)
Bucur, D., Varchon, N.: Stabilité de la solution d’un problème de Neumann pour des variations de frontière. C. R. Acad. Sci. Paris Sér. I Math., 331(5):371–374 (2000)
Carpio, A., Rapún, M.L.: Topological Derivatives for Shape Reconstruction. In Inverse Problems and Imaging, vol. 1943 of Lecture Notes in Math., pp. 85–133. Springer, Berlin (2008)
Carraturo, M., Rocca, E., Bonetti, E., Hömberg, D., Reali, A., Auricchio, F.: Graded-material design based on phase-field and topology optimization. Comput. Mech. 64(6), 1589–1600 (2019)
Chambolle, A., Doveri, F.: Continuity of Neumann linear elliptic problems on varying two-dimensional bounded open sets. Commun. Partial Differ. Eq. 22(5–6), 811–840 (1997)
Chenais, D.: On the existence of a solution in a domain identification problem. J. Math. Anal. Appl. 52(2), 189–219 (1975)
Ciarlet, P.G.: Mathematical elasticity. Vol. I, volume 20 of Studies in Mathematics and Its Applications. North-Holland Publishing Co., Amsterdam (1988). Three-dimensional elasticity
Dal Maso, G.: An introduction to \(\Gamma \)-convergence. Progress in Nonlinear Differential Equations and their Applications, vol. 8. Birkhäuser Boston Inc, Boston (1993)
Deckelnick, K., Elliott, C.M., Styles, V.: Double obstacle phase field approach to an inverse problem for a discontinuous diffusion coefficient. Inverse Probl., 32(4):045008, 26 (2016)
Doubova, A., Fernández-Cara, E.: Some geometric inverse problems for the Lamé system with applications in elastography. Appl. Math. Optim. 82(1), 1–21 (2020)
Eberle, S., Harrach, B.: Shape reconstruction in linear elasticity: standard and linearized monotonicity method. Inverse Probl. 37(4):045006, 27 (2021)
Eiliat, H., Urbanic, J.: Visualizing, analyzing, and managing voids in the material extrusion process. Int. J. Adv. Manuf. Technol. 96, 4095–4109 (2018)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions. Revised Textbooks in Mathematics. CRC Press, Boca Raton (2015)
Garcke, H., Hecht, C., Hinze, M., Kahle, C.: Numerical approximation of phase field based shape and topology optimization for fluids. SIAM J. Sci. Comput. 37(4), A1846–A1871 (2015)
Garcke, H., Lam Fong, K., Nürnberg, R., Signori, A.: Overhang penalization in additive manufacturing via phase field structural topology optimization with anisotropic energies. arXiv:2111.14070 (2021)
Giacomini, A.: A stability result for Neumann problems in dimension \(N\ge 3\). J. Convex Anal. 11(1), 41–58 (2004)
He, X., Yang, P.: The primal-dual active set method for a class of nonlinear problems with \(T\)-monotone operators. Math. Probl. Eng. pages Art. ID 2912301, 8 (2019)
Henrot, A., Pierre, M.: Shape Variation and Optimization, volume 28 of EMS Tracts in Mathematics. European Mathematical Society (EMS), Zürich, 2018. A geometrical analysis, English version of the French publication [ MR2512810] with additions and updates
Hintermüller, M., Ito, K., Kunisch, K.: The primal-dual active set strategy as a semismooth Newton method. SIAM J. Optim. 13(3), 865–888 (2003)
Hubmer, S., Sherina, E., Neubauer, A., Scherzer, O.: Lamé parameter estimation from static displacement field measurements in the framework of nonlinear inverse problems. SIAM J. Imaging Sci. 11(2), 1268–1293 (2018)
Ikehata, M., Itou, H.: On reconstruction of an unknown polygonal cavity in a linearized elasticity with one measurement. J. Phys. 290, 012005 (2011)
Ikehata, M., Itou, H.: On reconstruction of a cavity in a linearized viscoelastic body from infinitely many transient boundary data. Inverse Prob. 28(12), 125003 (2012)
Jin, B., Zou, J.: Numerical estimation of the Robin coefficient in a stationary diffusion equation. IMA J. Numer. Anal. 30(3), 677–701 (2010)
Kang, H., Kim, E., Lee, J.-Y.: Identification of elastic inclusions and elastic moment tensors by boundary measurements. Inverse Probl. 19(3), 703–724 (2003)
Karageorghis, A., Lesnic, D., Marin, L.: The method of fundamental solutions for the detection of rigid inclusions and cavities in plane linear elastic bodies. Comput. Struct. 106 (2012)
Kurahashi, T., Maruoka, K., Iyama, T.: Numerical shape identification of cavity in three dimensions based on thermal non-destructive testing data. Eng. Optim. 49(3), 434–448 (2017)
Lam, K.F., Yousept, I.: Consistency of a phase field regularisation for an inverse problem governed by a quasilinear Maxwell system. Inverse Probl. 36(4):045011, 33, (2020)
Liu, H., Rondi, L., Xiao, J.: Mosco convergence for \(H(\rm curl)\) spaces, higher integrability for Maxwell’s equations, and stability in direct and inverse EM scattering problems. J. Eur. Math. Soc. (JEMS) 21(10), 2945–2993 (2019)
Martínez-Castro, A.E., Faris, I.H., Gallego, R.: Identification of cavities in a three-dimensional layer by minimization of an optimal cost functional expansion. Comput. Model. Eng. Sci. 87(3), 177–206 (2012)
Menegatti, G., Rondi, L.: Stability for the acoustic scattering problem for sound-hard scatterers. Inverse Probl. Imaging 7(4), 1307–1329 (2013)
Modica, L.: The gradient theory of phase transitions and the minimal interface criterion. Arch. Ration. Mech. Anal. 98(2), 123–142 (1987)
Morassi, A., Rosset, E.: Stable determination of cavities in elastic bodies. Inverse Prob. 20(2), 453–480 (2004)
Morassi, A., Rosset, E.: Stable determination of an inclusion in an inhomogeneous elastic body by boundary measurements. Rend. Istit. Mat. Univ. Trieste 48, 101–120 (2016)
Ngo, T.D., Kashani, A., Imbalzano, G., Nguyen, K.T.Q., Hui, D.: Additive manufacturing (3d printing): a review of materials, methods, applications and challenges. Composites B 143, 172–196 (2018)
Ring, W., Rondi, L.: Reconstruction of cracks and material losses by perimeter-like penalizations and phase-field methods: numerical results. Interfaces Free Bound. 13(3), 353–371 (2011)
Rondi, L.: Reconstruction of material losses by perimeter penalization and phase-field methods. J. Differ. Eq. 251(1), 150–175 (2011)
Segall, P.: Earthquake and Volcano Deformation. Princeton University Press, Princeton, NJ (2010)
Shao, J., Shi, G., Qi, Z., Zheng, J., Chen, S.: Advancements in the application of ultrasound elastography in the cervix. Ultrasound Med. Biol. 47(8), 2048–2063 (2021)
Sherina, E., Krainz, L., Hubmer, S., Drexler, W., Scherzer, O.: Displacement field estimation from OCT images utilizing speckle information with applications in quantitative elastography. Inverse Probl. 36(12):124003, 27 (2020)
Shi, J., Beretta, E., de Hoop, M.V., Francini, E., Vessella, S.: A numerical study of multi-parameter full waveform inversion with iterative regularization using multi-frequency vibroseis data. Comput. Geosci. 24(1), 89–107 (2020)
Symes, W.W.: The seismic reflection inverse problem. Inverse Probl. 25(12):123008, 39 (2009)
Tronvoll, S.A., Welo, T., Elverum, C.W.: The effects of voids on structural properties of fused deposition modelled parts: a probabilistic approach. Int. J. Adv. Manuf. Technol. 97(9), 3607–3618 (2018)
Widlak, T., Scherzer, O.: Stability in the linearized problem of quantitative elastography. Inverse Probl., 31(3):035005, 27 (2015)
Acknowledgements
The authors deeply thank Dorin Bucur and Alessandro Giacomini for suggesting relevant literature and for useful discussions that led us to improve some of the results in this work. This research has been partially performed in the framework of the MIUR-PRIN Grant 2020F3NCPX “Mathematics for industry 4.0 (Math4I4)”. Andrea Aspri, Cecilia Cavaterra and Elisabetta Rocca are members of GNAMPA (Gruppo Nazionale per l’Analisi Matematica, la Probabilitá e le loro Applicazioni) of INdAM (Istituto Nazionale di Alta Matematica). Marco Verani has been partially funded by MIUR PRIN research grants n. 201744KLJL and n. 20204LN5N5. Marco Verani is a member of GNCS (Gruppo Nazionale per il Calcolo Scientifico) of INdAM.
Funding
Open access funding provided by Universitá degli Studi di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The authors have not disclosed any competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aspri, A., Beretta, E., Cavaterra, C. et al. Identification of Cavities and Inclusions in Linear Elasticity with a Phase-Field Approach. Appl Math Optim 86, 32 (2022). https://doi.org/10.1007/s00245-022-09897-6
Accepted:
Published:
DOI: https://doi.org/10.1007/s00245-022-09897-6