Monotonicity-based regularization for shape reconstruction in linear elasticity

Abstract

We deal with the shape reconstruction of inclusions in elastic bodies. For solving this inverse problem in practice, data fitting functionals are used. Those work better than the rigorous monotonicity methods from Eberle and Harrach (Inverse Probl 37(4):045006, 2021), but have no rigorously proven convergence theory. Therefore we show how the monotonicity methods can be converted into a regularization method for a data-fitting functional without losing the convergence properties of the monotonicity methods. This is a great advantage and a significant improvement over standard regularization techniques. In more detail, we introduce constraints on the minimization problem of the residual based on the monotonicity methods and prove the existence and uniqueness of a minimizer as well as the convergence of the method for noisy data. In addition, we compare numerical reconstructions of inclusions based on the monotonicity-based regularization with a standard approach (one-step linearization with Tikhonov-like regularization), which also shows the robustness of our method regarding noise in practice.

1 Introduction

The main motivation is the non-destructive testing of elastic structures, such as is required for material examinations, in exploration geophysics, and for medical diagnostics (elastography). From a mathematical point of view, this constitutes an inverse problem since we have only measurement data on the boundary and not inside of the elastic body. This problem is highly ill-posed, since even the smallest measurement errors can completely falsify the result.

There are several authors who deal with the theory of the inverse problem of elasticity. For the two dimensional case, we refer the reader to [14, 15, 17, 21]. In three dimensions, Nakamura and Uhlmann [22, 23] and Eskin and Ralston [8] gave the proof for uniqueness results for both Lamé coefficients under the assumption that $\mu$ is close to a positive constant. Beretta et al. [2, 3] proved the uniqueness for partial data, where the Lamé parameters are piecewise constant and some boundary determination results were shown in [17, 20, 22].

Further on, solution methods applied so far for the inverse problem, which will be solved in this paper, were presented in the following works: In Oberai et al. [24, 25], the time-independent inverse problem of linear elasticity is solved by means of the adjoint method and the reconstruction is simulated numerically. In addition, Seidl et al. [26] deals with the coupling of the state and adjoint equation and added two variants of residual-based stabilization to solve the inverse linear elasticity problem for incompressible plane stress. A boundary element-Landweber method for the Cauchy problem in stationary linear elasticity was investigated in Marin and Lesnic [19]. In Hubmer et al. [13], the stationary inverse problem was solved by means of a Landweber iteration as well and numerical examples were presented. Reciprocity principles for the detection of cracks in elastic bodies were investigated, for example, in Andrieux et al. [1] and Steinhorst and Sändig [27] or more recently in Ferrier et al. [9]. By means of a regularization approach, a stationary elastic inverse problem is solved in Jadamba et al. [16] and applied in numerical examples. Marin and Lesnic [18] introduces a regularized boundary element method. Finally, we want to mention the monotonicity methods for linear elasticity developed by the authors of this paper in Eberle and Harrach [5] as well as its application for the reconstruction of inclusions based on experimental data in Eberle and Moll [7].

We want to point out that the reconstruction of the support of the Lamé parameters, also called shape in this paper, and not the reconstruction of their values is the topic of this work. The key issue of the shape reconstruction of inclusions is the monotonicity property of the corresponding Neumann-to-Dirichlet operator (see [28, 29]). These monotonicity properties were also applied for the construction of monotonicity tests for electrical impedance tomography (EIT), e.g., in [12], as well as the monotonicity-based regularization in Harrach and Mach [11]. In practice however, data fitting functionals provide better results than the monotonicity methods but the data-fitting functionals are usually not convex (see, e.g. [10]). Even for exact data, therefore, it cannot generally be guaranteed that the algorithm does not erroneously deliver a local minimum. In addition, there is noise and ill-posedness. The local convergence theory of Newton-like methods requires non-linearity assumptions such as the tangential cone condition, which are still not proven even for simpler examples such as EIT. The convergence theory of Tikhonov-regularized data fitting functionals applies to their global minima, which in general cannot be found due to the non-convexity. Our method is based on the minimization of a convex functional and is to the knowledge of the authors the first rigorously convergent method for this problem, but only provides the shape of the inclusions. We combine the monotonicity methods (cf. [5, 6]) with data fitting functionals to obtain convergence results and an improvement of both methods regarding stability for noisy data. Here, we want to remark that compared to other data-fitting methods, we use the following a-priori assumptions: the Lamé parameters fulfill monotonicity relations, have a common support, the lower and upper bounds of the contrasts of the anomalies are known and we deal with a constant and known background material. Compared with Harrach and Mach [11], we expand the approach used there from the consideration of only one parameter to two parameters.

The outline of the paper is as follows: We start with the introduction of the problem statement. In order to detect and reconstruct inclusions in elastic bodies, we aim to determine the difference between an unknown Lamé parameter pair $(\lambda ,\mu )$ and that of the known background $(\lambda _0,\mu _0)$ and formulate a minimization problem. Similar to the linearized monotonicity tests in Eberle and Harrach [5], we also consider the Fréchet derivative, which approximates the difference between two Neumann-to-Dirichlet operators. For solving the resulting minimization problem, we first take a look at a standard approach (standard one-step linearization method). Therefore regularization parameters are introduced, which can only be determined heuristically. For this purpose, for example, a parameter study can be carried out. We would like to point out that this method is only a heuristic approach, but is commonly used in practice. Overall, this heuristic approach leads to reconstructions of the unknown inclusions without a rigorous theory. In Sect. 4, we focus on the monotonicity-based regularization in order to enhance the data fitting functionals. The idea of the regularization is to introduce conditions for the parameters / inclusions to be reconstructed for the minimization problem, which are based on the monotonicity properties of the Neumann-to-Dirichlet operator and the monotonicity tests. Further on, we prove that there exists a unique minimizer for this problem and that we obtain convergence even for noisy data. Finally, we compare numerical reconstructions of inclusions based on the monotonicity-based regularization with the one-step linearization, which also shows the robustness of our method regarding noise in practice.

2 Problem statement

We start with the introduction of the problems of interest, e.g., the direct as well as inverse problem of stationary linear elasticity.

Let $\Omega \subset \mathbb {R}^d$ ($d=2$ or 3) be a bounded and connected open set with Lipschitz boundary $\partial \Omega =\Gamma =\overline{\Gamma _{\mathrm {D}}\cup \Gamma _{\mathrm {N}}}$, $\Gamma _{\mathrm {D}}\cap \Gamma _{\mathrm {N}}=\emptyset$, where $\Gamma _{D }$ and $\Gamma _{N }$ are the corresponding Dirichlet and Neumann boundaries. We assume that $\Gamma _{D }$ and $\Gamma _{N }$ are relatively open and connected. For the following, we define

$$\begin{aligned} L_+^\infty (\Omega ):=\lbrace w \in L^\infty (\Omega ):\underset{x\in \Omega }{\text {essinf}}\,w(x)>0\rbrace . \end{aligned}$$

Let $u:\Omega \rightarrow \mathbb {R}^d$ be the displacement vector, $\mu ,\lambda :\Omega \rightarrow L^{\infty }_+(\Omega )$ the Lamé parameters, $\hat{\nabla } u=\tfrac{1}{2}\left( \nabla u + (\nabla u)^T\right)$ the symmetric gradient, n is the normal vector pointing outside of $\Omega$ , $g\in L^{2}(\Gamma _{N })^d$ the boundary force and I the $d\times d$-identity matrix. We define the divergence of a matrix $A\in \mathbb {R}^{d\times d}$ via $\nabla \cdot A=\sum \limits _{i,j=1}^d\dfrac{\partial A_{ij}}{\partial x_j}e_i$, where $e_i$ is a unit vector and $x_j$ a component of a vector from $\mathbb {R}^d$.

The boundary value problem of linear elasticity (direct problem) is that $u\in H^1(\Omega )^d$ solves

$$\begin{aligned} \nabla \cdot \left( \lambda (\nabla \cdot u)I + 2\mu \hat{\nabla } u \right)&=0 \quad \mathrm {in}\,\,\Omega , \end{aligned}$$

(1)

$$\begin{aligned} \left( \lambda (\nabla \cdot u)I + 2\mu \hat{\nabla } u \right) n&=g\quad \mathrm {on}\,\, \Gamma _{N }, \end{aligned}$$

(2)

$$\begin{aligned} u&=0 \quad \mathrm {on}\,\, \Gamma _{D }. \end{aligned}$$

(3)

From a physical point of view, this means that we deal with an elastic test body $\Omega$ which is fixed (zero displacement) at $\Gamma _{\mathrm {D}}$ (Dirichlet condition) and apply a force g on $\Gamma _{\mathrm {N}}$ (Neumann condition). This results in the displacement u, which is measured on the boundary $\Gamma _{\mathrm {N}}$.

The equivalent weak formulation of the boundary value problem (1)–(3) is that $u\in \mathcal {V}$ fulfills

$$\begin{aligned} \int _{\Omega } 2 \mu \, \hat{\nabla }u : \hat{\nabla }v + \lambda \nabla \cdot u \,\nabla \cdot v\,dx=\int _{\Gamma _{N }}g \cdot v \,ds \quad \text { for all } v\in \mathcal {V}, \end{aligned}$$

(4)

where $\mathcal {V}:=\left\{ v\in H^1(\Omega )^d:\, v_{|_{\Gamma _{D }}}=0\right\}$.

We want to remark that for $\lambda ,\mu \in L^{\infty }_+(\Omega )$ the existence and uniqueness of a solution to the variational formulation (4) can be shown by the Lax-Milgram theorem (see e.g., in [4]).

Measuring boundary displacements that result from applying forces to $\Gamma _{N }$ can be modeled by the Neumann-to-Dirichlet operator $\Lambda (\lambda ,\mu )$ defined by

$$\begin{aligned} \Lambda (\lambda ,\mu ): L^2(\Gamma _{N })^d\rightarrow L^2(\Gamma _{N })^d: \quad g\mapsto u_{|_{\Gamma _{N }}}, \end{aligned}$$

where $u\in \mathcal {V}$ solves (1)–(3).

This operator is self-adjoint, compact and linear (see Corollary 1.1 from [5]). Its associated bilinear form is given by

$$\begin{aligned} \langle g,\Lambda (\lambda ,\mu )h\rangle&=\int _{\Omega } 2 \mu \, \hat{\nabla }u^g_{(\lambda ,\mu )} : \hat{\nabla }u^h_{(\lambda ,\mu )}\nonumber \\&\quad + \lambda \nabla \cdot u^g_{(\lambda ,\mu )} \,\nabla \cdot u^h_{(\lambda ,\mu )}\,dx, \end{aligned}$$

(5)

where $u_{(\lambda ,\mu )}^g$ solves the problem (1)–(3) and $u_{(\lambda ,\mu )}^h$ the corresponding problem with boundary force $h\in L^2(\Gamma _{\mathrm {N}})^d$.

Another important property of $\Lambda (\lambda ,\mu )$ is its Fréchet differentiability (for the corresponding proof see Lemma 2.3 in [5]). For directions $\hat{\lambda }, \hat{\mu }\in L^\infty (\Omega )$, the derivative

$$\begin{aligned} \Lambda '(\lambda ,\mu )(\hat{\lambda },\hat{\mu }): L^2(\Gamma _{N })^d\rightarrow L^2(\Gamma _{N })^d \end{aligned}$$

is the self-adjoint compact linear operator associated to the bilinear form

$$\begin{aligned}&\langle \Lambda '(\lambda ,\mu )(\hat{\lambda },\hat{\mu })g,h\rangle \nonumber \\&\quad =-\int _{\Omega } 2 \hat{\mu }\, \hat{\nabla }u^g_{(\lambda ,\mu )} : \hat{\nabla }u^h_{(\lambda ,\mu )} + \hat{\lambda } \nabla \cdot u^g_{(\lambda ,\mu )} \,\nabla \cdot u^h_{(\lambda ,\mu )}\,dx. \end{aligned}$$

Note that for $\hat{\lambda }_0, \hat{\lambda }_1, \hat{\mu }_0, \hat{\mu }_1 \in L^\infty (\Omega )$ with $\hat{\lambda }_0\le \hat{\lambda }_1$ and $\hat{\mu }_0 \le \hat{\mu }_1$ we obviously have

$$\begin{aligned} \Lambda '(\lambda ,\mu )(\hat{\lambda }_0,\hat{\mu }_0)\ge \Lambda '(\lambda ,\mu )(\hat{\lambda }_1,\hat{\mu }_1), \end{aligned}$$

(6)

in the sense of quadratic forms.

The inverse problem we consider here is the following

$$\begin{aligned}&Find the support of (\lambda -\lambda _0,\mu -\mu _0)^T knowing the\\&\quad Neumann -to-Dirichlet operator \Lambda (\lambda ,\mu ). \end{aligned}$$

Next, we take a look at the discrete setting. Let the Neumann boundary $\Gamma _{N }$ be the union of the patches $\Gamma _{N }^{(l)}$, $l=1,\ldots ,M$, which are assumed to be relatively open and connected, such that $\overline{\Gamma _{N }}=\bigcup \nolimits _{l=1}^M\overline{\Gamma _{N }^{(l)}}$, $\Gamma _{N }^{(i)}\cap \Gamma _{N }^{(j)}=\emptyset$ for $i\ne j$ and we consider the following problem:

$$\begin{aligned} \nabla \cdot \left( \lambda (\nabla \cdot u)I + 2\mu \hat{\nabla } u \right)&=0 \quad \,\,\mathrm {in}\,\,\Omega , \end{aligned}$$

(7)

$$\begin{aligned} \left( \lambda (\nabla \cdot u)I + 2\mu \hat{\nabla } u \right) n&=g_l\quad \mathrm {on}\,\, \Gamma _{N }^{(l)},\end{aligned}$$

(8)

$$\begin{aligned} \left( \lambda (\nabla \cdot u)I + 2\mu \hat{\nabla } u \right) n&=0\quad \,\,\mathrm {on}\,\,\Gamma _{N }^{(i)},\quad i\ne l,\end{aligned}$$

(9)

$$\begin{aligned} u&=0 \quad \,\,\mathrm {on}\,\, \Gamma _{D }, \end{aligned}$$

(10)

where $g_l$, $l=1,\ldots , M$, denote the M given boundary forces applied to the corresponding patches $\Gamma _{\mathrm {N}}^{(l)}$. In order to discretize the Neumann-to-Dirichlet operator, we apply a boundary force $g_l$ on the patch $\Gamma _{\mathrm {N}}^{(l)}$ and set

$$\begin{aligned} \Lambda _l^{(k)}(\lambda ,\mu ):=\int _{\Gamma _{N }^{(l)}}g_l\cdot u^{(k)} \,ds \end{aligned}$$

(cf. (4) and (5)), where $u^{(k)}$ solves the corresponding boundary value problem (7)–(10) with boundary force $g_{k}$.

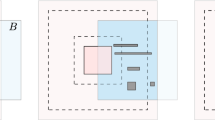
In Fig. 1 a simple example of possible boundary loads $g_l$ and patches $\Gamma _{\mathrm {N}}^{(l)}$ is shown.

Fig. 1

Illustration of possible boundary loads $g_l$ and patches $\Gamma _{\mathrm {N}}^{(l)}$. We consider here $l=1,\ldots ,5,$ Neumann patches and one Dirichlet patch (bottom of the cube). The boundary forces $g_l$ are normal vectors from the Euclidean space in each point of the patch

For the Neumann boundary forces as described here, we get an orthogonal system $g_l$ in $L^2(\Gamma _\mathrm{N})^d$. In practice, we additionally normalize the system $g_l$ and use more patches $\Gamma _{\mathrm {N}}^{(l)}$.

For the unknown Lamé parameters $(\lambda ,\mu )$, we obtain a full matrix

$$\begin{aligned} \varvec{\Lambda }(\lambda ,\mu )=\left( \Lambda ^{(k)}_l(\lambda ,\mu )\right) _{k,l=1,\ldots ,M}. \end{aligned}$$

3 Standard one-step linearization methods

In this section we take a look at one-step linearization methods. We want to remark that these methods are only a heuristical approach but commonly used in practice.

We compare the matrix of the discretized Neumann-to-Dirichlet operator $\varvec{\Lambda }(\lambda ,\mu )$ with $\varvec{\Lambda }(\lambda _0,\mu _0)$ for some reference Lamé parameter $(\lambda _0,\mu _0)$ in order to reconstruct the difference $(\lambda ,\mu )-(\lambda _0,\mu _0)$. Thus, we apply a single linearization step

$$\begin{aligned} \varvec{\Lambda }^\prime (\lambda _0,\mu _0)\left( (\lambda ,\mu )-(\lambda _0,\mu _0)\right) \approx \varvec{\Lambda }(\lambda ,\mu )-\varvec{\Lambda }(\lambda _0,\mu _0), \end{aligned}$$

where

$$\begin{aligned} \varvec{\Lambda }^\prime (\lambda _0,\mu _0): L^{\infty }(\Omega )^2\rightarrow \mathbb {R}^{M\times M} \end{aligned}$$

is the Fréchet derivative which maps $(\hat{\lambda }, \hat{\mu })\in L^\infty (\Omega )^2$ to

$$\begin{aligned}&-\left( \int _{\Omega }\hat{\lambda }\left( \nabla \cdot u^{(k)}_{(\lambda _0,\mu _0)}\right) \left( \nabla \cdot u^{(l)}_{(\lambda _0,\mu _0)}\right) \right. \\&\quad \left. +2\hat{\mu }\left( \hat{\nabla } u^{(k)}_{(\lambda _0,\mu _0)}\right) : \left( \hat{\nabla } u^{(l)}_{(\lambda _0,\mu _0)}\right) dx\right) _{1\le k, l\le M} . \end{aligned}$$

For the solution of the problem, we discretize the reference domain $\overline{\Omega }=\bigcup \nolimits _{j=1}^{p}\overline{\mathcal {B}}_j$ into p disjoint pixel $\mathcal {B}_j$, where each $\mathcal {B}_j$ is assumed to be open, $\Omega \setminus \mathcal {B}_j$ is connected and $\mathcal {B}_j \cap \mathcal {B}_i=\emptyset$ for $j\ne i$. We make a piecewise constant ansatz for $(\kappa ,\nu )\approx (\lambda ,\mu )-(\lambda _0,\mu _0)$ via

$$\begin{aligned} \kappa (x)=\sum _{j=1}^p \kappa _j \chi _{\mathcal {B}_j}(x)\quad \text {and}\quad \nu (x)=\sum _{j=1}^p \nu _j \chi _{\mathcal {B}_j}(x), \end{aligned}$$

(11)

where $\chi _{\mathcal {B}_j}$ is the characteristic function w.r.t. the pixel $\mathcal {B}_j$ and set

$$\begin{aligned} {\varvec{\kappa }}=(\kappa _j)_{j=1}^p\in \mathbb {R}^p \quad \text {and}\quad {\varvec{\nu }}=(\nu _j)_{j=1}^p\in \mathbb {R}^p. \end{aligned}$$

This approach leads to the linear equation system

$$\begin{aligned} \mathbf{S}^{\lambda }{\varvec{\kappa }}+ \mathbf{S}^{\mu }{\varvec{\nu }}= \mathbf{V}, \end{aligned}$$

(12)

where $\mathbf{V}$ and the columns of the sensitivity matrices $\varvec{S}^{\lambda }$ and $\varvec{S}^{\mu }$ contain the entries of $\Lambda (\lambda _0,\mu _0)-\Lambda (\lambda ,\mu )$ and the discretized Fréchet derivative for a given $\mathcal {B}_j$ for $j=1,\ldots ,p$, respectively. Here, we have

$$\begin{aligned} \mathbf{V}&=(V_i)_{i=1}^{M^2}\in \mathbb {R}^{M^2},\nonumber \\ V_{(l-1)M+k}&=\Lambda _l^{(k)}(\lambda _0,\mu _0)-\Lambda _l^{(k)}(\lambda ,\mu ), \end{aligned}$$

(13)

$$\begin{aligned} \mathbf{S}^{\lambda }&=(S^{\lambda }_{ij})\in \mathbb {R}^{M^2,p},\nonumber \\ S^{\lambda }_{(l-1)M+k,j}&=\int _{\mathcal {B}_j}\left( \nabla \cdot u^{(k)}_{(\lambda _0,\mu _0)}\right) \left( \nabla \cdot u^{(l)}_{(\lambda _0,\mu _0)}\right) dx, \end{aligned}$$

(14)

$$\begin{aligned} \mathbf{S}^{\mu }&=(S^{\mu }_{ij})\in \mathbb {R}^{M^2,p},\nonumber \\ S^{\mu }_{(l-1)M+k,j}&=\int _{\mathcal {B}_j}2\left( \hat{\nabla }u_{(\lambda _0,\mu _0)}^{(k)}\right) :\left( \hat{\nabla }u_{(\lambda _0,\mu _0)}^{(l)}\right) dx. \end{aligned}$$

(15)

Solving (12) results in a standard minimization problem for the reconstruction of the unknown parameters. In order to determine suitable parameters $(\varvec{\kappa },\varvec{\nu })$, we regularize the minimization problem, so that we have

$$\begin{aligned} \left\| \left( \mathbf{S}^{\lambda }\,\vert \,\, \mathbf{S}^{\mu }\right) \begin{pmatrix} \varvec{\kappa }\\ \varvec{\nu } \end{pmatrix} - \mathbf{V}\right\| _{2}^2 + \omega \Vert \varvec{\kappa }\Vert _{2}^2 + \sigma \Vert \varvec{\nu }\Vert _{2}^2\rightarrow \mathrm {min!} \end{aligned}$$

(16)

with $\omega$ and $\sigma$ as regularization parameters. For solving this minimization problem we consider the normal equation

$$\begin{aligned} \mathbf{A}^T \mathbf{A} \begin{pmatrix} \varvec{\kappa }\\ \varvec{\nu } \end{pmatrix} =\mathbf{A}^T \begin{pmatrix} \mathbf{V}\\ \mathbf{0}\\ \mathbf{0} \end{pmatrix} \end{aligned}$$

with $\mathbf{A}= \begin{pmatrix} \mathbf{S}^{\lambda } &{} \vert &{} \mathbf{S}^{\mu }\\ \omega \mathbf{I}&{}\vert &{} \mathbf{0} \\ \mathbf{0} &{} \vert &{} \sigma \mathbf{I} \end{pmatrix}.$

Obtaining a solution for this system is memory expensive and finding two suitable parameters $\omega$ and $\sigma$ can be time consuming, since we can only choose them heuristically. However, the parameter reconstruction provides good results as shown in the next part.

3.1 Numerical realization

We present a simple test model, where we consider a cube of a biological tissue with two inclusions (tumors) as depicted in Fig. 2.

Fig. 2

Cube with two inclusions (red) as considered in [5]

The Lamé parameters of the corresponding materials are given in Table 1.

Table 1 Lamé parameter of the test material in [Pa]

For our numerical experiments, we simulate the discrete measurements by solving

$$\begin{aligned} \left\{ \begin{array}{rcll} \nabla \cdot \left( \lambda _0 (\nabla \cdot u_0)I + 2\mu _0 \hat{\nabla } u_0 \right) &{}=&{}0&{}\mathrm {in}\,\,\Omega ,\\ -\nabla \cdot \left( ((\lambda _1-\lambda _0)\chi _D)(\nabla \cdot u_0)I+ 2((\mu _1-\mu _0)\chi _D)\hat{\nabla } u_0 \right) \\ +\nabla \cdot \left( \lambda (\nabla \cdot v)I + 2\mu \hat{\nabla } v \right) &{}=&{}0 &{}\mathrm {in}\,\,\Omega ,\\ \left( \lambda _0 (\nabla \cdot u_0)I + 2\mu _0 \hat{\nabla } u_0 \right) n&{}=&{}g_l&{}\mathrm {on}\,\, \Gamma _{\mathrm {N}},\\ \left( \lambda (\nabla \cdot v)I + 2\mu \hat{\nabla } v \right) n&{}=&{}0&{}\mathrm {on}\,\, \Gamma _{\mathrm {N}},\\ u_0&{}=&{}0 &{}\mathrm {on}\,\, \Gamma _{\mathrm {D}},\\ v&{}=&{}0 &{}\mathrm {on}\,\, \Gamma _{\mathrm {D}}, \end{array}\right. \end{aligned}$$

(17)

for each of the $l=1,\ldots ,M$, given boundary forces $g_l$, where $v:=u_0-u$ are the difference measurements. The equations regarding v in the system (17) result from substracting the boundary value problem (1) for the respective Lamé parameters.

We want to remark that the Dirichlet boundary is set to the bottom of the cube. The remaining five faces of the cube constitute the Neumann boundary. Each Neumann face is divided into 25 squares of equal size ($5\times 5$) resulting in 125 patches $\Gamma _{\mathrm {N}}^{(l)}$. On each $\Gamma _{\mathrm {N}}^{(l)}$, $l=1,\ldots ,125,$ we apply a boundary force $g_l$, which is equally distributed on $\Gamma _{\mathrm {N}}^{(l)}$ and pointing in the normal direction of the patch.

3.1.1 Exact data

First of all, we take a look at the example without noise, which means we assume we are given exact data.

In order to obtain a suitable visualization of the 3D reconstruction, we manipulate the transparency parameter function $\alpha : \mathbb {R} \rightarrow [0,1]$ of Fig. 4 as exemplary depicted for the Lamé parameter $\mu$ in Fig. 3. It should be noted that a low transparency parameter indicates that the corresponding color (here, the colors around zero) are plotted with high transparency, while a high $\alpha$ indicates that the corresponding color is plotted opaque. The reason for this choice is that values of the calculated difference $\nu =\mu -\mu _0$ close to zero are not an indication of an inclusion, while values with a higher absolute value indicate an inclusion. Hence, this choice of transparency is suitable to plot the calculated inclusions without being covered by white tetrahedrons with values close to zero. Further, the reader should observe that $\alpha (|\nu |)>0$ for all values of $\nu$, so that all tetrahedrons are plotted and that the transparency plot for $\kappa$ takes the same shape but is adjusted to the range of the calculated values.

The following results (Figs. 4 and 5) are based on a parameter search and the regularization parameters are chosen heuristically. Thus, we only present the results with the best parameter choice ($\omega =10^{-17}$ and $\sigma =10^{-13}$) and reconstruct the difference in the Lamé parameters $\mu$ and $\lambda$.

Fig. 3

Transparency function for the plots in Fig. 4 mapping the values of $|\nu |$ to $\alpha (|\nu |)$

Fig. 4

Shape reconstruction of two inclusions of the difference in the Lamé parameter $\mu$ (left hand side) and $\lambda$ (right hand side) for the regularization parameters $\omega =10^{-17}$ and $\sigma =10^{-13}$ without noise and transparency function $\alpha$ as shown in Fig. 3

Fig. 5

Shape reconstruction of two inclusions of the reconstructed difference in the Lamé parameter $\mu$ for the regularization parameters $\omega =10^{-17}$ and $\sigma =10^{-13}$ depicted as cuts without noise

With these regularization parameters, the two inclusions are detected and reconstructed correctly for $\mu$ (see Fig. 4 in the left hand side) and the value of $\mu -\mu _0$ is in the correct amplitude range as depicted in Fig. 5. Figure 4 shows us, that for $\lambda -\lambda _0$, the reconstruction does not work. The reason is that the range of the Lamé parameters differs from each other around $10^2$ Pa ($\lambda \approx 100\cdot \mu$), but

$$\begin{aligned} \Vert \mathbf{S}^\mu \Vert _2\approx 1.2\cdot 10^4 \Vert \mathbf{S}^\lambda \Vert _2, \end{aligned}$$

i.e. the signatures of $\mu$ are represented far stronger in the calculation of $\mathbf{V}$ than those of $\lambda$.

3.1.2 Noisy data

Next, we go over to noisy data. We assume that we are given a noise level $\eta \ge 0$ and set

$$\begin{aligned} \delta =\eta \cdot ||\varvec{\Lambda }(\lambda ,\mu )||_F. \end{aligned}$$

(18)

Further, we define $\varvec{\Lambda }^\delta (\lambda ,\mu )$ as

$$\begin{aligned} \varvec{\Lambda }^\delta (\lambda ,\mu )=\varvec{\Lambda }(\lambda ,\mu )+\delta \overline{\mathbf{E}}, \end{aligned}$$

(19)

with $\overline{\mathbf{E}}=\mathbf{E}/||\mathbf{E}||_F$, where $\mathbf{E}$ consists of $M\times M$ random uniformly distributed values in $[-1,1]$. We set

$$\begin{aligned} \mathbf{V}^\delta =\varvec{\Lambda }(\lambda _0,\mu _0)-\varvec{\Lambda }^\delta (\lambda ,\mu ). \end{aligned}$$

Hence, we have

$$\begin{aligned} \Vert \mathbf{V}^\delta - \mathbf{V}\Vert \le \delta . \end{aligned}$$

In the following examples, we consider relative noise levels of $\eta =1\%$ (Fig. 6 and 7 ) and $\eta =10\%$ (Fig. 8 and 9) with respect to the Frobenius norm as given in (19), where the regularization parameters are chosen heuristically and given in the caption of the figure.

In Fig. 6, we observe that for a low noise level with $\eta =1\%$, we obtain a suitable reconstruction of the inclusion concerning the Lamé parameter $\mu$ and the reconstruction of $\lambda$ fails again.

Fig. 6

Shape reconstruction of two inclusions of the difference in the Lamé parameter $\mu$ (left hand side) and $\lambda$ (right hand side) for the regularization parameters $\omega =1.1\cdot 10^{-17}$ and $\sigma =1.1\cdot 10^{-13}$ with relative noise $\eta =1\%$ and transparency function $\alpha$ as shown in Fig. 3

Fig. 7

Shape reconstruction of two inclusions of the reconstructed difference in the Lamé parameter $\mu$ for the regularization parameters $\omega =1.1\cdot 10^{-17}$ and $\sigma =1.1\cdot 10^{-13}$ depicted as cuts with relative noise $\eta =1\%$

In contrary to the low noise level ($\eta =1\%$), Figs. 8 and 9 show us that the standard one-step linearization method has problems in handling higher noise levels ($\eta =10\%$). As such, in the 3D reconstruction (see Fig. 8) it is hard to recognize the two inclusions even with respect to the Lamé parameter $\mu$. Further on in the plots of the cuts in Fig. 9, the reconstructions of the inclusions are blurred out.

Remark 1

All in all, the numerical experiments of this section motivate the consideration of a modified minimization problem in order to obtain a stable method for noisy data as well as a good reconstruction for the Lamé parameter $\lambda$. In doing so, we will combine the idea of the standard one-step linearization with the monotonicity method.

Fig. 8

Shape reconstruction of two inclusions of the difference in the Lamé parameter $\mu$ (left hand side) and $\lambda$ (right hand side) for the regularization parameters $\omega =6\cdot 10^{-17}$ and $\sigma =6\cdot 10^{-13}$ with relative noise $\eta =10\%$ and transparency function $\alpha$ as shown in Fig. 3

Fig. 9

Shape reconstruction of two inclusions of the reconstructed difference in the Lamé parameter $\mu$ for the regularization parameters $\omega =6 \cdot 10^{-17}$ and $\sigma =6\cdot 10^{-13}$ depicted as cuts with relative noise $\eta =10\%$

4 Enhancing the standard residual-based minimization problem

We summarize and present the required results concerning the monotonicity properties of the Neumann-to-Dirichlet operator as well as the monotonicity methods introduced and proven in [6] and Eberle and Harrach [5].

4.1 Summary of the monotonicity methods

First, we state the monotonicity estimates for the Neumann-to-Dirichlet operator $\Lambda (\lambda ,\mu )$ and denote by $u^g_{(\lambda ,\mu )}$ the solution of problem (1)–(3) for the boundary load g and the Lamé parameters $\lambda$ and $\mu$.

Lemma 1

(Lemma 3.1 from [6]) Let $(\lambda _1,\mu _1),(\lambda _2,\mu _2) \in L_+^\infty (\Omega )\times L_+^\infty (\Omega )$, $g\in L^2(\Gamma _{N })^d$ be an applied boundary force, and let $u_1:=u^{g}_{(\lambda _1,\mu _1)}\in \mathcal {V}$, $u_2:=u^{g}_{(\lambda _2,\mu _2)}\in \mathcal {V}$. Then

$$\begin{aligned}&\int _\Omega 2(\mu _1-\mu _2)\hat{\nabla }u_2:\hat{\nabla }u_2+(\lambda _1-\lambda _2)\nabla \cdot u_2\nabla \cdot u_2\,dx\nonumber \\&\quad \ge \langle g,\Lambda (\lambda _2,\mu _2)g\rangle -\langle g,\Lambda (\lambda _1,\mu _1)g\rangle \end{aligned}$$

(20)

$$\begin{aligned}&\quad \ge \int _\Omega 2(\mu _1-\mu _2)\hat{\nabla }u_1 :\hat{\nabla }u_1+(\lambda _1-\lambda _2)\nabla \cdot u_1 \nabla \cdot u_1\,dx. \end{aligned}$$

(21)

Lemma 2

(Lemma 2.2 from [5]) Let $(\lambda _1,\mu _1),(\lambda _2,\mu _2) \in L_+^\infty (\Omega )\times L_+^\infty (\Omega )$, $g\in L^2(\Gamma _{N })^d$ be an applied boundary force, and let $u_1:=u^{g}_{(\lambda _1,\mu _1)}\in \mathcal {V}$, $u_2:=u^{g}_{(\lambda _2,\mu _2)}\in \mathcal {V}$. Then

$$\begin{aligned}&\langle g,\Lambda (\lambda _2,\mu _2)g\rangle -\langle g,\Lambda (\lambda _1,\mu _1)g\rangle \nonumber \\&\quad \ge \int _{\Omega } 2\left( \mu _2-\frac{\mu _2^2}{\mu _1}\right) \hat{\nabla }u_2:\hat{\nabla }u_2\,dx\nonumber \\&\qquad +\int _{\Omega }\left( \lambda _2-\frac{\lambda _2^2}{\lambda _1}\right) \nabla \cdot u_2 \nabla \cdot u_2\,dx \end{aligned}$$

(22)

$$\begin{aligned}&\quad =\int _{\Omega } 2\frac{\mu _2}{\mu _1}\left( \mu _1-\mu _2\right) \hat{\nabla }u_2:\hat{\nabla }u_2\,dx\nonumber \\&\qquad +\int _{\Omega }\frac{\lambda _2}{\lambda _1}\left( \lambda _1-\lambda _2\right) \nabla \cdot u_2 \nabla \cdot u_2\,dx. \end{aligned}$$

(23)

As in the previous section, we denote by $(\lambda _0,\mu _0)$ the material without inclusion. Following Lemma 1, we have

Corollary 1

(Corollary 3.2 from [6]) For $(\lambda _0,\mu _0),(\lambda _1,\mu _1) \in L_+^\infty (\Omega )\times L_+^\infty (\Omega )$

$$\begin{aligned} \lambda _0\le \lambda _1 \text { and } \mu _0\le \mu _1 \quad \text { implies } \quad \Lambda (\lambda _0,\mu _0)\ge \Lambda (\lambda _1,\mu _1). \end{aligned}$$

(24)

Further on, we give a short overview concerning the monotonicity methods, where we restrict ourselves to the case $\lambda _1\ge \lambda _0$, $\mu _1\ge \mu _0$. In the following, let $\mathcal {D}$ be the unknown inclusion and $\chi _\mathcal {D}$ the characteristic function w.r.t. $\mathcal {D}$. In addition, we deal with “noisy difference measurements”, i.e. distance measurements between $u^g_{(\lambda ,\mu )}$ and $u^g_{(\lambda _0,\mu _0)}$ affected by noise, which stem from system (17).

We define the outer support in correspondence to Eberle and Harrach [5] as follows: let $\phi =(\phi _1,\phi _2):\Omega \rightarrow \mathbb {R}^2$ be a measurable function, the outer support $\underset{\partial \Omega }{\mathrm {out}}\,\mathrm {supp}(\phi )$ is the complement (in $\overline{\Omega }$) of the union of those relatively open $U\subseteq \overline{\Omega }$ that are connected to $\partial \Omega$ and for which $\phi \vert _{U}=0$, respectively.

Corollary 2

Linearized monotonicity test (Corollary 2.7 from [5])

Let $\lambda _0$, $\lambda _1$, $\mu _0$, $\mu _1\in \mathbb {R}^+$ with $\lambda _1>\lambda _0$, $\mu _1>\mu _0$ and assume that $(\lambda ,\mu )=(\lambda _0+(\lambda _1-\lambda _0)\chi _\mathcal {D},\mu _0+(\mu _1-\mu _0)\chi _{\mathcal {D}})$ with $\mathcal {D}=\mathrm {out}_{\partial \Omega }\,\mathrm {supp}((\lambda -\lambda _0,\mu -\mu _0)^T)$. Further on let $\alpha ^\lambda ,\alpha ^\mu \ge 0$, $\alpha ^\lambda +\alpha ^\mu >0$ and $\alpha ^\lambda \le \tfrac{\lambda _0}{\lambda _1}(\lambda _1 -\lambda _0)$, $\alpha ^\mu \le \tfrac{\mu _0}{\mu _1} (\mu _1 -\mu _ 0)$. Then for every open set $\mathcal {B}$

$$\begin{aligned}&\mathcal {B}\subseteq \mathcal {D}\quad \text {if and only if}\\&\quad \Lambda (\lambda _0,\mu _0)+\Lambda ^\prime (\lambda _0,\mu _0) (\alpha ^\lambda \chi _\mathcal {B}, \alpha ^\mu \chi _\mathcal {B})\ge \Lambda (\lambda ,\mu ). \end{aligned}$$

Corollary 3

Linearized monotonicity test for noisy data (Corollary 2.9 from [5])

Let $\lambda _0$, $\lambda _1$, $\mu _0$, $\mu _1\in \mathbb {R}^+$ with $\lambda _1>\lambda _0$, $\mu _1>\mu _0$ and assume that $(\lambda ,\mu )=(\lambda _0+(\lambda _1-\lambda _0)\chi _\mathcal {D},\mu _0+(\mu _1-\mu _0)\chi _{\mathcal {D}})$ with $\mathcal {D}=\mathrm {out}_{\partial \Omega }\,\mathrm {supp}((\lambda -\lambda _0,\mu -\mu _0)^T)$. Further on, let $\alpha ^\lambda ,\alpha ^\mu \ge 0$, $\alpha ^\lambda +\alpha ^\mu >0$ with $\alpha ^\lambda \le \frac{\lambda _0}{\lambda _1} (\lambda _1 -\lambda _0)$, $\alpha ^\mu \le \frac{\mu _0}{\mu _1} (\mu _1 -\mu _0)$. Let $\Lambda ^\delta$ be the Neumann-to-Dirichlet operator for noisy difference measurements with noise level $\delta >0$. Then for every open set $\mathcal {B}\subseteq \Omega$ there exists a noise level $\delta _0>0$, such that for all $0<\delta <\delta _0$, $\mathcal {B}$ is correctly detected as inside or not inside the inclusion $\mathcal {D}$ by the following monotonicity test

$$\begin{aligned}&\mathcal {B}\subseteq \mathcal {D}\quad \text { if and only if}\\&\quad \Lambda (\lambda _0,\mu _0)\! +\!\Lambda ^\prime (\lambda _0,\mu _0) (\alpha ^\lambda \chi _{\mathcal {B}},\alpha ^\mu \chi _{\mathcal {B}})\!-\!\Lambda ^\delta (\lambda ,\mu )\!+\!\delta I \!\ge \!0. \end{aligned}$$

Finally, we present the result (see Fig. 10) obtained from noisy data $\Lambda ^{\delta }$ with the linearized monotonicity method as described in Corollary 3, where we use the same pixel partition as for the one-step linearization method.

Fig. 10

Shape reconstruction of two inclusions (red) for $\alpha ^\lambda =0.28(\lambda _1-\lambda _0)\approx 4.6\cdot 10^5$Pa, $\alpha ^\mu =0.28(\mu _1-\mu _0)\approx 4.7\cdot 10^3$ Pa with relative noise $\eta =0.1\%$ and $\delta =1.88\cdot 10^{-10}$

Remark 2

The linearized monotonicity method converges theoretically rigorously, but in practice delivers poorer reconstructions even for small noise (see Fig. 10, where the two inclusions are not separated) than the theoretically unproven heuristic one-step linearization (see Fig. 6, where the two inclusions are separated). Thus, we improve the standard one-step linearization method by combining it with the monotonicity method without losing the convergence results.

4.2 Monotonicity-based regularization

We assume again that the background $(\lambda _0,\mu _0)$ is homogeneous and that the contrasts of the anomalies $(\gamma ^{\lambda },\gamma ^{\mu })^T\in L^\infty _+(\mathcal {D})^2$ with

$$\begin{aligned} \begin{pmatrix} \lambda (x)\\ \mu (x) \end{pmatrix} =\begin{pmatrix} \lambda _0+\gamma ^{\lambda }(x)\chi _\mathcal {D}(x)\\ \mu _0+\gamma ^{\mu }(x)\chi _\mathcal {D}(x) \end{pmatrix}, \end{aligned}$$

are bounded for all $x\in \mathcal {D}$ (a.e.) via

$$\begin{aligned} c^\lambda \le \gamma ^\lambda (x)\le C^\lambda \quad \text {and}\quad c^\mu \le \gamma ^\mu (x)\le C^\mu , \end{aligned}$$

with $c^\lambda$, $C^\lambda$, $c^\mu$, $C^\mu \ge 0$. $\mathcal {D}$ is an open set denoting the anomalies and the parameters $\lambda _0,\mu _0, c^\lambda ,c^\mu ,C^\lambda$ and $C^\mu$ are assumed to be known.

Remark 3

It should be noted that $\Omega \setminus \mathcal {D}$ has to be connected.

In doing so, we can also handle more general Lamé parameters and not only piecewise constant parameters as in the previous section.

Here, we focus on the case $\lambda \ge \lambda _0$, $\mu \ge \mu _0$, while the case $\lambda \le \lambda _0$, $\mu \le \mu _0$ can be found in the “Appendix”.

Similar as in the one-step linearization method, we make the piecewise constant ansatz (11) in order to approximate $(\gamma ^{\lambda },\gamma ^{\mu })$ by $(\kappa ,\nu ).$

The main idea of monotonicity-based regularization is to minimize the residual of the linearized problem, i.e.,

$$\begin{aligned} \left\| \left( \mathbf{S}^{\lambda }\,\vert \,\, \mathbf{S}^{\mu }\right) \begin{pmatrix} \varvec{\kappa }\\ \varvec{\nu } \end{pmatrix} - \mathbf{V}\right\| ^2_{2} \rightarrow \mathrm {min!} \end{aligned}$$

(25)

with constraints on $(\varvec{\kappa },\varvec{\nu })$ that are obtained from the monotonicity properties introduced in Lemma 1 and 2. Our aim is to rewrite the minimization problem (25) for the case $\mu _0\ne \mu ,\lambda _0\ne \lambda$ in $\mathcal {D}$ in order to be able to reconstruct the inclusions also with respect to $\lambda$. Our intention is to force that both Lamé parameters $\mu (x)$ and $\lambda (x)$ take the same shape but different scale.

In more detail, we define the quantities $a_{\max }$ and $\tau$ as

$$\begin{aligned} a_{\max }&:=\mu _0-\frac{\mu _0^2}{\mu _0+c^\mu }, \end{aligned}$$

(26)

$$\begin{aligned} \tau&:=\frac{1}{a_{\max }}\left( \lambda _0-\frac{\lambda _0^2}{\lambda _0+c^\lambda }\right) , \end{aligned}$$

(27)

such that

$$\begin{aligned} -2\left( \mu _0-\frac{\mu _0^2}{\mu }\right) +2a&\le 0, \end{aligned}$$

(28)

$$\begin{aligned} -\left( \lambda _0-\frac{\lambda _0^2}{\lambda }\right) +\tau a&\le 0 \end{aligned}$$

(29)

for all $0\le a\le a_{\max }$.

In addition, we set the residual $r(\nu )$ as

$$\begin{aligned} r(\nu ):=\Lambda (\lambda ,\mu )-\Lambda (\lambda _0,\mu _0)-\Lambda ^\prime (\lambda _0,\mu _0)(\tau \nu ,\nu ) \end{aligned}$$

and the components of the corresponding matrix $\mathbf{R}(\nu )$ are given by

$$\begin{aligned} (\mathbf{R}(\nu ))_{i,j=1,\ldots M}:=\left( \langle g_i,r(\nu )g_j\rangle \right) _{i,j=1,\ldots M}. \end{aligned}$$

We want to remark, that we use the same boundary loads $g_i$, $i=1,\ldots , M,$ as in Sect. 2.

Finally, we introduce the set

$$\begin{aligned} \mathcal {C}:=\bigg \lbrace \nu \in L^\infty (\Omega ): \nu&=\sum _{k=1}^p a_k \chi _{k},\,a_k\in \mathbb {R},\,0\le a_k\le \min (a_{\max },\beta _k)\bigg \rbrace \end{aligned}$$

with

$$\begin{aligned} \beta _k:=\mathrm {max}\left\{ a\ge 0:\, \Lambda (\lambda ,\mu )-\Lambda (\lambda _0,\mu _0)\le \Lambda ^\prime (\lambda _0,\mu _0) (\tau a\chi _k,a\chi _k)\right\} , \end{aligned}$$

(30)

where we set $\chi _k:=\chi _{\mathcal {B}_k}$.

Note that the set on the right hand side of (30) is non-empty since it contains the value zero by Corollary 1 and our assumptions $\lambda \ge \lambda _0, \mu \ge \mu _0$.

Then, we modify the original minimization problem (25) to

$$\begin{aligned} \min _{{\nu }\in \mathcal {C}}\Vert \mathbf{R}(\nu ) \Vert _F. \end{aligned}$$

Remark 4

We want to remark that $\beta _k$ is defined via the infinite-dimensional Neumann-to-Dirichlet operator $\Lambda (\lambda ,\mu )$ and does not involve the finite dimensional matrix $\mathbf{R}$. For the numerical realization we will require a discrete version $\tilde{\beta }_k$ of $\beta _k$ introduced later on.

4.2.1 Main results

In the following we present our main results and will show that the choices of the quantities $a_{\mathrm {max}}$ and $\tau$ will lead to the correct reconstruction of the support of $\kappa (x)$ and $\nu (x)$, which we introduced in (26) and (27), respectively, based on the lower bounds from the monotonicity tests as stated in (28) and (29).

Theorem 1

Consider the minimization problem

$$\begin{aligned} \min _{\nu \in \mathcal {C}}\Vert \mathbf{R}(\nu )\Vert _F. \end{aligned}$$

(31)

The following statements hold true:

• (i) Problem (31) admits a unique minimizer $\hat{\nu }$.

• (ii) $\mathrm {supp}(\hat{\nu })$ and $\mathcal {D}$ agree up to the pixel partition, i.e. for any pixel $\mathcal {B}_k$

  $$\begin{aligned} \mathcal {B}_k\subset \mathrm {supp}(\hat{\nu })\quad \text {if and only if}\quad \mathcal {B}_k\subset \mathcal {D}. \end{aligned}$$

  Moreover,

  $$\begin{aligned} \hat{\nu }=\sum _{\mathcal {B}_k\subseteq \mathcal {D}} a_{\max }\chi _{k}. \end{aligned}$$

Now we deal with noisy data and introduce the corresponding residual

$$\begin{aligned} r_\delta (\nu ):=\Lambda ^\delta (\lambda ,\mu )-\Lambda (\lambda _0,\mu _0)-\Lambda ^\prime (\lambda _0,\mu _0)(\tau \nu ,\nu ). \end{aligned}$$

(32)

Based on this, $\mathbf{R}_\delta (\nu )$ represents the matrix $(\langle g_i,r_\delta (\nu ) g_j\rangle )_{i,j=1,\ldots M}$.

Further on, the admissible set for noisy data is defined by

$$\begin{aligned} \mathcal {C}_\delta :=\bigg \lbrace \nu \in L^\infty (\Omega ): \nu&=\sum _{k=1}^p a_k \chi _{k},\,a_k\in \mathbb {R},\,0\le a_k\le \min (a_{\max },\beta _{k,\delta })\bigg \rbrace \end{aligned}$$

with

$$\begin{aligned} \beta _{k,\delta }&:=\mathrm {max}\left\{ a\ge 0:\, \Lambda ^{\delta }(\lambda ,\mu )-\Lambda (\lambda _0,\mu _0)-\delta I\right. \nonumber \\&\qquad \left. \le \Lambda ^\prime (\lambda _0,\mu _0) (\tau a\chi _k,a\chi _k)\right\} . \end{aligned}$$

(33)

Thus, we present the following stability result.

Theorem 2

Consider the minimization problem

$$\begin{aligned} \min _{\nu \in \mathcal {C}_\delta }\Vert \mathbf{R}_\delta (\nu )\Vert _F. \end{aligned}$$

(34)

The following statements hold true:

• (i) Problem (34) admits a minimizer.

• (ii) Let $\hat{\nu }=\sum \limits _{\mathcal {B}_k\subseteq \mathcal {D}}a_{\max }\chi _{k}$ be the minimizer of (31) and $\hat{\nu }_\delta =\sum \limits _{k=1}^p a_{k,\delta }\chi _{k}$ of problem (34), respectively. Then $\hat{\nu }_\delta$ converges pointwise and uniformly to $\hat{\nu }$ as $\delta$ goes to 0.

Remark 5

In [5], we used monotonicity methods to solve the inverse problem of shape reconstruction. In Theorems 1 and 2, we applied the same monotonicity methods to construct constraints for the residual based inversion technique. Both methods have a rigorously proven convergence theory, however the monotonicity-based regularization approach turns out to be more stable regarding noise.

4.2.2 Theoretical background

In order to prove Theorem 1 as well as Theorem 2, we have to take a look at the following.

Lemma 3

Let $a_{\mathrm {max}}$ and $\tau$ be defined as in (26) and (27), respectively, $\lambda ,\mu \in L^\infty _+(\Omega )$ and we assume that $\lambda \ge \lambda _0$, $\mu \ge \mu _0$, where $\lambda _0,\mu _0$ are constant. Then we have for any pixel $\mathcal {B}_k$, $\mathcal {B}_k\subseteq \mathcal {D}$ if and only if $\beta _{k}>0$, where $\beta _k$ is defined in (30).

Proof

We adopt the proof of Lemma 3.4 from [11].

Step 1: First, we verify that from $\mathcal {B}_k\subseteq \mathcal {D}$ it follows that $\beta _{k}>0$.

In fact, by applying the monotonicity principle (22) multiplied by $-1$ for

$$\begin{aligned} \lambda _1:=\lambda ,\mu _1:=\mu \,\,\,\mathrm {and}\,\,\, \lambda _2:=\lambda _0,\mu _2:=\mu _0, \end{aligned}$$

we end up with the following inequalities for all pixel $\mathcal {B}_k$, all $a\in [0,a_{\max }]$ and all $g\in L^2(\Gamma _{N })^d$

$$\begin{aligned}&\left\langle g,\left( \Lambda (\lambda ,\mu )-\Lambda (\lambda _0,\mu _0)- \Lambda ^{\prime }(\lambda _0,\mu _0)(\tau a\chi _{k},a\chi _{k})\right) g\right\rangle \\&\quad \le -\int _{\Omega } 2\left( \mu _0-\frac{\mu _0^2}{\mu }\right) \hat{\nabla }u_0^{g}:\hat{\nabla }u_0^{g} \,dx+ \int _{\Omega }2 a\chi _{k}\hat{\nabla }u_0^{g}:\hat{\nabla }u_0^{g}\,dx\\&\qquad -\int _{\Omega }\left( \lambda _0-\frac{\lambda _0^2}{\lambda }\right) \nabla \cdot u_0^{g} \nabla \cdot u_0^{g}\,dx + \int _{\Omega }\tau a\chi _{k}\nabla \cdot u_0^{g} \nabla \cdot u_0^{g}\,dx\\&\quad \le -\int _{\mathcal {D}} 2\left( \mu _0-\frac{\mu _0^2}{\mu }\right) \hat{\nabla }u_0^{g}:\hat{\nabla }u_0^{g}\,dx +\int _{\mathcal {B}_k}2 a_{\max }\hat{\nabla }u_0^{g}:\hat{\nabla }u_0^{g}\,dx\\&\qquad -\int _{\mathcal {D}}\left( \lambda _0-\frac{\lambda _0^2}{\lambda }\right) \nabla \cdot u_0^{g} \nabla \cdot u_0^{g}\,dx +\int _{\mathcal {B}_k}\tau a_{\max }\nabla \cdot u_0^{g} \nabla \cdot u_0^{g}\,dx\\&\quad \le 0. \end{aligned}$$

In the above inequalities, we used the shorthand notation $u_0^{g}$ for the unique solution $u_{(\lambda _0,\mu _0)}^{g}$. The last inequality holds due to the fact that $a_{\max }$ and $\tau$ fulfill

$$\begin{aligned} -2\left( \mu _0-\frac{\mu _0^2}{\mu }\right) +2a_{\max }&\le 0,\\ -\left( \lambda _0-\frac{\lambda _0^2}{\lambda }\right) +\tau a_{\max }&\le 0 \end{aligned}$$

in $\mathcal {D}$ and that $\mathcal {B}_k$ lies inside $\mathcal {D}$.

We want to remark, that compared with the corresponding proof in Harrach and Mach [11], this shows us that we require conditions on $a_{\max }$ as well as on $\tau$ (c.f. Eq. (28) and (29)) due to the fact that we deal with two unknown parameters ($\lambda$ and $\mu$) instead of one.

Step 2: In order to prove the other direction of the statement, let $\beta _{k}> 0$. We will show that $\mathcal {B}_k\subseteq \mathcal {D}$ by contradiction.

Assume that $\mathcal {B}_k\not \subseteq \mathcal {D}$ and $\beta _{k}>0$. Applying the monotonicity principle from Lemma 1,

$$\begin{aligned} \Lambda (\lambda ,\mu )-\Lambda (\lambda _0,\mu _0)\ge \Lambda ^{\prime }(\lambda _0,\mu _0)((\lambda ,\mu )-(\lambda _0,\mu _0)), \end{aligned}$$

with the definition of $\beta _k$ in (30), we are led to

$$\begin{aligned} 0&\ge \Lambda (\lambda ,\mu )-\Lambda (\lambda _0,\mu _0)-\Lambda ^{\prime } (\lambda _0,\mu _0)(\tau \beta _k\chi _k,\beta _k\chi _k)\\&\ge \Lambda ^{\prime }(\lambda _0,\mu _0)((\lambda ,\mu )-(\lambda _0,\mu _0))\\&\quad - \Lambda ^{\prime }(\lambda _0,\mu _0) (\tau \beta _k\chi _k,\beta _k\chi _k). \end{aligned}$$

Based on this, we conclude that for all $g\in L^2(\Gamma _{N })^d$

$$\begin{aligned}&\int _{\mathcal {B}_k}\tau \beta _{k}\nabla \cdot u_0^{g} \nabla \cdot u_0^{g}\,dx +2\int _{\mathcal {B}_k}\beta _{k}\hat{\nabla } u_0^{g} :\hat{\nabla } u_0^{g}\,dx\nonumber \\&\quad \le \int _{\Omega }(\lambda -\lambda _0)\nabla \cdot u_0^{g} \nabla \cdot u_0^{g}\,dx +2\int _{\Omega }(\mu -\mu _0)\hat{\nabla } u_0^{g} : \hat{\nabla } u_0^{g}\,dx\nonumber \\&\quad \le \int _{\mathcal {D}} C^{\lambda } \nabla \cdot u_0^{g} \nabla \cdot u_0^{g}\,dx +2\int _{\mathcal {D}}C^{\mu }\hat{\nabla }u_0^{g} : \hat{\nabla } u_0^{g}\,dx. \end{aligned}$$

(35)

On the other hand, using the localized potentials in a similar procedure as in the proof of Theorem 2.1 in [5], we can find a sequence $(g_m)_{m\in \mathbb {N}}\subset L^2(\Gamma _{N })^d$ such that the solutions $(u_0^m)_{m\in \mathbb {N}}\subset H^1(\Omega )^d$ of the forward problem (when the Lamé parameter are chosen to be $\lambda _0$, $\mu _0$ and the boundary forces $g=g_m$) fulfill

$$\begin{aligned}&\lim _{m\rightarrow \infty }\int _{\mathcal {B}_k}\hat{\nabla }u_0^{m}:\hat{\nabla }u_0^{m}\,dx=\infty ,\quad \,\,\, \lim _{m\rightarrow \infty }\int _{\mathcal {D}}\hat{\nabla }u_0^{m}:\hat{\nabla }u_0^{m}\,dx=0,\\&\lim _{m\rightarrow \infty }\int _{\mathcal {B}_k}\nabla \cdot u_0^{m} \nabla \cdot u_0^{m}\,dx=\infty ,\quad \lim _{m\rightarrow \infty }\int _{\mathcal {D}}\nabla \cdot u_0^{m} \nabla \cdot u_0^{m}\,dx=0, \end{aligned}$$

which contradicts (35). $\square$

Lemma 4

For all pixels $\mathcal {B}_k$, denote by $\mathbf{S}_k^\tau$ the matrix

$$\begin{aligned} \mathbf{S}_k^\tau :=\left( \langle g_i,-\Lambda ^\prime (\lambda _0,\mu _0)(\tau \chi _k,\chi _k)g_j\rangle \right) _{i,j=1,\ldots ,M}. \end{aligned}$$

Then $\mathbf{S}_k^\tau$ is a positive definite matrix.

Proof

We adopt the proof of Lemma 3.5 from [11] for the matrix $\mathbf{S}_k^\tau$, which directly yields the desired result. $\square$

Proof

(Theorem 1) This proof is based on the proof of Theorem 3.2 from [11].

to (i) Since the functional

$$\begin{aligned} \nu \mapsto \Vert \mathbf{R}(\nu )\Vert _F^2:=\sum _{i,j=1}^M\langle g_i,r(\nu )g_j\rangle ^2 \end{aligned}$$

is continuous, it admits a minimizer in the compact set $\mathcal {C}$.

The uniqueness of $\hat{\nu }$ will follow from the proof of (ii) Step 3.

to (ii) Step 1 We shall check that for all

$$\begin{aligned} \nu&=\sum _{k=1}^p a_k\chi _k\quad \text {satisfying}\quad 0\le a_k\le \min (a_{\max },\beta _k), \end{aligned}$$

it holds that $r(\nu )\le 0$ in quadratic sense. We want to remark that for $a_{\max }$ and $\tau$ the inequalities (28) and (29) hold in $\mathcal {D}$.

We proceed similar as in the proof of Lemma 3 and use Lemma 2 for $\lambda _1=\lambda , \mu _1=\mu , \lambda _2=\lambda _0$ and $\mu _2=\mu _0$. In addition, we multiply the whole expression with $-1$. Thus, it holds that

$$\begin{aligned}&\left\langle g,(\Lambda (\lambda ,\mu )-\Lambda (\lambda _0,\mu _0)-\Lambda ^\prime (\lambda _0,\mu _0)(\tau \nu ,\nu ))g\right\rangle \\&\quad \le -\int _{\mathcal {D}} 2 a_{\max }\hat{\nabla }u_0^{g}:\hat{\nabla }u_0^{g}\,dx+\sum _{k=1}^p\int _{\mathcal {B}_k} 2 a_k\hat{\nabla }u_0^{g}:\hat{\nabla }u_0^{g}\,dx\\&\qquad -\int _{\mathcal {D}}\tau a_{\max }\nabla \cdot u_0^{g} \nabla \cdot u_0^{g}\,dx+\sum _{k=1}^p\int _{\mathcal {B}_k}\tau a_k\nabla \cdot u_0^{g} \nabla \cdot u_0^{g}\,dx \end{aligned}$$

for any $g\in L^2(\Gamma _{N })^d$.

If $a_k>0$, it follows $\beta _k\ge a_k>0$, so that Lemma 3 implies that $\mathcal {B}_k\subseteq \mathcal {D}$. Since $a_k\le a_{\max }$, we end up with $\langle g,r(\nu ) g\rangle \le 0$ for $g\in L^2(\Gamma _{N })^d$.

Step 2: Let $\hat{\nu }=\sum \nolimits _{k=1}^p \hat{a}_k\chi _k$ be a minimizer of problem (31). We show that $\mathrm {supp}(\hat{\nu })\subseteq \mathcal {D}$.

Per definition of $\beta _k$, it holds that $\beta _k\ge \hat{a}_k$. This implies $\beta _k>0$. With Lemma 3 we have $\mathcal {B}_k\subseteq \mathcal {D}$.

Step 3: We will prove that, if $\hat{\nu }=\sum \nolimits _{k=1}^p \hat{a}_k\chi _k$ is a minimizer of problem (31), then the representation of $\hat{a}_k$ is given by

$$\begin{aligned} \hat{a}_k= {\left\{ \begin{array}{ll} 0&{}\text {for}\,\,\mathcal {B}_k\not \subseteq \mathcal {D},\\ a_{\mathrm {max}}&{}\text {for}\,\,\mathcal {B}_k\subseteq \mathcal {D}. \end{array}\right. } \end{aligned}$$

In fact, it holds that $\hat{a}_k< a_{\max }$. If there exists a pixel $\mathcal {B}_k$ such that $\hat{\nu }(x)<\min (a_{\max },\beta _k)$ in $\mathcal {B}_k$, we can choose $h^\nu > 0$, such that $\hat{\nu }+h^\nu \chi _k=a_{\max }$ in $\mathcal {B}_k$. We will show that then,

$$\begin{aligned} \Vert \mathbf{R}(\hat{\nu }+h^\nu \chi _k)\Vert _F < \Vert \mathbf{R}(\hat{\nu })\Vert _F, \end{aligned}$$

which contradicts the minimality of $\hat{\nu }$. Thus, it follows that $\hat{a}_k=\mathrm {min}\left( a_{\mathrm {max}},\beta _k\right)$.

To show the contradiction, let $\theta _1(\hat{\nu })\ge \theta _2(\hat{\nu })\ge \cdots \ge \theta _{M}(\hat{\nu })$ be M eigenvalues of $\mathbf{R}(\hat{\nu })$ and $\theta _1(\hat{\nu }+h^\nu \chi _k)\ge \theta _2(\hat{\nu }+h^\nu \chi _k)\ge \cdots \ge \theta _{M}(\hat{\nu }+h^\nu \chi _k)$ M eigenvalues of $\mathbf{R}(\hat{\nu }+h^\nu \chi _k)$.

Since $\mathbf{R}(\hat{\nu })$ and $\mathbf{R}(\hat{\nu }+h^\nu \chi _k)$ are both symmetric, all of their eigenvalues are real. By the definition of the Frobenius norm, we obtain

$$\begin{aligned}&\Vert \mathbf{R}(\hat{\nu }+h^\nu \chi _k)\Vert _F^2-\Vert \mathbf{R}(\hat{\nu })\Vert _F^2\\&\quad = \sum _{i=1}^M\vert \theta _i(\hat{\nu }+h^\nu \chi _k)\vert ^2-\sum _{i=1}^M\vert \theta _i(\hat{\nu })\vert ^2\\&\quad =\sum _{i=1}^M \left( \theta _i\left( \hat{\nu }+h^\nu \chi _k)+\theta _i(\hat{\nu }\right) \right) \cdot \left( \theta _i(\hat{\nu }+h^\nu \chi _k)-\theta _i(\hat{\nu })\right) . \end{aligned}$$

Due to Step 1, $r(\hat{\nu })\le 0$ and $r(\hat{\nu }+h^\nu \chi _k)\le 0$ in the quadratic sense. Thus, for all $x=(x_1,\ldots ,x_{M})^T\in \mathbb {R}^M$, we have

$$\begin{aligned} x^T \mathbf{R}(\hat{\nu })x=\sum _{i,j=1}^M x_i x_j \langle g_i, r(\hat{\nu })g_j\rangle = \langle g,r(\hat{\nu }) g\rangle \le 0, \end{aligned}$$

where $g=\sum \nolimits _{i=1}^M x_i g_i$. This means that $-\mathbf{R}(\hat{\nu })$ is a positive semi-definite symmetric matrix in $\mathbb {R}^{M\times M}$. Due to the fact, that all eigenvalues of a positive semi-definite symmetric matrix are non-negative, it follow that $\theta _i(\hat{\nu })\le 0$ for all $i\in \lbrace 1, \ldots , M\rbrace$. By the same considerations, $-\mathbf{R}(\hat{\nu }+h^\nu \chi _k)$ is also a positive semi-definite matrix. We want to remark, that $\mathbf{S}_k^\tau$ is positive definite as proven in Lemma 4 and hence, all M eigenvalues of $\theta _1(\mathbf{S}_k^{\tau }) \ge \cdots \ge \theta _{M}(\mathbf{S}_k^{\tau })$ are positive. Since

$$\begin{aligned} \mathbf{R}(\hat{\nu }+h^\nu \chi _k)= \mathbf{R}(\hat{\nu })+h^\nu \mathbf{S}_k^{\tau } \end{aligned}$$

and the matrices $\mathbf{R}(\hat{\nu }+h^\nu \chi _k)$, $\mathbf{R}(\hat{\nu })+h^\nu$ and $\mathbf{S}_k^\tau$ are symmetric, we can apply Weyl’s Inequalities to get

$$\begin{aligned} \theta _i(\hat{\nu }+h^\nu \chi _k)\ge \theta _i(\hat{\nu }) +\theta _{M}(h^\nu \mathbf{S}_k^{\tau }) >\theta _i (\hat{\nu }) \end{aligned}$$

for all $i\in \lbrace 1,\ldots ,M\rbrace .$

In summary we end up with

$$\begin{aligned} \Vert \mathbf{R}(\hat{\nu }+h^\nu \chi _k)\Vert _F < \Vert \mathbf{R}(\hat{\nu })\Vert _F, \end{aligned}$$

which contradicts the minimality of $\hat{\nu }$ and thus, ends the proof of Step 3.

Step 4: We show that, if $\mathcal {B}_k\subseteq \mathcal {D}$, then $\mathcal {B}_k\subseteq \mathrm {supp}(\hat{\nu })$. Indeed, since $\hat{\nu }$ is a minimizer of problem (31), Step 3 implies that

$$\begin{aligned} \hat{\nu }=\sum _{k=1}^p \min (a_{\max },\beta _k)\chi _k. \end{aligned}$$

Since $\mathcal {B}_k\subseteq \mathcal {D}$, it follows from Lemma 3 that $\min (a_{\max },\beta _k)>0$. Thus, $\mathcal {B}_k\subseteq \mathrm {supp}(\hat{\nu })$.

In conclusion, problem (31) admits a unique minimizer $\hat{\nu }$ with

$$\begin{aligned} \hat{\nu }=\sum _{k=1}^p \min (a_{\max },\beta _k)\chi _k. \end{aligned}$$

This minimizer fulfills

$$\begin{aligned} \hat{\nu }={\left\{ \begin{array}{ll} a_{\max }\,\,\,\,\text {in}\,\,\mathcal {B}_k,&{}\quad \text {if}\,\, \mathcal {B}_k\,\,\text {lies inside}\,\,\mathcal {D},\\ 0\,\,\quad \,\,\,\,\text { in}\,\,\,\,\mathcal {B}_k,&{}\quad \text {if}\,\,\mathcal {B}_k\,\,\text {does not lie inside}\,\,\mathcal {D}, \end{array}\right. } \end{aligned}$$

so that

$$\begin{aligned} \hat{\nu }=\sum _{\mathcal {B}_k\subseteq \mathcal {D}} a_{\mathrm {max}}\chi _k. \end{aligned}$$

$\square$

Next, we go over to noisy data and take a look at the following lemma, where we set $V^\delta :=\frac{1}{2}( V^\delta + (V^\delta )^{*})$, since we always can redefine the data $V^\delta$ in this way without loss of generality. Thus, we can assume that $V^\delta$ is self-adjoint.

Lemma 5

Assume that $\Vert \Lambda ^\delta (\lambda ,\mu )-\Lambda (\lambda ,\mu )\Vert \le \delta$. Then for every pixel $\mathcal {B}_k$, it holds that $\beta _k\le \beta _{k,\delta }$ for all $\delta >0$.

Proof

The proof follows the lines of Lemma 3.7 in [11] with the following modifications. We have to check that $\beta _k$ as given in (30) fulfills the relation

$$\begin{aligned} \vert V^\delta \vert +\Lambda ^\prime (\lambda _0,\mu _0)(\tau a \chi _k,a \chi _k)\ge -\delta I \quad \text {for all}\,\, a \in [0,\beta _k], \end{aligned}$$

where $\vert V^\delta \vert =\sqrt{(V^\delta )^*V^\delta }$.

As proven in [11], $V-V^\delta \ge -\delta I$ in quadratic sense. Further on Lemma 3.6 from [11] implies $\vert V^\delta \vert \ge V^\delta$, since $V^\delta$ is self-adjoint. Hence,

$$\begin{aligned}&\vert V^\delta \vert +\Lambda ^\prime (\lambda _0,\mu _0)(\tau \beta _k\chi _k,\beta _k\chi _k)\\&\quad \ge V^\delta +\Lambda ^\prime (\lambda _0,\mu _0)(\tau \beta _k\chi _k,\beta _k\chi _k)\\&\quad =V+\Lambda ^\prime (\lambda _0,\mu _0)(\tau \beta _k\chi _k,\beta _k\chi _k)+V^\delta -V\\&\quad \ge -\delta I. \end{aligned}$$

$\square$

Remark 6

As a consequence, it holds that

• 1. If $\mathcal {B}_k$ lies inside $\mathcal {D}$, then $\beta _{k,\delta }\ge a_{\max }$.

• 2. If $\beta _{k,\delta }=0$, then $\mathcal {B}_k$ does not lie inside $\mathcal {D}$.

Proof

(Theorem 2) This proof is based on the proof of Theorem 3.8 in [11].

to (i) For the proof of the existence of a minimizer of (34), we argue as in the proof of Theorem 1 (i). First, we take a look at the functional

$$\begin{aligned} \nu \mapsto \Vert \mathbf{R}_\delta (\nu )\Vert _F^2, \end{aligned}$$

(36)

which is defined by $(\mathbf{R}_{\delta }(\nu ))_{i,j=1,\ldots M}:=\left( \langle g_i,r_{\delta }(\nu )g_j\rangle \right) _{i,j=1,\ldots M}$ via the residual (32). Since the functional (36) is continuous, it follows that there exists at least one minimizer in the compact set $\mathcal {C}_\delta$.

to (ii) Step 1: Convergence of a subsequence of $\hat{\nu }_\delta$

For any fixed k, the sequence $\lbrace \hat{a}_{k,\delta }\rbrace _{\delta >0}$ is bounded from below by 0 and from above by $a_{\max }$, respectively. By Weierstrass’ Theorem, there exists a subsequence $(\hat{a}_{1,\delta _n},\ldots ,\hat{a}_{p,\delta _n})$ converging to some limit $(a_{1},\ldots ,a_p)$. Of course, $0\le a_k\le a_{\max }$ for all $k=1,\ldots ,p$.

Step 2: Upper bound and limit

We shall check that $a_k\le \beta _k$ for all $k=1,\ldots ,p$. As shown in the proof of Theorem 3.8 in [11], $\vert V^\delta \vert$ converges to $\vert V\vert$ in the operator norm as $\delta$ goes to 0, and hence, for any fixed k,

$$\begin{aligned}&\vert V\vert +\Lambda ^\prime (\lambda _0,\mu _0)(\tau a_k\chi _k,a_k\chi _k)\\&\quad = \lim _{\delta _n\rightarrow 0}(\vert V^{\delta _n}\vert +\Lambda ^\prime (\lambda _0,\mu _0) (\tau \hat{a}_{k,\delta _n}\chi _k,\hat{a}_{k,\delta _n} \chi _k)) \end{aligned}$$

in the operator norm. As in [11], we obtain that for all $g\in L^2(\Gamma _{\mathrm {N}})^d$,

$$\begin{aligned} \langle g, (\vert V\vert +\Lambda ^\prime (\lambda _0,\mu _0)(\tau a_k\chi _k,a_k\chi _k))g\rangle \ge 0. \end{aligned}$$

Step 3: Minimality of the limit

Due to Lemma 5, we know that $\min (a_{\max },\beta _k)\le \min (a_{\max },\beta _{k,\delta })$ for all $k=1,\ldots ,p$. Thus, $\hat{\nu }$ belongs to the admissible set $\mathcal {C}_\delta$ of the minimization problem (34) for all $\delta >0$. By minimality of $\hat{\nu }_\delta$, we obtain

$$\begin{aligned} \Vert \mathbf{R}_\delta (\hat{\nu }_\delta )\Vert _F\le \Vert \mathbf{R}_\delta (\hat{\nu })\Vert _F. \end{aligned}$$

Denote by $\nu =\sum \nolimits _{k=1}^p a_k\chi _k$, where $a_k$ are the limits derived in Step 1. We have that

$$\begin{aligned} \Vert \mathbf{R}_{\delta _n}(\hat{\nu }_{\delta _n})\Vert _F^2&= \sum _{i,j=1}^M\left\langle g_i,\left( -V^{\delta _n}-\sum _{k=1}^p \Lambda ^\prime (\lambda _0,\mu _0) (\tau \hat{a}_{k,\delta _n}\chi _k,\hat{a}_{k,\delta _n}\chi _k)\right) g_j\right\rangle ^2,\\ \Vert \mathbf{R}({\nu })\Vert _F^2&= \sum _{i,j=1}^M\left\langle g_i,\left( -V-\sum _{k=1}^p \Lambda ^\prime (\lambda _0,\mu _0)(\tau a_k\chi _k,a_k\chi _k)\right) g_j\right\rangle ^2. \end{aligned}$$

With the same arguments as in the proof of Theorem 3.8 in [11], i.e. that V converges to $V^\delta$ as well as $\hat{a}_{k,\delta }$ goes to $a_k$, we are led to

$$\begin{aligned} \Vert \mathbf{R}(\nu )\Vert _F\le \Vert \mathbf{R}(\hat{\nu })\Vert _F. \end{aligned}$$

Further on, by the uniqueness of the minimizer we obtain $\nu =\hat{\nu }$ that is

$$\begin{aligned} a_k=\hat{a}_k={\left\{ \begin{array}{ll} 0&{}\text {for}\,\,\mathcal {B}_k\not \subseteq \mathcal {D},\\ a_{\mathrm {max}}&{}\text {for}\,\,\mathcal {B}_k\subseteq \mathcal {D}. \end{array}\right. } \end{aligned}$$

Step 4: Convergence of the whole sequence $\hat{\nu }_\delta$

Again this is obtained in the same way as in [11] and is based on the knowledge that every subsequence of $(\hat{a}_{1,\delta },\ldots ,\hat{a}_{p,\delta })$ possesses a convergent subsubsequence, that goes to the limit $(\min (a,\beta _1),\ldots ,$ $\min (a,\beta _p))$. $\square$

Remark 7

All in all, we are led to the discrete formulation of the minimization problem for noisy data:

$$\begin{aligned} \min _{{\nu }\in \mathcal {C}_\delta }\Vert \mathbf{R}_\delta (\nu )\Vert _F, \end{aligned}$$

(37)

under the constraint

$$\begin{aligned} 0&\le \nu _k \le \min \left( a_{\max }, \tilde{\beta }_{k,\delta }\right) , \end{aligned}$$

(38)

where

$$\begin{aligned} a_{\max }&=\mu _0-\frac{\mu _0^2}{\mu _0+c^\mu }, \end{aligned}$$

(39)

$$\begin{aligned} \tau&=\dfrac{1}{a_{\mathrm {max}}}\left( \lambda _0-\dfrac{\lambda _0^2}{\lambda _0+c^{\lambda }}\right) , \end{aligned}$$

(40)

$$\begin{aligned} \tilde{\beta }_{k,\delta }&=\max \lbrace a \ge 0\,:\, - a \mathbf{S}^{\tau }_k\ge -\delta \mathbf{I}-\vert \mathbf{V}^\delta \vert \rbrace \end{aligned}$$

(41)

with $\vert \mathbf{V}^\delta \vert :=\sqrt{(\mathbf{V}^\delta )^{*} \mathbf{V}^\delta }$.

We want to mention, that $\mathbf {V}$ is positive definite, however, $\mathbf{V}^\delta$ is not in general, which leads to problems in the proofs. Hence, we use $\vert \mathbf{V}^\delta \vert$ instead.

Next, we take a closer look at the determination of $\tilde{\beta }_{k,\delta }$ (see [11]), where $\tilde{\beta }_{k,0}=\tilde{\beta }_{k}$:

First, we replace the infinite-dimensional operators $\vert { V}^\delta \vert$ and $\Lambda ^\prime (\lambda _0,\mu _0)$ in (33) by the $M\times M$ matrices $\mathbf{V}^\delta$, $\mathbf{S}_k^\tau$ such that we need to find $\tilde{\beta }_{k,\delta }$ with

$$\begin{aligned} - a \mathbf{S}_k^\tau&\ge -\delta \mathbf{I} -\vert \mathbf{V}^\delta \vert \end{aligned}$$

for all $a \in [0,\tilde{\beta }_{k,\delta }]$. Due to the fact that $\delta \mathbf{I} +\vert \mathbf{V}^\delta \vert$ is a Hermitian positive-definite matrix, the Cholesky decomposition allows us to decompose it into the product of a lower triangular matrix and its conjugate transpose, i.e.

$$\begin{aligned} \delta \mathbf{I} +\vert \mathbf{V}^\delta \vert = \mathbf{L} \mathbf{L}^{*}. \end{aligned}$$

We want to remark that this decomposition is unique. In addition, $\mathbf{L}$ is invertible, since

$$\begin{aligned} 0< \det (\delta \mathbf{I}+\mathbf{V}^\delta )=\det (\mathbf{L})\det (\mathbf{L}^{*})=\det (\mathbf{L})\overline{\det (\mathbf{L})}. \end{aligned}$$

For each $a>0$, it follows that

$$\begin{aligned}&-a\mathbf{S}_k^\tau + \delta \mathbf{I} +\vert \mathbf{V}^\delta \vert =-a \mathbf{S}_k^\tau + \mathbf{L} \mathbf{L}^{*} \\&\quad = \mathbf{L} (-a \mathbf{L}^{-1}\mathbf{S}_k^\tau (\mathbf{L}^{*})^{-1}+\mathbf{I})\mathbf{L}^{*}. \end{aligned}$$

Table 2 Lower and upper bounds $c^{\lambda },c^{\mu },C^{\lambda },C^{\mu }$ in [Pa]

Fig. 11

Transparency function for the plots in Fig. 12 mapping the values of $\nu$ to $\alpha (\nu )$

Based on this, we go over to the consideration of the eigenvalues and apply Weyl’s Inequality. Since the positive semi-definiteness of $-a \mathbf{S}_k^\tau +\delta \mathbf{I} +\vert \mathbf{V}^\delta \vert$ is equivalent to the positive semi-definiteness of $-a \mathbf{L}^{-1}{} \mathbf{S}_k^\tau (\mathbf{L}^{*})^{-1}+\mathbf{I}$, we obtain

$$\begin{aligned}&\theta _j(-a\mathbf{L}^{-1} \mathbf{S}_k^\tau (\mathbf{L}^*)^{-1}+\mathbf{I})= a\theta _j(-\mathbf{L}^{-1} \mathbf{S}_k^\tau (\mathbf{L}^{{*}})^{-1})+1,\quad \\&\quad j=1,\ldots ,M, \end{aligned}$$

where $\theta _1(A)\ge \cdots \ge \theta _{M}(A)$ denote the M-eigenvalues of some matrix A.

Further, let $\overline{\theta }_{M}(-\mathbf{L}^{-1} \mathbf{S}_k^\tau (\mathbf{L}^{*})^{-1})$ be the smallest eigenvalue of the matrix $-\mathbf{L}^{-1} \mathbf{S}^\tau _k (\mathbf{L}^{*})^{-1}$. Since $\mathbf{S}^\tau _k$ is positive definite, so is $\mathbf{L}^{-1} \mathbf{S}^\tau _k (\mathbf{L}^{*})^{-1}$. Thus, $\overline{\theta }_{M}(-\mathbf{L}^{-1} \mathbf{S}^\tau _k (\mathbf{L}^{*})^{-1})< 0$. Following the lines of [11], we obtain

$$\begin{aligned} \tilde{\beta }_{{k},{\delta }}=-\frac{1}{\overline{\theta }_{M}(-\mathbf{L}^{-1} \mathbf{S}_k^\tau (\mathbf{L}^*)^{-1})}\ge 0. \end{aligned}$$

(42)

4.2.3 Numerical realization

We close this section with a numerical example, where we again consider two inclusions (tumors) in a biological tissue as shown in Fig. 2 (for the values of the Lamé parameter see Table 1). In addition to the Lamé parameters, we use the estimated lower and upper bounds $c^{\lambda },c^{\mu },C^{\lambda },C^{\mu }$ given in Table 2.

Fig. 12

Shape reconstruction of two inclusions (red) of the reconstructed difference in the Lamé parameter $\mu$ (left hand side) and $\lambda$ (right hand side) without noise, $\delta =0$ and transparency function $\alpha$ as shown in Fig. 11. (Color figure online)

Fig. 13

Shape reconstruction of two inclusions (red) of the reconstructed difference in the Lamé parameter $\mu$ depicted as cuts without noise and $\delta =0$. (Color figure online)

Fig. 14

Shape reconstruction of two inclusions (red) of the reconstructed difference in the Lamé parameter $\mu$ (left hand side) and $\lambda$ (right hand side) with relative noise $\eta =10\%$, $\delta =8.3944\cdot 10^{-8}$ and transparency function $\alpha$ as shown in Fig. 11. (Color figure online)

Fig. 15

Shape reconstruction of two inclusions (red) of the reconstructed difference in the Lamé parameter $\mu$ depicted as cuts with relative noise $\eta =10\%$ and $\delta =8.3944\cdot 10^{-8}$. (Color figure online)

For the implementation, we again consider difference measurements and apply quadprog from Matlab in order to solve the minimization problem. In more detail, we perform the following steps:

(1):

Calculate

$$\begin{aligned} \langle (\Lambda (\lambda _0,\mu _0)-\Lambda ^\delta (\lambda ,\mu ))g_i,g_j\rangle _{i,j=1,\cdots ,M} \end{aligned}$$

with COMSOL to obtain $\mathbf{V}$ via (17).

(2):

Evaluate $\hat{\nabla }u^{g_i}_{(\lambda _0,\mu _0)}$ and $\nabla \cdot u^{g_i}_{(\lambda _0,\mu _0)}$ for $i=1,\cdots ,M$, in Gaussian nodes for each tetrahedron.

(3):

Calculate $\mathbf{S }^{\lambda }, \mathbf{S }^{\mu }$ (cf. Eqs. (14) and (15)) via Gaussian quadrature.

Note that $\mathbf{S }^{\lambda }$, $\mathbf{S }^{\mu }$ can also be calculated from the stiffness matrix of the FEM implementation without additional quadrature errors by the approach given in [10].

(4):

Calculate $\mathbf{S }^{\tau }=\mathbf{S }^{\mu }+\tau \mathbf{S }^{\lambda }$ with $\tau$ as in (27).

(5):

Calculate $\tilde{\beta }_{k,\delta }$, $k=1,\ldots ,p,$ as in (42).

(6):

Solve the minimization problem (34) with $\mathbf{R}_{\delta }(\nu )=\mathbf{S }^{\tau }\nu -\mathbf{V}^{\delta }$ with quadprog in Matlab to obtain

$$\begin{aligned} \tilde{\nu }_{\delta }=\sum _{k=1}^p a_{k,\delta }\chi _k. \end{aligned}$$

(7):

Set $\mu =\mu _{0}+\tilde{\nu }_{\delta }$, $\lambda =\lambda _0+\tau \tilde{\nu }_{\delta }$.

4.2.4 Exact data

We start with exact data, i.e. data without noise and due to the definition of $\delta$ given in (18), with $\delta =0$.

Remark 8

Performing the single implementation steps on a laptop with ${ 2\times 2.5}$ GHz and 8 GB RAM, we obtained the following computation times: Step (1), i.e., the determination of the matrix $\mathbf{V}$, was done in 9 min 1 s. The Fréchet derivative is computed in 53 s in steps (2)–(4). The solution of the minimization problem (steps (5)–(7)) is calculated in 6 min 27 s.

Figure 12 presents the results as 3D plots, while Fig. 13 shows the corresponding cuts for $\mu$. For the same reasons as discussed in Sect. 3, we change the transparency of the plots of the 3D reconstruction of Fig. 12 as indicated in Fig. 11. Thus, tetrahedrons with low values have a higher transparency, whereas tetrahedrons with large values are plotted opaque.

Figures 12 and 13 show that solving the minimization problem (37) indeed yields a detection and reconstruction with respect to both Lamé parameters $\mu$ and $\lambda$.

Remark 9

Compared with the results obtained with the one-step linearization method as depicted in Fig. 4 (right hand side), Fig. 12 shows an improvement because we are now able to also obtain information concerning $\lambda$ which is not possible with the heuristic approach considered in (16).

4.2.5 Noisy data

Finally, we take a look at noisy data with a relative noise level $\eta =10\%$, where the $\delta$ is determined as given in (18).

Figures 14 and 15 document that we can even reconstruct the inclusions for noisy data which is a huge advantage compared with the results of the one-step linearization (see Fig. 8- 9). This shows us, that the numerical simulations based on the monotonicity-based regularization are only marginally affected by noise as we have proven in theory, e.g., in Theorem 2.

5 Summary

In this paper we introduced a standard one-step linearization method applied to the Neumann-to-Dirichlet operator as a heuristical approach and a monotonicity-based regularization for solving the resulting minimization problem. In addition, we proved the existence of such a minimizer. Finally, we presented numerical examples.

Appendix

For the monotonicity-based regularization we focused on the case $\lambda \ge \lambda _0$, $\mu \ge \mu _0$ (see Sect. 5). For sake of completeness, we formulate the corresponding results for the case that $\lambda \le \lambda _0$, $\mu \le \mu _0$. Thus, we summarize the corresponding main results and define the set

$$\begin{aligned}&\mathcal {C}:= \bigg \lbrace \nu \in L^\infty (\Omega ):\nu =\sum _{k=1}^p a_k \chi _{k},\,a_k\in \mathbb {R},\,\\&\qquad 0\ge a_k \ge -\min (a_{\max },\beta _k)\bigg \rbrace \end{aligned}$$

where the quantities $a_{\max }$ and $\tau$ are defined as

$$\begin{aligned} a_{\max }&:=c^\mu \quad \text {and} \quad \tau :=\frac{c^\lambda }{c^\mu }, \end{aligned}$$

(43)

such that

$$\begin{aligned} -2\left( \mu -\mu _0\right) +2a&\ge 0,\end{aligned}$$

(44)

$$\begin{aligned} -\left( \lambda -\lambda _0\right) +\tau a&\ge 0 \end{aligned}$$

(45)

for all $0\ge a\ge - a_{\max }$.

Remark 10

The value $a_{\max }$ is obtained from the estimates in Lemma 1 which results in a different upper bound a compared with the case $\lambda \ge \lambda _0$, $\mu \ge \mu _0$.

Thus, the theorem for exact data is given by

Theorem 3

Consider the minimization problem

$$\begin{aligned} \min _{\nu \in \mathcal {C}}\Vert \mathbf{R}(\nu )\Vert _F. \end{aligned}$$

(46)

The following statements hold true:

• (i) Problem (46) admits a unique minimizer $\hat{\nu }$.

• (ii) $\mathrm {supp}(\hat{\nu })$ and $\mathcal {D}$ agree up to the pixel partition, i.e. for any pixel $\mathcal {B}_k$

  $$\begin{aligned} \mathcal {B}_k\subset \mathrm {supp}(\hat{\nu })\quad \text {if and only if}\quad \mathcal {B}_k\subset \mathcal {D}. \end{aligned}$$

  Moreover,

  $$\begin{aligned} \hat{\nu }=\sum _{\mathcal {B}_k\subseteq \mathcal {D}}-a_{\max }\chi _{k}. \end{aligned}$$

The corresponding results for noisy data is formulated in the following theorem, where $\mathbf{R}_\delta (\nu )$ represents the matrix $(\langle g_i,r_\delta (\nu ) g_j\rangle )_{i,j=1,\ldots ,M}$ and the admissible set for noisy data is defined by

$$\begin{aligned}&\mathcal {C}_\delta :=\bigg \lbrace \nu \in L^\infty (\Omega ): \nu =\sum _{k=1}^p a_k \chi _{k},\,a_k\in \mathbb {R},\\&\quad \,0\ge a_k\ge -\min (a_{\max },\beta _{k,\delta })\bigg \rbrace . \end{aligned}$$

Theorem 4

Consider the minimization problem

$$\begin{aligned} \min _{\nu \in \mathcal {C}_\delta }\Vert \mathbf{R}_\delta (\nu )\Vert _F. \end{aligned}$$

(47)

The following statements hold true:

• (i) Problem (47) admits a minimizer.

• (ii) Let $\hat{\nu }=\sum \limits _{\mathcal {B}_k\subseteq \mathcal {D}}-a_{\max }\chi _k$ be the minimizer of (46) and $\hat{\nu }_\delta =\sum \limits _{k=1}^{p} a_{k,\delta }\chi _k$ of problem (47), respectively. Then $\hat{\nu }_\delta$ converges pointwise and uniformly to $\hat{\nu }$ as $\delta$ goes to 0.