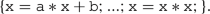Invariant relations for affine loops

Abstract

Invariant relations are used to analyze while loops; while their primary application is to derive the function of a loop, they can also be used to derive loop invariants, weakest preconditions, strongest postconditions, sufficient conditions of correctness, necessary conditions of correctness, and termination conditions of loops. In this paper we present two generic invariant relations that capture the semantics of loops whose loop body applies affine transformations on numeric variables.

1 Introduction

1.1 Position of the problem

This work is part of an effort to derive the function of C-like programs, including while loops. Given a while loop, an invariant relation thereof is a binary relation that includes pairs of states that are separated by an arbitrary number of iterations of the loop. Invariant relations are shown to be useful in analyzing while loop semantics: they can be used to derive the function of a loop [48, 49, 51], to generate loop invariants of a loop [31], to prove or disprove the correctness of a loop [45], to compute or approximate the weakest precondition and the strongest postcondition of a loop [19], to repair a faulty loop [18], and to compute or approximate the termination condition of a loop [10].

But invariant relations are useful in practice only to the extent that we can generate them automatically; to this effect, we adopt a pattern matching-based approach discussed in [10, 18, 19, 31, 45, 49, 51]. We define and store templates (which we call recognizers) that represent commonly occuring patterns in program functions (e.g. for a particular application domain), alongside the corresponding patterns that represent their invariant relations; these recognizers are selected to capture the requisite programming knowledge and domain knowledge that are needed to analyse programs in the targeted application domain. Invariant relations are generated by matching the actual function of the guarded loop body against formal recognizers; in case of a match, we generate an actual invariant relation for the loop by instantiating the formal invariant relation of the recognizer with the actual variables of the program. The success of this pattern matching approach is critically dependent on the availability of recognizers that are generally applicable and produce a precise invariant relation pattern. In this paper, we present two generic recognizers for loops that apply affine transformations on numeric variables; we argue that these two recognizers are sufficient to capture the semantics of any loop that performs affine transformations on numeric variables, regardless of their number. By extension, these two recognizers are also applicable to loops that perform a transformation of the form $X'=AX+B$, where X and B are vectors of size N and A is a matrix of size $N\times N$, provided A is diagonalisable.

1.2 Related work

Loops that perform affine transformations have been the focus of some research interest in the past [1, 21, 22, 28]. In [28] Jeannet et al. justify this level of interest by the fact that such loops occur very often in control and digital signal processing software, due to the presence of filters, integrators and iterative loops for solving equations or interpolating complex functions by means of splines. The analysis of affine loops has focused on deriving their loop invariants, and has generally been restricted to deriving loop invariants that have the form of affine equalities ($AX=B$) and affine inequalities ($AX\le B$) [1, 21, 22, 28, 32]. This has come to be known under the name Linear Relations Analysis [22] and has relied primarily on abstract interpretation [6] and an optimized version thereof, abstract acceleration [20]. In [1] Ancourt et al. propose to automate the analysis of affine loops by approximating loop behaviors with affine equalities and inequalities; but unlike the traditional approach that is based on state assertions [6], Ancourt et al. focus on state transformers, and attempt to capture approximations of the transitive closure of the function of the guarded loop body by means of affine formulae; as such, their quest is similar to the derivation of invariant relations, which we pursue in this paper.

In [12] Farzan and Kincaid present a semantic definition of C-like programs modeled by control flow automata where edges are labeled by program statements. A semantic function maps control flow edges to transformations of the state of the program, where the function of a path is the relational composition of the transformations associated with the edges that form the path. Since iteration creates an infinity of paths of unbounded length, Farzan and Kincaid proceed by formulating iterative transformations as recurrence equations, then solving the recurrence equation by eliminating the recurrence variable to derive relationships between the initial and final state variable values of iterative statements. Farzan and Kincaid make provisions for simple recurrence, where a variable is updated iteratively according to some recurrence formula, and stratified recurrence, where a variable that is defined by a recurrence formula is involved in the recurrence equation of another variable.

In [26], Humenberger et al. discuss the automatic generation of polynomial form loop invariants for a class of P-solvable loops that includes sums and products of hypergeometric and C-finite sequences; the technique is implemented in Mathematica (©Wolfram Research) on top of the loop invariant generator tool Aligator [24, 39]. The proposed method applies to loops whose loop body only includes a sequence of assignments of the form

$$\begin{aligned} \texttt {vi}\,\,\texttt {=}\,\,\texttt {fi}\,\, \texttt {(v1,}\,\,\texttt {v2,}\,\,\texttt {...}\,\,\texttt {vn);} \end{aligned}$$

where $v_1, v_2,..., v_n$ are scalar variables and $f_i$ are rational functions. This approach is applicable under some restrictive conditions on the control structure of the loop body. These restrictions are lifted in [27] where Humenberger et al. discuss how to derive loop invariants for multi-path loops with polynomial assignments; multi-path loops arise when we have branching logic in the loop body, rather than a single sequence of assignments. Humenberger et al. proceed in three steps: (i) turn the multi-path loop into a sequence of single-path loops; (ii) generate the polynomial invariant ideal of each single-path loop; then (iii) combine these ideals iteratively until the polynomial invariant ideal of the multi-path loop is derived. Humenberger et al. show that this process converges in time that is linear in the number of program variables and the number of inner loops. In our relational approach, the question of multi-path loops is posed in relational terms: while invariant relations are closed for intersection, they are not closed for union. Indeed, the union of two transitive relations is not transitive; to generate an invariant relation for a loop body that has the form of a union, say $B=B_1\cup B_2$, we can generate a reflexive transitive superset of $B_1$, say $R_1$ and a reflexive transitive superset of $B_2$, say $R_2$. In order to find an invariant relation for B, we must find a (the smallest, if possible) reflexive transitive superset of $R_1$ and $R_2$; this is discussed by Mraihi et al. in [30, 31, 50, 51].

In [25] Hrushovski et al. present an algorithm for deriving the strongest polynomial invariant for an affine program, i.e. an iterative program whose loop body is made exclusively of affine assignments to numeric variables. While other algorithms generate strongest affine invariants, or strongest polynomial invariants of a maximal degree (affine invariants being a special case of the latter condition for a degree 1), Hrushovski et al. present an algorithm that computes all the polynomial invariants of an affine loop of any degree; the strongest polynomial invariant is their conjunction. The proposed approach accommodates nested loops but does not accommodate deterministic conditional statements within the loop body; they replace such statements by non-deterministic choice, modeling a non-deterministic program.

In [35] Kincaid et al. contrast two orthogonal approaches to the analysis of while loops: The approach exemplified by the work of Rodriguez-Carbonell and Kapur [3] and Kovacs [39, 40], which aims to compute the strongest invariant relation of a loop, using special-purpose algorithms; the approach exemplified by the work of Farzan and Kincaid [12] and Kincaid et al. [33], which uses Compositional Recurrence Analysis (CRA) to over-approximate the semantic attributes of a broader class of loops. Whereas the first approach delivers very accurate results for a small class of loops, the second approach delivers approximate results for a large class of loops, including loops that have non-deterministic assignments and nested loops; CRA can also be applied to recursive procedures. Also, CRA is applied, not to the syntactic form of loops, but rather to their logical representation. Kincaid et al. present extensions to the numerical-reasoning techniques available under CRA, and show how these extensions enable them to generate non-linear numeric invariants.

In [34] Kincaid et al. go beyond the problem of generating loop invariants for numeric loops, to seek to derive (approximations of) the function of such loops, to which they refer as closed forms of loops. They present an algorithm for computing the closed form of a loop expressed using polynomials and exponentials over rational numbers. They argue that the logic for expressing closed forms is decidable, yielding decision procedures for verifying termination and safety of a class of numerical loops over rational numbers. They also show how the procedure for computing closed forms of loops can be used to over-approximate the behavior of arbitrary numeric programs, including programs with unrestricted control flow, non-deterministic assignment, and recursive calls.

In [54] Sankaranarayanan et al. use Farkas’ Lemma to generate a loop invariant for an affine loop whose body is made up of a deterministic or non-deterministic choice between several affine transformations of numeric program variables; Farkas’ Lemma is used to infer a loop invariant for the whole loop from invariants derived from each term in the form of an affine inequality. In [5] Colon et al. investigate a method to generate linear invariant relations by solving non-linear constraints, whose purpose is to ensure that the target is inductive. In [44], Liu et al. build on the results of Sankaranarayanan et al. [54] and Colon et al [5] to propose a scalable approach for the generation of tight(er) linear-invariants for affine programs, i.e. programs with affine conditions and assignments. Whereas Sankaranarayanan et al., and Colon et al. use Farkas’ Lemma to generate linear invariants of affine loops in the form of equalities and inequalities of linear expressions of program variables, Liu et al. generalize their results by addressing the scalability of the original algorithms. The first measure they deploy to achieve scalability is to separately generate several invariants at the same location, thereby enabling parallel computations and a better control of combinatorial explosion. The second measure they deploy is a more effective algorithm for identifying subsumption relations between clauses of invariants, hence faster convergence; they prove that this gain in efficiency does not cause a loss of precision in the generated invariants. Experimental evidence on representative benchmarks show orders of magnitude gains in run-time efficiency.

Farkas’s Lemma is also used by Ji et al. [29] to generate linear invariants for multi-path affine unnested loops. The method proposed by Ji et al. completely addresses the constraints derived from Farkas’ Lemma using matrix algebra. When the guard of the loop is an affine inequality or equality, the invariants can be generated by means of matrix inversion, and when the guard is TRUE (in non-terminating control loops, for example), the invariants can be generated by means of eigenvalue calculations.

Given how complex it is to generate loop invariants, some researchers have focused on obviating the need for loop invariants. In [36] Kondratyev and Nepomniaschy discuss a method for proving the correctness of iterative programs without using loop invariants. To this effect, they consider iterative programs written in a subset of C (C-light), which they characterize as definite iteration of sequences of data, where each iteration processes one element of the data sequence. To represent the semantics of definite iteration of the form

$$\begin{aligned} \texttt {for}\,\,\texttt {x}\,\,\texttt {in}\,\,\texttt {S}\,\,\texttt {do} \,\,\texttt {v=body}\,\texttt {(v,x)}\,\,\texttt {end}, \end{aligned}$$

where S is a sequence of data, x is of type element of S, v is a vector of variables, and body is assumed to change v but leave x intact. Kondratyev and Nepomniaschy define the replacement operator rep inductively as follows:

• $rep(0,S,v,body)=v0$, the initial state of state variables.

• $rep(i,S,v,body)=body(rep(i-1,S,v,body),si)$, for $i\ge 1$.

To the extent that this recurrence can be resolved or a closed form of rep() can be derived in some way, then one can reason about the semantics of the loop without recourse to its loop invariants.

Another effort to reason about iterative programs without resorting to loop invariants is attempted by Chakraborty et al. in [4]; not only does the proposed method analyze the semantics of iterative programs without using loop invariants, but it does so for an arbitrary number of iterations, including possibly nested iterations. It achieves this goal by using an inductive argument, not on the control structure of the program, as mandated by approaches that are based on loop invariants, but rather by induction on the size of the data the program operatoes on. The method of Chakratorty et al., known as full-program induction, applies to programs that manipulate arrays of parametric size, and can be used to prove a class of quantified as well as quantifier-free program specifications, in the form of pre/post conditions. If we let N be the size of the arrays manipulated by the program, then the proof of correctness proceeds by induction on N: the basis of induction is generated for $N=0$, and the induction step aims to prove that if the program satisfies its specification for $N-1$, then it does for N. This requires that we characterize the processing that is required to derive a solution for N from a solution for $(N-1)$. The derivation of the code that defines this transformation (called difference program) and the specification that this code must satisfy for the induction step to hold (called the difference precondition) are not always possible, nor easy even when they are possible. The characterization of the difference program is actually reminiscent of the operator of relational division introduced by Desharnais et al. [8] (which means that quotient program is perhaps a better name than difference program, since this operator is the inverse of relational product).

In [52] Myreen and Gordon report on a program verification tool that verifies the correctness of imperative programs by mapping them into a functional representation in the logic of a theorem prover; total correctness and partial correctness are then mere theorems to prove in the target logic. While statements are represented by recursive function definitions, according to the semantic identity:

$$\begin{aligned} \texttt {while}\,\,\texttt {(t)}\,\, \texttt {\{b;\}} = \texttt {if}\,\,\texttt {(t)}\,\, \texttt {\{b;\}} \,\,\texttt {while}\,\, \texttt {(t)}\,\, \texttt {\{b;\}} \end{aligned}$$

Among the benefits of the approach, the authors cite the following: proofs of correctness are readily applicable, once we formulate the pre/post specification of the program; the verification problem is reduced to its essence, the computation; it enables proof reuse, in the form of lemmas (proofs of subprograms can be used in proofs of encompassing programs); it is easier to implement than a verification condition generator. The tool is implemented in the HOL4 theorem prover and compared against alternative approaches on a number of illustrative examples.

In [43] Lefaucheux et al. consider the reachability problem for multi-path affine loops over the integers. They define the problem in the following terms: We consider a integer linear dynamical system that consists of a an initial vector $x_0\in \mathbb {Z}^d$, for some natural number d, and a set of update functions $f_1$, $f_2$,... $f_n$ on $\mathbb {Z}^d$, which represent the functions applied by paths of a multi-path loop. We consider a set Y and we ponder the question of whether we can ensure that the iterative application of the multi-path loop does not yield an element of Y; in practice, Y may represent a set of unsafe states and the reachability question is to check that no state generated by the loop is unsafe. To this effect, Lefaucheux et al. define an inductive invariant I as a set that satisfies the condition $f_i(I)\subseteq I$ for all i. Then the reachability query defined by the pair $(x_0,Y)$ can be solved by searching an inductive invariant I such that $x_0\in I$ and $Y\cap I=\emptyset$. Lefaucheux et al. consider a set of affine forms (redundant, counter-like, growing, inverting, etc) and present corresponding invariant forms. Then they discuss a tool that generates such invariants and addresses the question of unreachability, and illustrate the operation of the tool on a wide range of combinations of function types.

In [13] Frohn et al. discuss means to prove or disprove termination of triangular weakly non-linear loops (twn loops), which are loops of the form:

$$\begin{aligned} while (\phi ) \{x\leftarrow a(x)\}, \end{aligned}$$

where $x=(x_1, x_2,..., x_d)$ is the vector of program variables in some ring $\mathbb {S}$ ($\mathbb {Z}$, $\mathbb {Q}$, or $\mathbb {R}$), and a(x) has the following form:

$$\begin{aligned} a(x)=\left[ \begin{array}{c} c_1x_1+p_1\\ c_2x_2+p_2\\ ...\\ c_dx_d+p_d \end{array}\right] , \end{aligned}$$

where each $p_i$ is a possibly non-linear polynomial in variables $x_{i+1}, x_{i+2},... x_d$ (whence the qualifier triangular) and $c_i$ is a constant in $\mathbb {S}$. Frohn et al. are interested in proving or disproving termination, and they define non termination by means of the following formula, where $a^n$ represents the application of a n times:

$$\begin{aligned} \exists c\in \mathbb {S}^d: \forall n\in \mathbb {N}: \phi (a^n(c)). \end{aligned}$$

Such a c, if it exists, is called a witness to non-termination. To adjudge termination, Frohn et al. derive a closed form expression of $a^n(c)$, then the polynomial $\phi (a^n(c))$, which enables them to reason about the asymptotic behavior of this polynomial with respect to n.

1.3 Scope of the approach

Our approach differs from the works cited above in many meaningful ways; in this section, we characterize our approach (and distinguish it from others) in terms of its goals and premises; in Sect. 7.3, we distinguish it from related work in terms of its results (which we can only do after we present these results).

• Invariant relations versus invariant assertions Whereas much of the research on analyzing while loops has focused on generating and using their loop invariants (re: [7, 11, 12, 14, 24,25,26, 35, 37, 38, 41, 46, 47, 51, 57], to cite a few), our approach is geared towards generating and using their invariant relations. In [51], Mraihi et al. prove that all invariant assertions (aka loop invariants) stem from invariant relations, hence the search of invariant relations subsumes the search of invariant assertions, in the following sense: if all we do is search for invariant relations then convert them into invariant assertions using the formula of [51], we do not miss any invariant assertion.

• Derivation of invariant relations Our goal is to derive the invariant relations of while loops, where the invariant relation of a while loop is a binary relation that holds between two program states s and $s'$ that are separated by an arbitrary number of iterations.

• Context-independence Whereas loop invariants depend on the loop and its context (as defined by the precondition and the postcondition), invariant relations depend exclusively on the loop. Hence, whereas the generation of loop invariants juggles consideration of the precondition, the postcondition, and the loop, the generation of invariant relations focuses exclusively on the loop.

• Precise semantics Whereas much of linear relation analysis is geared towards the derivation of over-approximations of program behavior by means of convex polyhedra, our goal is to capture the semantics of loops programs in all its details. Also, many recent efforts focus explicitly on deriving approximations of the loop function, and overlook loop conditions and the branching logic of conditional statements; as a consequence, they do not analyze the program per se, but rather a non-deterministic approximation thereof.

• Free form invariant relations Whereas much of linear relation analysis is focused on deriving loop invariants of a prespecified form (e.g. affine equalities and inequalities, polynomial forms, polynomial forms of a prespecified degree, etc), our invariant relations are not restricted to any specific form; in fact the two invariant relation templates that we introduce in this paper are neither affine nor polynomial. The transformations that are applied by the guarded loop body are affine (more precisely: have affine clauses), but the corresponding invariant relations are not necessarily.

• Loops may have non-affine parts Our approach is not restricted to loops that only perform affine transformations; rather it is applicable to any loop that has an affine transformation, possibly alongside other non-affine transformations. We apply the formulas presented in this paper to the affine transformations of the loop, and apply other formulas to the other transformations.

• Loops may have non-numeric data types. Our approach is not restricted to numeric data types. We can handle any data type, provided:

  • We capture the semantics of the operations applied to the data type by means of relevant recognizers.

  • The equations that are generated by the recognizers can subsequently be solved or reasoned about to analyze the loop.

  We can also handle programs that mix numeric data types with non-numeric data type; see recognizer 2R3 in Table 1 as an example.

• Affine transformations may be hidden Our pattern matching algorithm is not applied to the source code of the program, but rather to its mathematical representation as a function. Hence we may have a clause of the form $(x'=a\times x+b)$ in the function of the loop body, even when no statement of the loop body has the form {x=a*x+b}:

  • {x=a*x; x=x+b;}. Affine clause: $x'=ax+b$.

  • {y=a*x+b; x=c*y+d;}. Affine clause: $x'=acx+cb+d$.

  • {y=x*x; x=(x+a)*(x+a)-y;}. Affine clause: $x'=2ax+a^2$.

  • {y=b; for (int k=a;k>0;k=k-1) {y=y+x}; x=y}. Affine clause: $x'=ax+b$, assuming a is a positive integer.

  Incidentally, we can also have an affine statement in the loop body, yet not have an affine clause in the function of the loop body:

  

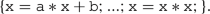
• Extension to matrices Whenever we have a loop body that performs an affine transformation of the form $(X'=AX+B)$, where X is a vector of size N, A is a matrix of size $N\times N$ and B is a vector of size N, and where A is a diagonalisable matrix, we can perform a change of variable $Y=V\times X$ in such a way that the transformations of $Y_i$ take the form $(Y_i'=a_i'\times Y_i+b_i')$; we discuss this case in Sect. 4.3.

• Invariant Generation Algorithm. All the related work cited above, as well as virtually all the work we know of on loop invariant generation, generates loop invariants on the fly, at run-time, by seeking to restrict the class of loops under consideration or the form of loop invariants under consideration. By contrast, we generate invariant relations by pattern matching against pre-stored code patterns for which we know invariant relation patterns. So while we may use similar techniques to other approaches (e.g. recurrence analysis), we use these techniques to generate the pattern matching templates off-line, not to generate invariant relations at run-time; at run-time, all we do is matching clauses of the program against prestored code patterns.

• Broader context Our work on affine loops is part of a broader effort to compute the function of C-like programs, including iterative programs. Our interest in affine loops stems from the fact that the semantics of affine loops can be captured by only two invariant relation templates, from which we generate two generic recognizers.

We assume the reader is familiar with simple relational mathematics [2, 56]; in Sect. 2 we briefly introduce some relational definitions and notations that we use in this paper. In Sect. 3 we discuss the concept of invariant relations, and show what they are useful for and how we can generate them. Section 4 presents the core ideas of this paper, in the form of explicit formulas for invariant relations that stem from affine transformations on scalar and vector variables of a loop. In Sect. 5 we discuss in what way and to what extent the invariant relations we generate in Sect. 4 are sufficient to capture the semantics of affine loops. These results are illustrated in Sect. 6 and assessed / critiqued in Sect. 7.

2 Definitions and notations

2.1 Relational definitions and notations

A relation on set S is a subset of the Cartesian product $S\times S$. Among the constant relations on set S, we cite the identity relation I and the universal relation, L. Among the operations on relations we cite, in addition to the set theoretic operations of union ($\cup$), intersection ($\cap$) and complement $\overline{R}$: The converse of relation R is denoted by $\widehat{R}$ and defined by: $\widehat{R} =\{(s,s')|(s',s)\in R\}.$ The product of two relations R and $R'$, is denoted by $R\circ R'$, or simply $RR'$, and defined by: $RR'=\{(s,s')|\exists s'':(s,s'')\in R\wedge (s'',s')\in R'\}.$ The transitive closure of relation R, denoted by $R^+$, and defined by: $R^+=\{(s,s')| \exists i\ge 1: (s,s')\in R^i\},$ where $R^1=R$, and $R^{i+1}=R\circ R^i$. The reflexive transitive closure of relation R, denoted by $R^*$, is defined by: $R^*=I\cup R^+$. The domain of relation R is denoted by ${ dom}(R)$ and defined by: ${ dom}(R)=\{s| \exists s': (s,s')\in R\}.$ The range (or codomain) of relation R is the domain of $\widehat{R}$.

A relation R is said to be reflexive if and only if $I\subseteq R$; a relation R is said to be transitive if and only if $R^2\subseteq R$; and a relation R is said to be deterministic if and only if $\widehat{R}R\subseteq I$; deterministic relations are referred to as functions. A vector T is a relation that satisfies the condition $TL=T$; given a predicate t on S, we denote by T the vector defined as $T=\{(s,s')| t(s)\}$; vectors are relational representations of subsets of S. Given a relation R and a vector T, we let the pre-restriction (resp. post-restriction) of R to T be defined as $T\cap R$ (resp. $\widehat{T}\cap R$).

We conclude this section with a simple Proposition from relational mathematics [2], which we present without proof, and will use throughout the paper.

Proposition 1

Two functions F and $F'$ are equal if and only if $F\subseteq F'$ and ${ dom}(F')\subseteq { dom}(F)$.

Generally, to prove that two relations are equal, we must prove inclusion in both directions; if they are deterministic, it suffices to prove inclusion in one direction, and inclusion of their domains in the opposite direction.

2.2 Program semantics

If we declare space S by means of variable declarations

$$\begin{aligned} \texttt {xType}\,\,\texttt {x;}\,\, \texttt {yType}\,\,\texttt {y;} \end{aligned}$$

then we mean that S is the Cartesian product of the sets of values taken by types xType and yType. An element of space S is referred to as a state, is usually denoted by lower case s and represents the tuple $s=\langle x, y\rangle$; we will usually let s stand for all the variables of the space, and we apply the same decoration to s and to the corresponding variables (e.g. $s'=\langle x',y'\rangle$, $s''=\langle x'',y''\rangle$, etc). Given a program p on state space S, the function of program p is denoted by P and defined as the set of pairs of states $(s,s')$ such that if p starts execution in state s it terminates normally (i.e. after a finite number of steps, without attempting any illegal operation) in state $s'$. As a result, the domain of P is the set of states s such that if p is executed on state s it terminates normally. By abuse of notation, we may sometimes denote a program p and its function P by the same symbol, P.

3 Invariant relations

In this section, we briefly present a definition of invariant relations, then we discuss in turn: what we use invariant relations for; then how we generate invariant relations.

Definition 1

Given a while loop w of the form {while (t) {b}}, an invariant relation of w is a reflexive transitive superset of $(T\cap B)$, where T is the vector that represents condition t and B is the function of {b}.

The following properties stem readily from the definition of invariant relations.

Proposition 2

Given a while loop w: {while (t) {b;}} on space S,

• The intersection of invariant relations of w is an invariant relation of w.

• $(T\cap B)^*$ is an invariant relation of w.

• $(T\cap B)^*$ is the smallest invariant relation of w: it is a subset of any invariant relation of w.

Proof

The first clause is a consequence of the property that the intersection of reflexive transitive relations is reflexive and transitive. The second and third clauses are properties of the reflexive transitive closure of a relation. $\square$

For illustration, we consider space S defined by natural variables n, f, k, and we let w be the following program:

For this program we find (using s as a stand-in for $\langle n,f,k\rangle$ and $s'$ as a stand-in for $\langle n',f',k'\rangle$):

$$\begin{aligned} T= & {} \{(s,s')| k\ne n+1\},\\ B= & {} \{(s,s')| n'=n\wedge f'=f\times k\wedge k'=k+1\}. \end{aligned}$$

We leave it to the reader to check that the following are invariant relations for w:

$$\begin{aligned} R_0= & {} \{(s,s')|n'=n\},\\ R_1= & {} \{(s,s')|k\le k'\},\\ R_2= & {} \left\{ (s,s')| \frac{f}{(k-1)!}=\frac{f'}{(k'-1)!}\right\} . \end{aligned}$$

Since these are invariant relations of w, so is their intersection $R= R_0\cap R_1\cap R_2$.

3.1 Using invariant relations

Invariant relations can be used for a wide range of applications in the analysis of loops; in this section we briefly discuss two applications, namely the derivation of the function of the loop, and the derivation of invariant assertions (aka loop invariants) of the loop. As background, the following Proposition gives a formula for the function of a loop.

Proposition 3

The function of the while loop w: {while (t) {b}} on space S is: $W=(T\cap B)^*\cap \widehat{\overline{T}}$, where T is the vector that represents condition t and B is the function of {b}.

A proof of this Proposition is given in [51]. The following Proposition is a simple corollary of Proposition 3; it stems readily from the property that any invariant relation R of w is a superset of $(T\cap B)^*$.

Proposition 4

Given a while loop of the form w: {while (t) {b}} on space S, and an invariant relation R of w the following inequality holds: $W\subseteq R\cap \widehat{\overline{T}}$.

As an illustration, we consider the factorial program above and we compute the proposed upper bound $W'$ of W:

$$\begin{aligned} W'= & {} R\cap \widehat{\overline{T}}= \left\{ (s,s')| k\le n+1\wedge n'=n\wedge k'=n+1 \wedge f'=n!\times \frac{f}{(k-1)!}\right\} . \end{aligned}$$

According to Proposition 4, W is a subset of $W'$ (given above). On the other hand, the loop converges for all s that satisfy the condition $(k\le n+1)$, hence ${ dom}(W')\subseteq { dom}(W)$. Since $W'$ is deterministic, we can apply Proposition 1, which yields $W=W'$. This is indeed the function of the (uninitialized) loop.

Invariant relations can also be used to derive loop invariants, as per the following Proposition.

Proposition 5

Due to [51]. If vector A represents a precondition of the loop w: {while (t) {b}} and relation R is an invariant relation thereof, then $\widehat{R}A$ is a loop invariant of the loop w

We consider a typical precondition of this factorial loop, namely: $A=\{(s,s')| n=n_0\wedge f=1\wedge k=1\}$, and we compute the resulting loop invariant.

$$\begin{aligned}{} & {} \quad \widehat{R}A \\{} & {} =\qquad \quad \{\text {inverting}\ R, \text {substituting}\ A\}\\{} & {} \quad \left\{ (s,s')| n'=n\wedge k\ge k'\wedge \frac{f}{(k-1)!} =\frac{f'}{(k'-1)!}\right\} \circ \{(s,s')|n=n_0\wedge f=1\wedge k=1\}\\{} & {} =\qquad \quad \{\text {relational product, substitution}\}\\{} & {} \quad \{(s,s')| n=n_0\wedge k\ge 1\wedge f=(k-1)!\}. \end{aligned}$$

This is clearly a loop invariant for this loop for the precondition A.

Note that by construction, $\widehat{R}A$ is a vector since A is a vector; hence $\widehat{R}A$ is a subset of the state space; it is in fact a relational representation of a set (the invariant set).

3.2 The elementary invariant relation

The following Proposition gives a constructive / explicit formula for a trivial invariant relation, which we call the elementary invariant relation.

Proposition 6

Due to [31]. Given a while loop of the form w: {while (t) {b}} on space S, the following relation is an invariant relation for w:

$$\begin{aligned} E=I\cup T(T\cap B) \end{aligned}$$

where T is the vector that represents the loop condition and B is the function of the loop body.

This relation includes pairs of states $(s,s')$ such that $s=s'$, reflecting the case when the loop does not iterate at all, and pairs of states $(s,s')$ when the loop iterates at least once, in which case s satisfies t and $s'$ is in the range of $(T\cap B)$.

As an illustration, we consider the factorial loop introduced above, in which we change the condition from t:(k!=n+1) to $\texttt {t':(k<n+1)}$:

This change does not affect the loop’s invariant relations. If we apply the formula of Proposition 4 to the invariant relation $R=R_0\cap R_1\cap R_2$, where

$$\begin{aligned} R_0= & {} \{(s,s')|n'=n\},\\ R_1= & {} \{(s,s')|k\le k'\},\\ R_2= & {} \left\{ (s,s')| \frac{f}{(k-1)!}=\frac{f'}{(k'-1)!}\right\} , \end{aligned}$$

we find the following upper bound of V:

$$\begin{aligned}{} & {} R\cap \widehat{\overline{T'}}\\{} & {} =\qquad \quad \{\text {Substitutions}\}\\{} & {} \left\{ (s,s')| k\le k'\wedge n'=n\wedge \frac{f}{(k-1)!}=\frac{f'}{(k'-1)!}\wedge k'\ge n+1\right\} . \end{aligned}$$

This is not a deterministic relation: unlike in the previous example (where we had $k'=n+1$) we do not have sufficient information to derive the final value of $k'$. The elementary invariant relation will help us derive the missing information:

$$\begin{aligned} E= & {} I\cup T'(T'\cap B)\\= & {} \qquad \qquad \{\text {Substitutions}\}\\{} & {} I\cup \{(s,s')| k<n+1\wedge \exists s'': k''<n''+1\wedge n'=n''\wedge k'=k''+1\wedge f'=f''\times k''\}\\= & {} \qquad \qquad \{\text {Simplification}\}\\{} & {} I\cup \{(s,s')| k<n+1\wedge k'<n'+2\wedge \exists f'': f'=f''\times (k'-1)\}. \end{aligned}$$

Applying Proposition 4 with the new invariant relation $R'=R\cap E$ yields the following upper bound $V'$ for V, where we abbreviate $(\exists f'': f'=f''\times (k-1))$ by ${ mult}(f',k'-1)$:

$$\begin{aligned} V'&=R_0\cap R_1\cap R_2\cap E\cap \widehat{\overline{T'}}\\&= \qquad \qquad \{\text {Factoring}\ E\}\\&\quad I\cap R_0\cap R_1\cap R_2\cap \widehat{\overline{T'}}\\&\quad \cup R_0\cap R_1\cap R_2\cap \{(s,s')|k<n+1\wedge k'<n+2\wedge { mult}(f',k'-1)\} \cap \widehat{\overline{T'}}\\&=\qquad \qquad \{\text {Substitutions, Simplifications}\}\\&\quad I\cap \overline{T'}\\&\quad \cup \{(s,s')|k<n+1\wedge n'=n\wedge k'\ge n+1 \\&\qquad \qquad \qquad \quad \wedge \frac{f}{(k-1)!} =\frac{f'}{(k'-1)!} \wedge k'<n+2\wedge { mult}(f',k'-1)\}\\&=\qquad \qquad \{\text {Simplifications, making} \ { mult}(f',k'-1)\ \text {redundant}\}\\&\quad \{(s,s')| k\ge n+1\wedge n'=n\wedge k'=k\wedge f'=f\} \\&\quad \cup \left\{ (s,s')|k<n+1\wedge n'=n\wedge k'=n+1\wedge f'=n!\times \frac{f}{(k-1)!}\right\} . \end{aligned}$$

We see that $V'$ is deterministic; on the other hand, the loop converges for all initial states, hence ${ dom}(V)=S$, from which we infer vacuously: ${ dom}(V')\subseteq { dom}(V)$. By Proposition 1, we infer $V'=V$; the elementary invariant relation was instrumental in enabling us to compute the function of the loop.

3.3 Generation of invariant relations

The elementary invariant relation is the only invariant relation we get for free, so to speak: we derive it constructively from the features of the loop, T and B; not surprisingly, it gives very little (yet sometimes crucial) information about the function of the loop. All the other invariant relations can only be derived by a meticulous analysis of T and B. The following Proposition is the basis of our approach to the generation of invariant relations.

Proposition 7

Given a while loop of the form w:{while (t) {b}} on space S, and a superset $B'$ of $(T\cap B)$, then $B'^*$ is an invariant relation for w.

Proof

If $B'$ is a superset of $(T\cap B)$, then so is $B'^*$; on the other hand, $B'^*$ is by construction reflexive and transitive. $\square$

To generate invariant relations, it suffices to isolate supersets of the function of the guarded loop body, and match them against recognizer patterns. In particular, if we decompose $(T\cap B)$ as the intersection of several terms, say:

$$\begin{aligned} (T\cap B)=B_1\cap B_2\cap B_3... \cap B_n, \end{aligned}$$

then we can compute the reflexive transitive closure (say $R_i$) of each $B_i$ then we take their intersection to find an invariant relation for the loop as: $R=\bigcap _{i=1}^n R_i.$

3.4 A database of recognizers

In order to automate the process of invariant relation generation, we create a database of recognizers, where each recognizer is made up of four components:

• Formal Space Declaration, $\sigma$. This includes C-like variable declarations and constant declarations (as needed). These are intended to be matched against actual variable declarations of the loop.

• Condition of Application, $\alpha$. Some recognizers can be applied only under some conditions, which we formulate in this column.

• Formal Clause, $\gamma$. This includes clauses that are formulated in terms of the variables declared above, and are intended to be matched against the function of the guarded loop body.

• Invariant Relation Template, $\rho$. This represents a superset of the reflexive transitive closure of the formal clause $\gamma$ (above).

The following pattern-matching algorithm is deployed to generate invariant relations of a loop, using the database of recognizers:

• For each recognizer in the database,

  • For each type-compatible mapping m from the formal variable declarations of the recognizer to the actual variable declarations of the program,

    • We check whether condition $m(\alpha )$ holds (i.e. the recognizer is applicable) and whether F logically implies $m(\gamma )$ (i.e. the function of the guarded loop body matches the formal clause of the recognizer, in which formal variable names are replaced by actual variable names).

    • In case of success, we generate $m(\rho )$; in other words, we instantiate the invariant relation template (formulated in formal variable names) with actual variable names. This gives us an invariant relation of the loop.

Table 1 shows some sample recognizers, for purposes of illustration, where $\otimes$ represents list concatenation and also (by abuse of notation) the operation of appending an element to a list; and Fib() represents the Fibonacci function. We distinguish between 1-recognizers, 2-recognizers and 3-recognizers, depending on the number of conjuncts in their Formal Clause component ($\gamma$); in practice we find that we seldom need to match more than three conjuncts at a time.

As an illustration, we consider the following loop on integer variables i and x, due to Kincaid et al. [34], where we assume, for simplicity, that $i\ge 0$:

The loop condition and the function of the loop are represented by the following relations:

$$\begin{aligned} T= & {} \{(s,s')| i\ne 10\wedge x<100\},\\ B= & {} \{(s,s')| i'=i+1\wedge x'=x+i+1\}. \end{aligned}$$

The elementary invariant relation of this while loop is derived from T and B as follows:

$$\begin{aligned}{} & {} E \\ ={} & {} \qquad \qquad \{\text {Definition}\}\\{} & {} \qquad I\cup T(T\cap B) \\ ={} & {} \qquad \qquad \{\text {Substitution}\}\\{} & {} \qquad I\cup \{(s,s')| i\ne 10\wedge x<100\qquad \qquad \qquad \qquad \qquad \qquad \\{} & {} \qquad \qquad \qquad \!\!\qquad \wedge (\exists s'': i''\ne 10\wedge x''<100\wedge i'=i''+1\wedge x'=x''+i''+1)\}\\ ={} & {} \qquad \qquad \{\text {Simplification}\}\\{} & {} \qquad I\cup \{(s,s')| i\ne 10\wedge x<100\wedge i'\ne 11\wedge x'-i'<100 \\{} & {} \qquad \qquad \quad \quad \!\!\qquad \wedge (\exists s'': i'=i''+1\wedge x'=x''+i''+1)\} \\ ={} & {} \qquad \qquad \{\text {Removing vacuous clause}\}\\{} & {} \qquad I\cup \{(s,s')| i\ne 10\wedge x<100\wedge i'\ne 11\wedge x'-i'<100\}. \end{aligned}$$

Application of recognizer 1R2 (with $a\equiv 1$) and recognizer 2R4 (with $f(i)\equiv i+1$) to this loop yields the following invariant relation:

$$\begin{aligned} R=\left\{ (s,s')| i\le i' \wedge x -\Sigma _{k=0}^{i-1}k+1=x'-\Sigma _{k=0}^{i'-1}k+1\right\} . \end{aligned}$$

We simplify this relation into:

$$\begin{aligned} R=\left\{ (s,s')| i\le i'\wedge x-\frac{i(i+1)}{2} =x'-\frac{i'(i'+1)}{2}\right\} . \end{aligned}$$

According to Proposition 3, the following relation $W'$ is a superset of (an approximation of) the function W of the loop: -

$$\begin{aligned}{} & {} \quad W' \\{} & {} =\qquad \quad \{\text {Proposition}~3\}\\{} & {} \quad E\cap R\cap \widehat{\overline{T}} \\{} & {} =\qquad \quad \{\text {Distributing}\ R\cap \widehat{\overline{T}} \ \text {over}\ E\}\\{} & {} \quad I\cap R\cap \widehat{\overline{T}} \\{} & {} \quad \cup \left\{ (s,s')| i\ne 10\wedge x<100\wedge i\le i'\wedge x-\frac{i(i+1)}{2}=x'-\frac{i'(i'+1)}{2} \wedge i'\ne 11\right. \\{} & {} \qquad \qquad \qquad \quad \left. \wedge x'-i'<100\wedge (i'=10\vee x'\ge 100)\right\} \\{} & {} =\qquad \quad \{\text {Since}\ R\ \text {is reflexive}, I\cap R=I; \text {also}, I\cap \widehat{\overline{T}} =I\cap \overline{T}\}\\{} & {} \quad \{(s,s')| (i=10\vee x\ge 100)\wedge i'=i\wedge x'=x\}\\{} & {} \quad \cup \left\{ (s,s')| i\ne 10\wedge x<100\wedge i\le i'\wedge x-\frac{i(i+1)}{2}=x'-\frac{i'(i'+1)}{2} \wedge i'\ne 11\right. \\{} & {} \qquad \quad \qquad \quad \quad \left. \wedge x'-i'<100\wedge (i'=10\vee x'\ge 100)\right\} \\{} & {} =\qquad \quad \{\text {Distributing the clause}\ (i'=10\vee x'\ge 100) \text {over the second term}\}\\{} & {} \quad \{(s,s')| (i=10\vee x\ge 100)\wedge i'=i\wedge x'=x\}\\{} & {} \quad \cup \left\{ (s,s')| i\ne 10\wedge x<100\wedge i\le i'\wedge x-\frac{i(i+1)}{2}=x'-\frac{i'(i'+1)}{2} \wedge i'\ne 11 \right. \\{} & {} \quad \quad \quad \qquad \qquad \left. \wedge x'-i'<100\wedge i'=10\right\} \\{} & {} \quad \cup \left\{ (s,s')| i\ne 10\wedge x<100\wedge i\le i'\wedge x-\frac{i(i+1)}{2}=x'-\frac{i'(i'+1)}{2} \wedge i'\ne 11\right. \\{} & {} \quad \quad \quad \quad \quad \quad \left. \wedge x'-i'<100\wedge x'\ge 100\right\} \\{} & {} =\qquad \quad \{\text {Simplifying the second term}\}\\{} & {} \quad \{(s,s')| (i=10\vee x\ge 100)\wedge i'=i\wedge x'=x\}\\{} & {} \quad \cup \left\{ (s,s')| i<10\wedge x<100\wedge i'=10\wedge x'=x+55-\frac{i(i+1)}{2} \wedge x'<110\right\} \\{} & {} \quad \cup \left\{ (s,s')| i\ne 10\wedge x<100\wedge i\le i'\wedge x-\frac{i(i+1)}{2}=x'-\frac{i'(i'+1)}{2} \wedge i'\ne 11 \right. \\{} & {} \qquad \quad \quad \quad \quad \quad \left. \wedge x'-i'<100\wedge x'\ge 100\right\} \\{} & {} =\qquad \quad \{\text {Replacing}\ x'\ \text {and}\ i'\ \text {in} \ (x'-i'<100)\ \text {by their expressions}\}\\{} & {} \quad \{(s,s')| (i=10\vee x\ge 100)\wedge i'=i\wedge x'=x\}\\{} & {} \quad \cup \left\{ (s,s')| i<10\wedge x<100\wedge x<\frac{i(i+1)}{2}+45 \wedge i'=10\wedge x'=x+55-\frac{i(i+1)}{2}\right\} \\{} & {} \quad \cup \left\{ (s,s')| i\ne 10\wedge x<100\wedge i\le i'\wedge x-\frac{i(i+1)}{2}=x'-\frac{i'(i'+1)}{2} \wedge i'\ne 11 \right. \\{} & {} \qquad \quad \quad \quad \quad \quad \left. \wedge x'-i'<100\wedge x'\ge 100\right\} \\{} & {} =\qquad \quad \{\text {The clause}\ (x<100)\ \text {is now redundant}\}\\{} & {} \quad \{(s,s')| (i=10\vee x\ge 100)\wedge i'=i\wedge x'=x\}\\{} & {} \quad \cup \left\{ (s,s')| i<10\wedge x<\frac{i(i+1)}{2}+45 \wedge i'=10\wedge x'=x+55-\frac{i(i+1)}{2}\right\} \\{} & {} \quad \cup \left\{ (s,s')|i\ne 10\wedge x<100\wedge i\le i'\wedge i'\ne 11 \right. \\{} & {} \qquad \qquad \qquad \qquad \left. \wedge x-\frac{i(i+1)}{2}=x'-\frac{i'(i'+1)}{2} \wedge x'-i'<100\wedge x'\ge 100\right\} . \end{aligned}$$

We use the three last clauses of the third term to derive an explicit expression of $i'$ and $x'$; to this effect, we replace $x'$ by

$$\begin{aligned} x-\frac{i(i+1)}{2}+\frac{i'(i'+1)}{2} \end{aligned}$$

in the inequations $x'-i'<100$ and $x'\ge 100$, which yields:

$$\begin{aligned}{} & {} x-\frac{i(i+1)}{2}+\frac{i'(i'+1)}{2}-i'<100,\\{} & {} x-\frac{i(i+1)}{2}+\frac{i'(i'+1)}{2}\ge 100. \end{aligned}$$

Isolating the term in $i'$ we rewrite this as:

$$\begin{aligned}{} & {} \frac{i'(i'-1)}{2}<100-x+\frac{i(i+1)}{2},\\{} & {} \frac{i'(i'+1)}{2}\ge 100-x+\frac{i(i+1)}{2}. \end{aligned}$$

The non-negative integer solution in $i'$ of these two inequations is the ceiling of the non-negative root of the quadratic equation:

$$\begin{aligned} \frac{i'(i'+1)}{2}=100-x+\frac{i(i+1)}{2}. \end{aligned}$$

Solving this quadratic equation and taking its ceiling yields the following expression for $i'$, from which we derive the expression of $x'$:

$$\begin{aligned} i'= & {} \bigg \lceil \sqrt{200.25-2x+i(i+1)}-0.5\bigg \rceil .\\ x'= & {} x+\frac{(i'-i)(i'+i+1)}{2}. \end{aligned}$$

We show briefly that $i\le i'$ is redundant with this equation of $i'$, hence it can be discarded from the formula:

$$\begin{aligned}{} & {} \quad i' \\{} & {} = \qquad \quad \{\text {hypothesis}\}\\{} & {} \quad \bigg \lceil \sqrt{200.25-2x+i(i+1)}-0.5\bigg \rceil \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\{} & {} \ge \qquad \quad \{\text {property of ceiling}\}\\{} & {} \quad \sqrt{200.25-2x+i(i+1)}-0.5\\{} & {} > \qquad \quad \{\text {clause}\ x<100 \}\\{} & {} \quad \sqrt{0.25+i(i+1)}-0.5 \\{} & {} >\qquad \quad \{\text {quadratic formula}\}\\{} & {} \quad \sqrt{(i+0.5)^2}-0.5\\{} & {} =\qquad \quad \{\text {simplification}\}\\{} & {} \quad i.\\ \end{aligned}$$

We rewrite $i'\ne 11$ as $(i'<11\vee i'>11)$, and decompose the third term into two terms, which yields after simplification:

$$\begin{aligned}{} & {} W' =\\{} & {} \{(s,s')| (i=10\vee x\ge 100)\wedge i'=i\wedge x'=x\} \\{} & {} \cup \left\{ (s,s')| i<10\wedge x<\frac{i(i+1)}{2}+45 \wedge i'=10\wedge x'=x+55-\frac{i(i+1)}{2}\right\} \\{} & {} \cup \left\{ (s,s')| i<10\wedge 45 +\frac{i(i+1)}{2}\le x<100\right. \\{} & {} \qquad \quad \quad \qquad \left. \wedge i'=\bigg \lceil \sqrt{200.25-2x+i(i+1)} -0.5\bigg \rceil \wedge x'=x+\frac{(i'-i)(i'+i+1)}{2}\right\} \\{} & {} \cup \left\{ (s,s')| i\ne 10\wedge x<100\wedge i'>11 \right. \\{} & {} \qquad \quad \quad \qquad \left. \wedge i'=\bigg \lceil \sqrt{200.25-2x+i(i+1)}-0.5\bigg \rceil \wedge x'=x+\frac{(i'-i)(i'+i+1)}{2}\right\} . \end{aligned}$$

To increase the reader’s confidence in our results we have run this program by varying i between 0 and 1000 and x between -990 and 110, and testing its function against an oracle derived verbatim from the formula of $W'$ above; all 1,102,101 tests returned TRUE.

Table 1 Sample recognizers

3.5 Condition of sufficiency

Given a while loop w:{while (t) {b;}} that we wish to analyze, we compute its invariant relation $E=I\cup T(T\cap B)$, then we use recognizers such as those of Table 1 to generate further invariant relations, take their intersection with E, say R, then use Proposition 4 to derive a superset (approximation) $W'$ of the function W of w. As we find more and more invariant relations and take their intersection, the resulting invariant relations grows smaller and smaller. The question we ask is: how small does R have to be to ensure that we actually find the exact function W. It is tempting to think that in order to derive the function of the loop ($W=(T\cap B)^*\cap \widehat{\overline{T}}$) by means of the approximation given in Proposition 4 ($W'=R\cap \widehat{\overline{T}}$), it is necessary to derive the smallest invariant relation ($R=(T\cap B)^*$). According to the following Proposition, this is not necessary.

Proposition 8

Given a while loop w:{while (t) {b;}} on space S and an invariant relation R of w, the function W of w equals $R\cap \widehat{\overline{T}}$ if and only if:

• $R\cap \widehat{\overline{T}}$ is deterministic.

• ${ dom}(R\cap \widehat{\overline{T}})\subseteq { dom}(W)$.

Proof

Necessity is trivial. For sufficiency, consider that because of the first hypothesis, we can use Proposition 1, since $R\cap \widehat{\overline{T}}$ and W are both deterministic. The condition $W\subseteq R\cap \widehat{\overline{T}}$ stems from Proposition 4; the condition ${ dom}(R\cap \widehat{\overline{T}})\subseteq { dom}(W)$ is given by hypothesis. By Proposition 1, $W=R\cap \widehat{\overline{T}}$. $\square$

Henceforth we use W to designate the function of the loop and $W'$ to designate the approximation $W'=R\cap \widehat{\overline{T}}$ that we can derive from some invariant relation R; we rename $W'$ as W once we ensure that $W'$ does satisfy the conditions of Proposition 8.

Fig. 1

Achieving $(T\cap B)^*\cap \widehat{\overline{T}} =R\cap \widehat{\overline{T}}$ does not require $R=(T\cap B)^*$

Given that we are approximating $W=(T\cap B)^*\cap \widehat{\overline{T}}$ by $W'=R\cap \widehat{\overline{T}}$ for some invariant relation R of w, it is tempting to think that we can achieve the condition $W=W'$ only with the invariant relation $R=(T\cap B)^*$. But this Proposition makes no mention of such a condition, and the following (counter-) example, due to [9], shows that we can achieve $W=R\cap \widehat{\overline{T}}$ while R is not equal to $(T\cap B)^*$, but is a superset thereof.

• Space, $S=\{0,1,2\}$.

• Loop Condition, $T=\{1,2\} \times S$. Whence, $\widehat{\overline{T}}=S\times \{0\}$.

• Loop Body Function, $B=\{(1,0),(2,0)\}$.

• Invariant Relation, $R=\{(0,0),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\}$.

We can easily check:

$$\begin{aligned} T\cap B=\{(1,0),(2,0)\}; \end{aligned}$$

whence

$$\begin{aligned} (T\cap B)^+=(T\cap B), \end{aligned}$$

from which we infer

$$\begin{aligned} (T\cap B)^*=I\cup (T\cap B)=\{(0,0),(1,0),(1,1),(2,0),(2,2)\}. \end{aligned}$$

Taking the intersection with $\widehat{\overline{T}}$, we find:

$$\begin{aligned} W=(T\cap B)^*\cap \widehat{\overline{T}}=\{(0,0),(1,0),(2,0)\}. \end{aligned}$$

Now we consider the approximation $W'=R\cap \widehat{\overline{T}}$ derived from relation R; first, we must check that R is indeed an invariant relation. Clearly, it is reflexive; on the other hand, we verify easily that $R^2\subseteq R$, hence R is transitive; finally it is also a superset of $(T\cap B)$, hence R is an invariant relation. We compute:

$$\begin{aligned} W'= & {} R\cap \widehat{\overline{T}} \\{} & {} = \qquad \qquad \{\text {Substitutions}\}\\{} & {} \{(0,0),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\} \cap \{(0,0),(1,0),(2,0)\} \\{} & {} = \qquad \qquad \{\text {Inspection}\}\\{} & {} (T\cap B)^*\cap \widehat{\overline{T}}. \end{aligned}$$

Hence we have shown on this example that the function of the loop $W=(T\cap B)^*\cap \widehat{\overline{T}}$ can be equal to the approximation derived from an invariant relation R, namely $W'=R\cap \widehat{\overline{T}}$ even though R is not equal to $(T\cap B)^*$, but is a superset thereof:

$$\begin{aligned} (T\cap B)^*= & {} \{(0,0),(1,0),(1,1),(2,0),(2,2)\},\\ R= & {} \{(0,0),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\}. \end{aligned}$$

Figure 1 shows in stark, plain terms why this is hardly surprising: just because two sets have the same intersection with a third set does not mean they are equal.

The practical implication of this result is that we can compute the function of a while loop without having to compute the reflexive transitive closure of its guarded loop body; in other words, we do not need to find the smallest invariant relation of a while loop; rather it suffices to find a small enough invariant relation R to satisfy the conditions of Proposition 8 (both of which impose upper bounds on R). This suggests that authors that approximate the function of a loop by computing the transitive closure of its loop body function may be aiming unnecessarily high, i.e. setting a goal that is unnecessarily difficult to achieve.

4 Recognizers for affine Loops

The success and effectiveness of our approach is contingent on our ability to capture as much programming and domain knowledge as possible, in as few recognizers as possible. The gist of our paper is that we can capture the semantics of any number of affine transformations in while loops with just two recognizers, which we present in this section.

4.1 A unary recognizer

We consider a while loop w of the form w:{while (t) {b}} and we assume that the function of its guarded loop body $(T\cap B)$ is a subset of a relation of the form:

$$\begin{aligned} B'=\{(s,s')| x'=a\times x+b\wedge a'=a\wedge b'=b\}, \end{aligned}$$

for some variables x, a and b (or variable x and constants a and b). In the remainder of this paper, we will refer to a and b as constants, regardless of whether they are declared as constants or declared as variables but are unmodified by the loop; also, for the sake of convenience we skip the clauses $a'=a$ and $b'=b$.

Proposition 9

We consider a while loop w of the form w:{while (t) {b}} and we assume that the function of its guarded loop body $(T\cap B)$ is a subset of a relation of the form:

$$\begin{aligned} B'=\{(s,s')| x'=a\times x+b\}, \end{aligned}$$

for some variable x, and constants a and b such that a is different from 0 and 1. Then the following is an invariant relation for w:

$$\begin{aligned} R_0= & {} \left\{ (s,s')|{ fr}({ log}_{|a|} \left( |x'+\frac{b}{a-1}|)\right) ={ fr}\left( { log}_{|a|} \left( \left| x+\frac{b}{a-1}\right| \right) \right) \right\} , \end{aligned}$$

where ${ fr}(x)$ is the fractional part of x, |x| is the absolute value of x, and ${ log}_a(x)$ is the ${ log}$ base a of x.

Proof

Relation $R_0$ is clearly reflexive and transitive. That it is a superset of $(T\cap B)$ can be easily verified by considering a pair $(s,s')$ in $(T\cap B)$ and proving that it is in $R_0$:

$$\begin{aligned}{} & {} { fr}\left( { log}_{|a|} \left( \left| x'+\frac{b}{a-1}\right| \right) \right) \\ ={} & {} \qquad \qquad \quad \{\text {replacing}\ x'\ \text {by}\ ax+b, \text {since}\ (s,s')\in T\cap B\}\\{} & {} { fr}\left( { log}_{|a|} \left( \left| ax+b+\frac{b}{a-1}\right| \right) \right) \\ ={} & {} \qquad \qquad \quad \{\text {common denominator, simplification}\}\\{} & {} { fr}\left( { log}_{|a|} \left( |a| \times \left| \left( x+\frac{b}{a-1}\right) \right| \right) \right) \\ ={} & {} \qquad \qquad \quad \{\text {property of}\ { log}_{|a|}\}\\{} & {} { fr}\left( 1+{ log}_{|a|} \left( \left| x+\frac{b}{a-1}\right| \right) \right) \\ ={} & {} \qquad \qquad \quad \{\text {property of}\ fr\}\\{} & {} { fr}\left( { log}_{|a|}\left( \left| x +\frac{b}{a-1}\right| \right) \right) . \end{aligned}$$

Hence $(s,s')$ is in $R_0$. $\square$

From this Proposition, we derive the following recognizer:

ID	Formal Space, $\sigma$	Formal Clause, $\gamma$	Condition, $\alpha$	Invariant Relation Template, $\rho$
1R0	$\begin{array}{l}{} \texttt {real x;}\\ \texttt {const real a,b}\end{array}$	$x'=ax+b$	$\begin{array}{l}a\ne 0 \\ \wedge a\ne 1\end{array}$	$\begin{array}{l}{} { fr}({ log}_{|a|}(|x+\frac{b}{a-1}|))\\ ={ fr}({ log}_{|a|}(|x'+\frac{b}{a-1}|))\end{array}$

In order to derive relation $R_0$, we had to assume that a is different from 0 and 1; of course, if $a=1$ then the job is even easier, we simply get:

$$\begin{aligned} R_0'=\left\{ (s,s')| { fr}\left( \frac{x}{b}\right) ={ fr}\left( \frac{x'}{b}\right) \right\} , \end{aligned}$$

assuming $b\ne 0$. If $b=0\wedge a\ne 1$ then relation $R_0$ applies, and if $b=0\wedge a=1$ then x is just preserved ($x'=x$).

4.2 A binary recognizer

Now we consider the case where we have two supersets of $(T\cap B)$ that have an affine form.

Proposition 10

We consider a while loop w of the form w:{while (t) {b}} and we assume that the function of its guarded loop body $(T\cap B)$ is a subset of two affine relations of the form:

$$\begin{aligned} B'= & {} \{(s,s')| x_0'=a_0\times x_0+b_0\},\\ B''= & {} \{(s,s')| x_1'=a_1\times x_1+b_1\}, \end{aligned}$$

for some variables $x_0, x_1$, and constants $a_0, a_1$ and $b_0, b_1$ such that $a_0, a_1$ are different from 0 and 1. Then the following is an invariant relation for w:

$$\begin{aligned} R_1= & {} \left\{ (s,s')| { log}_{|a_0|} \left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_1|}\left( \left| x_1'+\frac{b_1}{a_1-1}\right| \right) \right. \\{} & {} \qquad \qquad =\left. { log}_{|a_0|}\left( \left| x_0+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_1|}\left( \left| x_1+\frac{b_1}{a_1-1}\right| \right) \right\} . \end{aligned}$$

Proof

It is plain that $R_1$ is reflexive and transitive; it is an equivalence, in fact. To prove that $(T\cap B)$ is a subset of $R_1$, we consider a pair $(s,s')$ in $(T\cap B)$ and we show that it is necessarily in $R_1$.

To prove that $(s,s')$ is in $R_1$, we consider the expression ${ log}_{|a_0|}(|x_0'+\frac{b_0}{a_0-1}|) -{ log}_{|a_1|}(|x_1'+\frac{b_1}{a_1-1}|)$ and show that it is equal to: ${ log}_{|a_0|}(|x_0+\frac{b_0}{a_0-1}|) -{ log}_{|a_1|}(|x_1+\frac{b_1}{a_1-1}|)$.

$$\begin{aligned}{} & {} { log}_{|a_0|}\left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_1|}\left( \left| x_1'+\frac{b_1}{a_1-1}\right| \right) \\= & {} \quad \{\text {hypothesis}:\ (s,s')\in (T\cap B)\}\\{} & {} \qquad { log}_{|a_0|}\left( \left| a_0\times x_0+b_0+\frac{b_0}{a_0-1}\right| \right) - { log}_{|a_1|}\left( \left| a_1\times x_1+b_1+\frac{b_1}{a_1-1}\right| \right) \\= & {} \quad \{\text {arithmetic simplifications}\}\\{} & {} \qquad { log}_{|a_0|}\left( \left| a_0\times \left( x_0+\frac{b_0}{a_0-1}\right) \right| \right) -{ log}_{|a_1|}\left( \left| a_1\times \left( x_1+\frac{b_1}{a_1-1}\right) \right| \right) \\= & {} \quad \{\text {property of}\ { log}\}\\{} & {} \qquad 1+{ log}_{|a_0|}\left( \left| x_0+\frac{b_0}{a_0-1}\right| \right) -1-{ log}_{|a_1|}\left( \left| x_1+\frac{b_1}{a_1-1}\right| \right) \\= & {} \quad \{\text {arithmetic simplification}\}\\{} & {} \qquad { log}_{|a_0|}\left( \left| x_0+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_1|}\left( \left| x_1+\frac{b_1}{a_1-1}\right| \right) . \end{aligned}$$

Hence $(s,s')\in R_1$. $\square$

From this Proposition, we derive the following recognizer:

ID	Formal Space, $\sigma$	Formal Clause, $\gamma$	Condition, $\alpha$	Invariant Relation Template, $\rho$
2R1	$\begin{array}{l}{} \texttt {real x0, x1;}\\ \texttt {const int}\\ \texttt {a0,a1,b0,b1}\end{array}$	$\begin{array}{l}x_0'=a_0x_0+b_0\\ \wedge \\ x_1'=a_1x_1+b_1\end{array}$	$\begin{array}{l}a_0,a_1\ne 0\\ \wedge \\ a_0,a_1\ne 1\end{array}$	$\begin{array}{l}{} { log}_{|a_0|}(|x_0+\frac{b_0}{a_0-1}|)\\ - { log}_{|a_1|}(|x_1+\frac{b_1}{a_1-1}|)\\ = { log}_{|a_0|}(|x_0'+\frac{b_0}{a_0-1}|)\\ - { log}_{|a_1|}(|x_1'+\frac{b_1}{a_1-1}|)\end{array}$

In order to derive $R_1$, we had to assume that $a_0\ne 1$ and $a_1\ne 1$. If both $a_0$ and $a_1$ are equal to 1, then we get the following invariant relation:

$$\begin{aligned} R_1'=\{(s,s')| b_0x_1-b_1x_0=b_0x_1'-b_1x_0'\}. \end{aligned}$$

If only one coefficient is equal to 1 (e.g. $a_1=1$) then we get the following equations:

$$\begin{aligned}{} & {} { log}_{|a_0|}\left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) =i+{ log}_{|a_0|}\left( \left| x_0+\frac{b_0}{a_0-1}\right| \right) ,\\{} & {} x_1'=x_1+i\times b_1. \end{aligned}$$

Extracting i from the second equation and replacing it in the first equation, we derive the following invariant relation:

$$\begin{aligned} R_1''= \left\{ (s,s')| b_1\times { log}_{|a_0|} \left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) -x_1' = b_1\times { log}_{|a_0|} \left( \left| x_0+\frac{b_0}{a_0-1}\right| \right) -x_1\right\} . \end{aligned}$$

This is clearly a reflexive and transitive relation; to check that it is a superset of $(T\cap B)$, consider that if we replace $x_0'$ by $a_0x_0+b_0$ and $x_1'$ by $x_1+b_1$ in the expression on the left, we find $b_1\times (1+{ log}_{|a_0|}(|x_0 +\frac{b_0}{a_0-1}|))-x_1- b_1$, which cancels out to yield $b_1\times ({ log}_{|a_0|}(|x_0+\frac{b_0}{a_0-1}|))-x_1$.

The following corollary stems readily from Proposition 10, and is given without proof.

Corollary 1

We consider a while loop w of the form w:{while (t) {b}} and we assume that the function of its guarded loop body $(T\cap B)$ is a subset of two affine relations of the form:

$$\begin{aligned}{} & {} B'=\{(s,s')| x_0'=a_0\times x_0+b_0\},\\{} & {} B''=\{(s,s')| x_1'=a_1\times x_1+b_1\}, \end{aligned}$$

for some variables $x_0, x_1$, and constants $a_0, a_1$ and $b_0, b_1$ such that $a_0, a_1$ are different from 0 and 1. Then the following equation holds:

$$\begin{aligned}{} & {} { log}_{|a_0|}\left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_0|}\left( \left| x_0+\frac{b_0}{a_0-1}\right| \right) \\{} & {} \qquad = { log}_{|a_1|}\left( \left| x_1'+\frac{b_1}{a_1-1}\right| \right) -{ log}_{|a_1|}\left( \left| x_1+\frac{b_1}{a_1-1}\right| \right) . \end{aligned}$$

The following Proposition offers an interesting interpretation of this corollary: The two sides of this equation are equal because they both represent the number of iterations of the loop.

Proposition 11

We consider a while loop w of the form w:{while (t) {b}} and we assume that the function of its guarded loop body $(T\cap B)$ is a subset of an affine relation of the form:

$$\begin{aligned} B'=\{(s,s')| x'=a\times x+b\}, \end{aligned}$$

for some variable x, and constants a, b such that a is different from 0 and 1. Then the expression

$$\begin{aligned} { log}_{|a|}\left( \left| x'+\frac{b}{a-1}\right| \right) -{ log}_{|a|}\left( \left| x+\frac{b}{a-1}\right| \right) \end{aligned}$$

represents the number of affine applications of $B'$ that are needed to derive $x'$ from x.

Proof

This Proposition can be easily proved by induction on the number of iterations. For zero iterations we have $x'=x$, hence the formula returns zero. If $x'$ is derived from x by n iterations and $x''$ is derived from $x'$ by one more iteration then the formula returns:

$$\begin{aligned}{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{ log}_{|a|}\left( \left| x''+\frac{b}{a-1}\right| \right) - { log}_{|a|}\left( \left| x+\frac{b}{a-1}\right| \right) \\{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! =\qquad \quad \{\text {by hypothesis}:\ x''=ax'+b\}\\{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{ log}_{|a|}\left( \left| ax'+b+\frac{b}{a-1}\right| \right) -{ log}_{|a|}\left( \left| x+\frac{b}{a-1}\right| \right) \\{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! =\qquad \quad \{\text {reduction to common denominator, simplification}\}\\{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{ log}_{|a|}\left( |a|\times \left| x'+\frac{b}{a-1}\right| \right) -{ log}_{|a|}\left( \left| x+\frac{b}{a-1}\right| \right) \\{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! =\qquad \quad \{\text {property of} { log}()\}\\{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!1+{ log}_{|a|}\left( \left| x'+\frac{b}{a-1}\right| \right) -{ log}_{|a|}\left( \left| x+\frac{b}{a-1}\right| \right) \\{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! =\qquad \quad \{\text {induction hypothesis}\} \end{aligned}$$

$n+1$. $\square$

Hence Corollary 1 is merely saying that the affine transformations $B'$ and $B''$ are applied the same number of times, since each side of the equation is counting the number of times that the corresponding affine transformation is applied.

4.3 Extensions

In this section we consider two extensions of the results of the previous sections: first, the case of an arbitrary number of affine transformations; second, the case of a transformation of the form $X=AX+B$, where X and B are vectors of arbitrary size (say, N) and A is a diagonalisable matrix of size $N\times N$.

Proposition 12

We consider a while loop w of the form w:{while (t) {b}} and we assume that the function of its guarded loop body $(T\cap B)$ is a subset of N affine relations of the form:

$$\begin{aligned} B_i=\{(s,s')| x_i'=a_i\times x_i+b_i\}, \end{aligned}$$

where $0\le i\le N-1,$ for some variables $x_i$, and real constants $a_i$ and $b_i$ such that $a_i$ are different from 0 and 1. Then the following is an invariant relation for w:

$$\begin{aligned} R=\bigcap _{i=0}^{N-1} R_i, \end{aligned}$$

where

$$\begin{aligned} R_0= \left\{ (s,s')|{ fr}\left( { log}_{|a_0|} \left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) \right) ={ fr}\left( { log}_{|a_0|} \left( \left| x_0+\frac{b_0}{a_0-1}\right| \right) \right) \right\} , \end{aligned}$$

and for $1\le i\le N-1$,

$$\begin{aligned}{} & {} R_i=\left\{ (s,s')| { log}_{|a_0|} \left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_i|}\left( \left| x_i'+\frac{b_i}{a_i-1}\right| \right) \right. \\{} & {} \qquad \qquad \qquad \quad = \left. { log}_{|a_0|}\left( \left| x+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_i|}\left( \left| x_i+\frac{b_i}{a_i-1}\right| \right) \right\} . \end{aligned}$$

Proof

This invariant relation is obtained by applying Proposition 9 to $B_0$ and Proposition 10 to ($B_0$, $B_i$), for $1\le i\le N-1$. $\square$

As a generalization of Proposition 12, we want to derive invariant relations for while loops whose loop body has a function that is a subset of

$$\begin{aligned} \{(s,s')| X'=A\times X+B\} \end{aligned}$$

for some vector X of size N, some matrix A of size $N\times N$, and some vector B of size N.

Proposition 13

We consider a while loop w of the form w:{while (t) {b}} and we assume that the function of the guarded loop body of w is a subset of a relation of the form $\{(s,s')| X'=A\times X+B\}$ for some vector X of size N, some matrix A of size $N\times N$, and some vector B of size N. We further assume that A is diagonalizable, i.e. $A=V^{-1}\times D \times V$ for some invertible matrix V, and that all the (diagonal) entries of D are real values different from 0 and 1. Then the following is an invariant relation for w:

$$\begin{aligned} R=\bigcap _{i=0}^N R_i, \end{aligned}$$

where

$$\begin{aligned} R_0= \left\{ (s,s')|{ fr}\left( { log}_{|a_0|} \left( \left| y_0'+\frac{b_0}{a_0-1}\right| \right) \right) ={ fr}\left( { log}_{|a_0|} \left( \left| y_0+\frac{b_0}{a_0-1}\right| \right) \right) \right\} , \end{aligned}$$

and for $1\le i\le N$,

$$\begin{aligned}{} & {} R_i=\left\{ (s,s')|{ log}_{|a_0|} \left( \left| y_0'+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_i|}\left( \left| y_i'+\frac{b_i}{a_i-1}\right| \right) \right. \\{} & {} \qquad \qquad \qquad \quad = \left. { log}_{|a_0|}\left( \left| y_0+\frac{b_0}{a_0-1}\right| \right) -log_{|a_i|}\left( \left| y_i+\frac{b_i}{a_i-1}\right| \right) \right\} , \end{aligned}$$

where vector $Y=\left( \begin{array}{c}y_0\\ y_1\\ ..\\ y_{N-1} \end{array}\right)$ is defined by the equation $Y=V\times X$.

Proof

The equation $X'=A\times X+B$ can be rewritten as $X'=V^{-1}\times D \times V\times X+B$. Multiplying by V on the left and right and simplifying, we get $V\times X'=D\times V\times X+V\times B$; by making the change of variables $Y=V\times X$, $Y'=V\times X'$ and $C=V\times B$, we find an equation of the form $Y'=D\times Y+C$, which satisfies the conditions of Proposition 12; the proposed loop invariant stems from the application of this Proposition. $\square$

If a matrix is not diagonalisable then we can always apply $R_0$ and $R_1$ to its diagonal parts, i.e. transformations of the form $x'=ax+b$; for other transformations, we have to apply other recognizers, as appropriate; for illustration, see the example of Sect. 6.2.

5 Minimality properties

To say that some relation R is an invariant relation for some while loop w: {while (t) {b;}} is not big news; the universal relation L is reflexive and transitive, and it is a superset of any loop body function, but it does not tell us much of anything about any loop; what is important about an invariant relation is that it is small enough to give us useful information about the semantic properties of the loop. Proposition 8 provides the condition under which an invariant relation is small enough to derive the exact function of a loop. In this section, we show that the invariant relations given in Propositions 9 and 10 do satisfy the conditions of Proposition 8, hence are sufficient to compute the exact function of an affine loop.

5.1 One affine transformation

In this subsection we resolve to prove that the invariant relation given in Proposition 9 is sufficient to compute the function of an affine loop on a single variable; since we cannot prove this result for an arbitrary loop guard, we do so for a sample loop guard that tests the condition $\texttt {(x<c)}$ for some constant c. We consider the following affine loop on variable x, where a, b and c are constants, and we assume that a is different from 0 and 1:

$$\begin{aligned} \texttt {w0: while (x<c) \{x=a*x+b;\}}. \end{aligned}$$

Note that if this loop is executed on $x=\frac{-b}{a-1}$ where $\frac{-b}{a-1}<c$ then it does not terminate, since:

$$\begin{aligned} a\times \frac{-b}{a-1}+b=\frac{-ab+ab-b}{a-1}=\frac{-b}{a-1}. \end{aligned}$$

In other words, if this program is executed on an initial value of x equal to $\frac{-b}{a-1}$ that is less than c, it will remain less than c irrespective of the number of iterations, hence this loop would fail to terminate. Since x cannot be equal to $\frac{-b}{a-1}$, we must choose it either greater than, or less than $\frac{-b}{a-1}$. We assume, for the sake of argument, that a is greater than 1, then we find that $x<\frac{-b}{a-1}$ is equivalent to $ax+b<x$. In other words, if we start with x less than $\frac{-b}{a-1}$ and less than c, then each iteration of the loop brings x farther from c, hence the loop will fail to terminate; if $x=\frac{-b}{a-1}$ is greater than c, then the loop terminates vacuously without changing x.

The following Proposition provides that if a is greater than 1, then the invariant relation of Proposition 9 enables us to compute the function of the loop above; cases when a is not greater than 1 are discussed subsequently.

Proposition 14

We consider the following affine loop on variable x, where a, b and c are constants, and we assume that a is greater than 1:

w0: while (x<c) {x=a*x+b;}.

Then the function $W_0$ of w0 is:

$$\begin{aligned} W_0 = E\cap R_0\cap \widehat{\overline{T}}. \end{aligned}$$

Proof

We use Proposition 8.

Proof that $W'_0$ is deterministic. For the loop to terminate, we need $ax+b > x$, or $x > -\frac{b}{a-1}.$ Interestingly, this means that $(x+\frac{b}{a-1})$ is positive, hence we can remove the absolute values from the formula of $R_0$. The relations $R_0$ and the elementary invariant relation E imply

$$\begin{aligned}{} & {} x' + \frac{b}{a-1} = a^N\left( x+ \frac{b}{a-1}\right) , \quad \text{ and } \end{aligned}$$

(1)

$$\begin{aligned}{} & {} x' \ge c, \quad \frac{x'-b}{a} < c \end{aligned}$$

(2)

respectively. From (1), we get $x' = xa^N +(ba^N-b)/(a-1)$. Substituting this in (2), we have

$$\begin{aligned} x' \ge c&\Rightarrow xa^N + \frac{ba^N-b}{a-1} \ge c \\&\Rightarrow xa^N(a-1) + ba^N -b \ge c(a-1) \\&\Rightarrow a^N \ge \frac{c(a-1)+b}{x(a-1)+b} \equiv F \\&\Rightarrow N \ge \log _aF, \end{aligned}$$

and

$$\begin{aligned} \frac{x'-b}{a}< c&\Rightarrow xa^N + \frac{ba^N-b}{a-1}< ac+b \\&\Rightarrow a^N[x(a-1) + b)< (ac+b)(a-1)+b = a(c(a-1)+b)\\&\Rightarrow a^N< a\cdot \frac{(c(a-1)+b)}{x(a-1)+b} = aF \\&\Rightarrow N < 1 + \log _aF. \end{aligned}$$

Hence, with constants a, b, c, we have N a function of x, specifically $N = \text{ ceiling }(\log _aF)$. With N, $x'$ can be obtained with (1). Hence $W'_0$ is deterministic.

Proof of ${ dom}(W'_0)\subseteq { dom}(W_0)$. $W'_0$ is written as:

$$\begin{aligned} W'_0= & {} \{(x,x')| x\ge c\wedge x'=x\}\\{} & {} \cup \left\{ (x,x')| \frac{-b}{a-1}<x<c\wedge x'=a^{\lceil \log _a\left( \frac{c(a-1)+b}{x(a-1)+b}\right) \rceil } \times \left( x+\frac{b}{a-1}\right) -\frac{b}{a-1}\right\} . \end{aligned}$$

The domain of $W'_0$ can then be written as:

$$\begin{aligned} { dom}(W'_0)=\left\{ x| x\ge c\vee x<c\wedge x>\frac{-b}{a-1}\right\} . \end{aligned}$$

If $x\ge c$ then clearly the loop terminates vacuously; if x is less than c but strictly greater than $\frac{-b}{a-1}$ then, per the discussion above, each iteration of the loop increases x, eventually bringing it over the value of c. $\square$

If $0<a<1$, then, without the constraint $x<c$, x will converge to $\frac{-b}{a-1}$, regardless of the starting value. Thus, if c is less than $\frac{-b}{a-1}$, the loop will terminate in N steps, with $N=\text{ ceiling }(\log _a F)$, following arguments similar to the above.

In the case $(a<1)$, we note that N is also a function of x. If $c> x >\frac{-b}{a-1}$, then N is the even number between $\log _{|a|} F$ (inclusive) and $2+\log _{|a|} F$ (exclusive), whereas if $x <\frac{-b}{a-1}$, N is the maximum of 1 and the odd number between $\log _{|a|} |F|$ (inclusive) and $2+\log _{|a|} |F|$ (exclusive).

For $-1< a < 0$, the sequence $x = a x + b$ without constraints will also converge to $\frac{b}{1-a}$, like for $0<a<1$. However, unlike for $0<a<1$, for $-1<a<0$, the sequence oscillates around the limit $\frac{b}{1-a}$. Let’s call this limit X. So, if $x > X$, then either the loop doesn’t iterate (if $c\le x$), or it fails to converge (if $c>x$). On the other hand, (if $x < X$), then either the loop doesn’t iterate (if $c\le x$), or the loop fails to converge, (if $c\ge a x + b$) or it terminates after one iteration (if $x< c < a x + b$).

5.2 Two affine transformations

In this section, we consider a loop with two affine transformations.

Proposition 15

We consider the following affine loop on variables $x_0$, $x_1$, where $a_0$, $a_1$, $b_0$, $b_1$ and c are constants, and we assume that $a_0$ is greater than 1:

w1: while (x0<c){x0=a0*x0+b0; x1=a1*x1+b1;}.

Then the function $W_1$ of w1 is:

$$\begin{aligned} W_1 = E\cap R_0\cap R_1\cap \widehat{\overline{T}}, \end{aligned}$$

where E is the elementary invariant relation (Proposition 6) and $R_0$ is the unary invariant relation of affine loops (Proposition 9).

Proof

We let $W'_1$ be defined as: $W'_1=E\cap R_0\cap R_1\cap \widehat{\overline{T}}$, and we must prove that $W_1=W'_1$. We proceed the same way as for the proof of Proposition 14. The proofs that $W_1$ is a subset of $W'_1$ and the proof that ${ dom}(W'_1)$ is a subset of ${ dom}(W_1)$ is the same as the proof of Proposition 14, since $R_1$ is an invariant relation, and the termination of this loop is dependent exclusively on $x_0$. To prove that $W'_1$ is deterministic, we must prove that the equations of $W'_1$ uniquely determine the values of $x_0'$ and $x_1'$. For $x_0'$, the proof is the same as in Proposition 14. For $x_1'$, we consider the equation that stems from relation $R_1$:

$$\begin{aligned}{} & {} { log}_{|a_0|}\left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_1|}\left( \left| x_1'+\frac{b_1}{a_1-1}\right| \right) \\{} & {} \quad ={ log}_{|a_0|}\left( \left| x_0+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_1|}\left( \left| x_1+\frac{b_1}{a_1-1}\right| \right) . \end{aligned}$$

From this equation we derive:

$$\begin{aligned} { log}_{|a_1|}\left( \left| x_1'+\frac{b_1}{a_1-1}\right| \right)= & {} { log}_{|a_0|}\left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) \\{} & {} -{ log}_{|a_0|}\left( \left| x_0+\frac{b_0}{a_0-1}\right| \right) +{ log}_{|a_1|}\left( \left| x_1+\frac{b_1}{a_1-1}\right| \right) . \end{aligned}$$

From this equation we can extract the value of

$$\begin{aligned} \left( \left| x_1'+\frac{b_1}{a_1-1}\right| \right) . \end{aligned}$$

If we can determine the sign of $(x_1'+\frac{b_1}{a_1-1})$, then we can remove the absolute value from the equation above and uniquely determine $x_1'$. To this effect, we consider the equation:

$$\begin{aligned} \left( x_1'+\frac{b_1}{a_1-1}\right) =a_1^N\left( x_1+\frac{b_1}{a_1-1}\right) . \end{aligned}$$

If $a_1$ is positive then $(x_1'+\frac{b_1}{a_1-1})$ has the same sign as $(x_1+\frac{b_1}{a_1-1})$; and if $a_1$ is negative then whether $(x_1'+\frac{b_1}{a_1-1})$ and $(x_1+\frac{b_1}{a_1-1})$ have the same sign depends on the parity of N. In all cases, the absolute value can be removed and the equation can be solved in $x_1'$. Hence $W'_1$ is deterministic. $\square$

5.3 Multiple affine transformations

If we have more than two affine transformations, then we can apply $R_0$ to the variable that appears in the loop condition (let it be called the pivot variable), and we apply $R_1$ to the pair made up of the pivot and every non-pivot variable.

Proposition 16

We consider a while loop w of the form

where $a_0$ is greater than 1. Then the function $W_N$ of wN is:

$$\begin{aligned} W_1 = E\cap \left( \bigcap _{i=0}^{N}R_i\right) \cap \widehat{\overline{T}}, \end{aligned}$$

where

$$\begin{aligned} R_0= \left\{ (s,s')|{ fr}\left( { log}_{|a_0|} \left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) \right) ={ fr}\left( { log}_{|a_0|} \left( \left| x_0+\frac{b_0}{a_0-1}\right| \right) \right) \right\} , \end{aligned}$$

and for $1\le i\le N$,

$$\begin{aligned} R_i= & {} \left\{ (s,s')| { log}_{|a_0|} \left( \left| x_0'+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_i|}\left( \left| x_i'+\frac{b_i}{a_i-1}\right| \right) \right. \\{} & {} \qquad \qquad \qquad \qquad = \left. { log}_{|a_0|}\left( \left| x+\frac{b_0}{a_0-1}\right| \right) -{ log}_{|a_i|}\left( \left| x_i+\frac{b_i}{a_i-1} \right| \right) \right\} . \end{aligned}$$

Proof

This proof is the same as that of Proposition 15, except that the invariant relation of Proposition 10 is applied to each pair of variables $(x_0,x_i)$, for $1\le i\le N$. $\square$

6 Illustrative examples

We present three illustrative examples in this section: The first example will merely illustrate Propositions 9 and 10 by means of a loop that has two affine assignments; the second example serves to illustrate that the proposed results apply to loops that are not made up exclusively of affine assignments, but may include other types of instructions as well; the third example illustrates Propositions 12 and 13.

6.1 Two linear statements

We consider the following program on float variables x, y:

We propose to compute the function of w, the function of p, and an invariant assertion (loop invariant) of w. According to Propositions 9 and 10, the following are invariant relations for w:

$$\begin{aligned} R_0= & {} \left\{ (s,s')|{ fr}\left( { log}_5 \left( \left| x'+\frac{3}{4}\right| \right) \right) ={ fr}\left( { log}_5 \left( \left| x+\frac{3}{4} \right| \right) \right) \right\} ,\\ R_1= & {} \left\{ (s,s')| { log}_5\left( \left| x'+\frac{3}{4}\right| \right) -{ log}_3\left( \left| y'+\frac{5}{2}\right| \right) = { log}_5\left( \left| x+\frac{3}{4}\right| \right) -{ log}_3\left( \left| y+\frac{5}{2}\right| \right) \right\} . \end{aligned}$$

Because x and y are non-negative, we also have the following invariant relation:

$$\begin{aligned} R_2=\{(s,s')| x\le x'\wedge y\le y'\}. \end{aligned}$$

Finally, we use the elementary invariant relation:

$$\begin{aligned} E=I\cup \{(s,s')| x<200\wedge x'<1003\}. \end{aligned}$$

Adopting the invariant relation $R=R_0\cap R_1\cap R_2\cap E$ and applying Proposition 3, we find:

$$\begin{aligned}&W=\{(s,s')| x\ge 200\wedge s'=s\}\\&\cup \left\{ (s,s')|x<200\wedge x'=5^{\lceil \log _5 \left( \frac{200.75}{x+3/4}\right) \rceil } \left( x+\frac{3}{4}\right) -\frac{3}{4} \wedge \right. \\&\qquad \qquad \qquad \qquad \qquad \quad \left. y'=3^{\lceil \log _5\left( \frac{200.75}{x+3/4}\right) \rceil } \left( y+\frac{5}{2}\right) -\frac{5}{2}\right\} . \end{aligned}$$

The function of program p can be computed by replacing x and y by their initial values in W, which yields:

$$\begin{aligned}{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!P=\{(s,s')| 0\ge 200\wedge s'=s\}\\{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\cup \left\{ (s,s')|0<200\wedge x'=5^{\bigg \lceil \log _5 \left( \frac{200.75}{0+3/4}\right) \bigg \rceil } \left( 0+\frac{3}{4}\right) -\frac{3}{4} \wedge \right. \\{} & {} \qquad \qquad \left. y'=3^{\bigg \lceil \log _5 \left( \frac{200.75}{0+3/4}\right) \bigg \rceil } \left( 90+\frac{5}{2}\right) -\frac{5}{2}\right\} \\{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!=\{\text {the first term is empty, and} \ 0<200\ \text {is a tautology}\}\\{} & {} \quad \left\{ (s,s')| x'=5^4 \left( \frac{3}{4}\right) -\frac{3}{4} \wedge y'=3^4 \left( 90+\frac{5}{2}\right) -\frac{5}{2}\right\} \\{} & {} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!=\qquad \quad \{\text {arithmetic}\}\\{} & {} \quad \{(s,s')| x'=468 \wedge y'=7490\}. \end{aligned}$$

The same invariant relation $R=R_0\cap R_1\cap R_2\cap E$ can be used to generate a loop invariant for w, using Proposition 5 with precondition $A=\{(s,s')| x=0\wedge y=90\}$. According to this Proposition, we derive a loop invariant (in the form of a vector) as:

$$\begin{aligned}{} & {} V=\widehat{R}A\\{} & {} =\qquad \quad \{\text {substitution}\}\\{} & {} \qquad \qquad \left\{ (s,s')| { fr}\left( \log _5 \left( \left| x+\frac{3}{4}\right| \right) \right) ={ fr}\left( \log _5\left( \left| x'+\frac{3}{4} \right| \right) \right) \right. \wedge \\{} & {} \qquad \qquad \qquad \log _5\left( \left| x+\frac{3}{4}\right| \right) -\log _3\left( \left| y+\frac{5}{2}\right| \right) =\log _5\left( \left| x'+\frac{3}{4}\right| \right) -\log _3\left( \left| y'+\frac{5}{2}\right| \right) \wedge \\{} & {} \qquad \qquad \qquad \left. x\ge x'\wedge y\ge y'\wedge ((x=x'\wedge y=y') \vee (x'<200\wedge x<1003))\right\} \\{} & {} \qquad \qquad \circ \{(s,s')| x=0\wedge y=90\}\\{} & {} =\qquad \quad \{\text {performing the product, simplifying}\}\\{} & {} \qquad \qquad \quad \left\{ (s,s')| { fr}\left( \log _5 \left( \left| x+\frac{3}{4}\right| \right) \right) ={ fr}\left( \log _5\left( \frac{3}{4} \right) \right) \right. \wedge \\{} & {} \qquad \qquad \qquad \log _5\left( \left| x+\frac{3}{4}\right| \right) -\log _3\left( \left| y+\frac{5}{2}\right| \right) =\log _5\left( \frac{3}{4}\right) -\log _3\left( 90+\frac{5}{2}\right) \wedge \\{} & {} \qquad \qquad \qquad \left. x\ge 0\wedge y\ge 90\wedge ((x=0\wedge y=90)\vee (x<1003))\right\} . \end{aligned}$$

Table 2 (transcribed from an excel file) bears out all the clauses of this loop invariant: its columns represent, respectively, the ordinal of the iteration, then the values of x, y, $\log _5(x+\frac{3}{4})$, ${ fr}(\log _5(x+\frac{3}{4}))$, $\log _3(y+\frac{5}{2})$, ${ fr}(\log _3(y+\frac{5}{2}))$, and $\log _3(y+\frac{5}{2})-\log _5(x+\frac{3}{4})$. The invariance of $R_0$ can be observed in the columns of ${ fr}(\log _5(x+\frac{3}{4}))$ and ${ fr}(\log _3(y+\frac{5}{2}))$; the invariance of $R_1$ can be observed in the column of $\log _3(y+\frac{5}{2})-\log _5 (x+\frac{3}{4})$. We also note that the last row of columns x and y show the values indicated by function P, thereby further bearing out the correctness of our calculations. To further enhance the reader’s confidence, we have executed ten thousand versions of this loop, by varying the initial values of x and y from 1 to 100, and tested the invariants at each iteration; all tests of the loop invariant returned true.

For further illustration, we consider four versions of this small program, by varying the initial values of x and y as well as the coefficients of the affine transformations; the results of our analysis are summarized in Tables 3, 4, 5 and 6. These tables are all transcribed from Excel (©Microsoft) files; their columns represent, respectively:

• C1: The ordinal of the iteration (the number of times that the affine transformation has been applied),

• C2: Variable x.

• C3: Variable y.

• C4: The value of $\log _{|a|}(|x+\frac{b}{a-1}|)$.

• C5: The value of $\log _{|c|}(|y+\frac{d}{c-1}|)$.

• C6: The value of ${ fr}(\log _{|a|}(|x+\frac{b}{a-1}|))$.

• C7: The value of ${ fr}(\log _{|c|}(|y+\frac{d}{c-1}|))$.

• C8: The value of $\log _{|a|}(|x+\frac{b}{a-1}|) -\log _{|c|}(|y+\frac{d}{c-1}|)$.

• C9: The value of $\log _{|a|}(|x+\frac{b}{a-1}|) \log _{|a|}(|x0+\frac{b}{a-1}|)$, where x0 is the initial value of x.

• C10: The value of $\log _{|c|}(|y+\frac{d}{c-1}|) \log _{|c|}(|y0+\frac{d}{c-1}|)$, where y0 is the initial value of y.

These tables bear out the results of Sect. 4:

• Proposition 9 is borne out by the fact that columns C6 and C7 are uniform.

• Proposition 10 is borne out by the fact that column C8 is uniform.

• Corollary 1 is borne out by the fact that columns C9 and C10 are identical.

• Proposition 11 is borne out by the fact that columns C9 and C10 are identical to column C1.

Table 2 Invariant relation highlights

Table 3 {x=0;y=50; while(t) {x=5*x+3;y=3*y+5;}}

Table 4 {x=-40;y=50; while(t){x=5*x+3;y=3*y+5;}}

Table 5 {x=-40;y=50; while(t){x=-5*x+3;y=3*y+5;}}

Table 6 {x=-40;y=50;while(t){x=-5*x+3;y=-3*y+5;}}

6.2 A hybrid loop

In this section we generate the invariant relation of a loop whose loop body function includes affine transformations to which $R_0$ and $R_1$ can be applied, alongside other transformations for which we apply other recognizers. We consider the following loop on space S defined by float variables x, y, z and w:

We define the following supersets of the guarded loop body:

• $B_0=\{(s,s')| x'=5\times x+3\}$.

• $B_1=\{(s,s')| y'=3\times y+5\}$.

• $B_2=\{(s,s')| w'=3\times z+w\}$.

• $B_3=\{(s,s')| z'=z+6\}$.

Application of Proposition 9 to $B_0$ yields the following invariant relation:

$$\begin{aligned} R_0=\left\{ (s,s')|{ fr}\left( { log}_5 \left( \left| x+\frac{3}{4}\right| \right) \right) ={ fr}\left( { log}_5 \left( \left| x'+\frac{3}{4}\right| \right) \right) \right\} . \end{aligned}$$

Application of Proposition 10 to $(B_0,B_1)$ yields the following invariant relation:

$$\begin{aligned} R_1=\left\{ (s,s')| { log}_5\left( \left| x+\frac{3}{4}\right| \right) -{ log}_3\left( \left| y+\frac{5}{2}\right| \right) ={ log}_5\left( \left| x'+\frac{3}{4}\right| \right) -{ log}_3\left( \left| y'+\frac{5}{2}\right| \right) \right\} . \end{aligned}$$

In [17] Ghardallou presents a recognizer (recognizer 2R2, page 119) which, when applied to $(B_2,B_3)$, yields the following invariant relation:

$$\begin{aligned} R_2=\left\{ (s,s')|w-\frac{3z(z-6)}{12}=w'-\frac{3z'(z'-6)}{12}\right\} . \end{aligned}$$

In [17] Ghardallou presents a recognizer (recognizer 2R4, page 119) which, when applied to $(B_0,B_3)$, yields the following invariant relation

$$\begin{aligned} R_3=\left\{ (s,s')|\frac{4x+3}{5^{\frac{z}{6}}} =\frac{4x'+3}{5^{\frac{z'}{6}}}\right\} . \end{aligned}$$

Recognizer 1R2 (Table 1) applied to $B_3$ yields the following invariant relation:

$$\begin{aligned} R_4=\{(s,s')| z\le z'\wedge z ~mod~ 6=z'~mod~ 6\}. \end{aligned}$$

We further introduce the elementary invariant relation:

$$\begin{aligned} E=I\cup \left\{ (s,s')| x<y\wedge \frac{x'-3}{5}<\frac{y'-5}{3}\right\} . \end{aligned}$$

The invariant relation we generate for this loop is the intersection of all these relations:

$$\begin{aligned} R=R_0\cap R_1\cap R_2\cap R_3\cap R_4\cap E. \end{aligned}$$

From this invariant relation we derive a loop invariant for initial state $s0=\langle x0,y0,z0,w0\rangle$:

$$\begin{aligned}{} & {} { fr}\left( { log}_5\left( |x0+\frac{3}{4}|\right) \right) ={ fr}\left( { log}_5\left( |x+\frac{3}{4}|\right) \right) \wedge \frac{4x0+3}{5^{\frac{z0}{6}}} =\frac{4x+3}{5^{\frac{z}{6}}} \\{} & {} \quad \wedge { log}_5\left( \left| x0+\frac{3}{4}\right| \right) -{ log}_3\left( \left| y0+\frac{5}{2}\right| \right) ={ log}_5\left( \left| x+\frac{3}{4}\right| \right) -{ log}_3\left( \left| y+\frac{5}{2}\right| \right) \\{} & {} \quad \wedge w0-\frac{3z0(z0-6)}{12}=w-\frac{3z(z-6)}{12} \wedge z0\le z\wedge z ~mod~ 6=z0~mod~ 6\\{} & {} \quad \wedge \left( (x=x0\wedge y=y0\wedge z=z0\wedge w=w0) \vee \left( x0<y0\wedge \frac{x-3}{5}<\frac{y-5}{3}\right) \right) . \end{aligned}$$

To increase the reader’s confidence in this result, we test this loop invariant repeatedly by varying the initial values of the program variables (x0, y0, z0, w0); all the tests (for all the initial conditions and all the iterations of each initial condition, a total of 650 000 calls to the loop invariant) return true.

For the sake of comparison, we tried to run several published loop invariant generation tools on the same loop, to compare their results with ours.

• Aligator. When we run Aligator [37] on the same program, it declares that there no P-solvable solutions to this search, and returns no result, because it searches for loop invariants as polynomials.

• Daikon. Whereas our loop invariants can be parameterized in terms of the initial state, Daikon requires that we specify the initial values of the program variables. We initialize the program variables as follows: {x=0;y=90;z=0;w=1;}. Daikon returns the following loop invariant:

  $$\begin{aligned} x<y\wedge x\ne w\wedge y>z\wedge y>w\wedge z\ne w. \end{aligned}$$

  Note that the first conjunct ($x<y$) should not be part of the loop invariant, since it is the loop condition.

• Sting. When we run Sting [54] on this loop, with the same initialization as above, we find:

  $$\begin{aligned} x\le 1003\wedge y\ge 90\wedge -185x+403y\ge 36270. \end{aligned}$$

Multiple attempts to run other tools such as InvGen [23], ESMBC [15], and Dynamate [16] have failed.

6.3 Matrix transformation

In this section we briefly present an example that illustrates the application of Propositions 12 and 13: We consider a loop whose space S is defined by a vector X of size 4, whose body performs a transformation of the form $X'=A\times X+B$ where B is a vector of size 4 and A is a diagonalisable $4\times 4$ matrix whose diagonal form has coefficients that are different from 0 and 1. Specifically, we let A and B be defined as follows:

$$\begin{aligned} A=\left( \begin{array}{cccc} 0.634762 &{} 0.0347619 &{} -0.0380953 &{} 0.127143\\ 0.177143 &{} 0.577143 &{} 0.142857 &{} -0.0342857\\ -0.0919048 &{} 0.108095 &{} 0.795238 &{} 0.0871429\\ 0.211905 &{} 0.0119048 &{} 0.104762 &{} 0.692857\\ \end{array}\right) , B=\left( \begin{array}{c} -3\\ 5\\ -4\\ 6 \end{array}\right) . \end{aligned}$$

We find that A can be written as $A=V^{-1}\times D\times V$, where:

$$\begin{aligned} V=\left( \begin{array}{cccc} 5/12 &{} -1/12 &{} -1/3 &{} 1/4\\ -5/14 &{} 1/7 &{} -1/7 &{} 3/14\\ -1/4 &{} -1/4 &{} 0 &{} 1/4\\ 4/21 &{} 4/21 &{} 10/21 &{} 2/7\\ \end{array}\right) D=\left( \begin{array}{cccc} 0.8 &{} 0 &{} 0 &{} 0\\ 0 &{} 0.4 &{} 0 &{} 0\\ 0 &{} 0 &{} 0.6 &{} 0\\ 0 &{} 0 &{} 0 &{} 0.9\\ \end{array}\right) . \end{aligned}$$

The product of V by B yields the following vector:

$$\begin{aligned} C=\left( \begin{array}{c} 1.16667\\ 3.64286\\ 1\\ 0.190476 \end{array}\right) . \end{aligned}$$

According to Proposition 13, the following is an invariant relation of this loop:

$$\begin{aligned} R=\bigcap _{i=0}^3 R_i, \end{aligned}$$

where

$$\begin{aligned}{} & {} R_0= \left\{ (s,s')|{ fr}\left( { log}_{D[0,0]} \left( \left| Y'[0]+\frac{C[0]}{D[0,0]-1}\right| \right) \right) \right. \\{} & {} = \left. { fr}\left( { log}_{D[0,0]}\left( \left| Y[0] +\frac{C[0]}{D[0,0]-1}\right| \right) \right) \right\} , \end{aligned}$$

and for $1\le i\le 3$,

$$\begin{aligned} R_i= & {} \left\{ (s,s')| { log}_{D[0,0]}\left( \left| Y'[0]+\frac{C[0]}{D[0,0]-1}\right| \right) -{ log}_{D[i,i]}\left( \left| Y'[i]+\frac{C[i]}{D[i,i]-1}\right| \right) \right. \\{} & {} \qquad \qquad =\left. { log}_{D[0,0]}\left( \left| Y[0]+\frac{C[0]}{D[0,0]-1}\right| \right) -{ log}_{D[i,i]}\left( \left| Y[i]+\frac{C[i]}{D[i,i]-1}\right| \right) \right\} \end{aligned}$$

where $Y=V \times X$, $Y'=V\times X'$ and $C=V\times B$. We spare the reader the full expression of the loop invariant that can be generated from this invariant relation for the precondition $X=X0$; it can be obtained by replacing Y and $Y'$ by their expressions as a function of X and $X'$ in the formulas of R; then we replace X by X0 (the initial state) and $X'$ by X (the current state); this yields a unary predicate in X, where X0 represents the initial state (as a parameter of the loop invariant).

7 Conclusion

7.1 Summary

This work is part of a broader effort to derive the function of a C-like program through static analysis of its source code. To this effect, we map the source code onto an abstract syntax tree (AST) using a standard language parser; then we perform a recursive descent on the AST to derive an equation between the initial state and the final state of the program written in the syntax of a symbolic equation solver (specifically: Mathematica, ©Wolfram Research); then we invoke the symbolic equation solver to compute the final state of the program as a function of the initial state, thereby deriving the function of the program.

Not surprisingly, the most challenging aspect of this effort is the derivation of the function of iterative constructs, such as while loops, for loops, repeat loops, etc. We capture the semantics of loops by means of invariant relations, which are relations that hold between pairs of states $(s,s')$ such that $s'$ stems from s by an arbitrary number of iterations of the loop. To derive the function of a loop, we use a pattern matching algorithm which matches the clauses of the functional representation of the loop body against prespecified code patterns, for which we have the corresponding invariant relation pattern. This pattern-matching approach works best if we can analyze the broader possible set of loops with the smallest possible set of recognizers; hence we are very interested in recognizers that have a wide scope of application.

In this paper, we present two recognizers that are sufficient to analyze loops that apply affine transformations to numeric variables. We find that these two recognizers apply to loops that include an arbitrary number of affine transformations; also, we find that these recognizers are sufficient to derive the function of the while loop. Once we have the function of a loop, we can answer any question one may have about its semantic properties.

In particular, once we have the function W of a while loop w: {while (t) {b;}}, we can use it to generate the loop invariant

$$\begin{aligned} inv(s,s0)\equiv (W(s)=W(s0)), \end{aligned}$$

where s0 is the state of the program before execution of the loop. This loop invariant is strong enough to prove the correctness of the loop with respect to the following pre/post specification:

• Pre: $s=s0$.

• Post: $s=W(s0)$.

7.2 Extensions: branching logic and breaks

The approach we advocate in this paper for generating invariant relations relies on identifying supersets of the function of the loop body; this approach works best if we write the function of the loop body as an intersection of terms, such as:

$$\begin{aligned} (T\cap B) = B_0\cap B_1\cap B_2...\cap B_k. \end{aligned}$$

When $(T\cap B)$ is written in this form, each term of the intersection is a candidate for Proposition 9 and each pair of terms is a candidate for Proposition 10 (if these terms have the form $x'=a\times x+b$ and a satisfies the conditions of these Propositions). But we do not get to decide what form the function of $(T\cap B)$ has: if the loop body has branching logic (if-then statements, if-then-else statements, nested while loops) then the outer structure of the loop body’s function is a union of terms, not an intersection.

For the sake of argument, let us assume that the function of the loop body is the union of two terms, say

$$\begin{aligned} (T\cap B)=B_0\cup B_1. \end{aligned}$$

Let $R_0$ be a reflexive transitive superset of $B_0$ and $R_1$ be a reflexive transitive superset of $B_1$; then clearly $R=R_0\cup R_1$ is a reflexive superset of $B_0\cup B_1$. Unfortunately, R is not necessarily transitive, as the union of transitive relations is not necessarily transitive. Hence the derivation of an invariant relation in such cases is not straightforward: In [50] Mraihi investigates a number of heuristics for computing or approximating the smallest transitive superset of transitive relations; we envision to refine and specialize these heuristics for the case when $R_0$ and $R_1$ stem from affine transformations ($B_0$ and $B_1$).

The derivation of loop invariants becomes significantly more complex when we are dealing with break statements in the body of the loop [36]. All the mathematics we have developed for invariant relations are based on the assumption that a loop has a single exit, controlled by an explicit loop condition. Having break statements in the loop body means that the function of the loop is the union of several terms, one term for each break statement. Because such statements may be located anywhere in the body of a loop, we have to roll the statements of the loop body for each break statement in such a way that it is the last statement in the sequence. Also, each break statement is necessarily controlled by a condition (else the loop exits at the first iteration), hence we need to combine the condition of the break with the condition of the loop (unless the condition of the loop is TRUE). All of this adds complexity to the generation of invariant relations.

7.3 Comparison to related work

Our work partakes on four distinct research efforts, which we briefly discuss in this section: invariant relations, loop invariants, linear relationship analysis, and compositional recurrence analysis. We compare our work to these, in turn, below.

Invariant relations The closest thing we could find to invariant relations is the concept of transition invariants, which are transitive asymmetric supersets of the function of the guarded loop body [42, 53]; these are used to analyze termination properties of loops. Whereas transition invariants are transitive and asymmetric, invariant relations are transitive and reflexive; consequently, no relation can be a transition invariant and an invariant relation since asymmetry and reflexivity are mutually exclusive. Whereas transition invariants are used to capture termination properties of loops, invariant relations are used to capture the function of loops.

Loop invariant generation The automated generation of loop invariants has been an active research area for as long as loop invariants have been known, because this has been the main bottleneck/ obstacle to the automated correctness verification of software [7, 11, 12, 14, 24,25,26, 35, 37, 38, 41, 46, 47, 51, 57]; we discuss some of them in Sect. 6.

Linear relationship analysis Another area of research that is related to our work is the generation of loop invariants for loops that take the form of affine assignments and guards [1, 21, 22, 28]. This line of work, known under the name Linear Relation Analysis, differs from our approach in several important ways.

• Scope Most linear relation analysis is applicable to loops whose source code is restricted to specific syntactic forms of the loop body and the loop condition. In our approach, we impose no restriction on the loop condition, and we analyze the function of the guarded loop body, not its syntax. Also, our approach is applicable to any affine part of a loop body, alongside non-affine parts.

• Application Linear relation analysis usually aims to derive loop invariants in the form of affine equations and inequations; we have no such restriction, and we aim to capture all the semantic details of the loop, regardless of their form.

• Goal To the best of our understanding, the goal of linear relation analysis is to verify conditions that ensure the safe execution of affine loops; our goal is to capture all the semantic attributes of a loop, including its safe (abort-free) execution [10].

• Method Many of the techniques of linear relation analysis originally relied on abstract interpretation [6] to derive verification conditions of safety; abstract acceleration was subsequently used to enhance the precision of the generated formulas [1, 22, 28]. In our approach, we use a pattern-matching algorithm which attempts to match clauses of the function of the guarded loop body against code patterns for which we know an invariant relation template. Of course, this is restrictive, in the sense that we can only handle loops for which we have the necessary code patterns (recognizers); but we argue in this paper that with two recognizers (1R0, derived from Proposition 9, and 2R1, derived from Proposition 10), we can capture the semantics of any scalar affine transformation, as well as any matrix transformation of the form ($X'=A\times X+B$) that can be amenable to scalar affine transformations.

Compositional recurrence analysis (CRA) Recurrence analysis is used in [12, 25, 26, 35] to generate loop invariants and in [34] to generate the function of a loop (referred to as closed form of the loop, or its loop summary). This line of research differs from our approach in several different ways, which we discuss below; we refer to our approach as FX, acronym for Functional Extraction.

• In the use of recurrence In compositional recurrence analysis, the algorithm extracts the recurrence equations defined by the loop, then resolves it by eliminating the recurrence variable, to infer a relationship between program variables; the relationship derived in this manner is exactly the invariant relation that we are interested in. In the FX approach, recurrence analysis may be used to generate recognizers, but this is done off-line, not at run-time; at run-time, invariant relations are generated by pattern matching against pre-stored recognizers.

• Scope A consequence of the foregoing discussion is that whereas the CRA approach is restricted to loops that can be analyzed by compositional recurrence, the FX approach is not; as an example, consider recognizers 2R3, 2R4, 3R2. Of course, the consequence of this is that FX works only on loops for which it has applicable recognizers, whereas CRA works for any loop whose recurrence equation can be solved at run-time.

• On the role of recurrence The contrast between CRA and FX in terms of whether recurrence is deployed online or offline is not the only distinction. Most importantly, whereas recurrence is the core mechanism for loop analysis in CRA, it plays a minor role in generating recognizers in FX; very few recognizers are derived by recurrence analysis; most are derived by taking the reflexive transitive closure of selected code patterns. It is not difficult to verify that a generated recognizer is valid, but the generation of recognizers is a creative process that is difficult to automate.

• Top down versus bottom up Compositional Recurrence Analysis proceeds top-down, in the sense that it defines a general model of affine programs, then analyzes the programs that fall under that model; as with all modeling decisions, this involves a tradeoff between generality and precision. If the model is too general, it is difficult to derive precise results; if the model is too specific, it has limited scope of applicability. By contrast, FX proceeds by bottom up analysis of programs: we do not need to assume any specific structure of the program; we generate invariant relations by inspecting a few clauses of the loop body’s function at a time, a process that operates on a local scale. A global perspective is needed to analyze the equations generated from the invariant relations, not to generate the invariant relations. As an example, consider the following program on a space S defined by a variable v of type float and a variable x of type float:

  

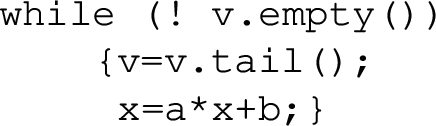
  Using the invariant relations E and $R_0$, alongside the following invariant relation that connects the two assignments:

  $$\begin{aligned} \left\{ (s,s')| \log _{|a|}\left( \left| x+\frac{b}{a-1}\right| \right) +length(v) =\log _{|a|}\left( \left| x'+\frac{b}{a-1}\right| \right) +length(v')\right\} \end{aligned}$$

  enables us to compute the function of the loop as:

  $$\begin{aligned} W=\left\{ (s,s')| v'=() \wedge x'=a^{length(v)}\times \left( x+\frac{b}{a-1}\right) -\frac{b}{a-1}\right\} . \end{aligned}$$

  The program does not have to fit any model; we just need to have all its invariant relations, which in turn requires that we have the proper recognizers to this effect.

Multi-Path Loops. Multi-path loops of affine transformations lend themselves to special solutions, such as Farkas’ Lemma [5, 29, 44, 54] or Porous Invariants [43]. In our approach, multi-path loops are addressed by means of a general solution, which makes no assumption on the form of the loop, nor the form of the loop invariant. This general solution aims to compute a small reflexive transitive superset of two (or more) reflexive transitive relations. Note that Propositions 9 and 10 give general formulas for invariant relations for affine loops, and Propositions 14 and 15 establish that these invariant relations are minimal, i.e. that they capture all the semantic information of the loop (since they enable us to compute the function of the loop). Since the invariant relations provided in Propositions 9 and 10 are not affine, we can infer that all the invariant generation methods that aim to generate affine loop invariants are, by construction, bound to generate suboptimal solutions, since they restrict their search space to a domain that is known not to contain optimal solutions.

We consider two possible solutions to the general problem of multi-path loops, which we interpret in relational term as the problem of generating a reflexive transitive superset of two or more reflexive transitive relations:

• We consider two reflexive transitive relations Q and $Q'$ and we assume that each is the intersection of reflexive transitive relations:

  $$\begin{aligned} Q= & {} Q_1\cap Q_2\cap ...\cap Q_n,\\ Q'= & {} Q'_1\cap Q'_2\cap ...\cap Q'_{n'}. \end{aligned}$$

  For each $Q_i$, $1\le i\le n$, we check whether $Q'$ is a subset of $Q_i$; if it is, we select $Q_i$. We do the same for each term of the decomposition of $Q'$. Then we let R be the intersection of all the selected components as a reflexive transitive superset of Q and $Q'$. In particular, if Q and $Q'$ are invariant relations of two paths in a loop body, then R is an invariant relation of the loop. This is briefly illustrated in the following example:

  

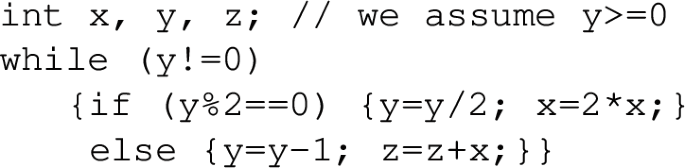
  We write the following reflexive transitive supersets of the first and second branch of the loop body:

  $$\begin{aligned} Q= & {} \{(s,s')| xy=x'y'\}\cap \{(s,s')| y'\le y\} \cap \{(s,s')| z'=z\}.\\ Q'= & {} \{(s,s')| x=x'\}\cap \{(s,s')| y'\le y\} \cap \{(s,s')| z+xy=z'+x'y'\}. \end{aligned}$$

  If we let $Q'_1$, $Q'_2$, $Q'_3$ be the three terms of $Q'$ (in the order in which they are listed) then we find:

  $$\begin{aligned}{} & {} Q\subseteq Q'_2\\{} & {} Q\subseteq Q'_3, \end{aligned}$$

  from which we infer that $R=Q'_2\cap Q'_3$ is an invariant relation of the loop.

  $$\begin{aligned} R=\{(s,s')| y'\le y\wedge x+yz=x'+y'z'\}. \end{aligned}$$

  The reader can easily check that this is an invariant relation of the loop: it holds for any two states $(s,s')$ that are separated by an arbitrary number of iterations, regardless of which branch of the if-else statement is executed at each iteration.

• The second option is to use a relational identity that characterizes the reflexive transitive closure of a union of relations [2, 55]:

  $$\begin{aligned} (Q\cup Q')^* = Q^*(Q'Q^*)^*=(Q^*Q')^*Q^*. \end{aligned}$$

  Here, since Q and $Q'$ are both reflexive and transitive, they equal their own reflexive transitive closure, hence we get the simplified version:

  $$\begin{aligned} (Q\cup Q')^* = Q(Q'Q)^*=(QQ')^*Q. \end{aligned}$$

  If we have recognizers against which we can match $QQ'$ or $Q'Q$, we can replace the transitive closures by the formula that is retrieved by the recognizer, and derive the invariant relation of the whole loop. The case when we have more than two terms of the union can be resolved by breaking down the union in two, but the logistics are certainly very onerous.

Termination Analysis. Given that we are interested to derive the function of a while loop, rather than its correctness with respect to a given specification, we do not analyze termination separately; rather, the condition of termination of a loop, or more generally a program, is merely the domain of the program function. To compute the termination condition of a loop, we generate its invariant relations, take their intersection to compute the function of the loop, then derive the domain of the computed function; in [10] we use invariant relations to integrate the analysis of termination with the analysis of abort conditions. Some of the developments of Frohn et al [13] perform a transformation that is similar to the generation of an invariant relation: when they give a closed form for $a^n(c)$ as a polynomial in n, it is possible to use this form to derive an invariant relation as:

$$\begin{aligned} R = \{(c,c')| \exists n\ge 0: c'=a^n(c)\}. \end{aligned}$$

Relation R is clearly reflexive, since $a^0(c)=c$; it is also transitive, since $a^n(a^m(c))=a^{n+m}(c)$; also, it is a superset of the function of the loop body since the function of the loop body is obtained by taking $n=1$.

7.4 Threats to validity

A significant limitation of our approach is that it can only handle loops for which we have pre-stored recognizers. We argue that it is impossible to analyze program semantics without some way to deploy the required programming knowledge and domain knowledge, and these recognizers are our way to capture this knowledge. Also, when our algorithm fails to capture the function of a loop in full, we have a way to identify the missing recognizers, so as to guide us in filling the missing gap.

Table 7 Supplemental recognizers

The most severe threat to the validity of the FX approach remains the difficulty of generating invariant relations from loop body functions that are not structured as intersections but as unions. The heuristics proposed in [30, 31, 51] are useful, in that they generate invariant relations that subsume terms of the union, but they are not guaranteed to generate smallest invariant relations. Alternatives and extensions are currently under investigation.

A comparative study

To give some sense of how the invariant relations approach to loop analysis compares with existing methods, we consider a number of sample programs from the SV-Comp benchmark. Whereas invariant relations of a loop can be used for a variety of purposes (deriving the function of the loop, its termination condition, its weakest preconditions, its strongest postconditions, etc), most other tools and methods are focused exclusively on generating loop invariants (aka invariant assertions); hence for the purposes of this experiment we use invariant relations solely to generate invariant assertions of the loops, to have a sound basis for comparison.

We have selected six sample programs from the SV-Comp benchmark; some of them were so trivial that we added lines to them, to make them more complex and more interesting. For each program, we derive the loop invariant that is generated from recognizers presented in this paper (1R0 to 1R3; 2R0 to 2R9; 3R1, 3R2); then we deploy four loop invariant generators that are available online, namely: Duet, Sting, Aligator and Daikon; for lack of a better name, we refer to our approach as InvRel (for: Invariant Relation). To accommodate these examples, we have added some recognizers, listed in Table 7.

Duet and InvRel do not require that the loop be initialized, and can refer to the initial state symbolically (by subscripting the program variables with zero, as in x0, y0, etc). Hence, for the sake of generality, we run them on uninitialized loops; we run the other tools on initialized loops, hence we will specify, for each sample program, the initialization that we use to this effect.

A demo of InvRel’s operation on these six sample programs can be seen at:

http://web.njit.edu/~mili/actademo.mp4.

Note that InvRel is usually deployed to compute the function of programs, in particular the function of loops, and is optimized to that effect. For the purposes of this experiment, we had to alter it to compute loop invariants instead. The process to generate invariant relations is the same, using a pattern-matching algorithm against pre-stored recognizers; but whereas loop functions are computed by means of the formula

$$\begin{aligned} W=R\cap \widehat{\overline{T}}, \end{aligned}$$

loop invariant assertions are computed by means of the formula

$$\begin{aligned} A=\widehat{R}P, \end{aligned}$$

where R is the loop’s invariant relation, T is the (vector representing) the loop’s condition, W is the loop’s function, P is the loop’s precondition and A is the corresponding loop invariant [51]. Because of this transition, we could not process examples of nested loops, because whereas the function of an inner loop can be used to compute the function of an outer loop, the invariant assertion of an inner loop cannot be used to infer the invariant assertion of an outer loop.

1.1 A.1 Sample 1: overflow

1.1.1 A.1.1 Source code

Initialization: x=0;

1.1.2 A.1.2 InvRel

1.1.3 A.1.3 Duet

1.1.4 A.1.4 Sting

1.1.5 A.1.5 Aligator

1.1.6 A.1.6 Daikon

1.1.7 A.1.7 Porous

The Porous Invariant Builder and Reachability Checker applies to integer linear dynamical systems and formulates loop invariants as sets of reachable states from some initial state; the tool takes as input an initial state $x_0$, a specification of the target set whose reachability is being considered Y, the loop condition, and a set of affine transformations that are applied by non-deterministic choice (defined by constants a, b in the transformation $x'=ax+b$). Because of this last requirement, this sample loop (which has only one variable and only one affine transformation) is the only example to which we can apply Porous as defined. Below are some of the sample executions we tried:

1.2 A.2 Sample 2: loop sum

1.2.1 A.2.1 Source code

Initialization: sn=0; a=2; i=1; size=8; x=5; y=2; z=2;

1.2.2 A.2.2 InvRel

1.2.3 A.3 Duet

1.2.4 A.2.4 Sting

1.2.5 A.2.5 Aligator

1.2.6 A.2.6 Daikon

1.3 A.3 Sample 3: linear1

1.3.1 A.3.1 Source code

Initialization: x=10; y=20; z=3; a=2;

1.3.2 A.3.2 InvRel

1.3.3 A.3.3 Duet

1.3.4 A.3.4 Sting

1.3.5 A.3.5 Aligator

1.3.6 A.3.6 Daikon

1.4 A.4 Sample 4: Gauss sum

1.4.1 A.4.1 Source code

Initialization: sum=0; i=1; n=10; j=4; a=3; b=7; k=2;

1.4.2 A.4.2 InvRel

1.4.3 A.4.3 Duet

1.4.4 A.4.4 Sting

1.4.5 A.4.5 Aligator

1.4.6 A.4.6 Daikon

1.5 A.5 Sample 5: jm2006

1.5.1 A.5.1 Source code

Initialization: i=10; j=10; x=i; y=j; a=2; b=6; z=2; t=8;

1.5.2 A.5.2 InvRel

1.5.3 A.5.3 Duet

1.5.4 A.5.4 Sting

1.5.5 A.5.5 Aligator

1.5.6 A.5.6 Daikon

1.6 A.6 Sample 6: Fibonacci

1.6.1 A.6.1 Source code

Initialization: cN=100; i=1; fb=1; np=1;

1.6.2 A.6.2 InvRel

1.6.3 A.6.3 Duet

1.6.4 A.6.4 Sting

1.6.5 A.6.5 Aligator

1.6.6 A.6.6 Daikon