Semigroups, keis and groups induced by knot diagrams: an experimental investigation with automated reasoning

Abstract

We apply automated reasoning to investigation of finite factors of algebraic structures associated with knot diagrams. We refute “double size” conjecture about cancellative semigroups and keis.

1 Definitions and context

1.1 Context and scope

The aim of this study is to improve our understanding of knot semigroups, $\pi$-orbifold groups and two-fold groups via experiments with specific knot diagrams such as those shown in Fig. 1. In this note we do not consider a wider context of this research in knot theory beyond algebraic constructions based on knot diagrams. Having said this, it makes sense to describe this context briefly. Knots are embeddings of a circle into 3-dimensional space. Two such embeddings are considered equivalent if one can be deformed into the other by an ambient isotopy. Speaking of a knot, depending on the context, one may mean an embedding or its equivalence class, or one can conveniently consider knot diagrams instead of knots.

One of the most famous problems in knot theory is checking if two knots are equivalent. An important role in solving this problem is played by knot invariants, that is, knot-related constructions which are preserved by ambient isotopies. Some of knot invariants are algebraic structures; arguably the best known and oldest examples of algebraic invariants are the Alexander polynomial and the knot group. Among the constructions used in this paper, keis, $\pi$-orbifold groups and two-fold groups are knot invariants. The authors conducted work in this area [5, 6], including estimating efficiency of different invariants [7, 10].

The authors have introduced and published several articles on what we call knot semigroups [10, 13, 14]. As we discuss below, knot semigroups are closely related to keis, $\pi$-orbifold groups and two-fold groups, see Sect. 1.5. Although knot semigroups are not knot invariants (see Section 8.2 in [13]), we have hopes that they solve another knot-theoretical problem, see the next paragraph.

The most important partial case of the knot equivalence problem is the unknotting problem, which asks whether a knot is trivial, that is, not knotted. For example, speaking of classical constructions, triviality can be detected using knot groups [2], but cannot be detected using Alexander polynomials (for example, see [8]). It was proved in 1969 that triviality can be detected using two-fold groups [15]; a more general result was proved in 1984; its proof is very involved and fills up a whole book [12]. The fact that triviality can be detected using keis was proved in 1984 as a corollary of [15] in an unpublished PhD thesis [16] and there seems to be no published proof of this fact. As to knot semigroups, it has been conjectured that they detect triviality, see Conjecture 1 below (this is Conjecture 24 in [13]; see also Conjecture 25 in [13]).

Below, we denote knot diagrams by letters such as ${\mathfrak {d}}$; we will denote semigroups (keis, groups) by letters S (K, G) and variations thereof.

1.2 Knot semigroups

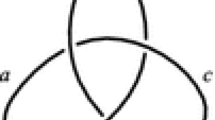
A semigroup is called cancellative if it satisfies two conditions: if $xz=yz$ then $x=y$, and if $xy=xz$ then $y=z$. For each given knot diagram ${\mathfrak {d}}$, we will define a cancellative semigroup which we call the knot semigroup of ${\mathfrak {d}}$ and denote by $S{\mathfrak {d}}$. By an arc we mean a continuous line on a knot diagram from one undercrossing to another undercrossing. For example, consider the knot diagram ${\mathfrak {t}}$ on the figure; it has three arcs, denoted by a, b and c. To denote a crossing on a knot diagram we shall use notation $x\dashv y\vdash z$, where x and z are the two arcs terminating at the crossing and y is the arc passing over the crossing. For example, the crossings on diagram ${\mathfrak {t}}$ are $b\dashv a\vdash c$, $b\dashv a\vdash a$ and $c\dashv a\vdash a$. To define the knot semigroup of a diagram ${\mathfrak {d}}$, assume that each arc is denoted by a letter. Then at every crossing $x\dashv y\vdash z$, ‘read’ two defining relations $xy=yz$ and $yx=zy$. The cancellative semigroup generated by the arc letters with these defining relations is the knot semigroup $S{\mathfrak {d}}$ of D. For example, on diagram ${\mathfrak {t}}$ we can read relations $ba=ac$ and $ab=ca$ at the left-top crossing, relations $ba=aa$ and $ab=aa$ at the right-top crossing and relations $ca=aa$ and $ac=aa$ at the bottom crossing. Using these relations, one can deduce equalities of words in $S{\mathfrak {t}}$. In particular, from $aa=ba=ca$, using cancellation, one can deduce $a=b=c$, that is, all generators are equal to one another; in other words, $S{\mathfrak {t}}$ is an infinite cyclic semigroup. The unusually simple structure of $S{\mathfrak {t}}$ may be related to the fact that ${\mathfrak {t}}$ is a diagram of the trivial knot: indeed, it is ‘tangled’, but it is not really ‘knotted’. A general conjecture was formulated in [13].

Conjecture 1

A knot diagram ${\mathfrak {d}}$ is a diagram of the trivial knot if and only if $S{\mathfrak {d}}$ is an infinite cyclic semigroup.

1.3 Keis

A kei (also known as an involutory quandle) is defined as an algebra with one binary operation $\rhd$ and three axioms

$$\begin{aligned} a\rhd a=a,\ (a\rhd b)\rhd b=a\ \hbox { and }(a\rhd b)\rhd c=(a\rhd c)\rhd (b\rhd c). \end{aligned}$$

For a given knot diagram ${\mathfrak {d}}$, the kei $K{\mathfrak {d}}$ of the knot is a kei generated by the arc letters with defining relations $x\rhd y=z$ and $z\rhd y=x$ for each crossing $x\dashv y\vdash z$ of ${\mathfrak {d}}$. The mnemonic behind notation $x\rhd y=z$ is expressed in [9]: ‘x under y gives z’. The three axioms of a kei directly correspond to the three Reidemeister moves [4].

1.4 $\pi$-Orbifold and two-fold groups

For a given knot diagram ${\mathfrak {d}}$, the $\pi$-orbifold group $G{\mathfrak {d}}$ of the knot is a group generated by the arc letters with the following relations. For each arc x of the diagram ${\mathfrak {d}}$, introduce a relation $x^{2}=1$. At every crossing $x\dashv y\vdash z$, introduce a defining relation $xy=yz$ (or, equivalently, $yx=zy$, or $yxy=z$, or $yzy=x$). Let A denote the generating set of $G{\mathfrak {d}}$ (i.e. the set of labels of the arcs of ${\mathfrak {d}}$), and consider the natural homomorphism from the free semigroup $A^{+}$ onto $G{\mathfrak {d}}$. It is easy to see that, for each element g of $G{\mathfrak {d}}$, either only words of an odd length are mapped to g or only words of an even length are mapped to g under the homomorphism. Accordingly, let us say that g is an element of odd (even) length in the former (latter) case. A subgroup of $G{\mathfrak {d}}$ consisting of the set of all elements of even length is called the fundamental group of the 2-fold branched cyclic cover space of a knot [12, 16]; we shorten this name to the two-fold group of a knot, and denote the group by $G^2{\mathfrak {d}}$.

1.5 Knot semigroups, keis and two-fold groups

Note that for every group G, one can define a kei K(G) whose elements are the elements of G, and in which the operation is $g\rhd h=hg^{-1}h$. Such a kei is also referred to as a core quandle of G in [1].

For a finite sequence of group elements $g_1, g_2, g_3, g_4, \dots$, define the alternating product of this sequence as the product $g_1 \cdot g_2^{-1} \cdot g_3 \cdot g_4^{-1} \cdot \dots$. Note that for every group G, one can define a semigroup S(G) whose elements are words over the alphabet G, and in which two words u, v are equal if and only if u and v have both the same length and the same alternating product in G.

For many types of knot diagrams, including those studied in [13], there is a simple connection between knot semigroups, keis and two-fold groups, as follows. Consider a knot diagram ${\mathfrak {d}}$ whose two-fold group is $G^2{\mathfrak {d}}$ and whose $\pi$-orbifold group is $G{\mathfrak {d}}$. In many examples, it turns out that the kei $K{\mathfrak {d}}$ is isomorphic to $K(G^2{\mathfrak {d}})$, and the knot semigroup $S{\mathfrak {d}}$ is isomorphic to $S(G{\mathfrak {d}})$.

However, there is no reason why it should be so for all knot diagrams; one can expect that at some point, knot semigroups, keis and two-fold groups will diverge. The aim of research reported in this note is to make progress towards finding counterexamples in which the simple correspondence described above does not hold anymore.

2 What conjectures we had

In [10] automated reasoning was applied to search for non-trivial cancellative factor semigroups of minimal sizes for knot semigroups of all knots up to 9 crossings.¹ Out of 84 standards knots diagrams with no more than 9 crossings, in 55 cases cancellative factor semigroups of a minimal size were found, in 9 cases cancellative factor semigroups were found which are not necessarily minimal, and in 20 cases the search took a long time and was abandoned, and no cancellative factor semigroups were found. After comparing the sizes of the found cancellative factor semigroups with the minimal sizes of factor keis, found in our earlier work [5], we formulated the following conjecture.

Conjecture 2

[10] Consider a knot diagram ${\mathfrak {d}}$. Suppose the kei of $K{\mathfrak {d}}$ has a factor kei of size k. Then semigroup $S{\mathfrak {d}}$ has a cancellative factor semigroup of size 2k.

Since we concentrate on minimal sizes of factors, the conjecture above can be usefully amended in the following two ways, both consistent with data from our experiments from [5, 10].

Conjecture 3

Consider a knot diagram ${\mathfrak {d}}$. Suppose $K{\mathfrak {d}}$ has finite factor keis, and $S{\mathfrak {d}}$ has finite cancellative factor semigroups. Let k and s be minimal sizes of a non-trivial factor kei of $K{\mathfrak {d}}$ and a non-trivial factor semigroup of $S{\mathfrak {d}}$, respectively. Then $s = 2k$

Conjecture 4

Consider a knot diagram ${\mathfrak {d}}$. Let k be the minimal size of a non-trivial factor kei of $K{\mathfrak {d}}$. Then there exists a non-trivial cancellative factor semigroup of $S{\mathfrak {d}}$ of size 2k.

Note that we do not know whether the kei $K{\mathfrak {d}}$ of every non-trivial knot diagram ${\mathfrak {d}}$ has a finite non-trivial factor kei, and we do not know whether the semigroup $S{\mathfrak {d}}$ of every non-trivial knot diagram ${\mathfrak {d}}$ has a finite non-trivial cancellative factor semigroup; hence, the more careful wording in Conjecture 3. As to our computational experiments, we still do not know whether the kei of the knot $10_{83}$ has finite factors [5], and only in this paper for the first time we find a finite cancellative factor semigroup of the knot semigroup of the knot $9_{22}$ [10].

3 Main results

The main result of this paper is that we refute all versions of the “double size” conjecture (Conjectures 2, 3, 4) by finding a suitable counterexample. Indeed, we find six knot diagrams with 9 crossings each, all having minimal factor keis of size 15, but having no cancellative factor semigroups of size 30. All these cases were left open in [10].

Namely, consider knot diagrams known as $9_{22}$, $9_{25}$, $9_{30}$, $9_{36}$, $9_{44}$,$9_{45}$ and shown in Fig. 1. The minimal non-trivial factor keis of keis of all these knots have size 15 [5]. However, we prove that their semigroups do not have cancellative factor semigroups of size 30.

Fig. 1

Knot diagrams with nine crossings which are counterexamples to double size conjecture(s)

If these six knot diagrams do not have cancellative factor semigroups of size 30, one can ask about the sizes of finite cancellative factor semigroups that they do have. For each of these diagrams $9_{22}$, $9_{25}$, $9_{30}$, $9_{36}$, $9_{44}$, $9_{45}$ we prove that their $\pi$-orbifold groups have factor groups of size 60; we also prove that this is the minimal size of finite non-trivial factor groups of $\pi$-orbifold groups of $9_{22}$, $9_{25}$, $9_{30}$, $9_{36}$, while minimal sizes for $9_{44}$, $9_{45}$ are 34 and 46, respectively.

Since for any knot diagram ${\mathfrak {d}}$ every finite factor group of $G{\mathfrak {d}}$ is a cancellative factor semigroup of $S{\mathfrak {d}}$, we conclude that for each of the diagrams $9_{22}$, $9_{25}$, $9_{30}$, $9_{35}$, $9_{44}$, $9_{45}$ their semigroups have cancellative factor semigroups of size 60. Furthermore, the semigroups of the diagrams $9_{44}$, $9_{45}$ have cencellative factor semigroups of sizes 34 and 46, respectively.

We do not know whether the corresponding sizes 60, 34, 46 of the cancellative factor semigroups are minimal for the inidcated knots diagrams, but we can conjecture that they are, as we state below.

Conjecture 5

The cancellative factor semigroups of semigroups of knots $9_{22}$, $9_{25}$, $9_{30}$, $9_{36}$ have all minimal size 60, and of knots $9_{44}$, $9_{45}$ have minimal sizes 34 and 46, respectively. More generally, one can conjecture that for any knot diagram ${\mathfrak {d}}$ the minimal factor semigroups of $S{\mathfrak {d}}$ are exactly the minimal factor groups of $G{\mathfrak {d}}$.

It is known that every finite cancellative semigroup is a group. Therefore, all finite cancellative factor semigroups of knot semigroups are groups. One can argue that perhaps there is a finite group which is a cancellative factor group of a knot semigroup of a knot diagram ${\mathfrak {d}}$ which is smaller than every factor group of the $\pi$-orbifold group of ${\mathfrak {d}}$. This is why, one can argue, experiments with cancellative factor semigroups still make sense, in addition to experiments with factor groups. Having said this, in these experiments we have never encountered a finite group which is a cancellative factor group of a knot semigroup of a knot diagram ${\mathfrak {d}}$ which has a smaller size than the smallest factor group of the $\pi$-orbifold group of ${\mathfrak {d}}$, hence, the following conjecture can be stated (and if the following conjecture is true that the previous Conjecture 5 is also true).

Conjecture 6

If a finite group is a cancellative factor group of a knot semigroup of a knot diagram ${\mathfrak {d}}$ then there is a factor group of the $\pi$-orbifold group of ${\mathfrak {d}}$ of the same or smaller size.

We describe how we obtained these results in the next section.

4 Automated reasoning and experimental results

Automated finite model building [3] is the area of automated reasoning concerning with developing efficient algorithms for solving the following task. Given a set of first-order sentences $\Phi$ build a finite model for $\Phi$ if it exists.

We use automated model finding to search for finite factor structures (cancellative semigroups, groups and keis), because these factors are, obviously, finite models for the corresponding first-order theories. To be more specific, let $\langle A \mid R \rangle$ be a presentation of a semigroup S with a finite set of generators A and a finite set of relations R. Then finite cancellative factor semigroups of S are precisely the finite models of a theory consisting of R and $(x *y) *z = x *(y *z)$, $(x *y = x *z) \rightarrow y = z$, $(y *x = z *x) \rightarrow y = z \}$. A similar statement can be formulated for $\pi$-orbifold groups, too.

In our experiments we used Mace4 finite model finder [11] implementing complete search algorithm. If there is a finite model of a specified finite size, then such a model will be found, is there no such model, this fact will be reported.

For each of the knots $9_{22}$, $9_{25}$, $9_{30}$, $9_{36}$, $9_{44}$, $9_{45}$ we built presentations for groups and semigroups according to definitions presented in Sect. 1, based on knot diagams shown in Fig. 1.

To be specific, the presentations of $\pi$-orbifold groups are as shown below, and the presentations of knot semigroups also contain inverted equalities $yx = wz$ for each equality $xy=zw$.

$9_{22}$::

$a_{1}a_{9}=a_{9}a_{2}$, $a_2a_7=a_7a_3$, $a_3a_1=a_1a_4$, $a_4a_2=a_2a_5$, $a_5a_8=a_8a_6$, $a_6a_3=a_3a_7$, $a_7a_5=a_5a_8$, $a_8a_6=a_6a_9$, $a_9a_4=a_4a_1$.

$9_{25}$::

$a_1a_4=a_4a_2$, $a_2a_6=a_6a_3$, $a_3a_1=a_1a_4$, $a_4a_8=a_8a_5$, $a_5a_3=a_3a_6$, $a_6a_9=a_9a_7$, $a_7a_5=a_5a_8$, $a_8a_7=a_7a_9$, $a_9a_2$=$a_2a_1$.

$9_{30}$::

$a_1a_9=a_9a_2$, $a_2a_6=a_6a_3$, $a_3a_1=a_1a_4$, $a_4a_2=a_2a_5$, $a_5a_8=a_8*_6$, $a_6a_3=a_3a_7$, $a_7a_5=a_5a_8$, $a_8a_7=a_7a_9$, $a_9a_4=a_4a_1$.

$9_{36}$::

$a_1a_4=a_4a_2$, $a_2a_7=a_7a_3$, $a_3a_5=a_5a_4$, $a_4a_1=a_1a_5$, $a_5a_8=a_8a_6$, $a_6a_9=a_9a_7$, $a_7a_3=a_3a_8$, $a_8a_6=a_6a_9$, $a_9a_2=a_2a_1$.

$9_{44}$::

$a_1a_4=a_4a2$, $a_2a_5=a_5a_3$, $a_3a_6=a_6a_4$, $a_4a_1=a_1a_5$, $a_5a_8=a_8a_6$, $a_6a_4=a_4a_7$, $a_7a_5=a_5a_8$, $a_8a_7=a_7a_9$, $a_9a_2=a_2a_1$.

$9_{45}$::

$a_1a_9=a_9a_2$, $a_2a_7=a_7a_3$, $a_3a_1=a_1a_4$, $a_4a_2=a_2a_5$, $a_5a_8=a_8a_6$, $a_6a_2=a_2a_7$, $a_7a_5=a_5a_8$, $a_8a_7=a_7a_9$, $a_9a_4=a_4a_1$.

In the first series of experiments for each knot diagram $9_{22}$, $9_{25}$, $9_{30}$, $9_{35}$, $9_{44}$, $9_{45}$, we used Mace4 to search for finite cancellative factor semigroups of size 30, as predicted by double size conjectures. In each case Mace4 has completed exhaustive search and returned result “no models exist”.

In the second series of experiments for each knot diagram $9_{22}$, $9_{25}$, $9_{30}$, $9_{35}$, $9_{44}$, $9_{45}$, we used Mace4 to search for finite factor groups of $\pi$-orbifold groups using default iterative search strategy of Mace4; that is, starting from size 2, it completes exhaustive search of models for a current size, and if a model is not found, the size increases by 1 and search continues. For each of the $9_{22}$, $9_{25}$, $9_{30}$, $9_{35}$ knots, the search is completed by finding the models of minimal size 60, while for $9_{44}$, $9_{45}$ the search yielded the models of minimal sizes 34 and 46, respectively.

We have placed experimental data including inputs and outputs of all reported experiments with Mace4 online; see https://zenodo.org/records/10003636.