Skip to main content
SpringerLink
Log in

Describing semigroups with defining relations of the form \(xy=yz\) and \(yx=zy\) and connections with knot theory

  • Research Article
  • Published:
Semigroup Forum Aims and scope Submit manuscript

Abstract

We introduce a knot semigroup as a cancellative semigroup whose defining relations are produced from crossings on a knot diagram in a way similar to the Wirtinger presentation of the knot group; to be more precise, a knot semigroup as we define it is closely related to such tools of knot theory as the twofold branched cyclic cover space of a knot and the involutory quandle of a knot. We describe knot semigroups of several standard classes of knot diagrams, including torus knots and torus links T(2, n) and twist knots. The description includes a solution of the word problem. To produce this description, we introduce alternating sum semigroups as certain naturally defined factor semigroups of free semigroups over cyclic groups. We formulate several conjectures for future research.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. Note that a knot semigroup is not a knot invariant; that is, there are cases when two different diagrams of the same knot produce non-isomorphic knot semigroups. See more in Sect. 8.

  2. The property of being thin relative to knot semigroups can be reformulated as follows: if two words \(u=au'\) and \(v=bv'\) are equal, where a, b are letters, then there are letters c, d such that \(ac=bd\) and \(u=acu''\) and \(v=bdv''\).

  3. It is known, see, for example, [15], that a presentation of a cancellative semigroup can be considerably more complicated than its cancellative presentation.

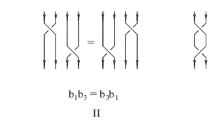
  4. Reidemeister moves are standard ways of transforming a knot diagram to produce other diagrams of the same knot.

  5. Note that the term ‘braid semigroup’ already has a well established meaning, namely, it is the subsemigroup of the braid group generated by clockwise half-twists (see, for example, [2]). To avoid confusion, we do not use the words ‘braid semigroup’ to mean the knot semigroup of a braid.

  6. A meridian is an element of the knot group corresponding to one arc.

References

  1. Diekert, V., Rozenberg, G.: The Book of Traces. World Scientific, Singapore (1995)

    Book  Google Scholar 

  2. Bokut, L.A., Fong, Y., Ke, W.F., Shiao, L.S.: Gröbner-Shirshov bases for the braid semigroup. Adv. Algebra 10, (2003)

  3. Cain, A.J., Gray, R., Malheiro, A.: On finite complete rewriting systems, finite derivation type, and automaticity for homogeneous monoids. submitted

  4. Kudryavtseva, G., Mazorchuk, V.: On three approaches to conjugacy in semigroups. In Semigroup Forum, vol. 78, no. 1 (Springer, Berlin, 2009), pp. 14–20

  5. Araújo, J., Konieczny, J., Malheiro, A.: Conjugation in semigroups. J. Algebra 403, 93–134 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Dehornoy, P.: Thin groups of fractions. Contemp Math 296, 95–128 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  7. Picantin, M.: Garside monoids vs divisibility monoids. Math Struct in Comput Sci 15(02), 231–242 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  8. Lickorish, W.R.: An Introduction to Knot Theory, vol. 175. Springer, Boston (2012)

    MATH  Google Scholar 

  9. Livingston, C.: Knot Theory, vol. 24. Cambridge University Press, Cambridge (1993)

    MATH  Google Scholar 

  10. Burde, G., Heusener, M., Zieschang, H.: Knots. De Gruyter, Berlin (2013)

    Book  MATH  Google Scholar 

  11. Manturov, V.: Knot Theory. CRC Press, Boca Raton (2004)

    Book  MATH  Google Scholar 

  12. Gilbert, N., Porter, T.: Knots and Surfaces. Oxford University Press, Oxford (1994)

    MATH  Google Scholar 

  13. Murasugi, K.: Knot Theory and its Applications. Springer, Boston (2007)

    Google Scholar 

  14. Howie, J., Short, H.: The band-sum problem. J Lond Math Soc 2(3), 571–576 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  15. Spehner, J.: Présentations et présentations simplifiables d’un monoïde simplifiable. Semigroup Forum 14(1), 295–329 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  16. Kawauchi, A.: A Survey of Knot Theory. Birkhäuser, Boston (1996)

    MATH  Google Scholar 

  17. Morgan, J.W., Bass, H.: The Smith Conjecture. Elsevier, Orlando (1984)

    MATH  Google Scholar 

  18. Winker, S.K.: Quandles, knot invariants, and the n-fold branched cover. Ph.D. dissertation, University of Illinois at Chicago (1984)

  19. Fenn, R., Rourke, C.: Racks and links in codimension two. J Knot Theory Ramif 1(04), 343–406 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  20. Joyce, D.: A classifying invariant of knots, the knot quandle. J Pure Appl Algebra 23(1), 37–65 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  21. Harary, F., Kauffman, L.H.: Knots and graphs i – arc graphs and colorings. Adv Appl Math 22(3), 312–337 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  22. Manturov, V., Ilyutko, D.: Virtual Knots: The State of the Art. World Scientific, Hackensack (2012)

    Book  MATH  Google Scholar 

  23. Kauffman, L.H., Lambropoulou, S.: On the classification of rational tangles. Adv Appl Math 33(2), 199–237 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  24. Conway, J.H.: An enumeration of knots and links, and some of their algebraic properties. In: Computational problems in abstract algebra (Proc. Conf., Oxford, 1967), 1970, pp. 329–358

  25. Dynnikov, I.A.: Three-page approach to knot theory. Universal semigroup. Funct Anal Appl 34(1), 24–32 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  26. Auinger, K., Chen, Y., Hu, X., Luo, Y., Volkov, M.: The finite basis problem for Kauffman monoids. Algebra universalis 74(3–4), 333–350 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  27. Kassel, C., Turaev, V.: Braid groups. Springer, Boston (2008)

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, University of Essex, Colchester, UK

    Alexei Vernitski

Authors
  1. Alexei Vernitski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alexei Vernitski.

Additional information

Communicated by Victoria Gould.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vernitski, A. Describing semigroups with defining relations of the form \(xy=yz\) and \(yx=zy\) and connections with knot theory. Semigroup Forum 95, 66–82 (2017). https://doi.org/10.1007/s00233-016-9808-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00233-016-9808-7

Keywords

Search

Navigation