1 Introduction

Cleaning is an omnipresent topic whose importance has increased in recent decades. The food processing industry is a field where cleaning and decontamination is of utmost importance in order to avoid cross-contamination at product changeover or to comply to increasingly strict hygienic standards [1]. Although cleaning induces high economic and ecological costs [2], dimensioning of cleaning processes is often done empirically [3]. Modeling the cleaning process and a systematic variation of cleaning parameters can minimize these costs. Cleaning processes, however, are complex multiphase problems that cannot be simulated in every detail on industrial scale with a reasonable amount of computational effort. A cost-efficient way to model cleaning processes is using a boundary condition cleaning model (BCCM), first introduced by [4]. In a BCCM, the soil behavior is modeled as a boundary condition for a computational fluid dynamics (CFD) problem. The underlying concept is to differentiate between soils according to their cleaning mechanism, which in turn is determined by the specific combination of the factors soil, cleaning fluid and substrate. According to [5], the cleaning process is classified into four mechanisms diffusive dissolution, cohesive separation, adhesive detachment and viscous shifting. These cleaning mechanisms are also confirmed by other authors, e.g. [6, 7] and [8]. In the present work, cohesive separation is considered, which is characterized by the overcome of the cohesive tension inside the soil and the successive removal of the soil layer. In case of small particles (e.g. in the order of single molecules) removed, the particle transport is similar to diffusive dissolution. Over the last decades increasing experimental and numerical research in terms of modeling of cleaning has been conducted. Early work, e.g. from [9] deals with the prediction of a shear driven flow in an oil layer. Fernandes et al. [10] later applied these approaches to predict the cleaning of viscoplastic soils under usage of impinging water jets. Joppa et al. [11] developed a BCCM for the diffusive dissolution of a starch layer and validated it with cleaning experiments in a channel flow and with an impinging jet. This BCCM was based on the modeling approach of [12], developed for the mass transfer of whey protein. Wilson et al. [13] presented a first approach for the prediction of the cleaning of an adhesively detaching soil. This was done by balancing hydrodynamic loads and a soil specific resistance. Köhler et al. [14] later introduced a BCCM for the cleaning of an adhesively detaching soil in a channel flow. The model was recently validated by [15] in a square duct flow with a sudden expansion with locally varying flow properties.

Scope of the present work is to develop a model for a cohesively separating soil on basis of the BCCM of [14]. The model is used to investigate the influence of the local soil mass distribution on the cleaning kinetics. For this purpose, the same starch as in [16] is used as model soil and water as cleaning fluid. Transferability to the industrial case of cleaning with other agents, such as hot sodium hydroxide solutions, e.g., is expected, as long as the cleaning mechanism does not differ. For the development of the model, it is necessary to describe the binding forces of the starch under consideration of its swelling behavior. Therefore, a micromanipulation measurement technique, similar to the technique used by [17] or [18] is utilized.

2 Modeling of cohesive separation

2.1 Overview and modeling as boundary condition

For modeling, the process of cohesive separation is divided into the four subprocesses shown in Fig. 1. In the first step, the loads applied by the flow to the soil are calculated to determine a representative stress \(\tau _\textrm{hyd}\). This is done by evaluating CFD simulation results. Next, the swelling behavior is described to calculate the local water mass fraction \(\omega _\textrm{f}\) in the soil. This is crucial, since the water mass fraction is assumed to be the quantity determining the cohesive binding forces. In the next step, the cohesive binding forces are described as a function of the water mass fraction: \(\tau _\textrm{coh} = f\left( \omega _\textrm{f} \right)\). Finally, a failure criterion is defined, which compares the hydraulic load \(\tau _\textrm{hyd}\) and the cohesive binding stress \(\tau _\textrm{coh}\) to decide, which amount of soil is removed by the flow.

Fig. 1
figure 1

Division of cohesive separation in subprocesses for the modeling (similar to [14])

Full size image

The model is developed as a boundary condition for a CFD simulation. This relies on the following assumptions [14]:

  1. 1.

    Decoupling of flow and cleaning status of the soil. This means that the fluid forces acting on the soil are independent of the swelling or partial removal of the soil.

  2. 2.

    The height of the soil is negligible. Hence, the soil does not constitute an obstacle in the CFD simulation. There are just walls identified as soiled.

  3. 3.

    The swelling of the soil can be described with a one-dimensional diffusion equation with constant boundary conditions.

2.2 Modeling of the swelling kinetics

To model the swelling process a one-dimensional diffusion equation for the water mass fraction is used, since the thickness of the soil is small compared to the other dimensions. It reads

$$\begin{aligned} \frac{\partial \omega _\textrm{f}}{\partial t} = \frac{\partial }{\partial y} \left( D\left( \omega _\textrm{f} \right) \frac{\partial \omega _\textrm{f}}{\partial y} \right) . \end{aligned}$$
(1)

In Eq. (1), y is the wall-normal direction and D the diffusion coefficient. The latter, however, is not constant. In the present study, two different approaches for modeling the swelling behavior are tested. One is the power law approach \(D=D_0 \, \omega _\textrm{f}^a\) as used in [14] is tested. The other is the exponential approach \(D=D_0 \exp ( a \omega _\textrm{f} )\) of [16] to describe the swelling of starch. In both cases, \(D_0\) and a is are parameters to be fixed. The boundary conditions for the swelling process are given as

$$\begin{aligned} \frac{\partial \omega _\textrm{f}}{\partial y} \bigg |_{y\mathop{=}0} = 0 \text { and } \omega _\textrm{f}(y = h_\textrm{s}) = \omega _\textrm{max}, \end{aligned}$$
(2)

where \(y=0\) corresponds to the wall, with the zero gradient condition representing a non-penetrable substrate. At the top, \(y=h_\textrm{s}\), the maximum water mass fraction \(\omega _\textrm{max}\) is imposed, which needs to be estimated experimentally. Due to the swelling, the height of the soil layer \(h_\textrm{s}\) is time dependent. The initial state refers to a dried soil with a constant initial water mass fraction \(\omega _0\). The soil layer is discretized by means of a finite volume method, using central differences for the spatial, and an Euler forward scheme for the temporal discretization as described in [19]. When the water diffuses into the soil, the height of the soil layer increases, thus modifying the diffusion process itself. This effect is taken into account by stretching the numerical grid. A detailed explanation of this technique is given in [14]. The numerical grid is illustrated in Fig. 2. The notation \(\omega _{\textrm{f}, i}^n\) refers to the water mass fraction at \(t = t^n\) and \(y = y_i\).

Fig. 2
figure 2

Sketch of the numerical discretization and the binding stresses in the model of the swelling process

Full size image

2.3 Removal criterion and load calculation

Cohesive separation of a part of the soil layer occurs, once the hydrodynamic load overcomes the cohesive strength at some point within the soil. In the present finite volume framework the water mass fraction is known at the cell centers. Removal is discretized by introducing breakage at cell boundaries. To decide whether a cell is removed or not, the cohesive strength must be described at the cell-to-cell interfaces. To this end, the water mass fraction is interpolated linearly and the cohesive strength is computed using

$$\begin{aligned} \tau _{\mathrm{coh},\, i\mathop{-}1/2}^n = f(\omega _{\mathrm{f},\,i\mathop{-}1/2}^n) . \end{aligned}$$
(3)

The function f links the water mass fraction to the cohesive strength and needs to be determined experimentally. The location of the quantities is depicted in Fig. 2. Once the binding forces over the soil layer are described properly, the modeling approach inherently provides the opportunity to describe the change between the mechanisms cohesive separation and adhesive detachment, since the removal of the wall-adjacent cell amounts to adhesive detachment and thus \(\tau _{\mathrm{coh},\, 1/2} = \tau _{\textrm{ad}}\). Note that the water mass fraction at the soil-substrate interface can be determined evaluating the boundary condition (Eq. (2) at \(y=0\). With present approach the gradual removal of soil mass over time is described and the soil mass coverage at \(t^n\) determined by

$$\begin{aligned} m^{\prime \prime \, n}_\textrm{s} = \sum _{i\mathop{=}1}^{N^n} m''_{\mathrm{s},\,i} \end{aligned}$$
(4)

The mass of soil in each cell i is denoted by \(m''_{\mathrm{s},\,i}\). These masses refer to the dry soil mass within each cell and are not time dependent until removal since this is one of the core assumptions of the swelling model [14]. All results shown within this paper are with respect to the mass of the soil itself, i.e. the dry state. The last value \(N^n\) of the summation in Eq. (4) refers to the number of cells at the time \(t^n\) and is determined using the removal criterion

$$\begin{aligned} N^n= {\left\{ \begin{array}{ll} N^{n\mathop{-}1}, &{} \text {if } \min \limits _{i}\left( \tau _{\textrm{coh},\, i\mathop{-}1/2}^n\right) \ge C \tau _\textrm{hyd} \\ \min \limits _{i}\left( \left\{ i-1 |\tau _{\textrm{coh},\, i\mathop{-}1/2}^n < C \tau _\textrm{hyd} \right\} \right) , \, &{} \text {else.} \end{array}\right. } \end{aligned}$$
(5)

The first condition of Eq. (5) refers to the case that no cells are removed. In this case, the number of cells remains the same as in the previous time step. If at least one cell is removed, the number of cells \(N^n\) is changed to the index of the wall-closest cell removed minus one. Once a cell is removed, it is considered to be flooded with water, i.e., it contains the maximum water mass fraction afterwards. This moves down the upper boundary condition.

The hydrodynamic load \(\tau _\textrm{hyd}\) is determined by means of CFD. Within this paper, only wall shear stress is taken into account, i.e.

$$\begin{aligned} \tau _\textrm{hyd} = \frac{1}{A_\textrm{p}} \int _{A_\textrm{p}} \underline{\underline{\tau }} \cdot \underline{n} \textrm{d}A \end{aligned}$$
(6)

In Eq. (6) the magnitude of wall shear stress is averaged across the surface \(A_\textrm{p}\). The integral is evaluated numerically using midpoint rule.

Equation (5) also includes a correction factor C. This is necessary to account for the differences in load application between the micromanipulation experiment and the fluid flow and was first introduced by [14]. It is a suitable means to account for the complex dependence of measured binding forces on the way the load is applied, which was noticed, e.g., in earlier work of [20].

2.4 Flow simulation and computational algorithm

All fluid flow simulations were carried out using the OpenFOAM CFD library, running the pimpleFoam solver. The governing equations for the problem are the incompressible Navier–Stokes-Equations. For the turbulence modeling, a Reynolds averaged Navier Stokes (RANS) -framework is used. More precisely, a k-\(\omega\)-SST turbulence model with a low Reynolds number adaption by [21] is utilized. The setup is a two-dimensional channel flow with a height of \(5 \, {mm}\) and a given mean bulk velocity \(u_\textrm{b}\) between 0.5 and \(3.0 \, {m/s}\), which is described in detail in [4]. Note that in the cleaning experiments, described in Section 3.4, a duct with rectangular cross section (\({78\,\textrm{mm}} \times {5\,\textrm{mm}}\)) is used. However, three dimensional effects are only present in regions close to the walls neglected in the simulation. Since those regions are omitted in during the evaluation of the experiments, the simulations can be performed two-dimensional. The resulting Reynolds numbers \(Re = u_\textrm{b} d_\textrm{h}/\nu\) range from 5, 000 to 30, 000. Once the CFD simulation is carried out, the averaged flow field is used to conduct the cleaning simulation. Within the cleaning simulation, the flow field remains unchanged. The soil behaviour is implemented as a boundary condition. The following steps are computed in each time step:

  1. 1.

    Update the water mass fraction \(\omega _{\mathrm{f},\,i}^{n\mathop{+}1}\) in the soil layer using Eqs. (1) and (2).

  2. 2.

    Stretching of the numerical grid to account for the swelling of the soil layer.

  3. 3.

    Interpolation of the water mass fraction to the cell-to-cell interfaces and calculation of the cohesive strength using Eq.(3).

  4. 4.

    Evaluation of the removal criterion (Eq. (5)) to determine which cells are removed.

  5. 5.

    Compute the soil mass coverage after removal using Eq. (4).

2.5 Modeling locally varying soil distribution

In the simulation, only a single value for the initial soil mass coverage can be given. In reality, however, the soil mass coverage is non-uniform. Here, it is assumed to be randomly distributed according to a normal distribution with a mean value \(\mu\) and a standard deviation \(\sigma\), i.e. with a density function of

$$\begin{aligned} \varphi (z) = \frac{1}{\sqrt{2\pi \sigma ^2}} \exp \left( - \frac{(z - \mu )^2}{2 \sigma ^2} \right) . \end{aligned}$$
(7)

The parameters \(\mu\) and \(\sigma\) are determined by evaluating the experiments. To investigate the effect of the variable soil distribution within the model, the simulation is run with different initial soil mass coverages in the range: \(S = \left[ \mu - 3\sigma , \mu + 3 \sigma \right]\). This ensures, that \(99.73 \%\) of all possible outcomes are considered. It turns out, that an increment of \(1 \, \mathrm {g/m^2}\) for the simulation of the range described by S provides a sufficient resolution. After obtaining \(m''_\textrm{s} (t; \, m''_\mathrm{s,\,0} )\) for different initial soil mass coverages \(m''_\mathrm{s,\,0}\), the weighted average with respect to the normal distribution is computed as

$$\begin{aligned} \langle m''_{\textrm{s}} \rangle (t) =\sum _{m''_\textrm{s, 0} \in S} \varphi (m''_\textrm{s, 0}) \cdot m''_\textrm{s} (t; \, m''_\textrm{s, 0}). \end{aligned}$$
(8)

3 Materials and methods

3.1 Soiling procedure and water mass fraction

For parametrization and validation of the cleaning model, precleaned stainless steel coupons (AISI 304, cold-rolled 2B finish) were soiled exactly as described in previous work [4, 5, 11, 16]. Starch (pre-gelatinized waxy maize starch, C Gel - Instant 12410, Cargill Deutschland GmbH, \(150 \, \mathrm{g/l}\)) was mixed with fluorescent zinc sulphide tracer crystals (\(4 \, \mathrm{g/l}\)) in deionized water (30 °C) under stirring. The solution was sprayed on the test sheets and subsequently dried in a climate chamber (temperature of 23 °C , relative humidity of \(50 \%\)) for about \(20 \, {h}\). The resulting surface soil mass coverage \(m''_\textrm{s,0}\) was determined by differential weighing. The initial water mass fraction \(\omega _0\) of the dried samples was determined by measuring the dry matter using the gravimetric method. Three samples were dried at 103 °C for several hours until mass constancy was achieved. By assuming that water is the only fraction that evaporates, the initial water mass fraction was calculated to be \(\omega _0=0.138 \pm 0.013\).

3.2 Unsteady soil layer thickness measurements

Measurements of the unsteady soil layer growth due to swelling were performed similar to [14]. Soiled test samples with different values of \(m''_\mathrm{s,\, 0}\) were immersed in water at 23 °C. The samples were placed horizontally in a transparent basin. With the aid of a camera whose optical axis was aligned parallel to and within the substrate surface, a diffuse light source from behind, and a threshold-based image analysis procedure, the change in soil layer thickness was measured.

3.3 Micromanipulation measurements

The determination of the binding forces was conducted with a micromanipulation device as described in [14]. A soiled sample was immersed in water at 23 °C for a predefined soaking time of \(t_\textrm{soak} = 45 \, \textrm{s}\). Subsequently, the sample was lifted out of the bath and a scraper blade pulled off parts of the soil layer at a predefined gap \(\delta _\textrm{gap}\) which was adjusted between the substrate surface and the bottom tip of the scraper blade. During this process, the force was measured with a sensor (KD40s 2N, ME-Meßsysteme GmbH) directly coupled to the blade. The magnitude of the average force \(\overline{F}\) was obtained for the situation where the scraper blade is between the beginning and the end of the sample.

3.4 Cleaning experiments and evaluation procedure

Test samples with \(m''_\textrm{s, 0}\) in the range of \(30 \, {\mathrm{g}/\mathrm{m}^2}\) to \(80 \, {\mathrm{g}/\mathrm{m}^2}\) were cleaned in a test rig with a fully developed turbulent flow of deionized water at \((25 \pm 1)\) °C flowing through a duct with rectangular cross section (cross section: \(78 \, \mathrm{mm} \times 5 \, \mathrm{mm}\)) at a given mean bulk velocity \(u_\textrm{b} = (0.5, \, 1.0, \, 2.0, \,3.0 ) \, \mathrm{m/s}\). The test rig is described and depicted in [4]. A total of 41 valid experiments were conducted. One side of the duct was soiled and the opposite side transparent to measure the local cleaning progress with a gray scale camera in terms of the local intensity \(I_\textrm{raw}\). An exemplary image sequence and the data evaluation procedure are presented in [5]. The evaluation modification as described in [14] was applied here as well: a centered square area of \(40 \, \mathrm{mm} \times 40 \, \mathrm{mm}\) was subdivided into \(1 \, \mathrm{mm} \times 1 \, \mathrm{mm}\) large subareas, in which an average was taken over about 36 pixels. The initial local grey value \(I_\textrm{raw, 0}\) and a previously determined calibration [5] were used to calculate the local initial soil mass. Subsequently, an increase in the grey value was observed which resulting from the swelling of the starch. This can be corrected by using a swelling correction, employed in [11]. With that, the local cleaning time \(t_\textrm{c, 90}\), where \(10 \%\) of the initial soil mass remains, was determined. Finally, the mean \(90 \%\) cleaning time \(\overline{\overline{t}}_\textrm{c, 90}\) and its standard deviation were finally calculated over all subareas.

4 Results

4.1 Model parametrization

4.1.1 Swelling kinetics and binding forces

Figure 3 shows the measured soil layer thickness \(h_\textrm{s}\) over time (symbols). For all investigated soil mass coverages the pattern is similar: A steep increase of \(h_\textrm{s}\), at the beginning is followed by an asymptotic approach to a saturation value. The investigated height ratio is \(r_h=h_\textrm{max}/h_0 =10.72 \pm 0.46\), where \(h_0\) is the initial and \(h_\textrm{max}\) the final value of \(h_\textrm{s}\). The qualitative swelling behavior is similar to dried ketchup, observed by [14], although the height ratio is found to be three times lager here. Assuming that the amount of starch in the soil remains unchanged, the maximum water mass fraction was determined according to [14] to be \(\omega _\textrm{max} = 0.91\) in the present case.

The thickness measurements were used to estimate the diffusion parameters \(D_0\) and a in Eq. (1). This was done by a systematic variation of the parameters and evaluation of the root-mean-square-error (RSME). The best results were obtained for an exponential diffusion coefficient \(D(\omega _\textrm{f} )=D_0 \exp (a \omega _\textrm{f} )\) with the parameters \(D_0 = 0.5 \cdot 10^{-9} \, \mathrm{m^2/s}\) and \(a=2.06\). The numerical results with this model are shown in Fig. 3, labeled model best fit. Note that a second model is shown in the diagram, which will be motivated in the next paragraph.

To determine the binding forces, measurements with varying \(\delta _\textrm{gap}\) were conducted, using two different initial soil mass coverages, 50 and \(70 \, {g/m^2}\). The results are shown in Fig. 4, where the forces, normalized with the sample width \(B= {20\,\textrm{mm}}\), are plotted over the penetration height \(h_\textrm{pen}\). The penetration height is the vertical distance over which the cutting device intrudes into the soil. It cannot be not given a priori but was estimated using the swelling experiments (Fig. 3) by interpolating the value of the soil layer thickness \(h_\textrm{s}\) for the given wetting time, i.e. evaluating

$$\begin{aligned} h_\textrm{pen} = h_\textrm{s}\left( m''_{\textrm{s, 0}}, t_\textrm{soak} \right) - \delta _\textrm{gap} \end{aligned}$$
(9)
Fig. 3
figure 3

Swelling kinetics measured for different initial soil mass coverages compared to the results of the numerical model

Full size image

Figure 4 shows that the pull-off force increase exponentially with penetration height. Second, the forces measured do not depend on the initial soil mass coverages. This indicates that a waterfront is propagating through the soil layer and after \({45\,\textrm{s}}\), the waterfront has not reached the substrate so that the measured forces are independent of the initial thickness of the soil layer.

In the consecutive step, the measured pull-off forces were used to describe the cohesive binding forces. However, the measured pull-off forces are composed of the force necessary to deform the layer in front of the blade, the force required to move up the material, and the actual cohesive binding forces [3]. Since there is no valid approach in the literature to separate these shares, the measured force is assumed to be the cohesive binding force, accepting that this leads to a systematic difference. It is assumed here that the correction factor in Eq. (5) can also be used to compensate this effect. Finally, the forces are normalized with the area of the sample to obtain a comparative strength \(\tau _\textrm{coh}\) also shown in Fig. 4.

Fig. 4
figure 4

Measured averaged pull-off forces \(\overline{F}\), normalized with the sample width B (left axis) and the sample area \(B \cdot L\) (right axis). The dashed line corresponds to the exponential fit \(\overline{F}/B = 0.0096 \exp ( 0.0321 h_\textrm{pen} )\) with \(R^2 = 0.96\). Each datum is measured with \(N = 5\) repetitions

Full size image

In Fig. 5, the cohesive strength \(\tau _\textrm{coh}\) is plotted against the water mass fraction at the tip of the scraper blade, \(\omega _\textrm{f} \left( t=t_\textrm{wet}, y = \delta _\textrm{gap} \right)\), which was determined using the best fit swelling model. It can be seen, that this procedure results in two different exponential functions \(\tau _\textrm{coh} = f_{m''_{\textrm{s},\, 0}} ( \omega _\textrm{f})\), depending on the initial soil mass coverage. This is contrary to the observations made in Fig. 4. A possible explanation could be that the swelling model best fit provides a reasonable prediction of the total water mass fraction within the entire soil layer, which is proven by the accordance with the measured soil layer thicknesses (Fig. 3). The model, however, fails to describe the water mass distribution across the soil properly. The literature also states that the diffusion behavior of some polymers cannot be described sufficiently by using Fick’s law with constant boundary conditions, especially when extensive swelling of the polymers is caused [22]. The wetting of the polymer causes structural changes which can lead to internal stresses which in turn generating a in non-Fickian diffusion processes [23].

Fig. 5
figure 5

Cohesive strength related to the water mass fraction using the model best fit. Each datum is measured with \(N = 5\) repetitions. The exponential fits correspond to \(\tau _\textrm{coh} = 181 \, \textrm{kPa} \, \exp (-11.31 \omega _\textrm{f})\) (\(R^2 = 0.991\)) for \(m''_{\textrm{s},\,0} = {70\,\mathrm{g/cm^2}}\) and \(\tau _\textrm{coh} = 50 \, \textrm{GPa} \, \exp (-28.45 \omega _\textrm{f})\) (\(R^2 = 0.988\)) for \(m''_{\textrm{s},\,0} = {50\,\mathrm{g/cm^2}}\)  

Full size image

One approach to overcome this issue is to use extreme values for the diffusion model parameters \(D_0\) and a to obtain the behavior of a waterfront propagating through the soil layer. Using a power-law approach \(D \left( \omega _\textrm{f} \right) = D_0 \omega _\textrm{f}^a\) with the parameters \(D_0 = 0.75 \cdot 10^{-9} \, {m^2/s}\) and \(a=10\) leads to a swelling model with the described properties. This model is labeled model waterfront here. Figure 6 shows the difference between both models regarding the qualitative distribution of the water mass fraction over the penetration height.

Fig. 6
figure 6

Qualitative comparison between the model best fit and the model waterfront regarding the water mass distribution across the soil layer height

Full size image

Using the model waterfront the cohesive strength can be related to the water mass fraction, independent of the initial soil mass coverage. This is shown in Fig. 7. The predicted swelling kinetics can also be compared to the soil thickness measurements (Fig. 3). The comparison, however, does not show a good agreement with the experiments. This indicates again that a more complex diffusion model, including, e.g., non-Fickian diffusion, would be necessary to fully capture the swelling behavior of the starch.

Fig. 7
figure 7

Cohesive strength related to the water mass fraction using the model waterfront. Each datum is measured with \(N = 5\) repetitions. The linear fit corresponds to \(\tau _\textrm{coh} = -1.21 \, \textrm{kPa} \, \, \omega _\textrm{f} + 1.13 \, \textrm{kPa}\) (\(R^2 = 0.961\))

Full size image

In the remainder of the paper both models are further evaluated in terms of applicability in cleaning simulations. For the model best fit the function \(\tau _\textrm{coh} = f(\omega _\textrm{f} )\) is determined for \(m''_{\textrm{s},\,0} = {50\,\mathrm{g/m^2}}\), since this is close to the majority of the investigated soil mass coverages in the cleaning experiments.

4.1.2 Estimating the correction factor

To determine the correction factor which completes the model, simulations accounting for non-uniform soil mass coverage were conducted and the results were adjusted to match the experimental data in terms of the \(90 \%\) cleaning time \(\overline{\overline{t}}_{ \textrm{c},\, 90 }\).

It was found that the correction factor is not independent from the flow velocity. It can be expressed in terms of the Reynolds number of the flow as

$$\begin{aligned} C = C_0 Re^{-0.88}. \end{aligned}$$
(10)

In a plane turbulent channel flow, quantities often show a dependency on the Reynolds number to the power of 0.88. For instance, the friction factor \(C_f\) can be expressed the same way [24]. The factor \(C_0\) in Eq. (10), finally, is estimated using a single cleaning experiment with a bulk velocity of \(u_ \textrm{b} = {1\,\mathrm{m/s}}\) and an initial soil mass coverage of \(m''_{\textrm{s},\,0} = ( 50 \pm 5) \, \mathrm{g/m^2}\). The values found are \(C_0=356.64\) for the model best fit and \(C_0=31974\) for the model waterfront.

4.2 Influence of the soil mass distribution

The cleaning experiments were evaluated with respect to the distribution of the initial soil mass coverage \(m''_{\textrm{s}, 0}\). Figure 8 a sample. Significant bright spots are attributed to tracer agglomerates.

Fig. 8
figure 8

Distribution of the initial soil mass coverage of a sample

Full size image

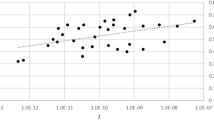
In the next step, the initial soil mass coverage of all the experiments was evaluated regarding the mean value \(\mu\) and the standard deviation \(\sigma\). The result is shown in Fig. 9.

Fig. 9
figure 9

Standard deviation \(\sigma\) of the initial soil mass distribution \(m''_{\textrm{s},0}\) over the mean value \(\mu\) in the cleaning experiments

Full size image

The evaluation shows no dependency of \(\sigma\) on \(\mu\). However, for mean values greater than \({60\,\mathrm{g/m^2}}\), larger standard deviations are observed in some cases. These are discarded here. Figure 9 shows that a value of \(\sigma = {5\,\mathrm{g/m^2}}\) provides a reasonable upper bound for the standard deviation. This value was utilized as standard deviation in all simulations as an realistic value. Tests conducted with \(\sigma = {7\,\mathrm{g/m^2}}\) showed only minor changes, thus backing the choice made here.

Using the information about the initial soil mass distribution obtained, the simulations were conducted and the influence of the distribution on the course of soil mass coverage over time evaluated. Figure 10 shows the dry soil mass coverage \(m''_{\textrm{s}}\) over time for the simulations with and without consideration of the distribution. A mean value of \({50\,\mathrm{g/m^2}}\) is investigated at a bulk velocity of \(u_\textrm{b} = {1\,\mathrm{m/s}}\). An experimental result is also shown for comparison. Note that the initial soil mass coverage of the experiment is slightly larger than in the simulation.

In the experiment, the cleaning starts after roughly \({40\,\textrm{s}}\) with a constant removal rate. Below \({10\,\mathrm{g/m^2}}\) the removal rate decays. In the simulation the start of the cleaning is not predicted correctly both with consideration of the soil mass distribution and without. Although both models detect a removal of the first layer after \({30\,\textrm{s}}\) (model waterfront) and \({70\,\textrm{s}}\) (model best fit). The cleaning appears to be slower than observed in the experiment until \(t \approx {200\,\textrm{s}}\). At this point, the consideration of the soil mass distribution becomes important: while in the simulation without considering the standard deviation the cleaning rate increases until total cleaning is observed, the cleaning rate remains constant in the simulations with consideration of the standard deviation. Below \({10\,\mathrm{g/m^2}}\) the removal rate decays as it was noticed in the experiments. Thus, the qualitative behavior of the simulations with consideration of the soil mass coverage distribution matches the experiments, although the cleaning at the beginning is predicted to slow and the removal rate in the middle of the process is overestimated. Both the model best fit and the model waterfront show a similar performance on the investigated case.

Note that the removal of the last remaining soil layer on the substrate only can be simulated properly when the information regarding the adhesion at the soil-substrate-interface is given. This is not investigated within this work.

Fig. 10
figure 10

Evolution of soil mass coverage over time for \(u_\textrm{b} = {1\,\mathrm{m/s}}\) and \(m''_{\textrm{s},\,0} \approx {50\,\mathrm{g/m^2}}\) comparing simulation data and experiments. The simulations were conducted with both diffusion models, best fit and waterfront. Both were used assuming constant soil coverage (solid lines) and spatial variation of soil mass (corresponding dashed lines)

Full size image

4.3 Variation of soil mass coverage and bulk velocity

4.3.1 Evaluation of 90% cleaning time

The influence of the soil mass coverage and the bulk velocity on the \(90 \%\) cleaning time is displayed in Fig. 11. Simulations were carried out at bulk velocities of \(u_\textrm{b}= (0.5, \, 1.0, \, 2.0, \, 3.0) \, \mathrm {m/s}\) with initial soil mass coverages of \(m''_ {\textrm{s},\,0} = (30, \, 50, \, 70) \, \mathrm {g/m^2}\) using both models. For the standard deviation of the initial soil mass coverage a value of \({5\,\mathrm{g/m^2}}\) was used.

In the experiments the cleaning time increases with the initial soil mass coverage. From the experiments at \({1.0\,\mathrm{m/s}}\) and \({2.0\,\mathrm{m/s}}\) the conclusion can be drawn, that the \(90 \%\) cleaning time increases about linearly with the initial soil mass coverage. However, this is uncertain due to scattering of the experiments. The decrease of the \(90 \%\) cleaning time appears to be approximately linearly with increasing bulk velocity for a soil mass coverage of \({40\,\mathrm{g/m^2}}\).

The simulations also yield a linear dependency of the \(90\%\) cleaning time on the initial soil mass coverages. For almost all cases shown, the predicted values are within the scatter of the experiments. However, for \(u_\textrm{b}= {3.0\,\mathrm{m/s}}\) the simulations underestimate the cleaning time. A reason for the difference could be that in the experiments the pump took roughly \({40\,\textrm{s}}\) to reach the target flow velocity. The simulation, on the other hand, assumes a developed flow right from the start. The simulated \(90 \%\) cleaning times increase slightly faster than linear with the bulk velocity. Both diffusion models provide similar results.

Fig. 11
figure 11

Experimental data (symbols) and simulation results (lines) for the \(90 \%\) cleaning time, with variation of bulk velocity and soil mass coverage. Error bars indicate standard deviations within each cleaning experiment

Full size image

4.3.2 Influence of soil mass coverage on cleaning rate

Three different initial soil mass coverages were further investigated regarding the cleaning rate, keeping the bulk velocity constant at \(u_\textrm{b}= {1.0\,\mathrm{m/s}}\). The results are shown in Fig. 12. For technical reasons the initial soil mass coverage in the experiment differed slightly from the ones in the simulation.

In the experiments, the cleaning rate is nearly independent of the initial soil mass coverage. This underlines the hypothesis that the cleaning time increases linearly with the initial soil mass coverage. The modeled cleaning rates are also nearly independent of the soil mass coverage. The predicted cleaning rates, however, are significantly larger than in the experiments. The beginning of the cleaning, on the other hand, is predicted too late, so that these effects compensate, and the predicted \(90 \%\) cleaning times exhibit a decent agreement. The experiments also show that the start of the removal is delayed with increasing cleaning time. This effect is also represented in the simulations, although it is overestimated. Both diffusion models perform in a similar way. The model waterfront, however, shows slightly better agreement with the experiments.

Fig. 12
figure 12

Evolution of cleaning rate over time for different initial soil mass coverages \(m''_{\textrm{s},\, 0}\) at a bulk velocity of \(u_\textrm{b} = {1.0\,\mathrm{m/s}}\). Symbols represent experimental data, lines correspond to simulations

Full size image
Fig. 13
figure 13

Evolution of cleaning rate over time for different bulk velocities \(u_\textrm{b}\) with an initial soil mass coverage of \(m''_{\textrm{s},\,0} = {40\,\mathrm{g/m^2}}\). Symbols represent experimental data, lines correspond to simulations

Full size image

4.3.3 Influence of bulk velocity on cleaning rate

Bulk velocities of \(u_\textrm{b} = (0.5, \, 1.0, \, 2.0) \, \mathrm {m/s}\) were used with an initial soil mass coverage of \(m''_{\textrm{s},0} = {40\,\mathrm{g/m^2}}\). The results are shown in Fig. 13. In the experiment, the observed cleaning rates increases approximately linearly with increasing bulk velocity. An increase of the cleaning rate with the bulk velocity is also observed in the simulations, although it is not linear. Furthermore, the simulations show the same discrepancies with the experiments as discussed in the previous section. For the two smaller velocities the difference is substantial, while for \({2.0\,\mathrm{m/s}}\) the simulation shows good agreement with the experiment. Hence, there is still room for improvement.

5 Conclusion

In this paper, a BCCM for a cohesively separating soil layer was presented. The model was parameterized using bench scale experiments. Extensive investigations on the modeling of the cohesive binding forces and the influence of the soil mass distribution were presented. The model results were compared with experimental data. The results of the investigation of the cohesive binding forces show, that a swelling model only considering Fickian diffusion is not sufficient to describe the swelling of starch. A workaround was created to represent some important swelling characteristics of starch. Furthermore, a methodology was developed that allows to account for statistical fluctuations of the soil mass coverage yielding significantly better agreement between simulations and experiments. The presented model mainly shows a good qualitative agreement with the experiments. Although the values predicted for the 90 In the future, the implementation of non-Fickian diffusion should be considered. Also, further investigation of the cohesive binding forces could be promising to separate the single load components. The presented model covers adhesive detachment as a limiting case by construction, so that the representation of a transition between these two cleaning mechanisms becomes feasible. If sufficient information about the binding forces is provided, the model has the potential to get close to the simulation of real industrial cleaning processes that involve changes in cleaning fluid and temperature.