1 Introduction

Fouling describes unwanted deposits on heat transfer surfaces and is a severe issue in the chemical and processing industries. Therefore, fouling has been a subject of scientific investigations for decades [1]. One of the most prevalent deposition mechanisms is crystallization fouling. The literature provides many examples of investigations and modeling of the time-dependent integral behavior of crystallization fouling from various scientific aspects [2,3,4,5,6,7,8,9], but only a few papers have been published on local investigations of crystallization fouling [10,11,12,13,14].

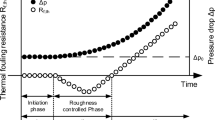
In accordance with Schoenitz et al. [15], the progress of crystallization fouling typically comprises three consecutive phases: An initiation phase is followed by a roughness controlled phase and then a layer growth phase. The first two phases make up the induction phase. Figure 1 schematically presents the progress of crystallization on a heat transfer surface. First, crystals are formed on the surface during initiation phase, but this initially has no noticeable influence on the heat transfer (phase I). Phase IIa is part of the roughness controlled phase. Increasing crystal size and surface coverage intensifies the surface roughness and leads to an enhanced heat transfer, thereby resulting in a negative thermal fouling resistance that ultimately reaches a maximum. This roughness effect is assumed to remain constant from that point on [11]. Subsequently, single crystals cross-link and the first fouling layers build up in clusters in direct contact with the heat transfer wall (Phase IIb). Phase IIb is also a part of the roughness controlled phase and can be defined as a transition zone. The additional thermal resistance starts to override the heat transfer enhancement caused by roughness until the thermal fouling resistance becomes zero. Subsequently, phase IIb extends into the phase of actual layer growth.

Fig. 1
figure 1

Consecutive phases of crystallization on a heat transfer surface; I: Inition phase with first crystals, IIa: Increasing crystal size and surface coverage, IIb: First fouling layers in clusters, III: Fouling layer covers the entire heat transfer surface

Full size image

Expansion causes the clusters to connect to each other and to form a dense bottom layer, which covers the entire heat transfer surface in phase III. Consequently, the fouling resistance becomes positive, due to increasing thermal resistance. In addition, the bottom layer grows with time and increasingly constricts the flow cross-section. When the flow rate is constant, the flow velocity increases due to constriction. Hence, the heat transfer impeding effect of the growing fouling layer is superimposed onto the simultaneous enhancement of the heat transfer due to fluid acceleration [11].

Conversely, the roughness and constriction increase the pressure drop already apparent in the induction phase [15]. Therefore, the fouling resistance must be differentiated into a thermal and a mass based expression. Kern and Seaton, in the 1950s, introduced a fundamental approach for modeling the integral fouling process [16], and this approach served as the basis for most fouling models developed subsequently [1]. The inlet and outlet temperatures of a heat exchanger quantify the change in the overall heat transfer resistance in the soiled \(\left(\frac{1}{{k}_{f}}\right)\) and clean \(\left(\frac{1}{{k}_{0}}\right)\) state and determine the integral thermal fouling resistance \({R}_{f,th}\) according to Eq. (1).

$${R}_{f,th}(t)=\frac{1}{{k}_{f}(t)}-\frac{1}{{k}_{0}}$$
(1)

 The increasing pressure drop of a heat exchanger indicates the integral mass based fouling resistance \({R}_{f,mass}\), which is described as a function of the deposited solid mass per unit area \({m}_{f}\) as well as the density and thermal conductivity of the fouling layer (Eq. 2 and 3)

$${m}_{f}={\rho }_{f}{x}_{f}$$
(2)
$$R_{f,mass}(t)=\frac{x_f(t)}{\lambda_f(t)}=\frac{m_f(t)}{\rho{}_f(t)\lambda_f(t)}$$
(3)

Albert et al. [11] eliminated the apparent negative fouling values by recalculating the integral thermal fouling resistances, taking into account the heat transfer enhancing roughness and constriction effects, as follows:

$${R}_{f,corr}\left(t\right)=\frac{1}{{k}_{f}\left(t\right)}-\frac{A}{{\alpha }_{i,0}{\left({\varepsilon }_{Nu,\xi }{\varepsilon }_{Nu,\omega }\right)}_{t}{A}_{i}}-\left(\frac{{x}_{w}A}{{\lambda }_{w}{A}_{m}}+\frac{A}{{\alpha }_{o}{A}_{o}}\right)$$
(4)

The effect of increasing surface roughness on heat transfer is considered by extending the common integral fouling description with the correction factor \({\varepsilon }_{Nu,\xi }\). This defines the ratio of heat transfer due to friction of the rough surface \({Nu}_{\xi }\) and the heat transfer due to friction of the smooth surface \({Nu}_{0}\), see Eq. (5). For this purpose, Albert et al. [11] applied various heat transfer correlations that accounted for the surface roughness effects developed by Nunner [17], Burck [18], Hughmark [19], and Ceylan and Kelbaliyev [20].

$${\varepsilon }_{Nu,\xi }=\frac{{Nu}_{\xi }}{{Nu}_{0}}$$
(5)

In addition, the constriction effect on heat transfer is considered by \({\varepsilon }_{Nu,\omega }\) which describes the ratio of the Nusselt numbers with and without constriction due to fouling. The increase in Nusselt number due to acceleration effects can be determined with the well-known correlation of Gnielinski [21] for turbulent pipe flow, see Eq. (7).

$${\varepsilon }_{Nu,\omega }=\frac{{Nu}_{\omega }}{{Nu}_{0}}$$
(6)
$${Nu}_{\omega }=\frac{\left({\xi}/ {8}\right)RePr}{1+12.7\sqrt{{\xi}/{8}}\left({Pr}^{^{2}/_{3}}-1\right)}\left[1+{\left(\frac{{d}_{i,f}(z)}{z}\right)}^{^{2}/_{3}}\right]$$
(7)

The recalculated fouling curves were obtained using Eq. (4) and applying the approaches of Burck [18] and Ceylan and Kelbaliyev [20]. This started with a physically unacceptable offset and showed unrealistically high fouling resistances [11]. More realistic results can be obtained using the empirical correlations of Nunner [17], Eq. (8), and Hughmark [19], Eq. (9).

$$\frac{{Nu}_{\xi }}{{Nu}_{0}}={\left(\frac{{\xi }_{f}}{{\xi }_{0}}\right)}^{^{1}/_{\left({Pr}/ {2}+1.5\right)}}$$
(8)
$$Nu=\sqrt{\frac{\xi }{8}}Re{\left[\begin{array}{c}\frac{1}{0.0303+0.0615{Pr}^{^{{1}/{2}}}}+\\ \frac{1}{0.625+0.062 {Pr}^{^{{1}/{3}}}}+\frac{1}{\frac{7.16}{\sqrt{\frac{\xi }{8}}Re}++2\sqrt{\frac{\xi }{8}}Pr}\end{array}\right]}^{-1}$$
(9)

The studies by Albert [10] and Goedecke et al. [13] showed local differences for the thermal fouling resistance along the inner tube of a counterflow double-pipe heat exchanger with a length of 2 m. Both studies reported that the integral assessment of the fouling process is not suitable for detection of local processes, for identification of the subsequent sub-processes and their interactions, and for explaining the underlying mechanisms. Therefore, both local and time-resolved acquisition, analysis, and modeling are essential for a deeper insight into the fouling process. Subsequently, various experimental investigations by Schlüter et al. [14] have extended the studies on local CaSO4 fouling.

As a continuation of this previous contributions, Schlüter et al. [22] introduced a new holistic concept to model fouling resistances presented as the first part of an extensive work. The aim of this concept is modeling and linking local and integral fouling resistances as well as the thermal and the mass based approaches. As the consequently following part, experimental results will be used in the present paper to calculate the input data required for modeling local thermal and local mass based fouling resistances based on Eqs. (1) and (3). The approach for recalculation of integral thermal fouling resistances by Eq. (4) will now also be applied to local thermal fouling resistances, obtained experimentally, to link the thermal and mass based approach. An overview of the applied modeling approach is presented in the following section.

2 Concept for modeling local fouling resistances

This section describes the concept of modeling local fouling resistances as a part of a new holistic approach to model and link fouling resistances. The core structure of this approach consists of six different expressions of the fouling resistance and is described comprehensively in Schlüter et al. [22].

Figure 2 shows in detail the composition of the local part of the holistic approach including all needed measured and calculated parameters as well as their connections. Rectangles indicate the measured data, while the calculated parameters are displayed as rectangles with rounded corners; these finally lead to the three target boxes. The modeling of the three different fouling resistances is described briefly in the following section. The experimental and theoretical approaches for obtaining the required parameters in the respective boxes are presented subsequently.

Fig. 2
figure 2

Measured (rectangles) and calculated (rectangles with rounded corners) variables integrated in the modeling of local fouling resistances

Full size image

2.1 Local thermal fouling resistance

The local thermal fouling resistances are determined by measuring the local temperatures at the wall and in the heating medium on the shell side and then using these measurements to quantify local overall heat transfer coefficients.

$${R}_{f,th,loc}=\frac{1}{{k}_{f}(t,z)}-\frac{1}{{k}_{0}(z)}$$
(10)

2.2 Corrected local fouling resistance

The corrected local fouling resistance is determined using the approach of Albert et al. [11] with a local perspective, see Eq. (11). This requires the local constrictions and the resulting local flow velocities, as well as the local friction coefficients based on the local layer roughness.

$${R}_{f,loc,corr}\left(t,z\right)=\frac{1}{{k}_{f}\left(t,z\right)}-\frac{1}{{k}_{0}\left(z\right){\left({\varepsilon }_{Nu,\xi }{\varepsilon }_{Nu,\omega }\right)}_{tz}}$$
(11)

2.3 Local mass based fouling resistance

The local mass based fouling resistances is calculated by applying a local consideration of Eq. (3).

$${R}_{f,mass,loc}(t,z)=\frac{{m}_{f}(t,z)}{{\rho}_{f}(t,z){ \lambda }_{f}(t,z)}$$
(12)

Accordingly, the local density and thermal conductivity are required, and these depend on the local void fraction of the fouling layer. The void fraction describes the part of a fouling layer that can be filled with fluid and is calculated from the local layer thickness and the local volume of the layer. The local deposited fouling mass per unit area is also used for calculations.

3 Experimental procedure

This section presents the experimental procedure for acquisition of the parameters displayed in the rectangles in Fig. 2.

Fouling experiments were carried out with a supersaturated aqueous CaSO4 solution in the test rig shown in Fig. 3. The test rig was equipped with two double-pipe heat exchangers (HX1 and HX2, 20 × 2 × 2000 mm) and has been described in detail by Schlüter et al. [14]. The heat exchangers operate in a counterflow with the salt solution entering the tube side at a 42 °C inlet temperature, 1 m s−1 flow velocity, and CaSO4 concentration of 0.027 mol L−1. Hot deionized water flows through the shell side, with an inlet temperature of 80 °C and a flow velocity of 0.25 m s−1. The resulting Reynolds numbers are 25,500 on the tube side and 20,700 on the shell side.

Fig. 3
figure 3

Fouling test rig equipped with two double-pipe heat exchangers, a heating circuit, and a product circuit

Full size image

One of the heat exchanger test sections is equipped with a fiber sensor in the wall of the inner tube and has six thermocouples in the annular gap. A schematic diagram of the test section is presented in Schlüter et al. [22]. This conformation allows determination of the temperature profiles at the tube wall and of the shell side flow. This information permits calculation of the local thermal fouling resistances [14]. The second heat exchanger is only equipped with six thermocouples in the shell side.

A fouling test run of approximately five days is conducted, and then the fouled inner tube of this heat exchanger is dismounted to investigate the axial distribution of the deposit in terms of its volume, mass, layer thickness, and roughness. A similar fouling progress is assumed in both test sections, due to identical process parameters and a similar integral pressure drop development; therefore, the fiber sensor provides the associated temperature profile.

The volume of the fouling layer is determined with an experimental setup consisting of the tube with the deposit inside and a connected translucent tube [22]. The system is filled incrementally with water and the principle of communicating tubes is used to record the corresponding water levels of the translucent tube. Comparison with the values of a tube without fouling provides information about the volume of water displaced by the deposit and therefore about the volume of the fouling layer [14]. After this volumetric investigation, the tube is cut into 10 segments of 200 mm length, as shown in Fig. 4.

Fig. 4
figure 4

Sketch of the fouled inner tube of the second heat exchanger, showing cuts into segments of 200 mm length for local investigations of the fouling layer thickness, roughness, and mass

Full size image

The local constriction, as well as the layer thickness and roughness height, at the different axial positions can be investigated by examining photographs of each tube cross-section with suitable image analysis software (Image J, Wayne Rasband, NIH). Other dimensions, such as the tube diameter, are specified and the program calculates the area of different circular shapes or a freehand selection. An example of analysis of the cross section of a fouled tube at z = 2 m is shown in Fig. 5, which displays the inner diameter \({d}_{i,f}\) corresponding to the fouling layer thickness \({x}_{f}\) and the diameter \({d}_{kr},\) taking into account the mean roughness height \({k}_{r}\).

Fig. 5
figure 5

Measurement of the cross section of a fouled tube at z = 2 m using image analysis software

Full size image

In addition, weighing the tube segments provides the deposited mass per segment and the resulting distribution of fouling mass along the tube. After an experiment with a duration of five days, the total fouling mass amounts to 3–5% of the tube weight.

4 Calculated parameters

The experimental results are used for the calculation of the local flow velocities, the resulting Reynolds numbers, and the local friction coefficients, as well as the local layer parameters of void fraction, thermal conductivity, and density. The calculation procedure is presented as follows.

4.1 Local flow velocity and local friction coefficient

The photographs of the tube segment cross-sections after a fouling experiment are analyzed using Image J to obtain the free flow cross-sectional area and the corresponding free inner diameter \({d}_{i,f}\), see Fig. 5. An increasing constriction along the tube length and operation of the heat exchanger at constant flow rate will result in an increase in the flow velocity as well:

$${w}_{f}(z)=\frac{\dot{V}}{^{\pi}/_{4}\cdot {{d}_{i,f}(z)}^{2}}$$
(13)

The approach of Nedderman and Shearer [23] describes the friction coefficient as a function of the sand roughness \({k}_{s}\):

$$\frac1{\sqrt\xi}=1,74-2\cdot\log_{10}\left(\frac{{2k}_s}{d_i}-\frac{10}{Re}\cdot\sqrt{\frac8\xi}\right)$$
(14)

This approach was chosen due to the similarity of the crystal layer roughness to the roughness type of affixed sand grains [10]. Hence, the mean local roughness height \({k}_{r}\), resulting from the image analysis, can be used in place of the sand roughness \({k}_{s}\). A conversion of Eq. (14) allows for an iterative calculation of the maximum local friction coefficient \({\xi }_{f,loc,max}\) based on the mean roughness height \({k}_{r}\) at the end of a fouling experiment:

$${k}_{r}=\frac{{d}_{i,f}}{2}\left[{10}^{\left(\frac{-1}{2 \sqrt{{\xi }_{f,loc,max}}}+\mathrm{0,87}+\frac{10}{{Re}_{f}} \sqrt{\frac{8}{{\xi }_{f,loc,max}}}\right)}\right]$$
(15)

4.2 Local void fraction, thermal conductivity, and density

The fouling layer is considered a porous system with a local void fraction \(\epsilon\). This local void fraction is calculated by applying the experimental results regarding the local thickness and the local volume of the layer. The displaced water is determined segmentally; therefore, the mean layer thickness within a tube segment is used. Both values are obtained from a fouled tube at its final condition after a fouling experiment. The mean local layer thickness \({x}_{f}\) defines the cross-sectional area occupied by deposits. Multiplying this area with the length of the segment gives the total layer volume \({V}_{f,tot}\). Subtracting the volume of water displaced by deposits within the respective tube segment from \({V}_{f,tot}\) then provides the volume of water \({V}_{{H}_{2}O,\epsilon }\) fitting in the void \(\epsilon\) of the theoretically available total layer volume \({V}_{f,tot}\). Finally, the ratio of both parameters yields the fouling layer void fraction per tube segment:

$$\epsilon (z)=\frac{{V}_{{H}_{2}O,\epsilon }}{{V}_{f,tot}}$$
(16)

The void fraction is determined for each tube segment, so all dependent values are also calculated per tube segment. The thermal conductivity is obtained from two alternative arrangements: the first is a solid matrix and a void acting as resistances in series, see Eq. (17), and the second is both acting in parallel, see Eq. (18) [24].

$$\lambda_{f,I}(z)=\epsilon(z)\cdot\lambda_{H_2O}+\left(1-\epsilon(z)\right)\cdot\lambda_{gyp}$$
(17)
$$\frac{1}{{\lambda }_{f,II}(z)}=\frac{\epsilon (z)}{{\lambda }_{{H}_{2}O}}+\frac{1-\epsilon (z)}{{\lambda }_{gyp}}$$
(18)

The void of the fouling layer is filled with the aqueous solution; therefore, the thermal conductivity of pure water (\({\lambda }_{{H}_{2}O}\) = 0.64 W m−1 K−1 at 45 °C) can be used and the thermal conductivity of gypsum (\({\lambda }_{gyp}\) = 1.3 W m−1 K−1) is applied for the solid [25]. The mean thermal conductivity of the fouling layer is calculated by averaging \({\lambda }_{f,I}\) and \({\lambda }_{f,II}\):

$${\lambda }_{f}(z)=\frac{{\lambda }_{f,I}(z)+{\lambda }_{f,II}(z)}{2}$$
(19)

The density of the fouling layer is calculated with Eq. (20) when considering the deposited salt (\({\rho }_{gyp}\) = 2,320 kg m−3) with the aqueous solution in the void fraction [26].

$$\rho_f(z)=\epsilon(z)\cdot\rho_{H_2O}+\left(1-\epsilon(z)\right){\cdot\rho}_{gyp}$$
(20)

5 Results

5.1 Local thermal fouling resistance

Figure 6 presents selected fouling curves obtained with the local temperature measurements using the fiber sensor. All curves clearly relate to the distance between the location of the measuring point and the hot water inlet of the heat exchanger. The respective local values for the fouling rate and the final fouling resistance increase in direction of the hot water inlet. A decrease in heat transfer over time was detected from the axial position z = 1.4 m onwards. The closest position to the heating water inlet that can be evaluated is z = 1.96 m. The corresponding fouling curves show the most significant enhancement of heat transfer after about one day. Therefore, a rapid development of the surface roughness and a high friction coefficient can be assumed at this location. At z = 1.2 m, only crystals that enhance the flow turbulence exist during the entire experimental time, resulting in a negative fouling resistance. Therefore, the fouling curve does not leave the roughness controlled phase [14].

Fig. 6
figure 6

Curves of local thermal fouling resistances at various local positions based on temperatures measured with the fiber sensor

Full size image

5.2 Corrected local fouling resistance

Figure 7 shows the axial distribution of the free tube diameter \({d}_{i,f}\) and the mean roughness height \({k}_{r}\) as a result of analyzing the cross sections of the second heat exchanger tube in accordance with Figs. 4 and 5. As expected, the free tube diameter is increasingly constricted along the tube length due to the increase in the fouling layer thickness starting at z = 1.0 m. No compact deposit was found between z = 0 m and z = 0.8 m. Conversely, the layer roughness increases strongly up to z = 0.8 m and remains constant as soon as a compact layer is formed.

Fig. 7
figure 7

Axial distribution of the constricted tube diameter and the mean roughness height of the fouling layer

Full size image

The values displayed in Fig. 7 are used to determine the local flow velocities, using Eq. (13), and the local friction coefficients, using Eq. (15), to calculate the maximum correction factors \({\varepsilon }_{Nu}\) while determining the heat transfer correlations of Nunner [17], Hughmark [19] and Gnielinski [21], using Eqs. (5–9). The comprehensive study of Albert et al. [11] revealed that the heat transfer correlations of Burck [18] and Ceylan and Kelbaliyev [20] are not suitable for this purpose; hence, these approaches are not considered here. The results for all the analyzed cross sections are presented in Table 1. The friction coefficient increases significantly within the first 800 mm of the tube due to the increasing layer roughness, and it remains constant thereafter. Accordingly, the constriction that has an effect on heat transfer starts at z = 1.0 m. The influence of roughness on heat transfer is given a higher weighting with Hughmark’s approach than with Nunner's approach [10], leading to higher correction factors \({\varepsilon }_{Nu,\xi }\) based on the friction coefficients.

Table 1 Local friction coefficients and correction factors based on layer roughness and thickness measurements
Full size table

Figure 8 shows the time dependency of the correction factors obtained by subdividing the curve of the local thermal fouling resistance at z = 1.96 m into different sections. In section A, \({\varepsilon }_{Nu,\xi }\) is time dependent until it reaches its maximum at the most negative fouling resistance. Subsequently, \({\varepsilon }_{Nu,\xi }\) remains constant, whereas \({\varepsilon }_{Nu,\omega }\) increases with increasing fouling resistance in section B. Ultimately, the constriction effect also remains constant in section C.  

Fig. 8
figure 8

Subdivision of the temporal course of the thermal fouling resistance at the axial position z = 1.96 m with regard to the roughness and constriction effects on heat transfer; A: Constriction effect can be neglected, B: Increasing constriction, C: Maximum constriction

Full size image

In accordance with Fig. 7, the roughness height does not change significantly when the compact layer initially starts to grow. Therefore, the local roughness heights measured at the end of the fouling experiment are assumed to correspond to the roughness heights at the time of the most negative values of the respective local fouling curves. Hence, the results shown in Table 1 are maximum friction coefficients and maximum correction factors \({\varepsilon }_{Nu,\xi ,max}\) related to roughness effects. The local correction factors \({\varepsilon }_{Nu,\omega }\) due to constriction, determined at the end of the experiment, are also considered maximum values. In the case of Fig. 8, the maximum is reached upon achieving an asymptotic local thermal fouling resistance, since the fouling layer thickness undergoes no further growth. For an axial position without an asymptotic fouling resistance, the correction factor increases until it reaches its highest value at the end of the experiment.

A direct determination of the temporal change of the correction factors is not possible. Therefore, the temporal change of \({\varepsilon }_{Nu,\xi }\) and \({\varepsilon }_{Nu,\omega }\) is aligned with the progress of the respective local fouling curve by normalization. This procedure is done separately for the different sections A, B and C displayed in Fig. 8. No temperature data is available at z = 2.0 m; therefore, the temporal change of the correction factors at this axial position is determined based on the fouling curve at z = 1.96 m.

Figure 9 shows the resulting development of the correction factors taking roughness and constriction effects into account by using the heat transfer correlations of Nunner, Hughmark, and Gnielinski. This approach was applied for all axial positions that had data for constriction and layer roughness determined from image analysis and the corresponding fouling curves.

Fig. 9
figure 9

Time-dependent courses of the correction factors for considering roughness and constriction effects on heat transfer for the axial position z = 1.96 m

Full size image

Recalculated local fouling resistances at z = 1.96 m, based on the method presented in Fig. 9, are plotted in Fig. 10 and compared with the local thermal fouling resistance based on a constant heat transfer coefficient extracted from Fig. 6. The increase in Nusselt numbers by both roughness and constriction effects is considered for calculation with Eq. (11).

Fig. 10
figure 10

Recalculated local fouling resistance at z = 1.96 m by considering heat transfer enhancing roughness effects and comparison with the measured fouling thermal resistance

Full size image

The negative fouling values are eliminated by taking into account the surface roughness and constriction effects on heat transfer. Furthermore, the corrected fouling resistances are higher than the fouling resistances calculated with a constant heat transfer coefficient at any given time. The correction factors in Table 1 indicate that higher fouling resistances result when using the correlation of Hughmark. This outcome could be confirmed at all the considered axial positions where corrected fouling resistances were calculated. However, the results of applying Hughmark's correlation provided unrealistically high fouling resistances, especially at the axial positions between z = 0.2 m and z = 0.8 m where only roughness exists. Therefore, this approach is not considered henceforth in this paper.

Overall, application of the heat transfer correlations described here and recalculating thermal fouling by taking into account roughness and constriction effects provides a local perspective of the fouling process that has been regarded integrally thus far. The next section presents a comparison of the axial distribution of the corrected local fouling resistances at the end of the experiment with the corresponding local thermal fouling resistances and local mass based fouling resistances.

5.3 Local mass based fouling resistance

Local mass based fouling resistances \({R}_{f,mass,loc}\) are calculated in accordance with Eq. (12) for all cross sections of the tube segments shown in Fig. 4. As shown in Fig. 2, the experimentally determined, locally deposited mass per area, the local deposit volume, and the local fouling layer thickness are needed for calculation of the mass based fouling resistances. These quantities are determined at the end of an experiment, so the local mass based fouling resistances are only calculated for this point; a time-resolved development is not available. The layer’s void fraction and the resulting thermal conductivity and density are calculated with Eqs. (16–20) for each axial position. Tables 2 and 3 list all the parameters for the available local positions extracted from the corresponding axial distributions along the heat exchanger tube length.

Table 2 Deposited mass, displaced water, and fouling layer thickness for all available axial positions
Full size table
Table 3 Calculated local void fraction, thermal conductivity, and density of the deposits at the different axial positions; assumed values are indicated in brackets
Full size table

Figure 7 and Table 2 show no fouling layer thickness up to z = 0.8 m. Hence, determining the corresponding local void fractions is not possible using Eq. (16), nor can the local density and thermal conductivity of the deposit be calculated for these axial positions; therefore, a determination of the mass based fouling resistance according to Eq. (12) is also not possible. However, the values of deposited mass per unit area at the positions z = 0.2 m to z = 0.8 m would theoretically allow quantification of local mass based fouling resistances. This calculation would require an assumption of a decreasing void fraction for the axial positions according to the increase of the volume of displaced water as well as the deposited mass, see Table 2. Thus, values for the local densities as well as the local thermal conductivities at these positions can also be calculated based on the assumed void fractions. All assumed values are indicated with brackets in Table 3. The resulting values for thermal conductivity and density all range between the applied material properties of water and pure gypsum, and they increase with a decreasing void fraction.

Figure 11 shows the resulting local mass based fouling resistances for all axial positions plotted over the tube length. The axial distribution of the local thermal fouling resistances and the corrected local fouling resistances, as determined by applying the correlation of Nunner at the end of the experiment, are also shown for comparison.

Fig. 11
figure 11

Axial distribution of local mass based fouling resistances at the end of the experiment and comparison to local thermal and corrected local fouling resistances

Full size image

5.4 Distinctions between the axial distributions of different fouling resistances

The curve of the local mass based fouling resistance shows an exponential course in the direction of the hot end of the heat exchanger. Therefore, it generally corresponds to the courses of thermal and corrected fouling resistances but has higher values, especially in the case where compact fouling layers appear from z = 1.0 m to z = 2.0 m. The latter local position is an exception and the corrected fouling resistance is much higher than the thermal and mass based fouling resistances.

According to Fig. 11, a correction of local thermal fouling resistances toward the higher values of local mass based fouling resistances was successfully achieved by applying the model that accounts for roughness and constriction effects on heat transfer at all axial positions except z = 2.0 m. Here, the modeling causes an increase in the local fouling resistance of about 1.7-fold, so that even the mass based fouling resistance is clearly exceeded. However, the correction factors \({\varepsilon }_{Nu,\xi }\) and \({\varepsilon }_{Nu,\omega }\) increase only slightly compared to the position z = 1.8 m; therefore, the corrected fouling resistance provides an unrealistically high value at z = 2.0 m, see Table 1. In accordance with Eq. (11), the correction factors are multiplied by \({k}_{0}\). Therefore, the modeling strongly depends on this term or, rather, the underlying local temperature measurement. Hence, the strong increase in fouling resistance is not only caused by the effects of the deposited fouling layer, but it is also mathematically justified.

In accordance with the points already mentioned, quantification of local fouling using the corrected local fouling resistance is particularly recommended if a compact fouling layer has not yet formed on the surface and only roughness is present. The mass based fouling resistance provides plausible values to describe the fouling behavior in this tube section, but it is based on assumptions regarding the material properties. By contrast, the quantification via \({R}_{f,mass,loc}\) is preferable as soon as a compact layer develops. The model for considering deposit-related influences on heat transfer corrects the local thermal fouling resistances at these axial positions in the direction of the values of \({R}_{f,mass,loc}\). Nevertheless, the fouling behavior still seems to be underestimated in terms of the amount of deposit formed and is more plausibly represented by the mass based quantification. In addition, the calculation at the local position z = 2.0 m showed that the values generated using the correction model can be too high.

6 Conclusions

This contribution presents the second part of an extensive work regarding a holistic fouling model with the aim of linking local and integral fouling resistances as well as the thermal and the mass based approaches to calculate fouling resistances. The part of the model dealing with the local fouling resistances is presented in detail by defining all measuring categories, as well as the resulting calculated parameters required for modeling local thermal fouling resistances, corrected local fouling resistances, and local mass based fouling resistances. The corrected fouling resistance is a recalculated form of the local thermal fouling resistance and accounts for the heat transfer enhancing effects due to surface roughness and constriction.

Data for modeling the local fouling resistances are generated by conducting fouling experiments in a double-pipe heat exchanger under constant process conditions. Crystallization fouling of an aqueous CaSO4 solution is examined with a local perspective. The fouling progress is investigated locally by measuring local temperatures with a fiber sensor along the heat exchanger. This allows the modeling of time-dependent local thermal fouling resistances. Further experimental methods (e.g., cutting the fouled tube into segments) provide data regarding the local fouling volume, mass, thickness, and roughness per tube segment. These parameters allow calculation of the fouling layer properties, such as void fraction, thermal conductivity, and density. All experimental and theoretical approaches are merged into the model for the determination of the corrected and mass based local fouling resistances.

Negative fouling resistances in the roughness controlled phase of the local thermal fouling resistances are eliminated by accounting for heat transfer enhancement through roughness. An additional consideration of constriction effects on heat transfer further increases the effective fouling resistances. Comparison of the values obtained by the thermal, mass based, and corrected approaches shows similar axial distribution at the end of the experiment. Overall, the correlation between the corrected local fouling resistance and the local mass based fouling resistance, as determined according to the introduced modeling concept, presents a major challenge. This task is further complicated by the differences resulting from the various experimental and computational approaches for determining the respective fouling resistances. Nevertheless, the use of the model to correct for thermal fouling resistance is a step forward in the development of a prospective holistic fouling model.