1 Introduction

One of the significant methods to increase a gas turbine output and its efficiency is to raise the turbine inlet temperature (TIT), which certainly exceeds the allowable blade material restrictions. A common method for blade cooling is to circulate coolant air through internal cooling passages within the turbine blades. An important aim of the turbine heat transfer community is to maximize the cooling efficiency of the internal cooling passages which can decrease the hot spot blade temperature and the maximum blade temperature gradient to insure appropriate engine longevity. Also manufacturing limitations and available volume space for internal cooling, aerodynamic losses, pressure drop penalties are imposed and these affect optimization and accurate quantification of the performance of the internal cooling technology. Consequently, numerous investigations have an emphasis on different considerations such as cross sectional geometries, different turbulator configurations, and different flow parameters for both stationary and rotating internal coolant passages. These studies have provided valuable insights on the effect of Coriolis and centrifugal buoyancy force on the flow and heat transfer characteristics for specific geometries, and have provided guidelines for applying developed internal-cooling strategies.

1.1 Heat transfer in smooth and ribbed channel under rotational condition

An enormous amount of literature related to heat transfer and fluid field for internal cooling of turbine blades have been reviewed by Han and coworkers [1, 2]. They presented two comprehensive review papers about recent studies in turbine blade cooling. Also, many studies were reviewed by Bunker [3], Sunden et al. [4] and Ligrani [5] about heat transfer augmentation technologies for internal cooling. The early research of the internal cooling of gas turbine blades started from the stationary condition and these focused on circular cross section tubes and rectangular smooth channels [6,7,8]. The rotating effect on gas turbine blade heat transfer has prompted some researchers such as Guidez et al. [9] to investigate secondary flow compelled via the Coriolis force on heat transfer. After that, Wagner and Johnson [10, 11] studied heat transfer in serpentine passages of smooth channels and they presented effects of the Coriolis and rotation induced buoyancy forces on it and described the Rotation number as the ratio of the Coriolis force to flow inertia force. Also, a series of valuable data about heat transfer enhancement because of rotation condition was prepared by means of their experimental reports. The role of the buoyancy force in gas turbine blade internal cooling because of high centrifugal acceleration generated by high rotational speed and a large difference of wall to coolant temperature is very significant and is not negligible [12]. A considerable increase about two to three times on the outward flow trailing wall and a decrease around 40% in the local heat transfer coefficient distributions on the outward flow leading wall were found by these researchers. This happens under rotating conditions compared to nonrotating flow conditions.

Investigation of high Rotation number around 0.4 has been done by means of increasing the operating pressure as evident by the survey of Wright et al. [13]. Furthermore high Reynolds number around 165,000 also has been researched via utilizing pressurized Freon R134a as the working fluid by Rallabandi et al. [14]. They expressed that the overall deviation and difference between the leading and trailing heat transfer coefficient was less as the Rotation number was increased largely and the Nusselt number ratio tendency is near the stationary condition as Reynolds number is increased. Several CFD simulations to investigate the heat transfer augmentation versus the pressure drop on both leading and trailing surfaces of a rotating rectangular channel with radially inward and outward flow were conducted by Iacovides et al. [15,16,17] Watanabe [18] Fransen [19] used RANS and LES turbulence modeling to simulate both a smooth channel and a channel equipped with skewed rib-roughening in rotation inward and outward flows. Many experimental studies by Han et al. [20,21,22] and Sunden et al. [23,24,25] were carried out to find out the influence of the rib configuration on the heat transfer augmentation against the pressure drop penalty. In general, these researches were considering the rib angle of attack [26, 27], V-shaped ribs [28, 29], staggered and inline arrangement of the ribs [30], and different aspect ratios of the ribbed channel [31, 32]. Indeed, they focused on boundary layers regenerated via the ribs and impacts of the secondary flow induced by rib turbulators. The outcomes showed considerable effects of these configuration parameters on heat transfer characteristics and pressure drop in the channel. Also, they reported that vortex pairs, which increase turbulent transport and secondary advection over the entire channel, are very essential. According to these authors, a considerable local heat transfer rate and averaged surface Nusselt number due to the rib turbulators are possible. Generally, it is concluded from previous studies that according to the results of [27], an increase of about 30% in heat transfer for angle ribs of 30 and 45 deg compared to a 90 deg rib angle of attack occurred. Also, the maximum thermal performance happened for a relative baffle width of 5.0 and thermo-hydraulic performance comparison displayed that the multi V-downstream pattern has better results compared to other baffle shapes in a rectangular duct [29]. Moreover, the most important conclusion for different aspect ratios in ribbed channels [32] is that the rotation influence is the main factor in low aspect ratio channels and the local enhancement due to the rib position is more dominant for high aspect ratio channels.

1.2 Heat transfer in view point of field synergy principle and secondary flow intensity

An innovative theory corresponding to convective heat transfer enhancement is called the field synergy principle proposed firstly by Guo et al. [33]. It states that the reduction of the intersection angle between the two vectors of velocity and temperature gradients in the flow field can effectively improve the convective heat transfer. A dimensionless number is determined as an indication of the synergy degree between the velocity and temperature fields for the entire flow and heat transfer domain. Undoubtedly, for an ideal heat transfer field, this number should be close to zero. A majority of investigations related to this concept concerns analysis of the enhancement mechanism in heat exchangers. A computational survey on the fin-and-tube surface with delta winglet vortex generators has been investigated by Wu et al. [34]. Their outcomes state that secondary flow generated by vortex generators reduces the intersection angle between the velocity and fluid temperature gradients and develop the heat transfer. Tao et al. [35] explored this for the wavy fin-and-tube heat exchanger numerically. Reynolds number effect and fin pitch were studied from the perspective of the field synergy principle. Also, a flow and heat transfer study for a porous wick of a CPL evaporator by Lio et al. [36] has been performed by applying the field synergy analysis. It can be concluded from previous studies that secondary flows associated with geometry parameters are certainly influential in decreasing the synergy angle and increasing the heat transfer. Investigations about heat transfer enhancement at an internal stationary channel with vortex generator have been presented by Song et al. [45,46,47] in view point of secondary flow intensity. In one of these references, Song [47] presented a quantitative relationship between heat transfer and secondary flow intensity in flat-tube-and-fin air heat exchanger.

1.3 Objectives of current study

As mentioned above, rotation effect on flow and heat transfer in smooth square U-ducts have been experimentally and numerically investigated. Some numerical approaches have been implemented to obtain the averaged or local heat transfer distributions in these channels. However, there are no investigations on heat transfer improvement considering the field synergy factors and secondary flow intensity analysis under rotation conditions. It is of interest to find out the effect of the secondary flow induced by the Coriolis force and U-bend on the synergy angle and secondary flow intensity. Our study aims to present the heat transfer and pressure drop characteristics in a rotating U-duct channel at various Reynolds number, Rotation numbers and Buoyancy number. The validation will be done by an experimental study carried out in an in-house rotating facility.

Three issues are included in this study:

First, a numerical study to provide additional flow field information compared to test results to quantify and to understand more of the flow physics and heat transfer.

Second, investigation of the influence of the secondary flow associated by Coriolis, buoyancy and bend in the first and second passages in an internal cooling channel.

Third, find out the effect of rotation, centrifugal buoyancy and Reynolds number on heat transfer enhancement through the synergy angle and secondary flow intensity.

Forth, analysis and comparison of two approaches of synergy angle and secondary flow intensity on heat transfer enhancement.

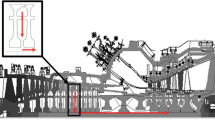
A representative sketch of gas turbine blade cooling is depicted in Fig. 1.

Fig. 1
figure 1

A representative sketch of blade internal and external cooling [48]

Full size image

2 Experimental setup and measurement techniques

2.1 Rotating facilities

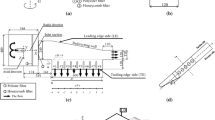
The experimental study was done at the Energy and Environment Laboratory of Iran University of Science and Technology (IUST). The test facility is depicted in Fig. 2. The rotating frame is driven by a 0.75 kW Electric Motor and can be varied from 1 to max 1500 rpm by a feedback AC Inverter Drive. A compressor-dryer-reservoir system with a maximum pressure of 10 bar delivers the coolant air to the rotating test set. Air passes through a flow meter, and is then transported to the rotating facility via a 1-in. rotary joint. The mass flow rate is controlled by using a throttle valve and is measured by means of an Acrylic Tube Rotameter with an uncertainty below 4%. The inlet and exit flow temperatures of the U-Turn channel are measured by two T-type thermocouples.

Fig. 2
figure 2

Rotation experimental facilities

Full size image

The test channel had a hydraulic diameter (Dh) of 40 mm and is equipped with screens and honeycombs to control the turbulence intensity of the main stream. The experimentally heated surfaces, including the leading surface and trailing surface were only heated and was used to support the copper plates and heaters.

The metal temperatures of the copper plate are measured with T-type thermocouples which is embedded into blind holes of each copper plates. The thickness of all copper plates was 4 mm. A strip of mica insulation with k = 0.12 W/mK with 1 mm in thickness was applied between adjacent copper plates to prevent conduction among different regions, and also help create a smooth contact surface between them. The thermocouples are connected with a reference junction to a data acquisition/ switch unit with a measurement accuracy of 0.5 K. For avoiding any undesirable effect on data acquisition and thermocouples.

The 4 × 4 cm silicone heaters are applied at the back surface of the copper plate to provide a constant heat flux during each test. This is shown in Fig. 2 (b). Biot numbers of the copper plates were calculated. The largest Biot number in this study is less than 0.022. The lumped capacitance method can be applied to determine the local wall temperature along the channel. Thus the passage can be divided into several regions based on the copper plate covered area. More details of the rotating facility have been introduced in our previous study [49].

2.2 Data reduction

To convert the raw measurements to the heat transfer coefficient and friction factor, the following equations are used:

The heat transferred to the fluid by each heater panel is calculated using Eq. (1). It represents the electrical power supplied by the heater minus the heat loss to the surroundings.

$$ {h}_i=\frac{Q_{input,n}-{Q}_{loss,n}}{A_n\times \left({T}_{w,n}-{T}_{b,n}\right)} $$
(1)

The heat losses are measured from several stationary and rotation calibration tests where the test-section is closed to avoid any air circulation. As the steady state condition is obtained, the heat supplied by the heaters is balanced by the heat lost during the actual measurement due to the heat conducted through the thermal insulating shell. Repeating this procedure for different power inputs, several calibration functions of the heat loss are obtained as a function of metal block temperature Tw,n with respect to the ambient temperature Tamb and these are used in the above mentioned data reduction procedure. In the current study, the percentage of the heat loss varies from 4% to 20.0%.

Also to determine the streamwise bulk temperatures, the enthalpy balance method is used as follows.

$$ {T}_{b,n}={T}_{b, in}+\frac{\sum {Q}_{net}}{\dot{m}.{c}_p} $$
(2)

The Nusselt Number can be normalized using the Dittus-Boelter equations [37]. It characterizes fully developed internal turbulent flow in circular passages with smooth surfaces as:

$$ \frac{Nu}{Nu_0}=\frac{hD_h/\lambda }{0.023{\operatorname{Re}}^{0.8}{\Pr}^{0.4}} $$
(3)

Reynolds, Rotation and Buoyancy numbers in the current study are calculated by using Eqs. (4) to (6).

$$ \operatorname{Re}=\frac{\rho {UD}_h}{\mu }=\frac{\dot{m}{D}_h}{A\mu} $$
(4)
$$ Ro=\frac{\Omega {D}_h}{U} $$
(5)
$$ Bu=\frac{\left({T}_w-{T}_b\right)}{\left({T}_w-{T}_b\right)/2}{Ro}^2\frac{r}{D_h} $$
(6)

Also, the friction factor in the numerical simulation is calculated based on the distance between the two pressure transducers and the passage hydraulic diameter. It can be normalized by the Blasius equation for fully developed turbulent flow in a circular tube [37].

$$ \frac{f}{f_0}=\frac{\Delta P}{4\left(L/{D}_h\right)\left(0.5\rho {U}^2\right)}\times \frac{1}{0.079{\operatorname{Re}}^{-0.25}} $$
(7)

The overall thermal performance factor is determined by dividing the overall averaged normalized Nusselt number by the normalized friction factor:

$$ TP=\frac{Nu/{Nu}_0}{{\left(f/{f}_0\right)}^{1/3}} $$
(8)

This performance factor helps to quantify the balance of the heat transfer increase against the friction factor penalty and is helpful for determining the optimal design.

Uncertainty analysis and propagation of error in the current investigation are estimated using the method by Moffat [44]. Table 1 illustrates the main measured parameters with their uncertainties in the experiment at Re = 10,000 and Ro = 0.1. The uncertainty of Reynolds number and Rotation number are estimated to be around ±3.6% and ± 2.3% based on the accuracy of measuring tools. Also, the estimated uncertainty of Nusselt number is calculated to be within ±7.5%. It is notable that each test has been repeated at least 3 times.

Table 1 Measured values and estimated uncertainty in the investigated channel in the case Re = 10,000, Ro = 0.1
Full size table

3 Computational investigation

3.1 Governing equations

The governing equations of fluid flow and heat transfer for different variables can be expressed as follows.

Continuity equation:

$$ \frac{\partial \left(\rho {\overline{u}}_i\right)}{\partial {x}_i}=0 $$
(9)

Momentum equations:

$$ \frac{\partial \left(\rho {\overline{u}}_i{\overline{u}}_j\right)}{\partial {x}_j}=-\frac{\partial \overline{P}}{\partial {x}_i}+\frac{\partial }{\partial {x}_j}\left(\left(\mu +{\mu}_t\right)\left(\frac{\partial {\overline{u}}_i}{\partial {x}_j}+\frac{\partial {\overline{u}}_j}{\partial {x}_i}\right)\right)-2{\rho e}_{ijk}{\Omega}_j{\overline{u}}_k-\rho {e}_{ilm}{e}_{mjk}{\Omega}_l{\Omega}_j{R}_k $$
(10)

where R is the rotation radius.

Energy equation:

$$ {c}_p\frac{\partial \rho {\overline{u}}_i\overline{T}}{\partial {x}_i}=\frac{\partial }{\partial {x}_i}\left(\lambda \frac{\partial \overline{T}}{\partial {x}_i}\right)-{c}_p\frac{\partial }{\partial {x}_i}\left(\left(\frac{\mu_t}{\Pr_t}\right)\frac{\partial \overline{T}}{\partial {x}_i}\right) $$
(11)

In accordance with Refs. [38,39,40], the k-ω SST model is a successful model for turbulence modeling in rotational heat transfer and wall function treatment is used automatically. The governing equations of this model are specified in Eqs. (12) to (15):

Turbulent kinetic energy k equation:

$$ \frac{\partial }{\partial {x}_i}\left(\rho {ku}_i\right)={\tau}_{ij}\frac{\partial {u}_j}{\partial {x}_i}-{\beta}^{\ast}\rho k\omega +\frac{\partial }{\partial {x}_i}\left(\left(\mu +{\alpha}_k{\mu}_t\right)\frac{\partial k}{\partial {x}_i}\right) $$
(12)

Rate of energy dissipation ω equation:

$$ \frac{\partial }{\partial {x}_j}\left(\rho \omega {u}_i\right)=\frac{\gamma }{\upsilon_t}{\tau}_{ij}\frac{\partial {u}_j}{\partial {x}_i}-{\beta \rho \omega}^2+\frac{\partial }{\partial {x}_i}\left(\left(\mu +{\alpha}_{\omega }{\mu}_t\right)\frac{\partial \omega }{\partial {x}_j}\right)+2\left(1-{F}_1\right){\alpha}_{\omega 2}\frac{\rho }{\omega}\frac{\partial k}{\partial {x}_i}\frac{\partial \omega }{\partial {x}_i} $$
(13)

In Eq. (13), F1 refers to the blending function defined in Eq. (14), where CDkω and the turbulent eddy viscosity υt are determined by Eqs. (15) and (16), respectively. F2 and S refer to the second blending function and the invariant measure of the strain rate, respectively and F2 is specified by Eq. (17).

$$ {F}_1=\tanh \left\{\min {\left[\left(\max \left(\frac{\sqrt{k}}{\beta^{\ast}\omega y},\frac{500\upsilon }{y^2\omega}\right),\frac{4{\sigma \omega}_2k}{CD_{k\omega}{y}^2}\right)\right]}^4\right\} $$
(14)
$$ {CD}_{k\omega}=\max \left(2{\rho \sigma}_{\omega 2}\frac{1}{\omega}\frac{\partial k}{\partial {x}_i}\frac{\partial \omega }{\partial {x}_i},{10}^{-10}\right) $$
(15)
$$ {\upsilon}_t=\frac{\alpha_1k}{\max \left({\alpha}_1\omega, {SF}_2\right)} $$
(16)
$$ {F}_2=\tanh \left\{{\left[\max \left(2\frac{\sqrt{k}}{\beta^{\ast}\omega y},\frac{500\upsilon }{y^2\omega}\right)\right]}^4\right\} $$
(17)

where:

$$ {\beta}^{\ast }=\frac{9}{100},{\alpha}_1=\frac{5}{9},{\alpha}_2=0.44,{\beta}_1=\frac{3}{40},{\beta}_2=0.0828,{\alpha}_{k1}=0.85,{\alpha}_{k2}=1,{\alpha}_{\omega 1}=0.5,{\alpha}_{\omega 2}=0.856 $$

3.2 Field synergy principle and secondary flow intensity

Mostly, heat transfer enhancement is normally accompanied by an additional large pumping power due to high flow resistances. The field synergy principle offers a useful tool to study the relation between fluid flow and heat transfer throughout the flow field that leads to a development series of novel enhanced solid boundaries with high energy efficiency.

For three-dimensional turbulent heat transfer without an internal heat source, the right-hand side is the heat flow rate between the solid wall and fluid. By transforming the volume integral to a surface integral, the turbulent thermal conductivity vanishes at the outer edge of the thermal boundary layer. Therefore, the integrated time-averaged energy conservation equation over the entire heat transfer domain Ω is simplified as:

$$ \underset{\Omega}{\iiint }{\rho c}_p\left(\overrightarrow{U}.\nabla T\right)d\forall =\underset{\Gamma}{\iint}\overrightarrow{n}.\left({\lambda}_{eff}\nabla T\right) dA $$
(18)

where \( \overrightarrow{U} \) and ∇T are the time-averaged velocity vector and the time-averaged temperature gradients respectively. λeff = λ + λturb is the effective thermal conductivity, which includes both fluid and turbulent thermal conductivity resulting from turbulent fluctuations.

Some dimensionless variables are introduced as,

$$ \overline{\overrightarrow{U}}=\frac{\overrightarrow{U}}{{\overrightarrow{U}}_{in}},\kern0.5em \nabla \overline{T}=\frac{\nabla T}{\left({T}_s-{T}_i\right)/\delta },\kern0.5em \overline{Y}=\frac{y}{\delta}\kern0.5em $$
(19)

The dot product of velocity vector and temperature gradient in Eq. (18) can be written as in the following equation:

$$ \left(\overline{U}.\nabla \overline{T}\right)=\left|\overline{U}\right|\left|\nabla \overline{T}\right|\cos \theta $$
(20)

From Eq. (20), it can be noted that the local synergy angle θ is the inclination angle between the time-averaged velocity vector and the time-averaged temperature gradient. Generally, it is considered to vary from 0 ~ 90 and can be calculated numerically in the form of,

$$ {\theta}_i=\operatorname{arccos}\left|\frac{u_i\frac{\partial {T}_i}{\partial x}+{v}_i\frac{\partial {T}_i}{\partial y}+{w}_i\frac{\partial {T}_i}{\partial z}}{\left|\overline{Ui}\right|\left|\nabla \overline{T_i}\right|}\right|=\operatorname{arccos}\left(\frac{\overline{U}.\nabla \overline{T}}{\left|\overline{U}\right|\left|\nabla \overline{T}\right|}\right) $$
(21)

Similarly, the area-weighted average synergy angle is given by:

$$ \theta =\underset{\Omega}{\iiint}\theta d\forall /\underset{\Omega}{\iiint }d\forall $$
(22)

where d∀iis the cell volume of each control volume. It should be noted that of the velocity vector is parallel to the temperature gradient (synergy angle equal zero) a fully-synergized flow field is valid and it is an ideal case for convective heat transfer [43], Therefore, a phenomenon leading to a decreasing synergy angle can improve convective heat transfer.

On the other hand, secondary flow generated by Coriolis force and angled rib turbulators plays a significant role on the heat transfer enhancement. Song et al. [47] presented a non-dimensional number, Se, to assess the intensity of the secondary flow. The local intensity of the secondary flow, Ses (x), is given as follows:

$$ {Se}_s(x)=\frac{\rho {D}_h^2}{\mu}\underset{\Gamma}{\iint}\left|{\omega}_n\right| dAdx/\underset{\Gamma}{\iint } dAdx $$
(23)

where, ω is the vorticity and ωn is the normal component of ω to the cross section.

By integration of the local intensity of the secondary flow, Ses(x), over the entire volume, the volume average value of Se can be obtained as follows:

$$ Se=\frac{\rho {D}_h^2}{\mu}\underset{\Omega}{\iiint}\left|{\omega}_n\right|d\forall /\underset{\Omega}{\iiint }d\forall $$
(24)

3.3 Description of physical models

The computational domain is set up as the rotation test channel but it is a little extended in length. The model is a square smooth channel with a hydraulic diameter of 40 mm. A heat flux is applied on two surfaces of the leading and trailing edge exactly as in the experiment.

As mentioned before, according to the investigation of ref. [38,39,40] on heat transfer in a smooth and rib roughened channel for both stationary and rotating conditions, the simulations by the RANS SST-k-ω model corresponded well with experimental results. Thus to satisfy the wall requirements of the k-ω SST model, the grids near the wall boundary are very refined to obtain y-plus values around 1.0. A non-uniform mesh distribution is adopted based on a numerical study for a grid independent solution and then the total number of control volumes for the whole channel is selected to be 3.6 M.

Table 2 illustrates the mesh independence study at a Reynolds number of 10,000 and heat flux of 8000 W/m2 in stationary condition. Six mesh systems of a computational model with 1.4 M, 2.1 M, 2.5 M, 3.1 M, 3.6 M and 4.4 M meshes were applied for the independence study, respectively. For all the mesh studies, the pressure drop and the averaged Nusselt number were obtained and changes less than 0.5% were considered acceptable. Thus, the 3.6 M mesh is selected in the present study.

Table 2 Grid independence study
Full size table

The computational channel and the structured meshes are demonstrated in Fig. 3.

Fig. 3
figure 3

Computational channel

Full size image

3.4 Boundary conditions

A constant heat flux is applied on the leading and trailing walls and all walls are considered as no-slip walls. The thermal boundary conditions for other walls such as the two vertical walls of the rectangular U-bend duct are zero heat flux, i.e., adiabatic conditions. Also, an adiabatic condition is applied for the inlet-extended part of the channel. A constant mass flow rate of air with a uniform temperature 293.15 K are applied at the inlet of channel. In accordance with the experiment, the inlet turbulence intensity level is set as 4%. The Reynolds number in all case studies is constant at 10,000 based on the channel hydraulic diameter. According to the aforementioned Reynolds number, the fluid flow can be considered as incompressible. The rotation number is changed from 0 to 0.25. The outflow boundary condition is set as an average static pressure of 1 bar. The flow in the computational channel is 3D-dimensional, turbulent, steady and rotating condition. ANSYS FLUENT 17.0 is employed to solve the governing equations. The discretized equations are solved by the SIMPLE algorithm. Second order difference formulae are selected for discretization of energy and momentum equations, turbulent kinetic energy and dissipation rate equations. To achieve converged solutions of the transport equations a series of appropriated relaxation factors been used.

4 Results and discussions

4.1 Data validation

Before the presentation and analysis of the numerical study and to guarantee the reliability, spanwise velocities at rotation condition and Nusselt numbers in non-rotating and rotating state are validated with experimental data. Because the mentioned rotating facility in the present study is only equipped to measure the Nusselt number in stationary and rotation conditions, the spanwise velocities at rotation condition are compared with the experimental data reported by Chen et al. [41]. Figure 4 presents the computed fluid flow results for the streamwise velocity at a Reynolds number of 10,000 and a Rotation number of 0.15. Comparison with experimental data [41] at the same condition is provided. The acceptable agreement between the present numerical study and experimental data expresses a good choice of the numerical treatment such as mesh density, turbulence modeling and etc.

Fig. 4
figure 4

Comparison between the numerical and experimental steamwise velocity in the rotating channel

Full size image

In Fig. 5, a comparison between experimental and computational axial distributions of the normalized Nusselt number at a Reynolds number of 10,000 in non-rotating condition and a Rotation number of 0.1 for the leading and trailing walls. Although, there are slight differences between our experimental data and our numerical results near the end of the first pass of the U-Turn channel, good agreement between experimental and predicted value is found. This ensures the sufficient accuracy of the present study. Also, a more validation between experimental and numerical thermal performance is visible in Fig. 22 as well.

Fig. 5
figure 5

Comparison between the numerical and experimental axial distributions of normalized Nusselt number in the rotating channel

Full size image

4.2 Fluid field study

Figure 6(a) shows corner a vortex at the top end of the first pass and a separation bubble in the second pass, also secondary flow induced by the turn is depicted in this Fig. in the non-rotating condition. Figure 6(b) displays the secondary-flow pattern in the cross-section at the outward flow first pass and inward flow second pass under rotation conditions. The images of the flow visualized with LLSV by Elfert et al. [42] are attached for comparison. It is evident that the flow in the smooth channel is influenced mainly by the bend around the U-turn. The centrifugal forces cause a secondary flow development of two counter-rotating vortices as illustrated in Fig. 6(a). Furthermore, because of the Coriolis force, a pair of vortices with secondary flow is generated symmetrically at the first pass of the rotating channel, but in the second pass, the specific separation and a dedicated vortex occur due to the U-bend disturb the Coriolis secondary flow. Undoubtedly at the first part of the second channel, the bend induced vortices dominate the whole cross section.

Fig. 6
figure 6

Secondary flow pattern in the first pass, second pass and U-turn region and compaction with images of the flow visualized with LLSV by Elfert et al. [42] for rotation and non-rotation state

Full size image

The Streamwise velocity profiles for the outward flow in the first pass of a rotating smooth channel are plotted in Fig. 7. Reynolds number is 10,000 and Rotation number is varied from 0 to 0.2. It is obvious that the flow is pushed from the leading wall to the trailing wall for the reason of the Coriolis vortex pairs. It is noteworthy that the overall relative deviations and skewness are diminished as the rotation number is increased quantitatively. This is in agreement with the findings of Chen et al. [41] in their experiments.

Fig. 7
figure 7

Axial velocity profiles for outward flow in the first pass of a rotating smooth channel at Re = 10,000 and various Rotation number

Full size image

Figures 8 (a) and (b) show the effect of the rotation force and rotational buoyancy force on the axial velocity skewness in outward flow in the first pass and inward flow in the second pass of the rotating smooth channel, respectively at Re = 10,000 and Ro = 0 and 0.2 and DR = 0 and 0.5, Indeed, these Figs. compare the axial velocity at stationary condition, rotation condition with only Coriolis force and rotation condition with both Coriolis force and centrifugal buoyancy force. An interesting point about the axial velocity skewness in the first pass in Fig. 8 (a), is the coincidence of the rotation force and rotational buoyancy force. This can amplify both effects to misguide the flow from the leading wall to the trailing wall. But in the second pass in Fig. 8 (b), the rotation force and rotational buoyancy force have opposite effects on the axial velocity deviation and thus makes the flow distribution more uniform. This will be used subsequently to justify the difference in heat transfer enhancement between the first and second passages of the square smooth channel under rotation condition.

Fig. 8
figure 8

Influence of rotation force and rotational buoyancy force on axial velocity skewness

Full size image

4.3 Heat transfer study at trailing and leading walls

Figures 9 (a) and (b) illustrate the local heat transfer results as axial distributions of the normalized Nusselt number ratio versus x/D at the trailing and leading wall at outward flow in the first pass of the U-turn channel for Re = 10,000 and four different Rotation number of 0.05, 0.1, 0.15 and 0.2, respectively.

Fig. 9
figure 9

Distribution of normalized local Nusselt number at outward flow first pass

Full size image

The numerical results of the stationary condition for both walls at the same heat flux condition are also included as a solid continuous curve for comparison with the rotating data. In general, in the first passage, the heat transfer enhancement is high at the inlet channel and then begins to decrease in the streamwise direction due to the growing of the boundary layer thickness. Also, along the trailing wall at the first passage, the numerical result predicts great heat transfer enhancement as the rotational speed increases. In some cross sections of the trailing surface, this enhancement of the normalized local heat transfer can reach about 1.5 times the non-rotating state at Rotation number of 0.2 and Re = 10,000.

Furthermore, in accordance with Fig. 9 (b) at the leading wall of the first passage, rotation causes the heat transfer to fall below the stationary case along the channel and in some cross sections, the Nu/Nu0 ratio is 35% lower than the non-rotating case. Also, at the leading wall, from x/D = 10 and above, the decrease in heat transfer does vary with increasing Rotation number, in contrast to the trailing wall. The difference in heat transfer coefficient on the leading and trailing surfaces between rotating and stationary conditions is assigned to the cross section secondary flow vortices generated by the Coriolis force and amplified by the centrifugal buoyancy force. In fact, because of the Coriolis force, a pair of vortices with secondary flow is generated symmetrically and by these the main flow is pushed from the leading wall to the trailing wall. Therefore, the boundary layer thickness at the trailing wall is decreased while at the leading wall it is increased.

Figures 10 (a) and (b) display the rotation effects on the average Nusselt number ratio in the outward flow in the first pass at the trailing wall and leading wall, respectively at Re = 10,000 and at three different Inlet Density Ratios. Rotation number is varied from 0 to 0.25. Similarly, variation of the average heat transfer ratio versus Rotation number variation are depicted in Figs. 11 (a) and (b) for the trailing and leading surface of radially inward flow in the second pass from the U-turn channel at the aforementioned conditions. For a square U-turn channel, it can be easily seen that Nu/Nu0 increases dramatically with rotation number at the trailing wall in the 1st passage and at the leading wall in the 2nd passage. In the first passage Nu/Nu0 at the trailing surface increases by 20% to 40% depending on various Density Ratio at Ro = 0.25 from its stationary value. In the second passage, the corresponding increase in Nu/Nu0 with rotation is only maximum 18% at Ro = 0.25 as shown in Figs. 10 (a) and 11 (b). On the other hand, Figs. 10 (b) and 11 (a) indicate that there is a gradual decrease of 12% in average Nu/Nu0 as rotation is increased to 0.25 at the leading wall at the 1st passage and a relative stable average Nu/Nu0 at trailing wall in the 2nd passage.

Fig. 10
figure 10

Effect of rotation on average Nusselt number ration variations in radially inward 1st pass trailing wall

Full size image
Fig. 11
figure 11

Effect of rotation on average Nusselt number ration variations in radially inward 2nd pass trailing wall

Full size image

Undoubtedly, the large increase in Nu/Nu0 allocated at the trailing wall in the first passage is due to the Coriolis-induced secondary flows and extra generation buoyancy-driven vortex in this channel. Also, due to rotation direction and flow direction, the directional Coriolis force in the first passage is different from that in the second passage. Accordingly, in the first passage the main flow is pushed from the leading wall to the trailing wall and in the second passage, the main flow is pressed from the trailing wall to the leading wall. Therefore, as expected, the Nusselt number variation on the trailing wall at first passage has qualitatively a behavior similar to that on the leading wall at second passage. Similar behavior occurs for the leading wall at first passage and trailing wall at second passage. It should be noted that because the bend is inducing dominating vortices, the Nusselt number in the second pass is larger than the corresponding value in the first pass for all rotation numbers.

4.4 Field synergy principle study

In addition to present heatlines principle, the field synergy principle is used to study the effect of both the velocity and the temperature fields on the heat transfer performance in a boundary-layer flow. Indeed, the hydrothermal performance of convective heat transfer is influenced by the magnitudes of both the temperature gradient vector and the velocity vector and even the intersection angle between these aforementioned vectors [33, 50]. Thus, Field Synergy Principle investigation for the convective heat transfer in the two-pass square smooth channel is presented in this section. Secondary flows generated by Coriolis forces and rotational buoyancy force and also bend induced vortices play an important role on the heat transfer augmentation. Figures 12 and 13 show the distributions of the temperature and velocity vectors in cross sections along the channel in the first and second passage, respectively, at the Reynolds Number of 10,000 and Rotation Number of 0.1. By considering Eq. (22), the field synergy angle analysis is calculated with a post-processor in-house code based on varying Rotation number, Inlet Density Ratio and Reynolds number. Tables 3, 4 and 5 present the variation of the synergy angle with Rotation number, Reynolds number and Density Ratio (as a representative of the Buoyancy number effect) respectively. The aforementioned variations and corresponding Nusselt number in each case studies are plotted in Figs. 14 to 16.

Fig. 12
figure 12

Temperature gradient vector and Temperature contour in a cross section along the channel

Full size image
Fig. 13
figure 13

Velocity vectors contour in a cross section along the channel

Full size image
Table 3 Numerical average synergy angles at Re = 10,000 and DR = 0.05
Full size table
Table 4 Numerical average synergy angles at Ro = 0.05 and DR = 0.5
Full size table
Table 5 Numerical average synergy angles at Re = 10,000 and Ro = 0.05
Full size table
Fig. 14
figure 14

Effect of Rotation number on synergy angle and average Nusselt number

Full size image
Fig. 15
figure 15

Effect of Reynolds number on synergy angle and average Nusselt number

Full size image
Fig. 16
figure 16

Effect of Density Ration on synergy angle and average Nusselt number

Full size image

According to Fig. 14, it is clear that in the 1st pass, the synergy angle decreases considerably from 89.02 to 70.58 as the Rotation number changes from 0 to 0.25. Also in the 2nd passage, the synergy deviates slightly from a perpendicular angle by changing the rotation. Indeed, the flow by the Coriolis-induced vortex pair leads to an increase of the fluid bulk motion from the boundary layer zone to the central core region and vice versa. Therefore, in the 1st pass, it can improve the synergy between the velocity and the temperature gradients as the basic mechanism for enhancing convective heat transfer, but in the 2nd pass, the Coriolis secondary flow cannot improve the synergy because of dominating bend vortex. These variations are exactly in compliance with Nusselt number variation by Rotation number in the first and second passages.

Moreover, according to Fig. 15, the changes of Reynolds number decrease the synergy angle slightly around 2%, while the turbulence properties are increased as the Reynolds number is increased and because of this, the heat transfer is enhanced dramatically with Re, but the field synergy principle does not show a considerable improvement in synergy angle with Re. This behavior is repeated in Fig. 16 as the Density Ratio increases. The changes of the Density Ratio, which affect the centrifugal buoyancy, do not have any remarkable influence on the synergy angle in the first and second passages, while the average Nusselt number increases with an increase in the Density Ratio. It seems that the synergy angle maybe has no close physical relation to heat transfer enhancement and it cannot predict correctly any factors that cause an increase heat transfer.

4.5 Secondary flow intensity

Figure 17 illustrates the contour plots of the secondary flow intensity at two cross sections of the first and second passages of the channel in stationary and rotating condition. The cross section stream lines are also included. According to Fig. 17 (a), in a stationary channel, the secondary flow intensity in the 1st pass is approximately zero but in the 2nd pass it will be considerable and the highest secondary flow intensity are coinciding with the streamline of the induced vortex by the bend effect. In a rotation state, the symmetrical pair vortices generated by Coriolis forces increase the secondary flow intensity 10 times in the 1st pass and to 2 ~ 3 times in the 2nd pass as shown in Fig. 17 (b).

Fig. 17
figure 17

Secondary flow intensity contours at first and second pass of channel l

Full size image

Figures 18 to 20 present the variation of the volume average of the secondary flow intensity as a function of Rotation number, Reynolds number and Density Ratio, respectively. For further comparison, the Nusselt number variation in all case studies are also included in these Figures. Referring to Fig. 18, the values of Se increase by an increase of Rotation number in both passages. Also the magnitude of Se in the second pass is larger than Se in the first pass which matches the high Nu value in the second pass compared to the first pass. This consistency is evident in the decrease of Nu and Se in the 2nd pass at Ro = 0.25. Also the percentage of variations in Nusselt number and secondary flow intensity are quite in compliance as Reynolds number increases in the first and second passages as depicted in Fig. 19. According to Fig. 20, despite the increase of the heat transfer coefficient with an increase of the Density Ratio, the secondary flow intensity remains relatively constant.

Fig. 18
figure 18

Effect of Rotation number on Secondary flow intensity and average Nusselt number

Full size image
Fig. 19
figure 19

Effect of Reynolds number on Secondary flow intensity and average Nusselt number

Full size image
Fig. 20
figure 20

Effect of Density Ration on Secondary flow intensity and average Nusselt number

Full size image

This means that for the heat transfer field, the secondary flow intensity criterion can predict better than the field synergy principle criterion and the effects of factors such as Re, Ro or geometric vortex generator, which substantially create or increase the secondary flow, can be covered accurately with the secondary flow intensity criterion.

4.6 Thermo-hydraulic performance factor

Figures 21 and 22 show friction factor ratio and thermal performance factor at constant Reynolds number of 10,000 and different Rotation number of 0 to 0.25. The pressure drops are calculated based on inlet and outlet pressure in the rotating U-turn channel and normalized by Eq. (7) and then are combined with the Nu/Nu0 to obtain thermal performance factors by Eq. (8).The friction factor ratio displays a very small fluctuation and remains relatively constant with altering Rotation number whereas the thermal performance factor increases with rotation due to increasing Nusselt number ratio and then remains fairly flat at around Ro = 0.2 and 0.25. Basically, it is obvious that rotation has no major influence on the friction factor.

Fig. 21
figure 21

Overall Nusselt number ration and friction factor ratio versus Rotation Number in Re = 10,000

Full size image
Fig. 22
figure 22

Thermal Performance factor versus Rotation Number in Re = 10,000

Full size image

5 Conclusions

The rotation effects on flow and heat transfer in a square smooth U-turn channel have been explored in the present study at various Rotation number, Reynolds number and Density Ratio numerically. A field synergy principle and secondary flow intensity analysis are consistent with the numerical results as well. Due to the comprehensive numerical results, the conclusions can be pointed out as follows:

1) The Coriolis force and rotational buoyancy force are two inevitable force in a rotating channel and it makes heat transfer to increase on the trailing edge and vice versa on the leading.

2) The symmetrical pair of secondary flows induced by Coriolis force and dean vortex generated by turn are two dominated factors for improvement of average Nusselt number in first and second passages.

3) Coriolis-induced secondary flows can considerably improve the synergy angle. This is the reason why the rotation affects the heat transfer enhancement. However, the heat transfer improvement due to Reynolds number and Density ratio is not predictable by the field synergy principle analysis.

4) The secondary flow intensity increases by the Rotation and Reynolds numbers and it reveals a close relationship between Nu and Se.