1 Introduction

The thermal comfort of the clothing user is closely related to the thermal balance between the human body and its environment. There is constant heat exchange between the human body and its environment through the following mechanisms: conduction, convection, radiation and evaporation of sweat. These phenomena are conditioned by the features of the human body (temperature, metabolism, respiration rate, sweat rate), as well as the environmental parameters, e.g. air temperature, thermal radiation, relative humidity and air velocity. The clothing constituting a barrier between the body and the environment is an important factor affecting the thermal balance of the human body. The influence of textile structure parameters (i.e. raw material, linear density of yarns, thickness and weave of fabrics, air permeability) on thermal comfort properties of clothing is an issue being studied by many researchers [1,2,3,4].

In moderate and hot environments, clothes support the thermoregulatory mechanism of the human body creating an microclimate in the gap between the clothing and the user’s body. This is a very important issue regarding protective clothing used among others by firefighters, rescuers, steelworks workers. They may be exposed to flame and to sources of radiant heat during firefighting operations and other professional activities. During firefighting operations the heat flux density in the environment is usually between 5 kW·m−2 to 20 kW·m−2 [5]. Therefore, their clothing must be designed to provide protection against fire and thermal hazards and to prevent skin burns [6,7,8].

Many geometric and thermal fabrics parameters (thickness, porosity, emissivity, absorptivity and thermal conductivity) affect the transfer of thermal energy through multilayer protective clothing and can affect their thermal protective performance [4, 7, 9]. The protection levels that are required from protective clothing worn during firefighting operations are defined and specified in the EN 469 [10]. This European Standard covers the general clothing design and testing methods to determine compliance with the aforementioned performance level according to EN ISO 15025 (flame spread properties) [11], EN ISO 9151 (heat transfer caused by flame) [12] and EN ISO 6942 (heat transfer caused by radiation) [13]. The test method [13] is based on measurement of a copper calorimeter temperature change. The calorimeter is placed behind a sample of protective clothing which is exposed to a specific level of radiant heat.

To achieve a good heat protection, the clothing must have a certain minimum weight and thickness, but clothing which is too heavy and too thick reduces ergonomics and thermophysiological comfort. It should be emphasized that in case of both thermal protective clothing and impermeable protective clothing (e.g. against liquid chemical agents), their thermophysiological properties may affect the user’s safety. This complex issues are the subject of research [1, 4, 14,15,16,17]. Houshyar et al. [4] found that it is possible to improve the thermophysiological comfort properties of firefighters protective clothing by incorporation of superabsorbent fibres into the inner-layer fabric. Su et al. [15] analyzed the effect of air gap thickness on thermal protection of protective clothing against hot steam and thermal radiation. The studies have shown that the air gap between the clothing and the skin provides better thermal protection during exposure to radiant heat. Rossi et al. [16] analyzed the steam transfer through different types of textile layers in firefighter’s clothing. Zhang et al. [17] studied a critical role of thermal liners in thermal protective performance for firefighter gear. The work revealed positive impact of incorporating aerogel and microencapsulated phase change materials on protective properties of functional clothing.

Currently, numerical simulations [18,19,20] are an effective and widely used tool to analyze among others thermal processes occurring in clothing, phenomena in porous materials [21, 22] as well as filtration processes occurring in fibrous materials [23,24,25]. Moreover, these tools use models of real clothing and numerical analysis of physical phenomena to predict their protective properties. It is becoming increasingly common to supplement typical experimental studies of real materials with simulations [26,27,28,29,30,31]. Many researchers developed numerical models of heat transfer through multilayer protective clothing. Some researchers attempted to model the metabolic heat and sweat (vapor) transfer through textile layers forming protective clothing [8, 32]. The aim of studies made by Onofrei et al. [28] was to develop a numerical model of heat transfer in firefighter’s clothing exposed to radiant heat flux. An engineering simulation software was used as a tool for simulation of heat transfer through the selected multilayer textile structure. Zhu and Zhou [29] presented a mathematical model for heat and moisture transfer through protective clothing exposed to heat flux. The model was developed on the basis of Fick’s second diffusion law, simulating an impinging fire jet drying a moist fabric and took into account the dynamic diffusion effect on the fire drying process. The finite volume method was applied by Tian et al. [33] to simulate the transient heat transfer through a flame manikin placed in a combustion chamber. The model was verified by comparison with an experiment performed using flame manikin system and then used as a fundamental model to investigate the heat flux transfer through protective clothing. Jiang et al. [34] presented an integrated numerical simulator that allows estimating burn injuries caused by heat and flame. In this simulator, a general goal of applied computational fluid dynamics (CFD) was to calculate the fluid flow and heat transfer in situ fire event, while one-dimensional model calculated the radiative–conductive heat transfer through the clothing and human skin was used. Wang et al. [35] presented a 3-D transient CFD simulations of heat and mass transfer in the flame manikin test of protective clothing.

The design of clothing, in particular functional clothing for protection against heat, is a time-consuming and material-intensive process. That is why it is increasingly supported by computer object modeling and advanced computational methods. With increase in computing power of computers it is possible to design more and more perfect models of textiles that faithfully reproduce not only the structure of real materials but also allow simulations of their key properties for a given application.

In the current work selected CAD software and finite volume methods to analyze heat transfer in protective clothing in order to predict its protection performance was applied. The work is continuation of research using the software to model physical phenomena occurred in functional clothing [2, 36, 37]. However, the mentioned articles concerned simulations of heat transfer performed under steady state conditions. In this work the software to analyze heat transfer in transient state through multilayer textile assembly used in thermal protective clothing exposed to radiant heat was used. The 3D model of real assembly in a CAD environment was developed. Different scales of resolution were applied for various layers, ranging from a homogenized nonwoven fabrics model to geometry of yarn in the woven fabrics model. Next, the finite volume method to model heat transfer through the assembly induced by radiation, was used. Finally, the usefulness of the developed model by comparison with experimental results was verified.

2 Experimental

2.1 Materials

Textile assembly intended for multilayer thermal protective clothing was investigated. The assembly consisted of five layers: A- outer shell (woven fabric), B- moisture barrier (membrane), C- nonwoven fabric, D- nonwoven fabric and E- lining (woven fabric). Layer B was laminated on layer C. Characteristic of all five layers was presented in Table 1.

Table 1 Characteristic of the layers forming the tested assembly
Full size table

For both woven fabrics (Layer A and Layer E), both nonwoven fabrics (Layer C and Layer D) and for membrane (Layer B), total porosity P were calculated according to the Eq. 1. Total porosity P was defined as the sum of the porosity of the yarn, Pyarn and the porosity resulting from the space between the warp and weft yarns, Pwarp-weft. Pyarn was determined based on cross-sectional images of yarns obtained by scanning electron microscopy and the Image J software application.

$$ P=\left(1-\frac{M_p\cdot {10}^{-3}}{d\cdot \rho}\right)\cdot 100\% $$
(1)

where: Mp– mass per unit area in g·m−2, d – thickness in mm, and ρ– density of the raw material in g·cm−3.

All the layers were made of flame retardant raw material, and perform different functions. Layer A is responsible for protection against mechanical wear and tear. Layer B is a waterproof, semi-permeable membrane, it provides water vapour (sweat) transfer from the skin to the environment. Layers C and D are thermal insulations. Finally, E is the lining. In the Fig. 1 images of cross-sections of the different layers obtained by scanning electron microscope, SEM (Nova Nanosem 230 FEI, USA) were presented.

Fig. 1
figure 1

SEM images of separated layers of tested assembly

Full size image

2.2 Test apparatus and method

The heat transfer through the multilayer assembly when exposed to heat radiation in a transient state was tested. Before testing the samples were conditioned for 24 h at the temperature of 22 °C and RH of 65%.

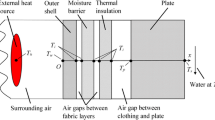
The tests were performed with a laboratory test apparatus conforming to the EN ISO 6942, under following ambient conditions: temperature of 25 °C and RH 35%. Figure 2 illustrates the measurement system.

Fig. 2
figure 2

Scheme of measurement system according to EN ISO 6942

Full size image

The measurement system consisted of a heat radiation source, a calorimeter, a thermometer and a dedicated software. During the course of the experiment the heat radiation source generates heat flux directed towards the outer surface of the sample (Layer A). The incident heat radiation caused rise of temperature of the sample outer surface and as the result the temperature rise of subsequent layers (from Layer A to Layer E). The inner surface of sample (Layer E) was in direct contact with the copper sensor of the calorimeter connected to a digital, computer driven thermometer. The purpose of the experiment was to determine the dependence of Layer E temperature versus time exposure of sample to heat radiation (Fig. 2). Results of measurements of the average temperature of Layer E were recorded in 1 s intervals until its temperature increased to 50 °C. The heat radiation was emitted by source of area equal to 320 cm2 and having the temperature of 1100 °C. The tests were performed for three values of incident heat flux density: 5 kW·m−2, 10 kW·m−2 and 20 kW·m−2, which corresponded to 35 cm, 24 cm and 17 cm, distances between the source and the sample. The results of these tests were the average values of three independent measurements performed for each of the three above mentioned levels of incident heat flux density.

On the basis of determined dependence T = f(t), the following parameters describing the thermal protection properties of heat protective clothing, crucial from commercial and legal point of view, were calculated according to EN ISO 6942:

  1. 1.

    Transmitted Heat Flux Density (THFD) – heat flux density transmitted through sample exposed to heat radiation,

  2. 2.

    Heat Transmission Factor (HTF) - ratio of the transmitted heat flux density through the sample to the incident heat flux density,

  3. 3.

    Radiant Heat Transfer Index (RHTI) - time to achieve a temperature rise of 24 °C in calorimeter when testing the sample with a specified incident heat flux density (this temperature rise indicates that the user experienced second degree burns).

3 Modeling

3.1 Model design

In the created 3-D model of multilayer assembly (Fig. 3) both woven fabrics (Layer A and Layer E) were mapped with the following geometric parameters: woven fabric thickness, distance between the weft yarns, distance between the warp yarns, elliptic shape of yarns cross-section.

Fig. 3
figure 3

3-D Model of tested assembly (a,b); cross section of assembly (c)

Full size image

Average values of all above mentioned geometric parameters were determined on the basis of images obtained by scanning electron microscope. Both nonwoven fabrics (Layer C and Layer D), membrane (Layer B) and yarn in both woven fabrics (Layer A and Layer E) due to their complicated internal structure, were mapped as the homogenized 3D objects with physical parameters (density, specific heat, thermal conductivity coefficient) resulting from appropriate porosity presented in Table 1. In case of two woven fabric models (Layers: A, E), the total porosity P resulted from the porosity of yarn Pyarn and porosity resulting from the free spaces between yarns of warp and weft Pwarp-weft. Pyarn was determined on the basis of images obtained by scanning electron microscopy.

3.2 Simulations

3.2.1 Physical basis of heat flow simulation

Heat flow in solids and gases

The Solidworks Flow Simulation was applied to model heat transfer using the finite volume method. The calculations are based on energy conservation equations and Navier-Stokes formulas [38] which describes fluid flow. The equations allows for simultaneous calculation of heat transfer in solid and fluid media and take into account energy exchange between these media. The equations mentioned above are supplemented by fluid state equations describing the nature of the fluid by empirical dependencies of fluid density, viscosity and thermal conductivity on temperature. Moreover, applied software allows to calculate (both in the steady state and transient state) 3D distributions of temperature created by: heat transfer in solids (conduction), free, forced, and mixed convection, and radiation [38].

Outer shell (Layer A) and lining (Layer E) in tested textile assembly were made of woven fabrics which were the complex structure of fibers and void spaces between fibers filled by air. In this type of material heat is transported in textile structure through both monofilaments (solid) and air (gas), with simultaneous exchange between these environments. The phenomenon of heat transfer in fluids describes the following conservation equation:

$$ \frac{\partial }{\partial t}\left[\rho \left(h+\frac{u^2}{2}\right)\right]+\frac{\partial }{\partial {x}_i}\left[\rho {u}_i\left(h+\frac{u^2}{2}\right)\right]=\frac{\partial }{\partial x{}_i}\left[{u}_j\left({\tau}_{ij}+{\tau}_{ij}^R\right)+{q}_i\right]+\frac{\partial p}{\partial t}-{\tau}_{ij}^R\frac{\partial {u}_i}{\partial {x}_j}+\rho \varepsilon +{S}_i{u}_i+{Q}_H $$
(2)

wherein Si = Siporous + Sigravity + Sirotation is the volume-distributed external force per unit volume (in N·m−3) due to porous media resistance (Siporous), buoyancy (Sigravity = −ρgi) and the coordinate system rotation (Sirotation). The subscripts denote summation over the three coordinate directions. The heat flux density expresses the following equation:

$$ {q}_i=\left(\frac{\mu }{P\kern0em r}+\frac{\mu_t}{\sigma_c}\right)\frac{\partial h}{\partial {x}_i};\kern1em i=1,\kern0.33em 2,\kern0.33em 3 $$
(3)

where:

$$ {\mu}_t=\frac{C_{\mu}\rho {k}^2}{\zeta } $$
(4)

The constant Cμ is determined according to [38] as equal to Cμ = 0.09, whereas σc = 0.9. The equations describe both laminar and turbulent flows. Additionally, transitions from one case to another and back are possible, k is turbulent kinetic energy while ζ, J·kg−1·s−1 is turbulence dissipation (rate at which turbulence kinetic energy is transformed into thermal internal energy). The parameters k and μt are zero in case of pure laminar flows. The anisotropic heat conductivity in solid media is described by the following equation:

$$ \frac{\partial \left(\rho e\right)}{\partial t}=\frac{\partial }{\partial {x}_i}\left({\lambda}_i\frac{\partial T}{\partial {x}_i}\right)+{Q}_H $$
(5)

where e = cT. The heat conductivity tensor is diagonal to the considered coordinate system and heat transport within textile is direction-independent, i.e. one can introduce an isotropic medium and can denote λ1 = λ2 = λ3 = λ. The energy exchange between the fluid and solid media is calculated via the heat flux in the direction normal to the solid/fluid interface, having the solid surface temperature and the gas boundary layer characteristics, if necessary.

Thermal radiation

The used software allows to simulate thermal radiation based on a so-called discrete transfer model. According the model the radiation leaving the surface element in a specified range of solid angles can be approximated by a single ray. The radiation heat is propagated along a series of rays emanating from the radiative surfaces only. Rays are then traced as they traverse through gas and transparent solid bodies until it hits another radiative surface. The thermal radiation defined by the surface or radiation source is expressed as a sum of material radiation (described by the surface emissivity and A prescribed area of radiation) and incoming radiative transfer. This problem is defined by the following equation [38]:

$$ {Q}_T^{out}=\varepsilon \cdot \sigma \cdot {T}^4\cdot A+\left(1-\varepsilon \right)\cdot {Q}_T^{in} $$
(6)

The main outcome of the radiation heat transfer calculation is temperature of surface of a solid or its internal temperature. But, these temperatures are also affected by heat conduction in solids and solid/fluid heat transfer. To see the results of radiation heat transfer calculation only one can view the leaving radiant flux over the selected radiative surfaces at surface plots.

3.2.2 Conditions of heat flow simulations

The main goal of the simulation was to calculate the time dependence of the inner surface average temperature of the multilayer assembly model for the same three levels of incident heat flux that were applied during the experiment. For this purpose a measurement system model was created (Fig. 4). This model consisted of a heat radiation source model and the sample model. The simplifying assumption that the heat radiation source was a rectangular plate with a surface area equal to 320 cm2 was made. The initial ambient conditions of simulations matched the initial conditions recorded during the experiment. The same three distances between models of the radiation source and the sample: 35 cm, 24 cm and 17 cm were modeled. These distances corresponded to the three values of incident heat flux density: 5 kW·m−2, 10 kW·m−2 and 20 kW·m−2, respectively.

Fig. 4
figure 4

Model of mulitalyer assembly (sample) and model of heat radiation source placed inside computational domain. Initial conditions: Tair = 25 °C, pair = 1013.25 hPa, Tsample = 25 °C, RH = 35%

Full size image

The heat radiation source model and the sample model were placed in a rectangular computational domain that was divided into 177,894–365,567 cells (8034–165,541 fluid cells, 1142–1666 solid cells and 168,718–365,580 partial cells). The number of cells depended on the distance between the heat radiation source and the sample. To eliminate the effects of asymmetric boundary conditions, software settings were applied to imitate an infinite five layers of multilayer assembly propagating outside of the domain in all four directions. Physical parameters of raw materials assigned to sample model were presented in Table 2 [39, 40].

Table 2 Physical parameters of raw materials applied in simulations
Full size table

4 Results and discussion

Experimental and simulated results (Fig. 5) showed a clear dependence between the average temperature of the inner surface of the tested textile assembly (Layer E) and the heat flux density incident on the outer surface of the assembly (Layer A).

Fig. 5
figure 5

The average temperature of layer E of the assembly versus exposure time of the layer A to heat radiation (solid line – experiment, dot line – simulation)

Full size image

Experimental results showed that the heating process of layer E can be divided into two stages. Duration of the first stage varies from 5 s for the smallest heat flux of 5 kW·m−2 to 1 s for the greatest heat flux density of 20 kW·m−2. During this time the temperature remains approximately constant. One can associate this stage with multilayer structure of the sample and thermal inertria of the calorimeter. This thermal inertria could affect the accuracy of layer E temperature measurements. During the second stage of the heating process the temperature of layer E is approximately a linear function of time with the slope proportional to the sample heating rate.

In contrast to the experimental results, performed simulations do not exhibit the first stage, during which the temperature of layer E remained constant. It should be noted that the temperature of layer E of the sample model was computed directly without taking a model of the calorimeter into account. As presented in Fig. 4 the measurement system model was created only from the heat radiation source model and the multilayer textile sample model. One can note that the simulations consistently underestimated the rate of heating of the sample model for all heat flux conditions. The slope of the temperature vs. time simulated curves is smaller than those determined experimentally.

In Table 3 the Transmitted Heat Flux Density (THFD), Heat Transmission Factor (HTF) and Radiant Heat Transfer Index (RHTI) determined from simulations and experiments were presented.

Table 3 Experimental and simulated thermal parameters of tested assembly
Full size table

Relative differences between experimental and simulated parameter depended on the level of incident heat flux density are: 7%–20% for THFD, 7%–20% for HTF and 3%–19% for RHTI. The comparison of the simulation and experiment values of these three parameters showed the highest compliance between the results for the smallest value of incident heat flux density (5 kW·m−2). As expected, the RHTI value decreases with an increase of the incident heat flux density. Both experimental and simulated results showed that as the incident heat flux density increases, the value of HTF parameter decreases (Table 3). This means that the tested textile assembly effectively reduces heat transfer when exposed to intense radiant heat.

Visualization of temperature growth in time resulting from heat radiation falling on the layer A of the tested five layers assembly model was presented in Fig. 6. Performed simulations show the largest increase in the temperature of the outer layer (Layer A) during the first 10 s of it exposure to heat radiation.

Fig. 6
figure 6

Temperature growth in time resulting from heat radiation falling on the layer A of multilayer assembly model (heat flux density of 5 kW·m−2)

Full size image

5 Conclusions

The objective of the study was to investigate the thermal performance of multilayer textile assembly used in protective clothing exposed to heat radiation. The 3D model of real textile assembly intended for clothing in a CAD environment was designed. The finite volume method to estimate the thermal protection properties of this multilayer textile assembly was used.

Performed simulations gave results correlating with experimental curves describing dependence of temperature of assembly inner layer versus exposure time of assembly outer layer to heat radiation. On the basis of the simulation and the experiment, the three thermal parameters of protective clothing (THFD, HTF and RHTI) were calculated. The results of experimental measurements correlated with simulation outcomes and the differences between them varied depending on the intensity of heat radiation incident on the tested multilayer assembly. These differences may result from both modeling issues (concerning above all simplification of complicated geometry of real textiles) like:

  • Homogenization (fibers raw materials and air) instead of taking into account individual fibers and spaces between them filled with air in the models of textiles,

  • In model of woven fabrics, elliptic cross-section of yarn equal in all repeat, was assumed. In the actual woven fabrics the yarn cross-section, as a result of frictional forces between the crossing of warp and weft, is changing,

  • Mutual contact of neighboring layers (affecting the phenomenon of inter-layer thermal conductivity) may be different in the designed model than in the real multilayer assembly.

and application of calorimeter with thermal inertria which could affect the accuracy of measurements of temperature of assembly inner layer.

Despite the above mentioned many simplifications, the applied software and developed geometrical model of multilayer assembly allows to predict three thermal parameters of protective clothing with an error of 3%–20%. Basing on the presented results of simulations performed by the computational fluid dynamics verified by experiment one can conclude that applied modeling method allows:

  • to examine the thermal properties of protective clothing still at the design stage (without the need to produce actual clothing),

  • to learn about the influence of geometric parameters and physical properties of individual layers of protective clothing on critical parameters that determine the thermal protection properties of protective clothing,

  • to optimize the thermal protection and comfort properties of functional clothing.