1 Introduction

The wet steam flow field in convergent-divergent (de Laval) nozzles has been analysed continuously by many researchers since the early 1960’s. Starting from the analytical approach, through experimental testing, to the application of Computational Fluid Dynamics (CFD) tools, the phenomenon of homo- and heterogeneous condensation in transonic flows of wet steam is identified better and better.

The strongest interest in steam condensing flows could be observed in the 1960’s and 1970’s. Gyarmathy’s works [1, 2] mark the greatest progress in the analytical approach to the problem. They prove that the moisture-related loss is affected first and foremost by the condensation zone location and the size of the droplets that arise in the process. The earliest examples of experimental testing of steam condensing flows in the de Laval nozzle are described in the works published by Barschdorff [3, 4], Barschdorff and Filippov [5], Moses and Stein [6] or Puzyrewski and Król [7, 8]. They concerned homogeneous (spontaneous) condensation in the first place, but they were used by many researchers to verify numerical models [e.g. 9]. Further experiments provided interesting quantitative results, such as the local measurement of the droplet size.

Numerical modelling of the flow field of the steam condensing flow in the de Laval nozzle became possible only in the late 1980’s, mainly owing to fast advancements in the computer technology. First attempts to perform two-dimensional numerical modelling of water vapour flows with the condensation phenomenon are presented in Bakhtar and Tochai’s work [10]. The works of Young [11] and Schnerr [12] are also worth mentioning.

Nowadays, the numerical research on condensing steam flows modelling in nozzles and turbine cascades are still valid and are under consideration of many researchers [13,14,15].

It seems that these complementary analytical, experimental and numerical studies conducted in the last 50 years or so should make it possible to thoroughly identify the physics of the wet steam condensation phenomenon in transonic flows and develop computational models offering an unequivocal flow field solution, regardless of the applied CFD numerical code. However, this is not the case, which is confirmed by numerical testing performed within the “Wet Steam Conference” in Prague in 2016. The project was carried out with the participation of scientists from many academic and research centres around the world (including industrial ones). The de Laval nozzle numerical calculations performed under the project gave significantly different results, despite the fact that the results were obtained using very similar methods and computational models [16]. The differences may first and foremost be the effect of the following factors:

  • the gas equations of state describing properties of water vapour, the gaseous phase in the wet steam (metastable) region mainly, that were implemented in the numerical CFD codes,

  • the small differences in the applied models of nucleation and droplets growth,

  • the differences in the flow conservation equations formulated either for the steam-water mixture (single-fluid model) or for the two phases individually (two-fluid model).

Revealing essential differences in the results of the flow field modelling carried out for wet steam flows with spontaneous condensation and performed by means of various numerical codes and models, both academic and commercial, the project proved that it was justified to continue works in this particular research area. It also emphasized the need for collaboration between scientific centres to develop more reliable methods and numerical models.

2 Subject of the analysis

Having almost 20 years of experience in numerical [9] and experimental [17, 18] testing of transonic steam condensing flows, the scientists at the Institute of Power Engineering and Turbomachinery of the Silesian University of Technology decided to find confirmation of the above-mentioned conclusions of the “Wet Steam Conference” by carrying out experimental and numerical tests for a selected geometry of the de Laval nozzle. The works were performed on an in-house experimental testing facility, and an in-house numerical code and the Ansys CFX commercial program were used. In order to raise the level of difficulty, the selected de Laval nozzle had a very small divergence in the supersonic part (cf. Fig. 1), corresponding to the outlet Mach number for the non-condensing (adiabatic) flow of 1.5. The effect of such a small divergence of the nozzle supersonic part is that the condensation wave location is strongly dependent on the boundary layer model, the applied condensation model and even slight changes in total temperature at the nozzle inlet. For a low expansion rate, the condensation wave location is also very sensitive to even small changes in the gaseous phase thermodynamic properties, which cannot be precisely calculated without using accurate equation of state for steam.

Fig. 1
figure 1

Geometry of the analysed de Laval nozzle for the Mach outlet number of approx. 1.5

Full size image

Numerical modelling was carried out using an in-house CFD code and the commercial Ansys CFX program. For both applied CFD codes the numerical simulation was based on time-dependent 3-D RANS equations. Together with mass, momentum and energy conservation equations formulated for the vapour/water mixture (single-fluid model), two equations for the SST turbulence model and three additional transport equations for the liquid phase are solved. For the two-phase non-equilibrium flow it is assumed that the volume occupied by droplets is negligibly small. The models does not take account of the interaction between droplets. The heat exchange between the liquid phase and the solid boundary, as well as the velocity slip between the vapour and the liquid phase are neglected.

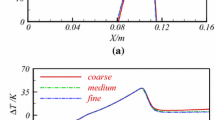
The numerical calculations were performed using the same numerical mesh with 501x121x3 computational nodes (cf. Fig. 2) for both codes mentioned earlier. The number of the nodes was selected to ensure a solution that would be independent of further refinement of the numerical mesh. Calculations carried out on coarser meshes indicated very similar locations of the condensation wave, but the wave intensity varied. Moreover, the condensation models used in both codes include identical relations describing the nucleation and the droplet growth models [9, 19]. For spatial discretization in both codes the high order of accuracy was applied, in the case of the in-house the third-order MUSCL scheme was used.

Fig. 2
figure 2

Numerical mesh for analyzed de Laval nozzle

Full size image

Solver criteria and many other relevant settings of the commercial code were set according to the Ansys recommendation for the wet steam flows calculations. A detailed description of the model applied in the in-house code can be found in e.g. [9] and in the Ansys CFX program in e.g. [19].

The numerical results were compared to the measurement results obtained on the laboratory stand (cf. Fig. 3), i.e. to the static pressure distribution along the nozzle, the flow field image obtained using the Schlieren technique and the measured wetness mass fraction and the mean size of droplets at the nozzle outlet. The experimental tests were carried out using the steam tunnel installation located in the SUT Thermal Machinery Hall. A more detailed description of the experimental facility and measured techniques used in the experiment are presented e.g. in [17, 18] and [20, 21].

Fig. 3
figure 3

Photograph of the laboratory stand with the installed measured nozzle

Full size image

Two measuring series were selected from a number of experimental measurements. They differ in the total temperature value at the nozzle inlet at an almost identical value of total pressure. In the first case, the total pressure and the total temperature values at the nozzle inlet are p0 = 124 kPa and t0 = 118°C, respectively. In the second case, p0 = 128 kPa and t0 = 121°C. Such a small difference in total pressure at the nozzle inlet does not affect the condensation wave location, but a change in total temperature, even as slight as 1 degree, may have a substantial impact [9], especially for nozzles with a low outlet Mach number.

The inlet boundary conditions for the selected test cases calculations are the values of total pressure and total temperature from experiment. In each case, inlet steam is superheated and at the outlet parameters are defined by means supersonic boundary conditions.

The results of numerical computations performed using the in-house code [9] and the commercial Ansys CFX program [19, 22, 23] and their comparison with own experimental testing results are presented below.

3 Analysis of results

3.1 Results for case 1; p0 = 124 kPa and t0 = 118°C

Figure 4 presents a comparison of the static pressure distribution along the nozzle obtained by means of CFD computations performed using the in-house code, the commercial Ansys CFX program and measured on the laboratory stand of the Institute of Power Engineering and Turbomachinery. It can be seen clearly that the pressure distributions produced by the in-house code and the commercial program are both different from the experimental data. The pressure distribution obtained from the computations using the Ansys CFX code points to the condensation wave location right downstream the nozzle critical cross-section, i.e. much earlier than suggested by the measurement results. In the case of the in-house code computations compared to the measurement results, the obtained pressure distribution indicates that the condensation wave is shifted slightly further downstream, towards the nozzle outlet.

Fig. 4
figure 4

Distributions of static pressure and the Mach number along the nozzle for p0 = 124 kPa and t0 = 118°C (ooo experiment, ––– in-house code, −•–•– Ansys CFX program)

Full size image

The symbols size of the static pressure measurement results presented in Fig. 4 and 9 take account of the range of the error and uncertainty of the measurement of pressure (totalling ±200 kPa) and the measuring point location.

The different location of the condensation wave indicated by the computations performed by means of the in-house code and the commercial program has also an impact on the value of the outlet Mach number, which totals 1.4 for the former and slightly above 1.2 for the latter. Such considerable differences between the results produced by the two CFD codes are difficult to explain, especially in view of the fact that the condensation model applied in them is almost identical, i.e. both the nucleation model and the droplet growth model are the same [9, 19].

The differences can also be observed comparing the wetness mass fraction distribution, the mean droplet size and the nucleation rate (cf. Fig. 5). The wetness mass fraction and the mean diameter of droplets for the in-house code computations are slightly higher compared to the Ansys CFX program and lower than the values obtained from measurements at the nozzle outlet.

Fig. 5
figure 5

Liquid phase parameter distribution along the nozzle for p0 = 124 kPa and t0 = 118°C (ooo experiment, ––– in-house code, –•–•– Ansys CFX program)

Full size image

Essential differences between the computation results obtained using the in-house code and the commercial program can also be seen on the expansion line (cf. Fig. 6). For the commercial Ansys CFX software package the increment in entropy on the condensation wave is relatively small, and the specific entropy value rises along the expansion line. The computations using the in-house code point to a considerable increment in entropy on the condensation wave, and the entropy value remains constant until the nozzle outlet. This is fairly justified because flow losses arising along the nozzle centre can increase only on the condensation wave or on the shock wave. In this case, the increment in entropy on the condensation wave is accompanied by a drop in total pressure and a rise in total temperature due to the heat exchange between the phases. A continuous rise in entropy along the nozzle, on the other hand, may lead to the conclusion that the longer the nozzle, the much higher the losses, which can be arguable. Despite the almost double increment in entropy for the in-house code, the losses are by less than 1% higher compared to those obtained for the results obtained from the commercial program. Isentropic efficiency calculated for the results produced by the in-house code and the Ansys CFX commercial program is 98 and 98.8%, respectively.

Fig. 6
figure 6

Expansion line along the nozzle for p0 = 124 kPa and t0 = 118°C (––– in-house code, –•–•– Ansys CFX program)

Full size image

The differences between the numerical computations performed using the in-house and the commercial CFD code can also be noticed in the flow field images obtained by means of the Schlieren technique (cf. Fig. 7) and in the Mach number isolines (cf. Fig. 8). The condensation wave location corresponds to the jump in static pressure presented in Fig. 3 for the three cases under consideration.

Fig. 7
figure 7

Numerical (∇ρ = −10÷10 kg/m4, Δ∇ρ = 0.2 kg/m4) and experimental Schlieren image for p0 = 124 kPa and t0 = 118°C

Full size image
Fig. 8
figure 8

Mach number isolines for p0 = 124 kPa and t0 = 118°C (M = 0÷1.2, ΔM = 0.05)

Full size image

3.2 Results for case 2; p0 = 128 kPa and t0 = 121°C

A change in total temperature at the nozzle inlet by 3 degrees, at a very similar total pressure value, had a substantial impact on the condensation wave location, which can be seen in the figures presented below. The comparison of static pressure values along the nozzle (cf. Fig. 9) indicates that for the modelling results produced by the Ansys CFX code, the condensation wave is located much closer to the nozzle critical cross-section compared to the experiment. Compared to previous results, the condensation wave location is shifted slightly downstream only, towards the nozzle outlet, which seems incomprehensible considering the rise in the total temperature value by as much as 3 degrees. Like in the previous case, the pressure distribution obtained using the in-house code shows that the condensation wave location is slightly shifted towards the nozzle outlet compared to measurements. Also the intensity of the condensation wave modelled by means of the in-house code is smaller than indicated by the measurements, unlike the results produced by the Ansys CFX code, where for both cases under analysis the condensation wave intensity is very high.

Fig. 9
figure 9

Distributions of static pressure and the Mach number along the nozzle for p0 = 128 kPa and t0 = 121°C (ooo experiment, ––– in-house code, –•–•– Ansys CFX program)

Full size image

The liquid phase parameters presented in Fig. 10 confirm the earlier observations concerning the intensity of the wave modelled by the two codes. They also show a fairly similar value of the wetness mass fraction and a higher value of the mean droplet size obtained from the in-house code. The measured Sauter diameter, D32, is by more than 50% bigger compared to the volume diameter obtained from the calculations.

Fig. 10
figure 10

Liquid phase parameter distribution along the nozzle for p0 = 128 kPa and t0 = 121°C (ooo experiment, ––– in-house code, −•–•– Ansys CFX program)

Full size image

The expansion line determined on the streamline (cf. Fig. 11), along the nozzle centre, demonstrates a clear jump in entropy in the condensation wave location. Compared to the in-house code, the entropy increment on the condensation wave is much smaller for the results obtained from the Ansys CFX code, although the wave intensity is much higher. The more abrupt rise in pressure on the condensation wave should involve bigger losses, which is suggested by the much lower outlet Mach number for the commercial code results – approx. 1.2 compared to almost 1.4 for the in-house code. The drop in velocity at the nozzle outlet from the adiabatic flow value (~1.5) is therefore significant. The different outlet Mach number values are mainly the effect of differences in absolute velocity because the outlet temperature value is similar in both cases, which means that the speed of sound should be similar too.

Fig. 11
figure 11

Expansion line along the nozzle for p0 = 128 kPa and t0 = 121°C (––– in-house code, −•–•– Ansys CFX program)

Full size image

The condensation wave location and intensity can be assessed easily and conveniently based on the flow field image obtained using the Schlieren technique, i.e. the density gradient (cf. Fig. 12) and the Mach number isolines (cf. Fig. 13). It can be seen clearly that the low intensity of the condensation wave modelled by the in-house code impedes determination of the wave location by means of the Schlieren technique. This is not the case for the results given by the commercial code or the Schlieren image obtained from the experiment.

Fig. 12
figure 12

Numerical (∇ρ = −10÷10 kg/m4, Δ∇ρ = 0.2 kg/m4) and experimental Schlieren image for p0 = 128 kPa and t0 = 121°C

Full size image
Fig. 13
figure 13

Mach number isolines for p0 = 128 kPa and t0 = 121°C (M = 0÷1.2, ΔM = 0.05)

Full size image

4 Summary and conclusions

The comparative analysis of the wet steam flow with spontaneous condensation through the de Laval nozzle provides unequivocal confirmation of significant differences that occur between the results obtained from numerical computations by means of different CFD codes and from measurements.

In the paper, the numerical and experimental results for one nozzle geometry and two inlet boundary conditions were discussed. For both applied CFD code the same flow governing equations formulated for stream/water mixture are solved. The set of five partial differential equations was supplemented by the same SST turbulence model and the same condensation theory. Also, the same numerical mesh was used. The presented results are complementary and all important flow quantities were compared, including expansions lines. The CFD results were validated against measurements in terms of static pressure distribution along the nozzle, droplet size at the nozzle outlet and Schlieren pictures.

Some thought should be given to decide which results should be considered as more reliable – those obtained on the laboratory stand, despite the measuring errors and uncertainty related mainly to the wetness mass fraction measurements, or those produced by the commercial CFD code, which is eagerly applied by academic researchers and often treated as the ultimate authority.

A definite conclusion is that research on numerical modelling and experimental testing of the steam condensing flow should be continued. Numerical studies should focus not on the existing models calibration, through introduction of calibration coefficients into the models of nucleation or the droplet growth, but rather on the search for a physical justification for the differences and divergence in the results compared to measurements.