1 Introduction

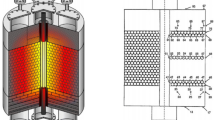
Iron ore pellets is a highly refined product supplied to the steel making industry to be used in blast furnaces or direct reduction processes. The use of pellets offers many advantages such as customer adopted products, transportability and mechanical strength. Yet the production is time and energy consuming. Being such, there is a natural driving force to enhance the pelletization in order to optimize production and improve quality. LKAB, a Swedish mining company, has several pelletizing plants of grate-kiln type. The grate-kiln plant consists of a grate, a rotating kiln and an annular cooler. Before being loaded onto a moving roster that goes through all the zones in the grate, the iron ore has already been processed in several steps, in the last step before the roster the ore has been rolled into so-called green pellets that consists of a relatively large amount of water, magnetite and different additives chosen to fit the demand from the customer. When these pellets are loaded onto the roaster a bed is formed with a mean height of 0.2 m. The grate is divided into four zones, see Fig. 1, in which the green pellets are first dried by forcing air through the pellet bed upwards, up draught drying (UDD), and downwards, down draught drying (DDD) [29, 30]. In the third zone the green pellets are heated to high temperatures in the tempered preheat (TPH) zone and then in the preheat (PH) zone where the pellets are oxidized to some extent. After the grate the green pellets are fed into a rotating kiln to sinter the pellets with aid of a burner fuelled with coal. In a last stage the pellets are cooled in an annular cooler supplying the rest of the system with heated air. Throughout these zones a temperature gradient is formed in the bed. This gradient should be as even as possible throughout the zones to ensure an even quality of the pellets.

Fig. 1
figure 1

Main components of a typical grate-kiln plant

Full size image

Heat transfer in a porous media is of great importance in a large number of areas, as the use of metal foams in applications such as heat exchangers [9] solar dryers for food and crop drying [7] and in pebble bed reactors [42] to mention a few.

Previous work has been conducted to study fluid dynamic phenomena in the traveling grate zone of a grate-kiln plant [4, 5] as well as in rotary kiln [23,24,25]. Of special interest is how the incoming process gas, leakage, and the detailed composition of the pellet bed influence the heat transfer through the bed. To be able to study this coupled behavior numerical models are here developed with which the heat transfer can be examined. To achieve the goals and create a trustful model for the heat transfer, the model must be built up in steps. Heat transfer to a bed of iron ore pellets is therefore examined numerically on several scales. In an earlier work by Burström et al. [6] a continuous model was compared against a discrete Voronoi discretization model showing that mean values can be approximated with a 1D model. Here a full Navier-Stokes model is added to the comparison with a turbulent flow and an uneven temperature profile on the inlet. Two different modelling strategies for the porous bed are compared. The first is a macro model approach that uses Computational Fluid Dynamics (CFD) with a continuum based porous media model for the bed of iron-ore pellets. In the second strategy a discrete micro-level model is applied where the pore space between the pellets is divided into cells with modified Voronoi diagrams. The convective heat transfer of hot fluid flow through the system including dispersion due to random configuration of the pellets is then modelled [16, 19, 31]. A random packing of spheres is considered and temperature distributions in time are compared resulting in conclusions about the advantages and drawbacks of respective model.

The discrete model in this article has earlier been used to model mass and heat transfer in a two-dimensional system of pellets [31]. The model has now been developed to handle a three-dimensional system of pellets [18] and it can now also be used to model compressible flows [6].

2 Theory

A main issue for a continuous model is the large quantity of pores in the domains of the porous media. This makes simulations that resolve the flow within each pore difficult to perform, or in many cases impossible. To solve the problems some kind of simplification is often required. One method is to volume average the transport equations to get averaged flow fields through the porous media [41].

2.1 Heat Transfer

When the thermal properties between the heated air and the pellets are similar, a Local Thermal Equilibrium (LTE) model can be used, i.e. in a LTE model just one energy equation has to be solved. The concept is that an effective thermal conductivity is introduced that takes care of both dispersion and effects of tortuosity [10]. If the thermal properties differ to a certain degree a Local Thermal Non-Equilibrium (LTNE) model has to be used. In that case two energy equations are set-up and solved, one for each phase. In models like this there is a need for exchange terms between the phases that are modelled either empirically [3] or by using constitutive equations [9, 36].

In a packed bed of pellets were the pellets are regarded as impermeable [28] heat can be transferred in various ways [43], including:

  • Conduction (Pellet-roster, pellet-pellet, within pellet)

  • Convection (Pellet-fluid, roster-fluid)

  • Radiation (pellet-pellet, pellet-roster)

as illustrated in Fig. 2.

Fig. 2
figure 2

Heat transfer in a porous bed: 1) Heat convection between wall and fluid; 2) Convective heat transfer between fluid and spheres; 3) Heat conduction between wall and sphere; 4) Heat conduction between spheres; 5) Radiation between wall and spheres; 6) Radiation between spheres; 7) Radiation between sphere and fluid; 8) Conduction through the fluid and heat transfer due to fluid mixing between particles (dispersion)

Full size image

In addition heat is generated and absorbed during phase changes and chemical reactions. This is primarily vaporization of water during the drying process and oxidation of magnetite to hematite. In the current study focus is on convection and how alterations in the flow influence the heat transfer. Conduction is considered as well as the influence from the convection by a defined relationship between the Nusselt number (Nu), Reynolds number (Re) and Prandl number (Pr) and will be outlined in an upcoming subchapter. Saying this, it should be mentioned that as temperature increases radiation becomes more and more important and chemical reactions kick-off generating heat. These mechanisms are, however neglected in the current study.

2.2 Fluid flow

Defining for the convection of heat in the bed is the fluid flow through it. In a random packed bed of mono-sized spheres the size of the pores will alter and there can be easy flow paths were the penetrating fluid may move faster than in other areas. This will be scrutinized in the current study. Wall effects are however, left for future studies.

The Darcy law is often used to model the flow through porous media for Re below 10 where viscous forces dominate, [17]. It is a linear continuum model that states that the superficial velocity is proportional to the pressure gradient in the same direction according to:

$$ {v}_s=-\frac{K}{\mu}\nabla p $$
(1)

where K is the permeability, μ the dynamic viscosity and p the pressure. Notice that v s is the averaged velocity outside the porous media and to get the averaged velocity inside it, it should be divided with the porosity, γ. For a media consisting of spherical particles the equation often refereed to as the Blake-Kozeny-Carman equation provides an estimation of the permeability as [12]:

$$ K=\frac{\gamma^3{D}_p^2}{150{\left(1-\gamma \right)}^2} $$
(2)

where D p is the diameter of the spheres. For inertia dominated flow experiment have yielded that there is a dependence on the velocity squared and the pressure gradient can be predicted according to the Burke-Plummer equation [12]:

$$ \nabla p=-\frac{\rho }{K}{v}_s^2 $$
(3)
$$ K=\frac{\gamma^3{D}_p}{1.75\left(1-\gamma \right)}. $$
(4)

It has turned out that these expressions are valid for turbulent flow, as well. It may also be argued that in a packed bed of spheres there is a wide range of Re and the flow can simultaneously be Darcian, inertia dominated and turbulent. An alternative should therefore be chosen that takes all the flow regimes and the transition between them into account. This may be done by usage of the empirical Ergun equation [12]:

$$ \frac{\varDelta p}{y}=150\frac{{\left(1-\gamma \right)}^2}{\gamma^3}\frac{\mu \frac{Q}{A}}{D_p^2}+1.75\frac{\left(1-\gamma \right)}{\gamma^3}\frac{\rho {\left(\frac{Q}{A}\right)}^2}{D_p} $$
(5)

where Q is the flow rate through an area A.

2.3 Transport phenomena

An important transfer mechanism in porous media is dispersion. Dispersion is caused by mechanical mixing achieved by motion of the fluid through the pore space and is caused by two different mechanisms: different paths caused by the tortuosity of the porous media and velocity differences within the pores, see Fig. 3. Dispersion is thus caused by the multitude of velocities existing in a porous media.

Fig. 3
figure 3

Schematic of mechanical dispersion

Full size image

The dispersion is not equal in all directions, the one taking place in the mean flow direction is called longitudinal dispersion and the other is called transverse dispersion and the effect can be seen in Fig. 4. The one taking place in the longitudinal direction is typically the larger one and for a certain Pe the dispersion coefficients are proportional to the averaged velocity. The dispersion depends on the arrangement of the material and the local mixing is, for instance, different for a material of foam and a packing of spheres. Any result or correlation is therefore dependent on the arrangement in which they were derived [10]. Dispersion coefficients are often reported in terms of the Pe. This dimensionless number is the ratio of advective transport to the diffusive transport. It is expressed in different ways dependent on which transport mechanism of dispersion that is of interest according to:

$$ Pe=\operatorname{Re} Sc\ or\ \mathrm{RePr} $$
(6)

in the case of species transport and heat transfer, respectively. Here Sc denotes the Schmidt number.

Fig. 4
figure 4

Schematic of the effect of longitudinal and transverse dispersion on mass/heat transport

Full size image

In a general sense the turbulent region for flow in porous media can be defined from a graph for pressure drop data. For a plot made for spheres, like the one in Ergun [12], Eq. (2) is valid for low Re, moving over to the turbulent regime where the effects of inertia takes over and where the Burke-Plummer equation, Eq. (4), is valid. It has been shown that the flow is Darcian for Re < 10 [17] thereafter there is a transition region, which includes effects of inertia up to the point where fully developed flow is achieved at about 1000, see Fig. 5. Experiments yield that there is a gradual transition between the two regions and the turbulence is affected by the packing and particle geometry [35]. Hence there is no definite limit for turbulent flow.

Fig. 5
figure 5

Comparison of different empirical representations for the pressure drop in a packed bed where the dimensionless pressure drop is plotted as a function of Re

Full size image

2.4 Volume averaging, continuous model

The volume averaging approach that is briefly explained below can be used to derive the macroscopic transport equations for mass and heat transfer in porous media [34]. When making the averaging, the size (V) of the representative elementary volumes (REV) is chosen in such a way that it is larger than the microscopic length, but much smaller than the macroscopic one (V c 1/3), see Fig. 6. Below two types of volume averaging are defined. The first is the extrinsic bulk-volume (superficial) average of a quantity Φ over the whole volume V, consisting of both phases:

Fig. 6
figure 6

Schematics of averaging volume when having a porous structure consisting of two phases

Full size image
$$ \left\langle {\phi}_i\right\rangle =\frac{1}{V}\underset{V_i}{\int }{\phi}_i dV $$
(7)

where i denotes the constituent that the property is associated with. To exemplify, the macroscopic velocity defined as 〈v f 〉, is also called superficial velocity.

To get the intrinsic averaged quantity value, i.e. the averaged values for each individual phase, an averaging over the pore/particle volume is carried out as:

$$ {\left\langle {\phi}_f\right\rangle}^f\frac{1}{V_f}\underset{V_f}{\int }{\phi}_f dV $$
(8)
$$ {\left\langle {\phi}_s\right\rangle}^s\frac{1}{V_s}\underset{V_s}{\int }{\phi}_s dV $$
(9)

The intrinsic value is what would be measured experimentally within a packed bed. This can for example be pressure or velocity. Regarding velocity it is often called interstitial or true velocity. Since the porosity is given as, γ = V f / V, the relationship between the superficial and true velocity may be written as v sup  = γv true.

The difference between the local microscopic and intrinsic value of a quantity is defined according to:

$$ {\phi}_i^{\prime }={\phi}_i-{\left\langle {\phi}_i\right\rangle}^i $$
(10)

where \( {\phi}_i^{\prime } \)is the local fluctuation. The following expression for the volume average of a product of two quantities can be expressed in the following way:

$$ \left\langle {\phi}_{i,1}{\phi}_{i,2}\right\rangle =\frac{1}{\gamma_i}\left\langle {\phi}_{i,1}\right\rangle \left\langle {\phi}_{i,2}\right\rangle +\left\langle {\phi}_{i,1}^{\prime }{\phi}_{i,2}^{\prime}\right\rangle $$
(11)

By the use of the definition of volume averaging and the equation above together with the spatial averaging theorem the macroscopic energy equations can be defined from the general transport equations.

2.5 Governing equations

Following Civan [8] the macroscopic formulation of the transport equations has been formed from the microscopic equations by means of the volume average method. The phases interact with each other through exchange terms, i.e. momentum source term that accounts for the pressure drop caused by the porous structure and a correlation to account for the heat exchange. The governing equations are presented on their compressible form and the continuity equation can be written in the following way:

$$ \frac{\partial }{\partial t}\left(\gamma {\left\langle {\rho}_f\right\rangle}^f\right)+\nabla \cdot \left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f\right)=0 $$
(12)

The momentum equation can, in its turn, be written as:

$$ {\displaystyle \begin{array}{l}\frac{\partial }{\partial t}\left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f\right)+\nabla \cdot \left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f\right)=\nabla \cdot \left(\gamma {\left\langle {\tau}_f\right\rangle}^f\right)\\ {}+\left(\gamma {\left\langle {\rho}_f\right\rangle}^f-{\rho}_{ref}\right)\mathrm{g}+\left\langle {S}_{M,f}\right\rangle -\nabla \left(\gamma {\left\langle {p}_f\right\rangle}^f\right)\ \end{array}} $$
(13)

where τ is the stress tensor, the second term to the right relates to gravity and the third term to the right is a momentum source that represent the interaction between the solid and fluid phases. In this case the interaction is, as already mentioned, modelled with the Ergun equation. The stress tensor for a Newtonian fluid is defined as:

$$ {\displaystyle \begin{array}{l}\nabla \cdot \left(\gamma {\left\langle {\tau}_f\right\rangle}^f\right)=\nabla \cdot \left(\mu \left[\nabla \left\langle {\mathrm{v}}_f\right\rangle +{\left(\nabla \left\langle {\mathrm{v}}_f\right\rangle \right)}^T-\frac{2}{3}\delta \nabla \cdot \left\langle {\mathrm{v}}_f\right\rangle \right]\right)\\ {}=\left(\mu \left[\nabla \cdot \nabla \left\langle {\mathrm{v}}_f\right\rangle +\nabla \cdot {\left(\nabla \left\langle {\mathrm{v}}_f\right\rangle \right)}^T-\frac{2}{3}\delta \nabla \cdot \nabla \cdot \left\langle {\mathrm{v}}_f\right\rangle \right]\right)\\ {}=\left(\mu \left[{\nabla}^2\left\langle {\mathrm{v}}_f\right\rangle +\nabla \cdot {\left(\nabla \left\langle {\mathrm{v}}_f\right\rangle \right)}^T-\frac{2}{3}\delta {\nabla}^2\cdot \left\langle {\mathrm{v}}_f\right\rangle \right]\right)\ \end{array}} $$
(14)

The conservation of energy for the fluid phase can be described in the following way:

$$ {\displaystyle \begin{array}{l}\frac{\partial }{\partial t}\left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {H}_f\right\rangle}^f\right)+\nabla \cdot \left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f{\left\langle {H}_f\right\rangle}^f\right)=\\ {}\nabla \cdot \left[{k}_{feff}\cdot \nabla {\left\langle {T}_f\right\rangle}^f\right]+\frac{\partial }{\partial t}\left(\gamma {\left\langle {p}_f\right\rangle}^f\right)+\nabla \cdot \left(\gamma {\left\langle {\mathrm{v}}_f\right\rangle}^f\cdot {\left\langle {\tau}_f\right\rangle}^f\right)\\ {}+{h}_{sf}{a}_{sf}\left[{\left\langle {T}_s\right\rangle}^s-{\left\langle {T}_f\right\rangle}^f\right]+{S}_f\end{array}} $$
(15)

where H is the total enthalpy. The solid phase energy equation can be written as:

$$ {\displaystyle \begin{array}{l}\frac{\partial }{\partial t}\left(\left(1-\gamma \right){\left\langle {\rho}_s\right\rangle}^s{\left\langle {h}_s\right\rangle}^s\right)+\nabla \cdot \left(\left(1-\gamma \right){\left\langle {\rho}_s\right\rangle}^s{\left\langle {\mathrm{v}}_s\right\rangle}^s{\left\langle {h}_s\right\rangle}^s\right)=\\ {}{\chi}_s\left(1-\gamma \right)\nabla \cdot \left[{k}_s\cdot \nabla {\left\langle {T}_s\right\rangle}^s\right]-{h}_{sf}{a}_{sf}\left[{\left\langle {T}_s\right\rangle}^s-{\left\langle {T}_f\right\rangle}^f\right]+{S}_s\end{array}} $$
(16)

where h is the static enthalpy. The second term disappears if the solid matrix is stationary as is the case in this study. In the continuous model the pellets itself form a continuous solid network, thus there is a direct heat transport from pellets to pellets and often a parallel heat assumption is applied. If the direct heat transport from pellets to pellets is disabled in the discrete model i.e. there is a tiny layer of gas between the pellets, the contact area of pellets is negligible or there is some essential heat resistance for the pellets in contact, it would respond to a value of k seff  = 0 in the continuous model. The conduction should be somewhere in between these two extremes and depends on the contact properties, i.e., on the roughness of the pellets, pressure applied on pellets, packing of pellets, porosity. To have a more valid approach for the thermal conductivity for the solid particles that is affected by the particle connections a factor can be used very much like the tortuosity in addition to the porosity. This factor, χ s , the reciprocal tortuosity coefficient is a dimensionless variable that varies from 0 to 1. It is included before k s as a multiplication factor. If the pellets just had point contact in the discrete model it would respond to an χ s  = 0 in the continuous model. In this work the conduction between the pellets modelled by an analytical expression in the discrete model and χ s is set to 0.2 as in Burström et al. [6]. The additional source terms S f and S s also appears in the transport equations for turbulence, therefore they will be described more explicitly in the next chapter. In Eqs. (15) and (16) the specific (effective) surface area between gas and pellets is computed as:

$$ {a}_{sf}=\frac{6\left(1-\gamma \right)}{D_p}. $$
(17)

As correlation for the heat transfer coefficient the empirical one proposed by Wakao et al. [39, 40] is applied. This correlation can be used up to a particle Re of 8500:

$$ {h}_{sf}=\left[2+1.1\mathrm{P}{\mathrm{r}}^{1/3}{\left(\frac{\rho_f{v}_s{D}_p}{\mu_f}\right)}^{0.6}\right]\frac{k_f}{D_p} $$
(18)

where Pr is expressed as:

$$ \Pr =\frac{\mu {c}_{pf}}{k_f}. $$
(19)

The fluid effective thermal conductivity is assumed to consist of a stagnant and dispersion part [1, 2]. Regarding dispersion, results from experiments [11, 40] from a thick bed yield the following approximate estimation for the longitudinal dispersion:

$$ {k}_{feff,z}=\gamma {k}_f+{\left(\rho {c}_p\right)}_f0.5{D}_p{v}_s $$
(20)

The expression yields an approximate asymptotic behavior at very low and high Pe. The real dependence can be different from this expression due to various factors such as: Sc, porosity, packing, dimensions, variation in particle size. For non-Darcian flow the first term is negligible due to a high interstitial velocity and low thermal conductivity and therefore the effective conductivity becomes proportional to velocity.

So far only the decrease in volume available for transport through the porous medium has been taken into account by the porosity, γ. Another often used non-dimensional parameter that accounts for the increase in path length for the fluid as it goes through the medium is tortuosity, ς. It is defined as the average ratio between a straight line between two points in the porous media and the actual flow path. In the work by Jourak et al. [19] it was concluded that the tortuosity factor for the gas phase within 3D randomly mono-sized spherical packing is in the range of 1.38–1.49. In the current study it is thus set to ς = 1.4 which also agrees well with what is suggested in other literature. For lower velocities diffusion becomes more important, and on a macroscopic scale the pure molecular diffusion transport coefficient can be rescaled by using the relationship [32]:

$$ D=\frac{\gamma }{\varsigma }{D}_{void} $$
(21)

When Re < 100 the following correlations has been used [11] for the longitudinal dispersion:

$$ {k}_{feff,z}=\gamma \left[\frac{k_f}{\varsigma }+{\left({\rho}_f{c}_p\right)}_f\frac{0.65{v}_{true}{D}_p}{1+7\sqrt{\frac{\varsigma }{\frac{v_{true}{D}_p}{\frac{k_f}{{\left({\rho}_f{c}_p\right)}_f}/\varsigma }}}}\right]. $$
(22)

For the transverse dispersion the following expression is applied regardless of Re [11]:

$$ {k}_{feff,x}=\frac{\gamma }{\varsigma }{k}_f+{\left({\rho}_f{c}_p\right)}_f\left(1/12\right){D}_p{v}_s. $$
(23)

The matching in the uneven temperature case was done by using a static transverse dispersion coefficient according to:

$$ {k}_{feff,x}=\frac{\gamma }{\varsigma }{k}_f+{\left({\rho}_f{c}_p\right)}_f{D}_{disp} $$
(24)

2.6 Turbulence modelling

Turbulent flow in a packed bed can be modeled in several ways. In many of the models macroscopic equations have been derived from microscopic equations by the use of volume averaging, resulting in additional source terms in the governing equations. These terms have often been derived for 2D structures. In the current study the Nakayama and Kuwahara (N-K) model [33] was chosen because of its simplicity, its closed formulation for the two different source terms and its realistic trend prediction for effective viscosity. The model was successfully validated against experiments for randomly packed monosized spheres in [15]. The N-K model is derived for fully turbulent flows and high Re and as discussed in Guo et al. [15] it is questionable how this model works in the laminar regime. For the case in this article the model should overestimate the effect of turbulence in the bed.

Following Guo et al. [15] the momentum equation for turbulent flow can be written as:

$$ {\displaystyle \begin{array}{l}\frac{\partial }{\partial t}\left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f\right)+\nabla \cdot \left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f\right)=\\ {}\nabla \cdot \left({\gamma \mu}_{eff}\left[\nabla {\left\langle {\mathrm{v}}_f\right\rangle}^f+{\left(\nabla {\left\langle {\mathrm{v}}_f\right\rangle}^f\right)}^T\right]-\gamma \frac{2}{3}{\left\langle {\rho}_f\right\rangle}^f{\left\langle {\kappa}_f\right\rangle}^f\right)\\ {}+\left(\gamma {\left\langle {\rho}_f\right\rangle}^f-{\rho}_{ref}\right)\mathrm{g}-\left\langle {S}_{M,f}\right\rangle -\nabla \left(\gamma {\left\langle {p}_f\right\rangle}^f\right)\kern5.5em \end{array}} $$
(25)

and the energy equation it is modified to the following form:

$$ {\displaystyle \begin{array}{l}\frac{\partial }{\partial t}\left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {H}_f\right\rangle}^f\right)+\nabla \cdot \left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f{\left\langle {H}_f\right\rangle}^f\right)=\\ {}\nabla \cdot \left[{k}_{feff}\cdot \nabla {\left\langle {T}_f\right\rangle}^f+\gamma \frac{\mu_t}{\mathrm{P}{\mathrm{r}}_t}\nabla {\left\langle {h}_f\right\rangle}^f\right]+\frac{\partial }{\partial t}\left(\gamma {\left\langle {p}_f\right\rangle}^f\right)\\ {}+\nabla \cdot \left(\gamma {\left\langle {\mathrm{v}}_f\right\rangle}^f\cdot {\mu}_{eff}\left[\nabla {\left\langle {\mathrm{v}}_f\right\rangle}^f+{\left(\nabla {\left\langle {\mathrm{v}}_f\right\rangle}^f\right)}^T\right]-\gamma \frac{2}{3}{\left\langle {p}_f\right\rangle}^f{\left\langle {\kappa}_f\right\rangle}^f\right)\\ {}+{h}_{sf}{a}_{sf}\left[{\left\langle {T}_s\right\rangle}^s-{\left\langle {T}_f\right\rangle}^f\right]+{S}_f\end{array}} $$
(26)

where:

$$ {\mu}_{eff}=\mu +{\mu}_t. $$
(27)

The Reynolds averaged Navier-Stokes turbulence model used is the k-ε model, where the eddy viscosity in both the momentum and fluid phase energy equation accounts for turbulence and is modelled in terms of the turbulent kinetic energy and its rate of dissipation in a similar way as for a pure fluid:

$$ {\mu}_t={C}_{\mu }{\left\langle {\rho}_f\right\rangle}^f\frac{{\left({\left\langle {\kappa}_f\right\rangle}^f\right)}^2}{{\left\langle {\varepsilon}_f\right\rangle}^f}. $$
(28)

Finally the flow resistance in the porous medium is added through the Ergun equation:

$$ \left\langle {S}_M\right\rangle =150\mu \frac{{\left(1-\gamma \right)}^2}{\gamma^3{d}_p^2}\left\langle {\mathrm{v}}_f\right\rangle +1.75\rho \frac{1-\gamma }{\gamma^3{d}_p}\left|\left\langle {\mathrm{v}}_f\right\rangle \right|\left\langle {\mathrm{v}}_f\right\rangle $$
(29)

The two transport equations for κ and ε can be written as:

$$ {\displaystyle \begin{array}{l}\frac{\partial }{\partial t}\left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\kappa}_f\right\rangle}^f\right)+\nabla \cdot \left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f{\left\langle {\kappa}_f\right\rangle}^f\right)=\\ {}\nabla \cdot \left[\gamma \left(\mu +\frac{\mu_t}{\sigma_k}\right)\nabla {\left\langle {\kappa}_f\right\rangle}^f\right]+\gamma {\left\langle {P}_k\right\rangle}^f-\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\varepsilon}_f\right\rangle}^f+\gamma {\left\langle {S}_k\right\rangle}^f\end{array}} $$
(30)
$$ {\displaystyle \begin{array}{l}\frac{\partial }{\partial t}\left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\varepsilon}_f\right\rangle}^f\right)+\nabla \cdot \left(\gamma {\left\langle {\rho}_f\right\rangle}^f{\left\langle {\mathrm{v}}_f\right\rangle}^f{\left\langle {\varepsilon}_f\right\rangle}^f\right)=\\ {}\nabla \cdot \left[\gamma \left(\mu +\frac{\mu_t}{\sigma_k}\right)\nabla {\left\langle {\varepsilon}_f\right\rangle}^f\right]+\gamma \frac{{\left\langle {\varepsilon}_f\right\rangle}^f}{{\left\langle {\kappa}_f\right\rangle}^f}\left({C}_{\varepsilon 1}{\left\langle {P}_k\right\rangle}^f-{C}_{\varepsilon 2}{\left\langle {\rho}_f\right\rangle}^f{\left\langle {\varepsilon}_f\right\rangle}^f\right)\\ {}+\gamma {C}_{\varepsilon 2}{\left\langle {S}_{\varepsilon}\right\rangle}^f\kern2.25em \end{array}} $$
(31)

where 〈P k 〉f is the generation of turbulent kinetic energy due to turbulent stress, modelled as:

$$ {\displaystyle \begin{array}{l}{\left\langle {P}_k\right\rangle}^f=\nabla {\left\langle {\mathrm{v}}_f\right\rangle}^f\cdot {\mu}_t\left[\nabla {\left\langle {\mathrm{v}}_f\right\rangle}^f+{\left(\nabla {\left\langle {\mathrm{v}}_f\right\rangle}^f\right)}^T\right]\\ {}-\frac{2}{3}\delta \nabla \cdot {\left\langle {\mathrm{v}}_f\right\rangle}^f\left(3{\delta \mu}_t\cdot {\left\langle {\mathrm{v}}_f\right\rangle}^f+{\left\langle {\rho}_f\right\rangle}^f{\left\langle {\kappa}_f\right\rangle}^f\right)\\ {}\kern9.75em .\end{array}} $$
(32)

In these equations 〈S k 〉fand 〈S ε 〉f are additional source terms added to account for the turbulence kinetic energy and dissipation rate caused by the presence of the porous media, see Table 1. As can be seen their influence vanishes in the case of no porous media (i.e. γ = 1). The standard k-ε turbulence model closure constants are [26]:

$$ {\displaystyle \begin{array}{l}{C}_{\varepsilon 1}=1.44\\ {}{C}_{\varepsilon 2}=1.92\\ {}{C}_{\mu }=0.09\kern0.5em .\\ {}{\sigma}_{\kappa }=1.0\\ {}{\sigma}_{\varepsilon }=1.3\end{array}} $$
(33)
Table 1. Source terms in the turbulence equations accounting for flow through a packing of spheres
Full size table

As in the models by Ljung et al. [31] and Burström et al. [6] additional source terms S f and S s have been incorporated into the energy equations to account for temperature gradients inside the spheres. This yields the following extra conduction term in the energy equation:

$$ {S}_f=\frac{3\left(1-\gamma \right)}{20} Nu\ {k}_f\frac{\partial^2{T}_s}{\partial {z}^2}. $$
(34)

In the same manner an additional term in the solid phase energy equation may be expressed as:

$$ {S}_s=\frac{3\left(1-\gamma \right)}{20} Nu\ {k}_f\frac{\partial^2{T}_f}{\partial {z}^2}. $$
(35)

2.7 Discrete model

The flow through a packed bed can also be modelled in detail were the flow in the voids between the particles is resolved. There are several methods to do this but here a method proposed in Hellström et al. [16] is applied. In this approach discrete Voronoi diagrams are used to divide the system of particles into cells, each containing one pellet. The pellets are regarded as impermeable and stationary and there is a non-slip boundary condition on their surfaces. The stream function is consequently constant along these surfaces and the flow field is obtained by minimization of the dissipation rate of energy. In this way dispersion of temperature and mass is introduced in a natural fashion through randomness of the arrangement of pellets. Treating the bed of pellets as a discrete system of particles makes it possible to a study statistical variations of the macroscopic heat transfer coefficients caused by microscopic stochasticity. Variations may originate from distribution of the size of the pellets and their position. The main procedures in the discrete model are:

  • Derivation of the stream function from a minimization of the vorticity.

  • Calculation of the velocity from the stream function distribution.

  • Calculation of heat and mass transfer from the velocity distribution.

Details about the discrete model can be found in Burström et al. [6], Jourak et al. [18] and Ljung et al. [31].

3 CFD Modelling

The flow in a generic slice of a packed bed was modelled and solved in ANSYS CFX15.0, and the simulations were run on a PC cluster with a capacity >400 cores. The porosity in the CFD model is assumed to be constant and equal to 0.41. In reality it is a function of the size and distribution of the pellets throughout the bed. The Ergun equation is used for the flow and the pellets are assumed to be perfectly spherical with a diameter of 12.0 mm. The chemical energy released by the oxidation from magnetite to hematite is not considered.

3.1 Convergence and grid independence, 1D/3D

To ensure a grid independent solution, a grid refinement study was preformed to estimate the discretization error. The continuous grid has one element in both the width and depth direction and the grid refinement was consequently done over the height of the bed. The study was preformed with sixteen hexahedral grids where the number of elements ranged from a crude resolution up to 5000 in the height direction of the bed. Several variables were investigated including the gas and solid temperature at different positions in the bed and at different times, as well as the pressure and the pressure recovery factor, F, which is an integrated quantity defined as:

$$ F=\frac{\frac{1}{A_{out}}{\int}_{A_{out}}p\; dA-\frac{1}{A_{in}}{\int}_{A_{in}}p\; dA}{\frac{1}{2}\rho\;{\left(\frac{Q_{in}}{A_{in}}\right)}^2}. $$
(36)

In this equation A is the area, p is the total pressure, ρ is the average density over the whole domain and Q is the flow rate. The representative edge length h 1D that is later used to visualize the results is defined as:

$$ {h}_{1D}=H/N $$
(37)

where N is the total number of hexahedra and H is bed height. The trend was the same for all variables and all positions. We have here chosen to present the results for the gas phase in a point about ¼ up in the bed early in the heating process since of the combinations investigated this is the one giving the largest error. A monotone convergence is achieved, see Fig. 7 and the polynomial curve shows that the solution is in the asymptotic range and that already grid number three with ten elements over the bed height gives an error no more than 0.8%. Since the 1D model is relatively simple the finest grid was anyway used in all the simulations.

Fig. 7
figure 7

Typical plot of gas temperature at a certain height at a certain time, slice

Full size image

The residuals and imbalances were also scrutinized in a sensitivity study to secure that they were small enough. This was carried out for both residuals and the progression of the time step used. The study yielded that the iteration error is negligible at the convergence criteria of max residuals below 1E-4 where the domain imbalances is below 0.5%. The time step used is:

$$ Timestep=1E-4\left[s\right]+0.0225\left[{s}^{0.25}\right]\ast {t}^{0.75}. $$
(38)

The results in Fig. 7 corresponds to the quantity giving the largest error of F, pressure and temperature tracked in five different locations evaluated at five different times. A grid consisting of 100 elements gives an error of maximum 0.2% for the quantities evaluated. For the 3D case the domain is 0.2*0.2*0.2 m, beginning with an even temperature of 573.15 K as for the slice and varying the spatial resolution uniformly yielded that an average edge size of h 3D  = 0.002 m, corresponding to 100 elements in each length direction gives the same order of error as in 1D. The average volume grid size is defined as:

$$ {h}_{3D}={\left[\frac{1}{N}\sum \limits_{i=1}^N\left(\varDelta {V}_i\right)\right]}^{1/3}. $$
(39)

As can be seen in Fig. 8, the same kind of convergence is attained.

Fig. 8
figure 8

Plot of the pressure recovery factor, 3D grid

Full size image

A maximum error of 0.2% in a part of the bed early in the heating process is good enough, and this resolution was used in the height direction for the uneven temperature case.

3.2 Boundary conditions and simulation settings

The full Navier-Stokes equations are solved, and the RANS k-ε model has been applied to model the turbulence. The boundary conditions employed in the numerical model mimic the boundary conditions that occur in the UDD zone in reality (the process described in the introduction). The gas heating the bed is treated as ideal and dry. Two different cases are run, one with even boundary conditions mimicking a slice of the bed and one with an uneven temperature profile, therefore also the transversal dispersion becomes important. In both cases the motion of the conveyor belt is neglected. Since the temperature is axisymmetric only 1/4th of the discrete model is modelled where the “walls” having symmetry boundary conditions, i.e. focus in on a section of the bed.

For the 1D model the bed inlet condition is set as a velocity with a superficial velocity of 1 m/s and a temperature of 573.15 K with the flow direction normal to the boundary. At the outlet an average relative static pressure of 0.0 Pa is applied. The turbulent quantity intensity, I, is set on the inlet in the turbulent runs as:

$$ {\kappa}_{inlet}=\frac{3}{2}{I}^2{v_s}^2 $$
(40)
$$ {\varepsilon}_{inlet}=\rho {C}_{\mu}\frac{\kappa^2}{\mu_t} $$
(41)

All simulations were carried out with a second-order discretization scheme and all the properties of the gas are functions of T. To describe the density change the ideal gas law is applied and Sutherland’s formula [38] is used to describe the dynamic viscosity and the thermal conductivity according to:

$$ c={c}_0\frac{T_{ref}+S}{T+S}{\left(\frac{T}{T_{ref}}\right)}^n. $$
(42)

In this expression c 0 is the reference quantity in question, T ref the reference temperature, S the Sutherland constant and n the temperature exponent. A polynomial is used to describe how the specific heat capacity changes with T, see Table 2 for the material properties used for the gas phase. Little is published about the thermal properties for the solid phase (magnetite) and it is assumed that constant material properties can be applied as presented in Table 3.

Table 2. Properties of air
Full size table
Table 3. Properties of solid phase (pellets, magnetite)
Full size table

The turbulence intensity is defined as:

$$ I=\frac{\sqrt{\frac{2}{3}\kappa }}{\sqrt{V_x^2+{V}_y^2+{V}_z^2}}. $$
(43)

In the work by Burström et al. [4, 5] a typical plot of I at the inlet of the bed in the PH and TPH-zone yielded a variation up to 80% as can be seen in Fig. 9. This variation is applied in this work.

Fig. 9
figure 9

Typical contour of the turbulent intensity plotted at a horizontal plane penetrating the inlet of the PH and TPH-zones of a grate-kiln plant

Full size image

3.3 Setup of the system, discrete model

The length of the system is set to be 0.20 m in the main flow direction. For the case of even temperature the other dimensions of the discrete model are 0.12 m giving a sufficient system size for the statistics inside parallel layers normal to the normal flow direction inside the bed. The simulations are run with the same settings as the v sup  = 1 m/s case in Burström et al. [6]. For the uneven temperature case a larger system size is needed of 0.2*0.2*0.2 m. The superficial velocity will vary inside of the layer since the transient heating of the layer is modelled and the density is a function of the pressure and temperature. For the uneven temperature case a Gaussian temperature profile has been set on the inlet as:

$$ {\displaystyle \begin{array}{l}T\left(x,y\right)=\left({265}^{\ast}\exp \right(-\Big({\left(\left(x/1\left[m\right]\right)-0.1\right)}^2+\\ {}{\left(\left(-y/1\left[m\right]\right)-0.1\right)}^2\left)/\left({2}^{\ast }0.04\hat{\mkern6mu} 2\right)\right)+308.15\Big)\left[K\right]\end{array}} $$
(44)

see Fig. 10. For this case the averaged inlet velocity is v sup  = 0.01 m/s. The velocity chosen is a trade-off between high velocity and computational resources noting that the discrete in-house code is not yet parallelized.

Fig. 10
figure 10

Temperature profile used on inlet boundary

Full size image

For both modelling strategies a two-phase heterogeneous energy model is used were different energy equations are solved for the different phases.

4 Results and discussions

As examples of numerical results snaps-shots of the temperature distributions derived from the CFD and discrete models for the even inlet temperature case are shown in Fig. 11. Naturally, the temperature front in the discrete model is not straight as in the CFD model as also shown in Ljung et al. [31]. This is because of the natural dispersion in the system due to the arrangement of the pellets and the uneven velocity distribution as disclosed numerically in Frishfelds et al. [14] and experimentally in Khayamyan et al. [21, 22].

Fig. 11
figure 11

Snaps-shots of gas temperature as derived from the CFD (a), and both the temperature of individual pellets and the gas from the discrete model (b)

Full size image

4.1 Even temperature

The inlet air temperature is 573.15 K and the initial bed temperature is 308.15 K yielding a ∆T = 265 K. When the air moves through the bed, it cool down as it heats the pellets in the bed. Since ρ = ρ(T, p) the volume average Rep (v s ρD p /μ) varies throughout the bed and, as an example, the propagation in time of Rep for the continuous model and v sup  = 1 and 3 m/s can be seen in Figs. 12 and 13, respectively. This variation is also captured with the discrete model and the two models gives nearly the same mean values in temperature history for the gas and for the pellets at different horizontal positions in the bed for v sup  = 1 m/s, see Fig. 14. Also a higher inlet velocity of v sup  = 3 m/s gives a good agreement, but the matching regarding the gas temperature is not as perfect as for the lower velocity, see Fig. 15.

Fig. 12
figure 12

Min, max and volume averaged Re through the bed as a function of time, continuous model, even temperature case, v sup = 1 m/s

Full size image
Fig. 13
figure 13

Min, max and volume averaged Re through the bed as a function of time, continuous model, even temperature case, v sup  = 3 m/s

Full size image
Fig. 14
figure 14

Comparison between discrete and continuous laminar model, the even temperature case. Averaged temperature as a function of time. Positions z = 0.0475 m, z = 0.0975 m and z = 0.1475 m, v sup  = 1 m/s

Full size image
Fig. 15
figure 15

Comparison between discrete and continuous laminar model, the even temperature case. Averaged temperature as a function of time. Positions z = 0.0475 m, z = 0.0975 m and z = 0.1475 m, v sup  = 3 m/s

Full size image

4.2 Turbulence

When the porosity is low and the permeability is not very high, the porous media flow cannot generally be treated as a conventional turbulent flow since the porous medium itself contribute to the turbulence, [27]. However, when using a RANS equation assumption and the N-K model there is a generation of 〈κ f 〉f due to the porous medium, see Chapter 2.6. The amount of mechanical energy that is converted into turbulence is depending on the properties of the porous matrix [17, 27], in this case the quantities of the fluid phase is continuously changing and both the gradient of 〈v f 〉f and the local value through the source term 〈S k 〉f influence the generation of turbulent kinetic energy inside the bed.

As apparent from the above discussion, the transition from laminar to turbulent flow in porous media is not definite and it is thus uncertain when a turbulent model should be activated. However, when varying the turbulence intensity at the inlet it turns out that the exact value does not influence the overall result, see Figs. 16, 17, 18, and 19 where the turbulence intensity values used are based on simulation done with a relevant up- and downstream geometry. The difference between laminar and turbulent gas temperature for five points in the bed is plotted as a function of time to highlight the influence of turbulence and inlet intensity. When comparing the results with and without the N-K model, ignoring wall effects, for an inlet superficial velocity 1–3 m/s and an inlet temperature of 300 °C the differences are small. For the case of v sup  = 1 m/s and a turbulence intensity of 3.7% on the inlet the mean difference is below 0.5 K when comparing the temperature in several points throughout the bed, see Fig. 16. The difference increases when increasing the inlet turbulence intensity to 80%, but this is only notable at the beginning of the bed, see Fig. 17. The reason to the fast decay is that the production and dissipation of turbulence inside the pores of a porous media will be balanced [20] so that the effect of inlet boundary condition disappears at the downstream, which is also seen in Fig. 20.

Fig. 16
figure 16

Comparison of ∆T between continuous laminar and RANS model in five points from the beginning to the end of bed, even temperature case, v sup  = 1 m/s, inlet intensity = 3.7%. Positions z = 0.0025 m, z = 0.0475 m, z = 0.0975 m, z = 0.1475 m and z = 0.1975 m

Full size image
Fig. 17
figure 17

Comparison of ∆T between continuous laminar and RANS model in five points from the beginning to the end of bed, even temperature case, vsup = 1 m/s, inlet intensity = 80%. Positions z = 0.0025 m, z = 0.0475 m, z = 0.0975 m, z = 0.1475 m and z = 0.1975 m

Full size image
Fig. 18
figure 18

Comparison of ∆T between continuous laminar and RANS model in five points from the beginning to the end of bed, even temperature case, vsup = 3 m/s, inlet intensity = 3.7%. Positions z = 0.0025 m, z = 0.0475 m, z = 0.0975 m, z = 0.1475 m and z = 0.1975 m

Full size image
Fig. 19
figure 19

Comparison of ∆T between continuous laminar and RANS model in five points from the beginning to the end of bed, even temperature case, vsup = 3 m/s, inlet intensity = 80%. Positions z = 0.0025 m, z = 0.0475 m, z = 0.0975 m, z = 0.1475 m and z = 0.1975 m

Full size image
Fig. 20
figure 20

Comparison of the turbulent intensity profile throughout the bed height for the continuous RANS model, even temperature case, vsup = 1 & 3 m/s, inlet intensity = 3.7 & 80%, t = 721 s

Full size image

If the velocity at the inlet is increased to v sup  = 3 m/s the difference decreases compared to the v sup  = 1 m/s case. The trend is otherwise the same when increasing the intensity at the inlet as can be seen in Figs. 18 and 19. The weak response when introducing the N-K model is somewhat surprising since the N-K model should over-predict the effect of turbulence. The Reynolds number is however still fairly low and it is not obvious whether the flow in reality should have been inertia dominated or turbulent. The dispersion is considered in all the models and in the next subchapter it will turn out that the influence of production of turbulence in the bed and its influence on the temperature profile is small compared with other mechanisms such as dispersion.

4.3 Importance of different mechanisms

The simulations revealed that the incorporation of generation of turbulence in the models has only a small effect on the temperature distribution. A scaling analysis will here be carried out, further demonstrating the importance of each term contributing to the distribution of temperature. As a verification of the results a comparison is made with the viscosity ratios reached in Guo et al. [15] and there is an agreement for a range of different Rep, ignoring the inlet effect. Knowing this effective viscosity profiles are showed in Fig. 21. It is again obvious that the effect of inlet turbulence intensity is only perceivable at the beginning of the bed.

Fig. 21
figure 21

Comparison of effective viscosity. Continuous RANS model, even temperature case, v sup  = 1 & 3 m/s, inlet intensity =3.7 & 80%, t = 721 s

Full size image

Turbulence affects the temperature distribution in packed beds mainly by convective heat transfer between solid and fluid and the variable k turbulence . Regarding the first mechanism, h sf is obtained from the experimental correlation by Wakao et al. and is identical for the laminar and turbulent simulations. Regarding the second mechanism, the thermal conductivity tensor in the turbulent flow model consists of terms taking care of molecular diffusion, mechanical dispersion and turbulence. Due to high interstitial velocity and low thermal conductivity the molecular diffusion is negligible. Based on the relationships for dispersion valid for Rep > 100 Eqs. (20 and 23), the terms that should be compared are summarized in Table 4:

Table 4 Terms of importance in the apparent thermal conductivity tensor
Full size table

Comparing Eq. (23) for traverse dispersion with the transverse component of turbulence, it is clear that a static ratio is achieved and that transverse dispersion effects are approximately 5 times greater than that predicted by Eq. (35) of Nakayama and Kuwahara [33]. A comparison between Eq. (20) with the k turbulence part of the thermal conductivity tensor during the runs furthermore reveals that the longitudinal dispersion is about 30 times greater that turbulence effects for both the v sup  = 1 and 3 m/s case. Hence, dispersion is much more important than turbulence for the temperature distribution in a porous bed up to a Rep value of at least 1000. This is especially true for longitudinal dispersion.

4.4 Uneven temperature

The standard deviation, σ, of the temperature in a cross section of the bed can be used as a measure of the variation of the temperature. The standard deviation is defined as:

$$ \sigma =\sqrt{\frac{1}{N}\sum \limits_{i=1}^N{\left({x}_i-\overline{x}\right)}^2} $$
(45)

where \( \overline{x} \) is mean value in the section of interest. Evaluating the result from the discrete model it can be seen that the effect of transverse dispersion is quite high as the profile is smeared out after just 0.1 m and σ in the cross section is 7 K. In a parallel cross section a couple of pellet rows from the inlet the standard deviation is reduced from 63 K to 9 K during the first second. The propagation of the temperature profile can be seen in Fig. 22, where snapshots from the discrete model are shown.

Fig. 22
figure 22

Snap shots of the temperature distribution as derived from the discrete model for uneven temperature

Full size image

Since the temperature profile is axisymmetric only a 1/4 of the geometry is modeled in the CFD model, see Fig. 23.

Fig. 23
figure 23

Figure of the inlet in the CFD model. (a) Full sized geometry. (b) Due to axisymmetric conditions just a ¼ of the domain is simulated

Full size image

Using Eqs. (22) and (23) in the continuous model results in a much lower transverse dispersion, see Figs. 24 and 25. However, by using a static dispersion coefficient in Eq. (24) a good comparison can be achieved as can be seen in Fig. 26 and Fig. 27. The use of a constant coefficient also displays that there is a difference in dispersion in different parts of the bed in the discrete model. Steady state profiles for different transverse dispersion coefficients can be seen in Fig. 24. Also σ is shown in Table 5 for five heights in the bed. The large difference in magnitude for the transverse dispersion is an issue for future research but will be shortly discussed here. The difference can be due to several topics related to the modelling of the physics and the steep temperature gradients generated. In particular the geometry for the conduction and dispersion in general are resolved in the discrete model while they are modelled in the CFD case. Hence step gradients in temperature and flow are blurred out in the latter. In a similar manner the continuum approach may fail with such large temperature gradients and relatively large pores. There may also be interplay between pellet conduction and dispersion of temperature that is not captured in the CFD and the transverse conduction may be somewhat over-predicted in the discrete model.

Fig. 24
figure 24

Gas temperature profiles for different dispersion coefficients for the continuous laminar model, for the longitudinal dispersion part is always Eq. (22) used, t = 50,000 s. (a) DT = Eq. (23). (b) DT = Eq. (24) with Ddisp = 0.000025 m2/s. (c) DT = Eq. (24) with Ddisp = 0.0004 m2/s. (d) DT = Eq. (24) with Ddisp = 0.0008 m2/s

Full size image
Fig. 25
figure 25

Continuous laminar model with Eqs. (22) and (23) compared with the discrete model for uneven temperature case. Averaged temperature as a function of time. Positions z = 0.0475 m, z = 0.0975 m and z = 0.1475 m

Full size image
Fig. 26
figure 26

Continuous laminar model with Eqs. (22) and (24) with Ddisp = 0.0004 m2/s compared with the discrete model for uneven temperature case. Averaged temperature as a function of time. Positions z = 0.0025 m, z = 0.0975 m and z = 0.1975 m. Standard deviation from the average value at given cross sections, hard drawn lines –discrete, coloured dashed –continuous

Full size image
Fig. 27
figure 27

Continuous laminar model with Eqs. (22) and (24) with Ddisp = 0.0008 m2/s compared with the discrete model for uneven temperature case. Averaged temperature as a function of time. Positions z = 0.0475 m and z = 0.1975 m. Standard deviation from the average value at given cross sections, hard drawn lines –discrete, coloured dashed –continuous

Full size image
Table 5 Standard deviation of temperature in cross sections throughout the packed bed, continuous laminar model in comparison with the discrete, uneven temperature case, t = 50,000 s
Full size table

5 Conclusions

The simulations indicate that the continuous model can be used if one is interested in mean predictions for even boundary conditions on the inlet to the bed. However, if local values are of great importance the discrete model should be used. It can be concluded that the discrete model can be used for non-Stokian flow as turbulent effects show little influence of the overall heat transfer rates in the continuous model.

For an uneven temperature on the inlet the dispersion is shifting heavily within the bed in the discrete model and cannot be matched by the correlation from a thick bed. The reasons to this are discussed and are topics for future research.