1 Introduction

Fluid motion within porous media takes place in geological, biological and technical processes. This includes ground water flows (Bear 2013; Das et al. 2015) composites manufacturing (Williams et al. 1996; Andersson et al. 2005), and forming and drying of iron ore pellets (Nath and Mitra 2005; Ljung et al. 2012). Due to the vast amount of applications, porous media flow has been a flourishing area of research for more than a century and several topics are still to be disclosed. This includes information about the detailed flow as the Reynolds number (\({Re} = {\textit{UL}}/\nu \) where U is velocity, L characteristic length scale and \(\nu \) kinematic viscosity) increases and the flow becomes inertia dominated, transitional and turbulent. In the review by Hlushkou and Tallarek (2006), it is, for example, stated that the physical reasons for the failure of Darcy law as Re increases are not completely understood although it has since long been proven to exist experimentally and been modelled by the Forchheimer equation.

In the current study, focus is on flow through a packed bed of spheres. Detailed measurements of all three velocity components will be done with stereoscopic particle image velocimetry (stereoscopic PIV) as Re is increased with the aim to reveal some of the details of the flow during different transitions and thereby increase the understanding of the flow. The traditional experimental approach to handle flow within porous media is to measure global parameters such as overall pressure drop and longitudinal and transverse dispersion. This gives empirical correlations that can be used to estimate the behaviour of the porous media (Dixon and Cresswell 1986; Ergun 1952; Gunn 1987). Global parameters can also be derived through modelling from first principles as, for instance, described in Lee and Howell (1987), Kuwahara et al. (1998) and Pedras and Lemos (2000). In Mei and Auriault (1991), theoretical analysis yields that if inertia is weak, inertia is more important locally than globally and in other studies the validity of Forchheimer equation is investigated by mathematical derivations based on first principles, e.g. Skjetne and Auriault (1999), Adler et al. (2013) and Soulaine and Quintard (2014). The general tactic is to derive and investigate additional terms added to Darcy law so that high Re laminar flow through porous media can be predicted on a global level. Also, turbulent flow through porous media has been treated theoretically and a quadratic dependence of the correction term for velocity has been derived in many studies (Skjetne and Auriault 1999; Lasseux et al. 2011). In Jouybari et al. (2016), the model by Nakayama and Kuwahara (1999) is extended to low Re turbulent flows by using a standard numerical model for a porous medium consisting of a staggered arrangement of square cylinders. Many researchers have modelled pore level flow, as such, theoretically or numerically, e.g. Geller and Hunt (1993), Hellström et al. (2010b), Ljung et al. (2012), Jourak et al. (2014) and Fabricius et al. (2016) and Pérez-Ràfols et al. 2016). Also, experiments have been performed on simplified geometries like parallel tubes (Khayamyan et al. 2014; Khayamyan and Lundström 2015).

To disclose more details of the flow experimentally, tomographic or optical techniques have been applied. Tomographic techniques include magnetic resonance imaging (MRI) (Baldwin et al. 1996; Sederman et al. 1998; Ogawa et al. 2001; Suekane et al. 2003), positron emission tomography (PET) (Khalili et al. 1998), nuclear magnetic resonance (NMR) imaging (Baldwin et al. 1996), gamma attenuation (Imhoff et al. 1994) and X-ray tomography (Imhoff et al. 1996). These methods involve rather expensive equipment and may give poor spatial and temporal resolution (Kutsovsky et al. 1996; Chang and Watson 1999; Gladden et al. 2006). For MRI there is a link between spatial and temporal resolution meaning that reducing the data acquisition time requires a decrease in spatial resolution (Gladden et al. 2006). To exemplify Sains et al. (2005) studied liquid flow through two columns of spheres with a diameter of 19 mm in a pipe and obtained an in-plane resolution of 0.8 \(\times \) 0.8 mm\(^{2}\) with a data acquisition time of 20 ms (50 Hz). For X-ray tomography, there is also a strong connection between spatial and temporal resolution. Regarding measurements with NMR of the flow in a 40 mm tube packed with spheres having a diameter of 6 mm a rather high resolution of 0.17 mm was achieved in the plane of measurements and 2 mm out-of-plane (Kutsovsky et al. 1996).

In contrast to the techniques described above, the relative simplicity, low cost and high resolution of optical techniques such as particle image velocimetry (PIV), micro-particle image velocimetry (\(\upmu \hbox {PIV}\)) and laser Doppler anemometry (LDA) make them attractive. The resolution of these systems is dependent on the set-up and to exemplify, Kähler et al. (2012) show that the resolution of PIV can be in the order of the sensor pixel size, about \(10\,\upmu \hbox {m}\), but due to the size of the tracer particles and the magnification it is typically somewhat larger. Usage of optical techniques in porous media requires all phases to be transparent and refractive index matched (RIM). Using RIM, Yarlagadda and Yoganathan (1989) studied a system of rods with LDA yielding a laminar and stable flow due to high viscous drag coefficients. Peurrung et al. (1995) applied particle tracking velocimetry (PTV) to low Re laminar flow in a bed of spheres and found that the flow rate measured with PTV is in good agreement with the flow rate given by the syringe pump used. In Moroni and Cushman (2001), the same technique was used to find 3D trajectories inside a porous medium to determine the dispersion tensor. Huang et al. (2008) used PTV to study the flow in a cylinder filled with monosized spheres at \(Re = 28\). The inner diameter of the tube is 50 mm, and all spheres have a diameter of 7 mm. Lachhab et al. (2008) designed a PTV system and investigated particle motion in match-index-refraction porous media. One purpose with the experiments is to study the spreading of small particles. In Patil and Liburdy (2013a), planar PIV measurements were carried out using RIM at discrete locations throughout a randomly packed bed with aspect ratio of 4.67 for steady, low Re flows. One result is that the velocity variance is nearly two times larger near the wall as compared to it in the bulk. In an additional study, Patil and Liburdy (2013b), turbulent flow through the same bed was studied. Main results are that recirculation zones have a large influence on the longitudinal dispersion, while tortuous channel region contributes to the transverse dispersion. For low Re flows, PIV has also been used to investigate flows through rectangular arrays of circular rods yielding good agreement between experiments and theory (Agelinchaab et al. 2006). In a similar geometry, Andersson et al. (2009) measured the interfacial velocity field near porous fibre bundles with \(\upmu \hbox {PIV}\). Notice that in \(\upmu \hbox {PIV}\) the whole volume is illuminated and the thickness of the plane of measurement is set by the focal depth of the microscope, while for PIV the thickness of the plane of measurement is set by the laser sheet. In Roman et al. (2016), flow in 2D etched micromodels with a typical grain size of 30 to 200 \(\upmu \hbox {m}\) was studied with \(\upmu \hbox {PIV}\). As in Andersson et al. (2009), no index matching needs to be performed and results are compared to 2D simulations with computational fluid dynamics. Although the experimental flow will be 3D due to the bounding walls (Fabricius et al. 2016) experimental results and results from simulations compare well to each other. Two-dimensional etched models were also studied with \(\upmu \hbox {PIV}\) in Blois et al. (2013). An additional possibility for flow on small scales is to apply confocal microscopy. With this technique, 2D fluid velocities have been derived for low Re flow through a porous medium of a sintered disordered packing of hydrophilic glass beads (Datta et al. 2013). A similar porous media model was studied in Sen et al. (2012) with \(\upmu \hbox {PIV}\) yielding 2D low Re velocity fields.

In a recent study by Khayamyan et al. (2016), PIV was used to measure the flow in a bed of spheres. Examples of results are that recirculation zones, that appear in inertia dominated flows, are suppressed by turbulent flow at higher Re and that the velocity distribution is self-similar with respect to Re for turbulent flow. In the current paper, new measurements from flow through the same bed of spheres with stereoscopic PIV are presented. This implies that all velocity components in different planes are captured and that the total velocity can be computed. This is especially important for flow within a bed of spheres since the flow is fully three dimensional. Stereoscopic PIV is a new technique for flow in porous media, but it is frequently used for a number of other applications (Willert 1997; Pokora and McGuirk 2015). In what follows the experimental set-up for measurement of relatively high Re flow through a bed a spheres with stereoscopic PIV is described. This includes the method of index matching used and an error analysis. The results are then presented and discussed, and finally some conclusions are drawn.

2 Experimental Set-Up

For flow through porous media Re may be defined in different ways, e.g. Hellström et al. (2010a). For packed beds, it is common practice to use the Particle Reynolds number, \({Re}_{{p}}=U_\mathrm{int} \,D_{p}/ \nu \), see Hlushkou and Tallarek (2006), for instance. In this equation, \(D_{p}\) is the (averaged) particle diameter \(U_\mathrm{int}=U_\mathrm{Darcy}/\phi \) where \(\phi \) is bed porosity and \(U_\mathrm{Darcy}=Q\)/\(A_\mathrm{bed}\) where Q and \(A_\mathrm{bed}\) are volumetric flow rate and bed cross-sectional area, respectively. One alternative Re is the pore Reynolds number that also includes porosity and tortuosity, see Seguin et al. (1998). Following Hlushkou and Tallarek (2006) \({Re}_{{p}}\) is employed in the present paper since it has a clear definition (i.e. the diameter), it can easily be related to the Peclet number (\({Pe} = U_\mathrm{int} \,D_{p}/ D_{m}\) where \( D_{m}\) is the molecular diffusion) and fewer sources to errors are introduced since solid fraction and tortuosity do not come into play. The latter can also be seen as a disadvantage of using \({Re}_{{p}}\).

Fig. 1
figure 1

Schematic of experimental set-up for measurements with stereoscopic PIV

Full size image

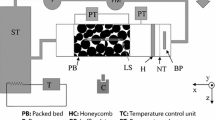
The experimental set-up used to measure the velocity field with stereoscopic PIV within the bed is shown in Fig. 1 and is comparable to that Patil and Liburdy (2013a, b) used for PIV measurements and the same as Khayamyan et al. (2016) also used for PIV measurements. The packed bed studied is made from a randomly packing of Plexiglas (PMMA, Precision Plastic Ball Co., www.PrecisionPlasticBall.com) spheres with a diameter of \(D_{p} = 12.7\) mm, and the typical size of the pores between the spheres is in the same range. Hence a fully 3D network of pore space is formed. The bed has a square cross section of \(100 \times 100\,\hbox {mm}^{2}\), and its length is 310 mm. This yields a bed width to \(D_{p}\) ratio of about 8 as compared to about 4 in the set-up in Patil and Liburdy (2013a, b). A ratio of 8 is large enough to avoid major effects of channelling near the confining walls on the flow in the middle of the bed (Chu and Ng 1989). The bed overall porosity (\(\phi )\), being the ratio of void volume to total bed volume, is about 0.414 from direct geometrical calculations. The fluid is circulated in a closed loop with a centrifugal pump, Tapflo HTM15PP, from an atmospheric pressure storage tank where the temperature of the fluid is regulated and kept at \(20 \pm 0.1\,^{\circ }\hbox {C}\) with a temperature control unit. The fluid is pumped through an electromagnetic flowmeter from ABB, ProcessMaster FEP300, to the Plexiglas box and finally back to the storage tank in a completely closed system. To ensure constant conditions during the measurement also the absolute pressure at the inlet to the Plexiglas box was monitored with a pressure transducer from General Electric, GE PTX5012. In addition, the pressure difference over the porous bed was recorded with the same type of pressure transducers.

The Plexiglas box is longer than the bed to enable a uniform flow entering and leaving the bed. To fulfil this requirement, the jet entering the box is broken and pushed towards the sidewalls by a baffle plate. The diameter of the baffle plate is 76 mm, being 50% larger than the jet or pipe diameter, and it is placed at 20 mm from the inlet to the box. After the baffle plate, the flow passes through a net and a honeycomb to reduce the fluctuations and also to break down large-scale eddies. The net and honeycomb are placed at 50 and 100 mm after the inlet, respectively. The net has square openings with a mesh size of \(2 \times 2 \,\hbox {mm}^{2}\), and the cells in the honeycomb have a circular cross section with a diameter of 2 mm. The thickness of the honeycomb in the flow direction is 25 mm. The inlet to the packed bed is 150 mm downstream the honeycomb. At the inlet and outlet of the packed bed, square meshes of \(4.4 \times 4.4\,\hbox {mm}^{2}\) and wire diameter of 0.65 mm are placed. The rather sudden contraction at the outlet of the box is placed 100 mm downstream the bed outlet.

Fig. 2
figure 2

Schematic of the index matching set-up

Full size image

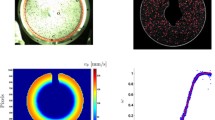
To have optical access to the flow field within the bed, the bed has to transmit light rays without distortion. To have such a medium, the refractive index of the fluid is matched to that of the spheres in the bed. For this purpose, an aqueous solution of ammonium thiocyanat (\(\hbox {NH}_{4}\,\hbox {SCN}\)) is used. This is a transparent liquid, and its refractive index can be tuned by variation of the concentration ammonium thiocyanat. The optimal concentration is found with the same optical method as in Khayamyan et al. (2016), see Fig. 2. The main idea is that the light will not refract and instead hit the reference point if the solution and sphere has the same refractive index. So a reference point was defined without any sphere. A sphere was then immersed into the fluid, and the indexed matched solution was found by adding water/salt to the initial solution until the light ray hit the reference point regardless of where the light ray passed the sphere. The concentration, kinematic viscosity and density of the final solution are 60.36%, \(1.83\,\times \,10^{-6}\,\hbox {m}^{2}/\hbox {s}\) and \(1127\,\,\hbox {kg}/\hbox {m}^{3}\), respectively. The viscosity was measured with a calibrated Ostwald viscometer due to the corrosive properties of the fluid.

A commercial stereoscopic PIV system from LaVision GmbH was set-up for the measurements. This system is based on a double-pulsed Nd:YAG laser at a wavelength of 532 nm with a maximum frequency of 100 Hz, a minimum interframe time for image pairs of \(5\,\upmu \hbox {s}\), and two LaVision double-frame FlowMaster Imager Pro cameras with spatial resolution of \(1280 \times 1024\) pixels per frame with pixel size of \(12\,\times \,12\,\upmu \hbox {m}^{2}\). This system has been used in a number of recent PIV studies, e.g. Larsson et al. (2012a, b), Larsson (2015a) and Saber et al. (2016), and comparisons to numerical modelling have been performed yielding very good agreement for proper turbulence models, e.g. Larsson et al. (2012b, 2015b). The thickness of the plane for measurement is about 1 mm. Stereoscopic PIV implies that velocities presented are averaged through this thickness. Two Nikon AF Nikkor 105 mm lenses were used, with an f-stop of 2.8. The time delay between image pairs was adjusted to restrict seeding particles mean displacements between 6 and 8 pixels. The laser and cameras were mounted on a 3D traversing system so that the laser sheet and cameras can be moved up to 500 mm in the x-, y- and z-directions. Hollow glass spheres with a diameter of \(10\,\upmu \hbox {m}\) from Dantec were used as seeding particles. The chosen seeding particles are sufficiently small, about 1000 times smaller than the typical pore size, and have a density near to that of the indexed matched solutions allowing them to closely follow the motion of the fluid (Raffel et al. 2013). According to Westerweel (2000), it can be concluded that the image of the particle should be 3–4 pixels of the theoretical uncertainty. As discussed in Overmars et al. (2010), in connection with Eq. 2 in their paper, this imaging is diffraction limited so the geometrical particle image size is not so relevant in this case. Moreover, if the (diffraction limited) particle image diameter is too small compared to the camera pixel size, it is common practice in PIV set-ups to use a very slight defocus in order for the particle image to cover a large enough region. This standard procedure was followed during the experiments for the different \({Re}_{{p}}\).

The two cameras are used to capture the particles in the light sheet from two different directions giving a stereovision in the same fashion as the human eyes, see Fig. 1. In the current set-up, the angle between the cameras is \(45^{\circ }\). A prism filled with the working liquid is placed in front of the bed to ensure that both cameras axis are perpendicular to the liquid–air interface. The slightly different image pairs include information about the third velocity component that can be extracted by comparing these images. The object plane and lens plane are not parallel since the axes of the two cameras intersect at the plane of the measurements. This results in geometric distortions, and in order to have the whole image in focus, the Scheimflug criterion must be met. This criterion states that the image plane, the lens plane and the object plane for each camera have to intersect in a common line and is full-filled by mounting standard LaVision Scheimpflug adapters between the cameras and the camera lenses. This set-up implies a variable magnification factor across the image plane and a perspective distortion. This is dealt with by a calibration procedure where two image pairs from a planar calibration target are captured. The images are parallel to the laser sheet with a defined distance from each other. To eliminate possible errors due to the motion of the planar calibration target towards the cameras, a dual-plane 3D calibration target with marks on both planes is used. The used calibration target has marks on one side, and both cameras were placed at one side of the calibration target illuminated by a light sheet cf. Fig. 1. This target is made from milling grooves on the surface of a flat slab. The groves define a second plane in the slab. In this way, marks can be on two levels. The target is specially designed since the standard target could not be used because of the corrosive salt.

To avoid false vector and facilitate the analysis, the images produced were masked. This was done manually, and the interior of spheres cut by the laser sheet and minor reflections from seeding particles trapped on the surface on the particles were covered. The PIV software DaVis 7.2.2 based on a cross-correlation algorithm was used to derive velocity vectors from the motion of the particles. A multi-step correlation processing algorithm with decreasing window size was used to evaluate recorded images with a final window size of \(32\,\times \,32\) pixels. The overlap of windows was constant at 75% for all steps. This final window size gives a vector spacing of 0.28 mm or 44 vectors per sphere diameter. Vectors, for which RMS exceeds 1.5 times of the neighbouring vectors’ RMS, were recognized as false vectors and were removed. At the end, a \(3\,\times \,3\) Gaussian kernel was used to smooth the vector field. The measurements were carried out in five planes directed with the main flow. The planes are located from the middle of the bed, plane P00 and towards the sidewall facing the cameras 6, 10, 14 and 18 mm from the midplane denoted P06, P10, P14 and P18, respectively. In each plane, measurements were carried out for \({Re}_{{p}}\approx 20\)–3220. The presented time-averaged velocity fields were derived from 712 instantaneous velocity fields recorded with a sampling frequency of 75 Hz, i.e. about 9.5 s. The limit is the storage capacity of the camera. This implies that frequencies from about 1 to 37 Hz can be captured according to the Nyquist sampling criteria. The velocity range is about \(3.5\, \hbox {mm}/\hbox {s}<U_\mathrm{int} < 0.5\,\hbox {m}/\hbox {s}\) or \(1.5\,\hbox {mm}/\hbox {s}< U_\mathrm{DARCY} < 0.2\, \hbox {m}/\hbox {s}\) as derived from the flow metre and knowledge of the volume fraction of the spheres and the cross-sectional area of the porous bed.

Systematic errors during stereoscopic PIV measurements (Coleman and Steele 1999) may be difficult to detect and are instead reduced by a careful set-up, and a biased error is approximated to 0.5%, following Larsson (2015a). Additional random errors may appear for the in-plane velocity components that is estimated to be about 5%. This is based on the error in the sub-pixel estimation during the cross-correlation, (10%) (Balakumar et al. 2009), the mean particle image diameter in pixels (3–4 pixels) and the typical displacement between image pairs (6–8 pixels). Since the angle between the cameras is \(45^{\circ }\) this approximate error is about 2.5 times larger for the out-of-plane velocity component, hence about 12.5% (Prasad 2000). The errors are still relatively small and will not influence the results to any large extent. New and advanced methods to derive the error in PIV measurements have recently been suggested, i.e. Charonko and Vlachos (2013) and Wienke (2015), but this has not yet resulted in a standard method.

3 Result and Discussion

Three types of velocities will be presented. The spatial distribution of time-averaged velocities, the time fluctuations of velocities in the measured planes and spatial and time-averaged velocities as a function of \({Re}_{{p}}\). Notice that all results are scaled with \(U_\mathrm{int}\), based on measurement of Q with the flow metre. The time- and spatial averaging were done over the pores area (just over the area covered by fluid). The time average was calculated for each point in the plane over the time series. Then the time-averaged velocity was area averaged over the area covered by fluid to get time- and spatial average values.

In the analyses of the results, the normalized probability distribution function (NPDF) and the cumulative distribution function (CDF) will be derived. The NPDF of the velocity yields the probability distribution of velocities normalized with the probability of the most probable velocity. In this context, the horizontal axis of the NPDF graph is scaled with \(U_\mathrm{int}\). The CDF of each velocity sums up all of the probabilities less than or equal to that velocity according to:

$$\begin{aligned} F\left( v \right) =P\left( {V<v} \right) =\mathop \sum \limits _{a\le v} p\left( a \right) . \end{aligned}$$
(1)

In the case of a continuous distribution, the function returns the area under the PDF from minus infinity to that velocity and is equal to the area under the PDF from minus infinity to that velocity which can be expressed as:

$$\begin{aligned} F\left( v \right) =P\left( {V<v} \right) =\mathop \smallint \nolimits _{-\infty }^{v} p\left( a \right) \mathrm{d}a. \end{aligned}$$
(2)
Fig. 3
figure 3

Colour plot of time-averaged and scaled total velocity in P00 for \({Re}_{{p}} = 20, 240, 1170\) and 3220

Full size image
Fig. 4
figure 4

Colour plot of time-averaged and scaled total velocity in P06 for \({Re}_{{p}} = 20, 240, 1170\) and 3220

Full size image
Fig. 5
figure 5

Colour plot of time-averaged and scaled total velocity in P10 for \({Re}_{{p}} = 20\), 240, 1170 and 3220

Full size image
Fig. 6
figure 6

Colour plot of time-averaged and scaled total velocity in P14 for \({Re}_{{p}} = 20\), 240, 1170 and 3220

Full size image
Fig. 7
figure 7

Colour plot of time-averaged and scaled total velocity in P18 for \({Re}_{{p}} = 20\), 240, 1170 and 3220

Full size image
Fig. 8
figure 8

Porosity of the five planes P00, P06, P10, P14 and P18

Full size image

3.1 Distribution of Time-Averaged Total Velocity Within the Planes

The distribution of the time-averaged total velocity, \(u_\mathrm{tot}\), is fairly uniform for all planes at \({Re}_{{p}} = 20\), and there are only a few areas with relatively high \(u_\mathrm{tot}\), see Figs. 3, 4, 5, 6 and 7 where colour plots of \(u_\mathrm{tot} /U_\mathrm{int}\) at four \({Re}_{{p}}\) and in the five planes are presented. At \({Re}_{{p}}\) = 240, more areas with high \(u_\mathrm{tot} /U_\mathrm{int}\) have formed and these areas are also present at \({Re}_{{p}} = 1170\) although the magnitude is a little bit lower. Hence, in all studied planes, flow structures appearing at \({Re}_{{p}}\) = 240 are still present at \({Re}_{{p}} = 1170\). For \({Re}_{{p}} = 3220\), the flow becomes more uniform again based on the resolution of the stereoscopic PIV system used and the time averaging done. In accordance with results in Khayamyan et al. (2016), this shows how the velocity distribution changes as the flow rate increases from close to creeping flow, \({Re}_{{p}} = 20\), to turbulent flow, \({Re}_{{p}} = 3220\), via an inertia dominated regime. The physics behind the more uniform distribution at \({Re}_{{p}} = 3220\) is that turbulence introduces mixing that will transport momentum from high velocity areas to low velocity areas and vice versa. This suggests that, for time-averaged plots, spatial variations will be smeared out including those that are smaller than the spatial resolution of the measuring system. Notice again that the trend is the same for all planes although the local porosities \(\phi \) varies between 0.16 and 0.35, see Fig. 8. In this figure, it can also be seen that the local \(\phi \) is lower than the one derived from volume calculations: on averaged \(\phi \approx 0.25\) in the planes studied as compared to \(\phi \approx 0.41\) in the whole volume. This can be explained with local variations, a higher \(\phi \) at all walls of the cell and that the masking is slightly outside the spheres. To quantify the observations in Figs. 3, 4, 5, 6 and 7, the NPDF and the CDF are plotted for all planes, see Figs. 9 and 10. It is clear that the distribution first increases in width with \({Re}_{{p}}\) and then it decreases with a maximum around \({Re}_{{p}} = 400\). It is likely that such behaviour of the flow should be reflected in overall measures such as resistance to flow and dispersion. It has been shown that the longitudinal dispersion coefficient \(C_{L}\) is reduced at \({Pe}\approx 2\,\times 10^{5}\) (Brenner 1980). With the following data for water at \(20\,^{\circ }\hbox {C}\,\nu = 1.004 \times 10^{-6}\,\hbox {m}^{2}/\hbox {s}\) and \(D_{m} = 2.023 \,\times \, 10^{-9}\, \hbox {m}^{2}/\hbox {s}\) (Holz et al. 2000) this corresponds to \({Re}_{p }= 400\). Hence the decrease in \(\hbox {C}_{L }\) obtained in Brenner (1980) is here indicated to relate to a narrowing of the velocity distribution. Regarding relation to resistance to flow, no clear connection can be found. Finally, the results also indicate that the measurement time is long enough since measurements in all five planes give the same overall result.

Fig. 9
figure 9

NPDF as a function of normalized total velocity \(u^{*}=u_\mathrm{tot}{/}U_\mathrm{int}\)

Full size image
Fig. 10
figure 10

CDF as a function of normalized total velocity \(u^{*}=u_\mathrm{tot}{/}U_\mathrm{int}\)

Full size image
Fig. 11
figure 11

Spatially averaged time fluctuations plotted as a function of \({Re}_{{p}}\) for five planes

Full size image

3.2 Spatial Averaged Time Fluctuations as a Function of \({Re}_{{p}}\)

The spatially averaged time fluctuations of the total velocity are plotted as a function of \({Re}_{{p}}\) for all planes in Fig. 11. The overall tendency is that the magnitude increases with \({Re}_{{p}}\) and reaches a maximum for \({Re}_{{p}} = 400\) being the same \({Re}_{p }\) as when the spatial variations are largest. The increase is not constant, and there are indications of a local maximum also at \({Re}_{{p}} = 80\) as was also obtained in Khayamyan et al. (2016) for the in-plane velocity component. The rather steep increase in the magnitude of fluctuations in the interval \(40< {Re}_{{p}}< 80\) is probably due to instabilities. A pallet of critical \({Re}_{{p}}\) for the onset of fluctuations was derived in Hill et al. (2001) for different random systems of spheres with aid of lattice Bolzmann simulations. The critical \({Re}_{{p}}\), range from 75 to 265 and thus, in the same range as fluctuations disclosed in Fig. 11. The fluctuations do not, however, influence the pressure measurements to any large extent until \(Re_{p}> 80\) as shown in Khayamyan et al. (2016). For \(Re_{p}> 400\), the level of velocity fluctuations becomes lower and for the highest Reps considered there is a tendency for a level out of the fluctuations which is an indication of turbulent flow, i.e. the energy of large-scale fluctuations is dissipated away by turbulent eddies on several scales.

There are two exceptions from the general trends. The fluctuations in P10 do not increase with \({Re}_{{p}}\) for \({Re}_{p }> 40\), and there is an additional increase in the fluctuations in plane P00 for \({Re}_{{p}} >1500\). In these two cross sections, the porosity is relatively low and there are only a few passages in the main flow direction, see Figs. 3 and 5. A low porosity and few passages may also be the reason for the varying but overall low magnitude of the fluctuations in P18, see Figs. 7 and 11. With these remarks, it can be concluded that the increase in fluctuations is likely to be due to both inertia and transitional effects and the decrease at high \({Re}_{{p}}\) is probably due to turbulence. One major difference between the velocity fluctuations of the in-plane velocity component (Khayamyan et al. 2016) and the velocity fluctuations of the total velocity derived in the current study is that the maximum for, respectively, case is at \({Re}_{{p}}\) about 800 and 400, respectively. The maximum is, however, relatively flat around these \({Re}_{{p}}\).

Fig. 12
figure 12

Time-averaged vector plots of the in-plane velocity for plane P06 and for four \({Re}_{{p}} = 20, 240, 1170, 3220\). Colour bar is the out-of-plane component

Full size image
Fig. 13
figure 13

Time-averaged vector plots of the in-plane velocity for plane P14 and for four \({Re}_{{p}} = 20, 240, 1170, 3220\). Colour bar is the out-of-plane component

Full size image

3.3 Distribution of Time-Averaged Velocity Components Within Two of the Planes

Time-averaged and normalized vector plots of the in-plane velocity (\(u_{x}\), \(u_{y}\)) for planes P06 and P14 are shown in Figs. 12a–d and 13a–d. In these plots, the colour denotes the normalized velocity magnitude of the out-of-plane component, \(u_{z}\) and the length of the vectors the normalized in-plane velocity magnitude. Three areas are marked, one in Fig. 12a–d and two in Fig. 13a–d. In the marked area in Fig. 12a (\({Re}_{{p}} = 20\)), most vectors are aligned. At \({Re}_{{p}} = 240\), the arrows are not aligned any more and the out-of-plane flow has changed direction, see Fig. 12b. The situation is nearly the same for \({Re}_{{p}} = 1170\), while at \({Re}_{{p}} = 3220\) there is a tendency for the arrows to align again, see Fig. 12c, d. By scrutinizing the marked areas in Fig. 13a–d, the trend is the same, ordered flow for \({Re}_{{p}} = 20\), disordered for \({Re}_{{p}} = 240\) and 1170 and ordered again at \({Re}_{{p}} = 3220\). Hence the flow structure within a porous bed is constantly evolving as \({Re}_{{p}}\) increases and both local magnitude and local direction of the velocity changes. This was also observed in Hill et al. (2001) when comparing flow structures obtained with Lattice-Boltzmann simulation for Stokes flow and \({Re}_{{p}} = 60\) and 113 for flow through a sparse and dense system of randomly distributed spheres, respectively. The conclusion is that for the sparse system with solid fraction of 10% there are significant differences in the flow already at \({Re}_{{p}} = 60\) as compared to \({Re}_{{p}}<< 1\). For the dense system, 59% solid fraction, only minor changes to the flow are observed. Hence the large alteration to the flow takes place at \({Re}_{{p}} > 113\) for highly packed systems. The likely reason for the time-averaged ordered flow at the highest \({Re}_{{p}}\) is that turbulence introduces mixing of momentum that will serve as a smoothening of large-scale structures and there is an interchange between high momentum and low momentum flow as well as between flows in different directions. The flow within the marked areas in Figs. 12 and 13 may be scrutinized further by zooming in the velocity fields, see Figs. 14, 15 and 16 and notice the scales are the same as in Figs. 12 and 13. From these figures, it becomes even more evident how much the flow changes in magnitude and direction as the \({Re}_{{p}}\) increases. One consequence of this is not only that dispersion varies with \({Re}_{{p}}\) but also that dispersion may increase if the flow is varied in some way, periodically, for instance since varying velocity in itself changes the flow pattern substantially. The change in flow pattern can be explained with the simple set-up presented in Khayamyan et al. (2014) and Khayamyan and Lundström (2015). The flow in a pore doublet model is studied, and one result is that during transitional flow in the larger pore, resistance increases and portions of the fluid are directed to the smaller pore. Such redistributions will constantly take place for certain \({Re}_{{p}}\) in a packed bed of spheres.

Fig. 14
figure 14

Zoomed in plot of marked area in Fig. 12. Notice that scales are the same as in Fig. 12

Full size image
Fig. 15
figure 15

Zoomed in plot of marked rectangular area in Fig. 13. Notice that scales are the same as in Fig. 13

Full size image
Fig. 16
figure 16

Zoomed in plot of marked elliptical area in Fig. 13. Notice that scales are the same as in Fig. 13

Full size image
Fig. 17
figure 17

Time- and spatially averaged magnitude of the axial velocity, \(u_{x}\)/\(u_\mathrm{tot}\)

Full size image

3.4 Time- and Spatially Averaged Portion of Axial Velocity as a Function of \({Re}_{{p}}\)

The time- and spatially averaged magnitude of the axial velocity \(u_{x}/u_\mathrm{tot}\) within five planes is shown in Fig. 17. The general trend is that the portion of this velocity has a minimum, around 40%, for \({Re}_{{p}} = 400\) and is then nearly independent of \({Re}_{{p}}\) for \({Re}_{{p}} > 1500\). Above \({Re}_{{p}} = 1500\), the fraction \(u_{x}\) is a little bit less than 50% of \(u_\mathrm{tot}\). Hence a considerable amount of the flow moves in the y- and z-directions, especially at \({Re}_{{p}} = 400\). A substantial flow perpendicular to the main flow direction is likely to result in a large transverse dispersion.

3.5 Stereoscopic PIV Versus PIV

In the current study, stereoscopic PIV was applied on the same set-up as in Khayamyan et al. (2016) where PIV was used for the measurement. Stereoscopic PIV discloses all velocity components in one shot, and flow in porous media is nearly always strongly 3D. Measurement with conventional PIV misses the out-of-plane component of velocity, which carries mass into or out of each volume of measurement. Hence the lack of the third velocity component in a measured 2D flow field will result in flow patterns, which violate the fundamental laws of fluid mechanics. However, if just two of the velocity components are of interest, PIV is a much easier technique to apply and calibrate.

4 Conclusion

For the first time, measurements of all components of a 3D-flow field with stereoscopic PIV within a porous media are reported. From these measurements, it is obvious that the velocity can be significantly different in neighbouring pores. It is also evident that the time-averaged velocity field in one pore can change direction and magnitude several times as \({Re}_{{p}}\) increases. This observation is important for dispersion driven processes. Specifically, the velocity range has a maximum at \({Re}_{{p}} = 400\) which is a critical \({Re}_{{p}}\) for when the longitudinal dispersion coefficient starts to decrease when increasing \({Re}_{{p}}\) according to Brenner (1980). It is also shown that the critical \({Re}_{{p}}\) for velocity fluctuations is about \({Re}_{{p}} = 40\) being in the same range as results obtained with numerical simulations performed in Hill et al. (2001). The velocity fluctuations have a maximum at \({Re}_{{p}} = 400\) and are then reduced, probably, since the flow becomes turbulent. Hence two effects are captured as \({Re}_{{p}}\) increases, namely a change in velocity distribution in space and the introduction of velocity fluctuations in time. When doing models of the flow from first principles it is therefore here suggested that both of these effects are accounted for. Furthermore, detailed studies of time-averaged velocity plots yield that the flow goes from spatially ordered to disordered and then ordered again when \({Re}_{{p}}\) increases. A considerable amount of the fluid moves in the perpendicular directions to the main flow direction and for \({Re}_{{p}}\) around 400 the spatial averaged \(u_{x}\) reaches a minimum and is only about 40% of \(u_\mathrm{tot}\). For \({Re}_{{p}}>\) 1500, this ratio is nearly constant and \( u_{x}\) is on average a little bit less than 50% of \(u_\mathrm{tot}\). Hence a great deal of the flow moves perpendicular to the main flow direction affecting variables such as the transverse dispersion.