1 Introduction

Evaporation of sessile droplets is vital for a number of applications. Dropwise evaporative cooling is, for example, often used in electronic industries, nuclear thermal management and metallurgics. Other areas where the behavior of sessile droplet evaporation is important is drying of paint and drying of dishes in a dishwasher. Generally questions are addressed both towards increasing the drying rate as well as on how to control the deposition of particles withheld in the fluid. To clarify such issues it is important that sessile droplet evaporation, including the internal flow, is further investigated.

Evaporating sessile droplets (from now on called droplets) have been studied frequently experimentally and numerically [1, 2]. Evaporation induced flow, natural convection and Marangoni convection are main mechanisms that have been coupled to the flow inside evaporating droplets [3, 4]. The appearance of Marangoni convection in water droplets has however been questioned in experimental investigations, with results indicating a suppression of Marangoni convection [4]. This is also in agreement with the experimental work of Savino et al. [5], where Marangoni convection was measured to be negligible for water droplets. It is therefore of interest to investigate both Marangoni convection as well as the isolated effect of buoyancy on the internal flow in droplets.

There are various examples of how the external flow, internal flow and evaporation rate can be coupled. Ruiz and Black [6] investigated the effect of internal thermocapillary convection, i.e. Marangoni convection, on the heat transfer between a droplet and a solid surface. Here a constant Nusselt number, (Nu = hD/k), and Sherwood number, (Sh = h m D/D av ), corresponding to conduction was applied at the surface in order to determine the rate of evaporation. Following the numerical work of Ruiz and Black, Mollaret et al. [7] investigated both numerically and experimentally how the substrate temperature affects the evaporation of a droplet. In the numerical model the Navier-Stokes and Energy equations inside the droplet were solved together with a diffusive equation corresponding to the vapor diffusion in the surrounding fluid. Sodtke et al. [8] investigated liquid droplet evaporation in a closed container filled with saturated vapor both numerically and experimentally, considering conduction as the main mode of heat transfer inside the droplet. Particle deposition was investigated by Girard et al. [9], further examining the mechanics behind the non-uniform deposition patterns of suspensions withheld within a droplet. In their article, internal motion of the liquid due to surface tensions effects, i.e. Marangoni flow, is considered, while the effects of natural convection are considered negligible. Strotos et al. [10] simultaneously studied the coupled fluid flow and heat transfer of a droplet, substrate and surroundings using volume of fluids (VOF). The model was compared to a simplified numerical approximation neglecting the internal flow, and the advanced model was found to give the best prediction when compared to experiments. Lu et al. [11] also showed an enhancement in the evaporation rate when Marangoni flow was accounted for. In their model, the effects of thermocapillary flow and viscous resistance was taken into account as well as the buoyancy force inside the droplet and the Hertz-Knudsen-Schrage formula was used to determine the evaporation rate. The effect of Marangoni number was further examined by Barmi and Meinhart [12] where the internal flow inside the droplet was coupled to diffusion of moisture in the surrounding air. The internal fluid motion in externally heated droplets was investigated both numerically and experimentally in Thokchom et al. [13], where a predicted temperature profile was applied at the droplet surface.

As apparent from the above discussion, various approaches to model the heat and mass transfer boundary condition at the surface of a droplet have been presented. Aiming for time efficient simulations it is of interest to determine the required level of details for the boundary conditions in general and that between the liquid droplet and surrounding air in particular. A comparatively efficient way to determine the rate of evaporation from this surface is to apply an average or locally dependent Nu together with the heat and mass transfer analogy [14]. With this approach the air and water domains can be simulated separately and the influence of vapor in the external flow is disregarded. The heat and mass transfer analogy has been applied on forced convection flows with good results [15, 16], but the validity of the method needs to be discussed if the flow is driven by density differences or if the external flow is influenced by other heat sources than the surface being dried, see Ljung et al. [17]. The inclusion of vapor due to evaporation will increase the computational complexity but as long as the heat and mass transfer coefficient can be regarded as relatively independent of the change in temperature at the surface, i.e. change due to latent heat or internal temperature distribution, it is still possible to simulate the domains separately. This enables, for example, simulation of various internal flow mechanism and particle transport without the added load of the external flow. For the separate domain approach it is, however, of interest to also investigate the effect of a locally resolved boundary condition on the internal flow. The influence of heat and mass transfer coefficients is furthermore of particular interest in transient simulations where the transfer coefficients are allowed to vary with contact angle.

To further clarify the influence of the droplet surface boundary condition, a numerical investigation of the combined effects of heat and mass transfer coefficient, internal flow and evaporation is here presented. Simulations are carried out on axi-symmetric water droplets at two predefined contact angles of θ = 90o and θ ≈ 53o, representing decreased volume due to evaporation. The computation of the heat and mass transfer coefficients is compared with correlations from literature and the results are verified through comparison between methods for calculation of evaporation rate.

2 Theory

Assuming laminar Newtonian flow the following continuity, momentum and energy equations apply for both the internal and external flow of the droplet [18]

$$ \frac{\partial \rho}{\partial t}+\nabla \cdot \left(\rho \mathbf{u}\right)=0, $$
(1)
$$ \frac{\partial \rho \mathbf{u}}{\partial t}+\nabla \cdot \left(\rho \mathbf{u}\otimes \mathbf{u}\right)\kern0.5em =-\nabla p+\nabla \cdot \uptau +{\mathbf{S}}_M $$
(2)

and

$$ \frac{\partial \left(\rho H\right)}{\partial t}+\nabla \cdot \left(\rho \mathbf{u} H\right)=\nabla \cdot \left( k\nabla T\right). $$
(3)

The viscous work and viscous dissipation is thus neglected in the energy equation due to the assumption of laminar, low-speed flow. The stress tensor, τ, is its turn determined from

$$ \uptau =\mu \left(\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^T-\frac{2}{3}\delta \nabla \cdot \mathbf{u}\right). $$
(4)

While a constant density is assigned to the water phase, the constituent equations for density and enthalpy of air and water vapor are calculated based on the ideal gas equations of state, i.e.

$$ \rho =\frac{wp_{abs}}{RT} $$
(5)

and

$$ dH={c}_p dT. $$
(6)

The material variables in Eq. (1)–(4) represent the air, water, or a mixture of air and water vapor depending on the studied case. The laminar μ and k, and specific heat c p , is derived as a mass fraction weighted average following the relationship here exemplified for μ as [18]

$$ \mu ={\mu}_a{\phi}_a+{\mu}_v{\phi}_v. $$
(7)

A mass fraction transport equation is also solved in addition to (1)–(3) to compute the transport of vapor in air according to

$$ \frac{\partial {\rho \phi}_v}{\partial t}+\nabla \cdot \left(\rho \mathbf{u}{\phi}_v\right)=\nabla \cdot \left(\rho {D}_{av}\nabla {\phi}_v\right) $$
(8)

while air is set as the constraint component with its mass fraction derived from

$$ \sum_i{\phi}_i=1. $$
(9)

Buoyancy in the surrounding flow is directly accounted for by the momentum source term [18]

$$ {\mathbf{S}}_M=\left(\rho -{\rho}_{ref}\right)\mathbf{g}. $$
(10)

The buoyance reference density, ρ ref , should be specified based on the average value of the domain density [19] and is here estimated from the external temperature and density of dry air. The internal flow of water due to natural convection is in its turn derived by the Boussinesq model, i.e. introducing a buoyancy source term approximated as

$$ \rho -{\rho}_{ref}=-{\rho}_{ref}{\alpha}_{\rho}\left( T-{T}_{ref}\right) $$
(11)

where α ρ is the thermal expansion

$$ {\alpha}_{\rho}={\left.-\frac{1}{\rho}\frac{\partial \rho}{\partial T}\right|}_p $$
(12)

and T ref is the buoyancy reference temperature. For the natural convection in the liquid phase, T ref is set explicitly in the model as an estimate of the average droplet temperature while ρ ref is specified as a constant material parameter valid for liquid water.

2.1 Interface boundary conditions

For a droplet subjected to evaporation, the source of energy at the surface may be expressed as

$$ {q}_{n, tot}^{"}={q}_n^{"}-{\dot{m}}_l{h}_{\lg } $$
(13)

where \( {q}_n^{"} \) is the local heat flux determined from Fourier’s law as [20]

$$ {q}_n^{"}=-{k}_f\frac{\partial T}{\partial n}. $$
(14)

It is also possible to express \( {q}_n^{"} \) in terms of a local heat transfer coefficient, h, as

$$ {q}_n^{"}= h\left({T}_s-{T}_{\infty}\right). $$
(15)

The mass flux, \( {\dot{m}}_l \), is based on the assumption that the air at the surface is fully saturated with vapor. The local mass flux of vapor at the surface may then, similarly to the heat flux, be determined from Fick’s law according to

$$ {\dot{m}}_l=-{D}_{av}\rho \frac{\partial {\phi}_v}{\partial n}. $$
(16)

The corresponding mass transfer coefficient is determined from

$$ {h}_m=\frac{{\dot{m}}_l}{\left({\rho}_{v, s}-{\rho}_{v,\infty}\right)}. $$
(17)

If the flow is mainly driven by temperature differences and h is known, h m may instead be obtained from the heat and mass transfer analogy according to

$$ \frac{h}{h_m}=\frac{k}{D_{av}{Le}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}} $$
(18)

enabling calculation of h m without including moisture in the simulations. Eq. 18 origin from the assumption that

$$ \frac{Nu}{Pr^e}=\frac{Sh}{Sc^e}. $$
(19)

It is generally adopted that e = 1/3 [14], and the value is confirmed for the objects studied in [21] as long as the thermal and concentration boundary layers have the same functional form. For the cases studied in this paper, the functional forms are not perfect, meaning that Nu ≈ Sh, and Pr ≈ Sc. It is thus of interest to compare the retrieved h m from Eq. (18) with results from Eq. (17). The gas properties in Eq. (18) are evaluated at the arithmetic mean temperature of the thermal boundary layer [14]. If h m is known, the mass flux may furthermore be determined from [14]

$$ {\dot{m}}_l={h}_m\frac{w_l}{R}\left(\frac{p_{v, sat}\left({T}_s\right)}{T_s}\right). $$
(20)

Hence, the air is in this work regarded as completely dry at the external boundaries. The saturated pressure, p v,sat ,(T), is the vapor pressure corresponding to saturation at temperature T as derived from Antonie’s Equation according to [22]

$$ \ln \left(\frac{p_{sat}}{1.333\cdot {10}^2}\right)= A-\frac{B}{C+ T} $$
(21)

with A = 18.3036, B = 3816.44 and C = −46.13. Thermo capillary fluid motion occurs at an interface of two immiscible fluids whenever a temperature gradient exists as the fluid tends to flow towards areas of higher surface tension, thus initiating so called Marangoni convection. The shear stress, τ, at the interface can be related to the surface tension by [23]

$$ \tau =\frac{\partial \sigma}{\partial T}{\nabla}_s T. $$
(22)

A correlation of the surface tension is found [24] as

$$ \sigma = F{\left(\frac{T_c- T}{T_c}\right)}^{\gamma}\left(1+ f\left(\frac{T_c- T}{T_c}\right)\right) $$
(23)

where F = 235.8e-3 N/m, T c  = 647.15 K, f = −0.625 and γ = 1.256 for water.

3 Model setup

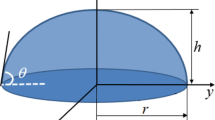
The simulations are carried out with the Computational Fluid Dynamics (CFD) software ANSYS CFX 14 and 15 being a hybrid method based solver. All simulations are carried out assuming laminar and Newtonian flow. A predefined axi-symmetrical geometry of the water droplet and ambient domain of air is used, i.e. a quasi-steady solution is presumed. The droplet and surrounding geometry is revolved 5ͦ around the y-axis, see Fig. 1.

Fig. 1
figure 1

Axi-symmetrical droplet in the form of a slice with symmetrical boundary conditions

Full size image

Assuming that the droplet remains in the form of a spherical cap, the height of the droplet h d changes as a function of the contact angle, θ, according to [25]

$$ {h}_d= r \tan \frac{\theta}{2}. $$
(24)

Two contact angles are examined in this work. In the first case the shape is half- spherical (h d  = r) yielding a contact angle of θ = 90o. In the second case h d is selected to be half of the original value, i.e. h d  = r/2. The contact radius is remained at its initial value [26]. This yields a contact angle of θ ≈ 53o. The contact radius, r, of the droplet is set to 0.001 m for all cases studied in this paper.

The geometry of the domain surrounding the droplet is constructed to not interfere with the heat transfer at the droplet surface. The heat transfer coefficient is considered to be sufficiently unaffected by the boundary of the external domain when the geometry is extruded 0.4 m above and beside the droplet. A free slip boundary condition is applied at the walls surrounding the domain. Fluid is thus not allowed to pass through the boundary and a constant temperature equal to T inf  = 293.15 K is applied at the external walls. The influence of a plate width or thickness on drying rate is not regarded in this study, and the boundary condition extended past the bottom of the droplet is set to a free slip isothermal boundary condition. A no slip condition is applied at the surface of the droplet facing towards the air. The part of the interface facing towards the droplet is assigned either a free slip boundary condition or a specified shear to account for the effect of Marangoni convection, see Eq. 22, while a no slip condition is applied at the bottom of the droplet with a specified temperature, T plate , to account for the heated plate.

Appropriate heat and mass transfer conditions at the droplet surface are evaluated through several modeling set-ups. To approximate Nu and Sh through separate simulations of droplet and external flow, the droplet surface temperature, T s , is set equal to the plate temperature, T plate . The heat and mass transfer coefficients between droplet surface and external flow are continuously updated if external and internal flow is considered simultaneous. The simulations conducted to determine the heat transfer coefficient are run in steady state mode, while the simulations with vapor included are run in transient mode and terminated when the evaporation rate has stabilized. A limitation in the model is that it is not possible to specify a value of the vapor density at the droplet surface. The specific mass density of water vapor is instead controlled with a source term through which a flux of vapor is added to the domain. A step function is then introduced to keep the level of vapor close to saturation. For stable convergence the average mass density of vapor is kept in an interval of maximum 1.0% from its theoretical value, assuming that the surface is fully saturated with vapor. Both air and vapor are regarded as temperature dependent ideal gases to account for the natural convection.

4 Results

Results from simulations are here presented and discussed. The convergence of the mesh is first ensured through a mesh study and the validity of the evaporation rates is then verified. The internal and ambient flows are evaluated, and simultaneous modeling of droplet and external flow is discussed. Finally the influence of local or average boundary conditions on the flow inside the droplet is examined, where the separate mechanisms of conduction, natural convection and Marangoni convection are studied.

4.1 Mesh convergence

A mesh convergence study based on results from simulations of three consecutive grids is carried out to estimate the magnitude of the discretization error. A structured mesh is applied on the axi-symmetrical geometry, with one element in the revolved direction (see Fig. 1). The advection scheme is solved with a specified blend factor of 1 and a RMS convergence criterion of 10−5 is applied. Conduction and natural convection inside the droplet is simulated simultaneously with the external flow, including thermal effects of evaporation, and the average evaporation rate on the droplet surface is chosen as key variable, see Table 1. With a plate surface temperature of T plate  = 333.15 K the results indicate that the simulations are in the asymptotic range and with a difference of less than 0.7% between Mesh no. 1 and Mesh no. 3 the accuracy is considered satisfactory and Mesh no. 3 is used in all further simulations.

Table 1 Mesh information
Full size table

4.2 External flow: Influence from vapor

The evaporation rate calculated from the ambient temperature field in air without vapor is compared with simulations including moisture to verify the results and to investigate the influence of vapor on the ambient flow. Constant droplet surface temperatures of T s  = 295.15 K, 297.15 K, 303.15 K, 313.15 K and 333.15 K are examined, while the surrounding air is set to T inf  = 293.15 K. The contact angle of the droplet is kept at θ = 90o.

An increased effect of natural convection due to temperature difference, ΔT, in air without moisture is shown for T s  = 333.15 K (Fig. 2 right), whereas the temperature field for T s  = 295.15 K (Fig. 2 left) show a behavior closer to conduction. Please note that only part of the external domain is displayed in Figs. 2 and 3. Inclusion of moisture due to evaporation will increase the maximum velocities in the external flow, and the largest effect of moist air is observed at T s  = 295.15 K; compare velocities in Figs. 2 and 3. A noticeable buoyancy effect due to vapor in the air is thus observed.

Fig. 2
figure 2

Temperature and velocity field of dry air arising from the heated droplet at T s  = 295.15 K (left) and T s  = 333.15 K (right). To enable visualization of the droplet, only part of the computational domain is displayed in the figure

Full size image
Fig. 3
figure 3

Temperature and velocity field of moist air arising from evaporation of the heated droplet at T s  = 295.15 K (left) and T s  = 333.15 K (right). To enable visualization of the droplet, only part of the computational domain is displayed in the figure

Full size image

Two methods to compute the evaporation rates are examined; Fick’s law at the droplet surface (Eq. 16) and the heat and mass transfer analogy (Eq. 18 in combination with Eq. 20). When the heat and mass transfer analogy is used, the drying rate is retrieved from simulations of the surrounding air without including the effect of water vapor (i.e. Fig. 2). Average Sh shows fairly good agreement between the methods, see Fig. 4. A maximum difference of around 8% is observed for T s  = 333.15 K. A possible reason for the discrepancy is the buoyancy effects, which are not accounted for in Eq. 18, but also the fact that the parameters in the heat and mass transfer analogy are retrieved at the arithmetic mean temperature of the thermal boundary layer. A value close to Sh = 2 is furthermore observed at low ΔT, beeing in agreement with correlations found in literature representing diffusive flows [14]. The variation of local Sh along the surface is increased with T s , see Fig. 5. At higher ΔT, it is thus of interest to investigate the importance of local heat and mass transfer boundary conditions at the droplet surface.

Fig. 4
figure 4

Influence of ΔT on the area average Sh retrieved from simulations considering dry air (heat and mass transfer analogy) and simulations including moisture (Fick’s law)

Full size image
Fig. 5
figure 5

Local Sh retrieved from simulations including moisture at θ = 90o

Full size image

In addition to thermal and buoyancy effects on Sh and Nu, it is also of interest to investigate the geometrical influence since, in reality, the contact angle decreases during drying. The average Nu in moist air is higher in the case of a receding contact angle; Nu = 2.31 at θ = 90o to be compared to Nu =2.66 at θ ≈ 53o, at T s  = 333.15 K. General for both shapes is that the maximum Nu is attained at the triple point (or triple line for a droplet) where fluid, air and substrate meet. It is also at this point that the largest difference in Nu between the contact angles appears, while the results are quite similar close to the apex, see Fig. 6. A characteristic length equal to the contact diameter is used for both geometries. Apparent is that the shape highly influences the local value of Nu close to the triple point, and that the use of a local, time-resolved Nu and Sh should be further investigated.

Fig. 6
figure 6

Local Nu for Ts = 333.15 K retrieved from simulations including moisture. Apex of the droplet is located at x = 0 m

Full size image

4.3 Internal flow: Influence from Marangoni convection

Although the theoretical Marangoni effect is significant for the internal flow, the presence of Marangoni convection in water droplets has been challenged [4, 5]. To further study this, simulations with and without Marangoni convection are here performed. In these simulations the external and internal domains are solved simultaneously with area average transfer coefficients applied at the interface between domains. The simulations are performed at T plate  = 333.15 K for θ = 90° and θ = 53°, where the lower contact angle corresponds to a smaller droplet volume due to evaporation. When combined with conduction, the simulations show that including Marangoni effects gives a distinct difference in results regarding both temperature distribution and velocity of the internal flow, see Figs. 7 and 8 where the results are displayed for θ = 90° and θ ≈ 53° respectively. In the case of natural convection the temperature profile inside the droplet is dominated by conduction due to low internal velocity. When both Marangoni and natural convection is present the velocity of the fluid is up to three orders of magnitude greater and this implies a larger convective heat transfer, as the minimum temperature inside the droplet is higher. The type of convection furthermore shows a distinct influence on the rotation direction of the fluid. In the case of Marangoni convection, fluid is moving from the triple point towards the apex along the surface while this motion is reversed when natural convection is dominating for T plate  = 333.15 K. The two types of convection will thus counteract for this case. The flow directions are consistent with results from Mollaret et al. [7] and Lu et al. [11].

Fig. 7
figure 7

Temperature and velocity distribution inside the droplet when conduction and natural convection are considered (left) and full model with Marangoni convection (right)

Full size image
Fig. 8
figure 8

Temperature and velocity distribution inside the droplet when conduction and natural convection are considered (left) and full model with Marangoni convection (right)

Full size image

Comparison of the separate mechanisms of the internal flow in Fig. 9 (θ = 90°) and Fig. 10 (θ ≈ 53°) confirms the result in Figs. 7 and 8. No apparent difference in T s is shown when the Marangoni convection is combined with natural convection as compared to the isolated dependence of Marangoni convection. A noticeable decrease in surface temperature is however observed if only natural convection and conduction are accounted for. At θ = 90° there is furthermore a small difference in temperature close to the apex between conduction and conduction combined with natural convection, while the difference is negligible for θ ≈ 53°.

Fig. 9
figure 9

Separate effects of internal flow mechanisms on T s . Apex of the droplet is located at x = 0 m. Contact angle θ = 90°

Full size image
Fig. 10
figure 10

Separate effects of internal flow mechanisms on T s . Apex of the droplet is located at x = 0 m. Contact angle θ ≈ 53°

Full size image

The large increase in velocity due to Marangoni convection will turn out to be of highest importance for as well the coupling of internal and external flow (chapter 4.4) as the influence of a spatially resolved heat and mass transfer coefficients on the evaporation rate (chapter 4.5).

4.4 Coupling of internal and external flow

Simultaneous and separate coupling between droplet and ambient flow is studied for θ = 90° and ≈ 53° at two different temperatures; T plate  = 295.15 K and 333.15 K. Notice that when the internal and external flow is simulated separately the mean transfer coefficients h and h m are retrieved from the simulations presented in Fig. 3, i.e. the area average coefficients applied in the simulations are determined at T s  = T plate .

The difference in drying rate between simultaneous (sim) and separate (sep) simulations is, due to the internal thermal gradient, largest at the start of drying as displayed in Figs. 11 and 12 for T plate  = 295.15 K and 333.15 K, respectively. The maximum differences of around 2% at T plate  = 295.15 K and 10% at T plate  = 333.15 K are attained when Marangoni convection is not accounted for, i.e. when the heat transfer inside the droplet is due to conduction and natural convection. A qualified estimation of average T s prior to the simulations could however increase the accuracy for separate simulations if T plate is high and the internal flow is low.

Fig. 11
figure 11

Average drying rate as a function of contact angle for comparison of simultaneous and separate modeling of droplet and ambient domains at T plate  = 295.15 K

Full size image
Fig. 12
figure 12

Average drying rate as a function of contact angle for comparison of simultaneous and separate modeling of droplet and ambient domains at T plate  = 333.15 K

Full size image

The drying rate at constant T s is of interest to further quantify the importance of the internal thermal transport. The difference in evaporation rate between T s  = T plate and Marangoni convection is around 10% at T s  = 333.15 K and θ = 90°, to be compared to 30% between natural convection and Marangoni convection (see Fig. 12). A small convective heat transfer inside the droplet will increase the internal temperature gradient, and hence increase the difference between T s and T plate . It is thus of special importance to model the internal heat transfer if Marangoni convection is suppressed, i.e. when the internal transfer is dominated by conduction and/or natural convection. The difference between natural convection and Marangoni convection is however reduced with decreased ΔT and θ, compare Figs. 11 and 12 where quasi steady results are retrieved for each θ at T plate  = 295.15 K and T plate  = 333.15 K, respectively.

Previous work has indicated suppression of Marangoni in water droplets, and for simultaneous simulations with conduction and natural convection the difference in evaporation rate between θ ≈ 53o and θ = 90o is almost constant at T plate  = 333.15 K, see Fig. 12. This indicates a rather constant evaporation rate throughout drying which is in correspondence with observations by Ruiz and Black [6] and Barmi and Meinhart [12]. The increased heat and mass transfer rates obtained at smaller contact angles might thus be balanced out by decreased surface area and internal conduction. Generally, the difference in total drying rate throughout the drying process is observed to increase with decreased thermal gradient inside the droplet, compare Figs. 11 and 12.

4.5 Influence of spatially resolved heat and mass transfer coefficients on the evaporation rate

The surface temperature of droplets will strongly influence the evaporation rate according to Eq. 20. The effect of local or area average heat and mass transfer coefficients on the surface temperature is therefore compared. The case of largest temperature difference, T s  = 333.15 K, and hence the largest local variation of Sh and Nu, is chosen for the investigation. Here a RMS convergence criteria of 10−7 is applied. Conduction, natural convection and Marangoni convection are compared for θ = 90° and θ ≈ 53°. When the circulation inside the droplet is weak, i.e. for conduction and natural convection, the differences between local and average boundary condition is pronounced, see Figs. 13 and 14 where results are displayed for θ = 90° and θ ≈ 53°, respectively. The application of an average heat transfer condition will thus reduce the surface temperature if the internal velocity is small. With Marangoni convection the heat transfer is, on the other hand, more significant and the two boundary conditions show almost identical results, see Figs.13 and 14. The latter also indicates that T s is nearly constant when Marangoni convection is present.

Fig. 13
figure 13

Comparison of T s between local and average boundary conditions. Contact angle θ = 90°. Tplate = 333.15 K

Full size image
Fig. 14
figure 14

Comparison of T s between local and average boundary conditions. Contact angle θ ≈ 53°. Tplate = 333.15 K

Full size image

As the local evaporation rate is strongly influenced by Nu and Sh, there are distinct differences in the spatial distribution of evaporation rate between local or average values at the surface. The total drying rates are however rather independent of this as the type of internal convection is more significant. The largest difference between local and average boundary conditions, approx. 5%, is found for θ ≈ 53o when only conduction and natural convection are accounted for the flow inside the droplet, see Table 2.

Table 2 Influence of a spatially resolved boundary condition
Full size table

5 Conclusions

For the studied conditions, simulations show a noticeable effect of buoyancy due to evaporation in the flow surrounding the droplet. The inclusion of moisture will hence increase the maximum velocities in the external flow. Including Marangoni convection will, in its turn, yield a flow within the droplet with velocities being up to three orders of magnitude greater than if this phenomenon is excluded. Results furthermore show that the internal and ambient flow can be simulated separately for the conditions studied here but the accuracy is improved if the internal temperature gradient is low, e.g. if Marangoni convection is present. A maximum difference in drying rate of 2–10% depending on T plate is observed between separate and simultaneous simulations when only conduction and natural convection is considered internally. Simultaneous simulations of the domains might thus be preferred at high plate temperatures if both internal and external flows are dominated by natural convection.

The importance of a spatially resolved heat and mass transfer boundary condition is, in its turn, increased if the velocity inside the sessile droplet is small or if there is a large variation of the transfer coefficients at the surface. Simulations show that the local variation of heat and mass transfer coefficients is increased with increased plate temperature and decreased contact angle. If the Marangoni convection is sufficiently high, the surface temperature and evaporation rate is on the other hand fairly independent of the type of heat transfer boundary condition. The inclusion of a locally dependent boundary condition will thus depend on the requested level of detail and accuracy.

If the internal convection is small, results further indicate that a rather constant evaporation rate may be obtained throughout drying at certain conditions. Modifications of boundary conditions and geometry during the course of evaporation are thus especially important if there is a large convective heat transfer inside the droplet.