1 Introduction

The transfer of thermal energy between fluids is one of the most important processes in engineering, which is possible through the use of different types of heat exchangers. They are broadly used in many thermal processes, both for the heating and cooling operations, and one of the simplest are the so-called double pipe heat exchangers. Despite their simplicity and low efficiency, they are very important due to their educational value in teaching the basics of heat exchanger design. Moreover, they form the structural basis for many more complex constructions, such as e.g. shell and tube heat exchangers or steam generators [24].

The steady-state properties of this class of thermal devices are very important from the point of view of their operation and control and thus are readily available since decades in many professional textbooks and scientific publications. However, since heat exchangers usually constitute part of larger industrial systems, their transient operations can occur frequently and thus can significantly influence overall system performance [21, 22, 25]. Therefore, contemporary mathematical models of heat exchangers should comprise not only their steady-state behaviour but also their dynamic properties, which are essential e.g. to impart effective control and to take preventive measures considering the safety aspect of the entire plant [5, 11].

The conventional tool for the mathematical description of the so-called distributed parameter systems (DPSs), which also include heat exchangers, are partial differential equations (PDEs) [13]. The development of the PDE-based mathematical modeling methods has progressed here in two parallel directions, with the use of either numerical or analytical approaches. For example, the numerical approach to some problems of plate fin and tube heat exchangers is presented in [23], whereas the same collection also includes the closed-form analytical solutions for the transient heat and moisture diffusion in a double-layer plate [8]. Moreover, there exist many professional software packages which allow to obtain numerical solutions to PDEs and make it possible to solve even very complex mathematical models, including the non-linear ones [19].

However, the use of such applications is usually limited to the personal computers or workstations. They are usually of little use for the real-time applications such as hardware-in-the-loop, or for implementation on embedded systems. From the control theory point of view, this kind of analytical representation is not fully effective because it does not express directly the relationships between the output (controlled) and the input (manipulated) variables of the system, and thus it is difficult to be used e.g. in the control system synthesis. In contrast, analytical methods allow for more thorough physical interpretation of the process and are more useful in the automatic control theory [20].

In this paper a method of the analytical description of a double pipe heat exchanger is considered, which is based on its transfer function representation. The main advantage of this approach, as compared to the numerical modelling, is that it constitutes a convenient starting point for computer implementation of different control algorithms. The knowledge of the transfer function make it to possible to determine not only the steady-state but also frequency- and time-domain responses of the system.

As opposed to the rational transfer function describing the dynamic properties of lumped parameter systems (LPSs), transfer functions of DPSs have the form of irrational functions [7, 27]. Due to the mathematical complexity, their analysis is more difficult, and possible applications are more limited than in the case of the finite-dimensional models. Therefore, in order to enable the implementation of the developed over the years techniques for the synthesis of control systems, the infinite-dimensional DPS models are usually replaced by their finite-dimensional approximations [3, 4, 9, 12, 16]. Nevertheless, regardless of the approximation method used, the starting point for the synthesis of a control system should be based on the possibly most accurate description of the DPS, taking into account its infinite-dimensional nature, e.g. a model in the form of the irrational transfer function.

Compared to the previously presented results, in the present paper the thermal capacity of the internal tube of the exchanger is taken into account, and two different typical flow configurations are considered, both for the steady-state and frequency domains. The remainder of the paper is organized as follows. Section 2 introduces a mathematical model of the considered thick-walled double pipe heat exchanger in the form of hyperbolic PDE system. In Sect. 3, transfer function matrices for the parallel- and counter-flow configurations are derived and analyzed. Based on the obtained transfer functions, Sect. 4 presents selected frequency responses of the exchanger, both in the form of three-dimensional graphs as well as classical, two-dimensional Bode and Nyquist plots. Next, Sect. 5 compares the steady-state temperature distributions for both flow configurations considered. Finally, short conclusions and future work prospects are given in Sect. 6.

Fig. 1
figure 1

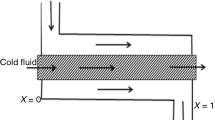
Schematic of a double pipe heat exchanger. \(v_s, v_t\)—shell-side and tube-side fluid velocities; \(\vartheta _s, \vartheta _t\)—shell-side and tube-side fluid temperatures; \(\vartheta _w\)—wall temperature; \(\vartheta _{si}, \vartheta _{ti}\)—shell-side and tube-side fluid inlet temperatures; \(\vartheta _{so}, \vartheta _{to}\)—shell-side and tube-side fluid outlet temperatures; \(L\)—heat exchanger length; \(d_{ti}, d_{to}\)—inner and outer diameters of the tube; \(d_{si}, d_{so}\)—inner and outer diameters of the shell. Solid arrows show flow directions for the parallel-flow mode, whereas dotted ones—for the counter-flow mode

Full size image

2 Governing PDEs

The considered heat exchanger consists of two concentric pipes (tubes) containing fluids flowing from the inlet of each tube towards its outlet (Fig. 1). In order to avoid ambiguity, throughout the rest of the paper the external tube will be referred as shell and the internal—simply as tube. Heat is transferred from one fluid to the other through the wall of the tube, either from tube side to shell side or vice versa. Depending on the flow arrangement, the fluids can enter the shell and the tube from the same or from the opposite ends of the exchanger. The first configuration is commonly known as parallel- while the second is usually referred to as counter-flow one.

In order to develop the mathematical model of the exchanger based on the energy balance equations, the following simplifying assumptions are made:

  • exchanger is perfectly insulated from the environment;

  • there are no internal thermal energy sources;

  • the flows are sufficiently turbulent to cause effective heat transfer;

  • only forced heat convection is considered (i.e. longitudinal heat conduction within the fluids and wall is neglected);

  • pressure drops of fluids along the shell and the tube are negligible;

  • the densities and heat capacities of the shell, tube and fluids are time and space invariant;

  • the convective heat transfer coefficients are constant and uniform over each surface.

According to the above assumptions, double pipe heat exchanger depicted in Fig. 1 is governed, based on the thermal energy balance equations, by the following PDE system [2, 6, 18]:

$$\begin{aligned} \frac{{\partial \vartheta _t \left( {l,t} \right) }}{{\partial t}} + v_t \frac{{\partial \vartheta _t \left( {l,t} \right) }}{{\partial l}}&= k_1 \big ( {\vartheta _w \left( {l,t} \right) - \vartheta _t \left( {l,t} \right) } \big ) \end{aligned}$$
(1)
$$\begin{aligned} \frac{{\partial \vartheta _s \left( {l,t} \right) }}{{\partial t}} + v_s \frac{{\partial \vartheta _s \left( {l,t} \right) }}{{\partial l}}&= k_2 \big ( {\vartheta _w \left( {l,t} \right) - \vartheta _s \left( {l,t} \right) } \big ) \end{aligned}$$
(2)
$$\begin{aligned} \frac{{\partial \vartheta _w \left( {l,t} \right) }}{{\partial t}}&= k_3 \big ( {\vartheta _t \left( {l,t} \right) - \vartheta _w \left( {l,t} \right) } \big ) \\ &\quad+ k_4 \big ( {\vartheta _s \left( {l,t} \right) - \vartheta _w \left( {l,t} \right) } \big ), \end{aligned}$$
(3)

where \(t\in [\,0,+\infty )\) represents time, \(l\in [\,0,L]\) stands for the space variable and the constant parameters \(k_1\), \(k_2\), \(k_3\), \(k_4\) depend on the shell and tube diameters, physical parameters of the fluids and the exchanger material [18]:

$$\begin{array}{*{20}l} {k_{1} = \frac{{4h_{t} }}{{\rho _{t} c_{t} d_{{ti}} }},} \hfill & {k_{2} = \frac{{4d_{{to}} h_{s} }}{{\rho _{s} c_{s} \left( {d_{{si}}^{2} - d_{{to}}^{2} } \right)}},} \hfill \\ {k_{3} = \frac{{4d_{{ti}} h_{t} }}{{\rho _{w} c_{w} \left( {d_{{to}}^{2} - d_{{ti}}^{2} } \right)}},} \hfill & {k_{4} = \frac{{4d_{{to}} h_{s} }}{{\rho _{w} c_{w} \left( {d_{{to}}^{2} - d_{{ti}}^{2} } \right)}},} \hfill \\ \end{array}$$
(4)

where \(\rho\) is the density, \(c\) is the specific heat and \(h\) is the heat transfer coefficient (subscripts as for the temperatures, see Fig. 1).

As one can notice, Eqs. (1–3) are weakly coupled, i.e. coupled only through the terms of convective heat exchange which do not contain derivatives. In contrast to the commonly adopted heat exchanger models such as those considered e.g. in [1, 11, 17], the abovementioned simplifications do not contain any assumption on the negligible thermal capacity of the tube, which results in the additional Eq. (3) representing heat conduction through the wall of the tube.

In order to obtain a unique solution of Eqs. (1–3), one must specify the appropriate initial and boundary conditions. The initial conditions can be specified in the following form:

$$\begin{aligned} \vartheta _t \left( {l,0} \right)&= \vartheta _{t0} \left( l \right) , \\ \vartheta _s \left( {l,0} \right)&= \vartheta _{s0} \left( l \right) , \\ \vartheta _w \left( {l,0} \right)&= \vartheta _{w0} \left( l \right) , \end{aligned}$$
(5)

where \(\vartheta _{t0}(l),\vartheta _{s0}(l),\vartheta _{w0}(l): [0,L] \rightarrow \mathbb {R}\) are given functions representing the initial (i.e. determined for \(t=0\)) temperature profiles along the heat exchanger.

The form of the boundary conditions for Eqs. (1–3) depends on the flow arrangement (see Fig. 1). For the case of the parallel-flow one obtains the following boundary conditions:

$$\begin{aligned} \vartheta _t \left( {0,t} \right)&= \vartheta _{ti} \left( t \right) , \\ \vartheta _s \left( {0,t} \right)&= \vartheta _{si} \left( t \right) , \end{aligned}$$
(6)

whereas for the counter-flow configuration the boundary conditions are expressed as follows:

$$\begin{aligned} \vartheta _t \left( {0,t} \right)&= \vartheta _{ti} \left( t \right) , \\ \vartheta _s \left( {L,t} \right)&= \vartheta _{si} \left( t \right) , \end{aligned}$$
(7)

where \(\vartheta _{ti}(t)\), \(\vartheta _{si}(l)\) represent the inlet temperatures which can be considered, from the control theory point of view, either as control signals or external disturbances.

3 Transfer function representation

For the heat exchanger under consideration one can distinguish two lumped input signals represented by the boundary conditions (6) or (7), and two output signals representing the distribution of the fluid temperatures along its axis. As shown e.g. in [7, 10], it is possible for the considered DPS with boundary inputs to obtain closed form expressions for the transfer functions by taking the Laplace transforms of the original PDEs and solving the resulting boundary value problem. In the following two subsections, transfer function matrices for the heat exchanger are introduced for two different boundary input configurations corresponding to the parallel- and counter-flow modes. Next, closed-form analytical expressions for those transfer functions are derived.

3.1 Parallel-flow mode

The transfer function matrix of the heat exchanger can be defined for the parallel-flow configuration described by the boundary conditions (6) as the matrix of the following form:

$$G(l,s) = \left[ {\begin{array}{*{20}l} {G_{{tt}} (l,s)} \hfill & {G_{{ts}} (l,s)} \\ {G_{{st}} (l,s)} \hfill & {G_{{ss}} (l,s)} \\ \end{array} } \right],$$
(8)

where

$$\begin{aligned} G_{tt} (l,s) = \frac{{\vartheta _t (l,s)}}{{\vartheta _t (0,s)}},\quad G_{st} (l,s) = \frac{{\vartheta _s (l,s)}}{{\vartheta _t (0,s)}}, \end{aligned}$$
(9)

for \(\vartheta _s(0,s)=0\), and

$$\begin{aligned} G_{ts} (l,s) = \frac{{\vartheta _t (l,s)}}{{\vartheta _s (0,s)}},\quad G_{ss} (l,s) = \frac{{\vartheta _s (l,s)}}{{\vartheta _s (0,s)}}, \end{aligned}$$
(10)

for \(\vartheta _t(0,s)=0\), all for zero initial conditions, \(\vartheta _t(l,0)=\vartheta _s(l,0)=0\), where

$$\begin{aligned} \vartheta \left( {l,s} \right) = {\mathcal {L}}_t \left\{ {\vartheta \left( {l,t} \right) } \right\} \end{aligned}$$
(11)

stands for the Laplace transform of \(\vartheta (l,t)\) in variable \(t\).

The vector of Laplace transforms of the fluid temperatures

$$\vartheta (l,s) = \left[ {\begin{array}{*{20}l} {\vartheta _{t} (l,s)} \hfill & {\vartheta _{s} (l,s)} \\ \end{array} } \right]^{T} ,$$
(12)

can therefore be determined, assuming zero initial conditions, based on the following equation:

$$\begin{aligned} \vartheta (l,s) = G(l,s) \vartheta (s), \end{aligned}$$
(13)

where

$$\vartheta (s) = \left[ {\begin{array}{*{20}l} {\vartheta _{t} (0,s)} \hfill & {\vartheta _{s} (0,s)}\\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}l} {\vartheta _{{ti}} (s)} \hfill & {\vartheta _{{si}} (s)}\\ \end{array} } \right]^{T}$$
(14)

can be considered as the vector of the boundary input signals for the parallel-flow mode.

Fig. 2
figure 2

Block diagram of the transfer function model of the heat exchanger (parallel-flow mode)

Full size image

A block diagram of the transfer function model for this mode is presented in Fig. 2. In order to find the elements of the transfer function matrix \(G(l,s)\) in (8), the Laplace transform approach can be used to solve Eqs. (1–3) with the boundary conditions (6). After Laplace transformation (11), Eqs. (1–3) take the following form:

$$\begin{aligned} s\vartheta _t\!\left( {l,\!s} \right) \! -\! \vartheta _t\! \left( {l,\!0} \right) \! + v_t \frac{{\partial \vartheta _t\!\! \left( {l,\!s} \right) }}{{\partial l}}\!&= \! k_1 \big ( {\vartheta _w\! \left( {l,\!s} \right) \! -\! \vartheta _t\! \left( {l,\!s} \right) }\big ), \end{aligned}$$
(15)
$$\begin{aligned} s\vartheta _s\!\! \left( {l,\!s} \right) \!-\!\vartheta _s\!\! \left( {l,\!0} \right) \! + v_s\! \frac{{\partial \vartheta _s\!\! \left( {l,\!s} \right) }}{{\partial l}}\!&= \! k_2 \big ( {\vartheta _w\! \left( {l,\!s} \right) \!-\!\vartheta _s\! \left( {l,\!s} \right) } \big ), \end{aligned}$$
(16)
$$\begin{aligned} s\vartheta _w\! \left( {l,\!s} \right) \! -\! \vartheta _w\! \left( {l,\!0} \right)&= k_3 \big ( {\vartheta _t\! \left( {l,\!s} \right) \! -\! \vartheta _w \left( {l,\!s} \right) } \big ) \\& \quad +k_4 \big ( {\vartheta _s \!\left( {l,\!s} \right) \! -\! \vartheta _w\! \left( {l,\!s} \right) } \big ). \end{aligned}$$
(17)

Assuming zero initial conditions and expressing the Laplace-transformed wall temperature \(\vartheta _w(l,s)\) from (17) as

$$\begin{aligned} \vartheta _w (l,s) = \frac{{k_3 \vartheta _t (l,s) + k_4 \vartheta _s (l,s)}}{{s + k_3 + k_4 }}, \end{aligned}$$
(18)

the equation set (15–17) can be reduced to the following two equations:

$$\begin{aligned} \frac{{\partial \vartheta _t \left( {l,s} \right) }}{{\partial l}}&= p_{tt} (s)\vartheta _t \left( {l,s} \right) + p_{ts} (s)\vartheta _s \left( {l,s} \right) , \end{aligned}$$
(19)
$$\begin{aligned} \frac{{\partial \vartheta _s \left( {l,s} \right) }}{{\partial l}}&= p_{st} (s)\vartheta _t \left( {l,s} \right) + p_{ss} (s)\vartheta _s \left( {l,s} \right) , \end{aligned}$$
(20)

where

$$\begin{aligned} p_{tt} (s)&= - \frac{{s^2 + (k_1 + k_3 + k_4 )s + k_1 k_4 }}{{v_t \left( {s + k_3 + k_4 } \right) }}, \end{aligned}$$
(21)
$$\begin{aligned} p_{ts} (s)&= \frac{{k_1 k_4 }}{{v_t \left( {s + k_3 + k_4 } \right) }}, \end{aligned}$$
(22)
$$\begin{aligned} p_{st} (s)&= \frac{{k_2 k_3 }}{{v_s \left( {s + k_3 + k_4 } \right) }}, \end{aligned}$$
(23)
$$\begin{aligned} p_{ss} (s)&= - \frac{{s^2 + (k_2 + k_3 + k_4 )s + k_2 k_3 }}{{v_s \left( {s + k_3 + k_4 } \right) }}, \end{aligned}$$
(24)

can be considered as elements of the following matrix:

$$P(s) = \left[ {\begin{array}{*{20}l} {p_{{tt}} (s)} \hfill & {p_{{ts}} (s)} \\ {p_{{st}} (s)} \hfill & {p_{{ss}} (s)} \\ \end{array} } \right].$$
(25)

By performing the Laplace transform again, now with respect to the space variable \(l\):

$$\begin{aligned} \vartheta \left( {q,s} \right) = \mathcal {L}_l \big \{ {\vartheta \left( {l,s} \right) } \big \} \end{aligned}$$
(26)

and taking into account that

$$\begin{aligned} \mathcal {L}_l \left\{ {\frac{{\partial \vartheta (l,s)}}{{\partial l}}} \right\} = q\vartheta (q,s) - \vartheta (0,s), \end{aligned}$$
(27)

one can transform the Eqs. (19) and (20) into the following algebraic form:

$$\begin{aligned} \vartheta _t \left( {q,s} \right)&= \frac{q - p_{ss}(s)}{{M(q,s)}} \vartheta _t \left( {0,s} \right) + \frac{p_{ts}(s)}{{M(q,s)}} \vartheta _s \left( {0,s} \right) , \end{aligned}$$
(28)
$$\begin{aligned} \vartheta _s \left( {q,s} \right)&= \frac{p_{st}(s)}{{M(q,s)}} \vartheta _t \left( {0,s} \right) + \frac{q - p_{tt}(s)}{{M(q,s)}}\vartheta _s \left( {0,s} \right) , \end{aligned}$$
(29)

where \(M(q,s)\) is the characteristic polynomial of the matrix \(P(s)\)

$$\begin{aligned} M\!(q,s)\! =\! \det \left( {qI\! -\! P(s)} \right) \! =\! \left( {q\! -\! \phi _1 \left( s \right) } \right) \left( {q\! -\! \phi _2 \left( s \right) } \right) , \end{aligned}$$
(30)

where \(\phi _1(s)\), \(\phi _2(s)\) are its eigenvalues given by

$$\begin{aligned} \phi _{1,2}(s) = \alpha (s) \pm \beta (s) \end{aligned}$$
(31)

with

$$\begin{aligned} \alpha (s) = \frac{1}{2}\left( {p_{tt}(s) + p_{ss}(s)} \right) \end{aligned}$$
(32)

and

$$\begin{aligned} \beta (s) = \frac{1}{2} {\sqrt{\left( {p_{tt}(s)-p_{ss}(s) } \right) ^2+4p_{ts}(s) p_{st}(s) } }. \end{aligned}$$
(33)

Finding the inverse Laplace transform of (28) and (29) with respect to \(q\) by taking advantage of the following property [14]:

$$\begin{aligned} \mathcal {L}_q^{ - 1} \left\{ {\frac{{S(q)}}{{T(q)}}\!=\!\frac{{S(q)}}{{\prod \limits _{j = 1}^N {\left( {q - \lambda _j } \right) } }}} \right\} \! =\!\sum \limits _{j = 1}^N {\frac{{S(\lambda _j )}}{{\left. {\frac{{dT(q)}}{{dq}}} \right| _{q = \lambda _j } }}\,{\text{e}}^{\lambda _j t} }, \end{aligned}$$
(34)

where \(S(q)\) and \(T(q)\) represent polynomials in \(q\) of degree \(M\) and \(N>M\), respectively, and \(\lambda _j\) is a single root of \(T(q)\), yields the following form of the equations:

$$\begin{aligned} \vartheta _t \left( {l,s} \right)&= G_{tt} \left( {l,s} \right) \vartheta _{t} \left( 0, s \right) + G_{ts} \left( {l,s} \right) \vartheta _{s} \left( 0, s \right) , \end{aligned}$$
(35)
$$\begin{aligned} \vartheta _s \left( {l,s} \right)&= G_{st} \left( {l,s} \right) \vartheta _{t} \left( 0, s \right) + G_{ss} \left( {l,s} \right) \vartheta _{s} \left( 0, s \right) , \end{aligned}$$
(36)

where the transfer functions are as follows:

$$\begin{aligned} G_{tt}(l,s)&= \frac{\phi _1(s) - p_{ss}(s)}{{\phi _1 (s) - \phi _2 (s)}}{\text{e}}^{\phi _1 (s)l} \\& \quad + \frac{\phi _2(s) - p_{ss}(s)}{{\phi _1 (s) - \phi _2 (s)}}{\text{e}}^{\phi _2 (s)l}, \end{aligned}$$
(37)
$$\begin{aligned} G_{ts}(l,s)&= \frac{p_{ts}(s)}{{\phi _1 (s) - \phi _2 (s)}}\left( {{\hbox {e}}^{\phi _1 (s)l} - {\hbox {e}}^{\phi _2 (s)l} } \right) , \end{aligned}$$
(38)
$$\begin{aligned} G_{st}(l,s)&= \frac{p_{st}(s)}{{\phi _1 (s) - \phi _2 (s)}}\left( {{\hbox {e}} ^{\phi _1 (s)l} - {\hbox {e}}^{\phi _2 (s)l} } \right) , \end{aligned}$$
(39)
$$\begin{aligned} G_{ss}(l,s)&= \frac{\phi _1(s) - p_{tt}(s)}{{\phi _1 (s) - \phi _2 (s)}}{\text{e}}^{\phi _1 (s)l} \\& \quad + \frac{\phi _2(s) - p_{tt}(s)}{{\phi _1 (s) - \phi _2 (s)}}{\text{e}}^{\phi _2 (s)l}, \end{aligned}$$
(40)

with \(p_{tt}(s)\), \(p_{ts}(s)\), \(p_{st}(s)\) and \(p_{ss}(s)\) being the elements of the matrix \(P(s)\) in (25) given by Eqs. (21–24) and \(\phi _1(s)\), \(\phi _2(s)\)—its eigenvalues given by (31–33).

3.2 Counter-flow mode

For the counter-flow configuration (7) the transfer function matrix of the exchanger can be defined in the following form:

$$\bar{G}(l,s) = \left[ {\begin{array}{*{20}l} {\bar{G}_{{tt}} (l,s)} \hfill & {\bar{G}_{{ts}} (l,s)} \\ {\bar{G}_{{st}} (l,s)} \hfill & {\bar{G}_{{ss}} (l,s)} \\ \end{array} } \right],$$
(41)

where

$$\begin{aligned} \bar{G}_{tt} (l,s) = \frac{{\vartheta _t (l,s)}}{{\vartheta _t (0,s)}},\quad \bar{G}_{st} (l,s) = \frac{{\vartheta _s (l,s)}}{{\vartheta _t (0,s)}}, \end{aligned}$$
(42)

for \(\vartheta _s(L,s)=0\), and

$$\bar{G}_{ts} (l,s) = \frac{{\vartheta _t (l,s)}}{{\vartheta _s (L,s)}},\quad \bar{G}_{ss} (l,s) = \frac{{\vartheta _s (l,s)}}{{\vartheta _s (L,s)}},$$
(43)

for \(\vartheta _t(0,s)=0\), all for zero initial conditions, \(\vartheta _t(l,0)=\vartheta _s(l,0)=0\).

The vector of Laplace transforms of the fluid temperatures

$$\vartheta (l,s) = \left[ {\begin{array}{*{20}l} {\vartheta _{t} (l,s)} \hfill & {\vartheta _{s} (l,s)} \\ \end{array} } \right]^{T} ,$$
(44)

can therefore be determined, assuming zero initial conditions, based on the following equation:

$$\begin{aligned} \vartheta (l,s) = \bar{G}(l,s) \bar{\vartheta }(s) \end{aligned}$$
(45)

where

$$\bar{\vartheta }(s) = \left[ {\begin{array}{*{20}l} {\vartheta _{t} (0,s)} \hfill & {\vartheta _{s} (L,s)} \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}l} {\vartheta _{{ti}} (s)} \hfill & {\vartheta _{{si}} (s)} \\ \end{array} } \right]^{T}$$
(46)

can be considered as the vector of the input signals for the counter-flow mode.

Fig. 3
figure 3

Block diagram of the transfer function model of the heat exchanger (counter-flow mode)

Full size image

A block diagram of the transfer function model for the counter-flow mode is presented in Fig. 3. In order to find the elements of the transfer function matrix \(\bar{G}(l,s)\), the similar approach as for parallel-flow can be applied, now with the boundary conditions (7). As a result one obtains the following equations:

$$\begin{aligned} \vartheta _t \left( {l,s} \right)&= \bar{G}_{tt} \left( {l,s} \right) \vartheta _{t} \left( 0, s \right) + \bar{G}_{ts} \left( {l,s} \right) \vartheta _{s} \left( L, s \right) , \end{aligned}$$
(47)
$$\begin{aligned} \vartheta _s \left( {l,s} \right)&= \bar{G}_{st} \left( {l,s} \right) \vartheta _{t} \left( 0, s \right) + \bar{G}_{ss} \left( {l,s} \right) \vartheta _{s} \left( L, s \right) , \end{aligned}$$
(48)

where

$$\begin{aligned} \bar{G}_{tt}(l,s) &= \frac{{{\text{e}}^{\phi _2 (s)L} {\text{e}}^{\phi _1 (s)l} \left( {\phi _1 (s) - p_{ss} (s)} \right) }}{{{\text{e}}^{\phi _2 (s)L} (\phi _1 (s) - p_{ss} (s)) - {\text{e}}^{\phi _1 (s)L} (\phi _2 (s) - p_{ss} (s))}} \\& \quad+ \frac{{{\text{e}}^{\phi _1 (s)L} {\text{e}}^{\phi _2 (s)l} \left( {\phi _2 (s) - p_{ss} (s)} \right) }}{{{\text{e}}^{\phi _2 (s)L} (\phi _1 (s) - p_{ss} (s)) - {\text{e}}^{\phi _1 (s)L} (\phi _2 (s) - p_{ss} (s))}}, \end{aligned}$$
(49)
$$\begin{aligned} \bar{G}_{ts}(l,s) = \frac{{p_{ts}(s) \left( {{\text{e}}^{\phi _2 (s)l} - {\text{e}}^{\phi _1 (s)l} } \right) }}{{{\text{e}}^{\phi _2 (s)L} (\phi _2 (s) - p_{tt} (s)) - {\text{e}}^{\phi _1 (s)L} (\phi _1 (s) - p_{tt} (s))}}, \end{aligned}$$
(50)
$$\begin{aligned} \bar{G}_{st}(l,s) = \frac{{p_{st} \left( {{\text{e}}^{\phi _2 (s)L} {\text{e}}^{\phi _1 (s)l} - {\text{e}}^{\phi _1 (s)L} {\text{e}}^{\phi _2 (s)l} } \right) }}{{{\text{e}}^{\phi _2 (s)L} (\phi _1 (s) - p_{ss} (s)) - {\text{e}}^{\phi _1 (s)L} (\phi _2 (s) - p_{ss} (s))}}, \end{aligned}$$
(51)
$$\begin{aligned} \bar{G}_{ss}(l,s) = \frac{{{\text{e}}^{\phi _2 (s)l} \left( {\phi _2 (s) - p_{tt} (s)} \right) - {\text{e}}^{\phi _1 (s)l} \left( {\phi _1 (s) - p_{tt} (s)} \right) }}{{{\text{e}}^{\phi _2 (s)L} \left( {\phi _2 (s) - p_{tt} (s)} \right) - {\text{e}}^{\phi _1 (s)L} \left( {\phi _1 (s) - p_{tt} (s)} \right) }}. \end{aligned}$$
(52)

As it can be easily noticed, the change in the boundary conditions imposed by the different flow configuration significantly affects the form of the transfer functions of the heat exchanger. This fact is reflected both in its steady-state and dynamic properties, as will be demonstrated later.

3.3 The case of zero heat transfer

As previously mentioned, the hyperbolic PDEs (1–3) are weakly coupled through the terms on the right-hand sides which represent the convective heat exchange. Assuming that no heat is transferred between the fluids through the wall, i.e. \(h_t=h_s=0\) in (4) which results in \(k_1=k_2=k_3=k_4=0\) in (1–3), one obtains the extremely simplified form of the equations

$$\begin{aligned}&\frac{{\partial \vartheta _t \left( {l,t} \right) }}{{\partial t}} + v_t \frac{{\partial \vartheta _t \left( {l,t} \right) }}{{\partial l}} = 0, \end{aligned}$$
(53)
$$\begin{aligned}&\frac{{\partial \vartheta _s \left( {l,t} \right) }}{{\partial t}} + v_s \frac{{\partial \vartheta _s \left( {l,t} \right) }}{{\partial l}} = 0, \end{aligned}$$
(54)

for which the matrix \(P(s)\) in (25) takes the following form:

$$P(s) = \left[ {\begin{array}{*{20}l} { - \frac{s}{{v_{t} }}} \hfill & 0 \hfill \\ 0 \hfill & { - \frac{s}{{v_{s} }}} \hfill \\ \end{array} } \right]{\text{ }}$$
(55)

with the eigenvalues

$$\begin{aligned} \phi _1(s)&= p_{tt}(s) = -\frac{s}{v_t}, \end{aligned}$$
(56)
$$\begin{aligned} \phi _2(s)&= p_{ss}(s) = -\frac{s}{v_s}, \end{aligned}$$
(57)

which consequently result in the following transfer function matrix:

$$G(l,s) = \left[ {\begin{array}{*{20}l} {{\text{e}}^{{ - s\tau _{t} (l)}} } \hfill & 0 \hfill \\ 0 \hfill & {{\text{e}}^{{ - s\tau _{s} (l)}} } \hfill \\ \end{array} } \right]$$
(58)

with

$$\begin{aligned} \tau _t(l)&= \frac{l}{v_t}, \quad \tau _s(l) = \frac{l}{v_s}, \end{aligned}$$
(59)

for the parallel-flow, and

$$\begin{aligned} \tau _t(l)&= \frac{l}{v_t}, \quad \tau _s(l) = \frac{l-L}{v_s}, \end{aligned}$$
(60)

for the counter-flow configuration.

The resulting system can thus be considered as two separate pure time-delay subsystems with time delays given by (59) or (60), representing two fluids of constant temperature profiles travelling along the exchanger.

4 Frequency responses

Based on the transfer functions derived in Sect. 3 it is straightforward to determine frequency responses of the heat exchanger. For this purpose, one should replace in the relationships (37–40) or (49–52) the operator variable \(s\) with the expression \(i\omega\), where \(i\) is the imaginary unit and \(\omega\) stands for the angular frequency.

Fig. 4
figure 4

Three-dimensional amplitude Bode plot of the frequency response \(G_{ts}(l,i\omega )\) for the parallel-flow heat exchanger

Full size image
Fig. 5
figure 5

Three-dimensional phase Bode plot of the frequency response \(G_{ts}(l,i\omega )\) for the parallel-flow heat exchanger

Full size image
Fig. 6
figure 6

Classical Bode plot of the frequency response \(G_{ts}(L,i\omega )\) for the parallel-flow heat exchanger

Full size image
Fig. 7
figure 7

Nyquist plot of the frequency response \(G_{ts}(L,i\omega )\) for the parallel-flow heat exchanger

Full size image

The graphical representation of these responses can take the form of three-dimensional graphs, taking into account their dependence on both the angular frequency \(\omega\) and the space variable \(l\). Another possibility is the representation in the form of classical two-dimensional plots, determined for fixed value of the space variable, e.g. \(l=0\) or \(l=L\). Considering as an example the Bode plot, the expressions for the logarithmic gain and phase take the following well-known form [14]:

$$\begin{aligned} L_m\left( {l,\omega } \right) = 20\log \big | {G\left( {l,i\omega } \right) } \big | \end{aligned}$$
(61)

and

$$\begin{aligned} \varphi \left( {l,\omega } \right) = \arg \big [ {G\left( {l,i\omega } \right) } \big ], \end{aligned}$$
(62)

where the expressions for the modulus and argument of the frequency response are as follows:

$$\begin{aligned} \big | {G\!\left( {l,\!i\omega } \right) } \big |\!=\!\sqrt{{\text{Re}}^2 \big \{ {G\!\left( {l,\!i\omega } \right) } \big \}\!+\!{\text{Im}}^2 \big \{ {G\!\left( {l,\!i\omega } \right) } \big \}} \end{aligned}$$
(63)

and

$$\begin{aligned} \arg \big [ {G\left( {l,i\omega } \right) } \big ] = \arctan \frac{{{\text{Im}}\big \{ {G\left( {l,i\omega } \right) } \big \}}}{{{\text{Re}}\big \{ {G\left( {l,i\omega } \right) } \big \}}}. \end{aligned}$$
(64)

Figures 4 and 5 show three-dimensional Bode plots of the frequency response \(G_{ts}(l,i\omega )\) of the exchanger operating in the parallel-flow mode, determined based on Eqs. (38) and (61–64) for the following parameter values: \(\rho _t = \rho _s = 1000\,{\text{kg/m}}^3\), \(\rho _w = 7800\, {\text{kg/m}^3}\), \(c_t = c_s = 4200\, {\text {J/(kg}\,\text{K)}}\), \(c_w = 500 {\text {J/(kg}\,\text{K)}}\), \(h_t = h_s = 6000\,{\text {W/(m}^2\, {\text{K}})}\), \(d_{ti} = 0.09\hbox { m}\), \(d_{to} = 0.1\hbox { m}\), \(d_{si} = 0.15\hbox { m}\), \(L = 5\hbox { m}\), \(v_t = 1\hbox { m/s}\), \(v_s = 0.1\hbox { m/s}\).

From the practical point of view, most important are the responses evaluated at the exchanger outlets, i.e. assuming \(l=0\) for \(\bar{G}_{st}, \bar{G}_{ss}\), and \(l=L\) for the remaining transfer functions. Fig. 6 shows classical two-dimensional Bode plots of the heat exchanger frequency responses \(G_{ts}(l,s)\) determined for \(l=L\). Next, the Nyquist plot for the same transfer function channel is presented in Fig. 7.

As seen from the Bode plots, the increase in the frequency of the sinusoidal input signal initially causes a decrease in the amplitude of the output signal, and then it gives rise to a local maximum. To a lesser extent this phenomenon is apparent in the phase characteristic. As the frequency increases, this effect repeats itself, which can be observed as oscillations on the Bode plot or as characteristic “loops” on the Nyquist plot. These oscillations are closely associated with the wave phenomena taking place inside the exchanger pipes [14].

Analysis of the frequency responses of the heat exchanger exhibits typical characteristics of systems with distributed delay [15]. In particular, in the case of the “straightforward” transfer function channels \(G_{tt}(l,s)\), \(G_{ss}(l,s)\) and their counter-flow counterparts, one can notice the dominant influence of the transport delay in the fluid flow. In order to confirm this conclusion, Nyquist plot of the frequency response \(G_{ss}(L,s)\) is shown in Fig. 8. The amplitude damping of the sinusoidal oscillations in the real and imaginary parts of the frequency response is relatively small, which is reflected here in the circular-shaped plot. On the other hand, in the case of the “crossover” transfer functions \(G_{ts}(l,s)\) and \(G_{st}(l,s)\), the damping of the input signal with increasing frequency is much greater as for the “straight-forward” channels (see Figs. 6, 7).

Fig. 8
figure 8

Nyquist plot of the frequency response \(G_{ss}(L,i\omega )\) for the parallel-flow heat exchanger

Full size image

5 Steady-state analysis

The steady-state temperature profiles along the heat exchanger can be determined directly from Eqs. (1–3) by assuming all time derivatives equal to zero, and solving the resulting boundary value problem

$$\begin{aligned} v_t \frac{{d \vartheta _t \left( {l} \right) }}{{d l}}&= k_1 \big ( {\vartheta _w \left( {l} \right) - \vartheta _t \left( {l} \right) } \big ), \end{aligned}$$
(65)
$$\begin{aligned} v_s \frac{{d \vartheta _s \left( {l} \right) }}{{d l}}&= k_2 \big ( {\vartheta _w \left( {l} \right) - \vartheta _s \left( {l} \right) } \big ), \end{aligned}$$
(66)
$$\begin{aligned} k_3 \big ( {\vartheta _t \! \left( {l} \right) \!- \!\vartheta _w \!\left( {l} \right) } \big ) \!+\! k_4 \big ( {\vartheta _s \!\left( {l} \right) \! -\! \vartheta _w \!\left( {l} \right) } \big )&= 0, \end{aligned}$$
(67)

with the boundary conditions representing constant inlet temperatures for the parallel-flow

$$\begin{aligned} \vartheta _t(0) = \vartheta _{ti}, \quad \vartheta _s(0) = \vartheta _{si}, \end{aligned}$$
(68)

or for the counter-flow configuration

$$\begin{aligned} \vartheta _t(0) = \vartheta _{ti}, \quad \vartheta _s(L) = \vartheta _{si}. \end{aligned}$$
(69)

The other possibility is to calculate the steady state responses of the exchanger from its transfer functions assuming \(s=0\) or, equivalently, from its frequency responses assuming \(\omega = 0\), and this approach will be applied below.

For \(s=0\) one obtains the following values of the parameters (21–24):

$$\begin{aligned} p_{tt}&= p_{tt} (0) = - \frac{{k_1 k_4 }}{{v_t \left( {k_3 + k_4 } \right) }}, \end{aligned}$$
(70)
$$\begin{aligned} p_{ts}&= p_{ts} (0) = \frac{{k_1 k_4 }}{{v_t \left( {k_3 + k_4 } \right) }} = - p_{tt}, \end{aligned}$$
(71)
$$\begin{aligned} p_{st}&= p_{st} (0) = \frac{{k_2 k_3 }}{{v_s \left( {k_3 + k_4 } \right) }}, \end{aligned}$$
(72)
$$\begin{aligned} p_{ss}&= p_{ss} (0) = - \frac{{k_2 k_3 }}{{v_s \left( {k_3 + k_4 } \right) }} = - p_{ts}, \end{aligned}$$
(73)

for which one obtains based on (32) and (33)

$$\begin{aligned} \alpha&= \alpha (0) = \frac{1}{2}\left( {p_{tt} + p_{ss}} \right) = - \frac{{k_1 k_4 v_s + k_2 k_3 v_t}}{{2 v_t v_s \left( {k_3 + k_4 } \right) }}, \end{aligned}$$
(74)
$$\begin{aligned} \beta&= \beta (0) = - \frac{1}{2} \left( {p_{tt}+p_{ss}}\right) = \frac{{k_1 k_4 v_s + k_2 k_3 v_t}}{{2 v_t v_s \left( {k_3 + k_4 } \right) }}, \end{aligned}$$
(75)

and consequently from (31)

$$\begin{aligned} \phi _1&= \phi _1(0) = \alpha + \beta = 0, \end{aligned}$$
(76)
$$\begin{aligned} \phi _2&= \phi _2(0) = \alpha - \beta = 2\alpha = - \frac{{k_1 k_4 v_s + k_2 k_3 v_t}}{{v_t v_s \left( {k_3 + k_4 } \right) }}. \end{aligned}$$
(77)

Based on the transfer functions determined in Sect. 3, it is now straightforward to obtain the formulas for the steady-state temperature profiles:

$$\begin{aligned} \vartheta _t \left( {l} \right)&= G_{tt} \left( {l} \right) \vartheta _{ti} + G_{ts} \left( {l} \right) \vartheta _{si}, \end{aligned}$$
(78)
$$\begin{aligned} \vartheta _s \left( {l} \right)&= G_{st} \left( {l} \right) \vartheta _{ti} + G_{ss} \left( {l} \right) \vartheta _{si}, \end{aligned}$$
(79)

where

$$\begin{aligned} G_{tt} (l)&= G_{tt} (l,0) = \frac{{p_{ss} }}{{\phi _2 }} + \left( {1 - \frac{{p_{ss} }}{{\phi _2 }}} \right) \text {e}^{\phi _2 l}, \end{aligned}$$
(80)
$$\begin{aligned} G_{ts} (l)&= G_{ts} (l,0) = \frac{{p_{ts} }}{{\phi _2 }} \left( {\text {e}^{\phi _2 l} - 1} \right) , \end{aligned}$$
(81)
$$\begin{aligned} G_{st} (l)&= G_{st} (l,0) = \frac{{p_{st} }}{{\phi _2 }} \left( {\text {e}^{\phi _2 l} - 1} \right) , \end{aligned}$$
(82)
$$\begin{aligned} G_{ss} (l)&= G_{ss} (l,0) = \frac{{p_{tt} }}{{\phi _2 }} + \left( {1 - \frac{{p_{tt} }}{{\phi _2 }}} \right) \text {e}^{\phi _2 l}, \end{aligned}$$
(83)

can be considered as the steady-state transfer functions of the heat exchanger, with \(p_{tt}\), \(p_{ts}\), \(p_{st}\), \(p_{ss}\) and \(\phi _2\) given by (70–77).

Similarly, for the counter-flow configuration one obtains based on Eqs. (47–52) and (70–77) the following steady-state equations:

$$\begin{aligned} \vartheta _t \left( {l} \right)&= \bar{G}_{tt} \left( {l} \right) \vartheta _{ti} + \bar{G}_{ts} \left( {l} \right) \vartheta _{si}, \end{aligned}$$
(84)
$$\begin{aligned} \vartheta _s \left( {l} \right)&= \bar{G}_{st} \left( {l} \right) \vartheta _{ti} + \bar{G}_{ss} \left( {l} \right) \vartheta _{si}, \end{aligned}$$
(85)

where

$$\begin{aligned} \bar{G}_{tt} (l)&= \bar{G}_{tt} (l,0) = \frac{{\text {e}^{\phi _2 L} p_{ss} + \text {e}^{\phi _2 l} \left( {\phi _2 - p_{ss} } \right) }}{p_{ss} \left( \text {e}^{\phi _2 L} - 1 \right) + \phi _2 }, \end{aligned}$$
(86)
$$\begin{aligned} \bar{G}_{ts} (l)&= \bar{G}_{ts} (l,0) = \frac{{p_{ts} \left( {\text {e}^{\phi _2 l} - 1} \right) }}{{\text {e}^{\phi _2 L} \left( {\phi _2 - p_{tt} } \right) + p_{tt} }}, \end{aligned}$$
(87)
$$\begin{aligned} \bar{G}_{st} (l)&= \bar{G}_{st} (l,0) = \frac{{p_{st} \left( {\text {e}^{\phi _2 l} - \text {e}^{\phi _2 L} } \right) }}{{p_{ss} \left( {\text {e}^{\phi _2 L} - 1} \right) + \phi _2 }}, \end{aligned}$$
(88)
$$\begin{aligned} \bar{G}_{ss} (l)&= \bar{G}_{ss} (l,0) = \frac{{{\text {e}}^{\phi _2 l} \left( {\phi _2 - p_{tt} } \right) + p_{tt} }}{{{\text {e}}^{\phi _2 L} \left( {\phi _2 - p_{tt} } \right) + p_{tt} }}. \end{aligned}$$
(89)

Having determined, based on Eqs. (78–83) or (84–89), the steady-state profiles of both fluids, it is straightforward to calculate also the temperature profiles for the wall from the algebraic Eq. (67) as

$$\begin{aligned} \vartheta _w (l) = \frac{{k_3 \vartheta _t (l) + k_4 \vartheta _s (l)}}{{k_2 + k_3 }}. \end{aligned}$$
(90)

Figure 9 shows the steady-state temperature profiles for the tube- and shell-side fluids, calculated based on Eqs. (78–83) for the following constant values of the inlet temperatures: \(\vartheta _s(0) = \vartheta _{si}=100\ ^\circ {\text {C}}\), \(\vartheta _t(0) = \vartheta _{ti}=50\ ^\circ {\text {C}}\), assuming \(v_s=0.1\ {\text{m/s}}\) and two different velocities of the tube-side fluid: \(v_t=1\ {\text{m/s}}\) (solid line) and \(v_t=0.2\ {\text{m/s}}\) (dashed line). Additionally, the steady-state temperature profiles of the wall are shown here, calculated based on Eqn. (90).

Figure 10 illustrates the steady-state temperature profiles calculated for the counter-flow configuration based on Eqs. (84–89) and (90) assuming: \(\vartheta _s(L) = \vartheta _{si}=100\ ^\circ {\text {C}}\), \(\vartheta _t(0) = \vartheta _{ti}=50\ ^\circ {\text {C}}\), \(v_s=-0.1\ {\text{m/s}}\) and two different velocities of the tube-side fluid: \(v_t=1\ {\text{m/s}}\) and \(v_t=0.2\ {\text{m/s}}\).

Fig. 9
figure 9

The steady state temperature profiles \(\vartheta _t(l)\), \(\vartheta _s(l)\) and \(\vartheta _w(l)\) for the parallel-flow heat exchanger (\(\vartheta _{si}=100\ ^\circ {\text {C}}\), \(\vartheta _{ti}=50\ ^\circ {\text {C}}\))

Full size image
Fig. 10
figure 10

The steady state temperature profiles \(\vartheta _t(l)\), \(\vartheta _s(l)\) and \(\vartheta _w(l)\) for the countercurrent-flow heat exchanger (\(\vartheta _{si}=100\ ^\circ {\text {C}}\), \(\vartheta _{ti}=50\ ^\circ {\text {C}}\))

Full size image

From the obtained results it is possible to determine e.g. the outlet temperatures of both fluids involved in the heat exchange. For example, for the parallel-flow configuration the outlet temperature \(\vartheta _t(L)\) of the heated fluid is about \(54.8 \ ^\circ {\text {C}}\) and the outlet temperature \(\vartheta _s(L)\) of the heating fluid is \(69 \ ^\circ {\text {C}}\) (see Fig. 9). Reducing the flow rate \(v_t\) of the heated fluid from 1 to \(0.2\ {\text{m/s}}\) increases its outlet temperature \(\vartheta _t(L)\) to about \(68.6 \ ^\circ {\text {C}}\) and also causes an increase in the outlet temperature \(\vartheta _s(L)\) of the heating fluid to \(75.9 \ ^\circ {\text {C}}\). As is apparent from Fig. 10, the change in the flow configuration causes further increase in the temperature of the heated fluid as compared to the parallel-flow mode. For example, when changing the flow rate \(v_t\) from 1 to \(0.2\ {{\text{m/s}}}\) its outlet temperature \(\vartheta _t(L)\) reaches \(71.3 \ ^\circ {\text{C}}\).

It is worth noting that the derived analytical expressions describing the steady-state properties not only make it possible to determine the outlet temperatures of the fluids but also allow an analysis of the temperature profiles along the heat exchanger, which may be of great importance from a technological point of view.

To sum up, the counter-flow mode has several advantages as compared to the parallel-flow one. The outlet temperature of the heated fluid can approach the inlet temperature of the heating fluid. The more uniform temperature difference between the two fluids prevents thermal stresses in the exchanger material. The other advantage is that the more uniform difference between temperatures \(\vartheta _t(l)\) and \(\vartheta _s(l)\) has an effect of more uniform heat transfer rate. The results presented above have been compared and found to be in general consistent with those well-known from the literature [18, 24, 26].

6 Conclusion

The closed-form analytical expressions have been derived for the individual elements of the 2 × 2 transfer function matrix of a double pipe heat exchanger working both in the parallel- and counter-flow modes. Unlike the case of lumped parameter systems, the transfer functions derived for this distributed parameter system contain irrational functions such as exponential and square root ones. As shown in the paper, the location of the boundary inputs of the system related to the flow configuration significantly affects its transfer function representation. Based on the obtained transfer functions, selected frequency responses of the heat exchanger have been presented both in the form of three-dimensional graphs as well as classical, two-dimensional Bode and Nyquist plots. Moreover, steady state temperature profiles have been determined and compared for both considered flow arrangements.

The future works could include determination of the space-time impulse responses for the individual transfer function channels, both for the parallel- and the counter-flow mode. Another issue to be thoroughly examined, which is very important from the control synthesis point of view, is selecting an appropriate method for the transfer functions and space-time responses approximation using the finite-dimensional models mentioned in Sect. 1.