Stability of pencils of plane sextics and Halphen pencils of index two

Abstract

We study the problem of classifying pencils of plane sextics up to projective equivalence via geometric invariant theory (GIT). In particular, we provide a complete description of the GIT stability of certain pencils of plane sextics called Halphen pencils of index two-classical geometric objects which were first introduced by G. Halphen in 1882. Inspired by the work of Miranda on pencils of plane cubics, we obtain explicit stability criteria in terms of the types of singular fibers appearing in their associated rational elliptic surfaces.

1 Introduction

Classification problems are often solved by constructing quotient spaces by the action of an algebraic group, and Geometric Invariant Theory (GIT) provides a tool for constructing such quotients. In this paper we are interested in the problem of classifying pencils of plane sextics up to projective equivalence.

If we let V denote the space of sections $H^0({\mathbb {P}}^2,{\mathcal {O}}_{{\mathbb {P}}^2}(1))$, then the space ${\mathscr {P}}_d$ of pencils of plane curves of degree d can be identified with the Grassmannian of lines $Gr(2,S^dV^{*})$, which can be embedded in ${\mathbb {P}}(\Lambda ^2 S^dV^{*})\simeq {\mathbb {P}}^N$ via Plücker coordinates. The group SL(V)¹ acts naturally on V, hence on the invariant subvariety ${\mathscr {P}}_d \subset {\mathbb {P}}^N$, and a classical problem consists of constructing the corresponding GIT quotient ${\mathscr {P}}_d// SL(V)$. This amounts to determining what are the (semi)stable pencils for this action.

In [1], we have related the GIT stability of a pencil ${\mathcal {P}} \in {\mathscr {P}}_d$ under the action of SL(V) to the log canonical threshold of the pair $({\mathbb {P}}^2,{\mathcal {C}}_d)$, where ${\mathcal {C}}_d$ is a curve in ${\mathcal {P}}$ (see e.g. [2, Sect. 8]); and also to the multiplicities of its generators at a base point. The results in [1] however only provide a partial description of the (semi)stable pencils.

In Sect. 2, we complete the description when $d=6$ obtaining explicit stability criteria in terms of some vanishing conditions on the Plücker coordinates of a pencil. This is the content of Propositions 2.2 and 2.3. In Sect. 3, we then focus on particular pencils of plane sextics and interpret such vanishing criteria geometrically.

In Sect. 4 we turn our attention to the so called Halphen pencils of index two, after the French mathematician Georges Henri Halphen who first studied them in [3]. We provide a complete and geometric description of their stability viewed as points in ${\mathscr {P}}_6$. Inspired by [4], we obtain explicit stability criteria in terms of the types of singular fibers appearing in their associated rational elliptic surfaces. The relevant definitions are as follows:

Definition 1.1

A Halphen pencil of index two is a pencil of plane curves of degree six with nine (possibly infinitely near) base points of multiplicity two.

Definition 1.2

A rational elliptic surface consists of a smooth and projective rational surface Y together with a fibration $f:Y\rightarrow {\mathbb {P}}^1$ such that the generic fiber is a smooth genus one curve and there are no $(-1)$-curves in any fiber. We define the index of the fibration as the positive generator of the ideal $\{D\cdot Y_{\eta } \,\,; \,\, D\in \text {Pic}(Y)\}$, where $Y_{\eta }$ denotes the generic fiber.

Moreover, the correspondence between Halphen pencils and rational elliptic surfaces is given by the following Proposition:

Proposition 1.3

[[5, Theorem 5.6.1]] If $f:Y \rightarrow {\mathbb {P}}^1$ is a rational elliptic surface of index two, then there exists a birational map $\pi : Y \rightarrow {\mathbb {P}}^2$ so that $f\circ \pi ^{-1}$ is a Halphen pencil of index two. Conversely, given a Halphen pencil of index two, taking the minimal resolution of its base points we obtain a rational elliptic surface of index two.

The surface Y has finitely many singular fibers and the configuration of all non-multiple singular fibers is exactly the same as the one in the associated Jacobian fibration (see e.g. [6, Chapter V.9]). In particular, the possible types of fibers have been classified by Kodaira and Néron [7,8,9]. Moreover, the possible configurations of singular fibers have been classified by Miranda and Persson [10, 11]. And, over a field of characteristic zero, any multiple fiber is of type $I_n$ for some $n\ge 0$ [5, Proposition 5.1.8].

The main results of this paper are given by Theorems 1.4, 1.5 and 1.6 below, where ${\mathcal {P}}$ denotes a Halphen pencil of index two and Y denotes the associated rational elliptic surface. We write ${\mathcal {P}}$ as $\lambda B + \mu (2C)=0$, where C is the unique cubic through the nine base points of ${\mathcal {P}}$ and the curve B corresponds to some (non-multiple) fiber of Y, which we denote by F.

One of the main ideas in our approach consists of observing that the group SL(V) is also acting on ${\mathbb {P}}(S^6V^*)$, the space of plane sextics. In [1] we have also related the stability of a pencil ${\mathcal {P}}\in {\mathscr {P}}_6$ to the stability of its generators, and the stability of plane curves of degree six is well known—it has been completely described by Shah in [12].

The other main ingredients are: (1) the explicit constructions of Halphen pencils of index two in [13] and the classification from Theorem 1.2 therein, (2) the inequalities provided by [13, Theorem 1.1], (3) the stability criteria given in [1] when $d=6$, and (4) the results from Sect. 3.

Using Kodaira’s notation for singular fibers of elliptic surfaces, and considering the actions of SL(V) on both ${\mathscr {P}}_6$ and the space of plane curves of degree six, we prove:

Theorem 1.4

When C is smooth the pencil ${\mathcal {P}}$ is stable if and only if one of the following statements hold

• (i) all fibers of Y are reduced

• (ii) Y contains exactly one (non-multiple) fiber F of type $I_n^*$ or $IV^*$

• (iii) Y contains exactly one (non-multiple) fiber F of type $II^*$ or $III^*$ and the corresponding plane curve B is semi-stable

• (iv) Y contains two fibers of type $I_0^*$ and there is no one-parameter subgroup $\lambda$ that destabilizes the two corresponding curves simultaneously.

Theorem 1.5

When C is singular the pencil ${\mathcal {P}}$ is stable if and only if one of the following statements hold

• (i) all fibers of Y are reduced

• (ii) Y contains a (non-multiple) non-reduced fiber F such that the corresponding curve B is semi-stable; and there is no one-parameter subgroup $\lambda$ that destabilizes 2C and B simultaneously

• (iii) Y contains a fiber of type $IV^*$ and B is unstable

Theorem 1.6

The pencil ${\mathcal {P}}$ is semi-stable if and only if every curve in ${\mathcal {P}}$ is semi-stable or Y does not contain a fiber F of type $II^*$.

We work over ${\mathbb {C}}$ throughout.

2 Stability of pencils of plane sextics

A fundamental tool for describing stability in the sense of GIT is the numerical criterion of Hilbert–Mumford. In our setting, it says a pencil ${\mathcal {P}} \in {\mathscr {P}}_6$ is unstable (resp. non-stable) if and only if there exists a 1-parameter subgroup ${\mathbb {C}}^{\times } \rightarrow SL(V)$ with respect to which all weights are positive (resp. non-negative). In particular, in order to determine which are the (semi)stable pencils, we need to know how the diagonal elements in SL(V) act on the Plücker coordinates.

if we choose a pencil ${\mathcal {P}} \in {\mathscr {P}}_6$ and two curves $C_f$ and $C_g$ as generators, these represented (in some choice of coordinates) by $f=\sum f_{ij}x^iy^jz^{6-i-j}=0$ and $g=\sum g_{ij}x^iy^jz^{6-i-j}=0$, respectively; then the Plücker embedding takes the $2\times 27$ matrix $\begin{pmatrix} f_{ij} \\ g_{ij} \end{pmatrix}$ to the point in ${\mathbb {P}}^{{28\atopwithdelims ()2}-1}$ whose coordinates are given by all the $2\times 2$ minors $m_{ijkl}\doteq \begin{vmatrix} f_{ij}&f_{kl} \\ g_{ij}&g_{kl} \end{vmatrix}$.

Now, if an element of SL(V) is given by $\begin{pmatrix} \alpha &{} 0 &{} 0\\ 0 &{} \beta &{} 0\\ 0 &{} 0 &{} \gamma \end{pmatrix}$ in some choice of coordinates [x, y, z] in ${\mathbb {P}}^2$, then its action on the coordinates of ${\mathbb {P}}^2$ is given by $[x,y,z] \mapsto [\alpha x,\beta y, \gamma z]$. Thus, the action on a point $(f_{ij})\in S^6 V^*$ representing $\sum f_{ij}x^iy^jz^{6-i-j}$ is given by $(f_{ij}) \mapsto (\alpha ^i\beta ^j\gamma ^{6-i-j}f_{ij})$ and, therefore, it acts on the Plücker coordinates by

$$\begin{aligned} (m_{ijkl}) \mapsto (\alpha ^{i+k}\beta ^{j+l}\gamma ^{12-i-j-k-l}m_{ijkl}) \end{aligned}$$

We can thus express the Hilbert–Mumford criterion for the stability of a pencil ${\mathcal {P}} \in {\mathscr {P}}_6$ as the vanishing of some of its Plücker coordinates $(m_{ijkl})$ (with respect to a convenient choice of basis in ${\mathbb {P}}^2$).

First, note that we may assume any one-parameter subgroup $\lambda$ of SL(V) is normalized, meaning we choose coordinates [x, y, z] in ${\mathbb {P}}^2$ so that $\lambda$ is given by

$$\begin{aligned} t \mapsto \begin{pmatrix} t^{a_x} &{} 0 &{} 0 \\ 0 &{} t^{a_y} &{} 0 \\ 0 &{} 0 &{} t^{a_z} \end{pmatrix} \end{aligned}$$

where $a_x,a_y,a_z \in {\mathbb {Z}}$ with $a_x \ge a_y \ge a_z, a_x>0$ and $a_x+a_y+a_z=0$.

In particular, the action of $\lambda (t)$ in the Plücker coordinates is given by

$$\begin{aligned} (m_{ijkl}) \mapsto (t^{e_{ijkl}} m_{ijkl}) \end{aligned}$$

where $e_{ijkl} \doteq a_x(2i+2k+j+l-12)+a_y(2j+2l+i+k-12)$.

Further, we can normalize the weights so that $a_x=1,a_y=a$ and $a_z=-1-a$ for some $a\in [-1/2,1]\cap {\mathbb {Q}}$. Then

$$\begin{aligned} e_{ijkl}=e_{ijkl}(a)= (2i+2k+j+l-12)+a(2j+2l+i+k-12) \end{aligned}$$

The sign of the Hilbert–Mumford weight $\mu ({\mathcal {P}},\lambda )$ (defined in (1) below) does not change under these reductions and the Hilbert–Mumford criterion becomes:

Proposition 2.1

A pencil ${\mathcal {P}}\in {\mathscr {P}}_6$ is unstable (resp. non-stable) if and only if there exists a rational number $a \in [-1/2,1]$ and coordinates in ${\mathbb {P}}^2$ such that if the pencil is represented in those coordinates by $(m_{ijkl})$, then $m_{ijkl}=0$ whenever $e_{ijkl}(a)\le 0$ (resp. $e_{ijkl}(a) < 0$).

A priori, for each choice of coordinates in ${\mathbb {P}}^2$ one would need to test all possible values of $a\in [-1/2,1]\cap {\mathbb {Q}}$ to verify the stability criterion. However, because the function (for a fixed ${\mathcal {P}}$ and some choice of coordinates)

$$\begin{aligned} \mu ({\mathcal {P}},\lambda ) \doteq \min \{e_{ijkl}(a)\,\,:\,\,m_{ijkl}\ne 0\} \end{aligned}$$

(1)

is piecewise linear, a key observation is that we only need to test its positivity for a finite number of critical values $a\in [-1/2,1]\cap {\mathbb {Q}}$.

In other words, the conditions $e_{ijkl}(a)\le 0$ (resp. $e_{ijkl}(a) < 0$) divide the interval $[-1/2,1]$ into finitely many subintervals $[a_n,a_{n+1}]$ within which the truthfulness of the inequality remains constant. That is, for each interval $[a_n,a_{n+1}]$ we can find values of i, j, k and l for which the inequality $e_{ijkl}(a)\le 0$ (resp. $e_{ijkl}(a) < 0$) remains true for all $a\in [a_n,a_{n+1}]$.

To find these intervals we proceed as follows. For computational reasons we first let $r=i+k$ and $s=j+l$. Then, for each possible pair (r, s) in the set

$$\begin{aligned} \{(r,s)\in \{0,1,\ldots ,12\}\times \{0,1,\ldots ,12\}\,\,:\,\, r+s \le 12\}, \end{aligned}$$

we test whether we can solve the inequality $2r+s-12+a(2s+r-12)\le 0$ (resp. $<0$) for the variable a, further imposing the restriction $a\in [-1/2,1]$.

There are ${14} \atopwithdelims (){2}$ possible pairs (r, s), and the corresponding values of a we find can be summarized as in Tables 1 and 2 below.

Table 1 Intervals for unstability

At this point, the corresponding vanishing conditions on the Plücker coordinates $m_{ijkl}$, however, are not independent. But a careful inspection of Tables 1 and 2 reveals the number of sub-intervals giving minimal conditions for unstability (resp. non-stability) is in fact six (resp. seven).

More precisely, in order to obtain minimal conditions for unstability, it suffices considering only the following six distinct subintervals:

$$\begin{aligned} (-1/3,-2/7),(-2/7,-1/5),(-1/11,0),(1/7,1/4),(1/4,2/5),(1/2,1) \end{aligned}$$

And, similarly, for non-stability it suffices taking

$$\begin{aligned} a\in \{-1/2,-2/7,-1/5,0,1/4,2/5,1\}. \end{aligned}$$

As a consequence, of this analysis of the data in Tables 1 and 2, we conclude the Hilbert–Mumford criterion for unstability (resp. non-stability) can be restated as in Proposition 2.2 (resp. Proposition 2.3) below, where we introduce the following sets:

$$\begin{aligned} M_{rs}\doteq \{m_{ijkl}\,:\,i+k=r\,\,\text{ and }\,\,j+l=s\} \end{aligned}$$

and

$$\begin{aligned} X_{m,n}\doteq \{(r,s)\,:\,r=m\,\,\text{ and }\,\,0\le s\le n\} \end{aligned}$$

Table 2 Intervals for non-stability

Proposition 2.2

A pencil ${\mathcal {P}}\in {\mathscr {P}}_6$ is unstable if and only if there exist coordinates in ${\mathbb {P}}^2$ so that if the pencil is represented in those coordinates by $(m_{ijkl})$, then either

Case U(1):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,12}\cup X_{1,11}\cup X_{2,10}\cup X_{3,8}\cup X_{4,4}$ and $a =-13/42$ will exhibit ${\mathcal {P}}$ as unstable; or

Case U(2):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,12}\cup X_{1,11}\cup X_{2,10}\cup X_{3,7}\cup X_{4,4}\cup X_{5,0}$ and $a= -8/35$ will exhibit ${\mathcal {P}}$ as unstable; or

Case U(3):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,12}\cup X_{1,10}\cup X_{2,8}\cup X_{3,6}\cup X_{4,4}\cup X_{5,1}$ and $a =-1/12$ will exhibit ${\mathcal {P}}$ as unstable; or

Case U(4):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,10}\cup X_{1,8}\cup X_{2,7}\cup X_{3,5}\cup X_{4,4}\cup X_{5,2} \cup X_{6,0}$ and $a =3/14$ will exhibit ${\mathcal {P}}$ as unstable; or

Case U(5):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,9}\cup X_{1,8}\cup X_{2,6}\cup X_{3,5}\cup X_{4,4}\cup X_{5,2} \cup X_{6,1}$ and $a=3/10$ will exhibit ${\mathcal {P}}$ as unstable; or

Case U(6):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,8}\cup X_{1,7}\cup X_{2,6}\cup X_{3,5}\cup X_{4,4}\cup X_{5,2} \cup X_{6,1}\cup X_{7,0}$ and $a =3/4$ will exhibit ${\mathcal {P}}$ as unstable.

Proposition 2.3

A pencil ${\mathcal {P}}\in {\mathscr {P}}_6$ is non-stable if and only if there exist coordinates in ${\mathbb {P}}^2$ so that if the pencil is represented in those coordinates by $(m_{ijkl})$, then either

Case NS(1):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,12}\cup X_{1,11}\cup X_{2,10}\cup X_{3,9}$ and $a=-1/2$ will exhibit ${\mathcal {P}}$ as non-stable; or

Case NS(2):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,12}\cup X_{1,11}\cup X_{2,10}\cup X_{3,7}\cup X_{4,3}$ and $a=-2/7$ will exhibit ${\mathcal {P}}$ as non-stable; or

Case NS(3):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,12}\cup X_{1,11}\cup X_{2,9}\cup X_{3,6}\cup X_{4,3}\cup X_{5,0}$ and $a=-1/5$ will exhibit ${\mathcal {P}}$ as non-stable; or

Case NS(4):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,11}\cup X_{1,9}\cup X_{2,7}\cup X_{3,5}\cup X_{4,3}\cup X_{5,0}$ and $a=0$ will exhibit ${\mathcal {P}}$ as non-stable; or

Case NS(5):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,9}\cup X_{1,8}\cup X_{2,6}\cup X_{3,5}\cup X_{4,3}\cup X_{5,2} \cup X_{6,0}$ and $a=1/4$ will exhibit ${\mathcal {P}}$ as non-stable; or

Case NS(6):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,9}\cup X_{1,7}\cup X_{2,6}\cup X_{3,5}\cup X_{4,3}\cup X_{5,2} \cup X_{6,1}$ and $a=2/5$ will exhibit ${\mathcal {P}}$ as non-stable; or

Case NS(7):

the $m_{ijkl}$ in $M_{rs}$ all vanish for all pairs (r, s) in $X_{0,7}\cup X_{1,6}\cup X_{2,5}\cup X_{3,4}\cup X_{4,3}\cup X_{5,2}\cup X_{6,1} \cup X_{7,0}$ and $a=1$ will exhibit ${\mathcal {P}}$ as non-stable.

Remark 2.4

Note that if a pencil ${\mathcal {P}}\in {\mathscr {P}}_6$ satisfies the vanishing conditions of Case U(i) in Proposition 2.2, then it satisfies the vanishing conditions of Case $NS(i+1)$ in Proposition 2.3.

3 Unstable and non-stable pencils

Given an unstable (resp. non-stable) pencil ${\mathcal {P}}\in {\mathscr {P}}_6$, if we choose coordinates [x, y, z] in ${\mathbb {P}}^2$ as in Proposition 2.2 (resp. 2.3) and generators $C_f$ and $C_g$, then each vanishing condition $m_{ijkl}=0$ can be translated into the vanishing of the coefficients of some pair $C_{f'}$ and $C_{g'}$ of generators (not necessarily the original pair). We can then visualize the stability criteria by representing $C_{f'}$ (and $C_{g'}$) in a triangle of coefficients in the plane as in [14, Sect. 1.9].

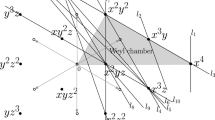
For instance, if we assume ${\mathcal {P}}$ satisfies the conditions of Case NS(1) (resp. NS(4)) of Proposition 2.3 then the coefficients of the defining polynomials $f'$ and $g'$ which are located below the corresponding lines in one of the cases in Fig. 1 (resp. 2) must all vanish.

Fig. 1

Pictorial description of Case NS(1) of Propositions 2.3

Fig. 2

Pictorial description of Case NS(4) of Propositions 2.3

One can draw similar pictures for each of the cases in Propositions 2.2 and 2.3 thus obtaining a characterization of the unstable and non-stable pencils in ${\mathscr {P}}_6$ in terms of explicit equations for their generators.

To illustrate what kind of computations are involved in this process we prove Proposition 3.1 below, which corresponds to Fig. 1. We use the notation $\langle m_1,\ldots ,m_n \rangle$ to denote the subspace of homogeneous polynomials of degree six in the variables x, y and z which is generated by the monomials $m_i$. Whereas $\rangle m_1,\ldots ,m_n \langle$ denotes the subspace of those polynomials which are generated by all the monomials which are different from the $m_i$. The result is the following:

Proposition 3.1

A pencil ${\mathcal {P}}\in {\mathscr {P}}_6$ satisfies the vanishing conditions in Case NS(1) of Proposition 2.3 if and only if there exist coordinates in ${\mathbb {P}}^2$ and generators $C_f$ and $C_g$ of ${\mathcal {P}}$ such that either

Case1:

$f \in \langle x^4z^2,x^4yz,x^4y^2,x^5z,x^5y,x^6 \rangle$ and g is arbitrary

Case2:

$f \in \langle x^3z^3,x^3yz^3,x^3y^2z,x^3y^3,x^4z^2,x^4yz,x^4y^2,x^5z,x^5y,x^6 \rangle$ and $g\in \rangle z^6,yz^5,y^2z^4,y^3z^3,y^4z^2,y^5z,y^6 \langle$

Case3:

f and $g \in \langle x^iy^jz^{6-i-j} \rangle$, where $2\le i \le 6, 0\le j \le 6$ and $i+j\le 6$

Proof

Let us assume ${\mathcal {P}}$ is non-stable and that its Plücker coordinates $(m_{ijkl})$ must vanish for all i, j, k and l satisfying $i+k=r$ and $j+l=s$ for all the pairs (r, s) in Case NS(1) of Proposition 2.3. Using the relations $m_{ijkl}=-m_{klij}$ and $m_{ijij}=0$ we can compute the minimal set of values $\{i,j,k,l\}$ (in order) so that the $m_{ijkl}$ vanish.

In other words, we find all integers i, j, k and l subject to the restrictions

• (i) $0\le i,j,k,l \le 6$,

• (ii) $i+j \le 6$,

• (iii) $k+l\le 6$, and

• (iv) $(i<k)\vee (i=k \wedge j<l)$

satisfying the inequality

$$\begin{aligned} (2i+2k+j+l-12)-1/2(2j+2l+i+k-12)<0 \end{aligned}$$

All possible solutions $\{i,j,k,l\}$ (in order) are:

$$\begin{aligned} \{0, 0, 0, 1\}, \{0, 0, 0, 2\}, \{0, 0, 0, 3\}, \{0, 0, 0, 4\}, \{0, 0, 0, 5\}, \{0, 0, 0, 6\}, \{0, 0, 1, 0\},\\ \{0, 0, 1, 1\}, \{0, 0, 1, 2\}, \{0, 0, 1, 3\}, \{0, 0, 1, 4\}, \{0, 0, 1, 5\}, \{0, 0, 2, 0\}, \{0, 0, 2, 1\}, \\ \{0, 0, 2, 2\}, \{0, 0, 2, 3\}, \{0, 0, 2, 4\}, \{0, 0, 3, 0\}, \{0, 0, 3, 1\}, \{0, 0, 3, 2\}, \{0, 0, 3, 3\}, \\ \{0, 1, 0, 2\}, \{0, 1, 0, 3\}, \{0, 1, 0, 4\}, \{0, 1, 0, 5\}, \{0, 1, 0, 6\}, \{0, 1, 1, 0\}, \{0, 1, 1, 1\}, \\ \{0, 1, 1, 2\}, \{0, 1, 1, 3\}, \{0, 1, 1, 4\}, \{0, 1, 1, 5\}, \{0, 1, 2, 0\}, \{0, 1, 2, 1\}, \{0, 1, 2, 2\}, \\ \{0, 1, 2, 3\}, \{0, 1, 2, 4\}, \{0, 1, 3, 0\}, \{0, 1, 3, 1\}, \{0, 1, 3, 2\}, \{0, 1, 3, 3\}, \{0, 2, 0, 3\}, \\ \{0, 2, 0, 4\}, \{0, 2, 0, 5\}, \{0, 2, 0, 6\}, \{0, 2, 1, 0\}, \{0, 2, 1, 1\}, \{0, 2, 1, 2\}, \{0, 2, 1, 3\}, \\ \{0, 2, 1, 4\}, \{0, 2, 1, 5\}, \{0, 2, 2, 0\}, \{0, 2, 2, 1\}, \{0, 2, 2, 2\}, \{0, 2, 2, 3\}, \{0, 2, 2, 4\}, \\ \{0, 2, 3, 0\}, \{0, 2, 3, 1\}, \{0, 2, 3, 2\}, \{0, 2, 3, 3\}, \{0, 3, 0, 4\}, \{0, 3, 0, 5\}, \{0, 3, 0, 6\}, \\ \{0, 3, 1, 0\}, \{0, 3, 1, 1\}, \{0, 3, 1, 2\}, \{0, 3, 1, 3\}, \{0, 3, 1, 4\}, \{0, 3, 1, 5\}, \{0, 3, 2, 0\}, \\ \{0, 3, 2, 1\}, \{0, 3, 2, 2\}, \{0, 3, 2, 3\}, \{0, 3, 2, 4\}, \{0, 3, 3, 0\}, \{0, 3, 3, 1\}, \{0, 3, 3, 2\}, \\ \{0, 3, 3, 3\}, \{0, 4, 0, 5\}, \{0, 4, 0, 6\}, \{0, 4, 1, 0\}, \{0, 4, 1, 1\}, \{0, 4, 1, 2\}, \{0, 4, 1, 3\}, \\ \{0, 4, 1, 4\}, \{0, 4, 1, 5\}, \{0, 4, 2, 0\}, \{0, 4, 2, 1\}, \{0, 4, 2, 2\}, \{0, 4, 2, 3\}, \{0, 4, 2, 4\}, \\ \{0, 4, 3, 0\}, \{0, 4, 3, 1\}, \{0, 4, 3, 2\}, \{0, 4, 3, 3\}, \{0, 5, 0, 6\}, \{0, 5, 1, 0\}, \{0, 5, 1, 1\}, \\ \{0, 5, 1, 2\}, \{0, 5, 1, 3\}, \{0, 5, 1, 4\}, \{0, 5, 1, 5\}, \{0, 5, 2, 0\}, \{0, 5, 2, 1\}, \{0, 5, 2, 2\}, \\ \{0, 5, 2, 3\}, \{0, 5, 2, 4\}, \{0, 5, 3, 0\}, \{0, 5, 3, 1\}, \{0, 5, 3, 2\}, \{0, 5, 3, 3\}, \{0, 6, 1, 0\}, \\ \{0, 6, 1, 1\}, \{0, 6, 1, 2\}, \{0, 6, 1, 3\}, \{0, 6, 1, 4\}, \{0, 6, 1, 5\}, \{0, 6, 2, 0\}, \{0, 6, 2, 1\},\\ \{0, 6, 2, 2\}, \{0, 6, 2, 3\}, \{0, 6, 2, 4\}, \{0, 6, 3, 0\}, \{0, 6, 3, 1\}, \{0, 6, 3, 2\}, \{0, 6, 3, 3\}, \\ \{1, 0, 1, 1\}, \{1, 0, 1, 2\}, \{1, 0, 1, 3\}, \{1, 0, 1, 4\}, \{1, 0, 1, 5\}, \{1, 0, 2, 0\}, \{1, 0, 2, 1\}, \\ \{1, 0, 2, 2\}, \{1, 0, 2, 3\}, \{1, 0, 2, 4\}, \{1, 1, 1, 2\}, \{1, 1, 1, 3\}, \{1, 1, 1, 4\}, \{1, 1, 1, 5\}, \\ \{1, 1, 2, 0\}, \{1, 1, 2, 1\}, \{1, 1, 2, 2\}, \{1, 1, 2, 3\}, \{1, 1, 2, 4\}, \{1, 2, 1, 3\}, \{1, 2, 1, 4\}, \\ \{1, 2, 1, 5\}, \{1, 2, 2, 0\}, \{1, 2, 2, 1\}, \{1, 2, 2, 2\}, \{1, 2, 2, 3\}, \{1, 2, 2, 4\}, \{1, 3, 1, 4\}, \\ \{1, 3, 1, 5\}, \{1, 3, 2, 0\}, \{1, 3, 2, 1\}, \{1, 3, 2, 2\}, \{1, 3, 2, 3\}, \{1, 3, 2, 4\}, \{1, 4, 1, 5\}, \\ \{1, 4, 2, 0\}, \{1, 4, 2, 1\}, \{1, 4, 2, 2\}, \{1, 4, 2, 3\}, \{1, 4, 2, 4\}, \{1, 5, 2, 0\}, \{1, 5, 2, 1\}, \\ \{1, 5, 2, 2\}, \{1, 5, 2, 3\}, \{1, 5, 2, 4\}\,\,\, \end{aligned}$$

The question then is how to determine which coefficients in the defining polynomials of the generators need to vanish.

Note that we have introduced an ordering on the Plücker coordinates coming from the restrictions on i, j, k and l. So, the first step is to look at the equation $m_{ijkl}=0$ for the first term $\{i,j,k,l\}$ in the list above, namely we look at the equation $m_{0001}=0$. It follows that either

• (1) $f_{00}=g_{00}=0$ or

• (2) $g_{00}\ne 0$ or

• (3) $f_{00}\ne 0$

Moreover, if (2) (or (3) by symmetry) holds, then taking $f'=f-\frac{f_{00}}{g_{00}}g$ we can assume $f_{00}=0$ and we must have $f_{01}=0$.

The next step then is, at each of the cases above, to look at the next vanishing condition $m_{0002}=0$ coming from the second term $\{i,j,k,l\}$ in the list. Again there are three possibilities: Either $f_{00}=g_{00}=0$ or $g_{02}\ne 0$ or $f_{02}\ne 0$.

We proceed in this manner until there are no more equations $m_{ijkl}=0$ to solve.

In fact our list tells us that $m_{00kl}$ vanish for all (appropriate) $0\le k \le 3$ and $0 \le l \le 6$. Thus, our algorithm tells us that if we are in the situation of case (2), then one of the generators belongs to $\rangle x^kj^lz^{6-k-l} \langle$ for all kl such that $m_{00kl}=0$. And, by symmetry, we reach the same conclusion if (3) holds. A similar reasoning applies to the next set of vanishing conditions $m_{01kl}=0$ and so on.

It is important to note, however, that at each step, when solving the equations $m_{ijkl}=0$ we have to take into account whether there are or there are not previous conditions on the coefficients $f_{ij},g_{ij},f_{kl}$ and $g_{kl}$.

By following the sketched algorithm we obtain the desired description for the pencil ${\mathcal {P}}$. $\square$

In particular,

Corollary 3.1.1

If ${\mathcal {P}}\in {\mathscr {P}}_6$ contains a curve of the form $4L+Q$, where L is a line and Q is a conic, then ${\mathcal {P}}$ is non-stable.

Now, the same algorithm as in the proof of Proposition 3.1 can be applied more generally whenever ${\mathcal {P}}$ is unstable (resp. non-stable) and satisfies one of the vanishing conditions in one of the cases in Proposition 2.2 (resp. 2.3). However, the computations involved are very lengthy, and a complete description can be found in [15]. We present here only the results which will be essential to our study of Halphen pencils of index two in Sect. 4. And we focus on pencils that contain a curve which has a multiple line as a component, and which are proper.

Definition 3.2

A pencil ${\mathcal {P}} \in {\mathscr {P}}_6$ is called proper if any two curves on it intersect properly, meaning its base locus is zero dimensional.

The first result we prove is the following:

Proposition 3.3

If we can find coordinates in ${\mathbb {P}}^2$ and generators $C_f$ and $C_g$ of ${\mathcal {P}}$ such that $f \in \langle x^5z,x^5y,x^6 \rangle$ and g is arbitrary, then the pencil ${\mathcal {P}}\in {\mathscr {P}}_6$ will satisfy the vanishing conditions in Case U(1) of Proposition 2.2. In particular, if ${\mathcal {P}}$ contains a curve of the form $5L+L'$, where L and $L'$ are lines, then ${\mathcal {P}}$ is unstable.

Proof

In fact, all the Plücker coordinates $m_{ijkl}$ vanish, except for (possibly): $m_{50kl},m_{51kl}$ and $m_{60kl}$. Note that $m_{ijkl}=-m_{klij}$ and $m_{ijij}=0$. $\square$

We also prove:

Proposition 3.4

Let ${\mathcal {P}}\in {\mathscr {P}}_6$ be a proper pencil which contains a curve $C_f$ of the form $4L+Q$, where L is a line and Q is a conic (possibly reducible). If ${\mathcal {P}}$ is unstable, then there exist coordinates in ${\mathbb {P}}^2$ and another generator $C_g$ of ${\mathcal {P}}$ such that $f\in \langle x^4z^2,x^4yz,x^4y^2,x^5z,x^5y,x^6 \rangle$ and either

• (i) L is tangent to $C_g$ at [0, 0, 1] with multiplicity $\ge 5$; or

• (ii) L is tangent to $C_g$ at [0, 0, 1] with multiplicity 4 and [0, 0, 1] has multiplicity $\ge 3$ in $C_g$; or

• (iii) L is tangent to $C_g$ at [0, 0, 1] with multiplicity $\ge 3$ and $[0,0,1]\in Q$.

Proof

We first note that by Corollary 3.1.1, ${\mathcal {P}}$ is always non-stable. In fact ${\mathcal {P}}$ satisfies the vanishing conditions in Case NS(1) of Proposition 2.3 (or, equivalently, Case 1 of Proposition 3.1). Now, using the algorithm described in the proof of Proposition 3.1, one can show that if ${\mathcal {P}}$ is unstable, then there exist coordinates in ${\mathbb {P}}^2$ and another generator $C_g$ of ${\mathcal {P}}$ such that either:

• (i) $f\in \langle x^4z^2,x^4yz,x^4y^2,x^5z,x^5y,x^6 \rangle$ and $g \in \rangle z^6,yz^5,y^2z^4,y^3z^3,y^4z^2 \langle$

• (ii) or

• (iii) $f \in \langle x^4yz,x^4y^2,x^5z,x^5y,x^6 \rangle$ and $g \in \rangle z^6,yz^5,y^2z^4,y^3z^3\langle$

• (iv) or

• (v) $f\in \langle x^4y^2,x^5z,x^5y,x^6 \rangle$ and $g \in \rangle z^6,yz^5,y^2z^4 \langle$

$\square$

Moreover, the same kind of reasoning as in the proof of Proposition 3.4 also shows:

Proposition 3.5

Let ${\mathcal {P}}\in {\mathscr {P}}_6$ be a proper pencil which contains a curve $C_f$ of the form $3L+C$, where L is a line and C is a cubic (possibly reducible). If ${\mathcal {P}}$ is unstable, then there exist coordinates in ${\mathbb {P}}^2$ and another generator $C_g$ of ${\mathcal {P}}$ such that

$$\begin{aligned} f\in \langle x^3z^3,x^3yz^2,x^3y^2z,x^3y^3,x^4z^2,x^4yz,x^4y^2,x^5z,x^5y,x^6 \rangle \end{aligned}$$

and either:

• (i) L is tangent to $C_g$ at [0, 0, 1] with multiplicity 6 and [0, 0, 1] has multiplicity $\ge 3$ in $C_g$; or

• (ii) L is tangent to $C_g$ at [0, 0, 1] with multiplicity 5, [0, 0, 1] has multiplicity $\ge 3$ in $C_g$ and and the intersection multiplicity of L and C at [0, 0, 1] is 1; or

• (iii) L is tangent to $C_g$ at [0, 0, 1] with multiplicity 5, [0, 0, 1] has multiplicity $\ge 2$ in $C_g$ and the intersection multiplicity of L and C at [0, 0, 1] is $\ge 2$; or

• (iv) L is tangent to $C_g$ at [0, 0, 1] with multiplicity 4, [0, 0, 1] has multiplicity $\ge 3$ in $C_g$ and the intersection multiplicity of L and C at [0, 0, 1] is 2; or

• (v) L is tangent to $C_g$ at [0, 0, 1] with multiplicity $\ge 3$, and the intersection multiplicity of L and C at [0, 0, 1] is 3.

Proposition 3.6

Let ${\mathcal {P}}\in {\mathscr {P}}_6$ be a proper pencil which contains a curve of the form $2L+Q$, where L is a line and Q is a quartic (possibly reducible). If ${\mathcal {P}}$ is unstable then there exist coordinates in ${\mathbb {P}}^2$ and generators $C_f$ and $C_g$ of ${\mathcal {P}}$ such that:

$$\begin{aligned} f\in \langle x^2yz^3,x^2y^2z^2,x^2y^3z,x^2y^4, x^iy^jz^{6-i-j} \rangle \end{aligned}$$

with $3\le i \le 6,0\le j \le 6, i+j \le 6$ plus $f_{2j}\ne 0$ for some $j=0,\ldots ,4$, L is tangent to $C_g$ with multiplicity 6 and [0, 0, 1] has multiplicity $\ge 4$ in $C_g$.

Proposition 3.7

Let ${\mathcal {P}}\in {\mathscr {P}}_6$ be a proper pencil which contains a curve $C_f$ of the form $3L+C$, where L is a line and C is a cubic (possibly reducible). If ${\mathcal {P}}$ is non-stable then there exist coordinates in ${\mathbb {P}}^2$ and another generator $C_g$ such that $f\in \langle x^3z^3,x^3yz^2,x^3y^2z,x^3y^3,x^4z^2,x^4yz,x^4y^2,x^5z,x^5y,x^6 \rangle$ and either:

• (i) L is tangent to $C_g$ at [0, 0, 1] with multiplicity 6

• (ii) L is tangent to $C_g$ at [0, 0, 1] with multiplicity 5 and [0, 0, 1] has multiplicity $\ge 3$ in $C_g$

• (iii) L is tangent to $C_g$ at [0, 0, 1] with multiplicity 4 and [0, 0, 1] has multiplicity $\ge 4$ in $C_g$

• (iv) L is tangent to $C_g$ at [0, 0, 1] with multiplicity 4 and the intersection multiplicity of L and C at [0, 0, 1] is $\ge 2$

• (v) L is tangent to $C_g$ at [0, 0, 1] with multiplicity $\ge 3$, [0, 0, 1] has multiplicity $\ge 3$ in $C_g$ and the intersection multiplicity of L and C at [0, 0, 1] is 2

• (vi) the intersection multiplicity of L and $C_g$ (resp. C) at [0, 0, 1] is $\ge 2$ (resp. 3).

4 Stability of Halphen pencils of index two

At last, we are in position of proving Theorems 1.4, 1.5 and 1.6. This is the goal of this section. Inspired by [4], we will provide a complete and geometric description of the stability of a Halphen pencil of index two ${\mathcal {P}}$ (Definition 1.1), in terms of the types of singular fibers appearing in the corresponding rational elliptic surface $Y \rightarrow {\mathbb {P}}^1$ (see Definition 1.2 and Proposition 1.3).

Our strategy can be summarized as follows: Combining the stability criteria we obtained in [1] with results from [13, 16, 17] (Lemmas 4.1, 4.3 and 4.4 below), we can first give some sufficient conditions for the (semi)stability of ${\mathcal {P}}$. This is achieved in Sect. 4.1. A complete characterization of the stability of ${\mathcal {P}}$ is then obtained by further studying the cases where Y contains a fiber F of type $II^*,III^*$ or $IV^*$ (Sects. 4.2, 4.3 and 4.4). And for these last steps we make use of the results from Sect. 3 and the explicit constructions from [13, Sect. 7].

Note that ${\mathcal {P}}$ contains exactly one multiple cubic 2C, which corresponds to a unique multiple fiber in Y [5, Proposition 5.61,(iii)]. Thus, ${\mathcal {P}}$ can be written in the following form $\lambda (B)+\mu (2C)=0$, where the curve B corresponds to some (non-multiple) fiber of Y that we denote by F. We will use these notations throughout.

4.1 Sufficient conditions for (semi)stability

In [13], we have studied the singularities of the curves B and C in terms of their log canonical threshold (lct) (see e.g. [2, Sect. 8]), and we have established some precise inequalities between the lct of the pair (Y, F) and the lct of the pair $({\mathbb {P}}^2,B)$. More precisely, denoting by $M_B$ (resp. $M_F$) the largest multiplicity of a component of B (resp. F), we have proved the following:

Lemma 4.1

([13, Theorems 1.1 and 1.2]) If F is any (non-multiple) fiber of Y, then the corresponding plane curve B is such that

$$\begin{aligned} lct({\mathbb {P}}^2,B)\le \frac{1}{M_B}\le 2lct(Y,F) \end{aligned}$$

Further,

• (i) if F is reduced, then B is reduced and we have that

  $$\begin{aligned} 1/2<lct({\mathbb {P}}^2,B)\le lct(Y,F) \end{aligned}$$

• (ii) if $M_F\ge 2$ (or, equivaletly, F is non-reduced), then $lct(Y,F)\le lct({\mathbb {P}}^2,B)$

• (iii) if $M_F\ge 3$, then B is non-reduced.

Remark 4.2

Note that the number lct(Y, F) is given by the table below, depending on the type of F:

$\varvec{lct(Y,F)}$	Type of $\varvec{F}$	$\varvec{lct(Y,F)}$	Type of $\varvec{F}$
1	$I_n$	1/2	$I_n^*$
5/6	II	1/6	$II^*$
3/4	III	1/4	$III^*$
2/3	IV	1/3	$IV^*$

And we have also proved:

Lemma 4.3

[[13, Proposition 4.9]] The curve C has at worst nodes as singularities. In particular, $lct({\mathbb {P}}^2,C)=1$.

In contrast, in [1] we have related the stability of any pencil ${\mathcal {P}} \in {\mathscr {P}}_6$ to: (i) the stability of the curves lying on it; (ii) the log canonical threshold of the pair $({\mathbb {P}}^2,{\mathcal {C}})$, where ${\mathcal {C}}$ is a curve in ${\mathcal {P}}$; and (iii) to the multiplicities of its generators at a base point.

Additionally, Hacking [16] and Kim-Lee [17] have observed the following:

Lemma 4.4

If ${\mathcal {C}}\subset {\mathbb {P}}^2$ is any plane curve of degree six and $lct({\mathbb {P}}^2, {\mathcal {C}})\ge 1/2$ (resp. $>1/2$), then ${\mathcal {C}}$ is semi-stable (resp. stable) for the natural action of SL(3).

In particular, we see that one can try to combine Lemmas 4.1, 4.3 and 4.4 above with some of the aforementioned results from [1] in order to obtain explicit stability criteria for Halphen pencils of index two. This is precisely what we pursue in this Section.

Concretely, the results we need from [1] are the following:

Lemma 4.5

([1, Theorem 1.1]) Let ${\mathcal {P}}$ be a pencil in ${\mathscr {P}}_6$ containing a curve $C_f$ such that $lct({\mathbb {P}}^2,C_f)=\alpha$. If ${\mathcal {P}}$ is unstable (resp. not stable), then ${\mathcal {P}}$ contains a curve $C_g$ such that $lct({\mathbb {P}}^2,C_g)< \frac{\alpha }{4\alpha -1}$ (resp. $\le$).

Lemma 4.6

([1, Theorem 1.3]) Let ${\mathcal {P}}$ be a pencil in ${\mathscr {P}}_6$. If we can find two curves $C_f$ and $C_g$ in ${\mathcal {P}}$ such that $mult_p(C_f) + mult_p(C_g)>8$ (resp. $\ge$) for some base point p, then ${\mathcal {P}}$ is unstable (resp. not stable).

Lemma 4.7

([1, Theorems 1.4 and 1.5]) Let ${\mathcal {P}}$ be a pencil in ${\mathscr {P}}_6$.

• (i) If ${\mathcal {P}}$ has only semi-stable (resp. stable) members, then ${\mathcal {P}}$ is semi-stable (resp. stable).

• (ii) If ${\mathcal {P}}$ contains at most one strictly semi-stable curve (and all other curves in ${\mathcal {P}}$ are stable), then ${\mathcal {P}}$ is stable.

Lemma 4.8

[[1, Theorem 1.6]] If ${\mathcal {P}}\in {\mathscr {P}}_6$ contains at most two semi-stable curves $C_f$ and $C_g$ (and all other curves in ${\mathcal {P}}$ are stable), then ${\mathcal {P}}$ is strictly semi-stable if and only if there exists a one-parameter subgroup $\lambda$ such that $C_f$ and $C_g$ are both non-stable with respect to this $\lambda$.

4.1.1 The criteria

With the above results in mind, let ${\mathcal {P}}$ be a Halphen pencil of index two, written in the form $\lambda (B)+\mu (2C)=0$. The first stability criterion we prove is the following:

Proposition 4.9

If ${\mathcal {P}}$ is non-stable, then Y contains a non-reduced fiber.

Proof

Since $lct({\mathbb {P}}^2,2C)=1/2$ (Lemma 4.3), we conclude from Lemma 4.5, with $\alpha =1/2$, that if the pencil ${\mathcal {P}}$ is non-stable, then ${\mathcal {P}}$ contains a curve B such that $lct({\mathbb {P}}^2,B)\le 1/2$. By Lemma 4.1 (i), this implies the corresponding rational elliptic surface $Y \rightarrow {\mathbb {P}}^1$ contains a non-reduced fiber F. $\square$

When C is smooth and B is semi-stable we also prove:

Proposition 4.10

If C is smooth and all curves in ${\mathcal {P}}$ are stable except (possibly) for one curve that is semi-stable, then ${\mathcal {P}}$ is stable.

Proof

It follows directly from Lemma 4.7 and the fact that 2C is stable [12]. $\square$

Corollary 4.10.1

If C is smooth, F is of type $II^*,III^*$ or $IV^*$ and the corresponding curve $B\doteq \pi (F)$ is semi-stable, then ${\mathcal {P}}$ is stable.

Proof

From the classification in [11] we know that any other fiber of Y is reduced. By Lemma 4.1 we also know that all other curves in ${\mathcal {P}}$ are reduced and have log canonical threshold greater than 1/2. As observed in Lemma 4.4, this implies all the curves in ${\mathcal {P}}$ are stable except for one curve that is semi-stable. The statement then follows from Proposition 4.10. $\square$

Corollary 4.10.2

If C is smooth and Y contains exactly one fiber F of type $I_n^*$, then ${\mathcal {P}}$ is stable.

Proof

Again, from the classification in [11] we know that any other fiber of Y is reduced. Since the curve B is such that $lct({\mathbb {P}}^2,B)\ge 1/2$ (Lemma 4.1), it is semi-stable by Lemma 4.4, and we can argue as in the proof of Corollary 4.10.1 to conclude all the curves in ${\mathcal {P}}$ are stable except (possibly) for one curve that is semi-stable. The result then follows from Proposition 4.10. $\square$

Proposition 4.11

If Y contains two fibers of type $I_0^*$, then ${\mathcal {P}}$ is strictly semi-stable if and only if there exists a one-parameter subgroup $\lambda$ (and coordinates in ${\mathbb {P}}^2$) such that the two curves corresponding to the fibers of type $I_0^*$ are both non-stable with respect to this $\lambda$.

Proof

By Lemma 4.1, if F is a fiber of type $I_0^*$, then the corresponding plane curve B is such that $lct({\mathbb {P}}^2,B)\ge 1/2$, hence it is semi-stable by Lemma 4.4. Moreover, by the classification in [11] we know that C has to be smooth, hence stable [12]; and all other fibers of Y must be reduced. In particular, ${\mathscr {P}}$ contains at most two semi-stable curves (and all other curves are stable), hence ${\mathcal {P}}$ is always semi-stable by Lemma 4.7 and the result follows from Lemma 4.8. $\square$

Corollary 4.11.1

If Y contains two fibers of type $I_0^*$ and ${\mathcal {P}}$ is strictly semi-stable, then ${\mathcal {P}}$ contains two curves $B_1$ and $B_2$ (different than 2C) such that $lct({\mathbb {P}}^2,B_i)= 1/2$. Moreover, each of these curves satisfies one of the following conditions:

• (i) it consists of a double line and a reduced quartic

• (ii) it is reduced and it has a (unique) point of multiplicity 4, which is (necessarily) a base point of ${\mathcal {P}}$

• (iii) it is reduced and it has a consecutive triple point, which is (necessarily) a base point of ${\mathcal {P}}$.

Proof

The curves $B_i$ are the two curves which correspond to the two fibers of type $I_0^*$. By Lemma 4.1, we have $lct({\mathbb {P}}^2,B_i)\ge 1/2$. On the other hand, if ${\mathcal {P}}$ is strictly semi-stable, then Proposition 4.11 implies both curves are non-stable, hence $lct({\mathbb {P}}^2,B_i)\le 1/2$, by Lemma 4.4. The description of the $B_i$ then follows from [12, Theorem 2.3]. These are the only non-stable sextics that could possibly yield a fiber of type $I_0^*$. $\square$

Combining Propositions 4.9, Corollaries 4.10.2 and 4.10.1 and Proposition 4.11 we have thus proved:

Proposition 4.12

Assume C is smooth and one of the following statements holds

• (i) all fibers of Y are reduced; or

• (ii) Y contains exactly one (non-multiple) fiber F of type $I_n^*$; or

• (iii) Y contains a (non-multiple) fiber F of type $II^*,III^*$ or $IV^*$ and the corresponding plane curve B is semi-stable; or

• (iv) Y contains two fibers of type $I_0^*$ and there is no one-parameter subgroup $\lambda$ that destabilizes the two corresponding curves simultaneously.

Then the pencil ${\mathcal {P}}$ is stable.

In Sect. 4.4 we will further show (Proposition 4.28) that when C is smooth, Y contains a (non-multiple) fiber F of type $IV^*$ and the corresponding plane curve B is unstable, then ${\mathcal {P}}$ is also stable. This will then complete the proof of the reverse implication in Theorem 1.4.

We now analyse the stability of ${\mathcal {P}}$ when C is singular. By the classification in [11], either all fibers of Y are reduced, or Y contains exactly one fiber of type $I_n^*,II^*,III^*$ or $IV^*$. It cannot contain two fibers of type $I_0^*$ (see e.g. [11]).

In view of Proposition 4.9, we will consider the case when ${\mathcal {P}}$ contains a non-reduced fiber F such that the corresponding curve B is semi-stable. In this case the pencil ${\mathcal {P}}$ will always be semi-stable (Lemma 4.7) since 2C is semi-stable by [12], and all other fibers must be reduced – hence the corresponding curves must be stable by Lemmas 4.5 and 4.4.

Applying Lemma 4.8 we can prove:

Proposition 4.13

If C is singular and Y contains exactly one fiber F of type $I_n^*$, then ${\mathcal {P}}$ is strictly semi-stable if and only if there exists a one-parameter subgroup $\lambda$ (and coordinates in ${\mathbb {P}}^2$) such that 2C and $B=\pi (F)$ are both non-stable with respect to this $\lambda$.

Proposition 4.14

If C is singular, Y contains a fiber F of type $II^*,III^*$ or $IV^*$ and the curve $B=\pi (F)$ is semi-stable, then ${\mathcal {P}}$ is strictly semi-stable if and only if there exists a one-parameter subgroup $\lambda$ (and coordinates in ${\mathbb {P}}^2$) such that 2C and B are both non-stable with respect to this $\lambda$.

In particular, combining Propositions 4.9, 4.13 and 4.14, we obtain the following, which is part of the statement of Theorem 1.5:

Proposition 4.15

Assume C is singular and one of the following statements holds

• (i) all fibers of Y are reduced; or

• (i) Y contains a (non-multiple) non-reduced fiber F such that the curve $B=\pi (F)$ is semi-stable and there is no one-parameter subgroup $\lambda$ that destabilizes 2C and B simultaneously.

Then the pencil ${\mathcal {P}}$ is stable.

Now, in order to complete the proofs of Theorems 1.4 and 1.5 we need to obtain necessary conditions for the estability of ${\mathcal {P}}$. In particular, we need to prove that whenever Y contains a (non-multiple) fiber F of type $II^*$ or $III^*$ and the corresponding curve B is unstable, then ${\mathcal {P}}$ is non-stable (Proposition 4.24). And we also need to better understand the stability of ${\mathcal {P}}$ when F is a fiber of type $IV^*$ (Sect. 4.4).

As already mentioned, for these last steps we will make use of the results from Sect. 3 and the constructions in [13, Sect. 7].

4.2 The stability of ${\mathcal {P}}$ when F is of type $II^*$

When F is of type $II^*$, then by [13, Theorem 5.15] the curve B can only be realized by one of the following plane curves:

• (i) a triple conic

• (ii) a nodal cubic and an inflection line, with the line taken with multiplicity three

• (iii) two triple lines

• (iv) a conic and a tangent line, with the line taken with multiplicity four

• (v) a line with multiplicity five and another line

By [12], if B is a triple conic, then B is strictly semi-stable and ${\mathcal {P}}$ will always be semi-stable (Lemma 4.7): The curve 2C is semi-stable by [12], and all other fibers must be reduced—hence the corresponding curves must be stable by Lemmas 4.5 and 4.4.

But there are two possibilities: either C is smooth, in which case ${\mathcal {P}}$ is stable (Corollary 4.10.1); or C is singular and then ${\mathcal {P}}$ is strictly semi-stable if and only if there exists a one-parameter subgroup $\lambda$ (and coordinates in ${\mathbb {P}}^2$) such that 2C and B are both non-stable with respect to this $\lambda$ (Proposition 4.14).

When B is one of the curves in (ii), (iii), (iv) or (v) then we can use the explicit constructions obtained in [13] to conclude ${\mathcal {P}}$ is unstable. In fact, we can find coordinates in ${\mathbb {P}}^2$ so that the Plücker coordinates of ${\mathcal {P}}$ with respect to these coordinates satisfy the conditions in Case U(1) of Proposition 2.2.

Therefore, we obtain the following characterization when F is of type $II^*$:

Proposition 4.16

If Y contains a fiber F of type $II^*$ and $B\doteq \pi (F)$ is not a triple conic, then ${\mathcal {P}}$ is unstable.

Proof

Since B is not a triple conic, there are four cases to consider:

• (ii) First, assume B consists of a nodal cubic and an inflection line, with the line taken with multiplicity three. Then [13, Example 7.58] we can find coordinates in ${\mathbb {P}}^2$ so that the curve B has equation $x^3(xz^2-y^2(y+x))=0$ and C is given by $x^2y+xz^2-y^3-xy^2=0$. In particular, the Plücker coordinates of ${\mathcal {P}}$ with respect to these coordinates satisfy the conditions in Case U(1) of Proposition 2.2 and we conclude ${\mathcal {P}}$ is unstable. Note that one can also easily check ${\mathcal {P}}$ is as in (v) in Proposition 3.5.

• (iii) Next, assume B consists of two triple lines. Then, one can show that one of the lines is an inflection line of C and the other line must be tangent to the cubic with multiplicity two [13, Example 7.57]. In particular, we can find coordinates in ${\mathbb {P}}^2$ so that B is given by $x^3y^3=0$ and C is given by $z^2x-y(y-x)(y-\alpha \cdot x)=0$, where $\alpha \in {\mathbb {C}}\backslash \{0,1\}$. In particular, the Plücker coordinates of ${\mathcal {P}}$ with respect to these coordinates satisfy the conditions in Case U(1) of Proposition 2.2. Moreover, again in this case, we can check ${\mathcal {P}}$ is as in (v) in Proposition 3.5.

• (iv) Assume now B consists of a conic and a tangent line, with the line taken with multiplicity four. Then [13, Example 7.59] ${\mathcal {P}}$ is as in (ii) in Proposition 3.4. In fact, one can show that C must be tangent to the conic (resp. the line) at the point $Q\cap L$ with multiplicity six (resp. two). In particular, we can find coordinates in ${\mathbb {P}}^2$ so that B is given by the zeros of the polynomial $x^4(y^2+xz)$ and C is given by $f=\sum f_{ij}x^iy^jz^{6-i-j}=0$, with $f_{00}=f_{01}=f_{02}=0$. Thus, the Plücker coordinates of ${\mathcal {P}}$ with respect to these coordinates satisfy the conditions in Case U(1) of Proposition 2.2 and we conclude ${\mathcal {P}}$ is unstable.

• (v) Lastly, assume B consists of a line with multiplicity five and another line. Then ${\mathcal {P}}$ is unstable by Proposition 3.3. In fact, we can choose coordinates so that B is the curve $x^5(x-z)=0$ and C is the cubic $y^2z=x(x-z)(x-\alpha \cdot z)$ for some $\alpha \in {\mathbb {C}}\backslash \{0,1\}$ [13, Example 7.59]. Note that, equivalently, the Plücker coordinates of ${\mathcal {P}}$ satisfy the vanishing conditions of Case U(1) in Proposition 2.2. $\square$

This proves the foward implication in Theorem 1.6. The other implication will then follow from Proposition 4.17 below, provided we can show whenever Y contains a fiber F of type $III^*$ or $IV^*$, then ${\mathcal {P}}$ cannot be unstable – this is achieved in Sects. 4.3 an 4.4 (Propositions 4.23 and 4.27).

Proposition 4.17

If ${\mathcal {P}}$ is unstable, then Y contains a fiber of type $II^*,III^*$ or $IV^*$.

Proof

The proof is very similar to the proof of Theorem 4.9. Since we know $lct({\mathbb {P}}^2,2C)=1/2$ by Lemma 4.3, we conclude from Lemma 4.5 (by taking $\alpha =1/2$) that if the pencil ${\mathcal {P}}$ is unstable, then ${\mathcal {P}}$ contains a curve B such that $lct({\mathbb {P}}^2,B)< 1/2$. Thus, Lemma 4.1 implies Y contains a fiber of type $II^*,III^*$ or $IV^*$. $\square$

4.3 The stability of ${\mathcal {P}}$ when F is of type $III^*$

We now consider the case when F is of type $III^*$.

By [13, Theorem 5.16] the curve B can only be realized by one of the following plane curves:

• (i) a double line, a cubic and another line

• (ii) a double conic and another conic (semi-stable)

• (iii) a triple conic (semi-stable)

• (iv) two triple lines

• (v) a triple line, a conic and a line

• (vi) a triple line, a double line and another line

• (vii) a triple line and a cubic

• (viii) a conic and a line, with the line taken with multiplicity four

• (ix) a line with multiplicity four and two other lines

If B is semi-stable, then arguing as in the case of a fiber of type $II^*$ (triple conic), we conclude ${\mathcal {P}}$ will always be semi-stable by Lemma 4.7. Again, there are two possibilities to consider: either C is smooth, in which case ${\mathcal {P}}$ is stable (Corollary 4.10.1); or C is singular and we can refer to Proposition 4.14.

When B is unstable we can once more use the explicit constructions obtained in [13, Sect. 7] to conclude ${\mathcal {P}}$ is strictly semi-stable. More precisely, arguing as in the case of a fiber of type $II^*$, we can first show:

Lemma 4.18

(i):

When the curve B is as in (i), (v) or (vi) (with the lines in general position), then we can find coordinates in ${\mathbb {P}}^2$ so that the Plücker coordinates of ${\mathcal {P}}$ with respect to these coordinates satisfy the conditions in Case NS(3) of Proposition 2.3.

(ii):

When B is one of the curves in (viii) or (ix) (resp. (vii)) we can find coordinates in ${\mathbb {P}}^2$ so that the corresponding Plücker coordinates satisfy the conditions in Case NS(1) of Proposition 2.3 (resp. Case NS(4) of Proposition 2.3).

Proof

If B is as in (i), (v) or (vi) (with the lines in general position), then ${\mathcal {P}}$ must be as in Example 7.45, Example 7.51 or Example 7.49 in [13], respectively. Similarly, if the curve B is as in (viii) or (ix) (resp. (vii)), then ${\mathcal {P}}$ must be as in Example 7.53 or Example 7.54 (resp. Example 7.52) in [13]. $\square$

Then, when B is one of the curves in (iv) or (vi) (with the lines concurrent at a point), we can apply the following Lemma to conclude ${\mathcal {P}}$ is also non-stable in these cases:

Lemma 4.19

If ${\mathcal {P}}$ contains a curve B and a base point p such that $\text {mult}_p(B)=6$, then ${\mathcal {P}}$ is non-stable.

Proof

Since $\text {mult}_P(C)\ge 1$, the result follows from Lemma 4.6 applied to the curves $C_f=B$ and $C_g=2C$ (and the base point p). $\square$

In particular, combining Lemmas 4.18 and 4.19 we obtain the following characterization when F is of type $III^*$:

Proposition 4.20

If Y contains a fiber F of type $III^*$ and $B\doteq \pi (F)$ is unstable, then ${\mathcal {P}}$ is non-stable.

Moreover, we can prove Propositions 4.21 and 4.22 below, which then further imply ${\mathcal {P}}$ can never be unstable.

Proposition 4.21

If Y contains a fiber F of type $III^*$ and $B\doteq \pi (F)$ contains either a line with multiplicity four or a triple line, then ${\mathcal {P}}$ is semi-stable.

Proof

If B contains a line with multiplicity four and ${\mathcal {P}}$ is unstable, then ${\mathcal {P}}$ (and B) must be as in one of the cases of Proposition 3.4. Similarly, if B contains a triple line and ${\mathcal {P}}$ is unstable, then ${\mathcal {P}}$ (and B) must be as in one of the cases of Proposition 3.5. Arguing as in [13, Sect. 5], it is routine to check none of these cases can yield a rational elliptic surface Y with a fiber of type $III^*$. $\square$

Proposition 4.22

If Y contains a fiber F of type $III^*$ and $B\doteq \pi (F)$ consists of a double line, a cubic and another line, then ${\mathcal {P}}$ is semi-stable.

Proof

If B consists of a double line, a cubic and another line, then ${\mathcal {P}}$ must be a pencil as in [13, Example 7.45]. More precisely, B must be of the form $2L_1+L_2+D$, where:

• (i) D is a nodal cubic, with node $P_1$;

• (ii) the line $L_1$ is a flex line of D, with flex point $P_2$; and

• (iii) the line $L_2$ is a line through $P_2$ that intersects D at two other points, say $P_3$ and $P_4$.

And, moreover, the cubic C is such that it passes through $P_1,\ldots ,P_4$; and it is tangent to D (resp. $L_1$) at $P_1$ with multiplicity 5 (resp. 3). Therefore, applying Proposition 3.6 we conclude ${\mathcal {P}}$ must be semi-stable.

Now, to see why the curves B and C must be as described above, note that if B consists of a double line, a cubic and another line, then the dual graph of F must be the following one:

Fig. 3

The dual graph of F

where we have labeled the components coming from B and the unlabeled black nodes indicate the missing components. See also [13, Lemma 4.1].

In particular, $\pi :Y\rightarrow {\mathbb {P}}^2$ is the blow-up of ${\mathbb {P}}^2$ at the points $P_1^{(1)},P_2^{(1)},\ldots ,P_2^{(6)},P_3^{(1)},P_4^{(1)}$, where $P_j=P_j^{(1)}$ is a point in ${\mathbb {P}}^2$ and $P_j^{(i+1)}$ is infinitely near to the previous point $P_j^{(i)}$ (of order 1). This tells us C must be tangent to D (resp. $L_1$) at $P_1$ with multiplicity 5 (resp. 3). $\square$

Concisely, we have thus proved:

Proposition 4.23

If Y contains a fiber F of type $III^*$, then ${\mathcal {P}}$ is semi-stable.

And, combining Propositions 4.16 and 4.20, we have also proved:

Proposition 4.24

If Y contains a (non-multiple) fiber F of type $II^*$ or $III^*$ and the corresponding curve B is unstable, then ${\mathcal {P}}$ is non-stable.

4.4 The stability of ${\mathcal {P}}$ when F is of type $IV^*$

Finally, we describe the stability of ${\mathcal {P}}$ when F is of type $IV^*$. We prove that either ${\mathcal {P}}$ is stable or C is singular and B is semi-stable, in which case we can refer to Proposition 4.14.

First, we observe that [13, Theorem 5.17] when F is of type $IV^*$, then B must be one of the following curves:

• (i) a double conic and a conic (semi-stable)

• (ii) a double line, a conic and two lines

• (iii) a double line, a cubic and a line

• (iv) a double line and two conics

• (v) two double lines and two lines

• (vi) two double lines and a conic

• (vii) a double conic and two lines (semi-stable)

• (viii) a triple conic (semi-stable)

• (xi) a triple line, a conic and a line

• (x) a triple line, a double line and another line

• (xi) a triple line and three lines

• (xii) a triple line and a cubic

Moreover, the constructions in [13, Sect. 5] further imply the following Lemma holds:

Lemma 4.25

Let ${\mathcal {P}}$ be a Halphen pencil of index two containing a curve B such that $B=2L+Q$, where L is a line and Q is a quartic (possibly reducible). The intersection multiplicity of L and Q at any point is at most 3. In particular, B is semi-stable by [12].

Proof

Arguing as in [13, Sect. 5], it is routine to check that if the intersection multiplicity of L and Q at some point p is four, then B cannot yield a fiber of type $IV^*$. Note that p has to be a base point of ${\mathcal {P}}$. $\square$

Now, if B is semi-stable, then arguing as in the case of a fiber of type $II^*$ (triple conic), we conclude ${\mathcal {P}}$ is always semi-stable by Lemma 4.7. Thus, in view of Lemma 4.25, it remains to consider the case where B contains a triple line. We prove:

Proposition 4.26

If Y contains a fiber F of type $IV^*$ and $B\doteq \pi (F)$ contains a triple line, then ${\mathcal {P}}$ is stable.

Proof

If ${\mathcal {P}}$ were non-stable, then ${\mathcal {P}}$ (and B) would be as in Proposition 3.7, by taking $B=C_f$. It is routine to check that ${\mathcal {P}}$ as in Proposition 3.7 cannot yield a rational elliptic surface Y with a fiber of type $IV^*$ (see e.g. [13, Sects. 5 and 7]). $\square$

In particular, we have proved Proposition 4.27 below.

Proposition 4.27

If Y contains a fiber of type $IV^*$, then ${\mathcal {P}}$ is semi-stable.

Moreover,

Proposition 4.28

If Y contains a fiber of type $IV^*$ and ${\mathcal {P}}$ is non-stable, then C is singular and B is semi-stable.

Proof

If ${\mathcal {P}}$ is non-stable, then it follows from Corollary 4.10.1 that either C is singular or B is unstable. The description by Shah in [12, Sect. 2] of unstable sextics, and a careful analysis of the possibilities for the curve B given at the beggining of this section, combined with Proposition 4.26 and Lemma 4.25 above, imply B cannot be unstable. $\square$

This concludes the proofs of Theorems 1.4, 1.5 and 1.6. Combining Propositions 4.12, 4.24 and 4.28 (resp. 4.15, 4.24 and 4.28) proves Theorem 1.4 (resp. 1.5), and the proof of Theorem 1.6 follows from combining Propositions 4.16, 4.17, 4.23 and 4.27.