Abstract
We calculate Chow quotients of some families of symmetric T-varieties. In complexity two we obtain new examples of Kähler–Einstein metrics by bounding the symmetric alpha invariant of their orbifold quotients. As an additional application we determine the homeomorphism class of the orbit space of the compact torus action.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we are interested in finding new Kähler–Einstein metrics on certain Fano manifolds. Whether or not a manifold X admits such a metric is characterized by the algebreo-geometric notion of K-stability, see [6, 7]. An equivariant version of K-stability has been used in the spherical [8], and complexity-one T-variety [12] settings to obtain an effective Kähler–Einstein criterion.
Generally, with group actions of complexity greater than one, K-stability is a difficult condition to check. Another approach is to apply the sufficient criterion of Tian [23]. In [20] it was shown that Tian’s criterion reduces to a related problem on the torus quotient if the original variety admits enough additional symmetries.
In the present paper the examples we consider are general arrangement varieties, that is they are T-varieties where the torus quotient is a projective space and the critical values of the quotient map form a general arrangement of hyperplanes in that projective space. Smooth projective general arrangement varieties of complexity and Picard rank 2 were classified according to their Cox ring in [11]. Following the methods of [20], we find three new examples of Kähler–Einstein metrics on some symmetric complexity two general arrangement varieties.
The first examples we are interested in are some hypersurfaces of bidegree (a, b). Consider the following varieties:
Let \(d = \gcd (a,b)\) and \(p= a/d, \ q = b/d\). There is an effective n-torus action prescribed by weights \((0|pI_n|0|-qI_n)\) on the homogeneous coordinates (x, y). Note, as an aside, that \(X^{2n-1}_{1,1}\) is a flag manifold of type \((1,n-1)\), which is known to admit a Kähler–Einstein metric as a homogeneous manifold, see remarks immediately preceeeding [18, Theorem 3] for example. By adjunction, \(X^{2n-1}_{a,b}\) is Fano iff \(a,b < n+1\). When \(a = 1\) then \(X^{2n-1}_{a,b}\) is smooth. Our first result is the following:
Theorem 1.1
\(X_{1,2}^5\) and \( X_{1,3}^5\) admit T-invariant Kähler–Einstein metrics.
Note that \(X_{1,2}^5, X_{1,3}^5\ \) appear in the classification of [11] as varieties 4E, 4F respectively. Secondly we consider an iterated blow-up of the even-dimensional quadric hypersurface. Consider the following representation:
Where we have labelled the projective coordinates \([x_0,\dots ,x_n,y_0,\dots ,y_n]\). There is a \(T \cong (\mathbb {C}^*)^{n+1}\) action on \(Q^{2n}\), specified on these coordinates by weight matrix \((I_n| - I_n)\). We obtain an effective \(T' := T / \langle \pm I_{n+1} \rangle \)-action on \(Q^{2n}\). Let \(Z_i := V(x_{i},y_i) \subset Q^{2n}\) for \(i=0,\dots ,n\). Consider the variety:
In Sect. 3.2 we show that \(W^{2n}\) is Fano, and independent with respect to permuting the indexing of the \(Z_i\). It is known as the wonderful compactification of the arrangement of subvarieties of Q built by \(Z_0,\dots ,Z_n\). Note that these blowups are equivariant with respect to the \(T'\)-action, and we may induce an effective \(T'\)-action on \(W^{2n}\). Our second result is the following:
Theorem 1.2
\(W^6\) admits a \(T'\)-invariant Kähler–Einstein metric.
We will use the following theorem of Tian, involving an invariant \(\alpha _{G}(X)\), the alpha invariant of a Fano manifold X.
Tian’s criterion
Let X be a Fano manifold and \(G \subset {{\,\mathrm{Aut}\,}}(X)\) reductive group of symmetries. If
Then X admits a G-invariant Kähler–Einstein metric.
In the case where G is finite, the alpha invariant coincides with the global log canonical threshold of X, denoted \({{\,\mathrm{g\mathbf {lct}}\,}}_G(X)\). A proof of this fact can be found in Demailley’s appendix of [5]. Suppose now X admits an effective action of an algebraic torus \(T = (\mathbb {C}^*)^{n+1} \subset {{\,\mathrm{Aut}\,}}(X)\). Let \(K \cong (S^1)^n\) be the maximal compact subtorus in T. Given a finite subgroup H of the normalizer \(\mathcal {N}_{{{\,\mathrm{Aut}\,}}(X)}(T)\), we have an induced H-action on the character lattice M of T.
Following [3], X is said to be symmetric with respect to the T-action if there exists such an H which fixes only the identity of M. Since H normalizes T then they generate a subgroup \(H T \subset {{\,\mathrm{Aut}\,}}(X)\). As H and T have trivial intersection this is a semidirect product of H and T. It can be shown that HT is the complexification of its maximal compact subgroup HK. Minor adjustments to Demailly’s proof give us that \( {{\,\mathrm{g\mathbf {lct}}\,}}_{HT}(X) = \alpha _{HT}(X) \) here also.
Let X be a symmetric T-variety. There is a natural quotient \(\pi :X \dashrightarrow Y\) by the torus action, the Chow quotient, first introduced by Kapranov [13]. Since H is in the normalizer of T then its action descends to Y. In the setting of this paper we assume that \(\pi \) is surjective. For any prime divisor Z on Y the generic stabilizer on a component of \(\pi ^{-1}(Z)\) is a finite abelian group. The maximal order across these components is denoted \(m_Z\). We then obtain a boundary divisor for \(\pi \) given by:
We call the pair (Y, B) the Chow quotient pair of the T-variety X. Süß, [20], showed that the global log canonical threshold of X with respect to HT coincides with that of the pair (Y, B) with respect to H:
Theorem 1.3
[20, Theorem 1.2] Let X be a symmetric log terminal Fano T-variety. Then
To prove Theorems 1.1, 1.2 we would like to apply Theorem 1.3 and then Tian’s criterion. We begin by calculating Chow quotients. The GIT quotients of X by T form a finite inverse system, and the inverse limit of this system contains a distinguished component, known as the limit quotient of X. In [2] it was shown that this limit quotient and the Chow quotient coincide. For the varieties \(X_{a,b}^{2n-1}\) we use the Kempf–Ness theorem to calculate GIT quotients. The inverse system is simple enough in this case to then deduce the Chow quotient pair.
For \(\gamma \in \mathbb {Q}\) define the \(\mathbb {Q}\)-divisor \(\gamma B := \gamma \sum _i H_i\), where \(H_1,\dots ,H_n\) are the coordinate hyperplanes of \(\mathbb {P}^{n-1}\) and \(H_0\) is the hyperplane \(V( \sum _{i=1}^n z_i)\). In Sect. 3.1 we will prove the following:
Lemma 1.4
The Chow quotient pair of \(X_{a,b}^{2n-1}\) by T is \((\mathbb {P}^{n-1},\gamma B)\) with \(\gamma = \max \left( \frac{p-1}{p}, \frac{q - 1}{q} \right) \).
By [21, Proposition 2.6] this allows us to calculate, as an additional application, the homeomorphism class of the quotient space \(X_{a,b}^n/T\). For the proof of the following corollary see Sect. 3.1.
Corollary 1.5
Let K be the maximal compact torus of T. There is a homeomorphism:
Where the later is the topological join of the \((n-1)\)-sphere and complex projective \((n-1)\)-space.
In particular, this shows that the K-orbit space of the flag manifolds \(F(1,n-1,\mathbb {C}^n) = X_{1,1}^{2n-1}\) is of this form.
Consider the variety \(W^{2n}\). Using results of [15] we may obtain the Chow quotient of \(W^{2n}\) from that of \(Q^{2n}\). In Sect. 3.2 we prove the following:
Lemma 1.6
The Chow quotient pair of \(W^{2n}\) by its \(T'\)-action is \((\mathbb {P}^{n-1},\frac{1}{2} B)\).
Remark 1.7
It is worth noting that Lemma 1.4 and Lemma 1.6 also follow from the basic theory of general arrangement varieties, see [11, Proposition 3.16, Remark 6.19]
Note that there is a natural \(S_{n+1}\)-action on \(X^{2n-1}_{a,b}\) permuting the indices of variables. Additionally, by results of [17], the \(S_{n+1}\)-action on \(Q^{2n}\) permuting the \(Z_i\) induces an action on \(W^{2n}\). These actions descend to the \(S_{n+1}\)-action on \(\mathbb {P}^{n-1}\) permuting the hyperplanes \(H_i\). We leave it to the reader to check that these finite group actions make \(X_{a,b}^{2n},Q^{2n},W^{2n}\) symmetric T-varieties.
We are now in a situation where we may be able to apply Theorem 1.3. For \(n=3\) we are able to calculate the log canonical threshold for the Chow quotient pairs. Let \(Y = \mathbb {P}^2\), with projective coordinates x, y, z, and consider the divisor B given by \(xyz(x+y+z) = 0\). Consider the \(S_4\)-actions on Y permuting the lines \(x=0, \ y=0, \ z=0, \ x+y+z=0\).
Lemma 1.8
Suppose \(\gamma < \frac{3}{4}\) so that the pair \((\mathbb {P}^2,\gamma B)\) is log Fano. We have:
2 Preliminaries
2.1 Chow and GIT quotients
Here we recall the definition of GIT, Chow, and limit quotients of a projective variety by a reductive algebraic group G. We also explain how, when G is a torus, they may be explicitely calculated via the Kempf–Ness theorem.
2.1.1 GIT quotients
Recall the basic setup of Mumford’s geometric invariant theory, which provides a method for finding geometric quotients on open subsets of a scheme X when the acting algebraic group G is reductive. A good reference for the material here is [19]. In [19] Mumford introduced the notion of a good categorical quotient, which can be shown to be unique if it exists.
Definition 2.1
A surjective G-equivariant morphism \(\pi : X \rightarrow Y\) is a good categorical quotient if the following hold:
-
(i)
We have \(\mathcal {O}_Y = (\pi _* \mathcal {O}_X)^G\);
-
(ii)
if V is a closed G-invariant subset of X then \(\pi (V)\) is closed;
-
(iii)
if V, W are closed G-invariant subsets of X and \(V \cap W = \emptyset \) then we have \(\pi (V) \cap \pi (W) = \emptyset \).
Good quotients do not always exist for a given scheme X, but we might hope that there exists some dense open subset of X which does admit a good quotient. Consider the affine case, where \(X = {{\,\mathrm{Spec}\,}}A\). For G reductive then it can be shown that  is a good categorical quotient.
is a good categorical quotient.
The same ansatz works in the projective case once we make a choice of a lift of the action to the ring of sections of a given ample line bundle. This choice is known as a linearization of the group action.
Definition 2.2
Let X be a projective scheme together with an action \( \lambda : G \times X \rightarrow X\) of a reductive algebraic group G. Let L be a line bundle on X. A linearization of the action \(\lambda \) on L is an action \({\tilde{\lambda }}\) on L such that:
-
The projection \(\pi \) is G-equivariant, \(\pi \circ {\tilde{\lambda }} = \lambda \circ \pi \)
-
For \(g \in G\) and \(x \in X\), the induced map \(L_x \mapsto L_{g \cdot x}\) is linear.
Note a linearization to L naturally induces linearizations to \(L^\vee \) and \(L^{\otimes r}\) for \(r \in \mathbb {N}\).
Example 2.3
A linearization of the trivial bundle on a projective variety X must be of the form:
for some \(\chi \in H^0(G \times X, \mathcal {O}_{G \times X}^*) \cong H^0(G, \mathcal {O}_G^*) = \mathfrak {X}(G).\)
The above example tells us that any two linearizations \(\lambda _1,\lambda _2\) of an action to the same line bundle differ by multiplication by some character \(\chi \) of G: fiberwise we have \({\tilde{\lambda }}_1 = \chi (g,x) {\tilde{\lambda }}_2\).
A linearization u of a group action G on X to L induces an action of G on the ring of sections \(R(X,L) := \bigoplus _{j \ge 0} H^0(X,L^{\otimes j}) \). Consider the scheme  . Note we have a birational map from X to
. Note we have a birational map from X to  , defined precisely at those \(x \in X\) such that there exists some \(m> 0 \) and \(s \in R(X,L)^G_m\) such that \(s(x) \ne 0\). Such a x are said to be semi-stable. If in addition \(G \cdot x\) is closed and the stabilizer \(G_x\) is of dimension zero, the point x is said to be stable. The sets of semi-stable and stable points will be denoted by \(X^{ss}(u)\) and \(X^{s}(u)\) respectively.
, defined precisely at those \(x \in X\) such that there exists some \(m> 0 \) and \(s \in R(X,L)^G_m\) such that \(s(x) \ne 0\). Such a x are said to be semi-stable. If in addition \(G \cdot x\) is closed and the stabilizer \(G_x\) is of dimension zero, the point x is said to be stable. The sets of semi-stable and stable points will be denoted by \(X^{ss}(u)\) and \(X^{s}(u)\) respectively.
Construction 2.4
[19, Chapter 1, Section 4] The canonical morphism  is a good categorical quotient.
is a good categorical quotient.
2.1.2 Chow and limit quotients
Recall the definition of the Chow quotient, as introduced in [13]. If G is any connected linear algebraic group and X is a projective G-variety, then orbit closures of points are generically of the same dimension and degree, and so define points in the corresponding Chow variety. The Chow quotient of the G-action on X is the closure of this set of points.
We now recall the definition of the limit quotient, from [19]. The limit quotient is discussed in detail in [2]. Let G be a reductive algebraic group, and X a projective G-variety. Suppose there are finitely many sets of semi-stable points \(X_1,\dots ,X_r\) arising from G-linearized ample line bundles on X. Whenever \(X_i \subseteq X_j\) holds, there is a dominant projective morphism  which turns the set of GIT quotients into an inverse system. The associated inverse limit Y admits a canonical morphism \(\bigcap _{i=1}^r X_i \rightarrow Y\). The closure of the image of this morphism is the limit quotient.
which turns the set of GIT quotients into an inverse system. The associated inverse limit Y admits a canonical morphism \(\bigcap _{i=1}^r X_i \rightarrow Y\). The closure of the image of this morphism is the limit quotient.
When G is an algebraic torus there are indeed finitely many semi-stable loci. Moreover, by [2, Corollary 2.7], we may calculate the limit quotient by taking the inverse limit of the subsystem obtained by only considering linearizations of powers of one fixed ample line bundle L. In [2, Proposition 2.5] it is shown that the Chow quotient and limit quotient coincide when G is an algebraic torus.
2.1.3 Kempf–Ness approach to GIT quotients
One approach to calculating GIT quotients is via the Kempf–Ness theorem. Let \(X \subseteq \mathbb {P}^N\) be a nonsingular complex projective variety and let G be reductive algebraic group acting effectively on \(\mathbb {P}^N\), restricting to an action on X. Let K be the maximal compact subgroup in G, with Lie algebra \(\mathfrak {k}\). The action of G is given by a representation \(\rho : G \rightarrow \text {GL}(N+1)\), and by choosing appropriate coordinates we may assume K maps to \(U(N+1)\) and so preserves the Fubini-Study form. It can be checked that a moment map \(\mu : X \rightarrow \mathfrak {k}^*\) is given by:
where x is any representative of \([x] \in X \subseteq \mathbb {P}^N\). Note we are now in the situation of the previous subsection, with \(L = \mathcal {O}_X(1)\) under the embedding \(X \subseteq \mathbb {P}^N\). This moment map is unique up to translations in \(\mathfrak {k}^*\). A different choice of linearization in this setting corresponds to multiplying \(\rho \) by some character \(\chi \in \mathfrak {X}(G)\).
Since \(\chi (K)\) is compact it sits inside \(S^1 \subset \mathbb {C}^*\), and hence we do not need to change coordinates when considering the effect on the moment map. When we plug this into (2) we see that we have translated the moment map by \(\chi \in \mathfrak {X}(G) \otimes \mathbb {R}\cong \mathfrak {k}^*\). Moreover, taking the rth power of L corresponds to scaling the moment map by a factor of r. This gives a correspondence between rational elements \(\chi \in \mathfrak {X}(G) \otimes \mathbb {Q}\subset \mathfrak {k}^*\) and linearizations of powers of L.
Example 2.5
Suppose \(G = T\) is an algebraic torus with character and cocharacter lattices M, N respectively. Then \(\rho \) is a diagonal matrix of characters \(u_0,\dots ,u_{N}\) and we obtain:
Then, by Atiyah [1], and Guillemin-Sternberg [10], the image of \(\mu \) is a convex polytope \(P \subset M\).
We will make use of the following theorem of Kempf and Ness. A proof is given in [19, Chapter 8]. See also the original work [14].
Theorem 2.6
[14, Theorem 8.3] Let \(X \subseteq \mathbb {P}^N\) be a nonsingular complex projective variety and let G be reductive algebraic group acting effectively on \(\mathbb {P}^N\), restricting to an action on X. Consider a linearization of some power of L corresponding to a rational element \(u \in \mathfrak {k}^*\).
-
(i)
\(X^{ss}(u) = \{ x \in X | {\overline{Gx}} \cap \mu ^{-1}(u) \ne \emptyset \} \).
-
(ii)
The inclusion of \(\mu ^{-1}(u)\) into \(X^{ss}(u)\) induces a homeomorphism

where \(\mu ^{-1}(u)/K\) is endowed with the quotient topology induced from the classical (closed submanifold topology) on \(\mu ^{-1}(u)\), and
 is endowed with its classical (complex manifold) topology
is endowed with its classical (complex manifold) topology
We can use Theorem 2.6 to calculate GIT quotients by inspection. To be explicit, suppose \(\mu ^{-1}(u)/K\) has the structure of a complex projective variety and \(\pi : X^{ss}(u) \rightarrow \mu ^{-1}(u)/K\) is a G-invariant morphism which restricts to the topological quotient map on the moment fibre, such that \(q_* \mathcal {O}_X^G = \mathcal {O}_Y\). The following fact is probably well known, but we prove it here for the reader’s convenience.
Lemma 2.7
The morphism q is a good categorical quotient and hence is isomorphic to the GIT quotient map  .
.
Proof
It is enough to show that q sends closed G-invariant subsets to closed subsets, and disjoint pairs of closed invariant subsets to disjoint pairs of closed subsets.
Firstly suppose that V is a G-invariant Zariski-closed subset of X. Then \(q(V) = q(V \cap \mu ^{-1}(u))\), and \(V \cap \mu ^{-1}(u)\) is K-invariant and closed in the classical topology of \(\mu ^{-1}(u)\). This implies that q(V) is closed in the classical topology on  . But q(V) is constructable, as the image of a Zariski-closed subset of X, and so we may conclude that q(V) is Zariski-closed in
. But q(V) is constructable, as the image of a Zariski-closed subset of X, and so we may conclude that q(V) is Zariski-closed in  .
.
Now suppose V, W are G-invariant and Zariski-closed in X, with \(x \in V\) and \(y \in W\) such that \(q(x) = q(y)\). By 2.6 we may take \({x'} \in {\overline{Gx}} \cap \mu ^{-1}(u), \ {y'} \in {\overline{Gy}} \cap \mu ^{-1}(u)\) such that \(q({x'}) = q({y'})\). These two points lie in the same K-orbit. By the G-invariance of V, W we have \(V \cap W \ne \emptyset \). \(\square \)
2.2 Log canonical thresholds
Here we recall the definition of the global log canonical threshold of a log pair, which features in Theorem 1.3 and Lemma 1.8. A log pair (Y, D) consists of a normal variety Y and a \(\mathbb {Q}\)-divisor D, where the coefficients of the irreducible components of D lie in [0, 1]. The canonical divisor of such a pair is \(K_Y+D\). A pair (Y, D) is called smooth if Y is smooth and D is a simple normal crossings divisor. A log resolution of a log pair (Y, D) is a birational map \(\varphi : {\tilde{Y}} \rightarrow Y\) such that \(({\tilde{Y}},\varphi ^*D)\) is smooth.
Definition 2.8
Suppose \(\varphi : {\tilde{Y}} \rightarrow Y\) is a log resolution of a pair (Y, D). Write \(D = \sum a_i D_i\) for prime \(D_i\) and rational \(a_i\). Then:
where \(\tilde{D_i}\) is the proper transform of \(D_i\) and the \(E_j\) are the \(\varphi \)-exceptional divisors. We say (Y, D) is log canonical at \(P \in Y\) if we have \(a_i \le 1 \) for \(P \in D_i\), and \(b_j \le 1\) for \(E_j\) such that \(\varphi (E_j) = P\). This condition is independent of the choice of resolution. If (Y, D) is log canonical at all \(P \in Y\) then we say (Y, D) is (globally) log canonical.
Example 2.9
Consider the pair \(Y = \mathbb {P}^2\) and \(D = \sum a_i L_i\) where \(L_i\) are all lines through a point \(P \in Y\). Blowing up at P we obtain the following:
where E is the exceptional divisor of the blow-up. Therefore (Y, D) is log-canonical whenever we have \(\deg D \le 2\) and all \(a_i \le 1\).
Recall the following consequence of the main theorem of [9], as stated in the proof of [5, Lemma 5.1]. This allows us to degenerate a pair under a \(\mathbb {C}^*\)-action if we want to show it is log canonical.
Proposition 2.10
Let (Y, D) be a log pair. Suppose \(\{ D_t | t \in \mathbb {C}\}\) is a family of \(\mathbb {Q}\)-divisors such that \(D_t \sim _\mathbb {Q}D\), \(D_1 = D\), and for \(t \ne 0\) there exists \(\phi _t \in {{\,\mathrm{Aut}\,}}(X)\) such that \(D_t = \phi _t(D)\). Then (Y, D) is log canonical if \((Y,D_0)\) is.
Now we recall the definition of the global log canonical threshold of a pair, as given in [21].
Definition 2.11
The global G-equivariant log canonical threshold of a log pair (Y, B) is defined to be
When B is trivial we will suppress it in our notation, writing \({{\,\mathrm{g\mathbf {lct}}\,}}_G(X)\) for the G-equivariant log canonical threshold of a normal variety X.
With the same notation as in (3), recall the following definitions, as a reference see [16]. The multiplier sheaf of a log pair (Y, D) is defined as follows:
the subscheme of log canonical singularities of the pair is the corresponding subscheme \(\mathcal {L}(Y,D)\) to the ideal sheaf \(\mathcal {I}(Y,D)\), and the support of \(\mathcal {L}(Y,D)\) is known as the locus of log canonical singularities, denoted \(\text {LCS}(Y,D)\). Note (Y, D) is not log canonical at \(P \in Y\) if and only if \(P \in \text {LCS}(Y,D)\).
Theorem 2.12
[16, Theorem 9.4.8] Suppose H is a big and nef \(\mathbb {Q}\)-divisor on Y such that \(K_Y+D+H=F\) for some Cartier divisor F on Y. Then
for every \(i \ge 1\).
Corollary 2.13
[22, Lemma 5.7] Suppose that \(-K_Y -D \) is nef and big. Then \(\text {LCS}(Y,D)\) is connected.
Corollary 2.13 is proved using a long exact sequence in cohomology. The following lemma is proved in a similar way, and is just a special case of [4, Lemma 2.9].
Lemma 2.14
Suppose that D is a \(\mathbb {Q}\)-divisor on \(\mathbb {P}^2\), with \(d:= \deg D\) satisfying \(3< d < 4\). Suppose \(\text {LCS}(\mathbb {P}^2,D)\) is a finite non-empty set of points. Then \(\text {LCS}(\mathbb {P}^2,D)\) consists of at most 3 points.
Proof
Let H be a line in \(\mathbb {P}^2\). Note \(K_{\mathbb {P}^2} + D \sim _\mathbb {Q}(d - 3) H\). By Theorem 2.12 we have an exact sequence:
Now \(|\text {LCS}(\mathbb {P}^2,D)| \le h^0(\mathcal {O}_{\mathcal {L}(\mathbb {P}^2,D)}) \le h^0(\mathcal {O}(\lceil d-3 \rceil )) = 3\). \(\square \)
Finally, in Demailly’s appendix of [5] it is shown that \({{\,\mathrm{g\mathbf {lct}}\,}}_{G}(X) = \alpha _G(X)\) for \(G \subseteq {{\,\mathrm{Aut}\,}}(X)\) a finite subgroup. The same proof may be easily extended to our setting, where G is the semidirect product of a torus T and a finite subgroup H of the normalizer of T in \({{\,\mathrm{Aut}\,}}(X)\). We outline one way of doing this in the following lemma.
Lemma 2.15
Suppose that X is a T-variety and H is a finite subgroup of the normalizer \( \mathcal {N}_{{{\,\mathrm{Aut}\,}}(X)}(T)\). Then \({{\,\mathrm{g\mathbf {lct}}\,}}_{HT}(X) = \alpha _{HT}(X)\).
Proof
One may define the log canonical threshold of a linear system \(|\Sigma | \subset |mL|\) for any line bundle L on X, see remarks succeeding [5, Definition A.2]. Note, by definition, if \(D \in |\Sigma |\) then \({{\,\mathrm{lct}\,}}(\frac{1}{m} D) \le {{\,\mathrm{lct}\,}}( \frac{1}{m} |\Sigma |)\) with equality when \(\Sigma \) is one-dimensional. As stated in [5, (A.1)] we have:
Clearly we have the inequality:
Now suppose \(|\Sigma | \subset |mL|\) is a HT-invariant linear system. Take \(D \in |\Sigma |\). We may repeatedly degenerate D along \(\mathbb {C}^*\)-actions to obtain \(D' \in |mL|^{T}\), with \({{\,\mathrm{lct}\,}}(\frac{1}{m}D') \le {{\,\mathrm{lct}\,}}(\frac{1}{m}D) \le {{\,\mathrm{lct}\,}}( \frac{1}{m}|\Sigma |)\) by Proposition 2.10. Let \(r = |H|\). Since H normalizes T, we may take \(D'':= \sum _{h \in H} h \cdot D'\), and then:
Then we have:
In particular when \(L = -K_X\) the left hand side is equal to \({{\,\mathrm{g\mathbf {lct}}\,}}_{HT}(X)\). \(\square \)
3 Examples
3.1 Bidegree (a, b) hypersurfaces \(X_{a,b}^{2n-1}\)
Recall the setup mentioned briefly in the introduction. Fix natural numbers \(n,a,b>0\), and consider:
Let \(p = a/d, q = b/d\), where \(d = \text {gcd}(a,b)\) and let T be the n-torus acting with weights \((0|q I_n|0|-p I_n)\). Let K denote the maximal compact torus in T. First we calculate our GIT and Chow quotients, proving Lemma 1.4. Let L be the restriction of \( \mathcal {O}(1,1)\) to X. Using (2) we can explicitely give a moment map for the torus action:
Where we take \(e_0 := 0\). The moment image polytope P is the convex hull of the vectors \(\{ q e_i - p e_j \}_{i,j}\). Consider a boundary point \(u \in \partial P\). In this case we show that the moment fibre of u is contained in one T-orbit, and so the GIT quotient is just contraction to a point. The key observation here is the following:
Lemma 3.1
Suppose \(\mu ([x],[y]) = \mu ([x'],[y'])\) and for each j we have
Then for each j we have \(x_i=0 \iff {x'}_i = 0\) and \(y_i = 0 \iff {y'}_i = 0 \).
Proof
Suppose first \(i>0\). We have:
For positive constants A, B, C, D. The conclusion follows by considering signs. Suppose now \(i =0\). By applying the affine linear functional \(l(w) := w \cdot \left( \sum e_j \right) - (b-a)\) to \(\mu (x,y) = \mu (x',y')\) we obtain:
For positive constants E, F, G, H. Again by signs we obtain the result. \(\square \)
Lemma 3.2
For \(u \in \partial P\) the moment fibre \(\mu ^{-1}(u)\) is contained in one T-orbit.
Proof
Suppose \(\mu ([x],[y]) = \mu ([{x'}],[{y'}]) \in \partial P\). Since \( (q-p)e_i \in P^\circ \) then \(x_iy_i = {x'}_i{y'}_i = 0\) for each \(i>0\). By the defining equation of X then also \(x_0y_0 = x_0y_0 = 0\). Applying Lemma 3.1 we are done. \(\square \)
Now consider moment fibres of points in the interior of P. We calculate the associated GIT quotient by selecting an appropriate rational map, as in Lemma 2.7.
Lemma 3.3
For \(u \in P^\circ \) the topological quotient \(\mu ^{-1}(u) \rightarrow \mu ^{-1}(u)/K \) is:
Proof
The map is clearly K-invariant. If \((x,y), ({x'},{y'}) \in \mu ^{-1}(u)\) Then for any representatives \(x,y,{x'},{y'}\) we have:
Fix a representative x of [x]. Pick a representative y of [y] such that \(|x||y| = 1\). For any representatives \({x'},{y'}\) of \([x'],[y']\) respectively, there is \(\lambda \in \mathbb {C}^*\) such that \( x_i^p y_i^q = \lambda {{x'_i}}^p {{y'_i}}^q\) for \(i>0\). Now, by Lemma 3.1 we may pick a representative \({x'}\) such that \(x_0 = {{x'_0}}\). Pick a representativeFootnote 1\({y'}\) such that \(\lambda = 1\). By the defining equation of X then \(x_0^a y_0^b = {x'_0}^a {y_0'}^b \). Applying Lemma 3.1 we have \(\nu \in \mathbb {C}^*\) such that \(y_0 = \nu {y'_0}\). As \(x_0 = {x'_0}\) then \(\nu \in S^1\), and we may rescale \({y'}\) by \(1/\nu \) so that \({y'_0} = y_0\).
If \(x_iy_i = 0\) then by Lemma 3.1 we can pick \(t \in \mathbb {C}^*\) such that \(x_i = t^b x_i', \ y_i = t^{-a} x_i'\). Suppose now \(x_iy_i \ne 0\). Then \(x_i,y_i,{x'_i},{y'_i} \ne 0\). Pick t such that \(t^p = {y'_i}/y_i\). Now \(x_i^p = t^{p q} {x'_i}^p\). Hence there exists some pth root of unity, say \(\xi \), such that \(x_i = \xi t^q {x'_i}\). Since p, q are coprime we may pick another pth root of unity \(\gamma \) such that \(\gamma ^q = \xi \). Picking s such that \(s^d = \gamma t\) we obtain \(x_i = s^b {x'}_i\) and \(y_i = s^{-q} {y'_i}\). We then have
Thus we have described a closed map with fibres precisely the S-orbits of \(\mu ^{-1}(u)\). This must be the topological quotient of the S-action. \(\square \)
By Lemma 2.7, we see for any \(u \in P^\circ \) the GIT quotient, according to the associated linearization of L, is given by:
By Lemma 2.7 this implies the Chow quotient is given by the same formula. We may now calculate the boundary divisor of this quotient, completing the proof of Lemma 1.4.
Proof of Lemma 1.4
From the above discussion we know the Chow quotient map is given by:
Suppose that Z is a prime divisor on the quotient, and D is a component of \(\pi ^{-1}(Z)\). If D intersects the open set where \(x_i,y_i \ne 0\), then \(t_i^p = t_i^q = 1\) for any t in the generic stabilizer of D. As p, q are coprime this would imply \(t_i = 1\). Suppose D is a component of \(\pi ^{-1}(Z)\) for some Z not of the form \(H_j\). Then for each i, D intersects the open set where \(x_i,y_i \ne 0\), so D has trivial generic stabilizer.
Now consider the prime divisor \(H_j\) on the quotient, for some fixed j. The irreducible components of \(\pi ^{-1}(H_i)\) are given by the homogeneous ideals \((x_j^p)\), \((y_j^q)\). The generic stabilizer of the first is a cyclic group of order p, generated by the element \(t \in T\) with \(t_i = 1\) for \(i \ne j\) and \(t_j\) a primitive pth root of unity. By symmetry the generic stabilizer of the second is a cyclic group of order q. This gives the required boundary divisor. \(\square \)
Proof of Corollary 1.5
By Lemmas 3.2 and 3.3 we see that the T-action on \(X^{2n-1}_{a,b}\) has almost trivial variation of GIT, as defined in [21, Definition 2.7], with \(Y = \mathbb {P}^{n-1}\). The result follows by [21, Proposition 2.9]. \(\square \)
3.2 Wonderful compactification of the quadric W
In this section we construct a wonderful compactification of an arrangement on an even dimensional quadric. We show that this compactification is Fano and we calculate the Chow quotient pair with respect to an induced torus action. First recall the notion of wonderful compactifications of arrangements of subvarieties, as introduced in [17].
Definition 3.4
Let X be a nonsingular algebraic variety. An arrangement of subvarieties of X is a finite collection \(\mathcal {S}\) of subvarieties closed under pairwise scheme-theoretic intersection. A building set of \(\mathcal {S}\) is a subset \(\mathcal {G} \subset \mathcal {S}\) such that for any \(S \in \mathcal {S} \backslash \mathcal {G}\) the minimal elements of \(\{G \in \mathcal {G} | G \supset S\}\) intersect transversally and the intersection is S. We will say that \(\mathcal {S}\) is built by \(\mathcal {G}\) if \(\mathcal {G}\) is a building set for \(\mathcal {S}\).
We will use the following result:
Theorem 3.5
[17, Theorem 1.3] Let X be a nonsingular projective variety, and \(V_1,\dots ,V_k\) a collection of subvarieties such any non-empty subset of \(\{V_1,\dots , V_k\}\) forms a building set for an arrangement of subvarieties. Consider the iterated blowup:
Then:
-
Each blowup is along a nonsingular variety;
-
W is isomorphic to the blowup along the ideal \(I_1 I_2 \cdots I_k\), where \(I_i\) is the homogeneous ideal corresponding to \(V_i\) for each i.
Following [17], we will call W the wonderful compactification of the arrangement built by \(V_1,\dots ,V_k\). Note that the composition of blowups \(\pi : W \rightarrow X\) is independent of the ordering of the \(V_i\).
We now turn to our particular example mentioned in the introduction. Let W be the wonderful compactification of the arrangement of subvarieties of Q built by \(Z_0,\dots ,Z_n\), where \(Z_i := V(x_{2i},x_{2i+1}) \subseteq Q\). We have the following:
Lemma 3.6
W is Fano.
Proof
By adjunction it is enough to show that \(-K_B - W\) is ample, where B is the wonderful compactification of the arrangement of subvarieties of \(\mathbb {P}^{2n+1}\) built by \(V_0,\dots ,V_n\), where \(V_i := V(x_{2i},x_{2i+1}) \subseteq \mathbb {P}^{2n+1}\).
For each i pick \(\sigma _i \in S_n\) such that \(\sigma _i(1) = i\). Each \(\sigma _i\) corresponds to a sequence of blowups whose composition is independent of i, as in Theorem 3.5. Denote by \( \psi _i: {{\,\mathrm{Bl}\,}}_{V_i} \mathbb {P}^{2n+1} \rightarrow \mathbb {P}^{2n+1}\) the first blowup of this sequence, and \(\pi _i: B \rightarrow {{\,\mathrm{Bl}\,}}_{V_i}\) the composition of the remaining blowups, so that the wonderful compactification is given by the composition \(\pi _i \circ \psi _i\). Denote the exceptional divisor of \(\psi _i\) by \(E_i\).
Consider the divisor \(D_i := \psi _i^* \mathcal {O}(1) - E_i\) on \({{\,\mathrm{Bl}\,}}_{V_i} \mathbb {P}^{2n+1}\). Note that \(D_i\) is nef, since for any curve C in \({{\,\mathrm{Bl}\,}}_{V_i} \mathbb {P}^{2n+1}\) we may pick a hyperplane \(H \subset \mathbb {P}^{2n+1} \) such that \(C \not \subset {\tilde{H}}\) but \(Z_i \subset {\tilde{H}}\), whereupon \((\pi ^* \mathcal {O}(1) - E_i) \cdot C = {\tilde{H}} \cdot C \ge 0\). Now
The divisors \((\pi \circ \psi )^* \mathcal {O}(1), \ \pi _0^* D_0, \dots , \pi _{n-1}^* D_{n} \) form a basis of the Picard group of W. Therefore they span a full dimensional subcone of the nef cone of B. Now \(-K_B - W\) is on the interior of this cone, and so is ample. \(\square \)
By construction there is a natural morphism \(\pi : W \rightarrow Q\) which is a composition of blowups, each centered at a smooth subvariety by Theorem 3.5. Fix the line bundle \(L = \mathcal {O}(1)_{|Q} \) on Q. Recall that there is an n-torus T acting on Q prescribed by \(\deg x_{2i} = e_{i+1}, \deg x_{2i+1} = -e_{i+1}\). This torus action may be extended to W. These torus actions are not effective, but we may quotient by the global stabilizer, a cyclic group of order two generated by \(-\text {Id} = (-1,\dots ,-1) \in T\), to obtain the action of an effective torus \(T'\) on Q and W. Quotienting does not affect the calculation of GIT quotients. In [21] the GIT quotients  were determined. They are either trivial contractions to a point, or of the following form:
were determined. They are either trivial contractions to a point, or of the following form:
The Chow quotient is also then given by (4). Following [15], there is an ample line bundle \({\tilde{L}}\) on W such that any linearization of \({\tilde{L}}\) is a lift of a linearization of L. Moreover, given a linearization, it can be shown that \(W^{ss} \subset \pi ^{-1}(X^{ss})\). By [ [15], Lemma 3.11] the GIT quotients of W given by a linearization of \({\tilde{L}}\) are precisely the restrictions of compositions \(q \circ \pi \), where q is the GIT quotient map for Q given by the corresponding linearization of L.
We can conclude that the Chow quotient is the restriction of a composition of the blowup map \(\pi \) followed by the map (4). We now calculate the boundary divisor of this quotient, proving Lemma 1.6:
Proof of Lemma 1.6
Recall the definition of the boundary divisor in the Chow quotient pair, see (1). From the formula (4) it is easy to calculate that the boundary divisor of the Chow quotient pair of Q is trivial. Therefore the only chance for \(m_Z >1\) occurs at the exceptional loci of blowups. If we construct W with the following sequence of blowups
The exceptional divisor of the composition of blowup maps is of the form \(E_{n-1} + \dots + E_0\), where \(E_i\) is the exceptional divisor of the \((i+1)\)th blowup in the sequence. By symmetry it is enough to calculate the generic stabilizer of \(E_0\). Consider \({{\,\mathrm{Bl}\,}}_{Z_0}Q\), realized as a subvariety of \(Q \times \mathbb {P}^1 \), given by the additional equation \(vx_0 - ux_1\), where u, v are the homogeneous variables in the second factor.
There is an induced T-action on \({{\,\mathrm{Bl}\,}}_{Z_0} Q\), under which the equation \(vx_0 - ux_1\) must be homogeneous with respect to the induced grading of the character lattice of T. This implies that \(\deg u = \deg v + 2e_1\), and we see that the generic stabilizer of the \(T' = T/ \langle \pm \text {Id} \rangle \)-action on the exceptional divisor must be a cyclic group of order 2, generated by the element \((-1,1,\dots ,1) + \langle \pm \text {Id} \rangle \). \(\square \)
4 Threshold Bounds and new Kähler–Einstein metrics
Let \(Y = \mathbb {P}^2\), with projective coordinates x, y, z, and consider the divisor B given by \(xyz(x+y+z) = 0\). Consider the \(S_4\)-actions on Y permuting the lines \(x=0, \ y=0, \ z=0, \ x+y+z=0\). First we prove Lemma 1.8:
Proof of Lemma 1.8
Set \(m = \min \left( \frac{2}{3-4 \gamma },\frac{4(1-\gamma )}{3-4\gamma } \right) \). In definition 2.2, considering the two cases
where C is the unique \(S_4\)-invariant conic in \(\mathbb {P}^2\), we see \({{\,\mathrm{g\mathbf {lct}}\,}}_{S_4}(\mathbb {P}^2, \gamma B) \le m \). Suppose, for a contradiction, that \({{\,\mathrm{g\mathbf {lct}}\,}}_{S_4}(\mathbb {P}^2, \gamma B) < m\). Pick \(D \in |-K_{\mathbb {P}^2} - \gamma B|^{S_4}_\mathbb {Q}\) such that \((\mathbb {P}^2, \gamma B + a D)\) is log canonical but not Kawatama log terminal, for some rational \(a<m\).
If \(\gamma B + aD = bC +R \) for some curve C, a rational number \(b>1\), and an effective \(\mathbb {Q}\)-divisor R, then \(C \ne B \) because \(a(3-4 \gamma ) < 4(1-\gamma )\). We must then have \(\deg C \le 1\), as now \(d< a(3-4\gamma ) <2\). No line is fixed under \(S_4\), so no such C exists, and so \(\text {LCS}(\mathbb {P}^2, \gamma B + aD)\) consists of finitely many points. Observe that
Now, by Lemma 2.14, \(\text {LCS}(\mathbb {P}^2,\gamma B + aD)\) consists of at most 3 points. As \(\text {LCS}(\mathbb {P}^2,\gamma B + aD)\) is \(S_4\)-invariant, it must be the points \([-1,1,1],[1,-1,1],[1,1,-1]\). Since these points do not lie in the support of B, then we see \(\text {LCS}(\gamma B+aD) = \text {LCS}(aD) \). But \(\deg aD <3\), so by Corollary 2.13\(\text {LCS}(aD) = \{[-1,1,1],[1,-1,1],[1,1,-1]\}\) is connected, which is a contradiction. \(\square \)
It is possible to obtain a rougher bound through another method, taking degenerations along \(\mathbb {C}^*\)-actions. This bound is still sufficient for our applications. We include it here for completeness:
Lemma 4.1
Consider the log pair \((\mathbb {P}^2,\gamma B)\), with \(\gamma < \frac{3}{4}\). We have:
Proof
To show \({{\,\mathrm{g\mathbf {lct}}\,}}_{G}(Y,\gamma B) \ge r\) it is sufficient to show that \(\gamma B + rD\) is log canonical for any \( D \in |-K_Y - \gamma B|_{\mathbb {Q}}^G\). Fix such a D and take \(P \in Y\). At most two of the \(H_i\) pass through P, so without loss of generality suppose \(H_0,H_3\) do not. Modify \(\gamma B+r D\) by removing any components supported at \(H_0,H_3\), to obtain a divisor \(D'\). Note \(\gamma B+r D\) is log canonical at P if \(D'\) is globally log canonical. Note also that although \(D'\) may not be G-invariant, it is still invariant under the involution \(\sigma \) swapping \(x_1\) and \(x_2\). Finally note \(D' \ge \gamma H_1 + \gamma H_2\).
Consider the \(\mathbb {C}^*\)-action \(t \cdot [x_1:x_2:x_3] = [ t x_1: t x_2 : x_3]\). By (2.10), \(D'\) is log canonical if \(D_0' := \lim _{t \rightarrow 0} \left( t \cdot D' \right) \) is log canonical. This \(\mathbb {C}^*\)-action commutes with \(\sigma \), and so \(D_0'\) is invariant under \(\sigma \). Moreover is is clear that each component of \(D_0'\) must be a line through the point [0, 0, 1]. By \(\sigma \)-invariance \(D_0'\) must be of the form:
for some \(a,b,c_i \in \mathbb {Q}\), where \(a + b + \sum _i 2 c_i \le 2 \gamma + 3 r - 4 \gamma r\). This is a divisor of the form described in Example 2.9. It is therefore log canonical iff the following inequalities hold:
Basic manipulation of inequalities gives our bounds on the global threshold. \(\square \)
Proof of Theorems 1.1 and 1.2
If X is \(X_{1,2}^5\) or \(W^6\) then X has Chow quotient \((\mathbb {P}^2,\frac{1}{2}B)\), and applying Theorem 1.3 and Lemma 1.8 we see that \(\alpha _{S_4}(X) = 2\). By Tian’s criterion then X admits an invariant Kähler–Einstein metric. Similarly the Chow quotient of \(X_{1,3}^5\) is \((\mathbb {P}^2,\frac{2}{3}B)\), and we see \(\alpha _{S_4}(X_{1,3}^5) \ge 2\), so \(X_{1,3}^5\) is also Kähler–Einstein. \(\square \)
Notes
Note that rescaling our chosen \({y'}\) by an element of \(S^1\) does not change anything here.
References
Atiyah, M.F.: Convexity and commuting Hamiltonians. Bull. Lond. Math. Soc. 14(1), 1–15 (1982)
Bäker, H., Hausen, J., Keicher, S.: On Chow quotients of torus actions. Michigan Math. J. 64(3), 451–473 (2015)
Batyrev, V.V., Selivanova, E.N.: Einstein-Kähler metrics on symmetric toric Fano manifolds. J. Reine Angew. Math. 512, 225–236 (1999)
Cheltsov, I., Shramov, C.: On exceptional quotient singularities. Geom. Topol. 15(4), 1843–1882 (2011). https://doi.org/10.2140/gt.2011.15.1843
Cheltsov, I.A., Shramov, K.A.: Log canonical thresholds of smooth Fano threefolds. Russ. Math. Surv. 63(5), 859 (2008)
Chen, X., Donaldson, S., Sun, S.: Kähler–Einstein metrics on Fano manifolds. III: limits as cone angle approaches \(2 \pi \) and completion of the main proof. J. Am. Math. Soc. 28(1), 235–278 (2015)
Chen, X.X., Donaldson, S., Sun, S.: Kähler-Einstein metrics and stability. Int. Math. Res. Not. IMRN 8, 2119–2125 (2014)
Delcroix, T.: K-stability of Fano spherical varieties. Ann. Sci. Éc. Norm. Supér. (4) 53(3), 615–662 (2020)
Demailly, J.P., Kollár, J.: Semi-continuity of complex singularity exponents and Kähler-Einstein metrics on Fano orbifolds. Annales scientifiques de l’Ecole normale supérieure 34, 525–556 (2001)
Guillemin, V., Sternberg, S.: Convexity properties of the moment mapping. II. Invent. Math. 77(3), 533–546 (1984). https://doi.org/10.1007/BF01388837
Hausen, J., Hische, C., Wrobel, M.: On torus actions of higher complexity. Forum Math. Sigma 7, Paper No. e38, 81 (2019)
Ilten, N., Süß, H.: K-stability for Fano manifolds with torus action of complexity 1. Duke Math. J. 166(1), 177–204 (2017)
Kapranov, M.M.: Chow quotients of Grassmannians. I. In: I. M. Gelfand Seminar, Adv. Soviet Math., vol. 16, pp. 29–110. American Mathematical Society, Providence (1993)
Kempf, G., Ness, L.: The length of vectors in representation spaces. In: Algebraic Geometry, pp. 233–243. Springer (1979)
Kirwan, F.: Partial desingularisations of quotients of nonsingular varieties and their Betti numbers. Ann. Math. 122(1), 41–85 (1985). https://doi.org/10.2307/1971369
Lazarsfeld, R.: Positivity in Algebraic Geometry II. Springer, Berlin (2004)
Li, L.: Wonderful compactification of an arrangement of subvarieties. Michigan Math. J. 58(2), 535–563 (2009)
Matsushima, Y.: Remarks on Kähler-Einstein manifolds. Nagoya Math. J. 46, 161–173 (1972)
Mumford, D., Fogarty, J., Kirwan, F.: Geometric invariant theory. Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)], vol. 34, 3rd edn. Springer, Berlin (1994). https://doi.org/10.1007/978-3-642-57916-5
Süß, H.: Kähler-Einstein metrics on symmetric Fano \(T\)-varieties. Adv. Math. 246, 100–113 (2013)
Süß, H.: Orbit spaces of maximal torus actions on oriented Grassmannians of planes (2018). http://arxiv.org/abs/1810.00981
Shokurov, V.: Three-fold log flips. Russ. Acad. Sci. Izvestiya Math. 40, 95–202 (1993)
Tian, G.: On Kähler-Einstein metrics on certain Kähler manifolds with \(C_1(M)>0\). Invent. Math. 89(2), 225–246 (1987). https://doi.org/10.1007/BF01389077
Acknowledgements
This work was partially supported by the Grant 346300 for IMPAN from the Simons Foundation and the matching 2015-2019 Polish MNiSW fund. I would like to thank my supervisor Hendrik Süß, Vanya Cheltsov, and my anonymous referee for many useful comments and suggestions while this paper was in preparation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cable, J. Kähler–Einstein metrics on symmetric general arrangement varieties. manuscripta math. 168, 119–135 (2022). https://doi.org/10.1007/s00229-021-01296-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00229-021-01296-5


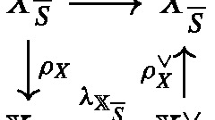



 is endowed with its classical (complex manifold) topology
is endowed with its classical (complex manifold) topology