Introduction

Among organisms, there is a high degree of commonality in how metabolism scales with body mass, and hence, the metabolic rate of an organism can be expressed as a function of its body mass by \({b}_{0}{M}^{b}\), where \({b}_{0}\) is the scaling coefficient and \(b\) is the allometric scaling coefficient (Bokma 2004; Brown et al. 2004; Glazier 2008). In effect \({b}_{0}\) and \(b\) are the intercept and slope of a log–log linear regression. The value of \(b\) has been under much investigation and debate, and has been proposed to be a constant, \(b\approx 3/4\), universal for all organisms (Brown et al. 2004), or to vary between \(2/3\) and 1 depending on the metabolic level of different taxonomic groups (Glazier 2008). Even though body mass is the master trait governing variation in metabolism, a fixed allometric coefficient is independent to and ignores, variation that may interact with body mass. The idea of a universal allometric coefficient has been criticized (Bokma 2004; Glazier 2006; Kozłowski et al. 2020), and although estimates of \(b\) often lie close to \(3/4\), there are clear differences between taxa in how metabolic rate scales with body size (Bokma 2004). Furthermore, the log–log relationship \(b\) describes a proportional or percent change in metabolic rate from the intercept \({b}_{0}\) (Gelman and Hill 2006 chapter 4). Hence, organisms with a higher log intercept (\({b}_{0}\)) will have a greater increase in metabolic rate per mass unit on the original scale even if they have the same slope (\(b\)) on the log scale. This means that b cannot describe an increase in metabolic rate with body mass on the original scale without information from an intercept (Fig. 1). Kozłowski et al. (2020) proposed that instead of focusing on the commonality, and one mechanistic explanation for all organisms, focus should be on the effect of natural selection on metabolic rate, through a life-history perspective. Hence, more research efforts are needed to explain how metabolic rate differs between species and to place metabolism in an eco-evolutionary context.

Fig. 1
figure 1

Exemplifies the relationship of log scale a and original scale b estimates of metabolic rate across mass. Panel (a) shows the log–log relationship between metabolic rate and mass where the lines have identical slopes of 0.75 but different intercepts of 0, 0.5, and 1, resulting in three parallel lines. In panel (b) the data in panel (a) has been transformed from the log scale to the original scale resulting in three non-parallel slopes where a greater intercept results in a steeper slope. In relation to hypothesis testing, panel (b) show an interaction, in effect, a difference in the relationship between metabolic rate and mass for the three groups (the three different lines) that is not visible on the log scale in panel (a). This illustrates a potential interpretation pitfall when the significance test of the interaction term is on the log scale (as the log scale often fulfills the assumptions of normality and homogeneity of variances) but estimates are presented on the original scale as this scale is biologically more meaningful. Hence, there is a risk of a discrepancy between the log scale test statistic and the original data

Full size image

Metabolic rate is a plastic trait and increases or decreases depending on physiological demands. Definitions and terminology are plentiful for measurements of metabolic rate (e.g., Burton et al. 2011; Morozov et al. 2018). For ectothermic organisms, the low metabolic rates are often termed standard or resting metabolic rates (SMR and RMR, respectively) and imply that the organism is inactive. SMR means that the organism has no spontaneous activity and no ongoing digestion, whereas spontaneous activity is allowed for RMR. In contrast, the maximum (MMR) and active metabolic rate (AMR) occur in organisms that perform strenuous activity and/or digest very large meals leading to considerably elevated metabolism (Clark et al. 2013). The original definition of MMR and AMR is the same, that is, peak/maximum aerobic activity (Fry 1971). RMR may be the better term when it is unknown whether the measured metabolic rate really is the lowest possible an individual could reach, i.e. SMR, or merely a proportion of it. Similarly, AMR may be the better term when it is unknown if the metabolic rate is the highest an individual possibly could achieve, i.e. MMR. In the present study, we will call the lowest resting and highest active rates RMR and AMR, respectively. However, the exact terminology may often be irrelevant to the study objectives (Morozov et al. 2018), as long as the experimental conditions are consistent and defined.

The difference between AMR and RMR is the aerobic scope and sets the organisms’ metabolic boundaries. The aerobic scope is the metabolism above the maintenance level and can be used for fitness-enhancing activities such as reproduction, growth and behavior (Pörtner and Farrell 2008). Hence, the greater the aerobic scope the more flexible the organism can be. Having either a high or a low metabolic rate can be beneficial under different environmental conditions, even for the same individual (Burton et al. 2011). For example, a low metabolic rate conserves energy when resources are scarce which is good during winter dormancy, whereas a higher rate can increase foraging efficiency and digestion which is good when resources are plentiful. Hence, metabolic rate data have to be interpreted contextually.

A key predictor of interspecific variation in metabolic rates is the species’ lifestyle (Glazier 2006; Seibel and Drazen 2007). For example, pelagic teleosts and cephalopods have a higher metabolism than their benthic and bathypelagic relatives (Seibel et al. 1997; Killen et al. 2010). This is believed to be caused by the requirement of a higher swimming performance for pelagic than benthic species, as they need to be more visually active to pursue prey or evade predators (Seibel and Drazen 2007). For teleost fish there is evidence suggesting that greater metabolic rates are correlated with morphological adaptations that lead to high swimming performance and a more efficient search for food (Killen et al. 2016; Morozov et al. 2018; Bergstrom et al. 2019), and hence, providing an adaptive link between physiology and ecology.

An organism’s lifestyle is defined as its degree of activity, and hence, variation in lifestyle leads to differing oxygen requirements and variations in metabolic rates. As such, much of the variation between taxa is driven by differences in locomotive activity, hence benthic and mesopelagic species typically have lower rates than the more active epipelagic species (Glazier 2006; Ikeda 2016). Similarly, variation within taxa can be explained by differences in lifestyle, as seen in four crab species. In this study, Johnson and Rees (1988) found that the predatory species had higher rates than their herbivorous relatives.

Strong seasonality in light and food availability characterize high-Arctic marine ecosystems (Daase et al. 2021), and the species here have evolved distinct lifestyles and their own particular ways of cope with the Arctic winter. This area is therefore an interesting setting to investigate the effects of lifestyle on metabolic rates. The Arctic mesozooplankton community is dominated by copepods, and in particular three Calanus species: C. finmarchicus, C. glacialis and C. hyperboreus. These are omnivorous grazers of different sizes that undergo a resting state during winter when they live off their large lipid reserves (Jónasdóttir et al. 2019). Sexual reproduction of C. glacialis and C. hyperboreus take place during the polar night, and the adult male is only present in high abundance for a brief period during which time the males are actively searching for mates (Hopkins et al. 1984; Daase et al. 2018). Two other calanoid copepod species, Metridia longa and Paraeuchaeta spp., do not undergo a resting state during winter but feed opportunistically, M. longa is an omnivorous grazer whereas the larger Paraeuchaeta spp. is a predator that hunts without vision and uses tactical cues (Olsen et al. 2000). Copepods often perform diel vertical migration, a behavior that is linked to predator avoidance (McLaren 1963). During the day copepods stay at depth to hide from visual predators, while during the night they actively feed on the surface (McLaren 1963; Hobbs et al. 2021). However, during the near-constant darkness of the Arctic winter, this behavior may be disrupted (Berge et al. 2020). Copepods undergo a distinct metamorphosis during development and thereby have easily identifiable life stages so that individuals can be partitioned between juveniles and adults, and males and females. Hence, the present study contains five species and their different life stages that all live in the same pelagic habitat.

The aim of this study is to link metabolic rate to the lifestyle of copepods that live in close proximity to the Arctic seas (Fig. 2). Our hypothesis was that the lifestyle of species and life stages during the polar night should be reflected in their metabolic rates. In addition, large individuals are expected to have higher metabolic rates in absolute terms than smaller individuals, even within the same species, but with lower metabolic rate per mass unit. This is because of the allometric relationship between metabolic rate and mass (Fig. 3). To conclude that differences in rate were due to lifestyle and not mass, comparisons were made between organisms of similar mass. Hence, variation in metabolic rate should be attributed to lifestyle differences alone.

Fig. 2
figure 2

Photos of the species and some of the life stages for which metabolic rate was measured. a Shows a female Calanus finmarchicus, b a cryptically colored juvenile (copepodid stage 5) Calanus glacialis which was mistaken as C. finmarchicus, c female C. glacialis, d male C. glacialis, e female Calanus hyperboreus, f male C. hyperboreus, g female Metridia longa, and h female Paraeuchaeta norvegica

Full size image
Fig. 3
figure 3

Exemplifies a confounding effect by the combination of mass and group on metabolic rate. The four lines in panel (a) and (b) show metabolic rate across mass for different groups. The metabolic rate shown in a is converted to per unit mass in b to clearly show the differences between linear and non-linear data. The two dashed lines in (a) and (b) are linear and hence across the full mass spectrum it is possible to determine that the difference in rate is due to group, as illustrated in panel (b) next to the letter A. The dotted and solid lines in panel (a) and (b) are non-linear and hence differences in metabolic rate can be caused solely by group as in B, or solely by mass as in C, or by the combination of mass and group as in D. By comparing organism groups of same mass when the relationship is non-linear, as in B, we can say for certain that differences in metabolic rate is due to group and not a mass effect nor a combination of the two. In the present study comparisons as in B were made

Full size image

Methods

Sampling

The copepods: Calanus finmarchicus, C. glacialis, C. hyperboreus, Metridia longa and Paraeuchaeta spp. -a mix of two species P. glacialis and P. norvegica, were sampled in the northern Barents Sea from the research vessel Kronprins Haakon (cutoff: 81.9819, 29.7942; 76.0057, 34.2815) during 1st – 13th of December 2019. Smaller species were collected by vertical net hauls with either a MultiNet or a bongo-net (Hydro-Bios®, Kiel), equipped with nets of 64-µm mesh size, and openings of 0.25 and 0.28 m2, respectively. If larger species were caught in the smaller nets they were sampled as well. Specifically for larger species we deployed a WP3 net with a 1 m2 opening and mesh size of 1000 µm to collect C. hyperboreus and Paraeuchaeta spp. The latter genus is not as delicate as the other species and were therefore also collected with an Isaac Kidd midwater trawl (MIK) with an opening of 3.14 m2 and a mesh size of 1.5 mm, where the last 1.5 m have a 500-µm mesh size. The MIK net was hauled vertically because of sea ice. Net haul speed was 0.3–0.5 ms−1 for the smaller nets, and 0.8–1 ms−1 for the larger nets. The net cod ends, in which the zooplankters were concentrated, were removable plastic net buckets with a side window of sieve gauze. Approximately 27% of the individuals were sampled within the range from a 100 m depth and up to the surface, 36% from a greater depth than 100 m and up to 100 m below the surface, and another 36% from a greater depth than 100 m and up to the surface. Sea temperatures ranged from  – 1.5 to 4 °C along the sampling transect, with the warmer Atlantic water mainly in the southern and northern parts (Van Engeland et al. 2023). Immediately after sampling, the samples were diluted in 30 L barrels with as much sea water as possible to mitigate stress caused by crowding and stored at 0 °C in a dark cold room. Larger gelatinous zooplankton were removed from the barrels as these can foul the water. A total of 3 barrels were used in rotation, using one barrel per net haul, as the last barrel filled up the first barrel was emptied to make space for the sample from the next haul. Typically one or two hauls were taken during a day, with one to three days between sampling days.

Species identification of Calanus finmarchicus and C. glacialis

Recent studies have highlighted the difficulties in correctly identifying Calanus finmarchicus and C. glacialis based on morphological criteria (Choquet et al. 2018). Before the measurements of metabolic rate, 283 individuals of C. finmarchicus and C. glacialis were identified as species solely based on their pigmentation. C. glacialis has more colorful red antennae, urosome, and female genital pore, while C. finmarchicus has a more transparent antennae, urosome, and the female genital pore is pale whitish (Fig. 1a–d). After measuring metabolic rate, a photo was taken of each individual before they were individually placed in tin cups and preserved at  – 20 °C for 5 months for later species genotyping. Prior to DNA extraction, the samples were freeze-dried to measure their dry weights. Extractions were made thereafter following the HotSHOT protocol presented by Montero‐Pau et al. (2008), following extraction a PCR was performed by adding the DNA extract to a master mix containing the primer G_150 that amplifies a region of 161 and 131 base-pairs in C. glacialis in C. finmarchicus, respectively, see Smolina et al. (2014). Amplicon size was examined by gel-electrophoresis; the gel was made of 2% agarose 100 ml TAE buffer and 5 µL GelRed, the gel ran for 25 min under 220 V. For every gel, two ladders, one negative control, and two positive controls of the respective species were added. Under ultraviolet light, an individual with a band that travelled a longer distance in the gel was determined as C. finmarchicus and a band that travelled shorter as C. glacialis.

The genetic species identification revealed that, based on coloration, only one out of 283 Calanus individuals were incorrectly classified, whereas 99.6% were correctly classified. This single individual was a C. glacialis with no pigmentation on the antennae which was incorrectly determined as C. finmarchicus. However, this individual had a small red pigmentation spot on the urosome which suggests that it is a C. glacialis (Fig. 2b).

Measurements of metabolic rate

Metabolic rates were measured on a microplate system from Loligo®, consisting of a glass dish with 24 wells with one optical sensor spot in each well. The glass dish was placed on top of a sensor dish reader that emitted light through the glass on to the optical sensor spot. Prior to the experiments each sensor spot was calibrated in both oxygen depleted and oxygen-saturated seawater at 0 °C. The sea water was deoxygenized by mixing water with 1% (w/w) sodium sulfite, and air saturated by circulating the water with air stones. Phase values were read once the values had stabilized for each two-point calibration and sensor spot. Calibration values were later used to convert the measured phase values to oxygen concentration. Measurements were taken in an incubator set at a constant temperature of 0 °C. During the experiments, the animals were in natural seawater that had been filtered through a 0.45-µm filter to remove respiring organisms, and thereafter oxygen saturated by circulating the water with air-stones. The sample size of individuals per species, sex and life stage (juvenile copepodid stage 5 and the adult female and male copepodid stage 6) were dependent on the individuals available in the nets. In the end, some combinations of species, sex and life stage were available in excess while others were few or even absent. Furthermore, the data were not analyzed until after the cruise so information on effect sizes and variance to find ideal sample sizes were not available.

Just prior to the measurements, copepods were pipetted one by one from their holding barrels to a small sieve placed in a container of sea water. Once the sieve had enough copepods for the experiments it was lifted and drained, leaving just the copepods, and thereafter immersed in a container with oxygen-saturated filtered seawater. From here the animals were transferred one by one to the wells of the sensor dish, which were filled with oxygen-saturated filtered seawater. Excess water in the wells was removed and the wells were sealed from the air. The seal was made by laying a silicon padding on top of the glass dish, and by making it adhere to the dish by supplying pressure from above with a weighted plate. The larger animals, C. hyperboreus and Paraeuchaeta spp. were measured in a dish with 1700-µl wells, whereas the smaller animals C. finmarchicus, C. glacialis and M. longa were measured in a dish with 500-µl wells. For every incubation, 20 wells were used to measure the metabolic rate of copepods, with one individual in each well. Four wells were left without copepods and only filled with filtered and oxygen-saturated seawater, these wells were used as a control to measure background respiration, i.e. changes in phase values that are not caused by the copepods. Oxygen measurements were taken in regular intervals every 5 or 30 s during the incubation, depending on the settings of the Loligo® software. Each incubation went on for at least 3 h. After the measurements, the copepods were photographed under a stereo microscope to determine species and life stage. Life stage and sex were determined by counting the number of segments on the urosome, which is species-specific and differs between males, females and juveniles, see Klekowski and Węsɫsawski (1991). Prosome length and 2D area were measured from the photos using the software tpsDig (Rohlf 2005) and used to calculate zooplankton volume by the formula of an ellipsoid \(\frac{4}{3}\pi abc\), assuming that width and depth are equal. A correction factor of 1.13 was used to correct for the volume of the antennas, legs, and urosome (Dubois et al. 2022). The animals were placed in pre-weighed tin cups and freeze dried at -50°Cand 0.2 mbar for at least 12 h in a LABCONCO FreeZone tray drier. The copepod dry weight was thereafter measured on a Mettler-Toledo XPR microbalance with 0.001 mg readability.

Data handling

Because of the initial handling of the copepods the metabolic rate was greater in the beginning of the measurement and became progressively lower as the copepods became more relaxed (Zhang et al. 2020). Hence, the oxygen (measured as phase values initially) concentrations decreased exponentially over time and were described by a linear model as: \(\left(phase\right)=time+ {e}^{time}\). The microplate system lacks any internal mixing mechanism; therefore, copepods could occasionally adhere to the optical sensor which caused small spikes in the phase values that go back to the curve trajectory once the animals move around and mix the water. Spikes, i.e. noise in phase values, were smoothed for every individual by fitting the linear model described above (Fig. 4a, Soulié et al. 2021). For every individual, predictions of phase values from the fitted curves were made for every 15 s to obtain curves without noise. Smoothing the raw data to remove noise before running the rolling regression analysis greatly improved the predictive power of the data (Fig. 4b).

Fig. 4
figure 4

Processing of raw data on oxygen concentration into active metabolic rate (AMR) and resting metabolic rate (RMR). Panel (a) shows a fitted curve to the raw data of a single individual, this smoothed the noisy raw data to suit it better for rolling regression. Panel (b) shows a comparison of rolling regression estimates on smoothed data and raw data for the whole data set of 447 copepods, smoothing greatly improved the correlation between dry weight and metabolic rate. In contrast, rolling regression directly on the noisy raw data made the estimates of metabolic rate go up or down haphazardly, and hence, weakened the relationship. c The fitted curves (displayed in panel a) were converted from phase to oxygen by use of calibration data, a rolling regression analysis was applied to every individual curve; regressions were made on 5 min intervals. The shaded area shows the sampling time 5 to 75 min. d Shows an example of a rolling regression analysis on random data, each regression is 5 observations long and the regression advances one point at a time until less than 5 observations remain. e The ‘densityMclust’ function was used to select AMR and RMR by taking the average of their normal distributions shown as dashed lines, see Chabot et al. (2016) for a review, the density distributions are from the data shown in panel (c)

Full size image

The fitted phase values of each individual were converted into µmol O2 L−1 (Fig. 4c). The relationship between phase value and oxygen concentration is linear. By dividing the oxygen concentration for air-saturated seawater at 0 °C (349 µmol O2 L−1) with the difference between the phase value at oxygen depletion and at oxygen saturation, we got a conversion factor of the oxygen concentration per unit phase value. The conversion factor was then multiplied by the difference between the phase value at oxygen depletion and the measured phase value in the experiment at time i. The subtraction is made because of the inverse relationship between phase value and oxygen concentration. The average oxygen concentration of the four control wells at time i was subtracted from every individuals’ oxygen concentration at time i. This was done to remove background respiration and sensor drift that is potentially caused by temperature variations. Finally, the curves were analyzed using rolling regression. The rolling regression rendered slope estimates (i.e., the metabolic rate) by continuously fitting linear regression models of 5 min length, advancing one observation (15 s, as defined above) per regression until less than 5 min remained, that is, from points \(i, i+1,\dots i+time \ window\) (Fig. 4d). Hence, the rolling regression analysis rendered as many estimates of metabolic rate as there were 5 min slots along the curve. The five-minute time window relies on the local linearity of a non-linear curve and helps to improve a linear fit (Morozov et al. 2019), and was short enough to capture rapid changes in metabolic rates. Rolling regressions were fitted by means of the ‘zoo’ package (Zeileis and Grothendieck 2005). Rolling regression estimates having the unit µmol O2 L−1 min−1 were transformed to µmol O2 day−1 by scaling it appropriate to the volume of water in the well after the volume of the zooplankton been subtracted, and by multiplying it by 60 (min) * 24 (h).

Different metabolic measurements

Active metabolic rate (AMR) was estimated soon after the zooplankton had been put into the wells. The preceding handling caused the zooplankton exertion (Norin and Clark 2016; Zhang et al. 2020), and hence, the metabolic rates were higher initially and gradually declined during the measurements. Metabolic recovery, the time it takes for the animal to go from a high metabolism active state to a low rate resting state is shorter the smaller mass an animal has (Goolish 1989, 1991). For example, Goolish (1991) estimated that the glycogen restoration in a 4 cm fish takes 1–3 h following anaerobic activity. For 1–3 g shrimps (Crangon crangon) performing burst tail contractions, recovery of ATP took 5 min and recovery of arginine phosphate took 30 min (Onnen and Zebe 1983). Copepods are considerably smaller than these shrimps, yet it can take several hours for their oxygen consumption to stabilize during incubation (Skjoldal et al. 1984; Båmstedt and Tande 1985). However, in the studies with copepods the incubations typically contained many individuals in the same container and had a resolution of hours between measures. To our knowledge, there are no studies showing how rates of individual copepods that are kept separately change during incubations with a resolution of seconds, as in the present study. Everything considered, we assumed that these small animals would recover during the experiment and that metabolic rate would become gradually lower.

The copepods were not fed before the experiments and were assumed to be in a post-absorptive state during the measurements since none of them had any visual signs of previous feeding as the gut and intestine were visible through their transparent bodies. The metabolic measurements started within 5 days from when the zooplankton were captured. Since the animals did not undergo fasting in the laboratory or a period of acclimation to the respirometer the minimum metabolic rates are here termed resting metabolic rate (RMR), meaning that the animals were in a quiescent state but may have low levels of spontaneous activity (Burton et al. 2011; Chabot et al. 2016). There was great individual variation in the present study. However, on a population level there was an overwhelming distinction between the measured AMR and RMR. The aerobic scope was calculated as the difference between AMR and RMR, and hence, describes the capacity for oxygen consumption above maintenance levels. Our estimate of aerobic scope is restrictive, as we know that the SMR can be lower than the RMR and that the MMR can be greater than the AMR. Hence, the aerobic scope based on SMR and MMR is equal or greater than what we have estimated. Key to this experimental setup is that the same method was used for each individual.

Providing a common environment for all individuals in the study enables the separation of inherent genetic variation and environmental variation in statistical models (Falconer and Mackay 1996 chapter 8). Here genetic variation is the variation that is caused by species, life stage, and sex. The environmental variation is caused by how the individuals were treated before the experiments, which affects their respective AMR and RMR. Hence, individual treatment should be as similar as possible so that variation in metabolic rate can be correctly attributed.

Metabolic rate values were selected within 75 min from the start of measurement, omitting 5 min initially as a wait time for sensor stability. The time frame of 75 min was chosen since a stable baseline was reached for many of the individuals of the smallest mass at that time, that is, the sensor could not detect a decrease in oxygen that was greater than the precision of the instrument after 75 min. This was also visible from the correlation between metabolic rate and dry weight which showed a greater correlation during the initial 75 min than during the remaining time (Fig. 4b). We decided to end the measurements after the same amount of time for each individual to give them as similar treatment as possible. The package ‘mclust’ (Scrucca et al. 2016) was used to select AMR and RMR by density estimation via model-based clustering within the 75-min time frame, see Chabot et al. (2016) for an example. Density estimation aims to estimate the underlying probability density distribution of observed continuous data using a local likelihood method. This differs from histograms’ that construct a density estimate by sorting data in discrete bins, and hence, if the data is continuous the bin placement becomes ambiguous and affects the underlying density distribution. Density estimation is useful when animal activity is unknown, as it assumes that AMR and RMR from each individual are measured with normally distributed errors (Chabot et al. 2016). For each individual the density algorithm detected 4 normal distributions within the data of rolling regression estimates (Fig. 4e). The mean of the lowest normal distribution was taken as the RMR and the mean of the highest normal distribution as the AMR.

Statistical analyses of metabolic rate

The response variable for the model was absolute metabolic rate with the unit µmol O2 day−1. A mixed model was fitted with two two-way interactions (Eq. 1). The first between species, with five categories, and metabolic measurement, with three categories: active metabolic rate (AMR), resting metabolic rate (RMR) and aerobic scope. The second, between the life stage, three categories: juveniles (C5), adult females (C6F) and adult males (C6M) and dry weight: a continuous variable.

$${\text{metabolic rate }}\sim {\text{ species }} \times {\text{ metabolic measurement }} + {\text{ life stage }} \times {\text{ dry weight }} + \, \left( {1 \, |{\text{ unique individual}}} \right)$$
(1)

The mixed linear model had the individual as a grouping variable (random effect), to account for the repeated measures, and was fitted with the function ‘lmer’ from the ‘lme4’ package (Bates et al. 2015) by restricted estimate maximum likelihood (REML) as the number of observations per group was unbalanced (Bolker et al. 2009). A mixed model was chosen because of the non-independence of the data where three metabolic measurements were taken on the same individual. An alternative approach would have been to split the data in three based on metabolic measurement and analyze each set individually, however, then the non-independence would not have been explicitly analyzed and the number of models would have tripled. The response variable and dry weight were both log transformed to reduce the effects of heteroscedasticity, and because of the non-linearity between metabolic rate and mass.

‘lmer’ model predictions and confidence intervals were calculated by the ‘Effect’ function in the ‘effects’ package and were transformed to the original scale (Fox and Weisberg 2018, 2019). Comparison of confidence intervals was done to assess the significance and to test our hypotheses. The ‘Effect’ function averages non-focal predictors and weigh levels of the factor in relation to sample size. All estimates in the result section were calculated from the two models stated above. We refrained from presenting p-values computed on the log scale data as these are not always sensible when scrutinizing model predictions on the original scale (Fig. 1).

The statistical analyses and data handling were carried out in R version 4. 0. 3 (R Core Team 2020) and the graphics were produced by the ‘ggplot2’ (Wickham 2016) and ‘patchwork’ (Pedersen 2020) packages.

Results

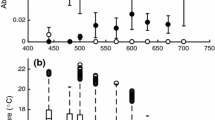
For copepod metabolic rates, each main effect: species, life stage or sex, metabolic measurement, and dry weight (body mass) was ‘significant’ in terms of non-overlapping 95% confidence intervals for one or more levels within each main effect and by not overlapping zero for dry weight (Fig. 5). The species main effect showed that Paraeuchaeta spp. had greater metabolic rates than Calanus hyperboreus; and for the smaller species, Metridia longa had greater rates than C. finmarchicus and C. glacialis. The life stage and sex main effect showed that males had greater metabolic rates than females and juveniles. In addition, the main effect of metabolic measurement showed that the active metabolic rate (AMR) was greater than the resting metabolic rate (RMR) and that the aerobic scope was intermediate. The main effect of dry weight showed that increasing mass leads to an increasing metabolic rate. Relative to each other, the main effect metabolic measurement (with the measurements: AMR, RMR, and aerobic scope) had the greatest effect on metabolic rate in our model, followed by dry weight, species, and life stage with the smallest effect on metabolic rate (Fig. 5).

Fig. 5
figure 5

Estimated main effects and their 95% confidence intervals from the model of copepod metabolic rate. The estimates were predicted for individuals of 1 mg dry weight, since for a log–log model the intercept is equivalent to 1, that is, \({ e}^{0}=1\). The covariates species, life stage, metabolic measurement, and mass are color coded. All coefficients are shown on the original scale. Life stages and sexes are abbreviated as juveniles C5, females C6F, and males C6M. Metabolic measurements are abbreviated as active metabolic rate AMR, resting metabolic rate RMR; aerobic scope is the difference between AMR and RMR. Main effects were averaged over the remaining focal predictors

Full size image

The interaction between metabolic measurements with three levels: active metabolic rate (AMR), resting metabolic rate (RMR) and aerobic scope, and the five different copepod species showed that metabolic rates differed between copepod species (Fig. 6; Table 1). For the small copepods (Fig. 6ab), predictions from the ‘lmer’ model on an individual of 0.4 mg dry weight (a weight that the three species could realistically take) confirmed that the AMR of Metridia longa 0.63 µmol O2 day−1 (95% CI: 0.51, 0.77) was greater than for both Calanus finmarchicus 0.34 (0.30, 0.38) and C. glacialis 0.36 (0.32, 0.41). In contrast, the RMR were similar for the three species: M. longa 0.08 (0.06, 0.10), C. finmarchicus 0.07 (0.06, 0.08), and C. glacialis 0.07 (0.06, 0.08). The greater AMR and similar RMR for M. longa resulted in a greater aerobic scope compared to C. finmarchicus and C. glacialis, which was 0.53 (0.43, 0.65) for M. longa and 0.25 (0.22, 0.28) for C. finmarchicus and 0.28 (0.25, 0.32) for C. glacialis.

Fig. 6
figure 6

Metabolic rates across dry weight for five Arctic copepod species. Lines are predicted estimates from the ‘lmer’ model with 95% confidence intervals in shaded areas and the species are color coded. Panel (a) and (b) shows the small copepods Calanus finmarchicus, C. glacialis, and Metridia longa. Panel (c) and (d) shows the large copepods Calanus hyperboreus and Paraeuchaeta spp. Points are the observed data where filled circles show active metabolic rate (AMR) and open circles the resting metabolic rate (RMR) in panels (a) and (c). Crosses show the aerobic scope in panels (b) and (d), this is the difference between AMR and RMR

Full size image
Table 1 Estimated active metabolic rate (AMR) and resting metabolic rate (RMR) at 0 °C from the ‘lmer’ models, estimates are given on the log scale as intercept (b0) and slope (b) with 95% confidence interval in parenthesis
Full size table

For the two larger copepods (Fig. 6c,d), predictions were made on an individual of 2 mg dry weight and showed that all metabolic measurements were greater for Paraeuchaeta spp. than for Calanus hyperboreus. The AMR was 2.06 µmol O2 day−1 (95% CI: 1.70, 2.50) for Paraeuchaeta spp. and 1.14 (0.99, 1.30) for C. hyperboreus, and the RMR was 0.61 (0.50, 0.74) for Paraeuchaeta spp. and 0.35 (0.30, 0.40) for C. hyperboreus, and the aerobic scope was 1.33 (1.10, 1.61) for Paraeuchaeta spp. and 0.74 (0.64, 0.84) for C. hyperboreus. The predictions of small and large copepod species are weighted averages over juveniles, females, and males.

The interaction between life stage and dry weight showed that the males had a greater increase in metabolic rate with dry weight than the females and juveniles (Fig. 7; Table 1). For a copepod of 0.4 mg dry weight the metabolic rate was 0.22 µmol O2 day−1 (95% CI 0.19, 0.26) for males and 0.23 (0.19, 0.27) for females and 0.21 (0.19, 0.24) for juveniles. In contrast, for a copepod of 2 mg dry weight the metabolic rate was 0.88 µmol O2 day−1 (95% CI 0.75, 1.04) for males and 0.57 (0.52, 0.63) for females and 0.54 (0.46, 0.62) for juveniles. These predictions were estimated as the weighted average over the five species and the three metabolic measurements.

Fig. 7
figure 7

Metabolic rates across dry weight for life stages and sexes, using the intercept for Calanus glacialis in panel (a) and (b) and C. hyperboreus in panel (c) and (d). Lines are predicted estimates from the ‘lmer’ model with 95% confidence intervals in shaded areas and the life stages and sexes are color coded. Points are the observed data where filled circles show active metabolic rate (AMR) and open circles the resting metabolic rate (RMR) in panels (a) and (c). Crosses show the aerobic scope in panels (b) and (d), this is the difference between AMR and RMR. Juveniles, females and males are abbreviated as C5, C6F and C6M in the legend, respectively

Full size image

Discussion

Our results show metabolic differences between overwintering Arctic copepod species and their life stages during the polar night. Even though the species live in the same pelagic habitat, their differences in ecology were reflected in their metabolic demand. Life stage and sex affected the metabolic rate probably due to differences in behavior between males and females and juveniles.

Of the small copepods, Metridia longa had higher active metabolic rates (AMR) and aerobic scope but a similar resting metabolic rate (RMR) as the two Calanus species C. finmarchicus and C. glacialis. The difference in AMR and aerobic scope is possibly due to the low activity by Calanus during winter, where feeding for the most part ceases and the species undergo a resting state (Båmstedt and Ervik 1984; Hopkins et al. 1984; Jónasdóttir et al. 2019). For example, Jónasdóttir et al. (2019) estimated that C. finmarchicus, the smallest of the three investigated Calanus species, has a lipid storage that can last up to 200 days for an adult female. In contrast, M. longa has a much smaller lipid storage and a greater loss in mass during winter and is therefore dependent on active search for non-phytoplankton food (Hopkins et al. 1984). Hence, M. longa is in need of a greater AMR and aerobic scope to feed during winter. As the RMR was similar for M. longa, C. finmarchicus, and C. glacialis this means that M. longa can switch to a lower metabolism that is nearly identical to the Calanus species’ while at rest and thereby holds a greater metabolic plasticity. It is well known that copepod species that are dormant during winter have lower metabolic rates than what they have when they are active during summer (Ingvarsdóttir et al. 1999; Maps et al. 2014). In the present study, we have showed that the metabolic rate of winter-active species can be greater than, or just as low as that in dormant species and that the metabolic rate can change greatly for an individual during a short time.

Of the large copepods, the tactile predator Paraeuchaeta spp. had a greater AMR, RMR and aerobic scope in comparison to the grazer Calanus hyperboreus. The consistent higher rates are likely beneficial because Paraeuchaeta spp. is not in need of a resting state during the polar night since it can feed on small mesozooplankton in the dark without visual cues (Yen 1987; Olsen et al. 2000).

We found contrasting metabolic rates between life stages and sexes, where the metabolic rate of males had a greater increase in body mass than adult females and juveniles. The difference was the greatest for the active metabolic rate. Hence, it takes a greater proportion of energy to sustain activity in large males than in large females and juveniles, in comparison to smaller individuals. This may be one reason why males of C. glacialis and C. hyperboreus were of considerably smaller mass than the females in the present study. Typically, Calanus males develop into adults during the winter and early spring and the adult males’ life span is only about two months, and hence, Calanus males are usually present only for a short time in high abundances (Daase et al. 2018; Hopkins et al. 1984; Tande 1982). Furthermore, the males have an increased swimming activity compared to the females (Daase et al. 2018), because they have to stay active to detect and mate with females (Tsuda and Miller 1998). Taken together with the expenses of spermatophore production and copulation, the male can lose up to 50–60% of its organic reserve in just two months (Hopkins et al. 1984). Hence, the greater metabolism by the male compared to the female and juvenile stage is likely due to its short and intense adult life span.

The fitness benefit of having a relatively high or low metabolism is conditional and context dependent. Organisms with lower metabolism conserve energy which is beneficial under deprived food conditions. On the other hand, organisms with higher metabolism process energy faster and can thereby sustain higher growth and reproductive rates when food conditions are good (Burton et al. 2011; Auer et al. 2015). Our results suggest that the juveniles and females of the Calanus species have a low metabolism during winter, likely as an adaptation to conserve energy and to cope with scarce food resources (Hopkins et al. 1984). In contrast, the metabolic rates we estimated for M. longa include a higher AMR than the Calanus species but a similar RMR. This greater plasticity may be beneficial during long periods of food deprivation with breaks of sudden short events with increased resource availability. Hopkins et al. (1984) found that M. longa is unable to store the amount of lipids needed for a continuous resting state during winter, and hence, the greater metabolic plasticity may be important to cope with the winter. Furthermore, Hopkins et al. (1984) found that the Calanus males do not conserve energy during winter to the same extent as the juveniles and females, hence, the males conserve energy as juveniles and spend it as adults. The strategy of the adult male is likely to convert stored energy into high reproductive rates by mating with as many females as possible in a time window of a few months, as they are present for a much shorter time than the females (Daase et al. 2018; Søreide et al. 2010; Hopkins et al. 1984). For the females, the adult life span is considerably longer and the conservation of energy during winter for future reproduction is more important (Søreide et al. 2010; Hopkins et al. 1984). This suggests that a lower metabolic rate during winter will increase fitness for Calanus females. Our findings confirm that species and sexes have distinct metabolic rates to meet their needs in activity, whether it is for feeding, locomotion, or mating.

In the present study, we had no detailed information about the copepods vertical placement in the water column. The vertical position is important as temperature affects metabolic rate and the temperature may be different in different water layers. The Arctic copepods are during the winter spread out in the water column from the surface down to great depths of thousands of meters (Auel et al. 2003; Gislason 2018). This means that copepods caught in the same haul may have been acclimated to different temperatures, which in turn may have an effect on their metabolic rate (Saumweber and Durbin 2006). Adding to the complexity is that the vertical position is to some degree species specific, where for example, Calanus hyperboreus is more associated with overwintering at great depths, whereas Metridia longa may perform daily vertical migrations during winter (Gislason 2018). In addition, Ingvarsdottir et al. (1999) found experimentally that seasonality was far more important than temperature in determining the metabolic rate of C. finmarchicus. Suggesting that copepods are resilient to vertical temperature differences, and perhaps not in need of a long acclimatization, as it is part of their lifestyle to move between water masses of different temperatures.

A general view is that the part of the Calanus populations that go the deepest down in the water column enter a state of diapause with a greatly reduced metabolic rate (Hirche 1996; Auel et al. 2003; Gislason 2018). For example, Auel et al. (2003) found that the metabolic rates of C. hyperboreus sampled from a 100 m depth up to the surface were greater than for individuals sampled from 2300 m depth. However, in the same study the authors also found that the metabolic rates of the surface population had far greater variance than the population in the depth. This means that there is an overlap in metabolic rates and that some individuals choose to overwinter higher up in the water column, and hence, depth cannot be the only variable affecting the metabolic rate in overwintering Calanus. This highlights the complexity of the vertical position of copepods in relation to their metabolic rates. Furthermore, for experiments run in the field it is exceedingly difficult to estimate the many variables that can affect metabolic rate. Hence, in the present study we investigate more general and simple hypotheses, such as the effects of species and life stage, since simple hypotheses are more likely to hold true across space and time.

Future directions

In the present study, the measurements on individual zooplankton allowed for a detailed description of the species metabolic rate and mass relationship. When measurements are taken on individuals we recommend reporting metabolic rate as a function of mass as this will be true across the full mass spectrum. In contrast to individual measurements, the typical “water bottle” method for zooplankton (Marshall et al. 1935; Ingvarsdóttir et al. 1999; Ikeda et al. 2001; Darnis et al. 2017) includes pooling of individuals and measuring their joint metabolic rate, which does not take into account individual variation in mass. The water bottle method results in an average metabolic rate and an average mass of the individuals. However, if the rate-mass relationship is exponential, the average rate does not necessarily correspond to an individual of average mass. Furthermore, a metabolic rate average cannot with certainty be extrapolated across a species mass spectrum if the true relationship is exponential, as the change in rate is not fixed for a given change in mass. Moreover, for any concave function (as in Table 1 and Figs. 6 and 7) the function output (metabolic rate) at the average input (mass) is greater or equal to the average output of the function, this is known as the Jensen’s inequality (Jensen 1906; Denny 2017), i.e. \(f\left(E\left[X\right]\right)\ge E\left[f\left(X\right)\right]\). Similarly, when metabolic rate per unit mass is described as a function of mass, the function is convex and Jensen’s inequality is \(f\left(E\left[X\right]\right)\le E\left[f(X)\right]\). These possible sources of error are to our knowledge rarely mentioned in ecological and evolutionary studies on the metabolic rate of zooplankton even though presenting results as averages are custom. Hence, it would be of tremendous help when comparing results within and between studies on zooplankton if metabolic rates are given as a function of mass instead of average estimates.