Introduction

Wood dust formed during abrasive sanding and by other means was recognized as a carcinogenic agent as early as 1994 (e.g., Meng et al. 2020). Wood dust particles, which are spread around workplaces, can also cause numerous other diseases (e.g., Jacobsen et al. 2010). Therefore, the application of dust exhaust systems has special importance for worker safety. Exhaust system components are located outside buildings to reduce the risk of fire. Under these conditions, dynamic interactions of wood dust with moist air cause water gain by wood dust when air cools as it is expelled to baghouse dust collectors. Under these circumstances, the effectiveness of filtration systems is often reduced by dust cake formation.

The filtration performance can be significantly affected by physical properties of gas. The effect of the air humidity on the filter performance depends on the filter type, gas properties, size and chemical composition of dust particles. Changes in air humidity induce variation in pressure drop, dust cake removal and filtration efficiency (Gupta et al. 1993; Schmidt and Pilz 1996; Hajra et al. 2003; Park et al. 2007). These problems are already found in the hygroscopic range and become more significant when condensation occurs. The presence of moisture during the filtration process leads to blinding and reduction in the life cycle of filter bags. Water condensation from air is responsible for forming a dust cake, which is difficult to clean. The dust cake adhesion strongly depends on the presence of water in the liquid phase. It induces higher energy demand for removing the dust cake. On the other hand, the blinding of the filter bags enhances filtration efficiency. Thanks to this, it is possible to reduce the content of carcinogenic wood dust particles in the air recycled into workplaces. However, other methods to reduce the concentration of dust should be chosen in order to reduce energy consumption and increase the life cycle of filter bags (Morris and Allen 1996; Chen et al. 2001; Mukhopadhyay 2009, 2010; Simon et al. 2014).

The hygroscopic and diffusion properties of dust acquired from beech wood were previously reported by Majka et al. (2019). However, that study considered dust obtained from untreated wood, while thermally modified wood has grown in popularity due to its reduced environmental impact compared to chemically modified wood and the desirable attributes of the product. Jones and Sandberg (2020) recently pointed out that thermal modification is the most common approach to wood modification. Thermal modification reduces wood hygroscopicity mainly by the removal of hydroxyl groups from degraded hemicellulose (e.g., Altgen et al. 2016; Liang and Wang 2016). Hemicellulose degradation also improves dimensional stability, which is attributed to ultrastructural changes in treated material (although some results suggest that cross-linking does not improve dimensional stability; e.g., Kocaefe et al. 2015).

The desirable properties of thermally modified wood are accompanied by a general decrease in favorable mechanical properties. Treated wood is more brittle due to the degradation of amorphous components (Esteves and Pereira 2009). Moreover, tensile strength and bending strength significantly decrease after treatment (e.g., Boonstra et al 2007). The mechanical properties of heat-treated wood also influence machining processes, including sawing and sanding. Only a few studies have analyzed wood dust obtained from thermally modified wood. Those analyses mainly focused on the particle size distribution of wood dust obtained from untreated and thermally modified wood. Aro et al. (2019) studied wood dust particle size obtained during sawing of thermally modified wood. They found that treatment had a minor influence on the size distribution of dust particles. Piernik et al. (2019) analyzed the effect of thermal modification and wood machining on wood dust formation, with higher treatment temperature increasing the production of the finest particles, which are a potential threat to workers’ health. A similar relationship was found by Očkajová et al. (2020), i.e., at higher treatment temperature values; there was an increase in the finest particle size of wood dust. Another problem in evaluating wood dust is differences in its properties for different wood species and with different machining operations, i.e., sawing (Aro et al. 2019) or milling (Očkajová et al. 2020; Piernik et al. 2019). The use of different laboratory grinders is one method for obtaining experimental material (e.g., Yuan et al. 2021), but this can produce significant differences in the shape and properties of wood dust particles.

Little is known about the hygroscopic properties of wood dust from thermally modified wood. Källbom et al. (2018) is the only study we are aware of that analyzed hygroscopicity of sawdust, in that case for heat-treated Norway spruce wood, with sorption isotherms evaluated over three adsorption–desorption cycles. They reported that equilibrium moisture content reduction is partially reversible. In comparison, the hygroscopic properties of thermally modified solid wood have been extensively studied. Olek et al. (2013) stated that monolayer moisture sorption was responsible for reduced equilibrium moisture content of thermally treated wood. It was also found that sorption hysteresis increased after wood modification, which was attributed to ultrastructural reorganization of wood.

Hygroscopic water transport in thermally modified solid wood has been examined less often. Pfriem et al. (2010) recognized non-Fickian behavior in thermally modified solid wood. Olek et al. (2016) applied the inverse method for analyzing water diffusion in native and thermally modified wood. Non-Fickian behavior was significant for heat-treated material, which was explained as being caused by a delay in obtaining hygroscopic equilibrium, compared to unmodified wood. To the authors` knowledge, a joint analysis of sorption isotherms and water diffusion in wood dust particles from thermally modified wood has not yet been reported.

The primary objective of this study was to determine sorption properties of dust particles produced by abrasive sanding of untreated and thermally modified beech wood. In addition, it was sought to quantify sorption properties by modeling sorption isotherms, which were used to design dynamic sorption experiments that could elucidate water diffusivity in wood dust.

Materials and methods

Thermal modification

European beech (Fagus sylvatica L.) wood was kiln dried to a moisture content of ca. 12% to prepare it for use in experiments. The material was then divided into two parts, one part was untreated and the other one subjected to thermal modification, which was done for samples having a cross section of ca. 40–50 mm and length of 300 mm. Thermal modification was carried out in a laboratory kiln (Olek et al. 2013). The first phase of heating was performed in moist air until the wood temperature reached ca. 130 °C. The second, main, phase of heating was done in superheated steam until reaching the target temperature of 220 °C. The duration of the main phase was 2 h during which the target temperature was maintained. After completing the main phase of treatment, the material was cooled, first in superheated steam and then in moist air.

Dust sample preparation

Wood dust was obtained from untreated and thermally modified solid wood by abrasive belt sanding along the direction of the wood grain. Wood dust was then sieved to separate the particles into fractions of distinctly different particle sizes, i.e., (a) < 25 and (b) 80–250 µm. An AS 200 Digit (Retsch, Germany) sieving machine was used to separate the dust fractions and a laser particle sizer (Analysette 22 Microtec Plus, Fritsch, Germany) quantified particle size distributions within each fraction. The cumulative particle size distribution (Q3) and density distribution (q3) are presented in Fig. 1 for unmodified and thermally modified wood. MaScontrol (Fritsch, Germany) software was used to calculate the diameter (d) of dust particles, with average diameter values of 22.75 and 24.99 µm for wood dust < 25 µm from untreated and thermally modified wood, respectively. Average diameters of the 80–250 µm fraction were 142.43 and 135.37 µm for untreated and thermally modified wood, respectively. Wood dust particle dimensions were smaller than the anatomical elements found in beech wood tissue. For example, the diameter of dust particles in each fraction was significantly lower than the mean length of fibers (600–1300 µm) and vessels (300–700 µm) of beech wood (Wagenführ 2006). Moreover, particle size analysis clearly showed that the dimensions of the smallest particles were less than the diameter of fibers and vessels, i.e., 16–20 µm and 10–85 µm, respectively (see Fig. 1).

Fig. 1
figure 1

Cumulative particle size distribution (Q3) and density distribution (q3) of untreated and thermally modified beech wood dust fractions

Full size image

Sorption experiments

Prior to testing, dust samples from untreated and thermally modified beech wood were stored in desiccators over phosphorus pentoxide to bring them close to a dry state. The initial mass of dust samples was ca. 7 mg. Sorption experiments were carried out in a dynamic vapor sorption apparatus (DVS Advantage 2, Surface Measurement Systems, London, the UK) at 25 °C. The experiments always started with samples equilibrated in dry gas in order to obtain a dry initial state. Equilibrium moisture content (EMC) values were measured at 11 levels of gas relative humidity (RH), ranging from 0 to 95%. The DVS apparatus uses two different options of a stop criterion, i.e., fixed time for a stage of a sorption experiment or a criterion based on the rate of mass change over a specified duration, which is applied at each RH level. The application of the fixed time criterion results in the problem that a stage lasts for a specified period of time regardless of the equilibrium state of a sample. Therefore, the rate of mass change over a specified duration was used in the study as the stop criterion. The default stop value of 0.002%/min over a 10 min window used in DVS Sorption Solution software was criticized by Glass et al. (2017, 2018) because it results in unacceptable errors in EMC estimation. Therefore, a modified stop criterion (0.001%/min with time window of 10 min and the minimum stability period of 60 min) was used in the present study. The analysis of the absolute error (uncertainty) of moisture content was performed to derive the criterion. The total differential method (e.g., Taylor 1997) was used to analyze the error. The current modified stop criterion is shorter than the recommendation of 0.0003% min−1 over 2 h and given by Glass et al. (2018), because wood dust approaches equilibrium more quickly than solid wood.

Sorption isotherm modeling

Adsorption and desorption isotherms were constructed for the four wood dust sample types (modified or unmodified and large or small size) and parametrized with the GAB (Basu et al. 2006) and GDW (Furmaniak et al. 2007a,b) models. The three-parameter GAB model was applied in the form:

$$EMC = M_{m} \frac{{K_{GAB} \cdot C_{GAB} \cdot RH}}{{\left( {1 - K_{GAB} \cdot RH} \right) \cdot \left( {1 - K_{GAB} \cdot RH + C_{GAB} \cdot K_{GAB} \cdot RH} \right)}}$$
(1)

where EMC—equilibrium moisture content, Mm (kg/kg)—monolayer capacity, CGAB—equilibrium constant related to monolayer sorption, and KGAB—equilibrium constant related to multilayer sorption. The model describes water molecule bonding to sorption sites to form a monomolecular layer. Water molecules in the monolayer become secondary sorption sites, and additional layers of water are formed (multilayer sorption).

The GDW model assumes the existence of the primary sorption sites on the adsorbent surface. It also postulates that water molecules bonded to those sites are converted into the secondary ones. However, the most important difference between the GAB and GDW models concerns the potential absorption of more than one water molecule by secondary sites. The four-parameter form of the GDW model is given by:

$$EMC = \frac{{m_{GDW} \cdot K_{GDW} \cdot RH}}{{\left( {1 + K_{GDW} \cdot RH} \right)}} \cdot \frac{{1 - k_{GDW} \cdot \left( {1 - w} \right) \cdot RH}}{{\left( {1 - k_{GDW} \cdot RH} \right)}}$$
(2)

where mGDW (kg/kg)—monolayer water content (the maximum content of water bound to primary sites), KGDW-—kinetic constant related to sorption on primary sites, kGDW—kinetic constant related to sorption on secondary sites, w—ratio of water molecules bound to the primary sites that become secondary sorption sites. The GDW model considers three scenarios of sorption, expressed through the w parameter: (a) w < 1—water molecules absorbed on primary sites are not completely converted into secondary sorption sites, (b) w = 1—all monolayer water molecules are converted into secondary sorption sites (in this case, the GDW model is reduced to the GAB model), and (c) w > 1—each monolayer water molecule is statistically converted into more than one secondary sorption site.

Diffusivity determination

As RH changes cause varying changes in EMC, the adsorption isotherms were used to design experiments for collecting data for diffusivity determination. The RH changes to be tested were determined to obtain even ranges of EMC. Data to estimate diffusivity were obtained from experiments made in the DVS apparatus in adsorption mode. The stepwise increase in RH was programmed to obtain a final EMC of 0.01 kg/kg at the end of the first adsorption stage, with the sample mass measured every 60 s. The test was terminated when the rate of mass change was less than 0.001%/min over 60 min. After finishing the first sub-experiment, RH was increased successively, with a total of 15 sub-experiments performed up to the maximum target EMC of 0.15 kg/kg. The results of the sub-experiments provided sets of input data for diffusivity determination.

Although wood dust particles can have a range of complex shapes, they are commonly modeled as spheres. The assumption of spherical shape was used in solving the initial-boundary-value problem of diffusion. Transient diffusion was described by Fick’s second law, with boundary condition of the first kind and the initial condition assuming uniform water content. A simplified solution of the diffusion problem derived by Peppas and Brannon-Peppas (1994) valid for short time behavior of the process, i.e., for E < 0.8 was applied, where:

$$E = 6\left( {\frac{D\tau }{{a^{2} }}} \right)^{\frac{1}{2}} \left\{ {\pi^{{ - \frac{1}{2}}} + 2\sum\limits_{n = 1}^{\infty } {\text{ierfc}} \frac{na}{{\sqrt {D\tau } }}} \right\} - 3\frac{D\tau }{{a^{2} }} \cong 6\left( {\frac{D\tau }{{\pi a^{2} }}} \right)^{\frac{1}{2}} - 3\frac{D\tau }{{a^{2} }}.$$
(3)

with a—sphere radius, D—water diffusivity, E—reduced water content, and τ—time. Water diffusivity values were obtained by fitting Eq. (3) to the results of the sorption sub-experiments.

Although it was already recognized that the thermal treatment of wood implies highly non-Fickian behavior the classic form of Fick’s second law together with the simplified analytical solution was used in the study. Olek et al. (2011, 2016) developed the modification of the diffusion model for non-Fickian behavior. The model accounted for an increased delay in obtaining the hygroscopic equilibrium of thermally modified wood. A relaxation mechanism was incorporated into the convective boundary condition of the model. Unfortunately, the model can be solved with numerical methods only. The implementation of the model for wood dust seems to be impossible.

Results

Sorption isotherms

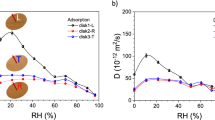
EMC measurements taken with the DVS apparatus provided data for individual sorption modes, i.e., adsorption and desorption. The discreet values of EMC were acquired after approaching the hygroscopic equilibria for prescribed RH levels at 25 °C. Sorption isotherms of untreated and thermally modified wood dust plotted after parameterization with the GAB model are presented in Fig. 2. Each plot depicts two sets of isotherm loops for wood dust fractions < 25 µm and 80–250 µm. The depicted isotherms formed closed loops. The EMC was influenced by particle size; higher EMC values were obtained for smaller particles of the same material, for both untreated and thermally modified wood dust. The influence of particle size was similar to that reported for dust of unmodified beech wood (Majka et al. 2019). A distinct reduction in EMC values was observed for thermally modified wood dust. Differences in EMC were quantified in detail by modeling sorption isotherms.

Fig. 2
figure 2

Sorption isotherms of untreated (left) and thermally modified (right) beech wood dust at 25 °C. Adsorption and desorption isotherms were parametrized with the GAB model, and symbols represent experimental data separately measured for each treatment option and dust fraction

Full size image

The three-parameter GAB and four-parameter GDW adsorption and desorption isotherm models were separately fitted for the four experimental options (two wood dust size fractions of untreated and thermally modified material). Coefficients of the best-fit sorption algorithms for each model were estimated using the Levenberg–Marquardt algorithm with SigmaPlot 9.0 software. The results of isotherm parametrization with both models are presented in Tables 1 and 2.

Table 1 Estimated coefficients of the GAB model for two fractions of untreated and thermally modified wood dust
Full size table
Table 2 Estimated coefficients of the GDW model for two fractions of untreated and thermally modified wood dust
Full size table

Thermal modification affected monolayer water content estimated using the GAB model during adsorption. The values of the Mm coefficient were reduced from 0.052 to 0.041 kg/kg for the dust fraction < 25 µm and from 0.047 to 0.035 kg/kg for the 80–250 µm fraction (Table 1). This supports the hypothesis that thermal modification reduces active sorption sites. Moreover, Mm was always lower for adsorption compared to desorption.

The CGAB coefficient is related to sorption enthalpy of the monolayer water. Values of this coefficient were higher than 2 in all analyzed isotherms. This satisfies the necessary condition for classifying these as type II isotherms. Lewicki (1997) states that type II isotherms should also satisfy the following two inequalities, in which 5.57 ≤ CGAB < ∞ and 0.24 < KGAB ≤ 1. These additional conditions were met for desorption isotherms only. Therefore, the adsorption isotherms cannot be fully classified as type II. The observed values of CGAB were always significantly higher than KGAB in corresponding isotherms (Table 1). This suggests that monolayer water molecules might be much stronger bound than those with multilayer bonding (e.g., Hess et al. 2018). Thermal modification increased CGAB for isotherms both in adsorption and desorption as well as for both size fractions of particles. This can be interpreted as meaning that thermal treatment increases the binding strength of water molecules in the monolayer. Some decrease in CGAB was found for larger dust particles, suggesting that monolayer water molecules are less tightly bound in larger wood dust particles. Higher CGAB values were noticed during desorption compared to adsorption (Table 1). This was observed for untreated and thermally modified wood as well as for both size fractions of wood dust. Hess et al. (2018) attributed differences in CGAB values for desorption and adsorption to sorption hysteresis.

The coefficient KGAB indicates the difference between the free enthalpy of multilayer water molecules and bulk water (Timmermann 2003). Values of KGAB were lower than 1 for all isotherms (Table 1), i.e., the necessary condition for preserving the physical soundness of the parameter was satisfied (e.g., Chirife et al. 1992). Higher values of KGAB indicate higher heat of sorption of multilayer water. It was observed during adsorption that neither thermal modification nor size of wood dust particles influenced the binding energy of water molecules during multilayer sorption. In the case of desorption, a decrease in KGAB was observed for thermally modified wood dust, while particle fraction had again no influence on the coefficient.

The influence of thermal modification on the reduction of water content in the monolayer was also evident when analyzing the GDW model. This reduction was evident from the lower maximum content of water bound to primary sites (mGDW), which has a similar physical meaning to that of the Mm coefficient in the GAB model. Values of mGDW were significantly lower with thermal modification for both adsorption and desorption as well as for both wood dust size fractions (Table 2). A similar reduction in monolayer water was found for thermally modified solid wood (Olek et al. 2013). The phenomenon can be explained by dehydration reactions of hemicelluloses, which are the most hygroscopic components of wood (Esteves and Pereira 2009), as well as by ultrastructural changes in wood components (Olek and Bonarski 2014).

Values of the w parameter in the GDW model were analyzed for the adsorption mode only as wood dust during its transport in the filtration installations only gains water. The w parameter is a measure of water molecules bound to primary sites that are converted into secondary ones. It indicates water gain and the creation of secondary sorption sites for binding water. For this reason, the analysis of w in desorption mode is questionable. The w parameter was less than 1 for the larger fraction (80–250 µm) of both untreated and thermally modified wood dust. This can be interpreted as indicating that not all primary sites are converted into secondary ones. Moreover, conversion ability decreased after thermal modification (Table 2). The number of secondary sites is smaller than the number of primary sites. In the case of the smaller dust fraction (< 25 µm), w was slightly greater than one, indicating that each water molecule bound to a primary sorption site was able to create more than one secondary site, promoting the formation of water clusters. Thermal modification only slightly decreased clustering ability. The values of w obtained for both size fractions of wood dust were significantly greater than has been reported for solid wood, for softwood species by Furmaniak et al. (2008) and especially for beech wood (Olek et al. 2013). Therefore, the mechanism of water molecules bonding on the secondary sorption sites in wood dust particles differs from that observed for solid wood, where clustering ability was practically not observed.

The applied GDW model was also used to classify sorption isotherms. Furmaniak et al. (2011) proposed an arbitrary criterion for distinguishing type II and type III isotherms. In the present study, KGDW was higher than unity for all treatment options. Therefore, all isotherms were classified as type II.

Sorption hysteresis was quantified with the hysteresis loop (H), the maximum difference of equilibrium moisture content for desorption and adsorption (ΔEMC) and corresponding relative humidity (RH) (Majka et al. 2016). The determined ΔEMC and corresponding RH values accounted for the EMC data obtained from the absorption isotherms being determined from the dry state and the scanning desorption isotherm initiated from RH of 95%. Therefore, the ΔEMC values were used for comparing the hysteresis phenomenon for each option of the sorption experiments. The estimated coefficients of hysteresis are presented in Table 3. Thermal modification significantly reduced hysteresis in both fractions of beech wood dust, as measured using the hysteresis loop. The significant influence of thermal modification on sorption hysteresis was also supported by values of the maximum difference of equilibrium moisture content for desorption and adsorption (ΔEMC). This estimator clearly indicated much greater influence of thermal modification on sorption hysteresis in wood dust, compared to solid wood. The phenomenon was found for both wood dust size fractions.

Table 3 Sorption hysteresis loop (H), maximum difference of equilibrium moisture content for desorption and adsorption (ΔEMC) and corresponding relative humidity (RH) for unmodified and thermally modified beech wood dust fractions at 25 °C
Full size table

Water diffusivity

Water diffusivity was studied for four sets of sorption experiments, i.e., for two size fractions of wood dust from untreated and thermally modified material. The values of the equivalent spherical diameter (d) of wood dust particles, as determined using MaScontrol software, were used to determine diffusivity according to the concept proposed by Ritger and Peppas (1987) for analyzing diffusion processes in particles of different sizes. The sets of input data for diffusivity determination were collected from 15 adsorption sub-processes. Adsorption isotherms obtained in the present study were used to design experiments in which changes in RH were selected so that each adsorption sub-process corresponded to a uniform range of wood dust moisture contents of ca. 0.01 kg/kg. The procedure enabled determination of the dependence of diffusivity on moisture content (Fig. 3).

Fig. 3
figure 3

Water diffusivity of unmodified and thermally modified beech wood dust (< 25 µm fraction—top and 80–250 µm fraction—bottom) as a function of moisture content (measured at 25 °C)

Full size image

The large number of observations of water content over time within the sorption sub-experiments allowed us to obtain high accuracy when fitting data to Eq. (3) and in determining water diffusivity. Much higher values of diffusivity were found for larger particles (Fig. 3, Table 4). This was consistent with the results of GAB model analysis, as CGAB values were lower for the 80–250 µm fraction. This was interpreted as indicative of lower mobility of water molecules in the monolayer in larger wood dust particles.

Table 4 Maximum values of diffusivity for unmodified and thermally modified beech wood dust fractions at 25 °C
Full size table

The highest values of diffusivity were found for the lowest values of moisture content, when water molecules were primarily bound to primary sorption sites. This was observed for both size fractions and for untreated and thermally modified wood. As moisture content increased and formation of the water monolayer proceeded, diffusivity significantly decreased until reaching a moisture content of ca. 0.06 kg/kg. This threshold corresponds to the maximum content of water bound to primary sites (mGDW) in the GDW model, estimated during adsorption (Table 2). After the monolayer was completely formed, there was a less significant decrease in diffusivity. This marked the beginning of the formation of additional layers of water. The decrease in diffusivity practically stopped at a moisture level of ca. 0.09 kg/kg. At higher moisture contents, diffusivity was fairly constant, which was probably related to decreased availability of secondary sorption sites with increasing moisture content and its influence on slowing diffusion rates.

The changes in diffusivity as a function of moisture content were found for both size fractions of wood dust as well as for untreated and thermally modified material. However, high differences in diffusivity were found for wood dust based on size. The influence of the size of wood dust was quantified by the ratio of the maximum values of diffusivity for the largest and smallest particles. Values of this ratio were calculated for data shown in Table 4, being equal to ca. 40 for untreated wood dust and ca. 30 for thermally modified material. Similar relations were reported for untreated wood dust at different temperatures during adsorption experiments (Majka et al. 2019).

The influence of thermal modification on water diffusivity was not clear. This probably was due to the fact that the diffusion model assumes wood dust particles were spherical, while the actual shapes of particles highly deviate from this assumption. It was previously found that the shape of wood dust particles is diverse, including irregular, conical, rectangular, cylindrical and spherical shapes (Gómez Yepes and Cremades 2011). Mazzoli and Favoli (2012) used scanning electron microscopy to determine size and shape of wood dust from different softwood and hardwood species. Their results confirmed that dust particles have a range of complex shapes, with spherical shape not predominant.

Another possible reason for uncertainty about diffusivity is related to the first kind boundary condition used in the model proposed by Ritger and Peppas (1987). The boundary condition assumes that hygroscopic equilibrium is instantly obtained at the surface of wood dust particles. Olek et al. (2016) previously reported that thermal modification alters the mechanism by which wood achieves hygroscopic equilibrium. Unfortunately, it was not possible in the present analysis to consider the already developed concept of the modified convective boundary condition, which incorporates a relaxation term. Moreover, Olek et al. (2016) found that thermal modification was responsible for increased non-Fickian behavior, so that the simplest diffusion models were unable to satisfactorily describe non-Fickian processes.

Conclusion

Dynamic sorption experiments of beech wood dust from untreated and thermally modified material were an effective and accurate approach to obtain adsorption and desorption isotherms. Adsorption isotherms were used to design another set of sorption experiments for collecting data to estimate water diffusivity. The analyses led to the following conclusions:

  1. 1.

    Thermal modification significantly decreased equilibrium moisture content of both smaller and larger size fractions of wood dust. The decrease was primarily caused by reduced primary sorption sites, as indicated by values of Mm and mGDW in the GAB and GDW models, respectively. The hypothesis of reduced wood dust hygroscopicity due to thermal modification was also supported by stronger binding of water molecules in the monolayer, as shown by CGAB values. The hygroscopic properties of dust obtained from thermally modified wood were significantly different compared to dust from untreated material. Therefore, the interactions between thermally treated wood dust and moist air will influence dust transport and filtration. These factors should be accounted for when designing, improving and controlling wood dust removal processes.

  2. 2.

    The relation between thermal modification and water diffusivity was not clearly established. This was probably the result of the model applied to describe water diffusion in wood dust, which assumes the geometry of dust particles is spherical. However, dust particles have diverse shapes and may be irregular, conical, rectangular, cylindrical and spherical. Another problem related to the modeling of water diffusion in wood dust is the assumption of the first kind boundary condition. The instantaneous hygroscopic equilibrium of dust particles has to be questioned, even for small particles of wood dust and especially those from thermally modified material, because thermal modification alters hygroscopic equilibrium. The model used to estimate water diffusion in wood dust particles did not allow consideration of a convective boundary condition to account for non-Fickian behavior.

  3. 3.

    Decreased water diffusivity with increasing moisture content was significant only from the dry state to the maximum water content for water binding to primary sites, i.e., over the range of monolayer sorption. For water molecules being linked to the secondary sorption sites, water diffusivity was largely independent of moisture content. This relationship was found for all experimental options tested in sorption experiments, i.e., for untreated and thermally modified material and for small and large dust fractions. Therefore, wood dust filtration can be significantly influenced only for wood dust at lowest moisture contents, while the majority of abrasive sanding processes are carried out for wood with moisture content higher than ca. 7–8%, at which there is limited influence of water–dust interactions. Another factor influencing filtration processes is particle size: The finest particles (wood dust fraction < 25 µm) had lower water diffusivity, being an order of magnitude less compared to wood dust particles of 80–250 µm diameter.