Introduction

Modeling of bound water diffusion in wood is most often required for investigations into wood drying, moisture buffering by timber constructions, etc. The quality of results of the modeling primarily depends on the structure of the model as well as on the values of wood properties represented by the mathematical model coefficients. The second Fick’s law, a combination of the Fick’s law of diffusion and the mass conservation equation, is usually used for the mathematical description of the transient bound water diffusion. However, in some cases, Fick’s law is unable to properly describe the diffusion. Therefore, some attempts were made to modify this law by introducing the diffusion coefficient dependence on bound water content (e.g., Simpson 1993; Simpson and Liu 1991).

Another problem related to the mathematical description of bound water diffusion in wood was related to the formulation of the boundary condition. It has already been recognized that wood surface being in contact with moist air is gradually approaching equilibrium moisture content (e.g., Skaar 1988). Therefore, the first kind boundary condition was considered as not valid in the case of bound water diffusion in wood. The problem was already mentioned in earlier studies on the diffusion coefficient determination (Comstock 1963; McNamara and Hart 1971; Stamm and Nelson 1961). It was only partially solved by introducing the third kind boundary condition, which assumed the convective vapor transfer in the near-surface layer of moist air. Therefore, the convective boundary condition has often been used in diffusion modeling. In order to improve the accuracy of the modeling, the analytical methods for the identification of the surface emission factor and diffusivity were developed (Choong and Skaar 1969, 1972).

However, Söderström and Salin (1993) reported experimental results that indicate the existence of the additional influence of porous and hygroscopic properties of wood on the surface emission factor. They also criticized the structure of the convective boundary condition with respect to the dependence of the equilibrium moisture content on temperature. Their statements were based on the erroneous assumption that the diffusion may be applied for modeling free and bound water transfer in wood, i.e., for moisture content values above fiber saturation point. An alternative approach for defining the boundary condition was proposed by Nakano (1994a, b). It was a modification of the first kind boundary condition, assuming that wood surface exponentially approached the equilibrium with moist air. Babiak (1995) discussed the proposed modification of the boundary condition and stated that the approach is frequently used to describe the process of obtaining equilibrium by different thermodynamic systems. Söderström (1996) compared the changes of surface moisture content with time as calculated for the convective boundary condition and the modified first kind boundary condition. The results showed significantly different character of approaching the equilibrium obtained for the two options.

Hrčka and Babiak (1999) studied a possible application of the modified first kind boundary condition for the diffusivity identification using the analytical solution of the diffusion problem. The accuracy of the identification was compared for the following boundary conditions: the first kind, the third kind, and the modified first kind with the wood surface exponential approach to the equilibrium. The worst accuracy of the identification was obtained for the unmodified first kind boundary condition. Practically, the same accuracy of the identification was obtained for the third kind and the modified first kind boundary conditions.

As reported in the literature, the choice of the relevant boundary conditions is an important question. Some works, due to applying analytical solutions, were limited by the difficulties in accounting for the dependency of the mass diffusivity with moisture content, the resistance to mass diffusion at the interface, or the coupling between heat and mass transfer. However, the choice of the boundary conditions can pose more serious questions. Among those is the deviation of material behavior from the linear Fickian diffusion. Such non-Fickian behavior was reported in the past years for polymers (Crank 1953; Long and Thompson 1955; Newns 1959). The deviation from Fick’s law can be seen in the expression of at least two time constants in the transient diffusion. The first one corresponds to the classical diffusion, whereas the second could be explained by the mobility of macromolecules, allowing for a configuration relaxation when the change in bound water molecules produces shrinkage or swelling. Similar results were also reported in the case of diffusion in wood, which is a composite of biomacromolecules (Wadsö 1993, 1994).

The recent progress in the development of numerical methods for the identification of material properties encouraged us to apply the finite element inverse approach to identify coefficients for the bound water diffusion model. The main objective of this study was to modify the boundary condition of the transient diffusion problem by implementing a relaxation equilibrium term, in order to increase the accuracy of the inverse and the direct modeling of diffusion.

Methods

Experimental data

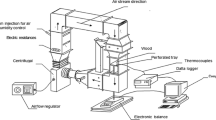
The sorption experiments were made in a setup designed and built in LERFoB, AgroParisTech, Nancy France (Perré et al. 2007). In the setup, the concept of a magnetic suspension balance was used. The balance was placed outside the main chamber of the setup in which a wooden sample was in contact with flowing moist air of controlled characteristics. The application of magnetic suspension resulted in increasing accuracy of mass measurements, eliminating air leakage through the chamber casing, and performing sorption experiments in temperatures beyond the range of balance operation. The air relative humidity inside the chamber was precisely controlled by mixing flows of dry and saturated air. A set of five-step changes in relative humidity was programmed for a single sample. In an adsorption experiment, a sample was initially equilibrated in dry air (i.e., relative humidity was equal to 0%) and then the stepwise change of relative humidity was made in order to obtain 18%. After mass increase in a sample was no longer observed (i.e., equilibrium was attained by a sample), air relative humidity was increased to 36%. The same procedure was repeated to obtain 54, 72, and 90% of relative humidity. The air temperature was constant during all phases of an experiment and was equal to 50°C.

In the present work, results obtained for beech wood were used. The thickness of samples was equal to 1 mm. It corresponded to either the tangential or the longitudinal directions depending on the test. The sides of the samples were sealed by covering them with two layers of an epoxy resin in order to obtain one-dimensional mass transfer only (Baronas and Ivanauskas 2002, 2004). Changes in the sample mass were recorded at constant time instants. The maximum load of the balance was 80 g with the weighing resolution of 0.01 mg and the reproducibility of ±0.02 mg.

Mathematical model

The mathematical structural model of the transient bound water diffusion was represented by the partial differential equation of the form:

$$ {\frac{\partial M}{\partial t}} = {\frac{\partial }{\partial x}}\left( {D{\frac{\partial M}{\partial x}}} \right),\quad (x,t) \in \Upomega \times \left( {0,t_{\text{F}} } \right] $$
(1)

with the initial condition

$$ M\left( {x,0} \right) = M_{0} ,\quad x \in \overline{\Upomega } $$
(2)

and the convective boundary condition:

$$ \left( { - D{\frac{\partial M}{\partial x}}} \right) = \sigma \cdot \left[ {M\left( {x,t} \right) - M_{\infty } } \right],\quad (x,t) \in \Upomega \times \left( {0,t_{\text{F}} } \right] $$
(3)

The convective boundary condition was used here for the description of the bound water diffusion in spite of the fact that the Biot number was higher than 10 for the majority of the analyzed options of the identification. In such cases, it is a typical approach to apply the first kind boundary condition that implies obtaining instant hygroscopic equilibrium at wood surface. However, for a sudden step of the external conditions, the boundary condition of the first kind would produce an infinite flux at time zero. Therefore, the external mass transfer resistance (i.e., surface emission coefficient) has a special importance at short times of the diffusion process. As the identification of the coefficients of the diffusion model was made for the entire processes, i.e., for the initial and the final phases, the convective boundary condition was applied to take into account the external mass transfer resistance.

The equilibrium bound water content (M ∞) used in the convective boundary condition was also modified in order to account for the exponential approach of the wood surface moisture content to the equilibrium with moist air. The modification proposed here is given in the following form:

$$ M_{\infty } = c + d \cdot \left[ {1 - \exp \left( { - t/\tau } \right)} \right] $$
(4)

This expression considers attaining the hygroscopic equilibrium as a process, i.e., it takes into account the time period for reorganization of wood ultrastructure due to bounding of water molecules during adsorption. Hill et al. (2010) reported that wood drying results in changes in cellulose ultrastructure due to the formation of intrachain hydrogen bonds. It was also shown that these bonds were partially broken during the course of water adsorption, and therefore, sorption sites were gradually becoming available for sorption. The reorganization of the wood ultrastructure in relation to sorption processes was also reported by Bonarski and Olek (2006). Additionally, Hartley et al. (1991) suggested that during sorption processes not only wood components changed the ultrastructure but also bound water molecules might form water clusters. In Eq. 4, coefficient c represents the equilibrium moisture content before macromolecule relaxation, coefficient d is the additional amount of bound water molecules allowed by relaxation and reorganization of already sorbed water (e.g., Olsson and Salmén 2004; Rawat and Khali 1998), and τ is the relaxation time resulting from macromolecules and water mobility. The expression proposed in the present work does not follow the model proposed by Crank (1953). The Crank model consisted of imposing an exponential variation of the surface moisture content and the expression of the authors allows for distinguishing between the resistance to mass transfer and the relaxation time due to the evolution of available sorption sites.

Inverse identification

The operational form of the direct diffusion model (1)–(4) was developed by the finite element approximation with an iterative procedure to deal with the quasi-linearity of equations and the recurrence scheme in time (Weres et al. 2009). The model was supplemented by the empirical submodels for the diffusivity:

$$ D = D_{0} $$
(5)
$$ D = D_{0} \cdot \exp \left[ { - a \cdot M\left( t \right)} \right] $$
(6)

where D 0 and a were the estimated coefficients. The equilibrium bound water content at the hygroscopic equilibrium (M ∞) was an additional parameter estimated in all options of the inverse analysis. The identification options as well as the estimated coefficients are illustrated in Table 1. The inverse identification comprised solving the direct diffusion problem controlled by the optimization procedure. In the algorithm of solving the direct problem, the procedure for calculating the average predicted bound water content M pred(t) was used. The average values were obtained for each time instant from all predicted nodal values of the bound water content in the geometrical domain. The applied approach allows for comparing the time evolution of the experimental and predicted global moisture contents and using them in the procedure for the coefficients estimation.

Table 1 Identification options applied in the inverse analysis of diffusivity
Full size table

The objective function was defined as the sum of the squares of the residuals of the measured and predicted global values of the bound water content

$$ S = \sum\limits_{i = 1}^{{{\text{NT}}_{\exp } }} {w_{i} \left[ {M_{ \exp } \left( {t_{i} } \right) - M_{\text{pred}} \left( {t_{i} } \right)} \right]}^{2} $$
(7)

As the experimental data were registered for constant time instants, constant weight values w i would result in overestimation for large instants in this case of the transient diffusion which is linear as a function of the square root of time. Instead of constant values, the weighting function should therefore be the highest at the beginning of the process and then it should decrease along with the process. Finally, the following expression was used, relevant for the diffusion process examined in this paper:

$$ w_{i} = \sqrt {t_{i} + \Updelta t} - \sqrt {t_{i} } $$
(8)

The optimization procedure was used to minimize the objective function (7). It was developed on the basis of the trust region algorithm combined with the secant-updating quasi-Newton procedure to approximate the Hessian (Weres et al. 2009). The inverse identification approach was implemented and coded in Lahey/Fortran 95 environment.

Results

The inverse identification of bound water diffusion in beech wood was made for three sets of processes: (a) adsorption in the radial direction, (b) adsorption in the longitudinal direction, and (c) desorption in the longitudinal direction. Each set of diffusion processes consisted of five stages with step changes of air relative humidity. The analysis was made separately for each stage and each identification option listed in Table 1. In the models chosen (Table 1), each analysis step represents an amount of 18 coefficients to be fitted. As a result, the total number of the identified coefficients describing the diffusivity and boundary condition amounted to 270. Therefore, only selected results were presented in the paper. The full results of identification for adsorption in the tangential direction are shown in Table 2, while the values presented in Table 3 concern the coefficients obtained for the three sets of processes and the highest values of bound water content in which non-Fickian diffusion could be expected. The estimated bound water content changes in time were compared with the data obtained from sorption experiments (Figs. 1, 2, 3, 4, 5, 6, 7).

Table 2 Values of the coefficients estimated by the inverse method (tangential direction, adsorption)
Full size table
Table 3 Values of the coefficients estimated by the inverse method (highest air relative humidity values)
Full size table
Fig. 1
figure 1

Comparison of estimated and measured bound water contents, tangential direction, adsorption, air relative humidity change 0–18%, identification options (i) and (iii)

Full size image
Fig. 2
figure 2

Comparison of estimated and measured bound water contents, tangential direction, adsorption, air relative humidity change 36–54%, identification options (i) and (iii)

Full size image
Fig. 3
figure 3

Comparison of estimated and measured bound water contents, tangential direction, adsorption, air relative humidity change 72–90%, identification options (i) and (iii)

Full size image
Fig. 4
figure 4

Comparison of estimated and measured bound water contents, longitudinal direction, adsorption, air relative humidity change 72–90%, identification options (i) and (iii)

Full size image
Fig. 5
figure 5

Comparison of estimated and measured bound water contents, longitudinal direction, desorption, air relative humidity change 90–72%, identification options (i) and (iii)

Full size image
Fig. 6
figure 6

Comparison of estimated and measured bound water contents, longitudinal direction, desorption, air relative humidity change 90–72%, identification options (i) and (ii)

Full size image
Fig. 7
figure 7

Comparison of estimated and measured bound water contents, longitudinal direction, desorption, air relative humidity change 90–72%, identification options (iii) and (iv)

Full size image

In order to quantify the quality of the estimation, two errors were defined and calculated (e.g., Olek and Weres 2007), i.e., the local relative error (e 1)

$$ e_{1} \left( {t_{i} } \right) = 100{\frac{{\left| {M_{\exp } \left( {t_{i} } \right) - M_{pred} \left( {t_{i} } \right)} \right|}}{{M_{\exp } \left( {t_{i} } \right)}}},\quad i = 1, \ldots ,{\text{NT}}_{\exp } $$
(9)

and the global relative error (e 2)

$$ e_{2} = 100{\frac{{\sqrt {\sum\nolimits_{i = 1}^{{{\text{NT}}_{ \exp } }} {\left[ {M_{ \exp } \left( {t_{i} } \right) - M_{\text{pred}} \left( {t_{i} } \right)} \right]}^{2} } }}{{\sqrt {\sum\nolimits_{i = 1}^{{{\text{NT}}_{ \exp } }} {M_{ \exp } \left( {t_{i} } \right)^{2} } } }}} $$
(10)

Each plot presented in Figs. 1, 2, 3, 4, 5, 6, 7 contains estimated values of bound water content for two identification options only. It allowed for analyzing the influence of different factors on the quality of the identification. As the primary objective of the paper was to study the role of modification of the convective boundary condition for the diffusion problem, Figs. 1, 2, 3 show the comparison of results obtained for the adsorption in the tangential direction as well as identification options (i) and (iii), i.e., the constant value of the diffusivity and unmodified and modified boundary conditions. A significant improvement of the identification was observed after the application of the boundary condition modified by Eq. (4). The improvement can be seen in Figs. 1 and 2 when analyzing results of the diffusion modeling for the step changes of the air relative humidity of 0-18% and 36–54%, respectively. The global relative error (e 2) was used to quantify the improvement of the identification. In both analyzed cases, the e 2 error was reduced by ca. four times after the application of the modified convective boundary condition. However, the same comparison was made for the air relative humidity change of 72–90% (Fig. 3), and the reported differences in results of diffusion modeling and measured values were almost insignificant. It was shown that the e 2 error was only reduced from 0.23 to 0.20%. Indeed, for this step of air relative humidity, the experimental data do not depict the relaxation phase. The analysis of adsorption and desorption processes in the longitudinal direction with the use of identification options (i) and (iii) (Figs. 4, 5) showed that the simplest form of the diffusion model, i.e., the model containing the constant value of diffusivity and unmodified convective boundary condition, was again unable to predict the bound water content changes in time appropriately. The modification of the convective boundary condition (identification option iii) was found an efficient way for improving the quality of diffusion identification.

The desorption process in the longitudinal direction was also used to study other futures related to the diffusion model development. It was already shown in our previous studies (e.g., Olek et al. 2005, Olek and Weres 2007) that the application of the diffusivity submodels accounting for the bound water content dependency and the unmodified convective boundary condition was improving the diffusion prediction. Unfortunately, the process was not studied for high values of the air relative humidity in which more pronounced non-Fickian diffusion could be expected. The comparison of the results presented in Fig. 6 clearly shows that the application of the diffusivity dependent on water content only insignificantly improved the prediction. The reduction of the e 2 error was small, i.e., from 0.84 to 0.66%. That observation can be supported by the analysis of the results presented in Fig. 7, i.e., for desorption in the longitudinal direction with identification options (iii) and (iv). The insignificant improvement of the prediction was found after introducing the diffusivity dependence on bound water content. The global relative error values were the same for both analyzed options of the diffusion modeling. Some additional studies for high values of the bound water content are required in order to get more general observations. It should therefore be emphasized that the non-Fickian behavior was more adequately modeled by the authors` modification of the convective boundary condition than the moisture content dependency of the mass diffusivity. Even though additional experimental results would be required for clear conclusions to be drawn, one may note that the non-Fickian term, represented by the coefficient d, tends to increase at high relative humidity, which is consistent with the data published by Wadsö (1993, 1994).

Conclusion

  1. 1.

    In order to account for the relaxation time associated with the equilibrium moisture content, a new formulation for the convective boundary condition was proposed for the bound water diffusion in wood. The original software for the inverse finite element analysis of heat and mass transport was appropriately modified.

  2. 2.

    The application of the modified convective boundary condition significantly improved the accuracy of the identification of the diffusion model coefficients.

  3. 3.

    The non-Fickian water diffusion in wood can be efficiently modeled when taking into account the diffusion coefficient dependency on moisture content and time-dependent equilibrium water content.

  4. 4.

    Some results are still to be confirmed using additional data, but it seems that the non-Fickian behavior, as predicted by the identifications, increases at high relative humidity values.