Abstract
Various studies on wood adhesives filled with conductive fillers for future application to structural monitoring showed a piezoresistive (resistance change with strain) response of the adhesive bond lines that is measurable under direct current. The results also showed a relatively high signal noise with low sensitivity. Using impedance spectroscopy as a measurement technique, the improvements in frequency-dependent piezoresistivity over DC (Direct Current) resistography of multifunctional bonded wood were studied. Beech specimens were bonded by one-component polyurethane prepolymer (1C-PUR) filled with carbon black and tested under shear load. The quality of the piezoresistive properties was described by calculating the signal-to-noise ratio (SNR) of the measured signal. A setup-specific frequency band with optimized SNR between 100 kHz and 1 MHz could be derived from the measurements. Several frequencies showed a signal with higher quality resulting in a higher SNR. Regardless of the variations in impedance spectra for all specimens, this frequency band provided several frequencies with improved signal quality. These frequencies give a more reliable signal with lower noise compared to the signal from DC resistography.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The use of wood adhesives as piezoresistive (resistance change with strain) sensor elements in engineered timber has been the focus of several previous studies conducted by the research group madera wood research (Winkler et al. 2020a, b; Winkler and Schwarz 2014, 2016). In these studies, adhesive joints between two wooden adherents—the bond line—have been modified by adding electrically conductive filler. Subsequently, the change of electrical properties could be used for measuring stress/strain differences. In contrast to the present study, the past work only used resistance under direct current as the leading sensory property. The long-term objective of these adhesive-based sensor elements is to provide affordable control and monitoring insights into the health of engineered timber under strain changes due to irregular loads as well as into moisture-induced changes of the wood’s material stiffness.
In 2015, it was reported that no state of the art in structural monitoring of timber construction exists (Kurz 2015), which could improve the durability of the construction and optimize maintenance. The main methods in non-destructive testing for assessment of timber structures have been summarized (Kasal and Tannert 2010; Kurz and Boller 2015), but are rarely used for long-term monitoring of structures. Several assessment techniques are in use to continuously prove public construction sites like bridges, but these assessments require ongoing investment. In contrast, monitoring methods have higher investment costs in the beginning and lower ongoing costs, while the integration of sensors into the monitored structure is needed (Adams 2007). Since the integration of discrete sensors can be very time consuming and is mostly done after production, the hurdle to use monitoring in timber constructions is still high. The utilization of the adhesive, which is generally used for production, can help at this point. The integration of the piezoresistive adhesive into the manufacturing process is easier and can be used to monitor locations inside the engineered timber element. Hence, bond lines in wood with high sensitivity (relative change with monitored stress) and reliability (small variability of the measured signal) are necessary.
The sensitivity of the sensor elements mainly originates in the compressibility differences between the filler material and the polymer, combining a theoretically dielectric polymer with electrical conductive filler material and thus creating a mostly linear and reversible change in the electrical resistance under strain (Dharap et al. 2004; Ferreira et al. 2013; Ferrreira et al. 2012; Hu et al. 2008; Li et al. 2008; Luheng et al. 2009; Pham et al. 2008).
The electrical conductivity and permittivity and therefore the electrical properties of dielectric polymers filled with conductive filler particles rely on four theoretical assumptions (Bao et al. 2012; Davidson 2005; Elhad Kassim et al. 2015; Elimat et al. 2010; Li et al. 2008; Sanli et al. 2016; Xia et al. 2017), which are also relevant for the change of electrical resistance under stress (Fig. 1). The four assumptions are the intrinsic electrical resistance of a conductive particle itself (1), the contact resistance of contacting particles (2), the tunneling effect between conductive particles which are not touching (3), and micro-capacitors formed through the Maxwell–Wagner-Sillars polarization in the interfaces between conductive particles (4), if insulating polymer can be found between two conductive particles (Elimat et al. 2010; Sanli et al. 2016; Sanli and Kanoun 2020; Xia et al. 2017). The impedance measured by impedance spectroscopy for a range of frequencies can be written as \(Z = Z^{\prime } + iZ^{{\prime \prime }}\) in the Cartesian form for each frequency, where Z′ is the real part (Re(Z)) and Z″ is the imaginary part (Im(Z)) of the impedance (Elimat et al. 2010; Sanli and Kanoun 2020). Compared to the DC-resistance the impedance for alternating current takes phase differences into account and can be carried out for different frequencies (Elimat et al. 2010; Sanli and Kanoun 2020) which gives the ability to receive more information on the electrical characteristics of the examined material. The effects (1) to (3) can be measured in the real part of the complex impedance (Xia et al. 2017), which describes the dissipation of electrical energy as thermal energy and includes all ohmic parts (Funke 1993). On the contrary, effect (4) can be measured in the imaginary part of the complex impedance (Elimat et al. 2010; Sanli et al. 2016; Sanli and Kanoun 2020; Xia et al. 2017) which describes the amount of electrical energy stored in the material containing induction and capacitance (Funke 1993).
Schematic visualization of the four mechanisms theoretically responsible for the change of electrical resistance in the bond line under stress. (1) Intrinsic electrical resistance of a conductive particle/aggregate itself. (2) Contact resistance of two contacting particles/aggregates. (3) Tunneling resistance between two conductive, but not touching particles/aggregates. (4) Micro-capacitors formed through Maxwell–Wagner-Sillars polarization in the interfaces between conductive particles/aggregates. The shapes of carbon black are shown according to Chang et al. (2012) (colour figure online)
In theory, the strain-dependent electrical resistance originates in the change of these four mechanisms, when the geometry of the polymer sample is deformed (Ferreira et al. 2013). Through the deformation of a conductive filler particle, it shows a change of its intrinsic resistance (Dharap et al. 2004; Elimat et al. 2010; Kang et al. 2006; Sanli et al. 2016; Zhang et al. 2006). In addition, the deformation of the conductive polymer could lead to changes in the mean filler distance which can separate two directly contacted particles (Park et al. 2008; Pham et al. 2008; Sanli et al. 2016; Yin et al. 2011) leading to increasing resistance. Furthermore, the change in distance between conductive particles affects the energy needed for the tunneling effect (Hu et al. 2008; Park et al. 2008; Sanli et al. 2016; Wichmann et al. 2009; Yasuoka et al. 2010; Yin et al. 2011). It also is possible that the change in distance exceeds or undercuts the maximal distance for the tunneling effect, whereby tunneling becomes possible or impossible. Therefore, the number of existing conductive paths decreases or increases. Additionally, the capacitance of the bond line can be altered through deformation by changing the distance between the particles separated through the insulating polymer matrix (Elimat et al. 2010; Sanli et al. 2016; Xia et al. 2017). These mechanisms creating the piezoresistive response can be measured in different frequency ranges between 20 Hz and 10 MHz according to the literature (Elimat et al. 2010; Xia et al. 2017). Impedance spectroscopy can be used to identify optimal frequencies with high signal quality and reliability in electrically conductive bond lines. The described mechanisms react to different applied frequency ranges in the measured signal to a varying extent (Sanli et al. 2016; Sanli and Kanoun 2020; Xia et al. 2017). Thus, this research study focuses on the piezoresistive response of bonded wood samples at various frequencies under compressive shear load as one of the critical load situations in timber engineering, for example shear load at the end face or inclined cut of curved glulam beams. Carbon black (CB) as opposed to carbon nanotubes (CNT) was used because of its higher sensitivity based on the findings from Winkler et al. (2020a).
Materials and methods
Sample preparation
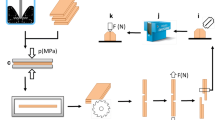
Figure 2 illustrates the process of producing the specimens, whereby defect-free lamellas of beechwood (Fagus sylvatica L.) were cut in pairs and conditioned for 14 days at 20 °C and 65% RH (20/65). Electrically conductive filler (Ketjenblack EC-300 J, Akzo Nobel Functional Chemicals B.V., Arnhem, Netherlands/Agglomerate size before dispersion 50 to 200 μm, primary aggregate size before dispersion 100 to 1000 nm, primary particle size of 30 to 50 nm according to data sheet) was dispersed into a one-component polyurethane prepolymer (Laboratory-Sample 1506-PV, Jowat, Detmold, Germany) by using a dissolver (Dispermat CV-SIP, VMA-Getzmann GMBH, Reichshof, Germany). A filler content of 4 wt% (≙ 25.35 vol%) was chosen, positioned at the upper limit of the percolation threshold area (2 wt% to 4 wt%) for this polymer-filler combination (Winkler et al. 2020a, 2020b) to reliably reach a usable sensitivity and at the same time a high reproducibility (Sanli et al. 2017). Based on the findings from Winkler et al. (2020b) that signal quality rises with rising amount of conductive adhesive, an amount of 640 ± 19.3 g/m2 of electrically conductive adhesive was applied to two pairs of lamellas using a glass scraper. Afterward, the two bonded beech lamellas were pressed in a laboratory press next to each other under a pressure of 0.9 MPa for 240 min at room temperature and were then stored in standard climate (20 °C/65% RH) for approximately 14 days. Nine samples of 60 mm × 20 mm × 10 mm were cut from the center of the lamellas according to DIN EN 302–1:2013–06 and formatted into the geometry that is described in Winkler et al. (2020a). To avoid changes in the contact resistance through deformation of the specimen in the contacting area, the shear area has been reduced by cutting two notches with dimensions of 10 mm length, 20 mm width, and 4.9 mm height as shown in Fig. 3 (Chung 2020). The adhesive joint was intact over the entire length of 60 mm but only subjected to compressive shear stress in an area of 40 mm × 20 mm. Finally, silver conductive paint (Leitsilber 200 N, Ferro GmbH, Hanau, Germany) was applied to the front faces of the specimens in the area of the bond line as described before (Winkler et al. 2020a, b)). Five replicas with a total outcome of 43 samples were manufactured and randomized during the test procedure.
Measuring setup
As shown in Fig. 4, the experimental setup for testing the electrical properties under alternating current at different frequencies consisted of an impedance spectroscope (ISX-3, Sciospec Scientific Instruments GmbH, Bennewitz, Germany) (a), connected to the specimen by two spring-loaded ring electrodes (b) via BNC-Cables (RF Cable Assemblies, RG-58C/U, Pomona Electronics Inc., USA) (c). A two-probe and four-wire method was used for the measurement. In this paper, measured values (e.g., Fig. 5) from impedance spectroscopy not only include the impedance values for the measured specimens but also the impedance of the whole measuring setup including the contact resistance between silver conductive paint and bond line or rather the silver conductive paint and the electrode. As the objective is not to provide an impedance spectroscopic analysis of the composite material, the frequency-dependent relative piezoresistive change in the measurements could be characterized instead. To counteract various possible influences on the measured values of impedance spectroscopic measurements (Bulst 2017; Chung 2020; Joffe and Lock 2010), the experimental setup was modified. To minimize the influence of external electromagnetic fields on the measured values, shielded coaxial cables were used, and the exposed electrodes (b) and specimen (d) were shielded by a grounded aluminum-encased box. To avoid distortions through movement in the experimental setup, the impedance spectroscope and the cables were fixed. Shielding ring electrodes were used to neutralize the electromagnetic field between electrodes, which could be disturbed by movements in the direct environment of the experimental setup. Through the usage of spring-loaded ring electrodes, pressure differences in the contact area between electrode and sample were minimized to keep the contact resistance as stable as possible (Chung 2020). Prior to the experiments, it was ensured that a change in pressure between electrode and silver conductive paste of the specimens does not have any influence on the measured values to avoid misleading signal changes by change in contact resistance. Through the conditioning of the specimens in the standard climate (20/65) prior to testing, the effect of the temperature and relative humidity was minimized. The actual testing was carried out under room climate conditions (20/40).
As shown in Fig. 6, this setup was used to measure impedance spectra while applying swelling shear stress to the bond line by applying pressure with a universal testing machine (Zwick/Roell Type 1484, load cell 200 kN, Ulm, Germany). For shear load application, a test setup was adapted from the standardized test for shear in adhesive joints (DIN EN 14,080:2013-09). As no shear test exists without any lateral stress at all, this setup includes transversal tension and transversal compression stress from a torsional moment. For simplification, the stress is labelled compression shear in the whole paper. The swelling shear load was used in earlier studies (Winkler et al. 2020b) with the intention to analyze the repeatability of the piezoresistive response. The swelling load rate of 0.1 Hz, compromising between a time-efficient testing cycle and a real load situation, ranks below the typically applied dynamic load rate, but above the quasi-static load. Typical load situations at these frequencies could be loads from wind-induced vibration as well as railroads and cars on bridges. A cyclic load over ten cycles has been applied in section I, changing from a basic load of 0.05 MPa to 0.25 MPa and back within 10 s (stress-controlled mode with a speed of 0.04 MPa/s) without leaving the elastic regime of the beech lamellas to avoid irreversible damage of the material. Section II consists of a relaxation phase for approx. 30 s. Followed by section III, which is equal to section I. Section IV was characterized by a uniform compression shear load at 0.25 MPa for 180 s. The measurements were performed at room temperature with a voltage amplitude of 500 mV over a frequency range from 10 kHz to 10 MHz with 101 log sized steps in between. The measurement range was set to 10 kOhm. For comparability, a four-wire DC-resistance measurement was performed on all samples. A pulsed DC with an amplitude of 1000 mV with a current pulse of \(f_{{{\text{measure}}}} = 100\;~{\text{ms}}\) and a break between every current pulse of \(f_{{{\text{breake}}}} = 50\;~{\text{ms}}\). To keep results comparable, the measurement setup and the environmental setting stayed the same. Only the impedance spectroscope and the cables were replaced by a digital multimeter (NI PXI 4071, National Instruments GmbH, Munich/Germany) and aluminum foil shielded commercial 3 mm cables.
Data analysis
The signal quality was evaluated by the signal-to-noise ratio (SNR) (Carminati 2017) calculated through Equation (1).
a describes the absolute sensitivity of the signal and \({\sigma }_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}\_\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}\) the standard deviation of the measured signal noise. Based on the assumption of a linear reaction of the response signal to the applied stress in the used experimental setup, the standard deviation of the measured signal noise was calculated from the values of the actually measured signal minus the measurement signal smoothed with the locally weighted scatterplot smoothing algorithm (LOWESS-algorithm with a 5 s time frame) (Cleveland 1979). The dividend a was extracted from a nonlinear model function in the form of \(X=a*\tau +b*{t}^{c}+d\) where X is the unit of impedance value (Re(Z) or Im(Z)) as a function of the compressive shear stress (τ) and time (t), by calculating the model parameters with a nonlinear least squares fitting algorithm. As mentioned before, the constant a represents the absolute sensitivity of the signal, b represents the drift factor, c the drift exponent over time and d the constant \({Z}_{0}\) (theoretical impedance base value) at time \({t}_{0}\) and compressive shear stress \({\tau }_{0}\). For further evaluation of the results, the relative standard errors for the constants a, b, c, and d were calculated.
Further, a ratio \({q}_{\overline{\text{SNR}}}\) between arithmetic mean SNR \(\left( {\overline{{{\text{SNR}}}} } \right)\) and relative standard deviation of the \(\overline{{{\text{SNR}}}} ~\left( {\sigma _{{{\text{rel}}{\text{.}}\overline{{{\text{SNR}}}} }} } \right)\) over all samples for each frequency was calculated by Equation (2). This calculated ratio can be used to evaluate the frequencies at which high signal quality and high reliability occur at the same time.
The standard deviation of the \({\overline{\text{SNR}}}\) values needed to be relativized to achieve comparability throughout all frequencies. The frequency with the maximum value for \({q}_{\overline{\text{SNR}}}\) was used to compare the results of the measurement with impedance spectroscopy to the DC resistography (measuring changes in electrical resistance under direct current). The signals measured with direct current were evaluated in the same way as the impedance spectroscopic signals to compare the quality of both modes.
Results and discussion
Figure 7 shows the \({\overline{\text{SNR}}}\) and \({\sigma }_{\mathrm{r}\mathrm{e}\mathrm{l}.{\overline{\text{SNR}}}}\) for each frequency over all measured samples. The real part of the complex impedance shows its highest values in the frequency band of 100 kHz to 1 MHz. These values are at least one third higher than the highest values for the imaginary part of the complex impedance, which occur in the higher frequencies above 8 MHz. The \({\sigma }_{\mathrm{r}\mathrm{e}\mathrm{l}.{\overline{\text{SNR}}}}\) for the real part of the complex impedance has its lowest values in the same frequency band where the \({\overline{\text{SNR}}}\) has its highest values. The imaginary part of the complex impedance, \({\sigma }_{\mathrm{r}\mathrm{e}\mathrm{l}.{\overline{\text{SNR}}}}\) has its lowest values at the same frequencies, where it has its highest values for the \({\overline{\text{SNR}}}\). The strong \({\overline{\text{SNR}}}\) drops at the frequencies 479 kHz and 631 kHz and the step-shaped form in the lower frequencies could depend on measurement system interferences, as reference measurements show similar shapes. Figure 7 further shows that a drop in the \({\overline{\text{SNR}}}\) goes along with a rise of noise in the signal while the sensitivity shows no significant change. This shows that calculating the SNR can be used to compare the sensor characteristics for the generated impedance data in this paper.
Left: Mean SNR and percental relative standard deviation of the SNR for each frequency over all samples for the real- and imaginary part of the complex impedance. Right: Examples of measured signals at two different frequencies with relatively different SNR. The spaces between measured points are interpolated
A drift in the measured signal can be seen and has also been reported in several studies (Abu-Abdeen et al. 2016; Kang et al. 2006; Wang and Ding 2010; Winkler et al. 2020b; Zhao et al. 2013). As the specimens are composites of two viscoelastic materials—the polymer-based bond line and the wood itself—it is possible that the drift is generated by the time-dependent material creep or strain hysteresis of the polymer, the wood or both components at the same time (Abu-Abdeen et al. 2016; Hunt 1999). A time-dependent creep or hysteresis can be caused by the relaxation motion speed of the macromolecular chain segments, not matching the change rate of the applied stress (Zhao et al. 2013). These effects could lead to a drifting resistance of the bond line over time because of the contained deformation of the polymer after each loading-cycle while testing the specimen and therefore cause a drifting signal (Abu-Abdeen et al. 2016; Zhao et al. 2013). Moreover, the wooden adherents could cause a drifting signal by applying a transferred stress to the bond line which leads to a creep or hysteresis in polymer deformation. Further, the possibility of an electrically induced signal drift (Chung 2020) must be considered, as measurements on mechanically unloaded specimens show the tendency of a drifting signal over time. Figure 8 gives an example of the relation between the strain of the specimen—measured by the traverse path sensor of the testing machine—and the change in resistance of the real part of the complex impedance over time that most of the measurements show while the gradients are varying with different specimens. The figure also shows the signal of the same specimen without mechanical load over time. The strain of the specimen shows a decent creep while keeping the signal of the stress constant in each loading-cycle (see above). The change in the real part of the complex impedance over time shows the same curve shape with a higher gradient. A positive drift also occurs in the signal of the mechanically unloaded specimen (electrically induced drift) which is relatively small compared to the drift of the mechanically loaded test. Nevertheless, the experimental results do not allow a conclusion about the possibly present quantity of material creep in each material of the composite. Further electrically induced drift seems to have an influence on the drifting signal under load at the same time. As other tests show the same creep in measurements of specimens that were not conditioned in a climate of 20 °C and 65% RH prior to testing, it is unlikely that the signal drift is caused by the change in wood moisture content during the testing process in room climate in the test procedure for these experiments. Additionally, the mean DC-resistance of the measurements is 124 kOhm with a standard deviation of 92 kOhm. Specimens produced in the same way, just without any kind of conductive filler, showed an overall resistance above 1 GOhm as also reported in Winkler et al. (2020a). Therefore, the ratio between the measured resistance with and without electrically conductive adhesive is at least 1/4000, resulting in a small part of the beechwood in the overall resistance.
Example of the strain (ε) and the resistance change of the real part over time for a mechanically loaded and a mechanically unloaded specimen at 549 kHz. The spaces between calculated points are interpolated. For better visibility, the signal of the mechanically loaded and unloaded measurements is smoothed by a LOWESS-algorithm
The mostly lower \({\overline{\text{SNR}}}\) for the imaginary part of the complex impedance means a lower change in inductive and capacitive properties of the test setup in comparison to the ohmic resistance change. Since three of the four known mechanisms of the piezoresistive response are measured in the real part of the complex impedance, a signal with higher sensitivity and lower noise in the real part of the complex impedance is most reasonable. In relation to the theory of the four mechanisms of piezoresistive response, it means that either the intrinsic change in resistance of the conductive particles or the change in contact resistance between contacting particles has the greatest impact on the piezoresistive response. This behavior fits to the conductive filler content above the percolation threshold as the arrangement of the particles changes from not contacting particles in the polymer to a larger number of direct contacts between the particles compared to a lower filler content. Thus, the described piezoresistive mechanisms (III) and (IV) are less likely to occur in the percolation network (Chung 2020).
The variation in \({\sigma }_{\mathrm{r}\mathrm{e}\mathrm{l}.{\overline{\text{SNR}}}}\) at different frequency bands shows that not only the value of the SNR is frequency-dependent but also the stability of the SNR values for different samples. The values for p of the real and imaginary parts of the complex impedance at all frequencies are shown in Fig. 9. The local maxima mark the frequencies, optimal for measuring the given specimens. Combining the manufactured specimens and the used test setup, the maximum \({q}_{\overline{\text{SNR}}}\) lies at 548 kHz for the real part and at 8710 kHz for the imaginary part of the complex impedance. The diagram also shows that the real part of the piezoelectric response has a nearly overall higher measurement quality compared to the imaginary part of the complex impedance for this set of samples at its best frequency. The real part of the complex impedance shows lower values for the mean relative standard error for the constants a, b, c, and d in the frequency bands where the real part of the complex impedance additionally has a higher \({q}_{\overline{\text{SNR}}}\) in comparison to the imaginary part of the complex impedance. As a sensor signal, the real part of the complex impedance is more reliable because of the lower values for the constants. Therefore, the frequency-dependent piezoresistive response of the real part of the complex impedance with the highest value for \({q}_{\overline{\text{SNR}}}\) will be used in the following comparison of the piezoresistive reaction measured by impedance spectroscopy and DC resistography. Figure 10 exemplarily shows the measurement of a specimen with DC and the measurement of the same specimen at the optimal frequency of 548 kHz with the impedance spectroscope. Both signals are representing the overall properties of the signal characteristics for each measuring mode. The noise of the piezoelectric response measured by impedance spectroscopy at the optimal frequency is lower compared to the response of the DC-resistance measurement. Furthermore, no clear signal is visible, even in the LOWESS-algorithm smoothed curve.
Of the 43 DC measurements, 19 could not be analyzed because the algorithm was not able to extract the values for the constants a, b, c, and d by the nonlinear regression. With impedance spectroscopy, there was an analyzable signal for each specimen. As shown in Table 1, the \({\overline{\text{SNR}}}\) for the analyzable impedance spectroscopic signals is more than four times higher compared to the \({\overline{\text{SNR}}}\) of the signals generated with DC resistography. Furthermore, for the DC-resistance measurements, the mean relative standard noise is more than three times higher. Besides the higher \({\overline{\text{SNR}}}\) and the lower mean relative standard noise, the mean relative standard errors for the constants a, b, c, and d are significantly lower for the impedance spectroscopic measured signals, as shown in Table 1. The 19 signals from DC measurements that cannot be analyzed led to the conclusion that the received signal shows no clear structure, which means that the signal must be of low quality and is not usable as a sensor signal. Furthermore, the high mean relative standard errors for the regression parameters b, c, and d for the DC-measurement data listed in Table 1, show that the model is not suitable for representing the measurements. In combination with the overall lower mean relative standard errors for the constants, the \({\overline{\text{SNR}}}\) evaluates the measurements with impedance spectroscopy as significantly higher in its quality and reliability. It should be noted that further work is needed to verify if the best frequencies defined in this paper remain the same over a long period of time or are applicable to other material combinations and specimen shapes. Further, experiments would be needed where the measuring setup used (device, cables, etc.) is changed in order to analyze the impact of the testing setup on the frequencies with the highest \({\overline{\text{SNR}}}\).
Thus, changes in the real part of the complex impedance can deliver an overall higher signal quality for the present measuring setup and the specimens used. This could be due to the dominance of the dynamic effects of the conductive mechanisms in the polymer used that are affected due to the change in material stress. In the low-frequency (DC) plateau regime (Funke 1993), static effects of conductivity mechanisms play the dominant role in the conductivity of the material which is captured in the signal including the effects of the conductivity mechanisms 1 to 3 (Elimat et al. 2010; Xia et al. 2017). With rising frequency in the following dispersive regime (Funke 1993), the ratio between static and dynamic effects of the conductivity mechanisms changes, and the dynamic effects of the conductivity mechanisms (the increase in the tunneling possibility with rising frequency (Xia et al. 2017)) gain the dominant role in the signal (Elimat et al. 2010; Xia et al. 2017). With DC resistography, only static effects of the conductivity mechanisms can be measured, whereas measurements with impedance spectroscopy detect dynamic and static effects at higher frequencies at the same time.
In comparison, the practical handling of the DC-resistance measurements is less prone to failure. One reason is that external influences have a smaller impact on DC-resistance measurements compared to impedance spectroscopic measurements. Further, the handling and analysis of the data require more knowledge if measurements are carried out by impedance spectroscopy because the data volume is much higher, and the interpreter needs a wider knowledge of electrodynamic processes in the current state. Additionally, the costs for the impedance spectroscopic devices exceed the costs for DC instruments. The objective of this study was a comparison of different methods for measuring the piezoresistive response of the previously described multifunctional adhesives in wood, which poses some challenges to the use of piezoresistive polymers (Winkler et al. 2020a). Therefore, the present study can only give an overview of the possible gain of impedance measurement. Covering the different influences and aspects associated with piezoresistive bond lines in wood, for example the influence of moisture or density, will be part of future studies. A well-adapted setup of the measurement for later applications to buildings could also avoid the influence of external disruptive factors. This development can only be the objective of further application-related work.
Conclusion
Overall, the results of this study suggest that the usability of electrically conductive wood bond lines for piezoresistive measurements of the engineered structure can be optimized by using frequency-dependent measurements. While with DC resistography, the piezoresistive effect was partly not measurable, the impedance spectroscopic analysis showed a distinctive piezoresistive behavior of each sample, making the technique more reliable for process integrated sensors.
The following conclusions can be drawn from the data and discussion:
-
(1)
Frequency-based measurements can enhance the reliability and usability of multifunctional bond lines in wood compared to DC-based resistography.
-
(2)
The real part of the complex impedance results in more reliable piezoresistive reactions compared to the imaginary part for the discussed data set, which is coherent with theory as the filler degree in the adhesive is above the percolation threshold and therefore the piezoresistive change is based on the assumptions 1 to 3 from the introduction (changes in intrinsic resistance, contact resistance and tunnel effects)
-
(3)
A method using the signal-to-noise ratio (SNR) as well as the calculated \({q}_{\overline{\text{SNR}}}\) was developed to evaluate the quality and reliability of the piezoresistivity of multifunctional bond lines in wood.
Availability of data and material
Available upon request: jesco.schaefer@hnee.de.
Code availability
Available upon request: jesco.schaefer@hnee.de.
References
Abu-Abdeen M, Aboud AI, Ramzy GH (2016) Effect of temperature on creep behavior of Poly(vinyl chloride) loaded with single walled carbon nanotubes. IJSEA 5:112–120. https://doi.org/10.7753/IJSEA0503.1001
Adams DE (2007) Health monitoring of structural materials and components: methods with applications. Wiley, Chichester, UK
Bao WS, Meguid SA, Zhu ZH, Weng GJ (2012) Tunneling resistance and its effect on the electrical conductivity of carbon nanotube nanocomposites. J Appl Phys 111:93726. https://doi.org/10.1063/1.4716010
Bulst M (2017) Impedance spectroscopy basics: choosing the instrumentation. In: Gruden R, Schweiger B, Pliquett U, Carminati M, Büschel P, Strunz W, Günther T, Radschun M, Bulst M, Errachid A, Danzer MA, Wagner N (eds) Advanced School on Impedance Spectroscopy (ASIS). Chair for measurement and sensor technology, pp. 199–217
Carminati M (2017) Advances in high-resolution microscale impedance sensors. J Sens 2017:1–15. https://doi.org/10.1155/2017/7638389
Chang C-C, Su H-K, Her L-J, Lin J-H (2012) Effects of chemical dispersant and wet mechanical milling methods on conductive carbon dispersion and rate capabilities of LiFePO 4 batteries. J Chinese Chem Soc 59:1233–1237. https://doi.org/10.1002/jccs.201200330
Chung DDL (2020) A critical review of piezoresistivity and its application in electrical-resistance-based strain sensing. J Mater Sci 55:15367–15396. https://doi.org/10.1007/s10853-020-05099-z
Cleveland WS (1979) Robust locally weighted regression and smoothing scatterplots. J Am Stat Assoc 74:829. https://doi.org/10.2307/2286407
Davidson T (2005) Conductive and Magnetic Fillers. In: Xanthos M (ed) Functional fillers for plastics. Wiley-VCH, Weinheim, pp 317–337
DIN EN 14080:2013–09 (2013) Timber structures—Glued laminated timber and glued solid timber—Requirements; German version EN 14080:2013. Deutsches Institut für Normung
DIN EN 302–1:2013–06 (2013) Adhesives for load-bearing timber structures - Test methods—Part 1: Determination of longitudinal tensile shear strength; German version EN 302–1:2013. Deutsches Institut für Normung
Dharap P, Li Z, Nagarajaiah S, Barrera EV (2004) Nanotube film based on single-wall carbon nanotubes for strain sensing. Nanotechnology 15:379–382. https://doi.org/10.1088/0957-4484/15/3/026
Elhad Kassim SA, Achour ME, Costa LC, Lahjomri F (2015) Prediction of the DC electrical conductivity of carbon black filled polymer composites. Polym Bull 72:2561–2571. https://doi.org/10.1007/s00289-015-1421-5
Elimat ZM, Hamideen MS, Schulte KI, Wittich H, La Vega A, de, Wichmann M, Buschhorn S, (2010) Dielectric properties of epoxy/short carbon fiber composites. J Mater Sci 45:5196–5203. https://doi.org/10.1007/s10853-010-4557-6
Ferreira A, Martínez MT, Ansón-Casaos A, Gómez-Pineda LE, Vaz F, Lanceros-Mendez S (2013) Relationship between electromechanical response and percolation threshold in carbon nanotube/poly(vinylidene fluoride) composites. Carbon 61:568–576. https://doi.org/10.1016/j.carbon.2013.05.038
Ferrreira A, Rocha JG, Ansón-Casaos A, Martínez MT, Vaz F, Lanceros-Mendez S (2012) Electromechanical performance of poly(vinylidene fluoride)/carbon nanotube composites for strain sensor applications. Sens Actuators A 178:10–16. https://doi.org/10.1016/j.sna.2012.01.041
Funke K (1993) Jump relaxation in solid electrolytes. Prog Solid State Chem 22:111–195. https://doi.org/10.1016/0079-6786(93)90002-9
Hu N, Karube Y, Yan C, Masuda Z, Fukunaga H (2008) Tunneling effect in a polymer/carbon nanotube nanocomposite strain sensor. Acta Mater 56:2929–2936. https://doi.org/10.1016/j.actamat.2008.02.030
Hunt DG (1999) A unified approach to creep of wood. Proc R Soc Lond A 455:4077–4095. https://doi.org/10.1098/rspa.1999.0491
Joffe EB, Lock K-S (2010) Grounds for grounding: a circuit to system handbook. Wiley, Hoboken, New Jersey
Kang I, Schulz MJ, Kim JH, Shanov V, Shi D (2006) A carbon nanotube strain sensor for structural health monitoring. Smart Mater Struct 15:737–748. https://doi.org/10.1088/0964-1726/15/3/009
Kasal B, Tannert T (eds) (2010) In Situ Assessment of Structural Timber. State of the Art Report of the RILEM, Springer, Heidelberg
Kurz JH (2015) Monitoring of timber structures. J Civil Struct Health Monit 5:97. https://doi.org/10.1007/s13349-014-0075-6
Kurz JH, Boller C (2015) Some background of monitoring and NDT also useful for timber structures. J Civil Struct Health Monit 5:99–106. https://doi.org/10.1007/s13349-015-0105-z
Li C, Thostenson ET, Chou T-W (2008) Sensors and actuators based on carbon nanotubes and their composites: a review. Compos Sci Technol 68:1227–1249. https://doi.org/10.1016/j.compscitech.2008.01.006
Luheng W, Tianhuai D, Peng W (2009) Influence of carbon black concentration on piezoresistivity for carbon-black-filled silicone rubber composite. Carbon 47:3151–3157. https://doi.org/10.1016/j.carbon.2009.06.050
Park M, Kim H, Youngblood JP (2008) Strain-dependent electrical resistance of multi-walled carbon nanotube/polymer composite films. Nanotechnology 19:55705. https://doi.org/10.1088/0957-4484/19/05/055705
Pham GT, Park Y-B, Liang Z, Zhang C, Wang B (2008) Processing and modeling of conductive thermoplastic/carbon nanotube films for strain sensing. Compos B Eng 39:209–216. https://doi.org/10.1016/j.compositesb.2007.02.024
Sanli A, Kanoun O (2020) Electrical impedance analysis of carbon nanotube/epoxy nanocomposite-based piezoresistive strain sensors under uniaxial cyclic static tensile loading. J Compos Mater 54:845–855. https://doi.org/10.1177/0021998319870592
Sanli A, Müller C, Kanoun O, Elibol C, Wagner MF-X (2016) Piezoresistive characterization of multi-walled carbon nanotube-epoxy based flexible strain sensitive films by impedance spectroscopy. Compos Sci Technol 122:18–26. https://doi.org/10.1016/j.compscitech.2015.11.012
Sanli A, Benchirouf A, Müller C, Kanoun O (2017) Piezoresistive performance characterization of strain sensitive multi-walled carbon nanotube-epoxy nanocomposites. Sens Actuators A 254:61–68. https://doi.org/10.1016/j.sna.2016.12.011
Wang P, Ding T (2010) Creep of electrical resistance under uniaxial pressures for carbon black–silicone rubber composite. J Mater Sci 45:3595–3601. https://doi.org/10.1007/s10853-010-4405-8
Wichmann MHG, Buschhorn ST, Gehrmann J, Schulte K (2009) Piezoresistive response of epoxy composites with carbon nanoparticles under tensile load. Phys Rev B. https://doi.org/10.1103/PhysRevB.80.245437
Winkler C, Schwarz U (2014) Multifunctional wood-adhesives for structural health monitoring purposes. In: Aicher S, Reinhardt H-W, Garrecht H (eds) Materials and joints in timber structures: recent developments of technology; [contributions from the RILEM International Symposium on Materials and Joints in Timber Structures that was held in Stuttgart, Germany from October 8 to 10, 2013. Springer, Dordrecht, pp 381–394
Winkler C, Schwarz U (2016) Wood Adhesives for Non-Destructive Structural Monitoring. e-J Nondestructive Testing 21:1–8
Winkler C, Konnerth J, Gibcke J, Schäfer J, Schwarz U (2020a) Influence of polymer/filler composition and processing on the properties of multifunctional adhesive wood bonds from polyurethane prepolymers I: mechanical and electrical properties. J Adhes 96:165–184. https://doi.org/10.1080/00218464.2019.1652601
Winkler C, Schäfer J, Jager C, Konnerth J, Schwarz U (2020b) Influence of polymer/filler composition and processing on the properties of multifunctional adhesive wood bonds from polyurethane prepolymers II: electrical sensitivity in compression. J Adhes 96:185–206. https://doi.org/10.1080/00218464.2019.1652602
Xia X, Wang Y, Zhong Z, Weng GJ (2017) A frequency-dependent theory of electrical conductivity and dielectric permittivity for graphene-polymer nanocomposites. Carbon 111:221–230. https://doi.org/10.1016/j.carbon.2016.09.078
Yasuoka T, Shimamura Y, Todoroki A (2010) Electrical resistance change under strain of CNF/Flexible-Epoxy Composite. Adv Compos Mater 19:123–138. https://doi.org/10.1163/092430410X490446
Yin G, Hu N, Karube Y, Liu Y, Li Y, Fukunaga H (2011) A carbon nanotube/polymer strain sensor with linear and anti-symmetric piezoresistivity. J Compos Mater 45:1315–1323. https://doi.org/10.1177/0021998310393296
Zhang W, Suhr J, Koratkar N (2006) Carbon nanotube/polycarbonate composites as multifunctional strain sensors. J Nanosci Nanotechnol 6:960–964. https://doi.org/10.1166/jnn.2006.171
Zhao J, Dai K, Liu C, Zheng G, Wang B, Liu C, Chen J, Shen C (2013) A comparison between strain sensing behaviors of carbon black/polypropylene and carbon nanotubes/polypropylene electrically conductive composites. Compos A Appl Sci Manuf 48:129–136. https://doi.org/10.1016/j.compositesa.2013.01.004
Acknowledgements
This work was supported by the German Government with the “Nachwachsende Rohstoffe” program (FNR, BMEL) under Grant 22005018.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was supported by the German Government with the “Nachwachsende Rohstoffe” program (FNR, BMEL) under Grant 22005018.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schäfer, J., Jager, C., Schwarz, U. et al. Improving the usability of piezoresistive bond lines in wood by using impedance measurements. Wood Sci Technol 55, 937–954 (2021). https://doi.org/10.1007/s00226-021-01311-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00226-021-01311-8