Introduction

Wood is a porous hygroscopic material where moisture exchanges freely depending on the environmental conditions to which it is exposed (Walker 2006; Zelinka et al. 2016). Wood has been used as building material for millennia (Ross 2010). However, some of the principal problems encountered with the use of wood are dimensional instability and durability, when it loses and gains moisture (Hill 2006; Xie et al. 2013). Hence, it is important to understand the wood–water interactions in wood processing and uses. Traditionally, water in wood exists in two main forms: as bound water within the cell wall, and as free water in the cell lumens. The fiber saturation point (FSP) is primarily used to distinguish these forms of water. The term fiber saturation point was originally applied to wood by Tiemann (1906). Siau (1995) paraphrased Tiemann’s definition of FSP as the moisture content at which all the free water was removed, but its cell wall was saturated throughout. However, the above two view points assume an ideal moisture state; thermodynamics indicates that free water will be present when relative humidity is less than 100%. Zelinka et al. (2016) provided an explicit definition of FSP from the perspective of the solution thermodynamics as the chemical potential of bound water equal to the chemical potential of free water. This definition endows the concept of FSP with an explicit physical meaning and also provides a scientific evaluation system for the study of the wood–water relationship.

There are many ways to measure FSP, and the different operational definitions of different methods may result in different FSP values (Zelinka et al. 2016). Conventional methods such as the sorption isotherm (Glass et al. 2017, 2018), compressive strength (Tiemann 1906) and electrical conductivity (Stamm 1929; James 1988) methods were used to estimate the FSP. The FSP determined by these conventional methods ranges from 23 to 33% (Stamm 1971). However, the FSP cannot be estimated accurately using the projection of the isotherm to 100% relative humidity. While the conventional methods give rough estimates of the FSP, the estimated FSP values could still serve for practical applications (Zelinka et al. 2016). In recent years, the dynamic vapor sorption (DVS) method has been used frequently (Jalaludin et al. 2010; Xie et al. 2010, 2011a; Hosseinpourpia et al. 2017) to determine the sorption isotherm. The DVS method provides highly reproducible data and is able to supply precise sorption isotherms over a wide range of relative humidity (Rautkari et al. 2013). Zhang et al. (2018) investigated the water vapor sorption behavior of 14 bamboo species using DVS method, and the FSP ranged from 16.37 to 27.91%. The solute exclusion method and pressure plate technique are also used to estimate FSP, but they give a much higher FSP (about 40%) (Tremblay et al. 1996) than the saturated salt solution method and DVS method. However, the solute exclusion method and pressure plate technique consume long testing times with tedious operations. The FSP determined by differential scanning calorimetry (DSC) is very close to the theoretical definition (Passarini et al. 2017). However, the DSC could not determine the FSP at room temperature (Zelinka et al. 2016). The nuclear magnetic resonance (NMR) technique was used to measure the transverse relaxation times and the relative amounts of bound and free water in wood and pulp and to study the nature of FSP (Riggin et al. 1979). Telkki et al. (2013) reported FSP value of 35% for Pinus sylvestris and 45% for Picea abies as determined by the NMR method. Compared with the disadvantages of small sample quality and the low signal-to-noise ratio associated with the DSC detection, the NMR tube of the NMR method can be adjusted according to requirements, and the NMR tube diameter is up to 150 mm. It can take samples directly from experimental materials, thus ensuring the stability and reliability of the test results.

Rattans are spiny climbing palms mainly distributed in tropical and subtropical regions. Like most monocotyledons, the rattan stem is anatomically composed of vascular bundles embedded in the parenchymatous tissue. In the vascular bundle, the fiber cell wall thickness, the fiber ratio and the vessel element diameter in the meta-xylem have important effects on the initial moisture content and volumetric shrinkage of rattan (Bhat 1991). While rattan canes have long been used by rural people in the manufacturing of baskets, cords and furniture, among many other uses, rattan exhibits certain undesirable properties when subjected to varying moisture levels, such as dimensional instability, mold growth, fungal decay and loss of strength (Shang 2014; Liu et al. 2014). A better understanding of rattan–moisture interactions will help develop effective methods of modifications and treatments to maintain its stability, durability and strength. FSP is the inflection point of the physical and mechanical properties of biomass material. The FSP of wood or chemically modified wood has been well documented (Passarini et al. 2015, 2017). However, there are very limited studies on the FSP of rattan. Therefore, it is important to quantify the FSP of rattan, so that suitable drying processes and safe storage methods in varying conditions could be developed.

The major objective of this study was to quantify the FSP of rattan by means of the low-field nuclear magnetic resonance (LF-NMR) and two conventional methods, namely the saturated salt solution method and the DVS method. The three methods were used to estimate the FSP of Calamus simplicifolius. The differences in FSP values as determined by the three methods were compared and explained.

Materials and methods

Materials

Cane samples of C. simplicifolius were collected from a plantation located in Pingxiang City, Guangxi Province, China. Three mature stems of rattan with an average diameter (D) of 20 mm were selected and collected at the height of 30 cm above the ground. All the samples were prepared from the middle portions of the cane.

Methods

Saturated salt solution method

The sample was cylindrical with a size of D mm (sample diameter) × 40 mm (height). The samples were tested at 9 moisture content levels, and there were 10 samples for each moisture content level. To plot the isotherms, 9 equilibrium points per isotherm were used to correspond to 9 different saturated salt solutions (Table 1). The samples in each saturated salt solution reached the equilibrium when the weight difference was no more than 0.1% in a 24-h interval (Esteban et al. 2015). It took 2 months to plot the sorption isotherms at a constant temperature of 20 °C. After this, the wet weight of the samples was obtained, and the test samples were placed in an oven at 103 °C until they reached the oven-dry weight. The equilibrium moisture content (EMC) was calculated as follows:

$${\text{EMC}} = \frac{{m_{\text{w}} - m_{0}}}{{m_{0}}} \times 100\%$$
(1)

where mw is wet weight (g), and m0 is the oven-dry weight (g).

Table 1 Saturated salt solutions and relative humidity
Full size table

When the oven-dry weight was reached, the adsorption isotherms were plotted. The sorption isotherm was extrapolated to 100% RH to estimate the FSP using the cubic function of one variable (Wang et al. 2010).

Dynamic vapor sorption method

A dynamic vapor sorption apparatus (DVS Intrinsic, Surface Measurement Systems, Ltd., UK) was used to determine the water vapor sorption behavior of the rattan. The rattan samples and reference holders were connected to a microbalance by hanging wires. They were both located in a thermostatically controlled chamber where there was a constant flow of dry nitrogen gas, and another flow of nitrogen containing water vapor was mixed to attain the pre-set RH values (Jalaludin et al. 2010; Hill et al. 2012; Popescu and Hill 2013). The sorption RH was changed in steps of 10% RH from 0 to 95% RH at a constant temperature of 25 ± 1 °C. The measurements were only taken from the adsorption process of water vapor for approximately 1.5 days. The instrument maintained the sample at a constant RH until the weight change was less than 0.002% per minute over a 10 min period (Popescu et al. 2014). Data on mass change were acquired every 20 s. The running time, target RH, actual RH and sample weight were recorded throughout the isotherm run.

The data obtained by the DVS technique were highly reproducible (Hill et al. 2009; Xie et al. 2011b). In this study, three measurements were taken for each rattan. Cylindrical sample pieces (diameter 20 mm, length 5 mm) were cut from the middle portion of the culm. To avoid rattan variability in the hierarchical architecture with vascular bundles non-uniformly distributed along the radial direction, small rattan blocks (around 30 mg) containing the epidermises and rattan core were cut from the rattan block with the final dimension of 1 × 3 × 3 mm3 (tangential × longitudinal × radial) (Fig. 1). The average initial mass of samples was 33.916 mg, 37.913 mg and 37.608 mg, respectively. The cubic function of one variable was used to calculate the FSP.

Fig. 1
figure 1

Rattan sample used in the experiment

Full size image

1H LF-NMR method

Sample preparation

Cylindrical sample pieces (diameter 20 mm, length 10 mm) were selected from the middle portion of the stems. The sample was inserted in a 10-mm OD 1H LF-NMR tube, which was then closed with a cap. The length of the 1H LF-NMR tube is 250 mm. To meet the inner diameter of the 1H LF-NMR tube and to avoid rattan variability in the hierarchical architecture with vascular bundles non-uniformly distributed along the radial direction, rattan blocks containing the waxy epidermises and rattan core were cut from the rattan block, with the final dimension of 8 × 9 × 10 mm3 (tangential × radial × longitudinal).

Instrument for 1H LF-NMR experiments

The 1H LF-NMR experiments were performed on a 23 MHz MiniMR Instrument (Niumag Instruments, Suzhou, China) at 25 °C. The temperature of the magnetic unit was set at 32 °C, within a variation of ± 0.01 °C. The Carr–Purcell–Meiboom–Gill (CPMG) pulse sequence was used to measure the T2 relaxation decay curve of the entire rattan sample. The CMPG experiments used the following parameters: sample frequency, 250 kHz; pulse width (90°), 5.2 μs; pulse width (180°), 10.4 μs; number of complex points, 200,008; recycle time, 3000 ms; echo time, 0.1 ms; number of echoes, 8000; number of accumulated scans, 128.

The sample temperatures considered include − 45 °C, − 40 °C, − 35 °C, − 30 °C, − 25 °C, − 20 °C, − 15 °C, − 10 °C, − 5 °C, − 3 °C, 0 °C, 3 °C and 5 °C and begins with the lowest temperature (Fig. 2). The temperature stabilization delay before the first experiment was about 45 min (Telkki et al. 2013). Generally, samples could reach the set temperature at about 10–20 min. The samples were scanned 30 min after the freezing treatment. Meanwhile, the sample chamber had also been adjusted to the same temperature, which ensured temperature stabilization during the process of the experiment (Gao et al. 2017).

Fig. 2
figure 2

a T2 relaxation time distributions of rattan at different temperatures and b partial enlarged drawing of T2 relaxation time distribution of rattan at − 5 to 5 °C

Full size image

Theoretical basis

Free water freezes below 0 °C, and the transverse relaxation time (T2) of ice is only 6 μs (Hartley et al. 1992), which is less than the response time of the MicroMR-10. Therefore, T2 of free water cannot be observed. In contrast, bound water freezes at very low temperatures. The FSP can be determined by comparing the measurements above and below the water melting point (Gao and Zhuang 2015; Gao et al. 2017; Telkki et al. 2013).

When determining the free water freezing temperature, the effects of the Gibbs–Thomson effect and the rattan extractives on the freezing point of free water were considered (Aksnes and Kimtys 2004). Park et al. (2006) and Zauer et al. (2014) used the Gibbs–Thomson equation to express the relationship between the liquid freezing point and the pore diameter as follows:

$$\Delta T_{\text{m}} = T_{\text{m}} - T_{\text{m}} (D) = \frac{{4\sigma T_{\text{m}} \cos \theta}}{{D\Delta H_{\text{f}} \rho}}$$
(2)

where Tm is the freezing point of macro-state water, 0 °C; Tm (D) is the freezing point of water in the tubule of diameter D, K; σ is the interfacial free energy, 12.1 mJ/m2; ρ is the density of water, 1.0 × 103 kg/m3; Hf is the specific enthalpy of water, 333.6 J/g; θ is the contact angle.

The tubule diameter can be obtained according to below equation:

$$D = \frac{K}{{\Delta T_{\text{m}}}} \approx \frac{39.6}{{\Delta T_{\text{m}}}}\,({\text{nm}}).$$
(3)

The rattan fiber cell cavity diameter is about 6 μm (Luo et al. 2013). Cell walls also contain micropores, and their maximum size is around 2–4 nm. (Hill 2006; Telkki et al. 2013). According to Eq. (3), the freezing point of free water is about − 0.007 °C, while that of the bound water is less than − 10 °C. Walker (2006) found that the concentration of dissolved sugars in the sap led the water in the lumens to freeze at a temperature between − 0.1 and − 2.0 °C. Therefore, the freezing temperature in this study was set at − 3 °C to ensure that the free water was fully frozen, while the bound water remained liquid.

After the 1H LF-NMR experiments, the moisture contents of the samples were determined by the weight difference between the wet and the dried (at 103 °C) samples.

The actual content of the bound water in the cell wall swelling state can be calculated using the following equation:

$$M_{\text{tx}} = C_{\text{MC}}.\frac{{S_{\text{tx}}}}{{S_{0}}}$$
(4)

where CMC is the ratio of the masses of the wet and dry rattan, %; Stx is the total number of integrals measured at the indicated temperatures; S0 is the total number of integrals measured at the reference temperatures.

The nuclear magnetic signal is inversely proportional to the temperature. Hence, to eliminate the temperature dependence of thermal equilibrium magnetization given by Curie’s law, the integrals of the signals measured at different temperatures were multiplied by the factor T/T0, where T is the actual temperature and T0 is the reference temperature (Kekkonen et al. 2014; Telkki et al. 2013).

Results and discussion

FSP determined by the saturated salt solution method

The water sorption isotherms of the rattans are plotted in Fig. 3a according to the EMC versus RH. The graph demonstrates that the isotherms of rattan cane exhibit a sigmoidal shape, have the characteristics of multi-molecular layer adsorption and belong to the second category of moisture adsorption isotherms (Brunauer et al. 1940; Liu and Zhao 2004). This curve feature is similar to that of bamboo and timber (Liu and Zhao 2004; Wang et al. 2010; Zhang et al. 2018). The tendencies of the moisture adsorption isotherms in different canes of C. simplicifolius are consistent. However, there is a certain degree of dispersion, which may be related to the rattan age. The harvested rattans were collected from the same site condition, but their ages and cane densities differ. Age was found to have a great influence on the water adsorption of biomaterials (Wang et al. 2010). Walker (2006) stated that the FSP of wood is inversely proportional to the basic wood density.

Fig. 3
figure 3

Moisture adsorption isotherms measured by a saturated salt solution method and b DVS. A, B and C represent the different canes of C. simplicifolius, respectively

Full size image

According to the concept of FSP (Stamm 1971), the regression equations of the moisture adsorption isotherm and the moisture content of FSP are presented in Table 2. It shows that the values of FSP determined based on the saturated salt solution method are 31.33%, 32.37% and 33.91%, respectively. There are some differences among the canes, but the differences are less than 1.6%.

Table 2 Regression equations and FSP values of rattan obtained by two conventional methods
Full size table

FSP determined by the DVS method

The curves of the moisture adsorption isotherms measured by the DVS method are similar to those obtained by adjusting the humidity with saturated salt solutions. In both cases, the isotherms are fitted to the type II sigmoid (Esteban et al. 2009) and display the characteristic sigmoidal shape (Fig. 3b). The adsorption isotherms of canes exhibit an upward bend above 60–70% RH, and similar results were obtained in bamboo (Zhang et al. 2018). However, there are differences in the EMC values among the various canes at certain RH levels, especially above 95% RH. The EMC of cane C at 100% RH was 30.63%, whereas that of cane A was 27.11%.

In addition, the values of FSP determined by the DVS method are lower than those determined by the saturated salt solution method, which is probably related to the test temperature and time. The DVS measurement temperature was higher than that of the saturated salt solution method measurement, indicating less hygroscopic capacity due to the changes induced in the rattan by the temperature and the high energy levels of the water molecules (Moreira et al. 2005). The test samples of the DVS method and the saturated salt solution method have the same anatomical and chemical composition, but the test times are different. Establishing a rapid water adsorption equilibrium is one important advantage of the DVS method. According to the moisture adsorption theory (Skaar 1988; Cao and Zhao 2001), the primary adsorption water was adsorbed directly on the free hydrogen bonds of the cell wall and had a higher bound energy. In the late period of water adsorption, dry nitrogen gas containing a preset amount of water vapor passed through the surfaces of the rattan samples. The secondary adsorption occurred on the base of the primary adsorption water, and the bound energy was small, which reduces the moisture adsorption quantity and led to the reduction in EMC.

FSP determined by LF-NMR method

Effects of temperature on T2 relaxation time distributions of rattan

The CPMG sequence was used to measure the T2 relaxation time distributions of the samples as a function of temperature (Fig. 2). Below 0 °C, only one component associated with bound water in the cell walls was observed, since free water was frozen, and its signal disappeared due to its short T2 (Hartley et al. 1992). Telkki et al. (2013) believed that a shorter T2 component with a larger amplitude arose from the water molecules hydrogen bonded to the hydroxyl groups and between the cellulose chains, whereas a longer T2 component with a smaller amplitude originated from water in the cell wall micropores.

Above 0 °C, four components can be observed (Fig. 2b). The two shortest T2 components were related to the bound water and had the same interpretation as that below 0 °C. The fast exchange between free water and the micropore water led to the increase in the relaxation time of the longer T2 component (Brownstein and Tarr 1979). Based on the investigations by Menon et al. (1989), the two longer T2 components arose from free water. According to the microstructure of rattan, the longest T2 component might have been caused by meta-xylem vessels, while the other components originated from protoxylem tracheary elements or parenchyma.

FSP of rattan determined by the LF-NMR method

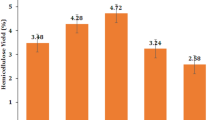
The freeze-thawing analysis technique was used to freeze the free water and obtain the bound water relaxation signal. LF-NMR method offers a straightforward and unambiguous means to determine the FSP. The FSP was accurately determined with the total moisture signal amplitudes below and above the bulk melting point. Consequently, 25 °C and − 3 °C were normally selected to calculate the FSP values of wood and bamboo (Telkki et al. 2013; Kekkonen et al. 2014; Gao and Zhuang 2015; Gao et al. 2017; Song et al. 2017). Equation (3) indicates that free water freezes at about − 0.007 °C, while the bound water freezes at temperatures lower than − 10 °C, as the concentration of dissolved sugars in the sap leads the water in the lumens to freeze at a temperature between − 0.1 and − 2.0 °C. The major monosaccharides of rattan are glucose and xylose, which account for more than 90% of the total sugars and are significantly higher than those of wood (Wu 2007). However, the temperature–signal curve of rattan had an obvious turning point at − 5 °C (Fig. 4). Therefore, the FSP values were measured at − 5 °C and are presented in Table 3.

Fig. 4
figure 4

Temperature-signal curve of rattan

Full size image
Table 3 Bound water content of rattan determined by LF-NMR cryoporometry at different temperatures
Full size table

Table 3 shows that the FSP values of rattan canes are 34.91%, 37.54% and 41.99%, respectively. The LF-NMR method gives a considerably higher FSP than the two other methods due to the different operational definitions. The conventional methods actually underestimate the cell wall saturation limit. Thermodynamics illustrate that free water will be present at a relative humidity of less than 100%, even in the ideal solution limit. Distinctly, the water in rattan is not an ideal solution. At a temperature below 0 °C, the free water relaxation time is not visible, and the FSP value is determined by the ratio of the measurements above and below the water melting point. Therefore, it is very close to the theoretical definition.

Discussion

The variation of FSP determined by the three methods is the same. Cane C has the maximum FSP value, while cane A has the minimum value. Images of the cross section from C. simplicifolius are presented in Fig. 5, indicating that the number of vascular bundles per unit area of cane C is higher than that of cane A and B. The main component of the vascular bundle is cellulose (Jia et al. 2016). Each glucose unit on the cellulose macromolecular chain has three hydroxyl bonds, and each hydroxyl bond has a strong capability of absorbing water molecules in the air and bonding with them (Huang and Wang 2014). However, the content of organic extractives in the parenchyma is higher than that in the vascular bundles, and hydrophobic compounds such as esters, ketones and higher aliphatic acid prevent the entry of water molecules. Therefore, the hygroscopic property of parenchymatous tissue is lower than that of vascular bundles. Engelund et al. (2013) reported that the hemicellulose was softened in the region 60–90% RH at room temperature, and the softening reduced the viscosity and rigidity of the polymeric network significantly, which might increase the capacity to accommodate water molecules in the cell wall. Therefore, the FSP of cane C is greater than that of cane A.

Fig. 5
figure 5

Images of the cross-section of different canes (a, b, c) from C. simplicifolius obtained by the trinocular microscope

Full size image

Density is another important factor that affects FSP (Walker 2006). With the decreasing basic density, the thickness of the cell walls decreases, and thus the walls exhibit weak resistance to swelling. The FSP represents a balance between the solution pressure within the swollen cell wall and resistance to this arising from the mechanical rigidity of the wall (Babiak and Kúdela 1995). Gao and Zhuang (2015) confirmed that the FSP is inversely proportional to the basic density. They also found that the FSP of high-density Mongolica is about 35%, and that the FSP of low-density balsa wood is close to 50%. The basic density of the C. simplicifolius is 0.47 g/cm3. The cell wall structure of the C. simplicifolius is relatively loose and less resistant to swelling, so it can hold more water as compared with wood and bamboo. Therefore, the FSP values of the rattan were slightly higher than those of bamboo (35%) (Song et al. 2017).

The results of the three methods demonstrated that the FSP values determined by the two conventional methods were lower than those of the LF-NMR method (Tables 2, 3). The projection of the saturated salt solution method and DVS method are based upon a thermodynamic interpretation of the FSP. The thermodynamics indicates that free water exists at a relative humidity of less than 100%. Babiak and Kúdela (1995) put the wood samples into a balanced condition of 100% relative humidity at a temperature of 20 °C for six months and then soaked them in distilled water. The results showed that the wood samples further swelled, which indicates that the moisture adsorption test does not reach the moisture adsorption limit of the wood cell walls. Although the two conventional methods have been used to estimate the fiber saturation point in recent years, they are considered basically as an empirical approach and thus are not as accurate as the LF-NMR method. In addition, they are not allowed to extend observations beyond a region in which measurements were taken. The projection of the isotherm to 100% relative humidity implies that this conventional method might not give an accurate estimation of the FSP values. The projected isotherm is a pseudo-equilibrium state. Therefore, the FSP values determined by the saturated salt solution method and DVS method are actually estimations. However, these conventional methods are simple, cost-effective and represent practical limits for the change in rattan properties with moisture (Zelinka et al. 2016). As a matter of fact, the three methods quantify different aspects of FSP. The moisture sorption isotherms obtained by conventional methods describe the amount of bound water and the NMR measures the amount of water distributed in microcapillaries. Therefore, the water content measured by the LF-NMR method is closer to FSP and higher than the values obtained by the conventional methods. Compared with the conventional methods, such as the saturated salt solution method and the DVS method, the LF-NMR method is able to quantify the amount of water in different states in wood (Telkki et al. 2013), and the test time of each sample can be controlled within 1 h. Thus, this method will give more accurate FSP values. Overall, this method appears to be a preferred method in the future for the determination of FSP.

Conclusion

FSP is an important parameter in the study of the physical and mechanical properties of rattan. In this study, the FSP of rattan was determined by the LF-NMR and two conventional methods. The experimental and theoretical analyses in this study led to the following conclusions.

  1. 1.

    The average FSP values of the rattan obtained by the saturated salt solution method, DVS method and LF-NMR method were 32.54%, 28.96% and 38.15%, respectively.

  2. 2.

    The different FSP values obtained by the three methods may be related to the operational definitions. The projection of the isotherm to 100% relative humidity is not an accurate description of the FSP, and the FSP values obtained by the two conventional methods are lower than the actual value of FSP. The LF-NMR method is able to measure the moisture content in the cell wall and thus gives more accurate FSP values.

  3. 3.

    FSP is also affected by the anatomical structure and density of rattan. Cane C with more vascular bundles has a higher FSP value than cane A. The basic density of C. simplicifolius cane is low, and the cell wall tissue is relatively loose and contains more water; thus, rattan has a higher FSP than higher-density bamboo and wood.