Abstract
We consider directed polymers in random environment in the critical dimension \(d = 2\), focusing on the intermediate disorder regime when the model undergoes a phase transition. We prove that, at criticality, the diffusively rescaled random field of partition functions has a unique scaling limit: a universal process of random measures on \({\mathbb {R}}^2\) with logarithmic correlations, which we call the Critical 2d Stochastic Heat Flow. It is the natural candidate for the long sought solution of the critical 2d Stochastic Heat Equation with multiplicative space-time white noise.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and main results
1.1 Overview
The model of directed polymer in random environment (DPRE) is by now a fundamental model in statistical physics and probability theory. It is one of the simplest and yet most challenging models for disordered systems, where the effect of disorder—which is synonymous with random environment—can be investigated. Originally introduced by Huse and Henley [59] in the physics literature to study interfaces of the Ising model with random impurities, over the years, DPRE has become an object of mathematical interest and lies at the heart of two areas of intense research in recent years. On the one hand, it is one of the canonical examples in the Kardar–Parisi–Zhang (KPZ) universality class of interface growth models, which has witnessed tremendous progress over the last two decades in spatial dimension \(d=1\) (see e.g. the surveys [34, 35, 73]); on the other hand, it provides a discretisation of the Stochastic Heat Equation (SHE) and (via the Cole-Hopf transformation) of the Kardar–Parisi–Zhang (KPZ) equation, for which a robust solution theory in \(d=1\) has been developed only recently in the larger context of singular stochastic partial differential equations (SPDE) [49, 53, 55, 56, 64].
Our goal in this paper is to consider DPRE in the critical spatial dimension \(d=2\), for which much remains unknown. Our main result shows that, in a critical window for the disorder strength, the family of partition functions of DPRE converges to a universal limit, which can be interpreted as the solution of the (classically ill-defined) 2-dimensional SHE. This is the first example of a singular SPDE for which a solution has been constructed in the critical dimension and for critical disorder strength.
In the remainder of the introduction, we first recall the definition of DPRE, its basic properties, and the works leading up to our current result. We then present our main results and discuss their connections with singular SPDEs and related research.
1.2 The model
The first ingredient in the definition of DPRE is a simple symmetric random walk \((S = (S_n)_{n\geqslant 0}, \mathrm P)\) on \({\mathbb {Z}}^d\), started at \(S_0 = 0\). To specify a different starting time m and position z, we will write \(\mathrm P(\,\cdot \,|S_m = z)\). The second ingredient is the disorder or random environment, encoded by a family of i.i.d. random variables \((\omega = (\omega (n,z))_{n\in {\mathbb {N}}, z\in {\mathbb {Z}}^d}, {{\mathbb {P}}} )\) with zero mean, unit variance and some finite exponential moments:
Given \(N\in {\mathbb {N}}\), \(\beta >0\), and a realization of \(\omega \), the polymer measure of length \(N\in {\mathbb {N}}\) and disorder strength (inverse temperature) \(\beta \) in the random environment \(\omega \) is given by
where
is the partition function. Note that \(\lambda (\beta )\) in the exponent ensures that \({{\mathbb {E}}} [Z_N^{\beta ,\,\omega }(z)]=1\).
In the mathematical literature, DPRE was first studied by Imbrie and Spencer [60]. There have been many results since then, although many fundamental questions remain open. We briefly recall what is known and refer to the recent monograph by Comets [30] for more details and references.
DPRE exhibits a phase transition between a weak disorder phase and a strong disorder phase. Using the martingale structure of the partition functions \((Z_N^{\beta ,\,\omega }(0))_{N\in {\mathbb {N}}}\), first identified by Bolthausen in [6], DPRE is said to be in the weak disorder (or strong disorder) phase if the martingale converges almost surely to a positive limit (or to 0). It was later shown in [33] that there is a critical value \(\beta _c\geqslant 0\) such that strong disorder holds for \(\beta >\beta _c\) and weak disorder holds for \(0 \leqslant \beta < \beta _c\), where \(\beta _c \in (0,\infty )\) for \(d\geqslant 3\) [6, 60], and \(\beta _c=0\) for \(d=1,2\) [22, 32] (see also [10, 65, 72]).
In the weak disorder phase, a series of works culminating in [33] showed that the random walk under the polymer measure converges to a Brownian motion under diffusive scaling of space and time, as if the disorder is not present. In the strong disorder phase, it is believed that under the polymer measure, the path should be super-diffusive, but this has only been proved for special integrable models in dimension \(d=1\), see [36, 61]. Even less is known in \(d\geqslant 2\) due to the lack of integrable models within the same universality class. We mention that the strong disorder phase can alternatively be characterised by the fact that two polymer paths sampled independently in the same random environment have positive overlap, see [22, 32, 77] and the more recent results [5, 8, 9, 24].
1.3 The case \(d=2\)
Henceforth, we will focus on dimension \(d=2\). Surprisingly, even though \(\beta _c=0\), there is still a weak to strong disorder transition, which was identified in [17]. More precisely, if we choose \(\beta =\beta _N={\hat{\beta }}/\sqrt{\log N}\), which is called an intermediate disorder regime, then it was shown in [17] that below the critical point \({\hat{\beta _c}} = \sqrt{\pi }\), the partition function \(Z_N^{\beta _N, \,\omega }(0)\) converges in distribution to a log-normal random variable, which is strictly positive, while at and above \({\hat{\beta _c}}\), it converges to 0 (such a transition does not occur in \(d=1\)). This raises many interesting questions about the 2-dimensional DPRE.
There are two main perspectives in the study of the partition functions of DPRE. One is to investigate the fluctuation of a single log-partition function \(\log Z_N^{\beta , \,\omega }(0)\) as \(N\rightarrow \infty \). In \(d=1\), this is conjectured to converge, under suitable rescaling, to the universal Tracy–Widom distribution whenever \(\beta >0\). Similar universal fluctuations are expected to arise in \(d\geqslant 2\) when \(\beta >\beta _c\), although only numerical results are available so far [57, 58]. In \(d=2\) and in the intermediate disorder regime \(\beta _N= {\hat{\beta }}/\sqrt{\log N}\) with a sub-critical interaction strength \({\hat{\beta }}<{\hat{\beta _c}}\), [17] showed that \(\log Z_N^{\beta , \,\omega }(0)\) converges to a universal normal limit independent of the law of \(\omega \). The super-critical case \({\hat{\beta \geqslant }} {\hat{\beta _c}}\) remains a difficult challenge.
Another perspective, which we take in this paper, is to study the diffusively rescaled field of partition functions indexed by all starting points in space-time:
as well as the diffusively rescaled field of log-partition functions:
The fields \({{\mathcal {U}}} _N\) and \({{\mathcal {H}}} _N\) provide natural discretizations of the solutions of the two-dimensional Stochastic Heat Equation (SHE) and Kardar–Parisi–Zhang equation (KPZ) respectively:
where \({\dot{W}} = {\dot{W}}(t,x)\) denotes space-time white noise. These stochastic PDEs are singular and ill-posed: even the recent breakthrough solution theories of regularity structures [55, 56] and paracontrolled distributions [53, 54] only apply in \(d=1\) but not in the critical dimension \(d=2\). Therefore, if \({{\mathcal {U}}} _N\) and \({{\mathcal {H}}} _N\) admit non-trivial limits, then these limits are natural candidates for the long-sought solutions of SHE and KPZ in \(d=2\).
The study of the random field \({{\mathcal {U}}} _N\) was initiated in [17], which showed that in the subcritical regime \({\hat{\beta }}<{\hat{\beta _c}}\), the centered and rescaled random field \(\sqrt{\log N}\big (\,{{\mathcal {U}}} _N(t,x) -1\big )\) converges to the solution of the so-called Edwards–Wilkinson equation, which is a Gaussian free field at each time t. The study of the random field \({{\mathcal {H}}} _N\) was first carried out in [25],Footnote 1 which showed that \(\sqrt{\log N}\big (\,{{\mathcal {H}}} _N(t,x) - {{\mathbb {E}}} [{{\mathcal {H}}} _N(t,x)]\big )\) is tight in N as a family of distribution-valued random variables for \({\hat{\beta }}\) sufficiently small; shortly after, [20] proved convergence to the solution of the same Edwards–Wilkinson equation as for \({{\mathcal {U}}} _N\) for all \({\hat{\beta }}<{\hat{\beta _c}}\) (simultaneously, the same result was proved in [50] for \({\hat{\beta }}\) sufficiently small).
In the much more interesting and delicate critical regime \({\hat{\beta }}= {\hat{\beta _c}}\)—there is in fact a critical window of width \(O(1/\log N)\) around \({\hat{\beta _c}}\), see (1.11) below—the random field \({{\mathcal {U}}} _N(t,x)\) no longer needs any centering and rescaling. Its limiting correlation structure was first identified in [7] through a different regularisation of the 2d SHE (1.6) (mollifying the noise \({\dot{W}}\) instead of discretizing space and time). In [19], the third moment of the averaged random field \({{\mathcal {U}}} _N(t,\varphi ) := \int {{\mathcal {U}}} _N(t,x) \, \varphi (x) \, \textrm{d}x\), for test functions \(\varphi \), was computed and shown to converge to a finite limit as \(N\rightarrow \infty \), which implies that all subsequential limits of \({{\mathcal {U}}} _N\) have the same correlation structure identified in [7] (tightness is trivial since \({{\mathbb {E}}} [{{\mathcal {U}}} _N]\equiv 1\)). Subsequently, [51] identified the limit of all moments of \({{\mathcal {U}}} _N(t, \varphi )\) (see also the more recent work [26]). However, the uniqueness of the limit of \({{\mathcal {U}}} _N\) remained elusive and challenging, because the limiting moments identified in [51] and [26] grow too fast to uniquely determine the law of the random field.
Our main result settles this question and shows that, in the critical window around \({\hat{\beta }} = {\hat{\beta _c}}\), the random field \({{\mathcal {U}}} _N\) indeed converges to a unique universal limit, which naturally provides a notion of solution of the 2d SHE (1.6) for disorder strength \(\beta \) in the critical window. Therefore, we name it the Critical 2d Stochastic Heat Flow.
1.4 Main results
To formulate our main results, we generalize the partition functions in (1.3) by introducing a point-to-point version, where both the starting and ending positions of the random walk are fixed: for \(M \leqslant N \in {\mathbb {N}}_0 = \{0,1,2,\ldots \}\) and \(w,z\in {\mathbb {Z}}^2\) we set
with the convention \(\sum _{n=M+1}^{N-1} \{\ldots \} := 0\) for \(N \leqslant M+1\).
To deal with parity issues, for \(x \in {\mathbb {R}}^2\) we denote by \([\![ x ]\!]\) the closest point \(z \in {\mathbb {Z}}^2_{\textrm{even}} :=\{(z_1, z_2)\in {\mathbb {Z}}^2: z_1+z_2 \text{ even }\}\); for \(s \in {\mathbb {R}}\) we define the even approximation \([\![ s ]\!] := 2 \, \lfloor s/2 \rfloor \in {\mathbb {Z}}_{\textrm{even}} := 2{\mathbb {Z}}\). We then introduce the process of diffusively rescaled partition functions:Footnote 2
where \(\textrm{d}x \, \textrm{d}y\) denotes the Lebesgue measure on \({\mathbb {R}}^2 \times {\mathbb {R}}^2\), and \(\beta _N\) will be defined shortly.
We regard \({{\mathcal {Z}}} ^{\beta _N}_{N;\, s,t}(\textrm{d}x, \textrm{d}y)\) as a random measure on \({\mathbb {R}}^2 \times {\mathbb {R}}^2\), where we equip the space of locally finite measures on \({\mathbb {R}}^2 \times {\mathbb {R}}^2\) with the topology of vague convergence:
Our main result proves weak convergence of the law of \({{\mathcal {Z}}} ^{\beta }_N\) as \(N\rightarrow \infty \), when \(\beta = \beta _N\) is rescaled in a suitable critical window, that we define next. Let us introduce the sequence
which is the expected overlap (number of collisions) between two independent simple symmetric random walks starting from the origin in \({\mathbb {Z}}^2\) up to time N. Recalling that \(\lambda (\cdot )\) is the disorder log-moment generating function, see (1.1), the critical window for \(\beta = \beta _N\) is
Since \(\lambda (\beta ) \sim \frac{1}{2} \beta ^2\) as \(\beta \downarrow 0\), see (1.1), we have \(\beta _N \sim {\hat{\beta _c}} / \sqrt{\log N}\) with \({\hat{\beta _c}} = \sqrt{\pi }\) irrespective of the parameter \(\vartheta \), which contributes to the second order asymptotics, see (3.12).
We can now state our main result, which will be proved in Sect. 9.
Theorem 1.1
(Critical 2d Stochastic Heat Flow) Fix \(\beta _N\) in the critical window (1.11), for some \(\vartheta \in {\mathbb {R}}\). As \(N\rightarrow \infty \), the family of random measures \({{\mathcal {Z}}} ^{\beta _N}_N = ({{\mathcal {Z}}} ^{\beta _N}_{N;\, s,t}(\textrm{d}x, \textrm{d}y))_{0\leqslant s \leqslant t < \infty }\) defined in (1.9) converges in finite dimensional distributions to a unique limit
which we call the Critical 2d Stochastic Heat Flow. This limit \({\mathscr {Z}}^\vartheta \) is universal, in that it does not depend on the law of the disorder \(\omega \) except for the assumptions in (1.1).
We can infer directly from its construction some basic properties of the Critical 2d Stochastic Heat Flow, which we collect in the next result, also proved in Sect. 9.
Theorem 1.2
The Critical 2d Stochastic Heat Flow \({\mathscr {Z}}^\vartheta \) is (space-time) translation invariant in law:
and it satisfies the following scaling relation:
The first and second moments of \({\mathscr {Z}}^\vartheta \) are given by
where g denotes the heat kernel in \({\mathbb {R}}^2\), see (3.20), and \(K^\vartheta \) is an explicit kernel, see (3.56).
Remark 1.3
The covariance kernel \(K_{t-s}^\vartheta (x,x'; y, y')\) was first identified in [7] (see also [19]) and is logarithmically divergent near the diagonals \(x=x'\) or \(y=y'\).
We now briefly explain the proof strategy. As noted before, the moments of \({\mathscr {Z}}^\vartheta \) identified in [51] and [26] grow too fast to uniquely characterize the law of \({\mathscr {Z}}^\vartheta \). The bounds given in these works suggest that the n-th moment is at most of order \(\exp (\exp (n^2))\), while our recent work [21] gives a lower bound of \(\exp (c n^2)\). Physical arguments on the Delta-Bose gas [74] suggest that the growth should be \(\exp (\exp (n))\). It may thus be surprising that we are still able to prove Theorem 1.1 and show that the limit is unique, without criteria to uniquely identify the limit. Another prominent result of this nature, which gave us inspiration, is the work of Kozma [63] on the convergence of the three-dimensional loop erased random walk with dyadic scaling of the lattice \(2^{-N}{\mathbb {Z}}^3\).
The basic strategy is to show that the laws of \(({{\mathcal {Z}}} ^{\beta _N}_{N})_{N\in {\mathbb {N}}}\) form a Cauchy sequence, i.e.
To accomplish this, we first construct a coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\,\cdot \, |\Theta )\), for each \(\varepsilon \in (0,1)\), which is a function of a family \(\Theta \) of coarse-grained disorder variables. We then perform a coarse-graining approximation of the partition function on the time-space scale \((\varepsilon N, \sqrt{\varepsilon N})\), which shows that \({{\mathcal {Z}}} ^{\beta _N}_{N}\) can be approximated by the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\,\cdot \, |\Theta )\) for a specific choice of coarse-grained disorder \(\Theta =\Theta _{N, \varepsilon }\) that depends on N and \(\varepsilon \), with an approximation error which is small for small \(\varepsilon \) and large N (shown via second moment bounds). As a consequence, we finally prove (1.14) by showing that the coarse-grained models \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\,\cdot \, |\Theta )\) with \(\Theta =\Theta _{N, \varepsilon }\) and \(\Theta =\Theta _{M, \varepsilon }\) are close in distribution, for small \(\varepsilon > 0\) and large \(N, M \in {\mathbb {N}}\) (shown via a Lindeberg principle).
We give a more detailed proof outline in Sect. 2. Let us just highlight here the key proof ingredients:
- A.:
-
Coarse-Graining, which leads to a coarse-grained model with the same structure as the original model, demonstrating a degree of self-similarity;
- B.:
-
Time-Space Renewal Structure, which sheds probabilistic light on second moment computations and leads in the continuum limit to the so-called Dickman subordinator;
- C.:
-
Lindeberg Principle for multilinear polynomials of dependent random variables, which controls the effect of changing \(\Theta \) in the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\,\cdot \, |\Theta )\);
- D.:
-
Functional Inequalities for Green’s Functions of multiple random walks on \({\mathbb {Z}}^2\), which yield sharp higher moment bounds for the coarse-grained model.
This framework is robust enough that it can also be used to show convergence of other approximations of SHE (1.6) to the Critical 2d Stochastic Heat Flow.
Remark 1.4
(Mollified SHE) The same proof steps A, B, C, D can be carried out for the solution \(u_\delta \) of the mollified SHE (1.6), where the space-time white noise \({\dot{W}}\) is mollified spatially on the scale \(\delta \) and \(\beta =\beta _\delta \) is chosen in the corresponding critical window, that is \(\beta ^2_\delta =\tfrac{2\pi }{|\log \delta |} +\tfrac{\vartheta +o(1)}{(\log \delta )^2}\) (cf. (3.12)). A key point is that coarse-graining \(u_\delta \) on the mesoscopic scale leads to exactly the same coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\,\cdot \, |\Theta )\) constructed in this paper, just with a different family of coarse-grained disorder variables \(\Theta = \Theta _{\delta ,\varepsilon }\). This means that the solution \(u_\delta \) of the mollified SHE would converge as \(\delta \downarrow 0\) to the same universal limit \({\mathscr {Z}}^\vartheta \) in Theorem 1.1. We will not carry out the details here since the paper is long enough.
We remark that Clark has proved in [28] an analogue of Theorem 1.1 for DPRE on the hierarchical diamond lattice, which is particularly useful for renormalization analysis and can mimic Euclidean lattices of different dimensions as the lattice parameters vary. Furthermore, in [27, 29], he also constructed the continuum polymer measures and studied their properties. This raises interesting questions as to whether similar results can be proved for DPRE on the Euclidean lattice, where exact renormalization analysis is no longer available. We point out that our work developed in parallel to that of Clark, and our proof strategies share some common features, such as coarse-graining and controlling distributional distances via a Lindeberg principle in our case vs. Stein’s method in [28], and showing that the laws of the partition functions form a Cauchy sequence.
Now that we have proved the existence of a unique limit \({\mathscr {Z}}^\vartheta \)—the Critical 2d Stochstic Heat Flow—the next challenge will be to investigate its properties and characterize its law.
Remark 1.5
(Alternative scaling) The simple random walk on \({\mathbb {Z}}^2\) is 2-periodic and each component has variance \(\frac{1}{2}\). As a consequence, the diffusively rescaled partition functions \({{\mathcal {U}}} _N(t,x)\) in (1.4) provide a discretization of a slightly modified SHE (1.6), namely
(see [21, Appendix A.3] for more details). The SHE with the usual parameters in (1.6) can be recovered via the change of variable \({{\mathcal {U}}} _N(t,\frac{x}{\sqrt{2}})\). Therefore to describe a candidate solution of (1.6), we should consider the rescaled Critical 2d Stochastic Heat Flow given by (recall (1.12))
which is also normalized to have mean 1 rather than \(\frac{1}{2}\) (see (1.13)).
1.5 Related literature
We next discuss the connection between our work and various results in the literature and point out some future directions of research.
1.5.1 Singular SPDEs
As explained in Sect. 1.3, the scaling limit \({\mathscr {Z}}^\vartheta \) in Theorem 1.1 can be interpreted as the solution of the 2-dimensional SHE (1.6) in the critical window. For SHE, dimension \(d=2\) marks the critical dimension in the language of singular SPDEs and renormalisation group theory. To define a solution for singular SPDEs, such as SHE and KPZ in (1.6)–(1.7), a standard approach is to mollify the space-time noise \({\dot{W}}\) in space on the scale of \(\varepsilon \), and then try to identify a scaling limit as \(\varepsilon \downarrow 0\). Discretizing space-time by considering a lattice model, such as the DPRE that we study in this paper, is just another way of removing the singularity on small scales (also known as ultraviolet cutoff).
All existing solution theories for singular SPDEs, including regularity structures [55, 56], paracontrolled distributions [53, 54], the renormalization group approach [64], or energy solutions [49], do not apply at the critical dimension. The only singular SPDEs for which progress has been made in defining its solution at the critical dimension are SHE and KPZ (via the Cole-Hopf transform). The phase transition identified in [17] was unexpected, and to the best of our knowledge no such transition has been established for other singular SPDEs in the critical dimension. Theorem 1.1 is thus the first result to define a solution for a singular SPDE at the critical dimension and for critical disorder strength.
In dimension \(d=2\), recently there has also been significant progress in understanding the solution of the anisotropic version of the KPZ equation (aKPZ), which differs from (1.7) in that \(|\nabla v|^2= (\partial _{x_1}v)^2+(\partial _{x_2}v)^2\) therein is replaced by \((\partial _{x_1}v)^2- (\partial _{x_2}v)^2\). This case is also beyond the reach of existing solution theories, and unlike the isotropic KPZ, it cannot be linearized via the Cole-Hopf transformation. Cannizzaro, Erhard, and Schönbauer [11] regularized the aKPZ via a cutoff in Fourier space, instead of discretizing space and time or mollifying the noise on the spatial scale \(\varepsilon \) (all are ultraviolet cutoffs). They showed that if the non-linear term \((\partial _{x_1}v)^2- (\partial _{x_2}v)^2\) is rescaled by a factor \(\lambda /\sqrt{|\log \varepsilon |}\), then the solution of the regularized aKPZ is tight with non-trivial limit points, which is the anisotropic analogue of [25]. Very recently, Cannizzaro, Erhard, and Toninelli [14] succeeded in proving that the limit is in fact Gaussian and solves the Edwards–Wilkinson equation, which is the anisotropic analogue of [20, 50]. In contrast to the isotropic case (1.7), there is no phase transition in \(\lambda \) for the aKPZ. The same authors also studied the aKPZ without scaling the non-linearity, and in a surprising result [12, 13], they showed that the solution exhibits logarithmic superdiffusive behaviour.
In the supercitical dimensions \(d\geqslant 3\), the transition between the weak and strong disorder phases for the directed polymer is long known [30] and has a natural counterpart for SHE and KPZ. In recent years, there have been many studies on the solutions of SHE and KPZ via mollification, namely, analogues of the random fields \({{\mathcal {U}}} _N\) and \({{\mathcal {H}}} _N\) defined in (1.4)–(1.5). These studies are all in the weak disorder regime and are analgous to results in \(d=2\), see e.g. [31, 37, 38, 41, 52, 68, 69, 71].
1.5.2 Coarse-graining
The first step in our approach is to construct a coarse-grained model. Coarse-graining has a long history in statistical mechanics and renormalisation theory. In the framework of directed polymer models, coarse-graining has played a crucial role in the studies by Lacoin [65] and Berger–Lacoin [10] on free energy asymptotics, which extended previous works in the literature of pinning models, see [47], from which we single out the fundamental work of Giacomin–Lacoin–Toninelli [48].
In our analysis, we need a family of coarse-grained models which provide a sharp approximation of the partition function at the critical point, while the works mentioned above used coarse-grained models to provide upper bounds away from the critical point. The need for a sharper approximation creates several challenges, which lead to the refined estimates in Sects. 5 and 8 and the development of the enhanced Lindeberg principle in Appendix A.
1.5.3 DPRE on hierarchical lattices
In a series of papers [27,28,29], Clark successfully treated the directed polymer model on hierarchical diamond lattices at the “critical dimension” and in the critical window of disorder strength, which contains an analogue of Theorem 1.1 and more. Due to their tree-like structure, hierarchical lattices are especially convenient for performing exact renormalization group calculations that are typically intractable on the Euclidean lattice. By tuning suitable parameters (such as the number of branches and the number of segments along each branch), hierarchical lattices can mimic Euclidean lattices with different spatial dimensions. When the branch number equals the segment number, hierarchical lattices mimic \({\mathbb {Z}}^2\). For DPRE on these lattices, Clark was able to prove in [28] the analogue of Theorem 1.1.
Exploiting the structure of hierarchical lattices, in [29], Clark was able to use the limiting partition functions obtained in [28] to construct a continuum version of the polymer measure and study its properties. Furthermore, in [27], he identified an interesting conditional Gaussian Multiplicative Chaos (GMC) structure among the continuum polymer measures with different parameter \(\vartheta \) (similar to \(\vartheta \) in Theorem 1.1). These results raise interesting questions as to whether similar results can be obtained for DPRE on the Euclidean lattice. In this respect, Theorem 1.1 provides the starting point.
1.5.4 Continuum polymer measure
A continuum version of the DPRE polymer measure in dimension \(d=1\) was constructed in [1, 2], exploiting the continuum limit of the point-to-point partition functions. The same approach was applied in [15] to pinning models with tail exponent \(\alpha \in (\frac{1}{2},1)\). An essential feature of these constructions, as well as the one by Clark [29] in the hierarchical setting in the critical regime, is that the continuum partition functions are random functions of the polymer endpoints. The same holds for DPRE in dimension \(d=2\) in the subcritical regime \(\beta _N \sim {\hat{\beta }} / \sqrt{\log N}\), with \({\hat{\beta }} < {\hat{\beta _c}} = \sqrt{\pi }\), where it was recently shown in [44] that the discrete polymer measure, diffusively rescaled, converges to the law of Brownian motion.
The situation for DPRE in dimension \(d=2\) in the critical window is radically different, because the continuum partition functions \({{\mathcal {Z}}} ^\vartheta _{z,t}(\textrm{d}x, \textrm{d}y)\) given in Theorem 1.1 are only random measures and undefined pointwise. The point-to-plane partition function \(Z^{\beta _N, \omega }_N\) defined in (1.3) in fact converges to 0 as \(N\rightarrow \infty \), as shown in [17]. For this reason, constructing a continuum version of the polymer measure—or studying the scaling properties of the discrete polymer measure—started from a fixed point, remains a significant challenge. However, if we consider discrete polymer measures with the starting point chosen uniformly from a ball on the diffusive scale, then the same proof strategy as that for Theorem 1.1 should be applicable to show that the measures converge to a continuum polymer measure starting from a ball, whose finite dimensional distributions are uniquely determined.
1.5.5 Schrödinger operators with point interactions
When the disorder \(\omega \) is standard normal, a direct calculation shows that for \(k\in {\mathbb {N}}\), the k-th moment of the polymer partition function in (1.3) is the exponential moment (with parameter \(\beta ^2\)) of the total pairwise collision local time up to time N among k independent random walks on \({\mathbb {Z}}^2\). When \(k=2\), by a classic result of Erdös and Taylor [42] (see also [46]), the collision local time rescaled by \(1/\log N\) converges to an exponential random variable with parameter \(\pi \). In the critical window we consider here, we have \(\beta _N={\hat{\beta _c}}/\sqrt{\log N}\) with \({\hat{\beta _c}}=\sqrt{\pi }\), and hence the parameter of the exponential moment matches exactly the parameter of the limiting exponential random variable, making the moment analysis particularly delicate.
Via the Feynman–Kac formula, it can also be seen that the k-th moment of the partition function is the solution of a discrete space-time parabolic Schrödinger equation with a potential supported on the diagonal (point interaction). In the continuum setting, there have been a number of studies on the Schrödinger operator with point interactions (also called Delta-Bose gas) in dimension \(d=2\) [3, 4, 39, 40]. Using ideas from these studies, especially the works of Dell’Antonio–Figari–Teta [39] and of Dimock–Rajeev [40], Gu, Quastel, and Tsai [51] were able to compute asymptotically all moments of the averaged solution of the mollified SHE, which are analogues of the averaged polymer partition functions \({{\mathcal {Z}}} ^{\beta _N}_{N;\, s,t}(\varphi , \psi ) :=\iint \varphi (x) \, \psi (y) \, {{\mathcal {Z}}} ^{\beta _N}_{N;\, s,t}(\textrm{d}x, \textrm{d}y)\) in (1.9), with \(\varphi \) and \(\psi \) assumed to be in \(L^2\) in [51]. Previously, only the third moment had been obtained in [19]. When \(\varphi \) is a delta function, the moments of \({{\mathcal {Z}}} ^{\beta _N}_{N;\, s,t}(\varphi , \psi )\) diverge as \(N\rightarrow \infty \), and the asymptotics of the third moment has been investigated in [43]. But all mixed moments of the form \(\mathrm E\big [\prod _{i=1}^n{{\mathcal {Z}}} ^{\beta _N}_{N;\, s,t}(\varphi _i, \psi _i)\big ]\) converge if \(\varphi _i\) are chosen to be distinct \(\delta \) functions, which was shown recently by Chen in [26].
As an input to the Lindeberg principle mentioned in the proof sketch for Theorem 1.1, we need to bound the fourth moment of the coarse-grained model, which approximates the original partition function. The results from the Schrödinger operator literature and [51] are not applicable in our setting, because they rely on explicit Fourier calculations. We therefore develop an alternative and more robust approach based on functional inequalities for Green’s function of multiple random walks on \({\mathbb {Z}}^2\), see Lemma 6.8. Instead of working with \(\varphi , \psi \in L^2\) as in [51], we can work with weighted \(L^p\)–\(L^q\) spaces with \(\frac{1}{p}+\frac{1}{q}=1\). The choice of a weight allows us to consider a wider class of boundary conditions, such as \(\psi \equiv 1\) and \(\varphi \) an approximate delta function, and also to control spatial decay when the support of \(\varphi \) and \(\psi \) are far apart, all of which are needed in our proof. See Sect. 6 for more details.
1.5.6 Lindeberg principle
A Lindeberg principle is said to hold when the law of a function \(\Phi \) of a family of random variables does not change much if the family of random variables is switched to another family with some matching moments. Lindeberg principles have been very powerful tools in proving universality. The usual formulation such as in [23] requires the family of random variables to be independent (or exchangeable), and \(\Phi \) needs to have bounded first three derivatives. This is not satisfied when \(\Phi \) is a multilinear polynomial, whose derivatives are unbounded. This case was addressed in [70, 76] when the arguments are independent random variables (see also [16]).
In the proof of Theorem 1.1, we need to deal with a multilinear polynomial of dependent random variables with a local form of dependence. We formulate an extension of the Lindeberg principle to this setting in Appendix A. Our calculations are inspired by a work of Röllin on Stein’s method [75], which is an analogue of [23] for a function \(\Phi \) (with bounded first three derivatives) of dependent random variables.
1.6 Structure of the paper
The rest of the paper is organized as follows.
-
In Sect. 2, we give a detailed proof outline.
-
In Sect. 3, we introduce some basic notation and tools that we need for the rest of the paper, which includes in particular the polynomial chaos expansion and second moment asymptotics for the partition function.
-
In Sect. 4, we define the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\,\cdot \, |\Theta )\) and the coarse-grained disorder \(\Theta = \Theta _{N,\varepsilon }\). Then in Sect. 5, we show that \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\,\cdot \, |\Theta _{N,\varepsilon })\) provides a good \(L^2\) approximation for the diffusively rescaled partition functions \({{\mathcal {Z}}} _N\) in (1.9).
-
In Sects. 6, 7 and 8, we derive key moment bounds for \({{\mathcal {Z}}} _N\), \(\Theta _{N, \varepsilon }\) and \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\,\cdot \, |\Theta )\).
-
In Sect. 9, we wrap up the proof of our main results: Theorems 1.1 and 1.2.
-
In Appendix A, we formulate an enhanced Lindeberg principle for multilinear polynomials of dependent random variables.
1.7 Notation
We denote by \(C_b({\mathbb {R}}^d)\), resp. \(C_c({\mathbb {R}}^d)\), the space of bounded, resp. compactly supported functions \(\varphi : {\mathbb {R}}^d \rightarrow {\mathbb {R}}\). The usual \(L^p\) norms will be denoted by \(\Vert \varphi \Vert _p\) for functions \(\varphi : {\mathbb {R}}^d \rightarrow {\mathbb {R}}\) and by \(\Vert X\Vert _{L^p}\) for random variables X. For notational simplicity, we will use \(c, C, C', C''\) to denote generic constants, whose values may change from place to place.
2 Proof outline
We elaborate in more detail our proof strategy for Theorem 1.1, especially the coarse-graining procedure. After reading the proof strategy, to see how the pieces fit together more precisely, we encourage the reader to go directly to Sect. 9.1 to read the proof of Theorems 1.1 and 1.2. The proof is contingent on some earlier results, such as Theorems 4.7 and 8.1, but otherwise is mostly self-contained.
Recalling (1.9), we just consider a single averaged partition function
for some \(\varphi \in C_c({\mathbb {R}}^2)\), \(\psi \in C_b({\mathbb {R}}^2)\), and \(\beta _N=\beta _N(\vartheta )\) chosen as in (1.11) for some fixed \(\vartheta \in {\mathbb {R}}\). To prove that \({{\mathcal {Z}}} _N\) converges in distribution to a limit as claimed in Theorem 1.1, we will show that the laws of \(({{\mathcal {Z}}} _N)_{N\in {\mathbb {N}}}\) form a Cauchy sequence.
The starting point of our analysis is a polynomial chaos expansion for \({{\mathcal {Z}}} _N\), which will be recalled in more detail in Sect. 3.3. In short, by introducing the i.i.d. random variables
which have mean 0 and variance \(\sigma _N^2\) as in (1.11), we can expand \({{\mathcal {Z}}} _N\) as a multilinear polynomial in the \(\xi _N\)’s as follows:
where \(q_{m,n}(x,y):= \mathrm P(S_n = y|S_m = x)\) is the random walk transition kernel, and \(q^N_{m,n}(\varphi , z_1)\), \(q^N_{m,n}(z_r, \psi )\), \(q^N_{m,n}(\varphi , \psi )\) are the averages of \(q_{m,n}(x,y)\) w.r.t. \(\varphi (x/\sqrt{N})\), \(\psi (y/\sqrt{N})\), or both (see (3.16)–(3.18)).
Each term in the sum in (2.1) contains a sequence of disorder variables \((\xi _N(n_j, z_j))_{1\leqslant j\leqslant r}\) linked by random walk transition kernels, and different terms in the sum are \(L^2\)-orthogonal. We will see that when it comes to second moment calculations, the sequence of points \((n_1, z_1), \ldots , (n_r, z_r)\) can be interpreted as a time-space renewal configuration.
Before explaining our proof strategy and ingredients, we first give a heuristic calculation that already shows universality, namely that as \(N\rightarrow \infty \), the limiting law of \({{\mathcal {Z}}} _{N}\) in (2.1) (if a unique limit exists) does not depend on the law of the i.i.d. random variables \(\xi _N(\cdot , \cdot )\) provided the first two moments are unchanged. The heuristic is based on a Lindeberg principle, which will help to illustrate some key ideas in our proof.
2.1 A heuristic calculation
Let us write \({{\mathcal {Z}}} _N(\xi _N)\) to emphasise the dependence on the i.i.d. family \(\xi _N(\cdot , \cdot )\), and let \({{\mathcal {Z}}} _N(\eta _N)\) be defined similarly with \(\xi _N\) replaced by an i.i.d. family \(\eta _N\) with matching first two moments and finite third moment. To show that \({{\mathcal {Z}}} _N(\xi _N)\) and \({{\mathcal {Z}}} _N(\eta _N)\) are close in law, it suffices to show that for any \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) with bounded first three derivatives,
This difference can be bounded by a Lindeberg principle. In particular, we can apply Theorem A.4 to the case of i.i.d. random variables (the sums in (A.9)–(A.10) will only contain indices \(k=l=m\) due to the i.i.d. assumption) to get the bound
where \(\xi _N^{(t)}:= \sqrt{t}\, \xi _N + \sqrt{1-t}\, \eta _N\) interpolates between \(\eta _N\) and \(\xi _N\), and \(\partial _{(n,z)}{{\mathcal {Z}}} (\xi _N)\) denotes partial derivative w.r.t. \(\xi _N(n,z)\). Since \({{\mathcal {Z}}} (\xi ^{(t)}_N)\) is a multilinear polynomial in \(\xi ^{(t)}_N(\cdot , \cdot )\), it is easily seen from (2.1) that
where \({{\mathcal {Z}}} ((n,z), \psi )\) is the point-to-plane partition function starting from the point (n, z) and terminating at time N with boundary condition \(\psi \), and \({{\mathcal {Z}}} (\varphi , (n,z))\) is the plane-to-point partition function with initial boundary condition \(\varphi \) and terminating at the point (n, z). Since \(\varphi \) has compact support, only (n, z) on the diffusive scale (n of order N and \(z\in {\mathbb {Z}}^2\) of order \(\sqrt{N}\)) contribute to the sum in (2.3), and there are \(N^2\) such terms. This sum is more than compensated by the factor \(\frac{1}{N^3}\) from \(\mathrm E[|\partial _{\xi _N(n,z)}{{\mathcal {Z}}} (\xi _N)|^3]= \frac{1}{N^3} \mathrm E[|{{\mathcal {Z}}} (\varphi , (n,z))|^3] \mathrm E[|{{\mathcal {Z}}} ((n,z), \psi )|^3]\), where we used the independence between \({{\mathcal {Z}}} (\varphi , (n,z))\) and \({{\mathcal {Z}}} ((n,z), \psi )\). To deduce (2.2), it suffices to show that the moment of the point-to-plane partition function \(\mathrm E[|{{\mathcal {Z}}} ((n,z), \psi )|^3] \ll N\) as \(N\rightarrow \infty \), which holds by Remark 6.5 below.
This heuristic can be made rigorous using the results we establish in Sect. 6. But this argument will not show that \({{\mathcal {Z}}} _N(\xi _N)\) has a unique limit in law. For that, we need to define coarse-grained models and compare \({{\mathcal {Z}}} _N(\xi _N)\), for different N, with the same coarse-grained model. We outline the proof strategy below, which contains many of the same ideas in the heuristic above, but in a more complicated setting.
2.2 A. Coarse-graining
As a first step, for each \(\varepsilon \in (0,1)\), we approximate \({{\mathcal {Z}}} _N\) in \(L^2\) by a coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi , \psi |\Theta _{N,\varepsilon })\), which is a multi-linear polynomial in suitable coarse-grained disorder variables \(\Theta _{N,\varepsilon }\) and depends on N only through \(\Theta _{N,\varepsilon }\). The details will be given in Sect. 4. Here we give a sketch.
We partition \({\mathbb {N}}\times {\mathbb {Z}}^2\) into mesoscopic time-space boxes
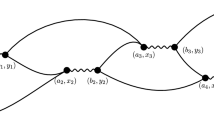
where \(({\textsf{i}}, {\textsf{a}}) \in {\mathbb {N}}\times {\mathbb {Z}}^2\) is the mesoscopic time-space index of \({{\mathcal {B}}} _{\varepsilon N}({\textsf{i}},{\textsf{a}})\), which has temporal width \(\varepsilon N\) and spatial side length \(\sqrt{\varepsilon N}\), and \(({\textsf{a}}-{\textsf{b}}, {\textsf{a}}] = ({\textsf{a}}_1-{\textsf{b}}_1,{\textsf{a}}_1] \times ({\textsf{a}}_2-{\textsf{b}}_2,{\textsf{a}}_2]\) for squares in \({\mathbb {R}}^2\). We then decompose the sum in (2.1) according to the sequence of mesoscopic time intervals \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_1), \ldots , {{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_k)\) visited by the renewal configuration \((n_1, z_1), \ldots , (n_r, z_r)\). For each \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_j)\), we then further decompose according to the first and last mesoscopic spatial boxes \({{\mathcal {S}}} _{\varepsilon N}({\textsf{a}}_j), {{\mathcal {S}}} _{\varepsilon N}({\textsf{a}}_j')\) visited in this time interval. This replaces the microscopic sum over \((n_1, z_1), \ldots , (n_r, z_r)\) in (2.1) by a mesoscopic sum over time-space renewal configurations \(({\textsf{i}}_1; {\textsf{a}}_1, {\textsf{a}}_1'), \ldots , ({\textsf{i}}_k; {\textsf{a}}_k, {\textsf{a}}_k')\), which specify the sequence of mesoscopic boxes \({{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}_j,{\textsf{a}}_j)\) and \({{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}_j,{\textsf{a}}_j')\) visited. See Fig. 1 for an illustration.
Ideally, we would like to replace each random walk kernel \(q_{n, m}(x,y)\) in (2.1) that connects two consecutive visited mesoscopic boxes \({{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}_j,{\textsf{a}}_j')\ni (n,x)\) and \({{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}_{j+1},{\textsf{a}}_{j+1})\ni (m,y)\) by a corresponding heat kernel. Namely, by the local limit theorem (3.21), replace \(q_{n, m}(x,y)\) by
where the factor 2 is due to periodicity. With such replacements, given a mesoscopic renewal configuration \(({\textsf{i}}_1; {\textsf{a}}_1, {\textsf{a}}_1'), \ldots , ({\textsf{i}}_k; {\textsf{a}}_k, {\textsf{a}}_k')\), as we sum over compatible microscopic renewal configurations \((n_1, z_1), \ldots , (n_r, z_r)\) in (2.1), the contributions of \(\xi _N(n,z)\) from each interval \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_j)\) would decouple, leading to a product of coarse-grained disorder variables of the form
with consecutive coarse-grained disorder variables \(\Theta _{N, \varepsilon }({\textsf{i}}_j; {\textsf{a}}_j, {\textsf{a}}_j')\) and \(\Theta _{N, \varepsilon }({\textsf{i}}_{j+1}; {\textsf{a}}_{j+1}, {\textsf{a}}_{j+1}')\) linked by the heat kernel \(g_{\tfrac{1}{2}({\textsf{i}}_{j+1}-{\textsf{i}}_j)}({\textsf{a}}_{j+1}-{\textsf{a}}_j')\) (we absorbed the factor \(\frac{2}{\varepsilon N}\) into (2.5)). This would give our desired coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi , \psi |\Theta _{N,\varepsilon })\).
An illustration of the chaos expansion for the coarse-grained model (2.7). The solid laces represent heat kernels linking consecutively visited mesoscopic time-space boxes. The grey blocks represent the regions defining the coarse-grained disorder variables \(\Theta _{N, \varepsilon }\). The double block in the middle represents a coarse-grained disorder variable \(\Theta _{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) visiting two mesoscopic time intervals \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\) and \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}')\) with \(|{\textsf{i}}'-{\textsf{i}}|\leqslant K_\varepsilon =(\log \frac{1}{\varepsilon })^6\) and cannot be decoupled
Unfortunately, this ideal procedure does not produce a sharp approximation of the partition function \({{\mathcal {Z}}} _N\) in (2.1). Indeed, the kernel replacement
induces an \(L^2\)-error, and this error is small (in the sense that it vanishes as \(\varepsilon \downarrow 0\), uniformly in large N) only if \({\textsf{i}}_{j+1}-{\textsf{i}}_j\) is sufficiently large (we will choose it to be larger than \(K_\varepsilon = (\log \frac{1}{\varepsilon })^6\)) and \(|{\textsf{a}}_{j+1}-{\textsf{a}}_j'|\) is not too large on the diffusive scale (we will choose it to be smaller than \(M_\varepsilon \sqrt{{\textsf{i}}_{j+1}-{\textsf{i}}_j}\) with \(M_\varepsilon =\log \log \frac{1}{\varepsilon }\)). We address this issue as follows.
The first crucial observation is that, modulo a small \(L^2\) error, microscopic renewal configurations \((n_1, z_1)\), ..., \((n_r, z_r)\) in (2.1) cannot visit three or more mesoscopic time intervals \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_j)\), \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_{j+1})\), and \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_{j+2})\) with both \({\textsf{i}}_{j+1}-{\textsf{i}}_j\leqslant K_\varepsilon \) and \({\textsf{i}}_{j+2}-{\textsf{i}}_{j+1}\leqslant K_\varepsilon \) (see Lemma 5.1 below). Furthermore, with a small \(L^2\) error, we can also enforce a diffusive truncation \(|{\textsf{a}}_{j+1}-{\textsf{a}}_j'| \leqslant M_\varepsilon \sqrt{{\textsf{i}}_{j+1}-{\textsf{i}}_j}\) (see Lemma 5.6 below). We will then make the random walk/heat kernel replacement (2.6) only between mesoscopic boxes \({{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}_j,{\textsf{a}}_j')\ni (n,x)\) and \({{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}_{j+1},{\textsf{a}}_{j+1})\ni (m,y)\) that satisfy the constraint \({\textsf{i}}_{j+1}-{\textsf{i}}_j > K_\varepsilon \).
After such kernel replacements, what are left between the heat kernels decouple and appear as a product of two types of coarse-grained disorder variables:
-
one type is as given in (2.5), which visits a single mesoscopic time interval \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\);
-
another type visits two mesoscopic time intervals \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\) and \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}')\), with \({\textsf{i}}' - {\textsf{i}}\leqslant K_\varepsilon \): we denote it by \(\Theta _{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) with \(\vec {\textsf{i}}=({\textsf{i}}, {\textsf{i}}')\) and \(\vec {\textsf{a}}=({\textsf{a}}, {\textsf{a}}')\), where \({\textsf{a}}\) identifies the first mesoscopic spatial box visited in the time interval \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\), while \({\textsf{a}}'\) identifies the last mesoscopic spatial box visited in the time interval \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}')\) (see (4.11)).
This leads to the actual coarse-grained model we will work with:
where \(\varphi _\varepsilon \) and \(\psi _\varepsilon \) are averaged versions of \(\varphi \) and \(\psi \) on the spatial scale \(\sqrt{\varepsilon }\), while \(g_{{\textsf{i}}/2}(\varphi _\varepsilon , {\textsf{a}})\), \(g_{{\textsf{i}}/2}({\textsf{a}}', \psi _\varepsilon )\), \(g_{{\textsf{i}}/2}(\varphi _\varepsilon , \psi _\varepsilon )\) are averages of the heat kernel \(g_{{\textsf{i}}/2}({\textsf{a}}-{\textsf{a}}')\) w.r.t. \(\varphi _\varepsilon \), \(\psi _\varepsilon \), or both.
In the sum in (2.7), we have hidden the various constraints on the mesoscopic time-space variables for simplicity (see (4.8) for the complete definition). Also note that in (2.7) we denote by \(\Theta = (\Theta (\vec {\textsf{i}},\vec {\textsf{a}}))\) a generic family of coarse-grained disorder variables; in order to approximate the averaged partition function \({{\mathcal {Z}}} _N\), we simply set \(\Theta =\Theta _{N, \varepsilon }\).
Remark 2.1
(Self-similarity) The coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta )\) in (2.7) has the same form as the original partition function \({{\mathcal {Z}}} _N\) in (2.1), with \(1/\varepsilon \) in place of N, \(\Theta _{N,\varepsilon }\) in place of \(\xi _N\), and the heat kernel \(g_{{\textsf{i}}/2}\) in place of the random walk kernel \(q_n\). This shows a remarkable degree of self-similarity: coarse-graining retains the structure of the model.
2.3 B. Time-Space Renewal Structure
Once we have defined precisely the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N,\varepsilon })\), see Sect. 4, we need to show that it indeed provides a good \(L^2\) approximations of the original partition function \({{\mathcal {Z}}} _N\), in the following sense:
This approximations will be carried out in Sect. 5, where we rely crucially on the time-space renewal interpretation of the sum in (2.1), which in the continuum limit with \(N\rightarrow \infty \) leads to the so-called Dickman subordinator [18]. This will be reviewed in Sect. 3.5.
2.4 C. Lindeberg Principle
In view of (2.8), given \(\varepsilon >0\) small, we can approximate \({{\mathcal {Z}}} _N\) by \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N,\varepsilon })\), where the \(L^2\) error is uniform in large N and tends to 0 as \(\varepsilon \downarrow 0\). To prove that the laws of \(({{\mathcal {Z}}} _N)_{N\in {\mathbb {N}}}\) form a Cauchy sequence, it then suffices to show that given \(\varepsilon >0\) we can bound the distributional distance between \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{M,\varepsilon })\) and \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N,\varepsilon })\) uniformly in \(M\geqslant N\) large, and furthermore, this bound can be made arbitrarily small by choosing \(\varepsilon >0\) sufficiently small. This would then complete the proof that \({{\mathcal {Z}}} _N\) converges in distribution to a unique limit.
The control of the distributional distance is carried out via a Lindeberg principle for the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N, \varepsilon })\), which is a multilinear polynomial in the family of coarse-grained disorder variables \(\Theta _{N, \varepsilon }=\{\Theta _{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\}\). We note that \(\Theta _{N, \varepsilon }(({\textsf{i}}, {\textsf{i}}'), ({\textsf{a}}, {\textsf{a}}'))\) and \(\Theta _{N, \varepsilon }(({\textsf{j}}, {\textsf{j}}'), ({\textsf{b}}, {\textsf{b}}'))\) have non-trivial dependence if \(({\textsf{i}}, {\textsf{a}})\) or \(({\textsf{i}}', {\textsf{a}}')\) coincides with either \(({\textsf{j}}, {\textsf{b}})\) or \(({\textsf{j}}', {\textsf{b}}')\). We thus need a Lindeberg principle for multilinear polynomials of dependent random variables, which we formulate in Appendix A and is of independent interest.
2.5 D. Functional Inequalities for Green’s Functions
To successfully apply the Lindeberg principle, we need to control the second and fourth moments of the coarse-grained disorder variables \(\Theta _{N, \varepsilon }\). We also need to control the influence of each \(\Theta _{N, \varepsilon }\), which boils down to bounding the fourth moment of the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N, \varepsilon })\), with the choice of boundary conditions \(\psi \equiv 1\) and \(\varphi (x)=\frac{1}{\varepsilon } \mathbb {1}_{|x|\leqslant \sqrt{\varepsilon }}\).
The moment bounds on \(\Theta _{N, \varepsilon }\) and \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N, \varepsilon })\) are technically the most delicate parts of the paper, especially since we need to allow \(\varphi (x)=\frac{1}{\varepsilon } \mathbb {1}_{|x|\leqslant \sqrt{\varepsilon }}\) and \(\psi \equiv 1\). Since the structure of \(\Theta _{N, \varepsilon }\) is similar to an averaged partition function, we will first derive general moment bounds on the averaged partition function \({{\mathcal {Z}}} _N\) in Sect. 6. The fourth moment bound on \(\Theta _{N, \varepsilon }\) then follows as a corollary in Sect. 7.
The approach we develop is different from the methods employed in [51] to bound the moments of the averaged solution of the mollified SHE. Our approach is based on functional inequalities for the Green’s function of random walks (see Lemma 6.8) and it is robust enough to be applied also to the coarse-grained model defined in (2.7), which will be carried out Sect. 8.
3 Notation and tools
In this section, we introduce some basic notation and tools, including the polynomial chaos expansion for the partition function, random walk estimates, the renewal interpretation for the second moment of partition functions and the Dickman subordinator that arises in the continuum limit.
3.1 Random walk and disorder
As in Sect. 1.2, let \((S = (S_n)_{n\geqslant 0}, \mathrm P)\) be the simple symmetric random walk on \({\mathbb {Z}}^2\), whose transition kernel we denote by
Let \((\omega = (\omega (n,z))_{n\in {\mathbb {N}}, z\in {\mathbb {Z}}^2}, {{\mathbb {P}}} )\) be the disorder, given by a family of i.i.d. random variables with zero mean, unit variance and locally finite exponential moments, see (1.1).
The expected overlap between two independent walks is (see [18, Proposition 3.2])
Note that \(R_N\) is the expected number of collisions up to time N between two independent copies of the random walk S when both start from the origin. Also note that \(\gamma \) is the Euler–Mascheroni constant. We further define
where the asymptotic behavior follows by the local limit theorem, see (3.21) below.
In order to deal with the periodicity of simple random walk, we set
Given \(x \in {\mathbb {R}}^d\) with \(d \geqslant 2\), we denote by \([\![ x ]\!]\) the point in \({\mathbb {Z}}^d_\textrm{even}\) closest to x (fix any convention to break the tie if \([\![ x ]\!]\) is not unique). More explicitly, we have
For \(s \in {\mathbb {R}}\) it is convenient to define the even approximation \([\![ s ]\!] \in 2{\mathbb {Z}}\) by
3.2 Partition functions at criticality
The point-to-point partition functions \(Z_{M,N}^\beta (w,z)\) were defined in (1.8). We mainly consider the case \(M=0\), for which we write
The field of diffusively rescaled partition functions \({\mathcal {Z}}^{\beta }_{N; s,t}(\textrm{d}x, \textrm{d}y)\) was introduced in (1.9). In the special case \(s=0\) we simply write:
where we recall that \(\textrm{d}x \, \textrm{d}y\) denotes the Lebesgue measure on \({\mathbb {R}}^2 \times {\mathbb {R}}^2\). We next define averaged partition functions \({\mathcal {Z}}^{\beta }_{N, t}(\varphi , \psi )\) for suitable \(\varphi , \psi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\):
We can rewrite the integrals in (3.8) as sums. For a locally integrable function \(\varphi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\), we define \(\varphi _N : {\mathbb {Z}}^2_\textrm{even}\rightarrow {\mathbb {R}}\) as the average of \(\varphi (\frac{\cdot }{\sqrt{N}})\) over cells \(B(v) \subseteq {\mathbb {R}}^2\), see (3.5):
If we similarly define \(\psi _N: {\mathbb {Z}}^2_\textrm{even}\rightarrow {\mathbb {R}}\) given \(\psi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\), we can rewrite the second line of (3.8) as a sum over the points \(v=[\![ x ]\!], w= [\![ y ]\!] \in {\mathbb {Z}}^2_\textrm{even}\) as follows:
Remark 3.1
(Parity issue) Let \({\mathbb {Z}}^d_\textrm{odd}:= {\mathbb {Z}}^d\backslash {\mathbb {Z}}^d_{\textrm{even}}\). If in (3.10) we sum over \(v,w \in {\mathbb {Z}}^2_\textrm{odd}\), we obtain an alternative “odd version” of the averaged partition function, which is independent of the “even version” because two simple random walks started at even vs. odd sites can never meet. This explains why we enforce a parity restriction in (3.10).
Finally, we recall the critical window of the disorder strength (inverse temperature) that was introduced in (1.11). Given the definition (3.2) of \(R_N\), for some fixed \(\vartheta \in {\mathbb {R}}\), we choose \(\beta = \beta _N=\beta _N(\vartheta )\) such that
We can spell out this condition more explicitly in terms of \(\beta _N\) (see [18, Appendix A.4]):
where \(\kappa _3, \kappa _4\) are the disorder cumulants, i.e. \(\lambda (\beta ) = \frac{1}{2}\beta ^2 + \frac{\kappa _3}{3!} \beta ^3 + \frac{\kappa _4}{4!} \beta ^4 + o(\beta ^4)\) as \(\beta \downarrow 0\), and \(\alpha \simeq 0.208\) is as in (3.2). Henceforth we always set \(\beta = \beta _N\).
3.3 Polynomial chaos expansion
We now recall the polynomial chaos expansion of the partition function. This is based on the following product expansion, valid for any set A and any family of real numbers \((h_n)_{n\in A}\) labelled by A:
If we apply (3.13) to the partition function \(Z^{\beta _N}_{d,f}(x,y)\) in (1.8), by (3.1) we obtain
Recalling (3.11), we introduce a family \((\xi _N(n,z))_{(n,z) \in {\mathbb {Z}}^2}\) of i.i.d. random variables by
These variables allow us to write
hence, by the Markov property for the random walk with kernel q, we get
where \(\prod _{j=2}^r (\ldots ) := 1\) if \(r=1\). We have expressed the point-to-point partition function as a multilinear polynomial (polynomial chaos) in the independent random variables \(\xi _N(n,z)\).
A similar polynomial chaos representation holds for the averaged partition function \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi ,\psi )\) given in (3.10). To simplify notation, it is convenient to define an averaged version of the random walk transition kernel \(q_{m,n}(x,y)\). Given suitable \(\varphi , \psi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\), a time horizon \(M \in (0,\infty )\), and two points \((m, w), (n, z) \in {\mathbb {Z}}^3_{\textrm{even}}\), recalling \(\varphi _N\) and \(\psi _N\) from (3.9), we define
Then (3.15) yields the following polynomial chaos expansion for \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi ,\psi )\) in (3.10):
As will be explained later, when it comes to second moment calculations, the time-space points \((n_1, z_1), \ldots , (n_r, z_r)\) in the sum can be interpreted as a time-space renewal configuration.
3.4 Random walk estimates
Let \(g_t: {\mathbb {R}}^2 \rightarrow (0,\infty )\) denote the heat kernel on \({\mathbb {R}}^2\):
where, unless otherwise specified, we denote by \(|\cdot |\) the Euclidean norm on \({\mathbb {R}}^d\).
The asymptotic behavior of the random walk transition kernel \(q_n(x) = \mathrm P(S_n = x)\) is given by the local central limit theorem: as \(n\rightarrow \infty \) we have, uniformly for \(x\in {\mathbb {Z}}^2\),
where the two lines are two different variants of the local central limit theorem for the simple symmetric random walk on \({\mathbb {Z}}^2\) given by Theorems 2.3.5 and 2.3.11 in [66]. We recall that \({\mathbb {Z}}^d_\textrm{even}\) is defined in (3.4), the multiplicative factor 2 comes from the periodicity of the simple random walk \(S_n = (S^{(1)}_n, S^{(2)}_n)\) on \({\mathbb {Z}}^2\), while the factor \(\frac{1}{2}\) in the time argument of the heat kernel comes from the fact that \(\mathrm E[S_n^{(i)} S_n^{(j)}] = \frac{n}{2} \, \mathbb {1}_{i=j}\). We also note that
Similar to the averaged random walk kernels \(q^N_{\cdot , \cdot }\) defined in (3.16)–(3.18), given \(\varphi \in L^1({\mathbb {R}}^2)\), \(\psi \in L^\infty ({\mathbb {R}}^2)\), \(t > 0\), and \(a,b \in {\mathbb {R}}^2\), we define the averaged heat kernels
Recall \(q^N_{0, Nt}(\varphi , \psi )\) from (3.18). By the local limit theorem (3.21), recalling (3.9) and (3.22), we have
where the prefactor \(\frac{1}{2}\) is due to periodicity.
We will also need the following lemma, which allows us to replace a random walk transition kernel by a heat kernel even if the time-space increments are perturbed.
Lemma 3.2
Let \(q_n(\cdot )\) be the transition kernel of the simple symmetric random walk on \({\mathbb {Z}}^2\), see (3.1), and let \(g_t(\cdot )\) be the heat kernel on \({\mathbb {R}}^2\), see (3.20). Then there exists \(C\in (0, \infty )\) such that, for all \(n \in {\mathbb {N}}\) and for all \(x \in {\mathbb {Z}}^2\) with \(|x|\leqslant n^{\frac{3}{4}}\), we have
Let \(\varrho _1, \varrho _2>0\) and set \(C := 2 e \, \varrho _1 \, \varrho _2\). Then, given an arbitrary \(m\in {\mathbb {N}}\), for all \(n_1, n_2 \in {\mathbb {N}}\) with \(n_1 \geqslant m\) and \(\frac{n_2}{n_1}\in [1/\varrho _1, \varrho _2]\), and for all \(x_1, x_2\in {\mathbb {R}}^2\) with \(|x_1-x_2|\leqslant \sqrt{m}\), we have
Proof
Let us prove (3.27): by the second variant of the local limit theorem in (3.21),
We next prove (3.28): by the assumption \(\frac{n_2}{n_1}\in [1/\varrho _1, \varrho _2]\), we have
where the last inequality holds because \(|x_2|^2 \leqslant 2 (|x_1|^2 + |x_2-x_1|^2) \leqslant 2 |x_1|^2 + 2 m\) and \(n_1 \geqslant m\) by assumption. \(\square \)
3.5 Renewal estimates and Dickman subordinator
We next present the time-space renewal process underlying the second moment calculations for the partition function. Under diffusive scaling, this leads to the so-called Dickman subordinator in the continuum limit. This approach was developed in [18, 19].
We first define a slight modification of the partition function \(Z_{d,f}^\beta (x,y)\) in (1.8), where we “attach” disorder variables \(\xi _N(n,z)\), see (3.14), at the boundary points (d, x) and (f, y) (which may coincide, if \(d=f\)):
Such quantities will appear as basic building blocks in our proofs. Note that \({{\mathbb {E}}} [X^{\beta _N}_{d,f}(x,y)] = 0\). The second moment of \(X^{\beta _N}_{d,f}(x,y)\) can be computed explicitly by the polynomial chaos expansion (3.15) and it can be expressed as follows:
where we recall that \(\sigma _N^2={\mathbb {V}}\textrm{ar}(\xi _N(a,x))\), and for \(n\in {\mathbb {N}}_0 = \{0,1,2,\ldots \}\) and \(x \in {\mathbb {Z}}^2\) we define
The quantity \(U_N(n,x)\), which plays an important role throughout this paper, admits a probabilistic interpretation as a renewal function. More precisely, let \((\tau ^{(N)}_r, S^{(N)}_r)_{r\geqslant 0}\) denote the random walk (time-space renewal process) on \({\mathbb {N}}_0 \times {\mathbb {Z}}^2\) starting at (0, 0) and with one-step distribution
where \(R_N\) is the random walk overlap defined in (3.2). Then we can write, recalling (3.11),
When \(\lambda _N=1\), we see that \(U_N(n,x)\) is just the renewal function of \((\tau ^{(N)}_r, S^{(N)}_r)_{r\geqslant 0}\). When \(\lambda _N\ne 1\), we can think of \(U_N(n,x)\) as an exponentially weighted renewal function, weighted according to the number of renewals. Note that the first component \(\tau ^{(N)} = (\tau ^{(N)}_r)_{r\geqslant 0}\) is a renewal process with one-step distribution
where \(u(n)=\sum _x q_n(x)^2\) is defined in (3.3). Correspondingly, we can define
The asymptotic behaviors of \(U_N(n,x)\) and \(U_N(n)\) were obtained in [18], exploiting the fact that \(\tau ^{(N)}\) is in the domain of attraction of the so-called Dickman subordinator, defined as the pure jump Lévy process with Lévy measure \(\frac{1}{x} \, \mathbb {1}_{(0,1)}(x) \, \textrm{d}x\). More precisely, we have the following convergence result, which is an extension of [18, Proposition 2.2] from finite dimensional distribution convergence to process level convergence.
Lemma 3.3
Let \((\tau ^{(N)}_r, S^{(N)}_r)_{r\geqslant 0}\) be the space-time random walk defined in (3.32). Let \((Y_s)_{s\geqslant 0}\) be the so-called Dickman subordinator [18], i.e. the pure jump Lévy process with Lévy measure \(\frac{1}{t}\mathbb {1}_{(0,1)}(t)\textrm{d}t\), and let \(V_s:= \frac{1}{2} W_{Y_s}\) where W is an independent Brownian motion. Then we have the convergence in distribution
on the space of càdlàg paths equipped with the Skorohod topology.
Proof
Denote \({\varvec{Y}}^{(N)}_s=(Y^{(N)}_s, V^{(N)}_s):= \Big (\frac{\tau ^{(N)}_{\lfloor s\log N\rfloor }}{N}, \frac{S^{(N)}_{\lfloor s\log N\rfloor }}{\sqrt{N}} \Big )\). The convergence of finite dimensional distributions was already proved in [18, Proposition 2.2]. We prove tightness by verifying Aldous’ tightness criterion [62, Theorem 14.11], namely that for any bounded sequence of stopping times \(\tau _N\) with respect to \(({\varvec{Y}}^{(N)}_s)_{s\geqslant 0}\) and any positive constants \(h_N\downarrow 0\), we have \({\varvec{Y}}^{(N)}_{\tau _N+h_N}-{\varvec{Y}}^{(N)}_{\tau _N}\rightarrow 0\) in probability as \(N\rightarrow \infty \). This follows immediately from the fact that the increments of \({\varvec{Y}}^{(N)}\) are i.i.d. and \({\varvec{Y}}^{(N)}_{h_N}\rightarrow (0,0)\) in probability as \(N\rightarrow \infty \). \(\square \)
For \(\vartheta \in (0,\infty )\), we define the exponentially weighted Green’s function for \({\varvec{Y}}= ({\varvec{Y}}_s)_{s\geqslant 0}\):
where \({\varvec{f}}_s(\cdot , \cdot )\) is the density of the law of \({\varvec{Y}}_s\) on \([0,\infty )\times {\mathbb {R}}^2\), given that \({\varvec{Y}}_0=(0,0)\) (we take notation from (3.36)). It was shown in [18] that
where \(g_\cdot (\cdot )\) is the heat kernel, see (3.20), and \({\widehat{G}}_\vartheta (t) :=\int _{{\mathbb {R}}^2} {\widehat{G}}_\vartheta (t,x) \textrm{d}x\) is closely related to the so-called Dickman function in number theory. For \(t\leqslant 1\), it can be computed explicitly as
with \(\gamma \) as in (3.2) (see [18]Footnote 3). We will also denote \(G_\vartheta (t,x) := G_\vartheta (t) \, g_{\frac{t}{4}}(x)\). Note that for \(t\leqslant 1\), \(G_\vartheta (t,x)\) and \(G_\vartheta (t)\) are the continuum analogues of \(U_N(n,x)\) and \(U_N(n)\), respectively. It is therefore no surprise that the asymptotics of \(U_N\) will be expressed in terms of \(G_\vartheta \), which we record below for later use.
In light of (3.30), it is convenient to define
Recalling (3.31), we can give a graphical representation for \(\overline{U}_N(b-a,y-x)\) as follows:

where in the second line we assign weights \(q_{n'-n}(x'-x)\) to any solid line going from (n, x) to \((n',x')\) and we assign weight \(\sigma _N^2\) to every solid dot.
Recall that \(\sigma _N^2 \sim \frac{\pi }{\log N}\), see (3.11) and (3.2). We now rephrase some results from [18]. Fix \(T>0\).
-
By [18, Theorem 1.4], for any fixed \(\delta > 0\), as \(N\rightarrow \infty \) we have
$$\begin{aligned} \overline{U}_N(n) = \frac{\pi }{N} \, \big ( G_\vartheta \big (\tfrac{n}{N}\big ) + o(1)\big ) \qquad \textrm{uniformly} \ \ \textrm{for} \ \ \delta N \leqslant n \leqslant T N ,\nonumber \\ \end{aligned}$$(3.42)and moreover there is \(C < \infty \) such that
$$\begin{aligned} \overline{U}_N(n) \leqslant \frac{C}{N} \, G_\vartheta \big (\tfrac{n}{N}\big ) \qquad \forall 0 < n \leqslant T N . \end{aligned}$$(3.43) -
By [18, Theorem 2.3 and 3.7], for any fixed \(\delta > 0\), as \(N\rightarrow \infty \) we have
$$\begin{aligned} \begin{aligned} \overline{U}_N(n,x)&= \frac{\pi }{N^2} \, \big ( G_\vartheta \big (\tfrac{n}{N}, \tfrac{x}{\sqrt{N}}\big ) + o(1)\big ) \, 2 \, \mathbb {1}_{(n,x) \in {\mathbb {Z}}^3_\textrm{even}} \\&\quad \text {uniformly for} \ \ \delta N \leqslant n \leqslant T N \ \ \text {and} \ \ |x| \leqslant \tfrac{1}{\delta } \sqrt{N} . \end{aligned} \end{aligned}$$(3.44)The prefactor 2 is due to periodicity and, moreover, there is \(C < \infty \) such that
$$\begin{aligned} \overline{U}_N(n,x) \leqslant \frac{C}{N} \, \frac{1}{n} \, G_\vartheta \big (\tfrac{n}{N}\big ) \qquad \forall 0 < n \leqslant T N , \ \forall x \in {\mathbb {Z}}^2 . \end{aligned}$$(3.45) -
By [18, Proposition 1.6], for \(t\in (0,1]\) the function \(G_\vartheta (t)\) is \(C^\infty \) and strictly positive, and as \(t \downarrow 0\) it has the following asymptotic behavior:
$$\begin{aligned} G_\vartheta (t) = \frac{1}{t(\log \frac{1}{t})^2} \bigg \{ 1 + \frac{2\vartheta }{\log \frac{1}{t}} + O\bigg (\frac{1}{(\log \frac{1}{t})^2}\bigg ) \bigg \} , \end{aligned}$$(3.46)hence as \(t \downarrow 0\)
$$\begin{aligned} \int _0^t G_\vartheta (s) \textrm{d}s = \frac{1}{\log \frac{1}{t}} \bigg \{ 1 + \frac{\vartheta }{\log \frac{1}{t}} + O\bigg (\frac{1}{(\log \frac{1}{t})^2}\bigg ) \bigg \} . \end{aligned}$$(3.47)
Remark 3.4
In the proof of (3.42)–(3.45), the case \(T>1\) has to be treated differently from \(T=1\). In [18], the case \(T>1\) was reduced to \(T=1\) through a renewal decomposition and recursion (see [18, Section 7]). Alternatively, we can reduce the case \(T>1\) to \(T=1\) by first setting \({\widetilde{N}}:=TN\), \({\tilde{\vartheta }}:= \vartheta +\log T+o(1)\) so that \(\sigma _{N}^{2}=\sigma _{N}^{2}(\vartheta ) = \sigma _{\widetilde{N}}^2(\tilde{\vartheta })\) by their definitions in (3.11), and then applying (3.42)–(3.45) with N replaced by \(\widetilde{N}\), using the observation that \(\frac{1}{T}G_{\vartheta +\log T}(\tfrac{t}{T}) = G_\vartheta (t)\).
We will also need the following bound to complement (3.44).
Lemma 3.5
There exists \(c\in (0,\infty )\) such that for all \(\lambda \geqslant 0\) and \(0\leqslant n\leqslant N\),
Note that by the Markov inequality and optimisation over \(\lambda >0\), (3.48) implies that the probability kernel \(\overline{U}_N(n,\cdot )/\overline{U}_N(n)\) has Gaussian decay on the spatial scale \(\sqrt{n}\).
Proof
Recall the definition of \(U_N(n,x)\) from (3.33). Conditioned on \(\tau ^{(N)}_1, \ldots , \tau ^{(N)}_r\) with \(\tau ^{(N)}_r=n\), we can write \(S^{(N)}_r=\zeta _1+\cdots +\zeta _r\) for independent \(\zeta _i\)’s with
where \(n_i:=\tau ^{(N)}_i - \tau ^{(N)}_{i-1}\) and \(x\in {\mathbb {Z}}^2\). For each i, denote by \(\zeta _{i,1}\) and \(\zeta _{i,2}\) the two components of \(\zeta _i\in {\mathbb {Z}}^2\). Then we note that there exists \(c>0\) such that for any \(\lambda \geqslant 0\), \(n_i \in {\mathbb {N}}\),
This can be seen by Taylor expanding the exponential and using that \(\mathrm E[\zeta _{i,\cdot }]=0\) by symmetry, \(|\mathrm E[\zeta ^{2k+1}_{i,\cdot }]| \leqslant \frac{1}{2}(\mathrm E[\xi ^{2k}_{i,\cdot }] + \mathrm E[\zeta ^{2k+2}_{i,\cdot }])\) by Young’s inequality, as well as \(\mathrm E[\zeta ^{2k}_{i,\cdot }] \leqslant (Cn_i)^k (2k-1)!!\) for some \(C>0\) uniformly in \(n_i, k\in {\mathbb {N}}\). The bound on \(\mathrm E[\zeta ^{2k}_{i,\cdot }]\) holds because by (3.21),
where \(q_{n_i}\) has the same Gaussian tail decay as the heat kernel \(g_{n_i/2}\). Using \(e^{|x|} \leqslant e^x+e^{-x}\), this then implies
The bound (3.48) then follows readily from the definitions of \(U_N(n,x)\) and \(U_N(n)\) in (3.33) and (3.35), recalling that \(\overline{U}_N(n,x)\) and \(\overline{U}_N(n)\) are defined in (3.40). \(\square \)
3.6 Second moment of averaged partition function
Using \(X^{\beta _N}_{d,f}(x,y)\) as introduced in (3.29), and recalling (3.15), we can now rewrite the chaos expansion for the averaged partition function \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi ,\psi )\) in (3.19) as follows:
so that by (3.30) and the fact that \(\overline{U}_N:=\sigma _N^2 U_N\), we have
We now compute the limit of \({{\mathbb {E}}} \big [{\mathcal {Z}}^{\beta _N}_{N, t}(\varphi ,\psi )^2 \big ]\) as \(N\rightarrow \infty \). This was first obtained for the Stochastic Heat Equation in [7] in the special case \(\psi \equiv 1\); see also [19, Theorems 1.2 and 1.7] for an alternative derivation, that also includes directed polymers.
Proposition 3.6
(First and second moments) Recall \(G_\vartheta (t)\) from (3.39) for all \(t>0\). For \(\varphi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\), defineFootnote 4
Then for all \(\varphi \) with \(\Vert \varphi \Vert _{{{\mathcal {G}}} _t}<\infty \) and all \(\psi \in L^\infty ({\mathbb {R}}^2)\), we have
where
and the kernel \(K_{t}^{\vartheta }\) is defined by
Proof
The first moment convergence (3.53) holds because by \({{\mathbb {E}}} \big [{\mathcal {Z}}^{\beta _N}_{N, t}(\varphi , \psi ) \big ]\! = q^{N}_{0,Nt}(\varphi ,\psi )\), see (3.50), in view of the asymptotic relation (3.26).
For the second moment computation (3.54) we exploit (3.51), where the first term in the r.h.s. converges to \(\frac{1}{4} \, g_{t/2}(\varphi ,\psi )^2\) by (3.26), which matches the first term in the r.h.s. of (3.54). It remains to show that the sum in (3.51) converges to the term \(\frac{1}{2} {\mathscr {V}}_{t}^{\vartheta }(\varphi ,\psi )\) in (3.54).
Recall the definition of \(q^N_\cdot \) in (3.16)–(3.17). By the local limit theorem (3.21) and in view of (3.22), we see that for any \(\varepsilon > 0\), uniformly for \(m > \varepsilon N\) and \(w \in {\mathbb {Z}}^2\), we have as \(N\rightarrow \infty \)
and similarly, uniformly for \(n \leqslant (1- \varepsilon ) Nt\) and \(z \in {\mathbb {Z}}^2\),
Applying the asymptotic relation (3.44) for \(\overline{U}_N(f-d,y-x)\), we see that the sum in (3.51) is a Riemann sum that converges as \(N\rightarrow \infty \) to the multiple integralFootnote 5
where the prefactor \(\frac{1}{2}\) results from combining the periodicity factor 2 in (3.44) with the volume factor \(\frac{1}{2} \cdot \frac{1}{2}\) which originates from the restrictions \((d,x), (f,y)\in {\mathbb {Z}}^3_{\textrm{even}}\) in (3.51). Then it follows by (3.23), (3.24) and (3.38) that the equality in (3.55) holds with
We can simplify both brackets via the identity \(g_t(x) \, g_t(y) = g_{2t}(x-y) \, g_{\frac{t}{2}}(\frac{x+y}{2})\), see (3.20). Performing the integrals over \(a,b \in {\mathbb {R}}^2\) we then obtain (3.56).
The bound in (3.55) follows by bounding \(\psi \) with \(\Vert \psi \Vert _\infty \) and then successively integrating out \(w, w'\), followed by u and s in (3.56). \(\square \)
Remark 3.7
(Point-to-plane partition function) For \(\psi (w) = \mathbb {1}(w) \equiv 1\), we can view \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi , \mathbb {1})\) as the point-to-plane partition function \(Z_N^{\beta _N}(z)\) in (1.3) averaged over its starting point z. By (3.53)–(3.56),
where we set
We note that both the asymptotic mean and the asymptotic variance of \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi , \mathbb {1})\) are half of those obtained in [19, eq. (1.19)–(1.20)]. This is because here we have defined \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi ,\psi )\) as a sum over \({\mathbb {Z}}^2_\textrm{even}\), see (3.10), while in [19], the sum is over both \({\mathbb {Z}}^2_\textrm{odd}\) and \({\mathbb {Z}}^2_\textrm{even}\), which give rise to two i.i.d. limits as \(N\rightarrow \infty \) by the parity of the simple random walk on \({\mathbb {Z}}^2\).
4 Coarse-graining
In this section, we give the details of how to coarse-grain the averaged partition function and what is the precise definition of the coarse-grained model, which were outlined in Sect. 2. The main result is Theorem 4.7, which shows that the averaged partition function \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi ,\psi )\), see (3.10), can be approximated in \(L^2\) by the coarse-grained model.
4.1 Preparation
The starting point is the polynomial chaos expansion (3.19) for the averaged partition function \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi ,\psi )\), which is a multilinear polynomial in the disorder variables \(\xi _N(n,z)\). We will call the sequence of time-space points \((n_1, z_1)\), ..., \((n_r, z_r)\in {\mathbb {N}}\times {\mathbb {Z}}^2\) in the sum in (3.19) a microscopic (time-space) renewal configuration. We assume that the disorder strength is chosen to be \(\beta _N=\beta _N(\vartheta )\) as defined in (3.11)–(3.12). For simplicity, we assume the time horizon to be tN with \(t=1\).
Given \(\varepsilon \in (0,1)\) and \(N\in {\mathbb {N}}\), we partition discrete time-space \(\{1,\ldots , N\} \times {\mathbb {Z}}^2\) into mesoscopic boxes
where \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\) is mesoscopic time interval and \({{\mathcal {S}}} _{\varepsilon N}({\textsf{a}})\) a mesoscopic spatial square.Footnote 6 These boxes are indexed by mesoscopic variables
Recall from Sect. 2 that to carry out the coarse-graining, we need to organize the chaos expansion (3.19) according to which mesoscopic boxes \({{\mathcal {B}}} _{\varepsilon N}\) are visited by the microscopic renewal configuration \((n_1, z_1)\), ..., \((n_r, z_r)\). To perform the kernel replacement (2.6), which allows each summand in the chaos expansion (3.19) to factorize into a product of coarse-grained disorder variables \(\Theta _{N, \varepsilon }\) connected by heat kernels, we will impose some constraints on the set of visited mesoscopic time intervals \({{\mathcal {T}}} _{\varepsilon N}(\cdot )\) and spatial boxes \({{\mathcal {S}}} _{\varepsilon N}(\cdot )\), which will be shown to have negligible costs in \(L^2\). We first introduce the necessary notation.
Let us fix two thresholds
We will require that the visited mesoscopic time intervals \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_1)\), ..., \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_k)\) belong to
We call this the no-triple condition, since it forbids three consecutive mesoscopic time indices \({\textsf{i}}_j, {\textsf{i}}_{j+1}, {\textsf{i}}_{j+2}\) with both \({\textsf{i}}_{j+1} -{\textsf{i}}_j< K_\varepsilon \) and \({\textsf{i}}_{j+2} -{\textsf{i}}_{j+1}< K_\varepsilon \). We can then partition \(({\textsf{i}}_1, \ldots , {\textsf{i}}_k)\) into time blocks such that \({\textsf{i}}_j, {\textsf{i}}_{j+1}\) belong to the same block whenever \({\textsf{i}}_{j+1}-{\textsf{i}}_j<K_\varepsilon \).
Definition 4.1
(Time block) We call a time block any pair \(\vec {\textsf{i}}= ({\textsf{i}}, {\textsf{i}}') \in {\mathbb {N}}\times {\mathbb {N}}\) with \({\textsf{i}}\leqslant {\textsf{i}}'\). The width of a time block is
The (non symmetric) “distance” between two time blocks \(\vec {\textsf{i}}, \vec {\textsf{m}}\) is defined by
and we write “\(\,\vec {\textsf{i}}< \vec {\textsf{m}}\)” to mean that “\(\,\vec {\textsf{i}}\) precedes \(\vec {\textsf{m}}\)” :
With the partitioning of the indices \(({\textsf{i}}_1, \ldots , {\textsf{i}}_k)\) of the visited mesoscopic time intervals into consecutive time blocks as defined above, which we denote by \(\vec {\textsf{i}}_1=({\textsf{i}}_1, {\textsf{i}}_1')\), ..., \(\vec {\textsf{i}}_r=({\textsf{i}}_r, {\textsf{i}}_r')\) with possibly \({\textsf{i}}_\ell ={\textsf{i}}_\ell '\), the constraint \({{\mathcal {A}}} _{\varepsilon }^{(\mathrm {no\, triple})}\) then becomes the following:
If the time horizon is Nt with \(t\ne 1\), then in (4.3) and (4.4) we just replace the upper bound \(\vec {\textsf{i}}_r \leqslant \lfloor \tfrac{1}{\varepsilon }\rfloor - K_\varepsilon \) by \(\vec {\textsf{i}}_r \leqslant \lfloor \tfrac{t}{\varepsilon }\rfloor - K_\varepsilon \).
Given a time block \(\vec {\textsf{i}}=({\textsf{i}}, {\textsf{i}}')\) with \({\textsf{i}}'-{\textsf{i}}+1\leqslant K_\varepsilon \) (possibly \({\textsf{i}}={\textsf{i}}'\)), which identifies two mesoscopic time intervals \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\) and \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}')\) visited by the microscopic renewal configuration \((n_1, z_1), \ldots , (n_r, z_r)\) from (3.19) and no intervals in-between is visited, we can identify the first and last mesoscopic spatial boxes visited in the time intervals \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\) and \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}')\), respectively. We call this pair of mesoscopic spatial indices a space block.
Definition 4.2
(Space block) We call a space block any pair \(\vec {\textsf{a}}= ({\textsf{a}},{\textsf{a}}') \in {\mathbb {Z}}^2 \times {\mathbb {Z}}^2\). The width of a space block is
with \(|\cdot |\) being the Euclidean norm. The (non symmetric) “distance” between two space blocks \(\vec {\textsf{a}}, \vec {\textsf{b}}\) is
Putting the time block and space block together, we have the following.
Definition 4.3
(Time-space block) We call a time-space block any pair \((\vec {\textsf{i}}, \vec {\textsf{a}})\) where \(\vec {\textsf{i}}\) is a time block and \(\vec {\textsf{a}}\) is a space block. We also define
In (3.19), we will restrict to \((n_1, z_1), \ldots , (n_r, z_r)\) (interpreted as a time-space renewal configuration) that satisfy condition (4.3), so that they determine a sequence of mesoscopic time-space blocks \(\{(\vec {\textsf{i}}_1, \vec {\textsf{a}}_1)\), ..., \((\vec {\textsf{i}}_r, \vec {\textsf{a}}_r)\} \in \vec {\varvec{{\mathcal {A}}}}_{\varepsilon }^{(\mathrm {no\, triple})}\). This would give the main contribution in (3.19). We now impose further constraints on the spatial components that still capture the main contribution.
Given two “boundary variables” \({\textsf{b}}, {\textsf{c}}\in {\mathbb {Z}}^2\) and a sequence of time blocks \((\vec {\textsf{i}}_1, \ldots , \vec {\textsf{i}}_r)\), we denote by \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; \,{\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})} = \vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; \, {\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}(\vec {\textsf{i}}_1, \ldots , \vec {\textsf{i}}_r)\) the following subset of space blocks \((\vec {\textsf{a}}_1, \ldots , \vec {\textsf{a}}_r)\), where we impose diffusive constraints on their widths and distances:
Given a sequence of mesoscopic time-space blocks \((\vec {\textsf{i}}_1, \vec {\textsf{a}}_1)\), ..., \((\vec {\textsf{i}}_r, \vec {\textsf{a}}_r)\) determined by the microscopic renewal configuration \((n_1, z_1), \ldots , (n_r, z_r)\) from (3.19), which satisfies the constraints \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon }^{(\mathrm {no\, triple})}\) and \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; \,{\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}\), we will perform the kernel replacement (2.6), which leads to a factorization of each summand in (3.19) as the product of coarse-grained disorder variables \(\Theta _{N, \varepsilon }(\vec {\textsf{i}}_j, \vec {\textsf{a}}_r)\), \(1\leqslant j\leqslant r\), connected by the heat kernels \(g_{\tfrac{1}{2}({\textsf{i}}_{j+1}-{\textsf{i}}_j)}({\textsf{a}}_{j+1}-{\textsf{a}}_j')\). See Fig. 2.
An illustration of the coarse-graining procedure. The solid lines represent the heat kernels after the kernel replacement (2.6), which connect adjacent coarse-grained disorder variables \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) consisting of sums over the dashed lines in each visited time-space block \({{\mathcal {B}}} _{\varepsilon N}(\vec {\textsf{i}},\vec {\textsf{a}})\) (see (4.11)). The solid and the dashed lines satisfy the diffusive constraint given in \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; \,{\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}\) and (4.11), respectively
4.2 Coarse-grained model
We are now ready to give the precise definition of the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta )\) given earlier in (2.7), which depends on \(\varepsilon \in (0,1)\) and is a multilinear polynomial of a given family of random variables \(\Theta =\{\Theta (\vec {\textsf{i}}, \vec {\textsf{a}})\}\) indexed by time-space blocks \((\vec {\textsf{i}},\vec {\textsf{a}})\).
Definition 4.4
(Coarse-grained model) Fix \(\varepsilon \in (0,1)\) and a family of random variables \(\Theta = (\Theta (\vec {\textsf{i}},\vec {\textsf{a}}))_{(\vec {\textsf{i}},\vec {\textsf{a}}) \in {{\mathbb {T}}} _\varepsilon }\) indexed by the set \({{\mathbb {T}}} _\varepsilon \) of time-space blocks defined in (4.5). Fix two locally integrable functions \(\varphi , \psi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\) and define \(\varphi _\varepsilon , \psi _\varepsilon : {\mathbb {Z}}^2 \rightarrow {\mathbb {R}}\) as follows:
Recall the heat kernel \(g_t(\cdot )\) from (3.20). Then the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta )\) is
Note that in (4.8), for technical reasons that will become clear later (to control the error induced by kernel replacements—see Sect. 5.3), we also imposed the constraint that the number of time-space blocks cannot exceed \((\log \frac{1}{\varepsilon })^2\). This coarse-grained model has the same structure as the original averaged partition function \({\mathcal {Z}}^{\beta _N}_{N, 1}(\varphi ,\psi )\) in (3.19), with \(1/\varepsilon \) replacing N, \(\Theta \) replacing \(\xi _N\), and the heat kernels replacing the random walk kernels. Note that when \(\varphi \) has compact support, (4.8) is a sum over finitely many terms.
Remark 4.5
To approximate the averaged partition function \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi ,\psi )\) with \(t\ne 1\), we define a corresponding coarse-grained model \({\mathscr {Z}}_{\varepsilon , t}^{(\textrm{cg})}(\varphi ,\psi |\Theta )\) which is obtained from (4.8) simply replacing \(g_{\frac{1}{2}}(\varphi , \psi )\) by \(g_{\frac{t}{2}}(\varphi , \psi )\) and \(g_{\frac{1}{2}(\lfloor \tfrac{1}{\varepsilon }\rfloor - {\textsf{i}}_r')}\) by \(g_{\frac{1}{2}(\lfloor \tfrac{t}{\varepsilon }\rfloor - {\textsf{i}}_r')}\), as well as modifying accordingly \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon }^{(\mathrm {no\, triple})}\) and \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; \, b,c}^{(\textrm{diff})}\) (replacing \(\lfloor \frac{1}{\varepsilon }\rfloor \) by \(\lfloor \frac{t}{\varepsilon }\rfloor \) therein).
4.3 Coarse-grained disorder variables
We now identify the coarse-grained disorder variables \(\Theta _{N, \varepsilon }^{\mathrm{(cg)}}\) so that the averaged partition function \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi , \psi )\) can be approximated in \(L^2\) by the coarse-grained model \({\mathscr {Z}}_{\varepsilon , t}^{(\textrm{cg})}(\varphi ,\psi |\Theta )\) with \(\Theta =\Theta _{N, \varepsilon }^\mathrm{(cg)}\).
Recall the point-to-point partition function \(Z_{d,f}^{\beta _N}(x,y)\) with its chaos expansion as in (3.15). Assuming \(f-d\leqslant \varepsilon N\), we introduce a diffusive truncation as follows, the effect of which will be negligible in \(L^2\), but it ensures that the coarse-grained disorder variable \(\Theta _{N, \varepsilon }^{\mathrm{(cg)}}\) will only depend on \(\xi _N(n,z)\) in a localized time-space window. In (3.15), let \({\textsf{a}}= {\textsf{a}}(x) \in {\mathbb {Z}}^2\) be such that \(x \in {{\mathcal {S}}} _{\varepsilon N}({\textsf{a}})\) (recall (4.1)). We then restrict y and all space variables \(z_j\) in (3.15) to those mesoscopic boxes \({{\mathcal {S}}} _{\varepsilon N}({\tilde{{\textsf{a}}}})\) with \(|{\tilde{{\textsf{a}}}} - {\textsf{a}}| \leqslant M_\varepsilon = \log \log \frac{1}{\varepsilon }\) as in (4.2), and define
Similar to the definition of \(X_{d,f}^{\beta _N}(x,y)\) in (3.29), we define
Note that we omit the dependence of \(Z^{(\textrm{diff})}_{d,f}(x,y)\) and \(X^{(\textrm{diff})}_{d,f}(x,y)\) on \(N, \varepsilon \).
The coarse-grained disorder variables \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) are defined as follows (see Fig. 2).
Definition 4.6
(Coarse-grained disorder variable) Given \(N\in {\mathbb {N}}\), \(\varepsilon \in (0,1)\) and a time-space block \((\vec {\textsf{i}},\vec {\textsf{a}})\), with \(\vec {\textsf{i}}= ({\textsf{i}},{\textsf{i}}')\) and \(\vec {\textsf{a}}= ({\textsf{a}},{\textsf{a}}')\), the associated coarse-grained disorder variable \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) is defined by
In the special case \(|\vec {\textsf{i}}|=1\), i.e., \({\textsf{i}}={\textsf{i}}'\), we will also write \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }({\textsf{i}}; {\textsf{a}}, {\textsf{a}}')\) in place of \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\).
We point out that the prefactor 2 in (4.11) is due to periodicity, because the sums are restricted to \({{\mathcal {B}}} _{\varepsilon N}({\textsf{i}},{\textsf{a}}) \subseteq {\mathbb {Z}}^3_\textrm{even}\), see (4.1).
4.4 Coarse-graining approximation
We can finally state the key result of this section, which approximates the averaged partition function \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi , \psi )\) in \(L^2\) by the coarse-grained model \({\mathscr {Z}}_{\varepsilon , t}^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N, \varepsilon }^{\mathrm{(cg)}})\), with an error which is much smaller than \({\mathbb {V}}\textrm{ar}({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi ,\psi ))\) in (3.55) when N is large and \(\varepsilon \) is small. Recall \(\Vert \cdot \Vert _{{{\mathcal {G}}} _t}\) from (3.52).
Theorem 4.7
(Coarse-graining) Let \({{\mathcal {Z}}} _{N,t}^{\beta _{N}}(\varphi , \psi )\) be the averaged partition function in (3.8), where \(\beta _{N}=\beta _{N}(\vartheta )\) satisfies (3.11) for some fixed \(\vartheta \in {\mathbb {R}}\). Let \({\mathscr {Z}}_{\varepsilon ,t}^{(\textrm{cg})}(\varphi ,\psi |\Theta )\) be the coarse-grained model from (4.8), with \(K_\varepsilon =(\log \frac{1}{\varepsilon })^6\) and \(M_\varepsilon =\log \log \frac{1}{\varepsilon }\) as in (4.2), and let \(\Theta (\vec {\textsf{i}},\vec {\textsf{a}}) = \Theta _{N,\varepsilon }^{(\textrm{cg})}(\vec {\textsf{i}},\vec {\textsf{a}})\) be the coarse-grained disorder variables from Definition 4.6. Then, for any \(T \in (0,\infty )\), there exists \({\textsf{C}}= {\textsf{C}}(T) < \infty \) such that, for \(\varepsilon > 0\) small enough, we have
uniformly in \(t\in [0,T]\), \(\psi \in L^\infty ({\mathbb {R}}^2)\) and \(\varphi :{\mathbb {R}}^2\rightarrow {\mathbb {R}}\) with \(\Vert \varphi \Vert _{{{\mathcal {G}}} _T}<\infty \).
Note that the r.h.s. of (4.12) tends to 0 as \(\varepsilon \downarrow 0\), because \(K_\varepsilon \, \varepsilon \rightarrow 0\). The whole of Sect. 5 is devoted to the proof of Theorem 4.7.
5 Second moment bounds for averaged partition functions
This section is devoted mainly to the proof of Theorem 4.7, which approximates the averaged partition function \({\mathcal {Z}}^{\beta _N}_{N, t}(\varphi ,\psi )\) from (3.10) by the coarse-grained model \({\mathscr {Z}}_{\varepsilon ,t}^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N,\varepsilon }^{(\textrm{cg})})\) from (4.8). We may assume \(t=T=1\) without loss of generality. The uniformity in \(t\leqslant T\) will be clear from the proof. Throughout this section we simply write \({\mathcal {Z}}_{N}(\varphi ,\psi )\), omitting the dependence on \(t=1\) and on \(\beta _N\).
The starting point of our proof of Theorem 4.7 is the polynomial chaos expansion (3.19). In the second moment calculations, the time-space renewal representation and the limiting Dickman subordinator presented in Sect. 3.5 play a crucial role. The proof will be carried out in three steps, presented in Sects. 5.1–5.3 below: given \(\varepsilon > 0\), we introduce two intermediate approximations \({{\mathcal {Z}}} _{N,\varepsilon }^{(\mathrm {no\, triple})}(\varphi ,\psi )\) and \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\) of the averaged partition function \({\mathcal {Z}}_{N}(\varphi ,\psi )\), and bound the following in \(L^2\).
-
Step 1. We bound \({{\mathcal {Z}}} _N(\varphi ,\psi ) - {{\mathcal {Z}}} _{N,\varepsilon }^{(\mathrm {no\, triple})}(\varphi ,\psi )\), see Lemma 5.1 in Sect. 5.1: this is the cost of imposing the constraints \({{\mathcal {A}}} _{\varepsilon }^{(\mathrm {no\, triple})}\) and \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon }^{(\mathrm {no\, triple})}\), see (4.3) and (4.4).
-
Step 2. We bound \({{\mathcal {Z}}} _{N,\varepsilon }^{(\mathrm {no\, triple})}(\varphi ,\psi ) - {{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\), see Lemma 5.6 in Sect. 5.2: this is the cost of imposing diffusive constraints, including \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; \, b,c}^{(\textrm{diff})}\) in (4.6) and the diffusive truncation in the definition of \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }\) in (4.11).
-
Step 3. We bound \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi ) - {\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N,\varepsilon })\), see Lemma 5.8 in Sect. 5.3: this is the cost of the kernel replacement (2.6).
Combining Lemmas 5.1, 5.6 and 5.8 then gives Theorem 4.7.
In the last Sect. 5.4, we will prove a separate second moment estimate for the coarse-grained model, which is needed later in Sect. 8 for higher moment bounds.
The proof details in this section are technically a bit heavy and could be skipped in a first reading.
5.1 Step 1: constraints on mesoscopic time variables
In this step, we introduce our first approximation \({{\mathcal {Z}}} _{N,\varepsilon }^{(\mathrm {no\, triple})}(\varphi ,\psi )\) and show that it is close to \({{\mathcal {Z}}} _N(\varphi ,\psi )\).
Recall the mesoscopic time intervals \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}) : = (({\textsf{i}}-1)\varepsilon N, \, {\textsf{i}}\varepsilon N]\) introduced in (4.1), to which we associate the mesoscopic time index \({\textsf{i}}\in \{1, \ldots , \frac{1}{\varepsilon }\}\). In the chaos expansion for \({{\mathcal {Z}}} _N^{\beta _N}(\varphi , \psi )\) in (3.19), each time index \(n_j\) belongs to \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\) for some \({\textsf{i}}\in \{1, \ldots , \frac{1}{\varepsilon }\}\). The first step of coarse-graining is to group the terms in the expansion in (3.19) in terms of the mesoscopic time intervals \({{\mathcal {T}}} _{\varepsilon N}(\cdot )\) visited by the sequence of time indices \(n_1, \ldots , n_r\). Namely, we can rewrite (3.19) as (omitting \(\beta _N\) from \({{\mathcal {Z}}} ^{\beta _N}_N(\varphi ,\psi )\), and expanding \(q^N_{0,n_1}(\varphi , z_1)\) and \(q^N_{n_r, N}(z_r, \psi )\) according to their definitions in (3.16)–(3.17)):
where \(\varphi _N\), \(\psi _N\) were defined in (3.9), and \(X_{d,f}(x,y)\) was defined in (3.29).
Recall from (4.2) that \(K_\varepsilon = (\log \frac{1}{\varepsilon })^6\). We will show that in (5.1), the dominant contribution (in \(L^2\)) comes from mesoscopic time variables \(({\textsf{i}}_1, \ldots , {\textsf{i}}_k)\) which contains no consecutive triples \({\textsf{i}}_j, {\textsf{i}}_{j+1}, {\textsf{i}}_{j+2}\) with both \({\textsf{i}}_{j+1}- {\textsf{i}}_j < K_\varepsilon \) and \({\textsf{i}}_{j+2}-{\textsf{i}}_{j+1} < K_\varepsilon \). This is encoded in \({{\mathcal {A}}} _{\varepsilon }^{(\mathrm {no\, triple})}\) from (4.3), which we recall here
We will further restrict the sum in (5.1) to \(({\textsf{i}}_1, \ldots , {\textsf{i}}_k)\) with \(k \leqslant (\log \frac{1}{\varepsilon })^2\), which leads to the following first approximation of \({{\mathcal {Z}}} _N(\varphi ,\psi )\):
The main result of this subsection is the following approximation, which constitutes part of the bound in (4.12). The proof is a bit lengthy, but it contains many important ingredients, including a key renewal interpretation of second moment bounds.
Lemma 5.1
(No close triples) Recall from (4.2) that \(K_\varepsilon =(\log \frac{1}{\varepsilon })^6\) and recall \(\Vert \cdot \Vert _{{{\mathcal {G}}} _t}\) from (3.52). There exists \({\textsf{C}}\in (0, \infty )\) such that for \(\varepsilon > 0\) small enough, we have: for all \(\varphi \) with \(\Vert \varphi \Vert _{{{\mathcal {G}}} _1}^2<\infty \) and \(\psi \in L^\infty ({\mathbb {R}}^2)\),
Proof
The random variables \(X_{d,f}(x,y)\) depend on the disorder variables \(\xi _N(n,x)\) for \(d \leqslant n \leqslant f\), see (3.29). They are centered and orthogonal in \(L^2\) and, by (3.30) and (3.40),
Since the sum which defines \({{\mathcal {Z}}} _{N,\varepsilon }^{(\mathrm {no\, triple})}(\varphi ,\psi )\) is a subset of that of \({{\mathcal {Z}}} _{N}(\varphi ,\psi )\), cf. (5.1) and (5.3), it follows that we can write
where \(\textrm{I}_{N,\varepsilon }\) and \(\textrm{II}_{N,\varepsilon }\) are the contributions of \(\{k > (\log \frac{1}{\varepsilon })^2\}\) and \(\{({\textsf{i}}_1, \ldots , {\textsf{i}}_k) \in ({{\mathcal {A}}} _\varepsilon ^{(\mathrm {no\, triple})})^c\}\). We split the proof in two parts, where we show that for some \({\textsf{C}}<\infty \) we have:
Remark 5.2
Let us sketch a probabilistic interpretation of (5.5). From (3.33), we recall that the expansion for \(\overline{U}_N(f-d, y-x)\) has a time-space renewal interpretation, and from (3.51) the expansion of \({{\mathbb {E}}} \big [{\mathcal {Z}}_{N}(\varphi ,\psi )^2 \big ]\) consists of a mixture of \(\overline{U}_N(f-d, y-x)\), with weight \(\frac{1}{N^2}q^N_{0,d}(\varphi , x)^2 q^N_{f, Nt}(y, \psi )^2\). We can therefore write
where denoting \({{\mathcal {S}}} =\{(n_1, z_1), \ldots , (n_r, z_r)\}\) with \(r=|{{\mathcal {S}}} |\), we define
The measure \({\textsf{M}}_N^{\varphi ,\psi }(\cdot )\) is called a spectral measure since \({\textsf{M}}_N^{\varphi ,\psi }({{\mathcal {S}}} )\) equals the square of the coefficient of \(\prod _{(n_i, z_i)\in {{\mathcal {S}}} } \xi _N(n_i, z_i)\) in the chaos expansion (3.19) for \({\mathcal {Z}}_{N}(\varphi ,\psi )\), where different terms in the expansion are orthogonal in \(L^2\), similar to a Fourier decomposition. For more on spectral measure, see e.g. [45].
The r.h.s. of (5.5) can then be written as
where given \({{\mathcal {S}}} \subseteq \{1,\ldots , N\} \times {\mathbb {Z}}^2\),
Thanks to Lemma 3.3, it can be shown that as \(N\rightarrow \infty \), \({\textsf{M}}_N^{\varphi ,\psi }\) converges to a similarly re-weighted measure for the continuum time-space renewal process introduced in Lemma 3.3, whose time component is the Dickman subordinator \((Y_s)_{s\geqslant 0}\) with exponentially weighted Green’s function \(G_\vartheta \), see (3.37) and (3.39).
Second Moment Bound via Renewal. We first explain the common steps in bounding \(\textrm{I}_{N,\varepsilon }\) and \(\textrm{II}_{N,\varepsilon }\) from (5.5), which also applies to the variance of \({{\mathcal {Z}}} _N(\varphi , \psi )\) and the mean squared error of later approximations. The common feature is that they all have the same expansion as in (5.5), except the summation constraints are different.
Consider \(\textrm{II}_{N,\varepsilon }\) from (5.5). We first sum out the space variables in (5.5). Recall (3.9) and note that
so that in (5.5) we can bound
We can plug this bound into (5.5) and sum over the space variables in reverse order, from \(y_k, x_k\) until \(y_2, x_2, y_1\), thus replacing \(\overline{U}_N(f_j-d_j,y_j-x_j)\) by \(\overline{U}_N(f_j-d_j)\) and \(q_{f_{j-1},d_j}(y_{j-1},x_j)^2\) by \(u(d_j - f_{j-1})\), see (3.40) and (3.3). Finally, we sum over \(x_1\) and observe that
where we introduced the function \(\Phi _N\). Substituting these bounds into (5.5) then gives
A similar estimate can be derived for \(\textrm{I}_{N,\varepsilon }\), with a corresponding summation constraint.
We now compute the limit as \(N\rightarrow \infty \) of the r.h.s. of (5.13). Recalling \(\varphi _N\) from (3.9), the local limit theorem (3.21), and (3.22), if \(d_1/N\rightarrow s\in (0,1)\), then for \(\Phi _N\) in (5.12) we have
where we note that, by the definition of \(\Vert \varphi \Vert _{{{\mathcal {G}}} _t}\) from (3.52),
We will use the following result, which says that as \(N\rightarrow \infty \), for each \({\textsf{I}}:=({\textsf{i}}_1, \ldots , {\textsf{i}}_k)\subset \{1, \ldots , \frac{1}{\varepsilon }\}\), the term in (5.13) converges to a limit that can be interpreted in terms of the Dickman subordinator, as mentioned in Remark 5.2.
Lemma 5.3
Let \(\Phi _N\) and \(\Phi \) be defined as in (5.14). For any fixed \(\varepsilon > 0\), \(k\in {\mathbb {N}}\) and \({\textsf{I}}:=\{{\textsf{i}}_1, \ldots , {\textsf{i}}_k\}\subset \{1, \ldots , \frac{1}{\varepsilon }\}\) with \({\textsf{i}}_1< {\textsf{i}}_2< \ldots < {\textsf{i}}_k\), we have
with
where \({{\mathcal {T}}} _{\varepsilon }({\textsf{i}}):= (\varepsilon ({\textsf{i}}-1), \varepsilon {\textsf{i}}]\), and \(G_\vartheta \) (see (3.39) and (3.37)) is the weighted Green’s function for the Dickman subordinator with Lévy measure \(\frac{1}{t}\mathbb {1}_{(0,1)}(t)\textrm{d}t\) introduced in Lemma 3.3.
Proof
If we introduce the macroscopic variables \(a_i := d_i/N\), \(b_i := f_i/N\) in (5.16), the sums converge to corresponding integrals as \(N\rightarrow \infty \) (for fixed \(\varepsilon > 0\)), by the asymptotic expansions (3.3), (3.11), (3.42) and (3.43) for \(u(\cdot )\), \(\sigma _N^2\), \(\overline{U}_N(\cdot )\) (also recall (3.2)), as well as the local limit theorem (3.21). This gives (5.16)–(5.17). \(\square \)
We can interpret \({{\mathcal {I}}} _\varepsilon ^{\Phi }({\textsf{I}})\) in (5.17) as the weight associated to a Dickman subordinator. More precisely, recall that \(G_\vartheta \) is the weighted Green’s function of the Dickman subordinator Y introduced in Lemma 3.3, and satisfies the following renewal property [18, eq. (6.14)]:
In (5.17), let us denote by \({{\mathcal {I}}} _\varepsilon ^{s,t}({\textsf{i}}_1, \ldots , {\textsf{i}}_k)\) the integral where the extreme variables \(a_1\) and \(b_k\) are not integrated out but rather fixed to be s and t respectively, namely,
This is the weight of renewal configurations that only visit the intervals \({{\mathcal {T}}} _\varepsilon ({\textsf{i}}_1)\), ..., \({{\mathcal {T}}} _\varepsilon ({\textsf{i}}_k)\), and \(a_j, b_j\) are the first and last renewal points in \({{\mathcal {T}}} _\varepsilon ({\textsf{i}}_j)\), while \(\frac{1}{a_{j}-b_{j-1}}\) comes from the Lévy measure of the Dickman subordinator. An iterative application of (5.18) then shows that
which is just a renewal decomposition by summing over the set of possible intervals \({{\mathcal {T}}} _\varepsilon ({\textsf{i}})\), \({\textsf{j}}\leqslant {\textsf{i}}\leqslant {\textsf{j}}'\), visited by the Dickman subordinator Y, given that s, t are in the range of Y.
Applying Lemma 5.3 to (5.13) then gives
With the same arguments, we obtain a corresponding bound for \(\textrm{I}_{N,\varepsilon }\):
To complete the proof of Lemma 5.1, it remains to derive (5.6) and (5.7) from these bounds. We start with \(\textrm{II}_{N,\varepsilon }\), which is more involved, but we first make a remark.
Remark 5.4
(Variance bound) If we remove any constraint on k and \(({\textsf{i}}_1, \ldots , {\textsf{i}}_k)\) from formula (5.5), summing over all \(k \in {\mathbb {N}}\) and \(0<{\textsf{i}}_1<\cdots <{\textsf{i}}_k\leqslant \frac{1}{\varepsilon }\), we obtain \({\mathbb {V}}\textrm{ar}({{\mathcal {Z}}} _N(\varphi , \psi ))\) (recall (3.19)). We thus have a simpler analogue of (5.21) and (5.22):
where in the second inequality we applied the renewal decomposition (5.20), with s and t being the first and last renewal points, we denoted \(c_\vartheta :=\int _0^1 G_\vartheta (t)\textrm{d}t\), see (3.46), and recalled (5.15). Note that this bound is the same as the one in (3.55) and does not depend on \(\varepsilon \).
Bound for \(\textrm{II}_{N,\varepsilon }\): proof of (5.7). We start with (5.21). The constraint \(({{\mathcal {A}}} _\varepsilon ^{(\mathrm {no\, triple})})^c\) contains \({\textsf{I}}=({\textsf{i}}_1,\ldots , {\textsf{i}}_k)\) with either \(1\leqslant {\textsf{i}}_1 <K_\varepsilon \), or \({\textsf{i}}_k > \frac{1}{\varepsilon } -K_\varepsilon \), or \({\textsf{i}}_{j+1}-{\textsf{i}}_j, {\textsf{i}}_{j+2}-{\textsf{i}}_{j+1} < K_\varepsilon \) for some j (hence \(k\geqslant 3\)). We will treat the three cases one by one.
For the first case \(1\leqslant {\textsf{i}}_1 <K_\varepsilon \), omitting the factor \(\Vert \psi \Vert _\infty ^2\), its contribution is bounded by
where we applied the renewal decomposition (5.20) as in (5.23), and recalled from (5.15) that \(\Vert \varphi \Vert _{{{\mathcal {G}}} _{\scriptscriptstyle K_\varepsilon \varepsilon }}^2= \int _0^{K_\varepsilon \varepsilon } \Phi (s) \textrm{d}s\). This gives the first term in (5.7).
For the second case \({\textsf{i}}_k > \frac{1}{\varepsilon } -K_\varepsilon \), omitting \(\Vert \psi \Vert _\infty ^2\), its contribution is bounded by
where in the second inequality, we used that \(\int _{a}^{a+K_\varepsilon \varepsilon } G_\vartheta (t) \, \textrm{d}t \leqslant C \int _0^{K_\varepsilon \varepsilon } G_\vartheta (t) \textrm{d}t\leqslant C/ \log \frac{1}{\varepsilon }\) uniformly in \(\varepsilon \) small enough and \(a\in (0,1)\) (by (3.46)–(3.47) and the choice (4.2) of \(K_\varepsilon \)). This bound is much smaller than the second term in (5.7).
For the third case with \({\textsf{i}}_{j+1}-{\textsf{i}}_j, {\textsf{i}}_{j+2}-{\textsf{i}}_{j+1} < K_\varepsilon \) for some j, we need to bound
where we again applied the renewal decomposition (5.20). Bounding the integral of \(G_\vartheta (t-a'')\) over t by \(c_\vartheta = \int _0^1 G_\vartheta (u) \, \textrm{d}u\), we obtain
Note that if we restrict the sum to \(2\leqslant {\textsf{i}}'-{\textsf{i}}, {\textsf{i}}''-{\textsf{i}}' \leqslant K_\varepsilon \), then using (3.47), it is not difficult to see that the integrals can be bounded by \(C \frac{(\log K_\varepsilon )^2}{\log \frac{1}{\varepsilon }}\int _0^1\Phi (s) \textrm{d}s\). Complications only arise when \({\textsf{i}}'={\textsf{i}}+1\) or \({\textsf{i}}''={\textsf{i}}'+1\).
We will proceed in three steps. The following bound will be used repeatedly:
Indeed, splitting the integral over \((0,\frac{\delta }{2})\) and \((\frac{\delta }{2}, \delta )\) and exploiting (3.46), we note that:
-
for \(x < \frac{\delta }{2}\) we have \(\log (1+\frac{z}{\delta -x}) \leqslant \log (1+\frac{z}{\delta /2}) \leqslant C \, \log (1+\frac{z}{\delta })\) and \(\int _0^{\delta /2} G_\vartheta (x) \, \textrm{d}x \leqslant \frac{C'}{\log \frac{1}{\delta }}\);
-
for \(x > \frac{\delta }{2}\) we can bound \(G_\vartheta (x) \leqslant \frac{C}{\delta (\log \frac{1}{\delta })^2}\) and, by the change of variable \(t := \frac{z}{\delta -x}\),
$$\begin{aligned} \int _{0}^\delta \log \bigg (1+\frac{z}{\delta -x}\bigg ) \, \textrm{d}x = z \int _{\frac{z}{\delta }}^\infty \frac{\log (1+t)}{t^2} \, \textrm{d}t \leqslant C' \, \delta \, \log \bigg ( 1+\frac{z}{\delta } \bigg ) .\nonumber \\ \end{aligned}$$(5.27)
We now continue to bound the r.h.s. of (5.25).
Step 1. Given \({\textsf{i}}' \in {\mathbb {N}}\) and \(a' \in {{\mathcal {T}}} _\varepsilon ({\textsf{i}}')\), we bound the integrals over \(a''\) and \(b'\) in (5.25):
where we used (5.26) and changed variable \(x := b'-a'\). Plugging it into (5.25), we obtain
Step 2. Given \({\textsf{i}}\in {\mathbb {N}}\) and \(b \in {{\mathcal {T}}} _\varepsilon ({\textsf{i}})\), we focus on the integral over \(a'\) in (5.28):
by the change of variables \(x := \varepsilon {\textsf{i}}'- a'\). We first bound the sum from \({\textsf{i}}'={\textsf{i}}+2\) onward, for which we note that for \(x \in (0,\varepsilon )\),
Moreover, by the change of variables \(x = \varepsilon \, e^{-t}\),
because \(t + \log \frac{1}{\varepsilon } \geqslant \log \frac{1}{\varepsilon }\) and \(1+K_\varepsilon e^t \leqslant (1+ K_\varepsilon ) e^t\). Therefore
Now for the case \({\textsf{i}}'={\textsf{i}}+1\), we have
Substituting the above bounds into (5.28) then gives
Step 3. Given \(s \in (0,1)\), we bound the integral over b in (5.31).
-
For \(s \in (\varepsilon ({\textsf{i}}-2),\varepsilon {\textsf{i}})\) we can bound, by (5.26) with \(\delta = \varepsilon {\textsf{i}}-s\),
$$\begin{aligned} \begin{aligned} \int _{s}^{\varepsilon {\textsf{i}}} G_\vartheta (b-s) \, \log \bigg (1+\frac{\varepsilon K_\varepsilon }{\varepsilon {\textsf{i}}-b}\bigg ) \, \textrm{d}b&\,\leqslant \, C \, \frac{\log (1+\frac{\varepsilon K_\varepsilon }{\varepsilon {\textsf{i}}-s})}{\log \frac{1}{\varepsilon {\textsf{i}}-s}}\\&\leqslant \, C' \, \log (1+K_\varepsilon ) , \end{aligned} \end{aligned}$$(5.32)where the last inequality (which is very rough) holds, say for \(\varepsilon \in (0,\frac{1}{4})\), uniformly for \(s \in (\varepsilon ({\textsf{i}}-2),\varepsilon {\textsf{i}})\) and \(K_\varepsilon \geqslant 1\), because \(x := \frac{1}{\varepsilon {\textsf{i}}-s} \geqslant \frac{1}{2\varepsilon } \geqslant 2\) and
$$\begin{aligned} \sup _{x\geqslant 2}\frac{\log (1+(\varepsilon K_\varepsilon ) x)}{\log x}{} & {} \leqslant \sup _{x\geqslant 2} \frac{\log ((1+ K_\varepsilon ) x)}{\log x} = \frac{\log ((1+ K_\varepsilon ) 2)}{\log 2}\\{} & {} \quad \leqslant \frac{2}{\log 2} \, \log (1+K_\varepsilon ) . \end{aligned}$$ -
For \(s \leqslant \varepsilon ({\textsf{i}}-2)\) we can bound \(G_\vartheta (b-s) \leqslant C \, G_\vartheta (\varepsilon ({\textsf{i}}-1)-s)\), see (3.46), and
$$\begin{aligned} \begin{aligned}&\int _{\varepsilon ({\textsf{i}}-1)}^{\varepsilon {\textsf{i}}} \log \bigg (1+\frac{\varepsilon K_\varepsilon }{\varepsilon {\textsf{i}}-b}\bigg ) \, \textrm{d}b \\ {}&\quad = \int _0^\varepsilon \log \bigg (1+\frac{\varepsilon K_\varepsilon }{x}\bigg ) \, \textrm{d}x \,\leqslant \, C' \, \varepsilon \, \log (1 + K_\varepsilon ) , \end{aligned} \end{aligned}$$by the change of variables \(x := \varepsilon {\textsf{i}}-b\) and the estimate (5.27) with \(\delta = \varepsilon \) and \(z =\varepsilon K_\varepsilon \).
Substituting these bounds into (5.31) then gives
where the last sum can be seen as a Riemann sum and bounded by a multiple of \(c_\vartheta = \int _0^1 G_\vartheta (x) \, \textrm{d}x\). This bound gives the second term in (5.7) and completes its proof.
Bound for \(\textrm{I}_{N,\varepsilon }\): proof of (5.6). In view of (5.22) and (5.15), we need to show that
By Markov’s inequality, we can bound
Recalling the renewal interpretation of \({{\mathcal {I}}} _\varepsilon ^{\Phi }({\textsf{I}})\) after Lemma 5.3 and the renewal decomposition (5.20), we can integrate over the first renewal visit s, the last visited point \(u\in {{\mathcal {T}}} _{\varepsilon }({\textsf{j}})\), the first visited point v after \({{\mathcal {T}}} _{\varepsilon }({\textsf{j}})\), and the last renewal visit \(t\leqslant 1\), to obtain the bound
Observe that the sum of the integrals is exactly the same as in the r.h.s. of (5.31) with \(K_\varepsilon \) replaced by \(\frac{1}{\varepsilon }\). Therefore the bounds leading to (5.33) also applies, which gives
This matches our goal (5.34) and completes the proof of (5.6). \(\square \)
5.2 Step 2: diffusive truncation in space
In this step, we introduce our second approximation \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\) and show that it is close to \({{\mathcal {Z}}} _{N,\varepsilon }^{(\mathrm {no\, triple})}(\varphi ,\psi )\).
For \({\textsf{a}}= ({\textsf{a}}^{(1)}, {\textsf{a}}^{(2)}) \in {\mathbb {Z}}^2\), recall from (4.1) the mesoscopic spatial square
to which we associate the mesoscopic space variable \({\textsf{a}}\). We now perform coarse-graining in space by grouping terms in the expansion of \({{\mathcal {Z}}} _{N,\varepsilon }^{(\mathrm {no\, triple})}(\varphi ,\psi )\) in (5.3) according to the mesoscopic spatial boxes visited by the space variables \(v, x_i, y_i, w\) in (5.3). Namely, recall the definition (4.1) of the mesoscopic time-space box
We can rewrite (5.3) by introducing the mesocopic space variables \({\textsf{b}}_0, {\textsf{a}}_1, {\textsf{b}}_1, \ldots , {\textsf{a}}_k, {\textsf{b}}_k, {\textsf{a}}_{k+1}\):
We now perform a diffusive scale truncation by replacing each \(X_{d_i,f_i}(x_i,y_i)\) in the above expansion by its truncated version \(X^{(\textrm{diff})}_{d_i,f_i}(x_i,y_i)\) defined in (4.10). Let us stress that
Furthermore, we restrict the mesoscopic space variables \(({\textsf{a}}_1, \, {\textsf{b}}_1, \,\ldots , {\textsf{a}}_k, \, {\textsf{b}}_k)\) in (5.37) to a “diffusive set” that depends on the initial and final space variables \({\textsf{b}}_0\) and \({\textsf{a}}_{k+1}\), and time variables \(({\textsf{i}}_0:=0, {\textsf{i}}_1, \ldots , {\textsf{i}}_k, {\textsf{i}}_{k+1}:=\frac{1}{\varepsilon })\):
Remark 5.5
Once \(({\textsf{i}}_1, \ldots , {\textsf{i}}_k)\in {{\mathcal {A}}} _{\varepsilon }^{(\mathrm {no\, triple})}\) are grouped into time blocks, see Definition 4.1, we can then group \(({\textsf{a}}_1, \, {\textsf{b}}_1, \,\ldots , {\textsf{a}}_k, \, {\textsf{b}}_k) \in {{\mathcal {A}}} _{\varepsilon ; {\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}\) into space-blocks, see Definition 4.2. The constraint \({{\mathcal {A}}} _{\varepsilon ; {\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}\) then maps to the constraint \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; {\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}\) defined in (4.6).
More explicitly, we can approximate \({{\mathcal {Z}}} _{N,\varepsilon }^{(\mathrm {no\, triple})}(\varphi ,\psi )\) from (5.37) by
where \(f_0:=0\). The main result of this subsection is the following, where the approximation error is much smaller than \({{\mathbb {V}}}\textrm{ar}({{\mathcal {Z}}} ^{\beta _N}_{N,1}(\varphi , \psi ))\) in (3.55).
Lemma 5.6
(Diffusive bound) Recall from (4.2) that \(M_\varepsilon = \log \log \frac{1}{\varepsilon }\) and recall \(\Vert \cdot \Vert _{{{\mathcal {G}}} _t}\) from (3.52). There exist \({\textsf{c}}, {\textsf{C}}\in (0, \infty )\) such that for \(\varepsilon > 0\) small enough, we have: for all \(\varphi \) with \(\Vert \varphi \Vert _{{{\mathcal {G}}} _1}^2<\infty \) and \(\psi \in L^\infty ({\mathbb {R}}^2)\),
Proof
We argue as in the proof of Lemma 5.1. Note that the chaos expansion for \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}\) is a restricted sum of terms in the expansion for \({{\mathcal {Z}}} _{N,\varepsilon }^{(\mathrm {no\, triple})}\) due to the following two effects:
-
(I)
the replacement of \(X_{d_j,f_j}(x_j,y_j)\) by \(X^{(\textrm{diff})}_{d_j,f_j}(x_j,y_j)\) (cf. (4.10)–(4.9) and (3.29));
-
(II)
the restriction of \(({\textsf{a}}_1, \, {\textsf{b}}_1, \,\ldots , {\textsf{a}}_k, \, {\textsf{b}}_k)\) to \({{\mathcal {A}}} _{\varepsilon ; {\textsf{b}}_0, {\textsf{a}}_{k+1}}^{(\textrm{diff})}\).
Since terms in the chaos expansion are mutually \(L^2\) orthogonal, we can write
where \(\textrm{I}_{N,\varepsilon }\) and \(\textrm{II}_{N,\varepsilon }\) are the squared \(L^2\) error as we first make the replacement in (I) and then impose the restriction in (II).
To be more precise, we can define \(X^{(\textrm{superdiff})}_{d,f}(x,y)\) by the equality
In view of (3.30) and (3.40), we define
Note that \(X^{(\textrm{superdiff})}_{d,f}(x,y)\) and \(X^{(\textrm{diff})}_{d,f}(x,y)\) are orthogonal in \(L^2\), see (4.10)–(4.9) and (3.29). As a consequence, if we plug (5.43) into (5.37) and expand the product, we obtain
The term \(\textrm{II}_{N,\varepsilon }\) in (5.42) accounts for the further restriction to \(({\textsf{a}}_1, \, {\textsf{b}}_1, \,\ldots , {\textsf{a}}_k, \, {\textsf{b}}_k) \in {{\mathcal {A}}} _{\varepsilon ; {\textsf{b}}_0, {\textsf{a}}_{k+1}}^{(\textrm{diff})} \cap {{\mathcal {A}}} _{\varepsilon ; {\textsf{b}}'_0, {\textsf{a}}'_{k+1}}^{(\textrm{diff})}\) for some \({{\textsf{b}}_0}, {{\textsf{b}}_0}', {\textsf{a}}_{k+1}, {\textsf{a}}_{k+1}' \in {\mathbb {Z}}^2\), and hence
To prove (5.41), it suffices to show that for some \({\textsf{c}}, {\textsf{C}}\in (0, \infty )\),
We need the following bound, which follows easily from Lemma 3.5. Recall \(U_N(n)\) and \(\overline{U}_N(n)\) from (3.35) and (3.40).
We are ready to bound \(\textrm{I}_{N,\varepsilon }\) in (5.46). As in the proof of Lemma 5.1, the last term \(\big ( \sum _{w\in {\mathbb {Z}}^2} q_{f_k, N}(y_k,w) \, \psi _N(w) \big )^2\) can be bounded as in (5.11). We then sum over all space variables in reverse order from \(y_k, x_k\) until \(y_1\). We will use \(\sum _{x \in {\mathbb {Z}}^2} q_{f,d}(y,x)^2 = u(d - f)\) by (3.3), apply (5.49) together with the fact that
and finally sum over \(x_1\), noting that, by (5.12),
We then obtain an analogue of (5.13):
For \(k \leqslant (\log \frac{1}{\varepsilon })^2\), recalling that \(M_\varepsilon = \log \log \frac{1}{\varepsilon }\), we can bound for \(\varepsilon > 0\) small enough
We now plug this bound into (5.52) and sum freely over all \(0< {\textsf{i}}_1< \ldots < {\textsf{i}}_k \leqslant \frac{1}{\varepsilon }\). As \(N\rightarrow \infty \), by Lemma 5.3 and similar to (5.21), we obtain (with \({\textsf{c}}= \frac{c}{2}\))
The renewal decomposition (5.20), together with \(c_\vartheta =\int _0^1 G_\vartheta (x) \, \textrm{d}x < \infty \), yields
By (5.15), this proves the first bound in (5.48).
We now prove the bound on \(\textrm{II}_{N,\varepsilon }\) in (5.48). Note from (5.39) that
The first union in (5.55) gives no contribution to (5.47) since \(\overline{U}^{(\textrm{diff})}_{N,d,f}(x,y) = 0\) when \(x \in {{\mathcal {S}}} _{\varepsilon N}({\textsf{a}})\) and \(y \in {{\mathcal {S}}} _{\varepsilon N}({\textsf{b}})\) with \(|{\textsf{b}}- {\textsf{a}}| > M_\varepsilon \), by (5.38) and (5.44). It remains to consider the contribution to (5.47) from the second union in (5.55), namely, \(|{\textsf{a}}_{j} - {\textsf{b}}_{j-1}| > M_\varepsilon \sqrt{{\textsf{i}}_j - {\textsf{i}}_{j-1}}\) for some \(j \in \{1,\ldots , k, k+1\}\).
In contrast to the bound on \(\textrm{I}_{N,\varepsilon }\) where a small factor \(Ce^{- c M_\varepsilon ^2}\) comes from the bound on \(\sum _{y_j\in {\mathbb {Z}}^2} \overline{U}^{(\textrm{superdiff})}_{N,\, d_j, f_j}(x_j, y_j)\) in (5.49), in the bound for \(\textrm{II}_{N,\varepsilon }\), the same small factor now comes from the following estimates: there exists \(c\in (0,\infty )\) such that for any \({\textsf{i}}<{\textsf{i}}'\), \(f\in {{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\), \(d'\in {{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}')\), \({\textsf{b}}\in {\mathbb {Z}}^2\), and \(y\in {{\mathcal {S}}} _{\varepsilon N}({\textsf{b}})\), we have
where recall from (3.3) that \(u(n):=\sum _{z\in {\mathbb {Z}}^2} q_n(z)^2 = q_{2n}(0)\). The first bound follows from the fact that \(q_n(\cdot )\) has Gaussian tail decay. The second bound is a consequence of the first bound, because \(\sup _z q_n(z) \leqslant \frac{C'}{n}\leqslant C u(n)\) by the local limit theorem (3.21) and (3.3).
The bound on \(\textrm{II}_{N,\varepsilon }\) then follows the same steps as that for \(\textrm{I}_{N,\varepsilon }\), where we take a union bound over all \(1\leqslant j\leqslant k+1\leqslant (\log \frac{1}{\varepsilon })^2+1\) with \(|{\textsf{a}}_j - {\textsf{b}}_{j-1}| > M_\varepsilon \sqrt{{\textsf{i}}_j - {\textsf{i}}_{j-1}}\).
-
For \(j=k+1\), bounding \(\psi \) by \(\Vert \psi \Vert _\infty \) and applying (5.56), the sum over \(w,w'\) and \({\textsf{a}}_{k+1}, {\textsf{a}}_{k+1}'\) in (5.47) under the super-diffusive constraint \(|{\textsf{a}}_{k+1} - {\textsf{b}}_k| > M_\varepsilon \sqrt{\frac{1}{\varepsilon } - {\textsf{i}}_k}\) leads to an extra factor of \(C e^{-c M_\varepsilon ^2}\) compared with the bound when this constraint is not present (see (5.11)).
-
For \(2\leqslant j\leqslant k\), by (5.57), the sum of \(q_{f_{j-1}, d_j}(y_{j-1}, x_j)^2\) over \(x_j\) in (5.47) under this super-diffusive constraint gives an extra factor of \(C e^{- c M_\varepsilon ^2}\) compared to the case when this constraint is not present.
-
For \(j=1\), given \({\textsf{b}}_0, {\textsf{b}}'_0\in {\mathbb {Z}}^2\), we could have either \(|{\textsf{a}}_1 - {\textsf{b}}_{0}| > M_\varepsilon \sqrt{{\textsf{i}}_1}\) or \(|{\textsf{a}}_1 - {\textsf{b}}'_{0}| > M_\varepsilon \sqrt{{\textsf{i}}_1}\); either way, given \(v\in {{\mathcal {S}}} _{\varepsilon N}({\textsf{b}}_0)\), \(v'\in {{\mathcal {S}}} _{\varepsilon N}({\textsf{b}}'_0)\) and \(d_1\in {{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_1)\), the sum of \(q_{0, d_1}(v, x_1)q_{0, d_1}(v', x_1)\) in (5.47) under this super-diffusive constraint gives a factor \(C e^{-c M_\varepsilon ^2}\) compared to the case when this constraint is not present.
Since there are at most \((\log \frac{1}{\varepsilon })^2+1\) choices of such j, this leads to the same bound we had for \(\textrm{I}_{N,\varepsilon }\) in (5.53), which establishes the second inequality in (5.48).
This completes the proof of Lemma 5.6. \(\square \)
5.3 Step 3: kernel replacement
In this step, we introduce a last approximation \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi ,\psi )\) and show that it is close both to \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\) and to the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N,\varepsilon }^{(\textrm{cg})})\). This completes the proof of Theorem 4.7.
Let us first summarize the previous steps. So far, we have performed coarse-graining by grouping terms in the chaos expansion for \({{\mathcal {Z}}} _N(\varphi , \psi )\) in (3.19) according to the mesoscopic time-space boxes \({{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}, {\textsf{a}})\) visited by the microscopic time-space renewal configuration \((n_1, z_1), \ldots , (n_r, z_r)\) in (3.19). Imposing suitable restrictions, we have defined the approximations \({{\mathcal {Z}}} _{N,\varepsilon }^{(\mathrm {no\, triple})}(\varphi ,\psi )\) in (5.3) and \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\) in (5.40). The next step is to replace the relevant random walk transition kernels in the expansion (5.40) for \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\) by heat kernels as in (2.6), i.e., replace the random walk transition kernels \(q_{f_{j-1}, d_j}(y_{j-1}, x_j)\) connecting the microscopic points \((f_{j-1}, y_{j-1})\in {{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}_{j-1}, {\textsf{b}}_{j-1})\) and \((d_j, x_j) \in {{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}_j, {\textsf{a}}_j)\) by a heat kernel that depends on the mesoscopic time-space variables \(({\textsf{i}}_{j-1}, {\textsf{b}}_{j-1})\) and \(({\textsf{i}}_j, {\textsf{a}}_j)\). However, such an approximation is only good if \({\textsf{i}}_j-{\textsf{i}}_{j-1}\) is sufficiently large, say at least \(K_\varepsilon =(\log \frac{1}{\varepsilon })^6\) as in (4.2).
This naturally leads to the decomposition of \(({\textsf{i}}_1, \ldots , {\textsf{i}}_k)\) into time blocks, where consecutive \({\textsf{i}}_{j-1}\), \({\textsf{i}}_j\) with distance less than \(K_\varepsilon \) are grouped into a single block. The constraint \({{\mathcal {A}}} _{\varepsilon }^{(\mathrm {no\, triple})}\) in (5.2) ensures that each time block consists of either a single \({\textsf{i}}_j\), or two consecutive \({\textsf{i}}_{j-1}\), \({\textsf{i}}_j\), leading to the definition of time blocks \(\vec {\textsf{i}}\) in Definition 4.1, while \({{\mathcal {A}}} _{\varepsilon }^{(\mathrm {no\, triple})}\) is mapped to the constraint \(\vec {\varvec{{\mathcal {A}}}}_\varepsilon ^{(\mathrm {no\, triple})}\) introduced in (4.4) for a sequence of time blocks. Given a sequence of time blocks \((\vec {\textsf{i}}_1, \ldots , \vec {\textsf{i}}_r)\) visited by the microscopic time-space renewal configuration, for each time block \(\vec {\textsf{i}}_l=({\textsf{i}}_l, {\textsf{i}}_l')\), we can identify the first mesoscopic box \({{\mathcal {S}}} _{\varepsilon N}({\textsf{a}}_l)\) visited by the renewal configuration in the time interval \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_l)\), as well as the last mesoscopic box \({{\mathcal {S}}} _{\varepsilon N}({\textsf{a}}_l')\) visited by the renewal configuration in the time interval \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}}_l')\). This produces a space block \(\vec {\textsf{a}}_l:=({\textsf{a}}_l, {\textsf{a}}_l')\) as in Definition 4.2.
Summarizing: we can rewrite the expansion for \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\) in (5.40) according to the sequence of visited time-space blocks \((\vec {\textsf{i}}_1, \vec {\textsf{a}}_1)\), ..., \((\vec {\textsf{i}}_r, \vec {\textsf{a}}_r)\), where the diffusive constraint \({{\mathcal {A}}} _{\varepsilon ; {\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}\) in (5.39) is mapped to \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; {\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}\) defined in (4.6) for the sequence of space blocks. See Fig. 2.
We are ready to define our last approximation \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi ,\psi )\): having rewritten the expansion (5.40) for \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\) in terms of the visited time-space blocks \((\vec {\textsf{i}}_1, \vec {\textsf{a}}_1)\), ..., \((\vec {\textsf{i}}_r, \vec {\textsf{a}}_r)\), we replace each random walk transition kernel connecting two consecutive time-space blocks by a heat kernel depending only on the mesoscopic variables \((\vec {\textsf{i}}_\cdot , \vec {\textsf{a}}_\cdot )\). More precisely, given \((f_{j-1}, y_{j-1})\in {{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}_{j-1}', {\textsf{a}}'_{j-1})\) and \((d_j, x_j) \in {{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}_j, {\textsf{a}}_j)\), we make within (5.40) the replacement
where the prefactor 2 is due to periodicity (note that \({\textsf{i}}_j-{\textsf{i}}'_{j-1}\geqslant K_\varepsilon \) by the constraint \(\vec {\varvec{{\mathcal {A}}}}_\varepsilon ^{(\mathrm {no\, triple})}\) from (4.4)). We similarly replace the “boundary kernels” in (5.40), namely
where the constraint \({{\mathcal {A}}} _\varepsilon ^{(\mathrm {no\, triple})}\) (which maps to \(\vec {\varvec{{\mathcal {A}}}}_\varepsilon ^{(\mathrm {no\, triple})}\)) ensures \({\textsf{i}}_1\geqslant K_\varepsilon \) and \(\frac{1}{\varepsilon }-{\textsf{i}}_k\geqslant K_\varepsilon \). We thus define \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi ,\psi )\) as the expression obtained from (5.40) via the replacements (5.58) and (5.59)–(5.61) (this description is useful to compare \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi ,\psi )\) with \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\)).
An alternative, equivalent description of \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi , \psi )\) is through the following formula:
where \({\textsf{i}}_0':=0\) and \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec {\textsf{i}}_j, \vec {\textsf{a}}_j)\) is the coarse-grained disorder variable defined in (4.11), which collects the contributions in (5.40) from a given visited time-space block \((\vec {\textsf{i}}_j, \vec {\textsf{a}}_j)\), and it arises thanks to the factorisations induced by the replacements in (5.58) and (5.59)–(5.61).
Remark 5.7
Only the prefactor \(\frac{2}{\varepsilon N}\) arising from the last replacement (5.61) appears explicitly in (5.62): all other factors of \(\frac{2}{\varepsilon N}\) arising from (5.58) and (5.60) have been absorbed in the coarse-grained disorder variable \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec {\textsf{i}}_j, \vec {\textsf{a}}_j)\) following the replaced kernel q, see (4.11).
Finally, to compare \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi , \psi )\) with the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})} (\varphi ,\psi |\Theta _{N,\varepsilon }^{(\textrm{cg})})\) defined in (4.8), we introduce the notation
which allows us to rewrite (5.62) more compactly as
Compare this with \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N,\varepsilon }^{(\textrm{cg})})\) in (4.8), the only difference is that \(\varphi _\varepsilon \) and \(\psi _\varepsilon \) in (4.8) are now replaced by \(\varphi ^{(N)}_\varepsilon \) and \(\psi ^{(N)}_\varepsilon \).
The main result of this subsection is the following \(L^2\) approximation, which completes the proof of Theorem 4.7.
Lemma 5.8
(Coarse graining) Recall \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi , \psi )\) from (5.62), \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N,\varepsilon }^{(\textrm{cg})})\) from (4.8) and \(\Vert \cdot \Vert _{{{\mathcal {G}}} _t}\) from (3.52). There exists \({\textsf{C}}\in (0, \infty )\) such that for \(\varepsilon > 0\) small enough, we have: for all \(\varphi \) with \(\Vert \varphi \Vert _{{{\mathcal {G}}} _1}^2<\infty \) and \(\psi \in L^\infty ({\mathbb {R}}^2)\),
Proof
We first prove (5.65). To define \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi ,\psi )\) from \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\) in (5.40), we first replaced the summation constraint \(1\leqslant k\leqslant (\log \frac{1}{\varepsilon })^2\) in (5.40) (on the number of visited mesoscopic time intervals) with the constraint \(1\leqslant r\leqslant (\log \frac{1}{\varepsilon })^2\) in (5.62) (on the number of visited coarse-grained disorder variables), where each coarse-grained disorder variable can visit either one or two mesoscopic time intervals. This amounts to adding some terms with \((\log \frac{1}{\varepsilon })^2<k \leqslant 2(\log \frac{1}{\varepsilon })^2\) in (5.40). The error from such additions is bounded as in (5.34) and agrees with the bound in (5.65). We then replaced the random walk kernels by heat kernels as in (5.58) and (5.59)–(5.61). We will make these replacements sequentially and control the error in each step, showing that it is bounded by the r.h.s. of (5.65).
First note that the replacement (5.59) simply changes the first term in (5.40), which is a deterministic constant. Since the l.h.s. of (5.59) converges to the r.h.s. as \(N\rightarrow \infty \), see (3.26), the \(L^2\) cost of the replacement (5.59) vanishes as \(N\rightarrow \infty \), which does not contribute to the bound in (5.65).
Next note that thanks to the diffusive constraint \({{\mathcal {A}}} _{\varepsilon ; {{\textsf{b}}_0, {\textsf{a}}_{k+1}}}^{(\textrm{diff})}\) in (5.40), which maps to \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; {\textsf{a}}'_0, {\textsf{a}}_{r+1}}^{(\textrm{diff})}\) in (5.62), the replacements in (5.58) and (5.60)–(5.61) are all of the form
for some \((s, x) \in {{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}, {\textsf{a}})\) and \((t,y) \in {{\mathcal {B}}} _{\varepsilon N}({\textsf{j}}, {\textsf{b}})\), with \((t-s, y-x)\in {\mathbb {Z}}^3_{\textrm{even}}\), \({\textsf{j}}-{\textsf{i}}\geqslant K_\varepsilon \), and \(|{\textsf{b}}-{\textsf{a}}|\leqslant M_\varepsilon \sqrt{{\textsf{j}}-{\textsf{i}}}\) (recall from (4.2) that \(M_\varepsilon =\log \log \frac{1}{\varepsilon }\)). We can then apply the local limit theorem (3.21) and refine the bounds in Lemma 3.2 as follows:
where since \(|(t-s) - \varepsilon N({\textsf{j}}-{\textsf{i}})| \leqslant \varepsilon N\) and \(|(y-x)-\sqrt{\varepsilon N}({\textsf{b}}-{\textsf{a}})| \leqslant \sqrt{2\varepsilon N}\) we can bound
so that for some \(c>0\), uniformly in \(\varepsilon >0\) small enough and N large, we have
Namely, every time we replace a random walk kernel by the corresponding heat kernel, we introduce an error factor of \(e^{\pm c M_\varepsilon /\sqrt{K_\varepsilon }}\).
We first estimate the cost of the bulk replacements (5.61). Consider each term in the sum in (5.40), which we abbreviate by \({{\mathcal {Z}}} _i\) for simplicity, where i gathers the indices k and \({\textsf{i}}_j, {\textsf{a}}_j, {\textsf{b}}_j, (d_j, x_j), (f_j, y_j)\) for \(1 \leqslant j \leqslant k\) (excluding \({\textsf{b}}_0, y_0\) and \({\textsf{a}}_{k+1}, x_{k+1}\)). Note that within each term \({{\mathcal {Z}}} _i\), we replace at most \((\log \frac{1}{\varepsilon })^2\) random walk kernels, which amounts to replacing \({{\mathcal {Z}}} _i\) by \(\gamma _i {{\mathcal {Z}}} _i\) with \(e^{-c (\log \frac{1}{\varepsilon })^2 M_\varepsilon /\sqrt{K_\varepsilon }}\leqslant \gamma _i \leqslant e^{c (\log \frac{1}{\varepsilon })^2 M_\varepsilon /\sqrt{K_\varepsilon }}\). We then have
since \(M_\varepsilon =\log \log \frac{1}{\varepsilon }\) and \(K_\varepsilon =\big (\log \frac{1}{\varepsilon }\big )^6\) by (4.2). Since the terms \({{\mathcal {Z}}} _i\) in the sum in (5.40) are mutually orthogonal, we can sum the bound above over i and we see that the contribution of the bulk replacements to (5.65) is at most
where the last bound follows from (5.23). This agrees with (5.65).
We next consider the boundary replacements (5.59) and (5.61). Replacing the leftmost random walk kernel \(q_{0,d_1}(y_0, x_1)\) in (5.40) by the corresponding heat kernel introduces an error factor \(e^{-c M_\varepsilon /\sqrt{K_\varepsilon }} \leqslant \gamma _{y_0, (d_1, x_1)} \leqslant e^{+c M_\varepsilon /\sqrt{K_\varepsilon }}\), see (5.67), which affects the \(L^2\) norm by \(\{\sum _{y_0} \varphi _N(y_0) (\gamma _{y_0, (d_1, x_1)}-1)\}^2 \leqslant C \frac{M_\varepsilon ^2}{K_\varepsilon } \{\sum _{y_0} |\varphi _N(y_0)|\}^2\) (no disorder variable is attached to \(y_0\)). Thus, as in (5.69), the left boundary replacement contributes to (5.65) at most by
which is a stronger bound than (5.65). The right boundary replacement (5.61) is controlled in a similar fashion, which completes the proof of (5.65).
Lastly, we prove (5.66). As noted before, the only difference between \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi ,\psi )\) and \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta ^\mathrm{(cg)}_{N,\varepsilon })\) is that \(\varphi _\varepsilon , \psi _\varepsilon \) in (4.8) are replaced by \(\varphi ^{(N)}_\varepsilon , \psi ^{(N)}_\varepsilon \) in (5.64). For \({\textsf{a}}\in {\mathbb {Z}}^2\), \(\varepsilon \varphi _\varepsilon ({\textsf{a}})\) is the integral of \(\varphi \) over the square \({{\mathcal {S}}} _{\varepsilon }({\textsf{a}})=(\sqrt{\varepsilon }{\textsf{a}}-(\sqrt{\varepsilon },\sqrt{\varepsilon }), \sqrt{\varepsilon }{\textsf{a}}]\), by the definition of \(\varphi _\varepsilon \) in (4.7). On the other hand, by the definition of \(\varphi _\varepsilon ^{(N)}\) in (5.63) and \(\varphi _N\) in (3.9), \(\varepsilon \varphi _\varepsilon ^{(N)}\) is the integral of \(\varphi \) over the region \({\tilde{{{\mathcal {S}}} }}_\varepsilon ({\textsf{a}}):= \bigcup _{v\in {{\mathcal {S}}} _\varepsilon ({\textsf{a}}) \cap ({\mathbb {Z}}^2_{\textrm{even}}/\sqrt{N}) } \,\{x\in {\mathbb {R}}^2: |x-v|_1\leqslant \frac{1}{\sqrt{N}}\}\). The difference between \({{\mathcal {S}}} _\varepsilon ({\textsf{a}})\) and \({\tilde{{{\mathcal {S}}} }}_{\varepsilon }({\textsf{a}})\) is contained in a shell of thickness \(1/\sqrt{N}\) around the boundary of \({{\mathcal {S}}} _\varepsilon ({\textsf{a}})\). Therefore, if \(\varphi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\) is locally integrable, then \(\varphi _\varepsilon ^{(N)}\) converges pointwise to \(\varphi _\varepsilon \) as functions on \({\mathbb {Z}}^2\), while if \(\psi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\) is also bounded, then \(\psi _\varepsilon ^{(N)}\) converges uniformly to \(\psi _\varepsilon \). If \(\varphi \) has bounded support, then (5.66) is easily seen to hold since we already have control over \({\mathbb {V}}\textrm{ar}({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi ,\psi ))\) that is uniform in N. General \(\varphi \) can then be handled by truncating its support. This concludes the proof of Lemma 5.8. \(\square \)
Combining Lemmas 5.1, 5.6 and 5.8 then gives Theorem 4.7.
5.4 A second moment bound for the coarse-grained model
In this subsection, we prove a second moment bound for the coarse-grained model, which is loosely speaking the analogue of Lemma 3.5. This is needed when we bound the fourth moment of the coarse-grained model in Sect. 8.
First we introduce some notation. Let us define the following variants of \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon }^{(\mathrm {no\, triple})}\) and \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; \,{\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}\) (see (4.4) and (4.6)), without dependence on the boundary conditions:
Recall the definition (3.40)–(3.41) of \(\overline{U}(n-m,x-y)\). We introduce an analogous quantity for the coarse-grained model defined in (4.8) (illustrated in Fig. 2). Given \({\textsf{n}}\in {\mathbb {N}}_0\) and \({\textsf{x}}\in {\mathbb {Z}}^2\), we define a coarse-grained analogue of \(X_{d,f}(x,y)\) in (3.29):
and define
We prove the following analogue of Lemma 3.5 (with an extra sum in the time index).
Lemma 5.9
For every \({\textsf{c}}\in (0,\infty )\), there exist \({\textsf{C}}= {\textsf{C}}({\textsf{c}}) \in (0, \infty )\) and \({\hat{\lambda }}_0={\hat{\lambda }}_0({\textsf{c}}) \in (0,\infty )\) such that: there exists \(\varepsilon _0 >0\) such that for all \(\varepsilon \in (0, \varepsilon _0)\) and \({\hat{\lambda }} \in ({\hat{\lambda }}_0,\infty )\), we have
Proof
The basic strategy is to first undo the replacement of the random walk kernels by heat kernels in the definition of the coarse-grained model \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi ,\psi )\) in Sect. 5.3. We then undo the summation constraints imposed in Sects. 5.1 and 5.2, which allows us to bound \(\overline{U}^{\mathrm{(cg)}}_{N, \varepsilon }({\textsf{n}}, {\textsf{x}})\), the second moment of \({\mathscr {X}}^{(\textrm{cg})}_{N, \varepsilon }({\textsf{n}}, {\textsf{x}})\), in terms of the second moment of the original partition function, so that Lemma 3.5 can be applied. The details are as follows.
Let us recall how the coarse-grained model \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{cg})}(\varphi , \psi )\) in (5.62) was defined from \({{\mathcal {Z}}} _{N,\varepsilon }^{(\textrm{diff})}(\varphi ,\psi )\) in (5.40) by replacing the random walk kernels with heat kernels in the chaos expansion (see (5.58), (5.60)–(5.61)). It was shown in the proof of Lemma 5.8, in particular, in (5.67) and (5.68), that the aggregate effect of such replacements is to change the second moment by a factor that is bounded between \(1-C/\log \frac{1}{\varepsilon }\) and \(1+ C/\log \frac{1}{\varepsilon }\). We can therefore undo these replacements, which only changes the second moment by a factor that is bounded between \(1-C'/\log \frac{1}{\varepsilon }\) and \(1+ C'/\log \frac{1}{\varepsilon }\) (\(\leqslant 2\) for \(\varepsilon \) small). More precisely, define
which is obtained by reversing the replacements of the random walk transition kernels by heat kernels in the definition of \({\mathscr {X}}^{(\textrm{cg})}_{N, \varepsilon }({\textsf{n}}, {\textsf{x}})\) in (5.72), plugging in the chaos expansion for the coarse-grained disorder variables \(\Theta ^{(\mathrm cg)}_{N,\varepsilon }\) from (4.11), (4.10) and (4.9), and then relaxing the constraints on the time-space summation indices. The pre-factor \(2/\varepsilon N\) comes from the first \(\Theta ^{(\mathrm cg)}_{N, \varepsilon }\) in (5.72) and is a normalising factor in its definition in (4.11). Since relaxing the summation constraint only increases the second moment because the terms of the chaos expansion are \(L^2\) orthogonal, we have that for \(\varepsilon \) sufficiently small and all N large,
where we have used the definition of \(\overline{U}_N(n-m,x-y)\) from (3.40)–(3.41). Substituting this bound into the l.h.s. of (5.74) then gives
We now observe that for \((m,y) \in {{\mathcal {B}}} _{\varepsilon N}(0,0)\) and \((n,x)\in {{\mathcal {B}}} _{\varepsilon N}({\textsf{n}}, {\textsf{x}})\) we have \(\frac{n-m}{\varepsilon N} \in [{\textsf{n}}-1, {\textsf{n}}+1]\) and \(\frac{|x-y|}{\sqrt{\varepsilon N}} \in [|{\textsf{x}}|-\sqrt{2}, |{\textsf{x}}|+\sqrt{2}]\), hence \(\varepsilon {\textsf{n}}= \frac{n-m}{N} + O(\varepsilon )\) and \(\sqrt{\varepsilon } |{\textsf{x}}| =\frac{x-y}{\sqrt{N}} + O(\sqrt{\varepsilon })\). Recalling that \(|{{\mathcal {B}}} _{\varepsilon N}(0,0)| = O((\varepsilon N)^2)\), the change of variables \((n-m, x-y) = (l, z)\) then yields
where we applied Lemma 3.5 and (3.43) in the second and third inequalities, then we chose \({\hat{\lambda }} \geqslant 2 c {\textsf{c}}^2=:{\hat{\lambda }}_0\) and applied (3.47) in the last line. This concludes the proof of Lemma 5.9. \(\square \)
6 Higher moment bounds for averaged partition functions
In this section, we bound higher moments of the averaged partition function \({{\mathcal {Z}}} _N^\beta (\varphi , \psi )\) (see (3.8) and (3.19)) in the critical window as specified in Theorem 1.1 and (3.11)–(3.12). As noted in Sect. 1.5 and the discussion therein on Schrödinger operators with point interactions, these bounds are very delicate in the critical window. Unlike in the sub-critical regime considered in [17, 20], where the chaos expansion of \({{\mathcal {Z}}} _N^\beta (\varphi , \psi )\) is supported (up to a small \(L^2\) error) on chaoses of finite order independent of N, for \(\beta =\beta _N\) in the critical window, the expansion is supported on chaoses of order \(\log N\), so hypercontractivity can no longer be used to bound higher moments in terms of the second moment. Instead, the expansion has to be controlled with much greater care. Bounds on the third moment were first obtained in [19]. Bounds on higher moments of the averaged solution of the mollified stochastic heat equation (continuum analogues of \({{\mathcal {Z}}} _N^\beta (\varphi , \psi )\)), for \(\varphi , \psi \in L^2\), were then obtained in [51] using techniques from the study of Schrödinger operator with point interactions (also called Delta-Bose gas) [39, 40]. The recent work [26] studied the semigroup associated with the Schrödinger operator and allowed \(\varphi \) to be delta functions.
Our goal is to develop similar moment bounds as in [51] for the averaged polymer partition function \({{\mathcal {Z}}} _N^\beta (\varphi , \psi )\). The approach of [51] used explicit Fourier calculations and the underlying space-time white noise, which cannot be easily adapted to lattice models with general disorder. We develop an alternative approach, where the key ingredient is a functional inequality for the Green’s function of multiple random walks on \({\mathbb {Z}}^2\) (see Lemma 6.8). This leads to Theorem 6.1, which is the main result of this section, where instead of working with \(\varphi , \psi \in L^2\) as in [51], we will work with weighted \(L^p\)–\(L^q\) spaces with \(\frac{1}{p}+\frac{1}{q}=1\), which allows \(\psi (y)\equiv 1\) and \(\varphi (x) = \varepsilon ^{-1} \mathbb {1}_{|x|\leqslant \sqrt{\varepsilon }}\) to be an approximate delta function on the scale \(\sqrt{\varepsilon }\), and it also gives spatial decay if the support of \(\varphi \) and \(\psi \) are far apart. Our approach is robust enough that it can be applied the coarse-grained disorder variables \(\Theta _{N,\varepsilon }^{(\textrm{cg})}\), which can be seen as an averaged partition functions (see Lemma 7.2), and it can also be adapted to the coarse-grained model \({\mathscr {Z}}_{\varepsilon ,t}^{(\textrm{cg})}(\varphi ,\psi |\Theta _{N,\varepsilon }^{(\textrm{cg})})\), as we will show in Theorem 8.1.
6.1 Statement and proof
Given a countable set \({{\mathbb {T}}} \) and a function \(f: {{\mathbb {T}}} \rightarrow {\mathbb {R}}\), we use the standard notation
while we let \(\Vert g\Vert _p\) denote the usual \(L^p\) norm of \(g: {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\). We will ignore parity issues, since this only affects the bounds by a constant multiple: for a locally integrable function \(\varphi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\), we consider its discretization \(\varphi _N: {\mathbb {Z}}^2 \rightarrow {\mathbb {R}}\) in (3.9) to be defined on the whole \({\mathbb {Z}}^2\) (rather than just on \({\mathbb {Z}}^2_\textrm{even}\)). Here is the main result of this section.
Theorem 6.1
(Higher moments) For \(N \leqslant {\tilde{N}} \in {\mathbb {N}}\), let \({{\mathcal {Z}}} _{N}^{\beta _{\tilde{N}}}(\varphi , \psi ) = {{\mathcal {Z}}} _{N,1}^{\beta _{{\tilde{N}}}}(\varphi , \psi )\) be the averaged partition function in (3.8), where \(\beta = \beta _{{\tilde{N}}}=\beta _{{\tilde{N}}}(\vartheta )\) satisfies (3.11) for some \(\vartheta \in {\mathbb {R}}\). Fix \(p, q \in (1,\infty )\) with \(\frac{1}{p}+\frac{1}{q}=1\), an integer \(h\geqslant 3\), and a weight function \(w: {\mathbb {R}}^2 \rightarrow (0,\infty )\) such that \(\log w\) is Lipschitz continuous. Then there exist \({\textsf{C}}, {\textsf{C}}' < \infty \) such that, uniformly in large \(N \leqslant {\tilde{N}}\in {\mathbb {N}}\) and locally integrable \(\varphi , \psi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\), we have
where \(\varphi _N, \psi _N, w_N: {\mathbb {Z}}^2 \rightarrow {\mathbb {R}}\) are defined from \(\varphi , \psi , w: {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\) by (3.9), we denote by \(B \subseteq {\mathbb {R}}^2\) a ball on which \(\psi \) is supported (possibly \(B={\mathbb {R}}^2\)), and we set \(B_N := B \sqrt{N}\).
Theorem 6.1 will be needed later in the proof of Lemma 7.2, where we consider \(N= \varepsilon {\tilde{N}}\) with \(\varepsilon \in (0,1)\); this is why we allow for \(\beta = \beta _{{\tilde{N}}}\) with \({\tilde{N}} \geqslant N\).
Remark 6.2
The second line of (6.2) follows from the first line by Riemann sum approximation (note that \(w(\frac{x+y}{\sqrt{N}}) = (1+O(\frac{|y|}{\sqrt{N}})) \, w(\frac{x}{\sqrt{N}})\) by the Lipschitz continuity of \(\log w\)).
Remark 6.3
Typically we will let \(w(x) = e^{-|x|}\), which allows \(\psi \equiv 1\) provided \(\varphi \) decays sufficiently fast at \(\infty \). If \(\psi \) is bounded with compact support, (6.2) also gives exponential spatial decay as the support of \(\psi \) moves to infinity. This answers the conjecture in [51, Remark 1.2] in our lattice setting, which can be extended to their continuum setting.
Remark 6.4
Similar to [51, Theorem 1.1], we can show that the moments in the l.h.s. of (6.2) converge as \(N\rightarrow \infty \). However, the limits are expressed as series of iterated integrals and are not very informative, so we will not state them here.
Remark 6.5
In the bound (6.2), we could first assign \(\varphi _N, \psi _N : {\mathbb {Z}}^2 \rightarrow {\mathbb {R}}\) and then define the corresponding \(\varphi , \psi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\), e.g. by piecewise constant extension \(\varphi (x) := \varphi _N([\![ \sqrt{N}x ]\!])\) and \(\psi (y) := \psi _N([\![ \sqrt{N}x ]\!])\), because \({{\mathcal {Z}}} _N^\beta (\varphi , \psi )\) depends on the functions \(\varphi , \psi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\) only through their discretizations \(\varphi _N, \psi _N\) in (3.9), see (3.10).
In particular, we can apply the bound (6.2) to the point-to-plane partition function \(Z_N^{\beta _N}(0)\) defined in (1.3). More precisely, we can write \(Z_N^{\beta _N}(0) = \sum _{y\in {\mathbb {Z}}^2}Z^{\beta _{N}}_N(0, y)=:{{\mathcal {Z}}} ^{\beta _{N}}_N(\varphi , \mathbb {1})\) with \(\varphi _N(w)= N \mathbb {1}_{\{w=0\}}\) and \(\psi _N(z) = \mathbb {1}(z) \equiv 1\), cf. (3.7) and (3.10), which correspond to \(\varphi (x) := \varphi _N([\![ \sqrt{N}x ]\!]) = N \, \mathbb {1}_{\{|x_1|+|x_2|\leqslant 1/\sqrt{N}\}}\) and \(\psi (y) \equiv 1\). Note that \(\Vert \varphi \Vert _p = O(N^{1-\frac{1}{p}})\). Then, applying (6.2) with \(w(x)= e^{-| x |}\) implies that for any integer \(h\geqslant 3\) and for any \(p>1\), there exists \(C_{p,h} < \infty \) such that for all \(N\in {\mathbb {N}}\),
Since we can take any \(p>1\), this shows that centered moments of any order \(h\geqslant 3\) of the point-to-plane partition function \(Z_N^{\beta _N}(0)\) diverge as \(N\rightarrow \infty \) more slowly than any polynomial.
Proof of Theorem 6.1
Our starting point is the polynomial chaos expansion of \({{\mathcal {Z}}} _N^{\beta _{{\tilde{N}}}}(\varphi , \psi )\) as in (3.19), which gives
where \(\xi (n,z) = \xi _{{\tilde{N}}}(n,z)\) is as defined in (3.14) with \(\beta _N\) therein replaced by \(\beta _{\tilde{N}}(\vartheta )\) so that \({\mathbb {V}}\textrm{ar}(\xi )=\sigma _{{\tilde{N}}}^2\). We will expand the h-fold product above, which gives a sum over h microscopic time-space renewals \((n^i_1, z^i_1), \ldots , (n^i_{r_i}, z^i_{r_i})\), \(1\leqslant i\leqslant h\). Given these h renewals, each lattice point (m, x) will contribute a factor of \({{\mathbb {E}}} [\xi (m,x)^{\#}]\), where \(\#\) is the number of times (m, x) appears among the h time-space renewals. Recall \(\xi \) and \(\sigma _{{\tilde{N}}}\) from (3.14) and (3.11), we have
Therefore a given configuration of h time-space renewals will give a non-zero contribution to the expansion in (6.4) if each (m, x) is visited by none or by at least two of the h renewals. We will rewrite the expansion by first summing over all possible choices of the set of time coordinates \(\bigcup _{i=1}^h \{n^i_1, \ldots , n^i_{r_i}\}\), then for each time n in this set, sum over the locations \(x\in {\mathbb {Z}}^2\) such that (n, x) is visited by (at least two) of the h renewals \((n^i_1, z^i_1), \ldots , (n^i_{r_i}, z^i_{r_i})\), and lastly, determine which of the h renewals visits (n, x). Note that in the expansion (6.4), for each of the h renewal sequences that visits (n, x), there is a random walk transition kernel q entering (n, x) and another one exiting (n, x), while for each renewal that does not visit the time plane \(\{(n,y): y \in {\mathbb {Z}}^2\}\), there is a transition kernel \(q_{a,b}(x, z)\) with \(a<n<b\), for which we will use Chapman–Kolmogorov to rewrite it as \(q_{a,b}(x,z) = \sum _{y\in {\mathbb {Z}}^2} q_{a,n}(x,y) q_{n,b}(y, z)\).Footnote 7
To expand the centred moment \(M_{N,{\tilde{N}}, h}^{\varphi , \psi }\) in (6.4) as described above, we first introduce some notation. Given \(h\geqslant 2\), let \(I \vdash \{1,...,h\}\) denote a partition \(I=I(1)\sqcup \cdots \sqcup I(m)\) of \(\{1,...,h\}\) into disjoint subsets I(1), ..., I(m) with cardinality \(|I|=m\). Write \(k{\mathop {\sim }\limits ^{I}} l\) if k and l belong to the same partition element of I. The interpretation is that, for a given time n, we have \(k{\mathop {\sim }\limits ^{I}} l\) if the k-th and l-th time-space renewals visit the same time-space point (n, x) for some \(x\in {\mathbb {Z}}^2\), which leads to a power of the disorder variable \(\xi (n,x)\). Given \(I \vdash \{1, \ldots , h\}\), denote
For \({\varvec{x}}\in ({\mathbb {Z}}^2)^h\), we denote
For \({\varvec{x}}, {\tilde{{\varvec{x}}}} \in ({\mathbb {Z}}^2)^h\), denote the h-component random walk transition probabilities by
where \(q^N_{0,t}(\varphi , x_i)\) and \(q^N_{0,t}(x_i, \psi )\) are defined in (3.16)–(3.17), and for \(I, J\vdash \{1, \ldots , h\}\), denote
We can then write
An illustration of the expansion for the fourth moment in (6.10). Solid dots are assigned weight  with
with  being the number of renewal sequences visiting the lattice site, while circles are assigned weight 1 and arise from the Chapman–Kolmogorov decomposition of \(q_{a,b}(x,y)\) at an intermediate time. Curly lines between sites (a, x), (b, y) (together with the solid dots at both ends) represent \(U_{\tilde{N}}(b-a,y-y)\) as in (6.14) and (3.41), while solid lines between sites (either solid dots or circles) (a, x), (b, y) are assigned weight \(q_{a, b}(x, y)\). As an illustration of the expansion in (6.17), we see the sequence of operators \({\textsf{P}}^{*,I_1}=Q^{*,I_1} U^{I_1}, {\textsf{P}}^{I_1,I_2} =Q^{I_1,I_2}U^{I_2}, {\textsf{P}}^{I_2,I_3}=Q^{I_2,I_3}, {\textsf{P}}^{I_3,I_4}=Q^{I_3,I_4}, {\textsf{P}}^{I_4,I_5}=Q^{I_4,I_5}\), with \(|I_1|=3, |I_2|=3, |I_3|=2, |I_4|=1, |I_5|=3\)
being the number of renewal sequences visiting the lattice site, while circles are assigned weight 1 and arise from the Chapman–Kolmogorov decomposition of \(q_{a,b}(x,y)\) at an intermediate time. Curly lines between sites (a, x), (b, y) (together with the solid dots at both ends) represent \(U_{\tilde{N}}(b-a,y-y)\) as in (6.14) and (3.41), while solid lines between sites (either solid dots or circles) (a, x), (b, y) are assigned weight \(q_{a, b}(x, y)\). As an illustration of the expansion in (6.17), we see the sequence of operators \({\textsf{P}}^{*,I_1}=Q^{*,I_1} U^{I_1}, {\textsf{P}}^{I_1,I_2} =Q^{I_1,I_2}U^{I_2}, {\textsf{P}}^{I_2,I_3}=Q^{I_2,I_3}, {\textsf{P}}^{I_3,I_4}=Q^{I_3,I_4}, {\textsf{P}}^{I_4,I_5}=Q^{I_4,I_5}\), with \(|I_1|=3, |I_2|=3, |I_3|=2, |I_4|=1, |I_5|=3\)
First note that we can bound \(|M_{N,{\tilde{N}},h}^{\varphi , \psi }|\) from above by replacing \({{\mathbb {E}}} [\xi ^{I_i}]\), \(\varphi \) and \(\psi \) with their absolute values. To simplify notation, we assume from now on \({{\mathbb {E}}} [\xi ^{I_i}]\), \(\varphi \) and \(\psi \) are all non-negative.
Next, we bound \(\psi \) by \(\Vert \psi \Vert _\infty \mathbb {1}_B\), where B is the ball of radius \(\varrho \in [1,\infty ]\) containing the support of \(\psi \). We then note that, uniformly in \(1\leqslant n_r\leqslant N\leqslant n_{r+1}\leqslant 2N\) and \({\varvec{y}}_r\), we can find \(C>0\) such that
Recalling the definition of \(q_{0,t}^N(y, \Vert \psi \Vert _\infty \mathbb {1}_B)\) from (3.17), this bound follows readily from the observation that, given that a random walk starting from y reaches \(\sqrt{N}B\) at time \(N-n_r\), the probability of being inside \(\sqrt{N}B\) at time \(n_{r+1}-n_r \in [0, 2N]\) is uniformly bounded away from 0.Footnote 8 Therefore we can sum the r.h.s. of (6.10) over \(N\leqslant n_{r+1}\leqslant 2N\) and then divide by N to get
We first single out consecutive appearances of the same I among \(I_1, \ldots , I_r\) with \(|I|=h-1\) (that is, I consists of all singletons except for a pair \(\{k,l\}\)). Given \(I\vdash \{1, \ldots , h\}\) with \(|I|=h-1\), for \(1\leqslant s_1 < s_2\leqslant N\) and \({\varvec{z}}_1, {\varvec{z}}_2 \in ({\mathbb {Z}}^2)^h\), define
(recall that the moments of \(\xi \) depend on \({\tilde{N}}\), see (6.5)) and define \({\textsf{U}}^I_{0,{\tilde{N}}}({\varvec{z}}_1, {\varvec{z}}_2) := \mathbb {1}_{\{{\varvec{z}}_1={\varvec{z}}_2\sim I\}} \). If \(\{k, l\}\) is the unique partition element of I with cardinality two, then we can write
where \(U_{{\tilde{N}}}(n,x)\) was defined in (3.31) (with \(\sigma _N^2\) therein replaced by \(\sigma _{{\tilde{N}}}^2\)). In (6.12), we can then contract the consecutive appearances of \(I_i = I_{i+1} =\cdots I_j=I\) with \(|I|=h-1\) into a single kernel \({\textsf{U}}^I_\cdot (\cdot , \cdot )\), so that each \(I_i\) with \(|I_i|=h-1\) does not appear twice in a row in the summation in (6.12).
With a slight overload of notation in order to avoid extra symbols, for \(\lambda > 0\) we set
for partitions \(I, J \vdash \{1, \ldots , h\}\), and we finally define, with operator notation,
To lighten notation, we will often omit the dependence of these operators on \(N, {\tilde{N}}\).
The introduction of the parameter \(\lambda \), especially the choice \(\lambda ={\hat{\lambda }}/N\) we will take later, will be crucial in decoupling the sum over \(n_1, n_2-n_1, \ldots , n_{r+1}-n_r=N-n_r\) in (6.10). Together with the replacement of \(n_{r+1}=N\) by averaging \(n_{r+1}\) over [N, 2N] in (6.12), this allows us to take Laplace transform and bound the r.h.s. of (6.10) in terms of the operators defined in (6.15)–(6.16). Furthermore, by taking \({\hat{\lambda }}\) large, we can extract a logarithmic decay in \({\hat{\lambda }}\) from \({\textsf{U}}_{\lambda , N, {\tilde{N}}}^{J}\), see (6.24). These ideas were used in [51] in a continuum setting.
To proceed with estimates along these lines, we first obtain an upper bound on (6.12) by inserting the factor \(e^{2\lambda N} e^{-\lambda \sum _{i=1}^{r+1} (n_i-n_{i-1})}\geqslant 1\), for \(\lambda >0\) to be determined later, and enlarging the range of summation for each \(n_i-n_{i-1}\) to [1, 2N]. Denoting by \(I=*\) the partition consisting of singletons (namely, \(I=\{1\}\sqcup \{2\}\cdots \sqcup \{h\}\)), we can then rewrite the sum in (6.12) and obtain the bound
where the sum is over r partitions \(I_1, \cdots , I_r \vdash \{1, \cdots , h\}\) such that \(|I_i|\leqslant h-1\) for all \(1\leqslant i\leqslant r\) and there is no consecutive \(I_{i-1}=I_i\) with \(|I_i|=h-1\); we also applied the definition of \(q^N_{0,n}(\varphi , z)\) and \(q^N_{0,n}(z, \psi )\) from (3.16)–(3.17), we set \(B_N:=\sqrt{N}B\) and, given \(f: {\mathbb {Z}}^2 \rightarrow {\mathbb {R}}\), for \({\varvec{y}}\in ({\mathbb {Z}}^2)^h\) we define \(f^{\otimes h}({\varvec{y}}) := \prod _{i=1}^h f({\varvec{y}}_i)\).
Our bounds will be in terms of the norms of operators acting on the function space \(\ell ^q(({\mathbb {Z}}^2)^h)\) for some \(q>1\). To allow for \(\psi = \mathbb {1}^{\otimes h}_{B_N}\) in (6.17), it is necessary to introduce spatial weights, which incidentally will also give bounds on the spatial decay if \(\psi \) has compact support and we shift its support toward \(\infty \). More precisely, for a function \(w: {\mathbb {R}}^2\rightarrow (0,\infty )\) such that \(\log w\) is Lipschitz, we define its discretized version \(w_N: {\mathbb {Z}}^2 \rightarrow {\mathbb {R}}\) by (3.9) and we introduce the weighted operators
with \({\widehat{{\textsf{P}}}}^{I, J}_{\lambda , N, {\tilde{N}}}\) defined from \({\widehat{Q}}\) and \({\widehat{U}}\) as in (6.16). Given a partition \(I\vdash \{1, \ldots , h\}\), denote
which is just a copy of \(({\mathbb {Z}}^2)^{|I|}\) embedded in \(({\mathbb {Z}}^2)^h\). Due to the delta function constraints in its definition (\(\mathbb {1}_{\{{\varvec{x}}\sim I, {\tilde{{\varvec{x}}}} \sim J\}}\) in (6.9)), we will regard \({\widehat{Q}}_{\lambda , N}^{I, J}({\varvec{x}}, {\tilde{{\varvec{x}}}})\) as an operator mapping from \(\ell ^q(({\mathbb {Z}}^2)^h_J)\) to \(\ell ^q(({\mathbb {Z}}^2)^h_I)\) for some \(q>1\), and similarly for \({\widehat{{\textsf{U}}}}_{\lambda , N, \tilde{N}}^{J}\) and \({\widehat{P}}_{\lambda , N, {\tilde{N}}}^{I, J}\). For \(p, q>1\) with \(\frac{1}{p}+\frac{1}{q}=1\), by Hölder’s inequality, we can then rewrite the bound (6.17) as
where \(\Vert \cdot \Vert _{\ell ^p({{\mathbb {T}}} )}\) is defined in (6.1), and given an operator \({\textsf{A}}: \ell ^q({{\mathbb {T}}} ) \rightarrow \ell ^q({{\mathbb {T}}} ')\), we set

In our case \({\widehat{{\textsf{P}}}}^{I, J}_{\lambda }, {\widehat{Q}}^{I, J}_{\lambda } : \ell ^q(({\mathbb {Z}}^2)^h_{J}) \rightarrow \ell ^q(({\mathbb {Z}}^2)^h_{I})\) (note that for \(I=*\) we have \(({\mathbb {Z}}^2)^h_{I} = ({\mathbb {Z}}^2)^h\)).
We will choose \(\lambda := {\hat{\lambda }}/N\) with \({\hat{\lambda }}\) large but fixed so that \(e^{\lambda N}\) remains bounded. We will show the following.
Proposition 6.6
Fix \(p, q>1\) with \(\frac{1}{p}+\frac{1}{q}=1\), an integer \(h\geqslant 2\) and \({\hat{\lambda }} > 0\). Then there exists \(c = c_{p,q,h,{\hat{\lambda }}} < \infty \) such that, uniformly for partitions \(I, J \vdash \{1, \ldots , h\}\) with \(1\leqslant |I|, |J| \leqslant h-1\) and \(I\ne J\) when \(|I|=|J|=h-1\), for large \(N \leqslant {\tilde{N}} \in {\mathbb {N}}\) and \(\lambda = \frac{{\hat{\lambda }}}{N}\) we have
Recall by (6.5) that \(|{{\mathbb {E}}} [\xi ^{I_i}]|=\sigma _{\tilde{N}}^2\) if \(|I_i|=h-1\), while \(|{{\mathbb {E}}} [\xi ^{I_i}]| \leqslant c' \, \sigma _{{\tilde{N}}}^3 = O ((\log {\tilde{N}})^{-\frac{3}{2}})\) if \(|I_i|<h-1\). Then, by the definition of \({\widehat{{\textsf{P}}}}\) analogous to (6.16), Proposition 6.6 implies that in (6.20), for each \(2\leqslant i\leqslant r\), we have for N sufficiently large
where for \(|I_i|=h-1\) with \({\widehat{{\textsf{P}}}}_\lambda ^{I_{i-1}, I_i}={\widehat{Q}}_{\lambda }^{I_{i-1}, I_{i}} \, {\widehat{{\textsf{U}}}}_{\lambda }^{I_i}\), we used the fact that \(\Vert \widehat{Q}_{\lambda }^{I_{i-1}, I_{i}} \, {\widehat{{\textsf{U}}}}_{\lambda }^{I_i}\Vert _{\ell ^q\rightarrow \ell ^q} \leqslant \Vert {\widehat{Q}}_{\lambda }^{I_{i-1}, I_{i}} \Vert _{\ell ^q\rightarrow \ell ^q} \Vert {\widehat{{\textsf{U}}}}_{\lambda }^{I_i} \Vert _{\ell ^q\rightarrow \ell ^q}\). Similarly,
Substituting these bounds into (6.20), bounding the number of choices for each \(I_i \vdash \{1, \ldots , h\}\) by a suitable constant \({\mathfrak {c}}_h\), choosing \({\hat{\lambda }}\) large such that \({\mathfrak {c}}_h \frac{c''}{\log {\hat{\lambda }}} \leqslant \frac{1}{2}\), and using the fact that \(|I_1|, |I_r|\leqslant h-1\), we then obtain that, for all N sufficiently large,
where the last inequality holds for \({\hat{\lambda }} \geqslant 2\). This concludes the proof of Theorem 6.1. \(\square \)
6.2 Functional inequalities
It only remains to prove the bounds in Proposition 6.6. The key ingredient is a Hardy–Littlewood–Sobolev type inequality. First we need the following bound on the Green’s function of a random walk on \(({\mathbb {Z}}^2)^h\).
Lemma 6.7
Given \(N\in {\mathbb {N}}\), \(\lambda \geqslant 0\), an integer \(h\geqslant 2\) and \({\varvec{x}}, {\varvec{y}}\in ({\mathbb {Z}}^2)^h\), denote \(Q_{\lambda ,N}({\varvec{x}}, {\varvec{y}}):= \sum _{n=1}^{2N} e^{-\lambda n} \prod _{i=1}^h q_n(y_i-x_i)\). Then for some \(C\in (0,\infty )\) uniformly in \(\lambda \), N and \({\varvec{x}}, {\varvec{y}}\),
Proof
We may assume \(\lambda =0\). Note that \(\prod _{i=1}^h q_n(\cdot )\) is the transition kernel of a random walk on \({\mathbb {Z}}^{2h}\). By the local central limit theorem [66, Theorem 2.3.11] and a Gaussian concentration bound, we have
for some \(C_1, C_2\in (0,\infty )\) uniformly in \(n\in {\mathbb {N}}\) and \({\varvec{x}}, {\varvec{y}}\in ({\mathbb {Z}}^2)^h\). We then have
where we used a Riemann sum approximation and we set \({\varvec{z}}_N:= ({\varvec{y}}-{\varvec{x}})/\sqrt{N}\). When \({\varvec{z}}_N=0\), we just use the constant upper bound \(Q_{\lambda , N}({\varvec{x}}, {\varvec{y}}) \leqslant 2C_1\). When \({\varvec{z}}_N\ne 0\), we write
where \(N|{\varvec{z}}_N|^2= |{\varvec{y}}-{\varvec{x}}|^2\), while the integral is bounded uniformly in \({\varvec{z}}_N\) and can be bounded by \(C_3 e^{-C_4|{\varvec{z}}_N|^2}\) when \(|{\varvec{z}}_N|\geqslant 1\). The bound (6.26) then follows. \(\square \)
The following crucial lemma proves a Hardy–Littlewood–Sobolev type inequality. This generalizes an inequality of Dell’Antonio–Figari–Teta in [39] (see Lemma 3.1 and inequalities (3.1) and (3.5) therein) which played an important role in [51] for moment bounds with \(L^2\) test functions and initial conditions.
Lemma 6.8
Fix \(p, q>1\) with \(\frac{1}{p}+\frac{1}{q}=1\) and an integer \(h\geqslant 2\). Consider partitions \(I, J \vdash \{1, \ldots , h\}\) with \(1\leqslant |I|, |J| \leqslant h-1\), and \(I\ne J\) if \(|I|=|J|=h-1\). Recall \(({\mathbb {Z}}^2)^h_I\) from (6.19) and the associated function space \(\ell ^p\big (({\mathbb {Z}}^2)^h_I\big )\). Let \(f\in \ell ^p\big (({\mathbb {Z}}^2)^h_I\big )\) and \(g \in \ell ^q\big (({\mathbb {Z}}^2)^h_J\big )\). Then there exists \(C = C_{p,q,h} < \infty \), independent of f and g, such that
In [39], an analogue of (6.27) was proved in the continuum for the special case \(p=q=2\) (i.e., \(L^2\) test functions) and \(|I|=|J|=h-1\) with \(I\ne J\). They presented their inequality in Fourier space, but in the \(L^2\) case, it is equivalent to (6.27) by the Plancherel theorem. Here we work on the lattice, which requires us to also consider partitions with \(|I|<h-1\) or \(|J|<h-1\), which cases are not present in the continuum. We also consider test functions in general \(\ell ^p\)-\(\ell ^q\) spaces (our proof steps can also be carried out in the continuum to extend the inequality of [39] to \(L^p\)-\(L^q\) spaces). Instead of working in Fourier space as in [39], we will work directly in real space, which allows the extensions mentioned above.
Remark 6.9
The inequality (6.27) is not expected to hold for \(|I|=|J|=h-1\) with \(I=J\), because it is exactly the borderline case of the Hardy–Littlewood–Sobolev inequality when it fails, see [67, Theorem 4.3].
Proof of Lemma 6.8
We first consider the case \(|I|=|J|=h-1\), and \(I\ne J\). Then I and J each contains a partition element with cardinality 2, say \(\{k, l\}\) and \(\{m, n\}\) respectively, and \(\{k, l\}\ne \{m, n\}\). In particular, \(x_k=x_l\) and \(y_m=y_n\) for \({\varvec{x}}\in ({\mathbb {Z}}^2)^h_{I}, {\varvec{y}}\in ({\mathbb {Z}}^2)^h_{J}\).
Fix any \(0<a<\frac{1}{p\vee q}\). We then apply Hölder to bound the left hand side of (6.27) by
We now bound the first factor in (6.28). Note that since \(y_m=y_n\), by the triangle inequality,
Substituting this inequality into \(\sum _{i=1}^h |x_i-y_i|^2\) then bounds the first factor in (6.28) by
Note that for \(r > 1\) we can bound \(\sum _{y \in {\mathbb {Z}}^2} \frac{1}{(s + |y - x|^2)^r} \leqslant \frac{C }{s^{r-1}}\) uniformly for \(s \geqslant 0\) and \(x\in {\mathbb {Z}}^2\). We can then successively sum over the variables \(y_j\) with \(j\ne k, l\): there are \(|J|-2\) such variables \(y_j\) and they are all present in the sum \(\sum _{i\ne m} |y_i-x_i |^2\) (recall that we sum over \({\varvec{y}}\in ({\mathbb {Z}}^2)^h_J\), hence \(y_m = y_n\) is a single variable), hence we get
Note that \(x_k=x_l\). Via the change of variables \({\tilde{y}}_1 = y_k-y_l\) and \({\tilde{y}}_2=y_k+y_l-2x_k\), and the observation that \(|y_k-x_k|^2 + |y_l-x_l|^2= ({\tilde{y}}_1^2 +{\tilde{y}}_2^2)/2\), we can bound the above sum by
where the last inequality is obtained by summing separately over \(|{\tilde{y}}_1|\leqslant |x_n-x_m|\) and \(|{\tilde{y}}_1|>|x_n-x_m|\), plus the assumption that \(ap<1\). Substituting this bound into (6.30), since we assume \(|J| = h-1\), we obtain that the first factor in (6.28) is bounded by \(C \Vert f \Vert _{\ell ^p}\). The second factor in (6.28) can similarly be bounded by \(C\Vert g\Vert _{\ell ^q}\). This concludes the proof of (6.27), and hence also (6.22), for the case \(|I|=|J|=h-1\) and \(I\ne J\).
We can adapt the proof to the case \(\min \{|I|, |J|\}<h-1\) as follows. If \(|I|, |J|<h-1\), then there is no need to introduce the factor \(\frac{1+|x_m-x_n|^{2a}}{1+|y_k-y_l|^{2a}}\) and its reciprocal in (6.28) because we already have \(\sum _{{\varvec{y}}\in ({\mathbb {Z}}^2)^h_J} \frac{1}{(1+ \sum _{i=1}^h |x_i-y_i|^2)^{h-1}}<\infty \). If \(|I|<h-1\) and \(|J|=h-1\), then we can still find k, l in the same partition element of I, but not the same partition element of J. We should then replace the factor \(\frac{1+|x_m-x_n|^{2a}}{1+|y_k-y_l|^{2a}}\) and its reciprocal in (6.28) by \(\frac{1}{1+|y_k-y_l|^{2a}}\). The rest of the proof is essentially the same. \(\square \)
6.3 Proof of Proposition 6.6
Proof of (6.22)
Note that (6.22) is equivalent to showing (recall (6.18))
uniformly for all \(f\in \ell ^p(({\mathbb {Z}}^2)^h_{I})\) and \(g\in \ell ^q(({\mathbb {Z}}^2)^h_{J})\). To control the effect of the weight \(w_N^{\otimes h}\), we split the summation into the regions
and \(A_N^c\) for some \(C_0\) to be chosen later. Note that \(\log w(\frac{y}{\sqrt{N}}) - \log w(\frac{x}{\sqrt{N}}) = O(\frac{|x-y|}{\sqrt{N}})\), because \(\log w\) is assumed to be Lipschitz. Since \(w_N: {\mathbb {Z}}^2 \rightarrow {\mathbb {R}}\) is obtained from \(w: {\mathbb {R}}^2 \rightarrow {\mathbb {R}}\) by (3.9), we have for all \({\varvec{x}}, {\varvec{y}}\in ({\mathbb {Z}}^2)^h\)
which is bounded by \(e^{CC_0}\) in \(A_N\). Therefore, the contribution of this region to the l.h.s. of (6.31) is controlled by the following uniform bound, that we prove below:
In the region \(A_N^c\), since \(Q_{\lambda , N}^{I,J} \leqslant Q_{\lambda , N}\) (recall (6.8)–(6.9)), we can apply Lemma 6.7 to bound
where the last inequality holds for \(|{\varvec{x}}- {\varvec{y}}|>C_0\sqrt{N}\) with \(C_0 := C(C+1)\). Thus
where the prefactor is bounded if \(|I|, |J|\leqslant h-1\). Combined with (6.33), this implies (6.31).
It only remains to prove (6.33), which follows from Lemmas 6.7 and 6.8 above. \(\square \)
Proof of (6.23)
It suffices to show that for \(p, q>1\) with \(\frac{1}{p}+\frac{1}{q}=1\) and for \(|I|\leqslant h-1\)
uniformly in \(f\in \ell ^p(({\mathbb {Z}}^2)^h_{I})\) and \(g\in \ell ^q(({\mathbb {Z}}^2)^h)\), which proves the second relation in (6.23); the first relation follows by interchanging f and g. (We recall that \(J=*\) denotes the partition of \(\{1,\ldots , h\}\) consisting of h singletons, i.e. \(J = \{1\}, \{2\}, \ldots , \{h\}\).)
The proof is similar to that of (6.31). When the sum in (6.36) is restricted to \(A_N^c\) with \(A_N:=\big \{({\varvec{x}},{\varvec{y}}) :|{\varvec{x}}-{\varvec{y}}|\leqslant C_0\sqrt{N}\big \}\), the same bound in (6.34)–(6.35) holds, which gives an upper bound of
It only remains to bound the sum in (6.36) restricted to \(A_N\) and show the following analogue of (6.27):
W.l.o.g., we may assume that 1 and 2 belong to the same partition element of I, so that \(x_1=x_2\). By Hölder’s inequality, we can bound the l.h.s. by
In the second factor, since \(x_1=x_2\), we can bound \(|x_2-y_2|^2 + |x_1-y_1|^2 \geqslant \frac{|y_1-y_2|^2 + |x_1-y_1|^2}{3}\) as in (6.29) to replace \(|x_2-y_2|^2\) by \(|y_1-y_2|^2\) inside \(\sum _{i=1}^h |x_i-y_i |^2\). By the same argument as that following (6.30), we can sum out the variables \(x_i\) for \(i \geqslant 3\). Since there are \(|I|-1\) such variables in \(({\mathbb {Z}}^2)^h_{I}\), for \(|I|\leqslant h-1\) we get
where the last bound holds because \(\sum _{x\in {\mathbb {Z}}^2:\, |x| \leqslant k} \frac{1}{s+|x|^2} \leqslant C \log (1 + \frac{k}{\sqrt{s}})\) uniformly in \(k, s \geqslant 1\), and furthermore \(|y_1-y_2|\leqslant |y_1-x_1| + |x_2-y_2| \leqslant 2C_0\sqrt{N}\) by \(|{\varvec{x}}-{\varvec{y}}|\leqslant C_0\sqrt{N}\). This implies that the second factor in (6.39) can be bounded by \(C\Vert g\Vert _{\ell ^q}\).
For the first factor in (6.39), we can first sum over \({\varvec{y}}\in ({\mathbb {Z}}^2)^h\) to bound
Recall \(x_1=x_2\). Let \(z_1:=y_1-y_2\) and \(z_2:=y_1+y_2-2x_1\), so that \(|z_1|, |z_2|\leqslant 2C_0\sqrt{N}\) and \(|z_1|^2 +|z_2|^2 = 2(|y_1-x_1|^2 +|y_2-x_2|^2)\). Summing over \(z_2\) then leads to the bound
by a Riemann sum approximation. Therefore the first factor in (6.39) can be bounded by \(C N^{\frac{1}{p}} \Vert f\Vert _{\ell ^p}\). Together with (6.40), this implies (6.38) and concludes the proof of (6.23). \(\square \)
Proof of (6.24)
Note that (6.24) is equivalent to showing
uniformly in \(f\in \ell ^p(({\mathbb {Z}}^2)^h_{I})\) and \(g\in \ell ^q(({\mathbb {Z}}^2)^h_{I})\). Without loss of generality, we may assume \(I\vdash \{1, \ldots , h\}\) consists of partition elements \(\{1, 2\}, \{3\}, \ldots , \{h\}\), so that \(x_1=x_2\) and \(y_1=y_2\).
Recall from (6.15) and (6.14) that
where \(U_{{\tilde{N}}}(n,x)\) is defined in (3.31), with \(\sigma _N^2\) replaced by \(\sigma _{{\tilde{N}}}^2\). Let us set \(T := \frac{{\tilde{N}}}{N} \geqslant 1\) for short. By (3.35), (3.43) where \(\overline{U}_{{\tilde{N}}}=\sigma _{{\tilde{N}}}^2 U_{{\tilde{N}}}\), and (3.46), we have
where the last inequality follows by bounding the integral separately over \(\big (0, \frac{1}{({\hat{\lambda }} T)^{1/2}}\big )\) and \(\big (\frac{1}{({\hat{\lambda }} T)^{1/2}}, \frac{1}{2} \wedge \frac{2}{T}\big )\), with the dominant contribution coming from the first interval.
On the other hand, for any \(C>0\), by (6.42) we have
where we applied (3.48) and (6.43).
We can now bound the l.h.s. of (6.41) as follows, recalling (6.32):
where we applied (6.44). Recalling that \(T = \frac{{\tilde{N}}}{N}\), this concludes the proof of (6.41). \(\square \)
7 Moment estimates for coarse-grained disorder
In this section, we derive second and fourth moment estimates for the coarse-grained disorder variables \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) defined in (4.11). These will be used later to bound moments of the coarse-grained model \({\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta )\) introduced in Definition 4.4, with \(\Theta = \Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\).
7.1 Second moment estimates
We first study the second moment of \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\).
Lemma 7.1
For each time-space block \((\vec {\textsf{i}}, \vec {\textsf{a}})=(({\textsf{i}}, {\textsf{i}}'), ({\textsf{a}}, {\textsf{a}}'))\in {{\mathbb {T}}} _\varepsilon \) defined in (4.5), the coarse-grained disorder variable \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) as defined in (4.11) has mean 0 and its second moment converges to a finite limit
see (7.4)–(7.5) below. Furthermore, there exist \(c, C>0\) independent of \(\varepsilon \), \(\vec {\textsf{i}}\), \(\vec {\textsf{a}}\) such that
Proof
(I) Random walk representation. We first express \( \mathrm E\big [\big (\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\big )^2\big ]\) in terms of the time-space renewal \((\tau ^{(N)}_\cdot , S^{(N)}_\cdot )\) defined in (3.32). First consider the case \(|\vec {\textsf{i}}|=1\), i.e., \({\textsf{i}}={\textsf{i}}'\). Recall from (4.11), (4.9) and (4.10) that
where we note that the terms are uncorrelated because \(\xi _N(\cdot , \cdot )\) are independent centred random variables with mean 0 and variance \(\sigma _N^2\) (recall (3.14) and (3.11)). Therefore
Note that this sum admits a representation in terms of the space-time random walk \((\tau ^{(N)}_k, S^{(N)}_k)_{k\geqslant 0}\) defined in (3.32), namely,
where \(\mathrm P^{N, \varepsilon }_{{\textsf{i}},{\textsf{a}}}\) denotes probability for \((\tau ^{(N)}_k, S^{(N)}_k)_{k\geqslant 0}\) with \((\tau ^{(N)}_0, S^{(N)}_0)\) sampled uniformly from \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\times {{\mathcal {S}}} _{\varepsilon N}({\textsf{a}})\cap {\mathbb {Z}}^3_{\textrm{even}}\). Changing variable \(k=s \log N\), using \(\sigma _N^2 R_N=1+ (\vartheta +o(1))/\log N\), and applying Lemma 3.3 on the convergence of \((\tau ^{(N)}_k, S^{(N)}_k)_{k\geqslant 0}\) to a Lévy process \({\varvec{Y}}_\cdot =(Y_\cdot , V_\cdot )\), we find that the sum above converges to the Riemann integral
where \(\mathrm P^\varepsilon _{{\textsf{i}},{\textsf{a}}}\) denotes the law of the Lévy process \({\varvec{Y}}_u=(Y_u, V_u)\) with \({\varvec{Y}}_0\) sampled uniformly from \({{\mathcal {T}}} _\varepsilon ({\textsf{i}})\times {{\mathcal {S}}} _\varepsilon ({\textsf{a}})\).
For \(|\vec {\textsf{i}}|\geqslant 2\), \(\Theta _{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) is defined in (4.11). The same argument as for the case \(|\vec {\textsf{i}}|=1\) gives
Here t is the time \((Y_\cdot , V_\cdot )\) jumps from \({{\mathcal {T}}} _\varepsilon ({\textsf{i}})\times {{\mathcal {S}}} _\varepsilon ({\textsf{b}})\) to \({{\mathcal {T}}} _\varepsilon ({\textsf{i}}')\times {{\mathcal {S}}} _\varepsilon ({\textsf{b}}')\).
(II) Proof of (7.2). First consider the case \(|\vec {\textsf{i}}|=1\). By translation invariance, we may assume \({\textsf{i}}={\textsf{i}}'=1\) and \({\textsf{a}}=0\). First note that
where \(G_\vartheta (t-s,y-x) := G_\vartheta (t-s) \, g_{\frac{t-s}{4}}(y-x)\) is the weighted Green’s function defined for the Lévy process \({\varvec{Y}}_s\), see (3.38) and (3.37).
When \({\textsf{a}}'=0\), we can relax the domain of integration in (7.6), use standard bounds on the Gaussian kernel g, and set \(u:=t-s\) to obtain
where we applied the asymptotics for \(\int _0^\varepsilon G_\vartheta \) in (3.47).
When \({\textsf{a}}'\ne 0\), the bound for \(\sigma _\varepsilon ^2(\vec {\textsf{i}}, \vec {\textsf{a}})\) can be improved with an extra factor of \(\frac{e^{-c|{\textsf{a}}'|^2}}{\log \frac{1}{\varepsilon }}\). Indeed, using polar coordinates (with respect to the \(|\cdot |_\infty \) norm) for \(x\in {{\mathcal {S}}} _\varepsilon (0)\), we have
If \(|{\textsf{a}}'|\geqslant 2\), then we can use (3.46) to bound the right hand side of (7.8) by
If \(1\leqslant |{\textsf{a}}'|<2\), then we can bound the right hand side of (7.8) by
This concludes the proof of the upper bound in (7.2).
We now bound \(\sigma _\varepsilon ^2(\vec {\textsf{i}}, \vec {\textsf{a}})\) for the case \(|\vec {\textsf{i}}|=2\). By relaxing all the constraints in (7.5) except \((Y_s, V_s) \in {{\mathcal {T}}} _\varepsilon ({\textsf{i}}')\times {{\mathcal {S}}} _\varepsilon ({\textsf{a}}')\), we note that except for a change of constants, the bound in (7.2) for \(|\vec {\textsf{i}}|=1\) also applies in this case. In particular, the bound in (7.2) holds for \(|\vec {\textsf{i}}|=2\) and \(|\vec {\textsf{a}}|\ne 0\). For \(|\vec {\textsf{i}}|=2\) and \(|\vec {\textsf{a}}|=0\), let us assume for simplicity that \({\textsf{i}}=1\), \({\textsf{i}}'=2\), and \({\textsf{a}}=0\). Again, relaxing all constraints in (7.5) except the constraint on \((Y_s, V_s)\), we have
The upper bound in (7.2) also holds.
We now consider the case \(|\vec {\textsf{i}}|\geqslant 3\). We first ignore the constraints on \(V_r\) for \(r\in (0,t)\cup (t,s)\) in (7.5). Using the weighted Green’s function \(G_\vartheta \) and the Lévy measure \(\frac{\mathbb {1}_{(0,1)}}{t} g_{t/4} \textrm{d}t \textrm{d}x\) for the Lévy process \({\varvec{Y}}_s=(Y_s, V_s)\) (see [18, Section 2]), we obtain the bound
Since \(|\vec {\textsf{i}}|={\textsf{i}}'-{\textsf{i}}+1\geqslant 3\), we can bound \(\frac{1}{s'-t}\leqslant \frac{1}{(|\vec {\textsf{i}}|-2)\varepsilon }\leqslant \frac{3}{|\vec {\textsf{i}}|\varepsilon }\) to obtain
where we first relaxed the constraints on \({\textsf{b}}\) and \({\textsf{b}}'\), then successively integrated out y, \(x'\), \(s'\), and t and applied (3.47), while in the last inequality, we applied a uniform bound on the heat kernel \(g_{\frac{t'-s}{4}}(y'-x)\). This concludes the proof of the upper bound in (7.2). \(\square \)
7.2 Fourth moment estimates
We next study the fourth moment.
Lemma 7.2
Let \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) be defined as in (4.11), with \((\vec {\textsf{i}}, \vec {\textsf{a}})=(({\textsf{i}}, {\textsf{i}}'), ({\textsf{a}}, {\textsf{a}}'))\in {{\mathbb {T}}} _\varepsilon \) defined in (4.5). There exist \(c, C\in (0,\infty )\) uniform in \((\vec {\textsf{i}}, \vec {\textsf{a}})\), such that for all \(\varepsilon >0\) sufficiently small,
Proof
We first prove (7.11) for \(|\vec {\textsf{i}}|={\textsf{i}}'-{\textsf{i}}+1\leqslant 2\). Consider a time-space block \((\vec {\textsf{i}}, \vec {\textsf{a}})=(({\textsf{i}}, {\textsf{i}}'), ({\textsf{a}}, {\textsf{a}}'))\) with \(|\vec {\textsf{a}}| \leqslant M_\varepsilon \sqrt{|\vec {\textsf{i}}|}\) and assume without loss of generality that \({\textsf{i}}={\textsf{i}}'=1\) and \({\textsf{a}}=0\). The case \(|\vec {\textsf{i}}|=2\) is similar (just replace \(\varepsilon \) by \(2\varepsilon \)). We will compare \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec 1, \vec {\textsf{a}})\) with an averaged partition function so that Theorem 6.1 can be applied.
Let us recall the polynomial chaos expansion of \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) from (4.11)
which is essentially an average of point-to-point partition functions with average over (d, x) and (f, y) in the bulk instead of through boundary conditions at time 0 and \(\varepsilon N\) respectively. To compare with an averaged partition function as in Theorem 6.1, we replace \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec 1, \vec {\textsf{a}})\) by
where \({{\mathcal {S}}} _{\varepsilon N}({\textsf{a}})=(({\textsf{a}}-(1,1))\sqrt{\varepsilon N}, {\textsf{a}}\sqrt{\varepsilon N}]\) and we note that uniformly in \((d,x)\in {{\mathcal {B}}} _{\varepsilon N}(1, 0)\) and \((f,y) \in {{\mathcal {B}}} _{\varepsilon N}(1, {\textsf{a}}')\), we have
Therefore \(\mathrm E[\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})^4] \leqslant C \mathrm E[\Theta ^4]\) because in the expansion for the fourth moment, all terms are non-negative if we assume \(\mathrm E[\xi _N^3]\geqslant 0\), which we may assume from now on since our bounds are in terms of \(|\mathrm E[\xi _N^k]|\) for \(1\leqslant k\leqslant 4\) (see the proof of Theorem 6.1). In the definition of \(\Theta \), we can further remove the constraint on y and the summation constraints in the definition of \(X_{d,f}^{(\textrm{diff})}(x,y)\) in (4.9)–(4.10), which gives the centred partition function
as defined in Theorem 6.1, with \(\varphi (x)=\mathbb {1}_{{{\mathcal {S}}} _1(0)}(x)\) and \(\psi (x)=\mathbb {1}_{{{\mathcal {S}}} _1({\textsf{a}}')}(x)\). Therefore for N large, we have
where we applied Theorem 6.1 with N set to \(\varepsilon N\), \(T=1/\varepsilon \), \(p=q=2\), \(h=4\), and \(w(x) = e^{-|x|}\). This proves (7.11) for \(|\vec {\textsf{i}}|\leqslant 2\).
We now consider the case \(|\vec {\textsf{i}}|\geqslant 3\). Recall the definition of \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) from (4.11), we can rewrite it as
where
For each \(({\textsf{b}}, {\textsf{b}}')\), because \({\textsf{i}}'-{\textsf{i}}\geqslant 2\), we can apply Lemma 3.2 (with \(m=\varepsilon N\)) to bound
uniformly in \((f,y) \in {{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}, {\textsf{b}})\) and \((d', x') \in {{\mathcal {B}}} _{\varepsilon N}({\textsf{i}}', {\textsf{b}}')\). We can make this replacement in the bound for the fourth moment to obtain
By triangle inequality, we can split the sum over \({\textsf{b}}, {\textsf{b}}'\) into three parts (with overlaps): (1) \(|{\textsf{b}}-{\textsf{a}}|\geqslant |\vec {\textsf{a}}|/3\); (2) \(|{\textsf{b}}'-{\textsf{a}}'|\geqslant |\vec {\textsf{a}}|/3\); \(|{\textsf{b}}'-{\textsf{b}}|\geqslant |\vec {\textsf{a}}|/3\). It suffices to bound the fourth moment of each part.
For part (1), we can bound
where the inequality can be justified if we first expand the power and take expectation and then bound \(\frac{e^{-c|{\textsf{b}}-{\textsf{b}}'|^2/|\vec {\textsf{i}}|}}{|\vec {\textsf{i}}|}<1\); we also used the independence of \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(({\textsf{i}}, {\textsf{i}}), \cdot )\) and \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(({\textsf{i}}', {\textsf{i}}'), \cdot )\). For the first factor in (7.17), we can expand the power and bound
where in the last inequality, we applied the fourth moment bound (7.13) for \(\Theta ^{(\textrm{cg})}_{N, \varepsilon }(\vec {\textsf{i}}, \cdot )\) with \(|\vec {\textsf{i}}|=1\). The second factor in (7.17) can be bounded the same way without the factor \(e^{-c|\vec {\textsf{a}}|}\). This implies that when the sum in (7.16) is restricted to \(|{\textsf{b}}-{\textsf{a}}|\geqslant |\vec {\textsf{a}}|/3\), we get a fourth moment bound of \(C e^{-c|\vec {\textsf{a}}|}/(\log \frac{1}{\varepsilon })^2\). The same bound holds if the sum is restricted to \(|{\textsf{b}}'-{\textsf{a}}'|\geqslant |\vec {\textsf{a}}|/3\).
When the sum in (7.16) is restricted to \(|{\textsf{b}}-{\textsf{b}}'|\geqslant |\vec {\textsf{a}}|/3\), we can bound \(\frac{e^{-c|{\textsf{b}}-{\textsf{b}}'|^2/|\vec {\textsf{i}}|}}{|\vec {\textsf{i}}|}\leqslant e^{-c|\vec {\textsf{a}}|^2/|\vec {\textsf{i}}|}\). The rest of the calculations is the same as before, which leads to a fourth moment bound of \(C e^{-c|\vec {\textsf{a}}|^2/|\vec {\textsf{i}}|}/(\log \frac{1}{\varepsilon })^2\). Combined with the previous estimates, it is clear that (7.11) holds. This concludes the proof of Lemma 7.2. \(\square \)
8 Moment estimates for the coarse-grained model
In this section, we will prove an analogue of Theorem 6.1 for the coarse-grained model (defined in (4.8)), that we rewrite for convenience:
with coarse-grained disorder variables \(\Theta (\vec {\textsf{i}}, \vec {\textsf{a}}):=\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) (see (4.11)) indexed by time-space blocks \((\vec {\textsf{i}}, \vec {\textsf{a}})=(({\textsf{i}}, {\textsf{i}}'), ({\textsf{a}}, {\textsf{a}}'))\) in the set \({{\mathbb {T}}} _\varepsilon \) (see (4.5)), while \(\varphi _\varepsilon , \psi _\varepsilon : {\mathbb {Z}}^2 \rightarrow {\mathbb {R}}\) are defined by (4.7) from \(\varphi \in C_c({\mathbb {R}}^2)\) and \(\psi \in C_b({\mathbb {R}}^2)\).
We will prove the following analogue of Theorem 6.1 for the 4-th moment of the coarse-grained model.
Theorem 8.1
Let \({\mathscr {Z}}_{N, \varepsilon }(\varphi ,\psi ) :={\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta ^{\mathrm{(cg)}}_{N, \varepsilon })\) be the coarse-grained model defined above. Further assume that \(\Vert \psi \Vert _\infty <\infty \) and \(\psi \) is supported on a ball B (possibly \(B={\mathbb {R}}^d\)). Then for any \(p, q \in (1,\infty )\) with \(\frac{1}{p}+\frac{1}{q}=1\) and any \(w: {\mathbb {R}}^2 \rightarrow (0,\infty )\) such that \(\log w\) is Lipschitz continuous, there exists \(C\in (0,\infty )\) such that uniformly in \(\varepsilon \in (0,1)\),
where \(w_\varepsilon :{\mathbb {Z}}^2 \rightarrow {\mathbb {R}}\) is defined from w by (4.7).
Proof
We will adapt the proof of Theorem 6.1 to the current setting. The complication is that the coarse-grained disorder variables \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) are assigned to time-space blocks \((\vec {\textsf{i}}, \vec {\textsf{a}})\) instead of individual lattice sites. We will therefore divide the proof into two parts: first, expand the fourth moment and perform a resummation to bring it into a similar framework as in the proof of Theorem 6.1; second, give the necessary bounds analogous to those in the proof of Theorem 6.1.
Part I. Expansion. First, as in (6.4) in the proof of Theorem 6.1, denote
By assumption, we have \(|\psi _\varepsilon |\leqslant \Vert \psi \Vert _\infty \mathbb {1}_{B_\varepsilon }\), where \(B_\varepsilon =B/\sqrt{\varepsilon }\). By the same reasoning as in the proof of Theorem 6.1 (see the discussion leading to (6.12)), we can replace \(\psi \) by \(\Vert \psi \Vert _\infty \mathbb {1}_{B_\varepsilon }\) and replace \(g_{\frac{1}{2}(\frac{1}{\varepsilon }- {\textsf{i}}_r')}(\cdot )\) by \(g_{\frac{1}{2}({\tilde{n}}- {\textsf{i}}_r')}(\cdot )\) (with \({\tilde{n}}\) first summed over \([\varepsilon ^{-1}, 2\varepsilon ^{-1}]\), then extended to \([1, 2\varepsilon ^{-1}]\)) to obtain the following bound
We then expand the product in (8.4) to obtain the sum over 4 sequences of time-space blocks, each time-space block contributing a \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\) variable. Because we will bound the sum by taking the absolute value of each summand, we can relax the summation constraint on r to obtain an upper bound. Also note that thanks to the assumption \(\varphi \in C_c({\mathbb {R}}^2)\) and the diffusive constraint \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; {\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}\) (see (4.6)), we have a sum with finitely many terms, which allows us to pass the limit \(N\rightarrow \infty \) inside the sum later. For each \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) with \(|\vec {\textsf{i}}|={\textsf{i}}'-{\textsf{i}}+1\geqslant 2\), we further expand it as
where \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, ({\textsf{a}}, {\textsf{b}}), ({\textsf{b}}', {\textsf{a}}'))\) is defined as \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\), except the sum in its definition in (4.11) is restricted to a fixed choice of \(\vec {\textsf{b}}:=({\textsf{b}}, {\textsf{b}}')\). The expansion of the product in (8.4) then gives 4 sequences of coarse-grained disorder variables \(\Theta ^\mathrm{(cg)}_{N, \varepsilon }\), some of which may visit two distinct mesoscopic time intervals with indices \({\textsf{i}}, {\textsf{i}}'\) due to the expansion in (8.5). If we record the indices of the visited mesoscopic time intervals and the mesoscopic spatial boxes of entry and exit in each time interval, then we obtain 4 sequences of time-space indices \(({\textsf{i}}^j_1, {\textsf{a}}^j_1, {\textsf{b}}^j_1)\), ..., \(({\textsf{i}}^j_{r_j}, {\textsf{a}}^j_{r_j}, {\textsf{b}}^j_{r_j})\), \(1\leqslant j\leqslant 4\). We will call each such sequence a mesoscopic time-space renewal sequence, or just renewal sequence (see Fig. 4).
A depiction of the expansion of the fourth moment of the coarse-grained model that satisfy conditions (a)–(g). There are four time-space renewal sequences, each depicted in a different colour. Different sequences visit different mesoscopic boxes \({{\mathcal {B}}} _{\varepsilon N}({\textsf{i}},{\textsf{a}})\), but each visited box must be visited by at least two sequences to give a non-zero contribution. The first two time strips are visited by the two renewal sequences coloured black and red, which match in the disorder they sample. These two strips are grouped together as a block of type \({\textsf{U}}\). The third and fourth time strips are visited by three renewal sequences, coloured black, red, and green, which form a block of type \({\textsf{V}}\) and its width cannot exceed 4. Within this \({\textsf{V}}\) block, the spatial boxes of entry by the three renewals are all within distance \(2M_\varepsilon \) of each other, 2 of which match exactly. The last time strip is only visited by two renewal sequences, coloured blue and red, which also forms a \({\textsf{U}}\) block
We will rearrange the expansion of (8.4) as follows:
-
(1)
Sum over the set \(\bigcup _{j=1}^4 \{{\textsf{i}}^j_1, \ldots , {\textsf{i}}^j_{r_j}\}=:\{n_1, \ldots , n_r\}\).
-
(2)
For each time index \(n_i\), \(1\leqslant i\leqslant r\), sum over the set of indices \(J_i\subset \{1, \ldots , 4\}\), which determine the renewal sequences that visit time interval \(n_i\).
-
(3)
For each \(j\in J_i\), i.e., a renewal sequence that visits time interval \(n_i\), sum over the indices \(({\textsf{a}}^j_i, {\textsf{b}}^j_i)\) that determine the spatial boxes of entry and exit in that time interval.
Given a choice of these summation indices, the summand contains a product of coarse grained disorder variables of either the form \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }((n_i, n_i), ({\textsf{a}}_i, {\textsf{b}}_i))=: \Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(n_i; {\textsf{a}}_i, {\textsf{b}}_i)\) or the form \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }((n_i, n_j), ({\textsf{a}}_i, {\textsf{b}}_i), ({\textsf{a}}_j, {\textsf{b}}_j))\), connected by heat kernels \(g_{\frac{1}{2}(n_k -n_l)}\, ({\textsf{a}}_k -{\textsf{b}}_l)\). For such a product to have non-zero expectation, we have the following constraints (see Fig. 4):
-
(a)
\(|J_i|\geqslant 2\) for each \(1\leqslant i\leqslant r\);
-
(b)
If \(|J_i|=2\), say \(J_i=\{k, l\}\subset \{1, \ldots , 4\}\), then we must have \({\textsf{a}}^k_i={\textsf{a}}^l_i\) and \({\textsf{b}}^k_i={\textsf{b}}^l_i\);
-
(c)
If \(|J_i|\geqslant 3\), then for each sequence \(k \in J_i\), there must be another sequence \(l\in J_i\) such that \(|{\textsf{a}}^k_i-{\textsf{a}}^l_i|\leqslant 2M_\varepsilon \), where \(M_\varepsilon =\log \log \frac{1}{\varepsilon }\) as in (4.2).
If (c) is violated, then by the spatial constraint in the definition of \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\) in (4.11), there will be a coarse-grained disorder variable visiting time interval \(n_i\), which is independent of all other coarse-grained disorder variables in the product, and hence leads to zero expectation.
The summation constraints \(\vec {\varvec{{\mathcal {A}}}}_\varepsilon ^{(\mathrm {no\, triple})}\) and \(\vec {\varvec{{\mathcal {A}}}}_{\varepsilon ; {\textsf{b}}, {\textsf{c}}}^{(\textrm{diff})}\) (see (4.4) and (4.6)) in the definition (8.1) of the coarse-grained model implies the following additional constraints on the summation indices r, \((n_i)_{1\leqslant i\leqslant r}\), \((J_i)_{1\leqslant i\leqslant r}\), and \(({\textsf{a}}^j_i, {\textsf{b}}^j_i)_{1\leqslant i\leqslant r, j\in J_i}\):
-
(d)
For all \(1\leqslant i\leqslant r\) and each renewal sequence with index \(j\in J_i\), \(|{\textsf{b}}^j_i-{\textsf{a}}^j_i|\leqslant M_\varepsilon \);
-
(e)
For \(1\leqslant j\leqslant 4\) and \(1\leqslant i_1 <i_2\leqslant r\), if \(j\in J_{i_1} \cap J_{i_2}\) and \(j\notin J_i\) for all \(i_1<i<i_2\) (namely renewal sequence j visits the mesoscopic time intervals with indices \(n_{i_1}\) and \(n_{i_2}\), but nothing in between), then \(|{\textsf{a}}^j_{i_2}-{\textsf{b}}^j_{i_1}|\leqslant M_\varepsilon \sqrt{n_{i_2}-n_{i_1}}\);
-
(f)
\(K_\varepsilon \leqslant n_1<n_2<\cdots <n_r \leqslant \frac{1}{\varepsilon } - K_\varepsilon \), where \(K_\varepsilon =(\log \frac{1}{\varepsilon })^6\) as in (4.2);
-
(g)
\((n_1, \ldots , n_r)\) can be partitioned into consecutive stretches \({{\mathcal {D}}} _1, \ldots , {{\mathcal {D}}} _m\) such that each \({{\mathcal {D}}} _i\) consists of consecutive integers, with a gap between \({{\mathcal {D}}} _i\) and \({{\mathcal {D}}} _{i+1}\). Then each \({{\mathcal {D}}} _\cdot =(n_{i}, n_{i+1}=n_i+1, \ldots , n_{j} = n_i + (j-i))\) has width \(n_{j}-n_{i}+1\leqslant 4\), since \(|J_{n_l}|\geqslant 2\) for \(i\leqslant l \leqslant j\) (namely the mesoscopic time interval with index \(n_l\) is visited by at least two renewal sequences), and each sequence can visit at most two mesoscopic time intervals with indices among \(n_{i}, n_{i+1}, \ldots , n_{j}\) by the constraint \(\vec {\varvec{{\mathcal {A}}}}_\varepsilon ^{(\mathrm {no\, triple})}\).
Conditions (d)–(e) follow from the definitions of \(\vec {\varvec{{\mathcal {A}}}}_\varepsilon ^{(\textrm{diff})}\) in (4.6) and \(\Theta ^\mathrm{(cg)}_{N, \varepsilon }\) in (4.11), while conditions (f)–(g) follow from the definition of \(\vec {\varvec{{\mathcal {A}}}}_\varepsilon ^{(\mathrm {no\, triple})}\) in (4.4).
To handle the dependency among the coarse-grained disorder variables in the expansion of (8.4), we perform a further resummation. First partition \((n_1, \ldots , n_r)\) into consecutive stretches \({{\mathcal {D}}} _1, \ldots , {{\mathcal {D}}} _m\) as in (g), so that \(\{n_1, \ldots , n_r\} = \bigcup _{i=1}^m {{\mathcal {D}}} _i\). For each \({{\mathcal {D}}} _i\), let \({\tilde{J}}_i :=\bigcup _{j \in {{\mathcal {D}}} _i} J_j\), which records which of the 4 renewal sequences visits the stretch \({{\mathcal {D}}} _i\). Next we group together consecutive \({{\mathcal {D}}} _{i_1}, {{\mathcal {D}}} _{i_1+1}, \ldots , {{\mathcal {D}}} _{i_2}\) with the same \({\tilde{J}}_i=\{k, l\}\) for some \(k\ne l\in \{1, \ldots , 4\}\), and only keep track of \(s:=\min {{\mathcal {D}}} _{i_1}\) and \(t:=\max {{\mathcal {D}}} _{i_2}\), thus effectively replacing \(\bigcup _{i_1\leqslant i\leqslant i_2} {{\mathcal {D}}} _i\) by [s, t]. This allows us to identify from \((n_1, \ldots , n_r)\) a sequence of disjoint time intervals (which we call blocks) \({{\mathcal {I}}} _i=[s_i, t_i]\cap {\mathbb {N}}\), \(1\leqslant i\leqslant k\), each associated with a label set \({{\mathcal {J}}} _i\subset \{1, \ldots , 4\}\). Some of these intervals arise from \(\bigcup _{i_1\leqslant i\leqslant i_2} {{\mathcal {D}}} _i\) as above, which are visited by exactly 2 renewal sequences, the rest coincide with the original \({{\mathcal {D}}} _i\)’s. We can then rewrite the expansion of (8.4) as follows:
-
(1’)
Sum over integers \(K_\varepsilon<s_1\leqslant t_1<s_2\leqslant t_2<\cdots<s_k\leqslant t_k < {\tilde{n}}\leqslant \frac{2}{\varepsilon }\), with \(s_{i+1}-t_i\geqslant 2\) for each i (recall the summation index \({\tilde{n}}\) from (8.4)). Denote \({{\mathcal {I}}} _i:=[s_i, t_i]\cap {\mathbb {N}}\).
-
(2’)
For each block \({{\mathcal {I}}} _i\), sum over the set of indices \({{\mathcal {J}}} _i \subset \{1, \ldots , 4\}\) with \(|{{\mathcal {J}}} _i|\geqslant 2\). If \(|{{\mathcal {J}}} _i|=2\), we call \({{\mathcal {I}}} _i\) a block of type U because it leads to contributions similar to \({\textsf{U}}_s({\varvec{z}}^1, {\varvec{z}}^2)\) in (6.14) (see also (3.41)); otherwise we call it a block of type V. There are no consecutive blocks \({{\mathcal {I}}} _i\), \({{\mathcal {I}}} _{i+1}\) of both type U with the same label set \({{\mathcal {J}}} _i={{\mathcal {J}}} _{i+1}\), and each block \({{\mathcal {I}}} _i\) of type V must have length \(|{{\mathcal {I}}} _i|\leqslant 4\). See Fig. 4 for an illustration.
-
(3’)
For each block \({{\mathcal {I}}} _i\) and each renewal sequence \(j\in {{\mathcal {J}}} _i\) that visits block \({{\mathcal {I}}} _i\), sum over time-space indices \((\sigma ^j_i, {\textsf{a}}^j_i)\) and \((\tau ^j_i, {\textsf{b}}^j_i)\) with \(s_i\leqslant \sigma ^j_i \leqslant \tau ^j_i \leqslant t_i\) and \({\textsf{a}}^j_i, {\textsf{b}}^j_i\in {\mathbb {Z}}^2\), which identifies the mesoscopic time-space blocks of entry and exit by the j-th renewal sequence in the time interval \({{\mathcal {I}}} _i=[s_i, t_i]\cap {\mathbb {N}}\).
The constraints imposed in (d)–(g) carry over, so we do not repeat them here.
To rewrite the expansion of (8.4) in a form that fits the framework developed in the proof of Theorem 6.1, we will carry out the following steps, that we describe below.
- (A):
-
To decouple different blocks, replace each coarse-grained disorder variable \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\) (it will arise as a summand in (8.5)) that visits two consecutive blocks \({{\mathcal {I}}} _i\) and \({{\mathcal {I}}} _{i+1}\) by the product of two coarse-grained disorder variables of the form \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}})\) with \(|\vec {\textsf{i}}|=1\), joined by a heat kernel.
- (B):
-
Bound the moments of the effective disorder variable associated with each U block and V block.
- (C):
-
Modification of the heat kernels \(g_{\frac{1}{2} (s_{i+1}-t_i)}(\cdot )\) connecting different blocks. In particular, carry out a Chapman–Kolmogorov type decomposition for the heat kernels as in the proof of Theorem 6.1, so that we sum over the spatial locations for all 4 renewal sequences at the beginning and end of each block \({{\mathcal {I}}} _i\).
This rewriting will introduce a constant factor for each block, but it will not affect our final result. We now give the details for (A)–(C).
(A) Note the technical complication that given a realisation of the summation indices in (1’)–(3’), there could be coarse-grained disorder variables \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }((\tau ^j_{i_1}, \sigma ^j_{i_2}), ({\textsf{a}}^j_{i_1}, {\textsf{b}}^j_{i_1}), ({\textsf{a}}^j_{i_2}, {\textsf{b}}^j_{i_2}))\) (see (8.5)) that visit two distinct blocks \({{\mathcal {I}}} _{i_1}=[s_{i_1}, t_{i_1}]\cap {\mathbb {N}}\) and \({{\mathcal {I}}} _{i_2}=[s_{i_2}, t_{i_2}]\cap {\mathbb {N}}\) for some \(i_1<i_2\), due to the contribution from the j-th renewal sequence for some \(j\in {{\mathcal {J}}} _{i_1}\cap {{\mathcal {J}}} _{i_2}\). In particular, \(\tau ^j_{i_1} \in {{\mathcal {I}}} _{i_1}\) and \(\sigma ^j_{i_2} \in {{\mathcal {I}}} _{i_2}\). Recall from (8.5) and (4.11) that
Note that by the definition of a U block, if \({{\mathcal {I}}} _{i_1}\) is a block of type U, then we must have \(\tau ^j_{i_1}=t_{i_1}\), the last time index in the block \({{\mathcal {I}}} _{i_1}\); while if \({{\mathcal {I}}} _{i_1}\) is a block of type V, then we must have \(\tau ^j_{i_1}\geqslant s_{i_1}\geqslant t_{i_1}-3\) because V blocks of length at most 4. Similarly, if \({{\mathcal {I}}} _{i_2}\) is of type of U, then we must have \(\sigma ^j_{i_2}=s_{i_2}\), the first time in the block \({{\mathcal {I}}} _{i_2}\); while if \({{\mathcal {I}}} _{i_2}\) is type V, then we must have \(\sigma ^j_{i_2}\leqslant t_{i_2}\leqslant s_{i_2} + 3\). Therefore \(d'-f\leqslant (s_{i_2}-t_{i_1}+7)\varepsilon N\). On the other hand, \({{\mathcal {I}}} _{i_1}\) and \({{\mathcal {I}}} _{i_2}\) are distinct blocks and hence \(s_{i_2}-t_{i_1}\geqslant 2\) and \(d'-f\geqslant \varepsilon N\). We can therefore apply Lemma 3.2 with \(m=\varepsilon N\), \(n_1=d'-f\), \(n_2=s_{i_2}-t_{i_1}\) and \(\varrho _1=10\) to bound
Applying this bound in (8.6) then allows us to make the replacement (recall the definition of \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\) from (4.11))
Of course this is not an upper bound since \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\) could be negative. However, when we compute the moment in (8.4), we end up with products of the moments of \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\)’s and its constituent \(\xi _N\)’s, which are then be bounded by their absolute values. Applying (8.7) at this point gives a true upper bound, which has the same effect as making the replacement (8.8) in the expansion before taking expectation, and then compute the moment as in (8.4). To keep the notation simple, we will assume this replacement from now on, so that the expansion of (8.4) now contains only \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }({\textsf{i}}; {\textsf{a}}, {\textsf{b}})\) that visits a single mesoscopic time interval \({{\mathcal {T}}} _{\varepsilon N}({\textsf{i}})\), which simplifies the expansion from (8.4). The cost is replacing some heat kernel \(g_{\frac{{\textsf{i}}}{2}}(\cdot )\) (more accurately, the associated random walk transition kernel) by \(C g_{10{\textsf{i}}}(\cdot )\) as in (8.7).
(B) We now consider a U block \({{\mathcal {I}}} =[s, t]\cap {\mathbb {N}}\). Assuming w.l.o.g. \({{\mathcal {J}}} =\{1,2\}\) so that only renewal sequences 1 and 2 in the expansion of (8.4) visit block \({{\mathcal {I}}} \). Let \({\textsf{a}}, {\textsf{b}}\in {\mathbb {Z}}^2\) be spatial indices for the mesoscopic boxes of entry and exit in the time interval \({{\mathcal {I}}} \). Then the coarse-grained disorder variables \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\) visited by renewal sequences 1 and 2 in the time interval \({{\mathcal {I}}} \) must match perfectly in order to have non-zero expectation. Taking expectation in (8.4), each U block in the expansion therein leads to the following quantity analogous to \(\overline{U}_N(n,x)\) defined in (3.40) and (3.41):
where \(\vec {\varvec{{\mathcal {A}}}}_\varepsilon ^{(\mathrm {no\, triple})}\) and \(\vec {\varvec{{\mathcal {A}}}}_\varepsilon ^{(\textrm{diff})}\) are defined in (5.70) and (5.71). Because the sum above is a sum over finitely many terms, by Lemma 7.1, the following limit exists
We next consider a V block \({{\mathcal {I}}} =[s,t]\cap {\mathbb {N}}\) with size \(t-s+1\leqslant 4\). Let \({{\mathcal {J}}} \subset \{1, 2,3,4\}\) denote the set of renewal sequences that visit \({{\mathcal {I}}} \). To have non-zero expectation in the expansion of (8.4), we must have \(|{{\mathcal {J}}} |\geqslant 3\) (\(|{{\mathcal {J}}} |= 2\) would make it a U block instead). Each renewal sequence can visit at most two mesoscopic time intervals with indices in \({{\mathcal {I}}} \). For each renewal sequence \(j\in {{\mathcal {J}}} \) that visits block \({{\mathcal {I}}} \), let \((\sigma ^j, {\textsf{a}}^j)\) and \((\tau ^j, {\textsf{b}}^j)\) be the indices of the mesoscopic time-space boxes of entry and exit in \({{\mathcal {I}}} \). In the expectation in (8.4), such a V block then leads to the following factor
where the indicators follow from the local dependence of \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\) from its definition in (4.11). Applying (7.11) with \(|\vec {\textsf{i}}|\leqslant 4\) (since V blocks have length at most 4) then gives
(C) We next modify the heat kernels connecting different blocks \({{\mathcal {I}}} _i\). First, we will contract each V block \({{\mathcal {I}}} _i=[s_i, t_i]\cap {\mathbb {N}}\) into a block of size 1. Note that every heat kernel in the expansion connects two different blocks \({{\mathcal {I}}} _{i_1}=[s_{i_1}, t_{i_1}]\cap {\mathbb {N}}\) and \({{\mathcal {I}}} _{i_2}=[s_{i_2}, t_{i_2}]\cap {\mathbb {N}}\), \(i_1<i_2\), and are of the form \(g_{\frac{1}{2}(\sigma _{i_2}-\tau _{i_1})}({\textsf{a}}_{i_2}-{\textsf{b}}_{i_1})\) for some \(\tau _{i_1}\in {{\mathcal {I}}} _{i_1}\) and \(\sigma _{i_2}\in {{\mathcal {I}}} _{i_2}\) with \(|{\textsf{a}}_{i_2}-{\textsf{b}}_{i_1}|\leqslant M_\varepsilon \sqrt{\sigma _{i_2}-\tau _{i_1}}\). The heat kernel \(g_{\frac{1}{2}(\sigma _{i_2}-\tau _{i_1})}(\cdot )\) from time \(\tau _{i_1}\) to \(\sigma _{i_2}\) may jump over multiple blocks of type V. If we contract the time span \([\tau _{i_1}, \sigma _{i_2}]\) of the heat kernel by shrinking each block of type V that intersects \([\tau _{i_1}, \sigma _{i_2}]\) into a block of size 1, and let u denote the length of the reduced time span for the heat kernel, then \(u\geqslant \frac{1}{4}(\sigma _{i_2}-\tau _{i_1})\) since blocks of type V have length at most 4. Therefore
The heat kernels introduced in (8.7) are of the form \(g_{10(\sigma _{i_2}-\tau _{i_1})}({\textsf{a}}_{i_2}-{\textsf{b}}_{i_1})\) and can similarly be bounded by \(8 g_{80u}({\textsf{a}}_{i_2}-{\textsf{b}}_{i_1})\). For consistency, we will further bound \(g_{2u}(\cdot ) \leqslant 20 g_{80u}(\cdot )\). This shows that at the cost of introducing a constant factor C for each block \({{\mathcal {I}}} _i\), we can assume from now on that all blocks \({{\mathcal {I}}} _i\) of type V have length 1, namely \(s_i=t_i\), and all heat kernels appearing in the expansion (as an upper bound for the expansion of (8.4)) are of the form \(g_{80(s_{i_2}-t_{s_{i_1}})}(\cdot )\).
Lastly, we perform a Chapman–Kolmogorov type decomposition for each heat kernel \(g_{80(s_{i_2}-t_{i_1})}({\textsf{b}}_{i_1}, {\textsf{a}}_{i_2}) :=g_{80(s_{i_2}-t_{i_1})}({\textsf{a}}_{i_2}-{\textsf{b}}_{i_1})\) at each \(s_j, t_j \in (t_{i_1}, s_{i_2})\cap {\mathbb {N}}\), similar to what was done in the proof of Theorem 6.1. To simplify notation, let \(u_0=t_{i_1}, u_1, \ldots , u_{k-1}, u_k=s_{i_2}\), with \(u_1, \ldots , u_{k-1}\) being the times at which we want to perform the decomposition. Let \({\textsf{x}}_0:={\textsf{b}}_{i_1}\), \({\textsf{x}}_k:={\textsf{a}}_{i_2}\). Then we can bound
where we have discretized the spatial integral into a sum over the lattice and introduced a factor 2 for each intermediate time \(u_i\), \(1\leqslant i<k\), as a crude upper bound.
The steps (A)–(C) we have performed so far basically allow us to bound the expansion (8.4) in a form that is similar to (6.12), and ready to lead to the analogue of (6.17). The U blocks we have introduced correspond to \({\textsf{U}}^I\) introduced in (6.14), while V blocks correspond to the disorder variable \(\xi \), which even after contracting each V block into a block length 1, still has non-trivial spatial dependence. Due to the heavy notation, we will not write down the analogue of (6.12) here. Instead, we explain below how the analogues of (6.17) and (6.20) can be derived.
Part II. Bounds. Based on the considerations above, we can write down an upper bound for (8.4) that allows us to adapt the proof of Theorem 6.1. First, we introduce some notation that parallels those in the proof of Theorem 6.1. Similar to (6.8), for \({\textsf{a}}=({\textsf{a}}^j)_{1\leqslant j\leqslant 4}, {\textsf{b}}=({\textsf{b}}^j)_{1\leqslant j\leqslant 4} \in ({\mathbb {Z}}^2)^4\) and \(\varphi :{\mathbb {Z}}^2\rightarrow {\mathbb {R}}\), define
Similar to (6.14), for \({{\mathcal {J}}} =\{k, l\}\subset \{1, 2,3,4\}\), define (recall \(\overline{U}^{\mathrm{(cg)}}_{\infty , \varepsilon }\) from (8.10))
with \(g_0({\textsf{a}}^j, {\textsf{b}}^j):=\mathbb {1}_{\{{\textsf{a}}^j={\textsf{b}}^j\}}\). Similarly, define (recall \({\textsf{V}}^{\mathrm{(cg)}, {{\mathcal {J}}} }_{\infty , \varepsilon }({\textsf{a}}, {\textsf{b}})\) from (8.11))
To be consistent with the notation in the proof of Theorem 6.1, we will replace \({{\mathcal {J}}} \subset \{1, 2,3,4\}\), which determines which mesoscopic renewal sequences collect coarse-grained disorder variables at time t, by a partition \(I\vdash \{1, 2,3,4\}\), which specifies which sequences interact with each other through the coarse-grained disorder variables at time t. In particular, in \({\textsf{U}}^{\mathrm{(cg), {{\mathcal {J}}} }}_{\infty , \varepsilon }\) corresponding to a U block, the associated partition I consists of \({{\mathcal {J}}} \) and \(\{j\}\) for \(j\notin {{\mathcal {J}}} \), so that \(|I|=3\). In \(V^{\mathrm{(cg), {{\mathcal {J}}} }}_{\infty , \varepsilon }\) corresponding to a V block, if \(|{{\mathcal {J}}} |=3\), then the associated partition I consists of \({{\mathcal {J}}} \) and \(\{j\}\) for \(j\notin {{\mathcal {J}}} \), so \(|I|=2\); if \(|{{\mathcal {J}}} |=4\), then the associated partition I is given by the connected components of \(\{1,2,3,4\}\) with an edge between i and j whenever \(|{\textsf{a}}^i-{\textsf{a}}^j|\leqslant 6M_\varepsilon \), and there can be no singletons in the partition to ensure that \({\textsf{V}}^{\mathrm{(cg), {{\mathcal {J}}} }}_{\infty , \varepsilon }\ne 0\) (in particular, \(|I|=1\) or 2).
From now on, we write \({\textsf{U}}^{\mathrm{(cg)}, I}_{\infty , \varepsilon } (t; {\textsf{a}}, {\textsf{b}})\) and \({\textsf{V}}^{\mathrm{(cg)}, I}_{\infty , \varepsilon } (t; {\textsf{a}}, {\textsf{b}})\), replacing \({{\mathcal {J}}} \) by the associated partition \(I\vdash \{1, 2,3,4\}\). Define
We can now write down the following upper bound for (8.4) in the limit \(N\rightarrow \infty \):
where C does not depend on \(\varepsilon \), \({\textsf{a}}_{r+1}:=\mathbb {1}_{B_\varepsilon }\), the sum in (8.15) contains no consecutive \(I_i=I_{i+1}\) with \(|I_i|=3\), and when \(|I_i|\leqslant 2\), we must have \(s_i=t_i\) thanks to the contraction of the V blocks.
For \(\lambda >0\) to be chosen later, we can insert the factor \(e^{\frac{2\lambda }{\varepsilon }} e^{-\lambda \sum _{i=1}^{r+1} (s_i-t_{i-1})-\lambda \sum _{i=1}^r (t_i-s_i)}\geqslant 1\) into (8.15) to obtain a bound similar to (6.17):
where given two partitions \(I, J \vdash \{1, \ldots , 4\}\), with \(I=*\) denoting the partition consisting of singletons, \({\textsf{P}}^{I, J}_{\lambda , \varepsilon }\) are integral operators with kernels given by
where for \({\textsf{a}}, {\textsf{b}}\in ({\mathbb {Z}}^2)^4\),
Here, given \({\textsf{a}}=({\textsf{a}}^j)_{1\leqslant j\leqslant 4} \in ({\mathbb {Z}}^2)^4\) and a partition \(I\vdash \{1, 2,3,4\}\), with \(k{\mathop {\sim }\limits ^{I}} l\) denoting k, l belonging to the same partition element in I,
We will denote \(({\mathbb {Z}}^2)^4_I := \{ {\textsf{b}}\in ({\mathbb {Z}}^2)^4: {\textsf{b}}\sim I\}\). The main difference from (6.17) and (6.15) is that the spatial constraint there are delta functions (see (6.7)), that is, \({\textsf{a}}\sim I\) with \(M_\varepsilon \) set to 0. Here we also have the additional operator \({\textsf{V}}_{\lambda , \varepsilon }^{J}({\textsf{a}}, {\textsf{b}})\) because we allow \({\textsf{b}}\ne {\textsf{a}}\). The analogue of \({{\mathbb {E}}} [\xi ^p]\) are the moments of the coarse-grained disorder variables \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\), which are now captured in \({\textsf{V}}_{\lambda , \varepsilon }^{J}\) and \({\textsf{U}}_{\lambda , \varepsilon }^{J}\).
As in (6.18), for a weight function \(w_\varepsilon :{\mathbb {Z}}^2 \rightarrow {\mathbb {R}}\), see (4.7), we define the weighted operators
and define \({\widehat{{\textsf{U}}}}_{\lambda , \varepsilon }^{J}({\textsf{a}}, {\textsf{b}})\), \({\widehat{{\textsf{V}}}}_{\lambda , \varepsilon }^{J}({\textsf{a}}, {\textsf{b}})\), and \(\widehat{\textsf{P}}^{I, J}_{\lambda , \varepsilon }\) similarly. For \(p, q>1\) with \(\frac{1}{p}+\frac{1}{q}=1\), we can then bound (8.16) via the following analogue of (6.20):
where we still have \(({\mathbb {Z}}^2)^4_I := \{ {\textsf{b}}\in ({\mathbb {Z}}^2)^4: {\textsf{b}}\sim I\}\), but the definition of the constraint \({\textsf{b}}\sim I\) has changed as in (8.19). We still regard \({\widehat{{{\mathcal {Q}}} }}_{\lambda , \varepsilon }^{I; J} (\cdot , \cdot )\) and \({\widehat{{\textsf{P}}}}_{\lambda , \varepsilon }^{I; J} (\cdot , \cdot )\) as operators from \(\ell ^q(({\mathbb {Z}}^2)^4_J) \rightarrow \ell ^q(({\mathbb {Z}}^2)^4_I)\), and similarly for \({\widehat{{\textsf{U}}}}_{\lambda , \varepsilon }^{J}\) and \({\widehat{{\textsf{V}}}}_{\lambda , \varepsilon }^{J}\).
We choose \(\lambda := {\hat{\lambda }} \varepsilon \) with \({\hat{\lambda }}\) large but fixed so that \(e^{\lambda \varepsilon }\) remains bounded. We have the following analogue of Proposition 6.6, where we again omitted \(({\mathbb {Z}}^2)^4_I\) from \(\Vert \cdot \Vert _{\ell ^p(\cdot )}\).
Proposition 8.2
For some c uniformly in \(\lambda = \frac{{\hat{\lambda }}}{N}>0\), \(\varepsilon \in (0,1)\), and \(I, J\subset \{1, \ldots , 4\}\) with \(1\leqslant |I|, |J| \leqslant 3\) and \(I\ne J\) when \(|I|=|J|=3\), we have
We now substitute these bounds into (8.20) and note that when \(|I|=|J|=3\), each factor \(\Vert {\widehat{{{\mathcal {Q}}} }}^{I; J}_{\lambda , \varepsilon }\Vert _{\ell ^q\rightarrow \ell ^q}\) can be controlled by \(\Vert \widehat{\textsf{U}}^{I}_{{\hat{\lambda }} \varepsilon , \varepsilon }\Vert _{\ell ^q\rightarrow \ell ^q}\), and when \(|I|\wedge |J|\leqslant 2\), the powers of \(M_\varepsilon =\log \log \frac{1}{\varepsilon }\) from (8.21)–(8.23) can be controlled by \(\Vert {\widehat{{\textsf{V}}}}^{I}_{\lambda , \varepsilon } \Vert _{\ell ^q\rightarrow \ell ^q}^{1/2} \Vert {\widehat{{\textsf{V}}}}^{J}_{\lambda , \varepsilon } \Vert _{\ell ^q\rightarrow \ell ^q}^{1/2}\) (set \(\Vert \widehat{\textsf{V}}^{I}_{\lambda , \varepsilon } \Vert _{\ell ^q\rightarrow \ell ^q}:=1\) if \(|I|=3\)). This leads to a convergent geometric series similar to (6.25), which gives
for some C depending only on \({\hat{\lambda }}\). This proves Theorem 8.1. \(\square \)
To conclude this section, we sketch the proof of Proposition 8.2.
Proof of Proposition 8.2
We will sketch how the proof of Proposition 6.6 can be adapted to the current setting.
Proof of (8.21). First note that it is equivalent to
uniformly for all \(f\in \ell ^p(({\mathbb {Z}}^2)^4_{I})\) and \(g\in \ell ^q(({\mathbb {Z}}^2)^4_{J})\). We split the region of summation into \(A_\varepsilon =\{|{\varvec{x}}-{\varvec{y}}|\leqslant C_0/\sqrt{\varepsilon |}\}\) and \(A_\varepsilon ^c\). Note that the analogue of Lemma 6.7 holds for \({{\mathcal {Q}}} _{\lambda , \varepsilon }\). Therefore following the same argument as in (6.35), the region \(A_\varepsilon ^c\) gives the contribution
where the spatial constraints in \({\varvec{x}}\in ({\mathbb {Z}}^2)^4_{I}\) and \({\varvec{y}}\in ({\mathbb {Z}}^2)^4_{J}\) (see (8.19)) led to the factor in the bracket in the third line.
In the region \(A_\varepsilon \), the factor \(w_\varepsilon ^{\otimes 4}({\varvec{x}})/w_\varepsilon ^{\otimes 4}({\varvec{y}})\) is bounded. By the analogue of Lemma 6.7 for \({{\mathcal {Q}}} _{\lambda , \varepsilon }\), it suffices to show
When \(|I|=|J|=3\), the proof is exactly the same as that of (6.27). When \(|I|, |J|<3\), we can apply Hölder to bound the l.h.s. of (8.29) by
When \(|I|<3\) and \(|J|=3\) (the case \(|I|=3\) and \(|J|<3\) can be treated identically), we can find \(k, l\in \{1,2,3,4\}\) that belong to the same partition element in I, but to different partition elements in J; in particular, \({\varvec{x}}\in ({\mathbb {Z}}^2)^4_{I}\) implies \(|x_k-x_l|\leqslant 20 M_\varepsilon \). Fix any \(a\in (0, 1/q)\). We can then apply Hölder to bound the l.h.s. of (8.29) by
where in the first bracket, the sum over \({\varvec{y}}\) is uniformly bounded by the same argument as in the bound for (6.28), while in the second bracket, we can distinguish between two cases: either \(|y_k-y_l|\leqslant 40M_\varepsilon \), in which case we apply this bound and sum over \({\varvec{x}}\) to get a bound of \(M_\varepsilon ^{\frac{4}{q}+2a}\Vert g\Vert _{\ell ^q}\); or \(|y_k-y_l|>40M_\varepsilon \geqslant 2|x_k-x_l|\), in which case we apply the triangle inequality
and follow the same argument as for (6.30) to get a bound of \(M_\varepsilon ^{4/q}\Vert g\Vert _{\ell ^q}\), where \(M_\varepsilon ^{4/q}\) comes from summing over the redundant components of \({\varvec{x}}\) after selecting one component of \({\varvec{x}}\) for each partition element of I. This concludes the proof of (8.21).
Proof of (8.22)–(8.23). Similar to (6.36), we need to show
uniformly in \(f\in \ell ^p(({\mathbb {Z}}^2)^4_{I})\) and \(g\in \ell ^q(({\mathbb {Z}}^2)^4)\). Restricted to \(({\varvec{x}}, {\varvec{y}}) \in A_\varepsilon ^c\), we note that the bound (8.28) can now be replaced by
Restricted to \(A_\varepsilon \), it suffices to bound the following analogue of (6.38):
When \(|I|=3\), this follows by exactly the same proof as that of (6.38). When \(|I|\leqslant 2\), the estimate is simpler and we can apply the Hölder inequality to bound the l.h.s. of (8.32) by
Since \(|I|\leqslant 2\), the second factor can be bounded by \(C M_\varepsilon ^4 \Vert g\Vert _{\ell ^q}\). For the first factor, summing over \({\varvec{y}}\) gives
uniformly in \({\varvec{x}}\in ({\mathbb {Z}}^2)^4_I\). Collecting all the bounds obtained so far then gives (8.31).
Proof of (8.24). Assume w.l.o.g. that \(I\vdash \{1,2,3,4\}\) consists of the partition elements \(\{1,2\}, \{3\}, \{4\}\). Recall from (8.18) and (8.12) that for \({\varvec{x}}, {\varvec{y}}\in ({\mathbb {Z}}^2)^4_I\),
We then have the following analogues of (6.43) and (6.44):
both of which follows from Lemma 5.9 by Fatou’s Lemma (recall \(\overline{U}^{\mathrm{(cg)}}_{\infty , \varepsilon }\) from (8.10)). The rest of the proof is exactly the same as that of (6.24).
Proof of (8.25). Given a partition \(I\vdash \{1,2,3,4\}\) with \(|I|\leqslant 2\), recall the definition of \({\widehat{{\textsf{V}}}}^{I}_{\lambda , \varepsilon }\) from (8.18). We need to show that
uniformly for all \(f\in \ell ^p(({\mathbb {Z}}^2)^4_I)\) and \(g\in \ell ^q(({\mathbb {Z}}^2)^4_I)\). As before, we consider the sum of \({\varvec{x}}, {\varvec{y}}\) over \(A_\varepsilon =\{|{\varvec{x}}-{\varvec{y}}|\leqslant C_0/\sqrt{\varepsilon |}\}\) and \(A_\varepsilon ^c\) separately and apply Hölder’s inequality. The bound (8.25) will follow if we show that uniformly in \({\varvec{x}}\in ({\mathbb {Z}}^2)^4_I\),
These bounds hold because (8.13) and (8.11) imply that
This concludes the proof of Proposition 8.2. \(\square \)
9 Proof of the main results: Theorems 1.1 and 1.2
9.1 Proof of Theorem 1.1
We can rephrase Theorem 1.1 as follows.
Theorem 9.1
Assume the same setup as in Theorem 1.1. Let \(k\in {\mathbb {N}}\). For \(i=1,\ldots , k\), assume \(0 \leqslant s_i \leqslant t_i < \infty \), \(\varphi _i \in C_c({\mathbb {R}}^2)\) has compact support, and \(\psi _i \in C_b({\mathbb {R}}^2)\) is bounded. Then the following convergence in distribution holds as \(N\rightarrow \infty \):
where \({{\mathcal {Z}}} ^{\beta _N}_{N;\, s,t}(\varphi , \psi ) :=\iint \varphi (x) \,\psi (y) \, {{\mathcal {Z}}} ^{\beta _N}_{N;\, s,t}(\textrm{d}x, \textrm{d}y)\).
We will prove Theorem 9.1 by showing that the random vector in the l.h.s. of (9.1) converges in distribution as \(N\rightarrow \infty \) to a unique random limit. This in turn implies that \(({{\mathcal {Z}}} ^{\beta _N}_{N;\, s,t}(\textrm{d}x, \textrm{d}y))_{0\leqslant s \leqslant t < \infty }\) converges to a unique limit, denoted \({\mathscr {Z}}^\vartheta = ({\mathscr {Z}}_{s,t}^\vartheta (\textrm{d}x, \textrm{d}y))_{0 \leqslant s \leqslant t < \infty }\).
The convergence of the one point distribution in Theorem 9.1 follows from the following result. We will explain how this can be adapted to finite dimensional distributions in Remark 9.5.
Proposition 9.2
Given \(\varphi \in C_c({\mathbb {R}}^2)\) and \(\psi \in C_b({\mathbb {R}}^2)\), let \({{\mathcal {Z}}} _N(\varphi , \psi ) := {{\mathcal {Z}}} ^{\beta _N}_{N,0,1}(\varphi , \psi ) = \iint \varphi (x) \psi (y) {{\mathcal {Z}}} ^{\beta _N}_N(\textrm{d}x, \textrm{d}y)\) be as in Theorem 9.1 with \(N\in 2{\mathbb {N}}\). Then \({{\mathcal {Z}}} _N(\varphi , \psi )\) converges in distribution to a unique limit as \(N\rightarrow \infty \).
Proof
Since
it follows that \(\mathrm E[|{{\mathcal {Z}}} _N(\varphi , \psi )|]\) is uniformly bounded in N and hence \(({{\mathcal {Z}}} _N(\varphi , \psi ))_{N\in {\mathbb {N}}}\) is a tight family and admits subsequential weak limits.
To show that the limit is unique, it then suffices to show that for every bounded \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\), with uniformly bounded first three derivatives, the limit
exists. To this end, we will show that \((\mathrm E[f({{\mathcal {Z}}} _N(\varphi , \psi ))])_{N\in {\mathbb {N}}}\) is a Cauchy sequence.
Theorem 4.7 allows us to approximate \({{\mathcal {Z}}} _N(\varphi , \psi )\) by the coarse-grained model \( {\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta )\) with coarse-grained disorder variables \(\Theta = \Theta _{N,\varepsilon }^{(\textrm{cg})}\), with an \(L^2\) error that is arbitrarily small, uniformly in large N, if \(\varepsilon >0\) is chosen sufficiently small. Therefore it only remains to show
We will prove (9.2) by applying the Lindeberg principle for multilinear polynomials of dependent random variables formulated in Lemmas A.2–A.4.
Let us set \(\Phi (\Theta ):= {\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta )\), and note from its definition in (4.8) that \(\Phi (\Theta )\) is a multilinear polynomial in the variables \(\Theta :=(\Theta (\vec {\textsf{i}}, \vec {\textsf{a}}))_{(\vec {\textsf{i}}, \vec {\textsf{a}}) \in {{\mathbb {T}}} _\varepsilon }\), where recall from (4.5) that
We write \(\Theta _n\) for the coarse-grained disorder variables \(\Theta ^{\mathrm{(cg)}}_{n, \varepsilon } := (\Theta ^{\mathrm{(cg)}}_{n, \varepsilon }(\vec {\textsf{i}}, \vec {\textsf{a}}))_{(\vec {\textsf{i}}, \vec {\textsf{a}}) \in {{\mathbb {T}}} _\varepsilon }\), see (4.11). These satisfy Assumption A.1 with the following dependency neighborhoods:
-
for each \({\textsf{z}}_1:=(\vec {\textsf{i}}_1, \vec {\textsf{a}}_1)\in {{\mathbb {T}}} _\varepsilon \), its dependency neighbourhood is given by
$$\begin{aligned} A_{{\textsf{z}}_1} =&\Big \{{\textsf{z}}_2=(\vec {\textsf{i}}_2, \vec {\textsf{a}}_2)\in {{\mathbb {T}}} _\varepsilon : \{{\textsf{i}}_2, {\textsf{i}}_2'\} \cap \{{\textsf{i}}_1, {\textsf{i}}_1'\}\ne \emptyset , \\&\qquad \textrm{dist}(\{{\textsf{a}}_2\}, \{{\textsf{a}}_1, {\textsf{a}}_1'\}) \wedge \textrm{dist}(\{{\textsf{a}}_2'\}, \{{\textsf{a}}_1, {\textsf{a}}_1'\}) \leqslant 2M_\varepsilon \Big \} ; \end{aligned}$$ -
given \({\textsf{z}}_1 \in {{\mathbb {T}}} _\varepsilon \) and \({\textsf{z}}_2\in A_{{\textsf{z}}_1}\), the dependency neighbourhood of \(\{{\textsf{z}}_1, {\textsf{z}}_2\}\) is given by
$$\begin{aligned} A_{{\textsf{z}}_1 {\textsf{z}}_2} = A_{{\textsf{z}}_1}\cup A_{{\textsf{z}}_2}. \end{aligned}$$
Recalling the definition of \({{\mathbb {T}}} _\varepsilon \), we see that, uniformly in \(\varepsilon > 0\) and \({\textsf{z}}\in {{\mathbb {T}}} _\varepsilon \),
In order to apply Lemma A.4, we first verify that condition (A.8) is satisfied by \(\Phi (\Theta )\).
Lemma 9.3
The multilinear polynomial \(\Phi (\Theta ) := {\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta )\) satisfies condition (A.8).
Proof
Condition (A.8) reads as
where \(\partial _{{\textsf{z}}}\) denotes derivative w.r.t. \(\Theta ({\textsf{z}})\). Since \(\Phi \) is multilinear in \((\Theta ({\textsf{z}}))_{{\textsf{z}}\in {{\mathbb {T}}} _\varepsilon }\), this condition is equivalent to the claim that no term in the expansion of \(\Phi \) (recall its definition from (4.8)) contains more than one of the factors \(\Theta ({\textsf{z}}_i)\), \(1\leqslant i\leqslant 3\). From the definition of \(\Phi \), clearly the product \(\Theta ({\textsf{z}}_1)\Theta ({\textsf{z}}_2)\) cannot appear because \({\textsf{z}}_1=(({\textsf{i}}_1, {\textsf{i}}_1'), ({\textsf{a}}_1, {\textsf{a}}_1'))\) and \({\textsf{z}}_2=(({\textsf{i}}_2, {\textsf{i}}_2'), ({\textsf{a}}_2, {\textsf{a}}_2'))\) have an overlapping time index. Similarly, if \({\textsf{z}}_3\in A_{{\textsf{z}}_i}\) for either \(i=1\) or 2, then the factor \(\Theta ({\textsf{z}}_i)\Theta ({\textsf{z}}_3)\) cannot appear. The last case is if \({\textsf{z}}_3\in A_{{\textsf{z}}_2}\), but \({\textsf{z}}_3\notin A_{{\textsf{z}}_1}\) (the case \({\textsf{z}}_3\in A_{{\textsf{z}}_1}\), \({\textsf{z}}_3\notin A_{{\textsf{z}}_2}\) is the same by symmetry, since \({\textsf{z}}_2\in A_{{\textsf{z}}_1}\) if and only if \({\textsf{z}}_1 \in A_{{\textsf{z}}_2}\)): let us show that \(\Theta ({\textsf{z}}_1)\Theta ({\textsf{z}}_3)\) does not appear in \(\Phi (\Theta )\). Both \(\vec {\textsf{i}}_1\) and \(\vec {\textsf{i}}_3\) have an overlapping time index with \(\vec {\textsf{i}}_2\), hence \(\textrm{dist}(\vec {\textsf{i}}_1, \vec {\textsf{i}}_3)\leqslant {\textsf{i}}_2'-{\textsf{i}}_2= |\vec {\textsf{i}}_2|-1\leqslant K_\varepsilon -1\), which contradicts the constraint imposed by \(\vec {\varvec{{\mathcal {A}}}}_\varepsilon ^{(\mathrm {no\, triple})}\) in (4.4), that for \(\Theta ({\textsf{z}}_1)\Theta ({\textsf{z}}_3)\) to appear, we must have \(\textrm{dist}(\vec {\textsf{i}}_1, \vec {\textsf{i}}_3)\geqslant K_\varepsilon \). This verifies condition (A.8). \(\square \)
We can then apply Lemmas A.2–A.4 to bound
where \(I_1^{(m)}\) and \(I_2^{(m)}\) are the terms from applying Lemma A.2 to \(h(\cdot ) = f(\Phi (\cdot ))\) and \(X = \Theta _m\), see (A.4) and (A.5), similarly for \(I_1^{(n)}\) and \(I_2^{(n)}\), while \(I_3^{(m,n)}\) is the term from applying Lemma A.3 to two Gaussian families \(Z = \Theta ^{(\mathrm{G)}}_m\) and \({\tilde{Z}} = \Theta ^{(\mathrm{G)}}_n\) with the same mean and covariance structure as \(\Theta _m\) and \(\Theta _n\), respectively, but independent of them, see (A.6).Footnote 9
We are now ready to prove (9.2) exploiting (9.4). It suffices to prove that
We will prove these relations separately, exploiting (A.9), (A.10) and (A.11) from Lemma A.4. This will conclude the proof of Proposition 9.2.
Bound on \(\limsup \limits _{n\rightarrow \infty } I_1^{(n)}\). By (A.9), we have
where for \(s,t,u\in [0,1]\),
with \(\Theta _n^A({\textsf{z}}) := \Theta _n({\textsf{z}}) \mathbb {1}_{\{{\textsf{z}}\in A\}}\).
First note that by the assumption \(\varphi \in C_c({\mathbb {R}}^2)\) and the definition of the multilinear polynomial \(\Phi (\Theta )\) in (4.8), \(\Phi (\Theta )\) depends only on \(\Theta ({\textsf{z}})\) for a finite set of \({\textsf{z}}\in {{\mathbb {T}}} _\varepsilon \). In particular, the sum in (9.6) is finite, and we can pass \(\limsup _{n\rightarrow \infty }\) inside the sum.
Note that \(\Vert f'''\Vert _\infty \) is bounded by assumption, and by (7.11),
The sum in (9.6) can be bounded by
Given \({\textsf{z}}=(\vec {\textsf{i}}, \vec {\textsf{a}})=(({\textsf{i}}, {\textsf{i}}'), ({\textsf{a}}, {\textsf{a}}'))\in {{\mathbb {T}}} _\varepsilon \), by the definition of \(\Phi (\Theta )={\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}(\varphi ,\psi |\Theta )\) in (4.8),
where \(\bar{{\mathscr {Z}}}^{(\textrm{cg})}_{[0, {\textsf{i}}]}(\varphi ,\mathbb {1}_{\{{{\mathcal {S}}} _\varepsilon ({\textsf{a}})\}}|\Theta )\) denotes the centred coarse-grained model with initial condition \(\varphi \) at time 0 and terminal condition \(\mathbb {1}_{{{\mathcal {S}}} _\varepsilon ({\textsf{a}})}\) at time \({\textsf{i}}\): this is just the original coarse-grained model in (4.8) with time horizon \({\textsf{i}}\) instead of \(\lfloor 1/\varepsilon \rfloor \) and with the constant term \(\frac{1}{2} \, g_{\frac{1}{2}}(\varphi , \psi )\) omitted. (We recall that \({{\mathcal {S}}} _\varepsilon ({\textsf{a}})\) is a square of side length \(\sqrt{\varepsilon }\) defined as in (5.35).) The definition of \(\bar{{\mathscr {Z}}}^{(\textrm{cg})}_{[{\textsf{i}}', 1/\varepsilon ]}(\mathbb {1}_{{{\mathcal {S}}} _\varepsilon ({\textsf{a}}')},\psi |\Theta )\) is similar, which is independent of \( \bar{{\mathscr {Z}}}^{(\textrm{cg})}_{[0, {\textsf{i}}]}(\varphi ,\mathbb {1}_{\{{{\mathcal {S}}} _\varepsilon ({\textsf{a}})\}}|\Theta )\). Each of \(\partial _{\Theta ({\textsf{z}})} {\mathscr {Z}}_{\varepsilon }^{(\textrm{cg})}\), \(\bar{{\mathscr {Z}}}^{(\textrm{cg})}_{[0, {\textsf{i}}]}\) and \(\bar{{\mathscr {Z}}}^{(\textrm{cg})}_{[{\textsf{i}}', 1/\varepsilon ]}\) contains a factor of \(\varepsilon /2\) by the defintion of the coarse-grained model in (4.8), which is why there is a prefactor of \(2/\varepsilon \) in (9.10). We then have
where we interchanged initial and terminal conditions by symmetry and used translation invariance and independence.
We can bound the two factors in the r.h.s. of (9.11) by applying slight variants of Theorem 8.1, which was formulated for the original coarse-grained model. Let us focus on the first factor in the r.h.s. of (9.11), for which we need to take into account two differences: the time range \([0,{\textsf{i}}]\) instead of \([0,\varepsilon ^{-1}]\) and the disorder \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\) instead of \(\Theta _n\).
The first difference is immaterial, because our moment estimate Theorem 8.1 is monotone increasing in the time length \({\textsf{i}}\in [1, \varepsilon ^{-1}]\) (see the argument leading to (8.4)). As a consequence, we can apply the bound in Theorem 8.1 with \(w(x)=e^{-|x|}\) to \(\bar{{\mathscr {Z}}}^{(\textrm{cg})}_{[0, {\textsf{i}}]}(\varphi ,\psi |\Theta _n)\), which yields
where C depends on the choice of p, q, but is uniform in \({\textsf{i}}\) and \({\textsf{a}}\) and in n sufficiently large, while \(B_\varphi \) is a ball that contains the support of \(\varphi \).
The second difference is also immaterial, that is we can replace \(\Theta _n\) by \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\) in (9.12). This is recorded in the following result, which we prove later.
Lemma 9.4
The bound (9.12) also holds if \(\Theta _n\) is replaced by \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\), uniformly in \({\textsf{z}}_1, {\textsf{z}}_2 \in {{\mathbb {T}}} _\varepsilon \) and \(s,t,u\in [0,1]\), and n large.
Similarly, we can also bound the second factor in the r.h.s. (9.11) by
Substituting these bounds into (9.11) and then (9.9) gives (for n sufficiently large)
where we used the symmetry in the dependency structure between \({\textsf{z}}_1, {\textsf{z}}_2, {\textsf{z}}_3\) (\({\textsf{z}}_2 \in A_{{\textsf{z}}_1}\) if and only if \({\textsf{z}}_1\in A_{{\textsf{z}}_2}\)) to reduce \(\sum _{i=1}^3\) to the case \(i=1\), and in the last inequality, we first summed out \({\textsf{z}}_2, {\textsf{z}}_3\) and applied the bounds \(|A_{z_1}| , |A_{{\textsf{z}}_1{\textsf{z}}_2}| \leqslant C M_\varepsilon ^4 K_\varepsilon ^2\) from (9.3), then summed out \(({\textsf{i}}_1', {\textsf{a}}_1')\) in \({\textsf{z}}_1=(({\textsf{i}}_1, {\textsf{i}}_1'), ({\textsf{a}}_1, {\textsf{a}}_1'))\) where the sum over \({\textsf{i}}_1'\) gives another factor of \(K_\varepsilon \) and the sum over \({\textsf{a}}_1'\) gives another factor of \(M_\varepsilon ^2 \, K_\varepsilon \), and lastly we summed out \(({\textsf{i}}_1, {\textsf{a}}_1)\), noting that \({\textsf{i}}_1 \in \{1,\ldots , \varepsilon ^{-1}\}\) while the sum over \({\textsf{a}}_1\) gives a factor \(O((\sqrt{\varepsilon })^{-2}) = O(\varepsilon ^{-1})\) because of the exponential decay on the scale \((\sqrt{\varepsilon })^{-1}\) (we recall that \(\varphi \) has compact support).
We recall from (4.2) that \(K_\varepsilon =(\log \frac{1}{\varepsilon })^6\) and \(M_\varepsilon =\log \log \frac{1}{\varepsilon }\). Choose \(p>1\) sufficiently close to 1 and substitute the above bound into (9.9) and then (9.6), together with (9.8), we then obtain that for any \(\delta \in (0,1)\), there exists \(C_\delta \) such that
This proves the first relation in (9.5).
Bound on \(\limsup \limits _{n\rightarrow \infty } I_2^{(n)}\). By (A.10),
where \(W_{t,u}^{{\textsf{z}}_1, {\textsf{z}}_2} := u\sqrt{t}\Theta _n^{A_{{\textsf{z}}_1{\textsf{z}}_2}} + \sqrt{t} \Theta _n^{A_{{\textsf{z}}_1{\textsf{z}}_2}^c} +\sqrt{1-t}\Theta ^{(\mathrm{G)}}_n\) for \(t,u\in [0,1]\). The bounds are exactly the same as for \(|I^{(1)}_n|\), which gives \(\limsup _{n\rightarrow \infty } |I^{(n)}_2| \leqslant C_\delta \varepsilon ^{\delta }\) for any \(\delta \in (0,1)\). This proves the second relation in (9.5).
Bound on \(\limsup \limits _{m,n\rightarrow \infty }I_3^{(m,n)}\). By (A.11) and the fact that \(\Theta _n\) is a family of mean zero uncorrelated random variables,
where \(W_t:= \sqrt{t}\Theta ^{(\mathrm{G)}}_n + \sqrt{1-t}\Theta ^{(\mathrm{G)}}_m\) for \(t\in [0,1]\). Note that by definition, \(\Phi (\Theta )\) depends only on a finite set of \(\Theta _{\textsf{z}}\), \({\textsf{z}}\in {{\mathbb {T}}} _\varepsilon \). Therefore the sum in (9.14) contains finitely many terms. For each \({\textsf{z}}\in {{\mathbb {T}}} _\varepsilon \),
by Lemma 7.1. On the other hand, uniformly in \(t\in [0,1]\), \(\mathrm E\big [ \big |\partial _{{\textsf{z}}} \Phi (W_t)\big |^2\big ]\) converges to a finite limit as \(m,n\rightarrow \infty \) because \(\partial _{{\textsf{z}}} \Phi (W_t)\) is a multilinear polynomial in \(W_t({\textsf{z}})\) for finitely many \({\textsf{z}}\in {{\mathbb {T}}} _\varepsilon \), while its second moment is a multilinear polynomial of \(\mathrm E[W^2_t({\textsf{z}})]\), \({\textsf{z}}\in {{\mathbb {T}}} _\varepsilon \), each of which converges by Lemma 7.1. It follows that \(\limsup _{m,n\rightarrow \infty } |I_3^{(m,n)}|=0\), which is stronger than the third relation in (9.5).
Conclusion. Assuming Lemma 9.4, we have proved (9.5). This implies (9.2) and finally completes the proof of Proposition 9.2. \(\square \)
Remark 9.5
(Extension to finite-dimensional distribution) Finally, to prove the finite-dimensional distribution convergence in Theorem 9.1, we argue as in the proof of Proposition 9.2. First we approximate the components \({{\mathcal {Z}}} _{N, s_i, t_i}^{\beta _N}(\varphi _i, \psi _i)\) of the random vector in the l.h.s. of (9.1) by coarse-grained models \({\mathscr {Z}}_{\varepsilon , s_i, t_i}^{(\textrm{cg})}(\varphi _i,\psi _i|\Theta )\), with the same coarse-grained disorder variables \(\Theta = \Theta _{N,\varepsilon }^{(\textrm{cg})}\), which we can do with a small \(L^2\) error, uniformly in large N, provided we choose \(\varepsilon > 0\) small enough, by Theorem 4.7.
It remains to apply a Lindeberg principle for a vector of multilinear polynomials, which is given in Remark A.5. The estimates needed are exactly the same as in the Lindeberg principle for a single multilinear polynomial. This concludes the proof of Theorem 9.1.
Proof of Lemma 9.4
We re-examine the proof of Theorem 8.1. First note that, similar to the \(L^2\) orthogonal decomposition of \(\Theta _n({\textsf{i}}, {\textsf{a}})\) with \(|\vec {\textsf{i}}|\geqslant 1\) as in (8.5), we can write
where \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}(\vec {\textsf{i}}, ({\textsf{a}}, {\textsf{b}}), ({\textsf{b}}', {\textsf{a}}'))\) are defined through the same mixture as in (9.7) between \(\Theta _n(\vec {\textsf{i}}, ({\textsf{a}}, {\textsf{b}}), ({\textsf{b}}', {\textsf{a}}'))\) and \(\Theta ^{(\mathrm{G)}}_n(\vec {\textsf{i}}, ({\textsf{a}}, {\textsf{b}}), ({\textsf{b}}', {\textsf{a}}'))\), with the latter being independent normals with mean 0 and the same variance as \(\Theta _n(\vec {\textsf{i}}, ({\textsf{a}}, {\textsf{b}}), ({\textsf{b}}', {\textsf{a}}'))\). We can then carry out the same expansion as for (8.4), and note that: whenever a product of coarse-grained disorder variables \(\Theta _n\) has zero expectation because of the presence of some \(\Theta _n({\textsf{i}}, {\textsf{a}})\) with either \(({\textsf{i}}, {\textsf{a}})\) or \(({\textsf{i}}', {\textsf{a}}')\) unmatched by any other \(\Theta _n\) in the product, the same is true if the family \(\Theta _n\) is replaced by \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\); similarly, whenever two collections of \(\Theta _n\) variables are independent of each other, the same is true if \(\Theta _n\) is replaced by \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\). This implies that the expansion and re-summation carried out for the r.h.s. of (8.4), as well as the accompanying constraints on summation indices, also apply when \(\Theta _n\) is replaced by \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\).
Next we claim that, for \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}(({\textsf{i}}_1, {\textsf{i}}_2), ({\textsf{a}}_1, {\textsf{b}}_1), ({\textsf{a}}_2, {\textsf{b}}_2)) \) that visits two distinct blocks \({{\mathcal {I}}} _1, {{\mathcal {I}}} _2\) (see the exposition leading to (8.6)), although we no longer have a chaos expansion representation as in (8.6) due to the Gaussian component of \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\), we can still make a replacement similar to (8.8) in order to bound the r.h.s. of (8.4), with \(\Theta _n\) replaced by \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\):
To see this, note that \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\) is a mixture of \(\Theta _n\) and \(\Theta ^{(\mathrm{G)}}_n\) with mixture coefficients given in (9.7). When we expand the r.h.s. of (8.4) with \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\) in place of \(\Theta ^{\mathrm{(cg)}}_{N, \varepsilon }\), we can further expand \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\) in terms of its mixture. Each term in the expansion then consists of a product of \(\Theta _n\) variables and \(\Theta ^{(\mathrm{G)}}_n\) variables, whose expectation factorises due to the independence between \(\Theta _n\) and \(\Theta ^{(\mathrm{G)}}_n\). For terms that contain the factor \(\Theta _n(({\textsf{i}}_1, {\textsf{i}}_2), ({\textsf{a}}_1, {\textsf{b}}_1), ({\textsf{a}}_2, {\textsf{b}}_2))\), the decomposition (8.6) applies, and the same argument justifying the replacement (8.8) can be applied here. For terms that contain the Gaussian factor \(\Theta ^{(\mathrm{G)}}_n(({\textsf{i}}_1, {\textsf{i}}_2), ({\textsf{a}}_1, {\textsf{b}}_1), ({\textsf{a}}_2, {\textsf{b}}_2))\), the expectation will be non-zero only if this factor appears exactly twice or four times. The resulting contribution will be either the second or the fourth moment of \(\Theta ^{(\mathrm{G)}}_n(({\textsf{i}}_1, {\textsf{i}}_2), ({\textsf{a}}_1, {\textsf{b}}_1), ({\textsf{a}}_2, {\textsf{b}}_2))\). Its second moment coincide with that of \(\Theta _n(({\textsf{i}}_1, {\textsf{i}}_2), ({\textsf{a}}_1, {\textsf{b}}_1), ({\textsf{a}}_2, {\textsf{b}}_2))\), while its fourth moment can be bounded in terms of its second moment by Gaussianity. Then as in (8.8), we make the following replacement in the expansion:
Therefore in the mixture of \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}(({\textsf{i}}_1, {\textsf{i}}_2), ({\textsf{a}}_1, {\textsf{b}}_1), ({\textsf{a}}_2, {\textsf{b}}_2))\) (recall (9.7)), we can replace the \(\Theta _n\) and \(\Theta ^{(\mathrm{G)}}_n\) components each by its factorisation as in (9.17). The mixture coefficient of the term \(C\Theta _n ({\textsf{i}}_1; {\textsf{a}}_1, {\textsf{b}}_1)g_{10({\textsf{i}}_2 - {\textsf{i}}_1)}\, ({\textsf{a}}_2 -{\textsf{b}}_1)\Theta _n({\textsf{i}}_2; {\textsf{a}}_2, {\textsf{b}}_2)\) is equal to \(\alpha \sqrt{t}\) with either \(\alpha =su\), u or 1, while the mixture coefficient of the term \(C\Theta ^{(\mathrm G)}_n ({\textsf{i}}_1; {\textsf{a}}_1, {\textsf{b}}_1)g_{10({\textsf{i}}_2 - {\textsf{i}}_1)}\, ({\textsf{a}}_2 -{\textsf{b}}_1)\Theta _n^{(\mathrm G)}({\textsf{i}}_2; {\textsf{a}}_2, {\textsf{b}}_2)\) equals \(\sqrt{1-t}\). This mixture can be further replaced by the r.h.s. of (9.16), which just contains extra terms and larger coefficients, where the choice of \(s=u=1\) and \(t=1/2\) in the first factor \(W_{1,1/2,1}^{{\textsf{z}}_1, {\textsf{z}}_2}({\textsf{i}}_1; {\textsf{a}}_1, {\textsf{b}}_1)\) helps to bound the mixture coefficients.
The remaining parts of the proof of Theorem 8.1 depends on the coarse-grained disorder variables \(\Theta _n=\Theta ^\mathrm{(cg)}_{n,\varepsilon }\) only through their second and fourth moments. Note that uniformly in \(s,t,u\in [0,1]\) and \({\textsf{z}}_1, {\textsf{z}}_2\), the second moment of \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\) is bounded by that of \(\Theta _n\), and modulo a constant multiple, the fourth moment of \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\) can be bounded by that of \(\Theta _n\). Therefore the remaining parts of the proof of Theorem 8.1 carries through without change if \(\Theta _n\) is replaced by \(W_{s,t,u}^{{\textsf{z}}_1, {\textsf{z}}_2}\). In particular, the bound on \(U^{\mathrm{(cg)}}_{N, \varepsilon }\) in (8.10) still holds since it only depends on the second moment of \(\Theta _n\), and the bound on \(V^\mathrm{(cg)}_{N,\varepsilon }\) in (8.11) still holds because it only depends on the fourth moment of \(\Theta _n\). \(\square \)
9.2 Proof of Theorem 1.2
The translation invariance of the law of \({\mathscr {Z}}^\vartheta \) is obvious.
To prove the scaling relation (1.12), let us write \(\beta _N(\vartheta )\) to emphasize that \(\beta _N\) as specified in (1.11) depends on a parameter \(\vartheta \). Given \({\textsf{a}}>0\), let \({\tilde{N}}=N/{\textsf{a}}\). Then using (1.11) and the fact that \(R_N=\frac{1}{\pi }(\log N+ \alpha +o(1))\) given later in (3.2), we have
so that \(\beta _N(\vartheta ) = \beta _{{\tilde{N}}}(\vartheta - \log {\textsf{a}})\), or equivalently, \(\beta _N(\vartheta +\log a) = \beta _{{\tilde{N}}}(\vartheta )\).
By (9.1), for \(\varphi , \psi \in C_c({\mathbb {R}}^2)\), we have
On the other hand, recall (1.9), we can rewrite the l.h.s. of (9.19) as
where we again applied (9.1). Combined with (9.19), this implies (1.12).
The first and second moments of \({\mathscr {Z}}^\vartheta \) can be identified from the limits in (3.53) and (3.54), since for \(\varphi \in C_c({\mathbb {R}}^2)\) and \(\psi \in C_b({\mathbb {R}}^2)\), the averaged partition function \({\mathcal {Z}}^{\beta _N}_{N, t-s}(\varphi , \psi )\) has a finite fourth moment that is uniformly bounded in N, see Theorem 6.1.
Notes
Note that \({{\mathbb {E}}} [Z_{M,N}^{\beta _N,\, \omega }(w,z)] = \mathrm P(S_{N} = z \,|\, S_{M} = w) = O(\frac{1}{N-M}) = O(\frac{1}{N})\) for \(M/N \leqslant c < 1\), by the local limit theorem, which explains the prefactor N in (1.9). The extra factor \(\frac{1}{4}\) is due to periodicity.
In [18], there was no separate notation \({\widehat{G}}_\vartheta \) for the weighted Green’s function, which might cause some confusion.
The positivity of \(\Vert \varphi \Vert _{{{\mathcal {G}}} _t}^2\) can be seen via Fourier transform.
We use the notation \(({\textsf{a}}-{\textsf{b}}, {\textsf{a}}] = ({\textsf{a}}_1-{\textsf{b}}_1,{\textsf{a}}_1] \times ({\textsf{a}}_2-{\textsf{b}}_2,{\textsf{a}}_2]\) for squares in \({\mathbb {R}}^2\).
This is the key difference between the expansions in [19] and [51]. This decomposition was used in [51], which allows a functional analytic interpretation of the iterated sums and helps bypass the combinatorial complexity encountered in [19], which the authors could control for the third moment but seemed intractable for higher moments.
Since \((\Theta _n({\textsf{z}}))_{{\textsf{z}}\in {{\mathbb {T}}} _\varepsilon }\) are uncorrelated, \((\Theta ^{(\mathrm{G)}}_n({\textsf{z}}))_{{\textsf{z}}\in {{\mathbb {T}}} _\varepsilon }\) are in fact independent Gaussian random variables.
References
Alberts, T., Khanin, K., Quastel, J.: The intermediate disorder regime for directed polymers in dimension \(1+1\). Ann. Probab. 42, 1212–1256 (2014)
Alberts, T., Khanin, K., Quastel, J.: The continuum directed random polymer. J. Stat. Phys. 154, 305–326 (2014)
Albeverio, S., Fenstad, J.E., Hoegh-Krohn, R., Karwowski, W., Lindstrom, T.: Schrödinger Operators with Potentials Supported by Null Sets. Ideas and Methods in Quantum and Statistical Physics, pp. 63–95. Cambridge Univeristy Press, Cambridge (1992)
Albeverio, S., Gesztesy, F., Hoegh-Krohn, R., Holden, H.: Solvable Models in Quantum Mechanics. AMS Chelsea Publishing, New York (2005)
Bates, E.: Full-path localization of directed polymers. Electron. J. Probab. 26, 1–24 (2021)
Bolthausen, E.: A note on the diffusion of directed polymers in a random environment. Commun. Math. Phys. 123, 529–534 (1989)
Bertini, L., Cancrini, N.: The two-dimensional stochastic heat equation: renormalizing a multiplicative noise. J. Phys. A: Math. Gen. 31, 615 (1998)
Bates, E., Chatterjee, S.: The endpoint distribution of directed polymers. Ann. Probab. 48, 817–871 (2020)
Bates, E., Chatterjee, S.: Localization in Gaussian disordered systems at low temperature. Ann. Probab. 48, 2755–2806 (2020)
Berger, Q., Lacoin, H.: The high-temperature behavior for the directed polymer in dimension \(1+2\). Ann. Institut Henri Poincaré Prob. et Statistiques 53, 430–450 (2017)
Cannizzaro, G., Erhard, D., Schönbauer, P.: \(2D\) anisotropic KPZ at stationarity: scaling, tightness and nontriviality. Ann. Prob. 49, 122–156 (2021)
Cannizzaro, G., Erhard, D., Toninelli, F.L.: Logarithmic superdiffusivity of the 2-dimensional anisotropic KPZ equation. arXiv:2009.12934 (2020)
Cannizzaro, G., Erhard, D., Toninelli, F.L.: The stationary AKPZ equation: logarithmic superdiffusivity. arXiv:2007.12203 (2020)
Cannizzaro, G., Erhard, D., Toninelli, F.L.: Weak coupling limit of the anisotropic KPZ equation. arXiv:2108.09046 (2021)
Caravenna, F., Sun, R., Zygouras, N.: The continuum disordered pinning model. Probab. Theory Related Fields 164, 17–59 (2016)
Caravenna, F., Sun, R., Zygouras, N.: Polynomial chaos and scaling limits of disordered systems. J. Eur. Math. Soc. 19, 1–65 (2017)
Caravenna, F., Sun, R., Zygouras, N.: Universality in marginally relevant disordered systems. Ann. Appl. Probab. 27, 3050–3112 (2017)
Caravenna, F., Sun, R., Zygouras, N.: The Dickman subordinator, renewal theorems, and disordered systems. Electron. J. Probab. 24, 1–24 (2019)
Caravenna, F., Sun, R., Zygouras, N.: On the moments of the (2+1)-dimensional directed polymer and stochastic heat equation in the critical window. Commun. Math. Phys. 372, 385–440 (2019)
Caravenna, F., Sun, R., Zygouras, N.: The two-dimensional KPZ equation in the entire subcritical regime. Ann. Prob. 48, 1086–1127 (2020)
Caravenna, F., Sun, R., Zygouras, N.: The critical 2d stochastic heat flow is not a gaussian multiplicative chaos. arXiv:2206.08766 (2022)
Carmona, P., Hu, Y.: On the partition function of a directed polymer in a Gaussian random environment. Probab. Theory Related Fields 124(3), 431–457 (2002)
Chatterjee, S.: A generalization of the Lindeberg principle. Ann. Probab. 34, 2061–2076 (2006)
Chatterjee, S.: Proof of the path localization conjecture for directed polymers. Commun. Math. Phys. 370, 703–717 (2019)
Chatterjee, S., Dunlap, A.: Constructing a solution of the \((2+1)\)-dimensional KPZ equation. Ann. Prob. 48, 1014–1055 (2020)
Chen, Y.-T.: The critical 2D delta-Bose gas as mixed-order asymptotics of planar Brownian motion. arXiv:2105.05154 (2021)
Clark, J.T.: The conditional Gaussian multiplicative chaos structure underlying a critical continuum random polymer model on a diamond fractal. arXiv:1908.08192 (2019)
Clark, J.T.: Weak-disorder limit at criticality for directed polymers on hierarchical graphs. Commun. Math. Phys. 386, 651–710 (2021)
Clark, J.T.: Continuum models of directed polymers on disordered diamond fractals in the critical case. Ann. Appl. Prob. 32, 4186–4250 (2022)
Comets, F.: Directed Polymers in Random Environments. Lecture Notes in Mathematics, vol. 2175. Springer, Cham (2017)
Comets, F., Cosco, C., Mukherjee, C.: Renormalizing the Kardar–Parisi–Zhang equation in \(d\ge 3\) in weak disorder. J. Stat. Phys. 179, 713–728 (2020)
Comets, F., Shiga, T., Yoshida, N.: Directed polymers in a random environment: path localization and strong disorder. Bernoulli 9, 705–723 (2003)
Comets, F., Yoshida, N.: Directed polymers in random environment are diffusive at weak disorder. Ann. Probab. 34, 1746–1770 (2006)
Corwin, I.: The Kardar–Parisi–Zhang equation and universality class. Random Matrices Theory Appl. 1, 1130001 (2012)
Corwin, I.: Kardar–Parisi–Zhang universality. Not. AMS 63, 230–239 (2016)
Corwin, I., Hammond, A.: KPZ line ensemble. Probab. Theory Relat. Fields 166, 67–185 (2016)
Cosco, C., Nakajima, S.: Gaussian fluctuations for the directed polymer partition function in dimension \(d\ge 3\) and in the whole \(L^2\)-region. Ann. Inst. H. Poincaré Prob. Stat. 57, 872–889 (2021)
Cosco, C., Nakajima, S., Nakashima, M.: Law of large numbers and fluctuations in the sub-critical and \(L^2\) regions for SHE and KPZ equation in dimension \( d\ge 3\). Stoch. Process. Appl. 151, 127–173 (2022)
Dell’Antonio, G.F., Figari, R., Teta, A.: Hamiltonians for systems of \(N\) particles interacting through point interactions. Ann. Inst. H. Poincaré Phys. Théor. 60, 253–290 (1994)
Dimock, J., Rajeev, S.: Multi-particle Schrödinger operators with point interactions in the plane. J. Phys. A: Math. Gen. 37(39), 9157 (2004)
Dunlap, A., Gu, Y., Ryzhik, L., Zeitouni, O.: Fluctuations of the solutions to the KPZ equation in dimensions three and higher. Probab. Theory Related Fields 176, 1217–1258 (2020)
Erdös, P., Taylor, S.J.: Some problems concerning the structure of random walk paths. Acta Math. Acad. Sci. Hungar. 11, 137–162 (1960)
Feng, Z.S.: Rescaled directed random polymer in random environment in dimension 1+2. Ph.D. thesis, Ann Arbor, MI (2016). https://www.proquest.com/docview/1820736587
Gabriel, S.: Central limit theorems for the (2+1)-dimensional directed polymer in the weak disorder limit. arXiv:2104.07755 (2021)
Garban, C., Steif, J.: Lectures on noise sensitivity and percolation. In: Proceedings of the Clay Mathematics Institute Summer School (Buzios, Brazil), Clay Mathematics Proceedings 15, pp. 49–154 (2012)
Gärtner, J., Sun, R.: A quenched limit theorem for the local time of random walks on \(\mathbb{Z} ^2\). Stoch. Process. Appl. 119, 1198–1215 (2009)
Giacomin, G.: Disorder and Critical Phenomena Through Basic Probability Models. Lecture Notes in Mathematics, vol. 2025. Springer, Heidelberg (2011)
Giacomin, G., Lacoin, H., Toninelli, F.L.: Marginal relevance of disorder for pinning models. Commun. Pure Appl. Math. 63, 233–265 (2010)
Goncalves, P., Jara, M.: Nonlinear fluctuations of weakly asymmetric interacting particle systems. Arch. Ration. Mech. Anal. 212, 597–644 (2014)
Gu, Y.: Gaussian fluctuations from the 2D KPZ equation. Stoch. Partial Differ. Equ. Anal. Comput. 8, 150–185 (2020)
Gu, Y., Quastel, J., Tsai, L.-C.: Moments of the 2D SHE at criticality. Prob. Math. Phys. 2, 179–219 (2021)
Gu, Y., Ryzhik, L., Zeitouni, O.: The Edwards-Wilkinson limit of the random heat equation in dimensions three and higher. Commun. Math. Phys. 363, 351–388 (2018)
Gubinelli, M., Imkeller, P., Perkowski, N.: Paracontrolled distributions and singular PDEs. Forum Math. Pi 3, e6 (2015)
Gubinelli, M., Perkowski, N.: KPZ reloaded. Commun. Math. Phys. 349, 165–269 (2017)
Hairer, M.: Solving the KPZ equation. Ann. Math. 178, 559–664 (2013)
Hairer, M.: A theory of regularity structures. Invent. Math. 198, 269–504 (2014)
Halpin-Healy, T.: \((2+1)\)-dimensional directed polymer in a random medium: scaling phenomena and universal distributions. Phys. Rev. Lett. 109, 170602 (2012)
Halpin-Healy, T.: Extremal paths, the stochastic heat equation, and the three-dimensional Kardar-Parisi-Zhang universality class. Phys. Rev. E 88, 042118 (2013)
Huse, D.A., Henley, C.L.: Pinning and roughening of domain walls in Ising systems due to random impurities. Phys. Rev. Lett. 54, 2708–2711 (1985)
Imbrie, J.Z., Spencer, T.: Diffusion of directed polymers in a random environment. J. Stat. Phys. 52, 609–626 (1988)
Johansson, K.: Transversal fluctuations for increasing subsequences on the plane. Probab. Theory Related Fields 116, 445–456 (2000)
Kallenberg, O.: Foundations of Modern Probability. Springer (1997)
Kozma, G.: The scaling limit of loop-erased random walk in three dimensions. Acta Math. 199, 29–152 (2007)
Kupiainen, A.: Renormalization Group and Stochastic PDEs. Ann. H. Poincaré 17, 497–535 (2016)
Lacoin, H.: New bounds for the free energy of directed polymers in dimension \(1+1\) and \(1+2\). Commun. Math. Phys. 294, 471–503 (2010)
Lawler, G.F., Limic, V.: Random Walk: A Modern Introduction. Cambridge University Press, Cambridge (2010)
Lieb, E.H., Loss, M.: Analysis. Graduate Studies in Mathematics, vol. 14, 2nd edn. American Mathematical Society, Providence (2001)
Lygkonis, D., Zygouras, N.: Edwards-Wilkinson fluctuations for the directed polymer in the full \(L^2\)-regime for dimensions \(d\ge 3\). Ann. Inst. Henri Poincaré Probab. Stat. 58, 65–104 (2022)
Magnen, J., Unterberger, J.: The scaling limit of the KPZ equation in space dimension 3 and higher. J. Stat. Phys. 171, 543–598 (2018)
Mossel, E., O’Donnell, R., Oleszkiewicz, K.: Noise stability of functions with low influences: invariance and optimality. Ann. Math. 171, 295–341 (2010)
Mukherjee, C., Shamov, A., Zeitouni, O.: Weak and strong disorder for the stochastic heat equation and continuous directed polymers in \(d\ge 3\). Electron. Commun. Probab. 21, 1–12 (2016)
Nakashima, M.: Free energy of directed polymers in random environment in \(1+1\)-dimension at high temperature. Electron. J. Probab. 24, 1–43 (2019)
Quastel, J., Spohn, H.: The One-dimensional KPZ equation and tts universality class. J. Stat. Phys. 160, 965–984 (2015)
Rajeev, S. G.: A condensation of interacting Bosons in two dimensional space. arXiv preprint arXiv:hep-th/9905120 (1999)
Röllin, A.: Stein’s method in high dimensions with applications. Ann. Inst. Henri Poincaré Probab. Stat. 49, 529–549 (2013)
Rotar, V.I.: Limit theorems for polylinear forms. J. Multivar. Anal. 9, 511–530 (1979)
Vargas, V.: Strong localization and macroscopic atoms for directed polymers. Probab. Theory Related Fields 138, 391–410 (2007)
Acknowledgements
We especially thank Te LI for showing us how Hardy–Littlewood–Sobolev type inequalities can be proved without using Fourier transform. F.C. is supported by INdAM/GNAMPA. R.S. is supported by NUS grant R-146-000-288-114. N.Z. is supported by EPRSC through grant EP/R024456/1.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Enhanced Lindeberg principle
Appendix A. Enhanced Lindeberg principle
In this appendix, we prove a Lindeberg principle for multilinear polynomials of dependent random variables with a local form of dependence. This extends [75], which requires the function to have bounded first three derivatives and is not applicable to multilinear polynomials, and it extends [70], which considers multilinear polynomials of independent random variables. We first introduce the necessary setup. Let \({{\mathbb {T}}} \) be a finite index set.
Assumption A.1
(Local dependence) Let \(X = (X_i)_{i\in {{\mathbb {T}}} }\) be random variables satisfying:
-
\(\mathrm E[X_i] = 0\) and \(\mathrm E[X_i X_j] = \sigma _{ij}\);
-
for every \(k \in {{\mathbb {T}}} \) there is \(A_k \subseteq {{\mathbb {T}}} \) such that \(X_k\) is independent of \((X_i)_{i\in A_k^c}\);
-
for all \(k \in {{\mathbb {T}}} \), \(l \in A_k\) there is \( A_{kl} \subseteq {{\mathbb {T}}} \) such that \((X_k, X_l)\) is independent of \((X_i)_{i\in A_{kl}^c}\).
The sets \((A_k)_{k\in {\mathbb {T}}}\) and \((A_{kl})_{k\in {\mathbb {T}}, l\in A_k}\) will be called dependency neighbourhoods of \(X = (X_i)_{i\in {{\mathbb {T}}} }\).
Let \(Z = (Z_i)_{i\in {{\mathbb {T}}} } \sim N(0, \sigma _\cdot )\) be a Gaussian vector independent of X, but with the same covariance matrix as X. For \(u, t \in [0,1]\), \(k\in {{\mathbb {T}}} \) and \(l\in A_k\), we define
where for any subset of indices \(B \subseteq {{\mathbb {T}}} \) we write
For \(s, u, t\in [0,1]\), \(k\in {{\mathbb {T}}} \) and \(l\in A_k\), we define
We have the following Lindeberg type result, which controls the distributional distance between X and Z through smooth test functions.
Lemma A.2
(Lindeberg principle for dependent random variables) Let X, Z, \(W_{t,u}^{k, l}\) and \(W_{s,t,u}^{k, l}\) be defined as above. Let \(h: {\mathbb {R}}^{|{{\mathbb {T}}} |} \rightarrow {\mathbb {R}}\) be bounded and thrice differentiable. Then
where
assuming that the integrals and expectations above are all finite.
To control the distributional distance between X and another random vector \({\widetilde{X}}=({\widetilde{X}}_i)_{i\in {{\mathbb {T}}} }\) with slightly perturbed covariance matrix \(({\tilde{\sigma }}_{ij})_{i, j\in {{\mathbb {T}}} }\) and dependency neighbourhoods \({\tilde{A}}_k, {\tilde{A}}_{kl}\), we will apply Lemma A.2 to X and \({\widetilde{X}}\) separately, plus the following result that compares two Gaussian vectors.
Lemma A.3
Let \(Z=(Z_i)_{i\in {{\mathbb {T}}} }\sim N(0, \sigma _\cdot )\) and \({\widetilde{Z}}=({\widetilde{Z}}_i)_{i\in {{\mathbb {T}}} }\sim N(0, {\widetilde{\sigma }}_\cdot )\) be centred Gaussian random vectors with covariance matrices \((\sigma _{ij})_{i,j\in {{\mathbb {T}}} }\) and \(({\tilde{\sigma }}_{ij})_{i,j\in {{\mathbb {T}}} }\) respectively. Let \(h: {\mathbb {R}}^{|{{\mathbb {T}}} |} \rightarrow {\mathbb {R}}\) be bounded and twice differentiable. Denote \(W_t:=\sqrt{t}{\widetilde{Z}} +\sqrt{1-t}Z\). Then we have
assuming that the integrals and expectations above are all finite.
We now specialise Lemmas A.2 and A.3 to our case of interest, where h is a function of a multi-linear polynomial \(\Phi (X)\).
Lemma A.4
Assume that \(h(X) := f(\Phi (X))\) for some bounded \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) with bounded first three derivatives, and
for some fixed coefficients \(c_I \in {\mathbb {R}}\). Furthermore, assume that
Then for \(I_1\), \(I_2\) and \(I_3\) as in (A.4), (A.5) and (A.6), we have
Remark A.5
We can extend Lemma A.4 to the vector setting, i.e. for a function \(h(X) = f(\Phi ^{(1)}(X), \ldots , \Phi ^{(k)}(X))\) of a finite number k of multi-linear polynomials \(\Phi ^{(i)}(X)\) as in (A.7), each satisfying (A.8), where \(f: {\mathbb {R}}^k \rightarrow {\mathbb {R}}\) has bounded partial derivatives of order up to three. The bounds (A.9)–(A.10) are simply modified replacing \(\Vert f'''\Vert _\infty \) by \(\max _{1\leqslant i,j,l \leqslant k} \Vert \partial _{i,j,l} f\Vert _\infty \) and the three occurrences of \(\Phi \) by \(\Phi ^{(i)}\), \(\Phi ^{(j)}\), \(\Phi ^{(l)}\), and then summing over \(1 \leqslant i,j,l \leqslant k\); similar modifications apply to the bound (A.11). The adaptation of the proof is straightforward.
We now give the proofs of Lemmas A.2–A.4.
Proof of Lemma A.2
Let \(Y_t:=\sqrt{t}X +\sqrt{1-t}Z\), \(t\in [0,1]\). Then we can write
Given \(C \subseteq {{\mathbb {T}}} \), let us denote
In particular, \(Y_t=U_t^{{\mathbb {T}}} \). Observe that \(\mathrm E[X_k \, \partial _k h(U_t^{A_k^c}) ] = \mathrm E[X_k] \mathrm E[\partial _k h(U_t^{A_k^c}) ] = 0\) by independence. We recall Gaussian integration by parts: for smooth functions \(\varphi \),
since \(\sigma _{kl} = 0\) for \(l \not \in A_k\). Then
Let us expand the first term. We can interpolate between \(U^{{\mathbb {T}}} _t\) and \(U_t^{A_k^c}\) by
Then
Note that we can restrict the sum to \(l \in A_k\) because \(X^{A_k}_l = 0\) otherwise. This leads to
Note that \(\mathrm E[X_k \, X_l \,\partial ^2_{kl} h\big ( U^{A_{kl}^c}_t \big ) ] = \mathrm E[X_k \, X_l] \mathrm E[\partial ^2_{kl} h\big ( U^{A_{kl}^c}_t \big ) ] = \sigma _{kl} \mathrm E[\partial ^2_{kl} h\big ( U^{A_{kl}^c}_t \big ) ]\) by the independence assumption. By adding and subtracting this term, we get
where
where we performed the integration on s in \(I_2\) (whose integrand does not depend on s).
Let us deal with \(I_1\). Note that
We can therefore interpolate between \(U^{A_{kl}^c}_t\) and \(U^{A_k^c}_t + s \sqrt{t} X^{A_k}\) by
Note that \((sX^{A_k} + X^{A_{kl}\backslash A_k})_m=0\) for \(m \not \in A_{kl}\). We can then write
This yields the final form of \(I_1\):
Let us now deal with \(I_2\). We can interpolate between \(U^{A^c_{kl}}_t\) and \(U^{{\mathbb {T}}} _t\) by
Then
This yields the final form of \(I_2\):
This concludes the proof of Lemma A.2. \(\square \)
Proof of Lemma A.3
Let \(W_t:=\sqrt{t}{\widetilde{Z}} +\sqrt{1-t}Z\), \(t\in [0,1]\). Using Gaussian integration by parts as in the proof of Lemma A.2, we have
which proves the lemma. \(\square \)
Proof of Lemma A.4
We can easily compute
which by assumption (A.8), gives
We can then substitute this into (A.4) to bound
where we used the fact that \(\partial _k\Phi (\ldots )\) is independent of \(X_k\) since assumption (A.8) implies that \(\partial _k \Phi (\ldots )\) does not depend on \((X_m)_{m\in A_{kl}}\). This immediately implies (A.9).
The proof of (A.10) is the same if in (A.5), we write \(\sigma _{kl}= \mathrm E[{\widetilde{X}}_k {\widetilde{X}}_l]\) for \(({\widetilde{X}}_k, {\widetilde{X}}_l)\) with the same distribution as \((X_k, X_l)\) but independent of X. The proof of (A.11) is even simpler. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Caravenna, F., Sun, R. & Zygouras, N. The critical 2d Stochastic Heat Flow. Invent. math. 233, 325–460 (2023). https://doi.org/10.1007/s00222-023-01184-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-023-01184-7
Keywords
- Directed polymer in random environment
- Stochastic heat equation
- KPZ equation
- Coarse-graining
- Renormalization
- Lindeberg principle