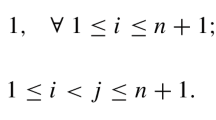On mixing diffeomorphisms of the disc

Abstract

We prove that a $C^k$, $k\ge 2$ pseudo-rotation f of the disc with non-Brjuno rotation number is $C^{k-1}$-rigid. The proof is based on two ingredients: (1) we derive from Franks’ Lemma on free discs that a pseudo-rotation with small rotation number compared to its $C^1$ norm must be close to the identity map; (2) using Pesin theory, we obtain an effective finite information version of the Katok closing lemma for an area preserving surface diffeomorphism f, that provides a controlled gap in the possible growth of the derivatives of f between exponential and sub-exponential. Our result on rigidity, together with a KAM theorem by Rüssmann, allow to conclude that analytic pseudo-rotations of the disc or the sphere are never topologically mixing. Due to a structure theorem by Franks and Handel of zero entropy surface diffeomorphisms, it follows that an analytic conservative diffeomorphism of the disc or the sphere that is topologically mixing must have positive topological entropy.

Appendix

Proof of Proposition 3.5

We denote the first and second coordinates of $g_n$ as $\bar{v},\bar{w}$. We expand $g_n$ into linear terms and higher order terms at the origin. For each $(v,w) \in U_n$, we have

$$\begin{aligned} \bar{v}(v,w)= & {} A_nv+f_n(v,w) \end{aligned}$$

(4.1)

$$\begin{aligned} \bar{w}(v,w)= & {} B_nw+h_n(v,w) \end{aligned}$$

(4.2)

where $\partial _{v}f_n(0,0)=\partial _{w}f_n(0,0)=\partial _{v}h_n(0,0)=\partial _{w}h_n(0,0)=0$. ($f_n,h_n$ are uniquely determined by these conditions). Following the notations in Sect. 3.2, we have

$$\begin{aligned} A_n = e^{\lambda ^u_n}, B_n =e^{\lambda ^s_n} \end{aligned}$$

Recall that we have assumed $\Vert Dg\Vert \le A$ and $\Vert D^2g\Vert \le D$. By Lemma 3.6, we have the following lemmata which are essentially proved in [4].

Lemma 4.1

For all $0 \le n \le L-1$ we have

$$\begin{aligned} \Vert D^2f_n\Vert , \Vert D^2h_n\Vert \le C_0D\beta _{n+1} \end{aligned}$$

As a consequence, for all $0 \le n \le L-1$ we have

$$\begin{aligned} |\partial _vf_n(v,w)|,|\partial _wf_n(v,w)|,|\partial _vh_n(v,w)|,|\partial _wh_n(v,w)| \le C_0D\beta _{n+1} (|v| + |w|) \end{aligned}$$

Here $C_0$ is a constant depending only on S and the norm is taken restricted to $U_n$.

Denote $\epsilon _n=2C_0D\beta _{n+1}r_n(1+\kappa _n)$, then we have the following estimate:

Lemma 4.2

For each $0\le n \le L-1$, we have

$$\begin{aligned} \Vert \partial _v f_n\Vert _{C^0} \le \epsilon _n, \Vert \partial _wf_n\Vert _{C^0} \le \epsilon _n \\ \Vert \partial _v h_n\Vert _{C^0} \le \epsilon _n, \Vert \partial _w h_n\Vert _{C^0} \le \epsilon _n \end{aligned}$$

Here $C^{0}$ norm is taken restricted to $U_n$.

It is easy to see that

$$\begin{aligned} \epsilon _n = 2C_0D\beta _{n+1}r_n(1+\kappa _n)\le & {} 2C_0D\max (A^{2}c_n^{-1}, \frac{1}{100}) {\bar{\beta }} \bar{r} c_n^3(1+c_n^{-1}{\bar{\kappa }}) \\\le & {} 400C_0c_nDA^2{\bar{\beta }} \bar{r} \end{aligned}$$

Then by (3.31) and (3.32), we have

$$\begin{aligned} \epsilon _n\le & {} D^{-\frac{M}{2}}{\bar{\kappa }} \end{aligned}$$

(4.3)

$$\begin{aligned} \epsilon _n \kappa _n\le & {} D^{-M}{\bar{\kappa }} \end{aligned}$$

(4.4)

$$\begin{aligned} \epsilon _n {\tilde{\kappa }}_{n}\le & {} D^{-M}{\bar{\kappa }} \end{aligned}$$

(4.5)

when D is sufficiently large depending only on S.

Then by Lemma 4.1 and (4.1), for any $(v,w) \in U_n$ we have,

$$\begin{aligned} |\bar{v}|\ge & {} A_n|v| - |f_n(v,w)| \nonumber \\\ge & {} A_n|v| - \epsilon _n(|v| + |w|) \nonumber \\\ge & {} (A_n - \epsilon _n - \epsilon _n \kappa _n)|v| - \epsilon _n \tau _n \end{aligned}$$

(4.6)

and by (4.2)

$$\begin{aligned} |\bar{w}|\le & {} B_n|w| + |h_n(v,w)| \nonumber \\\le & {} B_n|w| + \epsilon _n(|v| + |w|) \nonumber \\\le & {} B_n(\tau _n + \kappa _n |v|) + \epsilon _n((1+\kappa _n)|v| + \tau _n) \nonumber \\\le & {} (B_n \kappa _n + \epsilon _n + \epsilon _n \kappa _n) |v| + B_n \tau _n + \epsilon _n \tau _n \end{aligned}$$

(4.7)

We will first show that:

$$\begin{aligned} g_n(U_n) \text{ is } \text{ contained } \text{ in } \text{ the } \text{ interior } \text{ of } U(\infty , \tau _{n+1}, \kappa _{n+1}) \end{aligned}$$

(4.8)

Combining (4.6) and (4.7), (4.8) follows from:

$$\begin{aligned} \kappa _{n+1}> & {} \frac{e^{\lambda _n^s} \kappa _n + \epsilon _n + \epsilon _n \kappa _n}{ e^{\lambda _n^u} - \epsilon _n - \epsilon _n \kappa _n } \end{aligned}$$

(4.9)

$$\begin{aligned} \tau _{n+1}> & {} (e^{\lambda _n^s} + \epsilon _n + \epsilon _n \frac{e^{\lambda _n^s} \kappa _n + \epsilon _n + \epsilon _n \kappa _n}{ e^{\lambda _n^u} - \epsilon _n - \epsilon _n \kappa _n }) \tau _n \end{aligned}$$

(4.10)

By (4.3), (4.4), then when D is sufficiently large we get (4.9) from

$$\begin{aligned} \frac{e^{\lambda _n^s} \kappa _n + \epsilon _n + \epsilon _n \kappa _n}{ e^{\lambda _n^u} - \epsilon _n - \epsilon _n \kappa _n }< & {} e^{-\lambda _n^u + \frac{1}{2}\delta }(e^{\lambda _n^s} \kappa _n + D^{-\frac{1}{4}M}{\bar{\kappa }}) \\\le & {} \max (e^{ - \lambda _n^u + \lambda _n^s + \delta } \kappa _n, \frac{1}{100}{\bar{\kappa }}) \\\le & {} \kappa _{n+1} \end{aligned}$$

Similarly, by (4.3),(4.4), (3.30), we have (4.10) when D is sufficiently large.

Now we get to the proof of (1) in Proposition 3.5. Differentiate (4.1) and (4.2), we get

$$\begin{aligned} \frac{d\bar{v}}{dv}= & {} A_n + \partial _v f_n(v,w) \end{aligned}$$

(4.11)

$$\begin{aligned} \frac{d\bar{v}}{dw}= & {} \partial _w f_n(v,w) \end{aligned}$$

(4.12)

$$\begin{aligned} \frac{d\bar{w}}{dv}= & {} \partial _v h_n(v,w) \end{aligned}$$

(4.13)

$$\begin{aligned} \frac{d\bar{w}}{dw}= & {} B_n + \partial _w h_n(v,w) \end{aligned}$$

(4.14)

Take any $(a,b) \in C_n$, $(v,w) \in U_n$, then

$$\begin{aligned} (Dg_{n})_{(v,w)}(a,b)= & {} (\bar{a}, \bar{b}) \end{aligned}$$

with

$$\begin{aligned} \bar{a}= & {} (A_n + \partial _v f_n(v,w)) a + \partial _w f_n(v,w) b \\ \bar{b}= & {} \partial _v h_n(v,w) a + (B_n + \partial _w h_n(v,w))b \end{aligned}$$

Since $|b| \le \kappa _n|a|$, by Lemma 4.2 we have

$$\begin{aligned} |\bar{a} |\ge & {} (e^{\lambda _n^u } - \epsilon _n) |a| - \epsilon _n |b| \nonumber \\\ge & {} (e^{\lambda _n^u } - \epsilon _n - \epsilon _n\kappa _n) |a| \end{aligned}$$

(4.15)

and

$$\begin{aligned} |\bar{b}|\le & {} \epsilon _n a + (e^{\lambda _n^s} + \epsilon _n)b \nonumber \\\le & {} (\epsilon _n \kappa _n + e^{\lambda _n^s} \kappa _n + \epsilon _n) |a| \end{aligned}$$

(4.16)

Then we have

$$\begin{aligned} |\bar{b}| \le |\bar{a}|\frac{\epsilon _n \kappa _n + e^{\lambda _n^s} \kappa _n + \epsilon _n}{e^{\lambda _n^u } - \epsilon _n - \epsilon _n\kappa _n } \end{aligned}$$

Then by (4.9), we have that $(\bar{a}, \bar{b}) \in C_{n+1}$.

On the other hand, take any $(\bar{a},\bar{b}) \in \tilde{C}_{n+1}, (v,w) \in g_n(U_n) \bigcap U_{n+1}$, denote $(a,b) = (Dg_n^{-1})_{(v,w)}(\bar{a}, \bar{b})$, by (4.15) and (4.16) we have

$$\begin{aligned} {\tilde{\kappa }}_{n+1}(\epsilon _n |a| + (e^{\lambda _n^s} + \epsilon _n)|b|) \ge {\tilde{\kappa }}_{n+1}|\bar{b}| \ge |\bar{a}| \ge (e^{\lambda _n^u } - \epsilon _n) |a| - \epsilon _n |b| \end{aligned}$$

hence

$$\begin{aligned} |a|\le & {} |b|\frac{{\tilde{\kappa }}_{n+1}(e^{\lambda _n^s}+ \epsilon _n) + \epsilon _n}{e^{\lambda _n^u} - \epsilon _n - {\tilde{\kappa }}_{n+1}\epsilon _n} \end{aligned}$$

In order to prove that $(a,b) \in \tilde{C}_n$, it is enough to verify that

$$\begin{aligned} \frac{{\tilde{\kappa }}_{n+1}(e^{\lambda _n^s}+ \epsilon _n) + \epsilon _n}{e^{\lambda _n^u} - \epsilon _n - {\tilde{\kappa }}_{n+1}\epsilon _n} \le {\tilde{\kappa }}_n \end{aligned}$$

that is

$$\begin{aligned} {\tilde{\kappa }}_{n+1} \le \frac{{\tilde{\kappa }}_n e^{\lambda _n^u }- \epsilon _n {\tilde{\kappa }}_n - \epsilon _n}{e^{\lambda _n^s} + \epsilon _n + \epsilon _n {\tilde{\kappa }}_n} \end{aligned}$$

when D is sufficiently large. This is proved in a similar way as (4.9) using (4.3), (4.5). This completes the proof of (1).

Now we prove (2) in Proposition 3.5. If $\Gamma$ is $\kappa _n$-full horizontal graph of $U_n$, we can denote $\Gamma$ as the graph of $\phi : [-r_n, r_n] \rightarrow {\mathbb {R}}$, such that:

• (1) The Lipschitz constant of $\phi$ is smaller than $\kappa _n$ everywhere;

• (2) For any $v \in [-r_n, r_n]$, we have $(v,\phi (v)) \in U_n$.

By (4.11), we have for any $(v,w) \in U_{n}$

$$\begin{aligned} \frac{d\bar{v}}{dv}(v,w)> & {} e^{\lambda _n^u} - \epsilon _n(|v| + |w|) \\\ge & {} e^{\lambda _n^u} - \epsilon _n(|v| + \kappa _n|v| + \tau _n) \\\ge & {} e^{\lambda _n^u} - \epsilon _n(r_n + \kappa _nr_n + \tau _n) \\> & {} 0 \end{aligned}$$

when D is sufficiently large. By (4.6), for any w such that $(r_n, w) \in U_n$, if D is sufficiently large then

$$\begin{aligned} \bar{v}(r_n, w)\ge & {} (A_n - \epsilon _n - \epsilon _n \kappa _n) r_n - \epsilon _n \tau _n\\> & {} e^{\lambda _n^u - \frac{1}{2}\delta } r_n > r_{n+1} \end{aligned}$$

Here the second inequality follows from (4.3), (4.4) and (3.40). Similar calculation shows that $\bar{v}(-r_n, w) < -r_{n+1}$ for all w such that $(-r_n, w) \in U_n$. Then $\bar{v}^{-1}$ is defined over $[-r_{n+1}, r_{n+1}]$, and we have that the image of the vertical boundary of $U_n$ under $g_n$ is disjoint from the vertical boundary of $U_{n+1}$.

Then by (4.8), we have

$$\begin{aligned}&g_n(\Gamma ) \bigcap U_{n+1} \text{ is } \text{ contained } \text{ in } U_n \\&\text{ and } \text{ disjoint } \text{ from } \text{ the } \text{ horizontal } \text{ boundary } \text{ of } U_n \end{aligned}$$

Moreover, $g_n(\Gamma ) \bigcap U_{n+1}$ is the graph of function $\phi \bar{v}^{-1}$ restricted to $[-r_{n+1}, r_{n+1}]$. Since we already showed (1), we know that $g_n(\Gamma ) \bigcap U_{n+1}$ is a $\kappa _{n+1}$-full horizontal graph, and the image of the horizontal boundary of $U_n$ under $g_n$ is disjoint from the horizontal boundary of $U_{n+1}$.

This completes the proof of (2). $\square$