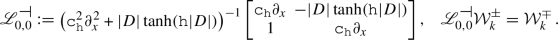Stokes Waves at the Critical Depth are Modulationally Unstable

Abstract

The paper fully answers a long standing open question concerning the stability/instability of pure gravity periodic traveling water waves—called Stokes waves—at the critical Whitham–Benjamin depth $\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}= 1.363...$ and nearby values. We prove that Stokes waves of small amplitude $\mathcal {O}( \epsilon )$ are, at the critical depth $\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$, linearly unstable under long wave perturbations. The same holds true for slightly smaller values of the depth $\texttt{h}> \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}- c \epsilon ^2$, $c > 0$, depending on the amplitude of the wave. This problem was not rigorously solved in previous literature because the expansions degenerate at the critical depth. To solve this degenerate case, and describe in a mathematically exhaustive way how the eigenvalues change their stable-to-unstable nature along this shallow-to-deep water transient, we Taylor-expand the computations of Berti et al. (Arch Ration Mech Anal 247:91, 2023) at a higher degree of accuracy, starting from the fourth order expansion of the Stokes waves. We prove that also in this transient regime a pair of unstable eigenvalues depict a closed figure “8”, of smaller size than for $\texttt{h}> \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$, as the Floquet exponent varies.

1 Introduction and Main Result

In the last years a substantial mathematical progress has been obtained in the classical problem of determining the stability/instability of the Stokes waves, i.e. periodic traveling waves of the gravity water waves equations in any depth, subject to long wave perturbations.

Let us briefly summarize the state of the art. The existence of small amplitude Stokes waves, pioneered by the famous work of Stokes [40] in 1847, was first rigorously proved by Struik [43], Levi-Civita [33], and Nekrasov [36] one century ago, and then extended to global branches containing extreme waves in [1, 15, 30, 35, 38, 44]. In the sixties Benjamin and Feir [3, 4], Whitham [45], Lighthill [34] and Zakharov [48, 50] discovered, through experiments and formal arguments, that small amplitude Stokes waves in sufficiently deep water are unstable, proposing a heuristic mechanism which leads to the disintegration of wave trains. More precisely, these works predicted the existence of a critical depth—that we shall call the Whitham–Benjamin depth—

$$\begin{aligned} \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}:= 1.363... \,, \end{aligned}$$

such that $2\pi \kappa$-space periodic Stokes waves in an ocean of depth $\mathtt h > \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}\kappa ^{-1}$ are unstable: in correspondence with small Floquet exponents $\mu$ (i.e. long-wave perturbations) the linearized equations at the Stokes wave possess a pair of eigenvalues with non-zero real part close to zero. This phenomenon is nowadays called “Benjamin–Feir”—or modulational—instability, and it is supported by an enormous amount of physical observations and numerical simulations, see e.g. [18, 19, 31]. We refer to [51] for a historical survey of the modulational theory of wave packets for several dispersive and fluid PDE models. We remark that modulational instability has indeed been observed also in a variety of approximate water waves models, such as KdV, gKdV, NLS and the Whitham equation, see [11, 12, 22,23,24,25, 27, 32, 39, 46].

For the water waves equations, the first mathematically rigorous proof of a local branch of unstable Benjamin–Feir eigenvalues close to zero for $\kappa \mathtt h > \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$ was obtained by Bridges-Mielke [10] in finite depth (see also Hur-Yang [26]) through a center manifold reduction, and recently by Nguyen-Strauss [37] by a Lyapunov-Schmidt decomposition. In deep water we mention the nonlinear modulational result by Chen-Su [13].

Very recently Berti-Maspero-Ventura [7, 8] developed a completely different rigorous spectral approach, based on a symplectic version of Kato’s theory of similarity transformations and a block diagonalization technique inspired by KAM theory, which provided the full topological splitting of all the four eigenvalues close to zero as the Floquet exponent $\mu$ is turned on. More precisely the works [7, 8], that, with no loss of generality, are formulated for $2\pi$-periodic Stokes waves, i.e. with wave number $\kappa =1$, rigorously prove that:

• Shallow water case: for any $0< \mathtt h < \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$ the eigenvalues close to zero are purely imaginary for Stokes waves of sufficiently small amplitude $\epsilon$, see Fig. 1-left;

• Sufficiently deep water case: for any $\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}< \mathtt h \le \infty$, there exists a pair of eigenvalues with non-zero real part, which traces a complete closed figure “8” (as shown in Fig. 1-right) parameterized by the Floquet exponent $\mu$. As ${\mathtt h} \rightarrow \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}^{\, +}$ the set of unstable Floquet exponents shrinks to zero and the Benjamin–Feir unstable eigenvalues collapse to the origin (we remark that the case $\texttt{h}= + \infty$ is not a consequence of the finite depth case). The figure “8” had been numerically observed in Deconinck-Oliveras [18].

Fig. 1

The left picture shows that for $\texttt{h}< \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$ the eigenvalues $\lambda ^\pm _{1} (\mu ,\epsilon )$ and $\lambda ^\pm _{0} (\mu ,\epsilon )$ are purely imaginary. The picture on the right shows that for $\texttt{h}> \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$ the eigenvalues $\lambda ^\pm _1 (\mu ,\epsilon )$ at fixed $|\epsilon | \ll 1$ as $\mu$ varies. This figure “8 ” depends on $\texttt{h}$ and shrinks to 0 as $\texttt{h}\rightarrow \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}^+$. Some higher order formal expansions have been computed in Creedon-Deconinck [16]

A question remained open: to determine the stability or instability of the Stokes waves at the critical Whitham–Benjamin depth $\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$ and analyze in detail the change of stable-vs-unstable behavior of the eigenvalues along this shallow-to-deep water transient.

Some formal answers have been given so far [27, 29, 41, 42]. Water waves solutions in the modulational instability ansatz are formally approximated by an equation for the wave envelope which is, if $\texttt{h}< \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$, a defocusing cubic nonlinear Schrodinger equation (NLS) whereas, if $\texttt{h}> \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$, it is a focusing cubic NLS (this is in agreement with the rigorous stability/instability results in shallow/deep water stated above). The transient behaviour at the critical depth $\texttt{h}= \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$ corresponds to the vanishing of the cubic coefficients, and, in this case, it is required to determine a higher order effective NLS. In the seventies, formal computations by Johnson [28] suggested a stability scenario for the Stokes waves for nearby larger values of $\texttt{h}> \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$. On the contrary, some years later Kakutani-Michihiro [29] derived a different quintic NLS equation and claimed the modulational instability of Stokes waves. The instability was further confirmed by Slunyaev [42] who computed how the coefficients of the quintic effective NLS depend on $\texttt{h}$.

In this paper we prove with mathematical rigor the occurrence of the latter scenario: Stokes waves of the pure gravity water waves equations at the critical depth are linearly unstable under long wave perturbations. Unlike all the previous mentioned works, we do not use any formal approximation argument with some quintic NLS equation, but prove directly the existence of unstable eigenvalues of the linearized water waves equations at the Stokes wave. Informally speaking the main result we prove is the following:

Theorem 1.1

(Modulational instability of the Stokes wave at $\texttt{h}= \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$). If $\texttt{h}= \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$ then small amplitude Stokes waves of amplitude $\mathcal {O}(\epsilon )$ are linearly unstable subject to long wave perturbations. Actually Stokes waves are modulational unstable also at nearby depths $\texttt{h}< \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$: there is an analytic function defined for $\epsilon$ small, of the form

$$\begin{aligned} \underline{ \texttt{h}}(\epsilon ) = - c \epsilon ^2 + \mathcal {O}(\epsilon ^3) \,, \quad c > 0 \,, \end{aligned}$$

such that, for any $(\texttt{h}, \epsilon )$ satisfying

$$\begin{aligned} \texttt{h}> \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}+ \underline{ \texttt{h}}(\epsilon ) \,, \end{aligned}$$

(1.1)

then the linearized equations at the Stokes wave have two eigenvalues with nontrivial real part for any Floquet exponent $\mu$ small enough, see Fig. 2. In particular for $\texttt{h}= \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$ the unstable eigenvalues depict a closed figure “8” as $\mu$ varies in an interval of size $[0, c_1 \epsilon ^2)$, see Fig. 3, whose height and width are much smaller than for $\texttt{h}> \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$, see Fig. 1.

Fig. 2

The values of ($\texttt{h}, \epsilon$) in $(0,\infty ) \times (0, \epsilon _1)$ for which there are Benjamin–Feir unstable eigenvalues fill the zone above the red curve, where $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};0,\epsilon )>0$

Fig. 3

The figure “8” at the critical depth, which has a smaller size with respect to the one in Fig. 1

For a more rigorous statement we refer to Theorems 1.3 and 1.4. Actually Theorems 1.3 and 1.4 provide a necessary and sufficient condition for the existence of unstable eigenvalues: the Benjamin–Feir discriminant function $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};\mu ,\epsilon )$ that appears in the matrix entry $[\mathtt U]_{21}$ in (1.18) has to be positive. We prove in Theorem 1.3 that the Benjamin–Feir discriminant function admits the expansion

$$\begin{aligned} \Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};\mu ,\epsilon ):= 8\texttt{e}_{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}) \epsilon ^2+ 8\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}) \epsilon ^4 + r_1(\epsilon ^5,\mu \epsilon ^3)-\texttt{e}_{22} (\texttt{h}) \mu ^2\big (1+r_1''(\epsilon ,\mu )\big )\nonumber \\ \end{aligned}$$

(1.2)

where

$$\begin{aligned} \texttt{e}_{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}):= \frac{1}{{\texttt{c}}_{\texttt{h}}} \Big [ \frac{9{\texttt{c}}_{\texttt{h}}^8-10{\texttt{c}}_{\texttt{h}}^4+9}{8{\texttt{c}}_{\texttt{h}}^6} - \frac{1}{\texttt{h}- \frac{1}{4}\texttt{e}_{12}^2} \Big (1 + \frac{1-{\texttt{c}}_{\texttt{h}}^4}{2} + \frac{3}{4} \frac{(1-{\texttt{c}}_{\texttt{h}}^4)^2}{{\texttt{c}}_{\texttt{h}}^2}\texttt{h}\Big ) \Big ]\nonumber \\ \end{aligned}$$

(1.3)

is called the Benjamin–Feir function, the coefficient $\texttt{e}_{22} (\texttt{h}) > 0$ is defined in (3.4c), and the coefficient $\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h})$ is computed in (1.20). The graph of the Benjamin–Feir function $\texttt{e}_{\scriptscriptstyle {\textsc {WB}}}(\texttt{h})$ is as in Fig. 4.

Fig. 4

The Whitham–Benjamin function $\texttt{e}_{\scriptscriptstyle {\textsc {WB}}}(\texttt{h})$ has a unique root $\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}=1.363\dots$

Thus, for any $\texttt{h}> \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$, resp. $\texttt{h}< \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$, it results $\texttt{e}_{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}) > 0$, resp. $\texttt{e}_{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}) < 0$, and therefore for $\mu$ and $\epsilon$ small enough $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};\mu ,\epsilon ) > 0$, resp. $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};\mu ,\epsilon ) < 0$, proving the existence of unstable, resp. stable, eigenvalues. This is the result proved in [9].

On the other hand at $\texttt{h}=\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$ the coefficient $\texttt{e}_{\scriptscriptstyle {\textsc {WB}}}( \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}) = 0$ vanishes and the sign of the Benjamin–Feir function $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};\mu ,\epsilon )$ in (1.2) is determined by the sign of the coefficient $\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}})$ (note that in (1.2) no pure term of order $\epsilon ^3$ appears; such a degeneracy is a consequence of symmetries of the problem). The constant $\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}})$ is computed in (1.20) and it turns out to be strictly positive (Fig. 5).

Fig. 5

The plot of the function $\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h})$ looks positive for every depth

This proves the linear instability of the Stokes wave at $\texttt{h}= \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$, stated in Theorem 1.1. In addition the regions where $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};0,\epsilon )> 0$, respectively $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};0,\epsilon ) < 0$, are delimited by the graph of an analytic curve of the form (obtained by the analytic implicit function theorem)

$$\begin{aligned}{} & {} \epsilon \mapsto \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}+\underline{\texttt{h}}(\epsilon ) \,, \quad \underline{ \texttt{h}}(\epsilon ) = - \frac{\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}})}{\texttt{e}_{\scriptscriptstyle {\textsc {WB}}}'(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}})} \epsilon ^2 + \mathcal {O}(\epsilon ^3) \,,\qquad \text {solving}\\{} & {} \Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}+\underline{\texttt{h}}(\epsilon );0,\epsilon )= 0\,, \end{aligned}$$

see Fig. 2. It turns out that $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};\mu ,\epsilon ) > 0$ if the condition (1.1) holds.

In order to prove (1.2)—which is the the major achievement of Sects. 3 and 4—we need to expand the Stokes waves up to order $\epsilon ^4$, as provided in Appendix A, and to explicitly compute the Taylor expansion of [9] at the fourth order of accuracy. We implement an effective algorithm to compute (1.2) observing several analytical cancellations in the symplectic Kato reduction process. We now present rigorously the main results.

Main result.

We first shortly introduce the pure gravity water waves equations, their Hamiltonian formulation, and the linearized water waves equations at the Stokes waves. We refer to [9] for more details.

The water waves equations. We consider the Euler equations for a 2-dimensional incompressible, irrotational fluid under the action of gravity. The fluid fills the region

$$\begin{aligned} { {\mathcal {D}}}_\eta := \left\{ (x,y)\in \mathbb {T}\times \mathbb {R}:\; -\texttt{h}\le y< \eta (t,x)\right\} \,, \quad \mathbb {T}:=\mathbb {R}/2\pi \mathbb {Z}, \end{aligned}$$

with finite depth and space periodic boundary conditions. The irrotational velocity field is the gradient of a harmonic scalar potential $\Phi =\Phi (t,x,y)$ determined by its trace $\psi (t,x)=\Phi (t,x,\eta (t,x))$ at the free surface $y = \eta (t, x )$. Actually $\Phi$ is the unique solution of the elliptic equation $\Delta \Phi = 0$ in ${{\mathcal {D}}}_\eta$ with Dirichlet datum $\Phi (t,x,\eta (t,x)) = \psi (t,x)$ and $\Phi _y(t,x,y) = 0$ at $y = - \texttt{h}$.

The time evolution of the fluid is determined by two boundary conditions at the free surface. The first is that the fluid particles remain, along the evolution, on the free surface and the second one is that the pressure of the fluid is equal, at the free surface, to the constant atmospheric pressure. Then, as shown by Zakharov [49] and Craig–Sulem [15], the time evolution of the fluid is determined by the following equations for the unknowns $(\eta (t,x), \psi (t,x))$,

$$\begin{aligned} \eta _t = G(\eta )\psi \,, \quad \psi _t = - g \eta - \dfrac{\psi _x^2}{2} + \dfrac{1}{2(1+\eta _x^2)} \big ( G(\eta ) \psi + \eta _x \psi _x \big )^2 \,, \end{aligned}$$

(1.4)

where $g > 0$ is the gravity constant and $G(\eta ):= G(\eta , \texttt{h})$ denotes the Dirichlet-Neumann operator $[G(\eta )\psi ](x):= \Phi _y(x,\eta (x)) - \Phi _x(x,\eta (x)) \eta _x(x)$. In the sequel, with no loss of generality, we set the gravity constant $g = 1$.

The equation (1.4) are the Hamiltonian system

$$\begin{aligned} \partial _t \begin{bmatrix}\eta \\ \psi \end{bmatrix} = \mathcal {J}\begin{bmatrix}\nabla _\eta \mathcal {H} \\ \nabla _\psi \mathcal {H} \end{bmatrix}, \quad \quad \mathcal {J}:= \begin{bmatrix} 0 &{} \textrm{Id}\\ -\textrm{Id}&{} 0 \end{bmatrix}, \end{aligned}$$

(1.5)

where $\nabla$ denote the $L^2$-gradient, and the Hamiltonian $\mathcal {H}(\eta ,\psi ):= \frac{1}{2} \int _{\mathbb {T}} ( \psi \,G(\eta )\psi +\eta ^2) \textrm{d}x$ is the sum of the kinetic and potential energy of the fluid. In addition of being Hamiltonian, the water waves system (1.4) is reversible with respect to the involution

$$\begin{aligned} \rho \begin{bmatrix}\eta (x) \\ \psi (x) \end{bmatrix}:= \begin{bmatrix}\eta (-x) \\ -\psi (-x) \end{bmatrix}, \quad \text {i.e. } \mathcal {H} \circ \rho = \mathcal {H} \,, \end{aligned}$$

(1.6)

and it is space invariant.

Stokes waves. The Stokes waves are traveling solutions of (1.4) of the form $\eta (t,x)=\breve{\eta }(x-ct)$ and $\psi (t,x)=\breve{\psi }(x-ct)$ for some real c and $2\pi$-periodic functions $(\breve{\eta } (x), \breve{\psi } (x))$. In a reference frame in translational motion with constant speed c, the water waves equation (1.4) become

$$\begin{aligned} \eta _t = c\eta _x+G(\eta )\psi \,, \quad \psi _t = c\psi _x - \eta - \dfrac{\psi _x^2}{2} + \dfrac{1}{2(1+\eta _x^2)} \big ( G(\eta ) \psi + \eta _x \psi _x \big )^2\qquad \end{aligned}$$

(1.7)

and the Stokes waves $(\breve{\eta }, \breve{\psi })$ are equilibrium steady solutions of (1.7).

Small amplitude Stokes waves were constructed by Struik [43] in finite depth, and Levi-Civita [33], and Nekrasov [36] in infinite depth.

Theorem 1.2

(Stokes waves). For any $\texttt{h}\in (0,+\infty ]$ there exist $\epsilon _*=\epsilon _*(\texttt{h}) >0$ and a unique family of real analytic solutions $(\eta _\epsilon (x), \psi _\epsilon (x), c_\epsilon )$, parameterized by the amplitude $|\epsilon |<\epsilon _*$, of

$$\begin{aligned} c \, \eta _x+G(\eta )\psi = 0 \,, \quad c \, \psi _x - \eta - \dfrac{\psi _x^2}{2} + \dfrac{1}{2(1+\eta _x^2)} \big ( G(\eta ) \psi + \eta _x \psi _x \big )^2 = 0 \,, \end{aligned}$$

(1.8)

such that $\eta _\epsilon (x)$ and $\psi _\epsilon (x)$ are $2\pi$-periodic; $\eta _\epsilon (x)$ is even and $\psi _\epsilon (x)$ is odd, of the form

$$\begin{aligned}&\begin{aligned} \eta _\epsilon (x)&= \epsilon \cos (x) + \epsilon ^2 \big (\eta _{2}^{[0]} + \eta _{2}^{[2]} \cos (2x)\big ) + \epsilon ^3 \big (\eta _{3}^{[1]} \cos (x) + \eta _{3}^{[3]} \cos (3x)\big ) \\&\quad +\epsilon ^4 \big (\eta _{4}^{[0]} +\eta _{4}^{[2]} \cos (2x)+ \eta _{4}^{[4]} \cos (4x)\big ) + \mathcal {O}(\epsilon ^5)\, , \end{aligned} \end{aligned}$$

(1.9a)

$$\begin{aligned}&\begin{aligned} \psi _\epsilon (x)&= \epsilon {\texttt{c}}_{\texttt{h}}^{-1} \sin (x) + \epsilon ^2 \psi _{2}^{[2]} \sin (2x) + \epsilon ^3 \big (\psi _{3}^{[1]} \sin (x)+\psi _{3}^{[3]} \sin (3x) \big ) \\&\quad + \epsilon ^4 \big (\psi _{4}^{[2]} \sin (2x)+\psi _{4}^{[4]} \sin (4x)\big ) +\mathcal {O}(\epsilon ^5) \, , \end{aligned} \end{aligned}$$

(1.9b)

$$\begin{aligned}&\begin{aligned} c_\epsilon = {\texttt{c}}_{\texttt{h}}+ \epsilon ^2 c_2 +\epsilon ^4 c_4 + \mathcal {O}(\epsilon ^5) \, , \qquad {\texttt{c}}_{\texttt{h}}= \sqrt{\tanh (\texttt{h})} \, ,\end{aligned} \end{aligned}$$

(1.9c)

with coefficients given in (A.2).

The expansions (1.9) are derived in Proposition A.1 (they coincide with [21] after some suitable rescaling, translation and choice of the moving frame, see Remark A.3).

Remark. More general time quasi-periodic traveling Stokes waves—which are nonlinear superpositions of multiple Stokes waves traveling with rationally independent speeds—have been recently proved for (1.4) in [6] in finite depth, in [20] in infinite depth, and in [5] for capillary-gravity water waves in any depth.

Linearization at the Stokes waves.

In order to determine the stability/instability of the Stokes waves given by Theorem 1.2, we linearize the water waves equation (1.7) with $c = c_\epsilon$ at $(\eta _\epsilon (x), \psi _\epsilon (x))$. In [9] we obtain the autonomous real linear Hamiltonian and reversible system

$$\begin{aligned}{} & {} \begin{bmatrix}{\hat{\eta }}_t \\ {\hat{\psi }}_t \end{bmatrix}\\{} & {} \quad = \begin{bmatrix} -G(\eta _\epsilon )B-\partial _x \circ (V-c_\epsilon ) &{} G(\eta _\epsilon ) \\ -1+B(V-c_\epsilon )\partial _x - B \partial _x \circ (V-c_\epsilon ) - BG(\eta _\epsilon ) B &{} - (V-c_\epsilon )\partial _x + BG(\eta _\epsilon ) \end{bmatrix} \begin{bmatrix}{\hat{\eta }} \\ {\hat{\psi }} \end{bmatrix}\nonumber \end{aligned}$$

(1.10)

where the functions (V(x), B(x)) are the horizontal and vertical components of the velocity field $(\Phi _x, \Phi _y)$ at the free surface. The real system (1.10) is Hamiltonian and reversible, i.e. of the form $\mathcal {J}{\mathcal {A}}$ with ${\mathcal {A}} = {\mathcal {A}}^\top$, where ${\mathcal {A}}^\top$ is the transposed operator with respect the scalar product of $L^2(\mathbb {T}, \mathbb {R}^2)$, and $\mathcal {J}{\mathcal {A}}$ anti-commutes with the involution $\rho$ in (1.6).

The linear system (1.10) assumes a simpler form by performing the time-independent symplectic and reversibility preserving “good unknown of Alinhac” and “Levi-Civita" conformal change of variables. As proved in [2, 9] there exists a diffeomorphism of $\mathbb {T}$, $x\mapsto x+\mathfrak {p}(x)$, with a small $2\pi$-periodic odd function $\mathfrak {p}(x)$, such that, defining the associated composition operator $(\mathfrak {P}u)(x):= u(x+\mathfrak {p}(x))$, system (1.10) is conjugated under the change of variable

$$\begin{aligned} h = \mathcal {P} Z^{-1} \begin{bmatrix}{\hat{\eta }} \\ {\hat{\psi }} \end{bmatrix} \,, \quad \mathcal {P}:= \begin{bmatrix}(1+\mathfrak {p}_x)\mathfrak {P} &{} 0 \\ 0 &{} \mathfrak {P} \end{bmatrix} \circ \begin{bmatrix} 1 &{} 0 \\ -B &{} 1\end{bmatrix} \,, \end{aligned}$$

(1.11)

into the linear system $h_t = \mathcal {L}_\epsilon h$ where $\mathcal {L}_\epsilon$ is the Hamiltonian and reversible real operator

$$\begin{aligned} \mathcal {L}_\epsilon := \begin{bmatrix} \partial _x \circ ({\texttt{c}}_{\texttt{h}}+p_\epsilon (x)) &{} |D|\tanh ((\texttt{h}+\texttt{f}_\epsilon ) |D|) \\ - (1+a_\epsilon (x)) &{} ({\texttt{c}}_{\texttt{h}}+p_\epsilon (x))\partial _x \end{bmatrix}\nonumber \\ = \mathcal {J}\begin{bmatrix} 1+a_\epsilon (x) &{} -({\texttt{c}}_{\texttt{h}}+p_\epsilon (x)) \partial _x \\ \partial _x \circ ({\texttt{c}}_{\texttt{h}}+p_\epsilon (x)) &{} |D|\tanh ((\texttt{h}+\texttt{f}_\epsilon ) |D|) \end{bmatrix} \end{aligned}$$

(1.12)

where $p_\epsilon (x)$, $a_\epsilon (x)$ are even real functions and $\texttt{f}_\epsilon$ is small real constant. The functions $p_\epsilon$ and $a_\epsilon$ are analytic in $\epsilon$ as maps $B(\epsilon _0)\rightarrow H^{s} ({\mathbb {T}})$ and admit a Taylor expansion as in Proposition A.2. The function $\epsilon \mapsto \texttt{f}_\epsilon$ is analytic as well with a Taylor expansion as in (A.47)–(A.48).

Bloch-Floquet operator. Since the operator $\mathcal {L}_\epsilon$ in (1.12) has $2\pi$-periodic coefficients, Bloch-Floquet theory guarantees that the spectrum

$$\begin{aligned} \sigma _{L^2(\mathbb {R})} (\mathcal {L}_\epsilon ) = \bigcup _{\mu \in [- \frac{1}{2}, \frac{1}{2})} \sigma _{L^2(\mathbb {T})} (\mathcal {L}_{\mu , \epsilon }) \qquad \text {where} \quad \qquad \mathcal {L}_{\mu ,\epsilon }:= e^{- \textrm{i}\,\mu x} \, \mathcal {L}_\epsilon \, e^{\textrm{i}\,\mu x} \,, \end{aligned}$$

and, if $\lambda$ is an eigenvalue of $\mathcal {L}_{\mu ,\epsilon }$ on $L^2(\mathbb {T}, \mathbb {C}^2)$ with eigenvector v(x), then $h (t,x) = e^{\lambda t} e^{\textrm{i}\,\mu x} v(x)$ is a solution of $h_t = \mathcal {L}_{\epsilon } h$.

The Floquet operator associated with the real operator $\mathcal {L}_\epsilon$ in (1.12) turns out to be the complex Hamiltonian and reversible pseudo-differential operator

$$\begin{aligned} \mathcal {L}_{\mu ,\epsilon } :&= \begin{bmatrix} (\partial _x+\textrm{i}\,\mu )\circ ({\texttt{c}}_{\texttt{h}}+p_\epsilon (x)) &{}\quad |D+\mu | \tanh \big ((\texttt{h}+ \texttt{f}_\epsilon ) |D+\mu | \big ) \\ -(1+a_\epsilon (x)) &{}\quad ({\texttt{c}}_{\texttt{h}}+p_\epsilon (x))(\partial _x+\textrm{i}\,\mu ) \end{bmatrix} \\&= \underbrace{\begin{bmatrix} 0 &{} \textrm{Id}\\ -\textrm{Id}&{} 0 \end{bmatrix}}_{\displaystyle {=\mathcal {J}}} \underbrace{\begin{bmatrix} 1+a_\epsilon (x) &{}\quad -({\texttt{c}}_{\texttt{h}}+p_\epsilon (x))(\partial _x+\textrm{i}\,\mu ) \\ (\partial _x+\textrm{i}\,\mu )\circ ({\texttt{c}}_{\texttt{h}}+p_\epsilon (x)) &{}\quad |D+\mu | \tanh \big ((\texttt{h}+ \texttt{f}_\epsilon ) |D+\mu | \big ) \end{bmatrix}}_{\displaystyle {=:\mathcal {B}_{\mu ,\epsilon }}} \, ,\nonumber \end{aligned}$$

(1.13)

meaning that $\mathcal {B}_{\mu ,\epsilon } = \mathcal {B}_{\mu ,\epsilon }^*$ and $\mathcal {L}_{\mu ,\epsilon } \circ {\bar{\rho }}=- {\bar{\rho }}\circ \mathcal {L}_{\mu ,\epsilon }$, where ${\bar{\rho }}$ is the complex involution (cfr. (1.6))

$$\begin{aligned} {\bar{\rho }}\begin{bmatrix}\eta (x) \\ \psi (x) \end{bmatrix}:= \begin{bmatrix}{\bar{\eta }}(-x) \\ -{\bar{\psi }}(-x) \end{bmatrix} \, . \end{aligned}$$

Equivalently the self-adjoint operator $\mathcal {B}_{\mu ,\epsilon }$ is reversibility-preserving, i.e. $\mathcal {B}_{\mu ,\epsilon } \circ {\bar{\rho }}= {\bar{\rho }}\circ \mathcal {B}_{\mu ,\epsilon }$.

We regard $\mathcal {L}_{\mu ,\epsilon }$ as an operator with domain $H^1(\mathbb {T}):= H^1(\mathbb {T},\mathbb {C}^2)$ and range $L^2(\mathbb {T}):=L^2(\mathbb {T},\mathbb {C}^2)$, equipped with the complex scalar product

$$\begin{aligned} (f,g):= \frac{1}{2\pi } \int _{0}^{2\pi } \left( f_1 \bar{g_1} + f_2 \bar{g_2} \right) \, \text {d} x \,, \quad \forall f= \begin{bmatrix}f_1 \\ f_2 \end{bmatrix}, \ \ g= \begin{bmatrix}g_1 \\ g_2 \end{bmatrix} \in L^2(\mathbb {T}, \mathbb {C}^2).\nonumber \\ \end{aligned}$$

(1.14)

We also denote $\Vert f \Vert ^2 = (f,f)$.

In addition $(\mu , \epsilon ) \rightarrow \mathcal {L}_{\mu ,\epsilon } \in \mathcal {L}(H^1(\mathbb {T}), L^2(\mathbb {T}))$ is analytic, since the functions $\epsilon \mapsto a_\epsilon$, $p_\epsilon$ defined in (A.58) are analytic as maps $B(\epsilon _0) \rightarrow H^1(\mathbb {T})$ and ${{\mathcal {L}}}_{\mu ,\epsilon }$ is analytic with respect to $\mu$.

Remark. The spectrum $\sigma ({{\mathcal {L}}}_{-\mu ,\epsilon }) = \overline{ \sigma ({{\mathcal {L}}}_{\mu ,\epsilon }) }$ and we can restrict to $\mu > 0$. Furthermore $\sigma ({{\mathcal {L}}}_{\mu ,\epsilon } )$ is a 1-periodic set with respect to $\mu$, so one can restrict to $\mu \in [0, \frac{1}{2})$.

Dimensional reduction. In view of the Hamiltonian structure of $\mathcal {L}_{\mu ,\epsilon }$, eigenvalues with non zero real part may arise only from multiple eigenvalues of $\mathcal {L}_{\mu ,0}$ because if $\lambda$ is an eigenvalue of $\mathcal {L}_{\mu ,\epsilon }$ then also $-{\bar{\lambda }}$ is, and the total algebraic multiplicity of the eigenvalues is conserved under small perturbation. The Fourier multiplier matrix real operator

$$\begin{aligned} \mathcal {L}_{0,0} = \begin{bmatrix} {\texttt{c}}_{\texttt{h}}\partial _x &{}\quad |D| \, \tanh \big (\texttt{h}|D| \big ) \\ -1 &{}\quad {\texttt{c}}_{\texttt{h}}\partial _x \end{bmatrix} \end{aligned}$$

possesses the eigenvalue 0 with algebraic multiplicity 4, and geometric multiplicity 3. A real basis of the corresponding generalized eigenspace is

$$\begin{aligned} f_1^+:= \begin{bmatrix} {\texttt{c}}_{\texttt{h}}^{1/2} \cos (x) \\ {\texttt{c}}_{\texttt{h}}^{-1/2} \sin (x) \end{bmatrix}, \quad f_1^{-}:= \begin{bmatrix}- {\texttt{c}}_{\texttt{h}}^{1/2} \sin (x) \\ {\texttt{c}}_{\texttt{h}}^{-1/2}\cos (x) \end{bmatrix}, \quad f_0^+:=\begin{bmatrix}1 \\ 0 \end{bmatrix}, \quad f_0^-:=\begin{bmatrix}0 \\ 1 \end{bmatrix},\nonumber \\ \end{aligned}$$

(1.15)

where $f_1^+, f_1^{-}, f_0^-$ are eigenvectors of $\mathcal {L}_{0,0}$ and $f_0^+$ is a generalized eigenvector, namely $\mathcal {L}_{0,0}f_0^+ =-f_0^-$. Furthermore 0 is an isolated eigenvalue for $\mathcal {L}_{0,0}$, namely the spectrum $\sigma \left( \mathcal {L}_{0,0}\right)$ decomposes in two separated parts

$$\begin{aligned} \sigma \left( \mathcal {L}_{0,0}\right) = \sigma '\left( \mathcal {L}_{0,0}\right) \cup \sigma ''\left( \mathcal {L}_{0,0}\right) \quad \text {where} \quad \sigma '(\mathcal {L}_{0,0}):=\{0\} \end{aligned}$$

(1.16)

and $\sigma ''(\mathcal {L}_{0,0})$ is formed by non zero eigenvalues at a positive distance from 0. In this paper we study the spectrum of ${{\mathcal {L}}}_{\mu , \epsilon }$ near 0 (an interesting problem concerns the splitting of the other non zero eigenvalues, see [17]). By Kato’s perturbation theory (see Lemma 2.1 below) for any $\mu , \epsilon \ne 0$ sufficiently small, the perturbed spectrum $\sigma \left( \mathcal {L}_{\mu ,\epsilon }\right)$ admits a disjoint decomposition as $\sigma \left( \mathcal {L}_{\mu ,\epsilon }\right) = \sigma '\left( \mathcal {L}_{\mu ,\epsilon }\right) \cup \sigma ''\left( \mathcal {L}_{\mu ,\epsilon }\right)$ where $\sigma '\left( \mathcal {L}_{\mu ,\epsilon }\right)$ consists of 4 eigenvalues close to 0. We denote by $\mathcal {V}_{\mu , \epsilon }$ the spectral subspace associated with $\sigma '\left( \mathcal {L}_{\mu ,\epsilon }\right)$, which has dimension 4 and it is invariant by $\mathcal {L}_{\mu , \epsilon }: \mathcal {V}_{\mu ,\epsilon } \rightarrow \mathcal {V}_{\mu ,\epsilon }$. The next Theorem 1.3 provides the complete splitting of the eigenvalues of the $4\times 4$ matrix which represents the operator $\mathcal {L}_{\mu ,\epsilon }: \mathcal {V}_{\mu ,\epsilon } \rightarrow \mathcal {V}_{\mu ,\epsilon }$. Before stating it, we first introduce a notation used through all the paper:

Notation: we denote by $\mathcal {O}(\mu ^{m_1}\epsilon ^{n_1},\dots ,\mu ^{m_p}\epsilon ^{n_p})$, $m_j, n_j \in \mathbb {N}$ (for us $\mathbb {N}:=\{1,2,\dots \}$), analytic functions of $(\mu ,\epsilon )$ with values in a Banach space X which satisfy, for some $C > 0$ uniform for $\texttt{h}$ in any compact set of $(0, + \infty )$, the bound $\Vert \mathcal {O}(\mu ^{m_j}\epsilon ^{n_j})\Vert _X \le C \sum _{j = 1}^p |\mu |^{m_j}|\epsilon |^{n_j}$ for small values of $(\mu , \epsilon )$. Similarly we denote $r_k (\mu ^{m_1}\epsilon ^{n_1},\dots ,\mu ^{m_p}\epsilon ^{n_p})$ scalar functions $\mathcal {O}(\mu ^{m_1}\epsilon ^{n_1},\dots ,\mu ^{m_p}\epsilon ^{n_p})$ which are also real analytic.

Our complete spectral result is the following:

Theorem 1.3

(Complete Benjamin–Feir spectrum). There exist $\epsilon _0, \mu _0>0$, uniformly for the depth $\texttt{h}$ in any compact set of $(0,+\infty )$, such that, for any $0\,<\, \mu < \mu _0$ and $0\le \epsilon < \epsilon _0$, the operator $\mathcal {L}_{\mu ,\epsilon }: \mathcal {V}_{\mu ,\epsilon } \rightarrow \mathcal {V}_{\mu ,\epsilon }$ can be represented by a $4\times 4$ matrix of the form

$$\begin{aligned} \begin{pmatrix} \texttt{U} &{} \quad 0 \\ 0 &{}\quad \texttt{S} \end{pmatrix}, \end{aligned}$$

(1.17)

where $\texttt{U}$ and $\texttt{S}$ are $2 \times 2$ matrices, with identical purely imaginary diagonal entries each, of the form

$$\begin{aligned}&\texttt{U} = {\begin{pmatrix} \textrm{i}\,\big (({\texttt{c}}_{\texttt{h}}- \tfrac{1}{2}\texttt{e}_{12})\mu + r_2(\mu \epsilon ^2,\mu ^2\epsilon ,\mu ^3) \big ) &{} -\texttt{e}_{22}\frac{\mu }{8}(1+r_5(\epsilon ,\mu )) \\ -\frac{\mu }{8} \Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h}; \mu , \epsilon ) &{} \textrm{i}\,\big ( ({\texttt{c}}_{\texttt{h}}-\tfrac{1}{2}\texttt{e}_{12})\mu + r_2(\mu \epsilon ^2,\mu ^2\epsilon ,\mu ^3) \big ) \end{pmatrix}}\, , \end{aligned}$$

(1.18)

$$\begin{aligned}&\texttt{S} = \begin{pmatrix} \textrm{i}\,{\texttt{c}}_{\texttt{h}}\mu + \textrm{i}\,{ r_9(\mu \epsilon ^2, \mu ^2\epsilon )} &{} \tanh (\texttt{h}\mu )+ {r_{10}(\mu \epsilon )} \\ -\mu + {r_8(\mu \epsilon ^2, \mu ^3 \epsilon )} &{} \textrm{i}\,{\texttt{c}}_{\texttt{h}}\mu +\textrm{i}\,{r_9(\mu \epsilon ^2,\mu ^2\epsilon ) } \end{pmatrix}\, . \end{aligned}$$

(1.19)

The Benjamin–Feir discriminant function $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};\mu ,\epsilon )$ in (1.18) has the form (1.2), where $\texttt{e}_{\scriptscriptstyle {\textsc {WB}}}(\texttt{h})$ is the Whitham–Benjamin function in (1.3), the coefficient $\texttt{e}_{22} (\texttt{h}) > 0$ is in (3.4c), and

(1.20)

A numerical calculus performed by Mathematica reveals that

$$\begin{aligned} \eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}) \approx 5.65555 > 0 \end{aligned}$$

(1.21)

and we deduce Theorem 1.1 since eigenvalues with nonzero real part appear whenever the Benjamin–Feir discriminant $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};\mu ,\epsilon ) > 0$. In the following corollary of Theorem 1.3 we describe the unstable eigenvalues of ${{\mathcal {L}}}_{\mu ,\epsilon }$ at the critical depth $\texttt{h}= \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$ (for simplicity we avoid to state the result for any $(\texttt{h}, \epsilon )$ satisfying (1.1)).

Theorem 1.4

(Benjamin–Feir unstable eigenvalues at $\texttt{h}= \texttt{h}_{\scriptscriptstyle {\textsc {WB}}}$.). There exist $\epsilon _1, \mu _0 > 0$ and an analytic function ${\underline{\mu }}(\cdot ): [0,\epsilon _1)\rightarrow [0,\mu _0)$ of the form

$$\begin{aligned} {\underline{\mu }}(\epsilon ) = \underline{c} \, \epsilon ^2 \big (1+r(\epsilon )\big ) \,, \quad \underline{c}:= \sqrt{ \frac{8 \eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}})}{\texttt{e}_{22}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}) }} \,, \end{aligned}$$

(1.22)

such that, for any $\epsilon \in [0, \epsilon _1)$, the operator $\mathcal {L}_{\mu ,\epsilon }$ has two eigenvalues $\lambda ^\pm _1 (\mu ,\epsilon )$

$$\begin{aligned} {\left\{ \begin{array}{ll} \textrm{i}\,\frac{1}{2} \breve{\mathtt c}_\texttt{h}\mu +\textrm{i}\,r_2(\mu \epsilon ^2,\mu ^2\epsilon ,\mu ^3) \pm \tfrac{1}{8} \mu \sqrt{\texttt{e}_{22}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}})} (1+r(\epsilon ,\mu )) \sqrt{\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}};\mu ,\epsilon ) } &{} 0<\mu<{\underline{\mu }}(\epsilon )\!\!\! \\ \textrm{i}\,\frac{1}{2} \breve{\mathtt c}_\texttt{h}\mu +\textrm{i}\,r_2(\mu \epsilon ^2,\mu ^2\epsilon ,\mu ^3) \pm \textrm{i}\,\tfrac{1}{8} \mu \sqrt{\texttt{e}_{22}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}})} (1+r(\epsilon ,\mu )) \sqrt{|\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}};\mu ,\epsilon )|} &{} {\underline{\mu }}(\epsilon )\le \mu < \mu _0\,,\!\!\! \end{array}\right. }\!\!\!\nonumber \\ \end{aligned}$$

(1.23)

with $\breve{\mathtt c}_\texttt{h}:=2 {\texttt{c}}_{\texttt{h}}- \texttt{e}_{12}(\texttt{h}) >0$ and $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}};\mu ,\epsilon ) = 8\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}) \epsilon ^4 + r_1(\epsilon ^5,\mu \epsilon ^3)-\texttt{e}_{22} (\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}) \mu ^2\big (1+r_1''(\epsilon ,\mu )\big )$.

Proof of Theorem 1.4

Since $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}};0,\epsilon ) = 8\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}) \epsilon ^4 (1+r(\epsilon ))$, it results that $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}};\mu ,\epsilon ) > 0$, for any $\mu \in (0, {\underline{\mu }}(\epsilon ))$ as in (1.22) and $\epsilon$ small enough. The unstable eigenvalues $\lambda ^\pm _1 (\mu ,\epsilon )$ in (1.22) are those of the matrix $\texttt{U}$ in (1.18). In order to determine the value $\mu = {\underline{\mu }}(\epsilon )$ such that $\lambda ^\pm _1 (\mu ,\epsilon )$ touches the imaginary axis far from the origin, we set $\mu = c \epsilon ^2$ so that $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}};\mu ,\epsilon ) = 0$ if and only if

$$\begin{aligned} 0 = \epsilon ^{-4} \Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}};c \epsilon ^2,\epsilon ) = 8\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}) (1+r(\epsilon ))+ r_1(c \epsilon )-\texttt{e}_{22} (\texttt{h}_{\scriptscriptstyle {\textsc {WB}}}) c^2 \big (1+r_1(\epsilon )\big ) \, . \end{aligned}$$

This equation is solved by an analytic function $\epsilon \mapsto c_\epsilon = \underline{c} (1+r(\epsilon ))$ with $\underline{c}$ defined in (1.22). $\square$

We conclude this section describing the main steps of the proof and the organization of the paper.

Ideas and scheme of proof. In Sect. 2 we shortly report the results of [9] which reduce the problem to determine the eigenvalues of the $4 \times 4$ Hamiltonian and reversible matrix $\texttt{L}_{\mu ,\epsilon } =\texttt{J}\texttt{B}_{\mu ,\epsilon }$ in (2.8). Then in Sect. 3 we provide the Taylor expansion of the matrix $\texttt{B}_{\mu ,\epsilon }$ in (2.9) at an order of accuracy higher than in [9, Proposition 4.3]. In particular in Proposition 3.1 we compute the coefficients of the Taylor expansion up to order 4 in the matrix entries (3.3a)–(3.3c) which enter in the constant $\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h})$ (cfr. (4.9)) appearing in the Benjamin–Feir discriminant function (1.2). This explicit computation requires the knowledge of the Taylor expansions of the Kato spectral projectors $P_{\mu , \epsilon }$ up to cubic order, that we provide in Sect. 3.2 and prove in Appendix B, relying on complex analysis. In order to perform effective computations we observe several analytical cancellations in Sects. 3.3 and 3.4, which reduce considerably the number of explicit scalar products to compute. The proof of Proposition 3.1 requires ultimately the knowledge of the Taylor expansion up to order four of the Levi-Civita and Alinach good unknown transformations (1.11) and of the functions $a_\epsilon (x), p_\epsilon (x)$ in the operator ${{\mathcal {L}}}_{\mu ,\epsilon }$ in (1.13), which are derived in Appendix A.2. In turn, such expansions follow by those of the Stokes waves that we prove in Appendix A.1. Finally in Sect. 4 we implement the block-diagonalization procedure of [9, Sect. 5] which provides the block-diagonal matrix (1.18) and we analytically compute the expansion of the Benjamin–Feir discriminant function $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};\mu ,\epsilon )$, in particular of the constant $\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h})$ in (4.9) and thus (1.20).

We point out that the constant $\eta _{\scriptscriptstyle {\textsc {WB}}}$ in (4.9) is analytically computed in terms of the coefficients (4.4) which, in turn, are expressed in terms of the coefficients $\phi _{21}, \phi _{22}, \gamma _{12}, \eta _{12}, \gamma _{11}, \phi _{11}, \gamma _{22}, \phi _{12}, \texttt{f}_{11}$, and ultimately $\eta _{2}^{[0]}, \ldots , \eta _{4}^{[4]}, \psi _{2}^{[2]}, \dots , \psi _{4}^{[4]}$, $c_2, c_4$ of the Stokes wave provided in Appendix A.1. Then we used Mathematica to compute how the coefficients of the Stokes wave, of the functions $a_\epsilon (x)$, $p_\epsilon (x)$ in (1.13), and $\eta _{\scriptscriptstyle {\textsc {WB}}}(\texttt{h})$ in (1.20) depend on $\texttt{h}$, starting from their algebraic formulas. The Mathematica code employed can be found at https://git-scm.sissa.it/amaspero/benjamin-feir-instability.

2 Perturbative Approach to Separated Eigenvalues

In this section we shortly report the spectral procedure developed in [7, 9] to study the splitting of the eigenvalues of $\mathcal {L}_{\mu ,\epsilon }$ close to 0 for small values of $\mu$ and $\epsilon$. First of all we decompose the operator $\mathcal {L}_{\mu ,\epsilon }$ in (1.13) as

$$\begin{aligned} \mathcal {L}_{\mu ,\epsilon } = \textrm{i}\,{\texttt{c}}_{\texttt{h}}\mu + \mathscr {L}_{\mu ,\epsilon } \,, \qquad \mu > 0 \,, \end{aligned}$$

(2.1)

where $\mathscr {L}_{\mu ,\epsilon }$ is the Hamiltonian and reversible operator

$$\begin{aligned} \mathscr {L}_{\mu ,\epsilon }= & {} \mathcal {J}\, {{\mathcal {B}}}_{\mu , \epsilon } \,, \quad \nonumber \\ {{\mathcal {B}}}_{\mu , \epsilon }:= & {} \begin{bmatrix} 1+a_\epsilon (x) &{}\quad -({\texttt{c}}_{\texttt{h}}+p_\epsilon (x))\partial _x-\textrm{i}\,\mu \, p_\epsilon (x) \\ \partial _x\circ ({\texttt{c}}_{\texttt{h}}+p_\epsilon (x)) + \textrm{i}\,\mu \, p_\epsilon (x) &{}\quad |D+ \mu | \, \tanh \big ((\texttt{h}+\texttt{f}_\epsilon )|D+\mu |\big ) \end{bmatrix} \end{aligned}$$

(2.2)

with ${{\mathcal {B}}}_{\mu , \epsilon }$ selfadjoint. The operator $\mathscr {L}_{\mu ,\epsilon }$ is analytic with respect to $(\mu , \epsilon )$ as $\mathcal {L}_{\mu ,\epsilon }$ is. The operator $\mathscr {L}_{\mu ,\epsilon }: Y \subset X \rightarrow X$ has domain $Y:=H^1(\mathbb {T}):=H^1(\mathbb {T},\mathbb {C}^2)$ and range $X:=L^2(\mathbb {T}):=L^2(\mathbb {T},\mathbb {C}^2)$.

In view of (2.1), the spectrum

$$\begin{aligned} \sigma ({{\mathcal {L}}}_{\mu ,\epsilon }) = \textrm{i}\,{\texttt{c}}_{\texttt{h}}\mu + \sigma (\mathscr {L}_{\mu ,\epsilon }) \end{aligned}$$

and we focus on studying the spectrum of $\mathscr {L}_{\mu ,\epsilon }$. The unperturbed $\mathscr {L}_{0,0} = \mathcal {L}_{0,0}$ has zero as isolated eigenvalue with algebraic multiplicity 4, geometric multiplicity 3 and generalized kernel spanned by the vectors $\{f^+_1, f^-_1, f^+_0, f^-_0\}$ in (1.15). The following lemma is [9, Lemmata 3.1 and 3.2].

Lemma 2.1

(Kato theory for separated eigenvalues of Hamiltonian operators). Let $\Gamma$ be a closed, counterclockwise-oriented curve around 0 in the complex plane separating $\sigma '\left( \mathscr {L}_{0,0}\right) =\{0\}$ and the other part of the spectrum $\sigma ''\left( \mathscr {L}_{0,0}\right)$ in (1.16). There exist $\epsilon _0, \mu _0>0$ such that for any $(\mu , \epsilon ) \in B(\mu _0)\times B(\epsilon _0)$ the following statements hold:

1. The curve $\Gamma$ belongs to the resolvent set of the operator $\mathscr {L}_{\mu ,\epsilon }: Y \subset X \rightarrow X$ defined in (2.2).

2. The operators

$$\begin{aligned} P_{\mu ,\epsilon }:= -\frac{1}{2\pi \textrm{i}\,}\oint _\Gamma (\mathscr {L}_{\mu ,\epsilon }-\lambda )^{-1} \textrm{d}\lambda : X \rightarrow Y \end{aligned}$$

(2.3)

are well defined projectors commuting with $\mathscr {L}_{\mu ,\epsilon }$, i.e. $P_{\mu ,\epsilon }^2 = P_{\mu ,\epsilon }$ and $P_{\mu ,\epsilon }\mathscr {L}_{\mu ,\epsilon } = \mathscr {L}_{\mu ,\epsilon } P_{\mu ,\epsilon }$. The map $(\mu , \epsilon )\mapsto P_{\mu ,\epsilon }$ is analytic from $B({\mu _0})\times B({\epsilon _0})$ to $\mathcal {L}(X, Y)$. The projectors $P_{\mu ,\epsilon }$ are skew-Hamiltonian and reversibility preserving, i.e.

$$\begin{aligned} \mathcal {J}P_{\mu ,\epsilon }=P_{\mu ,\epsilon }^*\mathcal {J}\,, \quad {\bar{\rho }}P_{\mu ,\epsilon } = P_{\mu ,\epsilon } {\bar{\rho }}\, . \end{aligned}$$

(2.4)

Finally $P_{0,\epsilon }$ is a real operator, i.e. $\bar{P_{0,\epsilon }}=P_{0,\epsilon }$.

3. The domain Y of the operator $\mathscr {L}_{\mu ,\epsilon }$ decomposes as the direct sum

$$\begin{aligned} Y= \mathcal {V}_{\mu ,\epsilon } \oplus \text {Ker}(P_{\mu ,\epsilon }) \,, \quad \mathcal {V}_{\mu ,\epsilon }:=\text {Rg}(P_{\mu ,\epsilon })=\text {Ker}(\textrm{Id}-P_{\mu ,\epsilon }) \,, \end{aligned}$$

of closed invariant subspaces, namely $\mathscr {L}_{\mu ,\epsilon }: \mathcal {V}_{\mu ,\epsilon } \rightarrow \mathcal {V}_{\mu ,\epsilon }$, $\mathscr {L}_{\mu ,\epsilon }: \text {Ker}(P_{\mu ,\epsilon }) \rightarrow \text {Ker}(P_{\mu ,\epsilon })$. Moreover

$$\begin{aligned} \begin{aligned}&\sigma (\mathscr {L}_{\mu ,\epsilon })\cap \{ z \in \mathbb {C} \text{ inside } \Gamma \} = \sigma (\mathscr {L}_{\mu ,\epsilon }\vert _{{{\mathcal {V}}}_{\mu ,\epsilon }} ) = \sigma '(\mathscr {L}_{\mu , \epsilon }), \\&\sigma (\mathscr {L}_{\mu ,\epsilon })\cap \{ z \in \mathbb {C} \text{ outside } \Gamma \} = \sigma (\mathscr {L}_{\mu ,\epsilon }\vert _{Ker(P_{\mu ,\epsilon })} ) = \sigma ''( \mathscr {L}_{\mu , \epsilon }) \, . \end{aligned} \end{aligned}$$

4. The projectors $P_{\mu ,\epsilon }$ are similar one to each other: the transformation operators

$$\begin{aligned} U_{\mu ,\epsilon }:= \big ( \textrm{Id}-(P_{\mu ,\epsilon }-P_{0,0})^2 \big )^{-1/2} \big [ P_{\mu ,\epsilon }P_{0,0} + (\textrm{Id}- P_{\mu ,\epsilon })(\textrm{Id}-P_{0,0}) \big ] \end{aligned}$$

(2.5)

are bounded and invertible in Y and in X, with inverse

$$\begin{aligned} U_{\mu ,\epsilon }^{-1} = \big [ P_{0,0} P_{\mu ,\epsilon }+(\textrm{Id}-P_{0,0}) (\textrm{Id}- P_{\mu ,\epsilon }) \big ] \big ( \textrm{Id}-(P_{\mu ,\epsilon }-P_{0,0})^2 \big )^{-1/2} \,, \end{aligned}$$

and $U_{\mu ,\epsilon } P_{0,0}U_{\mu ,\epsilon }^{-1} = P_{\mu ,\epsilon }$ as well as $U_{\mu ,\epsilon }^{-1} P_{\mu ,\epsilon } U_{\mu ,\epsilon } = P_{0,0}$. The map $(\mu , \epsilon )\mapsto U_{\mu ,\epsilon }$ is analytic from $B(\mu _0)\times B(\epsilon _0)$ to $\mathcal {L}(Y)$. The transformation operators $U_{\mu ,\epsilon }$ are symplectic and reversibility preserving, namely

$$\begin{aligned} U_{\mu ,\epsilon }^* \mathcal {J}U_{\mu ,\epsilon }= \mathcal {J}\,, \qquad {\bar{\rho }}U_{\mu ,\epsilon } = U_{\mu ,\epsilon } {\bar{\rho }}\, . \end{aligned}$$

(2.6)

Finally $U_{0,\epsilon }$ is a real operator, i.e. $\bar{U_{0,\epsilon }}=U_{0,\epsilon }$.

5. The subspaces $\mathcal {V}_{\mu ,\epsilon }=\text {Rg}(P_{\mu ,\epsilon })$ are isomorphic one to each other: $\mathcal {V}_{\mu ,\epsilon }= U_{\mu ,\epsilon }\mathcal {V}_{0,0}.$ In particular $\dim \mathcal {V}_{\mu ,\epsilon } = \dim \mathcal {V}_{0,0}=4$, for any $(\mu , \epsilon ) \in B(\mu _0)\times B(\epsilon _0)$.

We consider the basis of the subspace ${{\mathcal {V}}}_{\mu ,\epsilon } = \textrm{Rg} (P_{\mu ,\epsilon })$,

$$\begin{aligned} \mathcal {F}:= & {} \big \{ f_{1}^+(\mu ,\epsilon ), \ f_{1}^- (\mu ,\epsilon ), \ f_{0}^+(\mu ,\epsilon ),\ f_{0}^-(\mu ,\epsilon ) \big \} \,, \quad \nonumber \\ f_{k}^\sigma (\mu ,\epsilon ):= & {} U_{\mu ,\epsilon } f_{k}^\sigma \,, \ \sigma =\pm \,, \,k=0,1 \,, \end{aligned}$$

(2.7)

obtained by applying the transformation operators $U_{\mu ,\epsilon }$ in (2.5) to the eigenvectors $f_1^+, f_1^-, f_0^+, f_0^-$ in (1.15) which form a basis of $\mathcal {V}_{0,0} =\textrm{Rg} (P_{0,0})$. Exploiting the property (2.6) that the transformation operators $U_{\mu ,\epsilon }$ are symplectic and reversibility preserving, it is proved in [9, Sect. 3] the following lemma.

Lemma 2.2

(Matrix representation of ${{\mathcal {L}}}_{\mu ,\epsilon }$ on $\mathcal {V}_{\mu ,\epsilon }$). The operator $\mathscr {L}_{\mu ,\epsilon }: \mathcal {V}_{\mu ,\epsilon }\rightarrow \mathcal {V}_{\mu ,\epsilon }$ in (2.2) defined for $(\mu , \epsilon ) \in B_{\mu _0}(0)\times B_{\epsilon _0}(0)$ is represented on the basis $\mathcal {F}$ in (2.7) by the $4\times 4$ Hamiltonian and reversible matrix

(2.8)

and is the $4 \times 4$ self-adjoint matrix

$$\begin{aligned} \begin{aligned} \texttt{B}_{\mu ,\epsilon }&:= \begin{pmatrix} \big (\mathfrak {B}_{\mu ,\epsilon } f_1^+, f_1^+ \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_1^-, f_1^+ \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^+, f_1^+ \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^-, f_1^+ \big ) \\ \big (\mathfrak {B}_{\mu ,\epsilon } f_1^+, f_1^- \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_1^-, f_1^- \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^+, f_1^- \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^-, f_1^- \big ) \\ \big (\mathfrak {B}_{\mu ,\epsilon } f_1^+, f_0^+ \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_1^-, f_0^+ \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^+, f_0^+ \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^-, f_0^+ \big ) \\ \big (\mathfrak {B}_{\mu ,\epsilon } f_1^+, f_0^- \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_1^-, f_0^- \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^+, f_0^- \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^-, f_0^- \big ) \\ \end{pmatrix} \end{aligned} \end{aligned}$$

(2.9)

where

$$\begin{aligned} \mathfrak {B}_{\mu ,\epsilon }:= P_{0,0}^* \, U_{\mu ,\epsilon }^* \, {{\mathcal {B}}}_{\mu ,\epsilon } \, U_{\mu ,\epsilon } \, P_{0,0} \, . \end{aligned}$$

(2.10)

The entries of the matrix $\texttt{B}_{\mu ,\epsilon }$ are alternatively real or purely imaginary: for any $\sigma = \pm$, $k = 0, 1$, the scalar product $\left( \mathfrak {B}_{\mu ,\epsilon } \, f^{\sigma }_{k}\,,\,f^{\sigma }_{k'}\right)$ is real and $\left( \mathfrak {B}_{\mu ,\epsilon } \, f^{\sigma }_{k}\,,\,f^{-\sigma }_{k'}\right)$ is purely imaginary. The matrix $\texttt{B}_{\mu ,\epsilon }$ is analytic in $(\mu ,\epsilon )$ close to (0, 0) .

We conclude this section recalling some notation. A $2n \times 2n$, $n = 1,2,$ matrix of the form $\texttt{L}=\texttt{J}_{2n} \texttt{B}$ is Hamiltonian if $\texttt{B}$ is a self-adjoint matrix, i.e. $\texttt{B}=\texttt{B}^*$. It is reversible if $\texttt{B}$ is reversibility-preserving, i.e. $\rho _{2n}\circ \texttt{B}= \texttt{B}\circ \rho _{2n}$, where $\rho _4:= \begin{pmatrix}\rho _2 &{} 0 \\ 0 &{} \rho _2\end{pmatrix}$, $\rho _2:= \begin{pmatrix} \mathfrak {c} &{} 0 \\ 0 &{} - \mathfrak {c} \end{pmatrix}$ and $\mathfrak {c}: z \mapsto {\bar{z}}$ is the conjugation of the complex plane. Equivalently, $\rho _{2n} \circ \texttt{L}= - \texttt{L}\circ \rho _{2n}$.

The transformations preserving the Hamiltonian structure are called symplectic, and satisfy $Y^* \texttt{J}_4 Y = \texttt{J}_4$. If Y is symplectic then $Y^*$ and $Y^{-1}$ are symplectic as well. A Hamiltonian matrix $\texttt{L}=\texttt{J}_4 \texttt{B}$, with $\texttt{B}=\texttt{B}^*$, is conjugated through a symplectic matrix Y in a new Hamiltonian matrix. We finally mention that the flow of a Hamiltonian reversibility-preserving matrix is symplectic and reversibility-preserving (see Lemma 3.8 in [7]).

3 Expansion of $\texttt{B}_{\mu ,\epsilon }$

In this section we provide the Taylor expansion of the matrix $\texttt{B}_{\mu ,\epsilon }$ in (2.9), i.e. (3.1), at an order of accuracy higher than in [9, Proposition 4.3]. In particular we compute the quadratic terms $\gamma _{11} \epsilon ^2$, $\phi _{21} \mu \epsilon$, the cubic ones $\eta _{12}\mu \epsilon ^2$, $\gamma _{12}\mu \epsilon ^2$,$\phi _{11} \epsilon ^3$, $\phi _{22} \mu ^2 \epsilon$, and the quartic terms $\eta _{11} \epsilon ^4$, $\gamma _{22} \mu ^2 \epsilon ^2$, $\phi _{12} \mu \epsilon ^3$ in the matrices (3.3a)–(3.3c) below. These are the coefficients which enter in the constant $\eta _{\scriptscriptstyle {\textsc {WB}}}$ (cfr. (4.9)) of the Benjamin–Feir discriminant function (1.2).

For convenience we decompose the $4 \times 4$ matrix $\texttt{B}_{\mu ,\epsilon }$ in (2.9) as

$$\begin{aligned} \begin{aligned} \texttt{B}_{\mu ,\epsilon }&= \begin{pmatrix} E(\mu ,\epsilon ) &{} F(\mu ,\epsilon ) \\ F^*(\mu ,\epsilon ) &{} G(\mu ,\epsilon ) \end{pmatrix} \end{aligned} \end{aligned}$$

(3.1)

where E, G are the $2 \times 2$ self-adjoint matrices

$$\begin{aligned}&E(\mu ,\epsilon ) :=\begin{pmatrix} E_{11}(\mu ,\epsilon ) &{} \textrm{i}\,E_{12}(\mu ,\epsilon ) \\ -\textrm{i}\,E_{12}(\mu ,\epsilon ) &{} E_{22}(\mu ,\epsilon ) \end{pmatrix} := \begin{pmatrix} \big (\mathfrak {B}_{\mu ,\epsilon } f_1^+, f_1^+ \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_1^-, f_1^+ \big ) \\ \big (\mathfrak {B}_{\mu ,\epsilon } f_1^+, f_1^- \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_1^-, f_1^- \big ) \end{pmatrix} \, , \end{aligned}$$

(3.2a)

$$\begin{aligned}&G(\mu ,\epsilon ) :=\begin{pmatrix} G_{11}(\mu ,\epsilon ) &{} \textrm{i}\,G_{12}(\mu ,\epsilon ) \\ -\textrm{i}\,G_{12}(\mu ,\epsilon ) &{} G_{22}(\mu ,\epsilon ) \end{pmatrix}:= \begin{pmatrix} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^+, f_0^+ \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^-, f_0^+ \big ) \\ \big (\mathfrak {B}_{\mu ,\epsilon } f_0^+, f_0^- \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^-, f_0^- \big ) \end{pmatrix} \, , \end{aligned}$$

(3.2b)

and

$$\begin{aligned}&F(\mu ,\epsilon ):=\begin{pmatrix} F_{11}(\mu ,\epsilon ) &{} \textrm{i}\,F_{12}(\mu ,\epsilon ) \\ \textrm{i}\,F_{21}(\mu ,\epsilon ) &{} F_{22}(\mu ,\epsilon ) \end{pmatrix}:= \begin{pmatrix} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^+, f_1^+ \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^-, f_1^+ \big ) \\ \big (\mathfrak {B}_{\mu ,\epsilon } f_0^+, f_1^- \big ) &{} \big (\mathfrak {B}_{\mu ,\epsilon } f_0^-, f_1^- \big ) \end{pmatrix} \, . \end{aligned}$$

(3.2c)

The main result of this section is the following proposition.

Proposition 3.1

The $2 \times 2$ matrices $E:=E(\mu ,\epsilon )$, $F:=F(\mu ,\epsilon )$, $G:=G(\mu ,\epsilon )$ defined in (3.2) admit the expansion

$$\begin{aligned}&E = \begin{pmatrix} \texttt{e}_{11} \epsilon ^2(1+ r_1'(\epsilon ^3,\mu \epsilon )) + \eta _{11} \epsilon ^4 - \texttt{e}_{22}\frac{\mu ^2}{8}(1+r_1''(\epsilon ,\mu )) &{} \quad \textrm{i}\,\big ( \frac{1}{2}\texttt{e}_{12}\mu {+\eta _{12}\mu \epsilon ^2}+ r_2 (\mu \epsilon ^3,\mu ^2\epsilon ,\mu ^3) \big ) \\ - \textrm{i}\,\big ( \frac{1}{2}\texttt{e}_{12} \mu {+\eta _{12}\mu \epsilon ^2}+ r_2(\mu \epsilon ^3,\mu ^2\epsilon ,\mu ^3) \big ) &{}\quad -\texttt{e}_{22}\frac{\mu ^2}{8}(1+r_5(\epsilon ^{{2}},\mu )) \end{pmatrix} \end{aligned}$$

(3.3a)

$$\begin{aligned}&G = \begin{pmatrix} 1 {+\gamma _{11} \epsilon ^2}+r_8(\epsilon ^3, \mu \epsilon ^2,\mu ^2\epsilon ) &{} {-\textrm{i}\,\gamma _{12} \mu \epsilon ^2} - \textrm{i}\,r_9(\mu \epsilon ^3,\mu ^2\epsilon ) \\ {\textrm{i}\,\gamma _{12} \mu \epsilon ^2}+ \textrm{i}\,r_9(\mu \epsilon ^3, \mu ^2\epsilon ) &{}\quad \mu \tanh (\texttt{h}\mu ) {+\gamma _{22} \mu ^2\epsilon ^2} +r_{10}(\mu ^2\epsilon ^3,\mu ^3\epsilon ) \end{pmatrix} \end{aligned}$$

(3.3b)

$$\begin{aligned}&F = \begin{pmatrix} \texttt{f}_{11}\epsilon {+\phi _{11} \epsilon ^3}+ r_3(\epsilon ^4,\mu \epsilon ^2,\mu ^2\epsilon ) &{}\quad \textrm{i}\,\mu \epsilon {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} {+\textrm{i}\,\phi _{12} \mu \epsilon ^3} +\textrm{i}\,r_4({\mu \epsilon ^{4}}, \mu ^2 \epsilon ^2, \mu ^3\epsilon ) \\ \textrm{i}\,{\phi _{21}\mu \epsilon }+ \textrm{i}\,r_6(\mu \epsilon ^{{3}}, \mu ^2\epsilon ) &{}\quad {\phi _{22}\mu ^2\epsilon }+ r_7(\mu ^2\epsilon ^{{3}}, \mu ^3\epsilon ) \end{pmatrix} \, , \end{aligned}$$

(3.3c)

where the coefficients

$$\begin{aligned}&\texttt{e}_{11} := \dfrac{9{\texttt{c}}_{\texttt{h}}^8-10{\texttt{c}}_{\texttt{h}}^4+9}{8{\texttt{c}}_{\texttt{h}}^7} = \dfrac{9 (1-{\texttt{c}}_{\texttt{h}}^4)^2 +8 {\texttt{c}}_{\texttt{h}}^4 }{8{\texttt{c}}_{\texttt{h}}^7} > 0 \, , \qquad \texttt{f}_{11} := \tfrac{1}{2} {\texttt{c}}_{\texttt{h}}^{-\frac{3}{2}}(1-{\texttt{c}}_{\texttt{h}}^4) \, , \end{aligned}$$

(3.4a)

$$\begin{aligned}&\texttt{e}_{12}:= {\texttt{c}}_{\texttt{h}}+{\texttt{c}}_{\texttt{h}}^{-1}(1-{\texttt{c}}_{\texttt{h}}^4)\texttt{h}> 0 \, , \end{aligned}$$

(3.4b)

$$\begin{aligned}&\texttt{e}_{22}:= \dfrac{(1-{\texttt{c}}_{\texttt{h}}^4)(1+3{\texttt{c}}_{\texttt{h}}^4) \texttt{h}^2+2 {\texttt{c}}_{\texttt{h}}^2({\texttt{c}}_{\texttt{h}}^4-1) \texttt{h}+{\texttt{c}}_{\texttt{h}}^4}{{\texttt{c}}_{\texttt{h}}^3} > 0 \, , \end{aligned}$$

(3.4c)

were computed in [9, Proposition 4.3], whereas

$$\begin{aligned}&\eta _{11} :=\frac{1}{256 {\texttt{c}}_{\texttt{h}}^{19} ({\texttt{c}}_{\texttt{h}}^2+1)}\big (-36 {\texttt{c}}_{\texttt{h}}^{26}-108 {\texttt{c}}_{\texttt{h}}^{24}-261 {\texttt{c}}_{\texttt{h}}^{22}-73 {\texttt{c}}_{\texttt{h}}^{20}+1429 {\texttt{c}}_{\texttt{h}}^{18}+1237 {\texttt{c}}_{\texttt{h}}^{16} \end{aligned}$$

(3.4d)

$$\begin{aligned}&~~~~ -3666 {\texttt{c}}_{\texttt{h}}^{14}-3450 {\texttt{c}}_{\texttt{h}}^{12}+3774 {\texttt{c}}_{\texttt{h}}^{10}+3654 {\texttt{c}}_{\texttt{h}}^8-873 {\texttt{c}}_{\texttt{h}}^6-765 {\texttt{c}}_{\texttt{h}}^4+81 {\texttt{c}}_{\texttt{h}}^2+81\big )\, , \nonumber \\&\eta _{12}:= \frac{{\texttt{c}}_{\texttt{h}}^2 \big (3 {\texttt{c}}_{\texttt{h}}^{12}-8 {\texttt{c}}_{\texttt{h}}^8+3 {\texttt{c}}_{\texttt{h}}^4+18\big )-\big ({\texttt{c}}_{\texttt{h}}^{16}-2 {\texttt{c}}_{\texttt{h}}^{12}+12 {\texttt{c}}_{\texttt{h}}^8-38 {\texttt{c}}_{\texttt{h}}^4+27\big ) \texttt{h}}{16 {\texttt{c}}_{\texttt{h}}^9} \, , \end{aligned}$$

(3.4e)

$$\begin{aligned}&\gamma _{11} := \frac{-{\texttt{c}}_{\texttt{h}}^8+6 {\texttt{c}}_{\texttt{h}}^4-5}{8 {\texttt{c}}_{\texttt{h}}^4} \, , \quad \gamma _{12} := \frac{2 {\texttt{c}}_{\texttt{h}}^{12}-{\texttt{c}}_{\texttt{h}}^8-9}{16 {\texttt{c}}_{\texttt{h}}^7}\, , \quad \gamma _{22} := \frac{{\texttt{c}}_{\texttt{h}}^4-5}{4 {\texttt{c}}_{\texttt{h}}^2} \, , \end{aligned}$$

(3.4f)

$$\begin{aligned}&\phi _{11} :=\frac{10 {\texttt{c}}_{\texttt{h}}^{20}+4 {\texttt{c}}_{\texttt{h}}^{18}-7 {\texttt{c}}_{\texttt{h}}^{16}-6 {\texttt{c}}_{\texttt{h}}^{14}-99 {\texttt{c}}_{\texttt{h}}^{12}+257 {\texttt{c}}_{\texttt{h}}^8-6 {\texttt{c}}_{\texttt{h}}^6-171 {\texttt{c}}_{\texttt{h}}^4+18}{64 {\texttt{c}}_{\texttt{h}}^{27/2}} \, , \end{aligned}$$

(3.4g)

$$\begin{aligned}&\phi _{12}:= \frac{2 {\texttt{c}}_{\texttt{h}}^{18}-2 {\texttt{c}}_{\texttt{h}}^{16}-33 {\texttt{c}}_{\texttt{h}}^{14}-27 {\texttt{c}}_{\texttt{h}}^{12}+34 {\texttt{c}}_{\texttt{h}}^{10}+34 {\texttt{c}}_{\texttt{h}}^8-33 {\texttt{c}}_{\texttt{h}}^6-27 {\texttt{c}}_{\texttt{h}}^4+18 {\texttt{c}}_{\texttt{h}}^2+18}{32 {\texttt{c}}_{\texttt{h}}^{25/2} ({\texttt{c}}_{\texttt{h}}^2+1)} \end{aligned}$$

(3.4h)

$$\begin{aligned}&\phi _{21} :=\frac{{\texttt{c}}_{\texttt{h}}^2 ({\texttt{c}}_{\texttt{h}}^4-5)-({\texttt{c}}_{\texttt{h}}^8+2 {\texttt{c}}_{\texttt{h}}^4-3) \texttt{h}}{8 {\texttt{c}}_{\texttt{h}}^{7/2}} \, , \quad \phi _{22}:= \frac{-{\texttt{c}}_{\texttt{h}}^4 \texttt{h}+{\texttt{c}}_{\texttt{h}}^2+\texttt{h}}{4 {\texttt{c}}_{\texttt{h}}^{5/2}}\, . \end{aligned}$$

(3.4i)

The rest of the section is devoted to the proof of this proposition.

In [9, Proposition 4.3] we showed that the matrices E, G, F in (3.3a), (3.3b), (3.3c) admit the following expansions

$$\begin{aligned}&E(\mu ,\epsilon )= \begin{pmatrix} \texttt{e}_{11} \epsilon ^2 - \texttt{e}_{22}\frac{\mu ^2}{8} &{}\quad \textrm{i}\,\frac{1}{2}\texttt{e}_{12}\mu \\ - \textrm{i}\,\frac{1}{2}\texttt{e}_{12} \mu &{}\quad -\texttt{e}_{22}\frac{\mu ^2}{8} \end{pmatrix} + \underbrace{ \begin{pmatrix} r_1(\epsilon ^3, \mu ^2 \epsilon ,\mu ^3) &{} \textrm{i}\,r_2(\mu \epsilon ^2,\mu ^2\epsilon ,\mu ^3) \\ - \textrm{i}\,r_2(\mu \epsilon ^2,\mu ^2\epsilon ,\mu ^3) &{} r_5(\mu ^2\epsilon ,\mu ^3) \end{pmatrix}}_{=:{{\mathcal {E}}}(\mu ,\epsilon )}\, , \end{aligned}$$

(3.5a)

$$\begin{aligned}&G(\mu ,\epsilon ) = \begin{pmatrix} 1 &{} \quad 0 \\ 0 &{}\quad \mu \tanh (\texttt{h}\mu ) \end{pmatrix} + \underbrace{ \begin{pmatrix} r_8(\epsilon ^2,\mu ^2\epsilon ) &{} - \textrm{i}\,r_9(\mu \epsilon ^2,\mu ^2\epsilon ) \\ \textrm{i}\,r_9(\mu \epsilon ^2, \mu ^2\epsilon ) &{}r_{10}(\mu ^2\epsilon ) \, , \end{pmatrix}}_{=:\Gamma (\mu ,\epsilon )} \end{aligned}$$

(3.5b)

$$\begin{aligned}&F(\mu ,\epsilon ) := \begin{pmatrix} \texttt{f}_{11}\epsilon &{}\quad \textrm{i}\,\mu \epsilon {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \\ 0 &{}\quad 0 \end{pmatrix} + \underbrace{\begin{pmatrix} r_3(\epsilon ^3,\mu \epsilon ^2,\mu ^2\epsilon ) &{}\textrm{i}\,r_4({\mu \epsilon ^2}, \mu ^2 \epsilon ) \\ \textrm{i}\,r_6(\mu \epsilon ) &{} r_7(\mu ^2\epsilon ) \end{pmatrix}}_{=: \Phi (\mu ,\epsilon )} \, . \end{aligned}$$

(3.5c)

In order to get the expansion of ${{\mathcal {E}}}(\mu ,\epsilon )$, $\Gamma (\mu ,\epsilon )$ and $\Phi (\mu ,\epsilon )$ in Proposition 3.1 we first expand the operators ${{\mathcal {B}}}_{\mu ,\epsilon }$ in (2.2) (Sect. 3.1), the projector $P_{\mu ,\epsilon }$ in (2.3) (Sect. 3.2) and the operator $\mathfrak {B}_{\mu ,\epsilon }$ in (2.10) (Sect. 3.3). Finally we prove Proposition 3.1 in Sect. 3.4.

Notation. For an operator $A=A(\mu ,\epsilon )$ we denote its Taylor coefficients as

$$\begin{aligned} A_{i,j}:= \frac{1}{i!j!} \big (\partial ^i_\mu \partial ^j_\epsilon A \big )(0,0)\,,\qquad A_k:= A_k (\mu ,\epsilon ):= \sum _{\begin{array}{c} i+j=k\\ i,j\ge 0 \end{array}} A_{i,j} \mu ^i \epsilon ^j\, . \end{aligned}$$

(3.6)

Moreover we shall occasionally split $A_{i,j}=A_{i,j}^{[\texttt{ ev}]} + A_{i,j}^{[\texttt{odd}]}$, where $A_{i,j}^{[\texttt{ ev}]}$ is the part of the operator $A_{i,j}$ having only even harmonics, whereas $A_{i,j}^{[\texttt{odd}]}$ is the part having only odd ones.

3.1 Expansion of ${{\mathcal {B}}}_{\mu ,\epsilon }$

In the sequel $\mathcal {O}_5$ means an operator which maps $H^1(\mathbb {T},\mathbb {C}^2)$ into $L^2(\mathbb {T},\mathbb {C}^2)$-functions with size $\epsilon ^5$, $\mu \epsilon ^4$, $\mu ^2\epsilon ^3$, $\mu ^3\epsilon ^2$, $\mu ^4\epsilon$ or $\mu ^5$.

Lemma 3.2

The operator ${{\mathcal {B}}}_{\mu ,\epsilon }$ in (2.2) has the Taylor expansion

$$\begin{aligned} {{\mathcal {B}}}_{\mu ,\epsilon } = {{\mathcal {B}}}_0 + {{\mathcal {B}}}_1 + {{\mathcal {B}}}_2+ {{\mathcal {B}}}_3+{{\mathcal {B}}}_4+\mathcal {O}_5 \,, \end{aligned}$$

(3.7)

where

(3.8a)

(3.8b)

(3.8c)

(3.8d)

(3.8e)

and $p_i(x)$ and $a_i(x)$, $i=1,\dots ,4$, are computed in (A.59a)–(A.60a), $\mathcal {J}$ is the symplectic matrix in (1.5),

$$\begin{aligned} \Pi _{\texttt{s}}:=\begin{bmatrix} 0 &{} 0 \\ 0 &{} \text {sgn}(D) \end{bmatrix}\,, \qquad \Pi _{\texttt{ev}}:=\begin{bmatrix} 0 &{} 0 \\ 0 &{} \textrm{Id}\end{bmatrix}\,, \end{aligned}$$

(3.9)

and

(3.10a)

(3.10b)

(3.10c)

(3.10d)

(3.10e)

with $\texttt{f}_2$ and $\texttt{f}_4$ in (A.48).

Proof

By Taylor expanding (2.2). $\square$

We observe that, using the notation introduced in (3.6), we have

$$\begin{aligned} {{\mathcal {B}}}_{i,j}^{[\texttt{ ev}]} = {\left\{ \begin{array}{ll} {{\mathcal {B}}}_{i,j} &{}if j is even \,, \\ 0 &{}if j is odd \,, \end{array}\right. } \qquad {{\mathcal {B}}}_{i,j}^{[\texttt{odd}]} = {\left\{ \begin{array}{ll} 0 &{}if j is even \,, \\ {{\mathcal {B}}}_{i,j} &{}if j is odd \, . \end{array}\right. } \end{aligned}$$

(3.11)

3.2 Expansion of the projector $P_{\mu ,\epsilon }$

The projectors $P_{\mu ,\epsilon }$ in (2.3) admit the expansion

$$\begin{aligned} P_{\mu ,\epsilon } = P_0 + P_1 + P_2 + P_3 + \mathcal {O}_4 \,, \end{aligned}$$

(3.12)

where

$$\begin{aligned} \begin{aligned}&P_0:= P_{0,0} \,, \quad P_1:= \mathcal {P} \big [{{\mathcal {B}}}_1\big ] \\&P_2:= \mathcal {P} \big [{{\mathcal {B}}}_2\big ] + \mathcal {P} \big [{{\mathcal {B}}}_1,{{\mathcal {B}}}_1 \big ] \,,\\&P_3:= \mathcal {P} \big [{{\mathcal {B}}}_3\big ] + \mathcal {P} \big [{{\mathcal {B}}}_2,{{\mathcal {B}}}_1 \big ] + \mathcal {P} \big [{{\mathcal {B}}}_1,{{\mathcal {B}}}_2 \big ] + \mathcal {P} \big [{{\mathcal {B}}}_1,{{\mathcal {B}}}_1,{{\mathcal {B}}}_1 \big ] \,, \end{aligned} \end{aligned}$$

(3.13)

and

$$\begin{aligned} \begin{aligned}&\mathcal {P} \big [A_1]: = \frac{1}{2\pi \textrm{i}\,} \oint _\Gamma (\mathcal {L}_{0,0}-\lambda )^{-1} \mathcal {J}A_1 (\mathcal {L}_{0,0}-\lambda )^{-1} \textrm{d}\lambda \,,\quad \text {and for }k\ge 2 \\&\mathcal {P} \big [A_1,\dots , A_k \big ]:= \frac{(-1)^{k+1} }{2\pi \textrm{i}\,} \oint _\Gamma (\mathcal {L}_{0,0}-\lambda )^{-1} \mathcal {J}A_1 (\mathcal {L}_{0,0}-\lambda )^{-1} \dots \mathcal {J}A_k (\mathcal {L}_{0,0}-\lambda )^{-1} \textrm{d}\lambda \, . \end{aligned} \end{aligned}$$

(3.14)

In virtue of (3.6), (3.13)–(3.14) and (3.11) we obtain

$$\begin{aligned} P_{i,j}^{[\texttt{ ev}]} = {\left\{ \begin{array}{ll} P_{i,j} &{}if j is even \,, \\ 0 &{}if j is odd \,, \end{array}\right. } \qquad P_{i,j}^{[\texttt{odd}]} = {\left\{ \begin{array}{ll} 0 &{}if j is even \,, \\ P_{i,j} &{}if j is odd \, . \end{array}\right. } \end{aligned}$$

(3.15)

Action of $P_{\ell ,j}$ on the unperturbed vectors. We now collect how the operators $P_{\ell ,j}$ act on the vectors $f_1^+, f_1^-, f_0^+, f_0^-$ in (1.15). We denote

$$\begin{aligned} f_{-1}^+ :=\begin{bmatrix}{\texttt{c}}_{\texttt{h}}^{1/2}\cos (x) \\ -{\texttt{c}}_{\texttt{h}}^{-1/2}\sin (x) \end{bmatrix}\, ,\qquad f_{-1}^- :=\begin{bmatrix}{\texttt{c}}_{\texttt{h}}^{1/2}\sin (x) \\ {\texttt{c}}_{\texttt{h}}^{-1/2}\cos (x) \end{bmatrix} \ . \end{aligned}$$

(3.16)

We first consider the first order jets $P_{0,1}$ and $P_{1,0}$ of $P_1$.

Lemma 3.3

(First order jets). The action of the jets $P_{0,1}$ and $P_{1,0}$ of $P_1$ in (3.13) on the basis in (1.15) is

$$\begin{aligned} \begin{aligned}&P_{0,1}f^+_1 = { \begin{bmatrix}\mathfrak {a}_{0,1} \cos (2x) \\ \mathfrak {b}_{0,1} \sin (2x) \end{bmatrix} } \,, \quad P_{0,1}f^-_1 = { \begin{bmatrix}-\mathfrak {a}_{0,1} \sin (2x) \\ \ \mathfrak {b}_{0,1}\cos (2x) \end{bmatrix} } \,, \\&P_{0,1}f^+_0 = \mathfrak {u}_{0,1} f^+_{-1} \,, \quad P_{0,1}f^-_0 =0 \,, \quad P_{1,0} f_0^+=0 \,,\quad P_{1,0} f_0^-=0 \,, \\&P_{1,0} f_1^+ = \textrm{i}\,\mathfrak {u}_{1,0} f^{-}_{-1} \,, \quad P_{1,0} f_1^- = \textrm{i}\,\mathfrak {u}_{1,0} f^+_{-1}\,, \end{aligned} \end{aligned}$$

(3.17)

where

$$\begin{aligned} \begin{aligned}&\mathfrak {a}_{0,1}:= \frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-\frac{11}{2}} (3+{\texttt{c}}_{\texttt{h}}^4) \,, \quad \mathfrak {b}_{0,1}:= \frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-\frac{13}{2}} (1+{\texttt{c}}_{\texttt{h}}^4)(3-{\texttt{c}}_{\texttt{h}}^4) , \\&\mathfrak {u}_{0,1}:= \tfrac{1}{4}{\texttt{c}}_{\texttt{h}}^{-\frac{5}{2}}(3+{\texttt{c}}_{\texttt{h}}^4) \,,\quad \mathfrak {u}_{1,0}:= \tfrac{1}{4} \big (1+{\texttt{c}}_{\texttt{h}}^{-2}\texttt{h}(1-{\texttt{c}}_{\texttt{h}}^4)\big )\, . \end{aligned} \end{aligned}$$

(3.18)

Proof

See [9, formula (A.16)]. $\square$

Lemma 3.4

(Second order jets). The action of the jet $P_{0,2}$ of $P_2$ in (3.13) on the basis in (1.15) is given by

$$\begin{aligned}&P_{0,2} f_1^+ = \mathfrak {n}_{0,2} f_1^+ +\mathfrak {u}_{0,2}^+ f_{-1}^+ + \begin{bmatrix}\mathfrak {a}_{0,2}\cos (3x) \\ \mathfrak {b}_{0,2} \sin (3x) \end{bmatrix}\, , \quad P_0 P_{0,2} f_0^+ = 0 \, , \end{aligned}$$

(3.19a)

$$\begin{aligned}&P_{0,2} f_1^- = \mathfrak {n}_{0,2} f_1^- + \mathfrak {u}_{0,2}^- f_{-1}^- + \begin{bmatrix}{\widetilde{\mathfrak {a}}}_{0,2}\sin (3x) \\ {\widetilde{\mathfrak {b}}}_{0,2} \cos (3x) \end{bmatrix} \, , \quad P_{0,2} f_0^- = 0\, , \end{aligned}$$

(3.19b)

where ${\widetilde{\mathfrak {a}}}_{0,2}, {\widetilde{\mathfrak {b}}}_{0,2} \in \mathbb {R}$ and

$$\begin{aligned}&\mathfrak {n}_{0,2} := \frac{{\texttt{c}}_{\texttt{h}}^{12}+{\texttt{c}}_{\texttt{h}}^8-9 {\texttt{c}}_{\texttt{h}}^4-9}{8 {\texttt{c}}_{\texttt{h}}^{12}} \, , \\ {}&\mathfrak {u}_{0,2}^+ := \frac{-2 {\texttt{c}}_{\texttt{h}}^{12}-7 {\texttt{c}}_{\texttt{h}}^8+8 {\texttt{c}}_{\texttt{h}}^4+9}{32 {\texttt{c}}_{\texttt{h}}^8}\,, \quad \mathfrak {u}_{0,2}^- := \frac{2 {\texttt{c}}_{\texttt{h}}^{12}-11 {\texttt{c}}_{\texttt{h}}^8+20 {\texttt{c}}_{\texttt{h}}^4-3}{32 {\texttt{c}}_{\texttt{h}}^8}\, , \nonumber \\&\mathfrak {a}_{0,2} := \dfrac{3 ({\texttt{c}}_{\texttt{h}}^{12}+17 {\texttt{c}}_{\texttt{h}}^8+51 {\texttt{c}}_{\texttt{h}}^4+27)}{64 {\texttt{c}}_{\texttt{h}}^{23/2}}\, , \quad \mathfrak {b}_{0,2} := \dfrac{3 (3 {\texttt{c}}_{\texttt{h}}^{12}-5 {\texttt{c}}_{\texttt{h}}^8+25 {\texttt{c}}_{\texttt{h}}^4+9)}{64 {\texttt{c}}_{\texttt{h}}^{25/2}}\, . \nonumber \end{aligned}$$

(3.19c)

The action of the jet $P_{2,0}$ on the vector $f_0^-$ in (1.15) is

$$\begin{aligned} P_{2,0} f_0^- = 0\, . \end{aligned}$$

(3.19d)

The action of the jet $P_{1,1}$ on the basis in (1.15) is

$$\begin{aligned}&P_{1,1} f_1^+ = \textrm{i}\,{\widetilde{\mathfrak {m}}}_{1,1} f_0^- + \textrm{i}\,\begin{bmatrix} {\widetilde{\mathfrak {a}}}_{1,1} \sin (2x) \\ {\widetilde{\mathfrak {b}}}_{1,1} \cos (2x) \end{bmatrix} \, , \qquad P_{1,1} f_1^- = \textrm{i}\,\begin{bmatrix}\mathfrak {a}_{1,1} \cos (2 x) \\ \mathfrak {b}_{1,1} \sin (2 x) \end{bmatrix} \, ,\nonumber \\&P_{1,1} f_0^- = -\frac{\textrm{i}\,}{2} {\texttt{c}}_{\texttt{h}}^{-3/2} f_{-1}^+ \, , \qquad P_{1,1} f_0^+ = \textrm{i}\,{\widetilde{\mathfrak {n}}}_{1,1} f_1^- + \textrm{i}\,{\widetilde{\mathfrak {u}}}_{1,1} f_{-1}^- \, , \end{aligned}$$

(3.19e)

where ${\widetilde{\mathfrak {m}}}_{1,1}, {\widetilde{\mathfrak {a}}}_{1,1}, {\widetilde{\mathfrak {b}}}_{1,1}, {\widetilde{\mathfrak {n}}}_{1,1}, {\widetilde{\mathfrak {u}}}_{1,1} \in \mathbb {R}$ and

$$\begin{aligned}{} & {} \mathfrak {a}_{1,1}:=-\dfrac{3 ({\texttt{c}}_{\texttt{h}}^8-6 {\texttt{c}}_{\texttt{h}}^4+5) \texttt{h}-3{\texttt{c}}_{\texttt{h}}^2 ({\texttt{c}}_{\texttt{h}}^4+3)}{8 {\texttt{c}}_{\texttt{h}}^{15/2}} \,,\nonumber \\ {}{} & {} \quad \mathfrak {b}_{1,1}:=\dfrac{({\texttt{c}}_{\texttt{h}}^8+8 {\texttt{c}}_{\texttt{h}}^4-9) \texttt{h}+3 ({\texttt{c}}_{\texttt{h}}^6+{\texttt{c}}_{\texttt{h}}^2)}{8 {\texttt{c}}_{\texttt{h}}^{17/2}} \, . \end{aligned}$$

(3.20)

Proof

In Appendix B. $\square$

Lemma 3.5

(Third order jets). The action of the jets $P_{0,3}$, $P_{1,2}$ and $P_{2,1}$ of $P_3$ in (3.13) on $f_1^+$, $f_0^-$ is

$$\begin{aligned} \begin{aligned}&P_{0,3} f_1^+ = \begin{bmatrix}\mathfrak {a}_{0,3} \cos (2x) \\ \mathfrak {b}_{0,3} \sin (2x) \end{bmatrix} + \begin{bmatrix}{\widetilde{\mathfrak {a}}}_{0,3} \cos (4x) \\ {\widetilde{\mathfrak {b}}}_{0,3} \sin (4x) \end{bmatrix} \,, \quad P_{0,3} f_0^- = 0 \,, \\&P_{1,2} f_0^- = \textrm{i}\,\begin{bmatrix}\mathfrak {a}_{1,2} \cos (2 x) \\ \mathfrak {b}_{1,2} \sin (2 x) \end{bmatrix} \,, \quad P_{2,1} f_0^- = {\widetilde{\mathfrak {n}}}_{2,1} f_1^- + {\widetilde{\mathfrak {u}}}_{2,1} f_{-1}^- \,, \end{aligned} \end{aligned}$$

(3.21)

where ${\widetilde{\mathfrak {a}}}_{0,3}, {\widetilde{\mathfrak {b}}}_{0,3}, {\widetilde{\mathfrak {n}}}_{2,1}, {\widetilde{\mathfrak {u}}}_{2,1} \in \mathbb {R}$ and

$$\begin{aligned} \begin{aligned}&\mathfrak {a}_{0,3}:= \frac{1}{64 {\texttt{c}}_{\texttt{h}}^{35/2}({\texttt{c}}_{\texttt{h}}^2+1)} \Big (6 {\texttt{c}}_{\texttt{h}}^{22}+2 {\texttt{c}}_{\texttt{h}}^{20}+27 {\texttt{c}}_{\texttt{h}}^{18}+21 {\texttt{c}}_{\texttt{h}}^{16}-379 {\texttt{c}}_{\texttt{h}}^{14} \\&\qquad \qquad -361 {\texttt{c}}_{\texttt{h}}^{12}+575 {\texttt{c}}_{\texttt{h}}^{10}+581 {\texttt{c}}_{\texttt{h}}^8-243 {\texttt{c}}_{\texttt{h}}^6-225 {\texttt{c}}_{\texttt{h}}^4-162 {\texttt{c}}_{\texttt{h}}^2-162 \Big )\,,\\&\mathfrak {b}_{0,3}:= \frac{1}{128 {\texttt{c}}_{\texttt{h}}^{37/2} ({\texttt{c}}_{\texttt{h}}^2+1)} \Big (6 {\texttt{c}}_{\texttt{h}}^{26}+10 {\texttt{c}}_{\texttt{h}}^{24}+35 {\texttt{c}}_{\texttt{h}}^{22}+21 {\texttt{c}}_{\texttt{h}}^{20}-146 {\texttt{c}}_{\texttt{h}}^{18}-146 {\texttt{c}}_{\texttt{h}}^{16}\\&\qquad \qquad -46 {\texttt{c}}_{\texttt{h}}^{14}-34 {\texttt{c}}_{\texttt{h}}^{12}+470 {\texttt{c}}_{\texttt{h}}^{10}+482 {\texttt{c}}_{\texttt{h}}^8-333 {\texttt{c}}_{\texttt{h}}^6-315 {\texttt{c}}_{\texttt{h}}^4-162 {\texttt{c}}_{\texttt{h}}^2-162\Big )\,,\\&\mathfrak {a}_{1,2} = -\frac{ {\texttt{c}}_{\texttt{h}}^4+3}{4 {\texttt{c}}_{\texttt{h}}^7}, \quad \mathfrak {b}_{1,2}:= \frac{{\texttt{c}}_{\texttt{h}}^4+1 }{4 {\texttt{c}}_{\texttt{h}}^4}\, . \end{aligned} \end{aligned}$$

(3.22)

Proof

In Appendix B. $\square$

3.3 Expansion of $\mathfrak {B}_{\mu ,\epsilon }$

In this section we provide the expansion of the operator $\mathfrak {B}_{\mu ,\epsilon }$ defined in (2.10). We introduce the notation ${\textbf {Sym}} [A]:= \frac{1}{2} A+ \frac{1}{2} A^*$.

Lemma 3.6

(Expansion of $\mathfrak {B}_{\mu ,\epsilon }$). The operator $\mathfrak {B}_{\mu ,\epsilon }$ in (2.10) has the Taylor expansion

$$\begin{aligned} \mathfrak {B}_{\mu ,\epsilon } = \sum _{j=0}^4 \mathfrak {B}_j +\mathcal {O}_5 \end{aligned}$$

(3.23)

where

$$\begin{aligned} \mathfrak {B}_0&:=P_0^*{{\mathcal {B}}}_0P_0, \quad \mathfrak {B}_1 :=P_0^* {{\mathcal {B}}}_1 P_0, \quad \mathfrak {B}_2 := P_0^* {\textbf {Sym}} \big [{{\mathcal {B}}}_2+{{\mathcal {B}}}_1P_1\big ]P_0 \, , \end{aligned}$$

(3.24a)

$$\begin{aligned} \mathfrak {B}_3&:= P_0^*{\textbf {Sym}} \big [{{\mathcal {B}}}_3+{{\mathcal {B}}}_2P_1 + {{\mathcal {B}}}_1(\textrm{Id}-P_0)P_2\big ]P_0\, , \end{aligned}$$

(3.24b)

$$\begin{aligned} \mathfrak {B}_4&:= P_0^*{\textbf {Sym}} \big [{{\mathcal {B}}}_4+ {{\mathcal {B}}}_3P_1 + {{\mathcal {B}}}_2(\textrm{Id}-P_0)P_2 + {{\mathcal {B}}}_1(\textrm{Id}-P_0)P_3 - {{\mathcal {B}}}_1P_1 P_0 P_2 \nonumber \\ {}&+ \mathfrak {N}P_0P_2\big ] P_0\, , \end{aligned}$$

(3.24c)

the operators $P_0, \ldots , P_3$ are defined in (3.13) and

$$\begin{aligned} \mathfrak {N}:= \frac{1}{4} \big ( P_2^* {{\mathcal {B}}}_0-{{\mathcal {B}}}_0 P_2 \big ) = - \mathfrak {N}^* \, . \end{aligned}$$

(3.25)

It results

$$\begin{aligned} \big (\mathfrak {N} f_k^\sigma , f_{k'}^{\sigma '} \big )= 0\,,\quad \forall f_k^\sigma , f_{k'}^{\sigma '}\in \{f_1^+,f_1^-,f_0^- \}\, . \end{aligned}$$

(3.26)

Proof

In order to expand $\mathfrak {B}_{\mu ,\epsilon }$ in (2.10) we first expand $U_{\mu ,\epsilon } P_0$. In view of (2.5) we have, introducing the analytic function $g(x):= (1-x)^{-\frac{1}{2}}$ for $|x|<1$,

$$\begin{aligned} U_{\mu ,\epsilon } P_0 = g((P_{\mu ,\epsilon }-P_0)^2) \, P_{\mu ,\epsilon }\, P_0 = P_{\mu ,\epsilon }\, g((P_{\mu ,\epsilon }-P_0)^2) \, P_0 \, \end{aligned}$$

(3.27)

using that $(P_{\mu ,\epsilon }-P_0)^2$ commutes with $P_{\mu ,\epsilon }$, and so does $g((P_{\mu ,\epsilon }-P_0)^2)$. The Taylor expansion $g(x) = 1+\frac{1}{2}x+\frac{3}{8} x^2+ \mathcal {O}(x^3)$ implies that

$$\begin{aligned} g((P_{\mu ,\epsilon }-P_0)^2) = \textrm{Id}+ \underbrace{\frac{1}{2} (P_{\mu ,\epsilon }-P_0)^2}_{=:g_2} +\underbrace{\frac{3}{8} (P_{\mu ,\epsilon }-P_0)^4}_{=:g_4} + \, \mathcal {O}_6 \,, \end{aligned}$$

(3.28)

where $\mathcal {O}_6 = \mathcal {O}((P_{\mu ,\epsilon }-P_0)^6) \in \mathcal {L}(Y)$.

Furthermore, since $P_{\mu , \epsilon } \mathscr {L}_{\mu ,\epsilon } = \mathscr {L}_{\mu ,\epsilon } P_{\mu , \epsilon }$ (see Lemma 2.1- item 2), applying $\mathcal {J}$ to both sides and using (2.4), yields

$$\begin{aligned} P_{\mu , \epsilon }^* {{\mathcal {B}}}_{\mu ,\epsilon } = {{\mathcal {B}}}_{\mu ,\epsilon } P_{\mu , \epsilon } \qquad \text {where} \qquad P_{\mu , \epsilon }^2 = P_{\mu , \epsilon }\, . \end{aligned}$$

(3.29)

Therefore the operator $\mathfrak {B}_{\mu , \epsilon }$ in (2.10) has the expansion

$$\begin{aligned} \nonumber \mathfrak {B}_{\mu , \epsilon }&=^{(3.27)} P_0^*\, g((P_{\mu ,\epsilon }-P_0)^2)^* \, P_{\mu ,\epsilon }^* \, {{\mathcal {B}}}_{\mu ,\epsilon } \, P_{\mu ,\epsilon } \, g((P_{\mu ,\epsilon }-P_0)^2) \, P_0 \\ \nonumber&{\mathop {=}\limits ^{(3.29)}} P_0^* \, g((P_{\mu ,\epsilon }-P_0)^2)^* \, {{\mathcal {B}}}_{\mu ,\epsilon } \, P_{\mu ,\epsilon } \, g((P_{\mu ,\epsilon }-P_0)^2) \, P_0 \\ \nonumber&{\mathop {=}\limits ^{(3.28)}} P_0^* \, (\textrm{Id}+ g_2^* + g_4^*+\mathcal {O}_6) \, {{\mathcal {B}}}_{\mu ,\epsilon } \, P_{\mu ,\epsilon } \, \big (\textrm{Id}+g_2+g_4+\mathcal {O}_6\big ) \, P_0 \\&\;\;\;=\;\;\, {\textbf {Sym}} \big [ P_{0}^* \big ({{\mathcal {B}}}_{\mu ,\epsilon }P_{\mu ,\epsilon } + 2{{\mathcal {B}}}_{\mu ,\epsilon }P_{\mu ,\epsilon } g_2 + g_2^* {{\mathcal {B}}}_{\mu ,\epsilon } P_{\mu ,\epsilon } g_2 + 2{{\mathcal {B}}}_{\mu ,\epsilon }P_{\mu ,\epsilon } g_4 \big ) P_{0} \big ] \, \nonumber \\ {}&\quad + \mathcal {O}_6 \end{aligned}$$

(3.30)

using (3.29) and that $g_2 = \mathcal {O}_2$ and $g_4 = \mathcal {O}_4$.

A further analysis of the term (3.30) relies on the following lemma.

Lemma 3.7

Let $\Pi _0^+$ be the orthogonal projector on $f_0^+$ in (1.15) and $\Pi ^\angle := \textrm{Id}-\Pi _0^+$. One has

$$\begin{aligned}&{{\mathcal {B}}}_0 \, P_0 = P_0^* \, {{\mathcal {B}}}_0 = \Pi _0^+ \, , \qquad {{\mathcal {B}}}_0 \, P_1 + {{\mathcal {B}}}_1 \, P_0 = P_1^* \, {{\mathcal {B}}}_0 + P_0^* \, {{\mathcal {B}}}_1 \, , \end{aligned}$$

(3.31)

$$\begin{aligned}&P_0 \, P_1 \, P_0 = 0 \, , \qquad P_0 \, P_2 \, P_0 = - P_1^2 \, P_0 = - P_0 \, P_1^2 \, , \end{aligned}$$

(3.32)

$$\begin{aligned}&(P_{\mu , \epsilon } - P_0)^2 P_{0} = P_{0} ( \textrm{Id}- P_{\mu ,\epsilon } ) \, P_{0} \, , \qquad (P_{\mu , \epsilon } - P_0)^4 P_{0} = P_{0} \big ( ( \textrm{Id}- P_{\mu ,\epsilon } ) P_{0} \big )^2 \, , \end{aligned}$$

(3.33)

$$\begin{aligned}&\mathcal {J}P_j = P_j^* \mathcal {J}\, , \ \ \forall j \in \mathbb {N}_0 \, , \qquad P_0^* {{\mathcal {B}}}_0 P_j \Pi ^\angle P_0 = \Pi _0^+ P_j\Pi ^\angle P_0 \, . \end{aligned}$$

(3.34)

Proof

We deduce that ${{\mathcal {B}}}_0 \, P_0 = \Pi _0^+$ because ${{\mathcal {B}}}_0 f_1^+ = {{\mathcal {B}}}_0 f_1^- = {{\mathcal {B}}}_0 f_0^- = 0$, ${{\mathcal {B}}}_0 f_0^+=f_0^+$ and the first identity in (3.31) follows also since $P_0^* {{\mathcal {B}}}_0 = {{\mathcal {B}}}_0 P_0$ by (3.29). The second one follows by expanding the identity in (3.29) at order 1, using the expansions of $P_{\mu ,\epsilon }$ and $B_{\mu ,\epsilon }$ in (3.12) and (3.7). The identities in (3.32) follow by expanding the identity $P_{\mu ,\epsilon }^2 = P_{\mu ,\epsilon }$ at order 1 and 2, getting $P_1 P_0 + P_0 P_1 = P_1$ and $P_2 P_0 + P_1^2 + P_0 P_2 = P_2$, and applying $P_0$ to the right and the left of the identities above. The first identity in (3.33) is verified using that $P_{\mu ,\epsilon }^2 = P_{\mu ,\epsilon }$ and the second one follows by applying the first one twice. Finally the first identity in (3.34) follows by expanding the identity $\mathcal {J}P_{\mu ,\epsilon } = P_{\mu ,\epsilon }^*\mathcal {J}$ in (2.4) into homogeneous orders. The last identity in (3.34) descends from the first of (3.31), since for any $g\in L^2(\mathbb {T},\mathbb {C}^2)$ and $f_k^\sigma \in \{f_1^+,f_1^-,f_0^-\}$ one has

$$\begin{aligned} \big (P_0^* {{\mathcal {B}}}_0 P_j f_k^\sigma ,g \big )= \big ( P_j f_k^\sigma , {{\mathcal {B}}}_0 P_0 g \big ) = \big ( P_j f_k^\sigma , \Pi _0^+ g \big ) = \big ( \Pi _0^+ P_j f_k^\sigma , g \big ) \, . \end{aligned}$$

This concludes the proof of the lemma. $\square$

By (3.33) and (3.32) the Taylor expansions of $g_2P_0$ and $g_4P_0$ in (3.28) are

$$\begin{aligned} g_2 P_0&= \frac{1}{2} P_0 (Id - P_{\mu ,\epsilon }) P_0 = -\frac{1}{2} P_0 \, P_2 \, P_0 - \frac{1}{2} P_0 \,P_3 \, P_0 - \frac{1}{2} P_0 \,P_4 \, P_0 + \mathcal {O}_5 \, , \end{aligned}$$

(3.35a)

$$\begin{aligned} g_4 P_0&= \frac{3}{8} P_0 (Id - P_{\mu ,\epsilon }) P_0 (Id - P_{\mu ,\epsilon }) P_0 = \frac{3}{8} P_0 \, P_2 \, P_0 \, P_2 \, P_0 + \mathcal {O}_5 \, . \end{aligned}$$

(3.35b)

We now Taylor expand the operators in (3.30) and collect the terms of the same order.

$\underline{\hbox {Expression of} \mathfrak {B}_0:}$ The term of order 0 in (3.30) is simply $\mathfrak {B}_0 = P_0^* {{\mathcal {B}}}_{0}P_0$.

$\underline{\hbox {Expression of} \mathfrak {B}_1:}$ The term of order 1 is

$$\begin{aligned} \mathfrak {B}_1 = \frac{1}{2} P_0^* \big ( {{\mathcal {B}}}_0 P_1 + {{\mathcal {B}}}_1 P_0 + P_1^* {{\mathcal {B}}}_0 + P_0^* {{\mathcal {B}}}_1 \big ) P_0 = P_0^* \, {{\mathcal {B}}}_1 \, P_0 \end{aligned}$$

using (3.32) and (3.31) and that ${{\mathcal {B}}}_0, {{\mathcal {B}}}_1$ are self-adjoint.

$\underline{\hbox {Expression of} \mathfrak {B}_2:}$ We compute the terms of order 2 in (3.30). By (3.35a) we get

$$\begin{aligned} \mathfrak {B}_2 = {\textbf {Sym}} [P_0^* \big ({{\mathcal {B}}}_2 P_0 + {{\mathcal {B}}}_1P_1 + {{\mathcal {B}}}_0P_2 - {{\mathcal {B}}}_0 P_0 P_2 \big ) P_0 ] \, . \end{aligned}$$

(3.36)

Moreover

and from (3.36) descends the expression of $\mathfrak {B}_2$ in (3.24a).

$\underline{\hbox {Expression of} \mathfrak {B}_3:}$ We compute the terms of order 3 in (3.30). By (3.35a), identity (3.24b) follows from

$$\begin{aligned} \mathfrak {B}_3&= {\textbf {Sym}} [P_0^* \big ({{\mathcal {B}}}_3 + {{\mathcal {B}}}_2 P_1 + {{\mathcal {B}}}_1 P_2 + {{\mathcal {B}}}_0 P_3 - ({{\mathcal {B}}}_0P_1 + {{\mathcal {B}}}_1P_0)P_0 \, P_2 \, P_0 - {{\mathcal {B}}}_0 \, P_0\, P_3 \, P_0 \big ) P_0] \\&= {\textbf {Sym}} [P_0^* \big ({{\mathcal {B}}}_3 + {{\mathcal {B}}}_2 P_1 + {{\mathcal {B}}}_1 P_2 - {{\mathcal {B}}}_1P_0P_2 \big ) P_0] , \end{aligned}$$

where we used $P_0^* {{\mathcal {B}}}_0 P_3 = P_0^* {{\mathcal {B}}}_0 P_0 P_3$ and $P_0^* {{\mathcal {B}}}_0 P_1 P_0 P_2 P_0 = 0$ by (3.31) and (3.32).

$\underline{\hbox {Expression of} \mathfrak {B}_4:}$ At the fourth order we get, in view of (3.35a) and (3.35b),

$$\begin{aligned} \nonumber \mathfrak {B}_4&= {\textbf {Sym}} \big [ P_0^* \Big ( {{\mathcal {B}}}_0 P_4 + {{\mathcal {B}}}_1 P_3 + {{\mathcal {B}}}_2 P_2 + {{\mathcal {B}}}_3 P_1 + {{\mathcal {B}}}_4 - {{\mathcal {B}}}_0 P_0 P_4 P_0 - ({{\mathcal {B}}}_0P_1 +{{\mathcal {B}}}_1P_0) P_0 P_3 P_0 \\ \nonumber&\quad - ({{\mathcal {B}}}_2 P_0 + {{\mathcal {B}}}_1P_1 + {{\mathcal {B}}}_0P_2)P_0P_2P_0 + \frac{3}{4} {{\mathcal {B}}}_0P_0 P_2 P_0 P_2 P_0 + \frac{1}{4} P_2^* P_0^* {{\mathcal {B}}}_0 P_0 P_2 P_0 \Big ) P_0 \big ] \nonumber \\&= {\textbf {Sym}} \big [ P_0^* \Big ( {{\mathcal {B}}}_1 (\textrm{Id}-P_0) P_3 + {{\mathcal {B}}}_2 (\textrm{Id}-P_0) P_2 + {{\mathcal {B}}}_3 P_1 + {{\mathcal {B}}}_4 - {{\mathcal {B}}}_1P_1 P_0 P_2 P_0 \nonumber \\ {}&\quad -\frac{1}{4} {{\mathcal {B}}}_0(P_0P_2P_0)^2+\frac{1}{4} P_2^* {{\mathcal {B}}}_0P_0P_2P_0 \Big ) P_0 \big ]\, , \end{aligned}$$

(3.37)

where to pass from the first to the second line we used $P_0^*{{\mathcal {B}}}_0 P_4 =P_0^*{{\mathcal {B}}}_0 P_0 P_4$ (by (3.31)) and $P_0^* {{\mathcal {B}}}_0 P_1 P_0 P_3 P_0 = 0$ (by (3.31) and (3.32)). We sum up the last two terms in (3.37) into ${\textbf {Sym}} [ P_0^* \mathfrak {N} P_0 P_2 P_0]$ where $\mathfrak {N}$ is in (3.25). We observe that, in view of (3.31)–(3.34), we have, for any $f_k^\sigma , f_{k'}^{\sigma '}\in \{f_1^+,f_1^-,f_0^- \}$, that (3.26) holds. Thus we obtain (3.24c). In conclusion, we have proved formula (3.23). $\square$

Action of the jets of $\mathfrak {B}_{\mu ,\epsilon }$ on the kernel vectors. We now collect how the operators $\mathfrak {B}_{i,j}$ (cfr. (3.6)) acts on the vectors $f_1^+, f_1^-, f_0^-$.

Lemma 3.8

The first jets of the operator $\mathfrak {B}_{\mu ,\epsilon }$ in (2.10) act, for $f_k^\sigma \in \{f_1^+,f_1^-,f_0^- \}$, as

$$\begin{aligned}&\mathfrak {B}_{0,2}f_k^\sigma =P_0^* \big ( {{\mathcal {B}}}_{0,2}+{{\mathcal {B}}}_{0,1}P_{0,1} \big ) f_k^\sigma \, ,\quad \mathfrak {B}_{2,0}f_k^\sigma = P_0^* \big ( {{\mathcal {B}}}_{2,0}+{{\mathcal {B}}}_{1,0}P_{1,0} \big ) f_k^\sigma \, , \end{aligned}$$

(3.38a)

$$\begin{aligned}&{\mathfrak {B}}_{1,1} f_k^\sigma =P_0^* \big ( {{\mathcal {B}}}_{1,1}+{{\mathcal {B}}}_{1,0}P_{0,1} +{{\mathcal {B}}}_{0,1}P_{1,0} + \frac{1}{2} \Pi _0^+ P_{1,1} \big ) f_k^\sigma \, , \end{aligned}$$

(3.38b)

$$\begin{aligned}&\begin{aligned}&{\mathfrak {B}}_{0,3}f_k^\sigma =P_0^*\big ( {{\mathcal {B}}}_{0,3} + {{\mathcal {B}}}_{0,2} P_{0,1} + {{\mathcal {B}}}_{0,1} P_{0,2} - {\textbf {Sym}} [{{\mathcal {B}}}_{0,1}P_0P_{0,2}]\big )f_k^\sigma \, , \\&{\mathfrak {B}}_{3,0}f_k^\sigma = P_0^*\big ({{\mathcal {B}}}_{3,0} + {{\mathcal {B}}}_{2,0} P_{1,0} + {{\mathcal {B}}}_{1,0} P_{2,0} - {\textbf {Sym}} [{{\mathcal {B}}}_{1,0}P_0P_{2,0}]\big ) f_k^\sigma \, , \end{aligned} \end{aligned}$$

(3.38c)

$$\begin{aligned}&{\mathfrak {B}}_{1,2} f_k^\sigma =P_0^* \big ( {{\mathcal {B}}}_{1,2} + {{\mathcal {B}}}_{1,1} P_{0,1}+ {{\mathcal {B}}}_{0,2} P_{1,0} + {{\mathcal {B}}}_{1,0} P_{0,2} + {{\mathcal {B}}}_{0,1} P_{1,1} + \frac{1}{2} \Pi _0^+ P_{1,2} \\ \nonumber&\qquad \qquad \qquad - {\textbf {Sym}} [{{\mathcal {B}}}_{1,0}P_0P_{0,2}+{{\mathcal {B}}}_{0,1} P_0 P_{1,1}] \big )f_k^\sigma \, , \end{aligned}$$

(3.38d)

$$\begin{aligned}&{\mathfrak {B}}_{2,1} f_k^\sigma = P_0^* \big ( {{\mathcal {B}}}_{2,1} + {{\mathcal {B}}}_{1,1} P_{1,0}+ {{\mathcal {B}}}_{2,0} P_{0,1} + {{\mathcal {B}}}_{0,1} P_{2,0} + {{\mathcal {B}}}_{1,0} P_{1,1} + \frac{1}{2} \Pi _0^+ P_{2,1} \\ \nonumber&\qquad \qquad \qquad - {\textbf {Sym}} [{{\mathcal {B}}}_{0,1}P_0P_{2,0}+{{\mathcal {B}}}_{1,0} P_0 P_{1,1}] \big )f_k^\sigma \, , \end{aligned}$$

(3.38e)

$$\begin{aligned}&{\mathfrak {B}}_{0,4} f_k^\sigma =P_0^* \big ( \mathcal{B}_{0,4}+ \mathcal{B}_{0,3} P_{0,1} + \mathcal{B}_{0,2}P_{0,2} + \mathcal{B}_{0,1} P_{0,3} \\ \nonumber&\qquad \qquad \qquad - {\textbf {Sym}} [\mathcal{B}_{0,2}P_0P_{0,2} + \mathcal{B}_{0,1}P_0P_{0,3} + \mathcal{B}_{0,1}P_{0,1} P_0 P_{0,2} -\mathfrak {N}_{0,2} P_0 P_{0,2} ] \big ) f_k^\sigma \, ,\\ \nonumber&{\mathfrak {B}}_{2,2} f_k^\sigma =P_0^* \big ( \mathcal{B}_{2,2}+ \mathcal{B}_{1,2} P_{1,0}+ \mathcal{B}_{2,1} P_{0,1} + \mathcal{B}_{0,2}P_{2,0} + \mathcal{B}_{1,1}P_{1,1}+ \mathcal{B}_{2,0} P_{0,2} \\ \nonumber&\qquad + \mathcal{B}_{0,1} P_{2,1} + \mathcal{B}_{1,0} P_{1,2}+ \frac{1}{2} \Pi _0^+ P_{2,2} \\ \nonumber&\qquad - {\textbf {Sym}} [\mathcal{B}_{0,2}P_0P_{2,0}+\mathcal{B}_{1,1}P_0P_{1,1} +\mathcal{B}_{2,0}P_0P_{0,2} + \mathcal{B}_{0,1}P_0P_{2,1} + \mathcal{B}_{1,0}P_0P_{1,2} \end{aligned}$$

(3.38f)

$$\begin{aligned}&\qquad \qquad \qquad + \mathcal{B}_{0,1}P_{0,1} P_0 P_{2,0}+ \mathcal{B}_{1,0}P_{0,1} P_0 P_{1,1}+ \mathcal{B}_{0,1}P_{1,0} P_0 P_{1,1}+ \mathcal{B}_{1,0}P_{1,0} P_0 P_{0,2} \\ \nonumber&\qquad \qquad \qquad - \mathfrak {N}_{2,0} P_0 P_{0,2} - \mathfrak {N}_{0,2} P_0 P_{2,0} - \mathfrak {N}_{1,1} P_0 P_{1,1} ] \big ) f_k^\sigma \, ,\\ \nonumber&{\mathfrak {B}}_{1,3} f_k^\sigma =P_0^*\big ( \mathcal{B}_{1,3}+ \mathcal{B}_{0,3} P_{1,0}+ \mathcal{B}_{1,2} P_{0,1} + \mathcal{B}_{0,2}P_{1,1}+ \mathcal{B}_{1,1}P_{0,2} + \mathcal{B}_{1,0} P_{0,3}+ \mathcal{B}_{0,1} P_{1,2} \\ \nonumber&\qquad \qquad + \frac{1}{2} \Pi _0^+ P_{1,3} - {\textbf {Sym}} [\mathcal{B}_{0,2}P_0P_{1,1} + \mathcal{B}_{1,1}P_0P_{0,2} + \mathcal{B}_{1,0}P_0P_{0,3} + \mathcal{B}_{0,1}P_0P_{1,2} \end{aligned}$$

(3.38g)

$$\begin{aligned}&\qquad \qquad \qquad + \mathcal{B}_{1,0}P_{0,1} P_0 P_{0,2}+ \mathcal{B}_{0,1}P_{1,0} P_0 P_{0,2}+ \mathcal{B}_{0,1}P_{0,1} P_0 P_{1,1} \nonumber \\&\qquad - \mathfrak {N}_{1,1} P_0 P_{0,2} - \mathfrak {N}_{0,2} P_0 P_{1,1} ] \big ) f_k^\sigma \, , \end{aligned}$$

(3.38h)

with ${{\mathcal {B}}}_j$, $j=0,\dots ,4$, in (3.2) and $P_j$, $j=0,\dots ,3$, in (3.13).

The proof of (3.8) relies on formulas (3.24a)–(3.24c) and Lemmata 3.9, 3.10 below.

Lemma 3.9

Let $f_k^\sigma \in \{ f_1^+, f_1^-,f_0^-\}$. For any $j \in \mathbb {N}$ we have

(3.39)

where $\Pi _0^+$ is the orthogonal projector on $f_0^+$.

Proof

By identity (3.29) the operator ${{\mathcal {B}}}_{\mu ,\epsilon } P_{\mu ,\epsilon }$ is, like ${{\mathcal {B}}}_{\mu ,\epsilon }$, self-adjoint, hence its j-th jet fulfills

$$\begin{aligned} {\textbf {Sym}} [{{\mathcal {B}}}_jP_0+ \dots + {{\mathcal {B}}}_1 P_{j-1} ] ={{\mathcal {B}}}_jP_0 + \dots + {{\mathcal {B}}}_{1} P_{j-1} + {{\mathcal {B}}}_0 P_j - {\textbf {Sym}} [ {{\mathcal {B}}}_0 P_j ] .\qquad \end{aligned}$$

(3.40)

We claim that, for $f_k^\sigma \in \{ f_1^+, f_1^-,f_0^-\}$ we have

$$\begin{aligned} P_0^* ( {{\mathcal {B}}}_0 P_j - {\textbf {Sym}} [{{\mathcal {B}}}_0 P_j] )P_0 f_k^\sigma = \frac{1}{2} P_0^* \Pi _0^+ P_j P_0 f_k^\sigma \,, \end{aligned}$$

(3.41)

which, together with (3.40), proves (3.39). Claim (3.41) follows, by observing that $f_k^\sigma$ fulfills ${{\mathcal {B}}}_0f_k^\sigma = 0$ and $\Pi ^\angle P_0 f_k^\sigma =f_k^\sigma$ (cfr. Lemma 3.7), then

(3.42)

Using again that $P_0^* {{\mathcal {B}}}_0 P_{j} f_k^\sigma = \Pi _0^+ P_j f_k^\sigma$ we obtain (3.41). $\square$

Lemma 3.10

For any $f \in \{f_1^+, f_{1}^-, f_0^- \}$ and $j \in \mathbb {N}$ we have $\Pi _0^+ P_{0,j} f = \Pi _0^+ P_{j,0} f = 0$.

Proof

We have that $\Pi _0^+ P_{0,j} f = 0$ if and only if $( P_{0,j} f, f_0^+ ) = 0$. By [9, formula (4.8)] we have that $P_{0,\epsilon } f_0^- = f_0^-$ for any $\epsilon$ and we have the chain of identities

for any $f \in \{f_1^+, f_{1}^-, f_0^- \}$, deducing, in particular, that $( P_{0,j} f, f_0^+ ) = 0$. The proof that $\Pi _0^+ P_{j,0} f = 0$ is obtained similarly, exploiting that $P_{\mu ,0} f_0^- = f_0^-$ as proved in [9, Lemma A.5]. $\square$

In virtue of (3.6), (3.11) and (3.15) and in view of (3.24)–(3.25) we obtain

$$\begin{aligned} \mathfrak {B}_{i,j}^{[\texttt{ ev}]} = {\left\{ \begin{array}{ll} \mathfrak {B}_{i,j} &{}if j is even \,, \\ 0 &{}if j is odd \,, \end{array}\right. } \qquad \mathfrak {B}_{i,j}^{[\texttt{odd}]} = {\left\{ \begin{array}{ll} 0 &{}if j is even \,, \\ \mathfrak {B}_{i,j} &{}if j is odd \, . \end{array}\right. } \end{aligned}$$

(3.43)

3.4 Proof of Proposition 3.1

Proposition 3.1 is a direct consequence of the next proposition.

Proposition 3.11

The $2\times 2$ matrices ${{\mathcal {E}}}:= {{\mathcal {E}}}(\mu ,\epsilon )$, $\Gamma := \Gamma (\mu ,\epsilon )$, $\Phi := \Phi (\mu ,\epsilon )$ in (3.5a)–(3.5c) admit the expansions

$$\begin{aligned}&{{\mathcal {E}}}:= \begin{pmatrix} \widetilde{\eta }_{11}\epsilon ^3 + \eta _{11} \epsilon ^4 + r_1( \epsilon ^5,\mu \epsilon ^3,\mu ^2\epsilon ,\mu ^3) &{}\quad \textrm{i}\,\left( \eta _{12}\mu \epsilon ^2 + r_2(\mu \epsilon ^3,\mu ^2\epsilon ,\mu ^3)\right) \\ - \textrm{i}\,\left( \eta _{12}\mu \epsilon ^2 + r_2(\mu \epsilon ^3,\mu ^2\epsilon ,\mu ^3)\right) &{}\quad {\widetilde{\eta }}_{22} \mu ^2 \epsilon + r_5(\mu ^2\epsilon ^2,\mu ^3) \end{pmatrix} \, , \end{aligned}$$

(3.44a)

$$\begin{aligned}&\Gamma := \begin{pmatrix} \gamma _{11} \epsilon ^2 + r_8(\epsilon ^3,\mu \epsilon ^2,\mu ^2\epsilon ) &{} \quad -\textrm{i}\,\gamma _{12} \mu \epsilon ^2- \textrm{i}\,r_9(\mu \epsilon ^3,\mu ^2\epsilon ) \\ \textrm{i}\,\gamma _{12} \mu \epsilon ^2 + \textrm{i}\,r_9(\mu \epsilon ^3, \mu ^2\epsilon ) &{}\quad {\widetilde{\gamma }}_{22} \mu ^2 \epsilon + \gamma _{22}\mu ^2 \epsilon ^2 + r_{10}(\mu ^2\epsilon ^3,\mu ^3\epsilon ) \end{pmatrix}\, , \end{aligned}$$

(3.44b)

$$\begin{aligned}&\Phi := \begin{pmatrix} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \phi _{11} \epsilon ^3 + r_3(\epsilon ^4,\mu \epsilon ^2,\mu ^2\epsilon ) &{} \textrm{i}\,{\widetilde{\phi }}_{12} \mu \epsilon ^2 + \textrm{i}\,\phi _{12} \mu \epsilon ^3 + \textrm{i}\,\widetilde{\psi }_{12} \mu ^2 \epsilon +\textrm{i}\,r_4(\mu \epsilon ^4, \mu ^2 \epsilon ^2,\mu ^3\epsilon ) \\ \textrm{i}\,\phi _{21}\mu \epsilon + \textrm{i}\,\widetilde{\phi }_{21} \mu \epsilon ^2 + \textrm{i}\,r_6(\mu \epsilon ^{3}, \mu ^2\epsilon ) &{} \phi _{22}\mu ^2\epsilon + \widetilde{\phi }_{22} \mu ^2 \epsilon ^2 + r_7(\mu ^2\epsilon ^3, \mu ^3\epsilon ) \end{pmatrix}, \end{aligned}$$

(3.44c)

where

$$\begin{aligned} \begin{aligned}&{\widetilde{\eta }}_{11}:= \big ({\mathfrak {B}_{0,3}} f_1^+,f_1^+ \big ) = 0 \,, \qquad {\widetilde{\eta }}_{22}:= \big ({\mathfrak {B}_{2,1}} f_1^-, f_1^- \big ) = 0 \,, \qquad {\widetilde{\gamma }}_{22}:= \big ({\mathfrak {B}_{2,1}} f_0^-, f_0^- \big ) = 0 \,, \\&\textrm{i}\,{\widetilde{\phi }}_{12}:= \big ({\mathfrak {B}_{1,2}} f_0^-,f_1^+ \big ) = 0 \,, \ \quad \textrm{i}\,{\widetilde{\phi }}_{21}:=\big ({\mathfrak {B}_{1,2}} f_0^+,f_1^- \big ) = -\big ({\mathfrak {B}_{1,2}} f_1^-,f_0^+ \big ) = 0 \,, \\&\widetilde{\phi }_{22}:= \big ({\mathfrak {B}_{2,2}} f_0^-,f_1^- \big ) = 0 \,, \qquad \textrm{i}\,\widetilde{\psi }_{12}:= \big ({\mathfrak {B}_{2,1}} f_0^-, f_1^+ \big )= 0\,, \end{aligned} \end{aligned}$$

(3.45a)

whereas the coefficients

$$\begin{aligned}{} & {} \eta _{11}:= \big ({\mathfrak {B}_{0,4}} f_1^+,f_1^+ \big ) \,, \qquad \ \textrm{i}\,\eta _{12}:= \big ({\mathfrak {B}_{1,2}} f_1^-,f_1^+ \big ) \,, \nonumber \\{} & {} \gamma _{11}:= \big ({\mathfrak {B}_{0,2}} f_0^+,f_0^+ \big ) \,, \qquad \textrm{i}\,\gamma _{12}:= \big ({\mathfrak {B}_{1,2}} f_0^-,f_0^+ \big ) \,, \qquad \gamma _{22}:= \big ({\mathfrak {B}_{2,2}} f_0^-,f_0^- \big ) \,, \nonumber \\{} & {} \phi _{11}:= \big ({\mathfrak {B}_{0,3}} f_0^+,f_1^+ \big ) = \big ({\mathfrak {B}_{0,3}} f_1^+,f_0^+ \big ) \,, \quad \textrm{i}\,\phi _{12}:= \big ({\mathfrak {B}_{1,3}} f_0^-,f_1^+ \big ) \,, \nonumber \\{} & {} \textrm{i}\,\phi _{21}:= \big ({\mathfrak {B}_{1,1}} f_0^+,f_1^- \big )= - \big ({\mathfrak {B}_{1,1}} f_1^-,f_0^+ \big ) \,, \quad \phi _{22} = \big ({\mathfrak {B}_{2,1}} f_0^-,f_1^- \big )\,, \end{aligned}$$

(3.45b)

are given in (3.4d)–(3.4i).

The rest of the section is devoted to the proof of Proposition 3.11.

Lemma 3.12

The coefficients ${\widetilde{\eta }}_{11}, {\widetilde{\eta }}_{22}, {\widetilde{\gamma }}_{22}, {\widetilde{\phi }}_{12}, {\widetilde{\phi }}_{21}, {\widetilde{\phi }}_{22}$ in (3.45a) vanish.

Proof

The first six coefficients in (3.45a) are (use also the self-adjointness of the jets of $\mathfrak {B}_{\mu ,\epsilon }$)

$$\begin{aligned}{} & {} \big ({\mathfrak {B}_{0,3}^{[\texttt{ ev}]}} f_1^+,f_1^+ \big ) \,,\ \big ({\mathfrak {B}_{2,1}^{[\texttt{ ev}]}} f_1^-,f_1^- \big ) \,,\ \big ({\mathfrak {B}_{2,1}^{[\texttt{ ev}]}} f_0^-,f_0^- \big ) \,, \ \big ({\mathfrak {B}_{1,2}^{[\texttt{odd}]}} f_0^-,f_1^+ \big ) \,,\\ {}{} & {} \quad \big ( f_0^+, {\mathfrak {B}_{1,2}^{[\texttt{odd}]}} f_1^- \big ) \,, \ \big ({\mathfrak {B}_{2,2}^{[\texttt{odd}]}} f_0^-,f_1^- \big ) \,, \end{aligned}$$

which are zero because, by (3.43), the operators $\mathfrak {B}_{0,3}^{[\texttt{ ev}]}\mathfrak {B}_{1,2}^{[\texttt{odd}]}=\mathfrak {B}_{2,1}^{[\texttt{ ev}]} = \mathfrak {B}_{2,2}^{[\texttt{odd}]} = 0$. $\square$

For the computation of the other coefficients we use the following lemma.

Lemma 3.13

We have

$$\begin{aligned}&{{\mathcal {B}}}_{0,1} f_1^+ = \begin{bmatrix}\frac{1}{2} (a_1^{[1]} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} - p_1^{[1]}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} )\cos (2x) \\ - p_1^{[1]}{\texttt{c}}_{\texttt{h}}^\frac{1}{2} \sin (2x) \end{bmatrix} + \mathfrak {h}^{[0]}(x) \, , \\ \nonumber&{{\mathcal {B}}}_{1,0} f_1^+ = \begin{bmatrix}0 \\ -\textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}\big ({\texttt{c}}_{\texttt{h}}^2+\texttt{h}(1-{\texttt{c}}_{\texttt{h}}^4)\big )\cos (x) \end{bmatrix}\, ,\\ \nonumber&{{\mathcal {B}}}_{1,1} f_1^+ = \frac{\textrm{i}\,p_1^{[1]}}{2}\begin{bmatrix}-{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}\sin (2x) \\ {\texttt{c}}_{\texttt{h}}^\frac{1}{2} \cos (2x) \end{bmatrix}+\mathfrak {h}^{[0]}(x) \, ,\\ \nonumber&{{\mathcal {B}}}_{0,2} f_1^+ = \begin{bmatrix}\big ( (a_2^{[0]} +\frac{1}{2} a_2^{[2]} ){\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} - (p_2^{[0]} +\frac{1}{2} p_2^{[2]} ){\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \big ) \cos (x) \\ \big (\texttt{f}_2 (1-{\texttt{c}}_{\texttt{h}}^4) {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}- (p_2^{[0]} +\frac{1}{2} p_2^{[2]}){\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} \big ) \sin (x) \end{bmatrix} \\ \nonumber&\quad + \begin{bmatrix}\frac{1}{2} \big ( a_2^{[2]} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} - p_2^{[2]} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \big ) \cos (3x) \\ -\frac{3}{2} p_2^{[2]}{\texttt{c}}_{\texttt{h}}^{\frac{1}{2}}\sin (3x) \end{bmatrix} \, ,\\ \nonumber&{{\mathcal {B}}}_{0,3} f_1^+ = \begin{bmatrix}\frac{1}{2} ( a_3^{[1]}{\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} -p_3^{[1]}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}) \\ 0 \end{bmatrix} \\ \nonumber&\quad + \begin{bmatrix}\frac{1}{2} \big (a_3^{[1]}{\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} + a_3^{[3]}{\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} -p_3^{[1]}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} - p_3^{[3]}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \big )\cos (2x) \\ -(p_3^{[1]}+p_3^{[3]}){\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} \sin (2x) \end{bmatrix}+\mathfrak {h}^{[4]}(x)\, ,\\ \nonumber&{{\mathcal {B}}}_{0,4} f_1^+ = \begin{bmatrix}\big ({\texttt{c}}_{\texttt{h}}^\frac{1}{2} (a_4^{[0]}+\frac{1}{2} a_4^{[2]}) -{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} (p_4^{[0]}+\frac{1}{2} p_4^{[2]})\big )\cos (x) \\ \big ({\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}(1-{\texttt{c}}_{\texttt{h}}^4)(\texttt{f}_4-\texttt{f}_2^2{\texttt{c}}_{\texttt{h}}^2)-{\texttt{c}}_{\texttt{h}}^{\frac{1}{2}}(p_4^{[0]}+\frac{1}{2}p_4^{[2]} \big )\sin (x) \end{bmatrix}+\mathfrak {h}^{[3,5]}(x) \, ,\\ \nonumber&{{\mathcal {B}}}_{1,0} f_1^- = \begin{bmatrix}0 \\ \textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}\big ({\texttt{c}}_{\texttt{h}}^2+\texttt{h}(1-{\texttt{c}}_{\texttt{h}}^4)\big )\sin (x) \end{bmatrix}\, ,\quad {{\mathcal {B}}}_{1,1} f_1^- =-\frac{\textrm{i}\,p_1^{[1]}}{2} \begin{bmatrix}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \\ 0 \end{bmatrix} +\mathfrak {h}^{[2]}(x) \, , \\ \nonumber&{{\mathcal {B}}}_{1,2} f_1^- = -\textrm{i}\,\begin{bmatrix}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}(p_2^{[0]}+\frac{1}{2} p_2^{[2]})\cos (x) \\ {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} (p_2^{[0]}-\frac{1}{2} p_2^{[2]})\sin (x) \end{bmatrix} + \mathfrak {h}^{[3]}(x) \, ,\\ \nonumber&{{\mathcal {B}}}_{0,1} f_0^+ = \begin{bmatrix}a_1^{[1]}\cos (x) \\ -p_1^{[1]}\sin (x) \end{bmatrix}\, ,\quad {{\mathcal {B}}}_{0,2} f_0^+ = \begin{bmatrix}a_2^{[0]} \\ 0 \end{bmatrix}+ \begin{bmatrix}a_2^{[2]}\cos (2x) \\ -2p_2^{[2]}\sin (2x) \end{bmatrix}\, ,\\ \nonumber&{{\mathcal {B}}}_{1,1} f_0^- =-\textrm{i}\,p_1^{[1]} \begin{bmatrix}\cos (x) \\ 0 \end{bmatrix} \, ,\quad {{\mathcal {B}}}_{1,2} f_0^- = -\textrm{i}\,p_2^{[0]}\begin{bmatrix}1 \\ 0 \end{bmatrix} - \textrm{i}\,p_2^{[2]} \begin{bmatrix}\cos (2x) \\ 0 \end{bmatrix} \, ,\\ \nonumber&{{\mathcal {B}}}_{1,3} f_0^- = -\textrm{i}\,p_3^{[1]}\begin{bmatrix}\cos (x) \\ 0 \end{bmatrix}+\mathfrak {h}^{[3]}(x) \,, \quad {{\mathcal {B}}}_{2,2} f_0^- = \begin{bmatrix}0 \\ \texttt{f}_2 \end{bmatrix}\, , \end{aligned}$$

(3.46)

with $p_j^{[i]}$ and $a_j^{[i]}$, $j =1,\dots ,4$, $i=0,\dots ,j$, in (A.59), (A.60) and $\texttt{f}_2$ in (A.48) and where $\mathfrak {h}^{[\kappa _1,\dots ,\kappa _\ell ]}(x)$ denotes a function supported on Fourier modes $\kappa _1,\dots ,\kappa _\ell \in {\mathbb {N}_0}$.

Proof

By (3.2)–(3.9) and (1.15). $\square$

We now compute the remaining coefficients in (3.45).

Computation of $\gamma _{11}$. In view of (3.45b) and (3.24a) we have

$$\begin{aligned} \gamma _{11} = \underbrace{\big ( {{\mathcal {B}}}_{0,2} f_0^+, f_0^+ \big )}_{a_2^{[0]} \ {\text {by} \ (3.8\textrm{c})} } + \underbrace{ \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} P_{0,1} f_0^+, f_0^+ \big ) + \frac{1}{2}\big ( {{\mathcal {B}}}_{0,1} f_0^+, P_{0,1} f_0^+ \big )}_{\mathfrak {u}_{0,1} \big ( f_{-1}^+, {{\mathcal {B}}}_{0,1} f_0^+ \big ) \ {\text {by} \ (3.17)} } \, . \end{aligned}$$

(3.47)

By (3.46) and (3.16) it results that (3.47) is equal to

$$\begin{aligned} \gamma _{11} = a_2^{[0]}+\frac{1}{2} \mathfrak {u}_{0,1} (a_1^{[1]}{\texttt{c}}_{\texttt{h}}^{\frac{1}{2}}+p_1^{[1]}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}})\,, \end{aligned}$$

which in view of (A.59), (3.18) gives the term in (3.4f).

Computation of $\phi _{21}$. In view of (3.45b) and (3.38b) we have

$$\begin{aligned} \begin{aligned} \textrm{i}\,\phi _{21}&=-\big (\mathfrak {B}_{1,1} f_1^-, f_0^+ \big ) \\&=- \big ( {{\mathcal {B}}}_{1,1} f_1^-, f_0^+ \big ) - \underbrace{ \big ( {{\mathcal {B}}}_{0,1} P_{1,0} f_1^-, f_0^+ \big )}_{\textrm{i}\,\mathfrak {u}_{1,0} \big ( f_{-1}^+, {{\mathcal {B}}}_{0,1} f_0^+ \big ) \ {\text {by} \ (3.17)} } -\underbrace{ \big ( {{\mathcal {B}}}_{1,0} P_{0,1} f_1^-, f_0^+ \big ) }_{0 \ {\text {by} \ (3.17)}}\\ {}&\quad -\underbrace{ \frac{1}{2} \big (\Pi _0^+ P_{1,1} f_1^-, f_0^+ \big )}_{0 \ {\text {by} \ (3.19\textrm{e})}} \, . \end{aligned} \end{aligned}$$

By (3.46), (1.15) and (3.16) it results

$$\begin{aligned} \phi _{21} = \frac{1}{2} \big ({\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} p_1^{[1]}-\mathfrak {u}_{1,0} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} a_1^{[1]}-\mathfrak {u}_{1,0} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} p_1^{[1]} \big ) \end{aligned}$$

which in view of (A.59), (3.18) gives the term in (3.4i).

Computation of $\eta _{12}$. In view of (3.45b) and (3.38d), (3.17), Lemmata 3.4 and 3.5 we have

$$\begin{aligned} \textrm{i}\,\eta _{12}&= \big ( {{\mathcal {B}}}_{1,2} f_1^- , f_1^+ \big ) + \underbrace{\big ( {{\mathcal {B}}}_{1,1} P_{0,1} f_1^- , f_1^+\big )}_{\big ( {\begin{bmatrix}-\mathfrak {a}_{0,1}\sin (2x) \\ \mathfrak {b}_{0,1}\cos (2x) \end{bmatrix}} ,{{\mathcal {B}}}_{1,1} f_1^+\big ) \ by (3.17) } + \underbrace{\big ( {{\mathcal {B}}}_{0,2} P_{1,0} f_1^- , f_1^+ \big )}_{\textrm{i}\,\mathfrak {u}_{1,0} \big ( f_{-1}^+, {{\mathcal {B}}}_{0,2} f_1^+ \big ) by (3.17) } \\&\quad + \underbrace{\big ( {{\mathcal {B}}}_{1,0} P_{0,2} f_1^- , f_1^+ \big )}_{\underline{\mathfrak {n}_{0,2}({{\mathcal {B}}}_{1,0} f_1^-, f_1^+)} + \mathfrak {u}_{0,2}^-( f_{-1}^-,{{\mathcal {B}}}_{1,0} f_1^+) by (3.19\textrm{b}) } +\quad \underbrace{\big ( {{\mathcal {B}}}_{0,1} P_{1,1} f_1^- , f_1^+ \big )}_{\textrm{i}\,\big (\begin{bmatrix}\mathfrak {a}_{1,1}\cos (2x) \\ \mathfrak {b}_{1,1}\sin (2x) \end{bmatrix}, {{\mathcal {B}}}_{0,1} f_1^+ \big ) by (3.19\textrm{e})}\\&\quad +\underbrace{\frac{1}{2} \big ( \Pi _0^+ P_{1,2} f_1^-, f_1^+ \big )}_{=0 since \Pi _0^+ f_1^+ =0} \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{1,0} P_0 P_{0,2} f_1^- , f_1^+ \big )}_{\underline{-\frac{1}{2} \mathfrak {n}_{0,2}({{\mathcal {B}}}_{1,0} f_1^-, f_1^+)} by (3.19\textrm{b})} \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} P_0 P_{1,1} f_1^- , f_1^+\big )}_{=0 by (3.19\textrm{e})}\\&\quad \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{1,0} f_1^- , P_0 P_{0,2} f_1^+ \big )}_{\underline{-\frac{1}{2} \mathfrak {n}_{0,2} ({{\mathcal {B}}}_{1,0} f_1^-, f_1^+)} by (3.19\textrm{a})}\ \ \quad \underbrace{ - \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} f_1^- , P_0 P_{1,1} f_1^+ \big ) }_{{\mathop {=}\limits ^{(3.19\textrm{e})}}+\textrm{i}\,\frac{1}{2}{\widetilde{\mathfrak {m}}}_{1,1}( f_1^-,{{\mathcal {B}}}_{0,1} f_0^-) =0} \, , \end{aligned}$$

where the three underlined terms cancel out. Hence, by (3.46), (1.15) and (3.16),

$$\begin{aligned} \eta _{12}&= - p_2^{[0]} - \frac{1}{4} p_1^{[1]} (\mathfrak {b}_{0,1} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} + \mathfrak {a}_{0,1} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}) + \mathfrak {u}_{1,0} \big ( \frac{1}{2} {\texttt{c}}_{\texttt{h}}a_2^{[0]} + \frac{1}{4} {\texttt{c}}_{\texttt{h}}a_2^{[2]} - \frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-1} \texttt{f}_2 (1-{\texttt{c}}_{\texttt{h}}^4) \big ) \\&\quad +\frac{1}{2} \mathfrak {u}_{0,2}^- ({\texttt{c}}_{\texttt{h}}^2+\texttt{h}(1-{\texttt{c}}_{\texttt{h}}^4)){\texttt{c}}_{\texttt{h}}^{-1} + \frac{1}{4} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} a_1^{[1]}\mathfrak {a}_{1,1} - \frac{1}{2} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} p_1^{[1]} \mathfrak {b}_{1,1} -\frac{1}{4}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} p_1^{[1]} \mathfrak {a}_{1,1} \end{aligned}$$

which in view of (A.59), (3.18) and (3.19c) gives the term in (3.4e).

Computation of $\gamma _{12}$. By (3.45b) and (3.38d), (3.17), Lemma 3.4 and 3.5 and since ${{\mathcal {B}}}_{0,1} f_0^- = 0$ and ${{\mathcal {B}}}_{1,0} f_0^- = 0$ we have

$$\begin{aligned} \textrm{i}\,\gamma _{12}&= \big ( {{\mathcal {B}}}_{1,2}f_0^- , f_0^+ \big ) \underbrace{+ \big ( {{\mathcal {B}}}_{1,1} P_{0,1} f_0^- , f_0^+\big )}_{= 0} \underbrace{+\big ( {{\mathcal {B}}}_{0,2} P_{1,0} f_0^- , f_0^+ \big )}_{=0} \\&\quad \underbrace{+\big ( {{\mathcal {B}}}_{1,0} P_{0,2} f_0^- , f_0^+ \big )}_{=0} \underbrace{+\big ( {{\mathcal {B}}}_{0,1} P_{1,1} f_0^- , f_0^+ \big ) }_{-\textrm{i}\,\frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-3/2} ( f_{-1}^+, {{\mathcal {B}}}_{0,1} f_0^+)} \underbrace{+\frac{1}{2} \big ( \Pi _0^+ P_{1,2} f_0^-, f_0^+ \big )}_{=0}\\&\quad \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{1,0} P_0 P_{0,2} f_0^- , f_0^+ \big )}_{=0} \underbrace{ - \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} P_0 P_{1,1} f_0^- , f_0^+\big )}_{=0} \\&\quad \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{1,0} f_0^- ,P_0 P_{0,2} f_0^+ \big )}_{=0} \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} f_0^- , P_0 P_{1,1} f_0^+ \big )}_{=0} \, . \end{aligned}$$

So, by (3.46), (1.15) and (3.16),

$$\begin{aligned} \gamma _{12} = -p_2^{[0]} - \frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-3/2} (a_1^{[1]}{\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} + p_1^{[1]}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} ) \end{aligned}$$

which in view of (A.59) gives the term (3.4f).

Computation of $\phi _{11}$. By (3.45b) and (3.38c), (3.17), Lemma 3.4 and 3.5 we have

$$\begin{aligned} \phi _{11}&= \big ( {{\mathcal {B}}}_{0,3}f_1^+ , f_0^+ \big ) + \underbrace{\big ( {{\mathcal {B}}}_{0,2} P_{0,1} f_1^+ , f_0^+\big )}_{\big ({\begin{bmatrix}\mathfrak {a}_{0,1}\cos (2x) \\ \mathfrak {b}_{0,1}\sin (2x) \end{bmatrix}}, {{\mathcal {B}}}_{0,2} f_0^+\big )}+\underbrace{\big ( {{\mathcal {B}}}_{0,1} P_{0,2} f_1^+ , f_0^+ \big ) }_{ \mathfrak {n}_{0,2}(f_1^+,{{\mathcal {B}}}_{0,1} f_0^+) + \mathfrak {u}_{0,2}^+(f_{-1}^+, {{\mathcal {B}}}_{0,1} f_0^+) }\\&\quad \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} P_0 P_{0,2} f_1^+ , f_0^+ \big )}_{ -\frac{1}{2} \mathfrak {n}_{0,2}(f_1^+, {{\mathcal {B}}}_{0,1} f_0^+) } \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} f_1^+ ,P_0 P_{0,2} f_0^+ \big ) }_{{\mathop {=}\limits ^{(3.19\textrm{a})}}0} \, . \end{aligned}$$

Thus, by (3.46), (1.15) and (3.16),

$$\begin{aligned} \begin{aligned} \phi _{11}&= \frac{1}{2} a_3^{[1]} {\texttt{c}}_{\texttt{h}}^\frac{1}{2} -\frac{1}{2} p_3^{[1]}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} + \frac{1}{2} \mathfrak {a}_{0,1} a_2^{[2]} - \mathfrak {b}_{0,1} p_2^{[2]} \\&\quad + \frac{1}{4} \mathfrak {n}_{0,2} (a_1^{[1]}{\texttt{c}}_{\texttt{h}}^\frac{1}{2} -p_1^{[1]}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} ) + \frac{1}{2} \mathfrak {u}_{0,2}^+ (a_1^{[1]}{\texttt{c}}_{\texttt{h}}^\frac{1}{2} +p_1^{[1]}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} ) \end{aligned} \end{aligned}$$

which in view of (A.59), (3.18), (3.19c), gives the term (3.4g).

Computation of $\phi _{22}$. By (3.45b) and (3.38e), (3.17), Lemma 3.4 and 3.5 and since ${{\mathcal {B}}}_{2,1}=0$ and ${{\mathcal {B}}}_{0,1} f_0^-=0$, ${{\mathcal {B}}}_{1,0} f_0^-=0$ we have

$$\begin{aligned} \phi _{22}&= \underbrace{ \big ( {{\mathcal {B}}}_{2,1}f_0^- , f_1^-\big )}_{0} + \underbrace{\big ( {{\mathcal {B}}}_{1,1} P_{1,0} f_0^- , f_1^-\big )}_{0} \underbrace{+\big ( {{\mathcal {B}}}_{2,0} P_{0,1} f_0^- , f_1^- \big )}_{0}\\&\quad \underbrace{+\big ( {{\mathcal {B}}}_{0,1} P_{2,0} f_0^- , f_1^- \big )}_{0} \underbrace{ +\big ( {{\mathcal {B}}}_{1,0} P_{1,1} f_0^- , f_1^- \big ) }_{-\frac{\textrm{i}\,}{2}{\texttt{c}}_{\texttt{h}}^{-3/2} \big (f_{-1}^+,{{\mathcal {B}}}_{1,0} f_1^-\big ) }+ \underbrace{\frac{1}{2} \big ( \Pi _0^+ P_{2,1} f_0^-, f_1^-)}_{\frac{1}{2} \big ( {\tilde{\mathfrak {n}}}_{2,1} \Pi _0^+ f_1^- +{\tilde{\mathfrak {u}}}_{2,1} \Pi _0^+ f_{-1}^-, f_1^-)=0} \\&\quad \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} P_0 P_{2,0} f_0^- , f_1^- \big )}_{=0} -\underbrace{\frac{1}{2} \big ( {{\mathcal {B}}}_{1,0} P_0 P_{1,1} f_0^- , f_1^-\big )}_{=0}\\&\quad - \underbrace{ \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} f_0^- ,P_0 P_{2,0} f_1^- \big )}_{=0} - \underbrace{ \frac{1}{2} \big ( {{\mathcal {B}}}_{1,0} f_0^- , P_0 P_{1,1} f_1^- \big )}_{=0} \, . \end{aligned}$$

So, by (3.46) and (3.16),

$$\begin{aligned} \phi _{22} = \frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-\frac{5}{2}} ({\texttt{c}}_{\texttt{h}}^2+\texttt{h}(1-{\texttt{c}}_{\texttt{h}}^4)) \end{aligned}$$

which is the term (3.4i).

Computation of ${\widetilde{\psi }}_{12}$. By (3.45a), (3.38e) and since ${{\mathcal {B}}}_{2,1} =0$, $P_{1,0} f_0^- = 0$, $P_{0,1} f_0^- = 0$ by (3.17), Lemmata 3.4 and 3.5 this term is given by

$$\begin{aligned} \textrm{i}\,{\widetilde{\psi }}_{12}&=\underbrace{ \big ( {{\mathcal {B}}}_{2,1}f_0^- , f_1^+ \big )}_{=0} + \underbrace{ \big ( {{\mathcal {B}}}_{1,1} P_{1,0} f_0^- , f_1^+\big )}_{=0}+\underbrace{\big ( {{\mathcal {B}}}_{2,0} P_{0,1} f_0^- , f_1^+ \big )}_{=0} \\&+\underbrace{\big ( {{\mathcal {B}}}_{0,1} P_{2,0} f_0^- , f_1^+ \big )}_{=0 \ {\text {by} \, (3.19\textrm{d})} } +\underbrace{\big ( {{\mathcal {B}}}_{1,0} P_{1,1} f_0^- , f_1^+ \big ) }_{-\frac{\textrm{i}\,}{2} {\texttt{c}}_{\texttt{h}}^{-\frac{3}{2}} \big (f_{-1}^+,{{\mathcal {B}}}_{1,0} f_1^+ \big ) \ \text {by} (3.19\textrm{e})} +\underbrace{\frac{1}{2} \big (\Pi _0^+ P_{2,1} f_0^-, f_1^+ \big )}_{ =0 \ \text {as } \Pi _0^+ f_1^+ = 0}\\&- \underbrace{\frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} P_0 P_{2,0} f_0^- , f_1^+ \big ) }_{=0 \ {\text {by} \, (3.19\textrm{d})} } - \frac{1}{2} \underbrace{\big ( {{\mathcal {B}}}_{1,0} P_0 P_{1,1} f_0^- , f_1^+\big )}_{=0 \ \text {by} \, (3.19\textrm{e}) } \\&- \frac{1}{2} \underbrace{\big ( {{\mathcal {B}}}_{0,1} f_0^- ,P_0 P_{2,0} f_1^+ \big )}_{=0 \ \text {since} \ {{\mathcal {B}}}_{0,1} f_0^- = 0 } - \frac{1}{2} \underbrace{\big ( {{\mathcal {B}}}_{1,0} f_0^- , P_0 P_{1,1} f_1^+ \big ) }_{=0 { \ \text {since} \ {{\mathcal {B}}}_{1,0} f_0^- = 0 } } \end{aligned}$$

and finally, by (3.16) and (3.46),

$$\begin{aligned} \textrm{i}\,{\widetilde{\psi }}_{12} = -\tfrac{\textrm{i}\,}{2 } {\texttt{c}}_{\texttt{h}}^{-3/2} \big (f_{-1}^+,{{\mathcal {B}}}_{1,0} f_1^+ \big ) = 0 \, . \end{aligned}$$

Computation of $\eta _{11}$. By (3.45b), (3.38f), (3.17), Lemma 3.4 and Lemma 3.5 and (3.26), we have

$$\begin{aligned} \eta _{11}&= \big ( {{\mathcal {B}}}_{0,4} f_1^+,f_1^+\big )+ \underbrace{ \big ({{\mathcal {B}}}_{0,3} P_{0,1} f_1^+,f_1^+\big ) }_{ \big ( {\begin{bmatrix}\mathfrak {a}_{0,1} \cos (2x) \\ \mathfrak {b}_{0,1} \sin (2x) \end{bmatrix}}, {{\mathcal {B}}}_{0,3} f_1^+ \big )} + \underbrace{\big ( {{\mathcal {B}}}_{0,2}P_{0,2} f_1^+,f_1^+\big )}_{\big (\underline{\mathfrak {n}_{0,2} f_1^+} + \mathfrak {u}_{0,2}^+ f_{-1}^+ + {\begin{bmatrix}\mathfrak {a}_{0,2} \cos (3x) \\ \mathfrak {b}_{0,2} \sin (3x) \end{bmatrix}}, {{\mathcal {B}}}_{0,2} f_1^+ \big )} \\&\quad + \underbrace{ \big ( {{\mathcal {B}}}_{0,1} P_{0,3}f_1^+,f_1^+\big )}_{\big ( {\begin{bmatrix}\mathfrak {a}_{0,3} \cos (2x) \\ \mathfrak {b}_{0,3} \sin (2x) \end{bmatrix}}, {{\mathcal {B}}}_{0,1} f_1^+ \big )} \underbrace{ - \frac{1}{2} \big ({{\mathcal {B}}}_{0,2}P_0P_{0,2} f_1^+,f_1^+\big )}_{\underline{-\frac{1}{2} \mathfrak {n}_{0,2} \big ({{\mathcal {B}}}_{0,2} f_1^+,f_1^+\big )}} \\&\quad \underbrace{- \frac{1}{2} \big ({{\mathcal {B}}}_{0,2} f_1^+, P_0P_{0,2} f_1^+\big )}_{\underline{-\frac{1}{2} \mathfrak {n}_{0,2} \big ({{\mathcal {B}}}_{0,2} f_1^+,f_1^+\big )}} -\underbrace{\frac{1}{2} \big ( {{\mathcal {B}}}_{0,1}P_0P_{0,3} f_1^+,f_1^+\big )}_{=0} \\&\quad -\frac{1}{2} \underbrace{\big ({{\mathcal {B}}}_{0,1} f_1^+,P_0 P_{0,3}f_1^+\big )}_{=0} \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1}P_{0,1} P_0 P_{0,2} f_1^+,f_1^+\big )}_{-\frac{1}{2} \mathfrak {n}_{0,2} \big ( {\begin{bmatrix}\mathfrak {a}_{0,1} \cos (2x) \\ \mathfrak {b}_{0,1}\sin (2x) \end{bmatrix}}, {{\mathcal {B}}}_{0,1} f_1^+\big )} \underbrace{- \frac{1}{2} \big ( {{\mathcal {B}}}_{0,1} f_1^+,P_{0,1} P_0 P_{0,2} f_1^+\big )}_{-\frac{1}{2} \mathfrak {n}_{0,2} \big ( {\begin{bmatrix}\mathfrak {a}_{0,1} \cos (2x) \\ \mathfrak {b}_{0,1}\sin (2x) \end{bmatrix}},{{\mathcal {B}}}_{0,1} f_1^+\big )} \\&\quad +\frac{1}{2} \underbrace{\big (\mathfrak {N}_{0,2} P_0 P_{0,2} f_1^+, f_1^+ \big )}_{=0} + \underbrace{\frac{1}{2} \big ( f_1^+, \mathfrak {N}_{0,2} P_0 P_{0,2} f_1^+ \big )}_{=0} \, , \end{aligned}$$

where the three underlined terms cancel out. Thus, in view of (3.46), (1.15) and (3.16), we get

$$\begin{aligned} \eta _{11}&= {\texttt{c}}_{\texttt{h}}\frac{a_4^{[0]}}{2} + {\texttt{c}}_{\texttt{h}}\frac{a_4^{[2]}}{4} - p_4^{[0]} - \frac{p_4^{[2]}}{2} + \frac{1}{2{\texttt{c}}_{\texttt{h}}} (1-{\texttt{c}}_{\texttt{h}}^4)(\texttt{f}_4-\texttt{f}_2^2{\texttt{c}}_{\texttt{h}}^2) \\ \nonumber&\quad + \frac{1}{4} \big ( {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} (a_3^{[1]} + a_3^{[3]})- {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} ( p_3^{[1]} + p_3^{[3]}) \big )\mathfrak {a}_{0,1} - \frac{1}{2} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} ( p_3^{[3]} + p_{3}^{[1]} ) \mathfrak {b}_{0,1} \nonumber \\ \nonumber&\quad + \frac{1}{4}\big ( a_{2}^{[2]} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} - p_{2}^{[2]} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \big ) \mathfrak {a}_{0,2} - \frac{3}{4} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} p_{2}^{[2]} \mathfrak {b}_{0,2} \\ \nonumber&\quad + \frac{1}{2} \mathfrak {u}_{0,2}^+ \big ( {\texttt{c}}_{\texttt{h}}a_2^{[0]} + \frac{1}{2} {\texttt{c}}_{\texttt{h}}a_2^{[2]} - {\texttt{c}}_{\texttt{h}}^{-1} \texttt{f}_2 (1-{\texttt{c}}_{\texttt{h}}^4) \big ) \nonumber \\ \nonumber&\quad + \frac{1}{4}\mathfrak {a}_{0,3} \big (a_1^{[1]} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} - p_{1}^{[1]} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \big ) -\frac{1}{2} \mathfrak {b}_{0,3} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} p_1^{[1]}\\ \nonumber&\quad - \frac{1}{4} \mathfrak {n}_{0,2} \mathfrak {a}_{0,1}(a_{1}^{[1]} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} - p_1^{[1]} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} ) + \frac{1}{2} \mathfrak {n}_{0,2} \mathfrak {b}_{0,1} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} p_{1}^{[1]} \end{aligned}$$

(3.48)

which in view of (A.59), (A.60c), (3.18), (3.19c), (3.22) gives (3.4d).

Computation of $\gamma _{22}$. By (3.45b), (3.38g), where we exploit that $\big ({\textbf {Sym}} [A] f,f\big )= \mathfrak {Re} \big (Af,f \big )$, (3.17), Lemma 3.4, Lemma 3.5 and since ${{\mathcal {B}}}_{0,1} f_0^-=0$ and ${{\mathcal {B}}}_{1,0} f_0^-=0$ we have

$$\begin{aligned} \gamma _{22}&= \underbrace{\big ( {{\mathcal {B}}}_{2,2} f_0^-, f_0^- \big )}_{\texttt{f}_2} + \underbrace{\big ( {{\mathcal {B}}}_{1,2} P_{1,0} f_0^-, f_0^- \big )}_{=0} + \underbrace{ \big ( {{\mathcal {B}}}_{2,1} P_{0,1}f_0^-, f_0^- \big )}_{=0} + \underbrace{\big ( {{\mathcal {B}}}_{0,2}P_{2,0}f_0^-, f_0^- \big )}_{=0}\\&\quad + \underbrace{\big ( {{\mathcal {B}}}_{1,1}P_{1,1}f_0^-, f_0^- \big )}_{-\frac{\textrm{i}\,}{2} {\texttt{c}}_{\texttt{h}}^{-3/2}\big ( f_{-1}^+,{{\mathcal {B}}}_{1,1} f_0^-\big ) } + \underbrace{\big ( {{\mathcal {B}}}_{2,0} P_{0,2} f_0^-, f_0^- \big )}_{=0} + \underbrace{\big ( {{\mathcal {B}}}_{0,1} P_{2,1} f_0^-, f_0^- \big )}_{\big ( P_{2,1} f_0^-,{{\mathcal {B}}}_{0,1} f_0^- \big )=0}\\&\quad + \underbrace{\big ( {{\mathcal {B}}}_{1,0} P_{1,2} f_0^-, f_0^- \big )}_{ = 0} + \frac{1}{2} \underbrace{\big ( \Pi _0^+ P_{2,2} f_0^-, f_0^-\big ) }_{=0}\\&\quad \underbrace{- \mathfrak {Re} \big ( {{\mathcal {B}}}_{0,2}P_0P_{2,0}f_0^-, f_0^- \big )}_{= 0} \underbrace{-\mathfrak {Re} \big ({{\mathcal {B}}}_{1,1}P_0P_{1,1}f_0^-, f_0^- \big )}_{ = 0 } \underbrace{-\mathfrak {Re} \big ({{\mathcal {B}}}_{2,0}P_0P_{0,2}f_0^-, f_0^- \big )}_{=0}\\&\quad \underbrace{ -\mathfrak {Re} \big ( {{\mathcal {B}}}_{0,1}P_0P_{2,1}f_0^-, f_0^- \big )}_{\big ( P_0P_{2,1}f_0^-, {{\mathcal {B}}}_{0,1} f_0^- \big )=0} \\&\quad \underbrace{-\mathfrak {Re} \big ( {{\mathcal {B}}}_{1,0}P_0P_{1,2}f_0^-, f_0^- \big )}_{ = 0} \underbrace{-\mathfrak {Re} \big ( {{\mathcal {B}}}_{0,1}P_{0,1} P_0 P_{2,0}f_0^-, f_0^- \big ) }_{=0} \\&\quad \underbrace{-\mathfrak {Re} \big ( {{\mathcal {B}}}_{1,0}P_{0,1} P_0 P_{1,1} f_0^-, f_0^- \big )}_{=0} \underbrace{-\mathfrak {Re} \big ( {{\mathcal {B}}}_{0,1}P_{1,0} P_0 P_{1,1}f_0^-, f_0^- \big ) }_{=0}\\ {}&\quad \underbrace{-\mathfrak {Re} \big ( {{\mathcal {B}}}_{1,0} P_{1,0} P_0 P_{0,2} f_0^-, f_0^- \big ) }_{=0}\\&\quad \underbrace{+\mathfrak {Re} \big ( \mathfrak {N}_{2,0} P_0 P_{0,2} f_0^-, f_0^- \big )}_{=0} \underbrace{+\mathfrak {Re} \big ( \mathfrak {N}_{0,2} P_0 P_{2,0}f_0^-, f_0^-)}_{=0} \underbrace{+\mathfrak {Re}\big ( \mathfrak {N}_{1,1} P_0 P_{1,1} f_0^-, f_0^- \big )}_{=0}\, . \end{aligned}$$

Then by (3.8e), (3.9), (3.10d), (3.16) and (3.46) we get

$$\begin{aligned} \gamma _{22} = \texttt{f}_2 + \frac{p_1^{[1]}}{4{\texttt{c}}_{\texttt{h}}} \end{aligned}$$

which, in view of (A.48), (A.59c) gives (3.4f).

Computation of $\phi _{12}$. By (3.45b), (3.38h), (3.17), Lemma 3.4, Lemma 3.5, (3.26) and since ${{\mathcal {B}}}_{0,2} f_0^-=0$, ${{\mathcal {B}}}_{1,0} f_0^-=0$ and ${{\mathcal {B}}}_{0,1} f_0^-=0$ we have

$$\begin{aligned} \textrm{i}\,\phi _{12}&= \big ( {{\mathcal {B}}}_{1,3} f_0^-, f_1^+ \big ) + \underbrace{\big ( {{\mathcal {B}}}_{0,3} P_{1,0}f_0^-, f_1^+ \big )}_{=0} + \underbrace{\big ( {{\mathcal {B}}}_{1,2} P_{0,1}f_0^-, f_1^+ \big )}_{=0} \\&\quad + \underbrace{\big ( {{\mathcal {B}}}_{0,2}P_{1,1}f_0^-, f_1^+ \big )}_{-\frac{\textrm{i}\,}{2}{\texttt{c}}_{\texttt{h}}^{-3/2} \big ( f_{-1}^+, {{\mathcal {B}}}_{0,2} f_1^+ \big )} + \underbrace{\big ( {{\mathcal {B}}}_{1,1}P_{0,2} f_0^-, f_1^+ \big )}_{=0} + \underbrace{\big ({{\mathcal {B}}}_{1,0} P_{0,3}f_0^-, f_1^+ \big )}_{=0} +\underbrace{\big ( {{\mathcal {B}}}_{0,1} P_{1,2}f_0^-, f_1^+ \big )}_{\textrm{i}\,\big ({\begin{bmatrix}\mathfrak {a}_{1,2}\cos (2x) \\ \mathfrak {b}_{1,2} \sin (2x) \end{bmatrix}}, {{\mathcal {B}}}_{0,1} f_1^+ \big )} \\&\quad +\underbrace{\frac{1}{2} \big ( \Pi _0^+ P_{1,3} f_0^- , f_1^+ \big )}_{=0} - \frac{1}{2} \underbrace{\big ( {{\mathcal {B}}}_{0,2}P_0P_{1,1}f_0^-, f_1^+ \big )}_{=0} - \frac{1}{2} \underbrace{\big ( {{\mathcal {B}}}_{0,2}f_0^-,P_0P_{1,1} f_1^+ \big )}_{=0} \\&\quad -\frac{1}{2} \underbrace{\big ({{\mathcal {B}}}_{1,1} P_0P_{0,2} f_0^-, f_1^+ \big )}_{=0} \underbrace{-\frac{1}{2}\big ({{\mathcal {B}}}_{1,1}f_0^-, P_0P_{0,2} f_1^+ \big )}_{-\frac{1}{2} \mathfrak {n}_{0,2} \big ({{\mathcal {B}}}_{1,1}f_0^-, f_1^+ \big ) } -\frac{1}{2} \underbrace{\big ({{\mathcal {B}}}_{1,0}P_0P_{0,3}f_0^-, f_1^+ \big )}_{=0} \\&\quad -\frac{1}{2} \underbrace{ \big ({{\mathcal {B}}}_{1,0}f_0^-, P_0P_{0,3} f_1^+ \big )}_{=0} -\frac{1}{2} \underbrace{\big ( {{\mathcal {B}}}_{0,1}P_0P_{1,2} f_0^-, f_1^+ \big )}_{=0} -\frac{1}{2} \underbrace{\big ( {{\mathcal {B}}}_{0,1}f_0^-,P_0P_{1,2} f_1^+ \big )}_{=0} \\&\quad -\frac{1}{2}\underbrace{\big ( {{\mathcal {B}}}_{1,0}P_{0,1} P_0 P_{0,2}f_0^-, f_1^+ \big )}_{=0} -\frac{1}{2}\underbrace{\big ( {{\mathcal {B}}}_{1,0}f_0^-, P_{0,1} P_0 P_{0,2} f_1^+ \big )}_{=0} -\frac{1}{2} \underbrace{\big ( {{\mathcal {B}}}_{0,1}P_{1,0} P_0 P_{0,2}f_0^-, f_1^+ \big )}_{=0}\\&\quad -\frac{1}{2} \underbrace{\big ( {{\mathcal {B}}}_{0,1}f_0^-, P_{1,0} P_0 P_{0,2} f_1^+ \big )}_{=0} -\frac{1}{2}\underbrace{\big ( {{\mathcal {B}}}_{0,1}P_{0,1} P_0 P_{1,1}f_0^-, f_1^+ \big )}_{=0} -\frac{1}{2} \underbrace{\big ( {{\mathcal {B}}}_{0,1}f_0^-, P_{0,1} P_0 P_{1,1} f_1^+ \big )}_{=0} \\&\quad +\underbrace{\frac{1}{2} \big ( \mathfrak {N}_{1,1} P_0 P_{0,2} f_0^-, f_1^+ \big )}_{=0} +\underbrace{\frac{1}{2} \big ( f_0^-, \mathfrak {N}_{1,1} P_0 P_{0,2} f_1^+ \big )}_{=0} \\&\quad +\underbrace{\frac{1}{2} \big ( \mathfrak {N}_{0,2} P_0 P_{1,1} f_0^-, f_1^+ \big ) }_{=0} +\underbrace{\frac{1}{2} \big ( f_0^-, \mathfrak {N}_{0,2} P_0 P_{1,1} f_1^+ \big ) }_{-\frac{\textrm{i}\,}{2} {\widetilde{\mathfrak {m}}}_{1,1} \big (f_0^- , \mathfrak {N}_{0,2} f_0^- \big ){\mathop {=}\limits ^{(3.26)}} 0 } \, . \end{aligned}$$

Hence by (3.46), (1.15), (3.16), we have

$$\begin{aligned} \begin{aligned} \phi _{12}&= - \frac{1}{2} p_3^{[1]} {\texttt{c}}_{\texttt{h}}^{1/2} - \frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} (a_2^{[0]} +\frac{1}{2} a_2^{[2]}) +\frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-\frac{5}{2}}\texttt{f}_2 (1-{\texttt{c}}_{\texttt{h}}^4) \\&\quad + \frac{1}{4} \mathfrak {a}_{1,2} (a_1^{[1]}{\texttt{c}}_{\texttt{h}}^\frac{1}{2} - p_1^{[1]}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}) - \frac{1}{2} \mathfrak {b}_{1,2} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} p_1^{[1]} +\frac{1}{4} \mathfrak {n}_{0,2} p_1^{[1]} {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} \,, \end{aligned} \end{aligned}$$

which, in view of (A.59), (3.22) gives the term (3.4h).

4 Block-Decoupling and Proof of Theorem 1.3

In this section we prove Theorem 1.3 by block-decoupling the $4 \times 4$ Hamiltonian matrix $\texttt{L}_{\mu ,\epsilon } = \texttt{J}_4 \texttt{B}_{\mu ,\epsilon }$ in (2.8) obtained in Proposition 3.1, expanding the computations of [9] at a higher degree of accuracy.

We first perform the singular symplectic and reversibility-preserving change of coordinates in [9, Lemma 5.1].

Lemma 4.1

(Singular symplectic rescaling) The conjugation of the Hamiltonian and reversible matrix $\texttt{L}_{\mu ,\epsilon } = \texttt{J}_4 \texttt{B}_{\mu ,\epsilon }$ in (2.8) obtained in Proposition 3.1 through the symplectic and reversibility-preserving $4 \times 4$-matrix

$$\begin{aligned} Y:= \begin{pmatrix} Q &{} 0 \\ 0 &{} Q \end{pmatrix} \quad \text {with} \quad Q:=\begin{pmatrix} \mu ^{\frac{1}{2}} &{} 0 \\ 0 &{} \mu ^{-\frac{1}{2}}\end{pmatrix} \,, \ \ \mu > 0 \,, \end{aligned}$$

yields the Hamiltonian and reversible matrix

$$\begin{aligned}&\texttt{L}_{\mu ,\epsilon }^{(1)} := Y^{-1} \texttt{L}_{\mu ,\epsilon } Y = \texttt{J}_4\texttt{B}^{(1)}_{\mu ,\epsilon } = \begin{pmatrix} \texttt{J}_2 E^{(1)} &{} \texttt{J}_2 F^{(1)} \\ \texttt{J}_2 [F^{(1)}]^* &{} \texttt{J}_2 G^{(1)} \end{pmatrix} \end{aligned}$$

(4.1)

where $\texttt{B}_{\mu ,\epsilon }^{(1)}$ is a self-adjoint and reversibility-preserving $4 \times 4$ matrix

$$\begin{aligned} \texttt{B}_{\mu ,\epsilon }^{(1)} = \begin{pmatrix} E^{(1)} &{} F^{(1)} \\ [F^{(1)}]^* &{} G^{(1)} \end{pmatrix}, \quad E^{(1)} = [E^{(1)}]^* \,, \ G^{(1)} = [G^{(1)}]^* \,, \end{aligned}$$

where the $2 \times 2$ reversibility-preserving matrices $E^{(1)}:= E^{(1)} (\mu , \epsilon )$, $G^{(1)}:= G^{(1)} (\mu , \epsilon )$ and $F^{(1)}:= F^{(1)} (\mu , \epsilon )$ extend analytically at $\mu = 0$ with the expansion

$$\begin{aligned}&E^{(1)} = \begin{pmatrix} \texttt{e}_{11} \mu \epsilon ^2(1+ r_1'(\epsilon ^3,\mu \epsilon )) + \eta _{11} \mu \epsilon ^4 - \texttt{e}_{22}\frac{\mu ^3}{8}(1+r_1''(\epsilon ,\mu )) &{}\quad \textrm{i}\,\big ( \frac{1}{2}\texttt{e}_{12}\mu +\eta _{12}\mu \epsilon ^2+ r_2 (\mu \epsilon ^3,\mu ^2\epsilon ,\mu ^3) \big ) \\ - \textrm{i}\,\big ( \frac{1}{2}\texttt{e}_{12} \mu +\eta _{12}\mu \epsilon ^2 + r_2(\mu \epsilon ^3,\mu ^2\epsilon ,\mu ^3) \big ) &{}\quad -\texttt{e}_{22}\frac{\mu }{8}(1+r_5(\epsilon ^2,\mu )) \end{pmatrix} \end{aligned}$$

(4.2a)

$$\begin{aligned}&G^{(1)} := \begin{pmatrix} \mu +\gamma _{11} \mu \epsilon ^2 +r_8( \mu \epsilon ^3, {\mu ^2\epsilon ^2},\mu ^3\epsilon ) &{} -\textrm{i}\,\gamma _{12} \mu \epsilon ^2 - \textrm{i}\,r_9(\mu \epsilon ^3,\mu ^2\epsilon ) \\ \textrm{i}\,\gamma _{12} \mu \epsilon ^2+\textrm{i}\,r_9(\mu \epsilon ^3, \mu ^2\epsilon ) &{} \tanh (\texttt{h}\mu )+\gamma _{22} \mu \epsilon ^2 +r_{10}(\mu \epsilon ^3,\mu ^2\epsilon ) \end{pmatrix} \end{aligned}$$

(4.2b)

$$\begin{aligned}&F^{(1)} := \begin{pmatrix} \texttt{f}_{11} \mu \epsilon +\phi _{11} \mu \epsilon ^3+ r_3( \mu \epsilon ^4,\mu ^2\epsilon ^2,\mu ^3\epsilon ) &{} \quad \textrm{i}\,\mu \epsilon {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} +\textrm{i}\,\phi _{12} \mu \epsilon ^3 +\textrm{i}\,r_4({\mu \epsilon ^4}, \mu ^2 \epsilon ^2, \mu ^3\epsilon ) \\ \textrm{i}\,\phi _{21}\mu \epsilon +\textrm{i}\,r_6(\mu \epsilon ^3,\mu ^2\epsilon ) &{} \quad \phi _{22}\mu \epsilon + r_7(\mu \epsilon ^3,\mu ^2\epsilon ) \end{pmatrix} \end{aligned}$$

(4.2c)

where the coefficients appearing in the entries are the same of (3.3).

Note that the matrix $\texttt{L}_{\mu ,\epsilon }^{(1)}$, initially defined only for $\mu \ne 0$, extends analytically to the zero matrix at $\mu = 0$. For $\mu \ne 0$ the spectrum of $\texttt{L}_{\mu ,\epsilon }^{(1)}$ coincides with the spectrum of $\texttt{L}_{\mu ,\epsilon }$.

Non-perturbative step of block-decoupling.

The following lemma computes the first order Taylor expansions (4.4) of the matrix entries in (4.3) and then the expansion (4.8) at a higher degree of accuracy with respect to [9, Lemma 5.4].

Lemma 4.2

(Step of block-decoupling) There exists a $2\times 2$ reversibility-preserving matrix X, analytic in $(\mu , \epsilon )$, of the form

$$\begin{aligned} X:= \begin{pmatrix} x_{11} &{} \textrm{i}\,x_{12} \\ \textrm{i}\,x_{21} &{} x_{22} \end{pmatrix} \,, \qquad x_{ij}\in \mathbb {R}\,, \ i,j=1,2 \,, \end{aligned}$$

(4.3)

with

$$\begin{aligned} x_{11}&= x_{11}^{(1)} \epsilon + r(\epsilon ^3,\mu \epsilon ) \, , \qquad x_{12} = x_{12}^{(1)} \epsilon + r(\epsilon ^3, \mu \epsilon )\\ \nonumber x_{21}&= x_{21}^{(1)} \epsilon + x_{21}^{(3)} \epsilon ^3 + r(\epsilon ^4,\mu \epsilon ^2,\mu ^2\epsilon ) \, , \qquad x_{22} = x_{22}^{(1)} \epsilon + x_{22}^{(3)} \epsilon ^3 + r(\epsilon ^4,\mu \epsilon ^2,\mu ^2\epsilon ) \, , \end{aligned}$$

(4.4a)

where

$$\begin{aligned} x_{21}^{(1)}:= - \tfrac{1}{2} \texttt{D}_\texttt{h}^{-1} \big ( \texttt{e}_{12} \texttt{f}_{11} + 2{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \big ) \,,\quad x_{22}^{(1)}:= \tfrac{1}{2} \texttt{D}_\texttt{h}^{-1} \big ( {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}\texttt{e}_{12} +2\texttt{h}\texttt{f}_{11} \big ) \,, \end{aligned}$$

(4.4b)

and

$$\begin{aligned} \begin{aligned} x_{11}^{(1)}:&= \texttt{D}_\texttt{h}^{-1} \big (\tfrac{1}{16} \texttt{e}_{12}\texttt{e}_{22} x_{21}^{(1)} -\tfrac{1}{2} \texttt{e}_{12} \phi _{21} + \phi _{22} -\tfrac{1}{8} \texttt{e}_{22} x_{22}^{(1)} \big ) \,,\\ x_{12}^{(1)}:&= \texttt{D}_\texttt{h}^{-1}\big (\tfrac{1}{8} \texttt{h}\texttt{e}_{22} x_{21}^{(1)}-\texttt{h}\phi _{21} +\tfrac{1}{2} \texttt{e}_{12} \phi _{22}-\tfrac{1}{16} \texttt{e}_{12}\texttt{e}_{22} x_{22}^{(1)} \big ) \,, \\ x_{21}^{(3)}:&= \texttt{D}_\texttt{h}^{-1}\big ( -\tfrac{1}{2} \texttt{e}_{11} \texttt{e}_{12} x_{11}^{(1)}+\tfrac{1}{2}(\gamma _{12}+\eta _{12} ) \texttt{e}_{12} x_{21}^{(1)}+\tfrac{1}{2} \texttt{e}_{12} \gamma _{11} x_{22}^{(1)} \\&\quad -\tfrac{1}{2} \phi _{11} \texttt{e}_{12} - \texttt{e}_{11} x_{12}^{(1)} -\gamma _{22} x_{21}^{(1)} -(\gamma _{12} +\eta _{12}) x_{22}^{(1)} -\phi _{12} \big ) \,,\\ x_{22}^{(3)}:&={\texttt{D}_\texttt{h}^{-1} \big (\texttt{h}\texttt{e}_{11} x_{11}^{(1)} -\texttt{h}(\gamma _{12} +\eta _{12})x_{21}^{(1)} -\texttt{h}\gamma _{11} x_{22}^{(1)} +\texttt{h}\phi _{11} } \\&\quad +\tfrac{1}{2} \texttt{e}_{11} \texttt{e}_{12} x_{12}^{(1)}+\tfrac{1}{2} \texttt{e}_{12} \gamma _{22} x_{21}^{(1)} +\tfrac{1}{2} \texttt{e}_{12} (\gamma _{12} +\eta _{12} )x_{22}^{(1)}+ {\tfrac{1}{2} \texttt{e}_{12}} \phi _{12} \big )\,, \end{aligned} \end{aligned}$$

(4.4c)

with $\texttt{e}_{12}$, $\texttt{e}_{22}$, $\texttt{e}_{11}$, $\phi _{21}, \phi _{22}, \gamma _{12}, \eta _{12}, \gamma _{11}, \phi _{11}, \gamma _{22}, \phi _{12}, \texttt{f}_{11}$ computed in (3.4) and (cfr. [9, (5.7)])

$$\begin{aligned} \texttt{D}_\texttt{h}:= \texttt{h}-\frac{1}{4}\texttt{e}_{12}^2>0\,, \quad \forall \texttt{h}>0 \,, \end{aligned}$$

(4.5)

such that the following holds true. By conjugating the Hamiltonian and reversible matrix $\texttt{L}_{\mu ,\epsilon }^{(1)}$, defined in (4.1), with the symplectic and reversibility-preserving $4 \times 4$ matrix

$$\begin{aligned} \exp \big (S^{(1)} \big ) \,, \quad \text { where } \qquad S^{(1)}:= \texttt{J}_4 \begin{pmatrix} 0 &{} \Sigma \\ \Sigma ^* &{} 0 \end{pmatrix} \,, \qquad \Sigma := \texttt{J}_2 X \,, \end{aligned}$$

(4.6)

we get the Hamiltonian and reversible matrix

$$\begin{aligned} \texttt{L}_{\mu ,\epsilon }^{(2)}:= \exp \big (S^{(1)} \big ) \texttt{L}_{\mu ,\epsilon }^{(1)} \exp \big (-S^{(1)} \big )= \texttt{J}_4 \texttt{B}_{\mu ,\epsilon }^{(2)} = \begin{pmatrix} \texttt{J}_2 E^{(2)} &{} \texttt{J}_2 F^{(2)} \\ \texttt{J}_2 [F^{(2)}]^* &{} \texttt{J}_2 G^{(2)} \end{pmatrix}\,, \end{aligned}$$

(4.7)

where the reversibility-preserving $2\times 2$ self-adjoint matrix $E^{(2)}$ has the form

$$\begin{aligned}&E^{(2)} = { \begin{pmatrix} \texttt{e}_{\scriptscriptstyle {\textsc {WB}}}\mu \epsilon ^2+ \eta _{\scriptscriptstyle {\textsc {WB}}}\mu \epsilon ^4 + r_1'(\mu \epsilon ^5, \mu ^2 \epsilon ^3 )-\texttt{e}_{22}\frac{\mu ^3}{8}(1+r_1''(\epsilon ,\mu )) &{}\quad \textrm{i}\,\big ( \frac{1}{2}\texttt{e}_{12}\mu + r_2(\mu \epsilon ^2,\mu ^2\epsilon ,\mu ^3) \big ) \\ - \textrm{i}\,\big ( \frac{1}{2}\texttt{e}_{12}\mu + r_2(\mu \epsilon ^2,\mu ^2\epsilon ,\mu ^3) \big ) &{}\quad -\texttt{e}_{22}\frac{\mu }{8}(1+r_5(\epsilon ,\mu )) \end{pmatrix} }\, , \end{aligned}$$

(4.8)

where $\texttt{e}_{\scriptscriptstyle {\textsc {WB}}}$ is the Whitham–Benjamin function in (1.3) and

$$\begin{aligned} \eta _{\scriptscriptstyle {\textsc {WB}}}&= \eta _{11} + { x_{21}^{(1)} \phi _{12} + x_{21}^{(3)} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} - x_{22}^{(1)}\phi _{11} - x_{22}^{(3)} \texttt{f}_{11} + \frac{3}{2} (x_{21}^{(1)})^2 x_{22}^{(1)}\phi _{22} +(x_{21}^{(1)})^2 x_{12}^{(1)}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}} \\ \nonumber&\quad {- \frac{3}{2} x_{21}^{(1)} x_{12}^{(1)} x_{22}^{(1)}\texttt{f}_{11}+ \frac{3}{2} (x_{22}^{(1)})^2 x_{21}^{(1)}\phi _{21} -\frac{3}{2} x_{22}^{(1)}x_{11}^{(1)} x_{21}^{(1)} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} + (x_{22}^{(1)})^2 {x_{11}^{(1)}\texttt{f}_{11}}} \end{aligned}$$

(4.9)

with $x_{11}^{(1)}$, $x_{12}^{(1)}$, $x_{22}^{(1)}$, $x_{21}^{(1)}$, $x_{21}^{(3)}$, $x_{22}^{(3)}$ in (4.4) and the remaining coefficients in (3.4), whereas the reversibility-preserving $2\times 2$ self-adjoint matrix $G^{(2)}$ has the form

$$\begin{aligned} G^{(2)} = \begin{pmatrix} \mu + r_8(\mu \epsilon ^2, \mu ^3 \epsilon ) &{} - \textrm{i}\,r_9(\mu \epsilon ^2,\mu ^2\epsilon ) \\ \textrm{i}\,r_9(\mu \epsilon ^2, \mu ^2\epsilon ) &{} \tanh (\texttt{h}\mu ) + r_{10}(\mu \epsilon ) \end{pmatrix}\,, \end{aligned}$$

(4.10)

and finally

$$\begin{aligned} F^{(2)}= \begin{pmatrix} r_3(\mu \epsilon ^3 ) &{} \textrm{i}\,r_4(\mu \epsilon ^3 ) \\ \textrm{i}\,r_6(\mu \epsilon ^3 ) &{} r_7(\mu \epsilon ^3) \end{pmatrix} \, . \end{aligned}$$

(4.11)

The rest of the section is devoted to the proof of Lemma 4.2. In Lemma 5.4 of [9] we proved the existence of a matrix X as in (4.3) such that we obtain (4.7) with matrices $G^{(2)}, F^{(2)}$ as in (4.10)–(4.11) and a $2 \times 2$-self adjoint and reversibility preserving matrix $E^{(2)}$ whose first entry has the form $[E^{(2)}]_{11} = \texttt{e}_{\scriptscriptstyle {\textsc {WB}}}\mu \epsilon ^2 + r_1 (\mu \epsilon ^3, \mu ^2 \epsilon ^2 )$. The main result of Lemma 4.2 is that the first entry $[E^{(2)}]_{11}$ has the better expansion

$$\begin{aligned}{}[E^{(2)}]_{11} = \texttt{e}_{\scriptscriptstyle {\textsc {WB}}}\mu \epsilon ^2 + r_1 (\mu \epsilon ^3, \mu ^2 \epsilon ^2 ) = \texttt{e}_{\scriptscriptstyle {\textsc {WB}}}\mu \epsilon ^2+ \eta _{\scriptscriptstyle {\textsc {WB}}}\mu \epsilon ^4 + r_1'(\mu \epsilon ^5, \mu ^2 \epsilon ^3 ) \, \end{aligned}$$

with $\eta _{\scriptscriptstyle {\textsc {WB}}}$ computed in (4.9), which is relevant to determine the stability/instablity of the Stokes wave at the critical depth. Clearly we could compute explicitly also other Taylor coefficients of the matrix entries of $E^{(2)}, G^{(2)}, F^{(2)}$, but it is not needed.

The coefficients $x_{21}^{(1)}$ and $x_{22}^{(1)}$ in (4.4b) were already computed in [9, Lemma 5.4].

We now expand in Lie series the Hamiltonian and reversible matrix $\texttt{L}_{\mu ,\epsilon }^{(2)} = \exp (S)\texttt{L}_{\mu ,\epsilon }^{(1)} \exp (-S)$ where for simplicity we set $S:= S^{(1)}$. We split $\texttt{L}_{\mu ,\epsilon }^{(1)}$ into its $2\times 2$-diagonal and off-diagonal Hamiltonian and reversible matrices

$$\begin{aligned}&\qquad \qquad \qquad \qquad \qquad \qquad \texttt{L}_{\mu ,\epsilon }^{(1)} = D^{(1)} + R^{(1)} \, , \nonumber \\&D^{(1)} :=\begin{pmatrix} D_1 &{} 0 \\ 0 &{} D_0 \end{pmatrix} := \begin{pmatrix} \texttt{J}_2 E^{(1)} &{} 0 \\ 0 &{} \texttt{J}_2 G^{(1)} \end{pmatrix}, \quad R^{(1)} := \begin{pmatrix} 0 &{} \texttt{J}_2 F^{(1)}\\ \texttt{J}_2 [F^{(1)}]^* &{} 0 \end{pmatrix} , \end{aligned}$$

(4.12)

and we perform the Lie expansion

$$\begin{aligned} \texttt{L}_{\mu ,\epsilon }^{(2)}&= \exp (S)\texttt{L}_{\mu ,\epsilon }^{(1)} \exp (-S) = D^{(1)} + [S,D^{(1)}] + \frac{1}{2} \big [ S, [S, D^{(1)}] \big ] + R^{(1)} + [S, R^{(1)}] \nonumber \\&\quad + \frac{1}{2} \int _0^1 (1-\tau )^2 \exp (\tau S) \text {ad}_S^3( D^{(1)} ) \exp (-\tau S) \, \textrm{d}\tau \nonumber \\ {}&\quad + \int _0^1 (1-\tau ) \exp (\tau S) \, \text {ad}_S^2( R^{(1)} ) \, \exp (-\tau S) \, \textrm{d}\tau \end{aligned}$$

(4.13)

where $\text {ad}_A(B):= [A,B]:= AB - BA$ denotes the commutator between the linear operators A, B.

We look for a $4 \times 4$ matrix S as in (4.6) that solves the homological equation $R^{(1)} +\left[ S\,,\, D^{(1)} \right] = 0$, which, recalling (4.12), reads

$$\begin{aligned} \begin{pmatrix} 0 &{} \texttt{J}_2F^{(1)}+\texttt{J}_2\Sigma D_0 - D_1\texttt{J}_2\Sigma \\ \texttt{J}_2{[F^{(1)}]}^*+\texttt{J}_2\Sigma ^*D_1-D_0\texttt{J}_2\Sigma ^* &{} 0 \end{pmatrix} =0 \, . \end{aligned}$$

(4.14)

Writing $\Sigma =\texttt{J}_2 X$, namely $X = - \texttt{J}_2 \Sigma$, the equation (4.14) amounts to solve the “Sylvester” equation

$$\begin{aligned} D_1 X - X D_0 = - \texttt{J}_2F^{(1)} \, . \end{aligned}$$

(4.15)

We write the matrices $E^{(1)}, F^{(1)}, G^{(1)}$ in (4.1) as

$$\begin{aligned} E^{(1)} = \begin{pmatrix} E_{11}^{(1)} &{} \textrm{i}\,E_{12}^{(1)} \\ - \textrm{i}\,E_{12}^{(1)} &{} E_{22}^{(1)} \end{pmatrix}\,, \quad F^{(1)} = \begin{pmatrix} F_{11}^{(1)} &{} \textrm{i}\,F_{12}^{(1)} \\ \textrm{i}\,F_{21}^{(1)} &{} F_{22}^{(1)} \end{pmatrix} \,, \quad G^{(1)} = \begin{pmatrix} G_{11}^{(1)} &{} \textrm{i}\,G_{12}^{(1)} \\ - \textrm{i}\,G_{12}^{(1)} &{} G_{22}^{(1)} \end{pmatrix}\nonumber \\ \end{aligned}$$

(4.16)

where the real numbers $E_{ij}^{(1)}, F_{ij}^{(1)}, G_{ij}^{(1)}$, $i, j = 1,2$, have the expansion in (4.2a), (4.2b), (4.2c). Thus, by (4.12), (4.3) and (4.16), the equation (4.15) amounts to solve the $4\times 4$ real linear system

$$\begin{aligned} \underbrace{ \begin{pmatrix} G_{12}^{(1)} - E_{12}^{(1)} &{} G_{11}^{(1)} &{} E_{22}^{(1)} &{} 0 \\ G_{22}^{(1)} &{} G_{12}^{(1)} - E_{12}^{(1)} &{} 0 &{} - E_{22}^{(1)} \\ E_{11}^{(1)} &{} 0 &{} G_{12}^{(1)} - E_{12}^{(1)} &{} - G_{11}^{(1)} \\ 0 &{} - E_{11}^{(1)} &{} -G_{22}^{(1)} &{} G_{12}^{(1)} - E_{12}^{(1)} \end{pmatrix}}_{=: {{\mathcal {A}}} } \underbrace{ \begin{pmatrix} x_{11} \\ x_{12} \\ x_{21} \\ x_{22} \end{pmatrix}}_{ =: \textbf{x}} = \underbrace{ \begin{pmatrix} -F_{21}^{(1)} \\ F_{22}^{(1)} \\ - F_{11}^{(1)} \\ F_{12}^{(1)} \end{pmatrix} }_{=: \textbf{f}}. \end{aligned}$$

(4.17)

By [9] system (4.17) admits a unique solution. We now prove that it has the form (4.4).

Lemma 4.3

The vector $\textbf{x} = (x_{11}, x_{12}, x_{21}, x_{22})$ with entries in (4.4) solves (4.17).

Proof

Since $\tanh (\texttt{h}\mu ) = \texttt{h}\mu + r(\mu ^3)$, we have

$$\begin{aligned}&G_{12}^{(1)} - E_{12}^{(1)} = - \texttt{e}_{12}\frac{\mu }{2}- (\gamma _{12}+\eta _{12}) \mu \epsilon ^2 +r( \mu \epsilon ^3, \mu ^2\epsilon ,\mu ^3 ) \, , \\ \nonumber&G_{11}^{(1)} =\mu + \gamma _{11} \mu \epsilon ^2+ r_8(\mu \epsilon ^3,{\mu ^2\epsilon ^2}, \mu ^3 \epsilon ) \, ,\ \ E_{22}^{(1)} =-\texttt{e}_{22}\frac{\mu }{8}(1+r_5(\epsilon ^2,\mu )) \, ,\\ \nonumber&G_{22}^{(1)} = \mu \texttt{h}+ \gamma _{22} \mu \epsilon ^2+ r( \mu \epsilon ^3, \mu ^2\epsilon , \mu ^3 )\, , \ \ E_{11}^{(1)} = \texttt{e}_{11} \mu \epsilon ^2 +r(\mu \epsilon ^4,\mu ^2\epsilon ^3, \mu ^3) \, , \end{aligned}$$

(4.18)

with coefficients $\texttt{e}_{12}$, $\gamma _{12}$, $\eta _{12}$, $\gamma _{11}$, $\texttt{e}_{22}$, $\gamma _{22}$ and $\texttt{e}_{11}$ computed in (3.4). We exploit that the terms $x_{21}^{(1)}$ and $x_{22}^{(2)}$ have been already computed in [9, Lemma 5.4], in order to get $x_{11}^{(1)}$ and $x_{12}^{(2)}$ in (4.4) as solutions of the system

$$\begin{aligned} \begin{pmatrix} -\tfrac{1}{2} \texttt{e}_{12} &{} 1 \\ \texttt{h}&{} -\tfrac{1}{2} \texttt{e}_{12} \end{pmatrix} \begin{pmatrix} x_{11}^{(1)} \\ x_{12}^{(1)} \end{pmatrix} = \begin{pmatrix} \tfrac{1}{8} \texttt{e}_{22} x_{21}^{(1)}-\phi _{21} \\ \phi _{22}-\tfrac{1}{8} \texttt{e}_{22} x_{22}^{(1)} \end{pmatrix} \,,\quad \det \begin{pmatrix} -\tfrac{1}{2} \texttt{e}_{12} &{} 1 \\ \texttt{h}&{} -\tfrac{1}{2} \texttt{e}_{12} \end{pmatrix} {\mathop {=}\limits ^{(4.5)}} - \texttt{D}_\texttt{h}< 0\,,\nonumber \\ \end{aligned}$$

(4.19)

given, using also (4.2c), by the first two lines in (4.17) at order $\mu \epsilon$. Similarly, $x_{21}^{(3)}$ and $x_{22}^{(3)}$ in (4.4) solve the system

$$\begin{aligned} \begin{pmatrix} -\tfrac{1}{2} \texttt{e}_{12} &{} -1 \\ -\texttt{h}&{} -\tfrac{1}{2} \texttt{e}_{12} \end{pmatrix} \begin{pmatrix} x_{21}^{(3)} \\ x_{22}^{(3)} \end{pmatrix} = \begin{pmatrix} -\texttt{e}_{11} x_{11}^{(1)} + (\gamma _{12} +\eta _{12}) x_{21}^{(1)}+\gamma _{11} x_{22}^{(1)}-\phi _{11} \\ \texttt{e}_{11} x_{12}^{(1)}+\gamma _{22} x_{21}^{(1)}+(\gamma _{12}+\eta _{12})x_{22}^{(1)}+\phi _{12} \end{pmatrix} ,\qquad \end{aligned}$$

(4.20)

which comes, also by (4.2c), from the last two lines of (4.17) at order $\mu \epsilon ^3$. The solutions of (4.19)–(4.20) are given in (4.4c). $\square$

We now prove the expansion (4.8). Since the matrix S solves the homological equation $\left[ S\,,\, D^{(1)} \right] + R^{(1)} =0$, identity (4.13) simplifies to

$$\begin{aligned} \texttt{L}_{\mu ,\epsilon }^{(2)} = D^{(1)} +\frac{1}{2} \big [ S, R^{(1)} \big ]+ \frac{1}{2} \int _0^1 (1-\tau ^2) \, \exp (\tau S) \, \text {ad}_S^2( R^{(1)} ) \, \exp (-\tau S) \textrm{d}\tau .\nonumber \\ \end{aligned}$$

(4.21)

By plugging the Lie expansion

$$\begin{aligned} \begin{aligned}&\exp (\tau S) \, \text {ad}_S^2( R^{(1)} ) \, \exp (-\tau S) \\&\qquad = \text {ad}_S^2( R^{(1)} ) + \tau \text {ad}_S^3( R^{(1)} ) +\tau ^2 \int _0^1 (1-\tau ') \exp (\tau '\tau S) \, \text {ad}_S^4( R^{(1)} ) \, \exp (-\tau '\tau S) \, \textrm{d}\tau ' \end{aligned} \end{aligned}$$

into (4.21) we get

$$\begin{aligned} \texttt{L}_{\mu ,\epsilon }^{(2)}&= D^{(1)} +\frac{1}{2} \big [ S, R^{(1)} \big ] + \frac{1}{3} \text {ad}_S^2( R^{(1)} )+ \frac{1}{8} \text {ad}_S^3( R^{(1)} ) \end{aligned}$$

(4.22a)

$$\begin{aligned}&\quad +\frac{1}{2} \int _0^1 (1-\tau ^2)\tau ^2 \int _0^1 (1-\tau ') \exp (\tau \tau 'S) \text {ad}_S^4(R^{(1)}) \exp (-\tau \tau ' S) \textrm{d}\tau ' \textrm{d}\tau \, . \end{aligned}$$

(4.22b)

Next we compute the commutators in the expansion (4.22a).

Lemma 4.4

One has

$$\begin{aligned} \frac{1}{2} \big [S, R^{(1)} \big ] = \begin{pmatrix} \texttt{J}_2 {\tilde{E}}_1 &{} 0 \\ 0 &{}\texttt{J}_2 {\tilde{G}}_1 \end{pmatrix} \end{aligned}$$

(4.23)

where ${\tilde{E}}_1$, ${\tilde{G}}_1$ are self-adjoint and reversibility-preserving matrices of the form

$$\begin{aligned} \begin{aligned}&{\tilde{E}}_1 = \begin{pmatrix} {\tilde{\texttt{e}}}_{11}\mu \epsilon ^2 + {\tilde{\eta }}_{11}^{(a)} \mu \epsilon ^4 + {\tilde{r}}_1(\mu \epsilon ^5,\mu ^2\epsilon ^3, \mu ^3\epsilon ^2) &{}\quad \textrm{i}\,\big ({\tilde{\texttt{e}}}_{12} \mu \epsilon ^2 + {\tilde{r}}_2(\mu \epsilon ^4, \mu ^2 \epsilon ^2)\big ) \\ - \textrm{i}\,\big ( {\tilde{\texttt{e}}}_{12} \mu \epsilon ^2 + {\tilde{r}}_2(\mu \epsilon ^4, \mu ^2 \epsilon ^2) \big ) &{}\quad {\tilde{r}}_5(\mu \epsilon ^2) \end{pmatrix} \,, \\&{\tilde{G}}_1 = \begin{pmatrix} {\tilde{{\texttt{g}}}}_{11}\mu \epsilon ^2 + {\tilde{r}}_8(\mu \epsilon ^4,\mu ^2\epsilon ^2) &{}\quad \textrm{i}\,\big ({\tilde{{\texttt{g}}}}_{12} \mu \epsilon ^2 + {\tilde{r}}_9(\mu \epsilon ^4, \mu ^2 \epsilon ^2)\big ) \\ - \textrm{i}\,\big ( {\tilde{{\texttt{g}}}}_{12} \mu \epsilon ^2 + {\tilde{r}}_9(\mu \epsilon ^4, \mu ^2 \epsilon ^2) \big ) &{}\quad {\tilde{{\texttt{g}}}}_{22} \mu \epsilon ^2 + {\tilde{r}}_{10}(\mu \epsilon ^4,\mu ^2\epsilon ^2) \end{pmatrix} \,, \end{aligned} \end{aligned}$$

(4.24)

where

$$\begin{aligned} \begin{aligned}&{\tilde{\texttt{e}}}_{11}:= x_{21}^{(1)} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} - x_{22}^{(1)}\texttt{f}_{11}\,,\quad {\tilde{\eta }}_{11}^{(a)}:= x_{21}^{(1)}\phi _{12}+x_{21}^{(3)}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}-x_{22}^{(1)}\phi _{11}-x_{22}^{(3)}\texttt{f}_{11} \,,\quad \\&{\tilde{\texttt{e}}}_{12}:= -{\tilde{{\texttt{g}}}}_{12}:={\frac{1}{2} \big ( x_{21}^{(1)}\phi _{22}+x_{22}^{(1)}\phi _{21} -x_{11}^{(1)}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}-x_{12}^{(1)}\texttt{f}_{11} \big )} \,, \\&{\tilde{{\texttt{g}}}}_{11}:= x_{11}^{(1)}\texttt{f}_{11}+x_{21}^{(1)}\phi _{21} \,,\quad {\tilde{{\texttt{g}}}}_{22}:= x_{22}^{(1)}\phi _{22} +x_{12}^{(1)}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \, . \end{aligned} \end{aligned}$$

(4.25)

Proof

By (4.6), (4.12), and since $\Sigma = \texttt{J}_2 X$, we have

$$\begin{aligned} \frac{1}{2} \left[ S\,,\, R^{(1)} \right] = \begin{pmatrix} \texttt{J}_2 {\tilde{E}}_1 &{} 0 \\ 0 &{}\texttt{J}_2 {\tilde{G}}_1 \end{pmatrix},\quad {\tilde{E}}_1 := {\textbf {Sym}} \big [ \texttt{J}_2 X \texttt{J}_2 [F^{(1)}]^* \big ] \,, \quad {\tilde{G}}_1 := {\textbf {Sym}} \big [ X^* F^{(1)} \big ] ,\nonumber \\ \end{aligned}$$

(4.26)

where ${\textbf {Sym}} [A]:= \frac{1}{2} (A+ A^* )$, see [9, (5.28)–(5.29)]. By (4.3), (4.16), setting $F=F^{(1)}$, we have

$$\begin{aligned} \texttt{J}_2 X \texttt{J}_2 F^*&= \begin{pmatrix} x_{21}F_{12}-x_{22}F_{11} &{}\quad \textrm{i}\,(x_{21}F_{22}+x_{22} F_{21}) \\ \textrm{i}\,(x_{11}F_{12}+x_{12}F_{11}) &{} \quad - x_{11}F_{22} + x_{12}F_{21} \end{pmatrix} \, , \end{aligned}$$

(4.27)

$$\begin{aligned} X^* F&= \begin{pmatrix} x_{11}F_{11}+x_{21}F_{21} &{} \textrm{i}\,( x_{11}F_{12} - x_{21}F_{22}) \\ \textrm{i}\,(x_{22}F_{21}-x_{12}F_{11} ) &{} x_{22}F_{22}+ x_{12}F_{12} \end{pmatrix} \, , \end{aligned}$$

(4.28)

and the expansions in (4.24) with the coefficients given in (4.25) follow by (4.27), (4.28), (4.4) and (4.2c). $\square$

Lemma 4.5

One has

$$\begin{aligned} \begin{aligned}&\frac{1}{3} \textrm{ad}_S^2( R^{(1)} ) = \begin{pmatrix} 0 &{} \texttt{J}_2 {\tilde{F}} \\ \texttt{J}_2 {\tilde{F}}^* &{} 0 \end{pmatrix}, \end{aligned} \end{aligned}$$

(4.29)

where ${\tilde{F}}$ is a reversibility-preserving matrix of the form

$$\begin{aligned} {\tilde{F}} = \begin{pmatrix} {\tilde{\texttt{f}}}_{11}\mu \epsilon ^3 + {\tilde{r}}_3(\mu \epsilon ^5,\mu ^2\epsilon ^3) &{} \textrm{i}\,{\tilde{\texttt{f}}}_{12}\mu \epsilon ^3 + \textrm{i}\,{\tilde{r}}_4(\mu \epsilon ^5,\mu ^2\epsilon ^3) \\ \textrm{i}\,{\tilde{r}}_6(\mu \epsilon ^3) &{} {\tilde{r}}_{7}(\mu \epsilon ^3) \end{pmatrix} \,, \end{aligned}$$

(4.30)

with

$$\begin{aligned} {\tilde{\texttt{f}}}_{11}:= & {} {\frac{4}{3} x_{21}^{(1)} x_{11}^{(1)} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} -\frac{4}{3} x_{22}^{(1)} x_{11}^{(1)} \texttt{f}_{11} -\frac{4}{3} x_{22}^{(1)} x_{21}^{(1)} \phi _{21} +\frac{2}{3} x_{21}^{(1)} x_{12}^{(1)} \texttt{f}_{11} - \frac{2}{3} (x_{21}^{(1)})^2 \phi _{22} } \,,\nonumber \\ {\tilde{\texttt{f}}}_{12}:= & {} {\frac{4}{3} x_{21}^{(1)} x_{22}^{(1)} \phi _{22} + \frac{4}{3} x_{12}^{(1)} x_{21}^{(1)} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} -\frac{4}{3} x_{12}^{(1)} x_{22}^{(1)} \texttt{f}_{11} + \frac{2}{3}(x_{22}^{(1)})^2 \phi _{21} -\frac{2}{3} x_{11}^{(1)} x_{22}^{(1)} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} } .\nonumber \\ \end{aligned}$$

(4.31)

Proof

Using the form of S in (4.6) and $[S, R^{(1)} ]$ in (4.23) we deduce (4.29) with

$$\begin{aligned} {\tilde{F}}:= \frac{2}{3} \big (\texttt{J}_2 X \texttt{J}_2 {\tilde{G}}_1 + {\tilde{E}}_1 X \big ) \end{aligned}$$

(4.32)

where ${\tilde{E}}_1$ and ${\tilde{G}}_1$ are the matrices in (4.24). Writing

we have, in view of (4.3),

$$\begin{aligned} \begin{aligned} \texttt{J}_2 X \texttt{J}_2 {\tilde{G}}_1&= \begin{pmatrix} x_{21} {[{\tilde{G}}_1]}_{12}- x_{22} {[{\tilde{G}}_1]}_{11} &{}\quad \textrm{i}\,\big (x_{21} {[{\tilde{G}}_1]}_{22}- x_{22} {[{\tilde{G}}_1]}_{12} \big ) \\ \textrm{i}\,\big (x_{11} {[{\tilde{G}}_1]}_{12}+ x_{12} {[{\tilde{G}}_1]}_{11} \big ) &{}\quad - x_{11} {[{\tilde{G}}_1]}_{22}- x_{12} {[{\tilde{G}}_1]}_{12} \end{pmatrix}\,, \\ {\tilde{E}}_1 X&= \begin{pmatrix} x_{11} {[{\tilde{E}}_1]}_{11}- x_{21} {[{\tilde{E}}_1]}_{12} &{} \quad \textrm{i}\,\big (x_{12} {[{\tilde{E}}_1]}_{11}+ x_{22} {[{\tilde{E}}_1]}_{12} \big ) \\ \textrm{i}\,\big (x_{21} {[{\tilde{E}}_1]}_{22}- x_{11} {[{\tilde{E}}_1]}_{12} \big ) &{}\quad x_{12} {[{\tilde{E}}_1]}_{12}+ x_{22} {[{\tilde{E}}_1]}_{22} \end{pmatrix}\, . \\ \end{aligned} \end{aligned}$$

(4.33)

By (4.32), (4.33), (4.4) and (4.24) we deduce that the matrix ${\tilde{F}}$ has the expansion (4.30) with

$$\begin{aligned} \begin{aligned} {\tilde{\texttt{f}}}_{11}&= \frac{2}{3} \big ( x_{21}^{(1)}{\tilde{{\texttt{g}}}}_{12} - x_{22}^{(1)} {\tilde{{\texttt{g}}}}_{11} + x_{11}^{(1)}{\tilde{\texttt{e}}}_{11}- x_{21}^{(1)} {\tilde{\texttt{e}}}_{12} \big ) \,,\\ {\tilde{\texttt{f}}}_{12}&= \frac{2}{3} \big ( x_{21}^{(1)}{\tilde{{\texttt{g}}}}_{22} - x_{22}^{(1)} {\tilde{{\texttt{g}}}}_{12} + x_{12}^{(1)}{\tilde{\texttt{e}}}_{11}+ x_{22}^{(1)} {\tilde{\texttt{e}}}_{12} \big ) \,, \end{aligned} \end{aligned}$$

which, by (4.25), gives (4.31). $\square$

Lemma 4.6

One has

$$\begin{aligned} \begin{aligned}&\frac{1}{8} \textrm{ad}_S^3( R^{(1)} ) = \begin{pmatrix} \texttt{J}_2 {\tilde{E}}_3 &{} 0 \\ 0 &{}\texttt{J}_2 {\tilde{G}}_3 \end{pmatrix}, \end{aligned} \end{aligned}$$

(4.34)

where the self-adjoint and reversibility-preserving matrices ${\tilde{E}}_3, {\tilde{G}}_3$ in (4.34) have entries of size $\mathcal {O}(\mu \epsilon ^4)$. In particular the first entry of the matrix ${\tilde{E}}_3$ has the expansion

$$\begin{aligned} {[{\tilde{E}}_3]}_{11} = {\tilde{\eta }}_{11}^{(b)}\mu \epsilon ^4 + r(\mu \epsilon ^5,\mu ^2\epsilon ^4) \end{aligned}$$

(4.35)

with

$$\begin{aligned} {\tilde{\eta }}_{11}^{(b)}&:= { \frac{3}{2} (x_{21}^{(1)})^2 x_{22}^{(1)}\phi _{22} +(x_{21}^{(1)})^2 x_{12}^{(1)}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} - \frac{3}{2} x_{21}^{(1)} x_{12}^{(1)} x_{22}^{(1)}\texttt{f}_{11}}\\ \nonumber&\ \quad {+ \frac{3}{2} (x_{22}^{(1)})^2 x_{21}^{(1)}\phi _{21} -\frac{3}{2} x_{22}^{(1)}x_{11}^{(1)} x_{21}^{(1)} {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} + (x_{22}^{(1)})^2 {x_{11}^{(1)}\texttt{f}_{11}}} \, . \end{aligned}$$

(4.36)

Proof

Since $\frac{1}{8} \textrm{ad}_S^3( R^{(1)} ) = \frac{3}{8} [S, \frac{1}{3} \textrm{ad}_S^2(R^{(1)})]$ and using (4.29), the identity (4.34) holds with

$$\begin{aligned} {\tilde{E}}_3:= \frac{3}{4}{\textbf {Sym}} \big [ \texttt{J}_2 X \texttt{J}_2 [{\tilde{F}}]^* \big ] \,, \qquad {\tilde{G}}_3:= \frac{3}{4} {\textbf {Sym}} \big [ X^* {\tilde{F}} \big ] \, . \end{aligned}$$

(4.37)

Since, by (4.4) the matrix X in (4.3) has entries of size $\mathcal {O}(\epsilon )$ and the matrix ${\tilde{F}}$ in (4.30) has entries of size $\mathcal {O}(\mu \epsilon ^3)$ we deduce that the matrices ${\tilde{E}}_3$, ${\tilde{G}}_3$ in (4.37) have entries of size $\mathcal {O}(\mu \epsilon ^4)$. By (4.37) and denoting ${{\tilde{F}} = {\small \begin{pmatrix} {\tilde{F}}_{11} &{} \textrm{i}\,{\tilde{F}}_{12} \\ \textrm{i}\,{\tilde{F}}_{21} &{} {\tilde{F}}_{22} \end{pmatrix} } }$, we deduce, similarly to (4.27), that ${[{\tilde{E}}_3]}_{11} =\frac{3}{4}( x_{21} {\tilde{F}}_{12} - x_{22} {\tilde{F}}_{11})$ which, by (4.4) and (4.30), gives (4.35) with ${\tilde{\eta }}_{11}^{(b)} = \frac{3}{4} \big ( x_{21}^{(1)} {\tilde{\texttt{f}}}_{12} - x_{22}^{(1)}{\tilde{\texttt{f}}}_{11} \big )$ which by (4.31) gives (4.36). $\square$

Finally we show that the term in (4.22b) is small.

Lemma 4.7

The $4 \times 4$ Hamiltonian and reversible matrix ${\small \begin{pmatrix} \texttt{J}_2 {\widehat{E}} &{} \texttt{J}_2 {\widehat{F}}\\ \texttt{J}_2 [ {\widehat{F}} ]^* &{} \texttt{J}_2 {\widehat{G}} \end{pmatrix}}$ given by (4.22b) has the $2 \times 2$ self-adjoint and reversibility-preserving blocks ${\widehat{E}}$, ${\widehat{G}}$ and the $2\times 2$ reversibility-preserving block ${\widehat{F}}$ all with entries of size $\mathcal {O}(\mu \epsilon ^5)$.

Proof

By the Hamiltonian and reversibility properties of S and $R^{(1)}$ the matrix $ad _S^4 (R^{(1)})$ is Hamiltonian and reversible and the same holds, for any $\tau ,\tau ' \in [0,1]$, for

$$\begin{aligned} \exp (\tau \tau ' S) \, ad _S^4( R^{(1)} ) \, \exp (-\tau \tau ' S) = [S,ad _S^3( R^{(1)} )] (1 + \mathcal {O}(\mu ,\epsilon ))\, . \end{aligned}$$

(4.38)

The claimed estimate on the entries of the matrix given by (4.22b) follows by (4.38) and because S in (4.6) has entries of size $\mathcal {O}(\epsilon )$ and $ad _S^3( R^{(1)} )$ in (4.34) has entries of size $\mathcal {O}(\mu \epsilon ^4)$. $\square$

Proof of Lemma 4.2

It follows by (4.22), (4.12) and Lemmata 4.4, 4.5, 4.6 and 4.7. The matrix $E^{(2)}:= E^{(1)} + {\tilde{E}}_1 + {\tilde{E}}_3 + \widehat{ E}$ has the expansion in (4.8), with

$$\begin{aligned} \texttt{e}_{\scriptscriptstyle {\textsc {WB}}}:= \texttt{e}_{11} + {\tilde{\texttt{e}}}_{11} = \texttt{e}_{11} - \texttt{D}_\texttt{h}^{-1} \big ( {\texttt{c}}_{\texttt{h}}^{-1} + \texttt{h}\texttt{f}_{11}^2 +\texttt{e}_{12}\texttt{f}_{11}{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \big ), \quad \eta _{\scriptscriptstyle {\textsc {WB}}}:= \eta _{11}+ {\tilde{\eta }}_{11}^{(a)}+ {\tilde{\eta }}_{11}^{(b)} \,, \end{aligned}$$

as in (4.9). Furthermore $G^{(2)}:= G^{(1)} + {\tilde{G}}_1 + {\tilde{G}}_3 + \widehat{G}$ has the expansion in (4.10) and $F^{(2)}:= {\tilde{F}} + \widehat{F}$ has the expansion in (4.11). $\square$

Complete block-decoupling and proof of the main result.

Finally Theorem 1.3 is proved as in [9] by block-diagonalizing the $4\times 4$ Hamiltonian and reversible matrix $\texttt{L}_{\mu ,\epsilon }^{(2)}$ in (4.7),

$$\begin{aligned}&\texttt{L}_{\mu ,\epsilon }^{(2)} = D^{(2)} + R^{(2)} \, , \quad D^{(2)}:= \begin{pmatrix} \texttt{J}_2 E^{(2)} &{} 0 \\ 0 &{} \texttt{J}_2 G^{(2)} \end{pmatrix}, \quad R^{(2)}:= \begin{pmatrix} 0 &{} \texttt{J}_2 F^{(2)} \\ \texttt{J}_2 [F^{(2)}]^* &{} 0 \end{pmatrix} . \end{aligned}$$

(4.39)

The next lemma is [9, Lemma 5.9].

Lemma 4.8

There exist a $4\times 4$ reversibility-preserving Hamiltonian matrix $S^{(2)}:=S^{(2)}(\mu ,\epsilon )$ of the form (4.6), analytic in $(\mu , \epsilon )$, of size $\mathcal {O}(\epsilon ^3)$, and a $4\times 4$ block-diagonal reversible Hamiltonian matrix $P:=P(\mu ,\epsilon )$, analytic in $(\mu , \epsilon )$, of size ${ \mathcal {O}(\mu \epsilon ^6)}$ such that

$$\begin{aligned} \exp (S^{(2)})(D^{(2)}+R^{(2)}) \exp (-S^{(2)}) = D^{(2)}+P \, . \end{aligned}$$

(4.40)

By (4.40), (4.8)–(4.10) and the fact that P has size ${ \mathcal {O}(\mu \epsilon ^6)}$ we deduce Theorem 1.3: there exists a symplectic and reversibility-preserving linear map that conjugates the matrix $\textrm{i}\,{\texttt{c}}_{\texttt{h}}\mu +\texttt{L}_{\mu ,\epsilon }$ (which represents ${{\mathcal {L}}}_{\mu ,\epsilon }$) with $\texttt{L}_{\mu ,\epsilon }$ in (2.8) into the Hamiltonian and reversible matrix (1.17) with $\texttt{U}$ in (1.18) and $\mathtt S$ in (1.19). The function $\Delta _{\scriptscriptstyle {\textsc {BF}}}(\texttt{h};\mu ,\epsilon )$ expands as in (1.2).

Appendices

Fourth-Order Expansion of the Stokes Waves

In this Appendix we compute the Taylor coefficients (A.2) of the fourth order expansions (1.9) of the Stokes waves. We also compute the fourth order expansion (A.58) of the $2 \pi$-periodic functions $p_\epsilon (x)$ and $a_\epsilon (x)$ and the expansion (A.47) of the constant $\texttt{f}_\epsilon$ in (1.12).

1.1 Expansion of Stokes waves

Proposition A.1

(Expansion of Stokes waves). The Stokes waves $\eta _\epsilon (x)$, $\psi _\epsilon (x)$ and the speed $c_\epsilon$ in Theorem 1.2 have the expansions (1.9) with coefficients

$$\begin{aligned}&\eta _{2}^{[0]} := \frac{{\texttt{c}}_{\texttt{h}}^4-1}{4{\texttt{c}}_{\texttt{h}}^2} \, , \qquad \eta _{2}^{[2]} := \frac{3-{\texttt{c}}_{\texttt{h}}^4}{4{\texttt{c}}_{\texttt{h}}^6} \, , \qquad \psi _{2}^{[2]} := \frac{3+{\texttt{c}}_{\texttt{h}}^8}{8{\texttt{c}}_{\texttt{h}}^7} \, , \qquad \end{aligned}$$

(A.2a)

$$\begin{aligned}&c_2:= \frac{9-10{\texttt{c}}_{\texttt{h}}^4+9{\texttt{c}}_{\texttt{h}}^8 }{16{\texttt{c}}_{\texttt{h}}^7} + {\frac{(1-{\texttt{c}}_{\texttt{h}}^4) }{2{\texttt{c}}_{\texttt{h}}}} \eta _2^{[0]} = \frac{-2 {\texttt{c}}_{\texttt{h}}^{12}+13 {\texttt{c}}_{\texttt{h}}^8-12 {\texttt{c}}_{\texttt{h}}^4+9}{16 {\texttt{c}}_{\texttt{h}}^7}\, , \end{aligned}$$

(A.2b)

$$\begin{aligned}&\begin{aligned}&\eta _{3}^{[1]} := \frac{-2{\texttt{c}}_{\texttt{h}}^{12}+3{\texttt{c}}_{\texttt{h}}^8+3}{16{\texttt{c}}_{\texttt{h}}^8(1+{\texttt{c}}_{\texttt{h}}^2)} \, , \qquad \eta _{3}^{[3]} := \frac{-3{\texttt{c}}_{\texttt{h}}^{12}+9{\texttt{c}}_{\texttt{h}}^8-9{\texttt{c}}_{\texttt{h}}^4+27}{64{\texttt{c}}_{\texttt{h}}^{12}} \, , \\&\psi _{3}^{[1]} := \frac{2{\texttt{c}}_{\texttt{h}}^{12}-3{\texttt{c}}_{\texttt{h}}^{8}-3}{16{\texttt{c}}_{\texttt{h}}^7(1+{\texttt{c}}_{\texttt{h}}^2)} \, , \qquad \psi _{3}^{[3]} := \frac{-9{\texttt{c}}_{\texttt{h}}^{12}+19{\texttt{c}}_{\texttt{h}}^{8}+5{\texttt{c}}_{\texttt{h}}^4+9}{64{\texttt{c}}_{\texttt{h}}^{13}}\, , \end{aligned} \end{aligned}$$

(A.2c)

$$\begin{aligned}&\begin{aligned}&\eta _{4}^{[0]} := \frac{-4 {\texttt{c}}_{\texttt{h}}^{20}-4 {\texttt{c}}_{\texttt{h}}^{18}+17 {\texttt{c}}_{\texttt{h}}^{16}+6 {\texttt{c}}_{\texttt{h}}^{14}-48 {\texttt{c}}_{\texttt{h}}^8+6 {\texttt{c}}_{\texttt{h}}^6+36 {\texttt{c}}_{\texttt{h}}^4-9}{64 {\texttt{c}}_{\texttt{h}}^{14}} \, , \\&\eta _{4}^{[2]} := \frac{1}{384 {\texttt{c}}_{\texttt{h}}^{18} ({\texttt{c}}_{\texttt{h}}^2+1)} \Big (-24 {\texttt{c}}_{\texttt{h}}^{22}+285 {\texttt{c}}_{\texttt{h}}^{18}+177 {\texttt{c}}_{\texttt{h}}^{16}-862 {\texttt{c}}_{\texttt{h}}^{14}-754 {\texttt{c}}_{\texttt{h}}^{12}\\&\qquad +1116 {\texttt{c}}_{\texttt{h}}^{10}+1080 {\texttt{c}}_{\texttt{h}}^8-162 {\texttt{c}}_{\texttt{h}}^6-54 {\texttt{c}}_{\texttt{h}}^4-81 {\texttt{c}}_{\texttt{h}}^2-81 \Big ) \, , \\&\eta _{4}^{[4]} := \frac{21 {\texttt{c}}_{\texttt{h}}^{20}+{\texttt{c}}_{\texttt{h}}^{16}-262 {\texttt{c}}_{\texttt{h}}^{12}+522 {\texttt{c}}_{\texttt{h}}^8+81 {\texttt{c}}_{\texttt{h}}^4+405}{384 {\texttt{c}}_{\texttt{h}}^{18} ({\texttt{c}}_{\texttt{h}}^4+5)} \, , \\&\psi _{4}^{[2]} := \frac{1}{768 {\texttt{c}}_{\texttt{h}}^{19} ({\texttt{c}}_{\texttt{h}}^2+1)} \Big (-12 {\texttt{c}}_{\texttt{h}}^{26}-36 {\texttt{c}}_{\texttt{h}}^{24}+57 {\texttt{c}}_{\texttt{h}}^{22}+93 {\texttt{c}}_{\texttt{h}}^{20}+51 {\texttt{c}}_{\texttt{h}}^{18}-21 {\texttt{c}}_{\texttt{h}}^{16}-646 {\texttt{c}}_{\texttt{h}}^{14}\, , \\&\qquad -502 {\texttt{c}}_{\texttt{h}}^{12}+1098 {\texttt{c}}_{\texttt{h}}^{10}+1098 {\texttt{c}}_{\texttt{h}}^8-243 {\texttt{c}}_{\texttt{h}}^6-135 {\texttt{c}}_{\texttt{h}}^4-81 {\texttt{c}}_{\texttt{h}}^2-81\Big ) \, ,\\&\psi _{4}^{[4]} := \frac{-21 {\texttt{c}}_{\texttt{h}}^{24}+60 {\texttt{c}}_{\texttt{h}}^{20}+343 {\texttt{c}}_{\texttt{h}}^{16}-1648 {\texttt{c}}_{\texttt{h}}^{12}+3177 {\texttt{c}}_{\texttt{h}}^8+756 {\texttt{c}}_{\texttt{h}}^4+405}{1536 {\texttt{c}}_{\texttt{h}}^{19} ({\texttt{c}}_{\texttt{h}}^4+5)} \, , \end{aligned} \end{aligned}$$

(A.2d)

$$\begin{aligned}&c_4=\frac{1}{1024 {\texttt{c}}_{\texttt{h}}^{19}({\texttt{c}}_{\texttt{h}}^2+1)}\Big (56 {\texttt{c}}_{\texttt{h}}^{30}+88 {\texttt{c}}_{\texttt{h}}^{28}-272 {\texttt{c}}_{\texttt{h}}^{26}-528 {\texttt{c}}_{\texttt{h}}^{24}-7 {\texttt{c}}_{\texttt{h}}^{22}+497 {\texttt{c}}_{\texttt{h}}^{20}+1917 {\texttt{c}}_{\texttt{h}}^{18}\\ \nonumber&\quad +1437 {\texttt{c}}_{\texttt{h}}^{16}-4566 {\texttt{c}}_{\texttt{h}}^{14}-4038 {\texttt{c}}_{\texttt{h}}^{12}+4194 {\texttt{c}}_{\texttt{h}}^{10}+3906 {\texttt{c}}_{\texttt{h}}^8-891 {\texttt{c}}_{\texttt{h}}^6-675 {\texttt{c}}_{\texttt{h}}^4+81 {\texttt{c}}_{\texttt{h}}^2+81 \Big ) \, . \end{aligned}$$

(A.2e)

The rest of this section is devoted to the proof of Proposition A.1.

In [9, Theorem 2.1] we have yet computed the second order expansion of the Stokes waves in (1.9) and proved that the coefficients $\eta _2^{[0]}$, $\eta _2^{[2]}$, $\psi _2^{[2]}$ are (A.2a) and $c_2$ is (A.2b). Then we write

$$\begin{aligned} \begin{aligned}&\eta _\epsilon (x) = \epsilon \cos (x) + \epsilon ^2 (\eta _2^{[0]}+\eta _2^{[2]}\cos (2x)) + \epsilon ^3 \eta _3(x)+ \epsilon ^4 \eta _4(x)+\mathcal {O}(\epsilon ^5) \,, \\&\psi _\epsilon (x) = \epsilon {\texttt{c}}_{\texttt{h}}^{-1} \sin (x) + \epsilon ^2 \psi _2^{[2]}\sin (2x) + \epsilon ^3 \psi _3(x)+\epsilon ^4 \psi _4(x)+ \mathcal {O}(\epsilon ^5) \,,\\&c_\epsilon = {\texttt{c}}_{\texttt{h}}+ \epsilon ^2 c_2+ \epsilon ^3 c_3 +\epsilon ^4 c_4+ \mathcal {O}(\epsilon ^5) \,, \end{aligned} \end{aligned}$$

(A.2)

where the functions $\eta _3(x)$, $\eta _4 (x)$ are even and $\psi _3(x)$, $\psi _4 (x)$ are odd. We rewrite the equations (1.8) as the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \eta -c \, \psi _x + \dfrac{\psi _x^2}{2} - \dfrac{\eta _x^2}{2(1+\eta _x^2)} ( c - \psi _x )^2 = 0 \\ c \, \eta _x+G(\eta )\psi = 0 \,, \end{array}\right. } \end{aligned}$$

(A.3)

where in the first equation we have replaced $G(\eta )\psi$ with $-c \, \eta _x$.

We Taylor expand the Dirichlet-Neumann operator $G(\eta )$ as

$$\begin{aligned} G(\eta )= G_0+ G_1(\eta ) + G_2(\eta )+ G_3(\eta ) + \mathcal {O}(\eta ^4) \end{aligned}$$

where, by [14, formulae (39)–(40)],

$$\begin{aligned} \begin{aligned}&G_0:= D\tanh (\texttt{h}D) = |D| \tanh (\texttt{h}|D|) , \\&G_1(\eta ):= -\partial _x \eta \partial _x-G_0\eta G_0,\\&G_2(\eta ):= -\frac{1}{2} G_0 \partial _x \eta ^2 \partial _x+ \frac{1}{2} \partial _x^2 \eta ^2 G_0 -G_0 \eta G_1(\eta ) \,, \\&G_3(\eta ):=\frac{1}{6} \partial _x^3 \eta ^3 \partial _x + \frac{1}{6} G_0 \partial _x^2 \eta ^3 G_0 - G_0 \eta G_2(\eta ) +\frac{1}{2}\partial _x^2 \eta ^2 G_1(\eta ) \\&G_4(\eta ):= \frac{1}{24} G_0 \partial _x^3 \eta ^4 \partial _x - \frac{1}{24} \partial _x^4 \eta ^4 G_0 + \frac{1}{2} \partial _x^2 \eta ^2 G_2 (\eta ) + \frac{1}{6} G_0 \partial _x^2 \eta ^3 G_1 (\eta ) - G_0 \eta G_3 (\eta ) . \end{aligned} \end{aligned}$$

(A.4)

Remark A.2

In order to check that (A.4) coincides with [14, formulae (39)–(40)] use the identity $D^2=-\partial _x^2$. We point out that (A.4) coincides with [15, formulae (2.13)–(2.14)] and the recursion formulae of [47, p. 24].

The ‘unperturbed” linear part of the system (A.3) is associated with the self-adjoint closed operator

$$\begin{aligned} {{\mathcal {B}}}_0= \begin{bmatrix} 1 &{} -{\texttt{c}}_{\texttt{h}}\partial _x \\ {\texttt{c}}_{\texttt{h}}\partial _x &{} G_0 \end{bmatrix}: \mathcal {D}\subset H^{\sigma ,s}_{ev}\times H^{\sigma ,s}_{odd} \longrightarrow H^{\sigma ,s}_{ev}\times H^{\sigma ,s}_{odd}\,, \end{aligned}$$

(A.5)

with domain $\mathcal {D}:=H^{\sigma ,s+1}_{ev}\times H^{\sigma ,s+1}_{odd}$. To compute the higher-order expansions one needs the following

Lemma A.3

The kernel of the operator ${{\mathcal {B}}}_0$ in (A.5) is

$$\begin{aligned} K:= \text {Ker}\;{{\mathcal {B}}}_0= \text {span}\,\Big \{\begin{bmatrix}\cos (x) \\ {\texttt{c}}_{\texttt{h}}^{-1}\sin (x) \end{bmatrix} \Big \} \end{aligned}$$

(A.6a)

and its range $R:=\text {Rn}\;{{\mathcal {B}}}_0= K^{\perp _{\mathcal {D}}}$ is given by $R=R_0\oplus R_1\oplus R_\varnothing$, where

$$\begin{aligned} \begin{aligned}&\quad R_0:= \text {span}\,\Big \{\begin{bmatrix}1 \\ 0 \end{bmatrix} \Big \}\,,\ \ R_1:= \text {span}\,\Big \{\begin{bmatrix}-\cos (x) \\ {\texttt{c}}_{\texttt{h}}\sin (x) \end{bmatrix} \Big \}\,, \\&R_\varnothing := \overline{\bigoplus _{k=2}^\infty R_k}\,,\ \ R_k:= \text {span}\,\Big \{\begin{bmatrix}\cos (kx) \\ 0 \end{bmatrix}\,,\;\begin{bmatrix}0 \\ \sin (kx) \end{bmatrix} \Big \}\, . \end{aligned} \end{aligned}$$

(A.6b)

Consequently there exists a unique self-adjoint bounded linear operator ${{\mathcal {B}}}_0^{-1}:R\rightarrow R$, given by

(A.7)

such that .

Proof

This is the content of [9, Lemma B.1]. Then (A.7) follows by inspection. $\square$

From the second-order expansion of the Stokes waves in [9, Appendix B] we recover

$$\begin{aligned} G_0\psi _1 = {\texttt{c}}_{\texttt{h}}\sin (x)\,,\quad G_1(\eta _1)\psi _1 =\frac{1-{\texttt{c}}_{\texttt{h}}^4}{{\texttt{c}}_{\texttt{h}}(1+{\texttt{c}}_{\texttt{h}}^4)}\sin (2x)\, . \end{aligned}$$

(A.8)

Third order in $\epsilon$. By plugging the expansion (A.2) in system (A.3) and discarding quartic terms we find the following linear system (we drop the dependence w.r.t. x)

$$\begin{aligned} {{\mathcal {B}}}_0 \begin{bmatrix}\eta _3 \\ \psi _3 \end{bmatrix} = \begin{bmatrix}c_2(\psi _1)_x - (\psi _1)_x (\psi _2)_x - (\eta _1)_x^2 (\psi _1)_x {\texttt{c}}_{\texttt{h}}+ (\eta _1)_x (\eta _2)_x {\texttt{c}}_{\texttt{h}}^2 \\ -c_2(\eta _1)_x - G_1(\eta _1)\psi _2- G_1(\eta _2)\psi _1 - G_2(\eta _1)\psi _1 \end{bmatrix}=: \begin{bmatrix}f_3 \\ g_3 \end{bmatrix}.\nonumber \\ \end{aligned}$$

(A.9)

In view of (1.9) we have

$$\begin{aligned} \begin{aligned}&(\psi _1)_x (\psi _2)_x = \frac{\psi _2^{[2]}}{{\texttt{c}}_{\texttt{h}}}(\cos (x)+ \cos (3x))\,,\\&(\eta _1)_x^2 (\psi _1)_x {\texttt{c}}_{\texttt{h}}= \frac{1}{4} (\cos (x)-\cos (3x))\,, \end{aligned} \quad {\texttt{c}}_{\texttt{h}}^2 (\eta _1)_x (\eta _2)_x = {\texttt{c}}_{\texttt{h}}^2 \eta _2^{[2]}(\cos (x)- \cos (3x))\, . \end{aligned}$$

(A.10)

By means of (A.4) and since

$$\begin{aligned} \tanh (\texttt{h})={\texttt{c}}_{\texttt{h}}^2\,,\quad \tanh (2\texttt{h}) = \frac{2{\texttt{c}}_{\texttt{h}}^2}{1+{\texttt{c}}_{\texttt{h}}^4}\,,\quad \tanh (3\texttt{h})= \frac{3{\texttt{c}}_{\texttt{h}}^2+{\texttt{c}}_{\texttt{h}}^6}{1+3{\texttt{c}}_{\texttt{h}}^4} \,, \end{aligned}$$

(A.11)

whereby

$$\begin{aligned} G_0\psi _2 = \frac{4{\texttt{c}}_{\texttt{h}}^2}{1+{\texttt{c}}_{\texttt{h}}^4}\psi _2^{[2]} \sin (2x) \,,\quad \end{aligned}$$

(A.12)

we have, in view of (A.8) too,

$$\begin{aligned} \begin{aligned}&G_1(\eta _1)\psi _2 =\psi _2^{[2]} \frac{1-{\texttt{c}}_{\texttt{h}}^4}{1+{\texttt{c}}_{\texttt{h}}^4}\sin (x)+ 3\psi _2^{[2]} \frac{1-2{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8}{1+4{\texttt{c}}_{\texttt{h}}^4+3{\texttt{c}}_{\texttt{h}}^8}\sin (3x)\,, \\&G_2(\eta _1)\psi _1=\frac{{\texttt{c}}_{\texttt{h}}}{4}\frac{3{\texttt{c}}_{\texttt{h}}^4-1}{1+{\texttt{c}}_{\texttt{h}}^4}\sin (x)-\frac{3}{4} {\texttt{c}}_{\texttt{h}}\frac{{\texttt{c}}_{\texttt{h}}^8-4{\texttt{c}}_{\texttt{h}}^4+3}{1+4{\texttt{c}}_{\texttt{h}}^4+3{\texttt{c}}_{\texttt{h}}^8}\sin (3x)\,, \\ {}&G_1(\eta _2)\psi _1 =\frac{1}{{\texttt{c}}_{\texttt{h}}}\big (\eta _2^{[0]}(1-{\texttt{c}}_{\texttt{h}}^4)+\frac{1}{2}\eta _2^{[2]}(1+{\texttt{c}}_{\texttt{h}}^4)\big )\sin (x)+ \frac{3}{2{\texttt{c}}_{\texttt{h}}} \eta _2^{[2]} \frac{1-{\texttt{c}}_{\texttt{h}}^8}{1+3{\texttt{c}}_{\texttt{h}}^4}\sin (3x)\, . \end{aligned} \end{aligned}$$

(A.13)

By (A.2b), (A.10), (A.13) and (A.2a) the right-hand side of system (A.9) is given by

$$\begin{aligned} \begin{bmatrix}f_3(x)\\ g_3(x)\end{bmatrix} = \begin{bmatrix} f_3^{[1]}\cos (x)+f_3^{[3]}\cos (3x) \\ g_3^{[1]}\sin (x)+g_3^{[3]}\sin (3x) \end{bmatrix}\,, \end{aligned}$$

(A.14)

with

$$\begin{aligned} \begin{aligned}&f_3^{[1]}:= \frac{-2{\texttt{c}}_{\texttt{h}}^{12}+3{\texttt{c}}_{\texttt{h}}^8+3}{16{\texttt{c}}_{\texttt{h}}^8} \,,\quad f_3^{[3]}:= \frac{3{\texttt{c}}_{\texttt{h}}^8-6{\texttt{c}}_{\texttt{h}}^4-3}{8{\texttt{c}}_{\texttt{h}}^8}\,, \\&g_3^{[1]}:= \frac{2{\texttt{c}}_{\texttt{h}}^{12}-3{\texttt{c}}_{\texttt{h}}^{8}-3}{16{\texttt{c}}_{\texttt{h}}^7} \,,\quad g_3^{[3]}:= \frac{-6{\texttt{c}}_{\texttt{h}}^8+15{\texttt{c}}_{\texttt{h}}^4-9}{4{\texttt{c}}_{\texttt{h}}^7(1+3{\texttt{c}}_{\texttt{h}}^4)}\, . \end{aligned} \end{aligned}$$

(A.15)

We recall that the term $c_2$ in (A.2b) is determined (cfr. [9, Appendix B]) to make the vector (f(x), g(x)) in (A.14) orthogonal to the kernel of the operator ${{\mathcal {B}}}_0$, therefore ensuring the existence of a solution

$$\begin{aligned} \begin{bmatrix}\eta _3(x) \\ \psi _3(x) \end{bmatrix}:= \begin{bmatrix}\eta _3^{[1]}\cos (x)+\eta _3^{[3]}\cos (3x) \\ \psi _3^{[1]} \sin (x)+\psi _3^{[3]}\sin (3x) \end{bmatrix}:={{\mathcal {B}}}_0^{-1}\begin{bmatrix}f_3(x) \\ g_3(x) \end{bmatrix} \, . \end{aligned}$$

By Lemma A.3 and (A.11) we have

$$\begin{aligned} \begin{bmatrix}\eta _3^{[3]}\cos (3x) \\ \psi _3^{[3]}\sin (3x) \end{bmatrix} = {{\mathcal {B}}}_0^{-1}\begin{bmatrix}\beta \cos (3x) \\ \delta \sin (3x) \end{bmatrix}&= -\frac{1+3{\texttt{c}}_{\texttt{h}}^4}{24{\texttt{c}}_{\texttt{h}}^6} \begin{bmatrix} |D|\tanh (\texttt{h}|D|) &{} {\texttt{c}}_{\texttt{h}}\partial _x \\ -{\texttt{c}}_{\texttt{h}}\partial _x &{} 1 \end{bmatrix}\begin{bmatrix}f_3^{[3]} \cos (3x) \\ g_3^{[3]} \sin (3x) \end{bmatrix} \end{aligned}$$

(A.16)

$$\begin{aligned}&= -\frac{1+3{\texttt{c}}_{\texttt{h}}^4}{24{\texttt{c}}_{\texttt{h}}^6} \begin{bmatrix}3\big (\frac{3{\texttt{c}}_{\texttt{h}}^2+{\texttt{c}}_{\texttt{h}}^6}{1+3{\texttt{c}}_{\texttt{h}}^4}f_3^{[3]}+{\texttt{c}}_{\texttt{h}}g_3^{[3]}\big )\cos (3x) \\ (3{\texttt{c}}_{\texttt{h}}f_3^{[3]} + g_3^{[3]})\sin (3x) \end{bmatrix}\, , \end{aligned}$$

(A.17)

and $\begin{bmatrix}\eta _3^{[1]}\cos (x) \\ \psi _3^{[1]}\sin (x) \end{bmatrix} = {{\mathcal {B}}}_0^{-1}\begin{bmatrix}f_3^{[1]}\cos (x) \\ g_3^{[1]}\sin (x) \end{bmatrix} = \frac{1}{1+{\texttt{c}}_{\texttt{h}}^2}\begin{bmatrix}f_3^{[1]}\cos (x) \\ g_3^{[1]}\sin (x) \end{bmatrix}$. The coefficients in (A.2c) follow.

Fourth order in $\epsilon$. By plugging the expansion (A.2) in system (A.3) and discarding quintic terms we find the linear system

$$\begin{aligned} {{\mathcal {B}}}_0 \begin{bmatrix}\eta _4 \\ \psi _4 \end{bmatrix} = \begin{bmatrix}f_4 \\ g_4 \end{bmatrix}\,, \end{aligned}$$

(A.18)

with

$$\begin{aligned} f_4&:= c_3(\psi _1)_x +c_2(\psi _2)_x - (\psi _1)_x (\psi _3)_x - \frac{1}{2} (\psi _2)_x^2 + {\texttt{c}}_{\texttt{h}}(\eta _1)_x^2 \big (c_2-(\psi _2)_x\big ) \\ \nonumber&\quad + (\eta _1)_x (\eta _3)_x {\texttt{c}}_{\texttt{h}}^2 +\frac{1}{2} (\eta _2)_x^2{\texttt{c}}_{\texttt{h}}^2+\frac{1}{2}(\eta _1)_x^2(\psi _1)_x^2 -\frac{1}{2}{\texttt{c}}_{\texttt{h}}^2 (\eta _1)_x^4 -2{\texttt{c}}_{\texttt{h}}(\eta _1)_x(\eta _2)_x(\psi _1)_x\, , \end{aligned}$$

(A.19a)

$$\begin{aligned} g_4&:= -c_3(\eta _1)_x-c_2(\eta _2)_x - G_1(\eta _1)\psi _3- G_1(\eta _2)\psi _2- G_1(\eta _3)\psi _1 \\ \nonumber&\quad - G_2'(\eta _1)[\eta _2]\psi _1-G_2(\eta _1)\psi _2- G_3(\eta _1)\psi _1 , \end{aligned}$$

(A.19b)

where, in view of (A.4),

$$\begin{aligned} G_2'(\eta )[{\hat{\eta ]}}:= -G_0 \partial _x \eta {\hat{\eta }} \partial _x +\partial _x^2 \eta {\hat{\eta }} G_0 - G_0 {\hat{\eta }} G_1(\eta ) - G_0 \eta G_1({\hat{\eta }})\, . \end{aligned}$$

(A.20)

Let us inspect the terms in (A.19a). In view of (1.9) we have

$$\begin{aligned}&c_3 (\psi _1)_x = {\texttt{c}}_{\texttt{h}}^{-1}c_3 \cos (x)\, , \quad c_3 (\eta _1)_x =- c_3 \sin (x) \, ,\quad c_2 (\psi _2)_x = 2c_2 \psi _2^{[2]} \cos (2x)\, ,\\ \nonumber&c_2(\eta _2)_x = -2c_2\eta _2^{[2]} \sin (2x)\, ,\quad \frac{1}{2}(\psi _2)_x^2 = (\psi _2^{[2]})^2 + (\psi _2^{[2]})^2\cos (4x)\, , \\ \nonumber&(\psi _1)_x(\psi _3)_x = \frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-1}\psi _3^{[1]} +\frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-1}\big (\psi _3^{[1]}+3\psi _3^{[3]}\big )\cos (2x)+ \frac{3}{2} {\texttt{c}}_{\texttt{h}}^{-1}\psi _3^{[3]}\cos (4x)\, , \\ \nonumber&{\texttt{c}}_{\texttt{h}}(\eta _1)^2_x (\psi _2)_x = -\frac{1}{2} {\texttt{c}}_{\texttt{h}}\psi _2^{[2]}+{\texttt{c}}_{\texttt{h}}\psi _2^{[2]}\cos (2x) - \frac{1}{2} {\texttt{c}}_{\texttt{h}}\psi _2^{[2]} \cos (4x) \, , \\ \nonumber&\frac{1}{2}{\texttt{c}}_{\texttt{h}}^2 (\eta _2)_x^2 = {\texttt{c}}_{\texttt{h}}^2(\eta _2^{[2]})^2-{\texttt{c}}_{\texttt{h}}^2(\eta _2^{[2]})^2\cos (4x)\, ,\quad {\texttt{c}}_{\texttt{h}}c_2 (\eta _1)_x^2 = \frac{1}{2} {\texttt{c}}_{\texttt{h}}c_2 \big (1-\cos (2x)\big )\, , \\ \nonumber&{\texttt{c}}_{\texttt{h}}^2 (\eta _1)_x (\eta _3)_x = \frac{1}{2} {\texttt{c}}_{\texttt{h}}^2 \eta _3^{[1]} + \frac{1}{2} {\texttt{c}}_{\texttt{h}}^2 \big (- \eta _3^{[1]} +3\eta _3^{[3]} \big ) \cos (2x) - \frac{3}{2} {\texttt{c}}_{\texttt{h}}^2 \eta _3^{[3]} \cos (4x)\, , \\ \nonumber&\frac{1}{2} (\eta _1)^2_x (\psi _1)^2_x = \frac{{\texttt{c}}_{\texttt{h}}^{-2}}{16} \big (1-\cos (4x)\big )\, ,\quad \frac{1}{2} {\texttt{c}}_{\texttt{h}}^2 (\eta _1)_x^4 = \frac{{\texttt{c}}_{\texttt{h}}^2}{16} \big ( 3 - 4\cos (2x) + \cos (4x) \big ) \, , \\ \nonumber&2{\texttt{c}}_{\texttt{h}}(\eta _1)_x(\eta _2)_x(\psi _1)_x = \eta _2^{[2]}-\eta _2^{[2]}\cos (4x)\, . \end{aligned}$$

(A.21)

Let us inspect the terms in (A.19b). In view of (A.4), (A.2), (A.11), whereby

$$\begin{aligned} G_0\psi _3 = {\texttt{c}}_{\texttt{h}}^2 \psi _3^{[1]}\sin (x) + 3{\texttt{c}}_{\texttt{h}}^2 \frac{3+{\texttt{c}}_{\texttt{h}}^4}{1+3{\texttt{c}}_{\texttt{h}}^4} \psi _3^{[3]}\sin (3x)\,, \end{aligned}$$

(A.22)

and since

$$\begin{aligned} \tanh (4\texttt{h}) = \frac{4{\texttt{c}}_{\texttt{h}}^2+4{\texttt{c}}_{\texttt{h}}^6}{1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8}\,, \end{aligned}$$

(A.23)

we have

$$\begin{aligned} \begin{aligned} G_1(\eta _1)\psi _3&=\Big (\frac{1-{\texttt{c}}_{\texttt{h}}^4}{1+{\texttt{c}}_{\texttt{h}}^4}\psi _3^{[1]} +\frac{3(1-{\texttt{c}}_{\texttt{h}}^4)^2 \psi _3^{[3]}}{(1+{\texttt{c}}_{\texttt{h}}^4)(1+3{\texttt{c}}_{\texttt{h}}^4)} \Big )\sin (2x) + 6\frac{(1-{\texttt{c}}_{\texttt{h}}^4)^3 \psi _3^{[3]}\sin (4x)}{(1+3{\texttt{c}}_{\texttt{h}}^4)(1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8)}\,,\\ G_1(\eta _2)\psi _2&=4\frac{(1-{\texttt{c}}_{\texttt{h}}^4)^2}{(1+{\texttt{c}}_{\texttt{h}}^4)^2}\psi _2^{[2]}\eta _2^{[0]} \sin (2x)+ 4 \frac{(1-{\texttt{c}}_{\texttt{h}}^4)^2\psi _2^{[2]}\eta _2^{[2]}}{1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8}\sin (4x)\,,\\ G_1(\eta _3)\psi _1&=\Big ( \frac{1-{\texttt{c}}_{\texttt{h}}^4}{{\texttt{c}}_{\texttt{h}}(1+{\texttt{c}}_{\texttt{h}}^4)}\eta _3^{[1]} + \frac{1+3{\texttt{c}}_{\texttt{h}}^4}{{\texttt{c}}_{\texttt{h}}(1+{\texttt{c}}_{\texttt{h}}^4)} \eta _3^{[3]} \Big ) \sin (2x)+ 2\frac{(1-{\texttt{c}}_{\texttt{h}}^4)(1+3{\texttt{c}}_{\texttt{h}}^4)}{{\texttt{c}}_{\texttt{h}}(1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8)}\eta _3^{[3]}\sin (4x)\, . \end{aligned} \end{aligned}$$

(A.24)

In view of (1.9), (A.20), (A.11), (A.8), (A.13) and (A.23), we have

$$\begin{aligned} G_2'(\eta _1)[\eta _2]\psi _1= & {} \Big (\frac{8{\texttt{c}}_{\texttt{h}}^5\eta _2^{[2]}}{(1+3{\texttt{c}}_{\texttt{h}}^4)(1+{\texttt{c}}_{\texttt{h}}^4)}- \frac{4{\texttt{c}}_{\texttt{h}}(1-{\texttt{c}}_{\texttt{h}}^4)}{(1+{\texttt{c}}_{\texttt{h}}^4)^2}\eta _2^{[0]}\Big )\sin (2x)\nonumber \\{} & {} - \frac{8{\texttt{c}}_{\texttt{h}}(1-{\texttt{c}}_{\texttt{h}}^8)\eta _2^{[2]}}{(1+3{\texttt{c}}_{\texttt{h}}^4)(1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8)}\sin (4x)\, . \end{aligned}$$

(A.25)

By (1.9), (A.4), (A.13), (A.11) and (A.23) we have

$$\begin{aligned} G_2(\eta _1)\psi _2= -\frac{8{\texttt{c}}_{\texttt{h}}^2(1-{\texttt{c}}_{\texttt{h}}^4)\psi _2^{[2]}}{(1+{\texttt{c}}_{\texttt{h}}^4)^2(1+3{\texttt{c}}_{\texttt{h}}^4)}\sin (2x)- \frac{16{\texttt{c}}_{\texttt{h}}^2(1-{\texttt{c}}_{\texttt{h}}^4)^2\psi _2^{[2]}}{(1+{\texttt{c}}_{\texttt{h}}^4)(1+3{\texttt{c}}_{\texttt{h}}^4)(1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8)}\sin (4x)\, .\qquad \end{aligned}$$

(A.26)

Finally, by (1.9), (A.4), (A.13), (A.8), (A.11) and (A.23), we have

$$\begin{aligned} G_3(\eta _1)\psi _1= & {} \frac{-1+14{\texttt{c}}_{\texttt{h}}^4-9{\texttt{c}}_{\texttt{h}}^8}{3{\texttt{c}}_{\texttt{h}}(1+{\texttt{c}}_{\texttt{h}}^4)^2(1+3{\texttt{c}}_{\texttt{h}}^4)}\sin (2x)\nonumber \\{} & {} +2 \frac{-1+15{\texttt{c}}_{\texttt{h}}^4-23{\texttt{c}}_{\texttt{h}}^8+9{\texttt{c}}_{\texttt{h}}^{12}}{3{\texttt{c}}_{\texttt{h}}(1+{\texttt{c}}_{\texttt{h}}^4)(1+3{\texttt{c}}_{\texttt{h}}^4)(1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8)}\sin (4x)\, . \end{aligned}$$

(A.27)

By (A.19), (A.21), (A.24), (A.25), (A.26), (A.27) and (A.2a)–(A.2c) system (A.18) reads as

$$\begin{aligned} \begin{bmatrix} f_4(x) \\ g_4(x) \end{bmatrix}=\begin{bmatrix} f_4^{[0]} + {\texttt{c}}_{\texttt{h}}^{-1}c_3\cos (x) + f_4^{[2]}\cos (2x) + f_4^{[4]}\cos (4x) \\ c_3\sin (x) + g_4^{[2]}\sin (2x) + g_4^{[4]}\sin (4x) \end{bmatrix} \,,\qquad \end{aligned}$$

(A.28)

with

$$\begin{aligned} \nonumber f_4^{[0]}&= \frac{-4 {\texttt{c}}_{\texttt{h}}^{20}-4 {\texttt{c}}_{\texttt{h}}^{18}+17 {\texttt{c}}_{\texttt{h}}^{16}+6 {\texttt{c}}_{\texttt{h}}^{14}-48 {\texttt{c}}_{\texttt{h}}^8+6 {\texttt{c}}_{\texttt{h}}^6+36 {\texttt{c}}_{\texttt{h}}^4-9}{64 {\texttt{c}}_{\texttt{h}}^{14}}\, ,\\ \nonumber f_4^{[4]}&= \frac{7 {\texttt{c}}_{\texttt{h}}^{16}-48 {\texttt{c}}_{\texttt{h}}^{12}+126 {\texttt{c}}_{\texttt{h}}^8-168 {\texttt{c}}_{\texttt{h}}^4-45}{128 {\texttt{c}}_{\texttt{h}}^{14}} \, ,\\ \nonumber f_4^{[2]}&= \frac{4 {\texttt{c}}_{\texttt{h}}^{22}+12 {\texttt{c}}_{\texttt{h}}^{20}-27 {\texttt{c}}_{\texttt{h}}^{18}-31 {\texttt{c}}_{\texttt{h}}^{16}+78 {\texttt{c}}_{\texttt{h}}^{14}+66 {\texttt{c}}_{\texttt{h}}^{12}-72 {\texttt{c}}_{\texttt{h}}^{10}-84 {\texttt{c}}_{\texttt{h}}^8+6 {\texttt{c}}_{\texttt{h}}^6-6 {\texttt{c}}_{\texttt{h}}^4+27 {\texttt{c}}_{\texttt{h}}^2+27}{128 {\texttt{c}}_{\texttt{h}}^{14}(1+{\texttt{c}}_{\texttt{h}}^2)}\, ,\\ g_4^{[2]}&=\frac{3 {\texttt{c}}_{\texttt{h}}^{16}-12 {\texttt{c}}_{\texttt{h}}^{14}-39 {\texttt{c}}_{\texttt{h}}^{12}+18 {\texttt{c}}_{\texttt{h}}^{10}+139 {\texttt{c}}_{\texttt{h}}^8-225 {\texttt{c}}_{\texttt{h}}^4+18 {\texttt{c}}_{\texttt{h}}^2+18}{48{\texttt{c}}_{\texttt{h}}^9 (1+{\texttt{c}}_{\texttt{h}}^4)}\, , \\ \nonumber g_4^{[4]}&=\frac{-21 {\texttt{c}}_{\texttt{h}}^{20}+61 {\texttt{c}}_{\texttt{h}}^{16}+14 {\texttt{c}}_{\texttt{h}}^{12}-198 {\texttt{c}}_{\texttt{h}}^8+279 {\texttt{c}}_{\texttt{h}}^4-135}{48 {\texttt{c}}_{\texttt{h}}^{13} ({\texttt{c}}_{\texttt{h}}^8+6 {\texttt{c}}_{\texttt{h}}^4+1)}\, . \end{aligned}$$

(A.29)

As a consequence of (A.28) we have

$$\begin{aligned} \Big (\begin{bmatrix}f_4(x) \\ g_4(x) \end{bmatrix}\,, \, \begin{bmatrix}\cos (x) \\ {\texttt{c}}_{\texttt{h}}^{-1}\sin (x) \end{bmatrix} \Big ) = {\texttt{c}}_{\texttt{h}}^{-1}c_3\, . \end{aligned}$$

By Lemma A.3, with $c_3=0$ as stated in (1.9c), one ensures that the system (A.18) is solved by

$$\begin{aligned} \begin{bmatrix}\eta _4(x) \\ \psi _4(x) \end{bmatrix} = {{\mathcal {B}}}_0^{-1} \begin{bmatrix}f_4(x) \\ g_4(x) \end{bmatrix}\,, \end{aligned}$$

(A.30)

where, in view of (A.7) and (A.28),

$$\begin{aligned} \begin{bmatrix} \eta _4(x) \\ \psi _4(x) \end{bmatrix}=\left[ \begin{array}{l} \eta _4^{[0]} + \eta _4^{[2]}\cos (2x) + \eta _4^{[4]}\cos (4x) \\ \psi _4^{[2]}\sin (2x) + \psi _4^{[4]}\sin (4x) \end{array}\right] \,, \end{aligned}$$

(A.31)

with, in view of (A.11) and (A.23) too,

$$\begin{aligned}&\eta _4^{[0]} :=f_4^{[0]}\, , \quad \begin{bmatrix} \eta _4^{[2]}\\ \psi _4^{[2]} \end{bmatrix} = - \frac{1+{\texttt{c}}_{\texttt{h}}^4}{4{\texttt{c}}_{\texttt{h}}^6} \begin{bmatrix} \frac{4{\texttt{c}}_{\texttt{h}}^2}{1+{\texttt{c}}_{\texttt{h}}^4} &{} 2{\texttt{c}}_{\texttt{h}}\\ 2{\texttt{c}}_{\texttt{h}}&{} 1 \end{bmatrix} \begin{bmatrix} f_4^{[2]}\\ g_4^{[2]} \end{bmatrix}\\ \nonumber&\quad = - \frac{1+{\texttt{c}}_{\texttt{h}}^4}{4{\texttt{c}}_{\texttt{h}}^6} \left[ \begin{array}{l}\frac{4{\texttt{c}}_{\texttt{h}}^2}{1+{\texttt{c}}_{\texttt{h}}^4} f_4^{[2]} +2{\texttt{c}}_{\texttt{h}}g_4^{[2]} \\ 2{\texttt{c}}_{\texttt{h}}f_4^{[2]} +g_4^{[2]} \end{array}\right] \, , \\ \nonumber&\begin{bmatrix} \eta _4^{[4]}\\ \psi _4^{[4]} \end{bmatrix} = - \frac{1+6{\texttt{c}}_{\texttt{h}}^4+ {\texttt{c}}_{\texttt{h}}^8}{16{\texttt{c}}_{\texttt{h}}^6(5+{\texttt{c}}_{\texttt{h}}^4)} \begin{bmatrix} 16{\texttt{c}}_{\texttt{h}}^2 \frac{1+{\texttt{c}}_{\texttt{h}}^4}{1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8} &{} 4{\texttt{c}}_{\texttt{h}}\\ 4{\texttt{c}}_{\texttt{h}}&{} 1 \end{bmatrix} \begin{bmatrix} f_4^{[4]}\\ g_4^{[4]} \end{bmatrix}\\ \nonumber&\quad = - \frac{1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8}{16{\texttt{c}}_{\texttt{h}}^6(5+{\texttt{c}}_{\texttt{h}}^4)} \begin{bmatrix} 16{\texttt{c}}_{\texttt{h}}^2 \frac{1+{\texttt{c}}_{\texttt{h}}^4}{1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8} f_4^{[4]}+ 4{\texttt{c}}_{\texttt{h}}g_4^{[4]} \\ 4{\texttt{c}}_{\texttt{h}}f_4^{[4]} + g_4^{[4]} \end{bmatrix} \, . \end{aligned}$$

(A.32)

By (A.31) we conclude the proof of (1.9a)–(1.9b) and, in view of (A.32) and (A.29), of (A.2d). The proof of (1.9), (A.2) needs only the computation of $c_4$.

Fifth order in $\epsilon$. By plugging the expansion (A.2) in system (A.3) and discarding sextic terms we find the linear system

$$\begin{aligned} {{\mathcal {B}}}_0 \begin{bmatrix}\eta _5 \\ \psi _5 \end{bmatrix} = \begin{bmatrix}{\mathtt f}_5 \\ {\mathtt g}_5 \end{bmatrix} + c_4 \begin{bmatrix}(\psi _1)_x \\ -(\eta _1)_x \end{bmatrix}\,, \end{aligned}$$

(A.33)

with

$$\begin{aligned} {\mathtt f}_5&:= c_2(\psi _3)_x - (\psi _1)_x (\psi _4)_x- (\psi _2)_x (\psi _3)_x+ (\eta _1)_x^2 \big (-{\texttt{c}}_{\texttt{h}}(\psi _3)_x-c_2 (\psi _1)_x+(\psi _1)_x(\psi _2)_x \big )\end{aligned}$$

(A.34a)

$$\begin{aligned}&\quad + (\eta _1)_x(\eta _2)_x \big ((\psi _1)_x^2 + 2{\texttt{c}}_{\texttt{h}}c_2 - 2{\texttt{c}}_{\texttt{h}}(\psi _2)_x \big ) -{\texttt{c}}_{\texttt{h}}(\psi _1)_x \big ( (\eta _2)_x^2 - (\eta _1)_x^4 + 2(\eta _1)_x (\eta _3)_x \big ) \nonumber \\&\quad + {\texttt{c}}_{\texttt{h}}^2 \big ( (\eta _1)_x (\eta _4)_x + (\eta _2)_x (\eta _3)_x - 2(\eta _1)_x^3(\eta _2)_x \big )\, , \nonumber \\ {\mathtt g}_5&:= -c_2 (\eta _3)_x- G_1(\eta _1)\psi _4 - G_1(\eta _2)\psi _3 - G_1(\eta _3)\psi _2- G_1(\eta _4)\psi _1- G_2(\eta _1)\psi _3 \nonumber \\&\quad -G_2(\eta _2)\psi _1 - G_2'(\eta _1)[\eta _2,\psi _2] - G_2'(\eta _1)[\eta _3,\psi _1] - G_3(\eta _1)\psi _2 - G_3'(\eta _1)[\eta _2,\psi _1] - G_4(\eta _1)\psi _1\,, \end{aligned}$$

(A.34b)

where $G_2'$ is in (A.20) and, by (A.4),

$$\begin{aligned} G_3'(\eta )[{\hat{\eta ]}}= & {} \frac{1}{2} \partial _x^3 \eta ^2 {\hat{\eta }} \partial _x + \frac{1}{2} G_0 \partial _x^2 \eta ^2 {\hat{\eta }} G_0 - G_0 {\hat{\eta }} G_2(\eta ) - G_0 \eta G_2'(\eta )[{\hat{\eta ]}}\nonumber \\ {}{} & {} + \partial _x^2 \eta {\hat{\eta }} G_1(\eta ) + \frac{1}{2} \partial _x^2 \eta ^2 G_1({\hat{\eta }}) \, . \end{aligned}$$

(A.35)

The term $c_4$ is obtained by imposing the expression on the right-hand side of (A.33) to be orthogonal to the kernel of the operator ${{\mathcal {B}}}_0$ in (A.6a), obtaining, in view of (1.14),

$$\begin{aligned} c_4 = -\dfrac{\big ( {\mathtt f}_5, \eta _1\big )+\big ( {\mathtt g}_5, \psi _1\big )}{\big ( (\psi _1)_x, \eta _1\big )-\big ( (\eta _1)_x, \psi _1\big )} = -{\texttt{c}}_{\texttt{h}}\Big (\big ( {\mathtt f}_5, \eta _1\big )+\big ( {\mathtt g}_5, \psi _1\big )\Big ) \, . \end{aligned}$$

(A.36)

By (A.34) and (1.9) we find that $c_4$ in (A.36) has the explicit expression in (A.2e).

Remark A.3

Expansion (1.9), (A.2) coincides with that in [21, formulae (12)–(14)], provided one rescales properly their amplitude $\varepsilon _{\textrm{Fen}} = \epsilon + f(\texttt{h}) \epsilon ^3$ with a suitable $f(\texttt{h})$, translates their bottom to $d:=\texttt{h}+\epsilon ^2 \eta _2^{[0]}+\epsilon ^4 \eta _4^{[0]}+\mathcal {O}(\epsilon ^5)$ (in [21] the water surface $\eta$ has zero average) and removes from the velocity potential a shear term $-\overline{u}x$ (which corresponds to a Galilean reference frame).

1.2 A.2 Expansions of $a_\epsilon (x)$ and $p_\epsilon (x)$

In this section we compute the fourth order expansion of the functions $a_\epsilon (x)$ and $p_\epsilon (x)$ and of the constant $\texttt{f}_\epsilon$ in (1.12).

By [9, formula (2.18)]) the functions $a_\epsilon (x)$ and $p_\epsilon (x)$ in (1.12) are given by

$$\begin{aligned} {\texttt{c}}_{\texttt{h}}+p_\epsilon (x)&:= \displaystyle {\frac{ c_\epsilon -V(x+\mathfrak {p}(x))}{ 1+\mathfrak {p}_x(x)}} \, , \nonumber \\ 1+a_\epsilon (x)&:= \displaystyle {\frac{1+ (V(x + \mathfrak {p}(x)) - c_\epsilon ) B_x(x + \mathfrak {p}(x)) }{1+\mathfrak {p}_x(x)}}\nonumber \\ {}&= \dfrac{1}{1+\mathfrak {p}_x(x)} - ({\texttt{c}}_{\texttt{h}}+p_\epsilon (x))B_x(x+\mathfrak {p}(x)) \, , \end{aligned}$$

(A.37)

and by [9, formula (2.14)]) the constant $\texttt{f}_\epsilon$ is

$$\begin{aligned} \texttt{f}_\epsilon = \frac{1}{2\pi } \int _\mathbb {T}\eta _\epsilon (x + \mathfrak {p}(x)) \textrm{d}x \, . \end{aligned}$$

(A.38)

Here the function ${\mathfrak {p}}(x)$ is determined (cfr. [9, formula (2.14)], [2, formula (A.15)]) by the fixed point equation

$$\begin{aligned} \mathfrak {p} (x) = \frac{\mathcal {H}}{\tanh \big ((\texttt{h}+ \texttt{f}_\epsilon )|D| \big )}[\eta _\epsilon ( x + \mathfrak {p}(x))] \,, \end{aligned}$$

(A.39)

where ${{\mathcal {H}}}:= -\textrm{i}\,\text {sgn}(D)$ is the Hilbert transform¹, whereas the functions V and B (cfr. [9, formula (2.10)]) are given by

$$\begin{aligned} V(x):= -B(x) \eta '_\epsilon (x) + \psi '_\epsilon (x) \,, \quad B(x):= \frac{ \psi '_\epsilon (x)- c_\epsilon }{1+(\eta '_\epsilon (x))^2} \eta '_\epsilon (x) \, . \end{aligned}$$

(A.40)

To provide the Taylor expansion of the functions in (A.37) we need some preparatory results.

Lemma A.1

(Fourth order expansion of $\mathfrak {p} (x)$ and $\texttt{f}_\epsilon$) The function $\mathfrak {p} (x)$ in (A.39) admits the following Taylor expansion

$$\begin{aligned} \begin{aligned} \mathfrak {p}(x)&= \epsilon {\texttt{c}}_{\texttt{h}}^{-2} \sin (x) + \epsilon ^2 \mathfrak {p}_2^{[2]}\sin (2x) + \epsilon ^3 \big ( \mathfrak {p}_3^{[1]}\sin (x) +\mathfrak {p}_3^{[3]}\sin (3x) \big ) \\&\quad + \epsilon ^4 \big ( \mathfrak {p}_4^{[2]}\sin (2x) + \mathfrak {p}_4^{[4]}\sin (4x) \big ) +\mathcal {O}(\epsilon ^5) \end{aligned} \end{aligned}$$

(A.41)

with coefficients

$$\begin{aligned}&\mathfrak {p}_2^{[2]}:=\frac{3+4{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8}{8{\texttt{c}}_{\texttt{h}}^8}\, , \end{aligned}$$

(A.42)

$$\begin{aligned}&\mathfrak {p}_3^{[1]} := \frac{4 {\texttt{c}}_{\texttt{h}}^{14}+2 {\texttt{c}}_{\texttt{h}}^{12}-17 {\texttt{c}}_{\texttt{h}}^{10}-14 {\texttt{c}}_{\texttt{h}}^8+10 {\texttt{c}}_{\texttt{h}}^6+10 {\texttt{c}}_{\texttt{h}}^4-15 {\texttt{c}}_{\texttt{h}}^2-12}{16 {\texttt{c}}_{\texttt{h}}^{10} ({\texttt{c}}_{\texttt{h}}^2+1)} \, , \end{aligned}$$

(A.43)

$$\begin{aligned}&\mathfrak {p}_3^{[3]} := \frac{9+41{\texttt{c}}_{\texttt{h}}^4+43{\texttt{c}}_{\texttt{h}}^8 +3{\texttt{c}}_{\texttt{h}}^{12}}{64{\texttt{c}}_{\texttt{h}}^{14}} \, , \end{aligned}$$

(A.44)

$$\begin{aligned}&\mathfrak {p}_4^{[2]}:= -\frac{1}{256 {\texttt{c}}_{\texttt{h}}^{20} ({\texttt{c}}_{\texttt{h}}^2+1)} \big (8 {\texttt{c}}_{\texttt{h}}^{24}-57 {\texttt{c}}_{\texttt{h}}^{22}-37 {\texttt{c}}_{\texttt{h}}^{20}+199 {\texttt{c}}_{\texttt{h}}^{18}+175 {\texttt{c}}_{\texttt{h}}^{16}+238 {\texttt{c}}_{\texttt{h}}^{14} \end{aligned}$$

(A.45)

$$\begin{aligned}&\qquad \qquad +190 {\texttt{c}}_{\texttt{h}}^{12}-130 {\texttt{c}}_{\texttt{h}}^{10}-178 {\texttt{c}}_{\texttt{h}}^8+171 {\texttt{c}}_{\texttt{h}}^6+135 {\texttt{c}}_{\texttt{h}}^4+27 {\texttt{c}}_{\texttt{h}}^2+27 \big ) \, , \nonumber \\&\mathfrak {p}_4^{[4]}:=\frac{{\texttt{c}}_{\texttt{h}}^{24}+44 {\texttt{c}}_{\texttt{h}}^{20}+557 {\texttt{c}}_{\texttt{h}}^{16}+2528 {\texttt{c}}_{\texttt{h}}^{12}+3595 {\texttt{c}}_{\texttt{h}}^8+1332 {\texttt{c}}_{\texttt{h}}^4+135}{512 {\texttt{c}}_{\texttt{h}}^{20} ({\texttt{c}}_{\texttt{h}}^4+5)} \, . \end{aligned}$$

(A.46)

The real constant $\texttt{f}_\epsilon$ in (1.12) has the Taylor expansion

$$\begin{aligned} \texttt{f}_\epsilon = \epsilon ^2 \texttt{f}_2 + \epsilon ^4 \texttt{f}_4 + \mathcal {O}(\epsilon ^5) \end{aligned}$$

(A.47)

with coefficients

$$\begin{aligned} \texttt{f}_2&:=\frac{{\texttt{c}}_{\texttt{h}}^4-3}{4{\texttt{c}}_{\texttt{h}}^2} \, ,\nonumber \\ \texttt{f}_4&:= \frac{1}{64 {\texttt{c}}_{\texttt{h}}^{14} ({\texttt{c}}_{\texttt{h}}^2+1)}\big (-4 {\texttt{c}}_{\texttt{h}}^{22}-8 {\texttt{c}}_{\texttt{h}}^{20}+5 {\texttt{c}}_{\texttt{h}}^{18}+23 {\texttt{c}}_{\texttt{h}}^{16}+40 {\texttt{c}}_{\texttt{h}}^{14}+22 {\texttt{c}}_{\texttt{h}}^{12}\nonumber \\&\quad -78 {\texttt{c}}_{\texttt{h}}^{10}-72 {\texttt{c}}_{\texttt{h}}^8+72 {\texttt{c}}_{\texttt{h}}^6+54 {\texttt{c}}_{\texttt{h}}^4-27 {\texttt{c}}_{\texttt{h}}^2-27\big ) \, . \end{aligned}$$

(A.48)

Proof

We expand

$$\begin{aligned} \begin{aligned} \mathfrak {p}(x)&= \epsilon \mathfrak {p}_1(x) + \epsilon ^2 \mathfrak {p}_2(x) + \epsilon ^3 \mathfrak {p}_3(x)+ \epsilon ^4 \mathfrak {p}_4(x) +\mathcal {O}(\epsilon ^5)\,, \\ \texttt{f}_\epsilon&= \epsilon ^2 \texttt{f}_2 + \epsilon ^3 \texttt{f}_3+ \epsilon ^4 \texttt{f}_4 + \mathcal {O}(\epsilon ^5) \,, \end{aligned} \end{aligned}$$

(A.49)

where, by [9, formula (2.15)], $\mathfrak {p}_1(x)$, $\mathfrak {p}_2(x)$ are given in (A.42) and $\texttt{f}_2$ in (A.48).

Let us denote derivatives w.r.t x with a prime $'$. By (A.38), (1.9) and (A.49), we get

$$\begin{aligned} \texttt{f}_3 =\frac{1}{2\pi } \int _\mathbb {T}\big ( \eta _3(x)+\eta _2'(x)\mathfrak {p}_1(x) + \eta _1'(x)\mathfrak {p}_2(x)+\frac{1}{2} \eta _1''(x)\mathfrak {p}_1^2(x)\big ) \textrm{d}x = 0 \end{aligned}$$

as stated in the expansion (A.47). In view of (A.39) and (A.48) we have

$$\begin{aligned} \begin{aligned} \mathfrak {p}_3(x)&= - \textrm{i}\,\frac{\text {sgn}(D)}{\tanh (\texttt{h}|D|)} \Big ( \eta _3(x) + \eta _2'(x) \mathfrak {p}_1(x) + \eta _1'(x) \mathfrak {p}_2(x) + \frac{1}{2} \eta _1''(x) \mathfrak {p}_1^2(x) \Big ) \\&\quad + \texttt{f}_2 \frac{\partial _x}{\tanh ^2(\texttt{h}|D|)} \big (1-\tanh ^2(\texttt{h}|D|) \big )\eta _1(x) \, . \end{aligned} \end{aligned}$$

(A.50)

In view of (A.50), (1.9), (A.41)–(A.42) and (A.11), we have

$$\begin{aligned} \begin{aligned} \mathfrak {p}_3(x)&= \frac{16\eta _3^{[1]}{\texttt{c}}_{\texttt{h}}^8 - 16 \eta _2^{[2]} {\texttt{c}}_{\texttt{h}}^6 - 3 -6{\texttt{c}}_{\texttt{h}}^4 -{\texttt{c}}_{\texttt{h}}^8-16 \texttt{f}_2 {\texttt{c}}_{\texttt{h}}^6+16 \texttt{f}_2 {\texttt{c}}_{\texttt{h}}^{10} {16{\texttt{c}}_{\texttt{h}}^{10}}}{\sin }(x) \\&\quad + \frac{(1+3{\texttt{c}}_{\texttt{h}}^4)(8\eta _3^{[3]}{\texttt{c}}_{\texttt{h}}^4 + 8 \eta _2^{[2]} {\texttt{c}}_{\texttt{h}}^2 + 4{\texttt{c}}_{\texttt{h}}^4\mathfrak {p}_2^{[2]}+1)}{8{\texttt{c}}_{\texttt{h}}^6(3+{\texttt{c}}_{\texttt{h}}^4)}\sin (3x)\,, \end{aligned} \end{aligned}$$

(A.51)

which, by (A.2a)–(A.2c), is (A.44). By (A.38), (1.9), (A.42) and (A.44), we have

$$\begin{aligned} \texttt{f}_4&= \frac{1}{2\pi } \int _\mathbb {T}\big ( \eta _4(x) + \eta _3'(x) \mathfrak {p}_1(x) +\eta _2'(x) \mathfrak {p}_2(x) + \eta _1'(x) \mathfrak {p}_3(x) \nonumber \\&\quad +\frac{1}{2} \eta _2''(x) \mathfrak {p}_1^2(x)+ \eta _1''(x) \mathfrak {p}_2(x)\mathfrak {p}_1(x)+\frac{1}{6} \eta _1'''(x)\mathfrak {p}_1^3(x) \big ) \textrm{d}x \nonumber \\&= \eta _4^{[0]} - \frac{\eta _3^{[1]}}{2{\texttt{c}}_{\texttt{h}}^2} - \mathfrak {p}_2^{[2]}\eta _2^{[2]} - \frac{1}{2} \mathfrak {p}_3^{[1]} +\frac{\eta _2^{[2]}}{2{\texttt{c}}_{\texttt{h}}^4} - \frac{\mathfrak {p}_2^{[2]}}{4{\texttt{c}}_{\texttt{h}}^2} + \frac{1}{16{\texttt{c}}_{\texttt{h}}^6} \, , \end{aligned}$$

(A.52)

which gives the fourth-order coefficient in (A.48). Finally, by (A.39) and (A.48),

$$\begin{aligned} \mathfrak {p}_4(x)&= -\textrm{i}\,\frac{\text {sgn}(D)}{\tanh (\texttt{h}|D|)} \big ( \eta _4(x) + \eta _3'(x) \mathfrak {p}_1(x) +\eta _2'(x) \mathfrak {p}_2(x) + \eta _1'(x) \mathfrak {p}_3(x) \\&\quad +\frac{1}{2} \eta _2''(x) \mathfrak {p}_1^2(x)+ \eta _1''(x) \mathfrak {p}_2(x) \mathfrak {p}_1(x)+\frac{1}{6} \eta _1'''(x)\mathfrak {p}_1^3(x) \big ) \\&\quad + \texttt{f}_2 \frac{\partial _x}{\tanh ^2(\texttt{h}|D|)}\big ( 1-\tanh ^2(\texttt{h}|D|) \big ) \big (\eta _2(x) + \eta _1'(x) \mathfrak {p}_1(x)\big ) \\&= \frac{1+{\texttt{c}}_{\texttt{h}}^4}{2{\texttt{c}}_{\texttt{h}}^2} \big (\frac{1}{2} \mathfrak {p}_3^{[1]}-\frac{1}{2} \mathfrak {p}_3^{[3]}-\frac{1}{12{\texttt{c}}_{\texttt{h}}^6}-\frac{ \eta _2^{[2]}}{{\texttt{c}}_{\texttt{h}}^4}+\frac{ \eta _3^{[1]}}{2{\texttt{c}}_{\texttt{h}}^2}-\frac{3 \eta _3^{[3]}}{2{\texttt{c}}_{\texttt{h}}^2}+ \eta _4^{[2]} \big ) \sin (2x) \\&\quad + \frac{1+6{\texttt{c}}_{\texttt{h}}^4+{\texttt{c}}_{\texttt{h}}^8}{4{\texttt{c}}_{\texttt{h}}^2(1+{\texttt{c}}_{\texttt{h}}^4)} \big (\frac{\mathfrak {p}_2^{[2]}}{4 {\texttt{c}}_{\texttt{h}}^2} +\frac{3\eta _3^{[3]}}{2{\texttt{c}}_{\texttt{h}}^2}+\mathfrak {p}_2^{[2]} \eta _2^{[2]}+\frac{1}{2} \mathfrak {p}_3^{[3]}+ \frac{1}{48 {\texttt{c}}_{\texttt{h}}^6}+\frac{\eta _2^{[2]}}{2 {\texttt{c}}_{\texttt{h}}^4}+\eta _4^{[4]} \big ) \sin (4x) \\&\quad - \texttt{f}_2 \frac{(1-{\texttt{c}}_{\texttt{h}}^4)^2(1+2{\texttt{c}}_{\texttt{h}}^2\eta _2^{[2]})}{4{\texttt{c}}_{\texttt{h}}^6} \sin (2x) \, , \end{aligned}$$

which, by (A.2a)–(A.2c), gives (A.41) with the coefficients computed in (A.45)–(A.46). $\square$

The second preparatory result is given by the following

Lemma A.2

(Expansion of B(x) and V(x)) The functions B(x) and V(x) in (A.40) admit the following Taylor expansion

$$\begin{aligned} \begin{aligned} B(x)&= \epsilon B_1(x)+ \epsilon ^2 B_2(x) + \epsilon ^3 B_3(x)+ \epsilon ^4 B_4(x)+\mathcal {O}(\epsilon ^5)\,, \\ V(x)&= \epsilon V_1(x) + \epsilon ^2 V_2(x)+\epsilon ^3 V_3(x)+\epsilon ^4 V_4(x) + \mathcal {O}(\epsilon ^5) \,, \end{aligned} \end{aligned}$$

(A.53)

where

$$\begin{aligned} \begin{aligned} B_1(x)&= {\texttt{c}}_{\texttt{h}}\sin (x) \,, \quad{} & {} B_2(x) = B_2^{[2]}\sin (2x) \,,\quad&B_2^{[2]}:=\frac{3-2{\texttt{c}}_{\texttt{h}}^4}{2{\texttt{c}}_{\texttt{h}}^5}\,,\\ V_1(x)&={\texttt{c}}_{\texttt{h}}^{-1} \cos (x) \,, \quad{} & {} V_2(x) =\frac{{\texttt{c}}_{\texttt{h}}}{2} + V_2^{[2]} \cos (2x)\,,\quad&V_2^{[2]}:=\frac{3-{\texttt{c}}_{\texttt{h}}^8}{4{\texttt{c}}_{\texttt{h}}^7}\,, \end{aligned}\qquad \end{aligned}$$

(A.54)

and

$$\begin{aligned} \begin{alignedat}{2}&B_3(x) = B_3^{[1]}\sin (x)+ B_3^{[3]}\sin (3x)\,,\quad{} & {} B_4(x) = B_4^{[2]} \sin (2x)+ B_4^{[4]}\sin (4x)\,, \\&V_3(x) = V_3^{[1]}\cos (x)+ V_3^{[3]}\cos (3x)\,,\quad{} & {} V_4(x) = V_4^{[0]} + V_4^{[2]}\cos (2x)+ V_4^{[4]}\cos (4x)\,, \end{alignedat} \end{aligned}$$

(A.55)

with

$$\begin{aligned}&B_3^{[1]}:=\frac{6+3{\texttt{c}}_{\texttt{h}}^2-8{\texttt{c}}_{\texttt{h}}^4-8{\texttt{c}}_{\texttt{h}}^6+6{\texttt{c}}_{\texttt{h}}^8+3{\texttt{c}}_{\texttt{h}}^{10}-4{\texttt{c}}_{\texttt{h}}^{12}-2{\texttt{c}}_{\texttt{h}}^{14}}{16{\texttt{c}}_{\texttt{h}}^7(1+{\texttt{c}}_{\texttt{h}}^2)} \, ,\nonumber \\ {}&B_3^{[3]}:= \frac{81-99{\texttt{c}}_{\texttt{h}}^4+43{\texttt{c}}_{\texttt{h}}^8-{\texttt{c}}_{\texttt{h}}^{12}}{64{\texttt{c}}_{\texttt{h}}^{11}}\, ,\nonumber \\&V_3^{[1]}:=\frac{2{\texttt{c}}_{\texttt{h}}^{12}-15{\texttt{c}}_{\texttt{h}}^{8}-12{\texttt{c}}_{\texttt{h}}^6+24{\texttt{c}}_{\texttt{h}}^4+24{\texttt{c}}_{\texttt{h}}^2-3}{16{\texttt{c}}_{\texttt{h}}^7 (1+{\texttt{c}}_{\texttt{h}}^{2})}\, ,\nonumber \\&V_3^{[3]}:= \frac{21{\texttt{c}}_{\texttt{h}}^{12}-39{\texttt{c}}_{\texttt{h}}^8+15{\texttt{c}}_{\texttt{h}}^4+27}{64{\texttt{c}}_{\texttt{h}}^{13}}\, , \end{aligned}$$

(A.56a)

and

$$\begin{aligned} \begin{aligned} V_4^{[0]}:&=\frac{-2 {\texttt{c}}_{\texttt{h}}^{18}-6 {\texttt{c}}_{\texttt{h}}^{16}+3 {\texttt{c}}_{\texttt{h}}^{14}+9 {\texttt{c}}_{\texttt{h}}^{12}-33 {\texttt{c}}_{\texttt{h}}^6-27 {\texttt{c}}_{\texttt{h}}^4+36 {\texttt{c}}_{\texttt{h}}^2+36}{32 {\texttt{c}}_{\texttt{h}}^{11} ({\texttt{c}}_{\texttt{h}}^2+1)} \,,\\ B_4^{[2]}:&=\frac{1}{192 {\texttt{c}}_{\texttt{h}}^{17} ({\texttt{c}}_{\texttt{h}}^2+1)} \big (-24 {\texttt{c}}_{\texttt{h}}^{22}+24 {\texttt{c}}_{\texttt{h}}^{20}+354 {\texttt{c}}_{\texttt{h}}^{18}+210 {\texttt{c}}_{\texttt{h}}^{16}\\&\quad -943 {\texttt{c}}_{\texttt{h}}^{14}-835 {\texttt{c}}_{\texttt{h}}^{12}+927 {\texttt{c}}_{\texttt{h}}^{10}+855 {\texttt{c}}_{\texttt{h}}^8-81 {\texttt{c}}_{\texttt{h}}^6+27 {\texttt{c}}_{\texttt{h}}^4-81 {\texttt{c}}_{\texttt{h}}^2-81\big ) \,,\\ V_4^{[2]}:&= \frac{1}{384 {\texttt{c}}_{\texttt{h}}^{19} ({\texttt{c}}_{\texttt{h}}^2+1)} \big ( 12 {\texttt{c}}_{\texttt{h}}^{26}+36 {\texttt{c}}_{\texttt{h}}^{24}-9 {\texttt{c}}_{\texttt{h}}^{22}-45 {\texttt{c}}_{\texttt{h}}^{20}+357 {\texttt{c}}_{\texttt{h}}^{18}+285 {\texttt{c}}_{\texttt{h}}^{16}\\&\quad -1060 {\texttt{c}}_{\texttt{h}}^{14}-988 {\texttt{c}}_{\texttt{h}}^{12}+1584 {\texttt{c}}_{\texttt{h}}^{10}+1584 {\texttt{c}}_{\texttt{h}}^8-243 {\texttt{c}}_{\texttt{h}}^6-135 {\texttt{c}}_{\texttt{h}}^4-81 {\texttt{c}}_{\texttt{h}}^2-81\big ) \,, \\ B_4^{[4]}:&=\frac{6 {\texttt{c}}_{\texttt{h}}^{20}-47 {\texttt{c}}_{\texttt{h}}^{16}-100 {\texttt{c}}_{\texttt{h}}^{12}+522 {\texttt{c}}_{\texttt{h}}^8-594 {\texttt{c}}_{\texttt{h}}^4+405}{96 {\texttt{c}}_{\texttt{h}}^{17} ({\texttt{c}}_{\texttt{h}}^4+5)}\,, \\ V_4^{[4]}:&= \frac{9 {\texttt{c}}_{\texttt{h}}^{24}-96 {\texttt{c}}_{\texttt{h}}^{20}-377 {\texttt{c}}_{\texttt{h}}^{16}+1484 {\texttt{c}}_{\texttt{h}}^{12}-1413 {\texttt{c}}_{\texttt{h}}^8+756 {\texttt{c}}_{\texttt{h}}^4+405}{384 {\texttt{c}}_{\texttt{h}}^{19} ({\texttt{c}}_{\texttt{h}}^4+5)} \, . \end{aligned} \end{aligned}$$

(A.56b)

Proof

The first jets of (A.53) in (A.54) were computed in [9, (B.12–B.13)].

On the other hand, in view of (A.40) and (1.9), (A.2), the third order terms are

$$\begin{aligned} B_3(x)&= -{\texttt{c}}_{\texttt{h}}\eta _3'(x) + {\texttt{c}}_{\texttt{h}}(\eta _1'(x))^3 + \psi _1'(x) \eta _2'(x) + (\psi _2'(x)-c_2)\eta _1'(x) \nonumber \\&= \big ({\texttt{c}}_{\texttt{h}}\eta _3^{[1]} - \frac{3}{4} {\texttt{c}}_{\texttt{h}}- \frac{1}{{\texttt{c}}_{\texttt{h}}} \eta _2^{[2]} + \psi _2^{[2]} + c_2 \big )\sin (x)\nonumber \\ {}&\quad + \big ( 3{\texttt{c}}_{\texttt{h}}\eta _3^{[3]} + \frac{1}{4} {\texttt{c}}_{\texttt{h}}- \frac{1}{{\texttt{c}}_{\texttt{h}}} \eta _2^{[2]} -\psi _2^{[2]} \big )\sin (3x) \end{aligned}$$

(A.57a)

and

$$\begin{aligned} V_3(x)&= \psi _3'(x) - B_1(x) \eta _2'(x) - B_2(x) \eta _1'(x)\nonumber \\&= \big (\psi _3^{[1]} + {\texttt{c}}_{\texttt{h}}\eta _2^{[2]} +\frac{1}{2} B_2^{[2]} \big )\cos (x) + \big ( 3\psi _3^{[3]} - {\texttt{c}}_{\texttt{h}}\eta _2^{[2]} -\frac{1}{2} B_2^{[2]} \big ) \cos (3x) \, . \end{aligned}$$

(A.57b)

The fourth order terms are given by

$$\begin{aligned} \nonumber B_4(x)&= \psi _3'(x) \eta _1'(x) + \big (\psi _2'(x)-c_2+3{\texttt{c}}_{\texttt{h}}(\eta _1'(x))^2\big ) \eta _2'(x) + \psi _1'(x) \eta _3'(x) - \psi _1'(x) (\eta _1'(x))^3 -{\texttt{c}}_{\texttt{h}}\eta _4'(x) \, , \\ \nonumber&= \big (\frac{3}{2} \psi _3^{[3]}-\frac{1}{2} \psi _3^{[1]}+2c_2 \eta _2^{[2]}-3{\texttt{c}}_{\texttt{h}}\eta _2^{[2]} - \frac{1}{2{\texttt{c}}_{\texttt{h}}} \eta _3^{[1]} - \frac{3}{2{\texttt{c}}_{\texttt{h}}} \eta _3^{[3]} + \frac{1}{4{\texttt{c}}_{\texttt{h}}}+2{\texttt{c}}_{\texttt{h}}\eta _4^{[2]} \big ) \sin (2x)\\&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\,\,\begin{aligned}&\quad \ \big (-\frac{3}{2} \psi _3^{[3]}- 2\eta _2^{[2]}\psi _2^{[2]}+\frac{3}{2} {\texttt{c}}_{\texttt{h}}\eta _2^{[2]} -\frac{3}{2{\texttt{c}}_{\texttt{h}}} \eta _3^{[3]} - \frac{1}{8{\texttt{c}}_{\texttt{h}}} +4{\texttt{c}}_{\texttt{h}}\eta _4^{[4]} \big ) \sin (4x) \, ,\\ V_4(x)&= \psi _4'(x) -B_1(x)\eta _3'(x) - B_2(x) \eta _2'(x) -B_3(x) \eta _1'(x) \end{aligned} \\ \nonumber&=\frac{1}{2} {\texttt{c}}_{\texttt{h}}\eta _3^{[1]}+B_2^{[2]}\eta _2^{[2]}+\frac{1}{2} B_3^{[1]}+ \big (4\psi _4^{[4]}-\frac{3}{2} {\texttt{c}}_{\texttt{h}}\eta _3^{[3]} -B_2^{[2]} \eta _2^{[2]} -\frac{1}{2} B_3^{[3]} \big ) \cos (4x) \\ \nonumber&\quad +\big (2\psi _4^{[2]} -\frac{1}{2} {\texttt{c}}_{\texttt{h}}\eta _3^{[1]}+\frac{3}{2} {\texttt{c}}_{\texttt{h}}\eta _3^{[3]}-\frac{1}{2} B_3^{[1]} +\frac{1}{2} B_3^{[3]}\big )\cos (2x) \, . \end{aligned}$$

(A.57c)

From (A.57) we obtain (A.55) with the coefficients in (A.56). $\square$

We now provide the fourth order expansion of the functions $p_\epsilon (x)$ and $a_\epsilon (x)$ in (1.12).

Proposition A.2

The functions $p_\epsilon (x)$ and $a_\epsilon (x)$ in (1.12) have a Taylor expansion

$$\begin{aligned} \begin{aligned} p_\epsilon (x)&= \epsilon p_1 (x) + \epsilon ^2 p_2 (x)+ \epsilon ^3 p_3(x) + \epsilon ^4 p_4(x) + \mathcal {O}(\epsilon ^5) \,, \\ a_\epsilon (x)&= \epsilon a_1(x) +\epsilon ^2 a_2 (x) + \epsilon ^3 a_3(x) + \epsilon ^4 a_4(x) + \mathcal {O}(\epsilon ^5) \,, \end{aligned} \end{aligned}$$

(A.58)

with

$$\begin{aligned} p_1(x)&= p_1^{[1]}\cos (x)\, , \quad p_1^{[1]} := - 2 {\texttt{c}}_{\texttt{h}}^{-1}\, , \end{aligned}$$

(A.59a)

$$\begin{aligned} p_2(x)&= p_2^{[0]}+p_2^{[2]}\cos (2x)\, , \quad p_2^{[0]} := \frac{9+12 {\texttt{c}}_{\texttt{h}}^4+ 5{\texttt{c}}_{\texttt{h}}^8-2 {\texttt{c}}_{\texttt{h}}^{12}}{16 {\texttt{c}}_{\texttt{h}}^7}\, , \quad p_2^{[2]}:= - \frac{3+{\texttt{c}}_{\texttt{h}}^4}{2{\texttt{c}}_{\texttt{h}}^7}\, , \nonumber \\ p_3(x)&= p_3^{[1]}\cos (x)+p_3^{[3]}\cos (3x)\, , \quad p_3^{[3]} := -\frac{{\texttt{c}}_{\texttt{h}}^{12}+17 {\texttt{c}}_{\texttt{h}}^8+51 {\texttt{c}}_{\texttt{h}}^4+27}{32{\texttt{c}}_{\texttt{h}}^{13}} \, , \nonumber \\ p_3^{[1]}&:=\frac{-2 {\texttt{c}}_{\texttt{h}}^{14}+14 {\texttt{c}}_{\texttt{h}}^{10}+11 {\texttt{c}}_{\texttt{h}}^8-10 {\texttt{c}}_{\texttt{h}}^6-10 {\texttt{c}}_{\texttt{h}}^4+24 {\texttt{c}}_{\texttt{h}}^2+21}{8 {\texttt{c}}_{\texttt{h}}^9 ({\texttt{c}}_{\texttt{h}}^2+1)} \, , \nonumber \\ p_4(x)&= p_4^{[0]}+p_4^{[2]}\cos (2x) + p_4^{[4]}\cos (4x) \, , \end{aligned}$$

(A.59b)

$$\begin{aligned} p_4^{[0]}&:=\frac{1}{1024 {\texttt{c}}_{\texttt{h}}^{19} ({\texttt{c}}_{\texttt{h}}^2+1)} \big ( 56 {\texttt{c}}_{\texttt{h}}^{30}+88 {\texttt{c}}_{\texttt{h}}^{28}-208 {\texttt{c}}_{\texttt{h}}^{26}-336 {\texttt{c}}_{\texttt{h}}^{24}+441 {\texttt{c}}_{\texttt{h}}^{22}+369 {\texttt{c}}_{\texttt{h}}^{20}-995 {\texttt{c}}_{\texttt{h}}^{18}\nonumber \\&\quad -899 {\texttt{c}}_{\texttt{h}}^{16}-630 {\texttt{c}}_{\texttt{h}}^{14}-294 {\texttt{c}}_{\texttt{h}}^{12}+1026 {\texttt{c}}_{\texttt{h}}^{10}+1314 {\texttt{c}}_{\texttt{h}}^8-27 {\texttt{c}}_{\texttt{h}}^6+189 {\texttt{c}}_{\texttt{h}}^4+81 {\texttt{c}}_{\texttt{h}}^2+81\big ) \, ,\nonumber \\ p_4^{[2]}&:= \frac{1}{64 {\texttt{c}}_{\texttt{h}}^{19} ({\texttt{c}}_{\texttt{h}}^2+1)}\big (-12 {\texttt{c}}_{\texttt{h}}^{22}-4 {\texttt{c}}_{\texttt{h}}^{20}-19 {\texttt{c}}_{\texttt{h}}^{18}-7 {\texttt{c}}_{\texttt{h}}^{16}+350 {\texttt{c}}_{\texttt{h}}^{14}\nonumber \\&\quad +314 {\texttt{c}}_{\texttt{h}}^{12}-256 {\texttt{c}}_{\texttt{h}}^{10}-268 {\texttt{c}}_{\texttt{h}}^8+198 {\texttt{c}}_{\texttt{h}}^6+162 {\texttt{c}}_{\texttt{h}}^4+27 {\texttt{c}}_{\texttt{h}}^2+27\big ) \, , \nonumber \\ p_4^{[4]}&:=\frac{-{\texttt{c}}_{\texttt{h}}^{20}-39 {\texttt{c}}_{\texttt{h}}^{16}-366 {\texttt{c}}_{\texttt{h}}^{12}-850 {\texttt{c}}_{\texttt{h}}^8-657 {\texttt{c}}_{\texttt{h}}^4-135}{64 {\texttt{c}}_{\texttt{h}}^{19} ({\texttt{c}}_{\texttt{h}}^4+5)}\, , \end{aligned}$$

(A.59c)

and

$$\begin{aligned} \begin{aligned}&a_1(x) = a_1^{[1]} \cos (x)\,, \quad a_1^{[1]}:= - ( {\texttt{c}}_{\texttt{h}}^2 + {\texttt{c}}_{\texttt{h}}^{-2})\,, \\&a_2(x) = a_2^{[0]}+a_2^{[2]}\cos (2x)\,,\quad a_2^{[0]}:=\frac{3}{2} + \frac{1}{2{\texttt{c}}_{\texttt{h}}^4}\,, \quad a_2^{[2]}:= \frac{9{\texttt{c}}_{\texttt{h}}^8-14{\texttt{c}}_{\texttt{h}}^4-3}{4{\texttt{c}}_{\texttt{h}}^8}\,, \end{aligned}\qquad \end{aligned}$$

(A.60a)

$$\begin{aligned}&\begin{aligned}&a_3(x) = a_3^{[1]}\cos (x)+a_3^{[3]}\cos (3x)\, , \quad a_3^{[3]}:= \frac{-{\texttt{c}}_{\texttt{h}}^{16}-98 {\texttt{c}}_{\texttt{h}}^{12}+252 {\texttt{c}}_{\texttt{h}}^8-318 {\texttt{c}}_{\texttt{h}}^4-27}{64{\texttt{c}}_{\texttt{h}}^{14}}\, ,\\&a_3^{[1]} := \frac{4 {\texttt{c}}_{\texttt{h}}^{18}+6 {\texttt{c}}_{\texttt{h}}^{16}-11 {\texttt{c}}_{\texttt{h}}^{14}-12 {\texttt{c}}_{\texttt{h}}^{12}-45 {\texttt{c}}_{\texttt{h}}^{10}-48 {\texttt{c}}_{\texttt{h}}^8+93 {\texttt{c}}_{\texttt{h}}^6+90 {\texttt{c}}_{\texttt{h}}^4+27 {\texttt{c}}_{\texttt{h}}^2+24}{16 {\texttt{c}}_{\texttt{h}}^{10} ({\texttt{c}}_{\texttt{h}}^2+1)}\, , \end{aligned} \end{aligned}$$

(A.60b)

$$\begin{aligned}&a_4(x) = a_4^{[0]}+a_4^{[2]}\cos (2x) + a_4^{[4]}\cos (4x) \, , \end{aligned}$$

(A.60c)

$$\begin{aligned}&\begin{aligned}&a_4^{[0]}:=\frac{-12 {\texttt{c}}_{\texttt{h}}^{20}-31 {\texttt{c}}_{\texttt{h}}^{18}-17 {\texttt{c}}_{\texttt{h}}^{16}+40 {\texttt{c}}_{\texttt{h}}^{14}+46 {\texttt{c}}_{\texttt{h}}^{12}-150 {\texttt{c}}_{\texttt{h}}^{10}-132 {\texttt{c}}_{\texttt{h}}^8+84 {\texttt{c}}_{\texttt{h}}^6+90 {\texttt{c}}_{\texttt{h}}^4+9 {\texttt{c}}_{\texttt{h}}^2+9}{32 {\texttt{c}}_{\texttt{h}}^{16} ({\texttt{c}}_{\texttt{h}}^2+1)}\,, \\&a_4^{[2]}:=\frac{1}{128 {\texttt{c}}_{\texttt{h}}^{20} ({\texttt{c}}_{\texttt{h}}^2+1)} \big (-72 {\texttt{c}}_{\texttt{h}}^{24}-431 {\texttt{c}}_{\texttt{h}}^{22}-211 {\texttt{c}}_{\texttt{h}}^{20}+1767 {\texttt{c}}_{\texttt{h}}^{18}\\&\quad +1623 {\texttt{c}}_{\texttt{h}}^{16}-2142 {\texttt{c}}_{\texttt{h}}^{14}-2070 {\texttt{c}}_{\texttt{h}}^{12}+1022 {\texttt{c}}_{\texttt{h}}^{10}+854 {\texttt{c}}_{\texttt{h}}^8+333 {\texttt{c}}_{\texttt{h}}^6+297 {\texttt{c}}_{\texttt{h}}^4+27 {\texttt{c}}_{\texttt{h}}^2+27\big )\, , \\&a_4^{[4]}:= \frac{9 {\texttt{c}}_{\texttt{h}}^{24}+238 {\texttt{c}}_{\texttt{h}}^{20}-233 {\texttt{c}}_{\texttt{h}}^{16}-1676 {\texttt{c}}_{\texttt{h}}^{12}+743 {\texttt{c}}_{\texttt{h}}^8-3042 {\texttt{c}}_{\texttt{h}}^4-135}{128 {\texttt{c}}_{\texttt{h}}^{20} ({\texttt{c}}_{\texttt{h}}^4+5)}\, . \end{aligned} \end{aligned}$$

(A.60d)

Proof

The first two jets $p_1 (x), p_2(x)$ in (A.59a) and $a_1 (x), a_2 (x)$ in (A.60a) of the expansion (A.58) have been computed in [9, Lemma 2.2]. Let us compute the third order terms. In view of (A.37), (A.53) and (A.41), we have

$$\begin{aligned} p_3(x)&= {\texttt{c}}_{\texttt{h}}\big (-\mathfrak {p}_3'(x) +2\mathfrak {p}'_1(x)\mathfrak {p}'_2(x)- (\mathfrak {p}_1'(x))^3 \big ) + V_1(x) \big (\mathfrak {p}_2'(x) - (\mathfrak {p}_1'(x))^2 \big ) \nonumber \\&\quad - \big (c_2 - V_2(x) - V_1'(x) \mathfrak {p}_1(x) \big )\mathfrak {p}_1'(x) \nonumber \\&\quad - V_3(x) - V_2'(x) \mathfrak {p}_1(x) - V_1'(x) \mathfrak {p}_2(x) -\frac{1}{2} V_1''(x)\mathfrak {p}_1^{{2}}(x) \nonumber \\&= \big (-{\texttt{c}}_{\texttt{h}}\mathfrak {p}_3^{[1]} +\frac{7}{2{\texttt{c}}_{\texttt{h}}}\mathfrak {p}_2^{[2]}-\frac{13}{8} {\texttt{c}}_{\texttt{h}}^{-5} -\frac{c_2}{{\texttt{c}}_{\texttt{h}}^2}+\frac{1}{2{\texttt{c}}_{\texttt{h}}} +\frac{3V_2^{[2]}}{2{\texttt{c}}_{\texttt{h}}^2}-V_3^{[1]} \big )\cos (x)\nonumber \\&\quad +\big (-3{\texttt{c}}_{\texttt{h}}\mathfrak {p}_3^{[3]} + \frac{5}{2{\texttt{c}}_{\texttt{h}}}\mathfrak {p}_2^{[2]} -\frac{3}{8{\texttt{c}}_{\texttt{h}}^5} - \frac{V_2^{[2]}}{2{\texttt{c}}_{\texttt{h}}^2}-V_3^{[3]}\big )\cos (3x)\, , \end{aligned}$$

(A.61a)

$$\begin{aligned} a_3(x)&= -\mathfrak {p}_3'(x)+2\mathfrak {p}_1'(x)\mathfrak {p}_2'(x) - (\mathfrak {p}_1'(x))^3 \nonumber \\&\quad - {\texttt{c}}_{\texttt{h}}\big (B_3'(x) + B_2''(x) \mathfrak {p}_1(x) + B_1''(x) \mathfrak {p}_2(x) +\frac{1}{2} B_1'''(x) \mathfrak {p}_1^2(x) \big ) \nonumber \\&\quad -p_1(x) \big (B_2'(x) + B_1''(x) \mathfrak {p}_1(x) \big ) - p_2(x) B_1'(x)\, , \nonumber \\&= \big (-\mathfrak {p}_3^{[1]}+2{\texttt{c}}_{\texttt{h}}^{-2} \mathfrak {p}_2^{[2]} -\frac{3}{4} {\texttt{c}}_{\texttt{h}}^{-6} - {\texttt{c}}_{\texttt{h}}B_3^{[1]}+2{\texttt{c}}_{\texttt{h}}^{-1} B_2^{[2]} +\frac{1}{2} {\texttt{c}}_{\texttt{h}}^2 \mathfrak {p}_2^{[2]} \nonumber \\&\quad +\frac{1}{8} {\texttt{c}}_{\texttt{h}}^{-2}-p_1^{[1]} B_2^{[2]} +\frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-1} p_1^{[1]} -{\texttt{c}}_{\texttt{h}}p_2^{[0]} -\frac{1}{2} {\texttt{c}}_{\texttt{h}}p_2^{[2]} \big )\cos (x) \nonumber \\&\quad +\big (-3\mathfrak {p}_3^{[3]}+2{\texttt{c}}_{\texttt{h}}^{-2} \mathfrak {p}_2^{[2]} -\frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-6} -3{\texttt{c}}_{\texttt{h}}B_3^{[3]} -2{\texttt{c}}_{\texttt{h}}^{-1}B_2^{[2]}\nonumber \\&\quad -\frac{1}{2} {\texttt{c}}_{\texttt{h}}^2 \mathfrak {p}_2^{[2]} -\frac{1}{8} {\texttt{c}}_{\texttt{h}}^{-2} -p_1^{[1]} B_2^{[2]} -\frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-1} p_1^{[1]} -\frac{1}{2} {\texttt{c}}_{\texttt{h}}p_2^{[2]} \big ) \cos (3x)\, , \end{aligned}$$

(A.61b)

and

$$\begin{aligned} p_4(x)&= c_4 - V_4(x) - V_3'(x)\mathfrak {p}_1(x) - V_2'(x) \mathfrak {p}_2(x) -V_1'(x)\mathfrak {p}_3(x) \nonumber \\&\quad -\frac{1}{2} V_2''(x)\mathfrak {p}^2_1(x) - V_1''(x) \mathfrak {p}_2(x)\mathfrak {p}_1(x) - \frac{1}{6} V_1'''(x) \mathfrak {p}_1^3(x) \nonumber \\&\quad +\mathfrak {p}_1'(x) \big ( V_3(x) + V_2'(x) \mathfrak {p}_1(x) + V_1'(x) \mathfrak {p}_2(x) + \frac{1}{2} V_1''(x) \mathfrak {p}_1^2(x) \big ) \nonumber \\&\quad + \big ( (\mathfrak {p}_1'(x))^2 -\mathfrak {p}_2'(x) \big ) \big ( c_2 -V_2(x) - V_1'(x) \mathfrak {p}_1(x)\big ) \nonumber \\&\quad + V_1(x) \big ( \mathfrak {p}_3'(x) - 2 \mathfrak {p}_2'(x)\mathfrak {p}_1'(x) + (\mathfrak {p}_1'(x))^3\big ) \nonumber \\&\quad +{\texttt{c}}_{\texttt{h}}\big ( -\mathfrak {p}_4'(x)+ 2\mathfrak {p}_3'(x)\mathfrak {p}_1'(x) + (\mathfrak {p}_2'(x))^2 -3\mathfrak {p}_2'(x) (\mathfrak {p}_1'(x))^2 + (\mathfrak {p}_1'(x))^4 \big ) \, , \nonumber \\&=\frac{3}{4}{\texttt{c}}_{\texttt{h}}^{-7}+\frac{1}{2} c_2 {\texttt{c}}_{\texttt{h}}^{-4}-\frac{5}{4}{\texttt{c}}_{\texttt{h}}^{-4} V_2^{[2]}-2{\texttt{c}}_{\texttt{h}}^{-3}\mathfrak {p}_2^{[2]}-\frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-3}+{\texttt{c}}_{\texttt{h}}^{-2}V_3^{[1]}+2 {\texttt{c}}_{\texttt{h}}(\mathfrak {p}_2^{[2]})^2 \nonumber \\&\quad +2{\texttt{c}}_{\texttt{h}}^{-1}\mathfrak {p}_3^{[1]}+2 \mathfrak {p}_2^{[2]} V_2^{[2]}+c_4-V_4^{[0]} +\big (\frac{13}{12}{\texttt{c}}_{\texttt{h}}^{-7}+\frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-4}c_2+\frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-4}V_2^{[2]}-6{\texttt{c}}_{\texttt{h}}^{-3}\mathfrak {p}_2^{[2]} \nonumber \\&\quad -\frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-3}+2{\texttt{c}}_{\texttt{h}}^{-2}V_3^{[3]}+{\texttt{c}}_{\texttt{h}}\mathfrak {p}_2^{[2]}+{\texttt{c}}_{\texttt{h}}^{-1}\mathfrak {p}_3^{[1]}+5{\texttt{c}}_{\texttt{h}}^{-1}\mathfrak {p}_3^{[3]}-2{\texttt{c}}_{\texttt{h}}\mathfrak {p}_4^{[2]}-2 \mathfrak {p}_2^{[2]} c_2-V_4^{[2]} \big ) \cos (2x) \nonumber \\&\quad +\big (\frac{1}{6} {\texttt{c}}_{\texttt{h}}^{-7}-\frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-4}V_2^{[2]}-2{\texttt{c}}_{\texttt{h}}^{-3}\mathfrak {p}_2^{[2]}-{\texttt{c}}_{\texttt{h}}^{-2}V_3^{[3]}+2 {\texttt{c}}_{\texttt{h}}(\mathfrak {p}_2^{[2]})^2+4 {\texttt{c}}_{\texttt{h}}^{-1}\mathfrak {p}_3^{[3]}-4 {\texttt{c}}_{\texttt{h}}\mathfrak {p}_4^{[4]}-V_4^{[4]} \big ) \cos (4x) \end{aligned}$$

(A.62a)

$$\begin{aligned} a_4(x)&=-\mathfrak {p}_4'(x) + (\mathfrak {p}_2'(x))^2+2\mathfrak {p}_1'(x)\mathfrak {p}_3'(x) - 3(\mathfrak {p}_1'(x))^2\mathfrak {p}_2'(x) + (\mathfrak {p}_1'(x))^4 \nonumber \\&\quad -{\texttt{c}}_{\texttt{h}}\big (B_4'(x) + B_3''(x) \mathfrak {p}_1(x) + B_2''(x) \mathfrak {p}_2(x) + B_1''(x) \mathfrak {p}_3(x) \nonumber \\ {}&\quad + \frac{1}{2} B_2'''(x) \mathfrak {p}_1^2(x) + B_1'''(x) \mathfrak {p}_1(x) \mathfrak {p}_2(x) + \frac{1}{6} B_1^{\scriptscriptstyle { IV }}(x) \mathfrak {p}_1^3(x) \big ) \nonumber \\ {}&\quad -p_1(x) \big (B_3'(x) + B_2''(x) \mathfrak {p}_1(x) + B_1''(x) \mathfrak {p}_2(x) +\frac{1}{2} B_1'''(x) \mathfrak {p}_1^2(x) \big ) \nonumber \\&\quad -p_2(x) \big (B_2'(x) + B_1''(x) \mathfrak {p}_1(x) \big ) - p_3(x) B_1'(x)\nonumber \\&=\frac{3}{8} {\texttt{c}}_{\texttt{h}}^{-8}-\frac{1}{16}{\texttt{c}}_{\texttt{h}}^{-4}-\frac{3}{2} {\texttt{c}}_{\texttt{h}}^{-4}\mathfrak {p}_2^{[2]}+ \frac{1}{16}{\texttt{c}}_{\texttt{h}}^{-3}p_1^{[1]}-{\texttt{c}}_{\texttt{h}}^{-3}B_2^{[2]}+{\texttt{c}}_{\texttt{h}}^{-2}B_2^{[2]}p_1^{[1]}+ {\texttt{c}}_{\texttt{h}}^{-2}\mathfrak {p}_3^{[1]}\nonumber \\&\quad +\frac{1}{2} {\texttt{c}}_{\texttt{h}}^2 \mathfrak {p}_3^{[1]}+2{\texttt{c}}_{\texttt{h}}\mathfrak {p}_2^{[2]}B_2^{[2]}+\frac{1}{4} {\texttt{c}}_{\texttt{h}}\mathfrak {p}_2^{[2]}p_1^{[1]}-\frac{1}{2} {\texttt{c}}_{\texttt{h}}p_3^{[1]}+\frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-1} B_3^{[1]}+\frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-1}p_2^{[0]}-\frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-1}p_2^{[2]}\nonumber \\&\quad + 2 (\mathfrak {p}_2^{[2]})^2+\frac{1}{4} \mathfrak {p}_2^{[2]}- B_2^{[2]} p_2^{[2]}-\frac{1}{2} B_3^{[1]} p_1^{[1]} + \big (\frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-8}-3{\texttt{c}}_{\texttt{h}}^{-4}\mathfrak {p}_2^{[2]}+\frac{1}{12}{\texttt{c}}_{\texttt{h}}^{-4}+2{\texttt{c}}_{\texttt{h}}^{-3}B_2^{[2]}\nonumber \\&\quad -\frac{1}{2} {\texttt{c}}_{\texttt{h}}^2 \mathfrak {p}_3^{[1]}+ {\texttt{c}}_{\texttt{h}}^{-2}\mathfrak {p}_3^{[1]}+\frac{1}{2} {\texttt{c}}_{\texttt{h}}^2 \mathfrak {p}_3^{[3]}+3{\texttt{c}}_{\texttt{h}}^{-2}\mathfrak {p}_3^{[3]}-\frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-1}B_3^{[1]}+\frac{9}{2} {\texttt{c}}_{\texttt{h}}^{-1}B_3^{[3]}-2{\texttt{c}}_{\texttt{h}}B_4^{[2]}-\frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-1}p_2^{[0]}\nonumber \\&\quad +\frac{1}{2} {\texttt{c}}_{\texttt{h}}^{-1} p_2^{[2]}-\frac{1}{2}{\texttt{c}}_{\texttt{h}}p_3^{[1]}-\frac{1}{2} {\texttt{c}}_{\texttt{h}}p_3^{[3]}-2B_2^{[2]}p_2^{[0]}-\frac{1}{2} B_3^{[1]}p_1^{[1]}-\frac{3}{2} B_3^{[3]}p_1^{[1]}-2\mathfrak {p}_4^{[2]} \big )\cos (2x)\nonumber \\&\quad + \big (\frac{1}{8} {\texttt{c}}_{\texttt{h}}^{-8}-\frac{3}{2} {\texttt{c}}_{\texttt{h}}^{-4}\mathfrak {p}_2^{[2]}-\frac{1}{48} {\texttt{c}}_{\texttt{h}}^{-4}-{\texttt{c}}_{\texttt{h}}^{-3}B_2^{[2]}-\frac{1}{16} {\texttt{c}}_{\texttt{h}}^{-3} p_1^{[1]}-{\texttt{c}}_{\texttt{h}}^{-2}B_2^{[2]}p_1^{[1]}-\frac{1}{2} {\texttt{c}}_{\texttt{h}}^2 \mathfrak {p}_3^{[3]}\nonumber \\&\quad +3{\texttt{c}}_{\texttt{h}}^{-2}\mathfrak {p}_3^{[3]}-2{\texttt{c}}_{\texttt{h}}\mathfrak {p}_2^{[2]} B_2^{[2]}-\frac{1}{4} {\texttt{c}}_{\texttt{h}}\mathfrak {p}_2^{[2]}p_1^{[1]}-\frac{9}{2} {\texttt{c}}_{\texttt{h}}^{-1}B_3^{[3]}-4{\texttt{c}}_{\texttt{h}}B_4^{[4]}-\frac{1}{4} {\texttt{c}}_{\texttt{h}}^{-1} p_2^{[2]} \nonumber \\&\quad -\frac{1}{2} {\texttt{c}}_{\texttt{h}}p_3^{[3]}+2 (\mathfrak {p}_2^{[2]})^2 -\frac{1}{4} \mathfrak {p}_2^{[2]}-B_2^{[2]}p_2^{[2]}-\frac{3}{2} B_3^{[3]}p_1^{[1]}-4 \mathfrak {p}_4^{[4]}\big )\cos (4x) \, . \end{aligned}$$

(A.62b)

The expansions of $p_3(x)$, $a_3(x)$, $p_4(x)$ and $a_4(x)$ in (A.59a)–(A.60a) descend from (A.61a), (A.61b), (A.62a) and (A.62b) respectively, in view of (A.46), (A.44) (A.42), (A.54), (A.2b), (A.57b), (A.57a) and (A.57c)–(A.56b). $\square$

Remark A.8

The functions V and B in (A.40) coincide respectively with the horizontal and vertical derivative of the velocity potential $\Phi$ in [21, formula (12)] after the rescaling procedure outlined in Remark A.3.

Expansion of the Projector $P_{\mu ,\epsilon }$

In this Appendix we prove Lemmata 3.4 and 3.5.

We denote, for any $k \in \mathbb {N}$,

$$\begin{aligned} \begin{aligned}&f_k^+:=\begin{bmatrix}{\texttt{c}}_{\texttt{h}}^{1/2}\cos (kx) \\ {\texttt{c}}_{\texttt{h}}^{-1/2}\sin (kx) \end{bmatrix} \,, \quad f_k^-:=\begin{bmatrix}-{\texttt{c}}_{\texttt{h}}^{1/2}\sin (kx) \\ {\texttt{c}}_{\texttt{h}}^{-1/2}\cos (kx) \end{bmatrix} \,, \\&f_{-k}^+:=\begin{bmatrix}{\texttt{c}}_{\texttt{h}}^{1/2}\cos (kx) \\ -{\texttt{c}}_{\texttt{h}}^{-1/2}\sin (kx) \end{bmatrix}\,, \quad f_{-k}^-:=\begin{bmatrix}{\texttt{c}}_{\texttt{h}}^{1/2}\sin (kx) \\ {\texttt{c}}_{\texttt{h}}^{-1/2}\cos (kx) \end{bmatrix} \,, \end{aligned} \end{aligned}$$

(B.1)

and we define for any $k\in \mathbb {Z}$ the spaces

$$\begin{aligned} \mathcal {W}_k:= \text {span}\left\{ f_k^+, \ f_k^-, f_{-k}^+, \ f_{-k}^- \right\} \,,\quad \mathcal {W}_k^\sigma := \text {span}_\mathbb {R}\{f_k^\sigma ,\ f_{-k}^\sigma \}\,,\quad \sigma =\pm \, . \end{aligned}$$

(B.2)

We have the following

Lemma B.2

The jets of the operator ${{\mathcal {B}}}_{\mu ,\epsilon }$ in (3.2) act on the spaces in (B.2) as follows²

$$\begin{aligned} {{\mathcal {B}}}_{\ell ,j} \mathcal {W}_k^\sigma = \underbrace{\textrm{i}\,^\ell \mathcal {W}_{k-j}^{(-1)^{\ell } \sigma }+_\mathbb {R}\textrm{i}\,^\ell \mathcal {W}_{k-j+2}^{(-1)^{\ell } \sigma } +_\mathbb {R}\dots +_\mathbb {R}\textrm{i}\,^\ell \mathcal {W}_{k+j}^{(-1)^{\ell } \sigma } }_{j+1 \ terms}\,,\quad f_0^- \notin {{\mathcal {B}}}_{0,j} \mathcal {W}_k^-\,,\qquad \end{aligned}$$

(B.3)

with $\ell ,j=0,\dots ,4$, while the operator $\mathcal {J}$ in (1.5) acts as .

Proof

The first formula in (B.3) follows by (3.2)–(3.9). Let us prove the second statement by contradiction supposing that there exists $g\in \mathcal {W}_k^-$ such that ${{\mathcal {B}}}_{0,j} g = f_0^-$. Then $1 =\big (f_0^-, f_0^- \big ) = \big ({{\mathcal {B}}}_{0,j} g, f_0^- \big ) = \big ( g, {{\mathcal {B}}}_{0,j} f_0^- \big ) = 0$, by (3.2), which is a contradiction. $\square$

We now include an extended version of [9, Lemma A.2].

Lemma B.2

The space $H^1(\mathbb {T})$ decomposes as $H^1(\mathbb {T}) = \mathcal {V}_{0,0} \oplus \mathcal {U}\oplus {\mathcal {W}_{H^1}}$, with where the subspaces $\mathcal {V}_{0,0}, \mathcal {U}$ and $\mathcal {W}_k$, defined below, are invariant under $\mathscr {L}_{0,0}$ and the following properties hold:

• (i) $\mathcal {V}_{0,0} = \text {span} \{ f^+_1, f^-_1, f^+_0, f^-_0\}$ is the generalized kernel of $\mathscr {L}_{0,0}$. For any $\lambda \ne 0$ the operator $\mathscr {L}_{0,0}-\lambda : \mathcal {V}_{0,0} \rightarrow \mathcal {V}_{0,0}$ is invertible and

  $$\begin{aligned}&(\mathscr {L}_{0,0}-\lambda )^{-1}f_1^+ = -\frac{1}{\lambda }f_1^+ \, , \ (\mathscr {L}_{0,0}-\lambda )^{-1}f_1^- = -\frac{1}{\lambda }f_1^-, \ (\mathscr {L}_{0,0}-\lambda )^{-1}f_0^- = -\frac{1}{\lambda }f_0^- \, , \end{aligned}$$

  (B.4a)
  $$\begin{aligned}&(\mathscr {L}_{0,0}-\lambda )^{-1}f_0^+ = -\frac{1}{\lambda }f_0^+ + \frac{1}{\lambda ^2} f_0^- \, . \end{aligned}$$

  (B.4b)

• (ii) $\mathcal {U}:= \text {span}\left\{ f_{-1}^+, f_{-1}^- \right\}$. For any $\lambda \ne \pm 2 \textrm{i}\,$ the operator $\mathscr {L}_{0,0}-\lambda : \mathcal {U}\rightarrow \mathcal {U}$ is invertible and

  $$\begin{aligned} \begin{aligned}&(\mathscr {L}_{0,0}-\lambda )^{-1} f_{-1}^+ = \frac{1}{\lambda ^2+4 {\texttt{c}}_{\texttt{h}}^2}\left( -\lambda f_{-1}^+ + 2 {\texttt{c}}_{\texttt{h}}f_{-1}^-\right) , \\&(\mathscr {L}_{0,0}-\lambda )^{-1} f_{-1}^- = \frac{1}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} \left( -2 {\texttt{c}}_{\texttt{h}}f_{-1}^+ - \lambda f_{-1}^-\right) \, . \end{aligned} \end{aligned}$$

  (B.4c)

• (iii) Each subspace $\mathcal {W}_k$ in (B.2) is invariant under $\mathscr {L}_{0,0}$. For any $|\lambda | < \delta (\texttt{h})$ small enough and any natural $k\ge 2$, the operator ${\mathscr {L}_{0,0}-\lambda : \mathcal {W}_k\rightarrow \mathcal {W}_k }$ is invertible and for any $f \in \mathcal {W}_k$ and any natural number N

  

  (B.4d)

  for some analytic function $\lambda \mapsto \varphi _{f,N}(\lambda , \cdot ) \in \mathcal {W}_k$, where 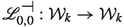is

  

  (B.5)

Remark B.3

We will use in the sequel the following decomposition formula, for any,

(B.6)

Notation. We denote by $\mathcal {O}(\lambda )$ an analytic function having a zero of order 1 at $\lambda =0$ and $\mathcal {O}_Z (\lambda ^m)$ an analytic function with valued in a subspace Z having a zero of order m at $\lambda =0$. We denote with $\mathcal {O}(\lambda ^{-1}:\lambda )$ any function having a Laurent series at $\lambda =0$ of the form $\sum _{\begin{array}{c} j\in \mathbb {Z}\setminus \{0\} \end{array}} a_j \lambda ^j$. We denote by $f_{{{\mathcal {W}}}_k}$ a function in ${{\mathcal {W}}}_k$.

If $h(\lambda ) = h_0 + \mathcal {O}(\lambda ^{-1}:\lambda )$, $h_0\in \mathbb {C}$, then, by the residue theorem,

$$\begin{aligned} \frac{1}{2\pi \textrm{i}\,} \oint _\Gamma \frac{h(\lambda )}{\lambda } \textrm{d}\lambda = h_0\, . \end{aligned}$$

(B.7)

We prepend to the proof of Lemma 3.4 a list of results given by straight-forward computations.

Lemma B.3

(Action of $(\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1}$ on $\mathcal {V}_{0,0}$, $\mathcal {U}$ and $\mathcal {W}_2$). One has

$$\begin{aligned} \begin{aligned}&(\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_1^+= \frac{\zeta _1^+}{\lambda } f_0^- + \textrm{A}_2^+ +\lambda \mathrm B_2^- + \lambda ^2 f_{\mathcal {W}_2^+} + \lambda ^3 f_{\mathcal {W}_2^-} + \mathcal {O}_{\mathcal {W}_2}(\lambda ^4)\,, \\&(\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_1^-= \textrm{A}_2^- + \lambda \textrm{B}_2^+ + \lambda ^2f_{\mathcal {W}_2^-} + \lambda ^3 f_{\mathcal {W}_2^+} + \mathcal {O}_{\mathcal {W}_2}(\lambda ^4) \,, \\&(\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_0^+= \frac{ \zeta _0^+}{\lambda } f_1^- + \frac{\alpha _0^+}{ \lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ + \lambda \frac{\beta _0^+ }{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^- \,, \\&(\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_0^-= 0 \,, \\&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{0,1} f^+_{-1} = \frac{\zeta _{-1}^+ }{ \lambda } f_0^- +\textrm{A}_{-2}^+ + \lambda f_{\mathcal {W}_2^-}+\mathcal {O}_{\mathcal {W}_2} (\lambda ^2) \,, \\&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{0,1} f^-_{-1} = f_{\mathcal {W}_2^-} + \mathcal {O}_{\mathcal {W}_2}(\lambda ) \,, \end{aligned} \end{aligned}$$

(B.8)

where $\zeta ^+_1, \zeta ^+_0$, $\alpha _0^+, \beta _0^+, \zeta _{-1}^+$ are real numbers, and

(B.9)

Moreover

$$\begin{aligned} \nonumber&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{0,1} \mathrm A_2^+ = \frac{\zeta _2^+}{\lambda } f_1^- + \frac{\alpha _2^+}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ + \mathrm A_3^+ +\frac{\lambda \beta _2^+}{\lambda ^2 + 4 {\texttt{c}}_{\texttt{h}}^2} f_{-1}^- +\lambda f_{\mathcal {W}_3^-} + \mathcal {O}_{ \mathcal {W}_3}(\lambda ^2) \, ,\\ \nonumber&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{0,1} \mathrm B_2^- = \frac{\zeta _3^+}{\lambda } f_1^+ + \frac{\alpha _3^+}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^- + f_{\mathcal {W}_3^-} + \frac{\lambda \beta _3^+}{\lambda ^2 + 4 {\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ + \mathcal {O}_{ \mathcal {W}_3}(\lambda ) \, ,\\ \nonumber&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{0,1} \mathrm A_2^- = \frac{\zeta _2^-}{\lambda } f_1^+ + \frac{\alpha _2^-}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^- + f_{\mathcal {W}_3^-} + \frac{\lambda \beta _2^- }{\lambda ^2 + 4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ + \lambda f_{\mathcal {W}_3^+} + \mathcal {O}_{\mathcal {W}_3}(\lambda ^2) \, ,\\&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{0,1} \mathrm B_2^+ = \frac{\zeta _3^-}{\lambda } f_1^- + \frac{\alpha _3^-}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ + f_{\mathcal {W}_3^+} + \frac{\lambda \beta _3^-}{\lambda ^2 + 4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^- + \mathcal {O}_{\mathcal {W}_3} (\lambda )\, , \end{aligned}$$

(B.10)

where $\zeta _2^-$, $\beta _2^\pm$, $\alpha _3^\pm$ and $\beta _3^{\pm }$ are real numbers and

$$\begin{aligned}&\zeta _2^+ := -\frac{(a_1^{[1]})^2 {\texttt{c}}_{\texttt{h}}^2-2 a_1^{[1]} ({\texttt{c}}_{\texttt{h}}^4+2) {\texttt{c}}_{\texttt{h}}p_1^{[1]}+(3 {\texttt{c}}_{\texttt{h}}^4+4) (p_1^{[1]})^2}{8 {\texttt{c}}_{\texttt{h}}^5} \, , \\ \nonumber&\alpha _2^+ := -\alpha _2^- := -\frac{(a_1^{[1]})^2 {\texttt{c}}_{\texttt{h}}-2 a_1^{[1]} ({\texttt{c}}_{\texttt{h}}^4+1) p_1^{[1]}+{\texttt{c}}_{\texttt{h}}^3 (p_1^{[1]})^2}{4 {\texttt{c}}_{\texttt{h}}^3 } \, , \\ \nonumber&\zeta _3^+ : = \zeta _3^- := \frac{({\texttt{c}}_{\texttt{h}}^4+1) (a_1^{[1]} {\texttt{c}}_{\texttt{h}}-2 p_1^{[1]}) \big ( ({\texttt{c}}_{\texttt{h}}^4+2) p_1^{[1]}-a_1^{[1]} {\texttt{c}}_{\texttt{h}}\big )}{8 {\texttt{c}}_{\texttt{h}}^{10}}\, , \\ \nonumber&\mathrm A_3^+(x) := \begin{bmatrix}\dfrac{ (a_1^{[1]})^2 ({\texttt{c}}_{\texttt{h}}^4+3) {\texttt{c}}_{\texttt{h}}^2-2{\texttt{c}}_{\texttt{h}}p_1^{[1]} a_1^{[1]} ({\texttt{c}}_{\texttt{h}}^8+9 {\texttt{c}}_{\texttt{h}}^4+6) + (11 {\texttt{c}}_{\texttt{h}}^8+29 {\texttt{c}}_{\texttt{h}}^4+12 ) (p_1^{[1]})^2 }{32 {\texttt{c}}_{\texttt{h}}^{19/2}} \cos (3 x) \\[4mm] \dfrac{(3 {\texttt{c}}_{\texttt{h}}^4+1) \big ((a_1^{[1]})^2 {\texttt{c}}_{\texttt{h}}^2-2 {\texttt{c}}_{\texttt{h}}p_1^{[1]} a_1^{[1]} ({\texttt{c}}_{\texttt{h}}^4+2) + (3 {\texttt{c}}_{\texttt{h}}^4+4) (p_1^{[1]})^2\big )}{32 {\texttt{c}}_{\texttt{h}}^{21/2}} \sin (3 x) \end{bmatrix} \, . \end{aligned}$$

(B.11)

Proof

Use the operator ${{\mathcal {B}}}_{0,1}$ in (3.8b), Lemma B.2 and that

$$\begin{aligned} \frac{1}{2\tanh (2\texttt{h}) - 4{\texttt{c}}_{\texttt{h}}^2} = - \frac{1+{\texttt{c}}_{\texttt{h}}^4}{4{\texttt{c}}_{\texttt{h}}^6}\,,\quad \frac{1}{3\tanh (3\texttt{h}) - 9{\texttt{c}}_{\texttt{h}}^2} = -\frac{1+3{\texttt{c}}_{\texttt{h}}^4}{24{\texttt{c}}_{\texttt{h}}^6}\,, \end{aligned}$$

which comes from the identities in (A.11). $\square$

Lemma B.5

(Action of $(\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,0}$ on $\mathcal {V}_{0,0}$ and $\mathcal {U}$). One has

$$\begin{aligned} \begin{aligned}&(\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,0}f_1^+ = - \textrm{i}\,\frac{\mu _\texttt{h}}{ \lambda } f_1^+ + \textrm{i}\,\frac{ 2{\texttt{c}}_{\texttt{h}}\mu _\texttt{h}}{\lambda ^2 + 4 {\texttt{c}}_{\texttt{h}}^2} f_{-1}^- - \textrm{i}\,\frac{\lambda \mu _\texttt{h}}{\lambda ^2 + 4 {\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ \,, \\&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{1,0}f_1^-= - \textrm{i}\,\frac{ \mu _\texttt{h}}{\lambda } f_1^- + \textrm{i}\,\frac{ 2 {\texttt{c}}_{\texttt{h}}\mu _\texttt{h}}{\lambda ^2 + 4 {\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ +\textrm{i}\,\lambda \frac{ \mu _\texttt{h}}{\lambda ^2 + 4 {\texttt{c}}_{\texttt{h}}^2} f_{-1}^- \,, \\&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{1,0}f_{0}^\pm =0\,, \\&(\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,0}f_{-1}^+ = \textrm{i}\,\frac{\mu _\texttt{h}}{ \lambda } f_1^+ - \textrm{i}\,\frac{2{\texttt{c}}_{\texttt{h}}\mu _\texttt{h}}{\lambda ^2 + 4 {\texttt{c}}_{\texttt{h}}^2} f_{-1}^- + \textrm{i}\,\frac{ \lambda \mu _\texttt{h}}{\lambda ^2 + 4 {\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ \,, \\&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{1,0}f_{-1}^-= -\textrm{i}\,\frac{ \mu _\texttt{h}}{\lambda } f_1^- + \textrm{i}\,\frac{ 2 {\texttt{c}}_{\texttt{h}}\mu _\texttt{h}}{\lambda ^2 + 4 {\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ + \textrm{i}\,\lambda \frac{ \mu _\texttt{h}}{\lambda ^2 + 4 {\texttt{c}}_{\texttt{h}}^2} f_{-1}^- \,, \end{aligned} \end{aligned}$$

(B.12)

with

$$\begin{aligned} \mu _\texttt{h}:=\dfrac{({\texttt{c}}_{\texttt{h}}^4-1) \texttt{h}-{\texttt{c}}_{\texttt{h}}^2}{2 {\texttt{c}}_{\texttt{h}}} \, . \end{aligned}$$

(B.13)

Proof

We apply the operator ${{\mathcal {B}}}_{1,0} = \ell _{1,0}(|D|) \Pi _{\texttt{s}}$ in (3.8b) to the vectors in $\mathcal {V}_{0,0}$ and use (B.6) and (B.4a)–(B.4c). $\square$

Lemma B.6

(Action of $(\mathscr {L}_{0,0} -\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2}$ on $\mathcal {V}_{0,0}$). One has

$$\begin{aligned} \nonumber&(\mathscr {L}_{0,0} -\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2} f_1^+ = \frac{\tau _1^+}{\lambda } f_1^- + \frac{\ell _{1}^+}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ + \mathrm L_3^+ + \frac{\lambda m_1^+}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^- + O_{\mathcal {W}_3}(\lambda ) \, , \\&(\mathscr {L}_{0,0} -\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2} f_1^- = \frac{\tau _1^-}{\lambda } f_1^+ + \frac{\ell _{1}^-}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^- + f_{\mathcal {W}_3^-} + \mathcal {O}_{\mathcal {U}\oplus \mathcal {W}_3}(\lambda ) \, , \\ \nonumber&(\mathscr {L}_{0,0} -\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2} f_{0}^+ = \frac{\tau _0^+}{\lambda } f_0^- + f_{\mathcal {W}_2^+}+ \mathcal {O}_{\mathcal {W}_2}(\lambda )\, , \quad (\mathscr {L}_{0,0} -\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2} f_{0}^- = 0 \, , \end{aligned}$$

(B.14)

where $m_1^+$, $\tau _1^-$, $\tau _0^+$, are real numbers, and

$$\begin{aligned}&\tau _1^+ :=\frac{1}{4 {\texttt{c}}_{\texttt{h}}} \big (2 a_2^{[0]} {\texttt{c}}_{\texttt{h}}^2+a_2^{[2]} {\texttt{c}}_{\texttt{h}}^2+2 \texttt{f}_2(1-{\texttt{c}}_{\texttt{h}}^4)-4 {\texttt{c}}_{\texttt{h}}p_2^{[0]}-2 {\texttt{c}}_{\texttt{h}}p_2^{[2]} \big ) \, , \nonumber \\&\ell _{1}^+ :=\frac{1}{2} \big ({\texttt{c}}_{\texttt{h}}^2 (2 a_2^{[0]}+a_2^{[2]})-2 \texttt{f}_2 (1-{\texttt{c}}_{\texttt{h}}^4) \big )\, , \quad \ell _{1}^- := \frac{1}{2} \big ( {\texttt{c}}_{\texttt{h}}^2 (-2a_2^{[0]}+a_2^{[2]})+2 \texttt{f}_2 (1-{\texttt{c}}_{\texttt{h}}^4) \big ) \, , \nonumber \\&\mathrm L_3^+(x) := \begin{bmatrix}-\dfrac{ \big (a_2^{[2]}{\texttt{c}}_{\texttt{h}}({\texttt{c}}_{\texttt{h}}^4+3)-2 (5 {\texttt{c}}_{\texttt{h}}^4+3) p_2^{[2]})}{16 {\texttt{c}}_{\texttt{h}}^{9/2}} \cos (3 x) \\[4mm] -\dfrac{(3 {\texttt{c}}_{\texttt{h}}^4+1) (a_2^{[2]} {\texttt{c}}_{\texttt{h}}-2 p_2^{[2]})}{16 {\texttt{c}}_{\texttt{h}}^{11/2}}\sin (3 x) \end{bmatrix} \, . \end{aligned}$$

(B.15)

Proof

We apply the operators ${{\mathcal {B}}}_{0,2}$ in (3.8c) and $\mathcal {J}$ in (1.5) to the vectors in $\mathcal {V}_{0,0}$. Then we use (B.6) and Lemma B.2 to obtain (B.14)–(B.15). $\square$

Lemma B.7

(Action of $(\mathscr {L}_{0,0}- \lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{1,1}$ on $\mathcal {V}_{0,0}$ and $\mathcal {U}$). One has

$$\begin{aligned} \begin{aligned}&(\mathscr {L}_{0,0}- \lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{1,1} f_1^+ = - \frac{\textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}}{\lambda ^2} f_0^- +\frac{\textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}}{\lambda } f_0^+ + \textrm{i}\,f_{\mathcal {W}_2^-} + \mathcal {O}_\mathcal {W}(\lambda ) \,,\\&(\mathscr {L}_{0,0}- \lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{1,1} f_1^- = \frac{\textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{3}{2}}}{\lambda } f_0^- +\textrm{i}\,\mathrm Q_{2}^++ \lambda \textrm{i}\,f_{\mathcal {W}_2^-} + \mathcal {O}_{\mathcal {W}_2}(\lambda ^2) \,,\\&(\mathscr {L}_{0,0}- \lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{1,1} f_0^+ = \frac{ \textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{3}{2}} }{\lambda } f_1^+ -\frac{2\textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^- + \lambda \frac{\textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{3}{2}}}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ \,, \\&(\mathscr {L}_{0,0}- \lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{1,1} f_0^- = \frac{ \textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}}{\lambda } f_1^- + \frac{2\textrm{i}\,{\texttt{c}}_{\texttt{h}}^{\frac{1}{2}}}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2}f_{-1}^+ + \lambda \frac{\textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}}}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^- \,, \end{aligned} \end{aligned}$$

(B.16)

where

$$\begin{aligned}&\mathrm Q_{2}^+(x) := \begin{bmatrix}\dfrac{ ({\texttt{c}}_{\texttt{h}}^4+3) p_1^{[1]} }{4 {\texttt{c}}_{\texttt{h}}^{9/2}} \cos (2x) \\[4mm] \dfrac{3({\texttt{c}}_{\texttt{h}}^4+1) p_1^{[1]} }{8 {\texttt{c}}_{\texttt{h}}^{11/2}} \sin (2x) \end{bmatrix} \, . \end{aligned}$$

(B.17)

Proof

We have ${{\mathcal {B}}}_{1,1} = - \textrm{i}\,p_1(x) \mathcal {J}$ by (3.8c), with $p_1(x) = p_1^{[1]} \cos (x)$ in (A.59a) and $p_1^{[1]} = -2{\texttt{c}}_{\texttt{h}}^{-1}$. Use also Lemma B.2. $\square$

Lemma B.8

(Action of $(\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{2,0}$ on $f_0^-$). One has

$$\begin{aligned} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{2,0} f_0^- = \frac{\texttt{h}}{\lambda ^2} f_0^- -\frac{\texttt{h}}{\lambda } f_0^+ \, . \end{aligned}$$

(B.18)

Proof

We apply ${{\mathcal {B}}}_{2,0} = \ell _{2,0}(|D|) \Pi _{\texttt{ev}}$ in (3.8c) and (B.4b). $\square$

Lemma B.9

(Action of $((\mathscr {L}_{0,0} - \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1})^2$ on $\mathcal {V}_{0,0}$) One has

$$\begin{aligned}&\begin{aligned}&[(\mathscr {L}_{0,0} - \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} ]^2 f_1^+ = \frac{\zeta _2^+ }{\lambda } f_1^- + \frac{\alpha _2^+}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ +\zeta _3^+ f_1^+ + \mathrm A_2^+ \\&\qquad \qquad \qquad \qquad \qquad \qquad +\lambda \big ( f_{\mathcal {W}_1^-} +f_{\mathcal {W}_3^-} \big ) + \lambda ^2 f_{\mathcal {W}_1^+} + \mathcal {O}_{\mathcal {W}_3}(\lambda ^2) + \mathcal {O}(\lambda ^3) \, , \\&[(\mathscr {L}_{0,0} - \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} ]^2 f_1^- = \frac{\zeta _2^-}{\lambda } f_1^+ + \frac{\alpha _2^-}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^- +\zeta _3^- f_1^- + f_{\mathcal {W}_3^-} +\lambda \big ( f_{\mathcal {W}_1^+ } + f_{\mathcal {W}_3^+} \big ) \\&\qquad \qquad \qquad \qquad \qquad \qquad + \lambda ^2 f_{\mathcal {W}_1^-} + \mathcal {O}_{\mathcal {W}_3} (\lambda ^2) + \mathcal {O}(\lambda ^3)\, , \end{aligned} \\ \nonumber&[(\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1}]^2 f_0^+ = \zeta _0^+ \mathrm B_2^+ + \frac{\alpha _0^+}{4 {\texttt{c}}_{\texttt{h}}^2} \textrm{A}_{-2}^+ + \mathcal {O}(\lambda ^{-1}:\lambda ) \, ,\ \ [(\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1}]^2 f_0^- = 0\, . \end{aligned}$$

(B.19)

Proof

Apply twice Lemma B.3 and use that

where $\alpha _5^\pm$, $\alpha _6^\pm$ are real numbers. $\square$

We further list a series of identities to exploit later.

By applying first Lemma B.5 and then Lemma B.3 we get

$$\begin{aligned} \nonumber&(\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,0}f_1^+ = - \textrm{i}\,\mu _\texttt{h}\Big [ \frac{ \zeta _1^+}{\lambda ^2} f_0^- + \frac{1}{\lambda }\mathrm A_2^+ + f_{\mathcal {W}_2^-} + \alpha _7 f_0^- + \mathcal {O}_{\mathcal {W}_2}(\lambda ) + \mathcal {O}_{\mathcal {W}_0}(\lambda ^2) \Big ] \, , \\ \nonumber&{(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{0,1} (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,0}f_1^- = -\textrm{i}\,\mu _\texttt{h}\Big [ \frac{1}{\lambda } \Big ( \textrm{A}_2^- - \frac{2{\texttt{c}}_{\texttt{h}}\zeta _{-1}^+}{\lambda ^2+ 4 {\texttt{c}}_{\texttt{h}}^2} f_0^- \Big ) + \textrm{J}_2^+ + \lambda f_{\mathcal {W}_2^-}+\mathcal {O}_{\mathcal {W}_2}(\lambda ^2)}\Big ] \, ,\\&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{0,1}(\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,0}f_0^\pm = 0\, , \end{aligned}$$

(B.20)

where $\alpha _7$ is a real number and

(B.21)

By applying first Lemma B.3 and then Lemma B.5, and since $\mathcal {J}{{\mathcal {B}}}_{1,0} \mathcal {W}_k \subseteq \mathcal {W}_k$, we get

$$\begin{aligned} \begin{aligned}&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{1,0} (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1}f_1^+ = \textrm{i}\,f_{\mathcal {W}_2^-}+\mathcal {O}_{\mathcal {W}_2}(\lambda ) \,,\\&(\mathscr {L}_{0,0}-\lambda )^{-1}\mathcal {J}{{\mathcal {B}}}_{1,0} (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1}f_1^- = \textrm{i}\,\mathrm S_2^+ +\textrm{i}\,\lambda f_{\mathcal {W}_2^-} + \mathcal {O}_{\mathcal {W}_2}(\lambda ^2) \,, \\&(\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,0} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_0^+ = \textrm{i}\,f_{\mathcal {W}_1^-} + \mathcal {O}(\lambda ^{-1}:\lambda ) \,,\\&(\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,0} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_0^- = 0\,, \end{aligned} \end{aligned}$$

(B.22)

where, using also (B.5), (3.8b)–(3.10a), (B.9)

(B.23)

We are now in position to prove Lemmata 3.4 and 3.5.

Proof of Lemma 3.4

The proof is divided in three parts, one for each group of formulas in (3.19).

Computation of $P_{0,2} f_j^\sigma$. Since $P_{0,\epsilon }f_0^-=f_0^-$ (cfr. [9, Lemma A.4]) we have

$$\begin{aligned} P_{0,2} f_0^- = 0\, . \end{aligned}$$

(B.24)

On the other hand, for $f_j^\sigma \in \{f_1^+, f_1^-,f_0^+ \}$, in view of (3.13) we have, by (B.4a)–(B.4b) and since ${{\mathcal {B}}}_{0,1} f_0^-={{\mathcal {B}}}_{0,2} f_0^- =0$,

$$\begin{aligned} P_{0,2} f_j^\sigma&= -\frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{0,2} f_j^\sigma \textrm{d}\lambda \\ \nonumber&+\frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{0,1} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_j^\sigma \textrm{d}\lambda =: \textrm{I}_j^\sigma + \mathrm {I\!I}_j^\sigma \, . \end{aligned}$$

(B.25)

In case $f_j^\sigma =f_0^+$ one readily sees, in view of (B.14) for $\textrm{I}_0^+$ and (B.19) for $\mathrm {I\!I}_0^+$, that $P_{0,2}f_0^+\in \mathcal {W}_2^+$ which implies the second statement in (3.19a). We now compute the remaining four terms.

First by Lemma B.6 and the residue theorem

$$\begin{aligned} \textrm{I}_1^+ = -\frac{\ell _1^+}{{4{\texttt{c}}_{\texttt{h}}^2}} f_{-1}^+ - \mathrm L_3^+ \,, \qquad \textrm{I}_1^- = -\frac{\ell _1^-}{{4{\texttt{c}}_{\texttt{h}}^2}} f_{-1}^- + f_{\mathcal {W}_3^-} \, . \end{aligned}$$

(B.26)

Then by (B.19) and the residue theorem

$$\begin{aligned} \mathrm {I\!I}_1^+ = \frac{\alpha _2^+}{4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^+ + \zeta _3^+ f_1^+ + \textrm{A}_3^+ \,, \qquad \mathrm {I\!I}_1^- = \frac{\alpha _2^-}{4{\texttt{c}}_{\texttt{h}}^2} f_{-1}^- + \zeta _3^- f_1^- + f_{\mathcal {W}_{3}^-} \ . \end{aligned}$$

(B.27)

In conclusion we have formulae (3.19a), (3.19b) with

$$\begin{aligned} P_{0,2} f_1^+= & {} \underbrace{\frac{\alpha _2^+ - \ell _1^+ }{4{\texttt{c}}_{\texttt{h}}^2} }_{\mathfrak {u}_{0,2}^+} f_{-1}^+ + \underbrace{\zeta _3^+}_{\mathfrak {n}_{0,2}} f_1^+ \underbrace{ - \textrm{L}_3^+ + \textrm{A}_3^+}_{\begin{bmatrix}\mathfrak {a}_{0,2} \cos (3x) \\ \mathfrak {b}_{0,2} \sin (3x) \end{bmatrix}}, \\ P_{0,2} f_1^-= & {} \underbrace{ \frac{\alpha _2^- - \ell _1^- }{4{\texttt{c}}_{\texttt{h}}^2} }_{\mathfrak {u}_{0,2}^-} f_{-1}^- + \underbrace{\zeta _3^-}_{\mathfrak {n}_{0,2}} f_1^- + f_{\mathcal {W}_{3}^-}\,, \end{aligned}$$

and we obtain the explicit expression (3.19c) of the coefficients given by

with $\zeta _3^+$, $\alpha _2^\pm$, $\mathrm A_3^+$ in (B.11) and $\ell _1^\pm$, $\mathrm L_3^+$ in (B.15).

Computation of $P_{2,0} f_0^-$. Since $P_{\mu ,0}f_0^-=f_0^-$ (cfr. [9, Lemma A.5]) we have

$$\begin{aligned} P_{2,0} f_0^- = 0\, . \end{aligned}$$

(B.28)

Computation of $P_{1,1} f_j^\sigma$. In case $f_j^\sigma \in \{f_1^+,f_1^-,f_0^- \}$ by (3.13), (3.14) and (B.4a), we have

$$\begin{aligned} \nonumber P_{1,1} f_j^\sigma&= - \frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{1,1} f_j^\sigma \textrm{d}\lambda + \frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{0,1} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,0} f_j^\sigma \textrm{d}\lambda \\&+ \frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{1,0} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_j^\sigma \textrm{d}\lambda =: \mathrm {I\!I\!I}_j^\sigma +\mathrm {I\!V}_j^\sigma +\textrm{V}_j^\sigma \, , \end{aligned}$$

(B.29a)

whereas, by (B.4b), (B.12), (B.8)

$$\begin{aligned} \nonumber P_{1,1} f_0^+&= - \frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{1,1} f_0^+ \textrm{d}\lambda + \frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda ^2} \mathcal {J}{{\mathcal {B}}}_{1,1} f_0^- \textrm{d}\lambda \\&+\frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{1,0} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_0^+ \textrm{d}\lambda =: \mathrm {I\!I\!I}_0^+ + \mathrm {I\!V}_0^+ +\textrm{V}_0^+\, . \end{aligned}$$

(B.29b)

When $f_j^\sigma =f_1^+$ one readily sees, in view of (B.16) for $\mathrm {I\!I\!I}_1^+$, (B.20) for $\mathrm {I\!V}_1^+$ and (B.22) for $\textrm{V}_1^+$, that $P_{1,1} f_1^+ \in \textrm{i}\,\mathcal {W}_0^- \oplus _\mathbb {R}\textrm{i}\,\mathcal {W}_2^-$ as stated in (3.19e). Similarly, when $f_j^\sigma =f_0^+$ one has, in view of (B.16) for $\mathrm {I\!I\!I}_0^+$ and $\mathrm {I\!V}_0^+$ and (B.22) for $\textrm{V}_0^+$, that $P_{1,1} f_0^+ \in \textrm{i}\,\mathcal {W}_1^-$ as stated in (3.19e).

We now compute the remaining terms. By Lemma B.7 and the residue theorem

$$\begin{aligned} \mathrm {I\!I\!I}_1^- = - {\textrm{i}\,\textrm{Q}_2^+} \,, \quad \mathrm {I\!I\!I}_0^- = -\frac{\textrm{i}\,}{2 {\texttt{c}}_{\texttt{h}}^{3/2}} f_{-1}^+ \, . \end{aligned}$$

(B.30)

By (B.20) we have

$$\begin{aligned} \mathrm {I\!V}_1^- = -\textrm{i}\,\mu _\texttt{h}{\mathrm J_2^+}, \quad \mathrm {I\!V}_0^- = 0 \, . \end{aligned}$$

(B.31)

By (B.22) we have

$$\begin{aligned} \textrm{V}_1^- = {\textrm{i}\,\mathrm S_2^+} \,, \quad \textrm{V}_0^- = 0\, . \end{aligned}$$

(B.32)

In conclusion we have formulae (3.19e) with

$$\begin{aligned} P_{1,1} f_1^- = \underbrace{ - {\textrm{i}\,\mathrm Q_2^+} + {\textrm{i}\,\mathrm S_2^+} - \textrm{i}\,\mu _\texttt{h}{ \mathrm J_2^+} }_{\textrm{i}\,{\begin{bmatrix}\mathfrak {a}_{1,1} \cos (2x) \\ \mathfrak {b}_{1,1} \sin (2x) \end{bmatrix}}} \,, \quad {P_{1,1} f_0^- = -\frac{\textrm{i}\,}{2 {\texttt{c}}_{\texttt{h}}^{3/2}} f_{-1}^+ }\,, \end{aligned}$$

(B.33)

and we obtain the explicit expression (3.20) of the coefficients given by

$$\begin{aligned} \begin{bmatrix}\mathfrak {a}_{1,1} \cos (2x) \\ \mathfrak {b}_{1,1} \sin (2x) \end{bmatrix}:= - \mathrm Q_2^+ +\mathrm S_2^+ - \mu _\texttt{h}\mathrm J_2^+ \end{aligned}$$

with $\mathrm S_2^+$ in (B.23), $\mu _\texttt{h}$ in (B.13), $\mathrm Q_2^+$ in (B.17) and $\mathrm J_2^+$ in (B.21).

This concludes the proof of Lemma 3.4.

Proof of Lemma 3.5

Computation of $P_{0,3} f_j^\sigma$. Similarly to (B.24) we have $P_{0,3}f_0^- = 0$ (as stated in (3.21)). Let us now compute $P_{0,3} f_1^+$. By (3.13), (3.14) and (B.4a)

$$\begin{aligned} \nonumber P_{0,3} f_1^+&= - \frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{0,3} f_1^+ \textrm{d}\lambda \\ \nonumber&+\frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{0,2} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_1^+ \textrm{d}\lambda \\ \nonumber&+\frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{0,1} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2} f_1^+ \textrm{d}\lambda \\ \nonumber&- \frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{0,1} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_1^+ \textrm{d}\lambda \\&=: \mathrm {V\!I} + \mathrm {V\!I\!I} + \mathrm {V\!I\!I\!I} + \mathrm {I\!X} \, . \end{aligned}$$

(B.34)

We now compute these four terms.

$\mathrm {V\!I} \big )$ By (3.8d) we have ${{\mathcal {B}}}_{0,3} = \begin{bmatrix} a_3(x) &{} -p_3(x)\partial _x \\ \partial _x\circ p_3(x) &{} 0 \end{bmatrix}$ with $p_3(x), a_3(x)$ in (A.59b)–(A.60b). Then ${{\mathcal {B}}}_{0,3} f_0^- = 0$ whereas $\mathcal {J}{{\mathcal {B}}}_{0,3} f_1^+ = \alpha _{10} f_0^- + {\textrm{W}_{2}^-} + f_{\mathcal {W}_4^-}$ where $\alpha _{10} \in \mathbb {R}$ and

$$\begin{aligned} {\textrm{W}_{2}^-} (x):= \begin{bmatrix} - {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}} (p_3^{[1]} + p_3^{[3]}) \, \sin (2x) \\[4mm] \dfrac{- {\texttt{c}}_{\texttt{h}}(a_3^{[1]} + a_3^{[3]}) + (p_3^{[1]} + p_3^{[3]})}{2 {\texttt{c}}_{\texttt{h}}^{\frac{1}{2}}} \cos (2x) \end{bmatrix} \ . \end{aligned}$$

(B.35)

Hence by (B.4d) we get

and, by (B.7), the term $\mathrm {V\!I}$ in (B.34) is

(B.36)

with

(B.37)

$\mathrm {V\!I\!I} \big )$ By Lemma B.3 and since ${{\mathcal {B}}}_{0,2} f_0^- = 0$, we get

$$\begin{aligned}&(\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_1^+ = (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2}\textrm{A}_2^+\\ \nonumber&\qquad +\lambda (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2} f_{\mathcal {W}_2^-} +\lambda ^2 (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2} f_{\mathcal {W}_2^+} +\mathcal {O}(\lambda ) \, . \end{aligned}$$

(B.38)

Applying the operators ${{\mathcal {B}}}_{0,2}$ in (3.8c) and $\mathcal {J}$ in (1.5) to the vector $\mathrm A_2^+$ in (B.9) one obtains

$$\begin{aligned} \mathcal {J}{{\mathcal {B}}}_{0,2} \mathrm A_2^+ = {\textrm{X}_2^-}+f_{\mathcal {W}_0^-} + f_{\mathcal {W}_4^-} \,, \end{aligned}$$

(B.39a)

where

$$\begin{aligned} {\textrm{X}_2^-}(x):= \begin{bmatrix}-\dfrac{({\texttt{c}}_{\texttt{h}}^4-1)^2 \texttt{f}_2 (a_1^{[1]} {\texttt{c}}_{\texttt{h}}-2 p_1^{[1]})+{\texttt{c}}_{\texttt{h}}({\texttt{c}}_{\texttt{h}}^4+1)p_2^{[0]} \big ( ({\texttt{c}}_{\texttt{h}}^4+2 ) p_1^{[1]}-a_1^{[1]} {\texttt{c}}_{\texttt{h}}\big )}{{\texttt{c}}_{\texttt{h}}^{11/2} ({\texttt{c}}_{\texttt{h}}^4+1)}\sin (2 x) \\[4mm] -\dfrac{a_2^{[0]} {\texttt{c}}_{\texttt{h}}\big (({\texttt{c}}_{\texttt{h}}^4+2) p_1^{[1]}-a_1^{[1]} {\texttt{c}}_{\texttt{h}}\big )+({\texttt{c}}_{\texttt{h}}^4+1) p_2^{[0]} (a_1^{[1]} {\texttt{c}}_{\texttt{h}}-2 p_1^{[1]})}{2 {\texttt{c}}_{\texttt{h}}^{11/2}} \cos (2 x) \end{bmatrix} .\nonumber \\ \end{aligned}$$

(B.39b)

On the other hand, in view of (B.3) and Lemma B.2, one has

$$\begin{aligned} \lambda (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2} f_{\mathcal {W}_2^-} = \mathcal {O}(\lambda ) \,,\quad \lambda ^2 (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,2} f_{\mathcal {W}_2^+} = \mathcal {O}(\lambda )\, .\qquad \end{aligned}$$

(B.39c)

Then Lemmata B.6, B.2, (B.38) and (B.39) give

and, by (B.7), the term $\mathrm {V\!I\!I}$ in (B.34) is

(B.40)

with, by (B.5) and (B.39b),

(B.41)

with

$\mathrm {V\!I\!I\!I}\big )$ By Lemma B.6, (B.15) and Lemma B.2 we get

(B.42)

Applying the operators ${{\mathcal {B}}}_{0,1}$ in (3.8b) and $\mathcal {J}$ in (1.5) to the vector $\mathrm L_3^+$ in (B.15) one obtains

$$\begin{aligned} \mathcal {J}{{\mathcal {B}}}_{0,1} {\mathrm L_3^+} = {\textrm{Y}_2^-} + f_{\mathcal {W}_4^-}\,, \end{aligned}$$

(B.43a)

where

(B.43b)

In view of (B.3) and Lemma B.2, one obtains by inspection

$$\begin{aligned} \frac{\lambda m_1^+}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_{-1}^- = \mathcal {O}(\lambda )\,,\quad (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} \mathcal {O}_{\mathcal {W}_3}(\lambda ) =\mathcal {O}(\lambda )\, .\nonumber \\ \end{aligned}$$

(B.43c)

Then (B.42), Lemmata B.3, B.2 and (B.43) give

and, by (B.7), the term $\mathrm {V\!I\!I\!I}$ in (B.34) is

(B.44)

where

(B.45)

with

$$\begin{aligned} \kappa _3 :&= \dfrac{a_1^{[1]} {\texttt{c}}_{\texttt{h}}\big (a_2^{[2]} {\texttt{c}}_{\texttt{h}}({\texttt{c}}_{\texttt{h}}^4+3)-2 (5 {\texttt{c}}_{\texttt{h}}^4+3)p_2^{[2]}\big ) -a_2^{[2]} {\texttt{c}}_{\texttt{h}}({\texttt{c}}_{\texttt{h}}^8+13 {\texttt{c}}_{\texttt{h}}^4+6) p_1^{[1]}+2 ({\texttt{c}}_{\texttt{h}}^4+3) (5 {\texttt{c}}_{\texttt{h}}^4+2) p_1^{[1]} p_2^{[2]}}{32 {\texttt{c}}_{\texttt{h}}^{19/2}} \, ,\\ \varsigma _3 :&= \dfrac{({\texttt{c}}_{\texttt{h}}^4+1)\big [ a_1^{[1]} {\texttt{c}}_{\texttt{h}}\big ( a_2^{[2]} {\texttt{c}}_{\texttt{h}}({\texttt{c}}_{\texttt{h}}^4+3)-2 (5 {\texttt{c}}_{\texttt{h}}^4+3) p_2^{[2]} \big )-2 a_2^{[2]} {\texttt{c}}_{\texttt{h}}(5 {\texttt{c}}_{\texttt{h}}^4+3) p_1^{[1]}+4 (7 {\texttt{c}}_{\texttt{h}}^4+3) p_1^{[1]} p_2^{[2]}\big ]}{64 {\texttt{c}}_{\texttt{h}}^{21/2}}\, . \end{aligned}$$

$\mathrm {I\!X} \big )$ By (B.19) we get

$$\begin{aligned}&[(\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1}]^3 f_1^+ = \frac{\zeta _2^+ }{\lambda } (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_1^-\\ \nonumber&+ \frac{\alpha _2^+}{\lambda ^2+4{\texttt{c}}_{\texttt{h}}^2} (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_{-1}^+ +\zeta _3^+ (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_1^+ +(\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} {\mathrm A_3^+} \end{aligned}$$

(B.46a)

$$\begin{aligned}&\begin{aligned}&+\lambda (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} \left( f_{\mathcal {W}_1^-} + f_{\mathcal {W}_3^-} \right) + \lambda ^2 (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_{\mathcal {W}_1^+} \\&+ (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} \mathcal {O}_{\mathcal {W}_3}(\lambda ^2) + (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} \mathcal {O}(\lambda ^3) \, .\end{aligned} \end{aligned}$$

(B.46b)

In view of (B.3) and Lemma B.2 the terms in the two lines in (B.46b) are

$$\begin{aligned}&\lambda (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1}\left( f_{\mathcal {W}_1^-} + f_{\mathcal {W}_3^-} \right) = \mathcal {O}(\lambda )\, ,\ \ \lambda ^2 (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} f_{\mathcal {W}_1^+} =\mathcal {O}(\lambda )\, ,\ \\&\ (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} \mathcal {O}_{\mathcal {W}_3}(\lambda ^2) =\mathcal {O}(\lambda ^2)\, , \quad (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} \mathcal {O}(\lambda ^3) = \mathcal {O}(\lambda )\, . \end{aligned}$$

The remaining terms in (B.46), again by Lemma B.3, are

(B.47)

By applying the operators ${{\mathcal {B}}}_{0,1}$ in (3.8b) and $\mathcal {J}$ in (1.5) to the vector ${\mathrm A_3^+}$ in (B.11) one gets

$$\begin{aligned} \mathcal {J}{{\mathcal {B}}}_{0,1} { \mathrm A_3^+} = {\textrm{Z}_2^-}+ f_{\mathcal {W}_4^-} \end{aligned}$$

(B.48)

where

$$\begin{aligned} {\textrm{Z}_2^-}(x):= - \begin{bmatrix} \frac{p_1^{[1]} \left( (a_1^{[1]})^2 \left( {\texttt{c}}_{\texttt{h}}^4+3\right) {\texttt{c}}_{\texttt{h}}^2 -2 a_1^{[1]}p_1^{[1]} \left( {\texttt{c}}_{\texttt{h}}^8+9 {\texttt{c}}_{\texttt{h}}^4+6\right) {\texttt{c}}_{\texttt{h}}+ (p_1^{[1]})^2 \left( 11 {\texttt{c}}_{\texttt{h}}^8+29 {\texttt{c}}_{\texttt{h}}^4+12\right) \right) }{32 {\texttt{c}}_{\texttt{h}}^{19/2}}\sin (2 x) \\[4mm] \frac{ (a_1^{[1]} {\texttt{c}}_{\texttt{h}}-p_1^{[1]}) \left( ( a_1^{[1]})^2 \left( {\texttt{c}}_{\texttt{h}}^4+3\right) {\texttt{c}}_{\texttt{h}}^2 -2 a_1^{[1]} p_1^{[1]} \left( {\texttt{c}}_{\texttt{h}}^8+13 {\texttt{c}}_{\texttt{h}}^4+6\right) {\texttt{c}}_{\texttt{h}}+3(p_1^{[1]})^2 \left( 9 {\texttt{c}}_{\texttt{h}}^8+15 {\texttt{c}}_{\texttt{h}}^4+4\right) \right) }{64 {\texttt{c}}_{\texttt{h}}^{21/2}} \cos (2 x) \end{bmatrix}\, .\nonumber \\ \end{aligned}$$

(B.49)

Finally, by (B.47) and (B.48), we get that the term $\mathrm {I\!X}$ in (B.34) is

(B.50)

where

(B.51)

where

$$\begin{aligned} \begin{aligned} \kappa _4&:= \frac{1}{64 {\texttt{c}}_{\texttt{h}}^{29/2}} \big ( -(a_1^{[1]})^3 ({\texttt{c}}_{\texttt{h}}^4+3) {\texttt{c}}_{\texttt{h}}^3 +(a_1^{[1]})^2 p_1^{[1]} (3 {\texttt{c}}_{\texttt{h}}^8+31 {\texttt{c}}_{\texttt{h}}^4+18) {\texttt{c}}_{\texttt{h}}^2 \\&\quad -a_1^{[1]}(p_1^{[1]})^2 (2 {\texttt{c}}_{\texttt{h}}^{12} +49 {\texttt{c}}_{\texttt{h}}^8+101 {\texttt{c}}_{\texttt{h}}^4+36) {\texttt{c}}_{\texttt{h}}+ (p_1^{[1]})^3 (11 {\texttt{c}}_{\texttt{h}}^{12}+67 {\texttt{c}}_{\texttt{h}}^8+86 {\texttt{c}}_{\texttt{h}}^4+24) \big ) \\ \varsigma _4&:= \frac{({\texttt{c}}_{\texttt{h}}^4+1)}{{128 {\texttt{c}}_{\texttt{h}}^{31/2}} } \big (-(a_1^{[1]})^3 ({\texttt{c}}_{\texttt{h}}^4+3) {\texttt{c}}_{\texttt{h}}^3+2 (a_1^{[1]})^2 p_1^{[1]} ({\texttt{c}}_{\texttt{h}}^8+14 {\texttt{c}}_{\texttt{h}}^4+9) {\texttt{c}}_{\texttt{h}}^2\\&\quad - a_1^{[1]}(p_1^{[1]})^2 (31 {\texttt{c}}_{\texttt{h}}^8+89 {\texttt{c}}_{\texttt{h}}^4+36) {\texttt{c}}_{\texttt{h}}+2 (p_1^{[1]})^3 (19 {\texttt{c}}_{\texttt{h}}^8+37 {\texttt{c}}_{\texttt{h}}^4+12) \big ) \end{aligned} \end{aligned}$$

In conclusion, by (B.34), (B.36), (B.40), (B.44) and (B.50) we deduce that

which proves the expansion of $P_{0,3} f_1^+$ in (3.21) with

$$\begin{aligned} \begin{bmatrix}\mathfrak {a}_{0,3}\cos (2x) \\ \mathfrak {b}_{0,3}\sin (2x) \end{bmatrix}&:= \begin{bmatrix}(\kappa _1 +\kappa _2 + \kappa _3 - \kappa _4 )\cos (2x) \\ (\varsigma _1 +\varsigma _2 + \varsigma _3 - \varsigma _4 )\sin (2x) \end{bmatrix}\\&\quad + (\tau _1^+ -\zeta _2^+) \mathrm B_2^+(x) + \frac{\ell _1^+- \alpha _2^+}{4{\texttt{c}}_{\texttt{h}}^2} \textrm{A}_{-2}^+(x) -\zeta _3^+\mathrm A_2^+(x) \, , \end{aligned}$$

with $\kappa _i$, $\varsigma _i$, $i=1,\dots ,4$ in (B.37), (B.41), (B.45), (B.51), $\mathrm B_2^+$, $\textrm{A}_{-2}^+$ $\mathrm A_2^+$ in (B.9), $\zeta _2^+$, $\alpha _2^+$, $\zeta _3^+$ in (B.11) and $\ell _1^+$, $\tau _1^+$ in (B.15), resulting in the coefficients $\mathfrak {a}_{0,3}$ and $\mathfrak {b}_{0,3}$ in (3.22).

Computation of $P_{1,2} f_0^-$. By (3.13), (3.14) and the fact that ${{\mathcal {B}}}_{1,0} f_0^- = {{\mathcal {B}}}_{0,1}f_0^- = {{\mathcal {B}}}_{0,2}f_0^- = 0$, the term $P_{1,2} f_0^-$ reduces to

$$\begin{aligned} P_{1,2}f_0^-&= -\frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{1,2} f_0^- \textrm{d}\lambda \nonumber \\&\quad +\frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{0,1} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,1}f_0^- \textrm{d}\lambda =: \textrm{X} + \mathrm {X\!I}\, . \end{aligned}$$

(B.52)

We now compute the two terms.

$\textrm{X}\big )$ By (3.46) we have $\mathcal {J}{{\mathcal {B}}}_{1,2} f_0^- =\textrm{i}\,a_3 f_0^- + {\textrm{i}\,\textrm{W}_{-2}^-}$ with and, by (B.4),

(B.53)

$\mathrm {X\!I}\big )$ By Lemmata B.7, B.3 one has

$$\begin{aligned} (\mathscr {L}_{0,0}-\lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{0,1} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,1} f_0^- = \textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} {\textrm{B}_2^+ }+ \textrm{i}\,\frac{1}{2 {\texttt{c}}_{\texttt{h}}^{3/2}} { \textrm{A}_{-2}^+} +\mathcal {O}(\lambda ^{-1}: \lambda )\,, \end{aligned}$$

and therefore

$$\begin{aligned} \mathrm {X\!I} = \textrm{i}\,{\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} {\textrm{B}_2^+ }+ \textrm{i}\,\frac{1}{2 {\texttt{c}}_{\texttt{h}}^{3/2}} {\textrm{A}_{-2}^+} \, . \end{aligned}$$

(B.54)

In conclusion, by (B.52), (B.53) and (B.54)

(B.55)

which, in view of (B.53), proves the expansion of $P_{1,2} f_0^-$ in (3.21) with

$$\begin{aligned} \begin{bmatrix}\mathfrak {a}_{1,2}\cos (2x) \\ \mathfrak {b}_{1,2} \sin (2x) \end{bmatrix}:= \begin{bmatrix}-p_2^{[2]} {\texttt{c}}_{\texttt{h}}^{-4} \cos (2x) \\ - p_2^{[2]}\frac{1+{\texttt{c}}_{\texttt{h}}^4}{2{\texttt{c}}_{\texttt{h}}^5}\sin (2x) \end{bmatrix}+ {\texttt{c}}_{\texttt{h}}^{-\frac{1}{2}} \textrm{B}_2^+(x) + \frac{1}{2 {\texttt{c}}_{\texttt{h}}^{3/2}}\textrm{A}_{-2}^+(x)\, , \end{aligned}$$

with $\textrm{B}_2^+$ and $\textrm{A}_{-2}^+$ in (B.9), resulting in the coefficients $\mathfrak {a}_{1,2}$ and $\mathfrak {b}_{1,2}$ given in (3.22).

Computation of $P_{2,1} f_0^-$. By (3.13) and the fact that ${{\mathcal {B}}}_{1,0} f_0^- = {{\mathcal {B}}}_{0,1}f_0^-$ and ${{\mathcal {B}}}_{2,1} = 0$ the term $P_{2,1} f_0^-$ reduces to

$$\begin{aligned} P_{2,1} f_0^-&= \frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{0,1} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{2,0} f_0^- \textrm{d}\lambda \\&\quad +\frac{1}{2\pi \textrm{i}\,} \oint _{\Gamma } \frac{(\mathscr {L}_{0,0}- \lambda )^{-1}}{\lambda } \mathcal {J}{{\mathcal {B}}}_{1,0} (\mathscr {L}_{0,0}- \lambda )^{-1} \mathcal {J}{{\mathcal {B}}}_{1,1} f_0^- \textrm{d}\lambda \, . \end{aligned}$$

By repeated use of (B.3) and Lemma B.2 one finds that $P_{2,1} f_0^- \in \mathcal {W}_1^-$ as stated in (3.21).