On Asymptotic Stability of the Sine-Gordon Kink in the Energy Space

Abstract

We consider the sine-Gordon (SG) equation in $1+1$ dimensions. The kink is a static, non symmetric exact solution to SG, stable in the energy space $H^1\times L^2$. It is well-known that the linearized operator around the kink has a simple kernel and no internal modes. However, it possesses an odd resonance at the bottom of the continuum spectrum, deeply related to the existence of the (in)famous wobbling kink, an explicit periodic-in-time solution of SG around the kink that contradicts the asymptotic stability of the kink in the energy space. In this paper we further investigate the influence of resonances in the asymptotic stability question. We also discuss the relationship between breathers, wobbling kinks and resonances in the SG setting. By gathering Bäcklund transformations (BT) as in Hoffman and Wayne (Differ Int Equ 26(3–4):303–320, 2013), Muñoz and Palacios (Ann. IHP C Analyse Nonlinéaire 36(4):977–1034, 2019) and Virial estimates around odd perturbations of the vacuum solution, in the spirit of Kowalczyk et al. (Lett Math Phys 107(5):921–931, 2017), we first identify the manifold of initial data around zero under which BTs are related to the wobbling kink solution. It turns out that (even) small breathers are deeply related to odd perturbations around the kink, including the wobbling kink itself. As a consequence of this result and Kowalczyk et al. (Lett Math Phys 107(5):921–931, 2017), using BTs we can construct a smooth manifold of initial data close to the kink, for which there is asymptotic stability in the energy space. The initial data has spatial symmetry of the form (kink + odd, even), non resonant in principle, and not preserved by the flow. This asymptotic stability property holds despite the existence of wobbling kinks in SG. We also show that wobbling kinks are orbitally stable under odd data, and clarify some interesting connections between SG and $\phi ^4$ at the level of linear Bäcklund transformations.

1 Introduction and Main Results

Consider the $1+1$ dimensional sine-Gordon (SG) equation, in physical coordinates (t, x), for a scalar field $\phi$:

$$\begin{aligned} \phi _{tt}-\phi _{xx}+\sin \phi =0. \end{aligned}$$

(1.1)

Here, $\phi =\phi (t,x)$ is a real-valued function, and $(t,x)\in \mathbb {R}^2$. A natural energy space for (1.1) is given by

$$\begin{aligned} (H_{sin}^1 \times L^2)(\mathbb {R}):= \left\{ \vec \phi := (\phi ,\phi _t) \in (\dot{H}^1 \times L^2) (\mathbb {R}) ~: ~ \sin \left( \frac{\phi }{2}\right) \in L^2 (\mathbb {R})\right\} , \end{aligned}$$

where we use the standard notation $\vec \phi :=(\phi ,\phi _t)$, corresponding to a wave-like dynamics. This fact essentially follows from the lower order conservation laws called energy and momentum, respectively:

$$\begin{aligned} E[\vec \phi ](t)=\dfrac{1}{2}\int _\mathbb {R}(\phi _x^2+\phi _t^2)(t,x)dx+\int _{\mathbb {R}}(1-\cos \phi (t,x))dx=E[\vec \phi ](0), \end{aligned}$$

(1.2)

and

$$\begin{aligned} P[\vec \phi ](t)=\dfrac{1}{2}\int _\mathbb {R}\phi _t(t,x)\phi _x(t,x)dx=P[\vec \phi ](0). \end{aligned}$$

(1.3)

Real-valued solutions of (1.1) that initially are in $H^1_{sin}\times L^2$ are preserved for all time, see e.g [19, 60]. Additionally, they are globally well-defined thanks to the fact that $\sin (\cdot )$ is a smooth bounded function. In what follows, we will assume that we have a real-valued solution of (1.1) (in vector form) $\vec \phi \in C(\mathbb {R}; H_{sin}^1\times L^2)$. Additionally, small perturbations of a given solution in $H_{sin}^1\times L^2$ are essentially in $H^1\times L^2$, and vice-versa.

Solutions of (1.1) are known to satisfy several symmetry properties: shifts in space and time $(t_0,x_0)$, i.e. the mapping $\vec \phi (t,x) \mapsto \vec \phi (t+t_0,x+x_0)$ among SG solutions is preserved, as well as Lorentz boosts: for each $\beta \in (-1,1)$, given $\vec \phi (t,x)=(\phi ,\phi _t)(t,x)$ solution, then

$$\begin{aligned} (\phi ,\phi _t)_\beta (t,x):= (\phi ,\phi _t)\big (\gamma (t-\beta x),\gamma (x-\beta t) \big ), \quad \gamma :=(1-\beta ^2)^{-1/2}, \end{aligned}$$

(1.4)

is another solution of (1.1). The parameter $\gamma$ is called Lorentz scaling factor, having an important role in the Physics of SG, and in what follows.

As for the motivation for studying SG, this equation has been extensively used in differential geometry (constant negative curvature surfaces), as well as relativistic field theory and soliton integrable systems. The interested reader may consult the monograph by Lamb [42, Section 5.2], and for more details about the physics of SG, see e.g. Dauxois and Peyrard [18], and the recent monographs [17, 29].

SG has particular (topological) stationary solutions, known as kinks [42]:

$$\begin{aligned} Q(x):= 4\arctan e^{x}. \end{aligned}$$

(1.5)

This exact solution connects the final states 0 and $2\pi$. Thanks to Lorentz boosts (1.4) and translation invariances, it is possible to define a kink of arbitrary speed $\beta \in (-1,1)$ and shift $x_0\in \mathbb {R}$, given by

$$\begin{aligned} Q(t,x;\beta ,x_0):= 4\arctan (e^{\gamma (x-\beta t+x_0)}), \qquad \gamma =(1-\beta ^2)^{-1/2}. \end{aligned}$$

(1.6)

From the integrability of SG [1, 72], interactions between kinks are elastic, i.e. they are “solitons” in the strict sense of the word [42]. Also, $-Q(x)$ is another stationary solution of SG, usually called anti-kink.

It is well-known that (Q, 0) is orbitally stable under small perturbations in the energy space $(H^1\times L^2)(\mathbb {R})$, see Henry-Perez-Wreszinski [25]. More precisely, there exists $C_0>0$ such that, for all sufficiently small $\eta >0$,

$$\begin{aligned} \begin{aligned}&\Vert (\phi ,\phi _t)(t=0) - (Q,0)\Vert _{H^1\times L^2}<\eta \\&\quad \implies \sup _{t\in \mathbb {R}} \Vert (\phi ,\phi _t)(t) - (Q,0)(\cdot -y(t))\Vert _{H^1\times L^2} <C_0\eta , \end{aligned} \end{aligned}$$

(1.7)

for some $y(t)\in \mathbb {R}$. Using the Bäcklund transformation present for SG, and extensively mentioned below, Hoffman and Wayne [27] extended this stability result to the case of the kink and sketched the case of several kink structures. Inspired by this work, and using the same technique, in a recent work [60] the three main 2-soliton solutions of SG were proved to be orbitally stable for small perturbations in the energy space. In that paper, 2-kinks solutions (1.11) were considered, but also breathers (see (2.1) below) and kink-antikinks, two additional 2-soliton solutions which are even in space. All of them were shown to be orbitally stable for small perturbations in $H^1\times L^2$.

In this paper we consider the asymptotic stability (AS) problem for the SG kink in the energy space. More precisely, we would like to understand the possible final states allowed by (1.7). As we will explain below, this is not a simple problem, because of several intriguing ingredients. Our main result, stated in few words, claims the following.

Theorem 1.1

There exists a smooth infinite codimensional manifold ${\mathcal {M}}_{\eta ,0}$ of initial data $(\phi _0,\phi _1)$ of the form

$$\begin{aligned} (\phi _0,\phi _1)= (Q + u_0, s_0), \quad u_0 \hbox { odd}, \; s_0 \hbox { even}, \quad \Vert (u_0, s_0) \Vert _{H^1\times L^2} <\eta \ll 1, \end{aligned}$$

(1.8)

of zero momentum (1.3), under which the SG kink Q in (1.5) is asymptotically stable in the energy space.

What do we mean by asymptotically stable in this setting, and what kind of manifold are we talking about, is something that we have to explain in detail, but it requires the introduction of several additional ingredients. These ingredients are the so-called wobbling kinks, breathers, (spectral) resonances and Bäcklund transformations, and we deeply think that they are certainly necessary to fully understand Theorem 1.1. A key element for the proof of Theorem 1.1 is to understand how spatial parity properties relate under Bäcklund transformations, a subject left out in our previous paper [60], and schematically explained in Figs. 4 and 5. The impatient reader can directly go to Theorem 6.1 to read a detailed description of our main result.

1.1 Wobbling kinks

Proving Theorem 1.1 is not direct, essentially because of the existence, near the static kink, of arbitrarily close wobbling kinks in SG [64, 65, 16, Thm. 2.6] (see also references therein and [36, Remark 1.3]).

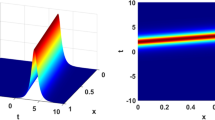
Recall the kink (1.5). Wobbling kinks are explicit solutions $W_\beta =W_\beta (t,x)$, $\beta \in (-1,1)$, to the SG equation (1.1), which behave as periodic in time, localized perturbations of the static kink solution¹:

$$\begin{aligned} \begin{aligned} W_\beta (t,x):=&~{} 4~\hbox {Arg} \left( U_\beta + i V_\beta \right) ,\\ U_\beta :=&~{} \cosh (\beta x) + \beta \sinh (\beta x) -\beta e^{ x} \cos (\alpha t) \\ V_\beta :=&~{} e^x \left( \cosh (\beta x) -\beta \sinh (\beta x) -\beta e^{-x} \cos (\alpha t) \right) , \quad \alpha :=\sqrt{1-\beta ^2}. \end{aligned} \end{aligned}$$

(1.9)

See Fig. 1 for a graphic depiction of this solution. Formally, wobbling kinks are solutions of the form kink $+$ breather, where a breather is a periodic in time solution of SG, for reasons to be explained below. Note also that $W_\beta$ reduces to the SG kink (1.5) as $\beta \rightarrow 0$. By construction, when $\beta \ne 0$, these modes never converge to a final state, no matter how close they are to the kink Q. Therefore, as already stated in [36, Remark 1.3] SG kinks are not asymptotically stable in the energy space.

Fig. 1

The wobbling kink (1.9) with $\beta =0.5$ at times $t=0$ (continuous curve), $t=2$ (dashed curve), and $t=6$ (dotted curve)

Consequently, any result concerning the long time behavior of SG kinks (see Theorem 1.1) will require to take into account these counterexamples (and probably others) to the existence of final states.

For further purposes, we will need the following standard notation: for $m=0,1,2,\ldots ,$ denote

$$\begin{aligned} \begin{aligned} H^m_e(\mathbb {R}):=&~{} \{ f \in H^m(\mathbb {R}) ~: ~ f \hbox { is even in space} \},\\ H^m_o(\mathbb {R}):=&~{} \{ f \in H^m(\mathbb {R}) ~: ~ f \hbox { is odd in space} \}. \end{aligned} \end{aligned}$$

(1.10)

As usual, we denote $L^2_e(\mathbb {R})=H^0_e(\mathbb {R})$ and $L^2_o(\mathbb {R})=H^0_o(\mathbb {R})$. Our second result of this paper is related to the orbital stability of the wobbling kink, under odd perturbations.

Theorem 1.2

The SG wobbling kink is orbitally stable under small $H^1_o\times L^2_o$ perturbations.

A more quantitative version of this result is given in Theorem 4.6. Whether or not the wobbling kink is orbitally stable under general perturbations depends on the definition of wobbling kink solution. Precisely, for some particular initial data one can see (see Lemma 4.7) that the wobbling kink structure as itself (periodic in time, odd perturbations of a kink) is destroyed; however, this is because the wobbling kink (1.9) is part of a more general family of topological 3-soliton solutions consisting of a kink and an attached static/moving breather. This phenomenon is similar to the case of NLS breathers/2-solitons, which are part of a whole family, see e.g. [2] for details. The stability of the whole 3-soliton family remains an interesting open problem.

SG can be also described using Inverse Scattering Techniques (IST) (recall that SG is an integrable model [1, 42, 72]). Some spatial decay hypotheses are needed to define the associated scattering data (or Riemann-Hilbert problem), and data only in the energy space are not well-suited for those methods. Also, the dynamics around kinks is usually not treated because of its unusual limit at infinity. Therefore, a description of the (wobbling) kink dynamics as in Theorems 1.1 and 1.2 for data only in the energy space is far from obvious, and not known as far as we understand. However, the IST description, when made rigorous, is far more accurate than ours. The interested reader can consult the recent monograph by Klein and Saut [31] for a complete description of this fascinating topic on IST vs. PDE techniques. See also a recent work by Chen-Liu-Lu [13] on the AS in some weighted smooth functional spaces by means of IST. The integrable character of SG was proved in [1, 72]. Some early descriptions of the dynamics can be found in Ercolani, Forest and McLaughlin, [23]. Birnir, McKean and Weinstein [11] studied nonexistence of breathers for perturbations of SG formally using Bäcklund transformations. Denzler [22] improved this result by considering more nonlinearities. See also Vuillermot [71] and Kichenassamy [30], and the monograph by Schuur [66] for more details on the methods. See also [52] for a recent construction of invariant soliton manifold for perturbed SG equations. A completely rigorous result on nonexistence of odd breathers can be found in [37].

The wobbling kink in SG (1.9) was first discovered by Segur [64] (see also [65]), while searching for wobbling kink solutions for $\phi ^4$ (see Sect. 2). Using IST and a permutability theorem [42], the wobble (1.9) is easily found as a solution consisting of a static kink plus an attached breather, exactly as expressed in (2.9). The same procedure for the $\phi ^4$ model (2.3) seems not to work (i.e. there is no wobbling kink), as the authors pointed out in [65]. A more rigorous proof was given in [36], in the case of (odd, odd) data, but for general data the question remains largely open. In this paper we answer parallel questions for the SG case, which enjoys far more algebraic properties than $\phi ^4$, although they meet nicely at the linear level, see Sect. 2. This close connection between SG and $\phi ^4$ has fascinated to plenty of authors in the mathematical physics community since past forty years; see e.g. the monographs [17, 29] for further details. In this paper, we also explore this connection in terms of the components needed for the proof of Theorems 1.1 and 1.2, see in particular the bridge between Theorems 1.2 and 1.1, which is Sect. 5.

Is the wobbling kink asymptotically stable for odd data? Clearly not. Fix $\beta \in (0,1)$. Then the initial perturbation of the wobbling kink $W_\beta (t,x)$ given by $W_{\beta '}(0,x)$, with $\beta '\sim \beta$ does not converge to the wobbling kink $W_\beta$. This means that wobbling kinks are not AS. The problem of asymptotic stability of the wobbling kink for a manifold of initial data just as in Theorem 1.1 remains an interesting open question.

Another point of view under which Theorem 1.1 can be put in context, is the one associated to generalized Korteweg-de Vries (gKdV), nonlinear Schrödinger (NLS) and Klein-Gordon (NLKG) equations and their associated soliton dynamics. We first focus on the NLKG case, closely related to SG. Soffer and Weinstein [68, 69] successfully solved the intriguing interaction between solitons and radiation in 3D NLKG. A complete description of the invariant manifolds around the 1D NLKG soliton for supercritical powers was also described in [41], recently extended in [38], based in previous results by Bizoń et. al. [12]. See the monograph [62] for a complete account of the methods developed by Krieger, Nakanishi and Schlag in the case of Klein-Gordon theories in several dimensions, and motivated by earlier fundamental results in this area by Bates and collaborators [9, 10]. For generalized KdV equations, see the works by Pego and Weinstein [63] and Martel and Merle [46,47,48]. Martel, Merle and Tsai [51] showed the stability of the sum of N solitons in general gKdV equations. The recently written review paper [39] contains a more complete description of the remaining NLS case, and of the literature around this important subject.

If the background is not soliton like, there are also important results to mention. Delort [20, 21] considered the global existence and scattering of small solutions to quasilinear NLS and NLKG equations. Bambusi and Cuccagna [8] considered the NLKG dynamics around the zero state. Other recent results concerning the scattering of small solutions in NLKG equations can be found in [45, 70].

As for kink structures is referred, and their asymptotic stability, there are several works on this subject. Merle and Vega [54] showed asymptotic stability of the modified KdV kink (see also [7, 57]). Kopylova and Komech [33, 34] considered the case of kink structures in scalar field models with higher nonlinearities. The kink in the $\phi ^4$ model was treated in [36], as previously explained. Finally, see [67] for the final state of a variable coefficients $\phi ^4$ kink.

Since the emergence of this work in 2020, several works on the AS of the kink in scalar field models have appeared. Closely related to this work we mention Luhrmann and Schlag [43], who proved AS of the SG kink in a weighted space and odd data. Note that this data considers the odd resonance as well. Related to other kink solutions in different settings, we mention the recent works [15, 24, 35, 40, 44].

The results previously proved in [36, 37], and the ones in this paper, make strong use of the parity of the initial data. Here we also consider particular parity for initial data even if it is not preserved in time. The use of parity in wave like equations is not a new subject, but it has had some increasing use in the previous years. Kenig et al. [28] considered energy channels for wave equations in odd dimensions, where initial data of the form (f, 0) and (0, g) were considered, much in the spirit of the generator of the manifold ${\mathcal {M}}_{\eta ,0}$ considered in this paper. However, it seems here that our results are the first ones where this symmetry is not respected by the flow.

We believe that some of the results here proved can be extended to more general solutions of SG, for instance, to the case of 2-kinks, wobbling kinks, or the so-called modified KdV kinks [54, 57]. Concerning the first case, a 2-kink is a solution of SG that behaves as the elastic interaction between two kinks. In the SG case, this 2-kink solution is explicit, and given by (see Lamb [42, pp. 145–149],²):

$$\begin{aligned} \begin{aligned} {{\mathcal {R}}}(t,x;\beta )=&~{} 4\arctan \left( \beta \frac{\sinh (\gamma x)}{\cosh (\gamma \beta t)} \right) , \quad \beta \in (-1,1),\quad \beta \ne 0. \end{aligned} \end{aligned}$$

(1.11)

Here $\beta$ is the scaling factor (or speed), and $\gamma =(1-\beta ^2)^{-1/2}$ is the usual Lorentz factor. The 2-kink represents the interaction of two SG kinks with speeds $\pm \beta$, with limits as $x\rightarrow \pm \infty$ equal to $-2\pi$ and $2\pi$ respectively (i.e., ${{\mathcal {R}}}$ does not decay to zero). Note that ${{\mathcal {R}}}$ is odd in x and even in t. Also recall that this solution was proved to be stable [60]. In another direction, the extension of Theorem 1.1 to the case of breathers (2.1) is a challenging problem, first of all, because it will be necessary to identify the correct perturbative manifold for decay. See also [5, 6, 59] for other early stability results in the case of breathers and [58] for a simple account of stability results in integrable and nonintegrable equations.

1.2 Organization of this article

This article is organized as follows. Section 2 presents preliminaries that we will need along this paper, in particular, resonances in $\phi ^4$ and SG around kink solutions. Section 3 deals with the Bäcklund transformations in the SG case. Section 4 refers to the action of the BT on certain parity manifolds, and contains the proof of Theorem 1.2 (see Theorem 4.6). Section 5 is devoted to the study of the linearized BT around the SG and $\phi ^4$ kinks. Section 7 contains the construction of the initial data and the zero-momentum manifold ${\mathcal {M}}_{\eta ,0}$. Section 8 deals with the modulation of the evolution. Section 9 concerns with the lifting of the data around zero towards the kink solution, Sect. 10 focus on estimates on the shift parameters on the kink, and finally Sect. 11 is devoted to the end of proof of Theorem 6.1.

2 Breathers and Resonances in $\phi ^4$ and SG: AS of the Vacuum Solution Under Odd Perturbations

This section is devoted to introduce some notation and key elements for forthcoming sections. Of particular interest will be the following three ingredients: (i) the introduction of the $\phi ^4$ model and its spectral properties (internal modes, resonances, etc.), useful in Sect. 5; (ii) the SG spectral problem and its connection to the wobbling kink, also useful for Sect. 5, and finally, (iii) the SG breather and its relationship via parity manifolds with the asymptotic stability problem around the vacuum, a result from [37] shall play a key role on the proof of Theorem 1.1 (see Theorem 2.1). We start out by recalling the definition of breather.

2.1 Breathers

A breather is a periodic in time, localized solution of SG around zero. The most famous example of breather is given by the formula [42]

$$\begin{aligned} B_\beta (t,x)= 4\arctan \left( \frac{\beta }{\alpha } \frac{\sin (\alpha t)}{\cosh (\beta x)} \right) , \quad \alpha =\sqrt{1-\beta ^2}, \quad \beta \ne 0, \quad \beta \in (-1,1). \qquad \end{aligned}$$

(2.1)

See Fig. 2 for a picture of the breather at different times. This solution is stable [6, 60], and for $\beta$ small contradicts the asymptotic stability of the vacuum in the energy space. The reader may consult [3, 4] for more details on breather solutions and their stability.

Fig. 2

Breather solution (2.1) with $\beta =0.5$ at times $t=0$ (continuous curve), $t=2$ (dashed curve) and $t=6$ (dotted curve)

2.2 The $\phi ^4$ kink and the even resonance

A step forward towards the understanding of the long time dynamics around kink solutions in $1+1$ dimensions was given in [36], where the authors considered odd perturbations of the (odd) kink

$$\begin{aligned} H(x)=\tanh \left( \frac{x}{\sqrt{2}} \right) , \end{aligned}$$

(2.2)

in the $1+1$ dimensional $\phi ^4$-model of Quantum Field Physics [18, 36]

$$\begin{aligned} \phi _{tt}-\phi _{xx}- \phi +\phi ^3=0. \end{aligned}$$

(2.3)

This model, in its 3D version, is deeply related to the Higgs boson description [26], via symmetry breaking around the global minima $|\phi |=1$. Although non integrable, $\phi ^4$ is closely related to SG (1.1). More precisely, after subtraction of $\pi$, SG solutions $\phi$ solve

$$\begin{aligned} \phi _{tt}-\phi _{xx}- \sin \phi =0, \end{aligned}$$

(2.4)

for which $\phi ^4$ (2.3) is a third order approximation, up to a suitable scaling factor. A beautiful description of the duality $\phi ^4$-SG can be found in the monograph by Dauxois and Peyrard [18], previously mentioned. In particular, many properties related to SG are also studied in $\phi ^4$ and viceversa [18, 64, 65]. However, SG is integrable and $\phi ^4$ is not.

In [36] it was proved that (under the oddness assumption on the initial data $(\phi ,\phi _t)(t=0)$, which is preserved by the flow),

$$\begin{aligned} \begin{aligned}&\Vert (\phi ,\phi _t)(t=0) - (H,0)\Vert _{H^1\times L^2} <\eta \ll 1 \\&\quad \implies \lim _{t\rightarrow \pm \infty } \Vert (\phi ,\phi _t)(t) - (H,0)\Vert _{(H^1\times L^2)(I)} =0, \end{aligned} \end{aligned}$$

(2.5)

for any compact interval of space I. This result was showed using fine virial estimates allowing to control the existence of an internal mode associated to the linear operator $\mathcal L_H$ around H:

$$\begin{aligned} {\mathcal {L}}_H:= -\partial _x^2 -1 +3H^2 =-\partial _x^2 +2 - 3{\text {sech}}^2\left( \frac{x}{\sqrt{2}}\right) . \end{aligned}$$

(2.6)

Recall that an internal mode here is a positive eigenvalue below the continuum spectrum. Here the internal mode and its eigenvalue are [36]

$$\begin{aligned} Y_1:= {\text {sech}}\left( \frac{x}{\sqrt{2}}\right) \tanh \left( \frac{x}{\sqrt{2}}\right) , \quad \lambda =\frac{3}{2}. \end{aligned}$$

(2.7)

The extension of the result (2.5) to the case of general data is far from being simple, and remains a challenging question, mainly because of the existence of an spectral resonance (a generalized eigenfunction of ${\mathcal {L}}_H$ in $L^\infty \backslash L^2$) at $\lambda =2$, given by

$$\begin{aligned} {\mathcal {L}}_H \left( 1-\frac{3}{2}{\text {sech}}^2\left( \frac{x}{\sqrt{2}}\right) \right) = 2 \left( 1-\frac{3}{2}{\text {sech}}^2\left( \frac{x}{\sqrt{2}}\right) \right) . \end{aligned}$$

(2.8)

Moreover, this resonance is even, and that is really important for the proof in [36]. See that work for more details.

2.3 Wobbling kinks and the odd resonance

Coming back to SG (1.1), and making a quick comparison with $\phi ^4$, we can notice that the kink Q (connecting 0 and $2\pi$) has no parity property, and the subtraction of $\pi$ above mentioned leads to an equation (see (2.4)) which is not stable around the zero state.

Recall that we have said that a wobbling kink can be recast as kink + breather, and we know that breathers are even. However, this conception is a somehow misleading because of the following really surprising fact.

Indeed, contrary to $\phi ^4$, one can notice from (1.9) that wobbling kinks $W_\beta$ can be recast as (odd, odd) perturbations of the SG kink (Q, 0). Indeed, from (1.9) one has (see also Fig. 3)

$$\begin{aligned} W_\beta (t,x) -Q(x)= & {} 4\,\hbox {Arg}\Big ( \left( \cosh x \cosh (\beta x) -\beta \sinh x \sinh (\beta x) -\beta \cos (\alpha t) \right) \nonumber \\{} & {} + i \beta \left( \sinh x \cos (\alpha t) -\sinh (\beta x) \right) \Big ) \nonumber \\= & {} 4\arctan \left( \frac{\beta \left( \sinh x \cos (\alpha t) -\sinh (\beta x) \right) }{\cosh x \cosh (\beta x) -\beta \sinh x \sinh (\beta x) -\beta \cos (\alpha t) }\right) .\qquad \end{aligned}$$

(2.9)

Even more surprising, is the following fact: if the initial data $\vec \phi (t=0)=(Q,0) +({\widetilde{u}}_0, {\widetilde{s}}_0)$ are such that $({\widetilde{u}}_0, {\widetilde{s}}_0)$ are odd, then the Eq. (1.1) formally preserves this property: one has $\vec \phi (t)=(Q,0) + ({\widetilde{u}}, {\widetilde{s}})(t)$, with $({\widetilde{u}}, {\widetilde{s}})(t)$ odd for all time.³ The wobbling case is a direct example of this property, and it seems the unique parity property around the kink preserved by SG.

Fig. 3

Evolution of the wobbling kink (2.9) minus Q in the case $\beta =0.5$. On the left, $W_\beta (t,x) -Q(x)$ for times $t=0$ (continuous curve), $t=2$ (dashed curve) and $t=6$ (dotted curve). On the right panel, $\partial _tW_\beta (t,x)$ for times $t=0$ (continuous curve), $t=2$ (dashed curve) and $t=6$ (dotted curve). Note the oddness character of both graphs. Contrary to the common belief that wobbling kinks are “kink+breather” structures, the even character of the breather (2.1) is not preserved by the wobbling kink

Consequently, and in view of (2.9), no result like (2.5) can be proved in the SG case in the ($Q+$ odd, odd) data case.

Another key point to have in mind, related to the odd parity in SG, is that the linear operator around Q given by

$$\begin{aligned} {\mathcal {L}}_Q:= -\partial _x^2 +\cos Q =-\partial _x^2 +1-2{\text {sech}}^2 x, \end{aligned}$$

(2.10)

has no internal modes (unlike $\phi ^4$), but a resonance at $\lambda =1$ with odd generalized eigenfunction ($=\tanh x$) at the bottom of its continuum spectrum. This property is in concordance with the existence of an odd perturbation of the kink which does not decay to the kink (the wobbling kink), since the resonance function is also odd. To add more substance to this analogy, in the $\phi ^4$ case the resonance above mentioned is associated to an even generalized eigenfunction. Moreover, the resonance $\tanh x$ of period $\lambda =1$ can be formally found as the spatial part of the $\beta \rightarrow 0$ limit of the derivative of $W_\beta$:

$$\begin{aligned} L:=\frac{1}{4}\lim _{\beta \rightarrow 0} \partial _\beta W_\beta (t,x) = \tanh x \cos t. \end{aligned}$$

Note that L does not decay in time, and solves $L_{tt} +\mathcal L_Q (L)=0.$ See also (5.4) for more properties about L. A natural question that arises from this observation is the following: Is there any corresponding connection between the $\phi ^4$ resonance (2.8) and a hypothetical $\phi ^4$ wobbling kink? In the odd-data case, such a connection does not exist in the case of small perturbations [36], but here we talk about even data.

2.4 Breathers and the AS manifold structure around zero

A key feature of the breather solution $(B_\beta ,\partial _t B_\beta )$ in (2.1) is its parity character in space. Indeed, note that SG preserves (even, even) and (odd, odd) parities around zero, and breathers are even solutions of SG. Also consider the following parity manifolds:

$$\begin{aligned} \begin{aligned} {\mathcal {E}}_0:=&~{} H^1_e\times L^2_e, \\ {\mathcal {O}}_0:=&~{} H^1_o\times L^2_o. \end{aligned} \end{aligned}$$

(2.11)

Both manifolds are preserved by the SG flow. Also, ${\mathcal {E}}_0$ is related to the manifold of initial data under which the zero solution is not asymptotically stable, since $(B_\beta ,\partial _t B_\beta )(t=0)\in {\mathcal {E}}_0.$

In [37], it was proved that ${\mathcal {O}}_0$ is indeed related to the manifold where asymptotic stability holds:

Theorem 2.1

(See also Fig. 4). There exists $\varepsilon _0>0$ such that, if $(y,v)\in C(\mathbb {R};H^1_o\times L^2_o)$ is a globally defined odd solution to SG such that $\sup _{t\in \mathbb {R}} \Vert (y,v)(t)\Vert _{H^1\times L^2} <\varepsilon _0$, then for any compact interval $I \subset \mathbb {R}$ one has

$$\begin{aligned} \lim _{t\rightarrow \pm \infty } \Vert (y,v)(t)\Vert _{(H^1\times L^2)(I)} =0. \end{aligned}$$

(2.12)

Moreover, there is integration in time of local norms: for any small $c_1>0$ fixed,

$$\begin{aligned} \int \int e^{-c_1|x|} (y_x^2 +y^2+ v^2)(t,x)dxdt \lesssim \varepsilon _0^2. \end{aligned}$$

(2.13)

Remark 2.1

Estimate (2.13) will be useful to prove Theorem 1.1, more precisely, the convergence result in Theorem 6.1, Eq. (6.4) (see Sect. 11, Step 4).

Fig. 4

A schematic representation of the initial-data manifolds ${\mathcal {E}}_0$ and ${\mathcal {O}}_0$ in (2.11). Here (o, o) and (e, e) mean odd-odd and even-even data in $H^1\times L^2$. The horizontal dark region represents a submanifold of small initial data for which no asymptotic stability (AS) around zero is present. The breather family $(B_\beta ,B_{\beta ,t})$ (for any small $\beta$) is part of this manifold (but it is not known yet if it is the only counterexample to AS). On the other hand, the vertical submanifold is related to AS thanks to Theorem 2.1, it has zero momentum P (see (1.3)) and it is part of the region in the energy space where AS is present. Finally, note that both manifolds ${\mathcal {E}}_0$ and ${\mathcal {O}}_0$ are preserved by the SG flow, intersect themselves only at the origin, and they are $H^1\times L^2$ orthogonal

3 Bäcklund Transformations

The previous discussion, mesmerizing in terms of allowing us to extend the techniques used in [36] to the SG case, opens a new window of possibilities where asymptotic stability could hold, this time in the complement of the odd parity manifold (note how different are parities between $\phi ^4$ and SG). But first we need to introduce the SG Bäcklund Transformations (BT). For more details, see e.g. [32]-[60].

3.1 Definitions

Let us write (1.1) in matrix form, that is $\vec \phi =(\phi ,\phi _t)=(\phi _0,\phi _1)$, in such a form that (1.1) reads now

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t \phi _0 =\phi _1,\\ \partial _t \phi _1 =\partial _x^2 \phi _0 -\sin \phi _0. \end{array}\right. } \end{aligned}$$

(3.1)

Now we introduce the Bäcklund transformation (BT) that we will use in this article. Recall that $H^1_{sin} = \{u\in L^\infty ~: ~ u_x\in L^2, ~ \sin (\frac{u}{2})\in L^2 \}$ represents the energy space introduced by de Laire and Gravejat [19]. Clearly, and restricted to our setting, solutions of the form (Q, 0) plus perturbations in $H^1\times L^2$ are included in this space..

Definition 3.1

(Bäcklund Transformation). Let $a\in \mathbb {C}$ be fixed. Let $\vec \phi =(\phi _0,\phi _1)(x)$ be a function defined in ${ H^1_{sin}(\mathbb {C})\times L^2(\mathbb {C})}$. We will say that $\vec \varphi$ in ${ H^1_{sin}(\mathbb {C})\times L^2(\mathbb {C})}$ is a Bäcklund transformation (BT) of $\vec \phi$ by the parameter a, denoted

$$\begin{aligned} \, \mathbb {B}(\vec \phi ) \xrightarrow {\ a \ }{\vec \varphi }, \end{aligned}$$

(3.2)

if the triple $(\vec \phi ,\vec \varphi ,a)$ satisfies the following equations, for all $x\in \mathbb {R}$:

$$\begin{aligned} \varphi _{0,x}-\phi _1&= \dfrac{1}{a}\sin \left( \dfrac{\varphi _0+\phi _0}{2}\right) +a\sin \left( \dfrac{\varphi _0-\phi _0}{2}\right) , \end{aligned}$$

(3.3)

$$\begin{aligned} \varphi _1-\phi _{0,x}&= \dfrac{1}{a}\sin \left( \dfrac{\varphi _0+\phi _0}{2}\right) -a\sin \left( \dfrac{\varphi _0-\phi _0}{2}\right) . \end{aligned}$$

(3.4)

The following result appears in an unpublished result by Nakanishi et al, justifying the introduction of the BT (3.3)–(3.4). Just denote

$$\begin{aligned} C_+:=\tfrac{1}{2a}\cos \left( \frac{\varphi _0 + \phi _0}{2} \right) ,\quad C_-:=\tfrac{a}{2}\cos \left( \frac{\varphi _0 - \phi _0}{2} \right) , \end{aligned}$$

(3.5)

and

$$\begin{aligned} S_+:=\tfrac{1}{a}\sin \left( \frac{\varphi _0+\phi _0}{2}\right) , \quad S_-:=a\sin \left( \frac{\varphi _0-\phi _0}{2}\right) . \end{aligned}$$

(3.6)

Lemma 3.2

(Nakanishi, [61]). Assume that $\vec {\phi }_0$ and $\vec {\varphi }_0$ are real-valued and related via a BT (3.3)–(3.4) with parameter $a\in \mathbb {R}$, and let $\phi (t)$ and $\varphi (t)$ global solutions to SG (3.1) with initial data $\phi _0$ and $\varphi _0$ respectively. Then $\phi (t)$ and $\varphi (t)$ are related via a BT of parameter a for all time.

Remark 3.1

The use of the Bäcklund transformation is not new in the field of integrable stability theory. The reader can consult the monograph [53] for a detailed introduction to the subject. In recent years, several works dealing with stability of solitonic structures via Bäcklund transformations have appeared: Hoffman and Wayne [27], Mizumachi and Pelinovsky [4, 5, 56, 60], but its use as a method for proving asymptotic stability results in this paper seems to be new in nonlinear wave like equations.

Proof of Lemma 3.2

Note that (3.3)–(3.4) can be rewritten as $\vec u=(u_0,u_1)=(0,0)$, where

$$\begin{aligned} {\left\{ \begin{array}{ll} u_0:=\partial _x \varphi _0 - \phi _1-S_+-S_-,\\ u_1:= \varphi _1 -\partial _x\phi _0 - S_+ + S_-. \end{array}\right. } \end{aligned}$$

(3.7)

With this definition of $\vec u$, we have

$$\begin{aligned} \begin{aligned}&\partial _tu_0=\partial _t\partial _x \varphi _0 - \partial _t\phi _1-C_+\partial _t\varphi _0-C_-\partial _t\phi _0,\\&\partial _tu_1=\partial _t\varphi _1 -\partial _t\partial _x\phi _0 - C_-\partial _t\varphi _0 - C_+\partial _t\phi _0, \end{aligned} \end{aligned}$$

(3.8)

where $C_+, C_-$ were introduced in (3.5). Now, using that

$$\begin{aligned} 2(C_+S_- + C_-S_+) = \sin \varphi _0, \quad 2(C_-S_+ - C_+S_-) = \sin \phi _0, \end{aligned}$$

(3.9)

we have for $C^\pm = C_+ \pm C_-$,

$$\begin{aligned} \begin{aligned}&\partial _xu_0=\partial _x^2\varphi _0- \sin \varphi _0 - \partial _x\phi _1 - C^+(u_0 + \phi _1) - C^-(\varphi _1 - u_1), \\&\partial _xu_1=-\partial _x^2\phi _0 + \sin \phi _0 + \partial _x\varphi _1 - C^-(u_0 + \phi _1) - C^+(\varphi _1 - u_1). \end{aligned} \end{aligned}$$

(3.10)

Finally we obtain

$$\begin{aligned} \begin{aligned}&(\partial _t+C^-)u_1-(\partial _x+C^+)u_0\\&\quad =[\partial _t\varphi _1 - \partial ^2_x\varphi _0 + \sin \varphi _0 - C^-(\partial _t\varphi _0 - \varphi _1)] - (\partial _x + C^+)(\partial _t\phi _0 - \phi _1)\\&(\partial _t-C^-)u_0-(\partial _x-C^+)u_1\\&\quad =-[\partial _t\phi _1 - \partial ^2_x\phi _0 + \sin \phi _1 + C^-(\partial _t\phi _0 - \phi _1)] + (\partial _x - C^+)(\partial _t\varphi _0 - \varphi _1). \end{aligned} \end{aligned}$$

(3.11)

Since $\vec \phi$ and $\vec \varphi$ satisfy SG in vectorial form, then injecting them into (3.11) yields

$$\begin{aligned} {\left\{ \begin{array}{ll} (\partial _t+C^-)u_1-(\partial _x+C^{+} )u_0=0,\\ (\partial _t-C^-)u_0-(\partial _x-C^+)u_1=0,\\ \end{array}\right. } \end{aligned}$$

(3.12)

which implies

$$\begin{aligned} \begin{aligned} \tfrac{d}{dt}\tfrac{1}{2}\Vert \vec u\Vert _{L^2}^2&=\langle \partial _tu_0|u_0\rangle + \langle \partial _tu_1|u_1\rangle \\&=\langle (\partial _x-C^+ )u_1+C^-u_0|u_1\rangle +\langle (\partial _x+C^+)u_0- C^-u_1|u_0\rangle \\&=\langle C^+||u_0|^2+|u_1|^2\rangle \le \Vert C^+\Vert _{\infty }\Vert \vec u\Vert _{L^2}^2. \end{aligned} \end{aligned}$$

(3.13)

Therefore, the Bäcklund relation (3.3)–(3.4) or $u = 0$ is propagated to all $t \in \mathbb {R}$. $\square$

We finish this subsection by considering Bäcklund functionals, in the sense considered in [4, 60].

Definition 3.3

(Bäcklund functionals). Let $(\varphi _0,\,\varphi _1,\,\phi _0,\,\phi _1,\,a)$ be data in a space $X(\mathbb {R})$ to be chosen later. Let us define the functional with vector values ${\mathcal {F}}:=({\mathcal {F}}_1,{\mathcal {F}}_2)$, where ${\mathcal {F}}={\mathcal {F}}(\varphi _0,\,\varphi _1,\,\phi _0,\,\phi _1,\,a) \in L^2(\mathbb {R}) \times L^2(\mathbb {R})$, given by the system:

$$\begin{aligned} {\mathcal {F}}_1 \big (\varphi _0,\varphi _1,\phi _0,\phi _1,a\big ) := \varphi _{0,x}-\phi _1 - \dfrac{1}{a}\sin \left( \dfrac{\varphi _0+\phi _0}{2}\right) -a\sin \left( \dfrac{\varphi _0-\phi _0}{2}\right) , \end{aligned}$$

(3.14)

$$\begin{aligned} {\mathcal {F}}_2 \big (\varphi _0,\,\varphi _1,\,\phi _0,\,\phi _1,\,a\big ) := \varphi _1-\phi _{0,x}- \dfrac{1}{a}\sin \left( \dfrac{\varphi _0+\phi _0}{2}\right) +a\sin \left( \dfrac{\varphi _0-\phi _0}{2}\right) . \end{aligned}$$

(3.15)

The choice of the space $X(\mathbb {R})$ heavily depends on the considered background solution. In our case, since Q does not belong to $L^2$, we will consider a different space for ${\mathcal {F}}$.

3.2 Kink profiles

Here we introduce the notion of kink profiles. See [6, 60] for more details.

Definition 3.4

(Kink profiles). Let $\beta \in (-1,1)$, $\beta \ne 0$, and $x_0\in \mathbb {R}$ be fixed parameters. We define the real-valued kink profile $\vec Q:=(Q,Q_t)$ with speed $\beta$ as

$$\begin{aligned} Q(x)&:= Q(x; \beta , x_0)=4\arctan \big (e^{\gamma (x - x_0)}\big ), \qquad \gamma := (1-\beta ^2)^{-1/2}, \end{aligned}$$

(3.16)

$$\begin{aligned} Q_x(x)&:= Q_x(x; \beta ,x_0)= \frac{4 \gamma e^{\gamma (x - x_0)}}{1+ e^{2\gamma (x - x_0)}} = \frac{2\gamma }{\cosh (\gamma (x-x_0))}, \end{aligned}$$

(3.17)

and

$$\begin{aligned} Q_t(x):= Q_t(x; \beta ,x_0)= \frac{-4\beta \gamma e^{\gamma (x - x_0)}}{1+ e^{2\gamma (x - x_0)}} = \frac{-2\beta \gamma }{\cosh (\gamma (x-x_0))}. \end{aligned}$$

(3.18)

Remark 3.2

(See also [60]). The profile $(Q,Q_t)$ is the standard profile associated to the kink solution (1.5). Although $(Q,Q_t)$ is not an exact solution of (3.7), it can be understood as follows: for each $(t,x)\in \mathbb {R}^2$, $(t,x) \mapsto (Q,Q_t)(x;\beta ,x_0{+}\beta t)$ is an exact solution of (3.1), moving with speed $\beta$.

In what follows, we prove connections between kink profiles and the zero solution in SG. Although some of these results are standard, recall that we prove them not only for exact solutions, but also for profiles which are not exact solutions of SG.

Lemma 3.5

(Kink as BT of zero, [60]). Let $(Q, Q_t)$ be a SG kink profile with scaling parameter $\beta \in (-1,1)$, $\beta \ne 0$, and shift $x_0$, see Definition 3.4. Then, for each $x\in \mathbb {R}$, $(Q, Q_t)$ is a BT of the origin (0, 0) with parameter

$$\begin{aligned} a= a(\beta ):= \left( \frac{1+\beta }{1-\beta }\right) ^{1/2}. \end{aligned}$$

(3.19)

That is,

$$\begin{aligned} Q_x = \ \dfrac{1}{a}\sin \Big (\dfrac{ Q}{2}\Big )+a\,\sin \Big (\dfrac{ Q}{2}\Big ), \qquad&Q_t = \ \dfrac{1}{a}\sin \Big (\dfrac{Q}{2}\Big )-a\,\sin \Big (\dfrac{Q}{2}\Big ). \end{aligned}$$

(3.20)

Note that (3.20) can be read as ${\mathcal {F}}(Q, Q_t,0,0,a)=0$, in terms of (3.14)–(3.15).

Remark 3.3

In (3.2), the parameter $a\in \mathbb {R}$ links $\vec \phi$ to $\vec \varphi$. In this paper, thanks to Lemma 3.5 we will connect the zero state with the kink state using this transformation, and then we will perturb both states (Theorems 1.1 and 6.1). However, since we know that asymptotic stability does not hold in the (odd, odd) regime (see Sect. 1.1), what we need is to ensure that our initial perturbation of the kink $\vec \varphi$, which will be of type (odd, even), could lead to a perturbation of the zero state $\vec \phi$ of type (odd, odd). And we need (odd, odd) data because decay of small data for SG occurs in this particular setting [37]. For instance, if the data is even, the breather (2.1) is a counterexample to decay, see Sect. 2.4 for more details.

Before proving its existence, we need some results about the parity properties satisfied by the Bäcklund functionals.

3.3 Parity properties associated to Bäcklund functionals

Recall the kink profile Q introduced in (3.16). Because of parity reasons, we will need a slight modification of Q, denoted ${\widetilde{Q}}$, and simply defined as

$$\begin{aligned} {\widetilde{Q}}(x;\beta ,x_0):= Q(x;\beta ,x_0) -\pi ,\qquad \widetilde{Q}_t(x;\beta ,x_0):= Q_t(x;\beta ,x_0). \end{aligned}$$

(3.21)

Note that ${\widetilde{Q}}$ is now odd in $x+x_0$, while $\widetilde{Q}_t$ is even, except when $\beta =0$. In such a case, it is also odd.

Lemma 3.6

(Parity properties for ${\mathcal {F}}$). Let $(Q, Q_t)=(Q,Q_t)(x;\beta ,x_0)$ be a kink profile of parameters $\beta \in (-1,1)$ and $x_0\in \mathbb {R}$. Consider the associated modified kink profile $({\widetilde{Q}},{\widetilde{Q}}_t)=({\widetilde{Q}},\widetilde{Q}_t)(x;\beta ,x_0)$ introduced in (3.21). Let also $({\widetilde{u}}_{0},{\widetilde{s}}_0)\in H^1\times L^2$ and $(y_0,v_0) \in H^1\times L^2$ be given functions. Finally, consider $a=a(\beta )$ as defined in (3.19), and $\delta \in \mathbb {R}$ sufficiently small. Then the following are satisfied:

• (a) One has from (3.14) and (3.15)

  $$\begin{aligned}&{\mathcal {F}}_1 \big (Q+{\widetilde{u}}_0, Q_t +{\widetilde{s}}_0 , y_0,v_0, a + \delta \big ) = \widetilde{{\mathcal {F}}}_1({\widetilde{u}}_0,{\widetilde{s}}_0,y_0,v_0,\delta ) \nonumber \\&\quad := {\widetilde{Q}}_x + {\widetilde{u}}_{0,x} -v_0 - \dfrac{1}{a+\delta }\cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}}_0 + y_0}{2}\right) -(a+\delta )\cos \left( \dfrac{{\widetilde{Q}} +\widetilde{u}_0-y_0}{2}\right) , \end{aligned}$$

  (3.22)
  $$\begin{aligned}&{\mathcal {F}}_2 \big (Q+{\widetilde{u}}_0, Q_t +{\widetilde{s}}_0 , y_0,v_0, a + \delta \big ) = \widetilde{{\mathcal {F}}}_2({\widetilde{u}}_0,{\widetilde{s}}_0,y_0,v_0,\delta ) \nonumber \\&\quad := {\widetilde{Q}}_t + {\widetilde{s}}_{0} -y_{0,x} - \dfrac{1}{a+\delta }\cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}}_0 + y_0}{2}\right) + (a+\delta )\cos \left( \dfrac{{\widetilde{Q}} +\widetilde{u}_0-y_0}{2}\right) . \end{aligned}$$

  (3.23)

• (b) If now ${\widetilde{u}}_{0},y_0\in H^1_o$ (see definitions in (1.10)), and $x_0=0$, then

  $$\begin{aligned} \cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}}_0 \pm y_0}{2}\right) \end{aligned}$$

  are even functions, with $\lim _{x\rightarrow \pm \infty } \cos \left( \frac{{\widetilde{Q}} +{\widetilde{u}}_0 \pm y_0}{2}\right) = \lim _{x\rightarrow \pm \infty }\cos \left( \frac{{\widetilde{Q}}}{2}\right) =0$. Moreover, both functions belong to $H^1_e$.

• (c) If now $x_0=0$, $({\widetilde{u}}_{0},{\widetilde{s}}_0)\in H^1_o\times L^2_e$ and $(y_0,v_0) \in H^1_o\times L^2_e$, then

  $$\begin{aligned} \widetilde{{\mathcal {F}}}_1({\widetilde{u}}_0,\widetilde{s}_0,y_0,v_0,\delta ) \in L^2_e,\quad \widetilde{\mathcal F}_2({\widetilde{u}}_0,{\widetilde{s}}_0,y_0,v_0,\delta ) \in L^2_e. \end{aligned}$$

  Consequently, $\widetilde{{\mathcal {F}}}:= (\widetilde{{\mathcal {F}}}_1, \widetilde{{\mathcal {F}}}_2)$ is a well-defined functional from $X(\mathbb {R}):= H^1_o\times L^2_e \times H^1_o\times L^2_e\times \mathbb {R}$ into $L^2_e\times L^2_e$, provided $\delta$ is chosen such that $a+\delta \ne 0$. It is also a $C^1$ functional among the considered spaces.

• (d) Assume $x_0=0$, $\beta =0$, $a=1$ and $\delta =0$. Then, if $({\widetilde{u}},{\widetilde{s}})\in H^1_o\times L^2_o$ and $(y,v) \in H^1_e\times L^2_e$, then

  $$\begin{aligned} \widetilde{{\mathcal {F}}}_1({\widetilde{u}},{\widetilde{s}},y,v, 0) \in L^2_e,\quad \widetilde{{\mathcal {F}}}_2({\widetilde{u}},\widetilde{s},y,v,0) \in L^2_o. \end{aligned}$$

  Consequently, abusing of notation, $\widetilde{{\mathcal {F}}}:= (\widetilde{{\mathcal {F}}}_1, \widetilde{{\mathcal {F}}}_2)$ is a well-defined functional from $X_0(\mathbb {R}):= H^1_o\times L^2_o \times H^1_e\times L^2_e$ into $L^2_e\times L^2_o$. It is also a $C^1$ functional among the considered spaces.

Proof

Equations (3.22)–(3.23) are just a rewrite of (3.14)–(3.15). The equality of the limit in statement (b) is a consequence of the Sobolev embedding for $H^1(\mathbb {R})$ and formula (3.24) below. On the other hand, the fact that $\cos (\tfrac{ \widetilde{Q}+\widetilde{u}_0\pm y_0}{2})$ belongs to $H^1_e$ follows from basic trigonometric identities, the hypothesis ${\widetilde{u}}_0,y_0\in H^1_o$ and the following identity:

$$\begin{aligned} \cos \left( \dfrac{\widetilde{Q}}{2}\right) ={\text {sech}}(\gamma (x+x_0)). \end{aligned}$$

(3.24)

Statement (c) is a direct consequence of the definitions (3.22)–(3.23) and part (b) of this Lemma (for the parity property).

Finally, (d) is consequence of ${\widetilde{Q}}_t=0$ under $\beta =0$ ($a=1$ in (3.19)), ${\widetilde{Q}}_x$ even if $x_0=0$, and the formulae

$$\begin{aligned} \begin{aligned}&~{} \widetilde{{\mathcal {F}}}_1({\widetilde{u}},{\widetilde{s}},y,v,0) = {\widetilde{Q}}_x + {\widetilde{u}}_{x} -v - \cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}} + y}{2}\right) -\cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}}-y}{2}\right) \in L^2_e, \\&~{} \widetilde{{\mathcal {F}}}_2({\widetilde{u}},{\widetilde{s}},y,v,0) = {\widetilde{s}} -y_{x} - \cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}} + y}{2}\right) +\cos \left( \dfrac{{\widetilde{Q}} +\widetilde{u}-y}{2}\right) \in L^2_o, \end{aligned} \end{aligned}$$

valid for $({\widetilde{u}},{\widetilde{s}},y,v) \in H^1_o\times L^2_o \times H^1_e\times L^2_e.$ Indeed, note that ${\widetilde{Q}}$ is odd, and

$$\begin{aligned} \cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}} + y}{2}\right) + \cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}}-y}{2}\right) =2\cos \left( \dfrac{{\widetilde{Q}} +\widetilde{u}}{2}\right) \cos \left( \dfrac{y}{2}\right) \in L_e^2, \end{aligned}$$

and

$$\begin{aligned} \cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}} + y}{2}\right) - \cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}}-y}{2}\right) =-2\sin \left( \dfrac{{\widetilde{Q}} +\widetilde{u}}{2}\right) \sin \left( \dfrac{y}{2}\right) \in L_o^2, \end{aligned}$$

thanks to (3.24). $\square$

4 The action of BT on Parity Manifolds: Proof of Theorem 1.2

4.1 BT and parity manifolds around 0 and Q

In what follows, we intend to get a better understanding of the image of the manifolds ${\mathcal {E}}_0$ and ${\mathcal {O}}_0$ under the Bäcklund Transformation (3.3)–(3.4), at least in the case of small data. Along this section, we will rigorously justify Fig. 5, continuation of Fig. 4. Our first result is the following:

Proposition 4.1

Every sufficiently small $H^1_e\times L_e^2$ perturbation of the vacuum state leads to a unique sufficiently small $H^1_o\times L_o^2$ perturbation of the SG static kink via a Bäcklund transformation.

Proof

See the appendix, Section A $\square$

Remark 4.1

In terms of the terminology introduced in [60], the previous result is a lifting lemma. We lift data from a neighborhood of zero towards data near the static kink. In [27, 60], such a property could not hold without the addition of an extra orthogonality condition around the kink solution (see Sect. 9 for another example). This extra condition was ensured via modulation techniques. Here we do not need such an additional condition because of the parities assumptions involved in the proof. It turns out that under (even, even) data around zero (e.g. small breathers), it is always possible to uniquely solve the BT leading to (odd, odd) data around the kink (e.g. the wobbling kink), no matter the time $t\in \mathbb {R}$ at which the lifting is performed.

Actually, the more impressing fact here is that the reciprocal of the previous result is also true.

Proposition 4.2

Every sufficiently small $H^1_o\times L_o^2$ perturbation of the SG static kink leads to a unique sufficiently small $H^1_e\times L_e^2$ perturbation of the vacuum state.

Remark 4.2

In the terminology of [60], Proposition 4.2 corresponds to a descent from a vicinity of the kink towards a corresponding vicinity of the zero solution. This property was previously established in [60] in the case of breathers, 2-kinks and kink-antikinks. However, it was always necessary to adjust the parameter $\delta$ in the BT (3.22)–(3.23) to ensure this property. Here, from the proof it will be clear that, under the correct parity conditions, such an additional adjustment is not necessary.

Remark 4.3

Note that if perturbations of the SG kink are uniformly bounded in time, the proof of Proposition 4.2 will ensure uniform bounds in time for perturbations of the zero solution as well.

Proof of Proposition 4.2

See the appendix, Section B. $\square$

Remark 4.4

As a consequence of Propositions 4.1 and 4.2, the section along the horizontal axis on the left panel in Fig. 5 is uniquely related to a section along the vertical axis on the right of the same figure.

Propositions 4.1 and 4.2 motivate the introduction of the first manifolds of initial data around the SG kink considered in this paper. Let

$$\begin{aligned} \begin{aligned} {\mathcal {O}}_Q:=&~{} \{ (Q+{\widetilde{u}}_0, {\widetilde{s}}_0) ~: ~ ({\widetilde{u}}_0, {\widetilde{s}}_0) \in {\mathcal {O}}_0= H^1_o\times L^2_o \}, \\ {\mathcal {E}}_Q:=&~{}\{ (Q+{\widetilde{u}}_0, {\widetilde{s}}_0) ~: ~ ({\widetilde{u}}_0, {\widetilde{s}}_0) \in {\mathcal {E}}_0= H^1_e\times L^2_e \}, \\ \mathcal{O}\mathcal{E}_Q:=&~{} \{ (Q+{\widetilde{u}}_0, {\widetilde{s}}_0) ~: ~ ({\widetilde{u}}_0, {\widetilde{s}}_0)\in H^1_o\times L^2_e \}. \end{aligned} \end{aligned}$$

(4.1)

Recall that only the first manifold is preserved by the flow in time, and that the wobbling kink $(W_\beta , \partial _t W_\beta )(t)$ in (1.9) belongs to ${\mathcal {O}}_Q$. For some reasons to be explained below, the manifold $\mathcal{O}\mathcal{E}_Q$ is well-suited for our problem, unlike an (even, even) manifold.

Where is the wobbling kink in Propositions 4.1 and 4.2? That is the purpose of the following paragraph.

4.2 Breather-Wobbling kink’s connection

Now we need the following classic connection between breathers and wobbling kinks, see e.g [16].

Lemma 4.3

Let $\beta \in (-1,1).$ Then breathers $B_\beta$ (2.1) and wobbling kinks $W_\beta$ (1.9) are connected via a BT of parameter $a=1$. More precisely, for all $t\in \mathbb {R}$,

$$\begin{aligned} \partial _x W_\beta - \partial _t B_\beta&= \sin \left( \dfrac{W_\beta +B_\beta }{2}\right) + \sin \left( \dfrac{W_\beta -B_\beta }{2}\right) , \end{aligned}$$

(4.2)

$$\begin{aligned} \partial _t W_\beta -\partial _x B_\beta&= \sin \left( \dfrac{W_\beta +B_\beta }{2}\right) - \sin \left( \dfrac{W_\beta - B_\beta }{2}\right) . \end{aligned}$$

(4.3)

Proof

The proof is somehow standard, but we include it in Appendix C. $\square$

Remark 4.5

Lemma 4.3 also works if breathers and kinks are perturbed, at the same time, by parameters $t\mapsto t+ x_1$ and $x\mapsto x+ x_2$, with $x_1,x_2$ free real parameters. This is just a consequence of the invariance of the Eq. (1.1) under space and time translations.

Remark 4.6

Lemma 4.3 is simple but it reveals a deep property of wobbling kinks. They are not immediately related to the zero solution (which is asymptotically stable under odd perturbations) as the breather was in [60]. Instead, even if they are odd solutions, wobbling kinks are related via BT to SG breathers, which are even nondecaying functions. The change in parity is a key element present in BT.

The following deep connections between the manifolds ${\mathcal {O}}_Q$ and ${\mathcal {E}}_0$ in (4.1), stated in Propositions 4.4 and 4.5, will be key ingredients for the proof of Theorem 1.2.

Proposition 4.4

Every sufficiently small $H^1_e\times L_e^2$ perturbation of the SG breather leads to a unique sufficiently small $H^1_o\times L_o^2$ perturbation of the SG wobbling kink via a Bäcklund transformation.

Remark 4.7

Once again, because of the parity assumptions, we will be able to prove this lifting result without using any type of modulation on the data. Compare with Proposition 4.1, which satisfies similar properties, but around the kink solution. This time, we will prove lifting around the wobbling kink.

Proof

We follow the proof of Proposition 4.1 very closely, but this time we need different Bäcklund functionals, as well as new parity properties not stated in Lemma 3.6 because of their lack of simplicity.

Without loss of generality we assume that $\beta$ is positive. For the sake of simplicity from now on we shall denote by $\widetilde{W}_\beta$ the function

$$\begin{aligned} {\widetilde{W}}_\beta :=W_\beta -\pi , \end{aligned}$$

(4.4)

which is odd in space. Now, let $(y,v)\in H^1_e\times L^2_e$ be small enough given perturbations and let $t\in \mathbb {R}$ fixed. Consider the system of perturbed equations given by the Bäcklund functionals (4.2)–(4.3)

$$\begin{aligned} \begin{aligned} {\mathcal {F}}_1&:={\widetilde{W}}_{\beta ,x} + {\widetilde{u}}_x-B_{\beta ,t} -v- \cos \left( \frac{{\widetilde{W}}_\beta + {\widetilde{u}} +B_\beta +y}{2}\right) -\cos \left( \frac{{\widetilde{W}}_\beta \!+\! {\widetilde{u}}\! -\!B_\beta -y}{2}\right) , \\ {\mathcal {F}}_2&:={\widetilde{W}}_{\beta ,t} + {\widetilde{s}} -B_{\beta ,x} -y_x - \cos \left( \frac{{\widetilde{W}}_\beta + {\widetilde{u}} +B_\beta +y}{2}\right) +\cos \left( \frac{{\widetilde{W}}_\beta + {\widetilde{u}} -B_\beta -y}{2}\right) , \end{aligned} \end{aligned}$$

(4.5)

where ${\mathcal {F}}_i={\mathcal {F}}_i(y,v,{\widetilde{u}},{\widetilde{s}})$ for $i=1,2$. Notice that for any given triplet $(y,v,\widetilde{u})\in H^1_e\times L^2_e\times H^1_o$, equation ${\mathcal {F}}_2\equiv 0$ is trivially solvable for $\widetilde{s}(\cdot )$ and defines a function in $L^2_o$. On the other hand,

$$\begin{aligned} {\mathcal {F}}_1:H^1_e(\mathbb {R})\times L^2_e(\mathbb {R})\times H^1_o(\mathbb {R})\times L^2_o(\mathbb {R}) \longrightarrow L^2_e(\mathbb {R}), \end{aligned}$$

defines a ${\mathcal {C}}^1$ functional in a neighborhood of zero and due to Lemma 4.3 we have ${\mathcal {F}}_1(0,0,0,0)\equiv 0$. Therefore, in order to conclude the proof it is enough to show that the Gâteaux derivative of ${\mathcal {F}}_1$ defines a invertible bounded linear operator with continuous inverse. In fact, notice that linearizing directly on the definition of ${\mathcal {F}}_1$ above and by using basic trigonometric identities we are lead to solve

$$\begin{aligned} {\widetilde{u}}_x = -\sin \left( \frac{{\widetilde{W}}_\beta }{2}\right) \cos \left( \frac{B_\beta }{2}\right) {\widetilde{u}} +f, \, \hbox { for some }\, f\in L^2_e. \end{aligned}$$

(4.6)

Now, in order to solve Eq. (4.6), we define $\mu _\beta (x)$ to be the solution of

$$\begin{aligned} \begin{aligned} \mu _{\beta ,x}-\sin \left( \dfrac{\widetilde{W}_\beta }{2}\right) \cos \left( \dfrac{B_\beta }{2}\right) \mu _\beta =&~{} 0, \\ \hbox { that is } \ \mu _\beta (x)=&~{} \exp \left( \int _0^x \sin \left( \dfrac{\widetilde{W}_\beta }{2}\right) \cos \left( \dfrac{B_\beta }{2}\right) \right) . \end{aligned} \end{aligned}$$

At this stage it is important to point out that $\mu _\beta (x)$ is an even function. Moreover, notice that by using the definitions of $\widetilde{W}_\beta$ and $B_\beta$ in (4.4)–(2.1) we conclude that there exists $R>1$ sufficiently large such that

$$\begin{aligned} \hbox {for all } \, x>R,&\quad \sin \left( \frac{{\widetilde{W}}_\beta }{2}\right) \cos \left( \frac{B_\beta }{2}\right) \sim 1- e^{- \beta x}, \end{aligned}$$

(4.7)

$$\begin{aligned} \hbox {and for all } \, x<-R,&\quad \sin \left( \frac{{\widetilde{W}}_\beta }{2}\right) \cos \left( \frac{B_\beta }{2}\right) \sim -1+ e^{ \beta x}. \end{aligned}$$

(4.8)

Therefore, we conclude that $\mu _\beta \rightarrow +\infty$ as $x\rightarrow \pm \infty$. On the other hand, due to the fact that both $\mu _\beta$ and f are even functions, we conclude that there is only one odd function solving (4.6), which is given by

$$\begin{aligned} {\widetilde{u}}(x)=\dfrac{1}{\mu _\beta (x)}\int _{0}^x \mu _\beta (z) f(z)dz. \end{aligned}$$

(4.9)

Finally, by using Young’s inequality, the explicit form of ${{\widetilde{u}}}$ and the exponential growth of $\mu _\beta$ given by (4.7)–(4.8) it is easy to check that

$$\begin{aligned} \Vert {\widetilde{u}}\Vert _{L^2(\mathbb {R})}\lesssim \Vert f\Vert _{L^2(\mathbb {R})}. \end{aligned}$$

We refer to [60] Section 6 for a complete proof of the latter inequality in a similar context. Notice that in order to conclude that ${\widetilde{u}}\in H^1_o$ it only remains to prove that ${\widetilde{u}}_x\in L^2$. Nevertheless, this is a direct consequence of the explicit form of ${\widetilde{u}}$ in (4.9) and the previous analysis. Therefore, we conclude the proof by applying the Implicit Function Theorem. $\square$

An even more striking property is that under no extra hypothesis we are able to prove a reciprocal theorem.

Proposition 4.5

Every sufficiently small $H^1_o\times L_o^2$ perturbation of the wobbling kink leads to a unique sufficiently small $H^1_e\times L_e^2$ perturbation of the SG breather.

Remark 4.8

The fact that we do not need any extra hypothesis to prove this theorem is (again) a consequence of restricting ourselves to $H^1_o\times L^2_o$ perturbations. An analogous statement for perturbations in the whole space $H^1\times L^2$ would require, for instance, some orthogonality condition hypothesis over the perturbations.

Proof

We shall closely follow the ideas of the proof of Proposition 4.4, with some key differences. Without loss of generality we assume that $\beta$ is positive. With $\widetilde{W}_\beta$ as in (4.4), let now $({\widetilde{u},\widetilde{s}})\in H^1_o\times L^2_o$ be small enough given perturbations and let $t\in \mathbb {R}$ fixed. Consider once again the system of perturbed equations given by the Bäcklund functionals (4.5):

$$\begin{aligned} \begin{aligned} {\mathcal {F}}_1&:={\widetilde{W}}_{\beta ,x} +\widetilde{u}_x-B_{\beta ,t} -v- \cos \left( \frac{{\widetilde{W}}_\beta + {\widetilde{u}} +B_\beta +y}{2}\right) -\cos \left( \frac{{\widetilde{W}}_\beta + {\widetilde{u}} -B_\beta -y}{2}\right) , \\ {\mathcal {F}}_2&:={\widetilde{W}}_{\beta ,t} +{\widetilde{s}} -B_{\beta ,x} -y_x - \cos \left( \frac{{\widetilde{W}}_\beta + {\widetilde{u}} +B_\beta +y}{2}\right) +\cos \left( \frac{{\widetilde{W}}_\beta + {\widetilde{u}} -B_\beta -y}{2}\right) , \end{aligned} \end{aligned}$$

where ${\mathcal {F}}_i={\mathcal {F}}_i(y,v,\widetilde{u},\widetilde{s})$ for $i=1,2$. Notice that for any given triplet $(y,{\widetilde{u},\widetilde{s}})\in H^1_e\times H^1_o\times L^2_o$, equation ${\mathcal {F}}_1\equiv 0$ is trivially solvable for $v(\cdot )$ and defines a function in $L^2_e$. On the other hand,

$$\begin{aligned} {\mathcal {F}}_2:H^1_e(\mathbb {R})\times L^2_e(\mathbb {R})\times H^1_o(\mathbb {R})\times L^2_o(\mathbb {R})\longrightarrow L^2_o(\mathbb {R}), \end{aligned}$$

defines a ${\mathcal {C}}^1$ functional in a neighborhood of zero and due to Lemma 4.3 we have ${\mathcal {F}}_2(0,0,0,0)\equiv 0$. Therefore, in order to conclude the proof it is enough to show that the Gâteaux derivative of ${\mathcal {F}}_2$ defines a invertible bounded linear operator with continuous inverse. In fact, notice that linearizing directly on the definition of ${\mathcal {F}}_2$ above and by using basic trigonometric identities we are lead to solve

$$\begin{aligned} y_x = \sin \left( \frac{{\widetilde{W}}_\beta }{2}\right) \cos \left( \frac{B_\beta }{2}\right) y +f, \, \hbox { for some }\, f\in L^2_o. \end{aligned}$$

(4.10)

Note that unlike (4.6) now we have a “$+$” sign in the right-hand side. As before, in order to solve Eq. (4.10), we define $\mu _\beta (x)$ to be the solution of

$$\begin{aligned} \mu _{\beta ,x}+\sin \left( \dfrac{\widetilde{W}_\beta }{2}\right) \cos \left( \dfrac{B_\beta }{2}\right) \mu _\beta =0, \end{aligned}$$

that is

$$\begin{aligned} \mu _\beta (x)=\exp \left( -\int _0^x \sin \left( \dfrac{\widetilde{W}_\beta }{2}\right) \cos \left( \dfrac{B_\beta }{2}\right) \right) . \end{aligned}$$

Note as before, that $\mu _\beta (x)$ is an even function. Moreover, notice that by using the definitions of $\widetilde{W}_\beta$ and $B_\beta$ in (4.4)–(2.1) we conclude that there exists $R>1$ sufficiently large such that

$$\begin{aligned} \hbox {for all } \, x>R,&\qquad \sin \left( \frac{{\widetilde{W}}_\beta }{2}\right) \cos \left( \frac{B_\beta }{2}\right) \sim 1- e^{- \beta x}, \end{aligned}$$

(4.11)

$$\begin{aligned} \hbox {and for all } \, x<-R,&\qquad \sin \left( \frac{{\widetilde{W}}_\beta }{2}\right) \cos \left( \frac{B_\beta }{2}\right) \sim -1+ e^{ \beta x}. \end{aligned}$$

(4.12)

Notice that, from the previous analysis, we deduce that in this case $\mu _\beta \rightarrow 0$ exponentially fast as $x\rightarrow \pm \infty$. Moreover since $\mu _\beta$ and f are even and odd functions respectively we conclude

$$\begin{aligned} \int _\mathbb {R}\mu _\beta (x) f(x)dx=0. \end{aligned}$$

Thus, solving (4.10) from $-\infty$ to x we conclude that there is only one solution to (4.10) which is given by

$$\begin{aligned} y=\dfrac{1}{\mu _\beta (x)}\int _{-\infty }^x \mu _\beta (z) f(z)dz. \end{aligned}$$

(4.13)

Finally, we claim that due to the explicit form of $y(\cdot )$ we have

$$\begin{aligned} \Vert {y}\Vert _{L^2(\mathbb {R})}\lesssim \Vert f\Vert _{L^2(\mathbb {R})}. \end{aligned}$$

In order to prove this we shall follow the ideas of [60]. In fact, first of all notice that by using (4.12) we deduce that for all $s\le x\ll -1$ we have

$$\begin{aligned} \left| \dfrac{\mu _\beta (s)}{\mu _\beta (x)}\right| \le C\left| \dfrac{\cosh (s)}{\cosh (x)}\right| \le C e^{s-x}, \end{aligned}$$

for some constant C only depending on $\beta$. Therefore, by using formula (4.13) we conclude that for $x\ll -1$ we have

$$\begin{aligned} \vert y(x)\vert \le Ce^{-x}\star \Big (f(\cdot ){1} \hspace{-3.40001pt}1_{(-\infty ,x]}(\cdot )\Big ), \end{aligned}$$

where $\star$ stands for the convolution in the space variable. Since $y(\cdot )$ is an even function the same bound holds for $x\gg 1$. Therefore, by using Young’s inequality we conclude that

$$\begin{aligned} \Vert {y}\Vert _{L^2(\mathbb {R})}\lesssim \Vert f\Vert _{L^2(\mathbb {R})}. \end{aligned}$$

Finally, notice that it only remains to prove that $y_x\in L^2$. Nevertheless, this is a direct consequence of the explicit form of $y(\cdot )$ in (4.13) and the previous analysis. Therefore, we conclude the proof by applying the Implicit Function Theorem. $\square$

As a corollary of Propositions 4.4–4.5 and the orbital stability of the SG breather for $H^1\times L^2$ perturbations (see [60], Theorem 1.1) we obtain the orbital stability of the SG wobbling kink (Theorem 1.2). See Fig. 5 for a graphic explanation of all previous results in this section.

4.3 Proof of Theorem 1.2

Now we state a quantitative version of Theorem 1.2.

Theorem 4.6

(Orbital stability of Wobbling kinks under odd perturbations). There exists $\eta _0{,~C_0>0}$ such that the following holds. Let $(W_\beta ,\partial _t W_\beta )$ be the wobbling kink written in (1.9). Consider initial data of the form $(W_\beta +u_0, \partial _tW_{\beta } +s_0)$, with $(u_0,s_0) \in H^1_o\times L^2_o$ satisfying

$$\begin{aligned} \Vert (u_0,s_0)\Vert _{H^1\times L^2}<\eta <\eta _0. \end{aligned}$$

(4.14)

Then, there exists $C_0>0$ and $x_1:\mathbb {R}\rightarrow \mathbb {R}$, $x_1=x_1(t)$ of class $C^1$ such that the solution $(\phi ,\phi _t)(t,x)$ to SG satisfies

$$\begin{aligned} \sup _{t\in \mathbb {R}} \Vert (\phi ,\phi _t) (t) - (W_\beta (t+x_1(t),\cdot ),(\partial _tW_{\beta }) (t+x_1(t),\cdot ){)}\Vert _{H^1\times L^2} <C_0\eta . \end{aligned}$$

Remark 4.9

Recall that no shift on the x variable is allowed in the wobbling kink since the data is odd. This implies, following the lines just below (2.9), that the solution is odd for all time.

Proof

We follow the ideas in [60]. Assume (4.14). Proposition 4.5 allows us to construct via BT a unique small, (even, even) perturbation $(y_0,v_0)$ of the breather solution $(B_\beta , B_{\beta ,t})$ from (2.1). Therefore, from [60] we know that the breather is stable, up to some shifts $x_1(t)$ and $x_2(t)$. By parity, in our case $x_2(t)=0$ and only $x_1(t)$ is not necessarily zero. Evolving in time the perturbation of the SG breather solution, and using Proposition 4.4 with a suitably chosen wobbling kink (it must have the same shift $x_1(t)$, see Remark 4.5 for details), we conclude the orbital stability. $\square$

Fig. 5

A schematic representation of the action of the BT at time $t=0$ on the initial-data manifolds ${\mathcal {E}}_0$ and $\mathcal O_0$ in (2.11), as well as why Theorem 1.2 holds. Here (o, o) and (e, e) mean odd-odd and even-even data in $H^1\times L^2$. The horizontal submanifold on the left (containing the breather $B_\beta$ in (2.1) and its time derivative) is sent via BT towards a vertical submanifold in ${\mathcal {O}}_Q$ (see (4.1) for definitions) containing the wobbling kink $W_\beta$ from (1.9), and its time derivative. See Propositions 4.1, 4.2 and Lemma 4.3 for the rigorous proofs. On the other hand, the vertical submanifold on the left for which there is AS (Theorem 2.1) is sent in Theorem 1.1, via BT, towards an “oblique” submanifold ${\mathcal {M}}_{\eta ,0}$ preserving the zero momentum condition. On the right, only the vertical manifold is preserved by the flow, and the image via BT of $(y_0,v_0)$ is $(Q+{\widetilde{u}}_0,{\widetilde{s}}_0)$, with zero momentum (see Sect. 7 for more details)

We finish this section with a simple lemma (see [55] for instance) stating that wobbling kinks cannot be orbitally stable for general data, in the sense that general perturbations may not lead to the evolution of a kink plus a perturbation which is periodic in time. In that sense, the wobbling kink (1.9) ceases to exist. However, there is a family of 3-soliton solutions which represents the interaction between a static kink and a moving breather. The stability of this family, as already stated in the introduction, is an open problem.

Lemma 4.7

There exists a family of SG 3-solitons with frequency $\beta \in (-1,1)$ and speed $v\in (-1,1)$, for which the wobbling kink (1.9) is the case of zero momentum, i.e. $v=0$. This family is explicitly given by

$$\begin{aligned} W_{\beta ,v}(t,x):=Q(x)-4\arctan \left( \dfrac{\beta }{i\alpha }\tan ( \Theta -{\overline{\Theta }})\right) , \end{aligned}$$

(4.15)

where ${\overline{\Theta }}$ denotes the complex conjugate of $\Theta$, which is given by

$$\begin{aligned} \Theta :=\arctan \left( \dfrac{\beta a_v+i\alpha a_v+1}{\beta a_v+i\alpha a_v-1}\tan \left( \arctan e^x-\arctan e^{\gamma (v)[\beta (x-vt)-i\alpha (t-vx)]}\right) \right) , \end{aligned}$$

and the parameters $a_v$, $\alpha$ and $\gamma (v)$ are given by

$$\begin{aligned} a_v:=\left( \dfrac{1+v}{1-v}\right) ^{1/2}, \quad \alpha =\sqrt{1-\beta ^2}, \quad \hbox {and}\quad \gamma (v)=\dfrac{1}{\sqrt{1-v^2}}. \end{aligned}$$

(compare with (3.19)).

Before finishing this section, some important remarks are in order.

Remark 4.10

Some snapshots of this 3-soliton family (4.15) are presented in Fig. 6.

Remark 4.11

The family $(W_{\beta ,v},\partial _t W_{\beta ,v})(t,x)$ in (4.15) converges naturally to the wobbling kink (1.9) when $v\rightarrow 0$. See Appendix 11 for details.

Remark 4.12

The family $(W_{\beta ,v},\partial _t W_{\beta ,v})(t=0)$ in (4.15) can also be regarded as an essentially (odd, even) perturbation of the kink (Q, 0). However, as we shall see in Sect. 7, it does not belong to the class of initial data under which Theorem 1.1 holds, due to the fact that it has nonzero momentum. Note also that these initial data leads to a perturbation on the position of the kink.

Fig. 6

The general 3-soliton or generalized wobbling kink (4.15) with $\beta =0.5$ and $v=0.4$ at times $t=-55.3$ (blue), $t=0$ (orange), and $t=55.3$ (green). This solution represents a breather colliding with a static kink. Notice that, after the “breather” collides against the kink, the latter shifts. Moreover, notice that at time $t=0$ this corresponds to an odd perturbation of the kink, that is, $(W_{\beta ,v}-Q)(t=0)$ is odd

5 Linearized Bäcklund Transformations and Resonances

Having proved Theorem 1.2, now we make an interesting digression from the proof of the remaining Theorem 1.1, which will start in the next Section.

An essential point where SG (1.1) and $\phi ^4$ (2.3) meet is at the level of linearized transformations, even when only one of them is integrable (this is one of the reasons why the AS for the $\phi ^4$ kink H (2.2) is harder). Section 2 first showed such an analogy at the level of linearized operators around kinks, as well as resonances.

In this section we present a new point of contact between both theories, maybe not recognized before in full detail. This connection is of independent interest, in view of recent advances in AS problem via dual methods [38].

5.1 The SG case

Let us consider the linearized Bäcklund transformations (LBT) around the SG kink solution (see (3.3)–(3.4) and (4.2)–(4.3))

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _x \phi -\partial _t \varphi =-\sin \left( \frac{{\widetilde{Q}}}{2}\right) \phi \\ \partial _t \phi -\partial _x \varphi = -\sin \left( \frac{{\widetilde{Q}}}{2}\right) \varphi , \end{array}\right. } \end{aligned}$$

(5.1)

where remember that

$$\begin{aligned} {\widetilde{Q}}(x;\beta ,x_0):= Q(x;\beta ,x_0) -\pi ,\qquad \widetilde{Q}_t(x;\beta ,x_0):= Q_t(x;\beta ,x_0), \end{aligned}$$

(5.2)

with $Q, Q_t$ defined in (3.16)–(3.18).

Here, $\phi$ and $\varphi$ are $C^2$ functions depending on (t, x). Some interesting properties of (5.1) are stated in the following result (maybe well-known in the literature), which are just consequence of (4.2)–(4.3).

Lemma 5.1

(LBT in the SG case). One has that

• (1) If $(\phi ,\varphi )$ solves (5.1), then they satisfy

  $$\begin{aligned} \phi _{tt} +{\mathcal {L}}_{Q} \phi =0 \qquad \hbox {and} \qquad \varphi _{tt} -\varphi _{xx} +\varphi =0, \end{aligned}$$

  (5.3)

  for ${\mathcal {L}}_Q$ given in (2.10), respectively. The converse is not necessarily true.

• (2) (Translations of kernels). $(\phi ,\varphi )=(Q',0)$ solves (5.1).

• (3) Let

  $$\begin{aligned} L:= \frac{1}{4}\partial _\beta W_\beta \Big |_{\beta =0} = \tanh x \cos t, \qquad M:= \frac{1}{4}\partial _\beta B_\beta \Big |_{\beta =0} = \sin t. \end{aligned}$$

  (5.4)

  be the corresponding resonances of SG around the kink and zero, generated by the wobbling kink and breather respectively. Then $(\phi ,\varphi )=(L,M)$ satisfies (5.1).

Remark 5.1

Similar conclusions as in item (3) above are obtained if the periodic functions in time are correctly changed: in (5.4) $({\tilde{L}}, {\tilde{M}}) = \Big (-\tanh x \sin t, \cos t\Big )$ is also solution of (5.1). This is consequence of the fact that time derivatives of solutions also solve (5.1) (and (5.3)).

Proof of Lemma 5.1

We start by proving the first point. In fact, by differentiating both equations in (5.1) with respect to space and time respectively we obtain

$$\begin{aligned} \partial _{tt}\phi -\partial _{tx}\varphi =-\sin \left( \tfrac{\widetilde{Q}}{2}\right) \partial _t\varphi \quad \hbox {and} \quad \partial _{xx}\phi -\partial _{xt}\varphi =-{\text {sech}}^2(x)\phi -\sin \left( \tfrac{\widetilde{Q}}{2}\right) \partial _x\phi . \end{aligned}$$

Therefore, using that $\sin \left( \tfrac{\widetilde{Q}}{2}\right) =\tanh (x)$ we obtain

$$\begin{aligned} \partial _{tt}\phi -\partial _{xx}\phi ={\text {sech}}^2(x)\phi -\sin \left( \tfrac{\widetilde{Q}}{2}\right) (\partial _t\varphi -\partial _x\phi )=-(1-2{\text {sech}}^2(x))\phi . \end{aligned}$$

In the same way, by differentiating both equations in (5.1) in the opposite order, that is, with respect to time and space respectively, we conclude

$$\begin{aligned} \partial _{tt}\varphi -\partial _{xx}\varphi =-{\text {sech}}^2(x)\varphi +\sin \left( \tfrac{\widetilde{Q}}{2}\right) \left( \partial _t\phi -\partial _x\varphi \right) =-\varphi . \end{aligned}$$

Now, recalling that the static kink satisfies (3.20) with $a=1$ we immediately obtain

$$\begin{aligned} Q''=2\left( \sin \left( \dfrac{Q}{2}\right) \right) '=2\cos \left( \dfrac{Q}{2}\right) \sin \left( \dfrac{Q}{2}\right) =\sin \left( \dfrac{\widetilde{Q}}{2}\right) Q'. \end{aligned}$$

(5.5)

Finally, differentiating (5.4) we obtain

$$\begin{aligned} L_x= {\text {sech}}^2 x\cos t,\quad L_t=-\tanh x \sin t, \quad M_x\equiv 0 \quad \hbox {and}\quad M_t=\cos t. \end{aligned}$$

Replacing these formulas into (5.1) we obtain

$$\begin{aligned} L_x-M_t=({\text {sech}}^2x-1)\cos t=-\tanh ^2(x)\cos t=-\sin \left( \tfrac{\widetilde{Q}}{2}\right) L, \end{aligned}$$

and

$$\begin{aligned} L_t-M_x=-\tanh x \sin t=-\sin \left( \tfrac{\widetilde{Q}}{2}\right) M. \end{aligned}$$

The proof is complete. $\square$

5.2 The $\phi ^4$ case as extension of SG

Which is the corresponding LBT for $\phi ^4$? Although $\phi ^4$ is not integrable, and apparently has no BT, it has essentially two suitable LBT around their soliton states. Indeed, for H as in (2.2),

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _x \phi -\partial _t \varphi =-\sqrt{2} H \phi \\ \partial _t \phi -\partial _x \varphi = - \sqrt{2} H \varphi , \end{array}\right. } \end{aligned}$$

(5.6)

is a LBT for $\phi ^4$. Recall that $H'=(1-H^2)/\sqrt{2}$. The resonance in (2.8) enters in (5.6) as follows:

Lemma 5.2

(LBT in the $\phi ^4$ case). Let (5.6) be the LBT of $\phi ^4$. Then one has the following properties.

• (1) If $(\phi ,\varphi )$ solves (5.6), then

  $$\begin{aligned} \phi _{tt} +{\mathcal {L}}_{H} \phi =0 \quad \hbox { and } \quad \varphi _{tt} +\widetilde{{\mathcal {L}}}_{H} \varphi =0, \end{aligned}$$

  for ${\mathcal {L}}_H$ given in (2.6) and

  $$\begin{aligned} \widetilde{{\mathcal {L}}}_{H}:= -\partial _x^2 +1 +H^2=-\partial _x^2 +2 -(1-H^2). \end{aligned}$$

  (5.7)

  The converse is not necessarily true. Note that $\widetilde{\mathcal L}_{H} \ge 0$ by definition.

• (2) $(\phi ,\varphi )=(H',0)$ solves (5.6).

• (3) $\sigma (\widetilde{{\mathcal {L}}}_{H})=\{\frac{3}{2}\} \cup [2,\infty )$. $\lambda =0$ is not an eigenvalue, $\lambda =\frac{3}{2}$ is the first eigenvalue associated to the eigenfunction $Y_0:=-\frac{1}{\sqrt{3}}{\text {sech}}\left( \frac{x}{\sqrt{2}}\right)$, and H is odd resonance at $\lambda =2$.

• (4) (Connection between internal modes). Recall $Y_1$ from (2.7). Then, $(\phi , \varphi )$ given by

  $$\begin{aligned} (\phi , \varphi ) = \Big (Y_1(x) \sin (t\sqrt{3/2}), Y_0(x) \cos (t\sqrt{3/2}) \Big ) \end{aligned}$$

  (5.8)

  solves (5.6).

• (5) Let

  $$\begin{aligned} L_4:=-\left( 1-\frac{3}{2}{\text {sech}}^2\left( \frac{x}{\sqrt{2}}\right) \right) \sin (\sqrt{2}t), \quad M_4:= \tanh \left( \frac{x}{\sqrt{2}}\right) \cos (\sqrt{2}t).\nonumber \\ \end{aligned}$$

  (5.9)

  be the corresponding resonances of $\phi ^4$ around the kink and “around the internal mode”, respectively. Then $(\phi ,\varphi )=(L_4,M_4)$ satisfies (5.6).

Remark 5.2

Similar conclusions in items (4) and (5) above are obtained if the periodic functions in time are correctly changed: in (5.8) $(\phi , \varphi ) = \Big (Y_1(x) \cos (t\sqrt{3/2}), -Y_0(x) \sin (t\sqrt{3/2}) \Big )$ is also solution of (5.6), and instead of (5.9),

$$\begin{aligned} \widetilde{L}_4:=-\left( 1-\frac{3}{2}{\text {sech}}^2\left( \frac{x}{\sqrt{2}}\right) \right) \cos (\sqrt{2}t), \qquad {\widetilde{M}}_4:= -\tanh \left( \frac{x}{\sqrt{2}}\right) \sin (\sqrt{2}t). \end{aligned}$$

are also solutions of (5.6). This is consequence of the fact that time derivatives of solutions also solve (5.6).

Remark 5.3

Note that $L_4$ already appeared in this paper in (2.8). Also, in item (5), $M_4$ is called “resonance around the internal mode” because it is exactly a resonance of $\widetilde{{\mathcal {L}}}_H$ in (5.7), which can be regarded as the linear operator for which the internal mode $Y_1$ in (2.7) is its generator, in the sense of [38].

Remark 5.4

Note that ${\mathcal {L}}_{H}$ and $\widetilde{{\mathcal {L}}}_{H}$ correspond, in the terminology of Schrödinger operators, to a linear operator and its dual, respectively, see e.g. [38] and references therein.

Proof of Lemma 5.2

The proof follows from straightforward computations. Nevertheless, for the sake of completeness we shall show them below. In fact, by differentiating both equations in (5.6) with respect to space and time respectively we obtain

$$\begin{aligned}{} & {} \partial _{tt}\phi -\partial _{tx}\varphi =-\sqrt{2}H\varphi _t \quad \hbox {and} \\{} & {} \partial _{xx}\phi -\partial _{tx}\varphi =-\sqrt{2}H'\phi -\sqrt{2}H\partial _x\phi . \end{aligned}$$

Thus, by replacing one equation into the other we conclude

$$\begin{aligned} \partial _{tt}\phi -\partial _{xx}\phi =(1-H^2)\phi -\sqrt{2}H(\partial _t\varphi -\partial _x\phi )=(1-3H^2)\phi . \end{aligned}$$

In the same way, deriving both equations in (5.6) with respect to time and space respectively we conclude

$$\begin{aligned} \partial _{tt}\varphi -\partial _{xx}\varphi =-\sqrt{2}H'\varphi +\sqrt{2}H(\partial _t\phi -\partial _x\varphi )=-(1+H^2)\varphi . \end{aligned}$$

This proves the first point.

Now, recalling that H satisfies the equation $H'=(1-H^2)/\sqrt{2}$, we immediately conclude

$$\begin{aligned} H''=\dfrac{1}{\sqrt{2}}(1-H^2)'=-\sqrt{2}HH', \end{aligned}$$

and hence $(H',0)$ solves (5.6).

The third point is consequence of standard Sturm-Liouville theory, and the fact that $Y_0$ has a sign and it is even.

Now we intend to prove point (4). In fact, let us start by some computations. By differentiating directly in the definition of $(\phi ,\varphi )$ we obtain

$$\begin{aligned} \partial _x\phi = -\dfrac{1}{\sqrt{2}}\left( 1-2{\text {sech}}^2\left( \dfrac{x}{\sqrt{2}}\right) \right) {\text {sech}}\left( \dfrac{x}{\sqrt{2}}\right) \tanh ^2\left( \dfrac{x}{\sqrt{2}}\right) \sin \left( \dfrac{\sqrt{3}t}{\sqrt{2}}\right) , \end{aligned}$$

and

$$\begin{aligned} \partial _x\varphi =\dfrac{1}{\sqrt{6}}{\text {sech}}\left( \dfrac{x}{\sqrt{2}}\right) \tanh \left( \dfrac{x}{\sqrt{2}}\right) \cos \left( \dfrac{\sqrt{3}t}{\sqrt{2}}\right) . \end{aligned}$$

Thus, by replacing these formulas into the system (5.6) we obtain

$$\begin{aligned} \partial _x\phi -\partial _t\varphi&=-\sqrt{2}\left( 1-{\text {sech}}^2\left( \dfrac{x}{\sqrt{2}}\right) \right) {\text {sech}}\left( \dfrac{x}{\sqrt{2}}\right) \sin \left( \dfrac{\sqrt{3}t}{\sqrt{2}}\right) \\ {}&= -\sqrt{2}H{\text {sech}}\left( \dfrac{x}{\sqrt{2}}\right) \tanh \left( \dfrac{x}{\sqrt{2}}\right) \sin \left( \dfrac{\sqrt{3}t}{\sqrt{2}}\right) =-\sqrt{2}H\phi , \end{aligned}$$

and

$$\begin{aligned} \partial _t\phi -\partial _x\varphi =\left( \sqrt{\dfrac{3}{2}}-\dfrac{1}{\sqrt{6}}\right) {\text {sech}}\left( \dfrac{x}{\sqrt{2}}\right) \tanh \left( \dfrac{x}{\sqrt{2}}\right) \cos \left( \dfrac{\sqrt{3}t}{\sqrt{2}}\right) =\sqrt{2}H\varphi , \end{aligned}$$

which finish the proof of the fourth statement. Finally, by differentiating (5.9) we obtain

$$\begin{aligned} L_{4,x}=-\dfrac{3}{\sqrt{2}}{\text {sech}}^2\left( \dfrac{x}{\sqrt{2}}\right) \tanh \left( \dfrac{x}{\sqrt{2}}\right) \sin (\sqrt{2}t) \end{aligned}$$

and

$$\begin{aligned} M_{4,x}=\dfrac{1}{\sqrt{2}}{\text {sech}}^2\left( \dfrac{x}{\sqrt{2}}\right) \cos (\sqrt{2}t). \end{aligned}$$

Therefore, by replacing these formulas into the left-hand side of the first equation in (5.6) we obtain

$$\begin{aligned} L_{4,x}-M_{4,t}&=-\dfrac{3}{\sqrt{2}}{\text {sech}}^2\left( \dfrac{x}{\sqrt{2}}\right) \tanh \left( \dfrac{x}{\sqrt{2}}\right) \sin (\sqrt{2}t)+\sqrt{2}\tanh \left( \dfrac{x}{\sqrt{2}}\right) \sin (\sqrt{2}t) \\ {}&= \sqrt{2}\left( 1-\dfrac{3}{2}{\text {sech}}^2\left( \dfrac{x}{\sqrt{2}}\right) \right) \tanh \left( \dfrac{x}{\sqrt{2}}\right) \sin (\sqrt{2}t), \end{aligned}$$

which proves that $(L_4,M_4)$ satisfy the first equation in (5.6). On the other hand, by replacing these formulas into the left-hand side of the second equation in (5.6) we obtain

$$\begin{aligned} L_{4,t}-M_{4,x}&=-\sqrt{2}\left( 1-\dfrac{3}{2}{\text {sech}}^2\left( \dfrac{x}{\sqrt{2}}\right) \right) \cos (\sqrt{2}t)-\dfrac{1}{\sqrt{2}}{\text {sech}}^2\left( \dfrac{x}{\sqrt{2}}\right) \cos (\sqrt{2}t) \\ {}&=-\sqrt{2}\left( 1-{\text {sech}}^2\left( \dfrac{x}{\sqrt{2}}\right) \right) \cos (\sqrt{2}t)=-\sqrt{2}HM_4. \end{aligned}$$

The proof is complete. $\square$

It turns out that the resonance $M_4$ in (5.9) plays the role of L in (5.4), and it is also related via LBT to a resonance of the zero solution of linear Klein-Gordon, as in Lemma 5.1, with a slight modification coming from the eigenvalue 3/2. What we prove now is in some sense similar to the factorization discussed in [38] and references therein: we can also connect $M_4$ with the even resonance associated to the vacuum state (the equivalent to M in (5.4)). For simplicity, we work with complex valued data. Let $\lambda _0:= i \sqrt{3/2},$ and consider the following LBT:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _x {\widetilde{\varphi }} -\partial _t{\widetilde{\psi }} =-\frac{1}{\sqrt{2}} H{\widetilde{\varphi }} \mp \lambda _0 {\widetilde{\psi }} \\ \partial _t {\widetilde{\varphi }}-\partial _x {\widetilde{\psi }}= -\frac{1}{\sqrt{2}} H {\widetilde{\psi }} \mp \lambda _0 {\widetilde{\varphi }}. \end{array}\right. } \end{aligned}$$

(5.10)

Note that we have two LBT depending on the sign ± on the right, but both are essentially the same. The following second LBT result for $\phi ^4$ follows:

Lemma 5.3

(LBT in the $\phi ^4$ case, second part). One has that

• (1) If $({\widetilde{\varphi }},{\widetilde{\psi }})$ solves (5.10), then

  $$\begin{aligned} {\widetilde{\varphi }}_{tt} + \widetilde{{\mathcal {L}}}_{H} \widetilde{\varphi }=0 \quad \hbox { and } \quad {\widetilde{\psi }}_{tt} -{\widetilde{\psi }}_{xx} +2{\widetilde{\psi }} =0. \end{aligned}$$

  (5.11)

  Once again, the converse is not necessarily true.

• (2) Let

  $$\begin{aligned} M_4:= \tanh \left( \frac{x}{\sqrt{2}}\right) e^{i\sqrt{2}t},\qquad N_4:= (-2i\mp \sqrt{2} \lambda _0)e^{i\sqrt{2}t}. \end{aligned}$$

  (5.12)

  Then $(M_4,N_4)$ satisfies (5.10).

Proof

Just differentiating both equations in (5.10) with respect to space and time respectively we obtain

$$\begin{aligned}{} & {} \partial _{xx} {\widetilde{\varphi }} -\partial _{tx}{\widetilde{\psi }} =-\frac{1}{\sqrt{2}} H'{\widetilde{\varphi }} -\frac{1}{\sqrt{2}} H{\widetilde{\varphi }}_x \mp \lambda _0 {\widetilde{\psi }}_x, \quad \hbox {and} \quad \\{} & {} \partial _{tt} {\widetilde{\varphi }}-\partial _{tx} {\widetilde{\psi }}= -\frac{1}{\sqrt{2}} H {\widetilde{\psi }}_t \mp \lambda _0 {\widetilde{\varphi }}_t. \end{aligned}$$

Thus, by replacing one equation into the other we conclude

$$\begin{aligned} \begin{aligned} \partial _{tt}{\widetilde{\varphi }}-\partial _{xx}{\widetilde{\varphi }}&=-\frac{1}{\sqrt{2}}H({\widetilde{\psi }}_t - {\widetilde{\varphi }}_x) + \frac{1}{\sqrt{2}}H'{\widetilde{\varphi }}\mp \lambda _0({\widetilde{\varphi }}_t-{\widetilde{\psi }}_x)\\&=-\frac{1}{2}H^2{\widetilde{\varphi }} \mp \frac{\lambda _0}{\sqrt{2}}H{\widetilde{\psi }} + \frac{1}{2}(1-H^2){\widetilde{\varphi }} \pm \frac{\lambda _0}{\sqrt{2}}H{\widetilde{\psi }}+\lambda _0^2{\widetilde{\varphi }}\\&=-(1+H^2){\widetilde{\varphi }}. \end{aligned} \end{aligned}$$

Namely, we get

$$\begin{aligned} {\widetilde{\varphi }}_{tt} + \widetilde{{\mathcal {L}}}_{H} \widetilde{\varphi }=0. \end{aligned}$$

In the same way, deriving both equations in (5.10) with respect to time and space respectively we conclude

$$\begin{aligned} \partial _{tt}{\widetilde{\psi }}-\partial _{xx}{\widetilde{\psi }}=-\frac{1}{\sqrt{2}}H'{\widetilde{\psi }}+\frac{1}{\sqrt{2}}H(\partial _t{\widetilde{\varphi }}-\partial _x{\widetilde{\psi }}) \pm \lambda _0({\widetilde{\psi }}_t-{\widetilde{\varphi }}_x)=-2{\widetilde{\psi }}. \end{aligned}$$

Namely, we get

$$\begin{aligned} {\widetilde{\psi }}_{tt} -\partial _{xx}{\widetilde{\psi }} + 2{\widetilde{\psi }} =0. \end{aligned}$$

This ends the proof of the first point.

Finally, by differentiating (5.10) we obtain

$$\begin{aligned} \begin{aligned}&M_{4x}=\frac{1}{\sqrt{2}}{\text {sech}}^2\left( \frac{x}{\sqrt{2}}\right) e^{i\sqrt{2}t},\quad N_{4x}=0,\\&M_{4t}=i\sqrt{2} \tanh \left( \frac{x}{\sqrt{2}}\right) e^{i\sqrt{2}t},\quad N_{4t}=i\sqrt{2}(-2i\mp \sqrt{2}\lambda _0)e^{i\sqrt{2}t}. \end{aligned} \end{aligned}$$

Now, subtracting we get

$$\begin{aligned} \begin{aligned} M_{4x} - N_{4t}&= \frac{1}{\sqrt{2}}{\text {sech}}^2\left( \frac{x}{\sqrt{2}}\right) e^{i\sqrt{2}t} - i\sqrt{2}(2\pm \sqrt{2}\lambda _0)e^{i\sqrt{2}t}\\&= -\frac{1}{\sqrt{2}} \tanh ^2\left( \frac{x}{\sqrt{2}}\right) e^{i\sqrt{2}t} + \left( \frac{1}{\sqrt{2}} - 2\sqrt{2} \pm 2i\lambda _0 \right) e^{i\sqrt{2}t}\\&= -\frac{1}{\sqrt{2}}HM_4 + \left( \sqrt{2}(i\sqrt{\frac{3}{2}})^2 \pm 2i\lambda _0 \right) e^{i\sqrt{2}t}\\&= -\frac{1}{\sqrt{2}}HM_4 + \lambda _0 \left( \sqrt{2}\lambda _0 \pm 2i \right) e^{i\sqrt{2}t}\\&= -\frac{1}{\sqrt{2}}HM_4 \mp \lambda _0[-2i\mp \sqrt{2}\lambda _0]e^{i\sqrt{2}t}=-\frac{1}{\sqrt{2}}HM_4\mp \lambda _0N_4.\\ \end{aligned} \end{aligned}$$

Similarly, we also get

$$\begin{aligned} \begin{aligned} M_{4t} - N_{4x}&= i\sqrt{2} \tanh \left( \frac{x}{\sqrt{2}}\right) e^{i\sqrt{2}t}\\&= -\frac{1}{\sqrt{2}}H[-2i\mp \sqrt{2}\lambda _0]e^{i\sqrt{2}t} \mp \lambda _0 \tanh \left( \frac{x}{\sqrt{2}}\right) e^{i\sqrt{2}t}\\&= -\frac{1}{\sqrt{2}}HN_4 \mp \lambda _0M_4. \end{aligned} \end{aligned}$$

This last fact ends the proof of the second point. $\square$

Remark 5.5

In terms of the results in [38], understanding the AS of the $\phi ^4$ under general data is related to the understanding of the corresponding AS around zero of the equation

$$\begin{aligned} {\widetilde{\psi }}_{tt} -{\widetilde{\psi }}_{xx} +2{\widetilde{\psi }} + N({\widetilde{\psi }})=0, \end{aligned}$$

for some $N({\widetilde{\psi }})$ determined after two consecutive reductions of $\phi ^4$ using Lemmas 5.2 and 5.3. This equation has the simplified $N_4$ in (5.12) as resonance, which is far simpler than $L_4$ in (5.9).

6 Asymptotic Stability Manifolds for the SG Kink: Theorem 1.1 Revisited

Now we have all the ingredients to fully understand Theorem 1.1: Theorem 4.6, the whole Sect. 5, and particularly Fig. 5.

Recall the manifold $\mathcal{O}\mathcal{E}_Q$ in (4.1). In this section, our goal is precisely to construct a smooth manifold of initial data of the form

$$\begin{aligned} \vec \phi (t=0)=(Q,0) + \hbox {(odd, even)} \in \mathcal{O}\mathcal{E}_Q, \end{aligned}$$

perturbations of (Q, 0), for which a final state is attained. Unlike the (odd, odd) configuration ${\mathcal {O}}_Q$ discussed in (4.1), in our present case the initial parities shall not be preserved by the flow. Recall the definitions of $H^m_e(\mathbb {R})$ and $H^m_o(\mathbb {R})$ given in (1.10). Theorem 1.1 will follow from the following static asymptotic stability manifold for the SG kink:

Theorem 6.1

(Zero momentum manifold for asymptotic stability in SG). There exists $\eta _0>0$ such that, for all $0<\eta <\eta _0$, the following holds. There exists a smooth manifold ${\mathcal {M}}_{\eta ,0}$ (of infinite codimension) of initial data $(\phi _0,\phi _1)$ of the form

$$\begin{aligned} (\phi _0,\phi _1)(x) = (Q(x) + {\widetilde{u}}_0(x), {\widetilde{s}}_0(x)), \qquad \Vert ({\widetilde{u}}_0,{\widetilde{s}}_0) \Vert _{H^1\times L^2}< \eta , \end{aligned}$$

(6.1)

where ${\widetilde{u}}_0\in H^1_o(\mathbb {R}),$ ${\widetilde{s}}_0\in L^2_e(\mathbb {R})$, and satisfying the following properties. Let $(\phi ,\phi _t)(t)$ be the global solution of (1.1) with initial data $(\phi _0,\phi _1)$. Then,

• (1) $(\phi ,\phi _t)(t)$ has zero momentum: $P[(\phi ,\phi _t)]=0$.

• (2) There exists a smooth $\rho (t)\in \mathbb {R}$ satisfying

  $$\begin{aligned} \sup _{t\in \mathbb {R}}| \rho '(t)| \lesssim \eta ^2, \end{aligned}$$

  (6.2)

  such that, for any sufficiently large bounded interval $I\subset \mathbb {R}$, the following alternative holds:

  • (a) there exists a sequence $t_n\rightarrow \pm \infty$ such that $|\rho (t_n) |\rightarrow +\infty$ and

    $$\begin{aligned} \lim _{n\rightarrow \pm \infty }\Vert (\phi ,\phi _t)(t_n)-(Q,0)(\cdot -\rho (t_n))\Vert _{(H^1\times L^2)(I)}=0; \end{aligned}$$

    (6.3)

  • (b) $\rho (t)$ stays bounded for all $t\in \mathbb {R}$ and

    $$\begin{aligned} \lim _{t\rightarrow \pm \infty }\Vert (\phi ,\phi _t)(t)-(Q,0)(\cdot -\rho (t))\Vert _{(H^1\times L^2)(I)}=0. \end{aligned}$$

    (6.4)

    Moreover, $\rho (t)\rightarrow {\bar{\rho }} \in \mathbb {R}$ in this case.

• (3) The manifold ${\mathcal {M}}_{\eta ,0}$ defining (6.1) is characterized as the image, under a Bäcklund transformation and the Implicit Function Theorem, of initial perturbations $(y_0,v_0)\in H_o^1\times L^2_e$ of the zero solution which satisfy $v_0=0$ and are connected to (6.1) in such a way that they preserve their total zero momentum.

Some remarks are certainly necessary.

Remark 6.1

Note that in Theorem 6.1 we do not specify the space where $(\phi ,\phi _t)$ are posed, this because (Q, 0)(t) in (1.5) does not belong to $H^1\times L^2$. However, it is possible to show local and global well-posedness (LWP), such that $H^1\times L^2$ perturbations are naturally allowed [19].

Remark 6.2

(Explicit examples) Note that the exact solution to SG (see (1.6) for the notation)

$$\begin{aligned} (\phi ,\partial _t \phi )(t,x) =(Q(t,x;\beta ,0), \partial _t Q(t,x;\beta ,0)), \end{aligned}$$

(6.5)

has nonzero momentum, provided $\beta \ne 0$. These data are not included in Theorem 6.1 precisely because of this nonzero momentum property. Indeed, with the terminology proposed above, for any $\beta$ small enough, one has the initial data $(\phi _0,\phi _1)(x) = (Q(x) + {\widetilde{u}}_0(x), {\widetilde{s}}_0(x))$, with ${\widetilde{u}}_0(x):=Q(0,x;\beta ,0)-Q(0,x;0,0)$ and $\widetilde{s}_0(x):=\partial _t Q(t,x;\beta ,0)\Big |_{t=0}$ (see (1.6) for definitions). Moreover, the evolution in this case is given by the exact solution (6.5). However, using a Lorentz transformation (1.4), it is possible to reduce the problem of data as in (6.5) to data of zero momentum, by changing the initial time (and also the data) considered at the new initial time.

Remark 6.3

(About the manifold ${\mathcal {M}}_{\eta ,0}$) Note that, unlike in the (odd, odd) case, data of the form (6.1) is not preserved by the SG equation. The clearest example is probably stated in the previous remark. The fact that $M_{\eta ,0}$ has infinite codimension should not be a surprise: by Theorem 1.2 a big part of the (kink + odd, odd) manifold does not satisfy the asymptotic stability property, or in other words, asymptotic stability manifolds are maybe far from being finite codimensional. Finally, recall that small shifts of kinks as initial data are not contained in the manifold ${\mathcal {M}}_{\eta ,0}$, because they break the parity assumptions.

Remark 6.4

It is worth noticing that, for any non-zero $\beta \in (-1,1)$ and any non-zero $v\in (-1,1)$, the wobbling kink $W_{\beta ,v}$ in (4.15) does not belong to ${\mathcal {M}}_{\eta ,0}$. This is a consequence of the fact that for such an election of $\beta$ and v, the wobbling kink $W_{\beta ,v}$ has non zero momentum.

Remark 6.5

Theorem 6.1 is in some sense sharp: if now ${\widetilde{s}}_0$ is general (e.g. odd), the convergence does not hold. Also, it seems to be the first asymptotic stability result in one dimension valid for perturbations of kinks in the energy space that lead to modifications in the shifts (that is to say, the parity symmetry is not preserved by the flow). We remark that Kopylova and Komech [34] also considered general perturbations in weighted Sobolev spaces of kink solutions for field theories with sufficiently flat nonlinearities, which do not contain SG nor $\phi ^4$.

Remark 6.6

(About the shift $\rho (t)$) It was not possible for us to show that, with data only in the energy space, $\rho (t)$ always converge to a final state. Indeed, because of the proof that we invoke, this fact is deeply related to the AS of the zero solution along moving in time space-intervals, a property that it is not known for odd data (note that in general this property fails to be true: any small moving breather contradicts that property). See Remarks 10.1 and 10.2 for full details. However, even in the case where $\rho (t)$ diverges along a subsequence, there is a sort of AS around any compact spatial interval. We conjecture that under some additional condition on the initial data, $\rho (t)$ is always convergent to a final state. See [34] for similar results.

Remark 6.7

(On the literature) The use of suitable choices of manifolds of initial data is not a new tool in analyzing stability issues in nonlinear models. Remember for instance the use of a $C^1$ center-stable manifold around the soliton solution of the NLKG equation [41]. Besides that, basic definitions of stable, unstable and center-stable manifolds can be found in [9] and [62]. In critical gKdV equations, smooth manifolds around the unstable soliton are constructed in [49, 50]. See also [38] for a very recent construction of the stable manifold leading to decay in monic subcritical NLKG equations.

The rest of this paper (Sects. 7–11) is devoted to the proof of Theorem 6.1, which is essentially divided in five parts:

• (1) Section 7: construction of the manifold of initial data ${\mathcal {M}}_{\eta ,0}$.

• (2) Section 8: modulation of the data around the kink.

• (3) Section 9: using BT, lifting of the data from (odd, odd) perturbations around the zero solution.

• (4) Section 10: improved estimates on the shift parameters.

• (5) Section 11: end of proof, essentially proving (6.3) and (6.4).

In next section, we will construct the manifold of initial data ${\mathcal {M}}_{\eta ,0}$, proving part (3) of Theorem 6.1.

Remark 6.8

(About the initial data) In what follows, and in order to avoid misunderstandings in the notation, we shall denote (see (3.16)–(3.18))

$$\begin{aligned} (Q^0, Q_t^0)&:=(Q,Q_t)(x;\beta =0,x_0=0), \nonumber \\ ({\widetilde{Q}}^0, {\widetilde{Q}}_t^0)&:=({\widetilde{Q}},{\widetilde{Q}}_t)(x;\beta =0,x_0=0). \end{aligned}$$

(6.6)

These functions are nothing but the background initial data “(Q, 0)” stated in Theorem 6.1, written this time in terms of kink profiles.

7 Proof of Theorem 6.1: Construction of the Manifold of Initial Data

In this Section we will construct the initial data (6.1). In order to prove this, we will solve the BT functionals (3.3)–(3.4) (more precisely, (3.22)–(3.23)) in the opposite sense to the one performed in [60]; that is to say, given any initial data near zero of (odd, odd) type, we will show the existence of (odd, even) type perturbation data around the kink.

The idea is to use the Implicit Function Theorem, choosing $(a,\phi _0,\phi _1)$ around (1, 0, 0) in (3.3)–(3.4) and uniquely solving for $(\varphi _0,\varphi _1)=\Phi (a,\phi _0,\phi _1)$ around the kink (Q, 0) ($\Phi$ represents the implicit function). Here the properties of the BT play a key role, in the sense that the only possibility for a solution to the previous question, because of strong parity constraints in BT, is to choose the initial perturbation $\phi _1$ on the velocity at time zero exactly equals to zero (more precisely, we need $\phi _1$ odd as above explained, but parity restrictions in BT only permit $\phi _1$ even). Here is when the manifold ${\mathcal {M}}_\eta$ in (7.5) will rise up ($\eta$ is an artificial smallness parameter, needed to run the Implicit Function Theorem), because that restriction to zero speed reduces the open character of the Implicit Function sets and solutions to the direct image of a graph of the form $\Phi (a,\phi _0,0)$. Finally, the zero momentum manifold $\mathcal M_{\eta ,0}$ appearing in Theorem 6.1 is just the image obtained by the set $\Phi (1,\phi _0,0)$, for which the momentum of both data is zero.

Recall $\widetilde{{\mathcal {F}}}_1$ and $\widetilde{{\mathcal {F}}}_2$ in (3.22)–(3.23). In what follows, we will prove that given $(y_0,v_0,\delta )\in H^1_o\times L^2_e\times \mathbb {R}$ sufficiently small, it is possible to uniquely solve the nonlinear system

$$\begin{aligned} \widetilde{{\mathcal {F}}}_1({\widetilde{u}}_0,\widetilde{s}_0,y_0,v_0,\delta ) =0,\quad \widetilde{{\mathcal {F}}}_2(\widetilde{u}_0,{\widetilde{s}}_0,y_0,v_0,\delta )=0, \end{aligned}$$

(7.1)

for $({\widetilde{u}}_0,{\widetilde{s}}_0) \in H^1_o\times L^2_e$ sufficiently small.

Lemma 7.1

(Construction of initial data). Assume $x_0=0$ as in (6.6). There exists $\eta _0>0$ such that, for all $0<\eta <\eta _0$, the following is satisfied.

• (1) Given any $(y_0,v_0,\delta )\in H^1_o\times L^2_e\times \mathbb {R}$ such that $\Vert (y_0,v_0)\Vert _{H^1\times L^2} +|\delta | <\eta$, there are unique $({\widetilde{u}}_0,{\widetilde{s}}_0):=\Phi (y_0,v_0,\delta ) \in H^1_o\times L^2_e$ small enough, and such that (7.1) are satisfied.

• (2) Moreover, the implicit mapping $\Phi$, defined from $(y_0,v_0,\delta )\in H^1_o\times L^2_e\times \mathbb {R}$ such that $\Vert (y_0,v_0)\Vert _{H^1\times L^2} +|\delta |<\eta$ into $H^1_o\times L^2_e$, is a $C^1$ diffeomorphism in its domain of definition.

Remark 7.1

Lemma 7.1 can be understood, in terms of the works [4] and [60], as a sort of lifting of the initial data from the zero background. In those papers, such a property holds only if suitable orthogonality conditions are imposed. Otherwise, the derivative mapping $D\widetilde{{\mathcal {F}}}$ does not define an homeomorphism. The novelty here is that, whenever we restrict ourselves to the subclass $H^1_o\times L^2_e\times \mathbb {R}$ (namely, we impose a fixed parity), these orthogonality conditions are not needed anymore.

Proof of Lemma 7.1

The proof follows the ideas in [60] (see also [27] for the first approach in the SG case), with the main difference being which function will be found in terms of the others. From (7.1), (6.6) and (3.22)–(3.23), we are lead to solve the equations

$$\begin{aligned} \widetilde{Q}^0_x+{\widetilde{u}}_{0,x}-v_0&= \dfrac{1}{1+ \delta }\cos \left( \dfrac{\widetilde{Q}^0+\widetilde{u}_0+y_0}{2}\right) + (1+\delta ) \cos \left( \dfrac{\widetilde{Q}^0+\widetilde{u}_0-y_0}{2}\right) , \end{aligned}$$

(7.2)

$$\begin{aligned} \widetilde{Q}^0_t+ {\widetilde{s}}_0-y_{0,x}&=\dfrac{1}{1+ \delta }\cos \left( \dfrac{\widetilde{Q}^0+{\widetilde{u}}_0+y_0}{2}\right) -(1+\delta )\cos \left( \dfrac{\widetilde{Q}^0+{\widetilde{u}}_0-y_0}{2}\right) . \end{aligned}$$

(7.3)

(Recall that $a=1$ because $\beta =0.$) A simple checking shows that $\widetilde{Q}^0_t=0$, see (3.18). Note also that knowing $(y_0,v_0,\delta )$ and ${\widetilde{u}}_0$, ${\widetilde{s}}_0$ is easily found using the second equation above. Therefore, we are only lead to show the existence of uniqueness of ${\widetilde{u}}_0$.

Thanks to Lemma 3.6, we are lead to consider the invertibility of the linear operator around $(\widetilde{u}_0,y_0)=(0,0)$ of $\widetilde{{\mathcal {F}}}_1$. Therefore, given $\delta \in \mathbb {R}$ small, we must solve

$$\begin{aligned} {\widetilde{u}}_{0,x} +\frac{1}{2} \left( \frac{1}{(1+ \delta )} + (1+\delta )\right) \sin \left( \frac{\widetilde{Q}^0}{2}\right) {\widetilde{u}}_{0} = f, \qquad {\widetilde{u}}_{0}\in H^1_o, \end{aligned}$$

(7.4)

for any $f \in L^2_e$.

The term $\sin \left( \frac{\widetilde{Q}^0}{2}\right)$ is odd and easily⁴ computed: $\sin \left( \frac{\widetilde{Q^0}}{2}\right) =\tanh x$. Consequently, (7.4) becomes

$$\begin{aligned} \left( {\widetilde{u}}_{0}\cosh ^{\nu _0} x \right) _x = f \cosh ^{\nu _0} x,\qquad \nu _0:= \frac{1}{2} \left( \dfrac{1}{(1+ \delta )} + (1+\delta )\right) \ge 1. \end{aligned}$$

Hence, since ${\widetilde{u}}_{0}$ must be odd,

$$\begin{aligned} \begin{aligned} {\widetilde{u}}_{0} (x) =&~{} {\widetilde{u}}_{0} (x=0) \cosh ^{-\nu _0} x + \cosh ^{-\nu _0} x \int _0^x f(s) \cosh ^{\nu _0} s \, ds \\ =&~{} \cosh ^{-\nu _0} x \int _0^x f(s) \cosh ^{\nu _0} s \, ds. \end{aligned} \end{aligned}$$

Note that, given $f\in L^2_e$, ${\widetilde{u}}_{0}$ is clearly odd. The proof that it belongs to $H^1$ and defines an homeomorphism is direct and can be found in [60]. $\square$

We finally describe the smooth manifold ${\mathcal {M}}_\eta$ of initial data $(Q^0,0)+ ({\widetilde{u}}_0, {\widetilde{s}}_0) \in H^1_o\times L^2_e$ required in Theorem 6.1.

First of all, recall the parameter $\eta \in (0,\eta _0)$ and the implicit function $\Phi$ obtained in Lemma 7.1. We will define

$$\begin{aligned} {\mathcal {M}}_\eta := \Big \{ (Q^0,0) + ({\widetilde{u}}_0, {\widetilde{s}}_0) ~: ~ ({\widetilde{u}}_0, {\widetilde{s}}_0):=\Phi (y_0, 0,\delta ), \quad y_0 \in H^1_o, \quad \Vert y_0\Vert _{H^1} +|\delta |<2\eta \Big \}.\nonumber \\ \end{aligned}$$

(7.5)

By definition ${\mathcal {M}}_\eta$ is a smooth manifold; it also satisfies some nice properties related to the uniqueness associated to the Implicit Function Theorem.

Lemma 7.2

(Basic properties of ${\mathcal {M}}_\eta$). Consider the manifold ${\mathcal {M}}_\eta$ introduced in (7.5), and recall $a=a(\beta )$ defined in (3.19). Then, the following properties are satisfied:

• (a) For any $0<\eta <\eta _0$, one has $(Q^0,0)\in {\mathcal {M}}_\eta$.

• (b) ${\mathcal {M}}_\eta -(Q^0,0) ~{\subseteq }~ H^1_o\times L^2_e$.

• (c) For any $\beta \in (-1,1)$, $\beta \ne 0$ sufficiently small (depending on $\eta _0$ in Lemma 7.1), let $(Q,Q_t)(x;\beta ,x_0)$ be the kink profile in (3.16). Then,

  $$\begin{aligned} ({\widetilde{u}}_0,{\widetilde{s}}_0)(x):=(Q(x;\beta ,0)-Q(x;0,0),Q_t(x;\beta ,0)) \end{aligned}$$

  belongs to ${\mathcal {M}}_\eta -(Q^0,0)$, with $y_0=0$ and $\delta =a(\beta )-a(0)=a(\beta )-1$. In other words, for $\beta$ sufficiently small,

  $$\begin{aligned} (Q(\cdot ;\beta ,0)-Q(\cdot ;0,0),Q_t(\cdot ;\beta ,0)) = \Phi (0,0,a(\beta )-1) \in H^1_o \times L^2_e. \end{aligned}$$

Proof

The proof of (a) follows from the fact that $\Phi (0, 0)=(0,0,0)$. The proof of (b) is direct from Lemma 7.1. The proof of (c) is also direct from Lemma 3.5 and the uniqueness for the values of $\Phi$ given by the Implicit Function Theorem. $\square$

It turns out that a very important quantity to consider when dealing with the asymptotic stability of kinks, is its momentum (see (1.3)), which is a key tool to find suitable rigidity and smoothness properties of the limit profile. For instance, in [36] all solutions considered had zero momentum. In Theorem 6.1, solutions do have zero momentum, but the kink itself may not have zero momentum, which makes its description harder than usual.

Lemma 7.3

(Momentum of the initial data). Let $\vec \phi =\vec \phi (t,x)$ be a solution issued of the initial data $(\phi _0,\phi _1) \in {\mathcal {M}}_\eta$ in (7.5). Then one has

$$\begin{aligned} P[\vec \phi ] = 2\left( \frac{1}{1+\delta } - (1+\delta ) \right) . \end{aligned}$$

(7.6)

In particular, the sign of the momentum depends on the sign of $\delta$, and the zero momentum submanifold is generated by the perturbation data $({\widetilde{u}}_0, {\widetilde{s}}_0):=\Phi (y_0, 0,0)$.

Proof

The proof of this result is consequence of Lemma 2.4 in [60], which states that

$$\begin{aligned} P[\vec \phi ] = P[y_0,0] +\frac{1}{a+\delta } (\ell _+^+-\ell _-^+)(t) -(a+\delta )(\ell _+^- -\ell _-^-)(t), \end{aligned}$$

and the fact that $P[y_0,0] =0$ and

$$\begin{aligned} \begin{aligned} \ell _+^\pm (t):=&~{} \lim _{x\rightarrow + \infty }\left( 1- \cos \left( \dfrac{Q +{\widetilde{u}}_0\pm y_0}{2}\right) \right) = 2, \\ \ell _-^\pm (t):=&~{} \lim _{x\rightarrow - \infty } \left( 1-\cos \left( \dfrac{Q+{\widetilde{u}}_0\pm y_0}{2}\right) \right) = 0. \end{aligned} \end{aligned}$$

(Note that both limits make sense because ${\widetilde{u}}_0$ and $y_0$ are in $H^1$ in one dimension.) $\square$

Since it will be important in the proof of Theorem 6.1, we will record the zero momentum submanifold ${\mathcal {M}}_{\eta ,0} \subseteq {\mathcal {M}}_\eta$ as

$$\begin{aligned} {\mathcal {M}}_{\eta ,0}:= \Big \{ (Q^0,0) + ({\widetilde{u}}_0, \widetilde{s}_0) ~: ~ ({\widetilde{u}}_0, {\widetilde{s}}_0):=\Phi (y_0, 0,0), \quad y_0 \in H^1_o, \quad \Vert y_0\Vert _{H^1} <\eta \Big \}.\nonumber \\ \end{aligned}$$

(7.7)

This manifold is characterized by taking $\delta =0$ in $\mathcal M_{\eta }$, see (7.6). As we will see below, working in this manifold will simplify and clarify the dynamics of the kink. However, we believe that some interesting properties are also possible to show in the general manifold ${\mathcal {M}}_{\eta }$.

We conclude this section with the following result, which ends the proof of Theorem 6.1, parts (1) and (3).

Corollary 7.4

For data in $(\phi ,\phi _t) \in {\mathcal {M}}_{\eta ,0}$, one has zero momentum: $P[(\phi ,\phi _t)]=0$.

8 Modulation of the Data in ${\mathcal {M}}_\eta$

In this section we will choose suitable modulation parameters to ensure a uniquely defined dynamics for the perturbation terms in (6.3).

8.1 Choice of final speed

In this subsection, we shall describe the final speed obtained by a perturbed kink. There are at least two ways to understand this final speed, but both are equivalent, as we will see below.

The first definition of final speed is motivated by the momentum of the kink profile, assuming that around it there is nothing close at infinity in time (which means that there is asymptotic stability).

Definition 8.1

(Final speed via conservation of momentum). Consider $0<\eta <\eta _0$ as given in Lemma 7.1. Let $y_0\in H^1_o$, and $({\widetilde{u}}_0,\widetilde{s}_0)=\Phi (y_0,0,\delta )$ such that $(Q^0,0)+ (\widetilde{u}_0,{\widetilde{s}}_0)$ is in ${\mathcal {M}}_\eta$ in (7.5). We define the final speed $\beta _1\in \mathbb {R}$ as the unique solution to the equation

$$\begin{aligned} P[(Q,Q_t)(\cdot ; \beta _1,0)] = \frac{1}{2}\int {\widetilde{s}}_0 (Q^0+{\widetilde{u}}_0)_x. \end{aligned}$$

(8.1)

where P is the momentum (1.3), and $(Q, Q_t)=(Q,Q_t)(x;\beta ,x_0)$ be a kink profile of parameters $\beta \in (-1,1)$ and $x_0\in \mathbb {R}$.

Remark 8.1

Under the smallness assumption $0<\eta <\eta _0$, equation (8.1) has always a unique solution for $\beta _1$. Indeed, from (3.16)–(3.18) one has

$$\begin{aligned} \begin{aligned} P[(Q,Q_t)(\cdot ; \beta _1,0)] =&~{} \frac{1}{2} \int (Q_xQ_t)(x; \beta _1,0)dx \\ =&~{} -\frac{1}{2} \beta _1\gamma (\beta _1) \int Q'^2 = -4 \beta _1 (1-\beta _1^2)^{-1/2}, \end{aligned} \end{aligned}$$

(8.2)

so that (8.1) has a unique solution thanks to the Inverse Function Theorem.

Remark 8.2

As we have already mentioned, the motivation for this choice is simple and comes from the conservation of momentum. If asymptotic stability holds around the kink solution, it must imply that around the kink there is no additional momentum.

The second option to define a final speed is given by the Bäcklund transformation. Indeed, from (7.2)–(7.3), there is a natural way to define a final speed in the presence of asymptotic stability, respecting the absence of additional energy/momentum at infinity. For this definition, recall Lemma 3.5 on the Bäcklund transformations for general kink profiles.

Definition 8.2

(Final speed via Bäcklund transformations). Consider $0<\eta <\eta _0$ as given in Lemma 7.1. Let $y_0\in H^1_o$, and $({\widetilde{u}}_0,\widetilde{s}_0)=\Phi (y_0,0,\delta )$ such that $(Q^0,0)+ (\widetilde{u}_0,{\widetilde{s}}_0)$ is in ${\mathcal {M}}_\eta$ in (7.5). Then, we define the final speed $\beta _2\in (-1,1)$ as the unique solution for the speed of a kink + no-dispersion in the Bäcklund equations with parameter $1+\delta :$

$$\begin{aligned} \widetilde{Q}_x&= \dfrac{1}{1+ \delta }\cos \left( \frac{\widetilde{Q}}{2}\right) + (1+\delta ) \cos \left( \frac{\widetilde{Q}}{2}\right) , \end{aligned}$$

(8.3)

$$\begin{aligned} \widetilde{Q}_t&=\dfrac{1}{1+ \delta }\cos \left( \frac{\widetilde{Q}}{2}\right) -(1+\delta )\cos \left( \frac{\widetilde{Q}}{2}\right) , \end{aligned}$$

(8.4)

in the sense that $a(\beta _2)=1+\delta$ (see (3.19)), and $({\widetilde{Q}}, {\widetilde{Q}}_t)=({\widetilde{Q}}, \widetilde{Q}_t)(x;\beta _2,0)$ be a kink profile of parameters $\beta _2\in (-1,1)$ and shift $x_0=0.$

The following result shows that both definitions of final speed are equivalent.

Lemma 8.3

For a given solution $\vec \phi =(\phi ,\phi _t)$ of SG with initial data of the form $(Q^0,0)+ ({\widetilde{u}}_0,{\widetilde{s}}_0) \in {\mathcal {M}}_\eta$ (see (7.5)), one has $\beta _1=\beta _2=:\beta$.

Proof

First of all, we recall that from (8.1) we have $P[\vec \phi ] = P[Q^0 + {\widetilde{u}}_0, {\widetilde{s}}_0] =: P[(Q,Q_t)(\cdot ; \beta _1,0)].$ Now notice that, on the one-hand, since $({\widetilde{u}}_0, {\widetilde{s}}_0)$ are constructed using (7.2) and (7.3), $\delta$ given and $v_0=0$, from Lemma 7.3 we have

$$\begin{aligned} P[Q^0 + {\widetilde{u}}_0, {\widetilde{s}}_0] = 2\left( \frac{1}{1+\delta } - (1+\delta ) \right) = P[(Q,Q_t)(\cdot ; \beta _2,0)]. \end{aligned}$$

On the other hand, by Definition 8.1 we have $P[(Q,Q_t)(\cdot ; \beta _1,0)] = -4 \beta _1 (1-\beta _1^2)^{-1/2}$. Hence, recalling that $a(\beta _2)=1+\delta$ and by using (3.19) we obtain

$$\begin{aligned} 2\left( \frac{1}{1+\delta } - (1+\delta ) \right) = -\frac{4\beta _2}{(1-\beta ^2_2)^{1/2}}, \ \, \hbox { and therefore } \ \, \frac{\beta _1}{(1-\beta ^2_1)^{1/2}}=\frac{\beta _2}{(1-\beta ^2_2)^{1/2}}. \end{aligned}$$

Finally, noticing that $f(x)=\tfrac{x}{(1-x^2)^{1/2}}$ is injective for $x\in (0,1)$, we conclude the desired result. $\square$

Consequently, in what follows, we will work with kink profiles of the form

$$\begin{aligned} (Q,Q_t)(\cdot ; \beta ,x_0), \end{aligned}$$

with $\beta$ given by any of the equivalent definitions 8.1 or 8.2, and $x_0\in \mathbb {R}$, possibly depending on time, to be chosen later.

8.2 Rewriting of the initial data

We need an additional makeover to fully introduce modulations, related to the initial data for general nonzero momentum. Recall that from (7.5) we have the initial data of the form

$$\begin{aligned} (Q^0,0) + ({\widetilde{u}}_0, {\widetilde{s}}_0) \quad \hbox {s.t.} \quad ({\widetilde{u}}_0, {\widetilde{s}}_0):=\Phi (y_0, 0,\delta ), \quad y_0 \in H^1_o, \quad \Vert y_0\Vert _{H^1} +|\delta |<\eta . \end{aligned}$$

(8.5)

These initial data can be conveniently written as follows:

$$\begin{aligned} (Q^0,0) + ({\widetilde{u}}_0, {\widetilde{s}}_0)= (Q,Q_t)(\cdot , \beta ,0) + ({\hat{u}}_0, {\hat{s}}_0), \end{aligned}$$

(8.6)

where

$$\begin{aligned} ({\hat{u}}_0, {\hat{s}}_0):= ((Q^0,0) -(Q,Q_t))(\cdot , \beta ,0)+ ({\widetilde{u}}_0, {\widetilde{s}}_0) \in H^1_o\times L^2_e. \end{aligned}$$

(8.7)

Note that, written this way, $({\hat{u}}_0, {\hat{s}}_0)$ is still (odd, even) and small enough. Moreover, the solutions to SG with initial data (8.5) and (8.6) are just the same.

Remark 8.3

The makeover (8.6) is made to precisely catch the final speed of the kink in the case where the data has general nonzero momentum. However, in Theorem 6.1, since the data has zero momentum, (8.6) will not be necessary, in the sense that we can take $\beta =0$ (since $\delta =0$) on the right hand side and $({\widetilde{u}}_0, {\widetilde{s}}_0)=({\hat{u}}_0, {\hat{s}}_0)$.

8.3 Modulation

Now we are ready to show a modulation result for the solution close to the kink profile. For a similar statement, see e.g. [4, 60]. Since Theorem 6.1 is equivalent for positive and negative times, we only consider the positive time case.

Let $(\phi ,\phi _t)$ be the solution to SG (1.1) with initial data (8.6). The perturbation data $({\hat{u}}_0, {\hat{s}}_0)$ is assumed small, depending on $\eta \in (0,\eta _0)$, parameter of the problem. Define, for $K^*>1$ large,

$$\begin{aligned} \begin{aligned} T^*:=&~{} \sup \Big \{ T>0 ~: ~ \forall ~ t\in [0,T], \, \exists ~ {\tilde{\rho }}(t)\in \mathbb {R}~ s.t. ~ \\&~{} \qquad \qquad \qquad \Vert (\phi ,\phi _t)(t)- (Q,Q_t)(x; \beta ,\beta t+ {\tilde{\rho }}(t))\Vert _{H^1\times L^2 } <K^* \eta \Big \}. \end{aligned} \end{aligned}$$

(8.8)

Clearly $T^*>0$ because of the continuity of the SG flow, the assumption (6.1) on the initial data and the fact that $K^*>1$. Suppose, as in [3, 60], that $T^*<+\infty$.

Lemma 8.4

(Modulation). By taking $\eta _0$ smaller if necessary, the following is satisfied. Let $\vec \phi _0:=(Q,Q_t)(\cdot , \beta ,0) + ({\hat{u}}_0, {\hat{s}}_0)$ be given initial data as in (8.6), and let $\vec \phi (t)$ be the corresponding solution to SG, with $\vec \phi (t=0)=\vec \phi _0$. Then, there is $\rho (t)\in \mathbb {R}$ such that,

$$\begin{aligned} ({\widetilde{u}},{\widetilde{s}})(t,x):= (\phi ,\phi _t)(t,x)- (Q,Q_t)(x; \beta ,\beta t + \rho (t)) \end{aligned}$$

(8.9)

satisfies, for all $t\in [0,T^*]$,

$$\begin{aligned} \int ({\widetilde{u}},{\widetilde{s}})(t,x)\cdot (\widetilde{Q}_x,{\widetilde{Q}}_{t,x})(x;\beta ,\beta t + \rho (t)) dx=0. \end{aligned}$$

(8.10)

Moreover, under this condition we have the following dynamical equations for $({\widetilde{u}},{\widetilde{s}})$ and $\rho '(t):$

$$\begin{aligned} \rho (0)=0, \quad ({\widetilde{u}},{\widetilde{s}})(t=0)=({\hat{u}}_0,{\hat{s}}_0), \end{aligned}$$

(8.11)

and

$$\begin{aligned} \left\{ \begin{array}{ll} {\widetilde{u}}_t = {\widetilde{s}}+\rho ' {\widetilde{Q}}_x, \\ {\widetilde{s}}_t={\widetilde{u}}_{xx} -\sin ( Q+{\widetilde{u}}) +\sin Q + \rho ' {\widetilde{Q}}_{t,x}. \end{array}\right. \end{aligned}$$

(8.12)

Proof

Let $z_0\in \mathbb {R}$ be fixed. The idea of the proof is to use the Implicit Function Theorem to ensure the existence of such decomposition with $({\widetilde{u}},{\widetilde{s}})(t,x)$ satisfying the orthogonality condition (8.10). First of all, let us consider the neighborhood

$$\begin{aligned} {\mathcal {U}}(\nu ):=\{(\phi ,\psi )\in H^1_{loc}\times L^2_{loc}: \ \Vert (\phi ,\psi )-(\widetilde{Q},{\widetilde{Q}}_t)(x;\beta ,z_0)\Vert _{H^1\times L^2}<\nu \}. \end{aligned}$$

Note that even when $(\phi ,\psi )$ does not belong to $H^1\times L^2$, its difference with $({\widetilde{Q}},{\widetilde{Q}}_t)$ does. Now, define the functional $Y:{\mathcal {U}}(\eta )\times (-\eta ,\eta )\rightarrow \mathbb {R}$, given by

$$\begin{aligned} Y(\phi ,\psi , \rho ):=\int _\mathbb {R}\big ((\phi ,\psi )(x)-(\widetilde{Q},{\widetilde{Q}}_t)(x;\beta ,z_0+ \rho )\big )\cdot (\widetilde{Q}_x,{\widetilde{Q}}_{t,x})(x;\beta ,z_0+ \rho ) dx. \end{aligned}$$

It is clear that Y is a $C^1$ functional. Moreover, we have

$$\begin{aligned} \dfrac{\partial Y}{\partial \rho }(\phi ,\psi , \rho )&=-\int _\mathbb {R}\Big ({\widetilde{Q}}^2_x(x;\beta ,z_0+ \rho )+\widetilde{Q}^2_{t,x}(x;\beta ,z_0+ \rho )\Big ) dx \\&\quad + \int _\mathbb {R}\big ((\phi ,\psi )(x)-({\widetilde{Q}},{\widetilde{Q}}_{t})(x;\beta ,z_0+ \rho )\big )\cdot ({\widetilde{Q}}_{xx},{\widetilde{Q}}_{t,xx})(x;\beta ,z_0+ \rho ) dx. \end{aligned}$$

Finally, note that at the point $({\widetilde{Q}},\widetilde{Q}_t)(x;\beta ,z_0)$ we have $Y({\widetilde{Q}},{\widetilde{Q}}_t,0)=0$ and

$$\begin{aligned} \dfrac{\partial Y}{\partial \rho }({\widetilde{Q}},\widetilde{Q}_t,0)=-\int _\mathbb {R}\Big ({\widetilde{Q}}_x^2(x;\beta ,z_0)+\widetilde{Q}_{t,x}^2(x;\beta ,z_0)\Big )dx\ne 0. \end{aligned}$$

(8.13)

Thus, by the Implicit Function Theorem we deduce the existence of ${\widetilde{\eta }}>0$ small enough and a ${\mathcal {C}}^1$ function $\rho (\phi ,\psi )$ defined on the neighborhood ${\mathcal {U}}({\widetilde{\eta }})\times (-{\widetilde{\eta }},\widetilde{\eta })$ to a neighborhood of zero such that

$$\begin{aligned} Y(\phi ,\psi , \rho )=0 \quad \hbox {for all }\ (\phi ,\psi )\in {\mathcal {U}}({\widetilde{\eta }})\times (-{\widetilde{\eta }},\widetilde{\eta }). \end{aligned}$$

Note that ${\widetilde{\eta }}$ only depends on (8.13) and not on the point $z_0\in \mathbb {R}$. Hence, for every $(\phi ,\psi )\in {\mathcal {U}}({\widetilde{\eta }})\times (-{\widetilde{\eta }},{\widetilde{\eta }})$ we define the shift $\rho _{z_0}(\phi ,\psi ):=z_0+\rho (\phi ,\psi )$. Finally, using the definition of $T^*$ we can define the mapping $t\mapsto {\widetilde{\rho }}(t)$ on $[0,T^*]$ by setting ${\widetilde{\rho }}(t):=\rho _{\beta t}((\phi ,\phi _t)(t))$. Thus we obtain

$$\begin{aligned} \int ({\widetilde{u}},{\widetilde{s}})(t,x)\cdot (\widetilde{Q}_x,{\widetilde{Q}}_{t,x})(x;\beta ,\beta t+\rho (t))=0, \quad \forall t\in [0,T^*]. \end{aligned}$$

Finally, (8.11) is direct from the chosen type of initial perturbative data (odd, even) and (8.10), and (8.12) are direct. $\square$

Note that $(Q,Q_t)(;\beta ,0)$ is indeed (Q, 0) if $\beta =0$ and we consider the general case $\beta \in (-1,1)$.

9 Lifting of the Data in ${\mathcal {M}}_\eta$

Let $(\phi _0,\phi _1)\in {\mathcal {M}}_\eta$ be initial data as described in Lemma 7.1 and (7.5). Then, there exist unique $(y_0, \delta )\in H^1_o\times \mathbb {R}$ with $\Vert y_0\Vert _{H^1} +|\delta |<\eta$ and such that $({\widetilde{u}}_0, {\widetilde{s}}_0)=\Phi (y_0, 0,\delta )\in H^1_o\times L^2_e$. Consider the SG Eq. (1.1) with initial data $(y_0,0)$. Since this data is (odd, odd), the evolution preserves this property. Namely, there exists a unique global solution $(y,v) \in C(\mathbb {R}; {H^1_o\times L^2_o})$ such that

$$\begin{aligned} \Vert (y,v)(t)\Vert _{H^1\times L^2} \lesssim \eta . \end{aligned}$$

Note additionally that, since $v_0=0$ in this case, one has that (y, v)(t) has zero momentum.

We shall use the results in [37] (see also [14] for earlier results), which claim that (odd, odd) small perturbations of the zero state in SG must converge to zero in compact intervals of space, as time tends to infinity. This is the key part of the paper, stated in Theorem 2.1, in the sense that if we are not able to get (odd, odd) data around zero, then we cannot use [37]. The construction of the manifold (odd, even) of initial data around Q is precisely the way we have to ensure that the data around zero have the right parity conditions.

Consider the (odd, odd) solution $(y,v)(t)\in H^1\times L^2$ of SG mentioned in Theorem 2.1, and constructed using the initial data in ${\mathcal {M}}_\eta$. The purpose of this Section is to connect this solution with the one described in Lemma 8.4, Eq. (8.9).

The main problem associated to this connection (if possible), is to arrive to the correct solution of SG. Here, the uniqueness of the solution (given the same initial data) will be essential to conclude this property. The correct choice of data will be given by (8.9).

9.1 Lifting via modified implicit function

Indeed, let $t\in [0,T^*]$ be fixed, and consider $(Q,Q_t)= (Q,Q_t)(x; \beta ,\beta t + \rho (t))$ and its corresponding modified profile $({\widetilde{Q}}, {\widetilde{Q}}_t):= ({\widetilde{Q}}, {\widetilde{Q}}_t)(x; \beta ,\beta t + \rho (t))$ (see (3.21)). Using (3.14)–(3.15), and given $(y(t),v(t),\delta )\in H^1_o\times L^2_o\times \mathbb {R}$, we will look for a solution $({\hat{u}},{\hat{s}})(t) \in H^1\times L^2$ of⁵

$$\begin{aligned} \widetilde{Q}_x+{\hat{u}}_{x}-v&= \dfrac{1}{1+\delta }\cos \left( \dfrac{\widetilde{Q}+ {\hat{u}}+ y}{2}\right) + (1+\delta ) \cos \left( \dfrac{\widetilde{Q}+{\hat{u}}-y}{2}\right) , \end{aligned}$$

(9.1)

$$\begin{aligned} \widetilde{Q}_t+ {\hat{s}} - y_{x}&=\dfrac{1}{1+\delta }\cos \left( \dfrac{\widetilde{Q}+{\hat{u}}+y}{2}\right) -(1+\delta )\cos \left( \dfrac{\widetilde{Q}+{\hat{u}}-y}{2}\right) , \end{aligned}$$

(9.2)

$$\begin{aligned} \text {with}\quad&\int ({\hat{u}},{\hat{s}})(t,x)\cdot (\widetilde{Q}_x,{\widetilde{Q}}_{t,x})(x;\beta ,\beta t + \rho (t)) dx = 0. \end{aligned}$$

(9.3)

As in [4, 27] and [60], the extra orthogonality condition (9.3) is essential to uniquely solve this nonlinear system. Note the similarity with (8.10).

Following the proof of Lemma 7.1, solving for ${\hat{s}}$ is trivial once we solve for ${\hat{u}}$. Hence, we must solve

$$\begin{aligned} {\hat{u}}_{x} +\frac{1}{2} \left( \frac{1}{(1+ \delta )} + (1+\delta )\right) \sin \left( \frac{\widetilde{Q}}{2}\right) {\hat{u}} = f, \qquad {\hat{u}} \in H^1, \end{aligned}$$

(9.4)

for any $f \in L^2$. We have $\sin \left( \frac{\widetilde{Q}}{2}\right) = \tanh (\gamma (x-\beta t -\rho (t))),$ and (9.4) becomes

$$\begin{aligned} \left( {\hat{u}}\cosh ^{\nu _0} (x-\beta t -\rho (t)) \right) _x = f \cosh ^{\nu _0} (x-\beta t -\rho (t)),\quad \nu _0 = \frac{1}{2\gamma } \left( \dfrac{1}{(1+ \delta )} + (1+\delta )\right) . \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} {\hat{u}} (x) =&~{} {\hat{u}} (x=\beta t+ \rho (t)) \cosh ^{-\nu _0} (x-\beta t -\rho (t)) \\&~{} + \cosh ^{-\nu _0} (x-\beta t -\rho (t)) \int _{\beta t + \rho (t)}^{x} f(s) \cosh ^{\nu _0} (s-\beta t -\rho (t)) \, ds. \end{aligned} \end{aligned}$$

Solving for ${\hat{s}}$ is also direct. Consequently, since from (3.16) we have ${\widetilde{Q}}_x(x;\beta ,\beta t+ \rho (t)) = 2\gamma {\text {sech}}(\gamma (x-\beta t -\rho (t)))$, we conclude that from the orthogonality condition in (9.3) we have ${\hat{u}} (x=\beta t+ \rho (t))$ uniquely determined. The rest of the proof is direct (as in Lemma 7.1), or as in [60].

9.2 Uniqueness of the lifted data

Now we discuss the uniqueness of the solution found, that is, $(\widetilde{Q},{\widetilde{Q}}_t)+ ({\hat{u}},{\hat{s}})$. Since (y, v)(t) is solution to SG (1.1), and $(Q, Q_t)(t)+ ({\widetilde{u}},{\widetilde{s}})(t)$ also solves SG (1.1), and their corresponding initial data are related by BT of parameter $1+\delta$, by Lemma 3.2 we have that they are always related via the same BT (9.1)–(9.2), for all time. Now consider the function $(Q, Q_t)(t)+ ({\hat{u}},{\hat{s}})(t)$. At time 0 one has

$$\begin{aligned} (Q, Q_t)(x;\beta ,0)+ ({\hat{u}},{\hat{s}})(0), \end{aligned}$$

since $\rho (0)=0$ (see (8.11)). Now, recall that $(y,v)(t=0)=(y_0,v_0)=(y_0,0)$, and by uniqueness associated to the Implicit Function (Lemma 7.1), we know that $(\widetilde{u}_0,{\widetilde{s}}_0)=\Phi (y_0,0,\delta )$. Consequently,

$$\begin{aligned} \begin{aligned} (Q, Q_t)(x;\beta ,0)+ ({\hat{u}},{\hat{s}})(0)= (Q^0,0) + ({\widetilde{u}}_0, {\widetilde{s}}_0), \end{aligned} \end{aligned}$$

and therefore $({\hat{u}},{\hat{s}})(0)= ((Q^0,0) -(Q,Q_t)(\cdot , \beta ,0))+ ({\widetilde{u}}_0, {\widetilde{s}}_0)=({\hat{u}}_0, {\hat{s}}_0)$ (see (8.6) and (8.7)). Therefore, one has the same initial data.

The previous argument and the uniqueness obtained via the Implicit Function Theorem applied at time t guarantees that the lifted data $(Q, Q_t)(t)+ ({\hat{u}},{\hat{s}})(t)$ is just $(Q, Q_t)(t)+ (\widetilde{u},{\widetilde{s}})(t)$ as in Lemma 8.4. Moreover, we have also proved that the kink is orbitally stable (see earlier results by [25, 27]).

10 Estimates on the Shift

In this section we prove further estimates on the shift $\rho (t)$ for the case $\beta =0$ that will allow us to prove the remaining parts in Theorem 6.1. Our aim is to prove Corollary 10.4, which relates $\rho '(t)$ with exponentially weighted, quadratic integrals only depending on $(y,y_x,v)$. We start out with the following mixed estimate.

Lemma 10.1

Assume $\beta =0$. Under the hypothesis of Lemma 8.4, for all $t\in \mathbb {R}$ the following bound holds: for any $\varepsilon >0$ small,

$$\begin{aligned} \vert \rho '(t)\vert \lesssim \int e^{-(1+\varepsilon )\vert x-\rho (t)\vert }({\widetilde{u}}^2+\widetilde{u}_x^2)(t,x)dx+\int e^{-(1-\varepsilon )\vert x-\rho (t)\vert }(y^2+y_x^2)(t,x)dx, \end{aligned}$$

(10.1)

with implicit constant independent of time and ${\widetilde{u}}$, y.

Remark 10.1

(About quadratic estimates and convergence) Estimate (10.1) reveals that, under the orthogonality condition (8.10) in the case $\beta =0$, the derivative of $\rho (t)$ is of quadratic order in ${\widetilde{u}}$ and y, a fact that should imply that $\rho (t)$ may converge as $t\rightarrow +\infty$. Unfortunately, there is no simple relationship between the weight $e^{-(1-\varepsilon )\vert x-\rho (t)\vert }$ and the dynamics of $(y^2+y_x^2)(t,x)$. This lack of evident connection for data only in the energy space makes the proof of convergence for $\rho (t)$ harder than usual. In any case, we are able to show in this paper (Theorem 6.1) that either $\rho (t_n)$ diverges for some sequence $t_n\rightarrow +\infty$, or it converges to a final state $\bar{\rho }.$ In both cases, a portion of the radiation term ${\widetilde{u}}$ converges in the energy space, on compact sets.

Remark 10.2

(Conditional convergence) A conditional result for convergence of $\rho (t)$ in every possible case is the following: if the data $(y_0,0)\in {\mathcal {M}}_{\eta ,0} \subseteq H_o^1\times L^2_{e}$ is such that the solution of SG $(y,v)(t)\in H^1_o\times L^2_o$ with initial data at $t=0$ given by $(y_0,0)$ satisfies

$$\begin{aligned} \int _0^\infty \!\!\! \int e^{-(1-\varepsilon )\vert x-\rho (t)\vert }(y^2+y_x^2)(t,x)dxdt <+\infty , \end{aligned}$$

then $\rho (t)\rightarrow {\bar{\rho }} \in \mathbb {R}.$ This result will transpire from the proof of Theorem 6.1.

Proof of Lemma 10.1

Recall that $Q_t=0$ in the $\beta =0$ case, see (3.18). In order to prove (10.1) we multiply (8.12) by $Q'$ and integrate in space, from where we obtain

$$\begin{aligned} \int {\widetilde{u}}_tQ'=\int {\widetilde{s}}Q'+\rho '\int Q'^2. \end{aligned}$$

(10.2)

Now notice that, due to the orthogonality condition and the uniformly smallness of $\widetilde{u}(t,x)$ we have

$$\begin{aligned} c\le \left| \int Q'^2-\int {\widetilde{u}}_tQ'\right| \le C, \end{aligned}$$

for some positive constants $c,C>0$. Therefore, using (11.5) in (10.2) we conclude

$$\begin{aligned} \vert \rho ' (t)\vert\lesssim & {} \left| \int y_xQ'-2\int Q'\left( \cos \left( \dfrac{\widetilde{Q}}{2}\right) \sin \left( \dfrac{\widetilde{u}}{2}\right) \right. \right. \nonumber \\{} & {} \left. \left. + \sin \left( \dfrac{\widetilde{Q}}{2}\right) \cos \left( \dfrac{\widetilde{u}}{2}\right) \right) \sin \left( \dfrac{y}{2}\right) \right| . \end{aligned}$$

(10.3)

On the other hand, notice that by using $Q'=-2\cos (\widetilde{Q}/2)$ and basic trigonometric identities we can rewrite the first and last term on the right-hand side of the latter inequality as

$$\begin{aligned} \left| \int y_xQ'-2Q'\sin \left( \dfrac{\widetilde{Q}}{2}\right) \cos \left( \dfrac{\widetilde{u}}{2}\right) \sin \left( \dfrac{y}{2}\right) \right| =\left| \int y_xQ'+2\int \cos \left( \dfrac{\widetilde{u}}{2}\right) \sin \left( \dfrac{y}{2}\right) Q''\right| , \end{aligned}$$

which, by integration by parts, is equal to

$$\begin{aligned} \left| \int \left( 1-\cos \left( \dfrac{\widetilde{u}}{2}\right) \cos \left( \dfrac{y}{2}\right) \right) Q'y_x+\int \sin \left( \dfrac{\widetilde{u}}{2}\right) \sin \left( \dfrac{y}{2}\right) Q'\widetilde{u}_x\right| . \end{aligned}$$

(10.4)

Finally, we recall that by basic trigonometric bounds together with the uniform smallness of the functions involved we have

$$\begin{aligned} 0\le 1-\cos \left( \dfrac{\widetilde{u}}{2}\right) \cos \left( \dfrac{y}{2}\right) \lesssim \widetilde{u}^2+y^2 \quad \hbox {and}\quad \left| \sin \left( \dfrac{\widetilde{u}}{2}\right) \sin \left( \dfrac{y}{2}\right) \right| \lesssim \vert \widetilde{u} y\vert . \end{aligned}$$

Therefore, plugging together the last identities and by using $ab\le 2a^2+2b^2$ we conclude

$$\begin{aligned} \begin{aligned}&\left| \int y_xQ'-2Q'\sin \left( \dfrac{\widetilde{Q}}{2}\right) \cos \left( \dfrac{\widetilde{u}}{2}\right) \sin \left( \dfrac{y}{2}\right) \right| \\&\quad \lesssim \int e^{-(1-\varepsilon )\vert x-\rho (t)\vert }(y^2+y_x^2)+\int e^{-(1+\varepsilon )\vert x-\rho (t)\vert }(\widetilde{u}^2+\widetilde{u}_x^2), \end{aligned} \end{aligned}$$

(10.5)

for any $0<\varepsilon \ll 1$ small. Notice that, in the same way as before, and by using the fact that $\cos \widetilde{Q}/2\lesssim {\text {sech}}(x-\rho (t))$, we also conclude in (10.3) that

$$\begin{aligned} \left| \int \cos \left( \dfrac{\widetilde{Q}}{2}\right) \sin \left( \dfrac{\widetilde{u}}{2}\right) \sin \left( \dfrac{y}{2}\right) Q'\right| \lesssim \int e^{-2\vert x-\rho (t)\vert }({\widetilde{u}}^2+y^2), \end{aligned}$$

which concludes the proof of the lemma. $\square$

Remark 10.3

Note that the nice cancelation produced in (10.4) is essentially due to the fact that (5.5) holds precisely under the orthogonality condition (8.10) in the case $\beta =0$.

Now our objective is to eliminate the term in ${\widetilde{u}}_x^2$ in (10.1).

Lemma 10.2

Assume $\beta =0$. Under the assumptions of Lemma 8.4, for any $0<\varepsilon \ll 1$ small and all $t\in \mathbb {R}$ the following bound holds

$$\begin{aligned} \int e^{-(1+\varepsilon )\vert x-\rho (t)\vert }\widetilde{u}_x^2\lesssim \int e^{-(1+\varepsilon )\vert x-\rho (t)\vert }(\widetilde{u}^2+y^2+v^2). \end{aligned}$$

(10.6)

Proof

To show (10.6) it is enough to notice that by using identity (11.3) and plugging it into Eq. (11.1) we deduce

$$\begin{aligned} \widetilde{u}_x=v-\sin \left( \dfrac{\widetilde{Q}}{2}\right) \sin \left( \dfrac{\widetilde{u}}{2}\right) \cos \left( \dfrac{y}{2}\right) -2\left( 1-\cos \left( \dfrac{\widetilde{u}}{2}\right) \cos \left( \dfrac{y}{2}\right) \right) \cos \left( \dfrac{\widetilde{Q}}{2}\right) . \end{aligned}$$

Therefore, bounding in the same way as in the proof of Lemma 10.1 we obtain

$$\begin{aligned} \int e^{-(1+\varepsilon )\vert x-\rho (t)\vert }\widetilde{u}_x^2\lesssim \int e^{-(1+\varepsilon )\vert x-\rho (t)\vert } (\widetilde{u}^2+y^2+v^2), \end{aligned}$$

which concludes the proof. $\square$

The final step to prove Corollary 10.4 is a control of ${\widetilde{u}}^2$ in terms of $(y^2+y_x^2+v^2)$, with a reasonable loss in the decaying exponentials involved in the weighted norms.

Lemma 10.3

Under the assumptions of Lemma 8.4, for any $0<\varepsilon \ll 1$ small and all $t\in \mathbb {R}$ the following bound holds

$$\begin{aligned} \int \widetilde{u}^2(t,x){\text {sech}}^{1+\varepsilon }(x-\rho (t))dx\lesssim \int (y^2+y_x^2+v^2)(t,x){\text {sech}}^{1-\varepsilon }(x-\rho (t))dx,\nonumber \\ \end{aligned}$$

(10.7)

with implicit constant independent of t and ${\widetilde{u}}, y, v$.

Proof

We start by rewriting the Bäcklund equation for $\widetilde{u}_x(t,x)$ in a more convenient form. In particular, notice that (11.1) is equivalent to

$$\begin{aligned} \widetilde{u}_x+\sin \left( \dfrac{\widetilde{Q}}{2}\right) \widetilde{u}=\widetilde{F}(t,x), \end{aligned}$$

where $\widetilde{F}(t,x)$ is given by

$$\begin{aligned} \widetilde{F}(t,x)&:=v-2\cos \left( \dfrac{\widetilde{Q}}{2}\right) \left( 1-\cos \left( \dfrac{\widetilde{u}}{2}\right) \cos \left( \dfrac{y}{2}\right) \right) \\&\quad +2\left( \dfrac{\widetilde{u}}{2}-\sin \left( \dfrac{\widetilde{u}}{2}\right) \cos \left( \dfrac{y}{2}\right) \right) \sin \left( \dfrac{\widetilde{Q}}{2}\right) \\ {}&=: v+\textrm{I}+\textrm{II}. \end{aligned}$$

Therefore, by solving the ODE and due to the fact that $\sin \big (\tfrac{\widetilde{Q}}{2}\big )=\tanh (x-\rho (t))$ we obtain

$$\begin{aligned} \widetilde{u}(t,x)=b(t){\text {sech}}(x-\rho (t))+{\text {sech}}(x-\rho (t))\int _{\rho (t)}^x\cosh (z-\rho (t))\widetilde{F}(t,z)dz.\nonumber \\ \end{aligned}$$

(10.8)

Notice that direct computations and Cauchy-Schwarz’s inequality lead us to

$$\begin{aligned}&\int \widetilde{u}^2{\text {sech}}^{1+\varepsilon }(x-\rho (t))dx \nonumber \\&\quad \lesssim b^2(t)+\int {\text {sech}}^{3+\varepsilon }(x-\rho (t))\left( \int _{\rho (t)}^x\cosh (z-\rho (t))\widetilde{F}(t,z)dz\right) ^2dx \nonumber \\&\quad \lesssim b^2(t)+\int {\text {sech}}^{3+\varepsilon }(x-\rho (t))\left( \int _{\rho (t)}^x\cosh ^3(z-\rho (t))dz\right) \nonumber \\&\qquad \left( \int _{\rho (t)}^x{\text {sech}}(z-\rho (t))\widetilde{F}^2(t,z)dz\right) dx \nonumber \\&\quad \lesssim b^2(t)+\int {\text {sech}}(x-\rho (t))\widetilde{F}^2(t,x)dx. \end{aligned}$$

(10.9)

Now we claim that there exists $0<\delta \ll 1$ such that

$$\begin{aligned} \int {\text {sech}}(x-\rho (t))\widetilde{F}^2(t,x)\lesssim & {} \int {\text {sech}}^{1-\varepsilon }(x-\rho (t))(y^2+y_x^2+v^2)\nonumber \\{} & {} +\delta \int {\text {sech}}^{1+\varepsilon }(x-\rho (t))\widetilde{u}^2. \end{aligned}$$

(10.10)

In fact, by using Cauchy-Schwarz’s inequality we obtain

$$\begin{aligned} \int \vert \textrm{I}\vert ^2{\text {sech}}(x-\rho (t))&\lesssim \int {\text {sech}}^4(x-\rho (t))(\widetilde{u}^4+y^4) \\ {}&\lesssim \sup _{t\in \mathbb {R}}\Vert y(t)\Vert _{H^1}^2\int {\text {sech}}(x-\rho (t))y^2 \\ {}&\quad + \sup _{t\in \mathbb {R}}\Vert {\widetilde{u}}(t)\Vert _{H^1}^2\int {\text {sech}}^{1+\varepsilon }(x-\rho (t))\widetilde{u}^2. \end{aligned}$$

On the other hand, by standard trigonometric inequalities and the uniform smallness of the functions involved we have

$$\begin{aligned} \left| \dfrac{\widetilde{u}}{2}-\sin \left( \dfrac{\widetilde{u}}{2}\right) \cos \left( \dfrac{y}{2}\right) \right| \lesssim \vert \widetilde{u}\vert y^2, \end{aligned}$$

and hence, by using again $2ab\le a^2+b^2$ we conclude

$$\begin{aligned} \int \vert \textrm{II}\vert ^2 {\text {sech}}(x-\rho (t))&\lesssim \sup _{t\in \mathbb {R}}\Vert u(t)\Vert _{H^1}^2\sup _{t\in \mathbb {R}}\Vert y(t)\Vert _{H^1}^2\int {\text {sech}}^{1+\varepsilon }(x-\rho (t))\widetilde{u}^2 \\ {}&\quad +\sup _{t\in \mathbb {R}}\Vert y(t)\Vert _{H^1}^4\int {\text {sech}}^{1-\varepsilon }(x-\rho (t))y^2, \end{aligned}$$

which concludes the claim. Finally, we are lead to estimate b(t).

Using (8.10) in the case $\beta =0$, and (3.17)–(3.18) (recall that $\gamma =1$), we have in (10.8)

$$\begin{aligned} |b(t)|^2 \lesssim \left( \int {\text {sech}}^2(x-\rho (t)) \left| \int _{\rho (t)}^x\cosh (z-\rho (t))\widetilde{F}(t,z)dz \right| dx \right) ^2. \end{aligned}$$

By Cauchy-Schwarz,

$$\begin{aligned} |b(t)|^2 \lesssim \int {\text {sech}}^{4-}(x-\rho (t)) \left| \int _{\rho (t)}^x\cosh (z-\rho (t))\widetilde{F}(t,z)dz \right| ^2 dx. \end{aligned}$$

(10.11)

Proceeding as in (10.9), we conclude

$$\begin{aligned} |b(t)|^2 \lesssim \int {\text {sech}}(x-\rho (t))\widetilde{F}^2(t,x)dx. \end{aligned}$$

Gathering this last estimate and (10.10), we conclude. $\square$

We finish this section gathering the main result concerning the quadratic behavior of $\rho '(t)$ in the case $\beta =0$.

Corollary 10.4

Assume $\beta =0$. Under the assumptions of Lemma 8.4, for all $t\in \mathbb {R}$ the following bound holds: for any $0<\varepsilon \ll 1$ small and fixed,

$$\begin{aligned} \vert \rho '(t)\vert \lesssim \int e^{-(1-\varepsilon )\vert x-\rho (t)\vert }(v^2+y^2+y_x^2)(t,x)dx, \end{aligned}$$

(10.12)

with implicit constant independent of time and (y, v).

This result proves (6.2) in Theorem 6.1, part (2). It only remains to show part (2), Eqs. (6.3) and (6.4).

11 End of Proof of Theorem 6.1

In this Section we prove Theorem 6.1, estimates (6.3) and (6.4). Recall that parts (1) and (3) of this result were already proved in Sect. 7 and 8.

Let us consider $\vec \phi _0:= (\phi _0,\phi _1)$ data belonging to the manifold ${\mathcal {M}}_\eta$ in (7.5). Let also $(\phi (t),\phi _t(t))$ be the unique solution of (1.1) with initial condition $(\phi ,\phi _t)(0)=(\phi _0,\phi _1)$. We restrict ourselves to the zero momentum submanifold ${\mathcal {M}}_{\eta ,0}$ introduced in (7.7). In particular, $\beta =0$ and $\gamma =1$ in the kink profile (see (3.21))

$$\begin{aligned} {\widetilde{Q}}(x;\beta ,\beta t + \rho (t))={\widetilde{Q}}(x;0, \rho (t)) =Q(x-\rho (t)) -\pi =: {\widetilde{Q}}(x-\rho (t)). \end{aligned}$$

Moreover, $\delta =0$ in (7.7).

Let us fix now a compact interval I. We divide the proof into several steps. The first two of them concern the limit of the $L^2$-norm of the functions $({\widetilde{u}},{\widetilde{s}})$. We shall only consider the case in which $t\rightarrow \infty$. Nevertheless, the same proof holds for the case when $t\rightarrow -\infty$ up to some obvious modifications.

Step 1. First of all consider (9.1)–(9.2) with ${\hat{u}}={\widetilde{u}}$ (see the discussion in Sect. 9.2):

$$\begin{aligned} \widetilde{Q}_x+{\widetilde{u}}_{x}- v&= \cos \left( \dfrac{\widetilde{Q}+{\widetilde{u}}+y}{2}\right) + \cos \left( \dfrac{\widetilde{Q}+\widetilde{u}-y}{2}\right) , \end{aligned}$$

(11.1)

$$\begin{aligned} \widetilde{Q}_t+{\widetilde{s}}-y_{x}&=\cos \left( \dfrac{\widetilde{Q}+{\widetilde{u}}+y}{2}\right) -\cos \left( \dfrac{\widetilde{Q}+{\widetilde{u}}-y}{2}\right) . \end{aligned}$$

(11.2)

Using that

$$\begin{aligned} \begin{aligned} \cos (A+B+C) =&~{} \cos A \cos B \cos C - \cos A \sin B \sin C \\&~{} - \cos B \sin A \sin C - \cos C \sin A \sin B, \end{aligned} \end{aligned}$$

we obtain

$$\begin{aligned} \begin{aligned}&\cos \left( \dfrac{\widetilde{Q}+{\widetilde{u}}+y}{2}\right) + \cos \left( \dfrac{\widetilde{Q}+{\widetilde{u}}-y}{2}\right) \\&\quad = 2\left( \cos \left( \dfrac{\widetilde{Q}}{2}\right) \cos \left( \dfrac{\widetilde{u}}{2}\right) -\sin \left( \dfrac{\widetilde{Q}}{2}\right) \sin \left( \dfrac{\widetilde{u}}{2}\right) \right) \cos \left( \dfrac{y}{2}\right) , \end{aligned} \end{aligned}$$

(11.3)

and

$$\begin{aligned} \begin{aligned}&\cos \left( \dfrac{\widetilde{Q}+{\widetilde{u}}+y}{2}\right) - \cos \left( \dfrac{\widetilde{Q}+{\widetilde{u}}-y}{2}\right) \\&\quad = -2\left( \cos \left( \dfrac{\widetilde{Q}}{2}\right) \sin \left( \dfrac{\widetilde{u}}{2}\right) + \sin \left( \dfrac{\widetilde{Q}}{2}\right) \cos \left( \dfrac{\widetilde{u}}{2}\right) \right) \sin \left( \dfrac{y}{2}\right) . \end{aligned} \end{aligned}$$

(11.4)

Both identities will be important in what follows. First of all, from (11.4) and the fact that $\widetilde{Q}_t =0$ in (11.2) (since $\beta =0$) one has

$$\begin{aligned} {\widetilde{s}} =y_x -2\left( \cos \left( \dfrac{\widetilde{Q}}{2}\right) \sin \left( \dfrac{\widetilde{u}}{2}\right) + \sin \left( \dfrac{\widetilde{Q}}{2}\right) \cos \left( \dfrac{\widetilde{u}}{2}\right) \right) \sin \left( \dfrac{y}{2}\right) . \end{aligned}$$

(11.5)

Recall the identities (see [60])

$$\begin{aligned} \sin \left( \frac{{\widetilde{Q}}}{2}\right) = \tanh ( x -\rho (t)), \qquad \cos \left( \frac{{\widetilde{Q}}}{2}\right) = {\text {sech}}(x -\rho (t)), \end{aligned}$$

(11.6)

and

$$\begin{aligned} |\sin x| \le |x| \quad \hbox {and} \quad 0\le 1-\cos x \le \min \left\{ 2,\frac{1}{2} x^2\right\} \quad \hbox {(valid for all } x\in \mathbb {R}). \end{aligned}$$

(11.7)

We have a.e. in $\mathbb {R}$

$$\begin{aligned} |{\widetilde{s}}(t,x)| \lesssim |y_x(t,x)| + |y(t,x)|, \end{aligned}$$

(11.8)

so that, from (2.13) and (2.12),

$$\begin{aligned} \int \int e^{-c_1|x|}{\widetilde{s}}^2(t,x)dxdt <+\infty , \qquad \lim _{t\rightarrow \pm \infty } \Vert {\widetilde{s}}(t)\Vert _{L^2(I)} =0, \end{aligned}$$

(11.9)

for any compact interval I. This proves the second component part of Theorem 6.1 in (6.3) and (6.4) (note that no particular sequence of times $t_n\rightarrow +\infty$ is needed in this case).

Step 2. In the case $\beta =0$, we have from (3.18) and (9.3)

$$\begin{aligned} \int {\widetilde{u}} Q'(x-\rho (t))=0. \end{aligned}$$

Taking derivative and using (8.12),

$$\begin{aligned} \rho ' \left( \int Q'^2 + \int {\widetilde{u}} Q'' (x-\rho (t))\right) =-\int {\widetilde{s}} Q'(x-\rho (t)). \end{aligned}$$

On the other hand, from the conservation of (zero) momentum, we have

$$\begin{aligned} 0= \int (Q'(x-\rho (t)) +{\widetilde{u}}_x) {\widetilde{s}} \implies -\int {\widetilde{s}} Q'(x-\rho (t)) = \int {\widetilde{u}}_x {\widetilde{s}}. \end{aligned}$$

We conclude that $\rho '$ is of quadratic order, and satisfies

$$\begin{aligned} |\rho '(t) | \lesssim \left| \int {\widetilde{u}}_x \widetilde{s}\right| \lesssim \eta ^2. \end{aligned}$$

This is also another proof of (6.2).

Step 3. In order to estimate the $\dot{H}^1$-norm of ${\widetilde{u}}$ we use (11.3) to re-write (11.1) as

$$\begin{aligned} \begin{aligned}&{\widetilde{u}}_{x}(t,x) + 2 \sin \left( \dfrac{\widetilde{Q}}{2}\right) \sin \left( \frac{{\widetilde{u}}(t,x)}{2}\right) \\&\quad +2 \cos \left( \dfrac{\widetilde{Q}}{2}\right) \left( 1-\cos \left( \frac{{\widetilde{u}}(t,x)}{2}\right) \right) \cos \left( \frac{y}{2}\right) = F(t,x), \end{aligned} \end{aligned}$$

(11.10)

where F is given by

$$\begin{aligned} F&:= - \widetilde{Q}_x + v +2 \cos \left( \dfrac{\widetilde{Q}}{2}\right) \cos \left( \dfrac{y}{2}\right) - 2 \sin \left( \dfrac{\widetilde{Q}}{2}\right) \left( \cos \left( \dfrac{y}{2}\right) - 1\right) \sin \left( \dfrac{{\widetilde{u}}}{2}\right) \\&= v + 2 \cos \left( \dfrac{\widetilde{Q}}{2}\right) \left( \cos \left( \dfrac{y}{2}\right) -1\right) - 2 \sin \left( \dfrac{\widetilde{Q}}{2}\right) \left( \cos \left( \dfrac{y}{2}\right) - 1\right) \sin \left( \dfrac{\widetilde{u}}{2}\right) . \end{aligned}$$

In the last line, we have used (3.20) which implies that ${\widetilde{Q}}_x = 2\cos \left( \frac{{\widetilde{Q}}}{2}\right)$. Note that since ${\widetilde{u}}\in L^\infty (\mathbb {R}; H^1(\mathbb {R}))$, we have ${\widetilde{u}}$ bounded independently of time. Therefore, F is bounded in $L^\infty (\mathbb {R})$, uniformly in time.

Now we prove that the $L^2_x(I)$-norm of F(t) goes to zero as $t\rightarrow +\infty$. In fact,

$$\begin{aligned} \begin{aligned} \left\| F \right\| _{L^2(I)}&~{} \lesssim \Vert v\Vert _{L^2(I)} + \left\| \cos \left( \dfrac{\widetilde{Q}}{2}\right) \right\| _{L^2(I)} \left\| \cos \left( \dfrac{y}{2}\right) -1 \right\| _{L^\infty (I)}\\&~{} \quad + \left\| \sin \left( \dfrac{\widetilde{Q}}{2}\right) \right\| _{L^\infty (I)} \left\| \cos \left( \dfrac{y}{2}\right) -1\right\| _{L^\infty (I)} \left\| \sin \left( \dfrac{{\widetilde{u}}}{2}\right) \right\| _{L^2(I)}. \end{aligned} \end{aligned}$$

(11.11)

On the other hand, the identities (11.6) imply that

$$\begin{aligned} \left\| F \right\| _{L^2(I)} \lesssim \Vert v\Vert _{L^2(I)} + \left\| \cos \left( \dfrac{y}{2}\right) -1 \right\| _{L^\infty (I)}. \end{aligned}$$

Hence, using Theorem 2.1, the inequalities (11.7), and the continuous embedding of $H^1(\mathbb {R})$ into $L^\infty (\mathbb {R})$ we obtain

$$\begin{aligned} \lim _{t\rightarrow +\infty }\left\| \cos \left( \dfrac{y}{2}\right) -1 \right\| _{L^\infty (I)}=0. \end{aligned}$$

Combining the previous limit and applying Theorem 2.1 again, we conclude

$$\begin{aligned} \lim _{t\rightarrow +\infty }\Vert F(t)\Vert _{L^2_x(I)}=0. \end{aligned}$$

(11.12)

Actually, we can prove even more. From (2.13), (11.6) and the second line in (11.11),

$$\begin{aligned} \begin{aligned} \int e^{-c_0|x|} F^2 (t,x)dx \lesssim&~{} \int e^{-c_0|x|}v^2(t,x)dx \\&~{} + \int e^{-c_0|x|} {\text {sech}}^2(x -\rho (t))y^4(t,x) dx \\&+\int e^{-c_0|x|} {\widetilde{u}}^2 y^4(t,x) dx\\ \lesssim&~{}\int e^{-c_1|x|}v^2(t,x)dx + \eta ^2 \int e^{-c_1|x|} y^2(t,x)dx. \end{aligned} \end{aligned}$$

Consequently, we obtain the stronger property

$$\begin{aligned} \int \int e^{-c_0|x|} F^2 (t,x)dx dt <+\infty . \end{aligned}$$

(11.13)

Assume now that $\Vert {\widetilde{u}}(t)\Vert _{L^2(I)}$ tends to zero as $t\rightarrow +\infty$. Using (11.10) and (11.12),

$$\begin{aligned} \Vert {\widetilde{u}}_{x}(t) \Vert _{L^2(I)} \lesssim \Vert {\widetilde{u}}(t) \Vert _{L^2(I)} + \Vert F(t) \Vert _{L^2(I)} \rightarrow 0 \end{aligned}$$

as $t\rightarrow +\infty .$ This last result shows that we only need to prove $L^2_{loc}$ decay on ${\widetilde{u}}(t)$.

Step 4. Proof of AS. Here we shall consider two cases.

Subcase 1. $|\rho (t_n)| \rightarrow +\infty$ for some $(t_n)$ tending to $+\infty$. With no loss of generality, we assume $\rho (t_n) \rightarrow +\infty$. Fix $x\in I$. Now the ODE (11.10) reads

$$\begin{aligned} {\widetilde{u}}_{x}(t,x) - 2 \sin \left( \frac{\widetilde{u}(t,x)}{2}\right) = {\widetilde{F}} (t,x), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {\widetilde{F}}(t,x):=&~{} F(t,x) - 2\left( 1+ \sin \left( \dfrac{\widetilde{Q}}{2}\right) \right) \sin \left( \frac{{\widetilde{u}}(t,x)}{2}\right) \\&~{} - 2 \cos \left( \dfrac{\widetilde{Q}}{2}\right) \left( 1-\cos \left( \frac{{\widetilde{u}}(t,x)}{2}\right) \right) \cos \left( \frac{y}{2}\right) . \end{aligned} \end{aligned}$$

Note that due to the fact that $\widetilde{u}\in L^\infty (\mathbb {R},H^1(\mathbb {R}))$ and the explicit form of $\widetilde{Q}$ we deduce

$$\begin{aligned} \sup _{t\in \mathbb {R}}\Vert {\widetilde{F}}(t)\Vert _{L^2(\mathbb {R})} <+\infty . \end{aligned}$$

Now, we conveniently rewrite (11.10) as

$$\begin{aligned} {\widetilde{u}}_{x}(t,x) + V(t,x) {\widetilde{u}}(t,x) =\widetilde{F}(t,x), \end{aligned}$$

(11.14)

where V(t, x) is given by

$$\begin{aligned} V(t,x):={\left\{ \begin{array}{ll}- \frac{2}{{\widetilde{u}}(t,x)} \sin \left( \frac{{\widetilde{u}}(t,x)}{2}\right) , &{} {\widetilde{u}}(t,x)\ne 0, \\ -1, &{} {\widetilde{u}}(t,x)=0.\end{array}\right. } \end{aligned}$$

Clearly V defines a bounded function in (t, x). Thus, solving this ODE we obtain the explicit solution

$$\begin{aligned} {\widetilde{u}}(t,x) = -\int _{x}^\infty e^{ \int _x^s V(t,\sigma )d\sigma } \widetilde{F}(t,s)ds. \end{aligned}$$

(11.15)

Using that $\sup _{x\in \mathbb {R}}| {\widetilde{u}}(t,x)| \lesssim \eta \ll 1$, uniformly for $t\in \mathbb {R}$, there exist $\nu =\nu (\eta )\ll 1$ such that

$$\begin{aligned} -1-\nu \le \sup _{x\in \mathbb {R}}V(t,x)\le -1+\nu , \end{aligned}$$

uniformly for $t\in \mathbb {R}$. Replacing this in (11.15) we obtain

$$\begin{aligned} \vert {\widetilde{u}}(t,x)\vert \le \int _x^\infty e^{-c_0(s-x)}\vert \widetilde{F}(t,s)\vert ds=\int _0^\infty e^{-c_0w} \vert \widetilde{F}(t,w+x)\vert dw, \quad c_0:=(1-\nu ). \end{aligned}$$

On the other hand, since all the functions involved belong to $L^\infty (\mathbb {R};H^1(\mathbb {R}))$ we have

$$\begin{aligned} \Vert \widetilde{F}(t)\Vert _{L^\infty _x(\mathbb {R})}\int _0^\infty e^{-c_0w}dw<\infty , \end{aligned}$$

uniformly for $t\in \mathbb {R}$. Finally, taking $L^2_x(I)$-norm and using that (11.12) holds for any bounded interval, we get that

$$\begin{aligned} \lim _{n\rightarrow +\infty }\Vert {\widetilde{u}}(t_n)\Vert _{L^2_x(I)}&\le \lim _{n\rightarrow \infty }\int _0^\infty e^{-c_0w}\Vert \widetilde{F}(t_n)\Vert _{L^2_x(I+w)}dw \\&\le \int _0^\infty e^{-c_0w}\lim _{n\rightarrow \infty }\Vert \widetilde{F}(t_n)\Vert _{L^2_x(I+w)}dw =0, \end{aligned}$$

where we have used Minkowski’s integral inequality and Dominated Convergence’s Theorem, which concludes this step. Therefore, we conclude

$$\begin{aligned} \lim _{n\rightarrow +\infty }\Vert (\widetilde{u}(t_n),\widetilde{s}(t_n))\Vert _{H^1_x(I)\times L^2_x(I)}=0. \end{aligned}$$

(11.16)

This proves (6.3).

Remark 11.1

Note that in the case $\rho (t_n) \rightarrow +\infty$ only $\widetilde{u}(t_n)$ converges along a subsequence. The remaining part $\widetilde{s}(t)$ converges, locally on compact sets of space, along any subsequence of time, no matter if $\rho (t)$ stays bounded or not (see (11.9)).

Subcase 2. $\rho (t)$ is bounded. In this case we have $e^{-(1-\varepsilon )\vert x-\rho (t)\vert } \le C e^{-(1-\varepsilon )\vert x\vert }$ for all time, with $C>0$ depending on $\max _\mathbb {R}\rho (t)<\infty$. From (10.12),

$$\begin{aligned} \vert \rho '(t)\vert \lesssim \int e^{-(1-\varepsilon )\vert x\vert }(v^2+y^2+y_x^2)(t,x)dx. \end{aligned}$$

(11.17)

Now let us recall that by (2.13) we have

$$\begin{aligned} \int _0^\infty \!\!\! \int e^{-(1-\varepsilon )\vert x\vert }(v^2+y^2+y_x^2)(t,x)dxdt <+\infty , \end{aligned}$$

and hence, (11.17) leads to

$$\begin{aligned} |\rho (s_n) -\rho (s_m)| \rightarrow 0, \quad n,m\rightarrow +\infty , \end{aligned}$$

for every sequence $(s_n)$ such that $s_n\rightarrow +\infty .$ Fix one such sequence $(s_n)$; we have $\rho (s_n)\rightarrow {\bar{\rho }}$ (this ${\bar{\rho }}$ still depends on the chosen sequence $(s_n)$, but we will prove that the whole $\rho (t)$ converges to this limit). Now, once again from (11.17),

$$\begin{aligned} |\rho (s_n) -\rho (t)| \lesssim \int _{t}^{s_n}\!\!\! \int e^{-(1-\varepsilon )\vert x\vert }(v^2+y^2+y_x^2)(t,x)dxdt<+\infty . \end{aligned}$$

Sending $n\rightarrow \infty$, and then $t\rightarrow +\infty$, we conclude $\rho (t)\rightarrow {\bar{\rho }}.$ This proves that, whenever $\rho (t)$ stays bounded, it must converge to a final position ${\bar{\rho }}.$

Finally, we prove (6.4). Note that from (8.12), (10.12) and after integration by parts we have

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt} \int ({\widetilde{s}}^2 + {\widetilde{u}}^2 + {\widetilde{u}}_x^2)(t,x){\text {sech}}^{1+\varepsilon }(x)dx=\int \big (\widetilde{s}_t\widetilde{s}+\widetilde{u}_t\widetilde{u}+\widetilde{u}_{tx}\widetilde{u}_x){\text {sech}}^{1+\varepsilon } (x)dx \\ {}&\quad \lesssim \int (\sin \widetilde{Q}-\sin (\widetilde{Q}+u))\widetilde{s}{\text {sech}}^{1+\varepsilon } (x)dx \\ {}&\quad +\int (\widetilde{u}\widetilde{s}+\vert \widetilde{u}_x\widetilde{s}\vert +{\dot{\rho }}\widetilde{u}_x\widetilde{Q}''){\text {sech}}^{1+\varepsilon } (x)dx. \end{aligned}$$

Thus, by using again the standard inequality $2ab\le a^2+b^2$ we deduce

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \int ({\widetilde{s}}^2 + {\widetilde{u}}^2 + {\widetilde{u}}_x^2)(t,x){\text {sech}}^{1+\varepsilon }(x)dx&\lesssim \int (\widetilde{u}^2+\widetilde{u}_x^2+\widetilde{s}^2){\text {sech}}^{1+\varepsilon } (x)dx. \end{aligned}$$

Using (11.8), (10.6) and (10.7), we simply obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \int ({\text {sech}}^{1+\varepsilon } x )({\widetilde{s}}^2 + {\widetilde{u}}^2 + {\widetilde{u}}_x^2)(t,x)dx \lesssim \int e^{-(1-\varepsilon )|x|} (y^2+y_x^2+v^2)(t,x)dx. \end{aligned}$$

Consequently, from (2.13) we conclude (11.16) (and therefore, (6.4)) exactly as it was done in [36].

Appendices

Appendix A: Proof of Proposition 4.1

We follow the ideas in [60], but with some important modifications. Let us consider the Bäcklund functionals introduced in (3.22) and (3.23) with $a=1$ and $\delta =0$ (i.e. $\beta =0$ from (3.19)):

$$\begin{aligned} 0= & {} \widetilde{{\mathcal {F}}}_1({\widetilde{u}},{\widetilde{s}},y,v,0) = {\widetilde{Q}}_x + {\widetilde{u}}_{x} -v - \cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}} + y}{2}\right) -\cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}}-y}{2}\right) , \nonumber \\ 0= & {} \widetilde{{\mathcal {F}}}_2({\widetilde{u}},{\widetilde{s}},y,v,0) = {\widetilde{s}} -y_{x} - \cos \left( \dfrac{{\widetilde{Q}} +{\widetilde{u}} + y}{2}\right) +\cos \left( \dfrac{{\widetilde{Q}} +\widetilde{u}-y}{2}\right) . \end{aligned}$$

(A.1)

Recall that ${\widetilde{Q}}_t =0$ in the case $\beta =0$ (see (3.18)). These functionals are well-defined, see Lemma 3.6, item (d).

Let $(y,v)\in H^1_e\times L^2_e$ be small enough given perturbations (maybe depending on time, but of size uniformly bounded for $t\in \mathbb {R}$). Notice that for any given triplet $(y,v, {\widetilde{u}})\in H^1_e\times L^2_e\times H^1_o$, equation $L_o^2\ni {\mathcal {F}}_2\equiv 0$ is trivially solvable for ${\widetilde{s}}$ and defines a function in $L^2_o$. On the other hand, with a slight abuse of notation,

$$\begin{aligned} \widetilde{{\mathcal {F}}}_1: H^1_o(\mathbb {R})\times L^2_o(\mathbb {R}) \times H^1_e(\mathbb {R})\times L^2_e(\mathbb {R}) \rightarrow L^2_e(\mathbb {R}), \quad \widetilde{\mathcal F}_1=\widetilde{{\mathcal {F}}}_1({\widetilde{u}},{\widetilde{s}},y,v), \end{aligned}$$

defines a ${\mathcal {C}}^1$ functional in a neighborhood of zero and due to Lemma 3.5 we have $\widetilde{{\mathcal {F}}}_1(0,0,0,0)\equiv 0$. Therefore, in order to conclude the proof it is enough to show that the Gâteaux derivative of ${\mathcal {F}}_1$ defines an invertible bounded linear operator with continuous inverse. In fact, notice that linearizing directly on the definition of ${\mathcal {F}}_1$ above and by using basic trigonometric identities we are lead to solve

$$\begin{aligned} {\widetilde{u}}_x =- \sin \left( \frac{{\widetilde{Q}}}{2}\right) \widetilde{u} +f, \, \hbox { for some }\, f\in L^2_e. \end{aligned}$$

(A.2)

Here, $\sin \left( \frac{{\widetilde{Q}}}{2}\right) =\tanh x.$ Now, in order to solve Eq. (A.2), we define $\mu _\beta (x)$ to be the solution of

$$\begin{aligned} \mu _{\beta ,x}-\sin \left( \dfrac{{\widetilde{Q}}}{2}\right) \mu _\beta =0, \, \hbox { that is } \quad \mu _\beta (x)=\cosh x. \end{aligned}$$

At this stage it is important to point out that $\mu _\beta (x)$ is an even function. On the other hand, due to the fact that both $\mu _\beta$ and f are even functions, we conclude that there is only one odd function solving (A.2), which is given by

$$\begin{aligned} {\widetilde{u}}(x)=\dfrac{1}{\mu _\beta (x)}\int _{0}^x \mu _\beta (z) f(z)dz. \end{aligned}$$

(A.3)

Finally, by using Young’s inequality, the explicit form of ${\widetilde{u}}$ and the exponential growth of $\mu _\beta$ it is a straightforward checking that

$$\begin{aligned} \Vert {\widetilde{u}}\Vert _{L^2(\mathbb {R})}\lesssim \Vert f\Vert _{L^2(\mathbb {R})}. \end{aligned}$$

We refer to [60] Section 6 for a complete proof of the latter inequality in a similar context. Notice that in order to conclude that ${\widetilde{u}}\in H^1_o$ it only remains to prove that ${\widetilde{u}}_x\in L^2$. Nevertheless, this is a direct consequence of the explicit form of u in (A.3) and the previous analysis. Therefore, we conclude the proof by applying the Implicit Function Theorem. $\square$

Appendix B: Proof of Proposition 4.2

We follow the guidelines of the proof of Proposition 4.1, with minor but essential differences. Once again, we put in the framework of Lemma 3.6, item (d).

Recall the setting of BT in (A.1). Now we will consider $({\widetilde{u}},{\widetilde{s}})\in H^1_o\times L^2_o$ be small enough given perturbations. Notice that for any given $({\widetilde{u}},y)\in H^1_o \times H^1_e$, equation $\widetilde{{\mathcal {F}}}_1\equiv 0$ is trivially solvable for $v(\cdot )$ and defines a function in $L^2_e$. On the other hand,

$$\begin{aligned} \widetilde{{\mathcal {F}}}_2:H^1_e(\mathbb {R})\times L^2_e(\mathbb {R})\times H^1_o(\mathbb {R})\times L^2_o(\mathbb {R})\rightarrow L^2_o(\mathbb {R}), \quad \widetilde{\mathcal F}_2=\widetilde{{\mathcal {F}}}_2({\widetilde{u}},{\widetilde{s}},y,v), \end{aligned}$$

defines a ${\mathcal {C}}^1$ functional in a neighborhood of zero and due to Lemma 3.5 we have $\widetilde{{\mathcal {F}}}_2(0,0,0,0)\equiv 0$. Therefore, linearizing directly on the definition of $\widetilde{{\mathcal {F}}}_2$ above and by using basic trigonometric identities we are lead to solve

$$\begin{aligned} y_x = \sin \left( \frac{{\widetilde{Q}}}{2}\right) y +f, \, \hbox { for some }\, f\in L^2_o. \end{aligned}$$

(B.1)

Note that unlike (A.2) now we have the opposite sign in the right-hand side. As before, in order to solve Eq. (B.1), we define $\mu _\beta (x)$ to be the solution of

$$\begin{aligned} \mu _{\beta ,x} + \sin \left( \dfrac{{\widetilde{Q}}}{2}\right) \mu _\beta =0, \qquad \hbox { that is } \qquad \mu _\beta (x)={\text {sech}}x. \end{aligned}$$

Notice that since $\mu _\beta$ and f are even and odd functions respectively we conclude

$$\begin{aligned} \int _\mathbb {R}\mu _\beta (x) f(x)dx=0. \end{aligned}$$

Therefore, solving (B.1) from $-\infty$ to x we conclude that there is only one solution to (B.1) which is given by

$$\begin{aligned} y(x)=\dfrac{1}{\mu _\beta (x)}\int _{-\infty }^x \mu _\beta (z) f(z)dz. \end{aligned}$$

(B.2)

Finally, by using Young’s inequality, the explicit form of y and the exponential decay of $\mu _\beta$ it is a straightforward checking that

$$\begin{aligned} \Vert y\Vert _{L^2(\mathbb {R})}\lesssim \Vert f\Vert _{L^2(\mathbb {R})} \quad \hbox {and}\quad \Vert y_x\Vert _{L^2(\mathbb {R})}\lesssim \Vert f\Vert _{L^2(\mathbb {R})}. \end{aligned}$$

We refer to [60] Section 6 for a complete proof of the latter inequality in a similar context. Therefore, we conclude the proof by applying the Implicit Function Theorem. $\square$

Appendix C: Proof of Lemma 4.3

Recall that the wobbling kink is given by (2.9)

$$\begin{aligned} W_\beta (t,x):= 4\arctan e^x + 4\arctan f,\quad f=\frac{g}{h}, \end{aligned}$$

(C.1)

where

$$\begin{aligned} \begin{aligned}&g:=\beta (\sinh (x)\cos (\alpha t) - \sinh (\beta x)),\\&h:=\cosh (x)\cosh (\beta x) - \beta \sinh (x)\sinh (\beta x) - \beta \cos (\alpha t). \end{aligned} \end{aligned}$$

(C.2)

Consequently,

$$\begin{aligned} W_{\beta ,t}=\dfrac{4f_t}{1 + f^2}, \qquad W_{\beta ,x}=2{\text {sech}}(x) + \dfrac{4f_x}{1 + f^2}. \end{aligned}$$

Moreover, directly from (2.1)

$$\begin{aligned} B_{\beta ,t}= \dfrac{4\alpha ^2\beta \cos (\alpha t)\cosh (\beta x)}{\alpha ^2\cosh ^2 (\beta x)+\beta ^2\sin ^2(\alpha t)}, \qquad B_{\beta ,x}=\dfrac{-4\alpha \beta ^2\sin (\alpha t)\sinh (\beta x)}{\alpha ^2\cosh ^2(\beta x)+\beta ^2\sin ^2(\alpha t)}, \end{aligned}$$

and

$$\begin{aligned} \sin \left( \dfrac{B_\beta }{2}\right)&=\dfrac{2\alpha \beta \sin (\alpha t)\cosh (\beta x)}{\alpha ^2\cosh ^2(\beta x)+\beta ^2\sin ^2(\alpha t)}, \\ \cos \left( \dfrac{B_\beta }{2}\right)&=\dfrac{\alpha ^2\cosh ^2(\beta x)-\beta ^2\sin ^2(\alpha t)}{\alpha ^2\cosh ^2(\beta x)+\beta ^2\sin ^2(\alpha t)}. \end{aligned}$$

On the other hand,

$$\begin{aligned} \begin{aligned} \sin \left( \dfrac{W_\beta }{2}\right) =&~{} \frac{1-f^2}{1+f^2}{\text {sech}}(x) - \frac{2f\tanh (x)}{1+f^2}, \\ \cos \left( \dfrac{W_\beta }{2}\right) =&~{} -\frac{1-f^2}{1+f^2}\tanh (x) - \frac{2f{\text {sech}}(x)}{1+f^2}. \end{aligned} \end{aligned}$$

Then we recast (4.2)–(4.3) as follows,

$$\begin{aligned}&(\alpha ^2\cosh ^2(\beta x)+\beta ^2\sin ^2(\alpha t))\Big (2(1+f^2){\text {sech}}(x) + 4f_x\Big ) \\&\qquad - 4\alpha ^2\beta \cos (\alpha t)\cosh (\beta x)(1+f^2)\\&\quad = 2(\alpha ^2\cosh ^2(\beta x) - \beta ^2\sin ^2(\alpha t)) \Big ((1-f^2){\text {sech}}(x) - 2f\tanh (x)\Big ), \end{aligned}$$

and

$$\begin{aligned}&4f_t(\alpha ^2\cosh ^2(\beta x)+\beta ^2\sin ^2(\alpha t)) + 4\alpha \beta ^2\sin (\alpha t)\sinh (\beta x)(1+f^2)\\&\quad =- 4\alpha \beta \sin (\alpha t)\cosh (\beta x) \Big ((1-f^2)\tanh (x) + 2f{\text {sech}}(x)\Big ), \end{aligned}$$

or in terms of g, h,  we get

$$\begin{aligned}{} & {} (\alpha ^2\cosh ^2(\beta x)+\beta ^2\sin ^2(\alpha t))\Big (2(h^2+g^2){\text {sech}}(x) + 4(g_xh - gh_x)\Big )\nonumber \\{} & {} \qquad - 4\alpha ^2\beta \cos (\alpha t)\cosh (\beta x)(h^2+g^2)\nonumber \\{} & {} \quad = 2(\alpha ^2\cosh ^2(\beta x) - \beta ^2\sin ^2(\alpha t)) \Big ((h^2-g^2){\text {sech}}(x) - 2gh\tanh (x)\Big ),\nonumber \\ \end{aligned}$$

(C.3)

$$\begin{aligned}{} & {} 4(g_th - gh_t)(\alpha ^2\cosh ^2(\beta x)+\beta ^2\sin ^2(\alpha t)) + 4\alpha \beta ^2\sin (\alpha t)\sinh (\beta x)(h^2+g^2)\nonumber \\{} & {} \quad = -4\alpha \beta \sin (\alpha t)\cosh (\beta x) \Big ((h^2-g^2)\tanh (x) + 2gh{\text {sech}}(x)\Big ). \end{aligned}$$

(C.4)

Now, having in mind that from (C.2),

$$\begin{aligned}&g_x=\beta (\cosh (x)\cosh (\beta x) - \beta \cosh (\beta x)),\\&g_t=-\alpha \beta \sinh (x)\sin (\alpha t),\\&h_x=\alpha ^2\sinh (x)\cosh (\beta x),\\&h_t=\alpha \beta \sin (\alpha t), \end{aligned}$$

substituting in (C.3)–(C.4) and after easy manipulations, we conclude and the proof is complete. $\square$

Appendix D: Proof of Remark 4.11

First of all, notice that by standard trigonometric identities we have

$$\begin{aligned} \tan (\Theta -{\overline{\Theta }})=\dfrac{\Upsilon -{\overline{\Upsilon }}}{1-\Upsilon {\overline{\Upsilon }}} \quad \hbox { where } \, \quad \Upsilon :=\left( \dfrac{\beta a_v+i\alpha a_v+1}{\beta a_v+i\alpha a_v-1}\right) \dfrac{e^x-e^{\gamma [\beta (x-vt)-i\alpha (t-vx)]}}{1+e^{x+\gamma [\beta (x-vt)-i\alpha (t-vx)]}}. \end{aligned}$$

Thus, after some easy manipulations we conclude that $\tan (\Theta -{\overline{\Theta }})=\tfrac{A_1}{A_2}$, where

$$\begin{aligned} A_1&=i(a_v^2-1)\cosh (x)\sin (\gamma \alpha (t-vx)) \\ {}&\quad -2ia_v\alpha \cos \big (\gamma \alpha (t-vx)\big )\sinh (x)-2ia_v\alpha \sinh \big (\gamma \beta (tv-x)\big ) \end{aligned}$$

and

$$\begin{aligned} A_2&=-2a_v\beta \cos \big (\gamma \alpha (t-vx)\big ) \\ {}&\quad +\cosh (\gamma v\beta t)\Big ((1+a_v^2)\cosh (x)\cosh (\gamma \beta x)-2a_v\beta \sinh (x)\sinh (\gamma \beta x)\Big ) \\ {}&\quad +\sinh (\gamma v\beta t)\Big (2a_v\beta \sinh (x)\cosh (\gamma \beta x)-(1+a_v^2)\cosh (x)\sinh (\gamma \beta x)\Big ). \end{aligned}$$

Notice that, if $v=0$, then $W_{\beta ,v}\equiv W_\beta$, where $W_\beta$ is given by (2.9).