Abstract
Three phases of macroscopic domains have been seen for large but finite periodic dimer models; these are known as the frozen, rough and smooth phases. The transition region between the frozen and rough region has received a lot of attention for the last twenty years and recently work has been underway to understand the rough–smooth transition region in the case of the two-periodic Aztec diamond. We compute uniform asymptotics for dimer–dimer correlations of the two-periodic Aztec diamond when the dimers lie in the rough–smooth transition region. These asymptotics rely on a formula found in Chhita and Johansson (Adv Math 294:37–149, 2016) for the inverse Kasteleyn matrix, they also apply to the infinite square grid dimer model with a variable weighting which interpolates between the rough and smooth phase (Kenyon et al. Ann Math (2) 163(3):1019–1056, 2006). In particular, we find that distant dimers initially decay exponentially when the magnetic coordinates are very close to the bounded complementary component of the associated amoebae, they then transition to a power law decay once far enough apart.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A dimer model on a bipartite planar graph G consists of a probability measure \({\mathbb {P}}\) on the set of dimer configurations of G. We recall that a dimer configuration of a graph G is a set of edges in G with the property that each vertex belongs to exactly one edge. We call an edge in a dimer configuration a dimer. Dimer configurations have a simple bijection to an associated set of tilings. The bijection is in terms of the dual graph \(G^*\) of G; since each dimer e crosses two faces of the dual graph, let the tile corresponding to e be the union of these two faces. In this paper we will focus on a graph G which is the subgraph of the grid graph of \({\mathbb {Z}}^2\) satisfying \(|x|+|y|\le n\). Since \({\mathbb {Z}}^2\) is its own dual graph, this is the study of domino tilings of the Aztec Diamond introduced in [14].
One can also define a set of surfaces in \({\mathbb {R}}^3\) called height functions which are in bijection with the dimer configurations of G. When the graph and probability measure have a certain double periodicity, [21] find that three classes of limiting Gibbs measures are possible. The three classes are referred to as frozen (solid), rough (liquid) and smooth (gas). Each of the three classes has a distinct decay of correlations for distant dimers, namely fixed (or zero decay), polynomial and exponential decay.
The above classes are also related to the fluctuations and average slope of the associated random height functions. As the system size becomes large, the induced measure on height functions localises on functions with distinct domains. The limiting global height function in these domains either has a smoothly varying, strictly non-zero curvature or zero curvature and a flat shape - called facets. The rough regions, in which the height functions curve, are rough in the sense that they have logarithmic fluctuations around their macroscopic shape. In these regions one expects the height fluctuations to be given by the Gaussian free field in an appropriate limit. The facets can have either no fluctuations (frozen) or bounded fluctuations (“smooth” but with small Poisson-like dislocations). The typical behaviour of the macroscopic height function at a rough to facet boundary point \(x_0\) is expected to be like \(\sim (x-x_0)^{3/2}\), see [7], the Pokrovsky-Talapov law. This has been proven rigorously by [1] for frozen boundaries in a large class of dimer models. In [1], there is also proof of the existence of smooth facets in the rather general setting of dimer models with polygonal boundary, this follows from a variational formula for the height function originating in [10]. In the context of random height functions our results relate to the correlations of the microscopic gradients of the height function at a rough–smooth boundary. We also remark that, aside from the formulas used here, the only other formulas available for the investigation of this type of transition are those of the type found in [4, 5, 13]. These formulas currently only pertain to the Aztec diamond graph, and there are currently none available for tilings of other domains with a smooth phase.
This article contains a uniform analysis of the decay of dimer correlations in different directions in a large two-periodic Aztec Diamond in the transition region between the rough and smooth phases. We study this decay in the finite model since if we let the size of the Aztec Diamond go to infinity first we only see a smooth pure phase in the transition region. Our analysis also applies to an infinite planar model with the same graph and weights induced to have the right slope of the height function. One result in this setting is the following theorem.
Theorem 1
Consider dimers in any large enough bounded region of the infinite grid graph (with vertices given by \({\mathbb {Z}}^2\)). There are Gibbs measures in the rough phase (or liquid phase) for which these dimers have exponential decay of correlations.
Proof
See Sect. 4.1. \(\square \)
This behavior of the correlations appears when the slope of the model is such that we are very close to a smooth phase. We will see that as we get closer to the smooth phase, the larger the corresponding region in which the dimers experience exponential decay of correlations. However for much larger distances we see the decay of correlations typically associated with the rough phase. Thus, although we are in a rough phase, if we look locally it seems like we are in a smooth phase and the rough phase only manifests itself at sufficiently long distances. The behavior at the rough–smooth boundary in the finite two-periodic Aztec diamond is given for dimers separated along the diagonal below in Theorem 2, and at arbitrary angles in Sect. 3.1.
As a further general background, the interpolation between exponential and power law decay of correlations has already been observed in a variety of two-dimensional models in statistical mechanics [7]. Whilst rigorous results are limited [15], physicists have used renormalisation group/mean field techniques along with numerical simulations to analyse the transition region of some of these models. As such, it is expected that a sharp transition occurs between the two regimes (exponential and power law decay). This is known as a Kosterlitz-Thouless phase transition, which was originally characterised by the appearance of "topological defects". For example, in the XY model the transition is associated with the appearance of vortices. The interpretation is that these vortices destroy the quasi-long range order present in the lower temperature regime giving rise to short range order and exponential decay of correlations. We discuss a kind of analogue of this and Fig. 3 for the infinite dimer model at the end of Sect. 4.1. For models with a similar transition which have been rigorously investigated more recently, see [6] and references therein.
1.1 Definition of the model
Consider the subset of \({\mathbb {Z}}^2\) given by \(V = W\cup B\), where
and
We define the vertex set V as the vertex set of the Aztec Diamond graph AD of size n with corresponding edge set given by all \(b-w=\pm \textbf{e}_1, \pm \textbf{e}_2\) for all \(b\in B, w\in W\), where \(\textbf{e}_1=(1,1)\), \(\textbf{e}_2=(-1,1)\). For an Aztec Diamond of size \(n=4m, m\in {\mathbb {N}}_{>0}\) define the weight as a function w from the edge set into \({\mathbb {R}}_{> 0}\) such that the edges contained in the smallest cycle surrounding the point (i, j) where \((i+j)\) mod \(4=2\), have weight \(a\in (0,\infty )\) and the edges contained in the smallest cycle surrounding the point (i, j) where \((i+j)\) mod \(4=0\) have weight \(b\in (0,\infty )\). Each of these cycles is the boundary of a face of AD and we call each of these faces an a face (b face) if the edges on its boundary each have weight a (b). We divide the white and black vertices into two different types. For \(i\in \{0,1\}\),
and
Define a probability measure \({\mathbb {P}}_{Az}\) on the finite set of all dimer configurations \({\mathcal {M}}(AD)\) of AD. For a dimer configuration \(\omega \in {\mathcal {M}}(AD)\),
is the partition function and the product is over all edges in \(\omega \). We call the probability space corresponding to \({\mathbb {P}}_{Az}\) and \({\mathcal {M}}(AD)\) the two-periodic Aztec Diamond, and note that the setup here is the same as in [8].
Fix \(a\in (0,1)\) and take, without loss of generality, \(b=1\). It is convenient to set \(c=a/(1+a^2)\in (0,1/2)\). Our goal is to take a very large n and compute uniform asymptotics of the correlation of two edges separated by a growing distance but for distances much smaller than n. We want to investigate the decay of correlations in the transition region between the rough and smooth phases of the model. As in [8] we only consider dimers in the the bottom left quadrant of AD. Let \(-1<\xi <0\) so that \((n(1+\xi ),n(1+\xi ))\) is the coordinate varying over the diagonal of the bottom left quadrant of the Aztec Diamond. We will use \((n(1+\xi ), n(1+\xi ))\) as a reference point so we want it to have integer coordinates, i.e. we assume that
The reference point should be close to the asymptotic rough–smooth boundary. Following the notation in [8], let \(\xi _c=-\frac{1}{2}\sqrt{1-2c}\) so that \(\xi =\xi _c\) corresponds to the limiting rough–smooth boundary. We will consider \(\xi \) close to \(\xi _c\).
Example 1
There are many possibilities for the location and orientation of the dimers. For our discussion of the correlations we will consider the following case. We take two dimers \(e_1=(x^{(1)},y^{(1)})\) and \(e_2=(x^{(2)},y^{(2)})\) in two separate a faces and both connecting the vertices of type \(W_0\) and \(B_0\), so \((x^{(i)},y^{(i)})\in W_0\times B_0\) for \(i=1,2\). We place one along the main diagonal. Explicitly
for \(r_1,r_2\in {\mathbb {Z}}\) such that \(r_1+r_2\) is even and \(2(|r_1|+|r_2|)\le r\).
Define the dimer–dimer correlation \(\text {corr}(e_1,e_2)\) of two dimers \(e_1,e_2\) to be the covariance of their indicators \(\mathbbm {1}_{e_1\in \omega }, \mathbbm {1}_{e_2\in \omega }\). We have
We first formulate a Theorem for the covariance in the setting of Example 1 with the dimers separated along the diagonal. This is found in Sect. 3.1, where it is restated as Theorem 7.
Define \(|G(i)|=(1-\sqrt{1-2c})/\sqrt{2c}\) and note that \(|G(i)|<1\), a function G will be introduced in general later. This function will come into the exponential decay rates of the correlations of dimers at arbitrary angles, however here we give a theorem for the case where dimers are separated along a direction parallel to the main diagonal, that is, parallel to the vector \(\textbf{e}_1=(1,1)\). Given a small \(\varepsilon >0\), we define \(\Lambda _\varepsilon \) to be the set of real numbers where we stay at least \(\varepsilon \) away from all \(n\pi \), \(n\ne 0\), i.e.
We use the convention that \(\sin (bx)/x=b\) when \(x=0\). We will use \(\simeq \) to say that two expressions are equal if we neglect subdominant terms. By this we mean that, for functions F, G, H of \(n,r,\xi \), the equality \(F_{r,\xi }^n=G_{r,\xi }^n+H_{r,\xi }^n\) is written \(F_{r,\xi }^n\simeq G_{r,\xi }^n\) if
where H is a subdominant term.
Theorem 2
Fix a small \(\varepsilon >0\), \(\gamma \in (1/2,1]\). Let \(\delta ^*_n>0\) be any sequence going to zero with n and take n so large that \(\delta ^*_n>0\) is sufficiently small. Let \(\xi _c-\xi =\delta ^*_n\) be such that \(n(\xi _c-\xi )>>n^{1/3}\). Let the distance between the two dimers \(r=\sqrt{r_1^2+r_2^2}\) lie in an interval \((r_{\text {min}},r_{n})\) where \(r_{\text {min}}>0\) is large but fixed and \(r_{n}\) is very large (growing with n) but less than \(\varphi _c^{\gamma -2}/2\). The function \(\varphi _c:=\varphi _c(\xi )\) is proportional to \(\sqrt{\xi _c-\xi }\) and is determined later. Let \(2r\varphi _c/\sqrt{1-2c}\in \Lambda _\varepsilon \) and take the direction pointing from one of the dimers to the other to be parallel to the main diagonal, that is, parallel to the vector (1, 1). Then
Looking at the formula in (6), observe how the behaviour of the term
changes as a function of r. If \(2r\varphi _c\) is small compared to \(\sqrt{1-2c}\) it is close to the constant \(\varphi _c\) (n is fixed), i.e. the smaller r is compared to the ratio \(\sqrt{1-2c}/(2\varphi _c)\) the closer the term (7) is to the constant \(\varphi _c\). Whereas for \(2r\varphi _c>\sqrt{1-2c}\) the term starts to slowly oscillate and decay like 1/r. This leads to three regimes for the correlation as a function of r. Pick any sequence \(M_n\) such that \(2M_n\varphi _c/\sqrt{1-2c}\) tends to zero, for example \(M_n=\varphi _c^{-1+\varepsilon }\), then for n fixed large enough
Regime I. As r varies from \(r_{\min }\) to \(\frac{1}{\log |G(i)|^{-2}}\log \frac{1}{\varphi _c}\),
which has exponential decay in r.
Regime II. As r varies from \(\frac{1}{\log |G(i)|^{-2}}\log \frac{1}{\varphi _c}\) to \(M_n\) then
which has no decay, so the correlation is constant.
Regime III. As r varies from \(M_n\) to \(r_n\),
which begins to oscillate and has a decay like \(1/r^2\).
The sign of the correlation changes depending on which type of dimers we pick. Here is some intuition behind the results. Think of the above case when the direction pointing from one dimer to the other is parallel to the main diagonal. There are two length scales in the problem. One is the lattice spacing and the other is the typical distance \(1/\sqrt{\xi _c-\xi }\) between the paths that we see in Fig. 3. These are the long (corridor) paths which connect sides of the Aztec diamond defined in [3]. As we increase the distance r between the dimers we first see the smooth phase exponential decay which takes place in the order of the lattice spacing. After that the correlations in some sense come from the paths, similar to what should happen at the rough-frozen boundary. In terms of the distance between the paths the lattice spacing is very short and hence we see constant correlations proportional to \(\xi _c-\xi \). At some point when the distance r is of order \(1/\sqrt{\xi _c-\xi }\), we start to see the type of decay that we have in a rough phase. Indeed here, if we set \(r=d/\sqrt{\xi _c-\xi }\) the correlations decay like \((\xi _c-\xi )\frac{\sin ^2(d)}{d^2}\) (omitting constants).
We can also consider the decay of the covariance in other directions, we summarise the results of Theorem 8. Take the direction pointing from one dimer to the other to be parallel to the anti-diagonal, i.e the vector \((-1,1)\). Let \(0<m<1\) be small and \(M>1\) large. As r varies from \(r_{\text {min}}\) to \(c_3\log (\frac{1}{\sqrt{\xi _c-\xi }})\),
then as r varies from \(\log (\frac{1}{\sqrt{\xi _c-\xi }})\) to \(m/(\xi _c-\xi )\),
then as r varies from \(m/(\xi _c-\xi )\) to \(M/(\xi _c-\xi )\) we see a transition to
and then as r varies from \(M/(\xi _c-\xi )\) to \(r_n\) we see a transition to
For a results on arbitrary directions, see Sect. 3, in particular Theorem 9.
1.2 Kasteleyn’s approach and dimer statistics
The classical approach to analyse the statistical behaviour of random dimer configurations of large bipartite graphs G is to follow an idea introduced by Kasteleyn. In this approach, one puts signs \(+1,-1\) (called a Kasteleyn orientation) into a submatrix of the weighted adjacency matrix indexed by \(B'\times W'\) for the black and white vertices, \(B'\) and \(W'\), of G. The resulting matrix K is called the Kasteleyn matrix and has the property that the partition function of the dimer model is equal to the absolute value of the determinant of K. The key idea in this approach is that the signs one introduced to construct the matrix K cause the non-zero terms in the sum of the determinant of K to all have the same sign. In general, the Kasteleyn orientation is not unique, and its values need not be restricted to \(1,-1\). Here we introduce the Kasteleyn matrix \(K_{a,1}\) that we use for the two-periodic Aztec Diamond model of size \(n=4m\). Define
where \(i=\sqrt{-1},\) \(j\in \{0,1\} \). For dimers \(e_1,...,e_n\), define the n-point correlation function
One can use the determinantal expression of the partition function to show that collections of dimers form a determinantal point process. Indeed, a theorem from Kenyon [20] (see also [19]) gives that for \(e_i=(b_i,w_i), \ i=1,...,n\), the n-point correlation functions are
with correlation kernel
In the above, \(K_{a,1}^{-1}(w_j,b_i)\) is the inverse of the Kasteleyn matrix \(K_{a,1}\) evaluated at \((w_j,b_i)\). From (3) we can write the covariance between two dimers in terms of \(K_{a,1}\) and \(K_{a,1}^{-1}\),
1.3 Dimer locations
We can specify that locations of arbitrary dimers as follows. Let \(\mathbbm {1}_{a_F}\) be an indicator function on the edge set so that \(\mathbbm {1}_{a_F}(e)=1\) if the edge e has weight a and \(\mathbbm {1}_{a_F}(e)=0\) otherwise. Take two dimers and label their positions as follows: For \(i=1,2\), let \(\varepsilon _1^{(i)},\varepsilon _2^{(i)}\in \{0,1\}\), the dimer \(e_i\) is given by a pair of vertices \((x_{\varepsilon _1}^{(i)},y_{\varepsilon _2}^{(i)}):=(x_{ \varepsilon _1^{(i)}}^{(i)},y_{\varepsilon _2^{(i)}}^{(i)})\in W_{\varepsilon _1^{(i)}}\times B_{\varepsilon _2^{(i)}}\) where
and \((r_1^{(i)}, r_2^{(i)})\in \{ (r_1^{(i)}, r_2^{(i)})\in {\mathbb {Z}}^2 : r_1^{(i)}+r_2^{(i)}\in 2{\mathbb {Z}}\ \text {and} \ |2r_1^{(i)}|+|2r_2^{(i)}| \le r\}\).
Note that the sum of \(r_1^{(i)}\) and \(r_2^{(i)}\) is always even and \((n(1+\xi )+1,n(1+\xi ))\) is always a \(W_0\)-type vertex. So \(x_0^{(i)}=(n(1+\xi )+2r_1^{(i)}+1,n(1+\xi )+2r_2^{(i)})\) generates all possible \(W_0\) vertices within a distance r of \((n(1+\xi )+1,n(1+\xi ))\). In (20) and (21) we have written the locations of the vertices x and y corresponding to the edge \(e=(x,y)\in W\times B\) as the sum of two coordinate vectors, the first corresponds to the \(W_0\) vertex in the same a or b face as e and the second is \((0,2\varepsilon _1^{(i)}(2\mathbbm {1}_{a_F}(e_i)-1))\) for the white vertex x or \(((-1+2\varepsilon _2^{(i)})(2\mathbbm {1}_{a_F}(e_i)-1),2\mathbbm {1}_{a_F}(e_i)-1)\) for the black vertex y.
1.4 Definitions and uniform asymptotic results
In order to investigate the dimer–dimer correlation (19) asymptotically we need asymptotic formulas for \(K_{a,1}^{-1}\). To prove these asymptotic results we need a good formula for \(K_{a,1}^{-1}\) as a starting point. A double contour integral formula for \(K_{a,1}^{-1}\) was derived in [8] starting from a quadruple integral formula found in [9]. Other versions of the result, not giving the inverse Kasteleyn matrix but a related particle kernel, have been derived in [13] and in [5] using a completely different approach. The rough–smooth boundary has also been investigated in [2] and [3] with the aim of establishing that right at the boundary we can see the Airy kernel point process. We will use the formula for \(K_{a,1}^{-1}\) derived in [8]. Before we can give the formula we first need to define the objects that come into it. For \(\varepsilon _1,\varepsilon _2\in \{0,1\}\), we write
In many cases the coordinates of the vertices giving the position of the dimers will enter into formulas via the following expressions. Let \((x_1,x_2)\in W_{\varepsilon _1}\), \((y_1,y_2)\in B_{\varepsilon _2}\) and define
Denote the open punctured unit disc \({\mathbb {D}}^*={\mathbb {D}}\setminus \{0\}\subset {\mathbb {C}}\). A basic role is played by the analytic function
with \(\sqrt{w^2 +2c}=i\sqrt{-\sqrt{2c}-iw}\sqrt{\sqrt{2c}-iw}\) where the previous two square roots are principal branch square roots. Let \(\sqrt{1/w^2 +2c}\) denote the previous function evaluated at 1/w. Equivalently,
where the previous square root is the principal branch square root. We note that G is the inverse of the analytic bijective map
J is related to the Joukovski map and the above claims about J and G follow from chapter 6 in [22]. From the definition, we have the symmetries
which give
We emphasise the fact that for all w in the domain of G we have the bound \(|G(w)|<1\), which follows from the definition of G, this fact gives the exponential decay of various asymptotic formulas.
Let \(k,\ell \) be non-zero integers. For \(k,\ell > 0\) define
where \(\Gamma _1\subset {\mathbb {C}}\) is the circle of radius 1 centred at the origin, and then for all \(k,\ell \) define
For vertices \((x_1,x_2)\in W_{\varepsilon _1}\), \((y_1,y_2)\in B_{\varepsilon _2}\), we define
where we used (23) and (24). This is the inverse Kasteleyn matrix in an infinite smooth phase planar model, see Sect. 4. In the asymptotic analysis of the inverse Kasteleyn matrix \(K_{a,1}^{-1}\) in [8], the following saddle-point function appears
We recall from [8] that for \(-\sqrt{1+2c}/2<\xi <\xi _c\), \(g_\xi \) has four critical points \(\pm \omega _c, \pm {\overline{\omega }}_c\), \(\omega _c=e^{i\theta _c}\), \(\theta _c\in [0,\pi /2]\), where \(g'_\xi (\pm \omega _c)=g'_\xi (\pm \overline{\omega _c})=0\). These four points satisfy the saddle-point equation
by (257), and will hence depend on \(\xi \). Define
where the contour \(\Gamma _{\omega _c}=\{e^{i\theta }:\theta \in (\theta _c,\pi -\theta _c)\cup (-\pi +\theta _c,-\theta _c)\}\) has positive orientation around the origin. For \(x=(x_1,x_2)\in W_{\varepsilon _1}\), \(y=(y_1,y_2)\in B_{\varepsilon _2}\), define
The elements of the inverse Kasteleyn matrix are given by the following theorem.
Theorem 3
For \(n=4m\), \(m\in {\mathbb {N}}_{>0}\), \((x_1,x_2)\in W_{\varepsilon _1}\), \((y_1,y_2)\in B_{\varepsilon _2}\) with \(\varepsilon _1,\varepsilon _2\in \{0,1\}\) then
We will not define \(B^*_{\varepsilon _1,\varepsilon _2}\) here. By lemma 3.6 in [8] there are positive constants \(C_1,C_2\) such that \(|B^*_{\varepsilon _1,\varepsilon _2}(a,x_1,x_2,y_1,y_2)|\le C_1e^{-C_2 n}\) when the vertices \((x_1,x_2)\), \((y_1,y_2)\) are distance \(O(\sqrt{n})\) from the line \((n(1+\xi ),n(1+\xi ))\), \(-1<\xi <0\). This means that for the purposes of this paper it will be negligible. The theorem follows from the results in [8], see Sect. 7. The term \(R_{\varepsilon _1,\varepsilon _2}\) is an error term in this paper. We have the following bound for \(R_{\varepsilon _1,\varepsilon _2}\).
Proposition 1
Let
If \(\delta ^*_n>0\) is a sequence going to zero as \(n\rightarrow \infty \) then there exists \(B,C>0\) such that for any n large enough and \(0< \xi _c-\xi \le \delta ^*_n\)
uniformly for all \(|a_i|,|b_i|\le \max \{n^{1/3},\sqrt{n\sqrt{\xi _c-\xi }}\}\) with \(i=1,2\).
We see that what we need is uniform asymptotics for \({\mathbb {K}}_{1,1}^{-1}\) and \(C_{\omega _c}\). The main results of this paper is the bound in Proposition 1 and uniform asymptotics for \({\mathbb {K}}_{1,1}^{-1}\) and \(C_{\omega _c}\).
Theorem 4
The asymptotic formulas (49), (50), (51), and (54) below together with (32) and (36), give uniform asymptotics for \({\mathbb {K}}_{1,1}^{-1}\) and \(C_{\omega _c}\), and hence for \(K_{a,1}^{-1}\) by (37).
Although these formulas give the asymptotics we need, it is not immediate to see how the the covariance (19) behaves if we fix n large and study how the covariance between two dimers in the transition region between the smooth and rough phases behaves as we increase the distance between them. We will discuss this in the setting of Example 1 in Sect. 3. Here we give a more informal summary.
2 Asymptotic Results
In this section we formulate the precise asymptotic results for \(E_{k,\ell }\) and \({\tilde{C}}_{\omega _c}(\ell ,k)\). The critical point \(\omega _c\) defined above is a function of \(\xi \) and lies on the unit circle so we can write \(\omega _c(\xi )=e^{i\theta _c(\xi )}\), where \(\theta _c(\xi )\in (0,\pi /2)\). It satisfies the Eq. (34). For convenience, we also define the function
since this will be a natural quantity that is small and can be related to \(\xi _c-\xi \), see Lemma 5. Note that when \(\xi =\xi _c\), \(g_\xi \) has a double critical point at both i and \(-i\) so \(\theta (\xi _c)=\pi /2\) and hence \(\varphi (\xi _c)=0\).
We need to assume that \(\xi _c-\xi \) is small, which means that we are close to the asymptotic rough–smooth boundary.
Assumption 1
We assume throughout the paper that \(\xi \) satisfies \(0<\xi _c-\xi <\delta \), where \(\delta <\xi _c+\frac{1}{2}\sqrt{1+2c}\) is a small number determined by a finite number of conditions below. We will not discuss the explicit value of \(\delta \).
We now relate the critical point \(\omega _c\) and \(\varphi _c\) to the value of \(\xi \) near \(\xi _c\).
Lemma 5
Let \(\xi \) be such that Assumption 1 holds and let \(\omega _c=e^{i\theta _c}\), \(\theta _c=\pi /2-\varphi _c\in [0,\pi /2]\) satisfy \(g'_\xi (\omega _c)=0\). Then there exists a bounded function \(R_1(\varphi _c)\) such that
Furthermore, there are bounded functions \(R_2(\xi ), R_3(\xi )\) such that
and
The proof of this lemma is given in Sect. 8. Note that Assumption 1 and Lemma 5 imply that there is a small \(\delta _1>0\) such that \(0<\varphi _c<\delta _1\) for all of the \(\xi \) we consider.
For the asymptotic analysis of \(E_{k,\ell }\) we need another saddle-point function. For \(\alpha \in [-1,1]\), define the function \({\tilde{g}}_\alpha : {\mathbb {C}}\setminus (i(-\infty ,1/\sqrt{2c}]\cup i[-\sqrt{2c},\sqrt{2c}]\cup i[\sqrt{2c},\infty ))\rightarrow {\mathbb {C}}\) by
where both logarithms have branch cuts on the negative real axis. Taking a derivative yields
and setting this equal to zero gives the equation \(2cw^4+(1-\alpha ^2)w^2-2c\alpha ^2=0\). Solving this gives the four critical points
It is straight forward to see that the four points solve \({\widetilde{g}}'_\alpha (w)=0\) if \(0<\alpha \le 1\) (and that there is no solution for \(-1\le \alpha \le 0\)) by using (28). Let
so that \(iw_\alpha \) is a critical point of \({\tilde{g}}_\alpha \).
Note that we have the properties
seen by the change of variables \(w\rightarrow 1/w\) in the definitions. By (48) we can assume that \(|k/\ell | \le 1\) without loss of generality. We are now in position to formulate our main asymptotic results.
Proposition 2
Let the integers \(\ell ,k\) be such that \(\ell +k\) is even and \(\alpha =|k|/|\ell |\) lie in a compact subset of (0, 1]. As \(|\ell |\rightarrow \infty \) there is a positive constant \(d_1\) and a bounded function \(R_4(k,\ell )\) such that
For fixed k, there is a positive constant \(d_2\) and a bounded function \(R_5(k,\ell )\) such that
as \(|\ell |\rightarrow \infty \).
Proposition 3
Fix \(\gamma \in (1/2,1]\) and \(\varepsilon >0\) small. Consider non-zero integers \(\ell ,k\) such that \(\ell +k\) is even, \(\alpha =k/\ell \) lies in \([-1,1]\) and \(\varphi _c^{2-\gamma }(|\ell |+|k|)\le 1\). If \(\varphi _c\ell (1-\alpha )/\sqrt{1-2c}\in \Lambda _\varepsilon \), then
where we have the estimate
for some constant \(C>0\) that only depends on \(\varepsilon \).
Set \(c'=c/(1-2c)^{3/2}\). For \(\theta \in {\mathbb {R}}\) define
It follows from (165) that \(R_{7}\) is bounded.
Proposition 4
Fix \({\tilde{\alpha }}\) in \([-1,1]\), \(\gamma \in (1/2,1]\) and \(\varepsilon >0\) small. Consider non-zero integers \(\ell ,k\) such that \(\ell +k\) is even, \(k/\ell ={\tilde{\alpha }}+\kappa _\ell \in [-1,1]\) and \((|\ell |+|k|)\varphi _c^{2-\gamma }\ge 1/2\). Here \(\kappa _\ell \) is an arbitrary sequence indexed by \(\ell \) such that \(|\kappa _\ell |<3/|\ell |\).
Assume that \(F(\varphi _c)(\ell -k)\in \Lambda _\varepsilon \). Then, when \(|\ell |\) is large enough, there is a bounded function \( R_{8}(\xi ,\ell ,k)\) such that
Furthermore, there is a constant \(C>0\) such that
We outline the arguments that lead to the above three Propositions. The proof of (49) in Proposition 2 is a standard steepest descent analysis, which is centred at the critical point \(iw_{\alpha }\in i[1,1/\sqrt{2c})\) of \({\tilde{g}}_{\alpha }\). This analysis works uniformly in \(\alpha \) in any compact subset of (0, 1]. For the regime in (50) (\(\alpha \) near/equal to zero), the critical point \(iw_\alpha \) merges into the branch cut along \(i[1/\sqrt{2c},\infty )\), so we perform a separate steepest descent analysis for this regime. This analysis/formula is independent of \(\varphi _c\).
In Proposition 3, the condition \(|\ell |+|k|\le \varphi _c^{\gamma -2}\) means we are considering the integral in (35) over a very small contour \(\Gamma _{\omega _c}\), but where the asymptotic parameters \(|\ell |,|k|\) still sit in a regime which is relatively small. We prove that an integration by parts argument suffices to obtain a uniformly small remainder in this "smaller" regime.
In Proposition 4 the regime is instead restricted to \(|\ell |+|k|\ge \varphi _c^{\gamma -2}/2\), which overlaps with the previous regime, but also consists of a range of larger \(|\ell |+|k|\). In this regime, integration by parts no long suffices in all regions of \((\ell ,k)\). The regime requires a mixture of integration by parts and methods in the spirit of the method of steepest descent to deal with the asymptotics. We also have to consider \(E_{k,\ell }-C_{\omega _c}(k,\ell )\) here, as in one region, the leading order terms of \(E_{k,\ell }\) and \(C_{\omega _c}\) are actually equal, and so they cancel if we compute the asymptotics of the integrals separately. Indeed, this is why we define \(D_{\omega _c}(k,\ell )=E_{k,\ell }-C_{\omega _c}(k,\ell )\) (defined in (195)) in a certain region of \((k,\ell )\).
3 Results on Dimer–Dimer Correlations
In this section we discuss the decay of the covariance between pairs of dimers in the transition region between the rough and smooth phases in the setting of Example 1. Recall the definitions (23), (24). For \(i=1,2\) label the evaluation of \(k_i, \ell _i\) at \((x^{(1)},y^{(2)})\) as \(k^{1,2}_i, \ell ^{1,2}_i\) and label their evaluation at \((x^{(2)},y^{(1)})\) as \(k^{2,1}_i, \ell ^{2,1}_i\). We have
and
This motivates us to think of
(where \(\sigma _1^2+\sigma _2^2=1\)) in the sense that \(r\sim \sqrt{r_1^2+r_2^2}\) gives the distance between two dimers and \(\pm (\sigma _1,\sigma _2)\) gives the direction.
Consider sequences \(\delta _n, \delta ^*_n, r_n>0\) such that \(\delta _n\le \delta ^*_n\),
and
as \(n\rightarrow \infty \). We assume that \(r_{\min }\le \sqrt{r_1^2+r_2^2}\le r_n\) and \(\delta _n\le \xi _c-\xi \le \delta ^*_n\), where \(r_{\min }\) is a positive number that will be taken large enough. For example we could take \(\delta _n=n^{-1/2}\) and \(\delta ^*_n = 1/\log (\log (n))\). Note that (60) implies
Recall Lemma 5, in particular (43) which gives a positive constant \(d_3\) such that
We see there are constants \(c_1,C_1>0\)
The dimer–dimer correlation is given by formula (19), which in the setting of Example 1 becomes
Let \((i,j)=(1,2)\) or (2, 1). By Theorem 3
Putting the coordinates in Example 1 into (38) yields Proposition 1 as
In the second inequality in 66 we used the following approximation; Set \(\alpha =0\) in (155) to get \({\mathcal {R}}[\psi (\theta _c)]=\log |G(\omega _c)|\), and then use (167) to obtain
Now we use (32) and (36) to write
where we recall \(l_1^{1,2}, k_1^{1,2}\)... as given in (56), (57).
Now we give a short lemma that we use to extract the leading order terms of \({\mathbb {K}}_{1,1}^{-1}\) from Proposition 2.
Lemma 6
For \(0< \alpha ,\alpha '\le 1\),
Proof
Since \(\alpha \rightarrow {\tilde{g}}_\alpha (iw_\alpha )\) is smooth, we use Taylor’s theorem and note that
by the chain rule. The lemma follows since \(iw_{\alpha '}\) is a critical point of \({\tilde{g}}_{\alpha '}\). \(\square \)
3.1 Dimer–dimer correlations parallel to \(\textbf{e}_1\)
We look at dimers separated along the diagonal, that is, we let \(r_1=r_2=r>0\). This implies \(k_1^{2,1}=l_1^{1,2}=r-1\), \(k_1^{1,2}=l_1^{2,1}=-r-1\) and \(k_2^{1,2}=l_2^{2,1}=-r\), \(k_2^{2,1}=l_2^{1,2}=r\). We obtain the formula
where we used (48). Take \(r_{\min }\) so large that we can neglect remainders in Proposition 2. Note that \(|G(i)|=(1-\sqrt{1-2c})/\sqrt{2c}<1\). Although other length scales can be analysed, for simplicity take \(\delta _n=\xi _c-\xi =\delta _n^*\).
Theorem 7
Take a very large n, a small \(\varepsilon >0\) and fix \(\gamma \in (1/2,1]\). Take \(\xi _c-\xi =\delta _n\), which gives \(\varphi _c\sim d\sqrt{\delta _n}\) with an explicit constant d. Assume that \(r_{\min }<r<r_n\),
and \(2r\varphi _c/\sqrt{1-2c}\in \Lambda _\varepsilon \), where \( \Lambda _\varepsilon \) is defined by (4). Then
Proof
It follows from our assumptions that \(r_n\varphi _c^2=o(1)\), together with (66) and (61) we have the estimate
An evaluation using (129) gives
We use lemma 6 with \(\alpha =(r-1)/(r+1)\), \(\alpha '=1\) to get \({\mathcal {R}}[{\tilde{g}}_{\alpha }(iw_\alpha )]={\mathcal {R}}[{\tilde{g}}_1(i)]-2\log |G(i)|/r+O(1/r^2)\). We can use this in Proposition 2, to get
We now apply Proposition 3 to the \({\tilde{C}}_{\omega _c}\) appearing in (70). By (63), the remainder \(R_{6}\) in (51) is very small compared to 1 and so we neglect this term. It follows from Proposition 3 that we can write
where \(a-|G(i)|^{-2}<0\). Now from (172) we obtain
Combining this with (61) we see that the error term \(o(n^{-1/3})\) can be neglected. A computation using (70) now gives (72). \(\square \)
3.2 Dimer–dimer correlations parallel to \(\textbf{e}_2\)
Now we look at dimers separated along the anti-diagonal. So we instead take \(r_1=-r_2=r>0\) for which we have \(k_1^{1,2}=\ell _1^{1,2}=r-1\), \(k_1^{2,1}=\ell _1^{2,1}=-r-1\), \(k_2^{2,1}=l_2^{2,1}=-r\), \(k_2^{1,2}=l_2^{1,2}=r\). So we obtain
Theorem 8
Take a very large n, a small \(\varepsilon >0\) and fix \(\gamma \in (1/2,1]\). Take \(\xi _c-\xi =\delta _n\), which gives \(\varphi _c\sim d\sqrt{\delta _n}\) with an explicit constant d. If \(r_{\min }<r<\varphi _c^{\gamma -2}/2\) then
If instead \(\varphi _c^{\gamma -2}/2\le r<r_n\) then
where \(c'=a\sqrt{1+a^2}/(1-a)^2\).
Proof
We can use (73)
where the remainder O(1/r) comes from estimating the difference between \(E_{(-1)^jr-1,(-1)^jr-1}\) and \(E_{(-1)^jr,(-1)^jr}\). Clearly (80) decays exponentially. Take \(r_{\min }\) large enough that the remainders in Proposition 3 are small. We can use Proposition 3 to write that for \(r\le 1/(2\varphi _c^{2-\gamma } )\),
Observe that there are no oscillations. By (60) and (66) we see the remainder in (77) is small compared to (81) for n large. So
now (78) follows by using (114) with \(\theta =-\pi /4\) which gives
and since \(1/\sqrt{r}>>\varphi _c\) in this regime.
If \(1/(2\varphi _c^{2-\gamma })\le r\le r_n \), by substitution in Proposition 4 we obtain
where
\(D_+, D_-\) are known as the Dawson function and Mills ratio, respectively. These functions are related to the imaginary and complementary error functions. We use 7.8.7 in [12] to write
for \(z>0\). We apply the upper bound \(|e^{-z^2}-1|\le z^2e^{z^2}\) to (86) on (0, 1]. We also have that for the same interval, the lower bounds \(e^{- z^2}\ge e^{-1}\), and \(t\ge 0\), \(e^{t^2}\ge 1\) hold, hence
For \(z\ge 1\), inequality (1) in [11] gives a lower bound and we apply the upper bound \(1-e^{-z^2}\le 1-e^{-1}\) to (86) to get
By 7.8.3 in [12] we have
for \(z\ge 0\). Hence
We can use (60) to show that both (90),(91) are much greater than \(1/\sqrt{n\sqrt{\xi _c-\xi }}\). Hence it follows from (83), (84) and (66) that the remainders in (77) are negligible. So we have
and
The O(1/r) error appearing in (93) arises from the difference in evaluating \(D_-(\sqrt{2 \cdot c'}\varphi _c)/\sqrt{2\cdot c'}\) at r and \(r-1\), similarly for \(D_+\) and (94). By (90) and (91) these errors are negligible in the current regime. Hence by (64) we have (79) for \(1/(2\varphi _c)^{2-\gamma }\le r \le r_n\) \(\square \)
We bring forward the asymptotics contained in (42.6) from [24] and (7.12.1), (7.6.2) in [12] (for which we note \(D_-(z)=\sqrt{\pi }e^{z^2}\text {erfc}(z)/2\)). For \(z>0\),
We see the following distinct decay rates.
Regime I. As r varies from \(r_{\min }\) to \(\frac{1}{\log |G(i)|^{-4}}\log \frac{1}{\varphi _c}\) ,
which decays exponentially.
For the next regime, we use (78) and (67) when r varies from \(\frac{1}{\log |G(i)|^{-4}}\log \frac{1}{\varphi _c}\) to \(1/(2\varphi _c^{2-\gamma })\). We then use (95) on (79) when r varies from \(1/(2\varphi _c^{2-\gamma })\) to small compared to \(1/(2c'\varphi _c^2)\). These two sub-regimes have the same leading order term which is just an artefact of how we proved the asymptotic formulas. We combine them into one regime.
Regime II. As r varies from \(\frac{1}{\log |G(i)|^{-4}}\log \frac{1}{\varphi _c}\) to small compared to \(1/(2c'\varphi _c^2)\),
which decays like \(1/\sqrt{r}\).
Regime III. As r varies from small compared to \(1/(2c'\varphi _c^2)\) to large compared to \(1/(2c'\varphi _c^2)\), corr\((e_1,e_2)\) is given by (79) and the integral is bounded below by a positive constant. Hence corr\((e_1,e_2)\) decays like 1/r.
For the next regime, we use (95) in (79).
Regime IV. As r varies from large compared to \(1/(2c'\varphi _c^2)\) to \(r_n\),
which decays like \(1/r^2\). One can also show that both \(a-|G(i)|^{-2}<0\) and \(|G(i)|^2-a<0\), hence we see that the correlation is positive in the four regimes above.
3.3 Dimer–dimer correlations at an arbitrary angle.
Now we analyse a third case which interpolates between the two previous cases. We consider \(2r_n\varphi _c^{2-\gamma }\le 1\) for a fixed \(\gamma \in (1/2,1)\). For an arbitrarily small fixed \(\varepsilon >0\), consider
if \(\theta =\pi /4\) this would correspond to separating the two dimers along the diagonal, when \(\theta =-\pi /4\) this corresponds to the anti-diagonal. In particular, it is interesting to examine the behaviour for \(\theta \) close to \(-\pi /4\).
Let \(\sigma :=\sigma _2/\sigma _1=\tan (\theta )\), so \(-1\le \sigma <1\). We now have \(l_1^{1,2}+1=l_2^{1,2}=r\sigma _1=-l_2^{2,1}=-l_1^{2,1}-1\) and \(k_1^{2,1}+1=k_2^{2,1}=r\sigma _2=-k_2^{1,2}=-k_1^{1,2}-1\). To state a formula for the correlation in the current setting we require the definitions of some functions, these functions come into the rate of exponential decay and leading term constants. Define \({\tilde{\sigma }}=\text {sign}(\theta )\), sign\((0)=1\) and note \(\sigma _1>0\). Define the piecewise continuous functions
where \(f(\alpha )=(\sqrt{2\pi |g''_\alpha (iw_\alpha )|}w_\alpha \sqrt{w_\alpha ^2-2c}\sqrt{1/w_\alpha ^2-2c})^{-1}\), \(\alpha \in (0,1]\).
Theorem 9
Take a very large n, a small \(\varepsilon >0\) and fix \(\gamma \in (1/2,1]\). Take \(\xi _c-\xi =\delta _n\), which gives \(\varphi _c\sim d\sqrt{\delta _n}\) with an explicit constant d. Assume that \(r_{\min }<r<r_n\),
and \(r(\sigma _1+\sigma _2)\varphi _c/\sqrt{1-2c}\in \Lambda _\varepsilon \), where \( \Lambda _\varepsilon \) is defined by (4). Then
Proof
We use Theorem 4 to establish (105) and (108). By (32), we have
Let \(\alpha ^{1,2}=(|r\sigma _2|+{\tilde{\sigma }}_2)/(r\sigma _1-1)\) and observe that \(C_\varepsilon \le |\alpha ^{1,2}|\le 1\), where \(C_\varepsilon \) is small, for large r by (99). By (49), we have
We have \(\alpha ^{1,2}-|\sigma |=(|\sigma |+{\tilde{\sigma }}_2)/(r\sigma _1)+O(1/r^2)\) and \(\frac{f(\alpha ^{1,2})}{\sqrt{r\sigma _1-1}}=\frac{f(|\sigma |)}{\sqrt{r\sigma _1}}+O(1/r)\) so
by lemma 6. Similarly,
We have
We see the remainder \(R_{0,0}\) in (65) is much smaller than (108) via (66). \(\square \)
Note the following facts about \(h_+\) and \(h_-\), since \((1+|\sigma |)\log |G(i)|\le (1-\sigma )\log |G(i)|\le (1-|\sigma |)\log |G(i)|\) lemma 13 gives
Since \(h_+-h_-=2(1-\sigma )\log |G(i)|\) we have \(h_+(\theta )<0\), it is also easy to compute \(h_-(-\pi /4)=0\). In fact, one can show that there is a positive \(c_5>0\) such that \(h_-(\theta )=-c_5(\theta +\pi /4)^2+O(\theta +\pi /4)^3\).
We have the following decay regimes. Let \(m>0\) be such that \(m/\sqrt{1-2c}\) is small.
Regime I. As r varies from \(r_{\min }\) to \(\frac{1}{\sigma _1|h_+(\theta )|}\log (\frac{1}{\varphi _c})\).
which decays exponentially. Note we used (115) here.
Regime II. As r varies from \(\frac{1}{\sigma _1|h_+(\theta )|}\log (\frac{1}{\varphi _c})\) to \(\min (\frac{1}{\sigma _1|h_-(\theta )|}\log (\frac{1}{\varphi _c}),m/((\sigma _1+\sigma _2)\varphi _c)\)
which decays exponentially for \(\theta \ne -\pi /4\), and like \(1/\sqrt{r}\) for \(\theta =-\pi /4\).
Regime III. As r varies from \(\min (\frac{1}{\sigma _1|h_-(\theta )|}\log (\frac{1}{\varphi _c}),m/((\sigma _1+\sigma _2)\varphi _c))\) to \(m/((\sigma _1+\sigma _2)\varphi _c)\)
which has zero or no decay.
Regime IV. As r varies from \(m/((\sigma _1+\sigma _2)\varphi _c)\) to \(r_n\),
which oscillates and decays like \(1/r^2\).
Hence we see that for \(\theta >-\pi /4\) close to \(-\pi /4\), there are two distinct exponential decay rates; a faster exponential decay in Regime I followed by a slower exponential decay in Regime II. As we vary the angle \(\theta \) closer to \(-\pi /4\), Regime II increases in size, and the decay in Regime II changes from exponential decay to a decay like \(1/\sqrt{r}\).
Remark 1
A simpler expression can be given for the product \(g_-(\theta )g_+(\theta )\) that appears when one expands the product over q in (103). This comes into the formula for Regime I (110). Through some manipulation one can show the identity
The identity (114) together with \(w_{|\sigma |}^2\sqrt{1/w_{|\sigma |}^2-2c}=\alpha \sqrt{w_{|\sigma |}^2-2c}\) and (129) can be used to obtain
4 Gibbs Measures and the Infinite Planar Graph
In [21], the authors describe the set of all translation invariant Gibbs measures of the infinite bipartite planar dimer models with a certain double periodicity. They also give an approach to compute the full plane inverse Kasteleyn matrix. The infinite planar graph \(G={\tilde{V}}\cup {\tilde{E}}\) relevant for the two-periodic Aztec diamond is the infinite version of what we defined above, and is defined as follows: for \(i\in \{0,1\}\), let
where \({\tilde{B}}={\tilde{B}}_0\cup {\tilde{B}}_1\) are the black vertices, \({\tilde{W}}={\tilde{W}}_0\cup {\tilde{W}}_1\) are the white vertices and \({\tilde{V}}={\tilde{W}}\cup {\tilde{B}}\). The edge set \({\tilde{E}}\) is all edges of the form \(b-w=\pm \textbf{e}_1+,\pm \textbf{e}_2\), for all \(b\in {\tilde{B}},w\in {\tilde{W}}\). Let the edges contained in the smallest cycle surrounding the point (i, j) where \((i+j)\) mod \(4=2\), have weight \(a\in (0,\infty )\) and the edges contained in the smallest cycle surrounding the point (i, j) where \((i+j)\) mod \(4=0\) have weight 1.
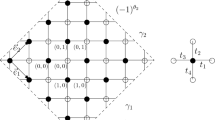
As a reference for the following we note [25], see also [18]. The graph G (together with its weights) is doubly periodic in the sense that the set T of shifts of the form \(n\mathbf {e_1}+m\mathbf {e_2}\), \((n,m)\in (2{\mathbb {Z}})^2\) preserve the colour of the vertices and edge weights. Define the graph \(G_1\) to be G mod the same shifts so that G is a collection of copies of \(G_1\) obtained by applying all shifts T. From its definition, \(G_1\) has periodic boundary conditions in both directions \(\textbf{e}_1\) and \(\textbf{e}_2\), so one can also think of \(G_1\) as a graph on the torus. Define the edge weights and Kasteleyn orientation of \(G_1\) as in figure 4, which induces a Kasteleyn orientation on all of G. The graph \(G_1\) is called the fundamental domain of G, note that it has vertices \(w_0\in {\tilde{W}}_0\), \(b_0=w_0+\textbf{e}_2\), \(b_1=w_0+\textbf{e}_1\), \(w_1=b_0+\textbf{e}_1\).
The authors of [21] introduce “magnetic coordinates” to parametrise the set of Gibbs measures. Following [21], let \((B_1,B_2)\in {\mathbb {R}}^2\) be the magnetic coordinates for the graph G and take two paths \(\gamma _1\), \(\gamma _2\) in each fundamental domain as shown in Fig. 4. Multiply the edge weight of an edge \(e=(b,w)\) by \(e^{B_1}\) (\(e^{-B_1}\)) if \(\gamma _1\) crosses e such that the white vertex w is on its right (left). Similarly multiply the edge weight of e by \(e^{B_2}\) (\(e^{-B_2}\)) if \(\gamma _2\) crosses e such that w is on its right (left). This yields the same graph with a different set of edge weights denoted \(G_{e^{B_1},e^{B_2}}\). Define the fundamental domain of \(G_{e^{B_1},e^{B_2}}\) to be \(G^1_{e^{B_1},e^{B_2}}\) as shown in the Fig. 4. The magnetic coordinates introduced in this way re-weight the average slope of the corresponding height functions. Note that \(B_1=B_2=0\) gives zero average slope in directions \(\textbf{e}_1\), \(\textbf{e}_2\) and gives the limiting smooth phase in the two-periodic Aztec diamond we are considering.
For \(L\in 2{\mathbb {N}}_{>0}\), define \(G^L=(V_L,E_L)\) to be the graph obtained by applying all shifts of the form \(n\textbf{e}_1+m\textbf{e}_2, (n,m)\in (2{\mathbb {Z}}\cap [-L,L])^2\) to \(G^1\) and with periodic boundary conditions, observe that \(G=\cup _L G^L\). If \(B_L\) are the black vertices and \(W_L\) are the white vertices so that \(V_L=B_L\cup W_L\) then viewing the Kasteleyn matrix \(K^L\) of the graph \(G^L\) as an operator \({\mathbb {C}}^{W_L}\rightarrow {\mathbb {C}}^{B_L}\), [21] block diagonalise \(K^L\) (along with three slightly modified variants of \(K^L\)). The authors of [21] then use an extension of Kasteleyn’s theory for dimer models on the torus to perform a limiting argument in L which yields a double contour integral formula for the free energy (per fundamental domain) of G, and posit a formula for the inverse Kasteleyn matrix. Following [21], denote the magnetically altered Kasteleyn matrix for the fundamental domain \(G_1\) by K(z, w) where one multiplies the edge weight of an edge \(e=(b,w)\) by z (or 1/z) if \(\gamma _1\) crosses e with the white vertex on its right (or left). Likewise multiply the edge weight of e by w (or 1/w) if \(\gamma _2\) crosses e such that w is on its right (or left). So for \(i,j\in \{0,1\}\) we obtain
The magnetically altered Kasteleyn matrix in magnetic coordinates \((B_1,B_2)\) corresponding to \(G^1_{e^{B_1},e^{B_2}}\) is \(K(e^{B_1}z,e^{B_2}w)\).
Suppose that \(x\in {\tilde{W}}_{\varepsilon _1}\) and \(y\in {\tilde{B}}_{\varepsilon _2}\), \(\varepsilon _1,\varepsilon _2\in \{0,1\}\). Let \((u,v)\in {\mathbb {Z}}^2\) be such that \(u (2\textbf{e}_1)+v(2\textbf{e}_2)\) is the translation to get from the fundamental domain containing x to the fundamental domain containing y. The whole plane inverse Kasteleyn matrix of \(G_{s_1,s_2}\) for the entries x, y in magnetic coordinates \((\log (s_1),\log (s_2))\) is
where \(\Gamma _r\) is a circle or radius r around the origin,
and
is called the characteristic polynomial. Note that \(K(z,w)^{-1}=Q(z,w)/P(z,w)\). The formula for \({\mathbb {K}}_{s_1,s_2}^{-1}\) differs compared to the one in [8] by multiplication of \(s_1^{-u+1}s_2^{-v+1}\).
If we set \(s_1=s_2=1\) in (117) we get \({\mathbb {K}}_{1,1}^{-1}\) which agrees with \({\mathbb {K}}_{1,1}^{-1}\) given by (32) as shown in [8]. We summarise a derivation of (32) from (117). Make the change of variables \(z=-u_1u_2\), \(w=u_2/u_1\) for \((u_1,u_2)\in \Gamma _1^2\) in the double contour integral (117) so that the characteristic polynomial is \(P(z,w)=-2(1+a^2)+a(u_1-1/u_1)(u_2-1/u_2)\). Then perform a small deformation in the \(u_1,u_2\) variables so that \((u_1,u_2)\in \Gamma _R^2\) for \(R<1\) very close to 1 (avoiding the zeros of P). Then recall that \(u\rightarrow \sqrt{\frac{c}{2}}(u-1/u)\) is a bijection from \(\{u;|u|<1\}\) to \({\mathbb {C}}\setminus i[-\sqrt{2c},\sqrt{2c}]\) with inverse \(w\rightarrow G(w)\). Then if we make another change of variables \(u_i=G(w_i)\) for \(i=1,2\) the characteristic polynomial becomes \(-2(1+a^2)(1-w_1w_2)\). Under the condition that \(k,\ell \ge 0\), one obtains a single contour integral from the pole \(w_1w_2=1\). One then checks that this single contour integral formula agrees with (32) in each of the cases of vertices \(\varepsilon _1,\varepsilon _2\in \{0,1\}\). The formula holds for all \(k,\ell \) by a symmetry argument. An extended summary of this derivation is given in [23]. For all the rest of the details, see [8].
In fact the whole plane inverse Kasteleyn matrix (117) can be related to the quantities whose asymptotics we analyze. We bring forward lemma 3.3 in [8].
Lemma 10
For \(x=(x_1,x_2)\in W_{\varepsilon _1}, y=(y_1,y_2)\in B_{\varepsilon _2}\), and \(s_1=1, s_2=1/|G(\omega _c)|^2\) we have
where \((u,v)\in {\mathbb {Z}}^2\) is such that \(u(2\textbf{e}_1)+v(2\textbf{e}_2)\) is the translation to get from the fundamental domain containing x to the fundamental domain containing y.
This means that Propositions 2, 3 and 4 also yield uniform asymptotics for the inverse Kasteleyn matrix for the infinite planar dimer model \(G_{s_1,s_2}\).
4.1 Discussion of dimer–dimer correlations on the infinite planar graph
Using (117) we can reformulate the discussion of dimer to dimer correlations in Sect. 3 in terms of the infinite planar graph \(G_{s_1,s_2}\). Instead of varying the distance \(n(\xi _c-\xi )\) of the two dimers to rough–smooth boundary, we can vary the magnetic coordinates in such a way that the Gibbs measure of the infinite dimer model varies between rough and smooth phases. Note that above we fixed n and chose \(\xi \) depending on n so the n-dependence now sits in the magnetic coordinates \((\log (s_1),\log (s_2))=(0,\log (1/|G(\omega _c)|^2))\). Using lemma 5 one can compute \(1/|G(\omega _c)|^2=1/|G(i)|^2+c_4(\xi _c-\xi )+O(\xi _c-\xi )^{3/2}\) for some \(c_4>0\) depending on a, so we have
where \(1/|G(i)|^{2}=2a/(\sqrt{1+a^2}-1+a)^2>1\). We see that varying \(\xi \) corresponds to varying \(s_2\) while keeping \(s_1\) fixed.
Take two dimers, \(e_i=(x^{(i)},y^{(i)})\in {\tilde{W}}_0\times {\tilde{B}}_0\), \(i=1,2\) with \(e_1\) placed arbitrarily. Define the coordinates of \(e_2\) as
where \(r_1,r_2\in {\mathbb {Z}}\) and \(r_1+r_2\) is even. Let \(\xi _c-\xi >0\) be sufficiently small and let the distance between the two dimers \(r=2\sqrt{r_1^2+r_2^2}\) lie in \([r_{\min },r_n)\) (\(r_{\min }\) is large but fixed and \(r_n=\infty \)). Note that this allows for any direction between the dimers. We see that the discussion in Sect. 3 of the dimer–dimer correlation between the dimers \(e_1,e_2\) translates into this setting.
Recall from [21] that the amoeba associated to the characteristic polynomial P is the image of the zero set of P(z, w) under the map \((z,w)\rightarrow (\log |w|,\log |z|)\). A picture of the amoeba of our characteristic polynomial (119) is given for \(a\sim 0.36\) as the right hand picture in figure 2 in [21], (i.e. the amoeba of \(z+z^{-1}+w+w^{-1}-6.25\)). The results of this paper together with the results in section 4 in [21] show that for the collection of weights \(s_1=e^{B_1}=1\), \(1\le s_2=e^{B_2} \le 1/|G(i)|^2\) the corresponding magnetic coordinates \((B_1,B_2)\) lie in the bounded complementary component of the amoeba of P(z, w), since we have exponential decay of correlations for these magnetic coordinates. This corresponds to a single unique (smooth) Gibbs measure with an average slope of (0, 0). When \(\varphi _c>0\) but small and \(s_1=1, s_2=1/|G(ie^{-i\varphi _c})|^2\) the corresponding magnetic coordinates \((B_1,B_2)\) lie in the interior of the amoeba of P(z, w), as here the long distance decay is polynomial for all \(\varphi _c>0\). For each \(\varphi _c>0\) there is a unique (rough) Gibbs measure with average slope \(t \textbf{e}_1\) for some \(t\in (0,1]\), and the regime of distances r for which dimers have exponential decay of correlations varies from some fixed number \(r_{\text {min}}\) to a term proportional to \(\log (1/\varphi _c)\) (see Regime I corresponding to (110)). For any large, bounded region, we can take \(\varphi _c\) so small that all of the dimers in the region have exponential decay of correlations between one another. From this we see Theorem 1 holds.
An interpretation is that when we have a non-zero average slope, there are infinitely long paths related to the level curves of the height function that are present. These infinite paths appear to imply quasi-long range order and power law decay. As we transition to the smooth phase these infinite paths typically become further and further apart, corresponding to a decreasing average slope of the height function. The length scales that are much smaller than the typical distance between these infinite paths experience exponential decay of correlations. If we move to the smooth phase the paths move infinitely far apart, disappearing and leaving only short range order.
5 Asymptotics of \({\mathbb {K}}_{1,1}^{-1}\)
In [8], the asymptotics of \(E_{k,\ell }\) are computed when \(\pm \ell \) is close to k, i.e when the vertices lie close to diagonal or cross-diagonal from one another. Here we extend the asymptotics to arbitrary angles. Note from the symmetry relation (48) we can restrict our attention to the case \(|k|\le |\ell |\) without loss of generality. Let \(\alpha = \frac{|k|}{|\ell |}\) and write
with saddle point function \({\widetilde{g}}_{\alpha }(w)\) defined in (44).
The integrand in (123) is analytic in the region \({\mathbb {C}}\setminus (i[-\sqrt{2c},\sqrt{2c}]\cup i[1/\sqrt{2c},\infty )\cup i(-\infty ,-1/\sqrt{2c}])\), so by Cauchy’s deformation theorem, for \(r>1\), we can deform \( \Gamma _1\) to \(\Gamma _{w_\alpha }(r)=\cup _{j=0}^3 \gamma _j(r)\) where
as sets \(\gamma _3(r)=-\gamma _1(r)\), \(\gamma _2(r)=-\gamma _0(r)\) and as curves each \(\gamma _j(r)\) has positive orientation counter-clockwise around the origin. For \(\eta _1,\eta _2, r\ge 0\), where \(\eta _2\) is small define \(\gamma _{\eta _1,\eta _2}(r)\) as
which is a path from \(i/\sqrt{2c}+i\eta _1+\eta _2+r\) to \(i/\sqrt{2c}-\eta _2 i\) consisting of three straight lines. Note we define the orientation of this curve to be in the direction of the path beginning at \(i/\sqrt{2c}+i\eta _1+\eta _2+r\) and ending at \(i/\sqrt{2c}-\eta _2 i\).
Let \({\mathcal {R}}[z]\) and \({\mathcal {I}}[z]\) denote the real and imaginary part of a complex number z, respectively. Denote the upper half plane \({\mathbb {H}}\subset {\mathbb {C}}\).
Lemma 11
For \(k,\ell \in {\mathbb {Z}}\),
If \(\ell +k\) is even, \(\eta _1,\eta _2\ge 0\) then
Proof
Take the integral (123), now perform the deformation of the contour \(\Gamma _1\) to \(\Gamma _{w_\alpha }(r)\) described above. Now from the definition of G in (25), clearly \(|G(w)|<1\) for all w in the domain of G. Using this fact we can see that for large |w|, the dominant factor in the integrand is \(w\sqrt{w^2+2c}\) appearing in the dominator. Hence the modulus of the integrand is bounded above by \(O(1/|w|^2)\) for large |w|. We can now take the limit \(r\rightarrow \infty \) and see that the contributions from \(\gamma _0(r)\) and \(\gamma _2(r)\) vanish. We split the integral up over the sections \(\gamma _1(\infty )\) and \(\gamma _3(\infty )\). Using the symmetries \(-\sqrt{w^2+2c}=\sqrt{(-w)^2+2c}\), \(-G(w)=G(-w)\) we rewrite the integral over \(\gamma _3(\infty )\) to be over \(\gamma _1(\infty )\), this causes us to a pick up a factor \((-1)^{|\ell |+|k|}\) which yields (125).
Similarly, for (126), we take the integral in (123) and deform \(\Gamma _1\) to \(\gamma _{\eta _1,\eta _2}(\infty )\cup \overline{\gamma _{\eta _1,\eta _2}(\infty )}\cup -\gamma _{\eta _1,\eta _2}(\infty )\cup -\overline{\gamma _{\eta _1,\eta _2}(\infty )}\) by an almost identical argument. Then (126) follows by further applications of the symmetries (28), (29) and noting that if \(\ell +k\) is even then \(|\ell |+|k|\) is even. \(\square \)
Next we give a lemma concerning the existence of descent paths.
Lemma 12
For \(\alpha \in [0,1]\), \(\beta \in [1,1/\sqrt{2c}]\) the mapping \((0,\infty )\ni t\rightarrow {\mathcal {R}} [{\widetilde{g}}_\alpha (i \beta +t)]\) is strictly decreasing. Moreover, if \(\alpha =0\) the same mapping is strictly decreasing for all \(\beta \in [1,\infty )\).
Proof
We use an integral representation of
which yields the correct branch cut and sheet of the square root. From (45) write
Now,
Let \(t<\beta \), the fact that the denominators in (128) are greater than zero and \(1\pm 2s\beta +s^2(t^2+\beta ^2)\ge 1\pm 2s\beta \) yields
The assertion that the previous expression is less than zero is equivalent to
The quartic above factorises into the form \(2\alpha (s^2-C_-)(s^2-C_+)/(t^2+\beta ^2)\) where explicitly
clearly \(C_-<0\) and \(C_+>\frac{1}{2\alpha }(t^2(1-2\alpha )+\beta ^2(1+2\alpha ))>t^2(1/\alpha -1)+\beta ^2>2c\) where the second last inequality holds since \(t<\beta \).
For \(t\ge \beta \), the function \(x\rightarrow 1/(1+x)\) is convex for \(x>-1\) so the sum of the first two terms in (128) is bounded above by
so from (128)
The assertion that the previous expression is less than zero is now equivalent to
The previous quartic factorises into the form \((t^2+\beta ^2)s^2(s-B_-)(s-B_+)\) where
It is obvious that since \(\beta \ge 1\), \(B_+>1>\sqrt{2c}\) and \(B_-\le 0\) is equivalent to
which is true when \(t\ge \beta \). So the mapping \((0,\infty )\times [0,\sqrt{2c}]\rightarrow {\mathbb {R}}\) such that \((t,s)\rightarrow {\mathcal {R}}f_\alpha (i\beta +t,s)\) is negative which proves the first result. The extension to \(\beta \in [1,\infty )\) when \(\alpha =0\) is immediate from (127). \(\square \)
Since \({\mathcal {R}}[{\widetilde{g}}_\alpha (i\beta -t)]={\mathcal {R}}[{\widetilde{g}}_\alpha (i\beta +t)]\) for \(t\in (-\infty ,\infty )\), lemma 12 also proves \((0,\infty )\rightarrow {\mathbb {R}};\) \(t\rightarrow {\mathcal {R}}[{\widetilde{g}}_\alpha (i\beta -t)]\) is decreasing.
Proof of Proposition 2
We perform a saddle point analysis on the right hand side of (125) and begin by proving the first statement. Multiply both sides of (45) by w, taking the derivative reveals
Recall that \(w_\alpha \in [1,1/\sqrt{2c})\). Computing \(\sqrt{(iw_\alpha )^2+2c}=i\sqrt{w_\alpha ^2-2c}\) and \(\sqrt{(1/iw_\alpha )^2+2c}=-i\sqrt{1/w_\alpha ^2-2c}\), and using \({\widetilde{g}}_\alpha '(iw_\alpha )=0\) we see that the above gives
We can simplify this as follows. Computing \(1/w_\alpha ^2=-\frac{1}{4c\alpha ^2}(1-\alpha ^2-\sqrt{(1-\alpha )^2+16c^2\alpha ^2})\), we see that \(1-\frac{2c}{w_\alpha ^2}=\frac{1}{\alpha ^2}(1-2cw_\alpha ^2)\) to get the identity \((w_\alpha ^2-2c)^{3/2}\frac{\alpha }{w_\alpha ^3}=\frac{w_\alpha ^3}{\alpha ^2}(1/w_\alpha ^2-2c)^{3/2}\). Hence,
Take \(\varepsilon >0\) small and less than \(\min (1/\sqrt{2c}-w_\alpha , w_\alpha -\sqrt{2c})\) and write (125) as
where \(C_{k,\ell }=\frac{(1+(-1)^{|\ell |+|k|})i^{-|k|-|\ell |}}{2(1+a^2)2\pi i}\). We parametrise \(\gamma _1(\infty )\) by
Taylor’s theorem yields
where
Here \(\partial {\mathbb {B}}(iw_\alpha ,\varepsilon )=\{\varepsilon e^{i\theta } + iw_\alpha : \theta \in [0,2\pi )\}\), so \(|R_{9}(t,\alpha )|\le C\) for \(t\in [-\varepsilon /2,\varepsilon /2]\) and all \(\alpha \). Since \(g_{\alpha }''(iw_\alpha )\) is less than some negative number for all \(\alpha \), we can take \(\varepsilon \) so small that
for some \(b>0\) uniformly in \(\alpha \) and \(t\in [-\varepsilon /2,\varepsilon /2]\). Setting \(\beta =w_\alpha \) in lemma 12, we have a descent contour so it follows from (130) and (131) that there are positive constants \(C_1, C_2\) so that
For the integral over \(\gamma _1(\varepsilon /2)\), in a similar fashion to above we parametrise \(\gamma _1(\varepsilon /2)\) as \(w(t)=iw_\alpha -t\) where \(t\in (-\varepsilon /2,\varepsilon /2)\). Now (130) gives
where \(V(w)=w\sqrt{w^2+2c}\sqrt{1/w^2+2c}\). We require three bounds. Taylors theorem applied to \(t\rightarrow V(iw_\alpha )/V(iw_\alpha -t)\) at \(t=0\) yields
We use the bound \(|e^{t}-1|\le |t|e^{|t|}\) to get
Finally,
Now take the absolute value of the integral in (132) minus the second term of the difference in (133). Write this as a sum of differences above, then use the triangle inequality and the three bounds. The main factor in (49) comes from the term \(\frac{\exp [|\ell |{\widetilde{g}}_\alpha (iw_\alpha )]}{V(iw_\alpha )}\) in (132).
The case \(\alpha =|k|/|\ell |\) for fixed k is handled differently. Recall the integral in (126) and write it as
The minus sign in (134) appears by defining \(\gamma '_{\eta _1,\eta _2}(\infty )\) to be \(\gamma _{\eta _1,\eta _2}(\infty )\) with reverse orientation. In this case the asymptotics come from the branch point \(i/\sqrt{2c}\), and the saddle point function \({\widetilde{g}}_0\) is analytic at this point. Parametrise \(w(t)=i(t+1/\sqrt{2c}) +\eta _2\) for \(t\in [0,\eta _1]\) and observe that
as \(\eta _2\rightarrow 0^+\). So
for a function f. A computation gives
We can get a bounded function \(R_{10}(t)\) such that
for \(t\in [0,\eta _1]\). From (45) we also have a bounded function \(R_{11}(t)\) such that
for \(t\in [0,\eta _1]\). Let \(b'=\sqrt{2c/(1-4c^2)}\). By lemma 12, the straight line from \(i/\sqrt{2c}+i\eta _1+\eta _2\) to infinity is a descent contour. Take \(\eta _1>0\) so small that
Then, by (138) and (139), there are positive constants \(C_4,C_5\) such that
Take \(\eta _2\rightarrow 0^+\) in (134). We consider a sequence of approximations and bound their differences. First, we have the estimate,
secondly,
and finally,
Furthermore,
Now note that when \(\ell +k\) is even, \(G(\frac{i}{\sqrt{2c}})^{|\ell |}G(-i\sqrt{2c})^{|k|}\) is a real number. The main contribution to the integral in (126) is the right hand side of (142). If we write the difference between the main contribution and the integral as sum of the differences above, then by the triangle inequality, (50) holds. \(\square \)
Remark 2
We can rewrite the expressions for \(E_{k,l}\) in lemma 2 as
when \(\alpha =\min {(\frac{|k|}{|\ell |},\frac{|\ell |}{|k|})}\) varies in compact subset of (0, 1]. If instead one of k or \(\ell \) is fixed, then
We know that \(|G(w)|<1\) for all w in the domain of G, which follows from the definition of G, from this we discern that \(E_{k,l}\) is exponentially decaying since \({\mathcal {R}}[{\tilde{g}}_\alpha (iw_\alpha )]=\log G(iw_\alpha )+\alpha \log G(1/(iw_\alpha ))<0\), where \(0\le \alpha \le 1\). However, we give the following quantitative estimate.
Lemma 13
For \(0\le \alpha < 1\),
Proof
Consider the integral
We see that
and
where \(1\le w_\alpha \le 1/\sqrt{2c}\). Define
We want to show that \(s(\alpha )\le 0\). Substituting \(u=1/v\) yields
and hence
For \(1\le u\le 1/\sqrt{2c}\),
which is equivalent to
or
Hence the integrand in (151) is less than or equal to zero, so \(s(\alpha )\le 0\). \(\square \)
6 Uniform Asymptotics of \(C_{\omega _c}\)
The goal of this section is to prove propositions 3 and 4, first we prove a lemma about descent paths.
Lemma 14
\(|G(e^{i\theta })|\) is strictly increasing for \(\theta \in (0,\pi /2)\).
Proof
Since \(|G(e^{i\theta })|^2=G(e^{i\theta })G(e^{-i\theta })\), taking the logarithm we can see the statement of this lemma is equivalent to assertion that the function \(\{e^{i\theta }: \theta \in (0,\pi /2)\}\rightarrow {\mathbb {R}}\) such that \({\widetilde{g}}_1(w)=\log (G(w))+\log (G(1/w))\) is strictly increasing over \(\theta \). From
changing variables \(w(\theta )=e^{i\theta }\) and from \(\sqrt{({\overline{w}})^2+2c}=\overline{\sqrt{w^2+2c}}\),
Once again we use the integral representation of the reciprocal square root to write
and since the integrand is positive for \(0<s<\sqrt{2c}\), \(0<\theta <\pi /2\) the lemma follows.
\(\square \)
Corollary 14.1
For \(\alpha \in (-1,\infty )\) (\(\alpha \in (-\infty ,-1)\)) the function \((0,\pi /2)\ni \theta \mapsto {\mathcal {R}}[g_\alpha (ie^{-i\theta })]\) is strictly decreasing (strictly increasing). If \(\alpha =-1\) the same function is zero.
Proof
Due to lemma 29
so the statement follows from lemma 14. \(\square \)
We write
to shorten the expressions. We require a few facts and approximations that will be used multiple times in the following proofs. From (155) and (29) we have
from which we see that \({\mathcal {I}}[\psi (\pi /2+\theta )]\) and \({\mathcal {R}}[\psi (\pi /2+\theta )]\) are odd and even functions on \([-\pi /2,\pi /2]\), respectively. In particular, (156) gives
A computation yields
from which we get
Further computation gives
Taylor’s theorem gives a bounded function \(R_{12}(\theta ,\theta _c,\alpha )\) such that
and there are also bounded functions \(R_{13}(\theta _c,\alpha ), R_{14}(\theta _c,\alpha ),R_{15}(\theta _c,\alpha )\) such that
From (157), (161) and (162) we obtain
We have a bounded function \(R_{16}(\theta ,\alpha )\) such that
which using (157), (159) gives a bounded function \(R_{8}(\theta )\) on \({\mathbb {R}}\) such that
We are now ready for the proof of Proposition 3.
Proof of Proposition 3
We parametrise \(w(\theta )=e^{i\theta }\) and use the fact that \(l+k\) is even to write
We rewrite (164) to get a \(R_{17}(\theta ,\alpha )\) such that
We use (167) and the bound \(|e^{t}-1|\le |t|e^{|t|}\) to get constants \(C_1,C_2>0\) such that
Next the second term in the difference in (168) can be approximated by (186). We get
Finally, the second them in the difference in (169) is
The two bounds (168), (169) together with (170) and (166) give a bounded function \(R_{18}(\xi ,\ell ,k)\) such that
Next, for all \(\varepsilon >0\) small if \(bx\in \Lambda _\varepsilon \) then there is a \(C(\varepsilon )>0\) such that
where we used the lower bound \(|\sin (x)/x|\ge 1-2|x|/\pi \) for \(x\in [-\pi /2,\pi /2]\). Hence if \(R_{6}\) is defined by (51),
Now \(\varphi _c^{2-\gamma }|\ell -k|\le \varphi _c^{2-\gamma }(|\ell |+|k|)<1\) implies \(\varphi _c^{1+\gamma }|\ell -k|\le \varphi _c^{-1+2\gamma }\) and \(\varphi _c^\gamma (1-2c)\le \varphi _c^{-1+2\gamma }\), so we obtain (52). \(\square \)
Now we give three propositions which go into the proof of Proposition 4.
Proposition 5
Let non-zero integers \(\ell ,k\) be such that \(\ell +k\le 2\) is even and \(\alpha = k/\ell \) lies in a compact subset of \([-1,1)\). There is a bounded function \(R_{19}(\xi ,\ell ,k)\) such that
Proof
We recall (166) as
Take the integral in (175), integrating by parts we have it equal to
where
Integrating by parts again, we have the integral in (176) as
Substituting this, we see that the integral in (175) is equal to
From (156) we get \(\psi '(\theta )=-\overline{\psi '(\pi -\theta )}\) and so \(b(\theta )=-\overline{b(\pi -\theta )}\). This gives
Note that because of (159) the term next to the exponential in the integrand in (178) is not defined when \(\alpha =1\). It is bounded when \(\alpha \) lies in a compact subset of \([-1,1)\), this follows from the change of variables \(w=e^{i\theta }\) in lemma (45) and noting that \(w_\alpha >1\) for \(0<\alpha <1\). When \(\ell +k<0\) and \(\alpha <1\) we have \(\ell <0\) so by corollary 14.1, \(l{\mathcal {R}}[\psi (\theta )]\) achieves its maximum over \([\theta _c,\pi -\theta _c]\) at the endpoints where \(l{\mathcal {R}}[\psi (\theta _c)]=l{\mathcal {R}}[\psi (\pi -\theta _c)]\). For \(\ell +k\in \{0,1,2\}\), \(\ell {\mathcal {R}}[\psi (\theta )]\) is bounded trivially on \([\theta _c,\pi -\theta _c]\). From this we obtain a bounded function \(R_{20}(\xi ,\ell ,k)\) such that
By (162) and (185) there is a bounded function \(R_{21}(\xi ,\alpha )\) such that
From (165), (181) and \(b(\pi /2)=i/[(1-\alpha )\sqrt{1-2c}]\) there are bounded functions \(R_{22}(\xi ,\alpha ), R_{23}(\xi ,\ell ,k)\) such that (180) equals
Hence (174) follows by (175), (180) and (182). \(\square \)
Proposition 6
Let non-zero integers \(\ell ,k\) be such that \(\ell +k< 0\) is even and \(\alpha = k/\ell \) lies in a compact subset of \((-1,1]\). There is a bounded function \(R_{24}(\xi ,\ell ,k)\) such that
Proof
Recall \({\tilde{C}}_{\omega _c}(k,\ell )\) as in (35) and that \(\Gamma _{\omega _c}=\{e^{i\theta }:\theta \in (\theta _c,\pi -\theta _c)\cup (-\pi +\theta _c,-\theta _c)\}\). We parametrise \(\Gamma _{\omega _c}\cap {\mathbb {H}}^+\) by \(w(\theta )=e^{i\theta }\) for \(\theta \in [\theta _c,\pi /2]\), use (196) and the fact that \(\ell +k\) is even to write
Now,
which is zero when \(\theta =\pi /2\), so there is a bounded function \(R_{25}(\theta )\) such that
Hence the integral in (184) can be approximated with an error bound given by
for some \(C>0\). We will return to this bound. Also note that the assumptions \(\ell +k<0\) and \(\alpha \in (-1,1]\) give \(\psi ''(\pi /2)>0\) and \(\ell <0\). We now focus on approximating the real part of the second integral appearing in the difference in (187)
Recalling (163), we see that
uniformly for \(\theta _c\le \theta \le \pi /2\). Note the inequality in (189) reverses upon multiplying both sides by \(\ell <0\). Now we use (163), (189) and the bound \(|e^t-1|\le |t|e^{|t|}\) to obtain a constant \(C>0\) such that
We return to the bound (187). By a similar argument to (190)
The second term in the difference in (191) is bounded by
for some \(C_1>0\). Hence by the triangle inequality (187) is bounded above by the sum of (192) and the right hand side of (193). Next, because of (156), the fact that \({\mathcal {I}}[\psi (\pi /2+\theta )]\) is odd on \([-\pi /2,\pi /2]\) and that \(\ell \pi (1-\alpha )=\pi (\ell -k)\) is an even multiple of \(\pi \), we have
The integral in (183) follows directly from (194) since (194) multiplied by \(1/(1-2c)\) gives the main contribution to the integral in (184). \(\square \)
We now note that by equation 4.21 in [8], the formula (30) in fact holds for \(k>0\) or \(\ell >0\) instead of just \(k,\ell >0\) as we stated it. Hence for non-zero integers \(k,\ell \) such that \(k>0\) or \(\ell >0\), define a function \(D_{\omega _c}(k,\ell )= E_{k,\ell }-{\tilde{C}}_{\omega _c}(k,\ell )\) where
and where \({\tilde{\Gamma }}_{\omega _c}=\Gamma _1\setminus \Gamma _{\omega _c}\) has positive orientation counterclockwise around the origin. Note that \(D_{\omega _c}(k,\ell )=D_{\omega _c}(\ell ,k)\) when \(k,\ell >0\).
One can use the symmetries in (28) to get
where \(\Gamma _{a,b}=\{e^{i\theta }:\theta \in [a,b]\}\), \(0\le a<b\le \pi /2\}\) and each curve has orientation counterclockwise around the origin.
Proposition 7
Let non-zero integers \(\ell ,k\) be such that \(\ell +k> 0\) is even and \(\alpha = k/\ell \) lies in a compact subset of \((-1,1]\). There exists a bounded function \(R_{26}(\xi ,\ell ,k)\) such that
Proof
From the definition of \(D_{\omega _c}(k,\ell )\) we see that
where we parametrised \({\tilde{\Gamma }}_{\omega _c}\cap {\mathbb {H}}^+\) by \(w(\theta )=e^{i\theta }\) for \(\theta \in [0,\theta _c]\) and \(\delta >0\) will be chosen small enough. The main contribution to \(D_{\omega _c}\) comes from the first integral in (198).
From (186) we have a constant \(C>0\) such that
We will return to this bound. First we will consider
since this contributes to the leading term of \(D_{\omega _c}\).
Recall (163) and take \(\delta \) so small that
for all \(\theta \in [\theta _c-\delta ,\theta _c]\). Now we use (163), the bound \(|e^t-1|\le |t|e^{|t|}\) and then (201) to give a constant C such that
Rewrite the integral on the right hand side of (202) as a sum of four integrals. We bound these four integrals separately. Here, and several times below, we will use that \(\psi ''(\pi /2)<0\) and \(\ell >0\). The first bound is
the third is
and the fourth is
We bound the second integral slightly differently by making the substitution \(\theta \rightarrow (\ell ^2\psi ''(\pi /2)^2\varphi _c)^{-1/3}\theta \) in
The integral in (206) is bounded because \(\int _0^{\infty }e^{-t\theta /2-\theta ^2/(4t)}\theta ^2d\theta \) is bounded uniformly for all \(t> 0\). We now return to the bound (199). Similar to how we got the bound (202), we obtain
The term appearing in the big brackets in (208) was bounded previously via (203), (205), (204) and (206). The second integral in the difference in (207) is
Hence we have established an upper bound on the right hand side of (199). The second integral appearing in the difference in (202) contributes to the main term and using similar manipulations leading to (194) we can rewrite it is as
We extend the integration in the last integral to infinity which gives an error term
Thus the infinite integral
gives the main term in (197).
It remains to bound the second integral in (198). Since \({\mathcal {R}}[\psi (\theta )]\) increases on \((0,\pi /2)\), there is a constant \(C>0\) such that
From (163) we can take \(\delta \) so small that
Hence (212) is bounded above by
\(\square \)
Now we give some lemmas from which we obtain the leading order terms in the preceding expansions.
Lemma 15
Let non-zero integers \(\ell ,k\) be such that \(\ell +k>0\) is even and \(\alpha =k/\ell \) lies in a compact subset of \([-1,1)\). There is bounded function \(R_{35}(\xi ,k,\ell )\) such that
If instead \(\alpha =1+\kappa _{\ell }\in [-1,1]\) such that \(\ell \kappa _{\ell }\) is bounded then there is a bounded function \(R_{38}\) such that
The proof of the above lemma is in Sect. 8
Lemma 16
Let \(\ell ,k\) be non-zero integers such that \(\ell +k<0\) and \(\alpha =k/\ell =1+\kappa _\ell \) for some \(\kappa _\ell =O(1/|\ell |)\). There is a bounded function \(R_{40}(\xi ,\kappa _\ell ,\ell )\) such that
Similarly, the proof of the above lemma is delayed to Sect. 8.
We now have all of the ingredients to prove Proposition 4.
Proof of Proposition 4
We divide the proof into five cases, one when \({\tilde{\alpha }}=-1\), the other four when \({\tilde{\alpha }}\in (-1,1)\) or \({\tilde{\alpha }}=1\) and \(\ell +k\) is positive or negative. Each case consists of defining \(R_9\) by the rearrangement of (54) and using the stated substitutions and bounds.
First the case \({\tilde{\alpha }}=-1\) for which the assumptions imply \(\ell +k\in \{-2,0,2\}\). By (172) we have
By lemma 13 and proposition 2 and there are \(C_1,C_2>0\) such that
We define \(R_9\) as the rearrangement of (54)
and use the formula for \(C_{\omega _c}\) given by Proposition 5 so that \(R_9\) is equal to
Now we use the upper bounds (217) and (218), and the conditions \(\varphi _c^{2-\gamma }(|\ell |+|k|)\ge 1/2, \ell +k\in \{-2,0,2\}\) to get
For the case \({\tilde{\alpha }}\in (-1,1)\) and \(\ell +k<-2\) we can set the two different expressions for \({\tilde{C}}_{\omega _c}\), (174) and (183), equal to one another so that bound (217) carries over to
for \(|\ell |\) large enough. We also have that \(\ell {\mathcal {R}}[\psi (\theta _c)]= (\ell +k)\log |G(e^{i\theta _c})|\ge (\ell +k)\log |G(i)|> 0\) which implies \(|G(\omega _c)|^{\ell +k}\) grows exponentially in \(|\ell |\). Just as in (219) we define \(R_9\) to be the rearrangement of (54) but now use the formula for \(C_{\omega _c}\) provided by Proposition 6 so that
Just as in (221), we use (223) together with (218), (222) to get the bound
For the case \({\tilde{\alpha }}=1\), \(\ell +k<-2\) we again define \(R_{9}\) as the rearrangement of (54). We then use Proposition 5 followed by lemma 16 on \(C_{\omega _c}\). Then using the bounds (218), (87), (88) we obtain a \(C>0\) such that
For the case \({\tilde{\alpha }}\in (-1,1)\), \(\ell +k>2\) we again define \(R_{9}\) as the rearrangement of (54). Then use Proposition 7 together with lemma 15 on the function \(E_{k,\ell }-C_{\omega _c}(k,\ell )\) appearing in the numerator of \(R_{9}\). Then use the bound (217) and \(\varphi _c^{2-\gamma }(|\ell |+|k|)\ge 1/2\) to obtain
For the case \({\tilde{\alpha }}=1\), \(\ell +k>2\) use lemmas 15 and 7 and the bound (89) to obtain
\(\square \)
7 Uniform Bound on \(R_{\varepsilon _1,\varepsilon _2}\)
We begin by proving Theorem 3. It is proved in [8] that for \(n=4m\), \(m\in {\mathbb {N}}_{>0}\), \((x_1,x_2)\in W_{\varepsilon _1}\), \((y_1,y_2)\in B_{\varepsilon _2}\) with \(\varepsilon _1,\varepsilon _2\in \{0,1\}\) we have the formula
where \(B_{\varepsilon _1,\varepsilon _2}(a,x_1,x_2,y_1,y_2)\) is given by (229) below and \(B^*_{\varepsilon _1,\varepsilon _2}\) is the sum of three double contour integrals related to \(B_{\varepsilon _1,\varepsilon _2}\) by symmetry.
We recall \(B_{\varepsilon _1,\varepsilon _2}\) as equation (3.11) in [8],
where equation (2.11) in [8] is
for integers \(0<x,y<n\) and G is defined in (25). The expression for \(V_{\varepsilon _1,\varepsilon _2}(w_1,w_2)\) is somewhat involved and we refer to equation (3.7) in [8]. The precise form is of \(V_{\varepsilon _1,\varepsilon _2}\) is not needed here. However we note that \(V_{\varepsilon _1,\varepsilon _2}\) is analytic in \(\big ({\mathbb {C}}\setminus (i(-\infty ,-1/\sqrt{2c}]\cup i[-\sqrt{2c},\sqrt{2c}]\cup i[1/\sqrt{2c},\infty ))\big )^2\). Thus the integrand of \(B_{\varepsilon _1,\varepsilon _2}\) is analytic in the same set minus the collection of points \(w_1=w_2\).
Define the error term
where desc\(_\xi \) and asc\(_\xi \) are the contours of steepest descent and ascent of the function \(g_{\xi }\) passing through \(\omega _c\), see [8] or lemmas 17 and 18 below. We want to show that
The formula (232) follows by a contour deformation in the contour integral formula for \(B_{\varepsilon _1,\varepsilon _2}\) as given in (229). For this section we use the coordinates in (38). From equations (230) and (33) we compute
We have lemma 3.15 from [8]
Lemma 17
For \(\xi =\xi _c\) there is a path of steepest descent for \(g_\xi \) leaving i at the angle \(-\pi /6\) going to 0 (via \({\mathbb {H}}^+\)) and a path of steepest ascent leaving at an angle \(\pi /6\) and going to infinity (via \({\mathbb {H}}^+\)).
Note \({\mathcal {R}}[g_\xi (w)]\) is symmetric across the real and imaginary axes so this also gives the paths on the upper left quadrant and bottom half of the plane. We have lemma 3.20 from [8]
Lemma 18
For \(\xi _c>\xi >-\frac{1}{2}\sqrt{1+2c}\), choose \(\omega _c=e^{i\theta _c}\) with \(\theta _c\in (0,\pi /2)\) such that \(g'_\xi (\omega _c)=0\). There is a contour of steepest ascent leaving \(\omega _c\) at an angle \(\theta _c-\pi /4\) ending at infinity (via \({\mathbb {H}}^+\)) and a contour of steepest ascent leaving \(\omega _c\) at an angle \(\theta _c+3\pi /4\) ending at a cut (via \({\mathbb {H}}^+\)) and an ascent contour ending at \(i\sqrt{2c}\) traveling via the cut \(i[0,\sqrt{2c}]\).
There is a contour of steepest descent leaving \(\omega _c\) at an angle \(\theta _c-3\pi /4\) ending at zero (via \({\mathbb {H}}^+\)) and a contour of steepest descent leaving \(\omega _c\) at an angle \(\theta _c+\pi /4\) ending at a cut (via \({\mathbb {H}}^+\)) and a descent contour ending at \(i/\sqrt{2c}\) traveling via the cut \(i[1/\sqrt{2c},\infty )\).
Now deform \(\Gamma _{r'}\) to the path of steepest descent, \(\text {desc}_{\xi }\), for \(g_{\xi }\) passing through the critical points \(\pm \omega _c\), \(\pm {\overline{\omega }}_c\). This can be done due to the following crude estimates for \(|w_2|=R\) large and \(|w_1|=1/R\) small,
which follow by Taylor expansions. Deform \(\Gamma _{1/r'}\) to path of steepest ascent of \(g_{\xi }\) passing through the points \(\pm \omega _c\), \(\pm \overline{\omega _c}\), label this contour asc\(_\xi \). Since the \(w_2\)-contour passes over the \(w_1\)-contour we pick up a contribution
by the residue theorem. Lemma (3.2) in [8] is
This together with the definitions in (23) and (24) give that the contribution (236) is equal to \(C_{\omega _c}(x,y)\) defined in (36). The rest of the integral is given by what we called the error term, (231). This proves the formula (232) and hence Theorem 3.
We now turn to the proof of Proposition 1. This involves an analysis of the steepest descent and ascent contours for the saddle point function \(g_\xi \), across a region of the parameter space \(\xi \) where two single critical points merge to form a double critical point. In order to carry out this analysis we note that the ascent contour is infinite and the descent contour travels to the origin, where the integrand is not analytic. In light of this, we make the following deformations.
Consider the upper right quadrant of \({\mathbb {C}}\). Take \(R>2\) very large, by lemmas 3.15 and 3.20 in [8], the path of steepest ascent of \(g_\xi \) in the upper right quadrant intersects the quarter circle centred at 0 that travels from R to iR. Deform the section of asc\(_\xi \) in the upper right quadrant that extends from the intersection to infinity to the section of the quarter circle starting at the intersection, travelling down the quarter circle and ending at the point \(R\in {\mathbb {C}}\). Make the equivalent symmetric deformations in the other three quadrants and label this contour \(\text {asc}^R_\xi \). Similarly, the path of steepest descent in the upper right quadrant intersects a small quarter circle centred at 0 of radius \(\varepsilon \), take \(\varepsilon =1/R\) for simplicity. Deform the section of desc\(_\xi \) starting at the intersection and going to zero to the contour starting from the intersection and travelling down along the small quarter circle to the point \(1/R\in {\mathbb {C}}\). Make the equivalent symmetric deformations in the other quadrants and label this new contour desc\(_{\xi ,1/R}\). Now note from (235) that we can take R so large and fixed so that \({\mathcal {R}}[g_{\xi }(\omega _c)]> {\mathcal {R}}[g_\xi (w_1)]+1\) and \({\mathcal {R}}[-g_\xi (\omega _c)]>{\mathcal {R}}[-g_\xi (w_2)]+1\) for \(|w_1|=1/R\), \(|w_2|=R\).
In order to deal with the contributions to the asymptotics coming from small neighbourhoods of the critical points we make the following local deformations.
Let \(0\le \xi _c-\xi \le \delta ^*_n\) where \(\delta ^*_n>0\) is a sequence going to zero. Consider the section of the contour desc\(_{\xi ,1/R}\) in \({\mathbb {H}}^+\). For \(\delta _0>0\) sufficiently small and n large enough, later we will prove that the section of desc\(_{\xi ,1/R}\) that leaves the small quarter circle centred at 0 of radius 1/R and travelling up to \(\omega _c'\) passes through the set \(\{i+\delta _0e^{i\theta }:\theta \in [-\pi /4-a^*,-\pi /6+a^*]\}\) for some positive \(a^*<\pi /24\). Label the contours intersection with this set as \(w^*_\xi \). Next consider the connected component of desc\(_{\xi ,1/R}\) with endpoints \(w^*_\xi \) and \(\omega _c\), deform this component to a straight line connecting the two endpoints. Also, deform the component of desc\(_{\xi ,1/R}\) starting at \(\omega _c\) and ending at the imaginary axis to the straight line starting from \(\omega _c\) and leaving at an angle \(3\pi /5\), extending to the imaginary axis. In the case \(\omega _c=i\) this last section vanishes. Make the equivalent symmetric deformations in the other three quadrants of \({\mathbb {C}}\). Label this deformed contour \(\widetilde{\text {desc}}_{\xi ,1/R}\) and note it now depends on \(\delta _0\) and \(\xi \), it has also only been defined for \(\delta _0\) sufficiently small and n large enough. We call the equivalent deformations to \(\text {asc}^R_\xi \) as \(\widetilde{\text {asc}}_{\xi }^R\).
We now have
So we have the bound
where
and \(\sup _1\) is the supremum over a compact subset A of \(( {\overline{{\mathbb {B}}}}(0,R)\setminus {\mathbb {B}}(0,1/R))^2\) such that \(V_{\varepsilon _1,\varepsilon _2}\) is analytic on A and \(\widetilde{\text {desc}}_{\xi ,1/R},\widetilde{\text {asc}}^R_\xi \subset A\) for every \(\xi \). Note that both \(\widetilde{\text {desc}}_{\xi ,1/R},\widetilde{\text {asc}}^R_\xi \subset {\overline{{\mathbb {B}}}}(0,R)\setminus {\mathbb {B}}(0,1/R)\) for all \(0\le \xi _c-\xi \le \delta ^*_n\). Now we are in a position to prove our bound on \(R_{\varepsilon _1,\varepsilon _2}\).
Proof of Proposition 1
We first formulate a few key lemmas. The first of these, provides us with the fact that the contours \(\widetilde{\text {desc}}_{\xi ,1/R}\), \(\widetilde{\text {asc}}_\xi ^R\) are well-defined.
Lemma 19
Let \(\delta ^*_n>0\) be a sequence that goes to zero as \(n\rightarrow \infty \), for \(\delta _0>0\) sufficiently small there is a natural number N such that for all \(n>N\) the section of desc\(_{\xi }\) with endpoints 0 and \(\omega _c\) intersects the set \(\{i+\delta _0 e^{i\varphi }:\varphi \in [-\pi /4,-\pi /12]\}\) for all \(0\le \xi _c-\xi \le \delta ^*_n\) and the section of \(\text {asc}_\xi \) starting at \(\omega _c\) and ending at infinity travelling via \({\mathbb {H}}^+\) intersects the set \(\{i+\delta _0 e^{i\varphi }:\varphi \in [\pi /12,\pi /4]\}\).
The next lemma gives control over the integral in a neighbourhood of the critical points.
Lemma 20
Let \(\delta ^*_n>0\) be a sequence going to zero as \(n\rightarrow \infty \). If \(\delta _0>0\) is sufficiently small then for \(w_1\in \widetilde{\text {desc}}_{\xi ,1/R}\cap \overline{{\mathbb {B}}}(i,\delta _0)\) and all n large enough, there exists \(C>0\) such that
for all \(0\le \xi _c-\xi \le \delta ^*_n\). Also, for \(w_2\in \widetilde{\text {asc}}_{\xi }^R\cap \overline{{\mathbb {B}}}(i,\delta _0)\) and n large enough,
for all \(0\le \xi _c-\xi \le \delta ^*_n\).
The next lemma gives control of the integral over sections of the descent path bounded away from the critical points, and follows from the above lemma.
Lemma 21
Let \(\delta ^*_n>0\) be a sequence that goes to zero as \(n\rightarrow \infty \), if \(\delta _0>0\) is sufficiently small and \(w^{*}_{\xi }\) is a point where desc\(_{\xi }\) intersects \(\partial {\mathbb {B}}(i,\delta _0)\) in \({\mathbb {H}}^+\), \(w_\xi ^{**}\) be a point where \(\text {asc}_\xi \) intersects \(\partial {\mathbb {B}}(i,\delta _0)\) in \({\mathbb {H}}^+\). There is a number \(C(\delta _0)>0\) such that
for all \(0\le \xi _c-\xi \le \delta ^*_n\), when n is large. We also have
for all \(0\le \xi _c-\xi \le \delta ^*_n\), when n is large.
Let \(\delta _0>0\) be small enough and n large enough such that the above lemmas hold. Define
It is enough to bound the integral in (240) restricted to \(({\mathbb {H}}^+)^2\),
In particular write this integral as a sum of integrals over products of sets of the form (246). The bound
holds by lemma 21 and the trivial bound \(\sup _{({\mathbb {B}}(0,R)\setminus {\mathbb {B}}(0,1/R))^2}|K(w_1,w_2)|\le e^{C'r}\) for some \(C'>0\). Since \({\mathcal {R}}[g_\xi (e^{i\theta })]=0\) for any real \(\theta \), \({\mathcal {R}}[g_\xi (\omega _c)]=0\). By an application of the Hayman-Wu theorem (see Garnett and Marshall [17]), the contours are finite length. To see this, recall a version of the Hayman-Wu theorem; If \(\varphi :{\mathbb {D}}\rightarrow {\mathbb {C}}\) is conformal on the unit disc and L is a straight line in \({\mathbb {C}}\) then length\((\varphi ^{-1}(L))\le 4\pi \). One can take \(\xi _c-\xi \) small enough that \(\widetilde{\text {desc}}_{\xi ,1/R}\) and \(\widetilde{\text {asc}}^R_\xi \) do not intersect the branch cuts so we can find a compact set \(A\subset {\mathbb {B}}(0,R+1)\setminus {\mathbb {B}}(i,\delta _0)\) such that \(g_\xi \) is analytic on A and A contains both \(\widetilde{\text {desc}}_{\xi ,1/R}\) and \(\widetilde{\text {asc}}^R_\xi \) for all \(\xi \). Cover A with finitely many open balls that do not intersect the branch cuts. Apply the Hayman-Wu theorem to the straight line \(\pm i{\mathcal {I}}[g_\xi (\omega _c)]+{\mathbb {R}}\) and \(g_\xi \) restricted to each open ball. Since the number of balls is finite the contours are finite. The same theorem gives the same bound for each contour and so the contours lengths are bounded uniformly in \(\xi ,\xi '\). The integrand in (248) is integrable since the two sections of the contours do not intersect. Hence the integral over \(\Gamma _{\text {d}}^{\text {out}}\times \widetilde{\text {asc}}^R_\xi \cap {\mathbb {H}}^+\) is \(O(e^{-C(\delta _0)n/2+C'r})\). One obtains the same bound for \(\Gamma _{\text {a}}^{\text {out}}\times \widetilde{\text {desc}}^R_\xi \cap {\mathbb {H}}^+\) in an analogous fashion. The integral over sections of the contours contained in \(({\mathbb {B}}(i,\delta _0)\cap {\mathbb {H}}^+)^2\) is
These contours are straight lines by definition
It is straightforward to see that the lengths of these straight lines are uniformly bounded in \(0\le \xi _c-\xi \le \delta ^*_n\), indeed, their endpoints all lie in a bounded region of \({\mathbb {C}}\). Define \(\gamma ^{\text {a},1}(t)=\omega _c+te^{i\theta _{\text {a},1} }\), \(\theta _{\text {a},1}=-3\pi /5\) for \(t\in [0,{\mathcal {R}}[\omega _c]/\sin (\pi /10)]\), \(\gamma ^{\text {a},2}(t)=\omega _c+te^{i\theta _{\text {a},2}}\), \(\theta _{\text {a},2}=\arg (w_\xi ^{**}-\omega _c)\) for \(t\in [0,|w_\xi ^{**}-\omega _c|]\), \(\gamma ^{\text {d},1}(s)=\omega _c+se^{i\theta _{\text {d},1}}\), \(\theta _{\text {d},1}=3\pi /5\) for \(s\in [0,{\mathcal {R}}{\omega _c}/\sin (\pi /10)]\), and finally, \(\gamma ^{\text {d},2}(s)=\omega _c+se^{i\theta _{\text {d},2}}\), \(\theta _{\text {d},2}=\arg {(w_\xi ^*-\omega _c)}\) for \(s\in [0,|w_\xi ^*-\omega _c|]\). These parametrise the straight lines in \(\Gamma _{\text {d}}^{\text {in}}\) and \(\Gamma _{\text {a}}^{\text {in}}\). For \(i,j=1,2\) consider the bound
which holds by lemma 20. We can take \(\delta _0\) small enough that for \(j\in \{1,2\}\)
for \(w_j\in {\mathbb {B}}(i,\delta _0)\cap {\mathbb {H}}^+\). From which we gain a \(C'''>0\) such that
Insert this bound into (251). Parametrising and recalling \({\mathcal {R}}[g_\xi (e^{ix})]=0\) for any real x, (251) is bounded by the prefactor \(|G(\omega _c)|^{b_1-a_1}|G(1/\omega _c)|^{a_2-b_2}\) multiplied by
when \(r\le n^{1/3}\). The double integral in (254) is bounded above by some positive constant uniformly for \(\xi ,n\). To prove the \(1/\sqrt{n\sqrt{\xi _c-\xi }}\) bound in (39), we instead use \({\mathcal {R}}[g_\xi (w_i)-g_\xi (\omega _c)]\le -C\sqrt{\xi _c-\xi }|w_i-\omega _c|^2\) in (251) and then make the change of variables \(s\rightarrow s/\sqrt{n\sqrt{\xi _c-\xi }}, t\rightarrow t/\sqrt{n\sqrt{\xi _c-\xi }}\) instead of \(s\rightarrow n^{-1/3}s, t\rightarrow n^{-1/3}t\) in (253). \(\square \)
We now turn to the proof of lemmas 19 to 21. Let \(\delta _0<1-\sqrt{2c}\) so that for \(-\frac{1}{2}\sqrt{1+2c}<\xi \le \xi _c\), \(g_\xi (w)\) is analytic in the annulus \({\mathcal {L}}(\delta _0)=\{z\in {\mathbb {C}}:1-\delta _0<|z|<1+\delta _0\}\). From Taylor’s theorem,
for \(\xi _c\ge \xi \ge \varepsilon ^*>-\frac{1}{2}\sqrt{1+2c}\). Where
for any \(0<\delta _1<\delta _0\) and \(R_{\omega _c}(w)(w-\omega _c)^4\) is \(O(|w-\omega _c|^4)\) uniformly in \(\xi \).
We have the equations
which follow by taking derivatives. Before we prove Lemmas 19, 20, 21 we relate the second and third derivatives of \(g_\xi \) at \(\omega _c\) to \(\xi _c-\xi \).
Lemma 22
There are functions \(R_{27}(\xi ),R_{28}(\xi )\) bounded for some interval \(0\le \xi _c-\xi < c_2\) such that
and
where \(d_2=4\sqrt{\frac{c(1+c)}{(1-2c)^{5/2}}}\), \(d_3=\frac{8c(1+c)|\xi _c|}{(1-2c)^{5/2}}\).
Proof
From (258) write
Define \(F_4(\theta _c)=e^{i\theta _c}/{((e^{i\theta _c})^2+2c)^{3/2}}\). For each \(\theta _c\in [0,\pi /2]\) there exists \(\chi \in [\theta _c,\pi /2]\) such that
with \(R_{29}(\xi )={\mathcal {I}}[F_4''(\chi )]\). Since \({\mathcal {I}}[F_4(\pi /2)]=0\),
where \(\varphi _cR_{30}(\xi )=e^{-2i\theta _c}+1\), \(R_{30}(\xi _c)=2i\) and \(|R_{30}(\xi )|\le 2e^{\pi -2\theta _c}\).
where \(R_{31}(\xi )=4ic\xi [{\mathcal {I}}[R_{29}(\xi )](-1-R_{30}(\xi ) \varphi _c)+R_{30}(\xi )F_4'(\pi /2)]\) is bounded.
A computation yields
Inserting (43) into (265) we have
for a bounded function \(R_{27}\).
For the third derivative, from (259) write
Define \(L_2(\theta _c)={\mathcal {R}}[\frac{2e^{i\theta _c}(c-e^{2i\theta _c})}{((e^{i\theta _c})^2+2c)^{5/2})}]\), for every \(\theta _c\in [0,\pi /2]\) there is a \(\chi \in [\theta _c,\pi /2]\) such that \(R_{32}(\xi )=-L_2'(\chi )\) and \(L_2(\theta _c)-L_2(\pi /2)=R_{32}(\xi )\varphi _c\). It is clear that \(L_2(\pi /2)=\frac{2(1+c)}{(1-2c)^{5/2}}\). So now
where \(|R_{33}(\xi )|\le 3e^{3\pi /2-3\theta _c}\), \(|R_{34}(\xi )|\le e^{\pi /2-\theta _c}\). The lemma follows by the statement on \(g''_\xi (\omega _c)\) and lemma 5. \(\square \)
Lemma 23
Let \(p\exp {(i\theta )}+\omega _c\) \((p>0,\theta \in (-\pi ,\pi ])\) be a point in the annulus \({\mathcal {L}}(\delta _0)\) satisfying
There are constants \(a_1,a_2>0\) sufficiently small such that the following holds. Set \(\delta =\delta (\varepsilon ) = \min \{\varepsilon a_1,a_2\}\). For every \(\varepsilon >0\), if \(0\le \xi _c-\xi \le \delta ^4\) and \(\delta /2\le p\le \delta \) then
If instead \({\mathcal {R}}[g_\xi (\omega _c+pe^{i\theta })]>{\mathcal {R}}[g_\xi (\omega _c)]\), then for every \(\varepsilon >0\) there is a \(\delta >0\) sufficiently small such that if \(0\le \xi _c-\xi \le \delta ^4\) and \(\delta /2\le p\le \delta \) then
Proof
Let \(0<\delta _1<1\) be small enough so that the remainders in equation (255) and lemma 22 are bounded for all \(0\le \xi _c-\xi \le \delta _1^{4}\) and \(0\le p\le \delta _1\). Insert the Taylor expansion (255) into the first condition in (270),
Now apply lemma 22 to the left hand side, a rearrangement gives
The absolute value of the right hand side of (274) is bounded above by
This is bounded by some constant \(C_1\) multiplied by \(\delta \) when \(\delta \le \delta _1\). Hence we take \(\delta =\min (\varepsilon /C_1,\delta _1)\) and \(a_1=1/C_1, a_2=\delta _1\). The remaining statements are proved by alterations to the above argument. \(\square \)
For \(s>0\) and a subset S of \({\mathbb {R}}\) define \({\overline{{\mathbb {B}}}}(S,s)=\cup _{x\in S}{\overline{{\mathbb {B}}}}(x,s)\). We now prove a lemma from which Lemma 19 follows.
Lemma 24
For every \(\varepsilon >0\) sufficiently small there is a \(\delta >0\) (with \(\delta \rightarrow 0\) when \(\varepsilon \rightarrow 0\)) such that desc\(_\xi \) intersects \(\{i+\varepsilon e^{i\varphi }:\varphi \in {\mathbb {B}}(-\pi /6,\delta )\}\) for all \(0\le \xi _c-\xi \le \varepsilon ^4\).
Proof
Let \(p>0\), \(\theta \in (-\pi ,\pi ]\) be such that \(p\exp {(i\theta )}+\omega _c\) is in the component \(\Gamma _\xi \) of desc\(_\xi \) with endpoints 0 and \(\omega _c\). By Lemma 23 and the fact the \(\cos (3\theta )\) is locally invertible near its roots; for every \(\varepsilon >0\) sufficiently small \(\theta \) is close to one of the points \(-5\pi /6,-\pi /6,\pi /2\) for all \(0\le \xi _c-\xi \le \varepsilon ^4\) and \(\varepsilon /2\le p \le \varepsilon \). Let us discount the cases where \(\theta \) is close to \(-5\pi /6\) or \(\pi /2\). By lemma 5 there is \(C>0\) such that \(|\omega _c-i|\le C \varepsilon ^2\). Take \(\varepsilon \) so small that \(|\omega _c-i|\le \varepsilon /8<\varepsilon /2\le p\). Because \(\Gamma _\xi \) can not cross the imaginary axis and by basic geometry, \(\theta \) is not close to \(-5\pi /6\). Since \(\Gamma _\xi \) leaves \(\omega _c\) at an angle \(\theta _c-3\pi /4\) and \({\mathcal {R}}[g_\xi (e^{ix})]=0\) for all real x, \(\Gamma _\xi \) can not cross the unit circle. So \(\theta \) is not close to \(\pi /2\).
Set \(i+\varepsilon e^{i\varphi }=\omega _c+pe^{i\theta }\). We have the inequality \(|p-\varepsilon |\le |pe^{i\theta }-\varepsilon e^{i\varphi }|=|\omega _c-i|\). So there is a constant \(C>0\) such that \(|\varphi +\pi /6|\le |\theta +\pi /6|+C|\omega _c-i|^2\le |\theta +\pi /6|+C\varepsilon ^2\).
\(\square \)
Lemma 25
Let \(\delta ^*_n>0\) be a sequence going to zero as \(n\rightarrow \infty \). If \(\delta _0>0\) is sufficiently small then for \(w_1\in \widetilde{\text {desc}}_\xi \cap \overline{{\mathbb {B}}}(i,\delta _0)\) and all n large enough, there exists \(C>0\) such that
for all \(0\le \xi _c-\xi \le \delta ^*_n\).
Proof
We give the proof for \(\widetilde{\text {desc}}_\xi \), the case for \(\widetilde{\text {asc}}_\xi \) is similar. Set \(w_1-\omega _c=pe^{i\theta }\). From lemma 22 and (255),
For \(\delta _0\) small enough and n large there is a \(C'>0\) such that \(|R_{\omega _c}(w_1)|,|R_8(\xi )|,|R_{12}(\xi )|\le C'\) using these inequalities in (277) we obtain
Next we recall a fact proved in the proof of lemma 24, for any \(\delta _0\) sufficiently small and n large enough, if \(w_\xi ^*\in \Gamma _\xi \cap \partial B(i,\delta _0)\) then \(\arg (w_\xi ^*-\omega _c)\in {\mathbb {B}}(-\pi /6, \pi /24)\). Recall also, that \(\widetilde{\text {desc}}_\xi \cap {\mathbb {B}}(i,\delta _0)\) consists of two straight lines: One leaving \(\omega _c\) at angle \(\theta =3\pi /5\), terminating at the imaginary axis and the other having endpoints \(\omega _c\), \(w_\xi ^*\). Hence take \(\delta _0\) so small that \(6C'\delta _0/d_3<1/8\), and n so large that \(\max (2C'\sqrt{\xi _c-\xi }/d_2,6C'/d_3(\sqrt{\xi _c-\xi }+|\omega _c-i|))<1/8\) so
since both \(\sin (2\theta ),\sin (3\theta )<-1/2\) when \(\theta =3\pi /5\) or \(\theta \in [-5\pi /24,-3\pi /24]\). Note this proof also yields Lemma 21. \(\square \)
8 Some Technical Lemmas
Now we give the proof of the lemma relating \(\omega _c\) and \(\xi \).
Proof of lemma 5
By (257), \(\xi =-1/(2{\mathcal {R}}[F_1(e^{i\theta _c})] )\) and \(\xi _c=-1/(2{\mathcal {R}}[F_1(i)])\) where we define \(F_1(w)=w/\sqrt{w^2+2c}\). Let \(F_2(\theta _c)=1/{\mathcal {R}}[F_1(e^{i\theta _c})]\), \(F_2\) is smooth on \([0,\pi /2]\). For any \(\theta _c\in [0,\pi /2]\) there exists \(\chi \) between \(\pi /2\) and \(\theta _c\) such that
Direct computation gives that \(F_2'(\pi /2)=F_2'''(\pi /2)=0\) and that \(F_2''(\pi /2)=-4c(1+c)/\sqrt{1-2c}\). (41) follows by defining \(R_{35}(\varphi _c)=F_2''''(\chi )\) for the corresponding \(\chi \) and the fact that \(\xi _c-\xi =(F_2(\pi /2)-F_2(\theta _c))/2\).
Define \(F_3(w)=F_1(w)+F_1(1/w)\). We are going to find a section of a small neighbourhood around i in which to invert \(F_3(w)\). Note \(F_3\) is not one-to-one in any neighbourhood of i. It is straightforward to compute \(F_3(i)=-1/\xi _c\), \(F_3'(i)=0\) and \(F_3''(i)=-8c(1+c)/(1-2c)^{5/2}\). One sees from the definition of \(F_3\) that \(F_3\) is analytic in the disc \({\mathbb {B}}(i,\delta _1)\) where \(\delta _1=1-\sqrt{2c}\). Define H such that \(F_3(i)-F_3(w)=H(w)(w-i)^2\) so that H is analytic in \({\mathbb {B}}(i,\delta _1)\) and \(H(i)=-F_3''(i)/2\) is a positive real number. Non-zero analytic functions have isolated zeros so we can find \(0<\delta _2<\delta _1\) so that \(0\notin H({\overline{{\mathbb {B}}}}(i,\delta _2))\) and define a branch of \(\sqrt{H(w)}\) so that \(\sqrt{H(w)}\) is analytic on \({\overline{{\mathbb {B}}}}(i,\delta _2)\). Now define the analytic function \(h(w)=(w-i)\sqrt{H(w)}\) on \({\overline{{\mathbb {B}}}}(i,\delta _2)\), one sees h has a non-vanishing derivative at i. Note \(h(w)^2=F_3(i)-F_3(w)\). Let \(c_1>0\) be chosen so that \(|h(w)|\ge 2c_1\) on \(|w-i|=\delta _2\). By Lagrange’s Inverse Function theorem (see [16]) we have
Now consider \(-\frac{1}{2}\sqrt{1+2c}<\xi \le \xi _c\) such that \(c_1^2\ge \frac{1}{\xi }-\frac{1}{\xi _c}\ge 0\) and label \(w_{\pm }(\xi )=h^{-1}(\pm \sqrt{\frac{1}{\xi }-\frac{1}{\xi _c}})\). Take a sequence \(\theta _c^{(n)}\rightarrow \pi /2^-\) such that \(e^{i\theta _c^{(n)}}\in {\overline{B}}(i,\delta _2)\cap {\mathbb {H}}^+\) for all n, by continuity \(\sqrt{H(e^{i\theta _c^{(n)}})}\rightarrow \sqrt{H(i)}\) which is a positive real number, so \(\arg (\sqrt{H(e^{i\theta _c^{(n)}})})\rightarrow 0\). Since \([-\pi /4,0)\ni \arg (e^{i\theta _c^{(n)}}-i)\rightarrow 0\) one can take n so large that \({\mathcal {R}}[h(e^{i\theta _c^{(n)}})]>0\). This discounts the possibility \(w_-=\omega _c\) and so we have \(w_+=\omega _c\). Hence we have obtained
For \(|t|<1\), \(\frac{1}{1-t}=1+t+\frac{t^2}{1-t}\),
Since h on \( {\overline{{\mathbb {B}}}}(i,\delta _2)\) only has a simple zero at \(\zeta =i\) the first term on the right hand side of (283) is i by Cauchy’s residue theorem. In the second term of (283) we have
By the mean value theorem for every \(-\frac{1}{2}\sqrt{1+2c}\le \xi \le \xi _c\) there exists \(\eta _\xi \in (0,(\xi -\xi _c)/\xi _c)\) such that \(\sqrt{\frac{1}{\xi }-\frac{1}{\xi _c}}=\frac{\sqrt{\xi _c-\xi }}{|\xi _c|}(1+\frac{(\xi _c-\xi )/\xi _c}{2(1+\eta _\xi )^{3/2}})\). (42) follows by letting
Since \(e^{-i\varphi _c}=-i(\omega _c-i)+1\), we can take the principle branch \(\log \) so
(43) follows from substituting (42) in to (285). \(\square \)
Now we have the proofs of the lemmas which extract the leading order terms in proposition 4.
Proof of lemma 15
Recall (155) and write the integral in (213) as
We use integration by parts to get (286) equal to
where
Note: Want to show that if \(G(e^{i\theta })\) is real and negative then \(\theta =0\).
Except for the discontinuities at \(\theta =2\pi n, n\in {\mathbb {Z}}\) caused by \(\arg \), one can check that \(\text {arg}(G(e^{i\theta }))\) has negative derivative bounded above by some negative number for all \(\theta \) and so f is smooth on \({\mathbb {R}}\setminus \{2\pi n\}\). Indeed, from (158) we can compute
where the integrand is bounded below by some positive number. Integrating by parts again we have (286) equal to
From (165)
Together with Taylors theorem applied to f, for each \(\varphi _c>0\) we get a \(\chi \in (0,\varphi _c)\) such that
where we used \(f(0)=i(1-\alpha )/\psi '(\pi /2)\) and the values of (157) and (159) computed earlier. By taking a derivative there is a \(C>0\) such that
since f is smooth. Similarly,
So by (293) the second term in (290) is bounded above by
Then if we use (294) in the third term (290) and integrate by parts, the third term in (290) is bounded above by
where in the last line we used the fact that there is a \(C'>0\) such that
for \(z>0\). Inserting (292) into (290) the two bounds (295) and (296) can be used to give (213).
Now we prove (214). We have
for a smooth h on \({\mathbb {R}}\) and bounded \(R_{39}\). Recall (53), we have that
where the last inequality follows since
Now recall the bound \(D_-(z)<1/(z+1)\) from (89). \(\square \)
Proof of lemma 16
We have (298) so
Now use the pair of inequalities
for \(z>0\). \(\square \)
Data Availability Statement
Not applicable.
References
Astala, K., Duse, E., Prause, I., Zhong, X.: Dimer models and conformal structures. arXiv preprint arXiv:2004.02599 (2020)
Beffara, V., Chhita, S., Johansson, K.: Airy point process at the liquid–gas boundary. Ann. Probab. 46(5), 2973–3013 (2018)
Beffara, V., Chhita, S., Johansson, K.: Local Geometry of the rough–smooth interface in the two-periodic Aztec diamond. arXiv:2004.14068
Berggren, T.: Domino tilings of the Aztec diamond with doubly periodic weightings. Ann. Probab. 49(4), 1965–2011 (2021)
Berggren, T., Duits, M.: Correlation functions for determinantal processes defined by infinite block Toeplitz minors. arXiv:1901.10877
Bauerschmidt, R., Park, J., Rodriguez, P-F.: The Discrete Gaussian model, I Renormalization group flow at the high temperature. arXiv:2202.02286
Chaikin, P.M., Lubensky, T.C.: Principles of Condensed Matter Physics. Cambridge University Press, Cambridge (1995)
Chhita, S., Johansson, K.: Domino statistics of the two-periodic Aztec diamond. Adv. Math. 294, 37–149 (2016)
Chhita, S., Young, B.: Coupling functions for domino tilings of Aztec diamonds. Adv. Math. 259, 173–251 (2014)
Cohn, H., Kenyon, R., Propp, J.: A variational principle for domino tilings. J. Am. Math. Soc. 14, 297–436 (2001)
Crstici, B., Tudor, G.: Compéments au Traité de D. S. Mitronovič (VII): Sur une inégalité de D. S. Mitrinovič. Publikacije Elektrotehničkog Fakulteta. Serija Matematika I Fizika, (498/541), 153–154 (1975)
DLMF. NIST Digital Library of Mathematical Functions. http://dlmf.nist.gov/
Duits, M., Kuijlaars, A.B.J.: The two-periodic Aztec diamond and matrix valued orthogonal polynomials. J. Eur. Math. Soc. (JEMS) 23(4), 1075–1131 (2021)
Elkies, N., Kuperberg, G., Larsen, M., et al.: Alternating-sign matrices and domino tilings (Part I). J. Algebr. Comb. 1, 111–132 (1992)
Fröhlich, J., Spencer, T.: The Kosterlitz–Thouless transition in two-dimensional Abelian spin systems and the Coulomb gas. Commun. Math. Phys. 81, 527–602 (1981)
Gamelin, T.: Complex Analysis. Springer-Verlag, New York (2000)
Garnett, J., Marshall, D.: Harmonic Measure. Cambridge University Press, New York (2005)
Gorin, V.: Lectures on Random Lozenge Tilings. Cambridge University Press, Cambridge (2021)
Johansson, K.: Edge fluctuations of limit shapes. arXiv e-prints arXiv:1704.06035 (2017)
Kenyon, R.: Local statistics of lattice dimers. Ann. Inst. H. Poincaré Probab. Stat. 33(5), 591–618 (1997)
Kenyon, R., Okounkov, A., Sheffield, S.: Dimers and amoebae. Ann. Math. (2) 163(3), 1019–1056 (2006)
Marshall, D.: Complex Analysis. Cambridge University Press, Cambridge (2019)
Mason, S.: Two-periodic weighted dominos and the sine-Gordon field at the free fermion point: I. arXiv preprint arXiv:2209.11111 (2022)
Myland, J., Oldham, K., Spanier, J.: An Atlas of Functions: With Equator, the Atlas Function Calculator, 2nd edn. Springer, New York (2009)
Toninelli, F.: Lectures on the Dimer model. http://math.univ-lyon1.fr/homes-www/toninelli/noteDimeri.pdf (unpublished)
Acknowledgements
We thank Craig Tracy for raising the question of how to understand the change from exponential to power law decay for dimer correlations in the two-periodic Aztec diamond at a meeting in Oberwolfach several years ago. We also thank Sunil Chhita for providing code to draw the figures 2 and 3 and for helpful comments on the introduction.
Funding
Open access funding provided by Royal Institute of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H. Spohn.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supported by the grant KAW 2015.0270 from the Knut and Alice Wallenberg Foundation.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Johansson, K., Mason, S. Dimer–Dimer Correlations at the Rough–Smooth Boundary. Commun. Math. Phys. 400, 1255–1315 (2023). https://doi.org/10.1007/s00220-023-04649-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-023-04649-1