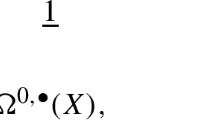Maximally Twisted Eleven-Dimensional Supergravity

Abstract

We perform the maximal twist of eleven-dimensional supergravity. This twist is partially topological and exists on manifolds of $G_2 \times SU(2)$ holonomy. Our derivation starts with an explicit description of the Batalin–Vilkovisky complex associated to the three-form multiplet in the pure spinor superfield formalism. We then determine the $L_\infty$ module structure of the supersymmetry algebra on the component fields. We twist the theory by modifying the differential of the Batalin–Vilkovisky complex to incorporate the action of a scalar supercharge. We find that the resulting free twisted theory is given by the tensor product of the de Rham and Dolbeault complexes of the respective $G_2$ and SU(2) holonomy manifolds as conjectured by Costello.

In conclusion, two things remain to be done with our theory. First, we are studying the reduction to four dimensions... (Cremmer, Julia and Scherk [1]).

1 Introduction

Eleven-dimensional supergravity [1] is the low energy limit of M-theory, a conjectural theory that is believed to unify type I, II, and heterotic superstring theories [2]. It realizes the maximal dimension that has a supersymmetric representation with particles of spin at most two [3], and the action of eleven-dimensional supergravity is unique [1]. M-theory compactifications on manifolds with $G_2$ holonomy result in four-dimensional field theories with minimal supersymmetry and have been intensely studied in relation to non-perturbative string dualities and phenomenology.

Over the past years, twists of supersymmetric field theories have mediated a lot of interactions between mathematics and physics. To this end, twisting can be used as a tool to construct new field theories which are topological or holomorphic in some spacetime directions from a given supersymmetric field theory. The observables of these twisted theories are often interesting mathematical invariants of the underlying spacetime manifold; the prime example here being the appearance of Donaldson polynomials as observables in Donaldson–Witten theory.

More recently, twisted supergravity theories have been studied in the light of the AdS/CFT correspondence [4,5,6,7,8]. As twisted theories are mathematically way more tractable than their untwisted versions, twisting on both sides of the correspondence is a promising way to provide rigorous manifestations of holography. Concretely, isomorphisms between certain algebras attached to the theories on each side of the correspondence have been established. Thus, for a thorough understanding of twisted holography, understanding twists of supergravity theories is crucial.

In this note, we consider a partial topological twist of eleven-dimensional supergravity on manifolds of $G_2 \times SU(2)$ holonomy. Partial topological twists are a natural arena where off-shell representations of supersymmetry, supersymmetric localization, special holonomy manifolds, and elliptic moduli problems converge. A partial topological twist can only be performed on a manifold of special holonomy. The equations of motion after twisting often simplify to elliptic complexes that are specific to the special holonomy manifold on which the twist is defined.

A conjectured partial topological twist of eleven-dimensional supergravity on manifolds, $M^7 \times M^4,$ of $G_2 \times SU(2)$ holonomy is given in [5, 9, 10]. As a free BV theory, the twisted theory is described by the cochain complex

$$\begin{aligned} \left( \Omega ^{\bullet }(M^7) \otimes \Omega ^{0,\bullet }(M^4) \, , \, D^{\textrm{tw}} \right) , \end{aligned}$$

(1.1)

where the differential $D^{\textrm{tw}}$ decomposes into

$$\begin{aligned} D^{\textrm{tw}} = d_{M^7} \otimes 1 + 1 \otimes \bar{\partial }_{M^4} \, . \end{aligned}$$

(1.2)

Here $d_{M^7}$ is the de Rham differential on $M^7$ and $\bar{\partial }_{M^4}$ is the Dolbeault differential on $M^4$. In principle, higher interaction terms will also be present, but here we restrict our attention to the free theory.

Already, twisted M-theory has had several applications to mathematical physics [5, 10]. While these works are rigorous mathematics in the sense of Jaffe–Quinn [11], our aim is to connect them to eleven-dimensional supergravity as originally envisioned by Cremmer–Julia–Scherk [1] and its more recent formulations in the pure spinor formalism [12, 13].

In this note we will show how to obtain the fields and BV differential by directly twisting the component fields of eleven-dimensional supergravity in the BV formalism [14]. After the twist, the three-form $C^{(3)}$ with its ghost system $C^{(2)},C^{(1)},C^{(0)},$ the spin-3/2 Rarita–Schwinger field $\psi ,$ and all of their corresponding antifields organize into a differential form $\mathcal {A}\in \Omega ^{\bullet }(M^7) \otimes \Omega ^{0,\bullet }(M^4)$, as conjectured by Costello. Its components are displayed in Table 1.

Table 1 Fields in maximally twisted supergravity

We will derive the conjectured form of the twisted fields and differential starting from the manifestly covariant formulation of eleven-dimensional supergravity [12, 13, 15, 16] in the pure spinor superfield formalism [17,18,19]. We use this formalism to obtain the BV complex of the three-form multiplet in eleven dimensional supergravity, including the full action of the supersymmetry algebra on the component fields. These results are then used to carry out the actual twist on the level of component fields. This gives an explicit understanding of the fields in the twisted theory as well as the formation of trivial pairs in terms of the fields of the untwisted supergravity multiplet.

The traditional approach to eleven-dimensional supergravity in superspace [20,21,22,23,24] starts with the supervielbein and imposes conventional constraints [25, 26] on torsions and curvatures. We will make some speculative remarks about the twist of the supervielbein at the end. A partially off-shell formulation of eleven-dimensional supergravity adapted to manifolds of $G_2 \times SU(2)$ holonomy is given in [27,28,29] and is closely related to the twisted theory.

We will work in Euclidean signature. We hope to return to the twist of the higher order terms and the formulation in Lorentzian signature in subsequent work.

From the outset you know, more or less, what became of the three-form multiplet, so most of your curiosity is invested in the question of how it all came to pass. (Adapted from A.O. Scott.)

Organization:

The rest of this work is structured as follows. In Sect. 2 we review supersymmetric theories in the BV formalism and explain how to twist them with respect to a supercharge. We describe the types of twists in eleven-dimensional supergravity and the $G_2 \times SU(2)$ invariant twist in detail. In Sect. 3 we specialize our general discussion of BV theories to eleven-dimensional supergravity. We introduce the BV complex for the three-form multiplet and describe the action of supersymmetry on its component fields. Finally, in Sect. 4 we describe the decomposition of the fields and supersymmetry transformations with respect to $G_2 \times SU(2).$ We then use the decomposition to determine the fields surviving the partial topological twist and the resulting action of the modified BV differential. We conclude with some thoughts on further directions in Sect. 5.

Note added:

The authors thank Ingmar Saberi and Brian Williams for informing them of their related paper [30] and coordinating submission to the arXiv. Their work derives the holomorphic twist of the eleven-dimensional three-form multiplet. Starting from the holomorphic twist of Saberi–Williams, Ingmar Saberi, Surya Raghavendran and Brian Williams independently derive the $G_2 \times SU(2)$ invariant twist in their forthcoming work [31]. Our work is complementary to that of Saberi–Williams and Raghavendran–Saberi–Williams in the sense that we determine the origin of the twisted fields in the untwisted theory, whereas their work cleverly bypasses the component fields of the untwisted theory. Further discussion of the relations between these different perspectives will appear in [32].

2 Twisting à la Costello

2.1 Supersymmetric field theories in the BV formalism

In the BV formalism, a field theory is described by a sheaf of cyclic (super) $L_{\infty }$ algebras over a spacetime M. This sheaf models the space of solutions to the equations of motion up to gauge equivalence [14, 33, 34]. Here we are only concerned with free field theories, which means that all involved $L_\infty$ algebras have no higher operations ($\mu _i=0$ for $i\ge 2$) and hence simply are cochain complexes. Given such an $L_\infty$ algebra L, the space $\mathcal {E}$ of BV fields is obtained by a homological shift $\mathcal {E} = L[1]$. The space of BV fields usually arises as the sections of a $\mathbb {Z}\times \mathbb {Z}/2\mathbb {Z}$ graded vector bundle $E \rightarrow M$ over the spacetime M,

$$\begin{aligned} (\mathcal {E}, D) = (\Gamma (M,E), D) \, , \end{aligned}$$

(2.1)

where the differential D arises as a differential operator of degree $(1,+)$. The $\mathbb {Z}$-grading is usually called ghost number, while the $\mathbb {Z}/2\mathbb {Z}$ grading corresponds to the usual parity distinguishing bosons and fermions. By assumption, E is equipped with a fiberwise non-degenerate, graded antisymmetric map of bidegree $(1,+)$

$$\begin{aligned} \omega : E \otimes E \longrightarrow \textrm{Dens}_M, \end{aligned}$$

(2.2)

which induces a pairing on compactly supported sections $\mathcal {E}_c \subseteq \mathcal {E}$ via integration. Due to its degree, this pairing connects fields and antifields.

A free classical BV theory, specified by the data $(E,D,\omega )$, can also be described in a second way that is, in a sense, dual to the above description. The pairing $\omega$ endows the functionals $\mathcal {O}(\mathcal {E})$ of the fields with an odd Poisson bracket $\{-,-\}$ of degree 1. The differential D induces a BV operator $Q_{BV} : \mathcal {O}(\mathcal {E}) \rightarrow \mathcal {O}(\mathcal {E})$ that can be written in the form

$$\begin{aligned} Q_{BV} = \{S_{BV} , -\} \end{aligned}$$

(2.3)

for the BV action $S_{BV}$, which satisfies the classical master equation $\{S_{BV}, S_{BV}\} = 0$. As we are dealing with free theories, the BV action can be written as

$$\begin{aligned} S_{BV}[\Phi ] = \int _M \omega (\Phi , D\Phi ) \, . \end{aligned}$$

(2.4)

Thus, for free theories and in the presence of a non-degenerate pairing $\omega$, the BV operator $Q_{BV}$, the differential D and the BV action $S_{BV}$ all contain the same information.

An important subset of all functionals of the fields are the local operators: For any point $x \in M$, we have local operators supported at x

$$\begin{aligned} \mathcal {O}_x(\mathcal {E}) = {{\,\textrm{Sym}\,}}^\bullet (J^\infty E|_x)^\vee \, , \end{aligned}$$

(2.5)

where $J^\infty$ denotes the infinite jet space. For example, given a field $\phi \in \mathcal {E}$, the corresponding local operator in $\mathcal {O}_x(\mathcal {E})$ evaluates $\phi$ at the point x.

Corresponding to these two point of views, there are also two ‘dual’ ways of encoding the action of supersymmetry in the BV formalism. Let us start from the perspective of fields. The endomorphisms $\textrm{End}(\mathcal {E})$, equipped with the commutator and the differential $[D,-]$, form a differential graded super Lie algebra. Inside $(\textrm{End}(\mathcal {E}), [D,-])$, there is a sub dg super Lie algebra denoted by $(\mathcal {D}(\mathcal {E}), [D,-])$, consisting of all endomorphisms of $\mathcal {E}$ acting by differential operators.

Now let $\mathfrak {p} = \mathfrak {p}_+ \oplus \mathfrak {p}_-$ denote a super Poincaré algebra. In a supersymmetric field theory, the action of supersymmetry is described on the fields by a map of super $L_\infty$ algebras

$$\begin{aligned} \rho : \mathfrak {p} \rightsquigarrow (\mathcal {D}(\mathcal {E}), [D,-]) \, . \end{aligned}$$

(2.6)

As such $\rho$ consists of component maps

$$\begin{aligned} \rho ^{(i)} : \mathfrak {p}^{\otimes i} \longrightarrow \mathcal {D}(\mathcal {E}) \, , \quad j \ge 1 \end{aligned}$$

(2.7)

of degree $1-i$ satisfying the usual consistency relations for morphisms of super $L_\infty$ algebras.

The action of supersymmetry can also be encoded on the operators of the theory. This is done by combining, for $Q \in \mathfrak {p}$, $\rho ^{(i)}(Q,\dots ,Q)^\vee$ the dual maps into a differential

$$\begin{aligned} \delta _Q = \sum _i \rho ^{(i)} (Q,\dots ,Q)^\vee : \mathcal {O}_x(\mathcal {E}) \longrightarrow \mathcal {O}_x(\mathcal {E}) \, . \end{aligned}$$

(2.8)

Note that this is the same procedure as encoding a gauge symmetry in the BRST differential. We will see in Sect. 3.4 how to describe the action of the supersymmetry algebra in the pure spinor formalism.

2.2 Twisting in the BV formalism

Let us fix a square zero element $Q \in \mathfrak {p}_-$ of the odd part of the supersymmetry algebra. Given a supersymmetric field theory in the BV formalism, the twist of the theory by Q is defined by deforming the BV operator

$$\begin{aligned} Q_{BV} \rightarrow Q_{BV} + t \delta _Q, \, \end{aligned}$$

(2.9)

where $t \in {\mathbb {C}}^{\times }$ and taking ${\mathbb {C}}^{\times }$-invariants [35, 36]. After taking invariants, we specialize to $t = 1.$ Equivalently, we can deform the BV action to

$$\begin{aligned} S^Q_{BV}[\Phi ] = S_{BV}[\Phi ] + \sum _{i} \int _M \omega (\Phi , \rho ^{(i)}(Q, \dots , Q) (\Phi ) ) \end{aligned}$$

(2.10)

following [37]. This defines the twisted theory as a classical BV theory $(E, S^{Q}_{BV}, \omega )$ with the same space of fields and odd-symplectic pairing, but with a new action. Deforming the differential typically breaks the grading on E. Importantly, the presence of new terms in the differential often results in the formation of trivial pairs that decouple and thus play no role in the dynamics of the twisted theory and hence can be neglected. More precisely, one can pass over to a theory with a smaller space of fields, where all trivial pairs are omitted. This gives an equivalent formulation of the twisted theory, which is often drastically simplified. One usually also refers to this formulation as the twisted theory.

2.3 Twisting and the Nilpotence Variety

Eleven-dimensional supergravity can be twisted in two distinct ways that correspond to the two types of nilpotent supercharges. In this note, we are exclusively concerned with the maximal twist, which is possible on a manifold with $G_2 \times SU(2)$ holonomy [5, 38, 39]. In addition, there is also a minimal (holomorphic) twist.

The possible twists of a supersymmetric field theory are described by the variety of square zero elements Y inside the supersymmetry algebra of the theory. The nilpotence variety

$$\begin{aligned} Y = \{ Q \in \mathfrak {p}_- | \{Q,Q\}=0 \} \end{aligned}$$

(2.11)

has a natural stratification such that each stratum can be identified with a twisted theory [40]. Different strata can be distinguished by the commutant

$$\begin{aligned} Z(Q) = \{ x \in A | [x,Q] = 0 \}, \end{aligned}$$

(2.12)

which is constant along the strata.

Recall that, in any dimension, the Dirac spinor representation S is obtained from a maximal isotropic subspace $L \subset V$ by setting

$$\begin{aligned} S = \wedge ^\bullet L^\vee \, . \end{aligned}$$

(2.13)

S forms a Clifford module for Cl(V) and thus in particular a representation of $\mathfrak {so}(V)$. In the case where $d= \textrm{dim}(V)$ is odd, this representation is irreducible. As we are interested in eleven-dimensional supergravity, we restrict to this case for the moment.

For $Q \in S$, the annihilator with respect to Clifford multiplication

$$\begin{aligned} \textrm{Ann}(Q) = \{ v \in V | v \cdot Q = 0 \} \end{aligned}$$

(2.14)

gives an isotropic subspace $\textrm{Ann}(Q) \subset V$. Q is called a Cartan pure spinor if $\textrm{Ann}(Q)$ is maximal isotropic. Every Cartan pure spinor is square zero. The converse, however, is in general not true as we will see below. More generally, one can define the varieties

$$\begin{aligned} \textrm{PS}_k = \{ Q \in S | \textrm{dim}(L) - \textrm{dim}(\textrm{Ann}(Q)) \le k \} \, , \end{aligned}$$

(2.15)

which define a filtration

$$\begin{aligned} \textrm{PS}_0 \subseteq \textrm{PS}_1 \subseteq \dots \textrm{PS}_n = S \, . \end{aligned}$$

(2.16)

2.4 Two families of twists

In eleven dimensions, the variety of square zero supercharges is described in coordinates by the eleven equations

$$\begin{aligned} \lambda ^\alpha \Gamma ^\mu _{\alpha \beta } \lambda ^\beta = 0 \, . \end{aligned}$$

(2.17)

This variety is closely related to the variety of Cartan pure spinors. In fact, one finds $Y = \textrm{PS}_3$ [40]. The variety of Cartan pure spinors sits inside Y as a subvariety $\textrm{PS}_0 \subset \textrm{PS}_3 = Y$. Furthermore, $\textrm{PS}_0$ is the singular locus of Y and can be described by imposing the additional equations

$$\begin{aligned} \lambda \Gamma ^{\mu \nu } \lambda = 0 \, . \end{aligned}$$

(2.18)

For Q on the singular locus, the degree zero part of the commutant is $Z^0(Q) = \mathfrak {u}(5)$. This corresponds to the holomorphic twist of eleven-dimensional supergravity. Away from the singular locus, the commutant is an algebra with Levi factor $\mathfrak {g}_2 \times \mathfrak {gl}(2)$. This corresponds to the maximal twist of eleven-dimensional supergravity that we will study.

Let us elaborate a little further on the maximal twist. The spinor representation in eleven dimensions decomposes as

$$\begin{aligned} S_{11} = S_{7} \otimes S_{4} \, . \end{aligned}$$

(2.19)

The Dirac Spin representation in four dimensions, $S_{4},$ decomposes into Weyl spinor representations $S_+$ and $S_-$:

$$\begin{aligned} S_{4} = \wedge ^\bullet L_{4}^\vee = \wedge ^{\textrm{even}} L_{4}^\vee \oplus \wedge ^{\textrm{odd}} L_{4}^\vee =: S_+ \oplus S_- \, . \end{aligned}$$

(2.20)

Identifying the group $Spin(4) \cong SU(2)_{+} \times SU(2)_{-},$ $S_{+}$ and $S_{-}$ are the fundamental representations of $SU(2)_{+}$ and $SU(2)_{-},$ respectively. On a manifold $M^7$ with $G_2$ holonomy, the spinor representation $S_{7}$ further decomposes as

$$\begin{aligned} S_{7} = 1_{G_2} \oplus V_{G_2} \, , \end{aligned}$$

(2.21)

where $V_{G_2}$ is the seven-dimensional representation of $G_2.$ Thus we have the decomposition

$$\begin{aligned} S_{11} = (1_{G_2} \oplus V_{G_2}) \otimes (\wedge ^0 L_{4}^\vee \oplus \wedge ^2 L_{4}^\vee \oplus S_-) \, . \end{aligned}$$

(2.22)

As a representation of $G_2 \times SU(2)_- \times U(1)_L$, where $U(1)_L$ is the Cartan subgroup of $SU(2)_+$ this gives

$$\begin{aligned} S_{11} = \left( (00) \oplus (10) \right) \otimes \left( 1_{-1} \oplus 1_{+1} \oplus 2_{0} \right) \, . \end{aligned}$$

(2.23)

Here we introduced Dynkin labels for the $G_2$-representation. $SU(2)\times U(1)$-representations are labeled by the dimension of the SU(2)-representation, with the U(1) charge as a subscript. To study the maximal twist, we choose a square zero supercharge

$$\begin{aligned} Q \in 1_{G_2} \otimes \wedge ^0 L_{4}^\vee = (00) 1_{-1} \, . \end{aligned}$$

(2.24)

Thus, we immediately see that Q is invariant under the action of $G_2 \times SU(2)_{-}$ and has $U(1)_L$ charge $-1,$.

The normal space to the nilpotence variety is spanned by the supercharges

$$\begin{aligned} {Q}_m\in & {} (V_{G_2} \otimes \wedge ^2 L_{4}^\vee ), \end{aligned}$$

(2.25)

$$\begin{aligned} Q_{\dot{\alpha }}\in & {} (1_{G_2} \otimes S_{-}). \end{aligned}$$

(2.26)

They satisfy the anticommutator relations

$$\begin{aligned} \{Q , Q_m \}= & {} P_m \end{aligned}$$

(2.27)

$$\begin{aligned} \{Q , Q_{\dot{\alpha }} \}= & {} P_{- \dot{\alpha }} \, . \end{aligned}$$

(2.28)

Here we already used that the vector representation decomposes under $G_2 \times SU(2) \times U(1)$ as

$$\begin{aligned} V_{11} = (10) \oplus 2_{-1} \oplus 2_1 \, . \end{aligned}$$

(2.29)

Our conventions are that indices $m,n, \dots$ are indices for the seven-dimensional vector representation, while $\dot{\alpha },\dot{\beta },\dots$ correspond to $SU(2)_-$.

The above anticommutator relations state that translations on $M^7$ and anti-holomorphic translations on $M^4$ are exact. Therefore, one can see already at this point that the twisted theory will depend only on the topological structures of $M^7$, but will be sensitive to holomorphic ones of $M^4$. Hence this twist is “partially topological” or “holomorphic-topological”.

3 Eleven-Dimensional Supergravity in the Pure Spinor Superfield Formalism

In this section, we give a short review of eleven-dimensional supergravity in the pure spinor superfield formalism. The pure spinor superfield formalism has been developed in the physics literature, in particular by Berkovits [41] and Cederwall [19]. In the context of eleven-dimensional supergravity, we in particular refer to [12, 13] and the references therein. The pure spinor superfield formalism was reinterpreted from a more modern mathematical perspective in [39]. For a detailed treatment in modern language, we refer to our forthcoming work [32]. Here we only use the pure spinor formalism as a tool to describe the action of supersymmetry on the BV complex of eleven-dimensional supergravity and therefore only give a brief treatment, exclusively tailored to the example of eleven-dimensional supergravity.

3.1 General remarks

The general idea of the pure spinor superfield formalism is to replace the usual BV complex $(\mathcal {E},D)$ by a much larger object, which we will denote by $(A,\mathcal {D})$, encoding the same information. In the case of eleven-dimensional supergravity, the construction can be carried out in the following way. Let $R= \mathcal {O}(S_{11}) = \mathbb {C}[\lambda ^1,\dots ,\lambda ^{32}]$ be the ring of polynomial functions on the eleven-dimensional spin representation $S_{11}$ and

$$\begin{aligned} I=(\lambda \Gamma ^\mu \lambda ) \end{aligned}$$

(3.1)

the ideal generated by the defining equation of the nilpotence variety. The quotient R/I can then be identified with the ring of functions on the nilpotence variety Y. Furthermore, let T denote the supertranslation subgroup of the super Poincaré group. There are two commuting actions of T on the smooth functions $C^\infty (T)$ on T, namely acting by left and right translations. Infinitesimally, these actions are described by Lie algebra maps

$$\begin{aligned} L,R : \mathfrak {t} \longrightarrow \textrm{Vect}(T) \, . \end{aligned}$$

(3.2)

We denote the images of a basis of $\mathfrak {t}_-$ under L and R by $\mathcal {Q}_\alpha$ and $\mathcal {D}_\alpha$. Introducing coordinates $\theta ^\alpha$ on $\mathfrak {t}_-$ and $x^\mu$ on $\mathfrak {t}_+= V_{11}$, these vector fields are the usual left and right translations on superspace.

$$\begin{aligned} \begin{aligned} \mathcal {Q}_\alpha&= \frac{\partial }{\partial \theta ^\alpha } - \Gamma ^\mu _{\alpha \beta } \theta ^\beta \frac{\partial }{\partial x^\mu }\\ \mathcal {D}_\alpha&= \frac{\partial }{\partial \theta ^\alpha } + \Gamma ^\mu _{\alpha \beta } \theta ^\beta \frac{\partial }{\partial x^\mu } \, . \end{aligned} \end{aligned}$$

(3.3)

Now we can define

$$\begin{aligned} \left( A ,\mathcal {D}\right) = \left( C^\infty (T) \otimes R/I \, , \, \mathcal {D} = \lambda ^\alpha \mathcal {D}_\alpha \right) \, . \end{aligned}$$

(3.4)

Note that the defining equation of the ideal I ensures that the differential $\mathcal {D}$ is indeed square zero. In coordinates, an element of this complex can be thought of as a function $\Psi (x,\theta ,\lambda )$ and is called a pure spinor superfield. With these coordinates, A takes the form

$$\begin{aligned} \left( A ,\mathcal {D}\right) = \left( C^\infty (V_{11}) \otimes {\mathbb {C}}[\theta ^1,\dots ,\theta ^{32}] \otimes R/I \, , \, \mathcal {D}\right) \, . \end{aligned}$$

(3.5)

The differential $\mathcal {D}$ has an obvious decomposition

$$\begin{aligned} \mathcal {D}= \mathcal {D}_0 + \mathcal {D}_1 \end{aligned}$$

(3.6)

where $\mathcal {D}_0 = \lambda ^\alpha \frac{\partial }{\partial \theta ^\alpha }$. This makes $(A,\mathcal {D})$ into a bicomplex. Note that

$$\begin{aligned} \left( A, \mathcal {D}_0 \right) = \left( K^\bullet (R/I) \otimes C^\infty (V_{11}) \, , \, d_K \otimes \textrm{id}_{C^\infty (V_{11})} \right) \end{aligned}$$

(3.7)

is simply the Koszul complex of R/I tensored with smooth functions on $V_{11}$.

The usual component field description is obtained by taking the cohomology with respect to $\mathcal {D}_0$ and transferring all relevant structures like the differential $\mathcal {D}_1$ (which gives to the differential D on the component field in the sense of Sect. 2.1), the action of the supersymmetry algebra (which gives rise to the $L_\infty$ module structure on the component fields), and possibly higher terms of an $L_\infty$ structure (which would rise to an $L_\infty$ structure encoding interactions on the component field level). For a systematic account of this perspective, we refer the reader to our future work [32]. In the next subsection, we will explain how the $\mathcal {D}_0$-cohomology can be computed and how the action of supersymmetry can be transferred for the case of eleven-dimensional supergravity.

3.2 $\mathcal {D}_0$-cohomology and representatives

The $\mathcal {D}_0$-cohomology can be identified with the tensor product

$$\begin{aligned} (L^\bullet \otimes _R {\mathbb {C}}) \otimes C^\infty (V_{11}) \, , \end{aligned}$$

(3.8)

where $L^\bullet$ is the minimal free resolution of R/I in R-modules. In our case the minimal free resolution of R/I takes the form

The resolution differential was already described in [12]. Let us choose a basis $(e_\mu )$ of $V_{11}$ and $(s_\alpha )$ of $S_{11}$. We will need the maps $d_1, \dots d_5$. In this basis they take the following form.

(3.9)

We do not specify the tensor $M_{\mu \nu }^{\alpha \beta }$ here, but just remark that it is a rather complicated expression in terms of $\Gamma$-matrices. The $\mathcal {D}_0$-cohomology is bigraded by $\lambda$ and $\theta$. The component fields organize according to degree in $\lambda$ and $\theta$ according to Table 2. We will call the $\lambda$ degree the BV degree. This convention is non-standard because it places the physical fields in BV degree three. However, we will see that it simplifies other aspects of our presentation.

Table 2 $\theta$ and $\lambda$ degrees for the supergravity three-form BV multiplet

To find explicit representatives for the cohomology classes corresponding to the component fields we define the adjoint differential

$$\begin{aligned} \mathcal {D}_0^\dagger = \theta ^\alpha \frac{\partial }{\partial \lambda _\alpha } \, . \end{aligned}$$

(3.10)

Representatives can then be found by applying the resolution differential and $\mathcal {D}_0^\dagger$ iteratively. This was already noted in [42] and will be elaborated on in [32]. For example we find for the one-form

(3.11)

such that the one-form field is represented by $(\lambda \Gamma ^\mu \theta ) C^{(1)}_\mu$.

Similarly one finds for the two-form

(3.12)

such that the two-form is represented by $(\lambda \Gamma ^\nu \theta )(\lambda \Gamma ^\mu \theta ) C^{(2)}_{\mu \nu }$. Likewise, the three-form is represented by $(\lambda \Gamma ^\nu \theta )(\lambda \Gamma ^\mu \theta ) (\lambda \Gamma ^\rho \theta ) C^{(3)}_{\mu \nu \rho }$.

Let us continue with the vector ghost v

(3.13)

Thus the representative is $(\lambda \Gamma _\mu \theta )(\lambda \Gamma ^{\mu \nu } \theta ) v_\nu$. For the graviton we find with a similar calculation $(\lambda \Gamma _\mu \theta )(\lambda \Gamma ^{\mu (\nu } \theta )(\lambda \Gamma ^{\rho )}\theta ) g_{\rho \nu }$.

Performing this procedure one can find representatives for the gravitino and its ghost. The results are summarized in Table 3.

Table 3 Representatives for the fields in 11D supergravity organized by $\theta$-degree

3.3 The BV differential

The differential D acting on the component fields is obtained by transferring $\mathcal {D}_1$ to the $\mathcal {D}_0$-cohomology. In general, this is done by a homotopy transfer of $D_\infty$-algebras but here we are only interested in the lowest order term that acts on the representatives simply by the usual formula of $\mathcal {D}_1$,

$$\begin{aligned} \mathcal {D}_1 = (\lambda \Gamma ^\mu \theta ) \partial _\mu \, . \end{aligned}$$

(3.14)

This gives part of the differential, that is first order in derivatives. For example, we can act on the $C^{(0)}$ ghost

$$\begin{aligned} \mathcal {D}_1 (C^{(0)}) = (\lambda \Gamma ^\mu \theta ) \partial _\mu C^{(0)} \, . \end{aligned}$$

(3.15)

Thus we see that the differential corresponds to the de Rham differential. This obviously generalizes to $C^{(1)}$ and $C^{(2)}$ such that we see that the ghost system of the three-form indeed corresponds to the usual ghost system of a higher form field. Moving on to the diffeomorphism ghost $v_\mu$ for the graviton, we find

$$\begin{aligned} \mathcal {D}_1( (\lambda \Gamma _\mu \theta ) (\theta \Gamma ^{\mu \nu } \theta )v_\nu ) = (\lambda \Gamma _\mu \theta ) (\theta \Gamma ^{\mu \nu } \theta ) (\lambda \Gamma ^\rho \theta ) \partial _\rho v_\nu \, . \end{aligned}$$

(3.16)

From our calculations of the representatives, we know that only the part where $\rho$ and $\nu$ are symmetrized corresponds to a non-trivial cohomology class. Thus we find

$$\begin{aligned} \mathcal {D}_1(v) = (\lambda \Gamma _\mu \theta ) (\theta \Gamma ^{\mu (\nu } \theta ) (\lambda \Gamma ^{\rho )} \theta ) (\partial _\rho v_\nu + \partial _\nu v_\rho ) \, . \end{aligned}$$

(3.17)

Written dually in terms of operators, we find that the BV operator acts by

$$\begin{aligned} Q_{BV} g_{\mu \nu } = \partial _\mu v_\nu + \partial _\nu v_\mu = (\mathcal {L}_v \eta )_{\mu \nu } \, , \end{aligned}$$

(3.18)

which is indeed the expected gauge transformation for the graviton.

A similar story also holds for the gravitino and its ghost. There we find

$$\begin{aligned} \mathcal {D}_1(\omega ) = (\lambda \Gamma ^\rho \theta )\left[ (\lambda \Gamma _\mu \theta )(\lambda \Gamma ^{\mu \nu }\theta )(\theta \Gamma _\nu )_\alpha + (\lambda \Gamma ^\mu \theta )(\lambda \Gamma ^\nu \theta )(\theta \Gamma _{\mu \nu })_\alpha \right] \partial _\rho \omega ^\alpha \, . \end{aligned}$$

(3.19)

This gives a gauge transformation

$$\begin{aligned} Q_{BV} \psi _\mu ^\alpha = \partial _\mu \omega ^\alpha \, . \end{aligned}$$

(3.20)

Thus we see that $\mathcal {D}_1$ encodes the usual gauge transformations, expected for the field content. Furthermore, one expects $\mathcal {D}_1$ to encode the Rarita–Schwinger equation between the gravitino and its antifield. In addition, homotopy transfer is expected to induce a second order differential giving the linearized equations of motions of the graviton and the three-form field.

3.4 The action of supersymmetry

As explained in Sect. 2.1, the supersymmetry algebra usually does not act strictly on the component fields. This is indeed the case for eleven-dimensional supergravity. Instead there is a $L_\infty$ map

$$\begin{aligned} \rho : \mathfrak {p} \rightsquigarrow \mathcal {D}(\mathcal {E}) \, . \end{aligned}$$

(3.21)

The components of $\rho$ can be obtained from the action of $Q_\alpha$ by left translation using a homotopy transfer procedure. The strict part is simply obtained by letting (3.3) act on the representatives. For an element $Q= \epsilon ^\alpha Q_\alpha$ of the supersymmetry algebra, this means

$$\begin{aligned} \rho ^{(1)}(Q) = \epsilon ^\alpha \frac{\partial }{\partial \theta ^\alpha } - \epsilon ^\alpha \Gamma ^\mu _{\alpha \beta } \theta ^\beta \partial _\mu \, . \end{aligned}$$

(3.22)

For the second order part one finds

$$\begin{aligned} \rho ^{(2)}(Q_1,Q_2) = p \circ \left( \rho ^{(1)}(Q_1) \circ \mathcal {D}_0^\dagger \circ \rho (Q_2) + \rho (Q_2) \circ \mathcal {D}_0^\dagger \circ \rho ^{(1)}(Q_1) \right) \circ i \, . \end{aligned}$$

(3.23)

Here i is the inclusion map from the $\mathcal {D}_0$-cohomology to the total complex (3.4) (mapping a component field to its representative, as computed above) and p is the projection back onto the $\mathcal {D}_0$-cohomology. The presence of $\rho ^{(2)}$ signals that the supersymmetry transformations only close up to the equations of motions and gauge transformations. In fact, $\rho ^{(2)}$ nullhomotopes the failure of the supersymmetry algebra to be represented strictly and thus exactly corresponds to what is called a “closure term” in the physics literature. Higher order components will not appear for eleven-dimensional supergravity. In [12], a close connection between the resolution differential and the non-derivative supersymmetry transformations and their closure terms was conjectured. We will explain this claim in modern language and provide a proof in [32]. Here it suffices to say that, as we will see momentarily, one can obtain the non-derivative part of $\rho$ by replacing $\lambda$ with $\epsilon$ in the resolution differential at appropriate places. Now let us start deriving the action of the supersymmetry algebra on the BV fields. The strict part gives the usual supersymmetry transformations known from the literature [12].

3.4.1 The three-form ghost system

We begin with the ghost system of the three-form. From degree reasons, it is obvious that $\rho ^{(1)}$ acts trivially on the ghost system for the three-form. Thus we have

$$\begin{aligned} \rho ^{(1)}(C^{(0)}) = \rho ^{(1)}(C^{(1)}) = \rho ^{(1)}(C^{(2)}) = 0 \, . \end{aligned}$$

(3.24)

However, this will be corrected by higher order contributions. There we find

$$\begin{aligned} \begin{aligned} \rho ^{(2)}(Q,Q)(C^{(1)})&= \rho ^{(2)}(Q,Q)(C^{(1)}_\mu (\lambda \Gamma ^\mu \theta )) \\&=(\epsilon \Gamma ^\mu \epsilon ) C^{(1)}_\mu \\&= \iota _{\{Q,Q\}} C^{(1)} \, . \end{aligned} \end{aligned}$$

(3.25)

Thus we find a map

$$\begin{aligned} \rho ^{(2)}(Q,Q) = \iota _{\{Q,Q\}} : \Omega ^1(M) \longrightarrow \Omega ^0(M) \, . \end{aligned}$$

(3.26)

Here we also see the relation to the resolution differential: $d_1$ acts on the one-form by $C^{(1)} \rightarrow (\lambda \Gamma ^\mu \lambda ) C^{(1)}_\mu ,$ thus replacing $\lambda$ with $\epsilon$ we obtain $\rho ^{(2)}$.

Written dually for operators, this gives a supersymmetry transformation rule

$$\begin{aligned} \delta C^{(1)}_\mu = (\epsilon \Gamma _\mu \epsilon ) C^{(0)} \, . \end{aligned}$$

(3.27)

With similar calculations, we also see that there are higher order transformations

$$\begin{aligned} \rho ^{(2)}(Q,Q) = \iota _{\{Q,Q\}} : \Omega ^2(M) \longrightarrow \Omega ^1(M) \end{aligned}$$

(3.28)

and

$$\begin{aligned} \rho ^{(2)}(Q,Q) = \iota _{\{Q,Q\}} : \Omega ^3(M) \longrightarrow \Omega ^2(M) \, . \end{aligned}$$

(3.29)

However, these transformations will not cancel any components in the twist since there the relevant supercharge satisfies $\{Q,Q\} = 0$ and thus the above maps all vanish.

3.4.2 The diffeomorphism ghost

The only non-derivative transformation for the diffeomorphism ghost appears in $\rho ^{(2)}$. It takes the form

$$\begin{aligned} \begin{aligned} \rho ^{(2)}(Q,Q)(v)&= \rho ^{(2)}(Q,Q)((\lambda \Gamma _\mu \theta )(\theta \Gamma ^{\mu \nu } \lambda )v_\nu ) \\&= (\lambda \Gamma _\mu \theta ) (\epsilon \Gamma ^{\mu \nu } \epsilon ) v_\nu \end{aligned} \end{aligned}$$

(3.30)

and thus gives a transformation rule

$$\begin{aligned} \delta C^{(1)}_\mu = (\epsilon \Gamma _{\mu \nu } \epsilon ) v^\nu . \end{aligned}$$

(3.31)

In addition, there is a $\rho ^{(1)}$-piece involving a derivative that can be seen to give rise to the usual supersymmetry transformation between the diffeomorphism and supertranslation ghost [12]

$$\begin{aligned} \delta \omega _\alpha = - \frac{1}{2} (\epsilon \Gamma ^{\mu \nu })_\alpha \partial _\mu v_\nu \,. \end{aligned}$$

(3.32)

3.4.3 The gravitino ghost

For the gravitino ghost, we obtain

$$\begin{aligned} \rho ^{(1)}(Q)(\omega ) = (\lambda \Gamma _\mu \theta )(\lambda \Gamma ^{\mu \nu } \theta ) (\epsilon \Gamma _\nu \omega ) + \frac{1}{2} (\lambda \Gamma _\mu \theta ) (\lambda \Gamma _\nu \theta ) (\epsilon \Gamma ^{\mu \nu } \omega ) \, . \end{aligned}$$

(3.33)

Again, note the relation to the free resolution. This gives two supersymmetry transformations

$$\begin{aligned} \begin{aligned} \delta v_\mu&= \epsilon \Gamma _\mu \omega \\ \delta C^{(2)}_{\mu \nu }&= \frac{1}{2} \epsilon \Gamma _{\mu \nu } \omega \, . \end{aligned} \end{aligned}$$

(3.34)

By now the methodology should be clear. In this style, one can derive the full higher order corrections to the supersymmetry transformations and encode them in the differential $\delta$.

We summarize the full non-derivative supersymmetry transformations in Table 4. These results first appeared in [12].

Table 4 Non-derivative supersymmetry transformations

In addition, we list the transformations including derivatives for the gravitino and its ghost in Table 5.

Table 5 Supersymmetry transformations with derivatives

4 Twisting the Free Theory

In this section, we will show that the fields of the twisted theory arrange into a differential form

$$\begin{aligned} \mathcal {A}\in \Omega ^{\bullet }(M^7) \otimes \Omega ^{0,\bullet }(M^4) \, . \end{aligned}$$

(3.35)

The strategy to establish this result is clear: we restrict the supersymmetry transformations from Table 4 to our $G_2 \times SU(2)$ invariant supercharge and look for fields that form trivial pairs under $\delta$. In the twisted theory these fields decouple and can be neglected. To find such cancellations we have to decompose the field content as well as the supersymmetry transformations equivariantly under $G_2 \times SU(2) \times U(1)$.

As a result, we will see that only certain components of the three-form, the three-form ghost system, the gravitino, and the corresponding antifields play a role in the twisted theory. These fields then arrange into the differential form described above.

We will see that the twisted differential takes the form

$$\begin{aligned} D^{\textrm{tw}} = d_{M^7} \otimes 1 + 1 \otimes \bar{\partial }_{M^4}. \end{aligned}$$

(4.1)

The fields in the untwisted theory have a have a $\mathbb {Z}\times \mathbb {Z}$-grading given by the BV degree $d_{BV}$ and the $U(1)_L$ charge $d_{U(1)_L}.$ After twisting, the new BV operator $Q_{BV} + \delta _Q$ breaks the $\mathbb {Z}\times \mathbb {Z}$-grading on the space of fields E to the $\mathbb {Z}$-grading

$$\begin{aligned} d^Q_{BV} = d_{BV} - d_{U(1)_L} , \end{aligned}$$

(4.2)

in the twisted theory. Note that $D^{\textrm{tw}}$ is not homogenous with respect to this grading since $\bar{\partial }_{M^4}$ operator carries $U(1)_L$ charge -1. The new BV degree of a component of $\mathcal {A}$ is simply its de Rham form degree on $M^7$. Alternatively, note that the twisted BV differential preserves the total form degree and we can assign a total form degree to the components of $\mathcal {A}.$ We observe that for component fields in $\mathcal {A}$ the total form degree agrees with their original $\theta$-degree. However, interactions might not preserve these degrees.

4.1 Decomposition of the field content

We now decompose the field content into representations of $G_2 \times SU(2)_- \times U(1)_L$. To do this, recall the following sequence of inclusions

$$\begin{aligned} Spin(11) \supset Spin(7) \times SU(2)_- \times U(1)_L \supset G_2 \times SU(2)_- \times U(1)_L \, . \end{aligned}$$

(4.3)

The branching of the relevant representations from Spin(11) to $Spin(7) \times SU(2)_- \times U(1)_L$ is described by Table 6.

Table 6 Branching of $Spin(11) \rightarrow Spin(7) \times SU(2)_{-} \times U(1)_L$-representations

Here we are using Dynkin labels to identify the Spin(11) and Spin(7) representations. We identify $SU(2) \times U(1)$-representations by the dimension of the SU(2)-representation and denote the U(1) charge as a subscript. Recall that the vector representation $V_{11}$ has Dynkin label (10000) and its second and third exterior powers are labeled by (01000) and (00100). The spinor representation $S_{11}$ has Dynkin label (00001). Furthermore, the gravitino representation already decomposes as a Spin(11) representation according to

$$\begin{aligned} S_{11} \otimes V_{11} \cong (00001) \oplus (10001) \, . \end{aligned}$$

(4.4)

Finally, the graviton transforms in the representation

$$\begin{aligned} {{\,\textrm{Sym}\,}}^2 V_{11} \cong (20000) \oplus (00000) \, . \end{aligned}$$

(4.5)

We also need the branching rules for $Spin(7) \rightarrow G_2,$ which we collect in Table 7.

Table 7 Branching of $Spin(7) \rightarrow G_2$-representations

We see that the three-form and its ghosts $C^{(p)}$ split into forms in $\Omega ^i(M^7) \otimes \Omega ^{j_1,j_2}(M^4),$ where $i + j_1 +j_2 = p$ is the total form degree. Thus, in the light of the conjecture, we expect all components with non-zero holomorphic form degree ($j_1 \ne 0$) to cancel in the twisted theory.

We now consider the decomposition of the gravitino field $\psi _{\mu }^{\alpha }$. It transforms in the product of the Spin(11) vector and spinor representations. We first consider its decomposition under $Spin(11) \rightarrow Spin(7) \times SU(2)_{-}$. We will later see that the only components that survive in the twisted multiplet have index $\mu$ transforming in a Spin(7)-vector representation whose components we denote by m.

On a manifold of $G_2$ holonomy the de Rham complex splits into three sub-complexes [43]

To define the space of differential forms $\Omega ^k_l$, recall that we can identify the differential forms $\Omega ^k$ in the de Rham complex with sections of the k-th exterior power of the cotangent bundle of $M^7.$ When $M^7$ has $G_2$ holonomy the exterior powers of the cotangent bundle decompose into irreducible representations of $G_2$ and we denote the sections by $\Omega ^k_l$, where the subscript denotes the respective dimension of the $G_2$-representation.

The spin 1/2 and spin 3/2 fields on $M^7$ decompose as [44, 45]

$$\begin{aligned} \Sigma _{1/2}&\cong \Omega ^0_1 \oplus \Omega ^1_7 \end{aligned}$$

(4.6)

$$\begin{aligned} \Sigma _{3/2}&\cong \Omega ^1_7 \oplus \Omega ^2_{14} \oplus \Omega ^3_{27}. \end{aligned}$$

(4.7)

Using the above decomposition and the $Spin(11) \rightarrow Spin(7) \times SU(2) \times U(1)_L$ branchings in Table 6, and the isomorphisms

$$\begin{aligned} \Sigma _{3/2} \oplus \Sigma _{1/2}&\cong \left( \Omega ^1_7 \oplus \Omega ^2_{14} \oplus \Omega ^3_{27} \right) \oplus \left( \Omega ^0_1 \oplus \Omega ^1_7 \right) \end{aligned}$$

(4.8)

$$\begin{aligned}&\cong \Omega ^2 \oplus \Omega ^3, \end{aligned}$$

(4.9)

we see that the gravitino, given by a pair of spin 3/2 and spin 1/2 fields on a $G_2$ holonomy manifold, can be identified with a pair of two- and three-forms on the manifold. We will find that the components of the gravitino that survive the twist are contained in the representation

$$\begin{aligned} (S_{+} \oplus S_{-}) \otimes (\Sigma _{3/2} \oplus \Sigma _{1/2} ) \cong (S_{+} \oplus S_{-}) \otimes (\Omega ^2 \oplus \Omega ^3) \, . \end{aligned}$$

(4.10)

However, not all of these components survive. We will find that the surviving components are $\Omega ^3 \otimes \wedge ^0 L_{4}^\vee$, $\Omega ^3 \otimes S_{-}$, and $\Omega ^2 \otimes \wedge ^2 L_{4}^\vee .$ The gravitino has BV degree 3 in the untwisted theory and the representations $\wedge ^0 L_{4}^\vee , S_{-}, \wedge ^2 L_{4}^\vee$ have U(1) charge $-1,0,$ and 1,  respectively. Thus their new BV defined by Eq. (4.3) are 4, 3, and 2. The components surviving the twist are therefore in $\Omega ^4(M^7) \otimes \Omega ^{0,0}(M^4)$, $\Omega ^3(M^7) \otimes \Omega ^{0,1}(M^4),$ and $\Omega ^2(M^7) \otimes \Omega ^{0,2}(M^4),$ where we have used the isomorphism $\Omega ^3 \cong \Omega ^4$ to ensure that the gravitino has its correct twisted BV degree.

The components of the three-form and its ghosts $C^{(p)}$, $p = 0 \dots 3$ and the gravitino along with their antifields that survive the twist therefore give exactly the right field content to be described by a form

$$\begin{aligned} \mathcal {A}\in \Omega ^{\bullet }(M^7) \otimes \Omega ^{0,\bullet }(M^4). \end{aligned}$$

(4.11)

4.2 Decomposition of the supersymmetry transformations

We now determine the supersymmetry transformations for the scalar supercharge Q. For the moment we are only interested in the supersymmetry transformations without derivatives since these are the ones responsible for the formation of trivial pairs. The transformations with derivatives will later be used to determine the twisted BV differential. Recall that the spin representation $S_{11}$ decomposes as

$$\begin{aligned} \left[ (00) \oplus (10) \right] (1_{-1} + 1_1 + 2_0) \, . \end{aligned}$$

(4.12)

This means that we can decompose the parameter $\epsilon$ from Table 4 into

$$\begin{aligned} \epsilon \rightarrow (\epsilon _{-} , \epsilon _{+}, \epsilon _{\dot{\alpha }} , \epsilon _{-m} , \epsilon _{+m}, \epsilon _{m \dot{\alpha }}) \, . \end{aligned}$$

(4.13)

Here m is an index for the seven-dimensional representation of $G_2$. To act by Q,  we specify $\epsilon _{-} = 1$ and set all other components to zero.

On general grounds, these transformation take a very simple form. As explained above, the supercharge Q is invariant under $G_2 \times SU(2)$ and has U(1) charge $-1$. As a consequence, $\delta _Q$ is an $G_2 \times SU(2)$-equivariant map. By decomposing the field content into irreducible $G_2 \times SU(2)$-representations, $\delta _Q$ splits up as a map between these irreducibles. However, since $\delta _Q$ is equivariant, we can apply Schur’s lemma and find, first, that there can not be any non-trivial maps between non-isomorphic components and, second, transformations between isomorphic $G_2 \times SU(2)$-representations are always of the form $\alpha \cdot \textrm{id}$ for some $\alpha \in {\mathbb {C}}$. Thus, to check whether there are any trivial pairs, we only have to see if there is a non-vanishing map between isomorphic representations. In addition, $\delta _Q$ carries a U(1) charge that simply equals minus the number of $\epsilon$’s appearing in the transformation, which can be used as a further criterion to establish that certain maps vanish.

To check whether or not supersymmetry transformation yields a trivial pair we need to decompose $\Gamma$-matrices.

4.2.1 Gamma matrix decomposition

In eleven dimensions the symmetric square of the spin representation decomposes as

$$\begin{aligned} {{\,\textrm{Sym}\,}}^2 S_{11} \cong V_{11} \oplus \wedge ^2 V_{11} \oplus \wedge ^5 V_{11} \, . \end{aligned}$$

(4.14)

Accordingly, there are maps denoted by $\Gamma ^\mu$, $\Gamma ^{\mu \nu }$ and $\Gamma ^{\mu _1 \dots \mu _5}$ given by projecting onto the summands in this decomposition. So for example, $\Gamma ^\mu$ is given by the composition

Recall the spin representation $S_{11}$ decomposes under $G_2 \times SU(2) \times U(1)$ as

$$\begin{aligned} S_{11} \rightarrow 1_{-1} + 1_{1} + 2_0 + (10) (1_{-1} + 1_1 + 2_0) \, . \end{aligned}$$

(4.15)

We are interested in $\epsilon _- \Gamma ^\mu \epsilon$ and $\epsilon _- \Gamma ^{\mu \nu } \epsilon$, where $\epsilon _- \in 1_{-1}$ in the above decomposition and $\epsilon$ is arbitrary. This means we are looking at a map $1_{-1} \otimes S_{11} \rightarrow V_{11}$ or $1_{-1} \otimes S_{11} \rightarrow \wedge ^2 V_{11},$ respectively. The representations $V_{11}$ and $\wedge ^2 V_{11}$ decompose as

$$\begin{aligned} \begin{aligned} V_{11}&\rightarrow 2_1 \oplus 2_{-1} \oplus (10) \\ \wedge ^2 V_{11}&\rightarrow (1_{-2} \oplus 1_0 \oplus 3_0 \oplus 1_2) \oplus (10)(2_{-1} \oplus 2_1) \oplus (10) \oplus (01). \end{aligned} \end{aligned}$$

(4.16)

We can now compare this with the decomposition of $1_{-1} \otimes S_{11}$ and read off the following results for $\Gamma ^\mu$:

$$\begin{aligned} \begin{matrix} \epsilon _- \Gamma ^\mu \epsilon _- &{} = &{} 0 \\ \epsilon _- \Gamma ^\mu \epsilon _+ &{} = &{} 0 \\ \epsilon _- \Gamma ^\mu \epsilon _{\dot{\alpha }} &{} \in &{} 2_{-1} \\ \epsilon _- \Gamma ^\mu \epsilon _{+ m} &{} \in &{} (10) \\ \epsilon _- \Gamma ^\mu \epsilon _{-m} &{} = &{} 0 &{} \\ \epsilon _- \Gamma ^\mu \epsilon _{m \dot{\alpha }} &{} = &{} 0. &{} \\ \end{matrix} \end{aligned}$$

(4.17)

For $\Gamma ^{\mu \nu }$ we find:

$$\begin{aligned} \begin{matrix} \epsilon _- \Gamma ^{\mu \nu } \epsilon _- &{} \in &{} 1_{-2} \\ \epsilon _- \Gamma ^{\mu \nu } \epsilon _+ &{} \in &{} 1_0 \\ \epsilon _- \Gamma ^{\mu \nu } \epsilon _{\dot{\alpha }} &{} = &{} 0 \\ \epsilon _- \Gamma ^{\mu \nu } \epsilon _{+ m} &{} = &{} 0 \\ \epsilon _- \Gamma ^{\mu \nu } \epsilon _{-m} &{} = &{} 0 &{} \\ \epsilon _- \Gamma ^{\mu \nu } \epsilon _{m \dot{\alpha }} &{} \in &{} (10) \, 2_{-1}. \\ \end{matrix} \end{aligned}$$

(4.18)

For example, we immediately see that all terms of the form $\epsilon _- \Gamma ^\mu \epsilon _-$ vanish and hence do not affect the twist. This is also a direct consequence of Q being nilpotent.

Let us start examining the supersymmetry transformations. Note that we are ignoring any potential non-zero scalar coefficients $\alpha$ as we are only interested in the formation of trivial pairs.

Furthermore, we are only considering cancellations between the fields of the multiplet as well as between the gravitino and its antifield. Since the action of supersymmetry respects the pairing on the BV complex, the same cancellations also occur for the respective antifields.

4.2.2 The zero-form $C^{(0)}$

For the zero-form ghost, we obviously have $\delta _Q C^{(0)} = 0$. Since there is no supersymmetry transformation generating $C^{(0)}$, it will become a field in the twisted theory.

4.2.3 The diffeomorphism ghost v

Next we consider the diffeomorphism ghost $v_\mu$. It decomposes into components

$$\begin{aligned} v_\mu \rightarrow (v_{m} , v_{+ \dot{\alpha }}, v_{- \dot{\alpha }}) \, . \end{aligned}$$

(4.19)

We have a supersymmetry transformation of the form

$$\begin{aligned} \delta _Q v_\mu = \epsilon \Gamma _\mu \omega \, . \end{aligned}$$

(4.20)

The gravitino ghost $\omega$ lives in the spinor representation and hence decomposes according to Eq. (4.15). From the $\Gamma$-matrix decomposition in Eq. (4.20), we know that $\epsilon _- \Gamma _\mu \omega$ is only non-vanishing for the components $\omega _{\dot{\alpha }}$ and $\omega _{+m}$ of $\omega$. Thus we get up to potential non-zero prefactors

$$\begin{aligned} \delta _Q v_{m} = \omega _{+m} \end{aligned}$$

(4.21)

and

$$\begin{aligned} \delta _Q v_{-\dot{\alpha }} = \omega _{\dot{\alpha }} \, . \end{aligned}$$

(4.22)

Finally we have,

$$\begin{aligned} \delta _Q v_{+ \dot{\alpha }} = 0 \, . \end{aligned}$$

(4.23)

Thus we already find that some components of the diffeomorphism ghost v form trivial pairs with parts of the gravitino ghost. In addition, it is interesting to note that $\delta _Q v_{+ \dot{\alpha }} = 0$. As $v_{+ \dot{\alpha }}$ will not be part of the twisted three-form multiplet, we expect it to be in the image of $\delta _Q$, forming a trivial pair with another field. Indeed, we will momentarily find that $v_{+ \dot{\alpha }}$ cancels the holomorphic part of the one-form $C^{(1)}$.

4.2.4 The one-form $C^{(1)}$

For the field $C^{(1)},$ we have a supersymmetry transformation rule

$$\begin{aligned} \delta _Q C^{(1)}_\mu = (\epsilon _- \Gamma _{\mu \nu } \epsilon _-) v^\nu \, . \end{aligned}$$

(4.24)

From the $\Gamma$-matrix decomposition, we know $\epsilon _- \Gamma _{\mu \nu } \epsilon _- \in 1_{-2}$. Thus we immediately find

$$\begin{aligned} \delta _Q C^{(1)}_{m} = 0 \end{aligned}$$

(4.25)

and

$$\begin{aligned} \delta _Q C^{(1)}_{+ \dot{\alpha }} = 0 \, . \end{aligned}$$

(4.26)

In addition, we have

$$\begin{aligned} \delta _Q C^{(1)}_{- \dot{\alpha }} = v_{+ \dot{\alpha }} \, . \end{aligned}$$

(4.27)

This shows that $C^{(1)}_{- \dot{\alpha }}$ and $v_{+ \dot{\alpha }}$ form a trivial pair and thus do not appear in the twisted theory. Recall that the choice $(\epsilon _{-} , \epsilon _{+} , \epsilon _{\dot{\alpha }}) = (1,0,0)$ defines a complex structure on $\mathbb {R}^4 \cong {\mathbb {C}}^2$. The four-dimensional vector representation decomposes as

$$\begin{aligned} V_4 = S_+ \otimes S_- = 2_1 \oplus 2_{-1} \, . \end{aligned}$$

(4.28)

The representation $2_{-1}$ corresponds to holomorphic and $2_1$ to the antiholomorphic components. Thus we see that, for this complex structure, the components $C^{(1)}_{- \dot{\alpha }}$ form the holomorphic parts of the one-form ghost $C^{(1)}$. As expected, only the anti-holomorphic part of the one-form plays a role in the twisted theory.

We can alternatively describe the cancellation using holomorphic geometry. With respect to the complex structure on ${\mathbb {C}}^2$,

$$\begin{aligned} \Omega = (\epsilon _- \Gamma _{\mu \nu } \epsilon _-) dx^\mu \wedge dx^\nu \end{aligned}$$

(4.29)

defines a holomorphic (2, 0)-form. Introducing coordinates $(z^{\dot{\alpha }}, \bar{z}^{\dot{\alpha }})$ on $V = 2_{-1} \oplus 2_1$, the holomorphic (2, 0)-form simplifies to

$$\begin{aligned} \Omega = dz^1 \wedge dz^2 \, . \end{aligned}$$

(4.30)

This allows us to rewrite the supersymmetry transformation of the one-form ghost as

$$\begin{aligned} \delta _Q C^{(1)} = \iota _v \Omega = v_{+ \dot{\alpha }} dz^{\dot{\alpha }} \, . \end{aligned}$$

(4.31)

Thus, we again see that the holomorphic components of $C^{(1)}$ cancel with the diffeomorphism ghost.

4.2.5 The two-form field $C^{(2)}$

Let us continue with the supersymmetry transformation of the two-form

$$\begin{aligned} \delta _Q C^{(2)}_{\mu \nu } = \frac{1}{2} \epsilon _- \Gamma _{\mu \nu } \omega + \epsilon _- \Gamma _{[\mu \rho } \epsilon _- g^\rho _{\nu ]} \, . \end{aligned}$$

(4.32)

The two-form and the graviton decompose into components

$$\begin{aligned} \begin{aligned} C^{(2)}_{\mu \nu }&\rightarrow (C^{(2)}_{mn}, C^{(2)}_{m + \dot{\alpha }}, C^{(2)}_{m - \dot{\alpha }}, C^{(2)}_{2} , C^{(2)}_{0} ,C^{(2)}_{(\dot{\alpha } \dot{\beta })} , C^{(2)}_{-2} ) \\ g_{\mu \nu }&\rightarrow (g_{mn}, g_{m + \dot{\alpha }}, g_{m - \dot{\alpha }}, g_{2 (\dot{\alpha } \dot{\beta })} , g_{(\dot{\alpha } \dot{\beta })}, g_0, g_{-2 (\dot{\alpha } \dot{\beta }) } , h) \, . \end{aligned} \end{aligned}$$

(4.33)

Consulting the $\Gamma$-matrix decomposition in Eq. (4.21), we get

$$\begin{aligned} \begin{aligned} \delta _Q C^{(2)}_{mn}&= 0 \\ \delta _Q C^{(2)}_{+ m \dot{\alpha }}&= 0 \\ \delta _Q C^{(2)}_{- m \dot{\alpha }}&= \omega _{m \dot{\alpha }} + g_{+ m\dot{\alpha }} \\ \delta _Q C^{(2)}_{2}&= 0 \\ \delta _Q C^{(2)}_{0}&= \omega _+ \\ \delta _Q C^{(2)}_{(\dot{\alpha } \dot{\beta })}&= g_{2 (\dot{\alpha } \dot{\beta })} \\ \delta _Q C^{(2)}_{-2}&= \omega _- + g_0 \, . \end{aligned} \end{aligned}$$

(4.34)

Thus we find that the components

$$\begin{aligned} C^{(2)}_{- m \dot{\alpha }} \quad C^{(2)}_{0} \quad C^{(2)}_{(\dot{\alpha } \dot{\beta })} \quad C^{(2)}_{-2} \end{aligned}$$

(4.35)

do not appear in the twisted multiplet, while

$$\begin{aligned} C^{(2)}_{mn} \quad C^{(2)}_{+ m \dot{\alpha }} \quad C^{(2)}_{2} \end{aligned}$$

(4.36)

are in the kernel of $\delta _Q$ and thus, since there are no supersymmetry transformations that could make these exact, part of the twisted multiplet. Note again that this matches with the expectation that only $(0,*)$-forms on $M^4$ play a role in the twisted multiplet.

Note that we can rewrite the piece of the supersymmetry transformation (4.35) involving the graviton using the holomorphic (2,0)-form $\Omega$ as

$$\begin{aligned} \delta _Q C^{(2)} = \iota _{g^\rho _\nu \partial _\rho } \Omega \wedge dx^\nu \, . \end{aligned}$$

(4.37)

However, due to the symmetry properties of the graviton, this transformation alone does not cancel all holomorphic component of the two-form. So one really needs the supersymmetry ghost to cancel the singlet $C^{(2)}_0$.

4.2.6 The three-form field $C^{(3)}$

For the three-form field, we have a supersymmetry transformation of the form

$$\begin{aligned} \delta _Q C^{(3)}_{\mu \nu \rho } = \frac{1}{4} \epsilon _- \Gamma _{[\mu \nu } \psi _{\rho ]} \, . \end{aligned}$$

(4.38)

The three-form decomposes into components

$$\begin{aligned} C^{(3)}_{\mu \nu \rho } \rightarrow (C^{(3)}_{mnp}, C^{(3)}_{mn+\dot{\alpha }}, C^{(3)}_{mn-\dot{\alpha }}, C^{(3)}_{m-2}, C^{(3)}_{m0}, C^{(3)}_{m(\dot{\alpha }\dot{\beta })}). \end{aligned}$$

(4.39)

To decompose this transformation, we write for the gravitino

$$\begin{aligned} \psi ^\alpha _\mu = \xi ^\alpha \otimes \chi _\mu \end{aligned}$$

(4.40)

where $\xi ^\alpha$ takes values in $S_{11}$ and $\chi _\mu$ in $V_{11}$. From (4.21), we see that $\xi ^\alpha$ has to live in

$$\begin{aligned} 1_{-1} \oplus 1_{1} \oplus (10) 2_0 \end{aligned}$$

(4.41)

to get a non-zero result. Decomposing $(1_{-1} \oplus 1_{1} \oplus (10) 2_0) \otimes V_{11}$ into irreducibles, we can identify the decomposed transformations. The results are listed in Table 8.

4.2.7 The supersymmetry ghost $\omega$

The non-derivative part of the supersymmetry transformation of $\omega _\alpha$ reads

$$\begin{aligned} \delta _Q \omega _\alpha = \frac{1}{2} (\epsilon _- \Gamma ^{\mu \nu })_{\alpha } (\epsilon _- \Gamma _{\mu } \psi _{\nu }) \, . \end{aligned}$$

(4.42)

Again decomposing the gravitino as we did for the three-form field and using the decomposition (4.20), we find that $\xi ^\alpha$ has to take values in

$$\begin{aligned} 2_0 \oplus (10) 1_1 \, . \end{aligned}$$

(4.43)

Tensoring with the vector representation $V_{11}$ and identifying matching representations gives the result listed below.

4.2.8 The graviton $g_{\mu \nu }$

The supersymmetry transformation

$$\begin{aligned} \delta _Q g_{\mu \nu } = \frac{1}{2} \epsilon _- \Gamma _{(\mu } \psi _{\nu )} \end{aligned}$$

(4.44)

again only allows for $\xi$ to come from $2_0 \oplus (10)1_1$. As before, we just list the results in Table 8.

In Table 8, we collect all decomposed non-derivative supersymmetry transformations. Here M is an index for the 14-dimensional representation (01) of $G_2$. It appears in the variation

$$\begin{aligned} \delta _Q C^{(3)}_{mn -\dot{\alpha }} = \psi _{M \dot{\alpha }} + \psi _{m \dot{\alpha }} \end{aligned}$$

(4.45)

where the notation describes the decomposition $\wedge ^2 (10) \rightarrow (10) \oplus (01)$ of $G_2$-representations.

Table 8 Decomposed supersymmetry transformations

4.3 Supersymmetry variation of the gravitino

The non-derivative supersymmetry transformation of the gravitino reads

$$\begin{aligned} \delta \psi ^\alpha _\mu = (\epsilon M_{\mu \nu }^{\alpha \beta } \epsilon ) \psi _{\beta }^{\dagger \nu } \, . \end{aligned}$$

(4.46)

This transformation reflects the fact that the supersymmetry algebra acts only up to the equations of motions of the gravitino. Correspondingly, there is a quadratic term in antifields appearing in the BV action [12, 46]

$$\begin{aligned} S^{(2)} \propto (\epsilon M \epsilon ) \psi ^{\dagger } \psi ^{\dagger } \, . \end{aligned}$$

(4.47)

The transformation (4.49) is responsible for the remaining cancellations between of the gravitino. To argue that indeed the correct components of $\psi$ cancel, we change our strategy. As the structure of $M^{\alpha \beta }_{\mu \nu }$ is very complicated, we will not decompose it directly under $G_2 \times SU(2)$. Instead we give an indirect argument.

For this, recall that (4.49) is precisely the term that corrects for the failure of the linearized supersymmetry transformation to act strictly. Denoting the linearized part of the supersymmetry transformation by $\delta _Q^{\textrm{lin}}$ and the quadratic transformation of the gravitino by $\delta _Q^{\textrm{quad}}$, we have

$$\begin{aligned} \begin{aligned} \{\delta _Q^{\textrm{lin}} ,\delta _Q^{\textrm{lin}} \} \psi&= \delta _{\{Q,Q\}}^{\textrm{lin}} \psi + \delta ^{\textrm{quad}}_Q Q_{BV} \psi ^\dagger \\&= \delta ^{\textrm{quad}}_Q Q_{BV} \psi ^\dagger \\&= (\epsilon _- M \epsilon _-) {Q}_{BV} \psi ^\dagger \, , \end{aligned} \end{aligned}$$

(4.48)

where we have used the fact that Q is square zero in the second equality.

Thus, for $\psi$ outside of the kernel of $Q_{BV}$,

$$\begin{aligned} \{\delta _Q^{\textrm{lin}} ,\delta _Q^{\textrm{lin}} \} \psi = 0 \implies \delta ^{\textrm{quad}}_Q \psi = 0 \, . \end{aligned}$$

(4.49)

For such components there can not be any cancellations between $\psi$ and $\psi ^\dagger$. Furthermore this reasoning suggests to view the cancellations between components of the gravitino and its antifield as a two-step procedure. First, the linearized transformation identifies a piece of $\psi$ with a component of $G^{(4)} = dC^{(3)}$. Then we can act with another linearized transformation to obtain a component of $\psi ^\dagger$. Clearly the U(1) charges of components connected in this way satisfy

$$\begin{aligned} d_{U(1)}(\psi ^\dagger ) = d_{U(1)}(G^{(4)}) +1 = d_{U(1)}(\psi ) +2 \, . \end{aligned}$$

(4.50)

Now recall that the linear part of supersymmetry transformations on the three-form and the gravitino are

$$\begin{aligned} \delta _Q^{\textrm{lin}} \psi _{\mu }&= (\Gamma ^{\nu \rho \sigma \tau }_{\mu } - 8 \Gamma ^{\rho \sigma \tau } \delta _{\mu }^{\nu } )G^{(4)}_{\nu \rho \sigma \tau } \epsilon _- \end{aligned}$$

(4.51)

$$\begin{aligned} \delta _Q^\textrm{lin} C^{(3)}_{\mu \nu \rho }&= \frac{1}{4} \epsilon _- \Gamma _{[\mu \nu } \psi _{\rho ]} \, . \end{aligned}$$

(4.52)

However, from Table 8 we know that the components

$$\begin{aligned} C^{(3)}_{mnp} \, , C^{(3)}_{mn + \dot{\alpha }} \, ,C^{(3)}_{m 2} \end{aligned}$$

(4.53)

are in the kernel of $\delta _Q$. Thus the pieces of $\psi$, which are mapped to the corresponding field strengths by (4.54) are annihilated by applying the second linear transformation (4.55) and hence satisfy $\{\delta _Q^\textrm{lin}, \delta _Q^{\textrm{lin}}\} \psi = 0$.

With this information, we can analyze the components of the gravitino. In Table 9, we display the $G_2 \times SU(2)$-equivariant decomposition of the gravitino, its antifield, and the field strength organized by U(1) charges. All components of $\psi$ and $\psi ^\dagger$ that form trivial pairs with other fields according to Table 8 are indicated with an arrow.

Table 9 Decomposition of the non-linear gravitino supersymmetry variation

We immediately see that the components of $\psi$ with U(1) charge 1 cannot be canceled and thus are part of the twisted multiplet. We circle these components in blue.

Furthermore, we can take a look at the remaining components of $\psi$ with U(1) charge $-1$. There we have a representation

$$\begin{aligned} (00)(1) \oplus (10)(1) \oplus (20)(1) \cong \Omega ^4(M^7) \otimes \Omega ^{0,0}(M^4) \, , \end{aligned}$$

(4.54)

which maps under $\delta _Q$ to $d_{M^7} C^{(3)}_{mnp}$. This means the corresponding components are part of the twisted multiplet. With similar reasoning the components

$$\begin{aligned} (00)(2) \oplus (10)(2) \oplus (20)(2) \cong \Omega ^3(M^7) \otimes \Omega ^{0,1}(M^4) \end{aligned}$$

(4.55)

with U(1) charge zero transform to the field strength of $d_{M^7} C^{(2)}_{mn + \dot{\alpha }}$ and $\bar{\partial } C^{(3)}_{mnp}$ under $\delta _Q$ and hence are also part of the twisted multiplet.

On the other hand, we see that different pieces of the gravitino are mapped to components of the field strength which are not part of the kernel of $\delta _Q$. These than can have $\{\delta _Q^\textrm{lin}, \delta _Q^{\textrm{lin}}\} \psi \ne 0$, such that a cancellation is possible. In Table 9 we indicate such components, the corresponding intermediate components of the field strength and the respective partners from $\psi ^\dagger$ with green rectangles.

Nevertheless one has to remain careful. As we explained above, these arguments only hold outside of the kernel of $Q_{BV}$. For U(1) charge zero, there is a component (00)(2) boxed in green. This can be viewed as a differential form

$$\begin{aligned} (00)(2) \cong \Omega _1^3(M^7) \otimes \Omega ^{0,1}(M^4) \subset \Omega ^3(M^7) \otimes \Omega ^{0,1}(M^4) \, . \end{aligned}$$

(4.56)

The corresponding field strength, however, does come from $C^{(3)}_{mn +\dot{\alpha }}$ which is in the kernel of $\delta _Q$. This is not a contradiction, since the corresponding representation (00)(2) is in the kernel of $Q_{BV}$. The trivial representation $(00) \subset \Omega ^3(M^7)$ corresponds to a covariantly constant spinor inside the tensor product $(TM^7)^{\mathbb {C}}\otimes SM^7$ [44], which is a zero-mode for the BV operator $Q_{BV}$ which acts as the Rarita–Schwinger operator. This means that the above argument does not apply here, in the light of the results so far and the conjecture, we nevertheless expect this component to cancel. An explicit investigation using a decomposition of the tensor $M^{\alpha \beta }_{\mu \nu }$ would still be interesting.

4.4 Summary of cancellations

We summarize the cancellations obtained in the previous sections in Table 10. The fields that do not form trivial pairs are circled in blue. They form the multiplet $\mathcal {A}\in \Omega ^{\bullet }(M^7) \otimes \Omega ^{0,\bullet }(M^4)$ and appear in Table 1. The bi-directional strike-through arrows indicate cancellations that occur between $\psi$ and its anti-field $\psi ^{\dagger }$ found in Sect. 4.3.

Special care should be taken for the variations of the components of $C^{(2)}$ that cancel with a linear combination of components of the graviton and supersymmetry ghost

$$\begin{aligned} \delta _Q C^{(2)}_{- m \dot{\alpha }}&= \omega _{m \dot{\alpha }} + g_{+ m\dot{\alpha }} \end{aligned}$$

(4.57)

$$\begin{aligned} \delta _Q C^{(2)}_{-2}&= \omega _- + g_0 \, \end{aligned}$$

(4.58)

that occur in Eq. (4.37). A subsequent variation yields

$$\begin{aligned} \delta _Q \omega _{m \dot{\alpha }}&= - \delta _Q g_{+ m\dot{\alpha }} = \psi _{2 m \dot{\alpha }} \end{aligned}$$

(4.59)

$$\begin{aligned} \delta _Q \omega _{-}&= -\delta _Q g_0 = \psi _{+} \end{aligned}$$

(4.60)

which is consistent with $\delta _Q^2 C^{(2)}= 0$. These extra cancellations are indicated by the strike-through arrows with labels x and y.

Table 10 Cancellations of fields under Q

4.5 The twisted differential

Recall that the BV differential of the twisted theory is the sum of two terms

$$\begin{aligned} Q_{BV}^{\text {tw}} = Q_{BV} + \delta _Q \, . \end{aligned}$$

(4.61)

We already examined how the non-derivative part of $\delta _Q$ leads to the formation of various trivial pairs; now we turn towards the parts containing derivatives in order to see how they act on the twisted multiplet.

The BV operator $Q_{BV}^{\textrm{tw}}$ is dual to a differential $D^{\textrm{tw}}$ acting on the fields of the twisted multiplet. We already know that D acts as the de Rham differential on the three-form ghost system. Under $G_2 \times SU(2)$ the de Rham differential decomposes

$$\begin{aligned} d = d_{M^7} + \bar{\partial }_{M^4} + \partial _{M^4} \, . \end{aligned}$$

(4.62)

As only $(0,*)$-forms are part of the twisted multiplet, this restricts to

$$\begin{aligned} d_{M^7} + \bar{\partial }_{M^4} \, . \end{aligned}$$

(4.63)

In addition, D acts on the gravitino by the Rarita–Schwinger equation. Identifying the gravitino as a spinor valued one-form, $\psi \in \Omega ^1(M) \otimes S_{11}$, the Rarita–Schwinger operator can be understood as a composition of the exterior differential and Clifford multiplication [45]. From this one can see that it also acts by $d_{M^7} + \bar{\partial }_{M^4}$ on the relevant pieces of the gravitino.

Finally, there is a contribution to $D^{\textrm{tw}}$ coming from the supersymmetry transformation (4.55). This transformation also acts by $d_{M^7} + \bar{\partial }_{M^4}$ and provides the missing differential between $C^{(3)}$ and $\psi$.

In summary, the twisted multiplet can thus be described by the cochain complex

$$\begin{aligned} \left( \Omega ^{\bullet }(M^7) \otimes \Omega ^{0,\bullet }(M^4) \, , \, D^{\textrm{tw}} = d_{M^7} + \bar{\partial }_{M^4} \right) \, , \end{aligned}$$

(4.64)

as conjectured by Costello.

Interestingly, the form of the differential can also be deduced directly from the explicit formulas in the pure spinor formalism. Recall that $\mathcal {D}_1$ acts on the representatives by

$$\begin{aligned} \mathcal {D}_1 = (\lambda \Gamma ^\mu \theta ) \partial _\mu \, , \end{aligned}$$

(4.65)

and that the one-form was represented by the cohomology classes $C^{(1)}_\mu (\lambda \Gamma ^\mu \theta )$. As we already know that the twisted multiplet forms the exterior algebra $\Omega ^{\bullet }(M^7) \otimes \Omega ^{0,\bullet }(M^4)$, we see that $\mathcal {D}_1$ simply acts by taking derivatives and wedging with the corresponding component of the one-form, i.e. precisely by $d_{M^7} + \bar{\partial }_{M^4}$.

In addition the derivative part of the supersymmetry transformation acts by

$$\begin{aligned} Q_{\partial _x} = (\epsilon _- \Gamma ^\mu \theta ) \partial _\mu \, . \end{aligned}$$

(4.66)

From the Gamma matrix decomposition (4.15), we see

$$\begin{aligned} (\epsilon _- \Gamma ^\mu \theta ) \in 2_{-1} \oplus (10) \, . \end{aligned}$$

(4.67)

Identifying the corresponding components with $d\bar{z}^{\dot{\alpha }}$ and $dx^m,$ we once again see that $Q_{\partial _x}$ acts as desired.

A more roundabout way of understanding the appearance of the de Rham differential is as follows. Recall that the gravitino field on $M^7$ can be organized into $\Omega ^2 \oplus \Omega ^3$ when $M^7$ has $G_2$ holonomy. Since there are $b^2(M^7) + b^3(M^7)$ zero modes of the gravitino on $M^7$ [44, 45, 47, 48], we see that the BV differential acts by the de Rham differential

$$\begin{aligned} d_{dR}: \Omega ^2 \oplus \Omega ^3 \rightarrow \Omega ^3 \oplus \Omega ^4. \end{aligned}$$

(4.68)

This is similar to the holomorphic twist of ten-dimensional abelian super Yang–Mills theory on ${\mathbb {C}}^5$. In that case, the analogous BV differential between the gaugino and its antifield expresses the Dirac equation. The relevant part of the differential in the twisted theory is

$$\begin{aligned} Q_{BV} (\lambda ^{mn})^{\dagger } = i \epsilon ^{mnpqr} \bar{\partial }_p \lambda _{qr}, \end{aligned}$$

(4.69)

and only involves the Dolbeault operator on $\Omega ^{0,\bullet }({\mathbb {C}}^5)$.

5 Conclusions and Future Directions

Eleven-dimensional supergravity in the pure spinor formalism incorporates both the three-form and super-vielbein multiplets. We have seen how the twist of the three-form multiplet is given by a differential form

$$\begin{aligned} \mathcal {A}\in \Omega ^{\bullet }(M^7) \otimes \Omega ^{0,\bullet }(M^4). \end{aligned}$$

(4.70)

The super-vielbein multiplet has the graviton, gravitino, and 4-form field strength $G^{(4)}$ as its physical fields. It is used in the traditional superspace formulation of supergravity. It is natural to expect that the twisted fields of the super-vielbein multiplet organize into a differential form

$$\begin{aligned} \partial \mathcal {A}\in \Omega ^{\bullet }(M^7) \otimes \Omega ^{1,\bullet }(M^4), \end{aligned}$$

(4.71)

with leading component $v_{+ \dot{\alpha }}$ from the diffeomorphism ghost. In future work [32], we plan to directly twist Cederwall’s pure spinor action [13] and compare to Costello’s conjectural action [5, 10] for the twisted theory.

The conjectural twist of type IIB supergravity was developed by Costello and Li to give a precise formulation of a sub-sector of AdS/CFT with rigorously defined mathematical objects [4, 49]. We hope that a similar approach can be used to derive the holomorphic twist of M-theory and Costello–Li’s conjectural form of the twist of type IIB supergravity as a BCOV theory using the presymplectic BV formalism of [50].

The AdS/CFT conjecture is a holographic duality between string and M-theory on anti-de Sitter spaces and gauge theories. In a particular limit it relates weakly coupled type IIB supergravity on products of five-dimensional AdS space $AdS_5$ with arbitrary Sasaki-Einstein manifolds $SE^5$ to four-dimensional supersymmetric gauge theories. A different form of the conjecture relates the weak coupling limit of M-theory on the products $AdS_4 \times SE^7$ to three-dimensional supersymmetric gauge theories. The cone over the Sasaki–Einstein manifold is a local Calabi–Yau manifold. One corollary of the conjecture is the equivalence of the superconformal index [51, 52] under gauge-gravity duality. The gravity superconformal index was computed in terms of holomorphic invariants of the Calabi–Yau manifold in [53, 54]. The corresponding field theory index was later shown to be most directly computed in the holomorphic twist [40, 55]. Thus a full derivation of the holomorphic twist of type IIB supergravity and eleven–dimensional supergravity should reproduce the index calculations of [53, 54]. This would serve as a natural bridge between physical and mathematical approaches to holography.

We hope that a further twist of the one considered in this paper can be used to derive twisted M-theory in the $\Omega$-background [5] following [56]. This could provide a physical origin for the applications in [57, 58] by coupling a twisted M5-brane [50] to twisted M-theory. Finally, we hope that twisted M-theory can shed new light on topological M-theory [59,60,61,62,63], which is believed to unify the Kähler [64] and Kodaira–Spencer theories of topological gravity.