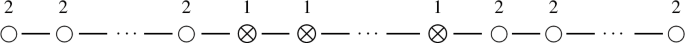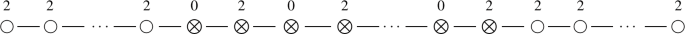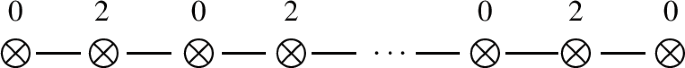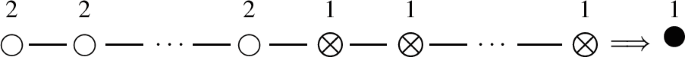On Free Field Realization of Quantum Affine W-Algebras

Abstract

We find an explicit formula for the conformal vector of any quantum affine W-algebra in its free field realization.

1 Introduction

The chiral part of a (super)conformal field theory is a vertex algebra which admits a conformal vector L, for which the eigenvalues of the energy operator $L_0$ lie in $\frac{1}{2}\mathbb {Z}_{\ge 0}$ and the multiplicity of the 0 eigenvalue is 1. An important class of such vertex algebras are quantum affine W-algebras $W^{k}(\mathfrak {g}, x, f)$ [KRW] , [KW] (see also [DSK]), attached to a “good” datum $(\mathfrak {g}, x , f, k)$ , where $\mathfrak {g}= \mathfrak {g}_{\bar{0}} \oplus \mathfrak {g}_{\bar{1}}$ is a basic Lie superalgebra, i.e. a simple finite-dimensional Lie superalgebra over an algebraically closed field $\mathbb {F}$ of characteristic 0 with reductive even part $\mathfrak {g}_{\bar{0}}$ and a fixed non-degenerate even invariant supersymmetric bilinear form $(. \, | \, .)$, $x\in \mathfrak {g}_{\bar{0}}$ is such that the eigenspace decomposition of $\mathfrak {g}$ with respect to $\mathop {\mathrm{ad}}\,x$ defines a $\tfrac{1}{2} \mathbb {Z}$-grading

$$\begin{aligned} \mathfrak {g}\ = \ \underset{j \in \tfrac{1}{2} \mathbb {Z}}{\bigoplus } \ \mathfrak {g}_{j}, \end{aligned}$$

(1.1)

$f\in \mathfrak {g}_{-1}$, and $k \in \mathbb {F}$.

A datum $(\mathfrak {g}, x , f, k)$ is called good if $f\in \mathfrak {g}_{-1}$ is such that

$$\begin{aligned} \mathfrak {g}^{f} \subset \mathfrak {g}^{}_{\le 0}. \end{aligned}$$

(1.2)

Hereafter $\mathfrak {g}^f$ (resp. $\mathfrak {g}_j^f$) denotes the centralizer of f in $\mathfrak {g}$ (resp. $\mathfrak {g}_j$), and we use notation $\mathfrak {g}^{}_{\le m} = \underset{{\mathrm{j}} \le {\mathrm{m}}}{\oplus } \ \mathfrak {g}_{j}$, and similarly for $\ge m$, or $< m$, or $> m$. We also denote by $p_{> 0}$, $p_{j}$, etc., the projection of $\mathfrak {g}$ to $\mathfrak {g}_{> 0}$, $\mathfrak {g}_{j}$, etc., along (1.1). A special case of a good datum is a Dynkin datum, defined by x and f from an $s\ell _2$-triple $\{ e,x,f\}$ in $\mathfrak {g}_{\bar{0}}$, where $[x,e] = e,[e , f] = x ,[x ,f] = -f$.

Recall that a bilinear form $(. \, | \, .)$ on $\mathfrak {g}$ is called even if $(\mathfrak {g}_{\bar{0}} | \mathfrak {g}_{\bar{1}}) = 0$, supersymmetric (resp. superskewsymmetric) if $(a | b) = (-1)^{p(a)p(b)} (b | a)$ (resp. $-(-1)^{p(a)p(b)} (b | a))$, and invariant if $([a,b] | c) = (a | [b,c])$.

In [KRW] for an arbitrary datum $(\mathfrak {g}, x, f ,k)$ a vertex algebra homology complex

$$\begin{aligned} (V^{k} (\mathfrak {g})\otimes F^{\mathrm{ch}}\otimes F^{\mathop {\mathrm{ne}}\,} \, , \, d^{}_{(0)}) \, \end{aligned}$$

(1.3)

was constructed, where $V^{k} (\mathfrak {g})$ is the universal affine vertex algebra of level k associated to $\mathfrak {g}$, and $F^{\mathrm{ch}}$ (resp. $F^{\mathop {\mathrm{ne}}\,})$ is the vertex algebra of free charged fermions based on $\mathfrak {g}^{}_{> 0} \oplus \mathfrak {g}^{*}_{> 0}$ with reversed parity (resp. of free neutral fermions based on $\mathfrak {g}_{1/2}$), and $d_{(0)}$ is an explicitly constructed odd derivation of the vertex algebra $\mathcal {C}^{k} (\mathfrak {g},x,f): = V^{k} (\mathfrak {g})\otimes F^{\mathrm{ch}}\otimes F^{\mathop {\mathrm{ne}}\,}$.

Recall [K2] that for the construction of the vertex algebra of free fermions based on a vector superspace A, one needs a superskewsymmetric bilinear form on A. In the case of $F^{\mathrm{ch}}$ this bilinear form is defined via the pairing of $\mathfrak {g}_{>0}$ and its dual $\mathfrak {g}^{*}_{> 0}$, which is identified with $\mathfrak {g}_{<0}$, using the bilinear form (.|.); the former is non-degenerate since the latter is. In the case of $F^{\mathop {\mathrm{ne}}\,}$ this bilinear form is defined by the formula

$$\begin{aligned} <a ,b>^{\mathop {\mathrm{ne}}\,} = (f | [a,b]), \ a ,b \in \mathfrak {g}^{}_{1/2}. \end{aligned}$$

(1.4)

The bilinear form (1.4) is non-degenerate if and only if

$$\begin{aligned} \mathop {\mathrm{ad}}\,f : \mathfrak {g}_{1/2} \rightarrow \mathfrak {g}_{-1/2} \,\, \hbox {is a vector superspace isomorphism}. \end{aligned}$$

(1.5)

Since property (1.2) is equivalent to $[f,\mathfrak {g}_j]=\mathfrak {g}_{j-1}$ if $j\le 1/2$ [KW], property (1.5) holds for any good datum.

The $\mathbb {Z}$-grading of the complex (1.3) is defined by

$$\begin{aligned} \deg V^{k} (\mathfrak {g}) = \deg F^{\mathop {\mathrm{ne}}\,} = 0 , \ \deg \mathfrak {g}^{}_{>0} = \ -\deg \mathfrak {g}^{*}_{>0} = 1. \end{aligned}$$

The homology of the complex (1.3) is called the quantum affine W-algebra, attached to the datum $(\mathfrak {g},x , f, k)$, and is denoted by $W^{k} (\mathfrak {g},x, f)$.

For a good datum, $[\mathfrak {g}_0, f]=\mathfrak {g}_{-1}$, hence the orbit $G_0 (f)$ is Zariski open in $\mathfrak {g}_{-1}$, and therefore the vertex algebra $W^k(\mathfrak {g}, x, f)$ is independent, up to isomorphism, of the choice of $f\in \mathfrak {g}_{-1}$, satisfying (1.2).

The main result of [KW] on the structure of the vertex algebra $W^{k} (\mathfrak {g},x, f)$ is Theorem 4.1, which states that for a good datum the j $^{\scriptstyle \text {th}}$ homology of the complex (1.3) is zero if $j \ne 0$, and the 0-th homology is the vertex algebra $W^{k} (\mathfrak {g},x, f)$, which is a subalgebra of the vertex algebra $\mathcal {C}^{k}(\mathfrak {g},x,f)$ freely generated by $d_{(0)}$-closed elements $J^{\{a_i\}}$, where $a_1 , \ldots , a_{s}$ is a basis of $\mathfrak {g}^{f}$ consisting of eigenvectors of $\mathop {\mathrm{ad}}\,x$. The elements $J^{\{a_i\}}$ can be recursively computed, using equations (4.11) and (4.12) from [KW]. The “building blocks” for construction of elements $J^{\{a_i\}}$ are the elements $J^{(a)}$, $a \in \mathfrak {g}^{f}$, defined in [KRW], see formula (2.7) in Sect. 2 of the present paper. Theorem 4.1(a) from [KW] states that for each $a \in \mathfrak {g}^{f}_{-j} \ (= \mathfrak {g}^{f} \cap \mathfrak {g}^{}_{-j})$ the element $J^{\{a\}} - J^{(a)}$ lies in the subalgebra of the vertex algebra $\mathcal {C}^{k} (\mathfrak {g},x, f)$, generated by elements $J^{(b)}$, where $b \in \mathfrak {g}^{}_{-s}$ with $0 \le s < j$ (recall that $\mathfrak {g}^{f}_{j} \ne 0$ only for $j \le 0$ by (1.2)), and by the neutral fermions.

Consider the subalgebra $\overline{\mathcal {C}}^k (\mathfrak {g},x, f)$ of the vertex algebra $\mathcal {C}^k (\mathfrak {g},x, f)$ generated by the elements $J^{(v)}$ with $v \in \mathfrak {g}_{\le 0}$, and by the neutral fermions. It follows from the above discussion that, for a good datum, all elements $J^{\{v\}}$, $v \in \mathfrak {g}^{f}$, lie in $\overline{\mathcal {C}}^k (\mathfrak {g},x,f)$. It is easy to see that the elements $J^{(v)}$ with $v \in \mathfrak {g}^{}_{0}$ and neutral fermions generate a subalgebra $\overline{\mathcal {C}}^k_{0} (\mathfrak {g},x, f)$ of the vertex algebra $\mathcal {C}(\mathfrak {g},x, f)$ , and that the $J^{(v)}$ with $v \in \mathfrak {g}^{}_{< 0}$ generate an ideal $U^{}_{< 0}$ of $\overline{\mathcal {C}}^k (\mathfrak {g},x, f)$ , such that $\overline{\mathcal {C}}^k_0 (\mathfrak {g},x, f) \ \cap \ U^{}_{< 0} = 0$. Hence, the canonical map $\overline{\mathcal {C}}^k (\mathfrak {g},x, f) \rightarrow \overline{\mathcal {C}}^k_{0} (\mathfrak {g},x,f)$ induces a vertex algebra homomorphism

$$\begin{aligned} W^{k} (\mathfrak {g},x, f) \ \xrightarrow \ {\overline{\mathcal {C}}}^k_{0} (\mathfrak {g},x,f). \end{aligned}$$

(1.6)

Since the vertex algebra $\overline{\mathcal {C}}^k_{0} (\mathfrak {g},x, f)$ is isomorphic to the tensor product of the universal affine vertex algebra $V^{k'} (\mathfrak {g}^{}_{0})$ of "shifted" level $k'$ ([KW] , formula (2.5)), and the vertex algebra $F^{\mathop {\mathrm{ne}}\,}$, the map (1.6) may be viewed as a free field realization (FFR) of the W-algebra $W^{k} (\mathfrak {g},x, f)$.

In the case of a good datum, for the $a^{}_{i} \in \mathfrak {g}^{f}_{j}$ with $j = 0$ or $- 1/2$ the elements $J^{\{a_i\}}$ are uniquely determined by the $a_i$ and they are explicitly constructed in [KW], Sect. 2. The construction of these elements is still valid for an arbitrary datum, satisfying property (1.5). Furthermore, provided that $k \ne -h^{\vee }$ (i.e. k is not the critical level), we also constructed there an energy-momentum element L, with respect to which the elements $J^{\{a_i\}}$ have conformal weight $1 - m_i$, where $[x ,a_i] = m^{}_{i} a^{}_{i}$, and this construction is again valid for an arbitrary datum satisfying property (1.5).

In [KW], Theorem 5.1(c), we found an explicit expression for L in terms of the elements $J^{(a_i)}$ and the neutral fermions in the case of minimal W-algebras, which allowed us to compute the FFR (1.6) for these W-algebras explicitly (see [KW], Theorem 5.2).

The main results of the present paper, valid for an arbitrary datum $(\mathfrak {g}, x,f,k)$ satisfying property (1.5), are Theorem 3.1, which gives an explicit expression of the element $J^{ \{ f \} }$ in terms of the elements $J^{(f)}$, $J^{(a)}$ with $a\in \mathfrak {g}_0$ and $\mathfrak {g}_{-1/2}$, and of neutral free fermions, and Theorem 3.2, which states that $L=-\frac{1}{k+h^\vee }J^{ \{ f \} }$, provided that $k \ne - h^{\vee }$. This leads to an explicit formula for the image of L under the FFR (1.6) for an arbitrary quantum affine W-algebra, attached to a good datum.

Our Theorem 3.2 assumes that $k\ne -h^\vee$, i.e. k is not critical, but the construction of the W-algebra and Theorem 3.1 hold for an arbitrary k. However the structure of the W-algebra $W^{-h^\vee }(\mathfrak {g},x,f)$ is dramatically different [FF1]. This W-algebra for $f=f_{pr}$ plays an important role in the geometric Langlands correspondence.

Throughout the paper the base field $\mathbb {F}$ is an algebraically closed field of characteristic 0.

2 The Complex $(\mathcal {C}^k(\mathfrak {g}, x, f), \,d_{(0)})$ and the W-Algebra $W^k (\mathfrak {g},x, f)$

First, recall the construction of vertex algebras $V^k (\mathfrak {g})$, $F^{\mathrm{ch}}$ and $F^{\mathop {\mathrm{ne}}\,}$. We shall use the very convenient language of non-linear Lie conformal superalgebras and $\lambda$-brackets [DSK].

Given a Lie superalgebra $\mathfrak {g}$ with an invariant supersymmetric bilinear form B, consider the $\mathbb {F}[\partial ]$-module $\mathbb {F}[\partial ] \otimes \mathfrak {g}$ with the following non-linear $\lambda$-bracket

$$\begin{aligned}{}[a^{}_{\lambda } b] = [a ,b] + \lambda B (a ,b) 1 , a ,b \in \mathfrak {g}, \end{aligned}$$

(2.1)

and the universal enveloping vertex algebra $V^{B} (\mathfrak {g})$ of this non-linear Lie conformal superalgebra. One often fixes such a bilinear form (. | .), lets $B (a ,b) = k (a | b)$, $k \in \mathbb {F}$, and uses the notation $V^k (\mathfrak {g}) = V^{B} (\mathfrak {g})$. Then $V^{k} (\mathfrak {g})$ is called the universal affine vertex algebra for $\mathfrak {g}$ of level k.

The vertex algebra F(A) of fermions based on the vector superspace A with a skewsupersymmetric bilinear form $< . , .>$ is defined as the universal enveloping vertex algebra of the $\mathbb {F}[\partial ]$-module $\mathbb {F}[\partial ] \otimes \mathfrak {g}$ with the non-linear $\lambda$-bracket

$$\begin{aligned}{}[a_{\lambda } b] = < a , b > 1, a ,b \in A . \end{aligned}$$

(2.2)

Given a datum $(\mathfrak {g},x , f, k)$ as described in the introduction, the associated homology complex $(\mathcal {C}^{k} (\mathfrak {g},x, f) ,d_{(0)})$ is constructed as follows. Let $A^{\mathrm{ch}} =\Pi ( \mathfrak {g}_{> 0} \oplus \mathfrak {g}^{*}_{> 0})$, where $\Pi$ stands for the reversal of parity, and define on it a skewsupersymmetric bilinear form $<. , .>^{\mathrm{ch}}$ by the pairing of the vector superspace $\Pi \mathfrak {g}_{>0}$ and its dual $\Pi \mathfrak {g}^{*}_{> 0}$, and let $A^{\mathop {\mathrm{ne}}\,} = \mathfrak {g}_{1/2}$ with the bilinear form $< a,b >^{\mathop {\mathrm{ne}}\,}$ defined by (1.4). Then $\mathcal {C}^{k} (\mathfrak {g},x, f)$ is the universal enveloping vertex algebra of the non-linear Lie confirmal superalgebra $\mathbb {F}[\partial ] (\mathfrak {g}\oplus A^{\mathrm{ch}} \oplus A^{\mathop {\mathrm{ne}}\,})$ with the $\lambda$-brackets defined by (2.1) and (2.2) on the summands and zero between the distinct summands. The vertex algebra $\mathcal {C}^k (\mathfrak {g},x, f)$ is isomorphic to $V^k (\mathfrak {g}) \otimes F^{\mathrm{ch}} \otimes F^{\mathop {\mathrm{ne}}\,}$, where $F^{\mathrm{ch}}=F(A^{\mathrm{ch}})$ and $F^{\mathop {\mathrm{ne}}\,}=F(A^{\mathop {\mathrm{ne}}\,})$. Letting

$$\begin{aligned} \deg V^k(\mathfrak {g}) = \deg F^{\mathop {\mathrm{ne}}\,} = 0 , \deg \mathfrak {g}_{> 0} = - \deg \mathfrak {g}^{*}_{> 0} = 1\,\, \hbox {on}\,\, F^{\mathrm{ch}}, \end{aligned}$$

(2.3)

defines a $\mathbb {Z}$-grading of this vertex algebra:

$$\begin{aligned} \mathcal {C}^{k} (\mathfrak {g},x, f) = \underset{j \in \mathbb {Z}}{\oplus } \, \mathcal {C}^{k}_{j}\, . \end{aligned}$$

(2.4)

In order to define the differential $d_{(0)}$ choose a basis $\{u_{i} \}^{}_{i \in S}$ of $\mathfrak {g}$, compatible with parity and the $\frac{1}{2} \mathbb {Z}$-grading (1.1), let $\{ u^i \}_{i \in S}$ be its dual basis of $\mathfrak {g}$ with respect to the bilinear form (.|.), i.e. $(u_i|u^j)=\delta _{i,j}$, and denote by $\{u_i \}^{}_{i \in S_{ > 0}}$ (resp. $\{ u_{i} \}_{i \in S_{j}}$) the part of $\{u_i\}_{i\in S}$, which is a basis of $\mathfrak {g}_{>0}$ (resp. $\mathfrak {g}_{j}$). Let $\{\varphi _{i} \}^{}_{i \in S_{ > 0}}$ be the corresponding to $\{u_{i} \}^{}_{i \in S_{>0}}$ basis of $\Pi \mathfrak {g}_{> 0}$, and let $\{\varphi ^{i} \}^{}_{i \in S_{ > 0}}$ be the dual basis of $\Pi \mathfrak {g}^{*}_{> 0}$. Let $\{\Phi _i\}_{{i \in S}_{1/2}}$ be the corresponding to $\{ u_{i} \}_{i \in S_{1/2}}$ basis of $A^{\mathop {\mathrm{ne}}\,}$. For $u \in \mathfrak {g}$ let $\Phi _{u} = {\sum }_{i \in S_{1/2}}$ $\gamma _{i} \Phi _{i}$ (resp. $\varphi _{u} = {\sum }_{i \in S_{> 0}} \gamma _{i} \varphi _{i}$) if $p_{1/2} u$ (resp. $p_{> 0}u$) $\gamma _{i} u_i$, where $\gamma _i\in \mathbb {F}$.

Introduce the following element of the vertex algebra $\mathcal {C}^{k} (\mathfrak {g},x, f)$:

$$\begin{aligned} d= & {} \underset{i \in S_{> 0}}{\sum } \big ((-1)^{p(i)} u_{i} \otimes \varphi ^{i} \otimes 1 + (f | u_{i}) \otimes \varphi ^{i} \otimes 1\big ) + \underset{i \in S_{1/2}}{\sum } 1 \otimes \varphi ^{i} \otimes \Phi _{i} \nonumber \\&+\frac{1}{2} \underset{i ,j \in S_{>0}}{\sum } (-1)^{p(i)} 1 \otimes : \varphi ^{i} \varphi ^{j} \varphi _{[u_j,u_i]}: \otimes 1, \end{aligned}$$

(2.5)

where p(i) stands for the parity $p(u_{i})$ in the Lie superalgebra $\mathfrak {g}$. The element d is independent of the choice of the basis of $\mathfrak {g}$. One checks that $[d_{\lambda } d] = 0$ ([KRW], Theorem 2.1), therefore $[d_{(0)} ,d_{(0)}] = 0$ and $d^{2}_{(0)} = 0$. Thus, $d_{(0)}$ is a homology differential of the vertex algebra $\mathcal {C}^{k} (\mathfrak {g},x, f)$. The homology of the complex $(\mathcal {C}^{k} (\mathfrak {g},x, f), d_{(0)})$ is the quantum affine W-algebra $W^{k} (\mathfrak {g},x, f)$.

One has the following formulas for the action of $d_{(0)}$ of the generators of the vertex algebra $\mathcal {C}^{k} (\mathfrak {g},x, f)$ (cf. [KRW], formula(2.4)), where $a \in \mathfrak {g}$, and thereafter we skip the tensor product signs:

$$\begin{aligned} d_{(0)} a= & {} \underset{j \in S_{> 0}}{\sum } \big ((-1)^{p (j)} :\varphi ^j [u_j,a]: + k(a|u_j)\partial \varphi ^j\big );\nonumber \\ d_{(0)} \varphi _a= & {} p_{> 0} (a) + (a|f) + (-1)^{p(a)} \Phi _{a} + \underset{j \in S_{> 0}}{\sum }: \varphi ^{j} \varphi _{[u_{j} ,p_{> 0} a]} :; \nonumber \\ d_{(0)} \varphi ^{i}= & {} - \frac{1}{2} \underset{j,s \in S_{> 0}}{\sum } (-1)^{p(i)p(j)}c_{j,s}^i :\varphi ^j \varphi ^s:, \,\,\hbox {where}\,\, [u_j,u_s]=\sum _i c_{j,s}^i u_i \ ; \nonumber \\ d_{(0)} \Phi _{a}= & {} \underset{j \in S_{1/2}}{\sum }(u_j|[a,f]) \varphi ^{j}. \end{aligned}$$

(2.6)

Recall that the “building blocks” for elements of the W-algebra $W^{k}(\mathfrak {g},x, f)$ are the following elements of $\mathcal {C}^{k}(\mathfrak {g},x, f)$ for $v\in \mathfrak {g}$:

$$\begin{aligned} J^{(v)} = v + \sum _{\begin{array}{c} j \in S_{> 0} \end{array}} (-1)^{p(v)+p(j)} : \varphi _{[v,u_j]}\varphi ^j :. \end{aligned}$$

(2.7)

Denote by $\mathcal {C}^k_- (\mathfrak {g},x, f)$ the subalgebra of the vertex algebra $\mathcal {C}^k (\mathfrak {g},x, f)$ , generated by the elements $J^{(v)}$ ($v\in S_{\le 0}$), $\varphi ^i$ ($i\in S_{>0}$), and $\Phi _i$ ($i\in S_{1/2}$). By (2.6), this subalgebra is $d_{(0)}$-invariant. Let, as above, $\overline{\mathcal {C}}^k (\mathfrak {g},x, f)$ be the subalgebra of $\mathcal {C}^k_- (\mathfrak {g},x, f)$, generated by the $J^{(v)}$ ($v\in S_{\le 0}$), and the $\Phi _i$ ($i\in S_{1/2}$). Then, by (2.6), we have

$$\begin{aligned} \overline{\mathcal {C}}^k (\mathfrak {g},x, f) \cap d_{(0)}\mathcal {C}^k_- (\mathfrak {g},x, f)=0. \end{aligned}$$

(2.8)

Let $\kappa (a ,b) = str_{\mathfrak {g}} (\mathop {\mathrm{ad}}\,a)(\mathop {\mathrm{ad}}\,b)$ be the Killing form on $\mathfrak {g}$. Recall that

$$\begin{aligned} \kappa (a,b)= 2h^\vee (a|b). \end{aligned}$$

(2.9)

For the projection $p_j : \mathfrak {g}\rightarrow \mathfrak {g}_j$ (resp $p_{>0}:\mathfrak {g}\rightarrow \mathfrak {g}_{> 0}$) along the grading (1.1), define the "partial" Killing forms

$$\begin{aligned} \kappa _{j} (a ,b) = \mathrm{str}_{\mathfrak {g}} (p_j (\mathop {\mathrm{ad}}\,a) (\mathop {\mathrm{ad}}\,b))\, (\hbox {resp.}\, \kappa _{> 0} (a ,b) = \mathrm{str}_{\mathfrak {g}} (p_{> 0} (\mathop {\mathrm{ad}}\,a) (\mathop {\mathrm{ad}}\,b)). \end{aligned}$$

(2.10)

Elements $J^{(v)}$ for $v \in \mathfrak {g}_0$ obey $\lambda$-brackets of the universal affine vertex algebra $V^{B_{0}} (\mathfrak {g}_{0})$ [KRW , Theorem 2.4(c)]:

$$\begin{aligned}{}[{J^{(a)}}_{\lambda } J^{(b)}] = J^{(a ,b)} + \lambda B_{0} (a ,b) , \ a ,b \in \mathfrak {g}_{0}, \end{aligned}$$

(2.11)

where

$$\begin{aligned} B_{0} (a ,b) = k(a | b) + \frac{1}{2} (\kappa (a ,b) - \kappa _{0} (a ,b)). \end{aligned}$$

(2.12)

In fact, (2.11) holds for $a \in \mathfrak {g}_{i}, \,b \in \mathfrak {g}_{j}$ with $ij \ge 0$ (of course $B_{0} (a ,b) = 0$ if $ij\ge 0$ and i or j is non-zero). Hence, we have the following

Corollary 2.1

The factor algebra of the vertex algebra $V^{B_{0}} (\mathfrak {g}_{\le 0})$ by the ideal, generated by $\mathfrak {g}_{<0}$, is isomorphic to the vertex algebra $V^{B_{0}} (\mathfrak {g}_ 0)$.

The proof of the following formula from [KW], formula (2.6), uses formulas (2.6):

$$\begin{aligned} d_{(0)} (J^{(v)})= & {} \sum _{j \in S_{>0}} ([f,v]|u_j) \varphi ^{j} + \sum _{ j \in S_{>0}} (-1)^{p(v)(p(j)+1)} :\varphi ^{j} \Phi _{p_{1/2}[v,u_{j}]}:\nonumber \\&\quad -\sum _{\begin{array}{c} j \in S_{>0}\\ {[}v,u_j{]} \in \mathfrak {g}_{\le 0} \end{array}} (-1)^{p(j) (p(v)+1)} : \varphi ^{j} J^{([v,u_{j}])} : + \sum _{j \in S_{>0}} (k(v|u_{j}) +\kappa _{>0} ( v, u_{j})) \partial \varphi ^j .\nonumber \\ \end{aligned}$$

(2.13)

From now on we shall assume that condition (1.5) holds, so that we can define the basis $\{\Phi ^i\}_{i\in S_{1/2}}$ of $A^{\mathop {\mathrm{ne}}\,}$, dual to $\{\Phi _i\}_{i\in S_{1/2}}$ with respect to the bilinear form (1.4). Then we have: $d_{(0)}\Phi ^i=\varphi ^i$.

As has been mentioned in the introduction, for a good grading the $d_{(0)}$-closed elements $J^{\{ a \}}$ are uniquely determined for $a \in \mathfrak {g}^{f}_{j}$ for $j = 0$ or $- 1/2$. The $d_{(0)}$-closed elements $J^{\{a \}}$ for $a \in \mathfrak {g}^{f}_{0}$ can be constructed, provided that (1.5) holds, and they are as follows (see [KRW], Theorem 2.4(a)):

$$\begin{aligned} J^{\{ a \}} = J^{(a)} \ + \frac{(-1)^{p (a)}}{2} \sum _{\begin{array}{c} j \in S_{1/2} \end{array}} : \Phi ^j \Phi _{[u_j ,a]} :. \end{aligned}$$

(2.14)

These elements obey $\lambda$-brackets of the universal affine vertex algebra $V^{B_{1/2}} (\mathfrak {g}^{f}_{0})$:

$$\begin{aligned}{}[{J^{\{a \}}}_{\lambda } J^{\{ b \}}] = J^{\{[a ,b] \}} + \lambda B_{1/2} (a ,b), \end{aligned}$$

(2.15)

where

$$\begin{aligned} B_{1/2} (a,b) = k (a|b) + \kappa _{> 0} (a,b) - \frac{1}{2} \kappa _{1/2} (a,b). \end{aligned}$$

(2.16)

The $d_{(0)}$-closed elements $J^{\{ v \}}$ for $v \in \mathfrak {g}^{f}_{-1/2}$ are as follows (see [KW] , Theorem 2.1(d)]):

$$\begin{aligned} J^{\{v \}}= & {} J^{(v)} - \frac{(-1)^{p(v)}}{3} \sum _{\begin{array}{c} i ,j \in S_{1/2} \end{array}} :\Phi ^{i} \Phi ^{j} \Phi _{[u_j,[u_{i},v]]}:\nonumber \\&+\underset{i \in S_{1/2}}{\sum }\big (:J^{([v, u_i])}\Phi ^i: -(k(v|u_i)+\kappa _{>0}(v,u_i))\partial \Phi ^i\big ), \end{aligned}$$

(2.17)

and one has ([KW], Theorem 2.1(e)):

$$\begin{aligned}{}[ {J^{\{ a \}}}_{\lambda } J^{\{v \}}] = J^{\{[a,v] \}} \ \ \hbox {if} \ \ a \in \mathfrak {g}^{f}_{0}, \,v \in \mathfrak {g}^{f}_{- 1/2}. \end{aligned}$$

(2.18)

Remark 2.1

The elements $\varphi ^i$ coincide with the elements, denoted by $\varphi _i^*$ in [KRW] and [KW], but are different from the elements, denoted by $\varphi ^i$ in [DSK]. The advantage of this less natural choice is that then the construction of the W-algebra $W^k(\mathfrak {g},x,f)$ works for an arbitrary finite-dimensional Lie superalgebra $\mathfrak {g}$ with an arbitrary supersymmetric (possibly degenerate) invariant bilinear form (.|.). (The simplicity of $\mathfrak {g}$ and the non-degeneracy of (.|.) are needed in the next sections.)

3 A Formula for $J^{\{f\}}$ and the Energy-Momentum Element L of $W^{k}(\mathfrak {g},x,f)$

Choose a Cartan subalgebra $\mathfrak {h}$ of $\mathfrak {g}_0$, containing a Cartan subalgebra of $\mathfrak {g}_0^f$. It is a Cartan subalgebra of $\mathfrak {g}$. Choose a set of positive roots of $\mathfrak {g}$, compatible with the grading (1.1). Recall that the dual Coxeter number $h^{\vee }$ of the simple Lie superalgebra $\mathfrak {g}$ with the given invariant bilinear form $(. \ | \ .)$ is the half of the eigenvalue of the Casimir operator $\sum _{j\in S} u^ju_j$ on $\mathfrak {g}$, and it is given by the formula

$$\begin{aligned} h^{\vee }\ = \ (\rho | \theta ) \ + \ \frac{1}{2} \ (\theta | \theta ) \ , \end{aligned}$$

(3.1)

where $\theta$ is the highest root and $\rho$ is the half of the difference between sums of positive even roots and positive odd roots. Provided that $k \ne - h^{\vee }$, the energy-momentum (or Virasaro) element of the vertex algebra $\mathcal {C}^{k} (\mathfrak {g},x, f)$ is defined by [KRW] for an arbitrary datum, satisfying (1.5):

$$\begin{aligned} L \ = \ L^{\mathfrak {g}} \ + \ \partial x \ + \ L^{\mathrm{ch}} \ + \ L^{\mathop {\mathrm{ne}}\,} , \end{aligned}$$

(3.2)

where

$$\begin{aligned} L^{\mathfrak {g}}= & {} \frac{1}{2 (k + h^{\vee })} \underset{j \in S}{\sum } \ : u^{j} u_{j} : , \\ L^{\mathrm{ch}}= & {} \underset{j \in S_{> 0}}{\sum } (1 - m_{j}) : (\partial \varphi ^{j}) \varphi _{j} : \ - \ m_{j} : \varphi ^{j} \partial \varphi _{j} : , \\ L^{ne}= & {} \frac{1}{2} \underset{j \in S_{1/2}}{\sum } \ : (\partial \Phi ^{j}) \Phi _{j} : , \end{aligned}$$

and the $m_{j}$ are defined by $[x ,u_{j}] = m_{j} u_{j}$.

The central charge of this Virasoro element is equal to (see [KRW], Remark 2.2)

$$\begin{aligned} c (\mathfrak {g},x ,k) \ = \mathop {\mathrm{sdim}} \, \mathfrak {g}_0 -\frac{1}{2}\mathop {\mathrm{sdim}} \, \mathfrak {g}_{1/2}- \frac{12}{k + h^\vee }|\rho -(k+h^\vee )x|^2. \end{aligned}$$

(3.3)

With respect to this L the elements $\varphi _{j}$ (resp. $\varphi ^{j}$) are primary of conformal weight $1 - m_{j}$ (resp. $m_{j}$), the $\Phi _{j}$ are primary of conformal weight 1/2, and $a \in \mathfrak {g}_{j}$ has conformal weight $1 - j$ and is primary, unless $j = 0$ and $(a | x) \ne 0$. Actually one has:

$$\begin{aligned}{}[L_\lambda a]=(\partial +\lambda )a -\lambda ^2 k(a|x)\,\, \hbox {for} \,\,a\in \mathfrak {g}_0. \end{aligned}$$

(3.4)

Furthermore, it was shown in [KRW] that the element d, defined by (2.5) is primary of conformal weight 1, hence $[d_{\lambda } L] = \lambda d$ and $d_{(0)} L = [d_{\lambda } L] |_{\lambda = 0} = 0$. Hence, the homology class of L defines an energy-momentum element of the vertex algebra $W^{k} (\mathfrak {g},x, f)$ , which is denoted again by L. Note that though, for a good datum, the W-algebra $W^{k} (\mathfrak {g},x, f)$ is independent, up to isomorphism, of the choice of x with given f [AKM], the element L does depend on x.

As has been mentioned in the introduction, the explicit expressions of the elements $J^{\{a\}}$ which generate the subalgebra $W^{k}(\mathfrak {g},x,f)$ of the vertex algebra ${\overline{\mathcal {C}}}^{k} (\mathfrak {g}, x, f)$, associated to a good datum, are known only for $a \in \mathfrak {g}_{-j}$, where $j = 0$ and $\frac{1}{2}$. In view of (1.6) it is important to find an explicit expression for $J^{\{ f \}}$. This is the first main result of the paper. The second main result is the formula $L=-\frac{1}{k+h^\vee }J^{\{f\}}$ in $W^k(\mathfrak {g},x,f)$. Both results hold for an arbitrary datum $(\mathfrak {g}, x,f,k)$, satisfying (1.5).

Let

$$\begin{aligned} \Omega _{0} \ = \ \underset{j \in S_{0}}{\sum } \ (\mathop {\mathrm{ad}}\,u^{j}) (\mathop {\mathrm{ad}}\,u_{j}). \end{aligned}$$

Proposition 3.1

The operator $\Omega _{0}$ is diagonalizable on $\mathfrak {g}_j$ for each $j> 0$.

Proof

Choose a Cartan subalgebra $\mathfrak {h}$ of $\mathfrak {g}_{0}$ ; it is a Cartan subalgebra of $\mathfrak {g}$, containing x. Choose a set of positive roots in $\mathfrak {h}^{*}$, compatible with the $\frac{1}{2} \mathbb {Z}$-grading (1.1), and let $e_{i} ,f_{i}$ be the Chevalley generators of $\mathfrak {g}$. Then for each $j>0$, the $\mathfrak {g}$-module $\mathfrak {g}_{j}$ is the sum of lowest weight modules with the lowest weight vectors that are commutators of the $e_{i}$, such that $e_{i}\in \mathfrak {g}_{>0}$. Since the restriction of $\Omega _{0}$ to each of these summands is diagonalizable, proposition follows. $\square$

Let $\rho _{> 0}$ (resp. $\rho _{j}$)$\in \mathfrak {h}^*=\mathfrak {h}$ be the half of the difference between the sums of positive even and positive odd roots of $\mathfrak {h}$ in $\mathfrak {g}_{> 0}$ (resp. $\mathfrak {g}_j$). (We idenitfy $\mathfrak {g}$ with $\mathfrak {g}^*$ using (.|.)).

Proposition 3.2

The element $\rho _{>0}$ lies in the center of $\mathfrak {g}_0$ if (1.5) holds.

Proof

Since $[{L^{\mathrm{ch}}}_\lambda J^{(a)}]=(\partial +\lambda )(J^{(a)}-a) +\lambda ^2(\rho _{>0}-h^\vee x|a)$ for $a\in \mathfrak {g}_0$, the Jacobi identity

$$\begin{aligned}{}[{J^{(a)}}_\lambda [{J^{(b)}}_\mu L]]-(-1)^{p(a)p(b)}[{J^{(b)}}_\mu [{J^{(a)}}_\lambda L]]=[[{J^{a)}}_\lambda J^{(b)}]_{\lambda +\mu } L],\,\, a,b\in \mathfrak {g}_0 \end{aligned}$$

is equivalent to the equation $0=-(\lambda +\mu )^2(\rho _{>0}|[a,b])$. Hence $([\rho _{>0},a]|b)=0$ for all $b\in \mathfrak {g}_0$. It follows that $[\rho _{>0},\mathfrak {g}_0]=0$. $\square$

Theorem 3.1

For the datum $(\mathfrak {g},x,f,k)$, satisfying (1.5), the following element of $\mathcal {C}^{k} (\mathfrak {g},x, f)$ is $d_{(0)}$-closed:

$$\begin{aligned} J^{\{ f \}} = J^{(f)} + \underset{j \in S_{1/2}}{\sum } (-1)^{p (j)} : \Phi ^{j} J^{([f , u_j])} : - \frac{1}{2} \underset{j \in S_0}{\sum } : J^{(u^j)} J^{(u_j)} :\\ - (k+h^\vee )\partial J^{(x)}+\partial J^{(\rho _{> 0} )} + \frac{k+h^\vee }{2} \underset{j \in S_{1/2}}{\sum } \ :\Phi ^{j} \ \partial \Phi _j: . \end{aligned}$$

Theorem 3.2

Assuming that the datum $(\mathfrak {g},x,f,k)$ satisfies (1.5), and that $k \ne -h^\vee$, the element $L + \frac{1}{k + h^\vee }J^{\{f\}}$ of $\mathcal {C}(\mathfrak {g},x,f)$ is $d_{(0)}$-exact. Consequently $L=-\frac{1}{k+h^\vee }J^{\{f\}}$ in $W^k(\mathfrak {g}, x,f)$.

As an immediate consequence of (2.11), (2.12), (2.14)–(2.17) and Theorems 3.1 and 3.2, we obtain the following corollary.

Corollary 3.1

Provided that the datum $(\mathfrak {g},x,f,k)$ is good and $k\ne -h^\vee$, one has a homomorphism of the vertex algebra $W^k (\mathfrak {g},x,f)$ to the vertex algebra $V^{B_{0}} (\mathfrak {g}_0) \otimes F^{\mathop {\mathrm{ne}}\,} (\mathfrak {g}_{1/2})$, such that

$$\begin{aligned}&J^{\{ a \}} \ \mapsto \ a \ + \ \frac{(-1)^{p(a)}}{2} \underset{j \in S_{1/2}}{\sum } :\Phi ^{j} \Phi _{[u_j ,a]}:\,\,\, \hbox {if}\,\,\, a \in \mathfrak {g}^{f}_{0} , \\&J^{\{ v \}} \ \mapsto \underset{i \in S_{1/2}}{\sum }:[v, u_i]\Phi ^i: - \frac{(-1)^{p(v)}}{3} \underset{i,j \in S_{1/2}}{\sum } : \Phi ^i \Phi ^j \Phi _{[u_j, [u_i ,v]]}: \\&\quad \qquad \qquad -\underset{i \in S_{1/2}}{\sum }\big (k(v|u_i)+\kappa _{>0}(v,u_i)\big )\partial \Phi ^i \,\,\, \hbox {if}\,\,\, v\in \mathfrak {g}^f_{-1/2} , \\&L \ \mapsto \ \frac{1}{k + h^\vee } \big (\frac{1}{2} \underset{j \in S_{0}}{\sum } : u^j u_j : \ + \ \partial ((k + h^\vee ) x - \rho _{>0})\big ) - \frac{1}{2} \underset{j \in S_{1/2}}{\sum } : \Phi ^j \partial \Phi _j: . \end{aligned}$$

Corollary 3.2

If $k=-h^\vee$, then $J^{\{f\}}$ is a central element of $W^k(\mathfrak {g}, x, f)$.

4 Proof of Theorem 3.1

Let U and V be finite-dimensional vector spaces over $\mathbb {F}$ with a non-degenerate even pairing $<.,.> : U \times V \xrightarrow {} \mathbb {F}$. Choose dual bases $\{ u_i \}_{i \in I}$ and $\{ u^i \}_{i \in I}$ of U and V respectively, i.e. $< u_i , u^j > = \delta _{ i , j}$. Then for any $A \in \mathop {\mathrm{End }}U$ and $B \in \mathop {\mathrm{End }}V$ we have:

$$\begin{aligned} \mathrm{str}_{U} A = \underset{i \in I}{\sum } (-1)^{p(i)}< A u_i , u^{i}> ,\,\, \mathrm{str}_{V} B = \underset{i \in I}{\sum } (-1)^{p(i)} < u_i , B u^i>, \end{aligned}$$

(4.1)

where, as before, p(i) stands for $p(u_i) (=p(u^i))$. This will be used to prove the following lemma.

Lemma 4.1

For $u, v \in \mathfrak {g}$ we have

$$\begin{aligned}&\kappa _{< 0} (u,v) = \kappa _{> 0} (u,v) - \mathrm{str}_{\mathfrak {g}{> 0}}\, p_{> 0} \mathop {\mathrm{ad}}\,[u,v], \end{aligned}$$

(4.2)

$$\begin{aligned}&\kappa _{> 0} (u,v) = \frac{1}{2} \big (\kappa (u,v) - \kappa _{0} (u,v) \ + \ \mathrm{str}_{\mathfrak {g}> 0} \,p_{> 0} \mathop {\mathrm{ad}}\,[u,v]\big ), \end{aligned}$$

(4.3)

$$\begin{aligned}&\kappa _{ 0} (u,v) = (\Omega _0 u | v) = (u | \Omega _0 v). \end{aligned}$$

(4.4)

Proof

We may assume that $(\mathop {\mathrm{ad}}\,u)(\mathop {\mathrm{ad}}\,v)$ preserves the $\frac{1}{2} Z$-grading (1.1) and that $p(u) = p(v)$. In order to prove (4.2), we use (4.1) with

$$\begin{aligned} U \ = \ \mathfrak {g}_{> 0} ,\, V = \mathfrak {g}_{< 0} ,\, <.,.> = ( .|. ),\, A =p_{>0} (\mathop {\mathrm{ad}}\,v)(\mathop {\mathrm{ad}}\,u), \,B =p_{>0} (\mathop {\mathrm{ad}}\,u)(\mathop {\mathrm{ad}}\,v). \end{aligned}$$

We have by the second and then the first formula in (4.1):

$$\begin{aligned}&\kappa _{< 0}(u,v) \ = \ \mathrm{str}_{\mathfrak {g}_{< 0}} B = \underset{i \in S_{>0}}{\sum } (-1)^{p(i)} (u_i | [u, [v,u^i] ]) \ = \ \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} ([ [u_i , u], v ] | u^i ) \\&\quad = \ (-1)^{p(u) p(v)} \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} \ ([v, [u, u_i]] | u^{i}) = (-1)^{p(u) p(v)} \mathrm{str}_{\mathfrak {g}_{> 0}} \ A \\&\quad = \ (-1)^{p(u)p(v)} \mathrm{str}_{\mathfrak {g}_{> 0}} \ \mathop {\mathrm{ad}}\,[v,u] \ + \ \mathrm{str}_{\mathfrak {g}_{> 0}} \ (\mathop {\mathrm{ad}}\,u )( \mathop {\mathrm{ad}}\,v) = - \mathrm{str}_{\mathfrak {g}_{> 0}} \mathop {\mathrm{ad}}\,[u,v] \ + \ \kappa _{> 0} (u,v). \end{aligned}$$

Formula (4.3) follows from (4.2) since $\kappa (u,v) = \kappa _{> 0} (u,v) + \kappa _0 (u,v) + \kappa _{< 0} (u,v)$. The proof of (4.4) is similar, by letting $U = V = \mathfrak {g}_0$, $A = (\mathop {\mathrm{ad}}\,u)(\mathop {\mathrm{ad}}\,v)$. $\square$

Lemma 4.2

Let, as before, $\{ u_i \}_{i \in S_{> 0}}$ be a basis of $\mathfrak {g}_{> 0}$ and $\{ u^i \}_{i \in S_{> 0}}$ the dual basis of $\mathfrak {g}_{< 0}$, i.e. $(u_i | u^j) = \delta _{i,j}$, and let $v \in \mathfrak {g}_0$. Then

$$\begin{aligned} \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} [u_i , u^i] = 2 \rho _{> 0}, \end{aligned}$$

(4.5)

$$\begin{aligned} \mathrm{str}_{\mathfrak {g}_{> 0}} \mathop {\mathrm{ad}}\,v = 2 (\rho _{>0} | v). \end{aligned}$$

(4.6)

Proof

Since the LHS is independent on the choice of dual bases, we may take for $\{ u_i \}_{i\in S_{>0}}$ the basis $\{ e_{\alpha } \}_{\alpha \in \Delta _{> 0}}$ of $\mathfrak {g}_{>0}$, so that the dual basis of $\mathfrak {g}_{<0}$ is $\{ e_{-\alpha } \}_{\alpha \in \Delta _{> 0}}$ with $(e_{\alpha } | e_{- \alpha }) = 1$, and hence $[e_{\alpha } , e_{- \alpha } ] = \alpha$. Then (4.5) follows.

For (4.6) we have:

$$\begin{aligned} \mathrm{str}_{\mathfrak {g}_{> 0}} \ \mathop {\mathrm{ad}}\,v \ = \ \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} ([v , u_i] | u^i) \ = \ \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} ( v | [u_i , u^i] ) = 2 (v | \rho _{> 0}) \end{aligned}$$

by (4.5). $\square$

Denote by I, II, ..., IV the operator $d_{(0)}$, applied to each of the six terms in the RHS of the formula for $J^{\{ f \}}$ in Theorem 3.1. We have to prove that the sum of these six elements of $\mathcal {C}^{k} (\mathfrak {g},x, f)$ is equal to 0.

By formula (2.13) for $v = f$, element I is equal to the sum of the following four elements:

$$\begin{aligned}&I_{A} = \underset{j\in S_{3/2}}{\sum } : \varphi ^{j} \Phi _{[f ,u_{i}]} : ,\,\, I_{B} = - \underset{j \in S_{1}}{\sum } (-1)^{p(j)} : \varphi ^{j} J^{([f ,u_{j}])}:, \end{aligned}$$

(4.7)

$$\begin{aligned}&I_{C} = - \underset{j \in S_{1/2}}{\sum } (-1)^{p(j)} : \varphi ^{j} J^{([f, u_{j}])} : , \,\,I_{D} = \underset{j \in S_{1}}{\sum } \big (k (f|u_{j}) + \kappa _{>0}(f,u_j)\big )\partial \varphi ^j.\nonumber \\ \end{aligned}$$

(4.8)

By (2.13) for $v = f$ and the last formula in (2.6), using that $d_{(0)}$ is an odd derivation of the vertex algebra $\mathcal {C}^{k}(\mathfrak {g},x, f)$, one obtains that element II is equal to the sum of the following five elements:

$$\begin{aligned}&II_{A} = \underset{j \in S_{1/2}}{\sum } (-1)^{p(j)} : \varphi ^{j} J^{([f ,u_j])} :, \,\, II_{B} = \underset{j \in S_{1/2}}{\sum }\ \underset{i \in S_{3/2}}{\sum } (f | [[f ,u_{j}] , u_{i}]) : \Phi ^{j} \varphi ^{i} :,\nonumber \\ \end{aligned}$$

(4.9)

$$\begin{aligned}&II_{C} = \underset{j \in S_{1/2}}{\sum } \ \underset{i \in S_{1}}{\sum } (-1)^{p(j) (p(i) + 1)} : \Phi ^{j} \varphi ^{i} \Phi _{[[f, u_{j}] , u_{i}]} : , \end{aligned}$$

(4.10)

$$\begin{aligned}&II_{D} = - \underset{i,j \in S_{1/2}}{\sum } (-1)^{p(i)(p(j)+1)} : \Phi ^{j} \varphi ^{i} J^{([[f,u_{j}],u_{i}])} :, \end{aligned}$$

(4.11)

$$\begin{aligned}&II_{E} = \underset{i,j \in S_{1/2}}{\sum } \big (k ([f,u_{j}]|u_{i}) + \kappa _{> 0} ([f,u_{j}],u_{i})\big ) : \Phi ^{j} \partial \varphi ^{i} :. \end{aligned}$$

(4.12)

It is easy to see that $I_{A} + II_{B} = 0$ , and since also $I_{C} + II_{A} = 0$ , we obtain

$$\begin{aligned} I + II = I_{B} + I_{D} + II_{C} + II_{D} + II_{E}. \end{aligned}$$

(4.13)

Lemma 4.3

One has

$\mathrm{(a)} II_{C} = 0.$

$\mathrm{(b)} II_{D} = \underset{i \in S_{1/2}}{\sum } \ \underset{k \in S_{0}}{\sum } : \Phi _{[u^{k} , u_{i}]} \varphi ^{i} \ J^{(u_{k})} : .$

Proof

By (4.10), using that

$$\begin{aligned} \Phi _{[[f,u_{j}],u_{k}]} = \underset{i \in S_{1/2}}{\sum } \langle u_{i} , [[f,u_{j}],u_{k}] \rangle ^{\mathop {\mathrm{ne}}\,} \Phi ^{i} , \end{aligned}$$

we obtain:

$$\begin{aligned} II_{C}= & {} \underset{i,j \in S_{1/2}}{\sum } \ \underset{k \in S_{1}}{\sum } (-1)^{p(j)(p(k) + 1)} \langle u_{i}, [[f,u_{j}],u_{k}] \rangle ^{\mathop {\mathrm{ne}}\,} : \Phi ^{j}\varphi ^k\Phi ^i: \\= & {} \underset{i,j \in S_{1/2}}{\sum } \underset{k \in S_{1}}{\sum } (-1)^{(p(i) + p(j)(p(k)+1)} \langle u_{i}, [[f,u_{j}],u_{k}] \rangle ^{\mathop {\mathrm{ne}}\,} : \Phi ^{j} \Phi ^{i} \varphi ^k: \\= & {} \underset{i,j \in S_{1/2}}{\sum } \ \underset{k \in S_{1}}{\sum } \ ([[f,u_{i}] , [f,u_{j}]] | u_{k}) : \Phi ^{j} \Phi ^{i} \varphi ^{k} : . \end{aligned}$$

If one exchanges i and j in the summation of the last expression, $II_{C}$ doesn’t change. On the other hand, looking at each summand in this expression, we see that it changes the sign, hence $II_{C} = - II_{C}$, proving (a).

By (4.11), using that, for $i , j \in S_{1/2}$,

$$\begin{aligned}{}[[f,u_{j}],u_{i}] = \underset{k \in S_{0}}{\sum } ([[f,u_{j}],u_{i}] | u^{k}) u_{k} , \end{aligned}$$

we obtain:

$$\begin{aligned} II_{D} = - \underset{i \in S_{1/2}}{\sum } \ \underset{k \in S_{0}}{\sum } (-1)^{p(i)p(k)} : \Phi _{[u_{i},u^{k}]} \varphi ^{i} J^{(u_{k})} : , \end{aligned}$$

proving (b). $\square$

Next, we treat the term III. For that introduce structure constants $c^{k}_{ij}$ and $c^{k}_{j} (v)$ for $i,j,k \in S_{> 0}$ and $v \in \mathfrak {g}_{0}$ by

$$\begin{aligned} {[}u_{i},u_{j}] = \underset{k}{\sum } c^{k}_{ij} u_{k},\,\, [v,u_{j}] = \underset{k}{\sum } c^{k}_{j} (v) u_{k}. \end{aligned}$$

Lemma 4.4

• (a) For $v \in \mathfrak {g}_{0}$ and $k \in S_{>0}$ one has:

  $$\begin{aligned}&\displaystyle [{\varphi ^{k}}_{\lambda } J^{(v)}] = \underset{j \in S_{> 0}}{\sum } c^{k}_{j} (v) \varphi ^{j} , \end{aligned}$$

  (4.14)
  $$\begin{aligned}&\displaystyle : \varphi ^{k} J^{(v)} : - (-1)^{p(v)(p(k)+1)} : J^{(v)} \varphi ^{k}:\, = \underset{j \in S_{> 0}}{\sum } c^{k}_{j} (v)\partial \varphi ^j . \end{aligned}$$

  (4.15)

• (b) For $u \in \mathfrak {g}_0, v\in \mathfrak {g}_{1/2}$ and $j \in S_{> 0}$ one has

  $$\begin{aligned}&{::} \Phi _{v} \varphi ^{j} : J^{(u)} {{:} {=} {:}} \Phi _{v} : \varphi ^{j} J^{(u)} {::} + \underset{k \in S_{> 0}}{\sum } c^{j}_{k} (u) : (\partial \Phi _{v}) \varphi ^k:, \end{aligned}$$

  (4.16)
  $$\begin{aligned}&{::} \varphi ^{j} \Phi _{v} : J^{(u)} {{:} {=} {:}} \varphi ^{j} : \Phi _{v} J^{(u)}{{:} {:}} + \underset{k \in S_{> 0}}{\sum } (-1)^{p(u)p(v)} c^{j}_{k} (u) : \varphi ^{k} \partial \Phi _{v} : . \end{aligned}$$

  (4.17)

Proof

It uses the $\lambda$-bracket calculus, see [K2, DSK]. Formula (4.14) follows by the non-commutative Wick formula, (4.15) by quasicommutativity, and (4.16) by quasiassociativity of a vertex algebra. As an example, we prove here (4.16). By quasiassociativity we have

$$\begin{aligned}&{::} \Phi _{v} \varphi ^{j} : J^{(u)} : - : \Phi _{v} : \varphi ^{j} J^{(u)} {{:} {:}} \\&\quad = (-1)^{p(u)(p(j)+1)} (\int ^{- \partial }_{0} : \Phi _{v} [{J^{(u)}}_{\lambda } \varphi ^{j}] d \lambda : - : \Phi _{v} \int ^{- \partial }_{0} [{J^{(u)}}_{\lambda } \varphi ^{j}] d \lambda :). \end{aligned}$$

Using (4.14), we obtain that the RHS is equal to

$$\begin{aligned}&- \underset{k \in S_{> 0}}{\sum } c^{j}_{k} (u) (\int ^{- \partial }_{0} : \Phi _{v} \varphi ^{k}: d \lambda - : \Phi _{v} \int ^{- \partial }_{0} \varphi ^{k} d \lambda :) \\&= \underset{k \in S_{> 0}}{\sum } c^{j}_{k} (u) (\partial : \Phi _{v} \varphi ^{k} : - : \Phi _{v} \partial \varphi ^{k} :) = \underset{k \in S_{> 0}}{\sum } c^{j}_{k} (u) : (\partial \Phi _{v}) \varphi ^k:, \end{aligned}$$

proving (4.16) $\square$

We have, by formula (2.13), for $i \in S_{0}$:

$$\begin{aligned} d_{(0)} J^{(u_i)} \ = \underset{j \in S_{1}}{\sum } (f | [u_{i},u_{j}]) \varphi ^{j} + \underset{j \in S_{1/2}}{\sum } (-1)^{p(i)(p(j)+1)} : \varphi ^{j} \Phi _{[u_i, u_j]}:. \end{aligned}$$

It follows that

$$\begin{aligned} d_{(0)} \underset{i \in S_{0}}{\sum } : J^{(u^{i})} \ J^{(u_{i})} : = A_{1} + A_{2} + A_{3} + A_{4} , \end{aligned}$$

(4.18)

where

$$\begin{aligned}&A_{1} = \underset{i \in S_{0}}{\sum } \ \underset{j \in S_{1}}{\sum } (f | [u^{i},u_{j}]) : \varphi ^{j} J^{(u_{i})} : , \end{aligned}$$

(4.19)

$$\begin{aligned}&A_{2} = \underset{i \in S_{0}}{\sum } \ \underset{j \in S_{1/2}}{\sum } (-1)^{p(i)(p(j)+1)} {{:} {:}} \varphi ^{j} \Phi _{[u^{i},u_{j}]} : J^{(u_{i})} : , \end{aligned}$$

(4.20)

$$\begin{aligned}&A_{3} = \underset{i \in S_{0}}{\sum } \ \underset{j \in S_{1}}{\sum } (-1)^{p(i)} (f | [u_{i},u_{j}]) : J^{(u^{i})} \varphi ^{j} : , \end{aligned}$$

(4.21)

$$\begin{aligned}&A_{4} = \underset{i \in S_{0}}{\sum } \ \underset{j \in S_{1/2}}{\sum } (-1)^{p(i)} (-1)^{p(i)(p(j)+1)} : J^{(u^{i})} \varphi ^{j} \Phi _{[u_{i},u_{j}]} :. \end{aligned}$$

(4.22)

In order to simplify expressions for those elements, recall the operator $\Omega _{0}$, defined by (3.4). By Proposition 3.1, this operator is diagonalizable in $\mathfrak {g}_{j}$. Hence we can choose $u_{i} \in \mathfrak {g}_{1/2}$ (resp. $\mathfrak {g}_{1})$ to be eigenvectors of $\Omega _{0}$ ; denote by $a_{i}$ (resp. $b_{i}$) the corresponding eigenvalues.

We have by (4.16):

$$\begin{aligned} A_{2} {=} \underset{i \in S_{0}}{\sum } \ \underset{j \in S_{1/2}}{\sum } (-1)^{p(i)(p(j)+1)} {:} \varphi ^{j} \Phi _{[u^{i},u_{j}]} J^{(u_{i})} {:} + \underset{k \in S_{1/2}}{\sum } \ \underset{i \in S_{0}}{\sum } \ \underset{j \in S_{1/2}}{\sum } c^{j}_{i,k} {:}\varphi ^k \partial \Phi _{[u^{i},u_{j}]}:. \end{aligned}$$

The first sum in this expression is equal to

$$\begin{aligned} A^{'}_{2} = \underset{i \in S_{0}}{\sum } \ \underset{j \in S_{1/2}}{\sum } : \Phi _{[u^{i},u_{j}]} \varphi ^{j} J^{(u_{i})} : , \end{aligned}$$

(4.23)

while the second sum is equal to

$$\begin{aligned} \underset{k \in S_{1/2}}{\sum } : \varphi ^{k} \underset{i \in S_{0}}{\sum } \ \ \partial \Phi _{[u^{i},[u_{i},u_{k}]]} : . \end{aligned}$$

Hence we obtain

$$\begin{aligned} A_{2} = A^{'}_{2} + \underset{k \in S_{1/2}}{\sum } a_{k} : \varphi ^{k} \partial \Phi _{k}: . \end{aligned}$$

(4.24)

Next, we obtain, using (2.6), (4.14) and (4.21),

$$\begin{aligned} A_{3} = A_{1} - \underset{k \in S_{1}}{\sum }\underset{i \in S_{0}}{\sum } \underset{j \in S_{1}}{\sum } c_{i,k}^j(f|[u^i, u_j])\partial \varphi ^k, \end{aligned}$$

hence

$$\begin{aligned} A_{3} = A_{1} - \underset{k \in S_{1}}{\sum } b_{k} (f|u_{k}) \partial \varphi ^{k}, \end{aligned}$$

(4.25)

since

$$\begin{aligned} \underset{j \in S_{1}}{\sum } c_{i,k}^j(f|[u^i, u_j])=(f|\Omega _0(u_k)). \end{aligned}$$

Finally, for $A_{4}$, given by (4.22), we have, using (4.15) and (4.23):

$$\begin{aligned} A_{4} = A^{'}_{2} - \underset{k \in S_{1/2}}{\sum } a_{k} : (\partial \varphi ^{k}) \Phi _{k} : . \end{aligned}$$

(4.26)

From (4.18)–(4.26) we obtain that the element III is equal to the sum of the four elements

$$\begin{aligned}&III_{A} = - \underset{i \in S_{0}}{\sum } \ \underset{j \in S_{1}}{\sum } (f | [u^{i},u_{j}]) : \varphi ^{j} J^{(u_{i})} : , \end{aligned}$$

(4.27)

$$\begin{aligned}&III_{B} = - \underset{i \in S_{0}}{\sum } \ \underset{j \in S_{1/2}}{\sum } : \Phi _{[u^{i},u_{j}]} \varphi ^{j} J^{(u_{i})}:, \end{aligned}$$

(4.28)

$$\begin{aligned}&III_{C} = \frac{1}{2} \underset{j \in S_{1}}{\sum } b_{j} (f | u_{j}) \partial \varphi ^{j} , \end{aligned}$$

(4.29)

$$\begin{aligned}&III_{D} = \frac{1}{2} \underset{j \in S_{1/2}}{\sum } a_{j} \big (:(\partial \varphi ^{j})\Phi _{j} : - : \varphi ^{j} \partial \Phi _{j} : \big ). \end{aligned}$$

(4.30)

We have:

$$\begin{aligned} III_{A} = \underset{j \in S_{1}}{\sum } (-1)^{p(j)} : \varphi ^{j} \underset{i \in S_{0}}{\sum } ([f,u_{j}|u^i]) J^{(u_{i})} : , \end{aligned}$$

hence, by (4.7),

$$\begin{aligned} III_{A} = - I_{B}. \end{aligned}$$

(4.31)

Using Lemma 4.3(b), we obtain

$$\begin{aligned} II_{D} = - III_{B}. \end{aligned}$$

(4.32)

Hence, by (4.13) and Lemma 4.3, we have

$$\begin{aligned} I + II + III = I_{D} + II_{E} + III_{C} + III_{D}. \end{aligned}$$

(4.33)

Next, we have

$$\begin{aligned} I_D + III_C= & {} \underset{j \in S_1}{\sum } \big ((k + h^\vee )(f|u_j) + (\rho _{>0}|[f,u_j])\big ) \partial \varphi ^j, \end{aligned}$$

(4.34)

$$\begin{aligned} II_E + III_D= & {} (k + h^\vee ) \underset{i \in S_{1/2}}{\sum } : \Phi _i \partial \varphi ^i : \ - \frac{1}{2} \underset{i \in S_{1/2}}{\sum } : (\partial \Phi _{\Omega _{0} u_{i}}) \varphi ^i : \nonumber \\&+ \underset{i \in S_{1/2}}{\sum } : \Phi _{[u_{i}, \rho _{> 0}]} \partial \varphi ^i : . \end{aligned}$$

(4.35)

Indeed, by (4.8) and (4.29), we have, using (4.3) and (2.9):

$$\begin{aligned} I_D + III_C \ {=} \ \underset{j \in S_1}{\sum } \big ((k + \frac{1}{2} b_j) (f|u_j) + h^\vee (f|u_j) {-} \frac{1}{2} \kappa _0 (f,u_j) {+} \frac{1}{2} \mathrm{str}_{\mathfrak {g}_{> 0}} \mathop {\mathrm{ad}}\,[f,u_j]\big ) \partial \varphi ^j. \end{aligned}$$

Applying (4.4) and (4.6) to the RHS, we obtain (4.34).

In order to prove (4.35), we rewrite (4.30) as follows:

$$\begin{aligned} III_D= & {} \frac{1}{2} \underset{k \in S_{1/2}}{\sum } \big (: (\partial \varphi ^k) \Phi _{\Omega _0 u_k} : - : \varphi ^k \partial \Phi _{\Omega _{0} u_{k}} :\big ) \\= & {} \frac{1}{2} \underset{k \in S_{1/2}}{\sum } \big (: \Phi _{\Omega _0 u_k} \partial \varphi ^k: - : (\partial \Phi _{\Omega _0 u_k}) \varphi ^k :\big ). \end{aligned}$$

We also rewrite (4.12), using (4.3), (4.4) and (4.6), as follows:

$$\begin{aligned} II_E \ = \ (k + h^\vee ) \ \underset{i \in S_{1/2}}{\sum } : \Phi _i \partial \varphi ^i : - \frac{1}{2} \underset{i \in S_{1/2}}{\sum } : \Phi _{\Omega _0 u_i} \partial \varphi ^i : + \underset{i \in S_{1/2}}{\sum } : \Phi _{[u_i , \rho _{> 0}]} \partial \varphi ^i : . \end{aligned}$$

Adding up these two expressions, we get (4.35).

Lemma 4.5

One has

$$\begin{aligned} \Omega _0 (u) \ = \ 2 [\rho _{> 0} , u] \,\,\, \hbox {for}\,\,\, u \in \mathfrak {g}_{1/2}. \end{aligned}$$

Proof

Since elements I, II, III lie in the image of $d_{(0)}$ and $d^{2}_{(0)} = 0$ , we obtain, using (4.33):

$$\begin{aligned} 0 \ = \ d_{(0)} (I_D \ + \ III_C) \ + \ d_{(0)} (III_E \ + \ III_D). \end{aligned}$$

Substituting here (4.34) and (4.35) and using formulas (2.6) for the action of $d_{(0)}$ , we obtain:

$$\begin{aligned} 0 \ = \underset{i, j \in S_{1/2}}{\sum } (-1)^{p(i)} < u_j , \frac{1}{2} \Omega _0 (u_i) - [\rho _{> 0} , u_i]>^{\mathop {\mathrm{ne}}\,} : \varphi ^i \partial \varphi ^j : . \end{aligned}$$

Due to the non-degeneracy of the bilinear form $< .,. >^{\mathop {\mathrm{ne}}\,}$, the lemma follows. $\square$

Finally, we treat the remaining three elements IV, V, and VI. Using (2.13), we obtain:

$$\begin{aligned}&IV = - (k + h^\vee ) \underset{j \in S_1}{\sum } \ (f|u_j) \partial \varphi ^j \ - \frac{k+h^\vee }{2} \underset{j \in S_{1/2}}{\sum } \partial : \Phi _j \varphi ^j : , \end{aligned}$$

(4.36)

$$\begin{aligned}&V = - \underset{j \in S_1}{\sum } (\rho _{> 0} | [f , u_j]) \partial \varphi ^j + \underset{j \in S_{1/2}}{\sum } \partial :\Phi _{[\rho _{> 0} , u_j]} \varphi ^j:. \end{aligned}$$

(4.37)

Using (2.6), we obtain

$$\begin{aligned} VI = \frac{k+h^\vee }{2} \underset{j \in S_{1/2}}{\sum } ( : \varphi ^j \partial \Phi _j : - : \Phi _j \partial \varphi ^j : ). \end{aligned}$$

(4.38)

Adding up (4.36)–(4.38), we obtain

$$\begin{aligned} \begin{array}{l} IV + V + VI = - (k + h^\vee ) \underset{j \in S_1}{\sum } (f | u_j) \partial \varphi ^j - \underset{j \in S_1}{\sum } (\rho _{> 0} | [f , u_j]) \partial \varphi ^j \\ - (k + h^\vee ) \underset{j \in S_{1/2}}{\sum } : \Phi _j \partial \varphi ^j : + \underset{j \in S_{1/2}}{\sum } \partial : \Phi _{[\rho _{> 0} , u_j]} \varphi ^j:. \end{array} \end{aligned}$$

(4.39)

Adding up (4.33) and (4.39), and using (4.34), (4.35) and Lemma 4.5, we conclude that $d_{(0)} J^{\{ f \}} \ = \ 0$, completing the proof of Theorem 3.1.

5 Proof of Theorem 3.2

First, introduce the following convenient notation. Let $\mathfrak {a}$ (resp. $\mathfrak {a}$’) be the sum of some $\mathfrak {g}_{j}$’s (resp. the remaining $\mathfrak {g}_{j}$’s) in (1.1). Then we let $\delta _{u,\mathfrak {a}} = 1$ (resp. 0 ) if $u \in \mathfrak {a}$ (resp. $\mathfrak {a}$’). Then we have for u , $v \in \mathfrak {g}$:

$$\begin{aligned}&\underset{i \in S_{> 0}}{\sum } ( u_{i} | v ) u^{i} \ = \ \delta _{v, \mathfrak {g}_{< 0}} v \text{; } \,\, \underset{i \in S_{> 0}}{\sum } ( v | u^{i} ) u_{i} \ = \ \delta _{v, \mathfrak {g}_{> 0}}v; \end{aligned}$$

(5.1)

$$\begin{aligned}&\underset{i \in S_{> 0}}{\sum } (u | u^{i}) (u_{i} | v) \ = \ \delta _{u , \mathfrak {g}_{> 0}} (u | v) \ = \ \delta _{v , \mathfrak {g}_{< 0}} (u | v); \end{aligned}$$

(5.2)

$$\begin{aligned}&\underset{i \in S_{> 0}}{\sum } ( u | u^{i} ) ( v | u_{i} ) \ = \ \delta _{u , \mathfrak {g}_{> 0}} ( v | u ) \ = \ \delta _{v , \mathfrak {g}_{< 0}} ( v | u ). \end{aligned}$$

(5.3)

Similar formulas hold if we replace $S_{> 0}$ by $S_{0}$ , and $\mathfrak {g}_{> 0}$ and $\mathfrak {g}_{< 0}$ by $\mathfrak {g}_{0}$ ; these formulas will be denoted by (5.1)’ , (5.2)’ and (5.3)’.

Next, let $v^{\mathrm{ch}}$ denote the second summand on the right in (2.7). Then

$$\begin{aligned} v^{\mathrm{ch}} \ = \ \underset{i,j \in S_{> 0}}{\sum } (-1)^{p(i)} ([v , u_{j}] | u^{i} ) :\varphi _{i} \varphi ^{j}: \ . \end{aligned}$$

(5.4)

Next, by condition (1.5), we have

$$\begin{aligned} u^{i} \ = \ [ u^{(i)} , f ] ,\,\, i \in S_{1/2} \ , \end{aligned}$$

(5.5)

where the $\{ u^{(i)} \}_{i \in S_{1/2}}$ is a basis of $\mathfrak {g}_{1/2}$ , dual to $\{ u_{i} \}_{i \in S_{1/2}}$ with respect to the bilinear form (1.4).

Next, by the quasiassociativity of the normally ordered product, we have for $i ,j ,k ,l \in S_{> 0}$

$$\begin{aligned}&{{:} {:}} \,\varphi _i \varphi ^j : \varphi _k : \ = \ : \varphi _i \varphi ^j \varphi _k : \ + \ (-1)^{p(j)} \delta _{j ,k} \partial \varphi _{i} \ ; \end{aligned}$$

(5.6)

$$\begin{aligned}&{{:} {:}}\, \varphi _i \varphi ^j : \varphi _k : \ = \ : \varphi _i \varphi ^j \varphi ^k : \ + \ (-1)^{(p(i) +1)(p(j) + 1)} \delta _{i ,k} \partial \varphi ^{j} \ ; \end{aligned}$$

(5.7)

$$\begin{aligned}&\ {{:} {:}}\, \varphi _i \varphi ^j {{:} {:}}\, \varphi _k \varphi ^l {{:} {:}} \ = \ : \varphi _i \varphi ^j \varphi _k \varphi ^l : \ + \ (-1)^{p(k)} \delta _{j ,k} :( \partial \varphi _i) \varphi ^l : \nonumber \\&\quad - \ (-1)^{p(j)p(k)} (-1)^{p(i)(p(j)+p(k))} \delta _{i ,l} : \varphi _{k} \partial \varphi ^j : \ . \end{aligned}$$

(5.8)

Lemma 5.1

We have, using (5.4):

$$\begin{aligned}&\underset{i \in S_0}{\sum } : u^i (u_i)^\mathrm{ch}: = \underset{i, j \in S_{> 0}}{\sum } (-1)^{p(i)} : p_0 ([u_j , u^i]) \varphi _i \varphi ^j : = \underset{i \in S_{0}}{\sum } : (u^{i})^\mathrm{ch}u_i : ; \end{aligned}$$

(5.9)

$$\begin{aligned}&\underset{i \in S_{0}}{\sum } : (u^i)^\mathrm{ch}(u_i)^\mathrm{ch}: = \underset{i, j, k, l \in S_{> 0}}{\sum }(-1)^{p(i)+p(k)} ([u_l , u^k ] | p_0 [u_j , u^i]) : \varphi _i \varphi ^j \varphi _k \varphi ^l : \nonumber \\&\quad + \underset{\underset{[u_{k} , u^{i}] \in \mathfrak {g}_{0}}{i ,j ,k \in S_{> 0}}}{\sum } \ (-1)^{p(i)} (u_{j} | [ u^k , [ u_k , u^i ] ]) ( :( \partial \varphi _i) \varphi ^j : - : \varphi _i \partial \varphi ^j :). \end{aligned}$$

(5.10)

Proof

Using the invariance of the bilinear form (. | .) and (5.1)’, we obtain

$$\begin{aligned} \underset{i \in S_{0}}{\sum } : u^i ( u_i )^\mathrm{ch}: = \underset{j ,k \in S_{> 0}}{\sum } (-1)^{p(j)} : p_0 ([ u_k , u^j ]) \varphi _{j} \varphi ^{k} : \ , \end{aligned}$$

which is the first equality in (5.9) after replacing indices j, k by i, j . The proof of the second equality in (5.9) is the same.

Using the invariance of the bilinear form (. | .) and (5.2)’, we obtain

$$\begin{aligned} \underset{i \in S_{0}}{\sum } : (u^i)^\mathrm{ch}(u_i)^\mathrm{ch}: = \underset{j ,k ,r ,s \in S_{> 0}}{\sum } (-1)^{p(j) + p(r)} ([u_s , u^r] | p_0 [u_k , u^j])\ {{:} {:}}\ \varphi _j \varphi ^k \ {{:} {:}}\ \varphi _{r} \varphi ^{s}\ {::} \ . \end{aligned}$$

Using (5.8), we see that this is equal to

$$\begin{aligned}&= \underset{j, k, r, s \in S_{> 0}}{\sum } (-1)^{p(j) + p(r)} ([u_s , u^r ] \ | \ p_{0} [u_k , u^j]) : \varphi _j \varphi ^k \varphi _{r} \varphi ^{s} : \\&\quad + \underset{j, k, s \in S_{> 0}}{\sum } (-1)^{p(j)} ([u_s , u^k] | p_0 [u_k , u^j] ) : (\partial \varphi _j) \varphi ^s : \\&\quad - \underset{j, k, s \in S_{> 0}}{\sum } (-1)^{p(j)} (u_s | [u^k , p_0 [u_k , u^j] \ ] ) : \varphi _j \partial \varphi ^s : \ . \end{aligned}$$

In the last term we used the invariance of (. | .) and relabeling of indices; we also used that $(a|b) \ne 0$ implies that $p(a) = p(b)$ in order to simplify the sign. Now (5.10) easily follows. $\square$

Lemma 5.2

Recalling that $[u_i , u_j] = \underset{k}{\sum } c^{k}_{ij} u_{k}$ for $i, j, k \in S_{> 0}$ , we have

$$\begin{aligned}&\underset{i, j, k, \in S_{> 0}}{\sum } (-1)^{p(i) + p(k)} c^{k}_{ij} :\varphi _k\varphi ^ju^i: = \underset{i ,j \in S_{> 0}}{\sum } (-1)^{p(i)} : p_{< 0} ([u_j , u^i]) \varphi _i \varphi ^j : \ ,\nonumber \\ \end{aligned}$$

(5.11)

$$\begin{aligned}&\underset{i, k \in S_{> 0}}{\sum } (-1)^{p(i)} : [u_k , u^i] \varphi _i \varphi ^k : - \underset{i, j, k \in S_{> 0}}{\sum } (-1)^{p(i) + p(k)} c^{k}_{ij} : \varphi _k \varphi ^j u^i : \end{aligned}$$

(5.12)

$$\begin{aligned} = \underset{i, j \in S_{> 0}}{\sum } (-1)^{p(i)} : p_{\ge 0} ([u_j , u^i]) \varphi _i \varphi ^j : \ . \end{aligned}$$

Proof

Using that $c^{k}_{ij} = ([u_i , u_j] | u^k)$, that the bilinear form $(. \ | \ .)$ is invariant, equation (5.1), and that $p(i) + p(k) \ = \ p(j)$ if $c^{k}_{ij}\ne \ 0$, we obtain :

$$\begin{aligned} \underset{i,j,k \in S_{> 0}}{\sum } (-1)^{p(i) + p(k)} c^{k}_{ij} : \varphi _k \varphi ^j u^i : = \underset{j,k \in S_{> 0}}{\sum } (-1)^{p(j)} : \varphi _k \varphi ^j p_{< 0} [u_j , u^k] : , \end{aligned}$$

from which (5.11) follows.

By (5.11), the LHS of (5.12) is equal to

$$\begin{aligned} (\underset{i,j \in S_{> 0}}{\sum } \ - \ \underset{\underset{[u_{j} , u^{i}] \in \mathfrak {g}_{< 0}}{i , j \in S_{> 0}}}{\sum }) (-1)^{p(i)} :[u_j,u^i] \varphi _i \varphi ^j : . \end{aligned}$$

Formula (5.12) follows. $\square$

Lemma 5.3

The expression

$$\begin{aligned} A_{< 0} \ = \ \underset{i, j, k, l \in S_{> 0}}{\sum } (-1)^{p(i) + p(k)} ([u_l , u^k] | p_{< 0}[u_j , u^i]) : \varphi _i \varphi ^j \varphi _k \varphi ^l : \end{aligned}$$

is equal to $\frac{1}{2} A_{\ne 0}$, where $A_{\ne 0}$ is obtained from $A_{< 0}$ by replacing $p_{< 0}$ by $p_{\ne 0}$ .

Proof

Exchanging i with k and j with l in $A_{< 0}$ , we obtain

$$\begin{aligned} A_{< 0} \ = \ \underset{i, j, k, l}{\sum } (-1)^{p(i) + p(k)} ([u_l , u^k] \ | \ p_{> 0}[u_j , u^i]) : \varphi _i \varphi ^j \varphi _k \varphi ^l : . \end{aligned}$$

Adding the two expressions for $A_{< 0}$, we obtain $A_{\ne 0}$. $\square$

From (5.4) we obtain

$$\begin{aligned} f^{\mathrm{ch}} \ = \ \underset{i, j \in S_{> 0}}{\sum } (-1)^{p(i)} (f | [u_j , u^i]) : \varphi _i \varphi ^j : . \end{aligned}$$

(5.13)

Lemma 5.4

We have

$$\begin{aligned} \underset{i \in S_{1/2}}{\sum } (-1)^{p(i)} : \Phi ^{i} [f , u_i]^{\mathrm{ch}} : = \underset{i, j \in S_{> 0}}{\sum } (-1)^{p(j)} : \Phi _{[u_j , u^i]} \varphi _i \varphi ^j: . \end{aligned}$$

Proof

Substituting in the LHS the expression (5.4) for $v = [f , u_i]$, we obtain, by invariance of (. | .) and (1.4) ,

$$\begin{aligned}&\underset{i \in S_{1/2}}{\sum } \underset{j, k \in S_{> 0}}{\sum } (-1)^{p(i) + p(k)} \ \langle u_i , [ u_j , u^k ] \rangle ^{\mathop {\mathrm{ne}}\,} : \Phi ^{i}\varphi _{k} \varphi ^j : \\&= \underset{j, k, \in S_{> 0}}{\sum } (-1)^{p(j)} \underset{i \in S_{1/2}}{\sum } \langle u_i , [ u_j , u^k ] \rangle ^{\mathop {\mathrm{ne}}\,} : \Phi ^{i} \varphi _{k} \varphi ^{j} : \\&= \underset{j, k \in S_{> 0}}{\sum } (-1)^{p(j)} : \Phi _{[ u_j , u^k ]} \varphi _k \varphi ^j : , \end{aligned}$$

proving the lemma. $\square$

Lemma 5.5

Let

Then

$$\begin{aligned} ( k + h^\vee ) L = d_{(0)} ( \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} : \varphi _i u^i : ) + P_0 . \end{aligned}$$

(5.14)

Proof

By (3.2) we have

$$\begin{aligned} ( k + h^\vee ) L = \frac{1}{2} \underset{j \in S}{\sum } : u^j u_j : + ( k + h^\vee ) \partial x + ( k + h^\vee ) L^{\mathrm{ch}} + ( k + h^\vee ) L^{\mathop {\mathrm{ne}}\,} . \end{aligned}$$

(5.15)

Choosing, as usual, dual bases $\{ h_i \}$ and $\{ h^i \}$, $i = 1 , \cdots , l$, of $\mathfrak {h}$ and root vectors $\{ e_\alpha \}_{\alpha \in \Delta _{+}}, \{ e_{-\alpha } \}_{\alpha \in \Delta _{+}}$ of $\mathfrak {g}$, where $( e_\alpha | e_{- \alpha }) = 1$, we obtain, using quasicommutativity of the normally ordered product, that the first term in the RHS of (5.15) is

$$\begin{aligned} \underset{\alpha \in \Delta _{+}}{\sum } (-1)^{p(\alpha )} : e_{\alpha } e_{ - \alpha } : + \frac{1}{2} \sum ^{l}_{i = 1} h^i h_{i} - \partial \rho= & {} \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} : u_i u^i : \nonumber \\&+ \frac{1}{2} \underset{i \in S_{0}}{\sum } : u^i u_i : - \partial \rho _{> 0} . \end{aligned}$$

(5.16)

We also have

$$\begin{aligned} \partial x^{\mathrm{ch}} = \underset{i \in S_{>0}}{\sum } (-1)^{p(i)} \ m_i \ \partial ( : \varphi _i \varphi ^i :) \ . \end{aligned}$$

(5.17)

Using (5.16) and (5.17), equation (5.15) can be rewritten as follows:

$$\begin{aligned} \begin{aligned}&( k + h^\vee ) L = \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} : u_i u^i : + \frac{1}{2} \underset{i \in S_{0}}{\sum } : u^i u_i : - \partial \rho _{> 0} \\&\qquad + ( k + h^\vee )\partial J^{(x)} - ( k + h^\vee ) \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} : \varphi _i \partial \varphi ^i : + \frac{ k + h^{\vee } }{2} \underset{i \in S_{1/2}}{\sum } : (\partial \Phi ^i) \Phi _i : \ . \end{aligned}\nonumber \\ \end{aligned}$$

(5.18)

Next, we compute $d_{(0)} (: \varphi _i u^i : )$, $i \in S_{> 0}$, using (2.6) and that $d_{(0)}$ is an odd derivation of the normally ordered product:

$$\begin{aligned}&d_{(0)} ( : \varphi _{i} u^{i} : ) = : u_{i} u^{i} : + \underset{j , k \in S_{> 0}}{\sum } (-1)^{p(k)} c^{k}_{i j} : \varphi _{k} \varphi ^{j} u^{i} : + ( f | u_{i} ) u^i \\&\qquad + (-1)^{p(i)} : \Phi _{u_i} [u^{(i)} , f] : - k : \varphi _{i} \partial \varphi ^{i} : - \underset{k \in S_{> 0}}{\sum } : [ u_k , u^i ] \varphi _i \varphi ^k : \ . \end{aligned}$$

We have used for the 3-rd term in the RHS that $(f | u_i ) = 0$ if $p(i) \ne 0$, and formula (5.5) for the 4-th term. It follows that

$$\begin{aligned}&\underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} d_{(0)} ( : \varphi _{i} u^{i} : ) {=} \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} {:} u_i u^i {:} + \underset{i , j , k \in S_{> 0}}{\sum } (-1)^{p(i) {+} p(k)} c^{k}_{i , j} {:} \varphi _{k} \varphi ^{j} u^{i} :\nonumber \\&\quad + f \ - \underset{i \in S_{1/2}}{\sum } (-1)^{p(i)} : \Phi ^{i} [ u_i , f ] : \nonumber \\&\quad - \underset{i , k \in S_{> 0}}{\sum } (-1)^{p(i)} : [ u_k , u^i ] \varphi _i \varphi ^k : - k \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} : \varphi _i \partial \varphi ^i : \ . \end{aligned}$$

(5.19)

We have used for the 3-rd term in the RHS that $f = \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} ( f | u_{i}) u^i$ , and for the 4-th term that

$$\begin{aligned} -\underset{i \in S_{1/2}}{\sum } (-1)^{p(i)} : \Phi ^i [ u_i , f ] : = \underset{i \in S_{1/2}}{\sum } (-1)^{p(i)} d_{(0)} ( : \varphi _i u^i : ). \end{aligned}$$

Therefore $(k+h^\vee )L - \sum _{i\in S_{>0}}(-1)^{p(i)}d_{(0)}(:\varphi _iu^i:)$ is the difference of the right hand sides of equations (5.18) and (5.19), which is $P_{0}$. $\square$

Lemma 5.6

We have

$$\begin{aligned} P_0 \ = - J^{ \{ f \} } + P_1 \ , \end{aligned}$$

where

Consequently, by (5.14), we have

$$\begin{aligned} (k + h^{\vee }) L + J^{ \{ f \}} \ \equiv \ P_1 \mod \mathop {\mathrm{Im}} \, d_{(0)} . \end{aligned}$$

(5.20)

Proof

First, we compute, using Lemma 5.1,

$$\begin{aligned}&\underset{i \in S_{0}}{\sum } : J^{(u^i)} J^{(u_i)} : \ = \underset{i \in S_0}{\sum } : u^i u_i : +2 \underset{i , j \in S_{> 0}}{\sum } (-1)^{p(i)} : p_0 ([u_j , u^i]) \varphi _i \varphi ^j : \nonumber \\&\quad + \underset{i,j,k, \ell \in S_{> 0}}{\sum } (-1)^{p(i) + p(k)} ([ u_{\ell } , u^k ] | p_0 [ u_j , u^i ]) : \varphi _i \varphi ^j \varphi _k \varphi ^{\ell } : \nonumber \\&\quad + \underset{i,j, k \in S_{> 0}}{\sum } (-1)^{p(i)} (u_j | [ u^k , p_0 [u_k , u^i]]) (: \partial \varphi _i \varphi ^j : - : \varphi _i \partial \varphi ^j :) . \end{aligned}$$

(5.21)

Hence, for $P_0$, defined in Lemma (5.5), and $J^{ \{ f \}}$, defined in Theorem 3.1, we have

$$\begin{aligned} P_0 + J^{ \{ f \} } \ = A , \end{aligned}$$

(5.22)

where

$$\begin{aligned} A= & {} (f^{\mathrm{ch}} + \underset{i \in S_{1/2}}{\sum } (-1)^{p(i)} : \Phi ^i [f , u_i]^{\mathrm{ch}} : ) + \frac{1}{2} \underset{i \in S_{0}}{\sum } (: u^i u_i : - : J^{(u^{i})} J^{(u_i)} : ) \nonumber \\&+ \underset{i ,j \in S_{> 0}}{\sum } (-1)^{p(i)} (\rho _{> 0}| [u_j , u^i] ) \partial : \varphi _i \varphi ^j: - h^{\vee } \underset{i \in S_{> 0}}{\sum } (-1)^{p(i)} : \varphi _i \partial \varphi ^i : \nonumber \\&+ \underset{i , j \in S_{> 0}}{\sum } (-1)^{p(i)} : p_{\ge 0} ([u_j , u^i]) \varphi _i \varphi ^j: . \end{aligned}$$

(5.23)

Here we used Lemma 5.4 for the first term, formula (5.21) for the second term and formula (5.12) for the last term.

From (5.23) it is straightforward to deduce that $A = P_1$. This completes the proof of Lemma 5.6. $\square$

Lemma 5.7

Let

Then

$$\begin{aligned} P_2 \ = P_1 - \frac{1}{2} d_{(0)} \underset{i ,j \in S_{> 0}}{\sum }(-1)^{p(j)} : \varphi _{[u_{i} , u^{j}]} \varphi _j \varphi ^i : . \end{aligned}$$

Consequently, by (5.20), we have

$$\begin{aligned} (k + h^{\vee }) L + J^{ \{ f \} } \ \equiv \ P_2 \mod \mathop {\mathrm{Im}} \, d_{(0)} . \end{aligned}$$

Proof

It is similar to that of Lemma 5.6, and therefore is omitted . $\square$

Lemma 5.8

Let

$$\begin{aligned} \varphi = \underset{i ,j \in S_{>0} }{\sum } (a_{ij} : (\partial \varphi _i) \ \varphi ^j : \ + b_{ij} \ : \varphi _i \ \partial \varphi ^j :) , \end{aligned}$$

where $a_{ij} , b_{ij} \in \mathbb {F}$.

Then $d_{(0)} \varphi = 0$ implies that $\varphi = 0$.

Proof

It is clear from (2.6). $\square$

Now it is easy to complete the proof of Theorem 3.2. By Lemma 5.7, $(k + h^{\vee }) L + J^{ \{ f \} } \ \equiv \ P_2 \mod \mathop {\mathrm{Im}} \, d_{(0)}$ , where $d_{(0)} P_2 = 0$ since $d_{(0)} L = 0 = d_{(0)} J^{ \{ f \} }$. But $P_2$ has the form of $\varphi$ in Lemma 5.8, hence $P_2 \ = 0$.

6 Examples

6.1 Minimal W-algebras

Let $\theta \in \mathfrak {h}^* =\mathfrak {h}$ be the highest root for some ordering of roots of the Lie superalgebra $\mathfrak {g}$. The W-algebra $W^{k} (\mathfrak {g}, \theta /2, e_{-\theta })$ is called a minimal W-algebra [KRW, KW] if the $\frac{1}{2} \mathbb {Z}$-grading (1.1) has the form

$$\begin{aligned} \mathfrak {g}= \oplus _{j = -1}^{1} \mathfrak {g}_{j} ,\, \text {where} \ \mathfrak {g}_{-1} = \mathbb {F} e_{- \theta } . \end{aligned}$$

In this case $f = e_{- \theta }$ lies in the non-zero nilpotent orbit of minimal dimension in one of the simple components of $\mathfrak {g}_{\overline{0}}$. Conversely, if f lies in the non-zero orbit of minimal dimension in a simple component of $\mathfrak {g}_{\overline{0}}$, then the corresponding W-algebra is a minimal W-algebra in all cases, except when $\mathfrak {g}=osp(3|n)$ and the simple component of $\mathfrak {g}_{\overline{0}}$ is $so_3$. Minimal W-algebras were studied in detail in [KRW] and [KW].

Obviously, for a minimal W-algebra, $\rho _{1} = x$, and it follows from [KW], formulas (5.6), (5.10), that $\rho _{1/2} = (h^{\vee } - 2)x$. Hence,

$$\begin{aligned} \rho _{> 0} \ = \ (h^{\vee } - 1)x. \end{aligned}$$

(6.1)

Therefore, $\rho _{> 0} - (k + h^{\vee })x \ = \ -(k + 1)x$, and the FFR, given by Corollary 3.1, coincides with that, given by [KW], Theorem 5.2.

6.2 Principal W-algebras

Let $\{e_*, \rho ^\vee , f_*\}$ be a principal $sl_2$-triple, where

$x = \rho ^{\vee }$ is the half of the sum of positive coroots of $\mathfrak {g}_{\overline{0}}$. Then the datum $(\mathfrak {g}, \rho ^\vee , f_*, k)$ is a Dynkin datum. The corresponding W-algebra $W^{k} (\mathfrak {g}, \rho ^{\vee }, f_*)$ is called the principal W-algebra, associated to $\mathfrak {g}$.

If $\mathfrak {g}$ is a Lie algebra, then $\mathfrak {g}_{\pm 1/2} = 0$ and $\mathfrak {g}_0 = \mathfrak {h}$, and therefore

$$\begin{aligned} \rho _{> 0} = \rho \, (\in \mathfrak {h}^{*} = \mathfrak {h}) ,\,\,\hbox {and}\,\, \mathfrak {g}^{f_*}_0=0, \end{aligned}$$

(6.2)

where $\rho$ is the half of the sum of positive roots of $\mathfrak {g}$. Hence the FFR in this case is a homomorphism $W^{k} (\mathfrak {g}, \rho ^{\vee }, f_*) \rightarrow V^{B_{0}} (\mathfrak {h})$, for which

$$\begin{aligned} L \ \mapsto \ \frac{1}{2(k + h^{\vee })} \underset{j \in S_{0}}{\sum } : u^{j} u_{j} : + \partial \rho ^\vee - \frac{1}{k+h^\vee }\partial \rho . \end{aligned}$$

(6.3)

The principal W-algebras for arbitrary simple Lie algebras were first constructed in [FF].

The element 2x is determined by its Dynkin labels $2\alpha _i(x),\, i=1,...,\mathrm{rank}\,\mathfrak {g}$, which are known to take values 0, 1, and 2. In the case when $\mathfrak {g}$ is a simple Lie algebra all the Dynkin labels of $2\rho ^\vee$ are equal to 2.

Let now $\mathfrak {g}$ be a basic Lie superalgebra, which is not a Lie algebra. Then $\mathfrak {g}$ may have several non-isomorphic sets of simple roots, and the Dynkin diagrams, corresponding to the choices of positive roots, compatible with the grading (1.1) may be different. Below we list the Dynkin labels $2\alpha _i(\rho ^\vee ),\, i=1,..., \mathrm{rank}\, \mathfrak {g}$, for all basic Lie superalgebras $\mathfrak {g}$, which are not Lie algebras. For exceptional Lie superalgebras $\mathfrak {g}$ they can be found in [H2]. We use notation for basic Lie superalgebras and their Dynkin diagrams from [K1].

I.:

$A(m, n), \,m > n \ge 0$, $m - n = 2k + 1$, $k \in \mathbb {Z}_ {\ge 0}$:

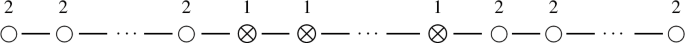
where the number of white nodes at the beginning and the end is equal to k, and the number of grey nodes is $2(n + 1)$.

II.:

$A(m, n),\, m > n \ge 0$, $m - n = 2k$, $k \in \mathbb {Z}_{\ge 1}$:

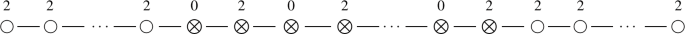
where the number of white nodes at the beginning (resp. end) is equal to k (resp. $k - 1$), and the number of grey nodes is $2 (n + 1)$ .

III.:

$A (m, m),\, m \ge 1$:

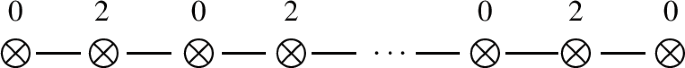
In all cases I–III the total number of nodes is $m + n + 1$ .

IV.:

$B (m, n),\, m \ge 0, \, n \ge 1$:

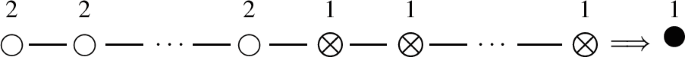
where the number of white nodes is $m - n$ if $m \ge n$, and is $n - m - 1$ if $m \ge n - 1$; the total number of nodes is $m + n$.

V.:

$C(n) \, , \, n \, \ge \, 3$:

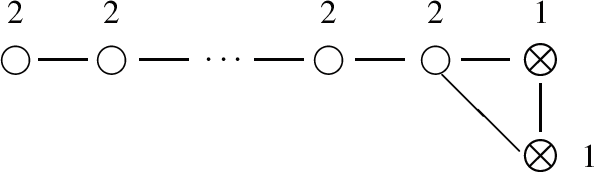
where the number of white nodes is $n - 2$.

VI.:

$D (m, n),\, \, m \ge 2 , \, n \ge 1$:

where the number of white nodes is $m - n - 1$, if $m \ge n +1$, and is $n - m$ if $m \le n$; the total number of nodes is $m + n$

VII.:

D(2, 1; a):

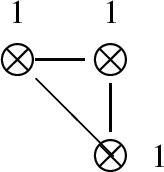
where the simple roots are $\{ \epsilon _{1} + \epsilon _{2} + \epsilon _{3} \, , \, \epsilon _{1} - \epsilon _{2} - \epsilon _{3} \, , \, - \epsilon _{1} - \epsilon _{2} + \epsilon _{3} \}$.

VIII.:

F(4):

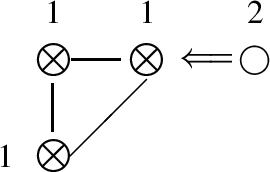
where the simple roots are $\{ \frac{1}{2} (\delta + \epsilon _{1} - \epsilon _{2} - \epsilon _{3}), \frac{1}{2} (\delta - \epsilon _{1} + \epsilon _{2} + \epsilon _{3}), \, \frac{1}{2} (- \delta + \epsilon _{1} - \epsilon _{2} + \epsilon _{3}), \, \epsilon _{2} - \epsilon _{3} \}$.

IX.:

G(3):

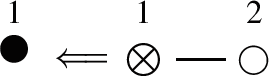
where the simple roots are $\{ \delta , - \delta + \epsilon _{1}, \, \epsilon _{2} - \epsilon _1 \}$.

Looking at these diagrams, we see that for all basic Lie superalgebras $\mathfrak {g}$, except for A(m, n) with $m-n$ even, which we shall exclude from consideration, the $\frac{1}{2}\mathbb {Z}$-grading (1.1), corresponding to the principal nilpotent element, is defined by

$$\begin{aligned} \alpha _i(\rho ^\vee )=1\,\, (\hbox {resp}=\frac{1}{2})\,\,\hbox {if}\,\, \alpha _i\, \,\hbox {is even (resp. odd)}, \end{aligned}$$

where $\alpha _i$, $i=1,...,\mathrm{rank}\,\mathfrak {g}$, are simple roots.. Hence this grading is compatible with the parity and $\mathfrak {g}_0=\mathfrak {h}$. It follows that (6.2) still holds. Furthermore, $\mathfrak {g}_{1/2}$ (resp. $\mathfrak {g}_{-1/2}$) is a purely odd space, spanned by the $e_{\alpha _i}$ (resp. $e_{-\alpha _i}$), where the $\alpha _i$ are all odd simple roots. The element $f\in \mathfrak {g}_{-1}$ can be chosen as follows. Let $f^0$ (resp. $f^1$) be the sum of all $e_{-\alpha _i}$ with $\alpha _i$ even (resp. odd); then

$$\begin{aligned} f=f^0 + [f^1,f^1]. \end{aligned}$$

Remark 6.1

It is probably impossible to write down a complete FFR of an arbitrary W-algebra, with explicit expressions for all elements beyond those of conformal weight 1, $\frac{3}{2}$, and L. However, in many cases (including the minimal one) the W-algebra $W^k(\mathfrak {g}, x,f)$ is generated by elements of conformal weight 1 and $\frac{3}{2}$ (this happens, for example, when $\mathfrak {g}^f_{-1/2}$ generates $\mathfrak {g}^f_{<0}$). In such cases formulas (2.14) and (2.17) can be extended to the complete FFR of this W-algebra.

Appendices

Appendix A. A more Conceptual Proof of Theorem 3.2 for Dynkin Datum

The proof uses the following properties of the Dynkin datum:

• (i) the restriction of the bilinear form $(. \ | \ .)$ to $\mathfrak {g}^{f}_{0}$ is non-degenerate;

• (ii) (even part of $\mathfrak {g}_{-1}$) $\cap$ (center of $\mathfrak {g}^{f}$) $= \mathbb {F} f$;

• (iii) $\mathfrak {g}_0^{f}$ is a direct sum of an abelian Lie algebra, basic Lie superalgebras, and gl(n|n) with $n\ge 1$;

• (iv) $(\mathfrak {g}_0^{f}|x)=0$.

Properties (i) and (iv) obviously hold. Property (ii) holds by the Brylinski-Kostant Theorem [BK, P] in the Lie algebra case, and its analogue in the Lie superalgebra case, which follows from [H1] and [H2]. Property (iii) for classical (resp. exceptional) basic Lie superalgebras holds by [Ho] (resp. [H1].

Lemma 7.1

Let L be the element of $\mathcal {C}^k (\mathfrak {g}, x, f)$, given by (3.1), and let $L^{'} = - \frac{1}{k + h^{\vee }} \ J^{\{ f \}}$ , where $J^{\{ f \}}$ is an element of $\mathcal {C}^k (\mathfrak {g}, x, f)$ given by Theorem 3.1. Let $a \in \mathfrak {g}^{f}_{0}$ and $J^{\{ a \}} \in \mathcal {C}^k (\mathfrak {g}, x, f)$ be defined by (2.14). Then

• (a) $[L_\lambda J^{\{ a \}}] = (\partial + \lambda ) J^{\{ a \}} + \lambda ^2 (\rho _{> 0} | a)$.

• (b) $[L^{'}_{\lambda } J^{\{ a \}}] = (\partial + \lambda ) J^{\{ a \}} + \lambda ^{2} (\rho _{> 0} | a)$.

Proof

From (2.11) and (2.14) we deduce

$$\begin{aligned}{}[{J^{\{ a \}}}_{\lambda } J^{(v)}] = J^{([a,v])} + \lambda B_{0} (a,b),\, a \in \mathfrak {g}^{f}_{0},\, v \in \mathfrak {g}_{\le 0} . \end{aligned}$$

(7.1)

Using (2.14) we obtain

$$\begin{aligned}{}[{J^{\{ a \}}}_\lambda \Phi _{u}] = (-1)^{p(a)} \Phi _{[a,u]},\, a \in \mathfrak {g}^{f}_{0},\, u \in \mathfrak {g}_{1/2}. \end{aligned}$$

(7.2)

From (7.1) and (7.2) we deduce, by making use of the non-commutative Wick formula, for $a \in \mathfrak {g}^{f}_{0}$, $i \in S_{0}$, $j \in S_{1/2}$:

$$\begin{aligned}&[{J^{\{ a \}}}_{\lambda } : J^{(u^{i})} J^{(u_{i})} :] =\, : J^{([a,u^{i}])} J^{(u_{i})} : + (-1)^{p(a)p(i)} : J^{(u^{i})} J^{([a,u_{i}])} : \\&{+} (-1)^{p(i)} \lambda J^{([u_{i}, [u^{i},a]])} {+} \lambda (B_{0} (a,u^{i}) J^{(u_{i})} {+} ({-}1)^{p(i)} B_{0} (a,u_{i}) J^{(u^{i})} ){+} \frac{1}{2} \lambda ^{2} B_{0} (a , [u^{i} , u_{i}]) , \\&[{J^{\{ a \}}}_{\lambda } : \Phi ^{j} \partial \Phi _{j} : ] \ = \ (-1)^{p (a) (p (j) + 1)}\lambda : \Phi ^{j} \Phi _{[a, u_{j}]} : + \frac{1}{2} (-1)^{p(a)} \lambda ^{2} \ \langle [a, u^{j}] , u_{j} \rangle ^{\mathop {\mathrm{ne}}\,} \\&+(-1)^{p(a)} \underset{i \in S_{1/2}}{\sum }(<u_i,[a,u^{(j)}]>^{\mathop {\mathrm{ne}}\,}:\Phi ^i\partial \Phi _j:-<u_j,[a,u^{(i)}]>^{\mathop {\mathrm{ne}}\,} :\Phi ^j\partial \Phi _i:), \\&[{J^{\{ a \}}}_{\lambda } {:} \Phi ^{j} J^{([f, u_{j}])} : ] {=} (-1)^{p(a)} \ : \Phi _{[a, u^{j}]} J^{([f, u_{j}])} : {+} (-1)^{p(a)p(j)} \ {:} \Phi ^{j} J^{([a, [f, u_{j}]])} : . \end{aligned}$$

Summing up both sides of the first formula over $i \in S_{0}$, the second and third formula over $j \in S_{1/2}$, we obtain the following three formulas for $a \in \mathfrak {g}^{f}_{0}$:

$$\begin{aligned}&\underset{i \in S_{0}}{\sum } [{J^{\{ a \}}}_{\lambda } : J^{(u^{i})} J^{(u_{i})} : ] = 2 (k + h^{\vee }) \lambda J^{(a)} , \end{aligned}$$

(7.3)

$$\begin{aligned}&\underset{j \in S_{1/2}}{\sum } [{a^{\mathop {\mathrm{ne}}\,}} _\lambda : \Phi ^{j} \partial \Phi _{j} : ] = -2 \lambda a^{\mathop {\mathrm{ne}}\,}, \end{aligned}$$

(7.4)

where $a^{\mathop {\mathrm{ne}}\,}$ is the secind term on the right in (2.14) ,

$$\begin{aligned} \underset{j \in S_{1/2}}{\sum } [{J^{\{ a \}}}_{\lambda } (-1)^{p(j)} : \Phi ^{j} J^{([f, u_{j}])} : ] = 0 . \end{aligned}$$

(7.5)

Using (7.1), we obtain

$$\begin{aligned}{}[{J^{\{ a \}}}_{\lambda } J^{(f)}] = 0 = [{J^{\{ a \}}}_{\lambda } J^{(x)}] \ \text {for} \, a \in \mathfrak {g}^{f}_{0}. \end{aligned}$$

(7.6)

Using Proposition 3.2,

we obtain from (7.1):

$$\begin{aligned}{}[{J^{\{ a \}}}_\lambda J^{(\rho _{> 0})}] = \lambda (k + h^{\vee })(a |\rho _{> 0}) . \end{aligned}$$

(7.7)

Now we can complete the proof of the lemma. Formula (a) is straightforward by the discussion in Sect. 3, cf. (3.4). Below we shall prove (b). We have for $a \in \mathfrak {g}^{f}_{0}$:

$$\begin{aligned}&[{J^{\{ a \}}}_{\lambda } J^{\{ f \}}] = [{J^{\{ a \}}}_{\lambda } J^{(f)}] + \ \underset{i \in S_{1/2}}{\sum } (-1)^{p(i)} [{J^{\{ a \}}}_{\lambda } : \Phi ^{i} J^{([f, u_{i}])} : ] \\&- \frac{1}{2} \underset{i \in S_{0}}{\sum } [{J^{\{ a \}}}_{\lambda } : J^{(u^{i})} J^{(u_{i})} : ] - (k + h^{\vee }) [{J^{\{ a \}}}_{\lambda } \partial J^{(x)}] \\&+ [{J^{\{ a \}}}_{\lambda } \ \partial J^{(\rho _{> 0})}] + \frac{1}{2} (k + h^{\vee }) \underset{i \in S_{1/2}}{\sum } [{J^{\{ a \}}}_{\lambda } : \Phi ^{i} \partial \Phi _{i} :]. \end{aligned}$$

The first and the fourth terms on the right are equal to 0 by (7.6), and the second term equals 0 by (7.5). The third term equals $-(k + h^{\vee }) \lambda J^{(a)}$ by (7.3). The fifth term equals $\lambda ^{2} (k + h^{\vee }) (a | \rho _{> 0})$ by (7.7). The sixth term equals $-(k + h^{\vee }) \lambda a^{\mathop {\mathrm{ne}}\,}$ by (7.4). Thus, we have :

$$\begin{aligned}{}[{J^{{\{ f \}}}}_{\lambda } J^{\{ a \}}]= & {} - [{J^{\{ a \}}}_{- \partial - \lambda } J^{\{ f \}}] = - (k + h^\vee ) (\partial + \lambda ) J^{\{ a \}} - \lambda ^2 (k + h^\vee ) (a | \rho _{> 0}) \\= & {} \ - (k + h^{\vee }) ((\partial + \lambda ) J^{\{ a \}} + \lambda ^{2} (a | \rho _{> 0}) ), \end{aligned}$$

proving formula (b). Here we have used property (iv) of a Dynkin data. $\square$

Remark 7.1

The same proof shows that Lemma 7.1 holds for arbitrary grading (1.1), satisfying (1.5), if we replace the coefficient of $\lambda ^2$ by $(\rho _{>0}|a)-(k+h^\vee )(x|a)$.

Lemma 7.2

Let M be an element of confirmal weight 2 (with respect to L), which lies in the subalgebra of $\mathcal {C}^{k} (\mathfrak {g}, x, f)$, generated by the elements $J^{\{ a \}}$, $a \in \mathfrak {g}^{f}_{0}$. Suppose that

$$\begin{aligned}{}[{J^{\{ a \}}}_{\lambda } M] = 0\,\, \hbox {for all}\,\,\, a \in \mathfrak {g}^{f}_{0}. \end{aligned}$$

(7.8)

Then $M = 0$.

Proof

By property (iii) of a Dynkin datum, the subalgebra of $\mathcal {C}^{k} (\mathfrak {g}, x, f)$ generated by the elements $J^{\{ a \}} , a \in \mathfrak {g}^{f}_{0}$, is the affine vertex algebra $V^{B_{1/2}} (\mathfrak {g}^{f}_{0})$ (see (2.15), (2.16)), associated to the Lie superalgebra $\mathfrak {g}^f_0$, which is a direct sum of its center, some basic Lie superalgebras and Lie superalgebras $gl(n|n), n\ge 1$, and a non-degenerative bilinear form on it, for all, but finitely many values of k.. Therefore, for all, but finitely many values of k, this vertex algebra carries the Sugawara element, with respect to which all elements $J^{\{ a \}}$, $a \in \mathfrak {g}^{f}_{0}$, have conformal weight 1 (see e.g. [K2]); for gl(n|n) we use the modification of the Sugawara construction, discussed in Appendix B. Hence, the center of $V^{B_{1/2}} (\mathfrak {g}^{f}_{0})$ consists of the multiples of the vacuum vector. Since condition (7.8) implies that M is a central element of $V^{B_{1/2}} (\mathfrak {g}^{f}_{0})$, we conclude that $M = 0$ for all, but finitely many k, hence for all k. $\square$

Now we can complete the proof of Theorem 3.2. Since L has conformed weight 2 (hereafter conformal weight is meant with respect to L), by [KW], Theorem 4.1(a), L is $d_{(0)}$-equivalent to an element of the form

$$\begin{aligned} J^{\{ f^{'} \}} \ = \ J^{(f^{'})} \ + \ M_{1} , \end{aligned}$$

(7.9)

where $f^{'} \in \mathfrak {g}^{f}_{-1}$ and $M_{1}$ lies in the subalgebra of $\mathcal {C}^k(\mathfrak {g}, x, f)$ generated by the $J^{(a)}$ with $a \in \mathfrak {g}_{0} + \mathfrak {g}_{-1/2}$ and the $\Phi _{i}, i \in S_{1/2}$ . Let $v \in \mathfrak {g}^{f}$ and let $J^{\{ v \}} \in \overline{\mathcal {C}}^{k} (\mathfrak {g}, x, f)$ be an element, given by [KW], Theorem 4.1(a). Since $J^{\{ f^{'} \}}$ is $d_{(0)}$-equivalent to L, we have in $W^{k} (\mathfrak {g}, x, f)$

$$\begin{aligned}{}[{J^{\{ f^{'} \}}}_{\lambda } J^{\{ v \}}] \ = \ \partial J^{\{ v \}} \ + \ O (\lambda ). \end{aligned}$$

(7.10)

But, due to (2.8), equation (7.10) is an equality in $\overline{\mathcal {C}}^{k} (\mathfrak {g}, x, f)$. It is easy to conclude from (7.9), using (2.11) (which can be used since $f^{'} \in \mathfrak {g}_{-1}$ and $v \in \mathfrak {g}_{\le 0}$), that we have the following equality in $\overline{\mathcal {C}}^{k} (\mathfrak {g}, x, f)$:

$$\begin{aligned}{}[{J^{\{ f^{'} \}}}_{\lambda } J^{\{ v \}}] \ = \ J^{\{ [f^{'} , v] \}} + A + B + O (\lambda ), \end{aligned}$$

(7.11)

where A is a linear combination of elements of the form $\sum \ : \partial ^{i_{1}} J^{(v_{1})} \dots \partial ^{i_{n}} J^{(v_{n})}:$ with $n \ge 2$ or $i_{1} \ + \dots + i_{n} \ge 1$, and B is a linear combination of normally ordered products, involving the $\Phi _{i}$. Comparing (7.10) and (7.11), we conclude that

$$\begin{aligned}{}[f^{'} , \mathfrak {g}^{f}] = 0. \end{aligned}$$

Hence, by condition (ii), we have

$$\begin{aligned} f^{'} = \gamma f \ \text {for some} \ \gamma \in \mathbb {F} . \end{aligned}$$

Therefore, L - $\gamma J^{(f)}$ is a sum of normally ordered products of elements of $\overline{\mathcal {C}}^{k} (\mathfrak {g}, x, f)$ of conformal weight $< 2$. It follows that, for $J^{\{ f \}}$ from Theorem 3.1, we have

$$\begin{aligned} L \ - \ \gamma J^{\{ f \}} \ = \ M , \end{aligned}$$

(7.12)

where M is a $d_{(0)}$-closed element of conformal weight 1. Hence, by [KW], Theorem 4.1(b) , M is a linear combination of elements of the form : $J^{\{ a \}} J^{\{ b \}}$: and $\partial J^{\{ c \}}$ , where $a, \ b, \ c \ \in \ \mathfrak {g}^{f}_{0}$. By Lemma 7.1, M satisfies (7.8), hence, by Lemma 7.2, $M = 0$, and we have

$$\begin{aligned} L = \gamma J^{\{ f \}}. \end{aligned}$$

(7.13)

In order to complete the proof of Theorem 3.2, it remains to show that

$$\begin{aligned} \gamma \ = \ - \frac{1}{k + h^{\vee }} . \end{aligned}$$

(7.14)

For that we use the following formula, which can be deduced from the discussion of properties of L in Sect. 3 :

$$\begin{aligned}{}[L_{\lambda } J^{(v)}] \ = \ (\partial + \Delta _v \lambda ) J^{(v)} \ + \ \lambda ^{2} (\rho _{> 0} | v),\,\, v \in \mathfrak {g}, \end{aligned}$$

(7.15)

where $\Delta _{v}$ is the conformal weight of $J^{(v)}$. Using formula (7.15), we obtain

$$\begin{aligned}{}[L_{\lambda } \gamma J^{\{ f \}}] \ = \ (\partial + 2 \lambda ) \gamma J^{\{ f \}} \ + \ \lambda ^{3} \big (- \gamma (k + h^\vee ) \frac{c (\mathfrak {g}, x, k)}{12}+\gamma \beta \big ). \end{aligned}$$

(7.16)

where

$$\begin{aligned} \beta = \ (\rho _{> 0} | \rho _{> 0}) - (\rho | \rho ) + \frac{1}{6} (\rho _{1/2} | \rho _{> 0}) + \frac{1}{24} \mathrm{str}_{\mathfrak {g}_{0} \oplus \mathfrak {g}_{1/2}} \Omega _0 . \end{aligned}$$

Using (7.13) and comparing (7.16) with

$$\begin{aligned}{}[L_\lambda L] \ = \ (\partial + 2 \lambda ) L \ + \ \frac{\lambda ^{3}}{12} \ c (\mathfrak {g}, x, k), \end{aligned}$$

where $c (\mathfrak {g}, x, k)$, given by (3.3), is non-zero for generic k, we obtain (7.14) (and also that $\beta = 0$). This completes the proof of Theorem 3.2.

Appendix B. Theorem 3.2 for $\mathfrak {g}$ = gl(n|n)

Let $\mathfrak {g}$ be a finite-dimensional Lie superalgebra over $\mathbb {F}$ with an even invariant supersymmetric bilinear form (. | .). In order to apply the Sugawara construction, we need two properties:

• (i) the bilinear form (. | .) is non-degenerate, so that we can choose dual bases $\{ u_i \}$ and $\{ u^i \}$ of $\mathfrak {g}$ with respect to this form and construct the Casimir operator

  $$\begin{aligned} \Omega \ = \ \underset{i}{\sum }\ u^i u_i \ \in U (\mathfrak {g}); \end{aligned}$$

• (ii) the Casimir operator $\Omega$ acts on $\mathfrak {g}$ as a scalar (which we denoted by $2 h^{\vee }$).

In this Appendix we consider $\mathfrak {g}= gl (n|n)$ with the bilinear form $(a|b) = \mathrm{str}\, ab$. The property (i) holds, but (ii) fails. However, we will show that the Sugawara operator $L^{\mathfrak {g}}$, appearing in the formula (3.2) for L can be modified, so that the resulting modified L is a Virasoro vector, which satisfies a modified Theorem 3.2 with the modified $J^{\{ f \}}$.

Let I be the identity matrix in $\mathfrak {g}$ and let

$$\begin{aligned} \omega \ = \ \underset{i}{\sum } \ : u^i u_i : \ \in V^{k} (\mathfrak {g}). \end{aligned}$$

(8.1)

The following formulas are obtained by straightforward computations, where $a \in \mathfrak {g}$:

$$\begin{aligned}&\Omega (a) \ = \ - 2 (a|I) I ; \end{aligned}$$

(8.2)

$$\begin{aligned}&[a_{\lambda } \omega ] \ = \ 2 \lambda k a - 2 \lambda (a|I) I ; \end{aligned}$$

(8.3)

$$\begin{aligned}&[a_{\lambda } I] \ = \ \lambda k (a|I) ; \end{aligned}$$

(8.4)

$$\begin{aligned}&[a_{\lambda } : I^2 :] \ = \ 2 \lambda k (a|I) I . \end{aligned}$$

(8.5)

Introduce the modified Sugawara operator

$$\begin{aligned} L^{\mathfrak {g}} \ = \ \frac{1}{2 k} \omega \ + \ \frac{1}{2 k^2} \ : I^2: . \end{aligned}$$

(8.6)

It is straightforward to deduce from (8.3)–(8.5) the following two formulas:

$$\begin{aligned}&[a_{\lambda } L^{\mathfrak {g}}] \ = \ \lambda a ,\,\, \text {hence}\,\, [{L^{\mathfrak {g}}}_{\lambda } a] \ = \ (\partial + \lambda )a ; \end{aligned}$$

(8.7)

$$\begin{aligned}&[{L^{\mathfrak {g}}}_\lambda L^{\mathfrak {g}}] \ = \ (\partial + 2 \lambda ) L^{\mathfrak {g}} . \end{aligned}$$

(8.8)

Hence, we have the following proposition.

Proposition 8.1

The element $L^{\mathfrak {g}}$ defined by (8.6) is a Virasoro vector of $V^k (\mathfrak {g})$ with central charge 0, for which $a \in \mathfrak {g}$ have conformal weight 1. Hence, $V^k (\mathfrak {g})$ is a conformal vertex algebra of CFT type for all $k \ne 0$.

Finally, we have the following version of Theorem 3.2 for $\mathfrak {g}= gl(n|n)$.

Theorem 8.1

Let $L^{\mathfrak {g}}$ be defined by (8.6), let L be defined by (3.2) with this $L^{\mathfrak {g}}$, and let $\tilde{J}^{\{ f \}}$ be the element, defined in Theorem 3.1 for $h^{\vee } = 0$. Then the element

$$\begin{aligned} J^{\{ f \}} \ = \ \tilde{J}^{\{ f \}} - \frac{1}{2 k} : I^{2} : \end{aligned}$$

is $d_{(0)}$-closed and $L = - \frac{1}{k} J^{\{ f \}}$ is an energy-momentum vector of $W^{k} (\mathfrak {g}, x , f)$ with central charge given by formula (3.3) with $h^{\vee } = 0$.

Proof

By the same proof as that of Theorem 3.1, the element $\tilde{J}^{\{ f \}}$ is $d_{(0)}$-closed, and also, by (2.6), the element I is $d_{(0)}$- closed, hence the same holds for $: I^{2} :$. Hence the element $J^{\{f\}}$ is $d_{(0)}$-closed.

Let $\tilde{L} \ = \frac{1}{2 k} \omega + \partial x + L^{ch} + L^{ne}$ (cf. (3.2)). By the same proof as that of Theorem 3.2, we have: $\tilde{L} + \frac{1}{k} \tilde{J}^{\{ f \}}$ is $d_{(0)}$-exact. Since this element coincides with $L + \frac{1}{k} J^{\{ f \}}$, the theorem is proved. $\square$