Blobbed Topological Recursion of the Quartic Kontsevich Model I: Loop Equations and Conjectures

Abstract

We provide strong evidence for the conjecture that the analogue of Kontsevich’s matrix Airy function, with the cubic potential $\mathrm {Tr}(\Phi ^3)$ replaced by a quartic term $\mathrm {Tr}(\Phi ^4)$, obeys the blobbed topological recursion of Borot and Shadrin. We identify in the quartic Kontsevich model three families of correlation functions for which we establish interwoven loop equations. One family consists of symmetric meromorphic differential forms $\omega _{g,n}$ labelled by genus and number of marked points of a complex curve. We reduce the solution of all loop equations to a straightforward but lengthy evaluation of residues. In all evaluated cases, the $\omega _{g,n}$ consist of a part with poles at ramification points which satisfies the universal formula of topological recursion, and of a part holomorphic at ramification points for which we provide an explicit residue formula.

1 Introduction

This paper achieves decisive progress in the complete solution of a quartic analogue of the Kontsevich model. The Kontsevich model [1] is a $N\times N$ Hermitian matrix model obtained by deforming a Gaußian measure $d\mu _0(\Phi )$ with covariance

$$\begin{aligned} \langle \Phi (e_{ij}) \Phi (e_{kl}) \rangle _c =\frac{\delta _{il}\delta _{jk}}{\lambda _k+\lambda _l} \end{aligned}$$

(1.1)

(where $(e_{kl})$ is the standard matrix basis and $\lambda _1,\dots ,\lambda _N$ are positive real numbers which we rename to $E_1,\dots ,E_N$ in this paper) by a cubic term $\exp (\frac{\mathrm {i}}{6} \mathrm {Tr}(\Phi ^3))$. Under ‘quartic analogue’ we understand the deformation of the same Gaußian measure (1.1) by a quartic term $\exp (-\frac{\lambda }{4} \mathrm {Tr}(\Phi ^4))$. The Kontsevich model proves a conjecture by Witten [2] that the generating function of intersection numbers of tautological characteristic classes on the moduli space $\overline{{\mathcal {M}}}_{g,n}$ of stable complex curves is a $\tau$-function for the KdV hierarchy. Thereby it beautifully connects several areas of mathematics and physics such as integrable models, matrix models, 2D quantum gravity, enumerative geometry, complex algebraic geometry and also noncommutative geometry.

Some 15 years ago it was understood that the Kontsevich model is also a prime example for a universal structure called topological recursion [3]. It starts with the initial data $(\Sigma ,\Sigma _0,x,\omega _{0,1},B)$, called the spectral curve. Here $x:\Sigma \rightarrow \Sigma _0$ is a ramified covering of Riemann surfaces, $\omega _{0,1}$ is a meromorphic differential 1-form on $\Sigma$ regular at the ramification points of x, and B the Bergman kernel, a symmetric meromorphic bidifferential form on $\Sigma \times \Sigma$ with double pole on the diagonal and no residue. From these initial data, topological recursion constructs a hierarchy $\{\omega _{g,n}\}$ with $\omega _{0,2}=B$ of symmetric meromorphic differential forms on $\Sigma ^n$ and understands them as spectral invariants of the curve. Other examples besides the Kontsevich model (which is described e.g. in [4, Sect. 6]) are the one- and two-matrix models [5], Mirzakhani’s recursions [6] for the volume of moduli spaces of hyperbolic Riemann surfaces, recursions in Hurwitz theory [7] and in Gromov-Witten theory [8].

This paper provides strong evidence that our quartic analogue of the Kontsevich model is a prime example¹ for blobbed topological recursion, an extension of topological recursion developed by Borot and Shadrin [9]. In this setting the differential forms

$$\begin{aligned} \omega _{g,n}(...,z)={\mathcal {P}}_z\omega _{g,n}(...,z) +{\mathcal {H}}_z\omega _{g,n}(...,z) \end{aligned}$$

decompose into a part ${\mathcal {P}}_z\omega _{g,n}$ with poles (in a selected variable z) at ramification points of $x:\Sigma \rightarrow \Sigma _0$ and a part ${\mathcal {H}}_z\omega _{g,n}$ with poles somewhere else. The ${\mathcal {P}}_z\omega _{g,n}$ are recursively given by the universal formula (for simple ramifications)

$$\begin{aligned} {\mathcal {P}}_z\omega _{g,n+1}(I,z)&=\sum _{\beta _i} \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i} K_i(z,q)\bigg ( \omega _{g-1,n+2}(I, q,\sigma _i(q)) \nonumber \\&\quad + \sum _{\begin{array}{c} g_1+g_2=g\\ I_1\uplus I_2=I\\ (g_1,I_1)\ne (0,\emptyset )\ne (g_2,I_2) \end{array}} \omega _{g_1,|I_1|+1}(I_1,q) \omega _{g_2,|I_2|+1}(I_2,\sigma _i(q))\!\bigg ) \end{aligned}$$

(1.2)

of topological recursion. Here $I=\{z_1,\dots ,z_n\}$ collects the other variables besides z, the sum is over the ramification points $\beta _i$ of x defined by $x'(\beta _i)=0$. The kernel $K_i(z,q)$ is defined in the neighbourhood of $\beta _i$ by $K_i(z,q)=\frac{\frac{1}{2}\int ^{q}_{\sigma _i(q)} B(z,q')}{\omega _{0,1}(q)-\omega _{0,1}(\sigma _i(q))}$, where $\sigma _i\ne \mathrm {id}$ is the local Galois involution $x(q)=x(\sigma _i(q))$ near $\beta _i$. There is no general formula for the other part ${\mathcal {H}}_z\omega _{g,n}$. The only requirement is that $\omega _{g,n}={\mathcal {P}}_z\omega _{g,n} +{\mathcal {H}}_z\omega _{g,n}$ satisfy abstract loop equations [10]. The $\omega _{g',n'}$ on the rhs of (1.2) contain both parts ${\mathcal {P}}$ and ${\mathcal {H}}$.

This paper identifies the $\omega _{g,n}$ for the quartic analogue of the Kontsevich model (which is probably the most innovative step) and establishes loop equations for them and for two families of functions interweaved with the $\omega _{g,n}$. These loop equations are very complicated. We succeed in solving them for $\omega _{0,2},\omega _{0,3},\omega _{1,1}$ and $\omega _{0,4}$. The results are remarkably simple and structured. We prove that, although our loop equations are much more complicated than familiar equations of topological recursion, the solutions satisfy exactly the blobbed topological recursion (1.2) in all four cases. This statement boils down to equality of more than 10 rational numbers. This is unlikely a mere coincidence so that we conjecture that the quartic analogue of the Kontsevich model obeys exactly the structures of blobbed topological recursion. In a subsequent work [11] we confirm the conjecture for genus $g=0$ (i.e. for all $\omega _{0,n}$). The loop equations established in this paper are shown in [11] to be equivalent to equations which express $\omega _{0,n+1}(z_1,\ldots ,z_n,-z)$ in terms of $\omega _{0,m+1}(z_1,\ldots ,z_m,+z)$ with $m\le n$. Their solution is a residue formula which implements blobbed topological recursion.

All these structures make the quartic analogue of the Kontsevich model a member of the family of models associated with the moduli space $\overline{{\mathcal {M}}}_{g,n}$ of stable complex curves.

We summarise central steps which went into the result. The model under consideration is the result of attempts to understand quantum field theories on noncommutative geometries. These QFT models have a matrix formulation [12, 13] which was a main tool in establishing perturbative renormalisability in four dimensions [14] and vanishing of the $\beta$-function [15]. Exact solutions of particular choices of these matrix models have been established in [13] for a complex model and most importantly in [16, 17] for a quantum field theory limit of the Kontsevich model (completed much later in [18]).

Building on [15], one of us (RW) with H. Grosse proved in [19] that the planar 2-point function of the Quartic Kontsevich Model satisfies a non-linear integral equation

$$\begin{aligned}&(\mu ^2{+}x{+}y)ZG^{(0)}(x,y) \nonumber \\&\quad = 1-\lambda \! \int _0^{\Lambda ^2} \!\!\! dt\;\varrho _0(t) \Big ( ZG^{(0)}(x,y) \;ZG^{(0)}(x,t) - \frac{ZG^{(0)}(t,y) -ZG^{(0)}(x,y)}{t-x}\Big ) \,. \end{aligned}$$

(1.3)

Here $\varrho _0$ is the spectral measure of a Laplacian on the noncommutative geometry, $\lambda$ the coupling constant and $\mu ^2(\Lambda ),Z(\Lambda )$ are renormalisation parameters to achieve existence of $\lim _{\Lambda \rightarrow \infty } G^{(0)}(x,t)$. For the purpose of this paper it is safe to set $\mu ^2=0=Z-1$. This equation is the first instance of a Dyson-Schwinger equation (or loop equation) in the Quartic Kontsevich Model. In [20] a fixed point formulation of (1.3) was found from which in the following years some qualitative results about the solution were deduced. But in spite of considerable efforts, a solution of (1.3) remained out of reach for 9 years. In 2018, one of us (RW) with E. Panzer found in [21] the solution of (1.3) for $\varrho _0(t)=1$, $\mu ^2=1-2\lambda \log (1+\Lambda ^2)$ and $Z=1$. A year later, two of us (AH, RW) with H. Grosse extended in [22] this solution to any Hölder-continuous $\varrho _0$ with $\int _0^\infty \frac{dt}{(1+t)^3}\varrho _0(t)<\infty$. The limit of (1.3) back to a matrix measure $\varrho _0(t)=\frac{1}{N}\sum _{k=1}^d r_k\delta (t-e_k)$, already considered in [22], was understood by RW with J. Schürmann in [23] as a problem in complex algebraic geometry. Also the next equation for the planar 2-point function of cycle type (2, 0) was solved in [23].

The present paper is a large-scale extension of [22, 23] to higher topological sectors. It was already pointed out in [20, 23] that, although all Dyson-Schwinger equations for higher topological sectors are affine equations, no solution theory for them seemed to exist. We succeed in finding one. In Definition 2.3 we identify three families $T_{q_1,...,q_m\Vert pq|},T_{q_1,...,q_m\Vert p|q|}$ and ${{\Omega }_{q_1,...,q_m}}$ of auxiliary functions for which we derive in Sect. 2.3 loop equations. These have a graphical interpretation which we provide in Appendix D. Knowing ${{\Omega }_{\dots }}$ and $T_{\dots }$ permits a straightforward solution of all cumulants $G_{\dots }$ of the quartically deformed measure along the lines of [23]. Section 3 extends the loop equations of Sect. 2.3 to functions of several complex variables. The solution for the function ${{\Omega }^{(0)}_2}(u,z)$ in Proposition 3.11 makes first contact with the Bergman kernel of topological recursion. We describe in Sect. 4 how all equations can be solved by evaluation of residues. Doing this in practice can be a longer endeavour, as demonstrated in Appendix G. The results strongly suggest that our auxiliary functions ${{\Omega }_{q_1,\ldots \,q_m}}$ descent from symmetric meromorphic differential forms $\omega _{g,m}$ which satisfy the main Eq. (1.2) of blobbed topological recursion. Moreover, we provide explicit residue formulae for ${\mathcal {H}}_z\omega _{g,n}(...,z)$.

2 The Setup

2.1 Matrix integrals

Our aim is the algebraic solution of the quartic analogue of the Kontsevich model, i.e. of a matrix model with the same weighted covariance as the Kontsevich model [1] but with quartic instead of cubic deformation. We employ the notation developed in [23] where further details are given.

Let $H_N$ be the real vector space of self-adjoint $N\times N$-matrices and $(E_1,\dots , E_{N})$ be pairwise different² positive real numbers. Let $d\mu _{E,0}(\Phi )$ be the probability measure on the dual space $H_N'$ uniquely defined by

$$\begin{aligned} \exp \Big (- \frac{1}{2N} \sum _{k,l=1}^{N} \frac{M_{kl}M_{lk}}{E_k+E_l}\Big ) = \int _{H_N'} d\mu _{E,0}(\Phi ) \,e^{\mathrm {i} \Phi (M)}\;, \end{aligned}$$

(2.1)

for any $M=M^*=\sum _{k,l=1}^{N} M_{kl} e_{kl}\in H_N$ where $(e_{kl})$ is the standard matrix basis. We deform $d\mu _{E,0}(\Phi )$ by a quartic potential to a measure

$$\begin{aligned} d\mu _{E,\lambda }(\Phi )&:= \frac{d\mu _{E,0}(\Phi )\; e^{-\frac{\lambda N}{4}\mathrm {Tr}(\Phi ^4)}}{ \int _{H_N'} d\mu _{E,0}(\Phi )\; e^{-\frac{\lambda N}{4}\mathrm {Tr}(\Phi ^4)}}\;, \end{aligned}$$

(2.2)

where $\mathrm {Tr}(\Phi ^4):= \sum _{j,k,l,m=1}^{N} \Phi (e_{jk})\Phi (e_{kl})\Phi (e_{lm})\Phi (e_{mj})$ when extending the linear forms via $\Phi (M_1+\mathrm {i}M_2):=\Phi (M_1)+\mathrm {i}\Phi (M_2)$ to complex $N\times N$-matrices.

The Fourier transform

$$\begin{aligned} {\mathcal {Z}}(M)= \int _{H'_N}\!\! d\mu _{E,\lambda } (\Phi ) \;e^{\mathrm {i}\Phi (M)} \end{aligned}$$

(2.3)

of the measure is conveniently used to organise moments

$$\begin{aligned} \langle e_{k_1l_1}\dots e_{k_nl_n}\rangle&:= \int _{H'_{N}} \!\! d\mu _{E,\lambda }(\Phi ) \;\Phi (e_{k_1l_1}) \cdots \Phi (e_{k_nl_n}) \\&= \frac{1}{\mathrm {i}^{n}} \frac{\partial ^n{\mathcal {Z}}(M)}{\partial M_{k_1l_1}\cdots \partial M_{k_nl_n}} \Big |_{M=0} \end{aligned}$$

and cumulants

$$\begin{aligned} \langle e_{k_1l_1}\dots e_{k_nl_n}\rangle _c&= \frac{1}{\mathrm {i}^{n}} \frac{\partial ^n\log {\mathcal {Z}}(M)}{\partial M_{k_1l_1}\cdots \partial M_{k_nl_n}} \Big |_{M=0}\;. \end{aligned}$$

(2.4)

As explained in [23], the cumulants (2.4) are only non-zero if $(l_1,\dots ,l_n)=(k_{\sigma (1)},\dots ,k_{\sigma (n)})$ is a permutation of $(k_1,\dots ,k_n)$, and in this case³ the cumulant only depends on the cycle type of this permutation $\sigma$ in the symmetric group ${\mathcal {S}}_n$. A non-vanishing cumulant of b cycles is thus of the form $\big \langle (e_{k_1^1k_2^1} e_{k_2^1k_3^1} \cdots e_{k_{n_1}^1k_1^1}) \cdots (e_{k_1^bk_2^b} e_{k_2^bk_3^b} \cdots e_{k_{n_b}^bk_1^b}) \big \rangle _c$ and gives, after rescaling by appropriate powers of N, for pairwise different $k_i^j$ rise to

$$\begin{aligned} \begin{aligned}&N^{n_1+\dots +n_b} \big \langle (e_{k_1^1k_2^1} e_{k_2^1k_3^1} \cdots e_{k_{n_1}^1k_1^1}) \cdots ( e_{k_1^bk_2^b} e_{k_2^bk_3^b} \cdots e_{k_{n_b}^bk_1^b}) \big \rangle _c \\&\quad =: N^{2-b} \cdot G_{|k_1^1\dots k_{n_1}^1|\dots |k_1^b\dots k_{n_b}^b|} \;. \end{aligned} \end{aligned}$$

(2.5)

The goal is to compute these ‘correlation functions’ $G_{\dots }$ after (at this point formal) expansion $G_{\dots }=\sum _{g=0}^\infty N^{-2g} G^{(g)}_{\dots }$, at least in principle. This was achieved in [22, 23] for $G^{(0)}_{|k_1k_2|}$ and in [23] for $G^{(0)}_{|k^1|k^2|}$. The results of [24] extend this solution to all $G^{(0)}_{|k_1\dots k_n|}$. But starting with $G^{(0)}_{|k^1_1k^1_2|k^2_1k^2_2|}$ and $G^{(1)}_{|k_1k_2|}$ a new structure arises which cannot be treated by the methods developed so far. The present paper gives the solution and shows that precisely these new structures provide the connection to the world of topological recursion [3, 4, 9].

2.2 Dyson-Schwinger equations

The Fourier transform (2.3) satisfies the equations of motion [23, Lemma 1+2]

$$\begin{aligned} \frac{1}{\mathrm {i}}\frac{\partial {\mathcal {Z}}(M)}{\partial M_{pq}}&= \frac{\mathrm {i} M_{qp}{\mathcal {Z}}(M)}{N(E_p+E_q)} -\frac{\lambda }{\mathrm {i}^3(E_p+E_q)} \sum _{k,l=1}^{N} \frac{\partial ^3 {\mathcal {Z}}(M)}{\partial M_{pk}\partial M_{kl}\partial M_{lq}}\;, \end{aligned}$$

(2.6)

$$\begin{aligned} \frac{1}{N} \frac{\partial {\mathcal {Z}}(M)}{\partial E_{p}}&= \Big (\sum _{k=1}^N \frac{\partial ^2}{\partial M_{pk} \partial M_{kp}} + \frac{1}{N}\sum _{k=1}^N G_{|pk|}+\frac{1}{N^2} G_{|p|p|}\Big ){\mathcal {Z}}(M)\;. \end{aligned}$$

(2.7)

The first one can be converted into [23, Eq. (50)]

$$\begin{aligned} -N\sum _{k=1}^{N} (E_p-E_q)\frac{\partial ^2 {\mathcal {Z}}(M)}{\partial M_{pk} \partial M_{kq}} = \sum _{k=1}^{N} \Big ( M_{kp} \frac{\partial {\mathcal {Z}}(M)}{\partial M_{kq}} -M_{qk} \frac{\partial {\mathcal {Z}}(M)}{\partial M_{pk}} \Big )\;. \end{aligned}$$

(2.8)

For $E_p\ne E_q$ it is safe to divide by $(E_p-E_q)$ to extract $\frac{\partial ^2 {\mathcal {Z}}(M)}{\partial M_{pk} \partial M_{kq}}$, whereas $\frac{\partial ^2 {\mathcal {Z}}(M)}{\partial M_{pk} \partial M_{kp}}$ has to be taken from (2.7).

Example 2.1

For $p\ne q$ one has with ${\mathcal {Z}}(0)=1$

$$\begin{aligned} G_{|pq|}&=-N \frac{\partial ^2 \log {\mathcal {Z}}(M)}{\partial M_{pq} \partial M_{qp}} \Big |_{M=0}= -N \frac{\partial ^2 {\mathcal {Z}}(M)}{\partial M_{pq} \partial M_{qp}} \Big |_{M=0} \\&= \frac{1}{E_p+E_q}-\frac{\lambda N}{E_p+E_q} \sum _{k,l=1}^N \frac{\partial ^2}{\partial M_{lq} \partial M_{qp}} \frac{\partial ^2 {\mathcal {Z}}(M)}{ \partial M_{pk} \partial M_{kl}}\Big |_{M=0}\;. \end{aligned}$$

The second line results when differentiating (2.6) with respect to $M_{qp}$. We split the l-sum into $l=p$ where (2.7) is used and $l\ne p$ where (2.8) for $q\mapsto l$ is inserted:

$$\begin{aligned} (E_p+E_q)G_{|pq|}&= 1 -\lambda \frac{\partial ^2}{\partial M_{pq} \partial M_{qp}} \Big [ \frac{\partial {\mathcal {Z}}(M)}{\partial E_p} -{\mathcal {Z}}(M)\Big (\sum _{k=1}^N G_{|pk|}+\frac{1}{N}G_{|p|p|} \Big )\Big ]\Big |_{M=0} \\&\quad -\lambda \sum _{k=1}^N \sum _{\begin{array}{c} l=1\\ l\ne p \end{array}}^N \frac{\partial ^2}{\partial M_{lq} \partial M_{qp}}\Big [ \frac{ M_{kp} \frac{\partial {\mathcal {Z}}(M)}{\partial M_{kl}} -M_{lk} \frac{\partial {\mathcal {Z}}(M)}{\partial M_{pk}} }{E_l-E_p}\Big ]\Big |_{M=0}\;. \end{aligned}$$

Inserting ${\mathcal {Z}}(M)= 1- \frac{1}{N^2} \sum _{j,k=1}^N \big (\frac{N}{2} G_{|jk|} M_{jk}M_{kj} + \frac{1}{2} G_{|j|k|} M_{jj}M_{kk}\big )+ {\mathcal {O}}(M^4)$, the differentiation yields the Dyson-Schwinger equation (DSE) for the 2-point function

$$\begin{aligned} (E_p+E_q)G_{|pq|} =&1+\frac{\lambda }{N} \frac{\partial G_{|pq|}}{\partial E_p} -\lambda G_{|pq|}\Big (\frac{1}{N}\sum _{k=1}^N G_{|pk|}+\frac{1}{N^2}G_{|p|p|} \Big ) \nonumber \\&+\frac{\lambda }{N} \sum _{\begin{array}{c} l=1\\ l\ne p \end{array}}^N \frac{G_{|lq|}-G_{|pq|}}{E_l-E_p} +\frac{\lambda }{N^2} \frac{G_{|q|q|}-G_{|p|q|}}{E_q-E_p}\;. \end{aligned}$$

(2.9)

Example 2.2

For $p\ne q$ one has with ${\mathcal {Z}}(0)=1$

$$\begin{aligned} G_{|p|q|}&=-N^2 \frac{\partial ^2 \log {\mathcal {Z}}(M)}{\partial M_{pp} \partial M_{qq}} \Big |_{M=0}= -N^2 \frac{\partial ^2 {\mathcal {Z}}(M)}{\partial M_{pp} \partial M_{qq}} \Big |_{M=0} \\&= -\frac{\lambda N^2}{E_p+E_p} \sum _{k,l=1}^N \frac{\partial ^2}{\partial M_{lp} \partial M_{qq}} \frac{\partial ^2 {\mathcal {Z}}(M)}{ \partial M_{pk} \partial M_{kl}}\Big |_{M=0}\;. \end{aligned}$$

The second line results when differentiating (2.6) taken at $q\mapsto p$ with respect to $M_{qq}$. We split the l-sum into $l=p$ where (2.7) is used and $l\ne p$ where (2.8) for $q\mapsto l$ is inserted:

$$\begin{aligned} (E_p+E_p)G_{|p|q|}&= -\lambda \frac{N\partial ^2}{\partial M_{pp} \partial M_{qq}} \Big [ \frac{\partial {\mathcal {Z}}(M)}{\partial E_p} -{\mathcal {Z}}(M)\Big (\sum _{k=1}^N G_{|pk|}+\frac{1}{N}G_{|p|p|} \Big )\Big ]\Big |_{M=0} \\&\quad -\lambda \sum _{k=1}^N \sum _{\begin{array}{c} l=1\\ l\ne p \end{array}}^N \frac{N \partial ^2}{\partial M_{lp} \partial M_{qq}}\Big [ \frac{ M_{kp} \frac{\partial {\mathcal {Z}}(M)}{\partial M_{kl}} -M_{lk} \frac{\partial {\mathcal {Z}}(M)}{\partial M_{pk}} }{E_l-E_p}\Big ]\Big |_{M=0}\;. \end{aligned}$$

Inserting ${\mathcal {Z}}(M)= 1- \frac{1}{N^2} \sum _{j,k=1}^N \big (\frac{N}{2} G_{|jk|} M_{jk}M_{kj} + \frac{1}{2} G_{|j|k|} M_{jj}M_{kk}\big )+ {\mathcal {O}}(M^4)$, the differentiation yields the Dyson-Schwinger equation for the $(1{+}1)$-point function

$$\begin{aligned} (E_p+E_p)G_{|p|q|} =&\frac{\lambda }{N} \frac{\partial G_{|p|q|}}{\partial E_p} -\lambda G_{|p|q|}\Big (\frac{1}{N}\sum _{k=1}^N G_{|pk|}+\frac{1}{N^2}G_{|p|p|} \Big ) \nonumber \\&+\frac{\lambda }{N} \sum _{\begin{array}{c} l=1\\ l\ne p \end{array}}^N \frac{G_{|l|q|}-G_{|p|q|}}{E_l-E_p} +\lambda \frac{G_{|qq|}-G_{|pq|}}{E_q-E_p}\;. \end{aligned}$$

(2.10)

The arising repeated differentiations with respect to the $E_q$ suggest to introduce:

Definition 2.3

Generalised correlation functions are defined for pairwise different $q_j, p^s_i$ by

$$\begin{aligned} T_{q_1,...,q_m\Vert p_1^1...p_{n_1}^1|p_1^2...p_{n_2}^2|...|p_1^b...p_{n_b}^b|} :=\frac{(-N)^m\partial ^m}{\partial E_{q_1}...\partial E_{q_m}}G_{|p_1^1...p_{n_1}^1|p_1^2...p_{n_2}^2|...|p_1^b...p_{n_b}^b|}\;. \end{aligned}$$

Moreover, assume that for

there is a function ${\mathcal {F}}(E,\lambda )$ with . Then functions , symmetric in their indices, are defined by

For the aim of the paper it will be sufficient to focus on the following special cases, the generalised 2-point and $1+1$-point functions:

$$\begin{aligned} T_{q_1,...,q_m\Vert pq|}&:=\frac{(-N)^m\partial ^m}{\partial E_{q_1}...\partial E_{q_m}}G_{|pq|}\;,&T_{q_1,...,q_m\Vert p|q|}&:=\frac{(-N)^m\partial ^m}{\partial E_{q_1}...\partial E_{q_m}}G_{|p|q|}\;. \end{aligned}$$

These functions will be considered as formal power series in $\frac{1}{N^2}$,

$$\begin{aligned} G=\sum _{g=0}^\infty N^{-2g} G^{(g)}\;,\quad T=\sum _{g=0}^\infty N^{-2g} T^{(g)}\;,\quad {\Omega }\,=\sum _{g=0}^\infty N^{-2g} {{\Omega }^{(g)}}\;, \end{aligned}$$

(2.11)

where g plays the rôle of a genus.

It is well-known that the 2-point function $G^{(g)}_{|pq|}$ and the $1+1$-point function $G^{(g)}_{|p|q|}$ have an expansion into ribbon graphs, see [25] for the definition of those ribbon graphs associated to the quartic Kontsevich model. The generalised correlation functions of Definition 2.3 have a topological meaning as well, since the derivative $\frac{\partial }{\partial E_{q_i}}$ acts on an internal edge and fixes it to $E_{q_i}$. This operation is extensively discussed in [25] and depends topologically on the labelling of the two faces adjacent to the edge. Let us briefly sum up the major ideas on which the detailed graphical discussion in Appendix D will build:

We consider genus-g Riemann surfaces X with b boundaries and m marked points. We let $\chi =2-2g-m-b$ be the Euler characteristic of X.

• 1. The ${{\Omega }^{(g)}}_{q_1,...,q_m}$ correspond to no boundary ($b=0$) and m marked points;

• 2. The $T^{(g)}_{q_1,...,q_m\Vert pq|}$ correspond to $b=1$ boundary and m marked points;

• 3. The $T^{(g)}_{q_1,...,q_m\Vert p|q|}$ correspond to $b=2$ boundaries and m marked points.

The ribbon graphs, consisting of vertices, edges and faces, are embedded into these Riemann surfaces. The faces carry a label from 1 to N, and we distinguish three types:

• 1. Internal faces whose labellings have to be summed over;

• 2. External faces in which at least one edge is part of the boundary (with fixed label);

• 3. Marked faces (with fixed label, too), where no edge is part of a boundary.

For the vertices, also three types show up:

• 1. 4-valent vertices in the interior, carrying the weight $(-\lambda )$;

• 2. 1-valent vertices on the boundaries belonging to one (in $G_{|p|q|}$) or two (in $G_{|pq|}$) external face(s);

• 3. One square-vertex within every marked face (see Fig. 1).

Fig. 1

The action of $\frac{\partial }{\partial E_{q_i}}$ on $G^{(g)}_{|pq|}$ (shown on the left, with $b=1$ boundary and no marked point) turns an inner face into a marked face with a square-vertex. The result of m such operations is depicted on the right; it corresponds to a genus g-Riemann surface with one boundary (carrying two 1-valent vertices) and m marked points. The operation is described in [25] in details

Let us return to the actual aim of the paper: We will show in this paper that a complexification of the ${\Omega }^{(g)}_{\dots }$ gives rise to meromorphic differentials $\omega _{g,n}$ conjectured to obey blobbed topological recursion [9]. This conjecture has been proved for $g=0$ in [11]. In a supplement [25] we express the functions ${{\Omega }_{q_1,...,q_m}}$ as distinguished polynomials in the correlation functions $G_{|\dots |}$, which themselves are quickly growing series in Feynman ribbon graphs. Both results together imply that intersection numbers [9] are accessible by a particular combination of graphs.

2.3 Dyson-Schwinger equations for generalised correlation functions

Definition 2.4

For a set $I=\{q_1,\dots ,q_m\}$ we introduce:

• $|I|=m$, $|\emptyset |=0$.

• $I,q:=I\cup \{q\}=\{q_1,\dots ,q_m,q\}$.

• $I{\setminus } q:=I\setminus \{q\}$, with $I{\setminus } q=\emptyset$ if $q\notin I$.

We let $\sum _{I_1\uplus I_2=I}$ be the sum over all disjoint partitions of I into two possibly empty subsets $I_1,I_2$.

Equations for $T_{\dots }$ result by application of $D_I:=\frac{(-N)^m \partial ^m}{\partial E_{q_1}\cdots \partial E_{q_m}}$ to (2.9) and (2.10) when taking Definition 2.3 into account. We will give three important types of Dyson-Schwinger equations that will determine the recursive structure of our model:

Proposition 2.5

Let $I=\{q_1,\dots ,q_m\}$. For pairwise different $q_j,p,q$, the generalised correlation functions $T_{\dots }$ and ${{\Omega }_{\dots }}$ satisfy the following three types of Dyson-Schwinger equations:

• (1) The DSE determining the generalised 2-point function:

  $$\begin{aligned}&\Big (E_q+E_p+\frac{\lambda }{N} \sum _{\begin{array}{c} l=1\\ l\ne p \end{array}}^N \frac{1}{E_l-E_p}\Big )T_{I\Vert pq|} - \frac{\lambda }{N}\sum _{\begin{array}{c} l=1 \\ l\notin I,p \end{array}}^N \frac{T_{I\Vert lq|}}{E_l-E_p} \nonumber \\&\quad = \delta _{0,|I|} - \lambda \bigg \{ \sum _{I'\uplus I''=I} {{\Omega }_{I',p}} T_{I''\Vert pq|} -\frac{1}{N}\frac{\partial T_{I\Vert pq|}}{\partial E_p} \nonumber \\&\qquad + \sum _{j=1}^m \frac{\partial }{\partial E_{q_j}} \Big (\frac{T_{I\setminus q_j\Vert q_jq|}}{E_{q_j}-E_p}\Big ) - \frac{1}{N^2}\frac{T_{I\Vert q|q|}-T_{I\Vert p|q|}}{E_q-E_p} \bigg \}\;. \end{aligned}$$

  (2.12)

• (2) The DSE determining the generalised 1+1-point function:

  $$\begin{aligned}&\Big (E_p+E_p+\frac{\lambda }{N} \sum _{\begin{array}{c} l=1\\ l \ne p \end{array}}^N \frac{1}{E_l-E_p}\Big ) T_{I\Vert p|q|} - \frac{\lambda }{N}\sum _{\begin{array}{c} l=1\\ l\notin I,p \end{array}}^N \frac{T_{I\Vert l|q|}}{E_l-E_p} \nonumber \\&\quad =(-\lambda ) \bigg \{ \sum _{I'\uplus I''=I} {{\Omega }_{I',p}}T_{I''\Vert p|q|} -\frac{1}{N}\frac{\partial T_{I\Vert p|q|}}{\partial E_p} \nonumber \\&\qquad +\sum _{j=1}^m \frac{\partial }{\partial E_{q_j}} \Big (\frac{T_{I\setminus q_j\Vert q_j|q|}}{E_{q_j}-E_p}\Big ) -\frac{T_{I\Vert qq|}-T_{I\Vert pq|}}{E_{q}-E_p} \bigg \}\;. \end{aligned}$$

  (2.13)

• (3) The DSE for ${{\Omega }_{I,q}}$ in terms of T:

  $$\begin{aligned}&{{\Omega }_{I,q}} = \frac{\delta _{|I|,1}}{ (E_{q_1}-E_q)^2} + \frac{1}{N}\sum _{\begin{array}{c} l=1\\ l\notin I \end{array}}^NT_{I\Vert ql|} - \sum _{j=1}^m \frac{\partial T_{I\setminus q_j\Vert qq_j|}}{\partial E_{q_j}} +\frac{1}{N^2} T_{I\Vert q|q|}\;, \end{aligned}$$

  (2.14)

  where $T_{\emptyset \Vert qq_j|}:=G_{|qq_j|}$ and $T_{\emptyset \Vert q_j|q|}:=G_{|q_j|q|}$.

Proof

We apply the operator $D_I:=\frac{(-N)^m \partial ^m}{\partial E_{q_1}\cdots \partial E_{q_m}}$ to (2.9) and take Definition 2.3 into account. Here we have

and, separating the cases $l\in I$ and $l\notin I$,

The last term in (**) cancels the contribution with $\delta _{|I_1|,1}$ in (*). All other derivatives are clear and arrange into (2.12).

The same considerations give (2.13) when applying $D_I$ to (2.10). Equation (2.14) is clear. $\square$

Remark 2.6

In a similar manner one can derive Dyson-Schwinger equations for $G_{|k_1^1\dots k_{n_1}^1|\dots |k_1^b\dots k_{n_b}^b|}$. In fact [20] they can be reduced to polynomials in correlation functions with $n_s\in \{1,2\}$, in $\lambda$ and in $\frac{1}{E_{k_i}-E_{k_j}}$. We refer to [26] for the precise form of the recursion. Applying $D_I$ then gives rise to Dyson-Schwinger equations for generalised correlation functions $T_{q_1,...,q_m\Vert k_1^1\dots k_{n_1}^1|\dots |k_1^b\dots k_{n_b}^b|}$. We have provided them in prior versions of this paper (e.g. https://arxiv.org/abs/2008.12201v3). For the sake of readability we decided to suppress them here.

The Dyson-Schwinger equations of Proposition 2.5 are in one-to-one correspondence with a graphical representation via a perturbative expansion into ribbon graphs. We derive them once again in Appendix D for illustrative purposes.

3 Loop Equations in Several Complex Variables

3.1 Complexification

The equations in Proposition 2.5 are not sufficient to determine the functions $G,T,{\Omega }$ because there is no equation for derivatives with respect to matrix indices (e.g. in $\frac{\partial T_{I\Vert pq|}}{\partial E_p}$ ) or functions with coincident matrix indices (e.g. $G_{|qq|}$, $G_{|q|q|}$ or $T_{p\Vert pq|}$), which however are needed. Our strategy is therefore to meromorphically extend these equations, where the extension is not necessarily unique, but unique at the points $E_p$.

Definition 3.1

Proposition 2.5 suggests the following extension:

• (a) Introduce holomorphic functions $G,T,{\tilde{\Omega }}$ in several complex variables, defined on Cartesian products of a neighbourhood ${\mathcal {V}}$ of $\{E_1,...,E_N\}$ in ${\mathbb {C}}$, which at $E_1,\dots ,E_N$ agree with the previous correlation functions:

  $$\begin{aligned} G(E_p,E_q)&\equiv G_{|pq|}\;,\qquad G(E_p|E_q)\equiv G_{|p|q|}\;, \\ T(E_{q_1},...,E_{q_m}\Vert E_p,E_q|)&\equiv T_{q_1,\dots ,q_m\Vert pq|}\;,\qquad \\ T(E_{q_1},...,E_{q_m}\Vert E_p|E_q|)&\equiv T_{q_1,\dots ,q_m\Vert p|q|}\;, \\ {\tilde{\Omega }}(E_{q_1},...,E_{q_m})&\equiv {{\Omega }_{q_1,\dots ,q_m}}\;. \end{aligned}$$

• (b) Write the equations in Proposition 2.5 in terms of $G,T,{\tilde{\Omega }}$ and postulate that they extend to pairwise different points $\{E_p\mapsto \zeta ,E_q\mapsto \eta ,E_{q_j} \mapsto \eta _j\}$ of ${\mathcal {V}}$.

• (c) Complexify the derivative by

  $$\begin{aligned} \frac{\partial }{\partial E_q} f(E_q)\mapsto \frac{f(\eta )-f(E_q)}{\eta -E_q} +\frac{\partial }{\partial E_q}\Big \vert _{E_q\mapsto \eta } f(\eta ) \end{aligned}$$

  such that the $\frac{\partial }{\partial E_q}\big \vert _{E_q\mapsto \eta }$-derivative acts in the sense of Definition 2.3 with extension to $E_q\mapsto \eta$, and a difference quotient which tends for $\eta \rightarrow E_q$ to the derivative on the argument of f.

• (d) Keep the $E_l$ in summations over $l \in \{1,\dots ,N\}$ and complete the l-summation with the difference quotient term of (c). Consider the equations for $\zeta ,\eta ,\zeta ^s_i,\eta _j \in {\mathcal {V}}\setminus \{E_1,\dots ,E_N\}$.

• (e) Define the values of $G,T,{\tilde{\Omega }}$ at $\zeta =E_p,\eta =E_q,\zeta ^s_i =E_{p^s_i},\eta _j=E_{q_j}$ and at coinciding points by a limit procedure.

Remark 3.2

The complexification of the derivative defined in (c) distinguishes between Definition 2.3 and a derivative acting on the argument of the function. The derivative on the argument is split into a difference quotient to generate all missing terms in the l-summation, e.g. for $l=q$ by

$$\begin{aligned} \lim _{\eta \rightarrow E_q}\frac{f(\eta )-f(E_q)}{\eta -E_q} =\lim _{E_l\rightarrow E_q} \frac{f(E_l)-f(E_q)}{E_l-E_q}=:\frac{\partial ^{ext}}{\partial E_q} f(E_q), \end{aligned}$$

(3.1)

where the analyticity property at $E_q$ holds by (b). Consequently, the summation over l gets unrestricted in the extension to ${\mathcal {V}}$ and coincides with Proposition 2.5 on the points $E_p$. Notice that the extension of Definition 3.1 is a meaningful extension but cannot be unique.

The complexification procedure allows to relax the condition that all $E_1,\dots ,E_N$ are pairwise different. From now on we agree that $(E_1,\dots ,E_N)$ is made of pairwise different $e_1,\dots ,e_d$ which arise with multiplicities $r_1,\dots ,r_d$ in the tuple, with $r_1+...+r_d=N$.

We search for a solution of the equations after expansion (2.11) of all arising functions as formal power series in $\frac{1}{N^2}$. It will become clear later on that g plays the rôle of the genus of a Riemann surface so that we call (2.11) the genus expansion. When splitting the equations into homogeneous powers of $N^{-2}$ we agree that $\frac{1}{N}\sum _{k=1}^d r_k G^{(g)}(e_k,\dots )$ contributes to order g. Similarly for $T^{(g)}$ and ${\tilde{\Omega }}^{(g)}$.

Example 3.3

The complexification procedure of Definition 3.1 turns (2.9) in Example 2.1 in presence of multiplicities of the $e_i$ into

$$\begin{aligned} (\zeta +\eta )G(\zeta ,\eta ) =&\, 1 -\frac{\lambda }{N^2} T(\zeta \Vert \zeta ,\eta ) -\lambda G(\zeta ,\eta ) {\tilde{\Omega }}(\zeta ) \nonumber \\&+\frac{\lambda }{N} \sum _{k=1}^d r_k \frac{G(e_k,\eta )-G(\zeta ,\eta )}{e_k-\zeta } +\frac{\lambda }{N^2} \frac{G(\eta |\eta )-G(\zeta |\eta )}{\eta -\zeta }\;. \end{aligned}$$

(3.2)

For instance, we have $\frac{\partial G_{|pq|}}{\partial E_p} \mapsto -\frac{1}{N} T(\zeta \Vert \zeta ,\eta )+ r_p \frac{G(\zeta ,\eta )-G(e_p,\eta )}{\zeta -E_p}$. The last term extends $\sum _{l=1, l\ne p}^N \frac{G_{|lq|}-G_{|pq|}}{E_l-E_p} \mapsto \sum _{l=1, l\ne p}^d r_l \frac{G(e_l,\eta )-G(\zeta ,\eta )}{e_l-\zeta }$ to the unrestricted sum in (3.2). After genus expansion and with ${\tilde{\Omega }}^{(0)}(\zeta ) = \frac{1}{N}\sum _{k=1}^d r_k G^{(0)}(\zeta ,e_k)$ from Definition 2.3 we have

$$\begin{aligned}&\Big (\zeta +\eta + \frac{\lambda }{N}\sum _{k=1}^d r_k G^{(0)}(e_k,\zeta ) +\frac{\lambda }{N} \sum _{k=1}^d \frac{r_k}{e_k-\zeta } \Big ) G^{(g)}(\zeta ,\eta ) -\frac{\lambda }{N} \sum _{k=1}^d \frac{r_k G^{(g)}(e_k,\eta )}{ e_k-\zeta } \nonumber \\&\quad = \delta _{g,0} -\lambda \sum _{g'=1}^g G^{(g-g')}(\zeta ,\eta ) {\tilde{\Omega }}^{(g')}(\zeta ) \nonumber \\&\qquad -\lambda T^{(g-1)}(\zeta \Vert \zeta ,\eta ) +\lambda \frac{G^{(g-1)}(\eta |\eta )-G^{(g-1)}(\zeta |\eta )}{\eta -\zeta }\;. \end{aligned}$$

(3.3)

Note that the sum over $g'$ restricts to $g'\ge 1$ because the case $g'=0$ is explicitly included in the lhs.

For $g=0$ this becomes a non-linear equation for the function $G^{(0)}(\zeta ,\eta )$ of $\zeta ,\eta \in {\mathcal {V}}$. It has been recently solved:

Theorem 3.4

([23], building heavily on [22]). Let $\lambda ,e_k>0$. Assume that there is a rational function $R:\hat{{\mathbb {C}}}\rightarrow \hat{{\mathbb {C}}}$ with

• 1. R has degree $d+1$, is normalised to $R(\infty )=\infty$ and biholomorphically maps a domain ${\mathcal {U}} \subset {\mathbb {C}}$ to a neighbourhood (which can be assumed to be ${\mathcal {V}}$) in ${\mathbb {C}}$ of a real interval that contains $e_1,\dots ,e_d$.

• 2. In terms of $G^{(0)}(R(z),R(w))=:{\mathcal {G}}^{(0)}(z,w)$ and $e_k=:R(\varepsilon _k)$ for $z,w,\varepsilon _k\in {\mathcal {U}}$ one has

  $$\begin{aligned} -R(-z)= R(z)+\frac{\lambda }{N}\sum _{k=1}^d \frac{r_k}{R(\varepsilon _k) -R(z)} +\frac{\lambda }{N} \sum _{k=1}^d r_k {\mathcal {G}}^{(0)}(z,\varepsilon _k)\;. \end{aligned}$$

  (3.4)

Then R and ${\mathcal {G}}^{(0)}$ are uniquely determined by the case $g=0$ of (3.3) to

$$\begin{aligned} R(z)&=z-\frac{\lambda }{N} \sum _{k=1}^d \frac{\varrho _k}{\varepsilon _k+z}\;,\qquad R(\varepsilon _k)=e_k\;,\quad \varrho _k R'(\varepsilon _k)=r_k\;, \nonumber \\ {\mathcal {G}}^{(0)}(z,w)&=\frac{\displaystyle 1 -\frac{\lambda }{N} \sum _{k=1}^d \frac{r_k}{ (R(z)-R(\varepsilon _k))(R(\varepsilon _k)-R({-}w))} \prod _{j=1}^d \frac{ R(w){-}R({-}\widehat{\varepsilon _k}^j)}{ R(w)-R(\varepsilon _j)} }{R(w)-R(-z)}\;. \end{aligned}$$

(3.5)

The ansatz (3.4) is identically fulfilled by (3.5). In these equations, the solutions of $R(v)=R(z)$ are denoted by $v\in \{z,{\hat{z}}^1,\dots ,{\hat{z}}^d\}$ with $z\in {\mathcal {U}}$ when considering $R:\hat{{\mathbb {C}}}\rightarrow \hat{{\mathbb {C}}}$. The function ${\mathcal {G}}^{(0)}(z,w)$ is symmetric. Its poles are located at $z+w=0$ and $z,w\in \{\widehat{\varepsilon _k}^j\}$ for $k,j\in \{1,...,d\}$.

Figure 2 sketches the map R. The rational function R introduces another change of variables.

Fig. 2

Illustration of the complexification procedure: The biholomorphic map $R:{\mathcal {U}}\rightarrow {\mathcal {V}}$ with $R(\varepsilon _k)=e_k$ will later be enlarged to a ramified cover $R:\hat{{\mathbb {C}}}\rightarrow \hat{{\mathbb {C}}}$. Functions on ${\mathcal {U}}$ will meromorphically continue to the Riemann sphere $\hat{{\mathbb {C}}}={\mathbb {C}}\cup \{\infty \}$

Definition 3.5

Let $G^{(g)},T^{(g)},{\tilde{\Omega }}^{(g)}$ be the functions in several complex variables obtained by the complexification of Definition 3.1, genus expansion and by admitting multiplicities of the $e_k$. Then functions ${\mathcal {G}}^{(g)},{\mathcal {T}}^{(g)},{\Omega }^{(g)}_m$ of several complex variables are introduced by

$$\begin{aligned} \begin{aligned} {\mathcal {G}}^{(g)}(z,w)&:=G^{(g)}(R(z),R(w))\;,\qquad {\mathcal {G}}^{(g)}(z|w):=G^{(g)}(R(z)|R(w))\;, \\ {\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z,w|)&:= T^{(g)}(R(u_1),...,R(u_m)\Vert R(z),R(w)|)\;, \\ {\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z|w|)&:= T^{(g)}(R(u_1),...,R(u_m)\Vert R(z)|R(w)|)\;, \\ {\Omega }^{(g)}_{m}(u_1,....,u_m)&:= {\tilde{\Omega }}^{(g)}(R(u_1),...,R(u_m)) \;. \end{aligned} \end{aligned}$$

We let ${\mathcal {T}}^{(g)}(\emptyset \Vert z,w|):= {\mathcal {G}}^{(g)}(z,w)$ and ${\mathcal {T}}^{(g)}(\emptyset \Vert z|w|):= {\mathcal {G}}^{(g)}(z|w)$.

Originally defined as holomorphic functions on Cartesian products of ${\mathcal {U}}$, we assume (and will show) that ${\mathcal {G}}^{(g)},{\mathcal {T}}^{(g)},{\Omega }^{(g)}_m$ extend to meromorphic functions on $\hat{{\mathbb {C}}} ={\mathbb {C}}\cup \{\infty \}$.

3.2 Complexified Dyson-Schwinger equations

We now combine the complexification according to Definition 3.1 with the change of variables of Definition 3.5:

Corollary 3.6

Let $I=\{u_1,...,u_m\}$. The complexification of Definition 3.1 turns after genus expansion (2.11), inclusion of multiplicities of $e_i$ and the change of variables given in Definition 3.5, which involves the rational function R of Theorem 3.4, the Dyson-Schwinger Eq. (2.12) of Proposition 2.5 into equations for meromorphic functions in several complex variables:

$$\begin{aligned}&(R(w)-R(-z)){\mathcal {T}}^{(g)}(I\Vert z,w|) -\frac{\lambda }{N}\sum _{k=1}^d \frac{r_k {\mathcal {T}}^{(g)}(I\Vert \varepsilon _k,w|)}{R(\varepsilon _k)-R(z)} \nonumber \\&\quad =\delta _{0,m}\delta _{g,0}-\lambda \bigg \{ \sum _{\begin{array}{c} I_1\uplus I_2=I,\;g_1+g_2=g \\ (g_1,I_1)\ne (0,\emptyset ) \end{array}} {{\Omega }^{(g_1)}_{|I_1|+1}}(I_1,z) {\mathcal {T}}^{(g_2)}(I_2\Vert z,w|) + {\mathcal {T}}^{(g-1)}(I,z\Vert z,w|) \nonumber \\&\qquad + \sum _{i=1}^m\frac{\partial }{\partial R(u_i)} \frac{{\mathcal {T}}^{(g)}(I\setminus u_i\Vert u_i,w|)}{ R(u_i)-R(z)} +\frac{{\mathcal {T}}^{(g-1)}(I\Vert z|w|) -{\mathcal {T}}^{(g-1)}(I\Vert w|w|)}{R(w)-R(z)} \bigg \}\,. \end{aligned}$$

(3.6)

Equation (3.6) reduces for $(g,m)=(0,0)$ to

$$\begin{aligned} {\mathcal {G}}^{(0)}(z,w)=\frac{1+\frac{\lambda }{N}\sum _{k=1}^d \frac{r_k {\mathcal {G}}^{(0)}(\varepsilon _k,w)}{ R(\varepsilon _k)-R(z)}}{R(w)-R(-z)}\;. \end{aligned}$$

(3.7)

Corollary 3.7

Let $I=\{u_1,...,u_m\}$. The complexification of Definition 3.1 turns after genus expansion (2.11), inclusion of multiplicities of $e_i$ and the change of variables given in Definition 3.5, which involves the rational function R of Theorem 3.4, the Dyson-Schwinger Eq. (2.13) of Proposition 2.5 into equations for meromorphic functions in several complex variables:

$$\begin{aligned}&(R(z)-R(-z)){\mathcal {T}}^{(g)}(I\Vert z|w|) -\frac{\lambda }{N}\sum _{k=1}^d r_k\frac{ {\mathcal {T}}^{(g)}(I\Vert \varepsilon _k|w|)}{R(\varepsilon _k)-R(z)} \nonumber \\&\quad =-\lambda \bigg \{ \sum _{\begin{array}{c} I_1\uplus I_2=I,\; g_1+g_2=g \\ (I_1,g_1)\ne (\emptyset ,0) \end{array}} {{\Omega }^{(g_1)}_{|I_1|+1}}(I_1,z) {\mathcal {T}}^{(g_2)}(I_2\Vert z|w|) +{\mathcal {T}}^{(g-1)}(I,z\Vert z|w|) \nonumber \\&\qquad +\sum _{i=1}^m \frac{\partial }{\partial R(u_i)}\frac{ {\mathcal {T}}^{(g)}(I\setminus u_i\Vert u_i|w|) }{R(u_i)-R(z)} +\frac{{\mathcal {T}}^{(g)}(I\Vert z,w|) -{\mathcal {T}}^{(g)}(I\Vert w,w|)}{R(w)-R(z)} \bigg \}\;. \end{aligned}$$

(3.8)

Remark 3.8

The DSE of Corollary 3.6 has a very intricate form. Actually, this structure of DSEs is well-known from the 2-matrix model. We refer to [27, Eqs. (2–19)] with the correspondence ${\Omega } \mapsto W$, ${\mathcal {T}}\mapsto H$ and $\sum _k\frac{{\mathcal {T}}(I\Vert \varepsilon _k,w|)}{R(\varepsilon _k)-R(z)} \mapsto {\tilde{U}}$. However, the last term of (3.6) does not have a corresponding counterpart. Thus, the quartic Kontsevich model is a priori similar to the 2-matrix model, but in some sense richer in its structure. This difference could explain why it is (conjecturally) governed by the extension to Blobbed Topological Recursion [9]. The fundamental building blocks in the 2-matrix model are the $W^{(g)}_{m,0}$ which were proved [5] to satisfy topological recursion. For this reason, the main interest lies on computation and structure of ${\Omega }^{(g)}_m$.

3.3 The DSE for ${\Omega }^{(g)}_m(u_1,...,u_m)$

To solve the system of Eqs. (3.6) and (3.8) we have to establish another DSE for ${{\Omega }^{(g)}_m}$. The same steps as in Corollaries 3.6 and 3.7 turn (2.14) into

$$\begin{aligned} \Omega ^{(g)}_{|I|+1}(I,z) =&\frac{\delta _{g,0}\delta _{|I|,1}}{(R(u_1)-R(z))^2} + \frac{1}{N}\sum _{k=1}^d r_k {\mathcal {T}}^{(g)}(I\Vert z,\varepsilon _k|) \nonumber \\&- \sum _{i=1}^m \frac{\partial {\mathcal {T}}^{(g)}(I{\setminus } u_i\Vert z,u_i|)}{ \partial R(u_i)} + {\mathcal {T}}^{(g-1)}(I\Vert z|z|)\,. \end{aligned}$$

(3.9)

We will prove another relation:

Proposition 3.9

Let $I=\{u_1,....,u_m\}$. The meromorphic functions ${{\Omega }^{(g)}_{m+1}}$ satisfy for $(g,m)\ne (0,0)$ the DSE

$$\begin{aligned}&R'(z){\mathfrak {G}}_0(z)\Omega ^{(g)}_{|I|+1}(I,z) -\frac{\lambda }{N^2}\sum _{n,k=1}^d r_nr_k \frac{{\mathcal {T}}^{(g)}(I\Vert \varepsilon _k,\varepsilon _n|)}{ (R(\varepsilon _k)-R(z))(R(\varepsilon _n)-R(-z))} \nonumber \\&\quad =\frac{\delta _{g,0}\delta _{|I|,1}}{(R(z)-R(u_1))^2} -\sum _{\begin{array}{c} I_1\uplus I_2=I,\; g_1+g_2=g\\ (I_1,g_1)\ne (\emptyset ,0)\ne (I_2,g_2) \end{array}} \Omega ^{(g_1)}_{|I_1|+1}(I_1,z) \frac{\lambda }{N}\sum _{n=1}^d r_n \frac{ {\mathcal {T}}^{(g_2)}(I_2\Vert z,\varepsilon _n|)}{ R(\varepsilon _n)-R(-z)} \nonumber \\&\qquad -\sum _{j=1}^m\frac{\partial }{\partial R(u_j)} \frac{\frac{\lambda }{N}\!\sum _{n=1}^d r_n \frac{{\mathcal {T}}^{(g)}(I\setminus u_j\Vert u_j,\varepsilon _n|) \!\!}{ R(\varepsilon _n)-R(-z)} }{R(u_j)-R(z)} -\frac{\lambda }{N}\sum _{n=1}^d r_n \frac{{\mathcal {T}}^{(g-1)}(I,z\Vert z,\varepsilon _n|)}{ R(\varepsilon _n)-R(-z)} \nonumber \\&\qquad -\frac{\lambda }{N}\sum _{n=1}^d r_n \frac{ {\mathcal {T}}^{(g-1)}(I\Vert z|\varepsilon _n|) - {\mathcal {T}}^{(g-1)}(I\Vert \varepsilon _n|\varepsilon _n|)}{ (R(\varepsilon _n)-R(z))(R(\varepsilon _n)-R(-z))} \nonumber \\&\qquad -\sum _{j=1}^m\frac{\partial }{\partial R(u_j)} {\mathcal {T}}^{(g)}(I\setminus u_j\Vert u_j,z|) +{\mathcal {T}}^{(g-1)}(I\Vert z|z|)\;, \end{aligned}$$

(3.10)

where ${\mathfrak {G}}_0(z):={{\,\mathrm{Res}\,}}_{v\rightarrow -z} {\mathcal {G}}^{(0)}(z,v)dv$.

Proof

Take (3.6), multiply it by $\frac{r_n}{N (R(w)-R(-z))}$, set $w=\varepsilon _n$ and sum over n. The lhs has the term $\frac{1}{N}\sum _{n=1}^d r_n {\mathcal {T}}^{(g)}(I\Vert z,\varepsilon _n|)$, which by (3.9) equals ${\Omega }_{m+1}^{(g)}(I,z)$ plus other terms. Another ${\Omega }_{m+1}^{(g)}(I,z)$ arises with a prefactor $\frac{\lambda }{N}\sum _n \frac{r_n {\mathcal {G}}^{(0)}(\varepsilon _n,z)}{R(\varepsilon _n)-R(-z)}$ from the case $(I_2,g_2)=(\emptyset ,0)$ in the second line of (3.6). Moving it to the lhs, we reconstruct a common prefactor $R'(z){\mathfrak {G}}_0(z)$ via (3.7). $\square$

Remark 3.10

The DSE of ${\Omega }^{(g)}_m$ gives the possibility for a comparison with the 2-matrix model as well. The DSE of Proposition 3.9 coincides (up to two additional terms) with [27, Eqs. (2–20)] after setting $q=p$, where those functions are related by ${\Omega }\mapsto W$, ${\mathcal {T}}\mapsto H$, $\sum _k\frac{{\mathcal {T}}(I\Vert \varepsilon _k,w|)}{ R(\varepsilon _k)-R(z)}\mapsto {\tilde{U}}$ and $\sum _{k,n}\frac{{\mathcal {T}}(I\Vert \varepsilon _k,\varepsilon _n|)}{ (R(\varepsilon _k)-R(z))(R(\varepsilon _n)-R(-z))}\mapsto E$. The two terms violating the exact coincidence are the last term and third last term of (3.10).

3.4 Solution for ${\Omega }^{(0)}_2(u,z)$

For $(g,m)=(0,1)$ the equation in Proposition 3.9 reduces to

$$\begin{aligned}&R'(z){\mathfrak {G}}_0(z){\Omega }^{(0)}_{2}(u,z) -\frac{\lambda }{N^2}\sum _{n,k=1}^d r_nr_k \frac{{\mathcal {T}}^{(0)}(u\Vert \varepsilon _k,\varepsilon _n|)}{ (R(\varepsilon _k)-R(z))(R(\varepsilon _n)-R(-z))} \nonumber \\&\quad = -\frac{\partial }{\partial R(u)} \frac{1+\frac{\lambda }{N}\sum _{n=1}^d r_n \frac{{\mathcal {G}}^{(0)}(u,\varepsilon _n)}{ R(\varepsilon _n)-R(-z)} }{R(u)-R(z)} -\frac{\partial }{\partial R(u)} {\mathcal {G}}^{(0)}(u,z) \nonumber \\&\quad =-\frac{\partial }{\partial R(u)}\big ( {\mathcal {G}}^{(0)}(u,-z)+ {\mathcal {G}}^{(0)}(u,z)\big )\;. \end{aligned}$$

(3.11)

The last line follows from (3.7). In [22] the following representation was proved:

$$\begin{aligned} {\mathcal {G}}^{(0)}(z,u) = \frac{1}{z+u} \Big (1+ \frac{\lambda ^2}{N^2} \sum _{k,l,m,n=1}^d \frac{C_{k,l}^{m,n}}{ (z-\widehat{\varepsilon _k}^m)(u-\widehat{\varepsilon _l}^n)} \Big )\;, \end{aligned}$$

(3.12)

where $C_{k,l}^{m,n}=\frac{(\widehat{\varepsilon _k}^m +\widehat{\varepsilon _l}^n) r_k r_l {\mathcal {G}}^{(0)}(\varepsilon _k,\varepsilon _l)}{ R'(\widehat{\varepsilon _k}^m)R'(\widehat{\varepsilon _l}^n) (R(\varepsilon _l)-R(-\widehat{\varepsilon _k}^m)) (R(\varepsilon _k)-R(-\widehat{\varepsilon _l}^n))}$. On one hand this shows

$$\begin{aligned} {\mathfrak {G}}_0(z)= 1- \frac{\lambda ^2}{N^2} \sum _{k,l,m,n=1}^d \frac{C_{k,l}^{m,n}}{ (z-\widehat{\varepsilon _k}^m)(z+\widehat{\varepsilon _l}^n)}\;, \end{aligned}$$

(3.13)

on the other hand we have the partial fraction decomposition

$$\begin{aligned} {\mathcal {G}}^{(0)}(z,u) = \frac{{\mathfrak {G}}_0(z)}{z+u} + \frac{\lambda ^2}{N^2} \sum _{k,l,m,n=1}^d \frac{C_{k,l}^{m,n}}{ (z+\widehat{\varepsilon _l}^n)(z-\widehat{\varepsilon _k}^m) (u-\widehat{\varepsilon _l}^n)}\;. \end{aligned}$$

(3.14)

Both together imply:

Proposition 3.11

Assume that (for generic u) the function $\Omega ^{(0)}_2(u,z)$ is regular at any zero z of ${\mathfrak {G}}_0$. Then

$$\begin{aligned} \Omega ^{(0)}_2(u,z)=\frac{1}{R'(z)R'(u)}\Big ( \frac{1}{(u-z)^2}+\frac{1}{(u+z)^2}\Big )\;. \end{aligned}$$

Proof

Inserting (3.12) and (3.14) into (3.11) gives

$$\begin{aligned}&R'(z)\Omega ^{(0)}_2(u,z) -\frac{1}{R'(u)(u+z)^2}-\frac{1}{R'(u)(u-z)^2} \\&\quad = \frac{1}{{\mathfrak {G}}_0(z)}\bigg [ \frac{\lambda }{N^2} \sum _{n,k=1}^d \frac{r_kr_n{\mathcal {T}}^{(0)} (u\Vert \varepsilon _k,\varepsilon _n|)}{ (R(\varepsilon _k)-R(z))(R(\varepsilon _n)-R(-z))} \\&\qquad +\frac{\lambda ^2}{N^2} \sum _{k,l,m,n=1}^d \frac{C_{k,l}^{m,n} \big (\frac{1}{R'(u)(u-\widehat{\varepsilon _l}^n)^2} +\frac{1}{R'(u)(u-\widehat{\varepsilon _k}^m)^2}\big ) }{ (z+\widehat{\varepsilon _l}^n)(z-\widehat{\varepsilon _k}^m)} \bigg ]\;. \end{aligned}$$

Since ${\mathfrak {G}}_0(z)$ has poles at every $z=\pm \widehat{\varepsilon _n}^j$, the rhs of the above equation has poles at most at the zeros of ${\mathfrak {G}}_0$. By assumption, the lhs is regular there. Thus, both sides must be constant by Liouville’s theorem and then, when considering $z\rightarrow \infty$, identically zero.

$\square$

Remark 3.12

Proposition 3.11 indicates that we are on the right track. The solution $\Omega ^{(0)}_2(u,z)$ is symmetric, and its part $\frac{1}{(u-z)^2}$ is closely related to the Bergman kernel $B(u,z)=\frac{du dz}{(u-z)^2}$ of topological recursion. Looking back into Remark 3.2 we can be confident that the complexification procedure of Definition 3.1 is reasonable.

Comparing again with the 2-matrix model, our DSE (3.11) of $\Omega ^{(0)}_{2}$ differs slightly. The last term ${\mathcal {G}}^{(0)}(u,z)$ in (3.11), which generates the pole on the antidiagonal, is not present in the 2-matrix model. We refer for instance to [27, Eqs. (2–20)] with the same identifications as in Remark 3.10 and with $g=0$, $q=p$, $\mathbf {p_K}=\emptyset$ and $|\mathbf {q_L}|=1$. The last term H in [27, Eqs. (2–20)] corresponds to our ${\mathcal {G}}^{(0)}(u,z)$, which is not present for $\mathbf {p_K}=\emptyset$. The distinction between the two different sets $\mathbf {p_K}$ and $\mathbf {q_L}$ is significant for the 2-matrix model.

4 Recursive Solution

In previous sections we have introduced and studied certain families of functions $\Omega ^{(g)}_m(u_1,..,u_m)$, ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z,w|)$, ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z|w|)$ and ${\mathcal {G}}^{(g)}(z,w)$, ${\mathcal {G}}^{(g)}(z|w)$. As already outlined after Definition 2.3, the integers (g, m, b) are interpreted as topological data of a Riemann surface X (see Fig. 3):

• g is the genus of X,

• m is the number of marked points on X,

• b is the number of boundary components of X; more precisely $b=1$ for ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z,w|)$ and $b=2$ for ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z|w|)$.

We let $\chi =2-2g-m-b$ be the Euler characteristic of X.

Fig. 3

The correlation functions relate to topological data of Riemann surfaces X. The Riemann surface corresponding to ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z,w|)$ has g handles, m marked points labelled $u_1,..,u_m$ and one boundary component with two defects (the 1-valent vertices) labelled z and w. The Riemann surface corresponding to ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z|w|)$ has g handles, m marked points labelled $u_1,...,u_m$ and two boundary components each with one defect labelled z or w, respectively. The Riemann surface corresponding to $\Omega ^{(g)}(u_1,...,u_m)$ has g handles, m marked points labelled $u_1,...,u_m$ and no boundary

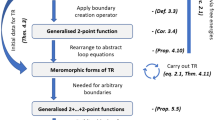
The Dyson-Schwinger equations for the generalised correlation functions $\Omega ^{(g)}_m(u_1,..,u_m)$, ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z,w|)$ and ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z|w|)$ follow a recursion in the Euler characteristic: To compute a generalised correlation function of negative Euler characteristic $-\chi =2g+(m+b)-2$ we need generalised correlation functions of negative Euler characteristic $-\chi '< -\chi$. In case of equality one builds ${\mathcal {T}}^{(g)}(u_1,...,u_{m-1}\Vert z,w|)$ from $\Omega ^{(g)}_m(u_1,...,u_{m-1},z)$. Figure 4 shows the recursive structure in solving the correlation function for small $-\chi$. This structure extends in obvious manner to higher topologies $(g,m+b)$.

Fig. 4

The three types of Dyson-Schwinger Eqs. (3.6), (3.8) and (3.10) are recursively built up and ordered in the negative Euler characteristic $-\chi$. This illustration shows for each $-\chi =2g+m+b-2$, where $b=0$ for $\Omega ^{(g)}_m(u_1,...,u_{m})$, $b=1$ for ${\mathcal {T}}^{(g)}(u_1,...,u_{m1}\Vert z,w|)$ and $b=2$ for ${\mathcal {T}}^{(g)}(u_1,...,u_{m}\Vert z|w|)$, the order in which to compute previous functions via solution of (3.6), (3.8) and (3.10), respectively. The initial case, $\chi =1$ is solved simultaneously by combining two equations

We will prove that the solution of ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z,w|)$ and ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z|w|)$ are obtained by a simple evaluation of residues. For that the following analyticity property is necessary:

Lemma 4.1

Let $I=\{u_1,...,u_m\}$. The generalised correlation functions ${\mathcal {T}}^{(g)}(I\Vert w,z)|$, ${\mathcal {T}}^{(g)}(I\Vert w|z|)$, and $\Omega ^{(g)}_m(I)-\frac{\delta _{g,0}\delta _{m,2}}{(R(u_1)-R(u_2))^2}$ are analytic at any two coinciding variables in the domain ${\mathcal {U}}$ which includes all $\varepsilon _k$ but excludes 0.

Proof

The analyticity property is proved by induction in the Euler characteristic. It is true for ${\mathcal {G}}^{(0)}(z,w)={\mathcal {T}}^{(0)}(\emptyset \Vert z,w|)$ by the explicit form (3.5) and ${\mathcal {G}}^{(0)}(z|w)={\mathcal {T}}^{(0)}(\emptyset \Vert z|w|)$ by the explicit form given in [23]. From Proposition  3.11, we have the limit $\lim _{u\rightarrow z} \big (\Omega ^{(0)}_2(u,z)-\frac{1}{(R(u)-R(z))^2} \big ) =\frac{1}{4z^2(R'(z))^2 }-\frac{R'''(z)}{6 (R'(z))^3} +\frac{(R''(z))^2}{4 (R'(z))^4}$.

Then by induction all terms ${\mathcal {T}}^{(g)}$ and $\Omega ^{(g_1)}_{|I_1|+1}$ with $2g_1+|I_1|\ge 2$ are analytic at coinciding arguments. The only critical terms for $z\rightarrow u_i$ arise in combination

$$\begin{aligned}&\Omega ^{(0)}_2(u_i,z){\mathcal {T}}^{(g)}(I\backslash u_i\Vert z,w|) +\frac{\partial }{\partial R(u_i)}\Big (\frac{{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i,w|)}{R(u_i)-R(z)}\Big ) \\&\quad = \Big (\Omega ^{(0)}_2(u_i,z)-\frac{1}{(R(u_i)-R(z))^2}\Big ) {\mathcal {T}}^{(g)}(I\backslash u_i\Vert z,w|) \\&\qquad +\frac{\partial }{\partial R(u_i)}\Big (\frac{{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i,w|)-{\mathcal {T}}^{(g)}(I\backslash u_i\Vert z,w|)}{R(u_i)-R(z)}\Big )\;, \end{aligned}$$

which is analytic for $z\rightarrow u_i$. Regularity for $w\rightarrow u_i$ is obvious, and regularity for $z\rightarrow w$ holds by induction. Thus, ${\mathcal {T}}^{(g)}(I\Vert z,w|)$ is regular for any $z,w\rightarrow u_i$ and $z\rightarrow w$. Similarly for (3.8). The same argument in the rhs of Proposition 3.9 shows analyticity of $\Omega ^{(g)}_{|I|+1}$ with $2g+I\ge 2$ at any $u_i\rightarrow u_j$. $\square$

4.1 Recursive solution of ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z,w|)$ and ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z|w|)$

The main observation when solving the DSEs (3.6) (or (3.8)) is the rationality of the second term of the lhs in R(z). After multiplication with $\prod _{k=1}^d(R(\varepsilon _k)-R(z))$, the resulting second term becomes a polynomial in R(z) of degree $d-1$. This observation suggests an application of the interpolation formula (see Lemma E.1), where the d distinct numbers are chosen as $x_j=R(-{\hat{w}}^j)$ (or $x_j=R(\alpha _j)$) in order to let the first term of the lhs vanish at $z=-{\hat{w}}^j$ (or at $z=\alpha _j$). The analyticity is easily shown by induction and similar to Lemma 4.1. For the sake of readability we have outsourced Propositions E.2 and E.4 and their proofs to the Appendix E. Here we only give their corollaries:

Corollary 4.2

Let $I=\{u_1,...,u_m\}$. The generalised 2-point function is given by

$$\begin{aligned} {\mathcal {T}}^{(g)}(I\Vert z,w|)&=\lambda {\mathcal {G}}^{(0)}(z,w)\mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow z,-{\hat{w}}^j,u_i,w} \frac{R'(t)\, dt}{(R(z)-R(t))(R(w)-R(-t)){\mathcal {G}}^{(0)}(t,w)} \\&\quad \times \bigg [\sum _{\begin{array}{c} I_1\uplus I_2=I \\ g_1+g_2=g\\ (I_1,g_1)\ne (\emptyset ,0) \end{array}} \Omega ^{(g_1)}_{|I_1|+1}(I_1,t){\mathcal {T}}^{(g_2)}(I_2\Vert t,w|) \\&\qquad + {\mathcal {T}}^{(g-1)}(I,t\Vert t,w|) +\frac{{\mathcal {T}}^{(g-1)}(I\Vert t|w|)}{R(w)-R(t)} \bigg ]. \end{aligned}$$

Fig. 5

Graphical illustration of Corollary 4.2

Instead of providing the technical proof, we have decided to give a graphical interpretation of Corollary 4.2 by cutting the Riemann surface corresponding to the generalised 2-point function. The cut operation itself, as shown in Fig. 5, generates for the generalised 2-point function the factor

$$\begin{aligned} \lambda {\mathcal {G}}^{(0)}(z,w) \frac{R'(t)\, dt}{(R(z)-R(t))(R(w)-R(-t)){\mathcal {G}}^{(0)}(t,w)} \end{aligned}$$

together with a residue operation of t at $z,-{\hat{w}}^j, u_i$ and w. Now, the generalised 2-point function can be cut in three topologically different ways:

• 1. The cut starts from t and ends at t by encircling the set $I_1\subset I$ of marked points and $g_1$ handles. This separates ${\mathcal {T}}^{(g)}(I\Vert z,w|)$ into $\Omega ^{(g_1)}_{|I_1|+1}(I_1,t)$ and ${\mathcal {T}}^{(g_2)}(I_2\Vert t,w|)$. Take the sum over all possibilities with Euler characteristic $\chi \le 0$.

• 2. The cut starts at t, paces through a handle and ends again at t. This removes the handle (reduces the genus by 1) at expense of an additional marked point labelled t.

• 3. The cut starts at t, paces through a handle and ends at the boundary next to w (not at t). This reduces the genus by one and generates the factor $\frac{1}{R(w)-R(t)}$ and two separated boundaries with one defect on each.

It seems that another possible case would be the variant of 3. where the cut does not pace through a handle but ends next to w. This would generate two separated correlation functions of the form ${\mathcal {T}}^{(g')}(I'\Vert t|)$, but these do no exist since the quartic Kontsevich model has no 1-point function (and therefore no generalised 1-point function).

Remark 4.3

This graphical description was already invented for the 2-matrix model to understand graphically any correlation function as a recursion depending on correlation functions of lower topology [28]. However, in the 2-matrix model two different sets of marked points exists, whereas the quartic Kontsevich model has a mixing of those sectors. In general, a proof of graphical rules is achieved by direct derivation via DSEs.

Corollary 4.4

Let $I=\{u_1,...,u_m\}$. Proposition E.4 is equivalent to

$$\begin{aligned}&{\mathcal {T}}^{(g)}(I\Vert z|w|) \\&\quad =\frac{\lambda \prod _{j=1}^d\frac{R(z)-R(\alpha _j)}{ R(z)-R(\varepsilon _j)}}{(R(z)-R(-z))} \mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow z ,\alpha _j,u_i,w} \frac{R'(t)\, dt\prod _{k=1}^d(R(t)-R(\varepsilon _k))}{(R(z)-R(t)) \prod _{k=1}^d(R(t)-R(\alpha _k))} \\&\qquad \times \bigg [\sum _{\begin{array}{c} I_1\uplus I_2=I\\ g_1+g_2=g\\ (I_1,g_1)\ne (\emptyset ,0) \end{array}}\!\!\!\!\! \Omega ^{(g_1)}_{|I_1|+1}(I_1,t) {\mathcal {T}}^{(g_2)}(I_2\Vert t|w|) + {\mathcal {T}}^{(g-1)}(I,t\Vert t|w|) +\frac{{\mathcal {T}}^{(g)}(I\Vert t,w|)}{R(w)-R(t)}\bigg ]\,. \end{aligned}$$

Fig. 6

Graphical illustration of Corollary 4.4

The graphical intepretation (see Fig. 6) of Corollary 4.4 differs slightly from Corollary 4.2 since the initial topological data of ${\mathcal {T}}^{(g)}(I\Vert z|w|)$ differs from ${\mathcal {T}}^{(g)}(I\Vert z,w|)$. The cutting operation itself generates the factor

$$\begin{aligned} \frac{\lambda \prod _{j=1}^d\frac{R(z)-R(\alpha _j)}{ R(z)-R(\varepsilon _j)}}{(R(z)-R(-z))} \frac{R'(t)\, dt\prod _{k=1}^d(R(t)-R(\varepsilon _k))}{(R(z)-R(t)) \prod _{k=1}^d(R(t)-R(\alpha _k))}, \end{aligned}$$

where residues of t are taken at $z ,\alpha _j,u_i,w$. This is due to the fact that the starting boundary has only one defect. The first two cases are essentially the same as in Corollary 4.2. However, the third case differs since two boundaries each with one defect are present. The third case has a cut starting at t and merging into the second boundary next to w. Both boundaries are merged to a single boundary with two defects. Furthermore, the cut not ending at its starting point generates again a factor $\frac{1}{R(w)-R(t)}$, similar to the third case of Corollary 4.2.

Remark 4.5

We have focused the computation in this paper to the generalised 2-point and $1+1$-point function. In a previous version of this paper (e.g. https://arxiv.org/abs/2008.12201v3) we have also defined more general correlation functions. These can be solved exactly with the same graphical rules, but with more possibilities in cutting the Riemann surfaces into different topologies.

4.2 Recursive solution for $\Omega ^{(g)}_m$ under Assumptions on its Poles

The solution of the DSE for $\Omega ^{(g)}_m(u_1,...,u_m)$ in Proposition 3.9 to low $2g+m$ (see Appendix G) suggests the following:

Conjecture 4.6

The function $\Omega ^{(g)}_{m+1}(u_1,...,u_m,z)$ is holomorphic in every $z\in \{\pm \widehat{u_l}^j,\pm \widehat{\varepsilon _k}^j, \pm \varepsilon _k,\pm \alpha _k\}$, where $k,j=1,...,d$ and $l=1,...,m$.

We prove this conjecture in Appendix F for the planar sector $g=0$. Conjecture 4.6 and Lemma 4.1 imply that $\Omega ^{(g)}_m(u_1,...,u_m,z)$ can only have poles at $z=\{0,-u_1,...,-u_m,\beta _1,...,\beta _{2d}\}$, where the $\beta _i$ are the ramification points of R given by $R'(\beta _i)=0$. Being by an easy induction argument a rational function, $\Omega ^{(g)}_m(u_1,...,u_m,z)$ must coincide with the partial fraction decomposition about its set of poles. This partial fraction decomposition can be written as a residue which applied to Proposition 3.9 gives:

Corollary 4.7

Assume Conjecture 4.6 is true for all (g, m). Then for $(g,m)\ne (0,0)$ and $(g,m)\ne (0,1)$ one has

$$\begin{aligned}&R'(z)\Omega ^{(g)}_{m+1}(u_1,...,u_m,z) \\&\quad =\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow 0,-u_l,\beta _i} \frac{dq}{(q-z){\mathfrak {G}}_0(q)} \bigg [\sum _{\begin{array}{c} I_1\uplus I_2=\{u_1,...,u_m\}\\ g_1+g_2=g\\ (I_1,g_1)\ne (\emptyset ,0)\ne (I_2,g_2) \end{array}} \Omega ^{(g_1)}_{|I_1|+1}(I_1,q)\frac{\lambda }{N}\sum _{n=1}^d \frac{ r_n{\mathcal {T}}^{(g_2)}( I_2\Vert q,\varepsilon _n|)}{R(\varepsilon _n)-R(-q)} \\&\qquad +\sum _{j=1}^m \frac{\partial }{\partial R(u_j)} {\mathcal {T}}^{(g)}(u_1,..\check{u_j}..,u_m\Vert u_j,q|) +\frac{\lambda }{N}\sum _{n=1}^d \frac{r_n{\mathcal {T}}^{(g-1)}(u_1,...,u_m,q\Vert q,\varepsilon _n|)}{ R(\varepsilon _n)-R(-q)} \\&\qquad +\frac{\lambda }{N}\sum _{n=1}^d \frac{r_n {\mathcal {T}}^{(g-1)}(u_1,...,u_m\Vert q|\varepsilon _n|)}{ (R(\varepsilon _n)-R(q))(R(\varepsilon _n)-R(-q))} -{\mathcal {T}}^{(g-1)}(u_1,...,u_m\Vert q|q|)\bigg ]\,. \end{aligned}$$

We evaluate in Appendix G the residues of Corollary 4.7 for $\Omega ^{(0)}_{3}(u_1,u_2,z)$, $\Omega ^{(0)}_{4}(u_1,u_2,u_3,z)$ and $\Omega ^{(1)}_{1}(z)$. For convenience we collect these results in Subsect. 4.3. The outcome suggests that the $\Omega ^{(g)}_m$ are closely related to structures in blobbed topological recursion (BTR) [9]. We review in Appendix B central aspects of the BTR. To make contact with BTR we reformulate the solution formulae of our loop equations in terms of meromorphic differential forms:

Definition 4.8

For integers $g\ge 0$ and $m\ge 1$ we introduce meromorphic differentials $\omega _{g,m}$ on $\hat{{\mathbb {C}}}^m$ by

$$\begin{aligned} \omega _{0,1}(z)&:= -R(-z)R'(z)dz \;, \nonumber \\ \omega _{g,m}(z_1,\dots ,z_m)&:= \lambda ^{2-2g-m} \Omega ^{(g)}_m(z_1,\dots ,z_m) \prod _{j=1}^m R'(z_j) dz_j\quad \text {for }2g+m\ge 2\;. \end{aligned}$$

(4.1)

Corollary 4.7 takes the following form:

$$\begin{aligned}&\omega _{g,m+1}(u_1,...,u_m,z) =\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow 0,-u_l,\beta _i} \frac{dz}{(q-z){\mathfrak {G}}_0(q)} \bigg [ \nonumber \\&\sum _{\begin{array}{c} I_1\uplus I_2=\{u_1,...,u_m\}\\ g_1+g_2=g\\ (I_1,g_1)\ne (\emptyset ,0)\ne (I_2,g_2) \end{array}} \omega _{g_1,|I_1|+1}(I_1,q) \frac{\lambda }{N}\sum _{n=1}^d \frac{ r_n{\mathfrak {t}}_{g_2,|I_2|}( I_2\Vert q,\varepsilon _n|)}{R'(q)(R(\varepsilon _n){-}R({-}q))} \nonumber \\&\quad +\sum _{j=1}^m d_{u_j}[{\mathfrak {t}}_{g,m-1}(u_1,..\check{u_j}..,u_m\Vert u_j,q|)]dq \nonumber \\&\quad +\frac{\lambda }{N}\sum _{n=1}^d \frac{r_n{\mathfrak {t}}_{g-1,m+1}(u_1,...,u_m,q\Vert q,\varepsilon _n|)}{ R'(q)(R(\varepsilon _n)-R(-q))} \nonumber \\&\quad +\frac{\lambda }{N}\sum _{n=1}^d \frac{r_n {\mathfrak {t}}_{g-1.m}(u_1,...,u_m\Vert q|\varepsilon _n|)}{ (R(\varepsilon _n)-R(q))(R(\varepsilon _n)-R(-q))}dq -{\mathfrak {t}}_{g-1,m}(u_1,...,u_m\Vert q|q|)dq\bigg ]\,, \end{aligned}$$

(4.2)

where $d_{u_j}$ is the exterior differential in $u_j$ and ${\mathfrak {t}}_{g,m}(u_1,...,u_m\Vert z,w|) := \lambda ^{2g-m} {\mathcal {T}}^{(g)}(z_1,...,z_m\Vert z,w|) \prod _{j=1}^m R'(z_j) dz_j$ as well as ${\mathfrak {t}}_{g,m}(u_1,...,u_m\Vert z|w|) := \lambda ^{-1-2g-m-} {\mathcal {T}}^{(g)}(z_1,...,z_m\Vert z|w|) \prod _{j=1}^m R'(z_j) dz_j$.

The residue in (4.2) provides a natural decomposition

$$\begin{aligned} \omega _{g,m+1}(u_1,...,u_m,z)= {\mathcal {P}}_{z}\omega _{g,m+1}(u_1,...,u_m,z) +{\mathcal {H}}_{z}\omega _{g,m+1}(u_1,...,u_m,z) \end{aligned}$$

(4.3)

into a part

$$\begin{aligned} {\mathcal {P}}_{z}\omega _{g,m+1}(u_1,...,u_m,z) :=\sum _{i=1}^{2d}\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i} \frac{dz}{(q-z){\mathfrak {G}}_0(q)}\Big [\dots \Big ] \end{aligned}$$

whose poles in z are located only at the ramification points $\beta _i$ of R and a part

$$\begin{aligned} {\mathcal {H}}_{z}\omega _{g,m+1}(u_1,...,u_m,z) :=\Big (\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow 0}+\sum _{l=1}^m \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow -u_l}\Big ) \frac{dz}{(q-z){\mathfrak {G}}_0(q)} \Big [\dots \Big ] \end{aligned}$$

which is holomorphic in z at the ramification points. We will discuss these projectors in the context of blobbed topological recursion in Appendix B, too.

4.3 Solution of $\omega _{g,m}$ to low degree

This subsection lists the results for $\omega _{0,3}$, $\omega _{0,4}$ and $\omega _{1,1}$ obtained by evaluating the residues in the system (4.2), (E.2) and (E.4). Appendix G gives details about the procedure and provides a few intermediate results.

We let $\sigma _i$ be the local Galois involution near the ramification point $\beta _i$, i.e. $R(z)=R(\sigma _i(z))$, $\lim _{z\rightarrow \beta _i} \sigma _i(z)=\beta _i$ and $\sigma _i\ne \mathrm {id}$. We let $B(z,w)=\frac{dz\,dw}{(z-w)^2}$ be the Bergman kernel and define $x(z)=R(z)$ and $y(z)=-R(-z)$. Moreover, we introduce two kernel forms

$$\begin{aligned} K_i(z,q)&=\frac{\frac{1}{2}\int _{q'=\sigma _i(q)}^{q'=q}B(z,q') }{ (y(q)-y(\sigma _i(q))dx(\sigma _i(q))}\;,&K_u(z,q)&=\frac{\int _{q'=-q}^{q'=-u} B(z,q')}{y(-q)-y(-u)}\;. \end{aligned}$$

(4.4)

The evaluation of $\omega _{0,3}$ and $\omega _{0,4}$ in Appendix G confirms⁴ for $m\in \{2,3\}$:

Conjecture 4.9

For any $I=\{u_1,..,u_m\}$ with $m\ge 2$ one has

$$\begin{aligned}&\omega _{0,m+1}(I,z) \nonumber \\&\quad = \sum _{i=1}^{2d}\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i} K_i(z,q) \sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1,I_2\ne \emptyset \end{array}} \omega _{0,|I_1|+1}(I_1,q) \omega _{0,|I_2|+1}(I_2,\sigma _i(q)) \nonumber \\&\qquad + \sum _{k=1}^{m} d_{u_k} \Big (\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow u_k} K_{u_k}(z,q) \!\!\!\! \sum _{\begin{array}{c} I_1\uplus ... \uplus I_s=I{\setminus } u_k\\ I_1,...,I_s \ne \emptyset \end{array}} \!\!\!\! \frac{\omega _{0,|I_1|+1}(I_1,-q)}{y(q)-y(u_k)} \prod _{r=2}^s \frac{\omega _{0,|I_r|+1}(I_r,u_k)}{(y(q)-y(u_k))dx(u_k)} \Big ). \end{aligned}$$

(4.5)

We remark that $\omega _{0,m}$ given by Conjecture 4.9 automatically satisfy the linear and quadratic loop equations given later in Definition B.1 or inside Conjecture 5.1.

The residues at $q=\beta _i$ can be evaluated with the formulae given in Appendix C; the residues at $q=u_k$ are straightforward. In terms of

$$\begin{aligned} x_{n,i}:=\frac{R^{(n+2)}(\beta _i)}{R''(\beta _i)}\;,\qquad y_{n,i}:=(-1)^n \frac{R^{(n+1)}(-\beta _i)}{R'(-\beta _i)}\;. \end{aligned}$$

(4.6)

and with $Q(u;z):= \frac{1}{u-z}+\frac{1}{u+z}$ arising in $\omega _{0,2}(u,z)=-d_u[Q(u;z)]dz$, we find

$$\begin{aligned} {\mathcal {P}}_z\omega _{0,3}(u_1,u_2,z)&= -d_{u_1}d_{u_2}\Big [\sum _{i=1}^d \frac{Q(u_1;\beta _i)Q(u_2;\beta _i)}{ R'(-\beta _i)R''(\beta _i) (z-\beta _i)^2}\Big ]dz\;, \end{aligned}$$

(4.7)

$$\begin{aligned} {\mathcal {H}}_z\omega _{0,3}(u_1,u_2,z)&= d_{u_1} \Big [\frac{\omega _{0,2}(u_2,u_1)}{(dR)(u_1) R'(-u_1)(z+u_1)^2}\Big ] +[u_1\leftrightarrow u_2] \end{aligned}$$

(4.8)

and

$$\begin{aligned}&{\mathcal {P}}_z\omega _{0,4}(u_1,u_2,u_3,z) \nonumber \\&\quad =d_{u_1}d_{u_2}d_{u_3}\Big [ \sum _{i=1}^{2d} \frac{Q(u_1;\beta _i)Q(u_2;\beta _i)}{ (R''(\beta _i))^2 (R'(-\beta _i))^2} \Big \{- \frac{Q(u_3;\beta _i)}{(z-\beta _i)^4} +\frac{Q(u_3;\beta _i)}{(z-\beta _i)^3} \frac{x_{1,i}}{3} \nonumber \\&\qquad +\frac{Q'(u_3;\beta _i)}{(z-\beta _i)^2}\frac{x_{1,i}}{2} - \frac{Q''(u_3;\beta _i)}{2(z-\beta _i)^2} +\frac{Q(u_3;\beta _i)}{(z-\beta _i)^2} \Big (\frac{x_{2,i}}{6} -\frac{x_{1,i}^2}{4} -\frac{y_{1,i}x_{1,i}}{6} +\frac{y_{2,i}}{6} \Big ) \Big \} \nonumber \\&\qquad - \frac{Q(u_3;\beta _i)}{R'(-\beta _i)R''(\beta _i) (z-\beta _i)^2} \Big \{ \frac{Q(u_2;u_1)}{R'(u_1)R'(-u_1)(u_1+\beta _i)^2} \nonumber \\&\qquad +\frac{Q(u_1;u_2)}{R'(u_2)R'(-u_2)(u_2+\beta _i)^2} + \sum _{n\ne i} \frac{Q(u_1;\beta _n)Q(u_2;\beta _n)}{ R'(-\beta _n)R''(\beta _n)(\beta _i-\beta _n)^2}\Big \} \nonumber \\&\qquad +[u_3\leftrightarrow u_1]+[u_3\leftrightarrow u_2] \Big ]dz\;, \end{aligned}$$

(4.9)

$$\begin{aligned}&{\mathcal {H}}_z\omega _{0,4}(u_1,u_2,u_3,z) \nonumber \\&\quad =d_{u_3}\Big [ \frac{2\omega _{0,2}(u_1,u_3)\omega _{0,2}(u_2,u_3)}{(dR(u_3))^2 (R'(-u_3))^2} \Big (-\frac{1}{(z+u_3)^3}+\frac{R''(-u_3)}{2R'(-u_3)(z+u_3)^2}\Big ) \nonumber \\&\qquad +\frac{\omega _{0,3}(u_1,u_2,u_3)}{dR(u_3) R'(-u_3) (z+u_3)^2} \Big ]dz +[u_3\leftrightarrow u_1]+[u_3\leftrightarrow u_2]\;, \end{aligned}$$

(4.10)

where in $Q'(u;z),Q''(u;z)$ the derivative is with respect to the second argument. We have simplified (4.10) using the reflection (G.14).

We also have a result for $g=1$:

Proposition 4.10

The solution of (4.2) for $m=0$ and $g=1$ is

$$\begin{aligned} {\mathcal {P}}_z\omega _{1,1}(z)&=\sum _{i=1}^{2d} \frac{dz}{R'(-\beta _i) R''(\beta _i)} \Big \{ -\frac{1}{8 (z-\beta _i)^4} + \frac{x_{1,i}}{24 (z-\beta _i)^3} \\&\quad +\frac{1}{(z-\beta _i)^2}\Big ( \frac{x_{2,i}}{48} - \frac{x_{1,i}^2}{48} -\frac{x_{1,i}y_{1,i}}{48} + \frac{y_{2,i}}{48} - \frac{1}{8 \beta _i^2}\Big ) \Big \} \;, \\ {\mathcal {H}}_z\omega _{1,1}(z)&= -\frac{dz}{8 (R'(0))^2 z^3} +\frac{R''(0)dz}{16(R'(0))^3z^2}\;. \end{aligned}$$

The differential form $\omega _{1,1}$ satisfies for z near $\beta _i$ the loop equations given in Definition B.1.

5 Main Conjecture

We established with the proof of Conjecture 4.9 for $m=2$ and $m=3$ as well as with Proposition 4.10 the unexpected result that all $\omega _{g,m}$ evaluated so far satisfy the linear and quadratic loop equations. This is very unlikely a mere coincidence, which suggests:

Conjecture 5.1

Let $R:\hat{{\mathbb {C}}}\rightarrow \hat{{\mathbb {C}}}$ be the ramified covering defined in (3.5). Let $\beta _1,...,\beta _{2d}$ be its ramification points and $\sigma _i$ the corresponding local Galois involution in the vicinity of $\beta _i$. For all $g\ge 0$ and $m\ge 1$, the meromorphic differentials $\omega _{g,m}$ given by $\omega _{0,1}(z)=-R(-z)R'(z)dz$, $\omega _{0,2}(u_1,z)=\frac{du_1\,dz}{(u_1-z)^2} +\frac{du_1\,dz}{(u_1+z)^2}$ and for $2-2g-m< 0$ by evaluation of the system (4.2), (E.2) and (E.4) are symmetric and satisfy the linear loop equation

$$\begin{aligned} \omega _{g,m}(u_1,...,u_{m-1},z)+ \omega _{g,m}(u_1,...,u_{m-1},\sigma _i(z))= {\mathcal {O}}(z-\beta _i)dz \end{aligned}$$

and the quadratic loop equation

$$\begin{aligned}&\omega _{g-1,m+1}(u_1,...,u_{m-1},z,\sigma _i(z)) + \sum _{\begin{array}{c} I_1\uplus I_2=\{u_1,...,u_{m-1}\}\\ g_1+g_2=g \end{array}} \omega _{g_1,|I_1|+1}(I_1,z) \omega _{g_2,|I_2|+1}(I_2,\sigma _i(z)) \\&\quad ={\mathcal {O}}((z-\beta _i)^2)(dz)^2\;. \end{aligned}$$

If the conjecture is true⁵, it is a general fact established in blobbed topological recursion [9] (and recalled in Appendix B) that the projection to the polar part is given by the universal formula of topological recursion:

$$\begin{aligned}&{\mathcal {P}}_z \omega _{g,m}(u_1,...,u_{m-1},z) \nonumber \\&\quad =\sum _{i=1}^{2d}\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i} \frac{\frac{1}{2}\int _{q'=\sigma (q)}^{q'=q} B(z,q')}{ \omega _{0,1}(q)-\omega _{0,1}(\sigma _i(q))} \Bigg ( \omega _{g-1,m+1}(u_1,...,u_{m-1},q,\sigma _i(q)) \nonumber \\&\qquad + \sum _{\begin{array}{c} I_1\uplus I_2=\{u_1,...,u_{m-1}\}\\ g_1+g_2=g \\ (I_1,g_1)\ne (\emptyset ,0)\ne (I_2,g_2) \end{array}} \omega _{g_1,|I_1|+1}(I_1,q) \omega _{g_2,|I_2|+1}(I_2,\sigma _i(q))\Bigg )\;, \end{aligned}$$

(5.1)

where $B(u,z)=\frac{du\,dz}{(u-z)^2}$ is the Bergman kernel.

6 Conclusion and Outlook

This paper makes the Quartic Kontsevich Model a member of a rich family of models affiliated with the moduli space $\overline{{\mathcal {M}}}_{g,n}$ of stable complex curves. Common to all these models is the possibility to construct all functions of interest (cumulants of a measure, correlation functions, generating functions of something) recursively in decreasing Euler characteristic $\chi =2-2g-n$. The quartic analogue of the Kontsevich model originates from attempts to put the $\lambda \varphi ^4$-quantum field theory model on a noncommutative geometry. It is a Hermitian matrix model in which a Gaußian measure with non-trivial covariance (2.1) is deformed by a quartic potential, see (2.2). This paper shows that the loop equation for the planar 2-point function of the Quartic Kontsevich model, found in [19] and eventually solved in [22], is indeed the initial datum for a novel structure affiliated with $\overline{{\mathcal {M}}}_{g,n}$.

We find that the primary structure of the Quartic Kontsevich Model is not the entirety of cumulants of the quartically deformed measure (as thought before) but a family of auxiliary functions $\Omega ^{(g)}_{q_1,...,q_m}$ introduced in Definition 2.3. They are particular polynomials of cumulants [25]. The $\Omega ^{(g)}_{q_1,...,q_m}$ are extended first to meromorphic functions $\Omega ^{(g)}_m$ and then to meromorphic forms $\omega _{g,m}$ on $\hat{{\mathbb {C}}}^m$. It is convenient to view $\hat{{\mathbb {C}}}^m$ as the space of (complex, compactified) lines through the m marked points of a Riemann surface of genus g, see Fig. 7. The $\Omega ^{(g)}_m$ do not exist alone; there are other families of functions $T^{(g)}_{\dots }$ which interpolate between cumulants and $\Omega$’s. These $T^{(g)}_{\dots }$ extend to meromorphic functions ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z,w|)$ and ${\mathcal {T}}^{(g)}(u_1,...,u_m\Vert z|w|)$ on the space of lines through

• 1. The m marked points of a bordered Riemann surface of genus g with $b=1$ or $b=2$ boundary components,

• 2. Defects on the boundary component(s); it is enough to consider two defects for $b=1$ and one defect on each boundary for $b=2$.

This distinction is nothing new for matrix models. It already appeared for the Hermitian 2-matrix model (2MM) [29] which has mixed-coloured and non-mixed coloured boundaries. The underlying structure of monochromatic boundary correlation functions of the 2MM was proved to follow a topological recursion [5]. However, to compute non-mixed coloured boundary correlation functions the knowledge of mixed-coloured boundary correlation functions is inevitable [27].

The Quartic Kontsevich Model, discussed here, almost shares its structure with the 2MM (cf. (3.6) with [28, Eqs. (1–3)]), even though it is by definition a completely different model. We have shown that the resulting Dyson-Schwinger equations are structurally almost of the same form. We have found an algorithm consisting of three steps (see Fig. 4) to compute a given correlation function of Euler characteristic $\chi -1$ from correlation functions of Euler characteristic $\ge \chi$. We showed that this calculation reduces to an evaluation of residues.

A look upon the explicitly given results for small $(-\chi )$ suggests that the quartic analogue of the Kontsevich model is governed by blobbed topological recursion [9]. This is an extension of topological recursion by an infinite family of initial data $\phi _{g,m}$. For convenience we provide in Appendix B some background information about the BTR.

The final proof of our Main Conjecture 5.1 is on the way. The proof for $g=0$ is accomplished in [11]; there remains little doubt that the result holds in general. The geometric structure is apparent: The spectral curve (of genus zero) is identified and parametrised by

$$\begin{aligned} x(z)&=R(z)\\ y(z)&=-R(-z),\qquad \text {where}\quad R(z)=z-\frac{\lambda }{N}\sum _{n=1}^d \frac{r_n}{R'(\varepsilon _n)(\varepsilon _n+z)}. \end{aligned}$$

The numbers $\varepsilon _n$ are related by $e_p=R(\varepsilon _p)$ to the distinct values $e_p$ occurring with multiplicity $r_p$ in the parameters $E_1,...,E_N$ of the Gaußian measure (2.1).

Our blobbed topological recursion is defined by:

• 1. The covering $x=R:\hat{{\mathbb {C}}}\rightarrow \hat{{\mathbb {C}}}$ of the Riemann sphere ramified at $\{\beta _1,\dots ,\beta _{2d}\}$;

• 2. Two meromorphic differentials

  $$\begin{aligned} \omega _{0,1}(z)&=y(z)dx(z) \qquad \text { on } \hat{{\mathbb {C}}}\;, \nonumber \\ \omega _{0,2}(z,u)&=B(z,u)+\phi _{0,2}(z,u) \qquad \text { on } \hat{{\mathbb {C}}}^2 \;, \end{aligned}$$

  (6.1)

  both regular at the ramification points, where $B(z,u)=\frac{dz\,du}{(z-u)^2}$ is the usual Bergman kernel and $\phi _{0,2}(z,u)=\frac{dz\,du}{(z+u)^2}$ a symmetric 2-form blob with a double pole on the antidiagonal;

• 3. The recursion kernel $K_i(z,q) =\frac{\frac{1}{2}\int _{q'=\sigma _i(q)}^{q'=q} B(z,q')}{ \omega _{0,1}(q)-\omega _{0,1}(\sigma _i(q))}$ constructed with the usual Bergman kernel and the local Galois involution $\sigma _i$ near $\beta _i$.

The presence of a blob $\phi _{0,2}(z,u)$ is an important difference to the standard approach [9]. Moreover, we recall that for the proof of BTR [9] it was sufficient to assume $\omega _{g,m}$ to be defined on disjoint unions $\cup _{i}U_i$ about the ramification points. In contrast, our differential forms $\omega _{g,m}$ are globally defined meromorphic forms on $\hat{{\mathbb {C}}}^m$.

We noticed an intriguing rôle of the global involution $z\mapsto -z$ on $\hat{{\mathbb {C}}}$. This involution is of central importance in [11] for proving Conjecture 5.1 for genus $g=0$. The blobs of higher genus have poles at the fixed point $z=0$ of this involution; also the other poles at $z_i=-z_j$ are related in this way. Since $z\rightarrow -z$ is a very natural structure, we expect that the corresponding intersection numbers have a topological significance. It seems worthwhile to work out details and to compute these numbers. Moreover, comparing our spectral curve (6.1) to [30], we already realised that a subset of the normalised part generates simple Hurwitz numbers. Our partition function is, however, considerably easier and more natural than that of [30].

One can take the point of view that the linear and quadratic loop equations [10] are the heart of TR. Their general solution is blobbed topological recursion [9]; further conditions are necessary to reduce it to pure TR. This raises the question why the original Kontsecich model [1] and a large class of generalisations [31] satisfy these further conditions, whereas the quartic analogue of the Kontsevich model does not. At the moment we do not have a good intuitive explanation, but on a technical level there are several reasons. In Remarks 3.8, 3.10, 3.12 and 4.3 we have indicated similarities and decisive differences to the Hermitean 2-matrix model. Precisely the additional terms compared with the 2-matrix model are responsible for the poles of $\omega _{g,n}$ away from ramification points of x (and the diagonal in case of $\omega _{0,2}$). The Laurent series about these additional poles is completely fixed by our global (on $\hat{{\mathbb {C}}}^n$) loop equations; there is absolutely no freedom in choosing the blobs. This is a clear difference with the original formulation of blobbed topological recursion [9] in which the abstract loop equations are only considered locally in a neighbourhood of the ramification points (so that the blobs can be chosen freely within the constraints of the loop equations).

Another technical reason for BTR is that the $\omega _{g,n}$ in matrix models are typically related to correlations of diagonal matrix elements $\Phi _{aa}$ (such as in the (generalised) Kontsevich model [31]) or correlations of resolvents $\mathrm {Tr}((z-\Phi )^{-1})$ (such as in the 2-matrix model [5]). Because of the invariance of the quartic Kontsevich model under $\Phi \mapsto -\Phi$, these special correlations only give rise to even Euler characteristics. In particular, the initial $\Omega ^{(0)}_1$ cannot be obtained in this way. We have shown in this paper that $\Omega ^{(0)}_1$ in the quartic Kontsevich model is built from the two-point function ${\mathcal {G}}^{(0)}(z,w)$, which has a pole at $z+w=0$. This pole at opposite diagonals proliferates into the $\omega _{g,n}$ for all $2g+n\ge 2$ and induces poles at $z_i=0$ for $g\ge 1$.

Private discussions with B. Eynard and E. Garcia-Failde also suggest that there is hope to formulate the current version of blobbed topological recursion in terms of pure TR by increasing the genus of the spectral curve by 1. The appearance of the same phenomenon in the O(n) model [32] and the remarkable structural analogies of holomorphic and polar parts in the quartic Kontsevich model make this hope a justified research goal for the future, among other stimulating questions arising from this model.

Appendices

Notations and Relations

For the sake of readability, and because we partly deviate from conventions in the literature, we list in the table below a few important notations and symbols used in this paper.

Symbol	Explanation
$E_1,...,E_N$; $\lambda$	Parameters of Gaußian measure and its quartic deformation
$e_k$, $r_k$, d	Distinct values in $(E_l)$, their multiplicities, their number
R(z)	Implicitly defined by $R(z) = z- \frac{\lambda }{N} \sum _{k=1}^d \frac{r_k}{R'(\varepsilon _k)(z+\varepsilon _k)}$, $e_k=R(\varepsilon _k)$
$\varepsilon _k$	Unique solutions in neighbourhood of $\lambda =0$ of $e_k=R(\varepsilon _k)$
${{\hat{z}}}^j$	d preimages with $R(z)=R({{\hat{z}}}^j)$ and $z\ne {\hat{z}}^j$
$\{0,\pm \alpha _i\}$	$2d+1$ solutions of $R(z)-R(-z)=0$
$\beta _i$	2d ramification points, solutions of $R'(z)=0$
$\sigma _i(z)$	Local Galois involution in the vicinity of $\beta _i$, with
	$R(z)=R(\sigma _i(z))$, $\lim _{z\rightarrow \beta _i}\sigma _i(z)=\beta _i$ and $\sigma _i\ne \mathrm {id}$
$G_{|\dots |}$	Correlation functions/cumulants of the deformed measure
${\mathcal {G}}^{(g)}(...)$	Complexification and transformation via R of $G_{|\dots |}$, plus genus expansion. Satisfies ${\mathcal {G}}(\varepsilon _k,...)=G_{|k...|}$
${\mathcal {G}}^{(0)}(z,w)$	Given in Theorem 3.4 as solution of a non-linear equation
$T_{...\Vert \dots |}$	Generalised correlation functions: $E_q$-derivatives of $G_{|\dots |}$ given in Definition 2.3
${\mathcal {T}}^{(g)}(...\Vert ...|)$	Complexification, transformation via R and genus expansion of $T_{...\Vert ...|}$
$\Omega _{q_1...q_m}$	Derivative of $\frac{1}{N}\sum _p G_{|q_1p|}+\frac{1}{N^2}G_{|q_1|q_1|}$ with respect to $E_{q_2},...,E_{q_{m}}$ (see Definition 2.3)
$\Omega ^{(g)}_m(z_1,...,z_m)$	Complexification, transformation via R and genus expansion of $\Omega _{q_1...q_m}$
$\omega _{g,m}(z_1,\dots ,z_m)$	Meromorphic differential $=\lambda ^{2-2g-m} \Omega ^{(g)}_m(z_1,\dots ,z_m) \prod _{j=1}^m R'(z_j) dz_j$
$L(x),L_w(x)$	Lagrange interpolation polynomials
$\chi$	Euler characteristic $\chi =2-2g-m-b$; the $\Omega ^{(g)}_m$ have $b=0$
${\mathfrak {G}}_0(z)$	Auxiliary function ${\mathfrak {G}}_0(z)=\mathop {{{\,\mathrm{Res}\,}}}\limits _{w\rightarrow -z} {\mathcal {G}}^{(0)}(z,w)dw$
$C_{k,l}^{m,n}$	Partial fraction coefficients of ${\mathcal {G}}^{(0)}(z,w)$

Symbol	Explanation
Q(w; z)	Auxiliary function $Q(w;z):=\frac{1}{w+z}+\frac{1}{w-z}$, derivatives $Q'$, $Q''$ etc. with respect to the second argument
B(z, u)	Bergman kernel $B(z,u)=\frac{dz\, du}{(z-u)^2}$
$\phi _{0,2}$	A blob given by $\frac{dz\, du}{(z+u)^2}$
$K_i(z,q)$	Recursion kernel
${\mathcal {H}}_z, {\mathcal {P}}_z$	Projections to holomorphic and polar parts (near ramification points) of meromorphic m-forms

Recap of Blobbed Topological Recursion

The outstanding applicability of topological recursion (TR) to a great bandwidth of mathematical phenomena is clearly undoubted. However, there exist models showing a certain recursive behaviour regarding their solutions of loop equations, but not perfectly fitting into the recursion of ordinary TR, for instance in the Hermitian 1-matrix model extended by multi-trace contributions [33] or in the quartic melonic tensor model [34]. The appearance of poles at $z\in \{0,-u_l\}$ in Corollary 4.7 gave a first hint⁶ to focus on a framework that even enlarges the mentioned bandwidth. Discovered in 2015, it extends the usual TR by additional topological quantities baptised blobs to blobbed topological recursion [9].

It was observed that the loop equations of several (matrix) models can be reduced to a system of linear and quadratic loop equations:

Definition B.1

Let $x:\Sigma \rightarrow \Sigma _0$ be a ramified covering with simple ramification points $\beta _i$ and $\sigma _i$ be the local Galois involution around $\beta _i$, i.e. $x(z)=x(\sigma _i(z))$, $\lim _{z\rightarrow \beta _i} \sigma _i(z)=\beta _i$ and $\sigma _i\ne \mathrm {id}$. A family of meromorphic differential forms $\omega _{g,m}$ on $\Sigma ^m$, with $g \ge 0$ and $m >0$, fulfils the linear loop equation if

$$\begin{aligned} \omega _{g,m+1}(u_1,...,u_m,z)+ \omega _{g,m+1}(u_1,...,u_m,\sigma _i(z))= {\mathcal {O}}(z-\beta _i)dz \end{aligned}$$

(B.1)

is a holomorphic linear form for $z \rightarrow \beta _i$ with (at least) a simple zero at $\beta _i$. The family of $\omega _{g,m}$ fulfils the quadratic loop equation if

$$\begin{aligned} Q^i_{g,m+1}&:=\omega _{g-1,m+2}(u_1,...,u_m,z,\sigma _i(z)) \nonumber \\&+ \sum _{\begin{array}{c} g_1+g_2=g \\ I_1\uplus I_2=\{u_1,...,u_m\} \end{array}} \omega _{g_1,|I_1|+1}(I_1,z) \omega _{g_2,|I_2|+1}(I_2,\sigma _i(z)) \nonumber \\&={\mathcal {O}}((z-\beta _i)^2)(dz)^2 \end{aligned}$$

(B.2)

is a holomorphic quadratic form with at least a double zero at $z \rightarrow \beta _i$.

An important subclass of solutions is given by differentials governed by TR [10]. The entirety of solutions, instead, is provided by BTR. According to Subsect. 4.3, the solutions $\omega _{0,2}$, $\omega _{0,3}$, $\omega _{0,4}$ and $\omega _{1,1}$ of the loop equations of the Quartic Kontsevich Model fulfil the linear and quadratic loop equations. We hope to provide in near future the proof of the natural Main Conjecture 5.1 that all $\omega _{g,m}$ obey these loop equations.

The suggestive notation in (4.3) was inspired by [9] and shall be explained now. In the framework of BTR, one defines projectors ${\mathcal {H}}_z$ and ${\mathcal {P}}_z$ acting on

$$\begin{aligned} \omega _{g,m}(...,z) = {\mathcal {H}}_z\omega _{g,m}(...,z)+ {\mathcal {P}}_z\omega _{g,m}(...,z). \end{aligned}$$

It is shown in [9] that the part ${\mathcal {P}}_z\omega _{g,m}(z_1...,z_{m-1},z)$ is produced by the universal formula of topological recursion from $\omega _{g',m'}$ with $2g'+m'-2<2g+m-2$. The mechanism of BTR can be depicted as in Fig. 7.

Fig. 7

Diagrammatic representation of blobbed topological recursion: $\omega _{g,m}$ is a meromorphic form on a product of $\hat{{\mathbb {C}}}$ (each shown as a line) each attached to a marked point (shown as black dot) on a genus-g Riemann surface (here $g=2$). It is recursively generated. The second and third graph on the rhs are copies of ordinary topological recursion; these provide the part of $\omega _{g,m}$ with poles in $z_1$ at ramification points of $x=R$. The first graph on the rhs, however, depicts the holomorphic part as an additional input of each recursion step. Its poles in $z_1$ are located outside the ramification points of $x=R$.

Applying these projections in every variable decomposes $\omega _{g,m}$ into $2^m$ pieces, among them the purely holomorphic part (for $2g+m-2>0$) $\phi _{g,m}(z_1,...,z_{m-1},z)= {\mathcal {H}}_{z_1}... {\mathcal {H}}_{z_{m-1}}{\mathcal {H}}_z\omega _{g,m}(z_1...,z_{m-1},z)$, called the blob, and the purely polar part ${\mathcal {P}}_{z_1}...{\mathcal {P}}_{z_{m-1}}{\mathcal {P}}_z \omega _{g,m}(z_1...,z_{m-1},z)$. In the special case where ${\mathcal {P}}_{z_1}...{\mathcal {P}}_{z_{m-1}}{\mathcal {P}}_z\omega _{g,m}(z_1...,z_{m-1},z) =\omega _{g,m}(z_1...,z_{m-1},z)$, the solution of abstract loop equations shall be called a normalised one, denoted by $\omega ^o_{g,m}$. In [9] there was developed a diagrammatic representation of (products of) projectors ${\mathcal {H}}$ and ${\mathcal {P}}$ acting on $\omega _{g,m}$.

We will slightly deviate from the above conventions by choosing the unstable blobs $\phi _{0,1},\phi _{0,2}$ differently and by adopting a global formulation. First, we set $\phi _{0,1}=0$ and $\phi _{0,2}(z,u)=\frac{dzdu}{(z+u)^2}$ with $\omega _{0,1}(z)=y(z)dx(z)$ as usual and $\omega _{0,2}(z,u)=B(z,u)+\phi _{0,2}(z,u)$, see (6.1). In the original formulation [9], the Riemann surface ${\mathcal {C}}$ is a disjoint union $\cup _{i}U_i$ of sufficiently small neighbourhoods of the ramification points $\beta _i$. Then ${\mathcal {H}}_z\omega _{g,m}$ is indeed holomorphic in every $z\in {\mathcal {C}}$. In contrast, our Quartic Kontsevich Model is defined globally on $\hat{{\mathbb {C}}}$ so that the term holomorphic part should be treated with more caution. It is rather a relic of previous namings and means holomorphic in ramification points, but with poles somewhere else on $\hat{{\mathbb {C}}}$.

The global formulation also suggests a more natural definition of the projection ${\mathcal {P}}_z$, namely

$$\begin{aligned} {\mathcal {P}}_z\omega (z)=\sum _{i=1}^{2d} {\mathcal {P}}^i_z\omega (z)\;,\qquad {\mathcal {P}}^i_z\omega (z):= \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i}\Big [\omega (q) \int _{\infty }^q B(z,.)\Big ] \end{aligned}$$

(B.3)

for a 1-form $\omega$ in a selected variable (in case there are 2d ramification points). Here $B(z,z')$ is the Bergman kernel; whereas [9] defines ${\mathcal {P}}_z$ with the given bidifferential $\omega _{0,2}(z,z')$. The global formulation allows us to start the contour integral at the special point $\infty \in \hat{{\mathbb {C}}}$ instead of $\beta _i$ chosen in [9]. In particular, our projector (B.3) sees the residue and thus gives the whole principal part of the Laurent series about $\beta _i$.

A main achievement in [9] is a simple proof (which adapts arguments of [10, Proposition 2.7]) that meromorphic m-forms $\omega _{g,m}$ which satisfy the abstract loop equations of Definition B.1 have a polar part given by the universal TR-formula. The essence of the proof remains unchanged when defining the polar part via (B.3). We find it convenient to sketch the arguments. For z near $\beta _i$ and $I=\{z_1,...,z_{m-1}\}$ define

$$\begin{aligned} {\mathcal {S}}^i_z \omega _{g,m}(I,z)&= \omega _{g,m}(I,z)+ \omega _{g,m}(I,\sigma _i(z))\;, \\ \Delta ^i_z \omega _{g,m}(I,z)&= \omega _{g,m}(I,z)- \omega _{g,m}(I,\sigma _i(z))\;. \end{aligned}$$

The quadratic loop Eq. (B.2) can be written as ${\mathcal {P}}^i_z \big [\frac{Q^i_{g,m}(I,z) }{\Delta ^i_z \omega _{0,1}(z)} \big ] = 0$. Indeed, $\Delta ^i_z \omega _{0,1}(z)$ has a double zero at every $z=\beta _i$ so that $\frac{Q^i_{g,m}(I,z) }{\Delta ^i_z \omega _{0,1}(z)}$ is holomorphic in $z=\beta _i$. Write $Q^i_{g,m}(I,z)=\omega _{0,1}(z) S^i_z\omega _{g,m}(I,z) -\omega _{g,m}(I,z)\Delta ^i_z\omega _{0,1}(z) +{\tilde{Q}}^i_{g,m}(I,z)$ where ${\tilde{Q}}^i_{g,m}(I,z)$ excludes both terms with $\omega _{0,1}$ in $Q^i_{g,m}$. Both $\omega _{0,1}(z)$ and (by the linear loop equation) $S^i_z\omega _{g,m}(I,z)$ have a simple zero at $z=\beta _i$ so that we arrive at

$$\begin{aligned} {\mathcal {P}}^i_z \omega _{g,m}(I,z)= {\mathcal {P}}^i_z \Big [\frac{{\tilde{Q}}^i_{g,m}(I,z)}{\Delta ^i_z\omega _{0,1}(z)}\Big ] =\frac{1}{2}{\mathcal {P}}^i_z \Big [\frac{{\tilde{Q}}^i_{g,m}(I,z)}{ \Delta ^i_z\omega _{0,1}(z)}\Big ] -\frac{1}{2}{\mathcal {P}}^i_{\sigma _i(z)} \Big [\frac{{\tilde{Q}}^i_{g,m}(I,z)}{\Delta ^i_z\omega _{0,1}(z)}\Big ]\;. \end{aligned}$$

The second equality follows from the antisymmetry of $\frac{{\tilde{Q}}^i_{g,m}(I,z)}{\Delta ^i_z\omega _{0,1}(z)}$ under the involution $z\leftrightarrow \sigma _i(z)$. Inserting this result into (B.3) establishes

$$\begin{aligned} {\mathcal {P}}_z \omega _{g,m}(I,z)&= \sum _{i=1}^{2d} \mathop {{{\,\mathrm{Res}\,}}}\limits _{q \rightarrow \beta _i} K_i(z,q) {\tilde{Q}}^i_{g,m}(I,q) \\ \text { with }K_i(z,q)&=\frac{\frac{1}{2}\int _{q'=\sigma _i(q)}^{q'=q} B(z,q')}{ \omega _{0,1}(q)-\omega _{0,1}(\sigma _i(q))}\;. \end{aligned}$$

It writes out as in (5.1).

Local Galois Involution and Recursion Kernel

Let $x:\hat{{\mathbb {C}}}\rightarrow \hat{{\mathbb {C}}}$ be a ramified covering of the Riemann sphere with simple ramification points, $\omega _{0,1}(z)=y(z)dx(z)$ a meromorphic 1-form which is holomorphic in the ramification points of x, and $B(z_1,z_2)=\frac{dz_1dz_2}{(z_1-z_2)^2}$ be the standard Bergman kernel on $\hat{{\mathbb {C}}}^2$. For a ramification point $\beta _i$ of x, determined by $x'(\beta _i)=0$, let $\sigma _i$ be the local Galois involution in a neighbourhood ${\mathcal {U}}_i$ of $\beta _i$, determined by $x(\sigma _i(z))=x(z)$, $\lim _{z\rightarrow \beta _i}\sigma _i(z)=\beta _i$ and $\sigma _i\ne \mathrm {id}$. Let

$$\begin{aligned} x_{n,i}:=\frac{x^{(n+2)}(\beta _i)}{x''(\beta _i)}\;,\qquad y_{n,i}:=\frac{y^{(n+1)}(\beta _i)}{y'(\beta _i)}\;. \end{aligned}$$

(C.1)

Lemma C.1

The local Galois involution $\sigma _i$ in ${\mathcal {U}}_i$ has a formal power series expansion $\sigma _i(q)=\beta _i+\sum _{n=0}^\infty c_{n,i}(q-\beta _i)^{n+1}$ whose coefficients are recursively given by $c_{0,i}=-1$ and for $n \ge 1$ by

$$\begin{aligned} c_{n,i}&=\frac{(-1)^n-1}{(n+2)!}x_{n,i} +\frac{1}{2}\sum _{k=1}^{n-1}c_{k,i}c_{n-k,i}+\frac{1}{(n+2)!} \sum _{k=3}^{n+1}x_{k-2,i}b_{n+2,k,i}(x)\;, \\&\quad \text {where } b_{n,k,i}(x):= B_{n,k}(1!c_{0,i},2!c_{1,i}, ...,(n{-}k{+}1)!c_{n-k,i})\;. \end{aligned}$$

Here $B_{n,k}$ are the Bell polynomials. The first examples are

$$\begin{aligned} c_{1,i}&=-\frac{x_{1,i}}{3}\;,&c_{2,i}&=-\frac{x_{1,i}^2}{9}\;,\quad \\ c_{3,i}&=-\frac{2 x_{1,i}^3}{27} +\frac{x_{1,i}x_{2,i}}{18}-\frac{x_{3,i}}{60}\;,\quad&c_{4,i}&= -\frac{4x_{1,i}^4}{81}+\frac{x_{1,i}^2x_{2,i}}{18} -\frac{x_{1,i}x_{3,i}}{60}\;. \end{aligned}$$

Proof

Insert the power series ansatz into the identity $0=x(\sigma _i(q))-x(q)$ for q in a neighbourhood of $\beta _i$. Then all derivatives with respect to q vanish at $q=\beta _i$ so that we have from Faà di Bruno’s formula and with $x'(\beta _i)=0$

$$\begin{aligned} x^{(n)}(\beta _i) = \sum _{k=2}^n x^{(k)}(\beta _i)\cdot b_{n,k,i}(x)\;. \end{aligned}$$

This gives $c_{0,i}^2=1$ for $n=2$. The solution $c_{0,i}=1$ selects the primary branch $c_{n,i}=0$ for all $n\ge 1$. For the local Galois involution we thus have $c_{0,i}=-1$. Solving the resulting equations by using the definition for the following Bell polynomials $b_{n,n,i}(x)=(-1)^n$ and

$$\begin{aligned} b_{n,2,i}(x)= n! \Big ( -c_{n-2,i}+\frac{1}{2}\sum _{k=1}^{n-3}c_{k,i}c_{n-2-k,i}\Big ) \end{aligned}$$

gives after shifting $n\rightarrow n+2$ and dividing by $x''(\beta _i)$ the desired recursion. $\square$

The recursion kernel near a ramification point $\beta _i$ specifies to

$$\begin{aligned} K_i(z,q) = \frac{\big (\frac{1}{z-q}-\frac{1}{z-\sigma _i(q)}\big )dz}{ 2 (y(q)-y(\sigma _i(q))) x'(\sigma _i(q)) d\sigma _i(q)}\;. \end{aligned}$$

(C.2)

In terms of $b_{n,k,i}(x)$, the terms in the recursion kernel expand into

$$\begin{aligned} \frac{1}{z-q}-\frac{1}{z-\sigma _i(q)}&=\sum _{n=1}^\infty \frac{(q-\beta _i)^n}{n!} \Big ( \frac{n!}{(z-\beta _i)^{n+1}} -\sum _{k=1}^n \frac{k!}{(z-\beta _i)^{k+1}}b_{n,k,i}(x)\Big )\;, \\ y(q)-y(\sigma _i(q))&= y'(\beta _i)\sum _{n=1}^\infty \frac{(q-\beta _i)^n}{n!}\Big ( y_{n-1,i} - \sum _{k=1}^n y_{k-1,i} b_{n,k,i}(x)\Big )\;, \\ x'(\sigma _i(q))&= x''(\beta _i)\sum _{n=1}^\infty \frac{(q-\beta _i)^n}{n!} \sum _{k=1}^n x_{k-1,i} b_{n,k,i}(x)\;. \end{aligned}$$

Up to order ${\mathcal {O}}((q-\beta _i)^3)$ we thus get

$$\begin{aligned}&K_i(z,q) \\&\quad =\frac{dz}{x''(\beta _i)y'(\beta _i) d\sigma _i(q)}\Big \{ -\frac{1}{2(z-\beta _i)^2(q-\beta _i)} -\frac{x_{1,i}}{12(z-\beta _i)^2} \\&\qquad +\Big [ \Big (- \frac{x_{1,i}^2 }{8} -\frac{x_{1,i} y_{1,i}}{12} + \frac{x_{2,i} }{12} + \frac{y_{2,i} }{12} \Big ) \frac{(q-\beta _i)}{(z-\beta _i)^2} \\&\qquad +\frac{x_{1,i}}{6}\frac{(q-\beta _i)}{(z-\beta _i)^3} -\frac{1}{2}\frac{(q-\beta _i)}{(z-\beta _i)^4}\Big ] \\&\qquad +\Big [\Big ( - \frac{37 x_{1,i}^3}{432} -\frac{x_{1,i}^2 y_{1,i}}{24} + \frac{x_{1,i} x_{2,i}}{12} + \frac{x_{1,i}y_{2,i} }{24} - \frac{x_{3,i}}{80} \Big ) \frac{(q-\beta _i)^2}{(z-\beta _i)^2} \\&\qquad + \frac{x_{1,i}^2}{12}\frac{(q-\beta _i)^2}{(z-\beta _i)^3} - \frac{x_{1,i}}{4} \frac{(q-\beta _i)^2}{(z-\beta _i)^4}\Big ] \\&\qquad +\Big [\Big ( - \frac{209 x_{1,i}^4}{2592} - \frac{19 x_{1,i}^3 y_{1,i} }{432} -\frac{x_{1,i}^2 y_{1,i}^2 }{72} + \frac{17 x_{1,i}^2 x_{2,i}}{144} + \frac{x_{1,i} x_{2,i} y_{1,i}}{36} \\&\qquad + \frac{19 x_{1,i}^2 y_{2,i}}{432} + \frac{x_{1,i} y_{1,i} y_{2,i}}{36} - \frac{x_{2,i}^2}{72} - \frac{23 x_{1,i} x_{3,i}}{720} - \frac{x_{3,i} y_{1,i}}{240} - \frac{x_{2,i} y_{2,i}}{72} \\&\qquad - \frac{y_{2,i}^2}{72} - \frac{x_{1,i} y_{3,i}}{72} + \frac{x_{4,i}}{240} + \frac{y_{4,i}}{240} \Big ) \frac{(q-\beta _i)^3}{(z-\beta _i)^2} \\&\qquad + \Big ( \frac{19 x_{1,i}^3}{216} +\frac{x_{1,i}^2 y_{1,i}}{36} - \frac{x_{1,i} x_{2,i}}{18} - \frac{x_{1,i} y_{2,i}}{36} + \frac{x_{3,i}}{120} \Big ) \frac{(q-\beta _i)^3}{(z-\beta _i)^3} \\&\qquad +\Big ( - \frac{19 x_{1,i}^2}{72} - \frac{x_{1,i} y_{1,i}}{12} + \frac{x_{2,i}}{12} + \frac{y_{2,i}}{12} \Big ) \frac{(q-\beta _i)^3}{(z-\beta _i)^4} \\&\qquad + \frac{x_{1,i}}{3} \frac{(q-\beta _i)^3}{(z-\beta _i)^5} - \frac{1}{2}\frac{(q-\beta _i)^3}{(z-\beta _i)^6}\Big ] \\&\qquad +{\mathcal {O}}((q-\beta _i)^4)\Big \}\;. \end{aligned}$$

Graphical Derivation of the Dyson-Schwinger Equations

Since all the correlation functions have a combinatorial interpretation, also the DSE’s of Proposition 2.5 can be described combinatorially in terms of ribbon graphs. The correlation function are generating series of those ribbon graphs; we refer to [25] for more details and precise definitions.

Before, we need two further relations between generalised correlation functions achieved by applying (2.8).

1.1 Ward-Takahashi identity for generalised correlation functions

We will represent higher correlation function through lower ones by summing over one of the indices:

Lemma D.1

Let $I=\{q_1,...,q_m\}$. Then we have the identity

$$\begin{aligned} -\frac{T^{(g)}_{I\Vert nq|}-T^{(g)}_{I\Vert pq|}}{E_n-E_p}&=\frac{1}{N}\sum _{\begin{array}{c} k=1\\ k\notin I \end{array}}^N T^{(g)}_{I\Vert pknq|}+\sum _{\begin{array}{c} g_1+g_2=g\\ I_1 \uplus I_2=I \end{array}} T^{(g_1)}_{I_1\Vert pq|}T^{(g_2)}_{I_2\Vert qn|} \nonumber \\&\quad -\sum _{q_i\in I}\frac{\partial }{\partial E_{q_i}} T^{(g)}_{I\setminus q_i\Vert pq_inq|} +T^{(g-1)}_{I\Vert p|pnq|}+T^{(g-1)}_{I\Vert n|pnq|}+T^{(g-1)}_{I\Vert pq|nq|}. \end{aligned}$$

Proof

The Ward-Takahashi identity for the 4-point function was already derived in [23, Eq. (B.5)], that is

$$\begin{aligned} -\frac{G^{(g)}_{|qn|}-G^{(g)}_{|pq|}}{E_n-E_p}&=\frac{1}{N}\sum _{k=1}^NG^{(g)}_{|pknq|} +\sum _{g_1+g_2=g} G^{(g_1)}_{|pq|}G^{(g_2)}_{|qn|}\\&\quad +G^{(g-1)}_{|p|pnq|}+G^{(g-1)}_{|n|pnq|} +G^{(g-1)}_{|pq|nq|}. \end{aligned}$$

Applying the operator $D_I:=\frac{(-N)^m \partial ^m}{\partial E_{q_1}\cdots \partial E_{q_m}}$ to the identity and making use of Definition 2.3 yields the assertion. $\square$

Lemma D.2

Let $I=\{q_1,...,q_m\}$. Then we have the identity

$$\begin{aligned} -\frac{T^{(g)}_{I\Vert p|q|}-T^{(g)}_{I\Vert n|q|}}{E_p-E_n}&=\frac{1}{N}\sum _{\begin{array}{c} k=1\\ k\notin I \end{array}}^NT^{(g)}_{I\Vert pkn|q|} -\sum _{q_i\in I}\frac{\partial }{\partial E_{q_i}} T^{(g)}_{I\setminus q_i\Vert pq_in|q|}+T^{(g)}_{I\Vert pqqn|} \nonumber \\&\quad + \!\! \sum _{\begin{array}{c} g_1+g_2=g\\ I_1 \uplus I_2=I \end{array}} T^{(g_1)}_{I_1\Vert pn|}\bigg (T^{(g_2)}_{I_2\Vert q|n|}+T^{(g_2)}_{I_2\Vert q|p|}\bigg ) +T^{(g-1)}_{I\Vert q|n|pn|}+T^{(g-1)}_{I\Vert q|p|pn|}. \end{aligned}$$

Proof

The Ward-Takahashi identity for the $3+1$-point function was already derived in [23, Eq. (B.6)], that is

$$\begin{aligned} -\frac{G^{(g)}_{|n|q|}-G^{(g)}_{|p|q|}}{E_n-E_p}&= \frac{1}{N}\sum _{k=1}^NG^{(g)}_{|pkn|q|} +G^{(g)}_{|pqqn|} + \!\!\! \sum _{g_1+g_2=g} \!\!\! G^{(g_1)}_{|pn|}\Big (G^{(g_2)}_{|q|n|}+G^{(g_2)}_{|q|p|}\Big )\\&+G^{(g-1)}_{|q|n|pn|}+G^{(g-1)}_{|q|p|pn|}. \end{aligned}$$

Applying the operator $D_I:=\frac{(-N)^m \partial ^m}{\partial E_{q_1}\cdots \partial E_{q_m}}$ to the identity and making use of Definition 2.3 yields the assertion. $\square$

1.2 Graphical derivation of (2.14)

We will start with the DSE (3) of Proposition 2.5, which is achieved combinatorially by an action of the operation $-N\frac{\partial }{\partial E_q}$ on $\Omega _{I}$ with $q\notin I$ (this was discussed in [25] in greater detail). The derivative acts on an edge adjacent to an internal face, splitting the edge and fixing the label of the internal face to q. There are three different cases depending on the other adjacent face to this edge:

• (a) If the other adjacent face is also an internal face labelled by l, a generalised 2-point function appears with a sum over this external face l, which is $\frac{1}{N}\sum _{l=1}^NT_{I\Vert ql|}$.

• (b) If the other adjacent face is labelled by $q_i\in I$, a generalised 2-point function appears with external faces q and $q_i$. A derivative of the form $-N\frac{\partial }{ \partial E_{q_i}}$ has to be taken only acting on the face labelled by $E_{q_i}$ since this face has one additional edge already split, that is $-\frac{\partial ^{ext} T_{I\setminus q_i\Vert qq_i|}}{\partial E_{q_i}}$ as defined in (3.1). A sum over all possible $q_i$ has to be taken.

• (c) If the other adjacent face is the same face, a generalised $1+1$-point function appears with one genus less and two external faces labelled by q each of length one, that is $\frac{1}{N^2}T_{I\Vert q|q|}$.

Combining case (a) and (b) via

$$\begin{aligned} -N\frac{\partial }{\partial E_{q_i}}T_{I\setminus q_i\Vert qq_i|} =T_{I\Vert qq_i|}-N\frac{\partial ^{ext} }{\partial E_{q_i}}T_{I\setminus q_i\Vert qq_i|}, \end{aligned}$$

(D.1)

where we have used (3.1), we obtain the DSE (2.14).

1.3 Graphical derivation of (2.12)

Fig. 8

Generic deletion of the first vertex for the generalised 2-point function, which separates the free propagator from the rest. This operation generates the factor $\frac{-\lambda }{E_p+E_q}$

The DSE (1) of Proposition 2.5 is achieved by a bijection between $T^{(g)}_{I\Vert pq|}$, a generating series of ribbon graphs with a certain structure, and other generating series via an operation we call vertex deletion (of the first vertex). The generic deletion is drawn in Fig. 8. We will distinguish between six topologically different cases depending on the choice of n in Fig. 8. For each choice of n, we get several subcases according to the choice of k, which we do not draw in general. However, it is evident by the distinctions in n how these different topologies for k should look like.

• (a) Generic n: Here, k can be an internal face label running from 1 to N with the prefactor $\frac{1}{N}$; the correlation function on the rhs of Fig. 8 therefore is

  $$\begin{aligned} \frac{1}{N}\sum _{k=1}^NT^{(g)}_{I\Vert pknq|}. \end{aligned}$$

  However, five further subcases occur, depending on the choice of k:

  • For $k=q$: The rhs can be split into two components with the structure $T^{(g_1)}_{I_1\Vert pq|}T^{(g_2)}_{I_2\Vert qn|}$ with $g_1+g_2=g$ and $I_1\uplus I_2=I$.

  • For $k=q_i\in I$: The rhs has an extra derivative on the face labelled by $q_i$ coming from the split edge of the square-vertex, that is $-\frac{\partial ^{ext}}{\partial E_{q_i}}T^{(g)}_{I\setminus q_i\Vert pq_inq|}$.

  • For $k=p$: A reduction of the genus by one can be generated with two boundary components one of length 1 and the other of length 3, so we obtain $T^{(g-1)}_{I\Vert p|pnq|}$.

  • For $k=n$: A reduction of the genus by one can be generated with two boundary components one of length 1 and the other of length 3, so we obtain $T^{(g-1)}_{I\Vert n|pnq|}$.

  • For $k=q$: A reduction of the genus by one can be generated with two boundary components of length 2, so we obtain $T^{(g-1)}_{I\Vert pq|nq|}$.

  These six terms can be combined and surprisingly the identity of Lemma D.1 can be applied exactly. Consequently, including the deleted free propagator and the vertex, we obtain after summation over n

  $$\begin{aligned}&\frac{-\lambda }{E_p+E_q}\frac{1}{N}\sum _{n=1}^N \bigg [\frac{1}{N}\sum _{k=1}^NT^{(g)}_{I\Vert pknq|} +\sum _{\begin{array}{c} g_1+g_2=g\\ I_1 \uplus I_2=I \end{array}} T^{(g_1)}_{I_1\Vert pq|}T^{(g_2)}_{I_2\Vert qn|} \nonumber \\&\qquad -\sum _{q_i\in I}\frac{\partial ^{ext}}{\partial E_{q_i}} T^{(g)}_{I\setminus q_i\Vert pq_inq|} +T^{(g-1)}_{I\Vert p|pnq|}+T^{(g-1)}_{I\Vert n|pnq|}+T^{(g-1)}_{I\Vert pq|nq|}\bigg ] \nonumber \\&\quad =\frac{\lambda }{E_p+E_q}\frac{1}{N}\sum _{n=1}^N \frac{T^{(g)}_{I\Vert nq|}-T^{(g)}_{I\Vert pq|}}{E_n-E_p}. \end{aligned}$$

  (D.2)

• (b) For $n=p$: There is one case where the correlation function is split into two components after deleting the first vertex. Depending on k, the three different subcases are drawn in Fig. 9.

  • For generic k: The sum over k is taken and the two components have the form $T^{(g_1)}_{I_1\Vert pk|}T^{(g_2)}_{I_2\Vert pq|}$ with $g_1+g_2=g$ and $I_1\uplus I_2=I$.

  • For $k=p$: A reduction of the genus by one can be generated with two boundaries for one of the correlation functions, we obtain $T^{(g_1-1)}_{I_1\Vert p|p|}T^{(g_2)}_{I_2\Vert pq|}$.

  • For $k=q_i\in I$: One correlation function gets an additional derivative wrt to the external face $q_i$ that is $(-\frac{\partial ^{ext}}{\partial E_{q_i}}T^{(g_1)}_{I_1\setminus q_i\Vert pq_i|})T^{(g_2)}_{I_2\Vert pq|}$.

  Including the deleted free propagator and applying the DSE (2.14) with $g_1$ and $I_1$, we finally obtain

  $$\begin{aligned}&\frac{-\lambda }{E_p+E_q}\sum _{\begin{array}{c} g_1+g_2=g\\ I_1 \uplus I_2=I \end{array}}T^{(g_2)}_{I_2\Vert pq|}\bigg [\frac{1}{N}\sum _{k=1}^NT^{(g_1)}_{I_1\Vert pk|} +T^{(g_1-1)}_{I_1\Vert p|p|}-\sum _{q_i\in I}\frac{\partial ^{ext}}{\partial E_{q_i}}T^{(g_1)}_{I_1\setminus q_i\Vert pq_i|}\bigg ]\nonumber \\&\quad =\frac{-\lambda }{E_p+E_q}\sum _{\begin{array}{c} g_1+g_2=g\\ I_1 \uplus I_2=I \end{array}}T^{(g_2)}_{I_2\Vert pq|}\Omega ^{(g_1)}_{I_1,p}. \end{aligned}$$

  (D.3)

• (c) For $n=p$: There is a second case where the correlation function is not split into two components, see Fig. 10. The genus is reduced by one and we can again distinguish between different k.

  • For generic k: There is an internal face labelled by k, we take the sum and have $\frac{1}{N}\sum _{k=1}^NT^{(g-1)}_{I\Vert pk|pq|}$.

  • For $k=q_i$: We have an additional derivative wrt to the external face labelled by $q_i$, that is $-\frac{\partial ^{ext}}{\partial E_{q_i}}T^{(g-1)}_{I\Vert pq_i|pq|}$.

  • For $k=p$: The genus can be reduced by one more. In total three boundaries are generated two with length 1 and one with length 2. The correlation function is of the form $T^{(g-2)}_{I\Vert p|p|pq|}$.

  • For $k=p$: Two boundaries can merge such that only one boundary of length 4 remains, $T^{(g-1)}_{I\Vert pppq|}$.

  • For $k=q$: Two boundaries can merge such that only one boundary of length 4 remains, $T^{(g-1)}_{I\Vert pqpq|}$.

  These cases sum again together to the following

  $$\begin{aligned}&\frac{-\lambda }{E_p+E_q}\bigg [ \frac{1}{N}\sum _{k=1}^NT^{(g-1)}_{I\Vert pk|pq|} -\sum _{q_i\in I}\frac{\partial ^{ext}}{\partial E_{q_i}}T^{(g-1)}_{I\Vert pq_i|pq|} \nonumber \\&\qquad +T^{(g-2)}_{I\Vert p|p|pq|}+T^{(g-1)}_{I\Vert pppq|}+T^{(g-1)}_{I\Vert pqpq|}\bigg ] \nonumber \\&\quad =\frac{-\lambda }{E_p+E_q}\,T^{(g-1)}_{I,p\Vert pq|}. \end{aligned}$$

  (D.4)

  This can be seen by deriving $-N\frac{\,\partial }{\partial E_{p'}}T^{(g)}_{I\Vert pq|}$, where we consider the same action as described in Sect. D.2 plus two additional cases: If the other adjacent face is an external face either labelled by p or q, then a boundary of length 4 is generated, that is $T^{(g)}_{I\Vert pp'pq|}$ or $T^{(g)}_{I\Vert qp'qp|}$:

  $$\begin{aligned}&\frac{1}{N}\sum _{k=1}^NT^{(g)}_{I\Vert p'k|pq|} -\sum _{q_i\in I}\frac{\partial ^{ext}}{\partial E_{q_i}}T^{(g)}_{I\Vert p'q_i|pq|} +T^{(g-1)}_{I\Vert p'|p'|pq|}+T^{(g)}_{I\Vert pp'pq|}+T^{(g)}_{I\Vert qp'qp|}\\&\quad =T^{(g)}_{I,p'\Vert pq|}. \end{aligned}$$

  This identity is then applied with $p'=p$ and $g\mapsto g-1$.

• (d) For $n=q_i\in I$: There is an overall derivative $-\frac{\partial ^{ext}}{\partial E_{q_i}}$. Combinatorially, all the cases are exactly the same as for generic n, but with $I\setminus q_i$ instead of I, see Fig. 11. So we conclude equivalently to case a)

  $$\begin{aligned} -\frac{\lambda }{E_p+E_q}\sum _{q_i\in I} \frac{\partial ^{ext}}{\partial E_{q_i}}\frac{T^{(g)}_{I\setminus q_i\Vert q_iq|} -T^{(g)}_{I\setminus q_i \Vert pq|}}{E_{q_i}-E_p} \end{aligned}$$

  (D.5)

• (e) For $n=q$: Fig. 12 shows that for generic k the genus is reduced by one. Here again, we have several subcases:

  • For generic k: The sum over k remains since k is an interal face, that is $\frac{1}{N}\sum _{k=1}^NT^{(g-1)}_{I\Vert pkq|q|}$.

  • For generic $k=q_i\in I$: One overall derivative appears such that we have $-\frac{\partial ^{ext}}{\partial E_{q_i}}T^{(g-1)}_{I\setminus q_i\Vert pq_iq|q|}$.

  • For $k=q$: Both boundaries can merge such that one boundary remains of length 4, $T^{(g-1)}_{I\Vert pqqq|}$.

  • For $k=q$: Also a splitting in two components can occur $T^{(g_1)}_{I_1\Vert pq|}T^{(g_2-1)}_{I_2\Vert q|q|}$ with $g_1+g_2=g$ and $I_1\uplus I_2=I$.

  • For $k=p$: A similar splitting in two components can occur $T^{(g_1)}_{I_1\Vert pq|}T^{(g_2-1)}_{I_2\Vert q|p|}$.

  • For $k=q$: Also a reduction by one further genus can occur, which has three boundaries of the form $T^{(g-2)}_{I\Vert q|q|pq|}$.

  • For $k=p$: Also a reduction by one further genus can occur, which has three boundaries of the form $T^{(g-2)}_{I\Vert q|p|pq|}$.

  Summing all subcases, the identity of Lemma D.2 applies perfectly, and we conclude

  $$\begin{aligned}&-\frac{\lambda }{E_p+E_q}\bigg [ \frac{1}{N}\sum _{k=1}^NT^{(g-1)}_{I\Vert pkq|q|} -\sum _{q_i\in I}\frac{\partial ^{ext}}{\partial E_{q_i}} T^{(g-1)}_{I\setminus q_i\Vert pq_iq|q|}+T^{(g-1)}_{I\Vert pqqq|} \nonumber \\&\qquad +\sum _{\begin{array}{c} g_1+g_2=g\\ I_1 \uplus I_2=I \end{array}} T^{(g_1)}_{I_1\Vert pq|}\bigg (T^{(g_2-1)}_{I_2\Vert q|q|}+T^{(g_2-1)}_{I_2\Vert q|p|}\bigg ) +T^{(g-2)}_{I\Vert q|q|pq|}+T^{(g-2)}_{I\Vert q|p|pq|}\bigg ]\nonumber \\&\quad =\frac{\lambda }{E_p+E_q}\,\frac{T^{(g-1)}_{I\Vert p|q|}-T^{(g-1)}_{I\Vert q|q|}}{E_p-E_q}. \end{aligned}$$

  (D.6)

Fig. 9

Three cases depending on k for the generalised 2-point function with $n=p$. The first vertex is drawn in the middle seperately

Fig. 10

The generalised 2-point function with $n=p$ but no seperation into two components. The first vertex is drawn in the middle seperately

Fig. 11

The generalised 2-point function with $n=q_i$, which is similar to the generic n case

Fig. 12

The generalised 2-point function with $n=q$ is reduced by one genus, but has at least two boundaries

Finally, including the free propagator for the genus $g=0$ and $I=\emptyset$ we obtain the DSE

$$\begin{aligned} T^{(g)}_{I\Vert pq|}=\frac{\delta _{0,g}\delta _{0,|I|}}{E_p+E_q} +\mathrm{(D.2)}+\mathrm{(D.3)} +\mathrm{(D.4)}+\mathrm{(D.5)} +\mathrm{(D.6)} \end{aligned}$$

which coincides with (2.12) after considering (D.1) and its definition (3.1).

1.4 Graphical derivation of (2.13)

The DSE 2) of Proposition 2.5 is also achieved by a bijection between $T^{(g)}_{I\Vert p|q|}$, a generating series of ribbon graphs with two boundaries of length 1 and other generating series via deletion of the first vertex. For the generalised $1+1$-point function, the prefactor after deletion becomes

$$\begin{aligned} \frac{-\lambda }{E_p+E_p} \end{aligned}$$

instead of $\frac{-\lambda }{E_p+E_q}$ as it was for the generalised 2-point function. The first four cases are (up to some small subtleties) the same as the cases (a)–(d) of the $T^{(g)}_{I\Vert pq|}$. The fifth case, however, is different:

• (e’) We have two separated boundaries each of length 1 labelled by p and q, see Fig. 13. The deletion of the first vertex is divided in several subcases:

  • For generic k: If k is an internal face, the sum is taken and one boundary of length 4 remains, $\frac{1}{N}\sum _{k=1}^NT^{(g)}_{I\Vert pkqq|}$.

  • For $k=q_i\in I$: The overall derivative is taken with $k=q_i$ and $I\setminus q_i$, that is $-\frac{\partial ^{ext}}{\partial E_{q_i}}T^{(g)}_{I\setminus q_i\Vert pq_iqq|}$.

  • For $k=q$: The graph can be split into two after deleting the first vertex. Two correlation functions occur each with boundary of length 2; we obtain $T^{(g_1)}_{I_1\Vert qq|}T^{(g_2)}_{I_2\Vert pq|}$ with $g_1+g_2=g$ and $I_1\uplus I_2=I$.

  • For $k=q$: There is also the case that two separated boundaries remain, but with one genus less, $T^{(g-1)}_{I\Vert q|qqp|}+T^{(g-1)}_{I\Vert qq|qp|}$.

  • For $k=p$: Two boundaries remain but genus is reduced by one, $T^{(g-1)}_{I\Vert p|qqp|}$.

  In summary, we find for the case e’) together with Lemma D.1

  $$\begin{aligned}&\frac{-\lambda }{E_p+E_p}\bigg [ \frac{1}{N}\sum _{k=1}^NT^{(g)}_{I\Vert pkqq|} -\sum _{q_i\in I}\frac{\partial ^{ext}}{\partial E_{q_i}} T^{(g)}_{I\setminus q_i\Vert pq_iqq|} \\&\qquad +\sum _{\begin{array}{c} g_1+g_2=g\\ I_1 \uplus I_2=I \end{array}} T^{(g_1)}_{I_1\Vert qq|}T^{(g_2)}_{I_2\Vert pq|}+T^{(g-1)}_{I\Vert q|qqp|} +T^{(g-1)}_{I\Vert qq|qp|}+T^{(g-1)}_{I\Vert p|qqp|}\bigg ] \\&\quad =\frac{\lambda }{E_p+E_p}\frac{T^{(g)}_{I\Vert qq|}-T^{(g)}_{I\Vert pq|}}{E_q-E_p}. \end{aligned}$$

Including the first four cases similar to the graphical derivation of the generalised 2-point function, we finally confirm the DSE (2.13) of the generalised $1+1$-point function $T^{(g)}_{I\Vert p|q|}$ with the same considerations as for the generalised 2-point function.

Fig. 13

The generalised $1+1$-point function with $n=q$ does not reduce the genus, but merges the two boundaries

Proofs for Sect. 4.1

We will use the following well-known interpolation formula:

Lemma E.1

Let f be a polynomial of degree $d-1\ge 0$ and $x_1,...,x_d$ be pairwise distinct complex numbers. Then, for all $x\in {\mathbb {C}}$,

$$\begin{aligned} f(x)=L(x)\sum _{j=1}^d\frac{f_j}{(x-x_j)L'(x_j)},\qquad \text {where } L(x)=\prod _{j=1}^d(x-x_j) \text { and } f_j=f(x_j). \end{aligned}$$

We recall [22] that (3.7) gives rise to the product representation

$$\begin{aligned} {\mathcal {G}}^{(0)}(z,w)=\frac{1}{R(w)-R(-z)} \prod _{k=1}^{d}\frac{R(z)-R(-{\hat{w}}^k)}{R(z)-R(\varepsilon _k)}\;. \end{aligned}$$

(E.1)

Proposition E.2

Let $I=\{u_1,...,u_m\}$. The DSE (3.6) is solved by

$$\begin{aligned}&{\mathcal {T}}^{(g)}(I\Vert z,w|) =\lambda {\mathcal {G}}^{(0)}(z,w)\mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow z,-{\hat{w}}^j} \frac{R'(t)\, dt}{(R(z)-R(t))(R(w)-R(-t)){\mathcal {G}}^{(0)}(t,w)} \nonumber \\&\quad \times \bigg [\sum _{\begin{array}{c} I_1 \uplus I_2=I\\ g_1+g_2=g\\ (I_1,g_1)\ne (\emptyset ,0) \end{array}} \Omega ^{(g_1)}_{|I_1|+1}(I_1,t) {\mathcal {T}}^{(g_2)}(I_2\Vert t,w|) +\sum _{i=1}^m\frac{\partial }{\partial R(u_i)} \frac{{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i,w|)}{R(u_i)-R(t)} \nonumber \\&\quad +\frac{{\mathcal {T}}^{(g-1)}(I\Vert t|w|) -{\mathcal {T}}^{(g-1)}(I\Vert w|w|)}{R(w)-R(t)} + {\mathcal {T}}^{(g-1)}(I,t\Vert t,w|)\bigg ], \end{aligned}$$

(E.2)

where $v\in \{w,{\hat{w}}^1,...,{\hat{w}}^d\}$ are the solutions of $R(v)=R(w)$. We employed the short-hand notation $\mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow z,-{\hat{w}}^j} \equiv \mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow z} + \sum _{j=1}^d\mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow -{\hat{w}}^j}$.

Proof

The second term of the lhs of the DSE (3.6) is conveniently written as

$$\begin{aligned} -\frac{\lambda }{N}\sum _{k=1}^d r_k \frac{{\mathcal {T}}^{(g)}(I\Vert \varepsilon _k,w|)}{R(\varepsilon _k)-R(z)}&=\frac{\frac{\lambda }{N}\sum _{k=1}^d r_k {\mathcal {T}}^{(g)}(I\Vert \varepsilon _k,w|) \prod _{i\ne k}^d (R(z)-R(\varepsilon _i))}{\prod _{j=1}^d(R(z)-R(\varepsilon _j))} \\&=:\frac{f(R(z);w|I)}{\prod _{j=1}^d (R(z)-R(\varepsilon _j))}\;, \end{aligned}$$

where $f(\,.\,;w|I)$ is now a polynomial of degree $d-1$. Applying Lemma E.1 with $L_w(t):=\prod _{j=1}^d (t-R(-{\hat{w}}^j))$, the interpolation formula yields

$$\begin{aligned} f(R(z);w|I)&= L_w(R(z))\sum _{j=1}^d\frac{f(R(-{\hat{w}}^j);w|I)}{ (R(z)-R(-{\hat{w}}^j)) L_w'(R(-{\hat{w}}^j))} \\&=L_w(R(z))\sum _{j=1}^d\mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow -{\hat{w}}^j} \frac{f(R(t);w|I)R'(t)dt}{(R(z)-R(t)) L_w(R(t))}\;, \end{aligned}$$

where the analyticity of f(R(z); w|I) at $z=-{\hat{w}}^j$ was used. Next, insert (3.6) again for $z\mapsto t$ near $t=-{\hat{w}}^j$ at which the first term of the lhs vanishes (here it is important that the integrand has only a simple pole at $t=-{\hat{w}}^j$). Inserting it for f(R(t); w|I) leads to

$$\begin{aligned}&-\frac{\lambda }{N}\sum _{k=1}^dr_k \frac{{\mathcal {T}}^{(g)}(I\Vert \varepsilon _k,w|)}{R(\varepsilon _k)-R(z)} \nonumber \\&\quad =-\lambda (R(w){-}R({-}z)){\mathcal {G}}^{(0)}(z,w) \sum _{j=1}^d \mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow -{\hat{w}}^j} \frac{R'(t)dt}{(R(z){-}R(t))(R(w){-}R({-}t)){\mathcal {G}}^{(0)}(t,w)} \nonumber \\&\qquad \times \bigg [\sum _{\begin{array}{c} I_1\uplus I_2=I\\ g_1+g_2=g\\ (I_1,g_1)\ne (\emptyset ,0) \end{array}} \Omega ^{(g_1)}_{|I_1|+1}(I_1,t){\mathcal {T}}^{(g_2)}(I_2\Vert t,w|) +\sum _{i=1}^m\frac{\partial }{\partial R(u_i)} \frac{{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i,w|)}{R(u_i)-R(t)} \nonumber \\&\qquad +\frac{{\mathcal {T}}^{(g-1)}(I\Vert t|w|) -{\mathcal {T}}^{(g-1)}(I\Vert w|w|)}{R(w)-R(t)} + {\mathcal {T}}^{(g-1)}(I,t\Vert t,w|)\bigg ]\;, \end{aligned}$$

(E.3)

where the product representation (E.1) was inserted.

Next, compute for the same integrand the residue at $t= z$ (for arbitrary z)

$$\begin{aligned}&\lambda (R(w)-R(-z)){\mathcal {G}}^{(0)}(z,w) \mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow z}\frac{R'(t)dt}{(R(z)-R(t))(R(w)-R(-t)) {\mathcal {G}}^{(0)}(t,w)} \\&\qquad \times \bigg [\sum _{\begin{array}{c} I_1\uplus I_2=I\\ g_1+g_2=g\\ (I_1,g_1)\ne (\emptyset ,0) \end{array}} \Omega ^{(g_1)}_{|I_1|+1}(I_1,t){\mathcal {T}}^{(g_2)}(I_2\Vert t,w|) +\sum _{i=1}^m\frac{\partial }{\partial R(u_i)} \frac{{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i,w|)}{R(u_i)-R(t)}\\&\qquad +\frac{{\mathcal {T}}^{(g-1)}(I\Vert t|w|) -{\mathcal {T}}^{(g-1)}(I\Vert w|w|)}{R(w)-R(t)} + {\mathcal {T}}^{(g-1)}(I,t\Vert t,w|)\bigg ]\\&\quad =-\lambda \bigg [\sum _{\begin{array}{c} I_1\uplus I_2=I\\ g_1+g_2=g\\ (I_1,g_1)\ne (\emptyset ,0) \end{array}} \!\!\!\!\!\! \Omega ^{(g_1)}_{|I_1|+1}(I_1,z){\mathcal {T}}^{(g_2)}(I_2\Vert z,w|) +\sum _{i=1}^m\frac{\partial }{\partial R(u_i)} \frac{{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i,w|)}{R(u_i)-R(z)} \\&\qquad +\frac{{\mathcal {T}}^{(g-1)}(I\Vert z|w|) -{\mathcal {T}}^{(g-1)}(I\Vert w|w|)}{R(w)-R(z)} + {\mathcal {T}}^{(g-1)}(I,z\Vert z,w|)\bigg ] \\&\quad =(R(w)-R(-z)){\mathcal {T}}^{(g)}(I\Vert z,w|) -\frac{\lambda }{N}\sum _{k=1}^d r_k \frac{{\mathcal {T}}^{(g)}(I\Vert \varepsilon _k,w|)}{R(\varepsilon _k)-R(z)}\;. \end{aligned}$$

Summing both expressions gives the assertion. $\square$

Remark E.3

The residue formula of Proposition E.2 is equivalent to the formula found in [23] via inversion of Cauchy matrices $\big (\frac{1}{R(\varepsilon _j)-R(-{\hat{w}}^k)}\big )_{j,k}$. This is not surprising as the derivation of the inverse Cauchy matrix in [35] is mainly based on the interpolation formula.

The proof of Corollary 4.2 is:

Proof

We rewrite one of the terms in Proposition E.2 as

$$\begin{aligned}&\frac{\partial }{\partial R(u_i)}\mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow z,-{\hat{w}}^j} \frac{R'(t)dt\prod _{k=1}^d(R(t)-R(\varepsilon _k)) }{(R(z)-R(t)) L_w(R(t))} \frac{{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i,w|)}{R(u_i)-R(t)}\\&\quad =\frac{\partial }{\partial R(u_i)}\mathop {{{\,\mathrm{Res}\,}}}\limits _{x\rightarrow R(z),R(-{\hat{w}}^j)} \frac{dx\prod _{k=1}^d(x-R(\varepsilon _k)) }{(R(z)-x) L_w(x)} \frac{{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i,w|)}{R(u_i)-x} \\&\quad =-\frac{\partial }{\partial R(u_i)}\mathop {{{\,\mathrm{Res}\,}}}\limits _{x\rightarrow R(u_i)} \frac{\prod _{k=1}^d(x-R(\varepsilon _k)) }{(R(z)-x) L_w(x)} \frac{{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i,w|)}{R(u_i)-x} \\&\quad =\frac{1}{R'(u_i)}\frac{\partial }{\partial u_i} \frac{\prod _{k=1}^d(R(u_i)-R(\varepsilon _k)) }{(R(z)-R(u_i)) L_w(R(u_i))}{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i,w|) \\&\quad =\mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow u_i}\frac{R'(t)dt \prod _{k=1}^d(R(t)-R(\varepsilon _k)) }{(R(z)-R(t)) L_w(R(t))}\Big \{\frac{1}{R'(u_i)R'(t)(t-u_i)^2 } {\mathcal {T}}^{(g)}(I\backslash u_i\Vert t,w|)\Big \}\;, \end{aligned}$$

where we substituted $t\mapsto x=R(t)$, then moved the integration contour and finally represented the result in form of a residue formula. Proposition 3.11 implies that $\frac{1}{R'(u_i)R'(t)(t-u_i)^2 }$ is partially given in $\Omega ^{(0)}_{2}(u_i,t)$. According to Lemma 4.1, $\Omega ^{(0)}_2(z,w)$ is the only correlation function divergent on the diagonal so that the terms in $\{~ \}$ extend to $\sum _{I_1,I_2,g_1,g_2} \Omega ^{(g_1)}_{|I_1|+1}(I_1;t){\mathcal {T}}^{(g_2)}(I_2\Vert t,w|)$ and finally to $\sum _{I_1,I_2,g_1,g_2} \Omega ^{(g_1)}_{|I_1|+1}(I_1;t){\mathcal {T}}^{(g_2)}(I_2\Vert t,w|)+ {\mathcal {T}}^{(g-1)}(I,t\Vert t,w|) +\frac{{\mathcal {T}}^{(g-1)}(I\Vert t|w|)}{R(w)-R(t)}$.

Analogously, the term

$$\begin{aligned}&\mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow z,-{\hat{w}}^j} \frac{R'(t)dt\prod _{k=1}^d(R(t)-R(\varepsilon _k)) }{(R(z)-R(t)) L_w(R(t))} \frac{{\mathcal {T}}^{(g-1)}(I\Vert w|w|)}{R(w)-R(t)} \end{aligned}$$

is represented by the w-residue in the Corollary, where again vanishing terms are added after substitution and moving the integration contour. $\square$

As argued in the proof of Corollary 4.2, Lemma 4.1 implies that the residue at $t=u_i$ contributes only via $\Omega ^{(0)}_2(u_i,t)$ and the residue at $t=w$ only via $\frac{{\mathcal {T}}^{(g-1)}(I\Vert t|w|)}{R(w)-R(t)}$.

Proposition E.4

Let $I=\{u_1,...,u_m\}$. The DSE (3.8) is solved by

$$\begin{aligned} {\mathcal {T}}^{(g)}(I\Vert z|w|)&=\frac{\lambda \prod _{j=1}^d\frac{R(z)-R(\alpha _j)}{ R(z)-R(\varepsilon _j)}}{(R(z)-R(-z))} \mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow z ,\alpha _j}\frac{R'(t)\, dt \prod _{k=1}^d(R(t)-R(\varepsilon _k))}{(R(z)-R(t)) \prod _{k=1}^d (R(t)-R(\alpha _k))} \nonumber \\&\quad \times \bigg [\sum _{\begin{array}{c} I_1\uplus I_2=I\\ g_1+g_2=g\\ (I_1,g_1)\ne (\emptyset ,0) \end{array}} \!\!\!\!\!\! \Omega ^{(g_1)}_{|I_1|+1}(I_1,t) {\mathcal {T}}^{(g_2)}(I_2\Vert t|w|) + {\mathcal {T}}^{(g-1)}(I,t\Vert t|w|) \nonumber \\&\quad +\sum _{i=1}^m\frac{\partial }{\partial R(u_i)} \frac{{\mathcal {T}}^{(g)}(I\backslash u_i\Vert u_i|w|)}{R(u_i)-R(t)} +\frac{{\mathcal {T}}^{(g)}(I\Vert t,w|) -{\mathcal {T}}^{(g)}(I\Vert w,w|)}{R(w)-R(t)}\bigg ], \end{aligned}$$

(E.4)

where $v\in \{0,\pm \alpha _j\}$ are the $2d+1$ solutions of $R(v)-R(-v)=0$.

Proof

Similar to the proof of Proposition E.2, but with d distinct points $x_k=R(\alpha _k)$ for the interpolation formula of Lemma E.1. $\square$

The proof of Corollary 4.4 works in a completely analogous way.

Proof of Conjecture 4.6 for g = 0

It is convenient to introduce

$$\begin{aligned} {\mathcal {T}}^{(g)}(u_1,..,u_m\Vert z,w|)&=:\frac{\partial ^m {\mathcal {U}}^{(g)} (u_1,..,u_m\Vert z,w|) }{\partial R(u_1)\cdots \partial R(u_m)} \,, \nonumber \\ {\mathcal {T}}^{(g)}(u_1,..,u_m\Vert z|w|)&=:\frac{\partial ^m{\mathcal {U}}^{(g)}(u_1,..,u_m\Vert z|w|) }{\partial R(u_1)\cdots \partial R(u_m)} \,, \nonumber \\ \Omega ^{(g)}_{m+1}(u_1,..,u_m,z)&=:\frac{\partial ^m {\mathcal {W}}^{(g)}_{m+1}(u_1,..,u_m;z)}{\partial R(u_1)\cdots \partial R(u_m)} \;. \end{aligned}$$

(F.1)

In these variables the DSE (3.6) reads for $g=0$ and $m\ge 1$

$$\begin{aligned}&(R(w)-R(-z)){\mathcal {U}}^{(0)}(u_1,...,u_m\Vert z,w|) -\frac{\lambda }{N}\sum _{k=1}^d \frac{r_k {\mathcal {U}}^{(0)}(u_1,...,u_m\Vert \varepsilon _k,w|)}{R(\varepsilon _k)-R(z)} \nonumber \\&\quad =-\lambda \!\!\!\!\!\! \sum _{\begin{array}{c} I_1\uplus I_2=\{u_1,...,u_m\}\\ I_1\ne \emptyset \end{array}} {\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;z) {\mathcal {U}}^{(0)}(I_2\Vert z,w|) -\lambda \sum _{j=1}^m \frac{{\mathcal {U}}^{(0)}(u_1,..\check{u_j}..,u_m\Vert u_j,w|)}{ R(u_j)-R(z)}\;, \end{aligned}$$

(F.2)

where ${\mathcal {U}}^{(0)}(\emptyset \Vert z,w|)={\mathcal {G}}^{(0)}(z,w)$. The DSE (3.10) becomes for $m\ge 2$

$$\begin{aligned}&R'(z){\mathfrak {G}}_0(z){\mathcal {W}}^{(0)}_{m+1}(u_1,...,u_m;z) -\frac{\lambda }{N^2}\sum _{n,k=1}^d \frac{r_nr_k {\mathcal {U}}^{(0)}(u_1,...,u_m\Vert \varepsilon _k,\varepsilon _n|)}{ (R(\varepsilon _k)-R(z))(R(\varepsilon _n)-R(-z))} \nonumber \\&\quad = -\sum _{\begin{array}{c} I_1\uplus I_2=\{u_1,...,u_m\}\\ I_1\ne \emptyset \ne I_2 \end{array}} {\mathcal {W}}^{(0)}_{|I_1+1|}(I_1;z)\frac{\lambda }{N}\sum _{n=1}^d \frac{r_n {\mathcal {U}}^{(0)}(I_2\Vert z,\varepsilon _n|)}{ R(\varepsilon _n)-R(-z)} \nonumber \\&\qquad -\sum _{j=1}^m \frac{\frac{\lambda }{N}\sum _{n=1}^d r_n \frac{{\mathcal {U}}^{(0)}(u_1,..\check{u_j}..,u_m\Vert u_j,\varepsilon _n|)}{ R(\varepsilon _n)-R(-z)} }{R(u_j)-R(z)} -\sum _{j=1}^m{\mathcal {U}}^{(0)}(u_1,..\check{u_j}..,u_m\Vert u_j,z|)\;. \end{aligned}$$

(F.3)

Lemma F.1

For all $m\ge 1$, the function ${\mathcal {W}}^{(0)}_{m+1}(u_1,\dots ,u_m;z)$ is holomorphic in every $z=\widehat{u_j}^k$, whereas ${\mathcal {U}}^{(0)}(u_1,\dots ,u_m\Vert z,w|)$ has simple poles there with residue

$$\begin{aligned}&\mathop {{{\,\mathrm{Res}\,}}}\limits _{z\rightarrow \widehat{u_j}^k} {\mathcal {U}}^{(0)}(u_1,...,u_m\Vert z,w|)dz \nonumber \\&\quad =-\sum _{l=1}^{m} \sum _{\begin{array}{c} I_1\uplus ...\uplus I_{l}=\{u_1,...\check{u_j}...,u_m\} \\ I_2,...,I_l\ne \emptyset \text { for }l>1 \end{array}} \frac{(-\lambda )^l{\mathcal {U}}^{(0)}(I_1\Vert u_j,w|) \prod _{i=2}^l {\mathcal {W}}^{(0)}_{|I_i|+1}(I_i;z) }{R'(z)(R(w)-R(-z))^l}\Big |_{z=\widehat{u_j}^k}\;. \end{aligned}$$

(F.4)

Proof

By induction in m, starting with Proposition 3.11 for $m=1$. Assume that the assertion concerning ${\mathcal {W}}_{k+1}^{(0)}$ is true for all $k\le m-1$. Then (F.4) is recursively obtained when taking the residue in (F.2) and inserting it repeatedly into itself. Next, taking (F.4) into account, the residue of (F.3) at $z=\widehat{u_j}^k$ collapses to

$$\begin{aligned}&\mathop {{{\,\mathrm{Res}\,}}}\limits _{z\rightarrow \widehat{u_j}^k} R'(z){\mathfrak {G}}_0(z){\mathcal {W}}^{(0)}_{m+1}(u_1,...,u_m;z)dz \\&\quad = \mathop {{{\,\mathrm{Res}\,}}}\limits _{z\rightarrow \widehat{u_j}^k}\Big [ \frac{1}{N} \sum _{n=1}^d r_n {\mathcal {U}}^{(0)}(u_1,...,u_m\Vert z,\varepsilon _n|) -\sum _{i=1}^m{\mathcal {U}}^{(0)}(u_1,..\check{u_i}..,u_m\Vert u_i,z|)\Big ]dz\;. \end{aligned}$$

But the rhs is $\mathop {{{\,\mathrm{Res}\,}}}\limits _{z\rightarrow \widehat{u_j}^k} {\mathcal {W}}^{(0)}_{m+1}(u_1,...,u_m;z)dz$ when expressing (3.9) in terms of ${\mathcal {W}}$ and ${\mathcal {U}}$. With $R'(\widehat{u_j}^k){\mathfrak {G}}_0(\widehat{u_j}^k)\ne 1$ we finish the proof. $\square$

Lemma F.2

For all $m\ge 1$, the function ${\mathcal {W}}^{(0)}_{m+1}(u_1,\dots ,u_m;z)$ is holomorphic in every $z=\pm \widehat{\varepsilon _k}^j$, whereas ${\mathcal {U}}^{(0)}(u_1,\dots ,u_m\Vert z,w|)$ has simple poles at $z=\widehat{\varepsilon _k}^j$ and is regular at $z=-\widehat{\varepsilon _k}^j$.

Proof

By induction in m, starting from the true statement for ${\mathcal {G}}^{(0)}(z,w)$ and ${\mathcal {W}}^{(0)}_{2}(u;z)$. If the statement is true for all ${\mathcal {W}}^{(0)}_{|I|+1}(I;z)$ with $|I|+1\le m$ and ${\mathcal {U}}^{(0)}(I\Vert ..|)$ with $|I|\le m-1$, then the rhs of (F.2) has at most simple poles at $z=\widehat{\varepsilon _k}^j$ and no poles at $z=-\widehat{\varepsilon _k}^j$. The same is true for the second term of the lhs of (F.2) so that the statement extends to ${\mathcal {U}}^{(0)}(u_1,\dots ,u_m\Vert z,w|)$. This means that the rhs and the second term of the lhs of (F.3) have at most simple poles at $z=\pm \widehat{\varepsilon _k}^j$. Since the prefactor ${\mathfrak {G}}_0(z)$ has simple poles at every $z=\pm \widehat{\varepsilon _k}^j$ and $R'(\pm \widehat{\varepsilon _k}^j)$ is regular, the function ${\mathcal {W}}^{(0)}_{m+1}(u_1,\dots ,u_m;z)$ must be regular at $z=\pm \widehat{\varepsilon _k}^j$. $\square$

Lemma F.3

The functions ${\mathcal {W}}^{(0)}_{m+1}(u_1,..,u_m;z)$ and ${\mathcal {U}}^{(0)}(u_1,..,u_m\Vert z,w|)$ are regular at $z=-\varepsilon _n$.

Proof

No term in (F.2) is singular for $z=-\varepsilon _n$, some of them even vanish because of $R(-\varepsilon _n)=\infty$. The singular denominators $\frac{1}{R(\varepsilon _n)-R(-z)}$ in (F.3) are protected by $\frac{1}{R'(z)}\rightarrow 0$ for $z\rightarrow -\varepsilon _n$. $\square$

By construction all functions are holomorphic at $z=\varepsilon _n$. This leaves the opposite diagonals $z=-u_k$ and the ramification points $z=\beta _i$ (from the prefactor $R'(z)$ in (F.3)) as the only possible location of poles in ${\mathcal {W}}^{(0)}_{m+1}(u_1,...,u_m;z)$. These are preserved by differentiation to $\Omega ^{(0)}_{m+1}(u_1,...,u_m,z)$, so that the proof of Conjecture 4.6 for $g=0$ is complete.

For $g\ge 1$ we also expect poles at $z=0$ inherited from the initial value ${\mathcal {G}}^{(g-1)}(z|z)$ and from the poles at $z=-z$ in ${\mathcal {T}}^{(g-1)}(u_1,...,u_m,z\Vert z,\varepsilon _n|)$. Also absence of poles at $z=\pm \alpha _k$ is only relevant for $g\ge 1$. We also note

Lemma F.4

We have

$$\begin{aligned}&\mathop {{{\,\mathrm{Res}\,}}}\limits _{z\rightarrow \widehat{u_j}^k} {\mathcal {U}}^{(0)}(u_1,...,u_m\Vert z|w|)dz \nonumber \\&\quad =-\sum _{l=1}^{m} \sum _{\begin{array}{c} I_1\uplus ...\uplus I_{l} =\{u_1,...\check{u_j}...,u_m\} \\ I_2,...,I_l\ne \emptyset \text { for }l>1 \end{array}} \frac{(-\lambda )^l{\mathcal {U}}^{(0)}(I_1\Vert u_j|w|) \prod _{i=2}^l {\mathcal {W}}^{(0)}_{|I_i|+1}(I_i;z) }{R'(z)(R(z)-R(-z))^l}\Big |_{z=\widehat{u_j}^k}\; \nonumber \\&\qquad -\lambda \sum _{n=1}^m \frac{1}{R'(z)(R(z)-R(-z))^n} \nonumber \\&\qquad \times \sum _{l=n}^{m} \sum _{\begin{array}{c} I_1\uplus ...\uplus I_{l}=\{u_1,...\check{u_j}...,u_m\} \\ I_2,...,I_l\ne \emptyset \text { for }l>1 \end{array}} \frac{(-\lambda )^l{\mathcal {U}}^{(0)}(I_1\Vert u_j,w|) \prod _{i=2}^l {\mathcal {W}}^{(0)}_{|I_i|+1}(I_i;z) }{(R(w)-R(z)) (R(w)-R(-z))^{l+1-n}} \Big |_{z=\widehat{u_j}^k}. \end{aligned}$$

(F.5)

Solution of the Recursion for Small Degree

1.1 Preparations for $g=0$

We formulate the proof in terms of ${\mathcal {U}}^{(0)}$ and ${\mathcal {W}}^{(0)}_m$ introduced in (F.1). Equation (E.3) then translates for $g=0$ to

$$\begin{aligned}&\frac{\lambda }{N}\sum _{k=1}^dr_k \frac{{\mathcal {U}}^{(0)}(I\Vert \varepsilon _k,w|)}{R(\varepsilon _k)-R(z)} \nonumber \\&\quad =\lambda (R(w){-}R({-}z)){\mathcal {G}}^{(0)}(z,w) \sum _{j=1}^d \mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow -{\hat{w}}^j} \frac{R'(t)dt}{(R(z){-}R(t))(R(w){-}R({-}t)){\mathcal {G}}^{(0)}(t,w)} \nonumber \\&\qquad \times \bigg [\sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1\ne \emptyset \end{array}} {\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;t){\mathcal {U}}^{(0)}(I_2\Vert t,w|) +\sum _{i=1}^m \frac{{\mathcal {U}}^{(0)}(I\backslash u_i\Vert u_i,w|)}{R(u_i)-R(t)} \bigg ], \end{aligned}$$

(G.1)

where $I=\{u_1,...,u_m\}$ and $m\ge 1$. Using the product representation (E.1) and the interpolation formula of Lemma E.1 it is straightforward to establish

$$\begin{aligned}&\sum _{j=1}^d \mathop {{{\,\mathrm{Res}\,}}}\limits _{t\rightarrow -{\hat{w}}^j} \frac{R'(t)dt}{(R(z){-}R(t))(R(u_i)-R(t))(R(w){-}R({-}t)){\mathcal {G}}^{(0)}(t,w)} \\&\quad = \frac{1}{R(z){-}R(u_i)} \Big (\frac{1}{(R(w)-R({-}u_i)){\mathcal {G}}^{(0)}(u_i,w)} -\frac{1}{(R(w)-R({-}z)){\mathcal {G}}^{(0)}(z,w)}\Big ). \end{aligned}$$

Defining ${\mathcal {U}}^{(g)}(I\Vert z,w|) =:{\mathcal {G}}^{(0)}(z,w)\tilde{{\mathcal {U}}}^{(g)}(I\Vert z,w|)$ (with $\tilde{{\mathcal {U}}}^{(g)}(\emptyset \Vert z,w|)\equiv 1$), Eq. (G.1) becomes

$$\begin{aligned}&\frac{\lambda }{N}\sum _{k=1}^dr_k \frac{{\mathcal {U}}^{(0)}(I\Vert \varepsilon _k,w|)}{R(\varepsilon _k)-R(z)} \nonumber \\&\quad =\lambda (R(w){-}R({-}z)){\mathcal {G}}^{(0)}(z,w) \Big (\sum _{i=1}^m \frac{\tilde{{\mathcal {U}}}^{(0)}(I\backslash u_i\Vert u_i,w|)}{(R(z)-R(u_i))(R(w)-R(-u_i))} \nonumber \\&\qquad +\sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1\ne \emptyset \end{array}} \sum _{j=1}^d \frac{R'({-}{\hat{w}}^j){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;{-}{\hat{w}}^j) \tilde{{\mathcal {U}}}^{(0)}(I_2\Vert {-}{\hat{w}}^j,w|)}{R'({\hat{w}}^j) (R(z)-R(-{\hat{w}}^j))} \Big ) \nonumber \\&\qquad -\sum _{i=1}^m \frac{\lambda {\mathcal {U}}^{(0)}(I\backslash u_i\Vert u_i,w|)}{R(z)-R(u_i)}\;. \end{aligned}$$

(G.2)

The limit $w=q$, $z\rightarrow -q$ of (G.2) is

$$\begin{aligned} \frac{\lambda }{N}\sum _{k=1}^dr_k \frac{{\mathcal {U}}^{(0)}(I\Vert \varepsilon _k,q|)}{R(\varepsilon _k)-R(-q)}&=\lambda R'(q){\mathfrak {G}}_0(q) {\mathfrak {U}}^{(0)}(I\Vert q) -\lambda \sum _{i=1}^m \frac{{\mathcal {U}}^{(0)}(I\backslash u_i\Vert u_i,q|)}{R(-q)-R(u_i)} \end{aligned}$$

(G.3)

where

$$\begin{aligned} {\mathfrak {U}}^{(0)}(I\Vert q)&=\sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1\ne \emptyset \end{array}} \sum _{j=1}^d \frac{R'(-{\hat{q}}^j){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;-{\hat{q}}^j) \tilde{{\mathcal {U}}}^{(0)}(I_2\Vert {-}{\hat{q}}^j,q|)}{R'({\hat{q}}^j) (R(-q)-R(-{\hat{q}}^j))} \nonumber \\&\quad -\sum _{i=1}^m \frac{\tilde{{\mathcal {U}}}^{(0)}(I\backslash u_i\Vert u_i,q|)}{(R(u_i)-R(-q))(R(q)-R(-u_i))} \;. \end{aligned}$$

(G.4)

On the other hand we insert (G.2) into the lhs of the Dyson-Schwinger Eq. (3.6), restricted to $g=0$ and translated to ${\mathcal {U}}^{(0)}$ and ${\mathcal {W}}^{(0)}_m$:

$$\begin{aligned} \tilde{{\mathcal {U}}}^{(0)}(I\Vert z,w|)&= \sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1\ne \emptyset \end{array}} \sum _{j=1}^d \frac{\lambda R'(-{\hat{w}}^j){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;-{\hat{w}}^j) \tilde{{\mathcal {U}}}^{(0)}(I_2\Vert {-}{\hat{w}}^j,w|)}{R'({\hat{w}}^j) (R(z)-R(-{\hat{w}}^j))} \nonumber \\&\quad +\sum _{i=1}^m \frac{\lambda \tilde{{\mathcal {U}}}^{(0)}(I\backslash u_i\Vert u_i,w|)}{(R(z)-R(u_i))(R(w)-R(-u_i))} \nonumber \\&\quad - \sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1\ne \emptyset \end{array}} \frac{\lambda {\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;z) \tilde{{\mathcal {U}}}^{(0)}(I_2\Vert z,w|) }{R(w)-R(-z)}\;. \end{aligned}$$

(G.5)

With these preparations we can eliminate ${\mathfrak {G}}_0$ in the residue formula of Corollary 4.7:

Proposition G.1

For $I=\{u_1,...,u_m\}$ and $m\ge 2$ one has

$$\begin{aligned}&R'(z){\mathcal {W}}^{(0)}_{|I|+1}(I;z) \nonumber \\&\quad =\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow -u_{1,...,m},\beta _{1,...2d}} \frac{\lambda \,dq}{(q-z)} \bigg [ \sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1,I_2\ne \emptyset \end{array}} R'(q){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;q) {\mathfrak {U}}^{(0)}(I_2\Vert q)\bigg ] \nonumber \\&\qquad - \lambda \sum _{k=1}^m \frac{{\mathfrak {U}}^{(0)}(I{\setminus }u_k \Vert u_k)}{z+u_k}\;. \end{aligned}$$

(G.6)

Proof

We insert (G.3) into Corollary 4.7, restricted to $g=0$ and translated to ${\mathcal {W}}^{(0)}_m$. The second term on the rhs (sum over i) then cancels the last line of (G.5):

$$\begin{aligned}&R'(z){\mathcal {W}}^{(0)}_{|I|+1}(I;z) \\&\quad =\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow -u_{1,...,m},\beta _{1,...2d}} \frac{\lambda \,dq}{(q-z)} \bigg [ \sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1,I_2\ne \emptyset \end{array}} R'(q){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;q) {\mathfrak {U}}^{(0)}(I_2\Vert q) \\&\qquad + \sum _{k=1}^m \frac{{\mathcal {G}}^{(0)}(u_k,q)}{{\mathfrak {G}}_0(q)} \Big \{ \sum _{\begin{array}{c} I_1\uplus I_2=I\setminus u_k\\ I_1\ne \emptyset \end{array}} \sum _{j=1}^d \frac{R'(-\widehat{u_k}^j){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;-\widehat{u_k}^j) \tilde{{\mathcal {U}}}^{(0)}(I_2\Vert {-}\widehat{u_k}^j,u_k|)}{R'(\widehat{u_k}^j) (R(q)-R(-\widehat{u_k}^j))} \\&\qquad +\sum _{\begin{array}{c} l=1 \\ l\ne k \end{array}}^m \frac{\tilde{{\mathcal {U}}}^{(0)}(I\backslash \{u_l,u_k\}\Vert u_l,u_k|)}{(R(q)-R(u_l))(R(u_k)-R(-u_l))} \Big \}\bigg ]\;. \end{aligned}$$

The last two lines only contribute to the residue at $q=-u_k$ via the first-order pole of ${\mathcal {G}}^{(0)}(u_k,q)$. The residue cancels ${\mathfrak {G}}_0$ and otherwise amounts to replace $q\mapsto -u_k$. This produces ${\mathfrak {U}}^{(0)}(I{\setminus }u_k \Vert u_k)$ according to (G.4). $\square$

We prove in the next subsections that the solution of (G.6) confirms the following conjecture for $m=2$ and $m=3$:

Conjecture G.2

For any $I=\{u_1,..,u_m\}$ with $m\ge 2$ one has

$$\begin{aligned}&R'(z) {\mathcal {W}}^{(0)}_{m+1}(I;z) \nonumber \\&\quad = \lambda \sum _{i=1}^{2d}\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i} {\tilde{K}}_i(z,q) \sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1,I_2\ne \emptyset \end{array}} R'(q){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;q) R'(\sigma _i(q)){\mathcal {W}}^{(0)}_{|I_2|+1}(I_2;\sigma _i(q)) \nonumber \\&\qquad + \sum _{k=1}^{m} \Big (\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow u_k} {\tilde{K}}_{u_k}(z,q) \!\!\!\! \sum _{\begin{array}{c} I_1\uplus ... \uplus I_s=I{\setminus } u_k\\ I_1,...,I_s \ne \emptyset \end{array}} \!\!\!\!\! \frac{\lambda R'({-}q){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;{-}q)}{R({-}u_k)-R({-}q)} \prod _{r=2}^s \frac{\lambda {\mathcal {W}}^{(0)}_{|I_r|+1}(I_r;u_k)}{ R(-u_k){-}R({-}q)}\Big )\,, \end{aligned}$$

(G.7)

where

$$\begin{aligned} {\tilde{K}}_i(z,q)&:= \frac{\frac{1}{2}(\frac{1}{z-q} -\frac{1}{z-\sigma _i(q)})dq}{ R'(\sigma _i(q))(-R(-q)+R(-\sigma _i(q)))}\;,&{\tilde{K}}_u(z,q)&:= \frac{(\frac{1}{z+q} -\frac{1}{z+u})dq}{ R(u)-R(q)}\;. \end{aligned}$$

Conjecture (G.2) is now a Theorem proved in [11]. The statement translates easily to Conjecture 4.9 about $\omega _{0,m}$.

In intermediate steps of the proof the following residues become important:

$$\begin{aligned} \nabla ^n_z f(z):= \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow z} \frac{f(q)dq}{(R(q)-R(z))^n (R(-z)-R(-q))}\;. \end{aligned}$$

(G.8)

Note that the upper index n is merely an index, not an exponent. The first such residues read

$$\begin{aligned} \nabla ^1_zf(z)&=\frac{f'(z)+ f(z)(\frac{R''(-z)}{2R'(-z)} -\frac{R''(z)}{2R'(z)})}{R'(z)R'(-z)}\;, \\ \nabla ^2_zf(z)&=\frac{\frac{1}{2}f''(z)+ f'(z)(\frac{R''(-z)}{2R'(-z)} -\frac{R''(z)}{R'(z)}) }{(R'(z))^2R'(-z)} \\&+\frac{f(z) (\frac{(R''(-z))^2}{4(R'(-z))^2} +\frac{3(R''(z))^2}{4(R'(z))^2} -\frac{R''(z) R''(-z)}{2R'(z) R'(-z)} -\frac{R'''(-z)}{6R'(-z)} -\frac{R'''(z)}{3R'(z)}) }{(R'(z))^2R'(-z)}\;. \end{aligned}$$

These operations arise in the limit $w=q,z\rightarrow -{\hat{q}}^j$ of (G.5):

$$\begin{aligned} \tilde{{\mathcal {U}}}^{(0)}(I\Vert {-}{\hat{q}}^j,q|)&= \sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1\ne \emptyset \end{array}} \sum _{\begin{array}{c} l=1 \\ l\ne j \end{array}}^d \frac{\lambda R'(-{\hat{q}}^l){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;-{\hat{q}}^l) \tilde{{\mathcal {U}}}^{(0)}(I_2\Vert {-}{\hat{q}}^l,q|)}{R'({\hat{q}}^l) (R(-{\hat{q}}^j)-R(-{\hat{q}}^l))} \nonumber \\&\quad +\sum _{i=1}^m \frac{\lambda \tilde{{\mathcal {U}}}^{(0)}(I\backslash u_i\Vert u_i,q|)}{ (R(-{\hat{q}}^j)-R(u_i))(R(q)-R(-u_i))} \nonumber \\&\quad - \sum _{\begin{array}{c} I_1\uplus I_2=I\\ I_1\ne \emptyset \end{array}} \lambda \nabla _z^1\big (R'(z){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;z) \tilde{{\mathcal {U}}}^{(0)}(I_2\Vert z,q|) \big )\big |_{z=-{\hat{q}}^j}\;. \end{aligned}$$

(G.9)

1.2 Proof of Conjectures 4.9 and G.2 for $m=2$

The case $m=1$ of (G.4) reduces to

$$\begin{aligned} {\mathfrak {U}}^{(0)}(u\Vert q)&=\sum _{j=1}^d \frac{{\mathcal {W}}^{(0)}_{2}(u;{\hat{q}}^j)}{(R(-q)-R(-{\hat{q}}^j))} -\frac{1}{(R(u)-R(-q))(R(q)-R(-u))}\;, \end{aligned}$$

(G.10)

where the symmetry $\frac{R'(-z)}{R'(z)} {\mathcal {W}}^{(0)}_{2}(u_1;-z)={\mathcal {W}}^{(0)}_{2}(u_1;z)$ has been used. This is inserted into (G.6) for $m=2$. The first term of the rhs of (G.10) contributes to the residue at $q=\beta _i$, the second term to the residue at $q=-u$. Moreover, $R'(q){\mathcal {W}}^{(0)}_{2}(u;q)=-\big (\frac{1}{u+q}+\frac{1}{u-q}\big )$ has a simple pole at $q=-u$. We thus arrive at

$$\begin{aligned}&R'(z) {\mathcal {W}}^{(0)}_3(u_1,u_2,z) \\&\quad = \sum _{i=1}^{2d} \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i} \frac{\lambda \,dq}{q-z} \sum _{j=1}^d \frac{\big [R'(q){\mathcal {W}}^{(0)}_2(u_1;q){\mathcal {W}}^{(0)}_2(u_2;{\hat{q}}^j) +u_1{\leftrightarrow } u_2\big ]}{ R( -q)-R(-{\hat{q}}^j)} \\&\qquad +\Big [ \frac{\lambda {\mathfrak {U}}^{(0)}(u_2\Vert {-}u_1)}{z+u_1} -\frac{\lambda {\mathfrak {U}}^{(0)}(u_2\Vert u_1)}{z+u_1} \\&\qquad - \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow -u_{1}} \frac{\lambda \,dq}{q-z} \frac{R'(q){\mathcal {W}}^{(0)}_2(u_2;q)}{ (R(u_1)-R(-q))(R(q)-R(-u_1))} + u_1{\leftrightarrow } u_2\Big ]\,. \end{aligned}$$

In the first line there is, under the assumption of simple ramification points, a unique preimage ${\hat{q}}^{j_i}=\sigma _i(q)$ with $\lim _{q\rightarrow \beta _i}{\hat{q}}^{j_i} =\beta _i$. Only this one contributes to the pole at $q=\beta _i$. In the last line we change variables $q\rightarrow -q$, arrange $\frac{\lambda \,dq}{z+q} =(\frac{\lambda \,dq}{z+q}-\frac{\lambda \,dq}{z+u_1})+\frac{\lambda \,dq}{z+u_1}$ and note that $\frac{\lambda \,dq}{z+u_1}$ produces the residue (G.8):

$$\begin{aligned}&R'(z) {\mathcal {W}}^{(0)}_3(u_1,u_2;z) \\&\quad = \sum _{i=1}^{2d} \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i} \frac{\lambda \,dq}{z-q} \frac{\big [R'(q){\mathcal {W}}^{(0)}_2(u_1;q)\,R'(\sigma _i(q)){\mathcal {W}}^{(0)}_2(u_2;\sigma _i(q)) +u_1{\leftrightarrow } u_2\big ]}{ R'(\sigma _i(q))(-R( -q)+R(-\sigma _i(q)))} \\&\qquad +\Big [ \frac{\lambda }{z+u_1} \Big \{{\mathfrak {U}}^{(0)}(u_2\Vert {-}u_1) -{\mathfrak {U}}^{(0)}(u_2\Vert u_1) +\nabla ^1_{-u_1} \big (R'(-u_1) {\mathcal {W}}^{(0)}_2(u_2;-u_1)\big )\Big \} \\&\qquad + \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow u_{1}} \Big (\frac{\lambda \,dq}{z+q}-\frac{\lambda \,dq}{z+u_1}\Big ) \frac{R'(-q){\mathcal {W}}^{(0)}_2(u_2;-q)}{ (R(u_1)-R(q))(R(-u_1)-R(-q))} + u_1{\leftrightarrow } u_2\Big ]\,. \end{aligned}$$

One checks that the terms in braces $\{~~\}$ sum up to zero. The first term on the rhs can be rearranged using the symmetry

$$\begin{aligned} \frac{dq}{(z-q)x'(\sigma _i(q))} = \frac{dq d\sigma _i(q)}{(z-q)x'(\sigma _i(q))d\sigma _i(q)} = \frac{dq d\sigma _i(q)}{(z-q) x'(q)dq} = \frac{d\sigma _i(q)}{(z-q) x'(q)}\;. \end{aligned}$$

Since an odd function under the involution $q\leftrightarrow \sigma _i(q)$ is integrated, we may replace $\frac{dq}{(z-q)}\mapsto \frac{1}{2} (\frac{dq}{(z-q)}-\frac{dq}{(z-\sigma _i(q))})$ and thus establish Conjecture G.2 for $m=2$. The result immediately translates into Conjecture 4.9 for $m=2$. The residue at $q=\beta _i$ is evaluated with formulae of Appendix C and translates to (4.7). It is straightforward to evaluate the residue at $q=u_1$ and $q=u_2$ to (4.8).

1.3 Proof of Conjectures 4.9 and G.2 for $m=3$

Lemma G.3

For $I=\{u_1,u_2\}$ one has

$$\begin{aligned} {\mathfrak {U}}^{(0)}(I\Vert q) =&\sum _{j=1}^d \frac{{\mathcal {W}}^{(0)}_{3}(I;{\hat{q}}^j) +\lambda \sum _{k=1}^2 {\mathcal {W}}^{(0)}_{2}(I{\setminus }u_k; {\hat{q}}^j) \check{{\mathfrak {U}}}_j^{(0)}(u_k\Vert q) }{(R(-q)-R(-{\hat{q}}^j))} \nonumber \\&+\sum _{k=1}^2 \frac{\lambda {\mathcal {W}}^{(0)}_2(I{\setminus } u_k;u_k) }{ (R(q)-R(-u_k))^2(R(u_k)-R(-q))} \nonumber \\&+\lambda \prod _{k=1}^2 \Big (\frac{1}{ (R(q)-R(-u_k))(R(u_k)-R(-q))}\Big ) \;, \end{aligned}$$

(G.11)

where

$$\begin{aligned} \check{{\mathfrak {U}}}^{(0)}_j(u\Vert q):= \sum _{\begin{array}{c} l=1 \\ l\ne j \end{array}}^d \frac{{\mathcal {W}}^{(0)}_2(u;{\hat{q}}^l) }{R(-{\hat{q}}^j)-R(-{\hat{q}}^l)} -\frac{1}{(R(u)-R(-q))(R(q)-R(-u))}\;. \end{aligned}$$

(G.12)

Proof

Inserting (G.9) for $I=u_k$ into the first line of (G.4) for $I=\{u_1,u_2\}$ and (G.5) into the second line of (G.4) leads after simplifications to

$$\begin{aligned}&{\mathfrak {U}}^{(0)}(u_1,u_2\Vert q) \nonumber \\&\quad = \sum _{j=1}^d \frac{R'(-{\hat{q}}^j) {\mathcal {W}}^{(0)}_{3}(u_1,u_2;-{\hat{q}}^j)}{R'({\hat{q}}^j) (R(-q)-R(-{\hat{q}}^j))} + \lambda \sum _{j=1}^d \frac{ \big [{\mathcal {W}}^{(0)}_{2}(u_1;{\hat{q}}^j) \check{{\mathfrak {U}}}_j^{(0)}(u_2\Vert q) + u_1\leftrightarrow u_2\big ] }{(R(-q)-R(-{\hat{q}}^j))} \nonumber \\&\qquad - \sum _{j=1}^d \frac{ \big [\lambda R'({\hat{q}}^j) {\mathcal {W}}^{(0)}_{2}(u_1;{\hat{q}}^j) \nabla _{-{\hat{q}}^j} \big (R'(-{\hat{q}}^j){\mathcal {W}}^{(0)}(u_2;-{\hat{q}}^j)\big ) + u_1\leftrightarrow u_2\big ] }{R'({\hat{q}}^j) (R(-q)-R(-{\hat{q}}^j))} \nonumber \\&\qquad + \frac{\lambda }{(R(q)-R(-u_1))(R(u_1)-R(-q)) (R(q)-R(-u_2))(R(u_2)-R(-q)) } \nonumber \\&\qquad + \Big [\frac{\lambda {\mathcal {W}}^{(0)}_2(u_2;u_1)}{(R(q)-R(-u_1))^2(R(u_1)-R(-q))} +u_1\leftrightarrow u_2\Big ]\;. \end{aligned}$$

(G.13)

The explicit formulae for ${\mathcal {W}}^{(0)}_3$ allow to prove the following identity⁷:

$$\begin{aligned}&R'(z){\mathcal {W}}^{(0)}_3(u_1,u_2;z)-R'(-z){\mathcal {W}}^{(0)}_3(u_1,u_2;-z) \nonumber \\&\quad =\big [\lambda R'(-z){\mathcal {W}}^{(0)}_{2}(u_1;-z) \nabla _z^1 (R'(z){\mathcal {W}}^{(0)}(u_2;z)) +u_1\leftrightarrow u_2\big ]\;. \end{aligned}$$

(G.14)

Inserted back into (G.13) for $z\mapsto -{\hat{q}}^j$ gives the assertion. $\square$

We insert (G.11) and (G.10) into (G.6) for $m=3$. Let again ${\hat{q}}^{j_i}=\sigma _i(q)$ be the unique (for simple ramification points) preimage with $\lim _{q\rightarrow \beta _i}\sigma _i(q)=\beta _i$. Only the first line of (G.11) contributes to the residue at $q=\beta _i$. More precisely, in the sum in this first line we have contributions from all terms with $j=j_i$, whereas for $j\ne j_i$ we only have poles in $\check{{\mathfrak {U}}}_{j}(u\Vert q)$, namely in the single term $\frac{\lambda {\mathcal {W}}^{(0)}_2(u;{\hat{q}}^{j_i})}{R(-{\hat{q}}^{j})-R(-{\hat{q}}^{j_i})}$ of the sum in (G.12). To the residue at $q=-u_3$ we have contributions from $R'(q){\mathcal {W}}^{(0)}_3(u_i,u_3;q)\mapsto \frac{\lambda {\mathcal {W}}^{(0)}_2(u_i,-u_3)}{(q+u_3)^2R'(u_3)}$, from $R'(q){\mathcal {W}}^{(0)}_2(u_3;q)\mapsto -\frac{1}{(q+u_3)}$, from ${\mathfrak {U}}^{(0)}(u_3\Vert q)\mapsto -\frac{1}{(R(u_3)-R(-q))(R(q)-R(-u_3))}$ according to (G.10) and from ${\mathfrak {U}}^{(0)}(u_i,u_3\Vert q)$ given by (G.11). Here the first line of (G.11) contributes via $\check{{\mathfrak {U}}}_j^{(0)}(u_3\Vert q) \mapsto -\frac{1}{(R(u_3)-R(-q))(R(q)-R(-u_3))}$, which together with the other lines amount to

$$\begin{aligned}&{\mathfrak {U}}^{(0)}(u_i,u_3\Vert q)\mapsto \frac{\lambda {\mathcal {W}}^{(0)}_2(u_i;u_3)}{(R(u_3)-R(-q))(R(q)-R(-u_3))^2} \\&\quad -\frac{\lambda {\mathfrak {U}}^{(0)}(u_i\Vert q)}{(R(u_3)-R(-q))(R(q)-R(-u_3))}\;. \end{aligned}$$

After partial rearrangement of permutations and change of variables $q\rightarrow -q$ to achieve the residue at $q=u_3$ we arrive at

As shown in the previous subsection, the line labelled by (*) is regular for $q\rightarrow \beta _i$ so that (*) and the line after can be discarded. In the two lines (**) we arrange $\frac{\lambda \,dq}{z+q} =(\frac{\lambda \,dq}{z+q}-\frac{\lambda \,dq}{z+u_3})+\frac{\lambda \,dq}{z+u_3}$ as before, where the second $\frac{\lambda \,dq}{z+u_3}$ produces the residue (G.8). The lines ($\dag$) have only a simple pole whose residue can also be written in terms of (G.8). We thus find

$$\begin{aligned}&R'(z) {\mathcal {W}}^{(0)}_4(u_1,u_2,u_3;z) \nonumber \\&\quad = \sum _{i=1}^{2d} \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i} \frac{\lambda \,dq}{q-z} \sum _{\begin{array}{c} I_1\uplus I_2=\{u_1,u_2,u_3\} \\ I_1,I_2\ne \emptyset \end{array}} \frac{R'(q){\mathcal {W}}^{(0)}_{|I_1|+1}(I_1;q) {\mathcal {W}}^{(0)}_{|I_2|+1}(I_2;\sigma _i(q)) }{R(-q)-R(-\sigma _i(q))} \nonumber \\&\qquad +\bigg \{ \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow u_3} \Big (\frac{\lambda \, dq}{z+q} -\frac{\lambda \,dq}{z+u_3}\Big ) \Big [ \frac{R'(-q){\mathcal {W}}^{(0)}_3(u_1,u_2;-q)}{(R(u_3)-R(q))(R(-u_3)-R(-q))} \nonumber \\&\qquad + \frac{\lambda R'(q)({\mathcal {W}}^{(0)}_2(u_1;q) {\mathcal {W}}^{(0)}_2(u_2;u_3)+ {\mathcal {W}}^{(0)}_2(u_2;q) {\mathcal {W}}^{(0)}_2(u_1;u_3))}{ (R(u_3)-R(-q))(R(-u_3)-R(-q))^2} \Big ] \nonumber \\&\qquad +\frac{\lambda X(u_1,u_2;-u_3)}{z+u_3} + [u_3\leftrightarrow u_1]+ [u_3\leftrightarrow u_2]\bigg \}\;, \end{aligned}$$

(G.15)

where the remaining collection of terms is shown to vanish identically⁸:

$$\begin{aligned} X(u_1,u_2;q)&:= {\mathfrak {U}}^{(0)}(u_1,u_2\Vert q) -{\mathfrak {U}}^{(0)}(u_1,u_2\Vert -q) + \nabla _q^1 \big (R'(q){\mathcal {W}}^{(0)}_3(u_1,u_2;q)\big ) \\&\quad + \lambda \big [{\mathfrak {U}}^{(0)}(u_2\Vert q) \nabla ^1_q\big (R'(q){\mathcal {W}}^{(0)}_2(u_1;q)\big ) +u_1\leftrightarrow u_2\big ] \\&\quad -\lambda \big [{\mathcal {W}}^{(0)}_2(u_2;-q) \nabla ^2_q\big ( R'(q){\mathcal {W}}^{(0)}_2(u_1;q)\big ) +u_1\leftrightarrow u_2\big ] \equiv 0\;. \end{aligned}$$

After symmetrisation $q\leftrightarrow \sigma _i(q)$ we confirm Conjecture G.2 for $m=3$. The result immediately translates into Conjecture 4.9 for $m=3$. The residue at $q=\beta _i$ is evaluated with the formulae given in Appendix C and translates to (4.9). The evaluation of the residue at $q=-u_3$ gives in a first step rise to ${\mathcal {W}}^{(0)}_3(u_1,u_2;-u_3)$ and derivatives $\partial _{u_3}{\mathcal {W}}^{(0)}_3(u_1;u_3)$ and $\partial _{u_3}{\mathcal {W}}^{(0)}_3(u_2;u_3)$. The reflection (G.14) simplifies this to an equation which translates into (4.10).

1.4 Proof of Proposition 4.10

According to Corollary 4.7 for $m=0$ and $g=1$ we have with (G.3)

$$\begin{aligned}&R'(z)\Omega ^{(1)}_{1}(z) \nonumber \\&\quad =\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow 0,\beta _i} \frac{dq}{(q-z){\mathfrak {G}}_0(q)} \Big [ \frac{\partial }{\partial R(u)} \Big (\lambda R'(q){\mathfrak {G}}_0(q) {\mathfrak {U}}^{(0)}(u\Vert q) -\frac{\lambda {\mathcal {G}}^{(0)}(u,q)}{R(-q)-R(u)} \Big ) \Big |_{u=q} \nonumber \\&\qquad +\frac{\lambda }{N}\sum _{n=1}^d \frac{r_n {\mathcal {G}}^{(0)}(q|\varepsilon _n)}{ (R(\varepsilon _n)-R(q))(R(\varepsilon _n)-R(-q))} -{\mathcal {G}}^{(0)}(q|q)\Big ]\,, \end{aligned}$$

(G.16)

provided that the part in $[\dots ]$ has only simple poles at $z=\pm \widehat{\varepsilon _k}^j$ (which we will confirm). From (3.8) at $m=0$ and $g=0$ we get

$$\begin{aligned}&\frac{\lambda }{N}\sum _{n=1}^d \frac{r_n {\mathcal {G}}^{(0)}(q|\varepsilon _n)}{ (R(\varepsilon _n)-R(q))(R(\varepsilon _n)-R(-q))} -{\mathcal {G}}^{(0)}(q|q) \nonumber \\&\quad = \lim _{u\rightarrow q} \Big ({\mathcal {G}}^{(0)}(u|{-}q) -\lambda \frac{{\mathcal {G}}^{(0)}(u,{-}q)}{(R(u)-R(-q))^2}\Big ) -\frac{\lambda R'(q){\mathfrak {G}}_0(q)}{(R(q)-R(-q))^3} \nonumber \\&\qquad -\frac{\partial }{\partial R(u)} \frac{\lambda {\mathcal {G}}^{(0)}(u,q)}{ (R(u)-R(-q))}\Big |_{u=q}\;. \end{aligned}$$

(G.17)

The limit in the second line follows with [23, Proposition 17],

$$\begin{aligned}&\lim _{u\rightarrow q}\Big ({\mathcal {G}}^{(0)}(u|{-}q) -\lambda \frac{{\mathcal {G}}^{(0)}(u,{-}q)}{(R(u)-R(-q))^2}\Big ) \nonumber \\&\quad = \frac{\lambda (R(q)+R(-q)-2R(0))}{(R(q)-R(-q))^4} \prod _{j=1}^d \frac{(R(q)-R(\alpha _j))(R(-q)-R(\alpha _j))}{ (R(q)-R(\varepsilon _j))(R(-q)-R(\varepsilon _j))}\;. \end{aligned}$$

(G.18)

With these considerations and (G.10) we get

$$\begin{aligned}&R'(z)\Omega ^{(1)}_{1}(z) \nonumber \\&\quad =\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow 0,\beta _i} \frac{\lambda \,dq}{(q-z)} \Big [ \sum _{j=1}^d \frac{R'(q) \Omega _2^{(0)}(q,{\hat{q}}^j)}{ R(-q)-R(-{\hat{q}}^j)} +\frac{R'(-q)}{(R(q)-R(-q))^3} \nonumber \\&\qquad +\frac{(R(q)+R(-q)-2R(0))}{{\mathfrak {G}}_0(q)(R(q)-R(-q))^4} \prod _{j=1}^d \frac{(R(q)-R(\alpha _j))(R(-q)-R(\alpha _j))}{ (R(q)-R(\varepsilon _j))(R(-q)-R(\varepsilon _j))} \Big ]\,. \end{aligned}$$

(G.19)

In particular, the terms in brackets are regular at $q=\pm \widehat{\varepsilon _n}^j$ so that Conjecture 4.6 is true for $g=1$, $m=0$. Being an even function of q, the expression (G.18) has a second-order pole at $q=0$ without residue; it is regular at $q=\beta _i$:

$$\begin{aligned} {}\mathrm{(G.18)} =\frac{\lambda R''(0)}{16 q^2 (R'(0))^4} \prod _{j=1}^d \frac{(R(0)-R(\alpha _j))^2}{(R(0)-R(\varepsilon _j))^2} +\text {regular terms at }q\in \{0,\beta _i\}\;. \end{aligned}$$

One has $\prod _{j=1}^d \frac{(R(0)-R(\alpha _j))^2}{(R(0)-R(\varepsilon _j))^2} =\lim _{q\rightarrow 0} \frac{(R(q)-R(-q))^2}{2R(q)-2R(0)}{\mathcal {G}}^{(0)}(q,q) =R'(0){\mathfrak {G}}_0(0)$ as shown in [23, Proposition 15]. The same discussion as for ${\mathcal {W}}^{(0)}_3$ shows that only one preimage ${\hat{q}}^{j_i}=\sigma _i(q)$ of the first term on the rhs of (G.19) contributes to the pole at $q=\beta _i$, and again the standard recursion kernel of topological recursion arises:

$$\begin{aligned} R'(z)\Omega ^{(1)}_{1}(z)dz&=\sum _{i=1}^{2d} \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i} \frac{\lambda dqdz}{z-q} \frac{ R'(q)R'(\sigma _i(q))\Omega ^{(0)}_2(q,\sigma _i(q))}{ R'(\sigma _i(q))(-R(-q)-(-R(-\sigma _i(q))))} \nonumber \\&\quad +\mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow 0}\frac{\lambda dqdz}{z-q}\Big [ -\frac{R'(-q)}{(R(q)-R(-q))^3} -\frac{R''(0)}{16q^2 (R'(0))^3}\Big ] \nonumber \\&=\lambda \sum _{i=1}^{2d} \mathop {{{\,\mathrm{Res}\,}}}\limits _{q\rightarrow \beta _i} \big [K_i(z,q) \omega _{0,2}(q,\sigma _i(q))\big ] \nonumber \\&\quad + \lambda dz \Big [-\frac{1}{8(R'(0))^2z^3}+ \frac{R''(0)}{16(R'(0))^3z^2}\Big ]\;. \end{aligned}$$

(G.20)

The expansion of the recursion kernel given in Appendix C evaluates the residue to the explicit formula given in Proposition 4.10. $\square$