Orbital Stability of Internal Waves

Abstract

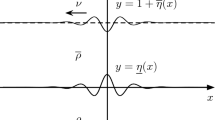
This paper studies the nonlinear stability of capillary-gravity waves propagating along the interface dividing two immiscible fluid layers of finite depth. The motion in both regions is governed by the incompressible and irrotational Euler equations, with the density of each fluid being constant but distinct. A diverse collection of small-amplitude solitary wave solutions for this system have been constructed by several authors in the case of strong surface tension (as measured by the Bond number) and slightly subcritical Froude number. We prove that all of these waves are (conditionally) orbitally stable in the natural energy space. Moreover, the trivial solution is shown to be conditionally stable when the Bond and Froude numbers lie in a certain unbounded parameter region. For the near critical surface tension regime, we prove that one can infer conditional orbital stability or orbital instability of small-amplitude traveling waves solutions to the full Euler system from considerations of a dispersive PDE model equation. These results are obtained by reformulating the problem as an infinite-dimensional Hamiltonian system, then applying a version of the Grillakis–Shatah–Strauss method recently introduced in Varholm et al. (Commun Pure Appl Math 73:2634–2684, 2020). A key part of the analysis consists of computing the spectrum of the linearized augmented Hamiltonian at a shear flow or small-amplitude wave. For this, we generalize an idea used by Mielke (R Soc Lond Philos Trans Ser A Math Phys Eng Sci 360:2337–2358, 2002) to treat capillary-gravity water waves beneath vacuum.

Appendix A. Elementary Identities

Here we give the proofs of the elementary first and second derivative formulas for the nonlocal operators $G_\pm (\eta )$ and $A(\eta )$.

Proof of Lemma 3.3

The formula (3.18) for $D G_\pm (\eta )$ can be derived using the same method as the standard one-fluid case. To obtain (3.20), it is easier to first consider the derivative of

$$\begin{aligned} A(\eta )^{-1} = G_+(\eta )^{-1} B(\eta ) G_-(\eta )^{-1} = \rho _+ G_+(\eta )^{-1} + \rho _- G_-(\eta )^{-1}. \end{aligned}$$

(A.1)

Then,

$$\begin{aligned} \left\langle D A(\eta ) {{\dot{\eta }}}, \, \psi \right\rangle&= -A(\eta ) \left\langle D (A(\eta )^{-1}) {{\dot{\eta }}}, A(\eta ) \psi \right\rangle \\&= \sum _\pm \rho _\pm A(\eta ) G_\pm (\eta )^{-1} \left\langle D G_\pm (\eta ) {{\dot{\eta }}}, G_\pm (\eta )^{-1} A(\eta ) \psi \right\rangle . \end{aligned}$$

Using the self-adjointness of $G_\pm (\eta )$ and the formula (3.18) for $D G_\pm (\eta )$, this leads immediately to (3.20). $\square$

Proof of Lemma 3.6

As in the proof of Lemma 3.3, we start by considering the corresponding formula for $A(\eta )^{-1}$. Recalling (A.1), we see that

$$\begin{aligned} \begin{aligned} D^2 (A(\eta )^{-1})[ {{\dot{\eta }}}, {{\dot{\eta }}}]&= \sum _{\pm } \rho _\pm D ^2 (G_\pm (\eta )^{-1})[ {{\dot{\eta }}}, {{\dot{\eta }}}] \\&= -\sum _{\pm } \rho _\pm G_\pm (\eta )^{-1} \left( D ^2G_\pm (\eta )[{{\dot{\eta }}},{{\dot{\eta }}}] \right. \\&\left. - 2 D G_\pm (\eta )[{{\dot{\eta }}}] G_\pm (\eta )^{-1} D G_\pm (\eta )[{{\dot{\eta }}}]\right) G_\pm (\eta )^{-1}. \end{aligned} \end{aligned}$$

On the other hand, we have the elementary identity

$$\begin{aligned} \begin{aligned} D ^2 A(\eta )[ {{\dot{\eta }}},{{\dot{\eta }}}]&= -A(\eta ) D ^2(A(\eta )^{-1})[{{\dot{\eta }}},{{\dot{\eta }}}] A(\eta ) + 2D A(\eta )[{{\dot{\eta }}}] A(\eta )^{-1} D A(\eta )[{{\dot{\eta }}}]. \end{aligned} \end{aligned}$$

(A.2)

Together, these will furnish a representation formula for the second variation of $A(\eta )^{-1}$ once we have fully expanded these expressions using (3.18) and (3.21).

Consider each of the terms on the right-hand side of (A.2). For the first, we have

$$\begin{aligned}&-\int _{\mathbb {R}} \psi A(\eta ) D ^2 (A(\eta )^{-1})[{{\dot{\eta }}},{{\dot{\eta }}}] A(\eta ) \psi \,d x= \sum _{\pm } \rho _\pm \int _{\mathbb {R}} \theta _\pm D ^2 G_\pm (\eta )[{{\dot{\eta }}},{{\dot{\eta }}}] \theta _\pm \,d x\\&\qquad -2 \sum _{\pm } \rho _\pm \int _{\mathbb {R}} \theta _\pm D G_\pm (\eta )[{{\dot{\eta }}}] G_\pm (\eta )^{-1} D G_\pm (\eta )[{{\dot{\eta }}}] \theta _\pm \,d x, \end{aligned}$$

where recall that $\theta _\pm = \theta _\pm (\eta , \psi )$ is given by (3.24). Throughout the remainder of the proof, $a_i^\pm$ will always be evaluated at $(\eta , \theta _\pm )$, so we suppress the arguments for readability. By the first variation (3.18) and second variation (3.21) formulas for $G_\pm (\eta )$, this becomes

$$\begin{aligned}&-\int _{\mathbb {R}} \psi A(\eta ) D ^2 (A(\eta )^{-1})[{{\dot{\eta }}}, {{\dot{\eta }}}] A(\eta ) \psi \,d x= \sum _\pm \rho _\pm \int _{\mathbb {R}} \left( a_4^\pm {{\dot{\eta }}}^2 + 2a_2^\pm {{\dot{\eta }}} G_\pm (\eta ) \left( a_2^\pm {{\dot{\eta }}} \right) \right) \,d x\\&\qquad -2 \sum _{\pm } \rho _\pm \int _{\mathbb {R}} a_1^\pm \left( G_\pm (\eta )^{-1} D G_\pm (\eta )[{{\dot{\eta }}}]\theta _\pm \right) ^\prime {{\dot{\eta }}} \,d x\\&\qquad -2 \sum _\pm \rho _\pm \int _{\mathbb {R}} a_2^\pm \left( D G_\pm (\eta )[{{\dot{\eta }}}] \theta _\pm \right) {{\dot{\eta }}} \,d x\\&\quad = \sum _\pm \rho _\pm \int _{\mathbb {R}} \left( a_4^\pm {{\dot{\eta }}}^2 + 2a_2^\pm {{\dot{\eta }}} G_\pm (\eta ) \left( a_2^\pm {{\dot{\eta }}} \right) \right) \,d x\\&\qquad -2 \sum _\pm \rho _\pm \int _{\mathbb {R}} {\mathscr {L}}_\pm [{{\dot{\eta }}}] D G_\pm (\eta )[{{\dot{\eta }}}] \theta _\pm \,d x, \end{aligned}$$

for the linear operator ${\mathscr {L}}_\pm$ given by (3.25). Using (3.18) once more allows us to simplify this to

$$\begin{aligned}&-\int _{\mathbb {R}} \psi A(\eta ) D ^2 (A(\eta )^{-1})[{{\dot{\eta }}}, {{\dot{\eta }}}] A(\eta ) \psi \,d x= \sum _\pm \rho _\pm \int _{\mathbb {R}} \left( a_4^\pm {{\dot{\eta }}} + 2a_2^\pm G_\pm (\eta ) \left( a_2^\pm {{\dot{\eta }}} \right) \right) {{\dot{\eta }}} \,d x\\&\qquad -2 \sum _{\pm } \rho _\pm \int _{\mathbb {R}} \left( a_1^\pm {\mathscr {L}}_\pm [{{\dot{\eta }}}]^\prime + a_2^\pm G_\pm (\eta ) {\mathscr {L}}_\pm [{{\dot{\eta }}}] \right) {{\dot{\eta }}} \,d x. \end{aligned}$$

So finally we have

$$\begin{aligned}&-\int _{\mathbb {R}} \psi A(\eta ) D ^2 (A(\eta )^{-1})[{{\dot{\eta }}},{{\dot{\eta }}}] A(\eta ) \psi \,d x\nonumber \\&\quad = \int _{\mathbb {R}} \Big ( a_4 {{\dot{\eta }}} + 2\sum _\pm \rho _\pm a_2^\pm G_\pm (\eta ) \left( a_2^\pm {{\dot{\eta }}} \right) - 2 {\mathscr {M}}{{\dot{\eta }}} \Big ) {{\dot{\eta }}} \,d x\end{aligned}$$

(A.3)

where recall $a_4 = a_4(\eta ,\psi )$ and ${\mathscr {M}} = {\mathscr {M}}(\eta ,\psi )$ were defined in (3.24) and (3.26), respectively.

Likewise, the second in term on the right-hand side of (A.2) can be treated as follows. Using (3.20), we calculate that

$$\begin{aligned}&\int _{\mathbb {R}} \psi D A(\eta )[ {{\dot{\eta }}}] A(\eta )^{-1} D A(\eta )[{{\dot{\eta }}}] \psi \,d x= \sum _{\pm } \rho _\pm \int _{\mathbb {R}} \Big ( a_1^\pm \left( G_\pm (\eta )^{-1} D A(\eta )[{{\dot{\eta }}}]\psi \right) ^\prime \\&\qquad +a_2^\pm A(\eta ) D A(\eta )[{{\dot{\eta }}}] \psi \Big ) {{\dot{\eta }}} \,d x\\&\quad = \sum _\pm \rho _\pm \int _{\mathbb {R}} {\mathscr {L}}_\pm [{{\dot{\eta }}}] D A(\eta )[{{\dot{\eta }}}] \psi \,d x= \int _{\mathbb {R}} {\mathscr {L}}[{{\dot{\eta }}}] D A(\eta )[{{\dot{\eta }}}] \psi \,d x. \end{aligned}$$

Applying (3.20) once more then yields

$$\begin{aligned} \begin{aligned}&\int _{\mathbb {R}} \psi D A(\eta )[ {{\dot{\eta }}}] A(\eta )^{-1} D A(\eta )[{{\dot{\eta }}}] \psi \,d x= \sum _{\pm } \rho _{\pm } \int _{\mathbb {R}} \Big ( a_1^{\pm } \left( A(\eta ) G_{\pm }(\eta )^{-1} {\mathscr {L}}[{{\dot{\eta }}}] \right) ^\prime \\&\qquad +a_2^{\pm } A(\eta ) {\mathscr {L}}[{{\dot{\eta }}}] \Big ) {{\dot{\eta }}} \,d x\\&\quad = \int _{\mathbb {R}} {{\dot{\eta }}}{\mathscr {N}} {{\dot{\eta }}} \,d x, \end{aligned} \end{aligned}$$

(A.4)

with ${\mathscr {N}} = {\mathscr {N}}(\eta ,\psi )$ defined in (3.27). Combining this with (A.2) and (A.3) gives the formula (3.23), completing the proof. $\square$