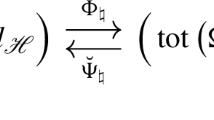Abstract
This paper is devoted to the study of the relation between ‘formal exponential maps,’ the Atiyah class, and Kapranov \(L_\infty [1]\) algebras associated with dg manifolds in the \(C^\infty \) context. We prove that, for a dg manifold, a ‘formal exponential map’ exists if and only if the Atiyah class vanishes. Inspired by Kapranov’s construction of a homotopy Lie algebra associated with the holomorphic tangent bundle of a complex manifold, we prove that the space of vector fields on a dg manifold admits an \(L_\infty [1]\) algebra structure, unique up to isomorphism, whose unary bracket is the Lie derivative with respect to the homological vector field, whose binary bracket is a 1-cocycle representative of the Atiyah class, and whose higher multibrackets can be computed by a recursive formula. For the dg manifold \((T^{0,1}_X[1],{\bar{\partial }})\) arising from a complex manifold X, we prove that this \(L_\infty [1]\) algebra structure is quasi-isomorphic to the standard \(L_\infty [1]\) algebra structure on the Dolbeault complex \(\Omega ^{0,\bullet }(T^{1,0}_X)\).
Similar content being viewed by others
References
Alexandrov, M., Schwarz, A., Zaboronsky, O., Kontsevich, M.: The geometry of the master equation and topological quantum field theory. Int. J. Mod. Phys. A 12(7), 1405–1429 (1997). https://doi.org/10.1142/S0217751X97001031
Bandiera, R.: Formality of Kapranov’s brackets in Kähler geometry via pre-Lie deformation theory. Int. Math. Res. Not. IMRN 21, 6626–6655 (2016). https://doi.org/10.1093/imrn/rnv362
Bandiera, R.: Homotopy abelian \(L_{\infty } \) algebras and splitting property. Rend. Mat. Appl. (7) 37(1–2), 105–122 (2016)
Bandiera, R., Chen, Z., Stiénon, M., Xu, P.: Shifted derived Poisson manifolds associated with Lie pairs. Commun. Math. Phys. 375(3), 1717–1760 (2020). https://doi.org/10.1007/s00220-019-03457-w
Behrend, K., Liao, H.-Y., Xu, P.: Derived Differentiable Manifolds (2020). arXiv:2006.01376 [math.DG]
Boardman, J.M.: The principle of signs. Enseign. Math. (2) 12, 191–194 (1966)
Bonavolontà, G., Poncin, N.: On the category of Lie \(n\)-algebroids. J. Geom. Phys. 73, 70–90 (2013). https://doi.org/10.1016/j.geomphys.2013.05.004
Bruce, A.J.: From \(L_\infty \)-algebroids to higher Schouten/Poisson structures. Rep. Math. Phys. 67(2), 157–177 (2011). https://doi.org/10.1016/S0034-4877(11)00010-3
Bruce, A.J., Grabowski, J., Vitagliano, L.: Representations up to homotopy from weighted Lie algebroids. J. Lie Theory 28(3), 715–737 (2018)
Căldăraru, A., Willerton, S.: The Mukai pairing. I. A categorical approach. N. Y. J. Math. 16, 61–98 (2010)
Carchedi, D., Roytenberg, D.: Homological Algebra for Superalgebras of Differentiable Functions (2012). arXiv:1212.3745 [math.AG]
Carchedi, D., Roytenberg, D.: On theories of superalgebras of differentiable functions. Theory Appl. Categ. 28(30), 1022–1098 (2013)
Cattaneo, A.S., Schätz, F.: Introduction to supergeometry. Rev. Math. Phys. 23(6), 669–690 (2011). https://doi.org/10.1142/S0129055X11004400
Chen, Z., Stiénon, M., Xu, P.: From Atiyah classes to homotopy Leibniz algebras. Commun. Math. Phys. 341(1), 309–349 (2016). https://doi.org/10.1007/s00220-015-2494-6
Chen, Z., Xiang, M., Xu, P.: Atiyah and Todd classes arising from integrable distributions. J. Geom. Phys. 136, 52–67 (2019). https://doi.org/10.1016/j.geomphys.2018.10.011
Chen, Z., Xiang, M., Xu, P.: Hochschild cohomology of dg manifolds associated to integrable distributions (2021). arXiv:2103.08096 [math.DG]
Cheng, J., Chen, Z., Ni, D.: Hopf algebras arising from dg manifolds. J. Algebra 584, 19–68 (2021). https://doi.org/10.1016/j.jalgebra.2021.05.004
Dolgushev, V.A.: Covariant and equivariant formality theorems. Adv. Math. 191(1), 147–177 (2005). https://doi.org/10.1016/j.aim.2004.02.001
Emmrich, C., Weinstein, A.: The differential geometry of Fedosov’s quantization. In: Lie Theory and Geometry, Vol. 123, pp. 217–239. Progr. Math. Birkhäuser Boston, Boston, MA (1994) https://doi.org/10.1007/978-1-4612-0261-5_7
Grabowska, K., Grabowski, J.: \(n\)-Tuple principal bundles. Int. J. Geom. Methods Mod. Phys. 15(12), 1850211, 18 (2018). https://doi.org/10.1142/S0219887818502110
Grabowski, J.: Modular classes of skew algebroid relations. Transform. Groups 17(4), 989–1010 (2012). https://doi.org/10.1007/s00031-012-9197-2
Jotz Lean, M.: Lie 2-algebroids and matched pairs of 2-representations: a geometric approach. Pac. J. Math. 301(1), 143–188 (2019). https://doi.org/10.2140/pjm.2019.301.143
Jotz Lean, M., Mehta, RA, Papantonis, T: Modules and representations up to homotopy of Lie n-algebroids (2020). arXiv:2001.01101 [math.DG]
Joyce, D.: An introduction to d-manifolds and derived differential geometry. In: Moduli Spaces. Vol. 411, pp. 230–281. London Math. Soc. Lecture Note Ser. Cambridge Univ. Press, Cambridge (2014)
Kapranov, M.: Rozansky–Witten invariants via Atiyah classes. Compos. Math. 115(1), 71–113 (1999). https://doi.org/10.1023/A:1000664527238
Kontsevich, M.: Deformation quantization of Poisson manifolds. Lett. Math. Phys. 66(3), 157–216 (2003). https://doi.org/10.1023/B:MATH.0000027508.00421.bf
Kontsevich, M.: Rozansky–Witten invariants via formal geometry. Compos. Math. 115(1), 115–127 (1999). https://doi.org/10.1023/A:1000619911308
Kotov, A., Strobl, T.: Characteristic classes associated to \(Q\)-bundles. Int. J. Geom. Methods Mod. Phys. 12(1), 1550006, 26 (2015). https://doi.org/10.1142/S0219887815500061
Lada, T., Markl, M.: Strongly homotopy Lie algebras. Commun. Algebra 23(6), 2147–2161 (1995). https://doi.org/10.1080/00927879508825335
Laurent-Gengoux, C., Stiénon, M., Xu, P.: Exponential map and \(L_\infty \) algebra associated to a Lie pair. C. R. Math. Acad. Sci. Paris 350(17–18), 817–821 (2012). https://doi.org/10.1016/j.crma.2012.08.009
Laurent-Gengoux, C., Stiénon, M., Xu, P.: Poincaré–Birkhoff–Witt isomorphisms and Kapranov dg-manifolds. Adv. Math. 387, Paper No. 107792, 62 pp. (2021). https://doi.org/10.1016/j.aim.2021.107792
Liao, H.-Y., Stiénon, M.: Formal exponential map for graded manifolds. Int. Math. Res. Not. IMRN 3, 700–730 (2019). https://doi.org/10.1093/imrn/rnx130
Liao, H.-Y., Stiénon, M., Xu, P.: Formality theorem for differential graded manifolds. C. R. Math. Acad. Sci. Paris 356(1), 27–43 (2018). https://doi.org/10.1016/j.crma.2017.11.017
Lyakhovich, S.L., Mosman, E.A., Sharapov, A.A.: Characteristic classes of \(Q\)-manifolds: classification and applications. J. Geom. Phys. 60(5), 729–759 (2010). https://doi.org/10.1016/j.geomphys.2010.01.008
Manetti, M.: On some formality criteria for DG-Lie algebras. J. Algebra 438, 90–118 (2015). https://doi.org/10.1016/j.jalgebra.2015.04.029
Markarian, N.: The Atiyah class, Hochschild cohomology and the Riemann–Roch theorem. J. Lond. Math. Soc. (2) 79(1), 129–143 (2009). https://doi.org/10.1112/jlms/jdn064
Mehta, R.A.: \(Q\)-Algebroids and their cohomology. J. Symplectic Geom. 7(3), 263–293 (2009)
Mehta, R.A., Stiénon, M., Xu, P.: The Atiyah class of a dg-vector bundle. C. R. Math. Acad. Sci. Paris 353(4), 357–362 (2015). https://doi.org/10.1016/j.crma.2015.01.019
Mehta, R.A.: Supergroupoids, double structures, and equivariant cohomology (2006). arXiv:math/0605356 [math.DG]
Pridham, J.P.: A differential graded model for derived analytic geometry. Adv. Math. 360, 106922, 29 (2020). https://doi.org/10.1016/j.aim.2019.106922
Pridham, J.P.: An outline of shifted Poisson structures and deformation quantisation in derived differential geometry (2018). arXiv:1804.07622 [math.DG]
Ramadoss, A.C.: The big Chern classes and the Chern character. Int. J. Math. 19(6), 699–746 (2008). https://doi.org/10.1142/S0129167X08004856
Roberts, J., Willerton, S.: On the Rozansky–Witten weight systems. Algebraic Geom. Topol. 10(3), 1455–1519 (2010). https://doi.org/10.2140/agt.2010.10.1455
Roytenberg, D.: On the structure of graded symplectic supermanifolds and Courant algebroids. In: Quantization, Poisson Brackets and Beyond (Manchester, 2001), Vol. 315, pp. 169–185. Contemp. Math. Amer. Math. Soc., Providence, RI (2002). https://doi.org/10.1090/conm/315/05479
Sawon, J.: Rozansky–Witten invariants of hyperkähler manifolds. Thesis (Ph.D.)–University of Cambridge (2000). arXiv:math/0404360 [math.DG]
Schwarz, A.: Geometry of Batalin–Vilkovisky quantization. Commun. Math. Phys. 155(2), 249–260 (1993)
Ševera, P.: Letters to Alan Weinstein about Courant algebroids (2017). arXiv:1707.00265 [math.DG]
Ševera, P.: Some title containing the words “homotopy” and “symplectic”, e.g. this one. In: Travaux Mathématiques. Fasc. XVI. Vol. 16, pp. 121–137. Trav. Math. Univ. Luxemb., Luxembourg (2005)
Shoikhet, B.: On the Duflo formula for \(L_\infty \)-algebras and \(Q\)-manifolds (1998). arXiv:math/9812009 [math.QA]
Spivak, D.I.: Derived smooth manifolds. Duke Math. J. 153(1), 55–128 (2010). https://doi.org/10.1215/00127094-2010-021
Stiénon, M., Xu, P.: Atiyah classes and Kontsevich–Duflo type theorem for DG manifolds. In: Homotopy Algebras, Deformation Theory and Quantization, Vol. 123, pp. 63–110. Banach Center Publ. Polish Acad. Sci. Inst. Math., Warsaw (2021). https://doi.org/10.4064/bc123-3
Vitagliano, L.: On the strong homotopy associative algebra of a foliation. Commun. Contemp. Math. 17(2), 1450026, 34 (2015). https://doi.org/10.1142/S0219199714500266
Voglaire, Y., Xu, P.: Rozansky–Witten-type invariants from symplectic Lie pairs. Commun. Math. Phys. 336(1), 217–241 (2015). https://doi.org/10.1007/s00220-014-2221-8
Voronov, T.T.: \(Q\)-Manifolds and higher analogs of Lie algebroids. In: XXIX Workshop on Geometric Methods in Physics. Vol. 1307, pp. 191–202. AIP Conf. Proc. Amer. Inst. Phys., Melville, NY (2010)
Voronov, T.T.: \(Q\)-Manifolds and Mackenzie theory. Commun. Math. Phys. 315(2), 279–310 (2012). https://doi.org/10.1007/s00220-012-1568-y
Voronov, T.T.: Graded geometry, \(Q\)-manifolds, and microformal geometry. Fortschr. Phys. 67(8–9), 1910023 (2019). https://doi.org/10.1002/prop.201910023
Yano, K., Ishihara, S.: Tangent and cotangent bundles: differential geometry. In: Pure and Applied Mathematics, No. 16, pp. ix+423. Marcel Dekker, Inc., New York (1973)
Acknowledgements
We would like to thank Ruggero Bandiera, Camille Laurent-Gengoux, Hsuan-Yi Liao, Rajan Mehta and Luca Vitagliano for fruitful discussions and useful comments. Seokbong Seol is grateful to the Korea Institute for Advanced Study for its hospitality and generous support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Schweigert.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research partially supported by NSF Grants DMS-1707545 and DMS-2001599.
Appendix A. Fedosov Construction for Graded Manifolds
Appendix A. Fedosov Construction for Graded Manifolds
This section is to give a brief description of the Fedosov construction for graded manifolds. We refer readers to [18, 19, 32] for more details.
Throughout this section, \({\mathcal {M}}\) is a finite-dimensional graded manifold and \(\nabla \) is a torsion-free affine connection on \({\mathcal {M}}\). By abuse of notation, the induced linear connection on \({\widehat{S}}(T_{{\mathcal {M}}}^{\vee })\) is denoted by the same symbol. The associated covariant derivative is written \(d^\nabla :\Omega ^{\bullet }({\widehat{S}}(T_{{\mathcal {M}}}^{\vee })) \rightarrow \Omega ^{\bullet +1}({\widehat{S}}(T_{{\mathcal {M}}}^{\vee }))\).
Consider the map \(\nabla ^{\lightning }:{\mathfrak {X}}({\mathcal {M}})\times \Gamma \big (S(T_{{\mathcal {M}}})\big ) \rightarrow \Gamma \big (S(T_{{\mathcal {M}}})\big )\) defined by
for all \(Y\in {\mathfrak {X}}({\mathcal {M}})\) and \({\varvec{X}}\in \Gamma \big (S(T_{{\mathcal {M}}})\big )\).
Lemma A.1
The above map \(\nabla ^{\lightning }\) defines a flat connection on \(S(T_{{\mathcal {M}}})\).
Abusing notation, we write the same symbol \(\nabla ^{\lightning }\) to denote the induced flat connection on \({\widehat{S}}(T_{{\mathcal {M}}}^{\vee })\). The associated covariant derivative \(d^{\nabla ^{\lightning }}:\Omega ^{\bullet }({\widehat{S}}(T_{{\mathcal {M}}}^{\vee })) \rightarrow \Omega ^{\bullet +1}({\widehat{S}}(T_{{\mathcal {M}}}^{\vee }))\) satisfies \((d^{\nabla ^{\lightning }})^{2}=0\).
We use the identification
The total degree of \(\omega \in \Omega ^{p}({\widehat{S}}(T_{{\mathcal {M}}}^{\vee }))\) is \(p+\left| \omega \right| \), where p is the cohomological degree and \(\left| \omega \right| \) is the internal degree of \(\omega \).
Define two operators
and
by
and
for all \(\omega \in \Omega ^{p}({\widehat{S}}(T_{{\mathcal {M}}}^{\vee }))\) and all homogeneous \(X_1,\cdots ,X_{p+1},Y_1,\cdots ,Y_{q+1}\in {\mathfrak {X}}({\mathcal {M}})\). The symbol \(\varepsilon \) denotes the Koszul signs: either \(\varepsilon (X_1,\cdots ,X_{p+1},Y_1,\cdots ,Y_{q-1})\) or \(\varepsilon (X_1,\cdots ,X_{p-1},Y_1,\cdots ,Y_{q+1})\), as appropriate.
Both \(\delta \) and \({\mathfrak {h}}\) are \(C^\infty ({\mathcal {M}})\)-linear, and \(\delta \) is the Koszul operator. Observe that \(\delta \) has total degree \(+1\) and \({\mathfrak {h}}\) has total degree \(-1\). However neither \(\delta \) nor \({\mathfrak {h}}\) change the internal degree: \(\left| \delta \omega \right| =\left| \omega \right| \) and \(\left| {\mathfrak {h}}\omega \right| =\left| \omega \right| \).
Remark A.2
In [18, 19, 32], the operator \({\mathfrak {h}}\) is written as \(\delta ^{-1}\). We avoid this notation because \({\mathfrak {h}}\) is not an inverse map of \(\delta \), and it is rather a homotopy operator.
Lemma A.3
The operator \(\delta \) satisfies \(\delta ^{2}=0\). That is,
is a cochain complex. Moreover, the operators \(\delta \) and \({\mathfrak {h}}\) satisfy
where \(\pi _{0}:\Omega ^{\bullet }({\widehat{S}}(T_{{\mathcal {M}}}^{\vee }))\rightarrow C^\infty ({\mathcal {M}})\) is the natural projection.
We have the following theorem
Theorem A.4
[32, Theorem 5.6]. Let \({\mathcal {M}}\) be a finite-dimensional graded manifold and let \(\nabla \) be a torsion-free affine connection on \({\mathcal {M}}\). Then the covariant derivative \(d^{\nabla ^{\lightning }}\) decomposes as
where the operator \({\widetilde{A^\nabla }}: \Omega ^{\bullet }\big ({\widehat{S}}(T_{{\mathcal {M}}}^{\vee })\big ) \rightarrow \Omega ^{\bullet +1}\big ({\widehat{S}}(T_{{\mathcal {M}}}^{\vee })\big )\) is the derivation of (total) degree \(+1\) determined by a certain element \(A^\nabla \) of \(\Omega ^{1}\big ({\mathcal {M}},{\widehat{S}}^{\ge 2}(T_{{\mathcal {M}}}^{\vee }) \otimes T_{{\mathcal {M}}}\big )\) satisfying
Remark A.5
The operator \(\widetilde{A^{\nabla }}\) increases the cohomological degree by \(+1\) and preserves the internal degree. That is, although the total degree of \(\widetilde{A^{\nabla }}\) is \(+1\), its internal degree is \(\left| \widetilde{A^{\nabla }}\right| =0\).
Write
Let \(R^\nabla \in \Omega ^{2}\big ({\mathcal {M}};{{\,\mathrm{End}\,}}(T_{{\mathcal {M}}})\big )\) denote the curvature of \(\nabla \).
Proposition A.6
We have the following recursive formula for \(A^\nabla _{n}\):
Proof
According to Theorem A.4 and Lemma A.1, we have \(d^{\nabla ^{\lightning }} = d^{\nabla }-\delta +A^\nabla \) and \((d^{\nabla ^{\lightning }})^{2}=0\).
By Lemma A.3, we know \(\delta ^{2}=0\) and \(\delta \circ {\mathfrak {h}}+{\mathfrak {h}}\circ \delta = {{\,\mathrm{id}\,}}-\pi _{0}\). Also, \((d^{\nabla })^{2}=R^\nabla \). Since \({\nabla }\) is torsion-free, we have
As a result, \((d^{\nabla ^{\lightning }})^{2}=0\) implies that
By applying the operator \({\mathfrak {h}}\), we get
because \( {\mathfrak {h}}\circ A^\nabla =0\) and \(\pi _{0}\circ A^\nabla =0\).
Since \({\mathfrak {h}}\big (\Omega ^2({\widehat{S}}^q(T^\vee _{\mathcal {M}})) \subset \Omega ^{1}({\widehat{S}}^{q+1}(T^\vee _{\mathcal {M}}))\), applying the canonical projections
(for each \(n\ge 2\)) to the equality
yields the relations
This completes the proof. \(\square \)
Corollary A.7
Under the same hypothesis as in Theorem A.4, the elements \(A^\nabla _{n}\) with \(n\ge 2\) are completely determined by the curvature \(R^\nabla \) and its higher covariant derivatives. In fact, the element \(A^\nabla _{n}\) is determined by the elements \(A^\nabla _k\) with \(k\le n-1\) by way of the recursive formula (65).
Rights and permissions
About this article
Cite this article
Seol, S., Stiénon, M. & Xu, P. Dg Manifolds, Formal Exponential Maps and Homotopy Lie Algebras. Commun. Math. Phys. 391, 33–76 (2022). https://doi.org/10.1007/s00220-021-04265-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04265-x