Abstract
We prove that any one-dimensional (1D) quantum state with small quantum conditional mutual information in all certain tripartite splits of the system, which we call a quantum approximate Markov chain, can be well-approximated by a Gibbs state of a short-range quantum Hamiltonian. Conversely, we also derive an upper bound on the (quantum) conditional mutual information of Gibbs states of 1D short-range quantum Hamiltonians. We show that the conditional mutual information between two regions A and C conditioned on the middle region B decays exponentially with the square root of the length of B. These two results constitute a variant of the Hammersley–Clifford theorem (which characterizes Markov networks, i.e. probability distributions which have vanishing conditional mutual information, as Gibbs states of classical short-range Hamiltonians) for 1D quantum systems. The result can be seen as a strengthening—for 1D systems—of the mutual information area law for thermal states. It directly implies an efficient preparation of any 1D Gibbs state at finite temperature by a constant-depth quantum circuit.





Similar content being viewed by others
Notes
In the following we always use 2 as the base of log.
\({{\mathcal {D}}}({{\mathcal {H}}}_{A_1} \otimes \cdots \otimes {{\mathcal {H}}}_{A_n})\) is the set of density matrices over the finite-dimensional Hilbert space \({{\mathcal {H}}}_{A_1} \otimes \cdots \otimes {{\mathcal {H}}}_{A_n}\).
A Markov network is a generalization of a Markov chain given by random variables \(X_{1}, \ldots , X_{n}\) defined on the vertices \(1, \ldots , n\in V\) of a graph \(G=(V,E)\), such that \(X_{i}\) is uncorrelated from all other random variables conditioned on the random variables \(\{ X_{j} \}_{(i,j)\in E }\) associated to neighboring vertices.
For Markov networks, in turn, the Hamiltonian is a sum of local functions of variables on all cliques of the graph.
In Ref. [8] a more general result was shown for quantum Markov networks. In contrast to the classical case, positive (i.e. full-rank) quantum Markov networks are only equivalent to Gibbs states of commuting Hamiltonians with terms on the cliques of the graph if the graph is triangle free.
Any quantum \(\varepsilon \)-approximate Markov chain \(\rho _{A_1\ldots A_m}\) satisfies \(I(A_i: A\backslash A_{i-1}A_iA_{i+1} | A_{i-1}A_{i+1})_\rho \le 2\varepsilon \) for all \(i \in [3,m-2]\).
Each \(|i\rangle \) depends on s as well as the eigenvalues \(E_i(s)\).
For instance, \({\tilde{E}}_{B \rightarrow BC}\) can be chosen to be
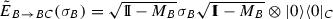 , where
, where 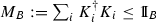 with \(\{K_i\}\) the Kraus operators of \({\tilde{\Lambda }}_{B\rightarrow BC}\).
with \(\{K_i\}\) the Kraus operators of \({\tilde{\Lambda }}_{B\rightarrow BC}\).Otherwise, we just pick the smallest p among \(p_i,i=1,\ldots ,l\) and redefine \({\tilde{\Lambda }}_i\) to be \(\frac{p}{p_i}{\tilde{\Lambda }}_i\) and \({\tilde{E}}_i\) to be \({\tilde{E}}_i+(1-\frac{p}{p_i}){\tilde{\Lambda }}_i\).
References
Ibinson, B., Linden, N., Winter, A.: Robustness of quantum markov chains. Commun. Math. Phys. 277(2), 289–304 (2008)
Fawzi, O., Renner, R.: Quantum conditional mutual information and approximate markov chains. Commun. Math. Phys. 340(2), 575–611 (2015)
Devetak, I., Yard, J.: Exact cost of redistributing multipartite quantum states. Phys. Rev. Lett. 100, 230501 (2008)
Berta, M., Brandao, F.G.S.L., Majenz, C., Wilde, M.M.: Deconstruction and conditional erasure of quantum correlations (2016). arXiv e-prints arXiv:1609.06994
Sharma, K., Wakakuwa E., Wilde, M.M.: Conditional quantum one-time pad (2017). arXiv e-prints arXiv:1703.02903
Hammersley, J.M., Clifford, P.E.: Markov field on finite graphs and lattices (1971). http://www.statslab.cam.ac.uk/grg/books/hammfest/hamm-cliff.pdf
Leifer, M.S., Poulin, D.: Quantum graphical models and belief propagation. Ann. Phys. 323(8), 1899–1946 (2008)
Brown, W., Poulin D.: Quantum Markov networks and commuting Hamiltonians (2012). arXiv e-prints arXiv:1206.0755
Brandao, F.G.S.L., Kastoryano, M.J.: Finite correlation length implies efficient preparation of quantum thermal states (2016). arXiv e-prints arXiv:1609.07877
Kim, I.H.: Determining the structure of the real-space entanglement spectrum from approximate conditional independence. Phys. Rev. B 87, 155120 (2013)
Flammia, S.T., Haah, J., Kastoryano, M.J., Kim, I.H.: Limits on the storage of quantum information in a volume of space. Quantum 1, 4 (2017)
Levin, M., Wen, X.-G.: Detecting topological order in a ground state wave function. Phys. Rev. Lett. 96, 110405 (2006)
Kato, K., Brandao, F.G.S.L.: Locality of edge states and entanglement spectrum from strong subadditivity (2018). arXiv preprints arXiv:1804.05457
Wolf, M.M., Verstraete, F., Hastings, M.B., Cirac, J.I.: Area laws in quantum systems: mutual information and correlations. Phys. Rev. Lett. 100, 070502 (2008)
Hastings, M.B.: Solving gapped Hamiltonians locally. Phys. Rev. B 73(8), 085115 (2006)
Swingle, B., McGreevy, J.: Mixed \(s\)-sourcery: building many-body states using bubbles of nothing. Phys. Rev. B 94(15), 155125 (2016)
Brandao, F.G.S.L.: Finite correlation length implies efficient preparation of quantum thermal states (2016). arXiv prepromts arXiv:1609.07877
Jaynes, E.T.: Information theory and statistical mechanics. Phys. Rev. 106, 620–630 (1957)
Jaynes, E.T.: Information theory and statistical mechanics. II. Phys. Rev. 108, 171–190 (1957)
Weis, S.: Information topologies on non-commutative state spaces. J. Conv. Anal. 21(2), 339–399 (2014)
Weis, S.: The MaxEnt extension of a quantum Gibbs family, convex geometry and geodesics. In: AIP Conference Proceedings, vol. 1641 (2015)
Alicki, R., Fannes, M.: Continuity of quantum conditional information. J. Phys. A: Math. Gen. 37, L55 (2004)
Hastings, M.B.: Quantum belief propagation: an algorithm for thermal quantum systems. Phys. Rev. B 76, 201102 (2007)
Kim, I.H.: Perturbative analysis of topological entanglement entropy from conditional independence. Phys. Rev. B 86, 245116 (2012)
Araki, H.: Gibbs states of a one dimensional quantum lattice. Commun. Math. Phys. 14(2), 120–157 (1969)
Lieb, E.H., Robinson, D.W.: The finite group velocity of quantum spin systems. Commun. Math. Phys. 28(3), 251–257 (1972)
Araki, H.: Expansional in banach algebras. Ann. Sci. Ecole Norm. S. 6(1), 67–84 (1973)
Brandao, F.G.S.L., Horodecki, M.: Exponential decay of correlations implies area law. Commun. Math. Phys. 333(2), 761–798 (2015)
Acknowledgements
Part of this work was done when both of us were working in the QuArC group of Microsoft Research. KK thanks Advanced Leading Graduate Course for Photon Science (ALPS) and JSPS KAKENHI Grant Number JP16J05374 for financial support. We thank Matthew Hastings and Michael Kastoryano for useful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. M. Wolf.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Another approach to prove Theorem 4
Appendix A: Another approach to prove Theorem 4
In Sect. 4, we employ a perturbative method to obtain a local operator O determined by the Hamiltonian and a local operator V such that
The existence of such operator plays a central role in the proof of Theorem 4. In this appendix, we introduce another approach to obtain similar operators, which is based on the previous work by Araki [25]. The main difference between these approaches is the origins of locality of the operator O. In the perturbative approach, the locality is originated in Lieb-Robinson bounds, which restrict real time evolutions of operators. Instead, in Araki’s approach, locality of O is originated in a restriction on imaginary-time evolutions of V.
Let us consider a 1D spin chain \(\Lambda =[-n,n]\), a short-range Hamiltonian H on \(\Lambda \), and a local operator V. We denote the maximum strength of H by J. A simple algebra show the following relation holds.
where we denote \(e^{-\frac{\beta }{2}(H+V)}e^{\frac{\beta }{2}H}\) by \(E_r(V; H)\). By denoting \(V(\beta )=e^{-\beta H}Ve^{\beta H}\), \(E_r(V; H)\) has another form written as [25]
Actually, \(E_r(V; H)\) can be approximated by a local operator.
Lemma 11
[25] The following statements hold for any region \(X\subset [-n,n]\) and any bounded operator V with \(supp(V)=[a,b]\subset [-n,n]\).
-
(i)
There exists a constant \(C\ge 0\) depending on \(\beta \), J and \(\Vert V\Vert \)such that
$$\begin{aligned} \Vert E_r(V; H_X)\Vert \le C\, \end{aligned}$$ -
(ii)
There exist constants \(C, q\ge 0\) depending on \(\beta \), J and \(\Vert V\Vert \) such that
$$\begin{aligned} \left\| E_r(V; H_X)-E_r(V; H_{X\cap [a-l,b+l]})\right\| \le C\frac{q^{1+\lfloor \frac{l}{2}\rfloor }}{(1+\lfloor \frac{l}{2}\rfloor )!}. \end{aligned}$$
Since \(\log x!\approx x\log x-x\), the denominator grows faster than the numerator with respect to l, and thus, the accuracy of the above approximation is exponentially good with respect to l. Note that similar properties hold for the inverse of \(E_r(V; H_X)\), \(E_l(V;H_X)\equiv e^{-\frac{\beta }{2}H_X}e^{\frac{\beta }{2}(H_X+V)}\). Therefore, by choosing \(V=H_{B^M}\), \(E_r(V; H)\) and its local approximation play the same role as \(O_{ABC}\) and \(O_B\) in Sect. 4.2.
Rights and permissions
About this article
Cite this article
Kato, K., Brandão, F.G.S.L. Quantum Approximate Markov Chains are Thermal. Commun. Math. Phys. 370, 117–149 (2019). https://doi.org/10.1007/s00220-019-03485-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-019-03485-6



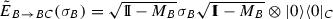 , where
, where 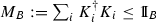 with
with