Abstract
We study the nonlinear equations of motion for equatorial wave–current interactions in the physically realistic setting of azimuthal two-dimensional inviscid flows with piecewise constant vorticity in a two-layer fluid with a flat bed and a free surface. We derive a Hamiltonian formulation for the nonlinear governing equations that is adequate for structure-preserving perturbations, at the linear and at the nonlinear level. Linear theory reveals some important features of the dynamics, highlighting differences between the short- and long-wave regimes. The fact that ocean energy is concentrated in the long-wave propagation modes motivates the pursuit of in-depth nonlinear analysis in the long-wave regime. In particular, specific weakly nonlinear long-wave regimes capture the wave-breaking phenomenon while others are structure-enhancing since therein the dynamics is described by an integrable Hamiltonian system whose solitary-wave solutions are solitons.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Earth’s rotation profoundly affects the dynamics of the atmosphere and of the ocean. However, an in-depth qualitative study of the governing equations for rotating fluids is analytically untractable and prohibitively expensive computationally. For this reason, it is imperative to derive simpler, manageable models which can be studied in detail. A significant feature of equatorial ocean dynamics is that the change of sign of the Coriolis force across the Equator produces an effective waveguide, with the Equator acting as a (fictitious) natural boundary that facilitates azimuthal flow propagation which is symmetric with respect to the Equator: wave–current interactions which propagate in the longitudinal direction and are symmetric with respect to the Equator, featuring so-called Kelvin-waves (large-scale wave motions affected by the Earth’s rotation and trapped at the Equator) and a depth-dependent underlying current field. Moreover, due to the pronounced density stratification of the equatorial regions, greater than anywhere else in the ocean, a rather sharp interface—the thermocline—separates a shallow near-surface layer of relatively warm water from a deep layer of colder and denser water, each layer being practically of constant density. Consequently, there are two types of equatorial Kelvin waves: surface and internal waves. These two types of waves have quite different spatial and temporal scales, the internal waves being significantly larger and slower, with much longer wavelengths. Let us also point out that, in the ocean, energy tends to be concentrated in the lower frequencies (see [16]). Internal equatorial Kelvin waves are slow (taking more than two months to cross the equatorial Pacific) and have very long wavelengths (measured in tens/hundreds of kilometres), being typically more strongly excited than other ocean waves. They play an essential role in the “El Niño”-phenomenon (see [22]): a spectacular, naturally occurring anomalous appearance, every few years, of unusually warm water in the central Pacific, transported eastwards by the internal Kelvin waves until a large expanse of the equatorial Pacific becomes much warmer than the average, thus altering the usual heat exchange process with the air above it and resulting in dramatic shifts of weather patterns in a chain reaction around the world. Moreover, the fact that a Kelvin wave is uni-directional facilitates the growth and accumulation of nonlinear perturbations as the wave propagates, so that nonlinear effects can become very large even if the initial amplitude is relatively small—it is not uncommon to record internal wave heights in excess of 40 m. Nonlinearity causes the often observed distortion of some internal equatorial Kelvin waves: the leading edge steepens while the trailing edge becomes flatter. These physical motivations prompted an intensive research activity, with the available studies of equatorial ocean waves falling into one of the following categories:
-
(I)
observational data and/or numerical simulations (see the discussion in [20]);
-
(II)
linear wave perturbations of a depth-dependent underlying current (see the discussion in [7]);
-
(III)
nonlinear studies assuming a passive equatorial current field (see the discussion in [29]).
Category (I) studies convey valuable information but, given the complexity of the encountered flows, by itself it does not suffice to identify clearly the important processes that are at work. Concerning the studies in category (II), the common occurence of nonlinear equatorial phenomena provides the impetus to go beyond the linear theory. As for (III), the importance of the interactions between waves and currents is highlighted by the fact that the underlying current field in the equatorial Pacific, generated by the prevailing westerly ambient wind pattern and the forces created by the Earth’s rotation (see the discussion in [3, 8]), presents flow-reversal: an eastward jet whose core resides in the thermocline (the Equatorial Undercurrent) is sandwiched between a westward surface flow and an abyssal layer of practically still water. The fact that a flow with piecewise constant vorticity (negative above the thermocline and positive below it) captures this salient feature within a Hamiltonian framework (see Sect. 3) opens up the possibility to develop a rigorous in-depth study of nonlinear wave–current interactions.
A detailed description of the salient physical features of the ocean flow in the equatorial Pacific and of the precise aims of our mathematical analysis is provided in Sect. 2. The analysis of the Hamiltonian structure of the governing equations is pursued in Sect. 3. In Sect. 4 we develop a Hamiltonian perturbation theory. The study of the linearised equations, performed in Sect. 4.1, reveals acute differences between the two most important physical regimes for wave propagation:
-
Internal linear short waves propagate slowly eastwards, while the short waves at the surface are fast and can propagate eastwards as well as westwards, with each propagation mode having no noticeable effect at the other interface.
-
The effects of linear long-wave propagation are practically confined to the motion of the thermocline, whose oscillations propagate slowly eastwards or westwards. The fact that the westward internal waves are slower is an outcome of the dynamic response of the ocean to the presence of strong underlying currents with flow reversal.
However, there are two major limitations of linear theory. Firstly, the ubiquitous wave-breaking phenomenon is outside the realm of linear waves. Moreover, in the context of equatorial wave–current interactions, the common occurrence of internal solitary waves—localised waves that maintain their coherence, propagating with constant speed and unaltered shape—is not captured by linear theory. In light of this, and given that most ocean energy is concentrated in the long waves, in Sect. 4.2 we lay out the foundations for carrying out a systematic weakly nonlinear analysis in the principal long-wave scaling regimes of geophysical relevance (see Table 1). Of particular interest is the derivation of model equations that capture the most striking geophysical manifestations of nonlinear phenomena:
-
Internal solitary waves of permanent form which owe their existence to a balance between wave-steepening effects and wave dispersion—these wave patterns are important because they are often large, very energetic events, and they have therefore a significant role in mass and momentum transport across the ocean. Actually, the corresponding model equation is not merely Hamiltonian, it is completely integrable and therefore the solitary waves present the enhanced structure of a soliton—solitary waves that have an elastic scattering property (after colliding with each other, they eventually emerge unscathed, retaining their shape and speed) and present remarkable stability properties. This opens up the possibility of a detailed analysis of the nonlinear interaction of several such wave patterns by means of an inverse scattering approach, based on an appropriate Riemann–Hilbert problem formulation.
-
Large-amplitude internal waves that break—other than their widespread occurrence, they are perceived as important for the turbulent mixing their death throes produce. This type of solutions correspond to a model similar to the classical nonlinear shallow water equations, modified to account for the presence of underlying currents in a stratified flow. We use the method of characteristics to provide insight into the fascinating process of wave breaking.
In Sect. 5 we overview the obtained results and we offer a perspective on promising future directions for related research.
We conclude this introduction by pointing out that, while we made a conscious effort to avoid being pedantic, there are some aspects of our investigation where a cavalier disregard for proper mathematical rigour is counter-productive. These are best illustrated by some conceptual and technical challenges that contrast to the situation encountered in the periodic setting, being specific for localised wave–current interactions. A central issue is the fact that the Hamiltonian cannot be the total energy of the flow since the kinetic energy contribution of the current is already infinite. Instead, we have to filter out the contribution from the current field and prove that this is achievable at the nonlinear level. Also, defining canonical variables of Schwartz class in the presence of depth-dependent underlying currents is not a foregone result; to the best of our knowledge, this problem has not been addressed in the research literature.
2 Preliminaries
The aim of this section is to briefly discuss the observational record as a physical background for the systematic mathematical approach developed in this paper.
2.1 Key features of equatorial ocean dynamics
Within a band of about 100–150 km of the Equator and extending longitudinally over about 16,000 km, the Pacific Ocean possesses some remarkable features: a significant density stratification (that is greater than anywhere else in the ocean, see [14]), an underlying current field with flow-reversal, and a wide variety of observed wave propagation phenomena. The hallmark of the pronounced density stratification is the presence of a rather sharp thermocline that separates a shallow near-surface layer of relatively warm water from a deep layer of colder and denser water; the assumption that each layer is of constant density is reasonable (see [31]). Within a band of width about 300 km, centred on the Equator, there is, confined to a depth of about 100 m, a westward current that is driven by the prevailing trade winds, below which lies the Equatorial Undercurrent (EUC)—an eastward jet whose core resides on the thermocline. Below the EUC the flow dies out rapidly so that, at depths in excess of about 500 m there is an abyssal region of almost still water (see [32]). This equatorial background state interacts with various oceanic wave propagation modes, including long waves (with wavelengths exceeding 50 km; see [16]) and short waves (with wavelengths of a few hundreds of metres; see [34]). A comprehensive model of this wave–current interaction must accommodate the density stratification as well as the coupling between the waves at the surface and on the thermocline. Observations provide evidence for highly nonlinear regimes of internal wave motion. While explicit nonlinear solutions can be obtained, they do not cope satisfactorily with the complexity of the equatorial flow due to the limitations on the permissible underlying currents (see the discussion in [7]). For this reason, it is necessary to perform approximations that capture the relevant dynamics. The available approaches rely on linear theory, whether they resort to a numerical treatment by means of finite differences (see [32, 39]) or to the method of multiple scales (see [7]). We aim to develop an approach that captures nonlinear effects which, in particular, can explain the propagation of observed equatorial solitary-like waves (see [38]). These are of special interest because they are completely missed by linear theory (see Sect. 4.1.3) and, as pointed out in [2], they are much more easily observable than nonlinear perturbations of an oscillatory wavetrain. Note also that geophysical fluid-dynamical considerations show that the Reynolds number is extremely large (see [30]), so that nonlinear effects typically dominate over viscosity. Field evidence for critical levels (locations where the wave speed equals the mean-flow speed) in the near-surface layer above the thermocline, where the flow-reversal of the underlying current occurs is available (see [34]). It is therefore advisable to rely on the nonlinear alternative to the conventional linear viscous boundary-layer approach for the description of the flow in the neighbourhood of critical levels, where Kelvin ‘cat’s eye’ flow patterns appear (see the discussion in [9] for the somewhat simpler case of gravity water flows with constant non-zero vorticity).
2.2 Basic modelling assumptions
A few realistic simplifying assumptions can be made. Firstly, since the Reynolds numbers are typically very large in geophysical ocean flows, it is reasonable to employ inviscid theory (see [30]). Secondly, because we are considering flows in the neighbourhood of the Equator, it is adequate to use the f-plane approximation in the governing equations (see [26]). Thirdly, since field data shows that the meridional velocities are much smaller than the zonal velocities at the Equator (see [20]), we study flow configurations which are latitude-independent and with a vanishing meridional velocity component. Consequently, we investigate two-dimensional inviscid flows which present no variation in the meridional direction, regarding them as wave–current interactions due to localised wave perturbations of a pure current background state. The presence of underlying depth-dependent currents places us within the framework of flows with non-zero vorticity. Since for wave–current interactions in which the waves are long compared with the mean depth of the effective flow region the importance of a non-zero mean vorticity preponderates that of its specific distribution (see [13]), the simplest realistic setting is that of flows with constant vorticity above and below the thermocline: negative above, to permit a reversal from the surface westward wind-drift to the eastward-flowing subsurface EUC, and positive below to model a flow that withers with increasing depth. This choice is propitious not just because in two-dimensional flows the vorticity of a particle remains constant as the particle moves about, as one can easily check. Remarkably, for two-dimensional stratified flows with constant vorticity in each layer, a separation of the flow into a pure current and an irrotational wave perturbation can be performed within the framework of the fully nonlinear theory, without recourse to approximations (see Sect. 3.3). This feature permits us to view the nonlinear wave–current interaction as an irrotational wave perturbation of a mean flow representing a pure current.
2.3 The Hamiltonian perspective
The ability to pursue in-depth nonlinear studies is contingent upon a rich structure. Since dissipation is not important, this motivates the quest for a Hamiltonian formulation. The Hamiltonian perspective results in a significant simplification, serving as a guide to the choice of new dependent and independent variables in which the equations take their simplest form. Note that the Hamiltonian formulation of the governing equations for two-dimensional gravity water flows was pioneered in [46] for irrotational flows, and was extended to rotational flows with constant vorticity in [43, 44]. A Hamiltonian approach to two-dimensional two-layer gravity water flows with a free surface was developed in [10], and recently the rotational counterpart, with constant vorticity in each layer, was obtained in [6] for periodic flows. This paper establishes the validity of a Hamiltonian perspective in the presence of Coriolis effects in the equatorial f-plane approximation, for zonal flows with no variation in the meridional direction which represent localised perturbations of an underlying pure current background state. A suitable nondimensionalisation reveals that in certain oceanographically relevant regimes the geophysical effects are not merely a small perturbation of the governing equations for gravity water waves: scaling ascertains the relative importance of the different components of the flow, and in this geophysical regime the (linear) contribution due to the Earth’s rotation to the longitudinal momentum equation balances the linear part of the material derivative, both being of the same order. We will also show that the Hamiltonian framework is adequate for structure-preserving perturbations. In particular, a specific weakly nonlinear long-wave regime turns out to be structure-enhancing since in this setting the dynamics is described by an integrable Hamiltonian system (with infinitely many degrees of freedom). In other regimes one can derive nonlinear models that capture wave breaking.
3 The Governing Equations
The objective of this section is to present the nonlinear governing equations and to elucidate the basic structure of the associated mean flow. Also, by specifying the associated geophysical scales we can introduce a set of non-dimensional variables which are useful for ascertaining the relative importance of the different components of the flow.
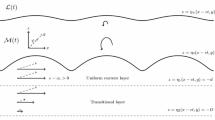
The fundamental model is that of an inviscid two-layer fluid which admits non-zero vorticity. Using the over-bar to represent the physical variables, we choose a coordinate system with its origin at a point on the Earth’s surface, with the \({\overline{x}}\)-axis horizontally due East, the \({\overline{y}}\)-axis horizontally due North and the \({\overline{z}}\)-axis upwards (see Fig. 1). Because we are considering flows in the neighbourhood of the Equator, we use the f-plane approximation (see [26]). Since observations show that the meridional velocities are much smaller than the zonal velocities at the Equator (see [20]) then, by assumption, our flow configuration is latitude-independent with vanishing meridional velocity component, and so we restrict the domain to be at a fixed latitude (see Fig. 2). Let \({\overline{z}}={\overline{h}}_1+{\overline{\eta }}_1({\overline{x}},\,{\overline{t}})\) be the free surface, \({\overline{z}}={\overline{\eta }}({\overline{x}},\,{\overline{t}})\) be the thermocline and \({\overline{z}}=-{\overline{h}}\) be the flat bed, where \({\overline{t}}\) stands for time. Here \({\overline{h}}_1\) and \({\overline{h}}\) are the mean depths of the near-surface layer and of the abyssal layer, with typical values about 120–250 m and 4 km, respectively (see [14]). The density of the fluid above the thermocline is constant, \({\overline{\rho }}_1 \approx 10^3\)\(\hbox {kg}\,\hbox {m}^{-3}\), and is replaced by \({\overline{\rho }}={\overline{\rho }}_1\,(1+r)\) for the fluid below the thermocline, where r is a small positive constant; typically r is about \(10^{-3}\) (see [22]).
Sketch of the cross-section of the fluid domain at a fixed latitude: the thermocline \({\overline{z}}={\overline{\eta }}({\overline{x}},{\overline{t}})\) separates the two layers of different constant densities, the lower boundary is a flat rigid bed, \({\overline{z}}=-{\overline{h}}\), while the upper boundary is a free surface of elevation \({\overline{z}}={\overline{h}}_1+{\overline{\eta }}_1({\overline{x}},{\overline{t}})\). The surface and internal waves are coupled, with the amplitude of the oscillations of the thermocline typically considerably larger
Denoting by \(({\overline{u}}_1({\overline{x}},{\overline{z}},{\overline{t}}),\,{\overline{v}}_1({\overline{x}},{\overline{z}},{\overline{t}}))\) and \(({\overline{u}}({\overline{x}},{\overline{z}},{\overline{t}}),\,{\overline{v}}({\overline{x}},{\overline{z}},{\overline{t}}))\) the velocity fields in the layers
above and below the thermocline, respectively, the equations of motion are the suitably adjusted Euler equations
where \({\overline{P}}={\overline{P}}({\overline{x}},{\overline{z}},{\overline{t}})\) is the pressure, \({\overline{g}} \approx 9.8\)\(\hbox {m}\,\hbox {s}^{-2}\) is the (constant) acceleration of gravity and \({\overline{\Omega }} \approx 7.29 \times 10^{-5}\) rad\(\,\hbox {s}^{-1}\) is the (constant) rotational speed of the Earth about the polar axis (towards the East), supplemented by the equations of mass conservation,
The vorticity distribution is specified by
for suitable (physical) constants \({\overline{\gamma }}_1\) and \({\overline{\gamma }}\). The appropriate boundary conditions are, at the free surface, the dynamic and kinematic boundary conditions
respectively, where \({\overline{P}}_{atm}\) is the constant pressure of the atmosphere at the surface of the ocean. At the thermocline we have the kinematic boundary conditions
together with the requirement that the pressure is continuous across the thermocline,
where \({\overline{P}}_\pm \) refer to the limits of the pressure \({\overline{P}}\) from above and below the interface. Finally, at the fixed, horizontal, impermeable bottom, we have the kinematic boundary condition
Note that (3.9)–(3.10) ensure the continuity of the normal component of the fluid velocity across the thermocline \({\overline{z}}={\overline{\eta }}({\overline{x}},{\overline{t}})\). Since within the inviscid setting the stress at an interface has no tangential component, due to the absence of any interaction derived from friction at the interface, in principle it is permissible for the tangential component of the fluid velocity to present discontinuities at the thermocline. Nevertheless, the available field data for equatorial flows suggests a continuous transition between the two layers (velocity discontinuities across the thermocline would correspond to a delta-sheet of vorticity—see also the discussion at the end of Sect. 3.3), so that we also require a tangential velocity balance:
Consequently, the velocity field is continuous across the thermocline. However, since the constant vorticities in the upper and lower layer have opposite signs, this continuity property is not valid in the continuously differentiable sense.
3.1 The pure current background state
A steady pure current solution of the governing equations, in a flow presenting no variations in the longitudinal direction and with a flat free surface \({\overline{z}} = {\overline{h}}_1\) and a flat thermocline \({\overline{z}}=0\), is provided by the velocity field \(({\overline{U}}_1({\overline{z}}),\,0)\) above the thermocline and \(({\overline{U}}({\overline{z}}),\,0)\) below it, where
the associated pressure distribution \(\overline{\mathfrak {P}}({\overline{z}})\) being given by
Depiction of the flow model in the absence of waves (pure current): constant negative vorticity \({\overline{\gamma }}_1\) in the near-surface homogeneous layer accommodates a flow-reversal from the westward wind-drift at the free surface \({\overline{z}}={\overline{h}}_1\) to an eastward jet whose core resides on the thermocline \({\overline{z}}=0\), while a constant positive vorticity in the abyssal homogeneous region below the thermocline permits the adjustment to practically still water at great depths (with no motion on the flat bed \({\overline{z}}=-{\overline{h}}\)). The corresponding velocity field is given by \({\overline{u}}_1({\overline{z}})={\overline{\gamma }}_1 {\overline{z}} + {\overline{\gamma }}\,{\overline{h}}\) and \({\overline{w}}_1=0\) in the near-surface layer \(0< {\overline{z}} < {\overline{h}}_1\), with \({\overline{u}}({\overline{z}})={\overline{\gamma }} \,( {\overline{z}} + {\overline{h}})\) and \({\overline{w}}=0\) in the abyssal layer \(-{\overline{h}}< {\overline{z}} < 0\); here \({\overline{\gamma }}> 0 > {\overline{\gamma }}_1\) and \(|{\overline{\gamma }}_1| {\overline{h}}_1 > {\overline{\gamma }} \,{\overline{h}}\)
The current profile (3.14)–(3.15) captures the salient features: a westward surface drift (since \(|{\overline{\gamma }}_1|{\overline{h}}_1> {\overline{\gamma }}{\overline{h}}\)) below which resides an eastward jet (the EUC) which overlies an abyssal layer where a gradual transition to no motion on the flat bed occurs (see Fig. 3). Note that
represents the mass transport per unit width (in \(\hbox {m}^2\,\hbox {s}^{-1}\)), so that for
there is a net eastward mass transport. Since typically (see below) \({\overline{h}}_1/{\overline{h}}\) and \({\overline{\gamma }}/{\overline{\gamma }}_1\) are both of order \(O(10^{-2})\), an eastward net flow occurs within 1\(^\circ \) from the Equator; this is compensated by a return flow at higher latitudes (see [36]). We seek nonlinear wave–current interactions arising as localised wave perturbations of the background flow (3.14–3.15).
3.2 Nondimensionalisation
The first stage in expressing the governing equations in a useful form is to introduce a suitable non-dimensionalisation of the variables; to this end we write
where the length scale is \({\overline{L}}=500\,\)m and \({\overline{U}}_0=0.5\,\hbox {m}\,\hbox {s}^{-1}\) is an appropriate speed scale. (The omission of the overbar now indicates that we are using the non-dimensional version of the corresponding variable.) Set
Above the thermocline, in the region
Eqs. (3.1), (3.3) and (3.5) therefore become
while below the thermocline, in the region
Eqs. (3.2), (3.4) and (3.6) become
where
for a flow reversal from a westward surface wind drift of \(0.5\,\hbox {m}\,\hbox {s}^{-1}\) to a maximal eastward EUC speed of \(1\,\hbox {m}\,\hbox {s}^{-1}\) in a layer of mean depth \({\overline{h}}_1=120\,\)m, with an abyssal layer of mean depth \({\overline{h}}=4\,\)km; these values, corresponding to \(h_1 \approx 0.24\) and \(h \approx 8\), are appropriate for the 6000 km stretch between about \(140^\circ \hbox {E}\) and \(150^\circ \hbox {W}\) (see [14]). For a flow that gradually dies out with depth, being motionless at the flat bed, we compute \(\overline{\gamma _1} \approx -1.25 \times 10^{-2}\,\hbox {s}^{-1}\) and \({\overline{\gamma }} \approx 2.5 \times 10^{-4}\,\hbox {s}^{-1}\). Written in nondimensional form, the boundary conditions (3.7)–(3.12) become
where \(p_\pm \) in (3.32) refer to the limits of the function p from above and below the common boundary \(z= \eta (x,t)\) of the regions \({{\mathcal {D}}}_1(t)\) and \({{\mathcal {D}}}(t)\).
The non-dimensional counterpart of the pure current background state (3.14)–(3.15) is
with \({\mathfrak {p}}(z)\), corresponding to the background pressure distribution (3.16), given by
3.3 Nonlinear flow separation
For wave–current interactions the “current” component of the flow is defined as the average velocity, and the localised perturbations that fluctuate around this average are ascribed to the wave motion, the direction of wave propagation being along the x-axis. We view the nonlinear equatorial wave–current interaction as a localised wave perturbation of the pure current solution (3.35)–(3.36) in a domain that is infinite in the x-direction. The localised nature of the wave disturbances is captured by assuming the smooth functions \(\eta _1(x,t)\) and \(\eta (x,t)\) to be of Schwartz class \({{\mathcal {S}}}({{\mathbb {R}}})\) in the x-variable at any instant t, with
The corresponding velocity fields \((u_1,w_1)\) and (u, w) are to be smooth in the domains \({{\mathcal {D}}}_1(t)\) and \({{\mathcal {D}}}(t)\), with both vector functions admitting continuous extensions to the closure of the domains and across their adjacent boundary. It is remarkable that the interpretation of (3.35)–(3.36) as the underlying current can be achieved within the framework of fully nonlinear theory, without performing approximations.
Theorem 1
If the flow approaches asymptotically the pure current state, then the velocity fields \((u_1,w_1)\) and (u, w) and the pressure p(x, z, t) are, at any instant t, smooth localised perturbations of the background flow (3.35)–(3.36) and of the corresponding background pressure distribution (3.37), in each of the domains \({{\mathcal {D}}}_1(t)\) and \({{\mathcal {D}}}(t)\), respectively.
Proof
Consider a solution to the governing equations (3.19)–(3.22), (3.23)–(3.26), (3.28)–(3.34), with no flow along the flat bed \(z=-h\). Let us denote by \({\mathfrak {U}}(z_0,t)=\displaystyle \lim _{\Lambda \rightarrow \infty } \frac{1}{2\Lambda } \int _{-\Lambda }^\Lambda u(x,z_0,t)\,dx\) the underlying current at a depth \(z_0\) below the trough of the thermocline \(z=\eta (x,t)\), obtained by averaging. Applying the divergence theorem to the divergence-free vector field \((-w,\,u-\gamma z)\) in the rectangular domain \(\{(x,z):\ -\Lambda< x< \Lambda ,\, -h< z < z_0\}\) yields
for \(\Lambda \rightarrow \infty \). Combining this with the absence of a flow on the flat bed, \(u=0\) on \(z=-h\), we get \({\mathfrak {U}}(z_0,t)=\gamma (z_0+h)\), which coincides with (3.36). Similarly, the underlying current at a depth \(z_0\) above the crest of the internal wave and below the trough of the surface wave is
Applying the divergence theorem in the domain \(\{(x,z):\ -\Lambda< x< \Lambda ,\, \eta (x,t)< z < z_0\}\) to the vector field \((-w_1,\,u_1-\gamma _1 z)\), we get
so that (3.38) and (3.34) yield
This leads to \({\mathfrak {U}}_1(z_0,t)=\gamma _1 z_0+ \gamma h\), which coincides with (3.35). Indeed, for this it suffices to apply the divergence theorem in the domain \(\{(x,z):\ -\Lambda< x< \Lambda ,\, -h< z < \eta (x,t)\}\) to the vector field \((-w,\,u-\gamma z)\), using (3.34) and (3.38) together with the vanishing of u on the flat bed \(z=-h\). \(\quad \square \)
Let us point out that the velocity field is actually Hölder continuous across the smooth thermocline. Indeed, the velocity field of the pure current background state (3.35)–(3.36) is Lipschitz continuous in the horizontal strip \(-h \le z \le h_1\). Since the wave–current interaction is a localized perturbation of this background flow, in an open horizontal strip \({{\mathbb {O}}}\) containing the thermocline, the velocity field \({{\mathbb {V}}}_{{\mathbb {F}}}\) of the wave motion is divergence-free, has a piecewise constant curl, decays as it approaches the lateral boundary components of \({{\mathbb {O}}}\) at infinity, and is smooth on the upper and lower boundary components \(\partial {{\mathbb {O}}}_\pm \) of \({{\mathbb {O}}}\) (since in the fluid domain away from the thermocline, the Laplacian of each velocity component is constant, so that the regularity for Poisson’s equation [15] applies). For \(s >3\), the a priori elliptic estimate
for the div-curl system, interpreted for \({{\mathbb {V}}}_{{\mathbb {F}}} \in L^\infty ({{\mathbb {O}}})\) in the sense of distributions (see [4, 42]), ensures, by means of a Sobolev imbedding (see [15]), that \({{\mathbb {V}}}_{{\mathbb {F}}}\) is Hölder continuous with exponent \(\alpha <1/3\) throughout \({{\mathbb {O}}}\). Consequently the velocity field of the wave–current interaction is Hölder continuous across the thermocline.
3.4 Hamiltonian formulation
We now present the Hamiltonian formulation of the governing equations (3.19)–(3.22), (3.23)–(3.26), (3.28)–(3.34).
As a first step towards the choice of new dependent and independent variables that reveal the Hamiltonian structure, we introduce the stream function and the perturbed velocity potential. The equations of mass conservation, (3.21) and (3.25), ensure the existence of a stream function in each layer, \(\psi _1(x,z,t)\) in \({{\mathcal {D}}}_1(t)\) and \(\psi (x,z,t)\) in \({{\mathcal {D}}}(t)\), determined, up to an additive term that depends only on time, by
Relying on (3.21), (3.25), (3.33) and (3.30), we may set
observing that (3.30) ensures that the first integral in (3.41) is well-defined. Each stream function has a smooth extension to the closure of its respective domain, \(\overline{{{\mathcal {D}}}(t)}\) and \(\overline{{{\mathcal {D}}}(t)}\). Actually, since the velocity field is a smooth localised perturbation of the background state (3.35)–(3.36), by evaluating \(\psi \) and \(\psi _1\) on \(z=\eta (x,t)\) as \(x \rightarrow -\infty \) we see that (3.40)–(3.41) ensure the existence of a continuous function \(\Psi (x,z,t)\) throughout the bulk of the fluid \({{\mathcal {K}}}(t)=\{(x,z):\ -d \le z \le h_1+\eta _1(x,t)\}\), with \(\Psi =\psi \) on \(\overline{{{\mathcal {D}}}(t)}\) and \(\Psi =\psi _1\) on \(\overline{{{\mathcal {D}}}(t)}\). The discussion after (3.13) shows that \(\Psi \) is continuously differentiable in \({{\mathcal {K}}}(t)\) without being twice continuously differentiable (due to discontinuities in the second order partial derivatives across the thermocline). For this reason, rather than using \(\Psi \) we prefer to use \(\psi \) and \(\psi _1\). With the vorticity distribution defined by (3.22) and (3.26), (3.39) yields
We now introduce harmonic perturbed velocity potentials, \(\varphi \) in \({{\mathcal {D}}}(t)\) and \(\varphi _1\) in \({{\mathcal {D}}}_1(t)\), by requiring
More precisely, since the velocity field is a smooth localised perturbation of the background state (3.35)–(3.36), with \(u=0\) on the flat bed \(z=-h\), we may set
to see that the first integral in (3.45) is well-defined, use (3.34) and subsequently the divergence theorem applied to the vector field \((-w,\,u-\gamma z)\) in \(\{(x',z):\ x^*<x'<x,\ -h< z <\eta (x',t)\}\) with \(x^*\rightarrow -\infty \). Both perturbed velocity potentials admit continuously differentiable extensions to the closures of their domains, \(\varphi \in C^1(\overline{{{\mathcal {D}}}(t)})\) and \(\varphi _1 \in C^1(\overline{{{\mathcal {D}}}_1(t)})\). However, in contrast with the stream functions, any oscillation of the thermocline impedes a continuous extension of the perturbed velocity potentials to the bulk of the fluid \({{\mathcal {K}}}(t)\): while smooth additive functions that depend solely on time may be added to the right sides of (3.44)–(3.45), this process does not lead to an equality of \(\varphi \) and \(\varphi _1\) on the interface. Indeed, for \(\eta \not \equiv 0\), (3.43) and the continuity of the velocity field across the thermocline show that differentiation of a presumed equality \(\varphi (x,\,\eta (x,t),\,t)=\varphi _1(x,\,\eta (x,t),\,t) +\varphi _0(t)\) with respect to the x-variable leads to a contradiction since \(\gamma \ne \gamma _1\).
The kinematic boundary conditions (3.29)–(3.31) can now be written as
respectively, where the subscript \(s_1\) means that we consider the traces of the involved functions on the free surface \(z=h_1+\eta _1(x,t)\), while the subscript s denotes traces on the interface \(z=\eta (x,t)\).
We can recast the Euler equations (3.19)–(3.20) and (3.23)–(3.24) as
respectively, so that the expressions on which the gradient operates are just time-dependent. Recalling (3.40)–(3.41), (3.44)–(3.45), and taking into account that the flow is a smooth localised perturbation of (3.35)–(3.36) with the background pressure distribution (3.37), we evaluate these expressions as \(x \rightarrow -\infty \) on \(z=\eta (x,t)\) and on \(z=-h\), respectively. We get
where
Consequently, we can write the dynamic boundary condition (3.28) as
while the continuity of the pressure across the thermocline, (3.32), becomes
where
Let us now show that the governing equations (3.19)–(3.22), (3.23)–(3.26), (3.28)–(3.34) can be tidied up as a Hamiltonian system by identifying
as the Hamiltonian, where
are the excess kinetic and potential energies, respectively. Other than the technical spur to avoid infinite energy, the rationale for the above choice is that not all potential energy can be converted into kinetic energy, the portion that is available for this conversion being the difference in the potential energy between the perturbed wave–current state and the pure current background state. In view of (3.17) and (3.27), the nondimensional expression in (3.54) corresponds to the total excess energy per unit width, \({\overline{H}}={\overline{\rho }}_1{\overline{U}}_0^2 {\overline{L}}^2\, H\). To see that \({\overline{\rho }}_1{\overline{U}}_0^2 {\overline{L}}^2 \approx 625 \times 10^5\)\(\hbox {m}\,\)kg\(\,\hbox {s}^{-2}\) is a suitable scale, note that, over the 16,000 km length of the EUC, it corresponds to a mean total energy of about 4 kg\(\,\hbox {s}^{-2}\), which is of the order of the mean kinetic energy at the surface of the equatorial Pacific (about 2 kg\(\,\hbox {s}^{-2}\); see [19]). As for the estimate of potential energy, field data gathered at 45 m depth indicates an average ratio between potential and kinetic energy of about 0.76, varying between 0.18 and 3.63 with means of the order of \(10^{-2}\) kg\(\,\hbox {s}^{-2}\) (see [28]). Moreover, the energy is dominated by the zonal component, which is about one order of magnitude greater than the meridional component, thus corroborating the realistic nature of an approach that invokes the f-plane approximation and the neglect of meridional variations.
Sketch of the geometric features that are relevant in the definition of the Dirichlet–Neumann operators associated with the two layers: at the instant t, the outward unit normals for the abyssal layer \({{\mathcal {D}}}(t)\) and for the near-surface layer \({{\mathcal {D}}}_1(t)\) at a point X on the thermocline are \(N^-(X)\) and \(N^+(X)\), respectively, while the outward unit normal at a point \(X_1\) on the free surface is \(N^+(X_1)\)
Using (3.43) and (3.38), we get
Since \(\Delta \varphi =0\) in \({{\mathcal {D}}}(t)\) with \(\varphi =0\) on \(z=-h\), setting
integration by parts yields
where \(G:=G(\eta )\) is the Dirichlet–Neumann operator on \({{\mathcal {D}}}(t)\), associating to \(\Phi \) the normal derivative of \(\varphi \) on the upper boundary \(z=\eta (x,t)\) with outward unit normal N; see Fig. 4. Similarly, denoting
we define on \({{\mathcal {D}}}_1(t)\) the Dirichlet–Neumann matrix operator
that associates to the boundary values of the harmonic function \(\varphi _1\) on the lower and upper boundaries, \(\Phi _1\) and \(\Phi _2\), respectively, the outward normal derivatives \(N\cdot \nabla \varphi _1\) at these boundaries. Then
On the other hand, since \(F=\psi -\frac{1}{2}\,\gamma \,(z+h)^2\) is harmonic in \({{\mathcal {D}}}(t)\), with \(\nabla F =(-\varphi _z,\,\varphi _x)\) and \(F=0\) on \(z=-h\), the divergence theorem applied to \(\frac{1}{2}\,\gamma \,(z+h)^2\, \nabla F\) yields
Similarly, the divergence theorem applied to \(\frac{1}{2}\,(\gamma _1 z^2+2\gamma h z) \nabla F_1\), where \(F_1=\psi _1 - \frac{1}{2}\,(\gamma _1 z^2+2\gamma h z)\) is harmonic in \({{\mathcal {D}}}_1(t)\) with \(\nabla F_1=(-\varphi _{1,z},\,\varphi _{1,x})\), yields
From the definition of the Dirichlet–Neumann operators, using (3.43) and (3.29)–(3.31), we see that
Adding up the relations (3.64) and (3.65), we obtain
Let us now define the operator
Introducing the variables
relation (3.67) enables us to express \(\Phi \) and \(\Phi _1\) in terms of \(\xi \) and \(\xi _1\):
Regarding \(h_1,\, h,\, \gamma _1,\,\gamma ,\,\omega \) as fixed parameters and gathering (3.54)–(3.57), (3.59), (3.61)–(3.63) and (3.70)–(3.71), we express H as a functional depending solely on the variables \(\eta \), \(\eta _1\), \(\xi \), \(\xi _1\):
Since \(x \mapsto \int \limits _{-\infty }^x \theta (x')\,dx' \in {{\mathcal {S}}}({{\mathbb {R}}})\) if and only if \(\theta \in {{\mathcal {S}}}({{\mathbb {R}}})\) satisfies \(\int \limits _{{{\mathbb {R}}}} \theta (x')\,dx'=0\), we see that the functions \(\varphi \) and \(\varphi _1\) defined by (3.44)–(3.45) are smooth localised perturbations. This property is passed on to \(\xi \) and \(\xi _1\), while for \(\eta \) and \(\eta _1\) it is part of our setup.
It is of interest to provide a concise explicit form of the functional \({{\mathcal {H}}}\) in (3.72). Since \(\Phi _1=(1+r)\Phi - \xi \) by (3.69), B and G are unbounded self-adjoint operators on \(L^2({{\mathbb {R}}})\) while \((G_{12})^*=G_{21}\), and using the relation \((1+r)B^{-1}G_{11}=\text {Id}-B^{-1}G\) that follows from (3.68), we get
We now compute variations of the functional \({{\mathcal {H}}}\), with respect to the inner product associated to square-integrable real functions defined on the real line. We consider variations of the wave field, regarding the underlying current field (3.35)–(3.36) as fixed; in particular, the flat bed, the vorticity and the mean depths of the layers do not change. Note that
On the other hand,
and
respectively. For harmonic variations of \(\varphi \), using the divergence theorem and the identity
we get
Similarly, for harmonic perturbations of \(\varphi _1\) we get
From (3.54)–(3.57) and (3.74)–(3.79), using (3.29)–(3.31), (3.40)–(3.41), (3.44)–(3.45), (3.51)–(3.52), we conclude that
since the invariance of the total mass in each layer ensures
Switching from the variables \((\eta ,\,\eta _1,\,\xi ,\,\xi _1)\) to the new variables \((\eta ,\,\eta _1,\,\zeta ,\,\zeta _1)\), where
using the identities
we can write (3.80) as
Recalling (3.53), note that \(\eta _t=-\partial _x\chi \) and \(\eta _{1,t}=-\partial _x\chi _1\), due to (3.31) and (3.29), while (3.40) and (3.41) yield the asymptotic behaviour \(\chi \rightarrow \frac{\gamma h^2}{2}\) and \(\chi _1 \rightarrow \int \limits _0^{h_1} (\gamma _1 z+\gamma h)\,dz + \frac{\gamma h^2}{2}= \frac{\gamma _1h_1^2 + 2\gamma hh_1+\gamma h^2}{2}\) for \(x \rightarrow -\infty \). Consequently
Since differentiation of (3.38) with respect to the t-variable yields \(\int _{{{\mathbb {R}}}} \eta _t \,dx= \int _{{{\mathbb {R}}}} \eta _{1,t}\,dx=0\), using integration by parts, (3.85) and (3.81), we get
Cancellations occur in (3.84) due to the above two relations in (3.84), so that
Therefore we proved the following result.
Theorem 2
Let \({\mathfrak {u}}=(\eta ,\,\eta _1,\,\zeta ,\,\zeta _1)^\intercal \). With \({{\mathcal {H}}}\) given by the explicit expression (3.73), the system
is the Hamiltonian form \(\partial _t {\mathfrak {u}}=J \,\delta _{\mathfrak {u}}\,{{\mathcal {H}}}\) of the governing equations with respect to the canonical symplectic structure induced by the matrix operator \(J = {\tiny \begin{pmatrix} 0 &{} I_2 \\ -I_2 &{} 0 \end{pmatrix}}\) with \(I_2={\tiny \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array}\right) }\), acting on the phase space \({{\mathcal {X}}}={{\mathcal {S}}}({{\mathbb {R}}}) \times {{\mathcal {S}}}({{\mathbb {R}}}) \times {{\mathcal {S}}}({{\mathbb {R}}}) \times {{\mathcal {S}}}({{\mathbb {R}}})\) of Schwartz-class functions.
The above variational derivative of \({{\mathcal {H}}}: {{\mathcal {X}}} \rightarrow {{\mathbb {R}}}\) at \({\mathfrak {u}}_0 \in {{\mathcal {X}}}\) is defined by \(\langle {\mathfrak {u}},\, \frac{\delta {{\mathcal {H}}}}{\delta {\mathfrak {u}}}( {\mathfrak {u}}_0)\rangle =\lim \limits _{\varepsilon \rightarrow 0} \,\frac{{{\mathcal {H}}}({\mathfrak {u}}_0 + \varepsilon {\mathfrak {u}})- {{\mathcal {H}}}({\mathfrak {u}}_0)}{\varepsilon }\), with respect to the inner product \(\langle \cdot ,\cdot \rangle \) in the Hilbert space \(L^2({{\mathbb {R}}}) \times L^2({{\mathbb {R}}}) \times L^2({{\mathbb {R}}}) \times L^2({{\mathbb {R}}})\).
4 Hamiltonian Perturbations
We regard the equatorial waves as localised perturbations of the background state, typical examples being solitary waves. A reasonable measure of the “wavelength” of a solitary wave is the spatial extent of the region where the deviation of the profile from its mean level is at least 1% of the maximum height. In the geophysical regime in which the wavelength is long compared to the average depth, both gravity and the rotation of the Earth play a role in the dynamics. In our nondimensional framework \(x=1\) corresponds to 500 m, so that the relevant spatial scaling is
with \(\varepsilon \ll 10^{-1}\). This defines a physical regime in which the dependent and independent variables are O(1), and the relation to the nondimensional variable x is by means of (4.1); in particular, a perturbation that mainly occurs for values \(x' \in (-1,1)\) corresponds to \(x \in (-1/\varepsilon ,\,1/\varepsilon )\) and thus represents a physical region spreading over more than 10 km. Our approach to systematic derivations of model equations is from the point of view of Hamiltonian perturbation theory. The parameter \(\varepsilon \) from (4.1) will also be introduced through choices of scaling of the dependent variables \((\eta ,\,\eta _1,\,\zeta ,\,\zeta _1)\), corresponding to scaling regimes of interest, in which dispersive and nonlinear effects are brought into play. Since our main interest is the propagation of internal waves, the representative scales are determined by the motion of the thermocline, and we use these scales also for the surface waves. This results in a Hamiltonian that is a function of the small parameter \(\varepsilon \). The approximating Hamiltonian systems are obtained by retaining a finite number of terms in the Taylor expansion in \(\varepsilon \) of the Hamiltonian.
Given a constant \(\alpha >0\) and a smooth local diffeomorphism \(f: {{\mathbb {R}}}^4 \rightarrow {{\mathbb {R}}}^4\), the change of variables \([\alpha t'= t, \,{\mathfrak {u}}'=f({\mathfrak {u}})]\) transforms the Hamiltonian system \(\partial _t {\mathfrak {u}}=J\,\delta _{\mathfrak {u}} {{\mathcal {H}}}\) to the Hamiltonian system \(\partial _{t'} {\mathfrak {u}}'=J'\,\partial _{{\mathfrak {u}}'} {{\mathcal {H}}}'\) with Hamiltonian \({{\mathcal {H}}}'({\mathfrak {u}}')={{\mathcal {H}}}({\mathfrak {u}})\) if the operator \(J'=\alpha (\delta _{\mathfrak {u}} f)J(\delta _{\mathfrak {u}} f)^\intercal \) is symplectic, that is, \((J')^\intercal J J'=J\) (see [35]); moreover, if the change of variables preserves the Hamiltonian form of all Hamiltonian equations, then \(J'\) must be symplectic (see [33]). Due to the physical interpretation in which the dynamics is governed by the perturbations of the two interfaces, the relevant coordinate transformation in our setting is the spatial scaling
for some positive scalars a and b. Since a \(2n \times 2n\) block matrix \({\tiny \begin{pmatrix} M_{11} &{} M_{12} \\ M_{21} &{} M_{22} \end{pmatrix}}\) is symplectic if and only if the \(n \times n\) matrices \(M_{11}^\intercal M_{21}\) and \(M_{12}^\intercal M_{22}\) are symmetric and \(M_{11}^\intercal M_{22} -M_{21}^\intercal M_{12}=I_n\) (see [33]), we see that the scaling transformation (4.2) coupled with the simultaneous temporal scale
is symplectic if and only if \(a=b=\sqrt{\alpha }\). Note for our nondimensionalisation \(t=1\) corresponds to about 17 min. The space-time scale (4.2)–(4.3) specifies the distance and time needed to bring about the balance
for the dynamics of the flow. Note that a regime of type (4.2) comes about due to wave perturbations of the pure current background state described in Sect. 3.1. Since these perturbations are harmonic, as shown by the considerations in Sects. 3.3 and 3.4, their overall effect is encoded in the way they operate at the surface and at the interface. Using the relations (3.43), (3.58), (3.60), (3.69), (3.82)–(3.83), one can render (4.2) in terms of the magnitude of the deviation of the surface/interface from the quiescent flat state and of the relative sizes of the wave/current components of the fluid velocity field at these boundaries. We will provide details of this interpretative aspect in each specific case that we discuss.
The linear Dirichlet–Neumann operators G and \(G^+\) are analytic in their dependence on \(\eta \) and \((\eta ,\eta _1)\), respectively, having convergent Taylor series expansions
with each linear operator \(G^{(j)}(\eta )\) homogeneous of degree j in \(\eta \) and each linear operator \(G_{ij}^{(m_0m_1)}(\eta ,\eta _1)\) with \(i,j=1,2\) homogeneous of degree \(m_0\) in \(\eta \) and of degree \(m_1\) in \(\eta _1\) (see the discussion in [10, 11]); moreover, each of the operators \(G^{(j)}(\eta )\) and \(G_{ii}^{(m_0m_1)}(\eta ,\eta _1)\) with \(i=1,2\) and \(m_0,\,m_1 \ge 0\) is self-adjoint, while \((G_{12}^{(m_0m_1)}(\eta ,\eta _1))^*=G_{21}^{(m_0m_1)}(\eta ,\eta _1)\). Denoting
and given a smooth function \(m: {{\mathbb {R}}} \rightarrow {{\mathbb {C}}}\) whose derivatives of any order have polynomial growth, the Fourier multiplication operator
maps \({{\mathcal {S}}}({{\mathbb {R}}})\) into \({{\mathcal {S}}}({{\mathbb {R}}})\) and extends to a self-adjoint operator in \(L^2({{\mathbb {R}}})\) if and only if m is real-valued; see [40]. The operator (4.7) is bounded if and only if \(m \in L^\infty ({{\mathbb {R}}})\), with m(D)f real-valued or imaginary-valued, for real-valued \(f \in {{\mathcal {S}}}({{\mathbb {R}}})\), if \(m(-x)=\overline{m(x)}\) or if \(m(-x)=-\overline{m(x)}\) for all \(x \in {{\mathbb {R}}}\), respectively. In terms of Fourier multipliers the leading order terms of the Dirichlet–Neumann operators G and \(G^+\) are given by
while
The above formulas are indicative of the nonlinear nonlocal dependence of the operators \(G(\eta )\) and \(G^+(\eta ,\eta _1)\) on \(\eta \) and \((\eta ,\eta _1)\), respectively. Concerning the effect of scaling, note that a simple change of variables confirms that the transformation (4.1) replaces the Fourier multiplier operator m(D) by \(m(\varepsilon D')\), with \(D'=-i\partial _{x'}\). More precisely, for \(f \in {{\mathcal {S}}}({{\mathbb {R}}})\) we have
where \(F(x)=f(x/\varepsilon )\). On the other hand, the effect of the scaling (4.2) is expressed by
with more intricate but workable scaling formulas expressing \(G_{ij}^{(m_0m_1)}(\eta ',\eta _1')\) in terms of \(G_{ij}^{(m_0m_1)}(\eta ,\eta _1)\) for \(1 \le i,j \le 2\) and \(m_0,\,m_1 \ge 0\).
4.1 The linearised equations
The quiescent state (no waves) corresponds to the trivial solution \(\eta =\eta _1=\zeta =\zeta _1=0\). Since most practical predictions of water waves use linear approximations, it is natural to investigate the linearised equations about the state of rest. An elegant way to derive them is to truncate the Taylor expansion of the Hamiltonian at its quadratic term. The quadratic part of the Hamiltonian (3.73) is
since \(B \approx D\tanh (hD) + (1+r)D\coth (h_1D)\), \(G \approx D\tanh (hD)\) and
To obtain the linearised form of (3.86) we have to exhibit in (4.15) a functional dependence on \({\mathfrak {u}}=(\eta ,\,\eta _1,\,\zeta ,\,\zeta _1)^\intercal \). This can be achieved as follows. Note that (3.82)–(3.83) yield
Using the calculus of pseudodifferential operators with smooth symbols, by means of (4.17) we can handle the last three terms in (4.15) by relying on the fact that although the functions and the operators of interest are all real-valued, the natural set-up for Fourier multipliers is the complex inner product on \(L^2({{\mathbb {R}}})\), which is also adequate for taking advantage of the self-adjointness of operators of the type (4.7). We get
The linearised equations of motion are
Given an initial data \({\mathfrak {u}}_0\), representing a localised wave perturbation of the pure current background state described in Sect. 3.1, we can solve the linear system (4.18) using the Fourier transform. Indeed, setting \({\hat{f}}(k)=\int _{{\mathbb {R}}} f(x)e^{-ikx}dx\) for \(f \in {{\mathcal {S}}}({{\mathbb {R}}})\) in each component of \({\mathfrak {u}}\), the system (4.18) is transformed for any fixed \(k \in {{\mathbb {R}}}\) into the linear autonomous system of ordinary differential equations
where
and
Note that in the absence of vorticity (\(\gamma =\gamma _1=0\)) the matrix M(k) is real but the context of equatorial wave–current interactions (for which \(\gamma \ne 0\)) brings about purely imaginary entries on the main diagonal. The complex system (4.19) can be cast in the form of a real Hamiltonian system with double degree of freedom (of dimension eight) by separating the real and complex part of each of the four components of the vector \(\hat{{\mathfrak {u}}} \in {{\mathbb {C}}}^4\). However, in our context it is advisable to work with the complex linear Hamiltonian system to avoid going beyond the treshold of Galois theory for roots of polynomials. In particular, finding the spectrum of M(k) is computationally within reach for a fixed value of \(\xi \) since explicit formulas are available for its quartic characteristic polynomial. On the other hand, since the available theoretical studies of Hamiltonian systems deal with systems in \({{\mathbb {R}}}^{2n}\), there is a need for theoretical adjustment but with guaranteed structural features. For example, the matrix M(k) being Hamiltonian means that JM(k) is self-adjoint, so \(M(k)=J^{-1} (-\overline{M(k)}^{\,\intercal }) J\). Therefore the matrices M(k) and \(\overline{M(k)}^{\,\intercal }\) are similar. Thus if \(\Lambda (k)\) is an eigenvalue of M(k), then so is \(-\overline{\Lambda (k)}\) and the whole Jordan block structure will be the same for \(\Lambda (k)\) and \(-\overline{\Lambda (k)}\).
The unique solution to (4.19) with initial data \(\hat{{\mathfrak {u}}}_0(k)=\int _{{\mathbb {R}}} {\mathfrak {u}}_0(x)\,e^{ikx}\,dx\), given by \(\hat{{\mathfrak {u}}}(k,t)=e^{M(k)t}\,\hat{{\mathfrak {u}}}_0(k)\) for \(t \ge 0\), corresponds, by means of the inverse Fourier transform, to the solution
of (4.18) with initial data \({\mathfrak {u}}_0 \in {{\mathcal {S}}}({{\mathbb {R}}})\). To a purely imaginary eigenvalue \(\Lambda (k)=- ikc\) with \(c \in {{\mathbb {R}}} {\setminus }\{0\}\) of M(k), with corresponding eigenvector \({\mathfrak {v}}(k) \ne 0\), we can associate the oscillatory mode solution \(e^{M(k)t}{\mathfrak {v}}(k)=e^{-ikct}\,{\mathfrak {v}}(k)\) of (4.19), and for the initial data \({\mathfrak {u}}_0 \in {{\mathcal {S}}}({{\mathbb {R}}})\) with \(\hat{{\mathfrak {u}}}_0(k)={\mathfrak {v}}(k)\), we can interpret the solution
as a linear superposition of such modes. This way a purely imaginary eigenvalue \(\Lambda (k)=- ikc\) of M(k) corresponds to the fundamental oscillation mode \(e^{ ik (x-ct)}\,{\mathfrak {v}}(k)\) with frequency \(\frac{|k|}{2\pi }\), propagating at the constant speed c. Due to (3.17), a fixed nondimensional value of \(k \ne 0\) corresponds in physical variables to a harmonic oscillation of wavelength \(\frac{2\pi }{|k|}\,{\overline{L}}\). With our choice \({\overline{L}}=500\,\)m, since ocean waves have wavelengths in excess of 50 m, the qualitative behaviour of the solutions to the linear system (4.19) for \(|k| < 64\) is physically relevant. Note that an eigenvalue \(\Lambda (k)\) with nonzero real part is the symptom of an oscillation mode whose amplitude grows exponentially in time since \(\Lambda (k)\) or \(-\overline{\Lambda (k)}\) leads to a coefficient of the type \(e^{\omega (k)t}\) with \(\omega (k)>0\). This Kelvin-Helmholtz instability corresponds to a situation when a wave is capable of extracting energy from the background pure current state, by drawing either kinetic energy from the pure current motion or potential energy from the stratification.Footnote 1 Since these instability phenomena are a prelude to mixing and turbulence, it is important to understand whether or not they are inherent to the equatorial wave–current interactions. For considerations of spectral type the explicit formulas for the roots of the quartic characteristic polynomial are too unwieldy. We advocate an approach that takes advantage of the fact that each entry of the matrix M(k) depends smoothly (actually, the dependence is real-analytic) on the parameter k. This ensures that the eigenvalues depend continuously on k, even if splitting and coalescence of eigenvalues may take place (see the discussion in [21], Chapter VII) and the eigenvalues need not be differentiable, which makes it difficult to translate this feature quantitatively. Also, note that the eigenspaces can behave quite singularly—they are not necessarily continuous. However, for simple eigenvalues the eigenvalue itself as well as the (unique) normalised eigenvector will exhibit a real-analytic dependence on k (see [25]). Note that the multiparameter version of this last result fails spectacularly: for simple eigenvalues, a locally Lipschitz-dependence holds but differentiability might fail and it may not even be possible to choose eigenvectors in a continuous way (see the discussion in [24]).
Since our main interest is the propagation of localised perturbations, it is advantageous to use the Paley-Wiener theorem to translate the feature that \(x \mapsto {\mathfrak {u}}(x,t)\) has compact support at every instant into the requirement that \(k \mapsto \hat{{\mathfrak {u}}}(k,t)\) is an analytic function of exponential type. The general solution of (4.19) is a linear combination of solutions of the form \(t^n e^{\Lambda (k) t} {\mathfrak {U}}\), where n is a nonnegative integer, \({\mathfrak {U}}\) is a constant vector and \(\Lambda (k)\) is an eigenvalue of M(k). Since the fact that no entry of the matrix M(k) exhibits a superlinear growth in k towards infinity ensures, by inspection of Ferrari’s classical algebraic solution to the quartic, the existence of a constant \(m>0\) such that \(|\Lambda (k)| \le m(1+|k|)\) for all \(k \in {{\mathbb {R}}}\), we deduce that \(k \mapsto \hat{{\mathfrak {u}}}(k,t)\) remains forever of exponential type if it is initially so. Consequently the linearised system captures the propagation of localised wave perturbations of the pure current background state.
A simple calculation shows that M(0) has \(\Lambda (0)=0\) as an eigenvalue of algebraic multiplicity four and geometric multiplicity two, with the eigenspace spanned by the eigenvectors \((1\, 0\,0\,0)^{\,\intercal }\) and \((0\, 1\,0\,0)^{\,\intercal }\). This behaviour is quite different from that encountered for waves in the physically relevant regime \(0<|k| < 64\).
Lemma
The matrix M(k) has four distinct purely imaginary eigenvalues for \(0<|k| < 64\).
Proof
Note that \(\Lambda (k) \in {{\mathbb {C}}}\) is an eigenvalue of M(k) with eigenvector \((v_1\ v_2\ v_3\ v_4)^{\,\intercal }\) if and only if \(\lambda (k)=\frac{i\Lambda (k)}{k}\) is an eigenvalue with corresponding eigenvector \((v_1\ v_2\ ikv_3\ ikv_4)^{\,\intercal }\) of the real matrix
To investigate the roots of the characteristic polynomial \(p(\lambda )=\hbox {det}(R-\lambda I_4)\), we first perform two sets of operations to simplify its structure. Add the first row multiplied by \(\mu \) to the third row, and the second row multiplied by \(\mu _1\) to the fourth row, and in the outcome add the third column multiplied by \(\mu \) to the first column and the fourth column multiplied by \(\mu _1\) to the second column to obtain a determinant edxpressed in terms of \(X=\lambda - \gamma h\), corresponding to the wave speed relative to the maximum speed of the EUC, as
where \({\hat{g}}=g+\gamma _1^2 h_1 - \omega \gamma h\) and \({\mathfrak {s}}={\mathfrak {s}}(k)= \text {sech}(h_1k)\). Expanding the above determinant by minors along the first column yields
since \(\Theta>0 >\Gamma \) and the inequality \(s < (1+s)\tanh (s)\) for \(s>0\), in combination with the relation
yields \(\gamma _1^2 h_1^2/(\Theta _1-{\mathfrak {s}}^2\Theta )=\gamma _1^2h_1h_1k/\tanh (h_1k)< \gamma _1^2h_1\,(1+h_1|k|) < {\hat{g}}\) for \(|k| <64\). On the other hand,
since the inequality \(\tanh (s)<s < (1+s)\tanh (s)\) for \(s>0\) yields
while \(\mu>0>\mu _1\), \(\Gamma <0\), and
Note that
An expansion of (4.23) by minors along the first column yields
since \(B=1+\sqrt{1-\Gamma /(\mu ^2\Theta )}>2\) satisfies \(B(2-B) \mu ^2\Theta = \Gamma \) and \({\hat{g}}+2\mu \mu _1\Theta B >0\).
We conclude from \( -\mu \Theta B< 0 < -\Gamma /(2\mu )\) and (4.24), (4.26), (4.29), that the quartic (4.23), with leading term \(X^4\), has four distinct real roots, two positive and two negative. \(\quad \square \)
4.1.1 Long waves
We now describe the main features of the linear wave propagation under the over-arching assumption of long waves, characterised by wavelengths in excess of 16 km and corresponding roughly to \(|k| < 0.2\).
The lemma in the preamble of this section validates the applicability of perturbation theory. Using the approximations
for \(k \rightarrow 0\), in combination with
we can approximate the determinant (4.23) by
An expansion of the above determinant by minors along the first column yields the polynomial
While the intricacy of the coefficients prevents us from using the explicit quartic formulas to gain insight into the location of the roots of \(p_0\), we can nevertheless take advantage of the approach used to reduce the solution of the quartic to solving the resolvent cubic. More precisely, we seek real numbers A, \(\alpha \) and \(\beta \) such that
a process factorising the quartic into a product of two quadratics whose roots are readily available. Expanding the brackets on the above right side and comparing the coefficients with (4.32), we get
and the two available expressions for \(4\alpha ^2\beta ^2\) yield a cubic equation for A,
It is a daunting task to use Cardano’s formulas to identify a real root A of the cubic (4.37) so that \(\alpha ^2\) and \(\beta ^2\), defined in (4.34)–(4.35), are positive. It turns out that a computational approach can be avoided by using the available structure. Indeed, in terms of \(a=A+ g(h+h_1)/2\), we can write the cubic \({{\mathcal {A}}}(a)\) on the left side of (4.37) in the form
Since
we see that \({{\mathcal {A}}}(-[\gamma _1h_1+\gamma h]^2/8)< 0 < {{\mathcal {A}}}(0)\). Thus \({{\mathcal {A}}}\) has a negative root \(a_0 >-(\gamma _1h_1+\gamma h)^2/8\) and the cubic (4.37) has a root \(A_0\) such that
Since \(\gamma _1h_1+\gamma h <0\), corresponding to \(A_0\) we get from (4.35) a value \(\alpha _0<0\) with
while (4.34) yields a value \(\beta _0>0\) with
Writing now (4.33) in the form
we see that the four real roots of the quartic \(p_0\) are given by
By (3.17) and (3.27), the numerical range of the relevant physical constants is
We will first obtain approximations of the roots (4.41)–(4.42) taking only into account the relative sizes of the above parameters, more precisely, the fact that
The specification (4.43) singles out the details for the ocean dynamics in the equatorial Pacific but other values, subject to (4.44), are relevant for flows in the equatorial regions of the Atlantic and Indian ocean, respectively.
The estimates (4.38), (4.39) and (4.40) yield
while Viète’s relations enable us to infer from (4.32) that
so that \(X_3^2+X_4^2 \approx \gamma _1^2h_1^2+\gamma ^2 h^2\). Using now (4.32) to write \(p_0(X)=0\) for \(X=X_3\) and \(X=X_4\) as
we can approximate \(X_{3,4}\) by the roots of the quadratic \(\Big \{ (h+h_1)X^2 - hh_1(\gamma _1-\gamma )X - \frac{rghh_1}{1+r}\Big \}\), that is,
Since \(c=\lambda =\gamma h +X\) and \({\overline{c}}=c\,{\overline{U}}_0 \), we obtain from (3.17)–(3.18) that the dispersion relations corresponding to (4.45) and (4.46) are, respectively,
and
Note that a root X of the quartic \({\hat{p}}(X)\) is related by means of \(\lambda =\gamma h +X\) to an eigenvalue \(\lambda \) of the matrix R(k), and the corresponding eigenvector \({{\mathbb {E}}}=(E_1\ E_2\ E_3\ E_4)^{\,\intercal }\) corresponds to the eigenvector \((E_1\ E_2\ \frac{E_3}{ik}\ \frac{E_4}{ik})^{\,\intercal }\) for the eigenvalue \(\Lambda (k)=-ik\lambda \) of the matrix M(k). If \({{\mathbb {E}}}\) is an eigenvector of R(k), then, multiplying the first equation of the system \(R(k){{\mathbb {E}}}=\lambda {{\mathbb {E}}}\) by \(\mu \) and adding it to the second equation yields
while the second equation multiplied by \(\mu _1\) and added to the fourth equation yields
and the first equation reads
Using the first two relations in the third yields
Taking (4.30) and (4.31) into account, (4.49) becomes
For \(X=X_{1,2}\), (4.45) and (4.44) yield \(E_1 \approx \frac{ghX}{X^3}\,E_2 \approx \frac{h}{h+h_1}\,E_2\), that is,
while for \(X=X_{3,4}\) the quadratic polynomial providing (4.46) yields \([(\gamma -\gamma _1) X-rg] hh_1 \approx -(h+h_1)X^2\), so that (4.50) simplifies to \(E_1 \approx \frac{h_1\{ g-\gamma _1 (X-\gamma _1h_1)\}}{X(X-\gamma _1h_1)} \,E_2 \approx \frac{h_1 g}{X(X-\gamma _1h_1)} \,E_2\), and in this case
for example, for the values specified in (4.43), the ratio \(\eta /\eta _1\) is about 500 (see Fig. 5). The above considerations prove the validity of the following result.
Theorem 3
Within the framework of linear theory, long waves in slow-mode propagate at speeds given by the formula (4.48), with the effects confined to the motion of the thermocline, due to (4.52), while the propagation speed of the fast long-waves is given by (4.47).
We showed that the Paley-Wiener theorem applied to the linear system (4.19) ensures that a localised disturbance occurring in the equatorial mid-Pacific will generate a unique solution in the form of a localised wave perturbation of the underlying pure current background state, that we can regard as a superposition of periodic modes by means of (4.22). Since in the ocean, energy tends to be concentrated in the lower frequencies, the physically most relevant regime is that of long waves, in which the asymptotic procedure implemented above supresses high frequencies by acting like a low-pass filter. From (4.47) and (4.48), using the values in (4.43), we obtain four possible propagation speeds in this regime:
The speed values (4.53) correspond to the extremely rare eventFootnote 2 of tsunami waves: if triggered by a submarine earthquake or by a meteorite impact, these would consist, in view of (4.51), of surface waves coupled with internal waves of roughly the same amplitude, propagating along the Equator eastwards at 727 k\(\hbox {m}\,\hbox {h}^{-1}\) and westwards at 720 k\(\hbox {m}\,\hbox {h}^{-1}\). While these fast waves are exceptional, note that on Sunday, 22 May 1960, several powerful earthquakes in rapid succession, occurred along 1000 km of fault parallel to the Chilean coastline, with the epicentre at about 200 km off the coast of Central Chile (see the discussion in [5]). Tsunami waves were generated which propagated across the Pacific Ocean and records of the travel time of the tsunami indicate a speed of about 720 k\(\hbox {m}\,\hbox {h}^{-1}\), which matches well our predictions. On the other hand, the two values (4.54) represent ubiquituous slow internal waves (known as eastward Kelvin waves and westward Rossby waves): (4.52) yields that the corresponding surface waves are insignificant, given that the typical amplitude of an internal wave is about 20 m. Note that the predicted speed values (4.54) for the slow internal waves fit reasonably well with reported field data (see the discussion in [7]). They highlight an important feature of the equatorial ocean dynamics in the Pacific: the eastward internal wave speed exceeds the maximum speed of the EUC, while the westward internal wave is slower than the maximum speed of the surface wind-driven current. Consequently, the dynamic response of the equatorial Pacific presents an east–west asymmetry due to the interaction between waves and the depth-dependent underlying currents.
4.1.2 Short waves
High-frequency ocean waves, with wavelengths of 50–100 m, correspond to the range \(31< |k| <64\), in which the approximations \(\tanh (h_1k) \approx 1\) and \(\tanh (kh) \approx 1\) are reasonable, so that \(\Theta (k) \approx \frac{1}{(2+r)|k|}\) and \(\Theta _1(k) \approx \frac{1}{|k|}\). On the other hand, the fact that \(s \mapsto s/\sinh (s)\) is decreasing for \(s>0\) yields
in particular, \(\sinh (kh_1)>817\) for \(k>31\) yields the upper bound 0.0189 above. Retaining only the leading order of each entry, we approximate the matrix M(k) in (4.19) by
with \(\Gamma ,\,\Gamma _1<0\). The characteristic polynomial
has the four disjoint purely imaginary eigenvalues
with eigenvectors \({\mathfrak {u}}_\pm (\xi )= \Big ( 1 \ 0 \ \pm i \sqrt{\tfrac{(2+r)|\Gamma |}{|k|}}\ 0\Big )^{\,\intercal }\) and \({\mathfrak {u}}^\pm (\xi )=\Big ( 0 \ 1 \ 0 \ \pm i \sqrt{\tfrac{g-\omega \Gamma _1}{|k|}}\ \Big )^{\,\intercal }\), respectively. Consequently we have four types of high-frequency oscillations: two modes in which periodic sinusoidal disturbances of the thermocline propagate at the speeds
without any effect on the (flat) free surface, and two modes in which periodic harmonic oscillations of the free surface propagate at the speeds
with an undisturbed (flat) thermocline (see Fig. 6). The appearance of dispersive effects is in marked contrast with the long waves: the initial disturbance can be thought of as being composed of the sum of a great many modes and, as time passes by, due to (4.57)–(4.58), the longer components (that is, those for which |k| is relatively smaller) will propagate faster than the shorter modes.
Let us point out succinctly the practical meaning of the nondimensional formulas (4.57)–(4.58). In view of (3.17), the nondimensional travelling mode \(e^{ik(x-ct)}\), of wavelength \(\frac{2\pi }{|k|}\), corresponds in physical variables to a harmonic oscillation of wavelength \(\frac{2\pi }{|k|}\, {\overline{L}}\), propagating at the speed \({\overline{c}}=c\,\overline{U_0}\). More precisely, due to (3.27), (3.18), (3.17), (3.82), (3.83) and (4.20), the dimensional counterpart of (4.57) for the wavelength \({\mathfrak {L}}=\frac{2\pi }{|k|}\, {\overline{L}}\) is
while that of (4.58) is
The previous considerations prove the following result.
Theorem 4
High-frequency linear waves can propagate as oscillations of the free surface and of the thermocline, with the corresponding speeds, provided by the formulas (4.60) and (4.59), respectively, imparting a dispersive character to the flow. The propagation modes (at the surface or at the termocline) are decoupled, with no noticeable effect occurring at the other interface.
Note that formula (4.60) predicts that sinusoidal surface waves with a wavelength \({\mathfrak {L}}=100\) m (corresponding to \(k=10\pi \)) propagate at speeds
These values of the wavelength and of the wave speeds are realistic for wind-generated surface waves in the Pacific (see [23]). On the other hand, by (4.59), the predicted propagation speeds of sinusoidal internal waves with a wavelength of 100 m are
Such values, close to the maximal speed of the Equatorial Undercurrent, are reported in field data (see the discussion in [7]).
4.1.3 Solitary waves
For the linear system (4.18) the existence of a smooth localised wave solution \({\mathfrak {u}}(x-c_0t)\) which propagates without change of shape at the constant speed \(c_0\) is equivalent, upon applying the Fourier transform, to \(\Lambda (k)=- i k c_0\) being an eigenvalue of M(k) with corresponding eigenvector \(\hat{{\mathfrak {u}}}(k)\) for every \(k \in {{\mathbb {R}}}\) for which \(\hat{{\mathfrak {u}}}(k) \ne 0\). In physical terms this means that the internal solitary wave profile \(\eta \in {{\mathcal {S}}}({{\mathbb {R}}})\) is expressed in Fourier integral form \(\eta (x)=\frac{1}{2\pi }\int _{{\mathbb {R}}} {\hat{\eta }}(k)\,e^{ i k x}dk\) as consisting of a superposition of harmonic wave components \(\frac{1}{2\pi }{\hat{\eta }}(\xi )\,e^{ i k x}\) of wavelength \(2\pi /|k|\) and amplitude \(\frac{1}{2\pi }\,|{\hat{\eta }}(k)|\), each travelling out at the same velocity so that the shape of the initial localised disturbance is not altered as time passes by, the only effect being a mere translation in the direction of wave propagation. We now prove that linear theory does not capture the solitary wave phenomenon.
Theorem 5
The linearised problem does not admit solitary wave solutions.
Proof
The existence of a solitary wave corresponding to some non-trivial \({\mathfrak {u}} \in {{\mathcal {S}}}({{\mathbb {R}}}^4)\) and some propagation speed \(c_0 \ne 0\) would ensure that \(c_0\) is a root of the characteristic polynomial \(p(\lambda )\) associated to the real \(4 \times 4\) matrix R(k) for all k in some open interval (a, b) where \(\hat{\mathfrak {u}}(k) \ne 0\). But since all entries of R(k) are real-analytic functions of the variable k, this would mean that the real-analytic function \(k \mapsto p(c_0)=\text {det}[R(k)-c_0 I]\) vanishes for \(k \in (a,b)\). Consequently it must be identically zero, so that \(p(c_0)=0\) for all \(k \in {{\mathbb {R}}}\). Since \(\lim _{k \rightarrow \infty } \text {sech}(h_1k)=\lim _{k \rightarrow \infty } \Theta (k)=\lim _{k \rightarrow \infty } \Theta _1(k)=0\), letting \(k \rightarrow \infty \) in the matrix \([R(k)-c_0 I]\) yields the singular matrix
Consequently we should have \(c_0=\gamma h\) or \(c_0=\Gamma _1\). Letting \(k \rightarrow 0\) in the identity (4.24) yields
which rules out the possibility \(c_0=\gamma h\). On the other hand, from (4.23) we can express \(\lim _{k \rightarrow 0} p(\Gamma _1)\) expanding by minors along the last row yields to obtain the value
so that \(c_0 \ne \Gamma _1\). The obtained contradiction completes the proof. \(\quad \square \)
4.2 Weakly nonlinear models
Even the most powerful computers cannot handle the full range of space and time scales that must be resolved to successfully simulate numerically the real-world equatorial flows. Model equations and conceptual simplifications can be brought to bear on the problem, thereby providing us with a considerable level of understanding of various physically relevant regimes for equatorial wave–current interactions. The results of the previous subsection show that linear models are not sufficient to capture the solitary wave phenomenon. Recall that linear theory corresponds to retaining only quadratic terms in the expansion of the Hamiltonian, with the expansion parameter describing the amplitude of the wave perturbation of a background pure current state. Weakly nonlinear models can be derived by expanding the Hamiltonian up to cubic terms in the wave amplitude, thereby permitting nonlinear interactions to become relevant.
It is more convenient to write the governing Hamiltonian system (3.86) in terms of the variables \((q,\,q_1,\,\eta ,\,\eta _1)\), where
Using (3.82)–(3.83), (3.69), (3.58), (3.60), (3.43) and (3.13) we get
so that \([q-(\mu +\gamma -\gamma _1)\eta |/r\) and \(q_1-\mu _1\eta _1\) are the tangential velocities of the wave perturbations at the interface and free surface, respectively. Therefore the variables \((q,\,q_1,\,\eta ,\,\eta _1)\) basically encode the profiles and the propagation speeds of the interface and of the free surface, whilst taking into account the vorticity values above and below the thermocline as well as the effect of the Earth’s rotation. Note that (3.38) in combination with (3.82)–(3.83) ensure \(q,\,q_1 \in {{\mathcal {S}}}({{\mathbb {R}}})\). Since for \(q=\zeta _x\) and \({\tilde{q}}={\tilde{\zeta }}_x\), using integration by parts, we see that
Similarly, since (3.82)–(3.83) yield \(\xi _x=q-\mu \eta \) and \(\xi _{1,x}=q_1-\mu _1 \eta _1\), we get
Therefore, in terms of the new variables, the Hamiltonian system (3.86) takes on the form
4.2.1 KdV equation describing the evolution of the thermocline
Taking \(\varepsilon \ll 1\) and \(\delta \ll 1\) to be small parameters, we consider the shallow-water (long wave) regime defined by the spatial scale
and the wave perturbation scales
in which \(\eta \) and q, as well as \(\eta _1\) and \(q_1\), are considered of the same order of magnitude, with the surface wave having a smaller amplitude than the internal wave—an impulse that generates wave perturbations of the background pure current state will typically have a pronounced oscillatory effect at the thermoclineFootnote 3 whereas the sea surface is hardly affected at all.Footnote 4 The interpretation of the scaling (4.65), in which the typical internal wave amplitude \(\varepsilon ^2\) and wavelength \(\varepsilon ^{-1}\) are in quadratic balance, is that \(x'\), t, \(\eta '\), \(q'\), \(\eta _1'\) and \(q_1'\) are all of order O(1), with (4.64) specifying the distance needed to bring about this balance for the dynamics of the flow. Note that the nondimensionalisation performed in Sect. 3.2 fixed the reference scales of 500 m for length and 0.5 \(\hbox {m}\,\hbox {s}^{-1}\) for speed, while typical amplitudes and propagation speeds of equatorial internal waves do not exceed 50 m and 0.1 \(\hbox {m}\,\hbox {s}^{-1}\), respectively. This is consistent with the choice \(\varepsilon \ll 1\) in (4.65). The time scale at the surface, introduced in (4.65), captures the fact that changes in the surface wave profile occur faster than at the thermocline; note also that the discussion of Hamiltonian perturbations at the beginning of Sect. 4 shows that to use different spatial scales for the two interfaces requires a different adjustment of the two time scales. The scaling (4.64)–(4.65) introduces the small parameters \(\varepsilon \) and \(\delta \) into the Hamiltonian (3.73), transforming (4.63) accordingly into the Hamiltonian system
with Hamiltonian \({{\mathcal {H}}'}={{\mathcal {H}}}\varepsilon ^{-3}\).
Due to (4.8), (4.9), (4.13), (4.14), under the scaling (4.65) the Taylor expansion for the Dirichlet–Neumann operator \(G(\eta )\) is
since \(\tanh (s)=s-\frac{1}{3}\,s^3 +\frac{2}{15}\,s^5+O(s^7)\) and for \(j \ge 2\) the terms \(G^{(j)}(\eta ')\) are of order \(O(\varepsilon ^8)\), while
since \(\text {coth}(s)=s^{-1}+\frac{1}{3}\,s -\frac{1}{45}\,s^3+O(s^5)\) and \(\text {csch}(s)=s^{-1}-\frac{1}{6}\,s +\frac{7}{360}\,s^3+O(s^5)\). Using (4.67)–(4.68) for the asymptotic expansion of the operator B, defined in (3.68), gives
and, with respect to this expansion, the inverse operator is
Similarly we see that
Let us now choose \(\delta =O(\varepsilon )\) in (4.64). Writing the Hamiltonian (3.73) as functionally dependent on \(\eta '\), \(\eta _1'\), \(\xi '\), \(\xi _1'\), we retain terms up to order \(O(\varepsilon ^5)\) and thus reduce the Hamiltonian (3.73) to
since (4.64) and (3.82)–(3.83) yield \(\xi =\varepsilon \xi '\) and \(\xi _1=\varepsilon ^2\xi '_1\), and the only pseudo-differential operators for which we have to take into account one term beyond leading order are \(G_{22}\) and
On the other hand, in analogy to (4.62), the relations
yield
where
We now neglect terms of order \(O(\varepsilon ^6)\) in the Hamiltonian \({{\mathcal {H}}}\), thus replacing (4.66) by a truncated Hamiltonian system. The canonical equations for the variables related to the free surface are linear
while those for the variables at the thermocline are nonlinear
For \(\delta \ll \varepsilon ^2\) we can neglect the \(\delta \)-terms above and decouple the internal wave motion from the oscillations of the free surface: the system (4.77)–(4.80) simplifies to
Note that (3.46)–(4.82) yield \((q_1' - \mu _1 \eta _1')_{t}=0\); these equations also show that the motion of the free surface is determined by the initial data and the characteristics \((\eta ',q')\) of the displacements of the thermocline. On the other hand, from (4.83)–(4.84) we infer that the leading order linear equations for \(\eta '\) and \(q'\) are
Therefore the wave speed c of a linear travelling wave, in which the \((x',t)\)-dependence is solely in terms of \((x'-ct)\), satisfies the quadratic equation
which, in view of (4.76), has the solutions
Note that \(g\gg \gamma h \omega \), so that the solutions are real. Recalling from (3.36) that \(\gamma h\) is the speed of the underlying current at the mean level \(z=0\) of the thermocline, we see that in (4.88) the plus sign corresponds to the speed of waves outrunning the current (downstream linear waves), while the minus sign corresponds to the speed of waves running counter to the current (upstream linear waves). At this (leading) order c is a constant and dispersion effects are not observable. To deal with nonlinear effects, setting
with c given by (4.88), we observe that (4.85)–(4.86) show that \(q'=((r+1) c_1 \eta ')/h\) at the leading order. We therefore expect that
for some constants \(b_{1,2}\) that are yet to be determined. With the Ansatz (4.90), we substitute \(q'\) in (4.83)–(4.84) and write both two equations in terms of \(\eta '\) only up to the order \(O(\varepsilon ^{2})\), thus obtaining two evolutionary equations for \(\eta '\), which should coincide up to \(O(\varepsilon )\). The equality of their coefficients allows us to find the constants \(b_1\) and \(b_2\), as follows:
The resulting evolution equation for \(\eta \) is
while the corresponding \(q'\) can be recovered from (4.90). Although we can write (4.93) in the standard form of the KdV-equation in a moving frame of reference by means of a scaling transformation (see [35]), we prefer to work with the form (4.93) to facilitate the physical interpretation of the mathematical results. One appealing feature of the KdV equation (4.93) is its bi-Hamiltonian structure: the equation has two expressions as a Hamiltonian evolutionary equation, with the two Hamiltonian operators compatible, that is, any linear combination is again a Hamiltonian operator (see [35]). The bi-Hamiltonian structure ensures the existence of infinitely many integrals of motion that are functionally independent. Moreover, the equation can be solved exactly using inverse scattering theory: starting with arbitrary initial data in the Schwartz class, the solution that evolves from this data develops into a finite number of localised solitary waves (solitons) with speeds proportional to the amplitude, plus an oscillatory tail (see the discussion in [5]). Each solitary wave recovers its localised identity after interacting with other solitary waves (re-emerging unscated after such interaction, the only hallmark of the interaction being a phase shift), while the oscillatory tail disperses and spreads out in space. Therefore the solution evolves in to an ordered set of solitons, with the tallest in front, followed by an oscillatory tail. The details of this general picture can be predicted fairly explicitly from detailed knowledge of the initial data. For example, the internal solitary wave solution is a wave of depression, given in the original variables by
with \(A>0\) and \(\mathcal {A}= \frac{1}{2c_1}\left( \frac{3c_0^2}{h}+ 3\gamma c_0 +h\gamma ^2 -\frac{h\gamma _1^2}{r+1}\right) <0\), \(\mathcal {B}=\frac{A_2 (r+1) c^2_0}{2h c_1 }>0\). We see that the propagation speed of the solitary wave, \(c+\tfrac{A|{{\mathcal {A}}}|}{3}\), exceeds the speed c of the leading-order linear wave by an amount that is proportional to the wave amplitude A. Therefore larger solitary waves travel faster. With regard to the soliton interaction of two solitary waves that are initially separated, with the larger (and faster) one overtaking the smaller (and slower) one, they emerge unscated from the interaction, but each is shifted, this being the hallmark of the nonlinear nature of the interaction—in contrast to mere superposition. More precisely, the faster/slower solitary wave is shifted forward/backward by \(\sqrt{\frac{12\mathcal {B}}{a_1|\mathcal {A}|} } \ln \frac{\sqrt{a_1}+\sqrt{a_2}}{\sqrt{a_1}-\sqrt{a_2}}\) and \(\sqrt{\frac{12\mathcal {B}}{a_2|\mathcal {A}|} } \ln \frac{\sqrt{a_1}+\sqrt{a_2}}{\sqrt{a_1}-\sqrt{a_2}}\), respectively, where \(a_1>a_2>0\) are the amplitudes of the solitary waves. We point out that case studies for such wave phenomena in equatorial regions are available in the literature (see the interpretation of space shuttle photographs in [47], which show the relevance of soliton theory to the propagation of equatorial internal waves, and the discussion in [2], where it is pointed out that internal solitons are likely to be generated by the relaxation of the trade winds at the western boundary of the equatorial Pacific that triggers the “El Niño” event), although in general the presence of underlying currents is neglected. We see that the effect of the currents is encoded in the coefficients of the equation, so that these currents alter the shape and speed of these solitons (in comparison to the classical irrotational setting).
4.2.2 Inviscid Burgers regime.
Equatorial ocean dynamics present peculiar features when compared to off-equatorial regions. A remarkable anomaly is that, despite high levels of internal wave energy and shear due to the presence of strong, zonal, basin-scale currents, study observations show that internal wave breaking is less frequent than one might anticipate, with rates near the Equator less than 10% of those typical at mid-latitudes for internal waves of comparable energy (see [18]). Nevertheless, internal wave breaking does occur in the equatorial Pacific: observations indicate that, in a process in which the interactions with the large shear caused by the EUC play a significant rôle (with the EUC enhancing the internal wave activity—see the discussion in [27]), a strong wind stress propagates downward and generates quite significant internal waves (see [45]) which often break. The breaking is preceded by a steepening of the internal wave profile which results in finite-time gradient blow-up. We will now indicate how the Hamiltonian perturbation approach yields in a specified physical regime model equations that capture this type of behaviour.
Taking \(\varepsilon \ll 1\) and \(\delta \ll 1\) to be small parameters, we consider the shallow-water regime defined by the spatial scale
and the wave perturbation scales
in which \(x'\), t, \(\eta '\), \(q'\), \(\eta _1'\), and \(q_1'\) are of the order of magnitude O(1), with the surface perturbations faster but less significant than those at the thermocline (in view of the fact that \(\delta \ll 1\)). The regime (4.94)–(4.95) captures internal waves of larger amplitude than the long-wave regime (4.64)–(4.65), transforming (4.63) into the Hamiltonian system
with Hamiltonian \(\tilde{{\mathcal {H}}}={{\mathcal {H}}}/\varepsilon \). For \(\delta =O(\varepsilon )\), we follow the approach pursued in Sect. 4.1 and expand the Hamiltonian (3.73) up to order \(O(\varepsilon ^{3})\), obtaining
with the notation in (4.76). We now neglect terms of order \(O(\varepsilon ^4)\) in the Hamiltonian \({{\mathcal {H}}}\), thus replacing (4.96) by a truncated Hamiltonian system with Hamiltonian \(H^{(3)}/\varepsilon \). The canonical equations for the variables related to the free surface are linear
while those for the variables at the thermocline are nonlinear
For \(\delta =O(\varepsilon ^2)\) we can neglect the \(\delta \)-terms and the \(\varepsilon ^2\)-terms above and decouple the motion of the thermocline from that of the free surface: the system (4.98)–(4.101) simplifies to
The Eqs. (4.102)–(4.103) show that the motion of the free surface is determined by the initial data and the characteristics \((\eta ',q')\) of the displacements of the thermocline, with \((q_1' - \mu _1 \eta _1')_{t}=0\). Note that (4.104)–(4.105) show that the leading order linear equations for \(\eta '\) and \(q'\) are (4.85)–(4.86), so that the wave speed c of a linear travelling wave, in which the \((x',t)\)-dependence is solely in terms of \((x'-ct)\), satisfies the quadratic equation (4.87) whose solutions are given by (4.88). The choice of the plus sign in (4.88) yields the speed of linear waves outrunning the current, while (3.82) shows that the minus sign corresponds to the linear waves propagating westwards. To investigate nonlinear effects, using the notation (4.89), we infer from (4.85)–(4.86) that \(q'=((r+1) c_1 \eta ')/h\) at leading order. We therefore expect that
for some constant \(b_1\) to be determined. With the Ansatz (4.106), we substitute q in (4.104)–(4.105) and write both two equations in terms of \(\eta '\) up to the order of \(O(\varepsilon ^2)\), thus obtaining two evolutionary equations for \(\eta '\), which should coincide up to \(O(\varepsilon )\). From the equality of their coefficients we obtain
The resulting evolution equation for \(\eta \) is the inviscid Burgers equation
while \(q'\) can be recovered from (4.106). It is well-known (see, for example, the discussion in [12]) that any initial data in the Schwartz class will lead to finite-time blow-up for the solution to (4.108) in the form of wave breaking: the solution remains bounded but its slope becomes unbounded in finite time.
5 Concluding Discussion
Within the framework of two-dimensional equatorial flows in the f-plane, with no meridional variations, we presented a Hamiltonian formulation of the nonlinear governing equations for wave–current interactions in a two-layer inviscid fluid with a flat bed and a free surface, for flows with constant vorticity in each layer. A key step was to prove, without recourse to approximations, that the flow can be viewed as an irrotational perturbation—possibly of the same order—of a mean flow that represents the underlying current field. We have also derived several simplified models for the equatorial wave–current interaction across the Pacific through systematic structure-preserving perturbation theory. These have genuine potential as simplified diagnostic and prognostic models since they accommodate all the salient features of equatorial ocean dynamics in the Pacific (strong stratification, as well as a current field with flow-reversal) and are able to capture nonlinear effects. In particular, at some specific geophysical scales the weakly nonlinear long-wave regime turns out to be structure-enhancing since in this setting the nonlinear dynamics is described by a KdV equation—an integrable infinite-dimensional Hamiltonian system. The derived models can discriminate between different physical effects in observations and simulations, dictated by different scales. For example, the variety of oceanographically relevant scales permits us to single out various types of interplay between dispersion and nonlinearity, ranging from regimes in which dispersion and nonlinearity balance each other and allow wave solutions that propagate without change of form to dispersionless regimes that favour wave breaking.
The general systematic approach developed in this paper is also useful for developing accurate numerical procedures. Note that, even within the framework of irrotational two-layer inviscid flow with a free surface, the problem of treating computationally the nonlinear interactions between the surface and internal modes of oscillation is challenging (see the discussion in [37]). For example, for fixed densities \({\overline{\rho }} >{\overline{\rho }}_1\) of the layers but allowing variations of their mean depths \({\overline{h}}\) and \({\overline{h}}_1\), in the rigid-lid approximation the polarity of the internal solitary waves (that is, whether they are waves of elevation or depression) changes once in the range \({\overline{h}}_1/{\overline{h}} \in (0,1)\), while no such change occurs in the coupled configuration (see [1, 10]). Furthermore, the presence of non-zero vorticity in each layer complicates considerably the dynamics. Showing that within the nonlinear framework it is possible to split the velocity field into an underlying steady current component and a harmonic wave velocity field opens up the possibility to find numerically solitary wave solutions to the fully-nonlinear problem using a boundary integral method based on Cauchy integral formula (see the discussion in [41]).
The Hamiltonian approach developed in this paper and the above mentioned topics open up exciting perspectives for future interdisciplinary research on equatorial wave–current interactions.
Notes
The wave motion involves lifting of denser fluid and sinking of lighter fluid, both of which cause a change in the centre of gravity which brings about a change of potential energy. In the absence of dissipation, the supply/loss of potential energy can only be provided by conversion of/into kinetic energy.
While four out of every five tsunamis happen in the Pacific Ocean, initiated by earthquakes along the boundary of one of the Earth’s main geologically active tectonic plates, those in the tropical Pacific tend to be modest in size. However, a few times every century, tsunami waves generated by great earthquakes in the North Pacific or along the Pacific coast of South America sweep across the entire Pacific. As for large asteriod impacts into the deep ocean, these are very rare—the only currently known deep-ocean impact event on Earth being the Eltanin asteroid impact and tsunami, ocurring about 2.5 million years ago when a asteriod exceeding 1 km in diameter did strike the ocean about 1500 km SSW of Chile (see [17]).
The impulse causes the denser water to rise above the flat equilibrium thermocline level, but gravity pulls it back down because the water beneath the thermocline is heavier than that above it, and the inertia acquired during the falling movement causes the water to penetrate below the level of equilibrium of the thermocline, thus setting up an oscillatory motion. This wave disturbance propagates horizontally since the local increase in pressure that occurs where a parcel of water rises above the equilibrium level pushes the fluid below it away from that place, generating in this process an acceleration (and thus also a force) which also comprises a horizontal component.
Since the internal restoring buoyancy force is much smaller than that at the surface, the density variation across the thermocline being about one-thousandth of that across the air-water interface.
References
Benjamin, T.B.: Internal waves of finite amplitude and permanent form. J. Fluid Mech. 25, 241–270 (1966)
Boyd, J .P.: Equatorial solitary waves. Part I: Rossby solitons. J. Phys. Oceanogr. 10, 1699–1717 (1980)
Boyd, J.P.: Dynamics of the Equatorial Ocean. Springer, Berlin (2018)
Cheng, C.H., Shkoller, S.: Solvability and regularity for an elliptic system prescribing the curl, divergence, and partial trace of a vector field on Sobolev-class domains. J. Math. Fluid Mech. 19, 375–422 (2017)
Constantin, A.: Nonlinear Water Waves with Applications to Wave–Current Interactions and Tsunamis. SIAM, Philadelphia (2011)
Constantin, A., Ivanov, R.I., Martin, C.-I.: Hamiltonian formulation for wave–current interactions in stratified rotational flows. Arch. Ration. Mech. Anal. 221, 1417–1447 (2016)
Constantin, A., Johnson, R.S.: The dynamics of waves interacting with the equatorial undercurrent. Geophys. Astrophys. Fluid Dyn. 109, 311–358 (2015)
Constantin, A., Johnson, R.S.: Ekman-type solutions for shallow-water flows on a rotating sphere: a new perspective on a classical problem. Phys. Fluids 31, 021401 (2019)
Constantin, A., Strauss, W., Varvaruca, E.: Global bifurcation of steady gravity water waves with critical layers. Acta Math. 195–262, 2016 (2017)
Craig, W., Guyenne, P., Kalisch, H.: Hamiltonian long-wave expansions for free surfaces and interfaces. Commun. Pure Appl. Math. 58, 1587–1641 (2005)
Craig, W., Guyenne, P., Sulem, C.: The surface signature of internal waves. J. Fluid Mech. 710, 277–303 (2012)
Dafermos, C.M.: Hyperbolic Conservation Laws in Continuum Physics. Springer, Berlin (2010)
DaSilva, A.F.T., Peregrine, D.H.: Steep, steady surface waves on water of finite depth with constant vorticity. J. Fluid Mech. 125, 281–302 (1988)
Fedorov, A.V., Brown, J.N.: Equatorial waves. In: Steele, J. (ed.) Encyclopedia of Ocean Sciences, pp. 3679–3695. Academic Press, Cambridge (2009)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (2001)
Gill, A.: Atmosphere-Ocean Dynamics. Academic Press, Cambridge (1982)
Goff, J., Chagué-Goff, C., Archer, M., Dominey-Howes, D., Turney, C.: The Eltanin asteroid impact: possible South Pacific palaeomegatsunami footprint and potential implications for the Pliocene–Pleistocene transition. J. Quat. Sci. 27, 660–670 (2012)
Gregg, M.C., Sanford, T.B., Winkel, D.P.: Reduced mixing from the breaking of internal waves in equatorial waters. Nature 422, 513–515 (2003)
Ishikawa, Y., Awaji, T., Akimoto, K.: Global surface circulation and its kinetic energy distribution derived from drifting buoys. J. Oceanogr. 53, 489–516 (1997)
Johnson, G.C., McPhaden, M.J.: Equatorial Pacific ocean horizontal velocity, divergence, and upwelling. J. Phys. Oceanogr. 31, 839–849 (2001)
Kato, T.: Perturbation Theory for Linear Operators. Springer, Berlin (1980)
Kessler, W.S., McPhaden, M.J.: Oceanic equatorial waves and the 1991–1993 El Niño. J. Clim. 8, 1757–1774 (1995)
Kinsman, B.: Wind Waves. Prentice-Hall, Englewood Cliffs (1965)
Kurdyka, K., Păunescu, L.: Hyperbolic polynomials and multiparameter real-analytic perturbation theory. Duke Math. J. 141, 123–149 (2008)
Lax, P.D.: Linear Algebra. Wiley, New York (1997)
LeBlond, P.H., Mysak, L.A.: Waves in the Ocean. Elsevier, Amsterdam (1978)
Lien, R.-C., D’Asaro, E.A., McPhaden, M.J.: Internal waves and turbulence in the upper central equatorial Pacific: Lagrangian and Eulerian observations. J. Phys. Oceanogr. 32, 2619–2639 (2002)
Lien, R.-C., McPhaden, M.J., Gregg, M.C.: High-frequency internal waves at 0\(^\circ \), 140\(^\circ \)W and their possible relationship to deep-cycle turbulence. J. Phys. Oceanogr. 26, 581–600 (1996)
Majda, A.J.: Introduction to PDEs and Waves for the Atmosphere and Ocean. Courant Lecture Notes in Mathematics. AMS, Providence (2003)
Maslowe, S.A.: Critical layers in shear flows. Ann. Rev. Fluid Mech. 18, 405–432 (1986)
McCreary, J.P.: Modeling equatorial ocean circulation. Ann. Rev. Fluid Mech. 17, 359–409 (1985)
McPhaden, M.J., Proehl, J.A., Rothstein, L.M.: The interaction of equatorial Kelvin waves with realistically sheared zonal currents. J. Phys. Oceanogr. 17, 1499–1515 (1986)
Meyer, K.H., Hall, G.R.: Introduction to Hamiltonian Dynamical Systems and the n-Body Problem. Springer, New York (1992)
Moum, J.N., Nash, J.D., Smyth, W.D.: Narrowband oscillations in the upper equatorial ocean. Part i: interpretation as shear instability. J. Phys. Oceanogr. 41, 397–411 (2011)
Olver, P.J.: Applications of Lie Groups to Differential Equations. Springer, New York (1993)
Pacanowski, R.C., Philander, S.G.H.: The generation of equatorial currents. J. Geophys. Res. 85, 1123–1136 (1980)
Parau, E.I., Woolfenden, H.C.: Numerical computation of solitary waves in a two-layer fluid. J. Fluid Mech. 688, 528–550 (2011)
Pinkel, R., Merrifield, M., McPhaden, M., Picaut, J., Rutledge, S., Siegel, D., Washburn, L.: Solitary waves in the western equatorial Pacific Ocean. Geophys. Res. Lett. 24, 1603–1606 (1997)
Proehl, J.A., McPhaden, M.J., Rothstein, L.M.: A numerical approach to equatorial oceanic wave-mean flow interactions. In: O’Brien, J.J. (ed.) Advanced Physical Oceanographic Modelling, pp. 111–126. D. Reidel Publishing Company, Dordrecht (1986)
Reed, P., Simon, B.: Methods of Modern Mathematical Physics. Fourier Analysis, Self-Adjointness, vol. II. Academic Press, New York (1975)
Vanden-Broeck, J.-M.: Solitary waves in water: numerical methods and results. In: Grimshaw, R.H.J. (ed.) Solitary Waves in Fluids, pp. 55–84. WIT Press, Southampton (2007)
von Wahl, W.: Estimating \(\nabla u\) by div\(\, u\) and curl\(\, u\). Math. Methods Appl. Sci. 15, 123–143 (1992)
Wahlén, E.: A Hamiltonian formulation of water waves with constant vorticity. Lett. Math. Phys. 79, 303–315 (2007)
Wahlén, E.: Hamiltonian long-wave approximations of water waves with constant vorticity. Phys. Lett. A 372, 2597–2602 (2008)
Wijesekera, H.W., Dillon, T.M.: Internal waves and mixing in the upper equatorial Pacific Ocean. J. Geophys. Res. 96, 7115–7125 (1991)
Zakharov, V.E.: Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9, 1990–1994 (1968)
Zheng, Q., Klemas, V., Yan, X.-H.: Dynamic interpretation of space shuttle photographs: deepwater internal waves in the western equatorial Indian Ocean. J. Geophys. Res. 100, 2579–2589 (1995)
Acknowledgements
Open access funding provided by University of Vienna. This research was supported by the WWTF research Grant MA16-009 and by the EPSRC Grant No. EP/K032208/1. The authors would also like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme “Nonlinear water waves”, where the final stages of the work on this paper were undertaken. The authors are very grateful to the referee for comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by W. Schlag
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Constantin, A., Ivanov, R.I. Equatorial Wave–Current Interactions. Commun. Math. Phys. 370, 1–48 (2019). https://doi.org/10.1007/s00220-019-03483-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-019-03483-8