Abstract
The equidensity orbitals (EO) are used in the resultant entropic description of molecular states which combines the probability and current contributions in the overall information content. Continuities of the modulus and phase components of electronic wavefunctions are examined, and the Harriman–Zumbach–Maschke (HZM) construction of Slater determinants yielding the prescribed electron density is explored. The conditional probability interpretation of (complex) HZM wavefunctions is formulated, the entropy/information contributions due to the state phase component are summarized, and a nonclassical origin of quantum dynamics of the resultant gradient information, related to average kinetic energy of electrons, is emphasized. The phase equilibria maximizing the resultant-entropy measures are explored, and “thermodynamic” phase minimizing the overall gradient information is determined. It generates finite orbital currents giving rise to the vanishing resultant flow of electrons in the system as a whole. Potential use of atomic and molecular EO bases in electronic structure calculations and interpretations in chemistry is discussed, and illustrative example of Gaussian probability distribution is examined in some detail.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The classical information theory (IT) [1,2,3,4] explores functionals of the entropy/information content in molecular probability distribution p(r) = ρ(r)/N, the shape factor of electron density ρ(r) in N-electron system. For example, the local (gradient) information measure I[p] of Fisher [1, 2] and the global (logarithmic) entropy descriptor S[p] of Shannon [3, 4] reflect the complementary “narrowness” and “spread” aspects of electron distributions. In accordance with modern density functional theory (DFT) [5,6,7,8,9,10], the ground-state densities ρ0(r) or p0(r) determine all molecular properties, e.g., the electronic energy for the given external potential v(r) due to the system fixed nuclei, E0 = Ev[ρ0] = Ev[N, p0], and its classical entropy/information contents: S0 = S[p0] or I0 = I[p0]. However, in general (non-stationary) quantum states or for approximate (trial) wavefunctions of molecular information principles one has to take into account also the nonclassical entropy/information contributions due to the state phase distribution ϕ(r), S[ϕ] or I[ϕ] [11,12,13,14,15], in the resultant-entropy/information measures S[p, ϕ] = S[p] + S[ϕ] or I[p, ϕ] = I[p] + I[ϕ].
The extrema of such overall global or gradient entropy descriptors determine the phase equilibria in molecules and their fragments [15,16,17,18,19,20]. These generalized IT descriptors allow one to distinguish the information content of states exhibiting the same electron density but differing in their current composition, e.g., the bonded (entangled) and nonbonded (disentangled) states of subsystems in the chemical reactivity theory [21, 22]. The entropic phase contributions play an important role in an information description of reactive systems [23,24,25,26,27,28] by precisely specifying the mutually open (bonded) and closed (nonbonded) states of reactants. To paraphrase Prigogine [29], the density distribution establishes the molecular “static” structure of being, while the current pattern establishes the complementary “dynamical” aspect of molecular organization—the structure of becoming: the latter determines the dynamics of the former.
The classical IT of Fisher and Shannon [1,2,3,4, 30,31,32,33] has been already successfully applied to interpret molecular probability distributions, e.g., [15, 34,35,36,37]. Information principles have been explored, and density pieces attributed to atoms-in-molecules (AIM) have been approached [38,39,40,41,42,43,44,45,46], providing the information basis for the intuitive (stockholder) division of Hirshfeld [47]. Patterns of chemical bonds have been extracted from electronic communications in molecules [15, 34,35,36,37, 48,49,50,51,52,53,54,55,56,57,58], and the entropy/information distributions in molecules have been explored [15, 34,35,36,37, 59, 60]. The nonadditive Fisher information [15, 34,35,36,37, 61, 62] has been linked [62] to electron localization function (ELF) [63,64,65] of modern DFT. This analysis has also formulated the contragradience (CG) probe [66] for determining the bond patterns in molecules, and orbital communication theory (OCT) has identified the bridge interactions originating from cascade propagations of information, which involve intermediate orbitals [15, 37, 67,68,69,70,71,72].
In present analysis, the phase/current feature of electronic states will be emphasized throughout. General quantum states of N electrons yielding the prescribed electron density involve Slater determinants constructed from the (orthonormal) (plane-wave)-type equidensity orbitals (EO) of Harriman, Zumbach and Maschke (HZM) [73, 74], each generating the specified molecular probability distribution and exhibiting the density-dependent local phase safeguarding the orbital orthogonality. This construction separates the modulus and phase aspects of multi-electronic states thus offering an attractive framework for studying the role of classical (probability) and nonclassical (current) entropy/information contributions in chemical processes. We shall examine the construction of orbital phases and electronic currents they generate, providing them an appropriate probabilistic interpretation in terms of conditional probabilities involving electron coordinates. This development will be illustrated for the special case of the Gaussian-type probability distributions.
The continuities of the physical, probability and phase descriptors of electronic states implied by the Schrödinger equation will be summarized, and probability interpretation of the key constructs of this orbital representation will be given. The dynamics of resultant gradient information will be explored, and a nonclassical character of the information production will be emphasized. The overlap extension of the equidensity orbitals [75] will be outlined, and possible applications of EO bases of constituent atoms in electronic structure calculations and interpretations in chemistry will be explored.
2 Continuities of probability and phase distributions
The evolution of molecular electronic wavefunctions is determined by the Schrödinger equation (SE) of quantum mechanics. It also determines the dynamics of probability- and current attributes of the abstract (complex) quantum states [26,27,28] and the associated information contributions. It is of interest to examine general implications of SE for the dynamics of these two physical descriptors of the modulus and phase components of molecular wavefunctions.
For simplicity, let us first consider a single electron at time t in state \( |\psi(t)\rangle\equiv|\psi\rangle \), described by the (complex) wavefunction in position representation,
where the real functions R(r, t) and ϕ(r, t) stand for its modulus and phase parts, respectively. They determine the electron probability distribution at time t,
and the corresponding current density
Here, the effective velocity of the probability “fluid,” V(r, t) = dr/dt, measures the local current per particle and reflects the state phase-gradient:
The state probability density p(r, t) and its flux j(r, t) thus constitute two independent physical degrees-of-freedom of such a general quantum state of an electron:
The phase component of molecular states reflects the coherence, current aspect of the system electronic structure.
In molecular scenario, the electron is moving in the external potential v(r) due to the “frozen” nuclei of the familiar Born–Oppenheimer (BO) approximation, thus being described by the Hamiltonian
where \( {\hat{\rm{T}}(}\varvec{r}\text{)} \) denotes its kinetic part. The dynamics of its quantum state ψ(r, t) is determined by SE,
which also generates the associated temporal evolutions of the state probability density and of its phase distribution.
The SE implies the sourceless continuity relation for the particle probability “fluid”:
The total time derivative dp(r, t)/dt of the electron probability density p(r, t) = p[r(t), t] defines its local production σp(r, t). It measures the time rate of change in an infinitesimal volume element around r(t) of the probability fluid moving with the local velocity dr/dt = V(r, t), while the partial derivative ∂p(r, t)/∂t refers to the volume element around the fixed point in space. The vanishing total derivative dp/dt of electron probability density thus reads:
Using the probability continuity also gives:
Therefore, comparing the two preceding equations implies the vanishing divergence of the effective velocity field, determined by the Laplacian of the phase component of molecular quantum states:
The probability continuity of Eq. (9) also determines the state modulus dynamics:
while the phase dynamics from SE reads:
The probability velocity V also drives the phase current
The SE then predicts a nonvanishing phase source in the associated continuity equation:
Using Eq. (13) finally gives the following production term of a local phase:
It follows from these continuity relations that a common velocity of the probability and phase currents, determined by the state phase-gradient, reflects the structure dynamical aspect, while the probability density at the specified time establishes its static facet. The former characterizes the temporal evolution of the latter. In other words, a structure of “becoming” determines the evolution of an instantaneous structure of “being.”
3 Equidensity orbitals
In DFT, one often explores the density-constrained (“entropic”) variational principles, e.g., the Levy [7] construction of the universal density functional for the sum of electronic kinetic and repulsion energies. They are also called the “vertical” or “thermodynamic” searches, by analogy to the minimum-energy and maximum-entropy criteria for determining equilibria in ordinary thermodynamics [76]. A related problem of constructing the antisymmetric wave functions of N fermions yielding the prescribed density ρ(r), vital for solving the familiar N-representability problem of DFT, has been solved by Harriman [73], who had used the crucial insights due to Macke [77, 78] and Gilbert [79]. Its three-dimensional generalization by Zumbach and Maschke [74] introduces the complete set of Slater determinants build using the density-dependent (orthonormal) equidensity orbitals (EO) of the plane-wave type,
each generating the molecular probability distribution
the shape factor of the system electron density ρ(r). Here,
denotes the (constant) reduced-momentum (wave-number) vector, and Φq(r) stands for the EO resultant phase, defined by the sum of the orthogonality-phase Fq(r) and thermodynamic-phase contribution ϕ(r), common to all occupied EO. The latter has to be eventually determined from the auxiliary maximum resultant-entropy principle, which establishes the system phase equilibrium. The vector function in Eq. (17),
ultimately generates the probability-dependent Jacobian determinant ∂f/∂r = |∂fm/∂xn| grouping partial derivatives \( \{ \partial f_{m} /\partial x_{n} \} \) of the phase-vector f ≡ {fm} components with respect to electron position coordinates r ≡ {xn}.
This construction can be thus viewed as transformation of the physical space into itself: for any r = (x, y, z) ∈ ℜ3 we define the (invertible) density-dependent transformation of r into the new vector f(r) ∈ ℜ3, with the familiar plane-wave type orthogonality relation between orbitals. The overall phase Φq(r) of EO involves the orbital-specific (geometric) internal contribution q·f(r) ≡ Fq(r), which enforces the independence of these one-particle states, and “thermodynamic” external phase \( \phi \left( \varvec{r} \right) \), common to all EO,
The latter has to be determined from a subsidiary variational principle for the extremum of the state resultant entropy [12,13,14,15,16,17,18,19,20,21, 36].
By definition, in the HZM construction one sets this transformation between local volume elements as being proportional to molecular probability distribution, \( {\text{d}}\varvec{f }\text{(}\varvec{r}) \propto p(\varvec{r}){\text{d}}\varvec{r} \), with the associated Jacobian determinant
As explicitly proposed by Zumbach and Maschke [74], the functional relations defining components of the phase vector field \( \varvec{f} = \varvec{f}[\rho ] \) read:
They define the functional determinant of Eq. (22):
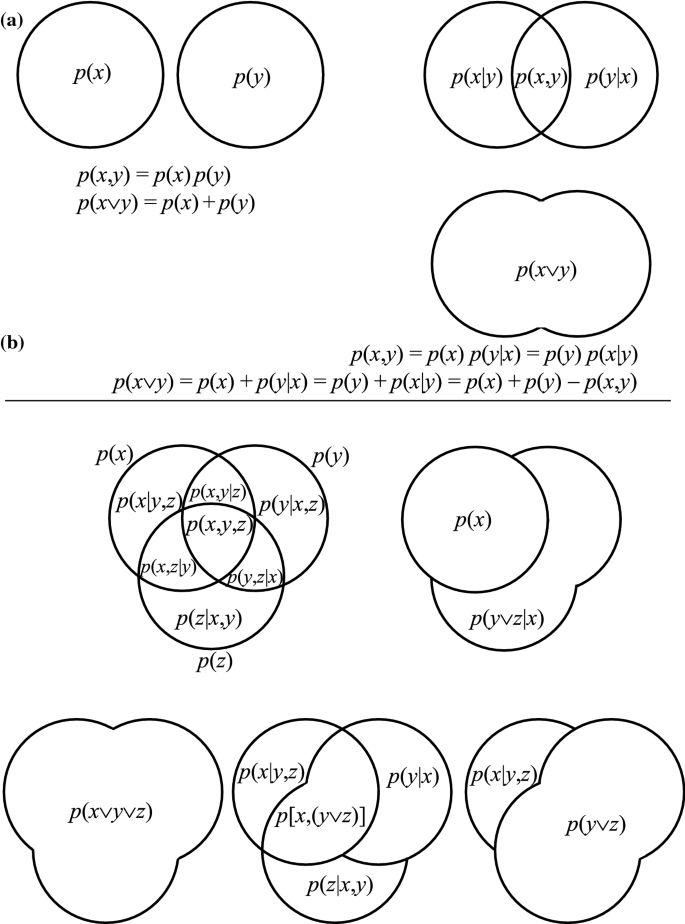
These “diagonal” derivatives \( \{ \partial f_{\alpha } /\partial x_{\alpha } \} \) can be expressed in terms of the relevant conditional probabilities [14] involving the position coordinates (see Figs. 1 and 2), defined by the corresponding ratios of the relevant joint probabilities:
The graphical representation of various joint and conditional probabilities of the electron position coordinates, r = xi + yj + zk ≡ (x∧y∧z) ≡ (x, y, z), e.g., p(r) = p(x∧y∧z) ≡ p(x, y, z), p(y|x) = p(x, y)/p(x), p(x,y|z) = p(x,y,z)/p(z), p(x|y,z) = p[x,y,z)]/p(y,z), etc. A single circle delineates probability of a separate coordinate, e.g., \( p\left( x \right) = \int {p\left( \varvec{r} \right){\text{d}}y{\text{d}}z} \), the envelope of the two or three overlapping circles represents the probability of the union (sum) of observing the specified (dependent) coordinates, e.g., p(x∨y) = p(x) + p(y) − p(x,y) = p(x) + p(y|x) = p(y) + p(x|y) or p(x∨y∨z) = p(x) + p(y∨z|x) = p(y∨z) + p(x|y,z) = [p(x|y,z) + p(y|x,z) + p(z|x,y)] + [p(y,z|x) + p(x,z|y) + p(x,y|z)] + p(x,y,z). The probabilities of the joint coordinate events (products), e.g., p(x,y) or p(x,y,z) similarly correspond to the overlap areas (intersections) of two or three circles, respectively. The non-overlapping circles in part (a) represent the independent, exclusive coordinate events
Schematic diagram of the partition of the probability density p[U(r)] ≡ p(x∨y∨z) of the union of spatial coordinates (x, y, z) of the electron position vector r = xi + yj + zk (see also Fig. 1), corresponding to the envelope of three probability circles {p(xn)} for the separate Cartesian coordinates, into partial areas representing the conditional probabilities of Eq. (25). Here, p(z) stands for the probability distribution of the coordinate “z,” p(y|z) is the conditional probability of observing coordinate “y” given “z,” and p(x|y,z) denotes conditional probability of observing coordinate “x,” when one has already simultaneously observed coordinates “y” and “z”
Here, p(a|b) ≡ p(a, b)/p(b) denotes the conditional probability of event a, given event b, while p(a, b) stands for the joint probability of simultaneously observing the two events. Substituting Eq. (25) into Eq. (24) then indeed generates the postulated density-dependent transformation between the volume elements dr and df:
The mutual orthogonality between such EO states then directly follows:
In “Appendix 1,” the illustrative case of Gaussian probability distribution is examined, where the key concepts of HZM construction have been examined, with the local phase vector f(r) expressed in terms of the error function of probability theory.
To summarize, the Slater determinants build from specific selections of N different equidensity orbitals,
then by construction generate the prescribed electron density \( \rho \left( \varvec{r} \right) \):
They constitute the complete orthonormal set of N-particle functions capable of representing the molecular ground state of N electrons for the associated electron distribution \( \rho_{0} \left( \varvec{r} \right) \) = \( \rho \left[ {N,v;\varvec{r}} \right] \), the equilibrium density for the system electronic Hamiltonian
in the HZM configuration interaction (CI) type expansion:
It should be emphasized, however, that such trial functions do not satisfy the phase constraint of Eq. (11), the implication of the probability-continuity relation, since ∇·f(r) ≠ 0. This phase requirement should be ultimately fulfilled by the exact solutions of SE, which reflect the system dynamical conditions.
The EO \( \{ \varphi_{{\varvec{q}}} \left( \varvec{r} \right) \, = \langle \varvec{r}|\varphi_{\varvec{q}} \rangle \equiv \langle \varvec{r}|\varvec{q}\rangle \} \) constitute the complete set of functions capable of representing any quantum state \( |\psi \rangle \) of a single electron or the associated wavefunction in the position representation:
They constitute the basis of the Harriman representation of electronic states [14, 36]. The coefficient function in the preceding equation,
the momentum representation of \( |\psi \rangle \) can be subsequently (r → f)-transformed,
where the transformed “volume” element
Here, \( \psi \left( \varvec{f} \right) \, = \langle \varvec{f}|\psi \rangle \) stands for the f representation of the state vector \( |\psi \rangle \), while \( \varphi_{\varvec{q}} \left( \varvec{f} \right) \) similarly expresses the state \( |\varphi_{{\varvec{q}}} \rangle \) in terms of the density-dependent spatial variable f.
These equations summarize the Fourier transformations between the momentum \( (|\varvec{q}\rangle ) \) and position (\( |\varvec{r}\rangle \) or \( |\varvec{f}\rangle \)) representations of \( |\psi \rangle \). Notice that in this vector interpretation, the orthogonality relation of Eq. (27) reads,
thus manifesting the completeness of the EO basis yielding the molecular probability density:
It is also of interest to express the HZM representation of \( |\psi \rangle ,\psi \left( \varvec{f} \right) = \langle \varvec{f}|\psi \rangle \), in terms of its standard position or momentum representations: \( \psi \left( \varvec{r} \right) = \langle \varvec{r}|\psi \rangle \) or \( \psi \left( \varvec{k} \right) =_{{}} \langle \varvec{k}|\psi \rangle \). Using the familiar Fourier transformation gives:
with \( \varvec{f}\left( \varvec{k} \right)_{{}} =_{{}} \langle \varvec{k}|\varvec{f}\rangle \) and \( \varvec{f}\left( \varvec{r} \right) \, = \langle \varvec{r}|\varvec{f}\rangle = \varvec{r}\left( \varvec{f} \right)^{*} \) standing for the momentum and position representations of \( |\varvec{f}\rangle \), respectively.
The admissible N-electron determinants \( \Psi_{{\mathbf{q}}} ({\mathbf{r}}) \equiv \left\langle {{\{ \varvec{r}_{i} \} }} \mathrel{\left | {\vphantom {{\{ \varvec{r}_{i} \} } {\Psi_{{\mathbf{q}}} }}} \right. \kern-0pt} {{\Psi_{{\mathbf{q}}} }} \right\rangle \equiv \left\langle {{\mathbf{r}}} \mathrel{\left | {\vphantom {{\mathbf{r}} {\mathbf{q}}}} \right. \kern-0pt} {{\mathbf{q}}} \right\rangle \) similarly span the complete N-electron basis in molecular Hilbert space,
which can be used in the CI-type expansion of Eq. (31) for the molecular ground state \( |\Psi_{0} \rangle \):
4 Resultant descriptors, phase equilibria and information production
For simplicity, let us first consider a single electron in the specified quantum state \( |\psi \rangle \) of Eq. (1). The average Fisher’s [1, 2] measure of the gradient information for locality events contained in the electronic probability density p(r) = R(r)2 [80], called the intrinsic accuracy, is reminiscent of von Weizsäcker’s [81] inhomogeneity correction to kinetic energy functional,
This classical measure characterizes an effective “narrowness” of the spatial probability distribution, a degree of electronic position determinicity. It represents the complementary measure to Shannon’s [3, 4] global entropy descriptor,
which reflects the position uncertainty, i.e., a “spread” of the distribution.
In quantum IT (QIT), these complementary classical descriptors are supplemented by the associated nonclassical complements in the resultant-entropy/information functionals, which combine the probability and phase/current contributions. The intrinsic accuracy concept generalizes naturally into the associated resultant descriptor of the gradient information content in the quantum state \( |\psi \rangle \) itself:
This overall Fisher-type measure is defined by the expectation value of the Hermitian information operator \( {\hat{\text{I}}}(\varvec{r}) \) [61], related to kinetic energy operator \( {\hat{\rm{T}}(}\varvec{r}\text{)} \) of Eq. (6),
Using the integration by parts then gives:
This quantum information concept thus combines the classical (probability) contribution I[p] of Fisher and (positive) nonclassical (phase/current) supplement \( I[\phi \left] { \, = I} \right[\varvec{j}] \). The sign of the latter expresses the fact that nonvanishing current pattern introduces more structural determinicity or order information about the system. This dimensionless measure is seen to also reflect the average kinetic energy of an electron
It is of interest to examine the resultant gradient information content of EO. One first observes that \( \varphi_{\varvec{q}} \left( \varvec{r} \right). \) satisfies the pseudo-eigenvalue problem of the momentum operator \( {\hat{\mathbf{p}}}(\varvec{r}) \) = − iħ∇,
which directly gives the expectation value of the information operator of Eq. (44):
Its first (classical) contribution thus amounts to the Fisher information in probability distribution p(r), while the second (nonclassical) component, due to the orthogonality phase of Eq. (17), amounts to the plane-wave contribution 4q2 multiplied by the EO-average value of the squared divergence of the phase vector field f(r).
One similarly generalizes the global entropy concept by supplementing the classical (probability) functional with the (negative) nonclassical contribution generated by the state (positive) phase [15,16,17,18,19,20,21]. Its sign implies a decrease in state overall structural indeterminicity due to its nonvanishing current distribution. The resultant global entropy measure then reads
while the overall gradient entropy is given by the expectation value
The negative character of the phase contribution M[ϕ] in the latter reflects the fact that a presence of a finite current decreases the overall structure-uncertainty (entropy) content in ψ.
The state extrema of these uncertainty descriptors identify the same optimum (nonnegative) equilibrium-phase solution,
This entropy equilibrium (“thermodynamic”) phase thus generates the associated EO current density reflecting the negative probability-gradient:
One also introduces the complex overall entropy concept [11], the quantum expectation value of the non-Hermitian entropy operator \( {\hat{\mathbf{S}}}(\varvec{r}) \) = − 2lnψ(r). In this “vector” measure of the state overall structural uncertainty, the two contributions of Eq. (49) constitute its real and imaginary parts:
In the Schrödinger dynamical picture, the time evolution of resultant gradient information, the operator of which does not depend on time explicitly, \( {\hat{\text{I}}}(\varvec{r}) \) = − 4∇2 = σ\( {\hat{\text{T}}}(\varvec{r}) \), results solely from the quantum dynamics of the system state vector \( \left| {\psi}({t})\right\rangle \), determined by SE. The time derivative of the resultant gradient information [20],
is then generated by the expectation value of the commutator
and the integration by parts implies:
Hence, the integral production (source) of this information descriptor reads:
This derivative is seen to be determined by the current content of molecular electronic state. Therefore, it identically vanishes for the zero-current density everywhere, when the local component of the state phase identically vanishes, thus confirming its nonclassical origin.
This qualitative conclusion also follows from the time-differentiation of the resultant gradient information I[p, ϕ] = I[p] + I[ϕ] [Eq. (45)]. Its vanishing classical source then indeed directly follows from the sourceless character of probability distribution [Eq. (8)],
while the phase continuity relations [Eqs. (11) and (16)] give the following expression for the nonclassical information source:
Therefore, the integral source of resultant gradient information in fact reflects the total time derivative of its nonclassical contribution I[ϕ]. Hence, the associated derivative of the overall gradient entropy of Eq. (50) reads:
This result confirms the intuitive expectation that an increase in the state overall structural determinicity (order) information, σI(t) > 0 implies the associated decrease in the structural indeterminicity (disorder) information (entropy): σM(t) < 0.
The above one-electron development can be straightforwardly generalized into a general N-electron system in the specified electronic state \( \left| {\Psi}({N})\right\rangle \), exhibiting the electron density ρ(r) = Np(r). The N-electron information operator then combines terms due to each particle,
and determines the state overall gradient information,
proportional to the system average kinetic energy T(N). The relevant separation of the modulus and phase components of N-electron states calls for wavefunctions yielding the specified electron density. For example, in DFT this goal can be effected using the HZM construction, which we have outlined in Sect. 3.
5 Probability currents and information equilibria
Both parts of the resultant EO phases Φq in Eq. (17) contribute to the overall probability current generated by the Slater determinant Ψq(N) describing an electron configuration. The given EO φq(r) generates the associated current density
Hence, the overall current in a trial configuration of N electrons, corresponding to the N-electron operator
where
denotes the resultant “wave-number” vector of \( \Psi_{{\mathbf{q}}} (N) \), independent of the spatial position r, and ∇·f(r) stands for the divergence of its phase vector field f(r).
A reference to Eq. (25) and Fig. 2 shows that this divergence corresponds to the probability density of the union (sum) U(r) = x∨y∨z of observing the specified position coordinates,
which is represented by the area enclosed by the envelope of three probability circles in the figure [14, 36].
Therefore, in the HZM construction of an antisymmetric wavefunction of N electrons the Jacobian of the r → f(r) transformation, expressing a dependence of the volume element df on the spatial volume dr, is proportional to molecular probability function of the product (joint) event involving the spatial coordinates of an electron, while its divergence—determining the current density—corresponds to the probability of the union of such elementary coordinate events.
The overall current of Eq. (66) consists of the resultant “orthogonality” component jf(r) in HZM construction, determined by the local electron density ρ(r), the average wave-number vector 〈q〉 and the divergence of the phase vector f(r), supplemented by the overall “thermodynamic” component jϕ(r) determined by the “thermodynamic” phase-gradient, ∇ϕ(r). The orbital contributions {jl(r)} to the former,
can be also regarded as the ∇·f(r)-enhanced plane-wave currents j(ql; r) of Ψq(N), with the local enhancement factor reflecting the probability density of Fig. 2.
It is also of interest to determine the information-optimum thermodynamic phase, which minimizes the nonclassical gradient information of EO, for the prescribed molecular probability distribution. Indeed, in such a vertical search, for the fixed (ground-state) probability density p0 = ρ0/N, it is the thermodynamic phase ϕ(r) of EO states {ψl[p0]}, which is being optimized, since their orthogonality phases are uniquely determined by the electron density ρ0: f(r) = f[ρ0; r] and {ql = ql[ρ0]}. The condition of the minimum overall gradient information in configuration Ψq[p0],
for the specified probability distribution p0, the shape factor of ρ0, then implies the minimum value of the overall nonclassical information,
with respect to thermodynamic part ϕ of the resultant EO phases {Φl[ϕ; p0]}:
This condition is satisfied by the optimum phase ϕopt.(r) satisfying the local gradient condition
This minimum value of G({gl}) implies the associated Euler equation for determining the information-optimum thermodynamic phase ϕopt.(r) ≥ 0:
This equation thus predicts, to a constant phase unspecified in QM,
Setting const. = 0 finally determines the optimum phase ϕopt.[p0; r] of EO that minimizes their overall nonclassical gradient information I[ϕ; p0] (see also “Appendix 2”):
One observes that this information-optimum local phase of EO differs from its entropy-optimum (“equilibrium”) analog of Eq. (52). It generates the orbital current in direction of the EO-average wave-number vector 〈q[p0]〉:
To summarize, the information-optimum thermodynamic phase of EO is determined by the average “wave-number” vector 〈q〉 in Ψq(N) = \( \Psi_{{\varvec{q}_{1} ,\varvec{q}_{1} , \ldots ,\varvec{q}_{N} }} (N) \). The associated information-“equilibrium” EO thus exhibits the overall phase determined by the deviation of its wave-number vector ql from configuration-average vector 〈q〉:
and generates the associated orbital current:
Such phase-transformed EO thus gives rise to the vanishing resultant probability current:
since
The information-optimum equilibria in EO, for the specified electron density, thus ascribe finite orbital currents, which sum up to the vanishing resultant probability current in the system as a whole. Moreover, since in the information-optimum state of Eq. (78) δq[p] replaces q[p], its resultant gradient information content [see Eq. (48)],
exhibits the current contribution proportional to the squared deviation of the EO wave-number vector q from the configuration-average value 〈q〉.
6 Atomic bases and orbitals reconstructing overlap distributions
The EO states{\( {{\varphi}_{\varvec{q}}({\text {X}}) \equiv {{\varphi}_{\varvec{q}}}^{\text{X}}({\varvec{r}})} \)} of constituent atoms X = A, B, … in a molecule,
form an admissible (non-orthogonal) molecular basis for electronic structure calculations. They give rise to a nonvanishing (complex) diatomic (X ≠ Y) overlap integral,
the projection of \(\big|\varphi_{{\varvec{q}}^{\prime}}^{\text{Y}} \rangle\) on \(\big|\varphi_{{\varvec{q}}}^{\text{X}} \rangle\) in the molecular Hilbert space, the element of the associated (Hermitian) EO-overlap matrix: O = {Oq,q′(X,Y)} = O†.
Since the complex AO are characterized by their probability and current distributions, the natural question arises about the chemically favorable combinations of these physical descriptors of AIM subsystems in a molecule. In particular, one would like to address the intriguing question, how to combine the probability currents to facilitate/enhance the chemical bonds between AIM or reactant fragments? The constructive superposition of subsystem probabilities in the bonding MO combinations of the real AO and their destructive superposition pattern in the antibonding MO states have been well established in the familiar MO theory of molecular electronic structure. Hence, the favorable MO combination of the subsystem EO calls for their summation in the probability-bonding combination,
while the EO difference,
should be associated with the probability-antibonding situation.
The phase/current factors of atomic EO dynamically influence a chemical character of the bonding MO combination describing a given X–Y bond. One recalls that directions of atomic currents in standard EO states, for ϕ = 0, are determined by the orbital wave-number vectors: qX = q and qY = q′. Therefore, in the probability-bonding combination of Eq. (85), the inward orientation of EO currents, toward the bonding region between the nuclei,
should enhance the covalent bond X–Y, while the outward pattern of EO currents,
is expected to weaken this bond component. Therefore, the (“static”) probability-bonding combination of Eq. (85) can assume both the (“dynamic”) current-bonding and current-antibonding characters of Eqs. (87) and (88), respectively. In such EO combinations, the current pattern (the structure of “becoming”) determines different time evolutions of the same initial (bonding) probability distribution (the structure of “being”).
Similar current-bonding and current-antibonding combinations of the subsystem MO, e.g., substrates in chemical reactions, can be encountered in molecular interactions. Consider two interacting (parallel) benzene rings of reactants, perpendicular to “z” axis passing through their centers. In the bonding combination of complex MO exhibiting finite ring currents, the conrotatory matching of the latter should indeed result in an attraction between the magnetic moments associated with these substrate currents, while their disrotatory pattern should produce a magnetic repulsion.
One can also design the EO bases for the specified probability distributions of molecular fragments, e.g., substrates in a chemical reaction. This application should facilitate an orbital interpretation of molecular interactions. The HZM construction of antisymmetric states can be generalized to generate any probability distribution. In particular, one can design the orthonormal EO of N electrons which yields the prescribed diatomic overlap distribution [75],
which represents the geometrical average of atomic probability densities {pZ(r)},
and then construct Slater determinants from alternative selections of different N such orbitals.
Following the development of Sect. 3, this overlap-HZM construction transforms r into
with the associated Jacobian relation between volume elements:
This can be effected through the overlap-dependent vector field FXY(r) = f[ΩXY, r] of the EO phase component,
It gives the functional Jacobian determinant of Eq. (88):
Again, the diagonal derivatives of the preceding equation can be also interpreted as the associated conditional distributions:
The orthonormality of such transformed EO conserving the given overlap distribution can be then demonstrated directly, following the substitution of Eq. (27):
The standard HZM construction, reproducing the prescribed molecular probability density p(r), can be thus considered as representing a special case of the above overlap development for the equal fragment distributions:
The generalized approach, however, allows one to generate the orthonormal basis for any average distribution, e.g., that resulting from the overlap between atomic orbitals, AIM, reactants, etc. Such an EO framework can be thus focused on the valence region of the overlap between the specified pair of AIM, which is mostly responsible for the chemical bond formation between such subsystems. It can be better suited for a more compact, chemical interpretation of the bonding patterns generated by atomic electron distributions.
As an illustrative example, consider an overlap between two spherical-Gaussian densities {Gα(Aα, Rα)} corresponding to subsystems α = (a, b) (see “Appendix 1”), centered in positions {Rα},
Their product can be transformed into an effective Gaussian function
where ρab = (ARa + BRb)/(A + B). It also generates the Gaussian average density,
which provides the distribution basis of the associated overlap EO of Eq. (90). As shown in “Appendix 1,” the HZM conditional probabilities and local phase-vector components for such an effective spherical-Gaussian distribution are readily available.
7 Conclusion
In this article, we have first summarized the probability and phase continuities of molecular states, as implied be SE. We have then reexamined the HZM construction of DFT, of antisymmetric states yielding the prescribed electron density, and provided the probability interpretation of its key phase concept. It has been argued that this transformed position representation in fact preserves main features of the momentum representation in molecular quantum mechanics. A need for the quantum extension of the familiar classical (probability) measures of the entropy/information content in molecular states, to accommodate the complex wave functions of the quantum–mechanical description, has been stressed, and resultant descriptors combining the probability and phase/current contributions have been introduced. This quantum generalization of Fisher’s gradient information, related to electronic kinetic energy, generates a nonvanishing information source. We have also demonstrated the nonclassical (current) origins of the associated resultant-information production. The present analysis and related treatments of reactivity phenomena [23,24,25,26,27,28] complement the previous classical information approaches to reactive systems, e.g., [82,83,84,85,86].
The orbital flows of electrons have been examined, and the information-optimum “thermodynamic” phases of the information-equilibrium EO states have been determined. It has been argued that the overall current of electron configurations in such information equilibria identically vanishes. The current orientations in the bonding combinations of atomic EO have been examined and the current-bonding or current-antibonding patterns have been identified. Finally, the EO basis reproducing the specified diatomic overlap density has been discussed and an illustrative example of the overlapping Gaussian distributions has been explored.
This article further develops the resultant-information description of molecular states [26,27,28, 86]. The electronic state exhibiting a nonvanishing probability current indeed contains more information, compared to the zero-current state of the same electron density, since the former exhibits an additional structural element, and thus also the associated coherence information of the phase/flux pattern, which is missing in the state specification by the probability distribution alone. Following Prigogine [29], one could refer at this point to the now famous picture of a complicated network of vortices on Jupiter. The current structure of “becoming” contains the information about the (subsequent) quantum evolution of the system temporary probability distribution, the structure of “being,” thus representing the state of a greater “knowledge” about the system, as reflected by the higher degree of the gradient “order” (determinicity) information, corresponding to lower level of the system “uncertainty,” corresponding to smaller gradient “disorder” (indeterminicity) information (entropy) measure.
References
Fisher RA (1925) Theory of statistical estimation. Proc Camb Philos Soc 22:700–725
Frieden BR (2004) Physics from the Fisher information—a unification. Cambridge University Press, Cambridge
Shannon CE (1948) The mathematical theory of communication. Bell System Tech J 27(379–493):623–656
Shannon CE, Weaver W (1949) The mathematical theory of communication. University of Illinois, Urbana
Hohenberg P, Kohn W (1964) Inhomogeneous electron gas. Phys Rev 136B:864–971
Kohn W, Sham LJ (1965) Self-consistent equations including exchange and correlation effects. Phys Rev 140A:133–1138
Levy M (1979) Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem. Proc Natl Acad Sci USA 76:6062–6065
Parr RG, Yang W (1989) Density-functional theory of atoms and molecules. Oxford University Press, New York
Dreizler RM, Gross EKU (1990) Density functional theory: an approach to the quantum many-body problem. Springer, Berlin
Nalewajski RF (ed) (1996) Density functional theory I–IV, topics in current chemistry vol 180–183
Nalewajski RF (2016) Complex entropy and resultant information measures. J Math Chem 54:1777–1782
Nalewajski RF (2014) On phase/current components of entropy/information descriptors of molecular states. Mol Phys 112:2587–2601
Nalewajski RF (2017) Quantum information measures and their use in chemistry. Curr Phys Chem 7:94–117
Nalewajski RF (2013) Exploring molecular equilibria using quantum information measures. Ann Phys (Leipzig) 525:256–268
Nalewajski RF (2016) Quantum information theory of molecular states. Nova Science Publishers, New York
Nalewajski RF (2014) On phase equilibria in molecules. J Math Chem 52:588–612
Nalewajski RF (2014) Quantum information approach to electronic equilibria: molecular fragments and elements of non-equilibrium thermodynamic description. J Math Chem 52:1921–1948
Nalewajski RF (2015) Phase/current information descriptors and equilibrium states in molecules. Int J Quantum Chem 115:1274–1288
Nalewajski RF (2015) Quantum information measures and molecular phase equilibria. In: Baswell AR (ed) Advances in mathematics research, vol 2. Nova Science Publishers, New York, pp 53–86
Nalewajski RF (2018) Information equilibria, subsystem entanglement and dynamics of overall entropic descriptors of molecular electronic structure. J Mol Model (Chattaraj PK issue) 24:212–227
Nalewajski RF (2017) Entropy continuity, electron diffusion and fragment entanglement in equilibrium states. In: Baswell AR (ed) Advances in mathematics research, vol 22. Nova Science Publishers, New York, pp 1–42
Nalewajski RF (2016) On entangled states of molecular fragments. Trends Phys Chem 16:71–85
Nalewajski RF (2018) Phase description of reactive systems. In: Islam N, Kaya S (eds) Conceptual density functional theory. Apple Academic Press, Waretown, pp 217–249
Nalewajski RF (2017) Chemical reactivity description in density-functional and information theories. Acta Phys Chim Sin 33:2491–2509
Nalewajski RF (2019) On entropy/information description of reactivity phenomena. In: Baswell AR (ed) Advances in mathematics research, vol 26. Nova Science Publishers, New York
Nalewajski RF (2019) Quantum information perspective on chemical reactivity. In: Islam N (ed) Recent trends in theoretical and computational research (in press)
Nalewajski RF (2019) Role of electronic kinetic energy and resultant gradient information in chemical reactivity. In: Berski S, Sokalski WA (eds) J Mol Model (Latajka Z issue) (in press)
Nalewajski RF (2019) Understanding electronic structure and chemical reactivity: quantum-information perspective. Appl Sci 9:1262–1292
Prigogine I (1980) From being to becoming: time and complexity in the physical sciences. Freeman WH & Co, San Francisco
Kullback S, Leibler RA (1951) On information and sufficiency. Ann Math Stat 22:79–86
Kullback S (1959) Information theory and statistics. Wiley, New York
Abramson N (1963) Information theory and coding. McGraw-Hill, New York
Pfeifer PE (1978) Concepts of probability theory. Dover, New York
Nalewajski RF (2006) Information theory of molecular systems. Elsevier, Amsterdam
Nalewajski RF (2010) Information origins of the chemical bond. Nova Science Publishers, New York
Nalewajski RF (2003) Electronic structure and chemical reactivity: density functional and information theoretic perspectives. Adv Quant Chem 43:119–184
Nalewajski RF (2012) Perspectives in electronic structure theory. Springer, Heidelberg
Nalewajski RF, Parr RG (2000) Information theory, atoms-in-molecules and molecular similarity. Proc Natl Acad Sci USA 97:8879–8882
Nalewajski RF (2003) Information principles in the theory of electronic structure. Chem Phys Lett 372:28–34
Nalewajski RF (2003) Information principles in the Loge theory. Chem Phys Lett 375:196–203
Nalewajski RF, Broniatowska E (2003) Information distance approach to Hammond postulate. Chem Phys Lett 376:33–39
Nalewajski RF, Parr RG (2001) Information theory thermodynamics of molecules and their Hirshfeld fragments. J Phys Chem A 105:7391–7400
Nalewajski RF (2002) Hirshfeld analysis of molecular densities: subsystem probabilities and charge sensitivities. Phys Chem Chem Phys 4:1710–1721
Parr RG, Ayers PW, Nalewajski RF (2005) What is an atom in a molecule? J Phys Chem A 109:3957–3959
Nalewajski RF, Broniatowska E (2007) Atoms-in-molecules from the stockholder partition of molecular two-electron distribution. Theor Chem Acc 117:7–27
Heidar-Zadeh F, Ayers PW, Verstraelen T, Vinogradov I, Vöhringer-Martinez E, Bultinck P (2018) Information-theoretic approaches to atoms-in-molecules: Hirshfeld family of partitioning schemes. J Phys Chem A 122:4219–4245
Hirshfeld FL (1977) Bonded-atom fragments for describing molecular charge densities. Theor Chim Acta (Berl) 44:129–138
Nalewajski RF (2000) Entropic measures of bond multiplicity from the information theory. J Phys Chem A 104:11940–11951
Nalewajski RF (2004) Entropy descriptors of the chemical bond in Information Theory: I. Basic concepts and relations. Mol Phys 102:531–546; II. Application to simple orbital models. Mol Phys 102:547–566
Nalewajski RF (2004) Entropic and difference bond multiplicities from the two-electron probabilities in orbital resolution. Chem Phys Lett 386:265–271
Nalewajski RF (2005) Reduced communication channels of molecular fragments and their entropy/information bond indices. Theor Chem Acc 114:4–18
Nalewajski RF (2005) Partial communication channels of molecular fragments and their entropy/information indices. Mol Phys 103:451–470
Nalewajski RF (2011) Entropy/information descriptors of the chemical bond revisited. J Math Chem 49:2308–2329
Nalewajski RF (2014) Quantum information descriptors and communications in molecules. J Math Chem 52:1292–1323
Nalewajski RF (2009) Multiple, localized and delocalized/conjugated bonds in the orbital-communication theory of molecular systems. Adv Quant Chem 56:217–250
Nalewajski RF, Szczepanik D, Mrozek J (2011) Bond differentiation and orbital decoupling in the orbital communication theory of the chemical bond. Adv Quant Chem 61:1–48
Nalewajski RF, Szczepanik D, Mrozek J (2012) Basis set dependence of molecular information channels and their entropic bond descriptors. J Math Chem 50:1437–1457
Nalewajski RF (2017) Electron communications and chemical bonds. In: Wójcik M, Nakatsuji H, Kirtman B, Ozaki Y (eds) Frontiers of quantum chemistry. Springer, Singapore, pp 315–351
Nalewajski RF, Świtka E, Michalak A (2002) Information distance analysis of molecular electron densities. Int J Quantum Chem 87:198–213
Nalewajski RF, Broniatowska E (2003) Entropy displacement analysis of electron distributions in molecules and their Hirshfeld atoms. J Phys Chem A 107:6270–6280
Nalewajski RF (2008) Use of Fisher information in quantum chemistry. Int J Quantum Chem (Jankowski K issue) 108:2230–2252
Nalewajski RF, Köster AM, Escalante S (2005) Electron localization function as information measure. J Phys Chem A 109:10038–10043
Becke AD, Edgecombe KE (1990) A simple measure of electron localization in atomic and molecular systems. J Chem Phys 92:5397–5403
Silvi B, Savin A (1994) Classification of chemical bonds based on topological analysis of electron localization functions. Nature 371:683–686
Savin A, Nesper R, Wengert S, Fässler TF (1997) ELF: the electron localization function. Angew Chem Int Ed Engl 36:1808–1832
Nalewajski RF, de Silva P, Mrozek J (2010) Use of nonadditive Fisher information in probing the chemical bonds. J Mol Struct: Theochem 954:57–74
Nalewajski RF (2011) Through-space and through-bridge components of chemical bonds. J Math Chem 49:371–392
Nalewajski RF (2011) Chemical bonds from through-bridge orbital communications in prototype molecular systems. J Math Chem 49:546–561
Nalewajski RF (2011) On interference of orbital communications in molecular systems. J Math Chem 49:806–815
Nalewajski RF, Gurdek P (2011) On the implicit bond-dependency origins of bridge interactions. J Math Chem 49:1226–1237
Nalewajski RF (2012) Direct (through-space) and indirect (through-bridge) components of molecular bond multiplicities. Int J Quantum Chem 112:2355–2370
Nalewajski RF, Gurdek P (2012) Bond-order and entropic probes of the chemical bonds. Struct Chem 23:1383–1398
Harriman JE (1980) Orthonormal orbitals for the representation of an arbitrary density. Phys Rev A 24:680–682
Zumbach G, Maschke K (1983) New approach to the calculation of density functionals. Phys Rev A28: 544–554; Erratum, Phys. Rev. A29: 1585–1587
Nalewajski RF (2000) Orthonormal orbitals from the overlapping densities of subsystems. J Mol Struct (Theochem) 501:529–534
Callen HB (1962) Thermodynamics: an introduction to the physical theories of equilibrium thermostatics and irreversible thermodynamics. Wiley, New York
Macke W (1955) Zur wellermechanischen behandlung von vielkoeperproblemen. Ann Phys 17:1–9
Macke W (1955) Wave mechanical treatment of the Fermi gas. Phys Rev 100:992–993
Gilbert TL (1975) Hohenberg–Kohn theorem for nonlocal external potentials. Phys Rev B 12:2111–2120
Sears SB, Parr RG, Dinur U (1980) On the quantum mechanical kinetic energy as a measure of the information in a distribution. Isr J Chem 19:165–173
von Weizsäcker CF (1935) Zur theorie der kernmassen. Z Phys 96:431–458
Hô M, Schmider HL, Weaver DF, Smith VH Jr, Sagar RP, Esquivel RO (2000) Shannon entropy of chemical changes: SN2 displacement reactions. Int J Quantum Chem 77:376–382
López-Rosa S, Esquivel RO, Angulo JC, Antolin J, Dehesa JS, Flores-Gallegos N (2010) Fisher information study in position and momentum spaces for elementary chemical reactions. J Chem Theory Comput 6:145–154
Esquivel RO, Liu SB, Angulo JC, Dehesa JS, Antolin J, Molina-Espiritu M (2011) Fisher information and steric effect: study of the internal rotation barrier in ethane. J Phys Chem A115:4406–4415
Liu SB (2016) Information-theoretic approach in density-functional reactivity theory. Acta Phys Chim Sin 32:98–118
Nalewajski RF (2019) Resultant information description of electronic states and chemical processes. J Phys Chem A (Geerlings P issue) (submitted)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The following notation is adopted: A denotes a scalar, A is the row or column vector, A represents a square or rectangular matrix, and the dashed symbol \( {\hat{\text{A}}} \) stands for the quantum–mechanical operator of the physical property A. The logarithm of Shannon’s information measure is taken to an arbitrary but fixed base: log = log2 corresponds to the information content measured in bits (binary digits), while log = ln expresses the amount of information in nats (natural units): 1 nat = 1.44 bits.
Appendices
Appendix 1: HZM construction for the spherical-Gaussian probability distribution
Consider the 1s-type spherical-Gaussian orbital (SGO) centered at the origin (R = 0) of the Cartesian coordinate system {xα},
and the probability density it generates,
expressed in terms of the coordinate distributions
The factorization of Eq. (A2) and partial normalization of Eq. (A3) then imply the following joint and conditional probability distributions:
Following the HZM prescription, the corresponding components of the local phase vector fμ[p; r] ≡ fμ(r) = {fμ,α(r)} are defined by the partial integrals of Eq. (23). One first observes that the construction definite integrals read:
Its indefinite integrals can be thus expressed in terms of the familiar error function of probability theory,
The resulting components of the phase vector for this spherical-Gaussian probability density thus read:
Finally, by direct differentiation one can verify Eq. (25) which determines the construction Jacobian of Eq. (24).
Appendix 2: Thermodynamic phase from extremum principle for nonclassical information
Consider first the resultant-information content [Eq. (45)] in the single original (nontransformed) EO of Eq. (17), for ϕ = 0,
This classical information term is thus uniquely determined by the electron probability distribution p(r). Indeed, both q and f are unique functionals of p: the former—by the energy—minimum principle of quantum mechanics, and the latter—by the HZM construction.
After the thermodynamic-phase transformation,
the overall classical information content in such an information-equilibrium state is supplemented by ϕ-dependent, nonclassical contributions:
The information-equilibrium thermodynamic phase, for the fixed probability distribution, then results from the extremum of the nonclassical information contribution,
which gives the following Euler’s equation for the information-optimum phase of EO:
where we have recognized the phase continuities of Eq. (11): ∇2Fq = ∇2ϕopt. = 0. It thus follows from the preceding equation that
Finally, for the specified configuration of N electrons [Eq. (28)], identified by the set of the occupied information-equilibrium EO {φlopt.}, one finds by summation over the orbital relations (B7),
and hence [see Eq. (76)]:
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nalewajski, R.F. Equidensity orbitals in resultant-information description of electronic states. Theor Chem Acc 138, 108 (2019). https://doi.org/10.1007/s00214-019-2487-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00214-019-2487-1