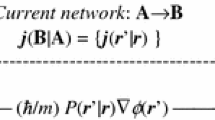Abstract
Several concepts of information theory (IT) are extended to cover the complex probability amplitudes (wave functions) of molecular quantum mechanics. The classical and non-classical aspects of the electronic structure are revealed by the electronic probability and phase distributions, respectively. The information terms due to the probability and current distributions are accounted for in the complementary Shannon and Fisher measures of the resultant information content of quantum states. Similar generalization of the information-distance descriptors is also established. The superposition principle (SP) of quantum mechanics, which introduces the conditional probabilities between quantum states, is used to generate a network of quantum communications in molecules, and to identify the non-additive contributions to physical and information quantities. The phase-relations in two-orbital model are explored. The orbital communication theory of the chemical bond introduces the entropic bond multiplicities and their partition into IT covalent/ionic components. The conditional probabilities between atomic orbitals, propagated via the network of the occupied molecular orbitals, which define the bond system and orbital communications in molecules, are generated from the bond-projected SP. In the one-determinantal representation of the molecular ground state the communication amplitudes are then related to elements of the charge and bond-order matrix. Molecular equilibria are reexamined and parallelism between the vertical (density-constrained) energy or entropy/information principles of IT and the corresponding thermodynamic criteria is emphasized.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Concepts and techniques of information theory (IT) [1–8] have been successfully applied to explore the molecular electron probabilities and the associated patterns of chemical bonds, e.g., [9–18]. In Schrödinger’s quantum mechanics the electronic state is determined by the system wave function, the (complex) amplitude of the particle probability-distribution, which carries the resultant information content. Both the electron density or its shape factor, the probability distribution determined by the wave-function modulus, and the system current-distribution, related to the gradient of the wave-function phase, ultimately contribute to the quantum information descriptors of molecular states. The former reveals the classical information term, while the latter determines its non-classical complement in the overall information measures [9, 10, 16, 17]. The phenomenological IT description of equilibria in molecular subsystems has also been proposed [11, 19–22], which formally resembles the ordinary thermodynamics [23].
In the present analysis we shall emphasize the non-classical, (phase/current)-related contributions to quantum information measures of electronic states in molecules. It is the main purpose of this work to identify the non-classical supplements of the classical cross (relative) entropy (information-distance) descriptors within both the Fisher and Shannon measures of the information content, and to explore the the role of the phase dependence of scattering amplitudes in the orbital communication theory (OCT) [12, 13, 18, 24–27]. The information-cascade (bridge) propagation of electronic probabilities in molecular information systems, which generates the indirect bond contributions due to orbital intermediaries [13, 28–32], will be also examined.
Throughout the article the following tensor notation is used: \(A\) denotes a scalar quantity, \({{\varvec{A}}}\) stands for the row or column vector, and A represents a square or rectangular matrix. The logarithm of the Shannon-type information measure is taken to an arbitrary but fixed base. In keeping with the custom in works on IT the logarithm taken to base 2 corresponds to the information measured in bits (binary digits), while selecting log = ln expresses the amount of information in nats (natural units): 1 nat = 1.44 bits.
2 Probability and current descriptors of electronic states
Consider the electron density \(\rho ({{\varvec{r}}}) = Np({{\varvec{r}}})\), or its shape (probability) factor \(p({{\varvec{r}}})\), and the current density \({{\varvec{j}}}({{\varvec{r}}})\) in the quantum state \(\Psi (N)\) of \(N\) electrons,
Here \(R(N)\) and \(\Phi (N)\) stand for the wave-function modulus and (spatial) phase parts, respectively, \({\varvec{\sigma }}^{N} = (\sigma _{1}, \sigma _{2}, {\ldots }, \sigma _{N})\) groups the spin orientations of all \(N\) (indistinguishable) electrons and \(\mathbf{r}^{N} = ({{\varvec{r}}}_{1}, {{\varvec{r}}}_{2}, {\ldots }, {{\varvec{r}}}_{N})\equiv ({{\varvec{r}}}_{1}, \mathbf{r}^{\prime })\) combines their spatial positions. These quantities are defined by the quantum-mechanical expectation values,
of the corresponding observables in the position representation,
where \(m\) denotes the electronic mass and the momentum operator \({\hat{\mathbf{p}}}_k =-\hbox {i}\hbar \nabla _k\).
The modulus part of the wave function generates the state electron distribution,
where the summation is over the admissible spin-orientations of all electrons,
and the integration covers the coordinates of positions \(\mathbf{r}^{\prime } = ({{\varvec{r}}}_{2}, {{\varvec{r}}}_{3}, {\ldots }, {{\varvec{r}}}_{N})\) of all these indistinguishable fermions but the representative “first” electron in \({{\varvec{r}}}, {{\varvec{r}}}_{1} ={{\varvec{r}}}\), as enforced by the Dirac delta function. The probability current density is similarly shaped by the state phase gradient:
These expressions assume particularly simple forms in the MO approximation,
e.g., in the familiar Hartree–Fock (HF) or Kohn–Sham (KS) self-consistent field (SCF) theories, in which \(\Psi (N)\) is given by the antisymmetrized product (Slater determinant) of \(N\) one-particle functions, spin molecular orbitals (SMO),
each determined by a product of the associated spatial function (MO) \(\varphi _{k}({{\varvec{r}}})\) and the corresponding spin-state
Indeed, since the observables of Eq. (2) combine one-electron operators their expectation values are given by the sum of the corresponding orbital expectation values:
where \(\{\rho _k ({{\varvec{r}}})\}\) and \(\{j_k({{\varvec{r}}})\}\) denote the orbital contributions to the system electron density and current distributions, respectively.
In the simplest case of a single (\(N = 1\)) electron in a general state described by the complex MO,
the modulus factor of this wave function determines the particle spatial probability/density distribution,
while the gradient of its phase component generates the associated current density:
The phase gradient is thus proportional to the current-per-particle, “velocity” field \({{\varvec{ V}}}({{\varvec{r}}}) ={{\varvec{j}}}({{\varvec{r}}})/p({{\varvec{r}}})\):
The probability and current densities manifest the complementary facets of electron distributions in molecules. They respectively generate the classical and non-classical contributions to the generalized measures of the information content in quantum electronic states [9, 10, 16, 17, 33], which we shall briefly summarize in the next section.
3 Information measures
In Sects. 3–5 we provide a short overview of the pertinent concepts and techniques of IT, including the classical measures of the information content and their quantum generalizations capable of tackling the complex probability amplitudes (wave functions). As already remarked above, these generalized quantities have to be used in diagnosing the full, quantum information content of electronic states [9, 10], exploring molecular equilibria [16, 17], probing the chemical bond multiplicities due to orbital bridges, and in treating the associated multiple (cascade) communications in molecular information channels. Some rudiments of the classical communication systems and the associated amplitude channels will also be given and the entropic descriptors of the orbital networks will be linked to the chemical bond multiplicities and their covalent/ionic composition.
The key element of the IT approach to molecular electronic structure is an adequate definition of a generalized measure of the information content in the given (generally complex) quantum state of electrons in molecules. The system electron distribution, related to the wave-function modulus, reveals only the classical, probability aspect of the molecular information content [1–7], while the phase (current) component gives rise to the non-classical entropy/information terms [9, 10, 16, 17, 33]. The resultant quantum measure then allow one to monitor the full information content of the non-equilibrium (variational) quantum states, thus providing the complete information description of their evolution towards the final equilibrium.
In density functional theory (DFT) [34, 35] one often refers to the density-constrained principles [9, 10, 36] and states [37–40], which correspond to the fixed electronic probability distribution. They determine the so called vertical equilibria, which are determined solely by the non-classical (current related) entropy/information functionals [9, 10, 16, 17]. The density-unrestricted principles associated with the resultant information measure similarly determine the horizontal (unconstrained) equilibria in molecules [9–11].
Of interest in the electronic structure theory also are the cross (or relative) entropy quantities, which measure the information distance between two probability distributions and reflect the information similarity between different states or molecules, as well as descriptors of the information propagation between bonded atoms and orbitals in the system chemical bonds. One also aims at formulating the adequate, consistent with the prevailing chemical intuition, measures of the chemical bond multiplicity in the system as a whole and its constituent fragments, as well as the entropy/information descriptors of the bond covalent/ionic composition.
The spread of information in molecular communication networks, among AIM or between AO they contribute to molecular bond system, is investigated in OCT in which molecular systems are regarded as the AO-resolved information channels. Their conditional-entropy (communication noise) and mutual-information (information-flow) descriptors [3, 7, 11–13] then provide a chemical resolution of the resulting IT bond multiplicities into the covalent and ionic bond components, respectively. One is also interested in mutual relations between analogous concepts developed within the SCF MO and IT approaches. Together they offer a deeper insight into the complex phenomenon called the chemical bonding.
The Shannon entropy [3] of the normalized probability vector \({{\varvec{p}}} = \{p_{i}\}, \sum _{i} p_{i} = 1\),
where the summation extends over labels of the elementary events determining the discrete probability scheme in question, provides a measure of the average indeterminacy in the argument probability distribution. One similarly introduces the associated functional of the spatial probability distribution \(p({{\varvec{r}}}) = {\vert }\varphi ({{\varvec{r}}}){\vert }^{2}\), for the continuous labels of the electron locality events \(\{{{\varvec{r}}}\}\):
These electron “uncertainty” quantities also measure the corresponding amounts of information, \(I^\mathrm{S}(p)=S(p)\) or \(I^\mathrm{S}[p] = S[p]\), obtained when the distribution indeterminacy is removed by an appropriate measurement (experiment). This familiar (global) information measure is classical in character, being determined by probabilities alone. This property distinguishes it from the corresponding quantum concept of the non-classical entropy contribution due to the phase of the complex quantum state in question. As argued elsewhere [9, 10, 16, 17], for a single particle in the MO state of Eq. (12) the density of the non-classical entropy complement to the classical Shannon entropy of Eq. (17) is proportional to the local magnitude of the phase function, \({\vert }\phi {\vert } = (\phi ^{2})^{1/2}\), the square root of the phase-density \(\phi ^{2}\), with the local particle probability density providing the relevant weighting factor:
Therefore, for the given quantum state \(\varphi \) of an electron the two components \(S[p] = S^{class.}[\varphi ]\) and \(S[p, \phi ] = S^{nclass.}[\varphi ]\) determine the resultant entropy descriptor:
The classical Fisher information for locality events [1, 2], also called the intrinsic accuracy, historically predates the Shannon entropy by about 25 years, being proposed in about the same time, when the final form of the modern quantum mechanics was shaped. This classical gradient measure of the information content in the probability density \(p({{\varvec{r}}})\) reads:
where \(A({{\varvec{r}}}) = \sqrt{p({{\varvec{r}}})}\) denotes the classical amplitude of this probability distribution.
This Fisher information is reminiscent of von Weizsäcker’s [41] inhomogeneity correction to the electronic kinetic energy in the Thomas-Fermi theory. It characterizes the compactness of the probability density \(p({{\varvec{r}}})\). For example, the Fisher information in the normal distribution measures the inverse of its variance, called the invariance, while the complementary Shannon entropy is proportional to the logarithm of variance, thus monotonically increasing with the spread of the Gaussian distribution. The Shannon entropy and intrinsic accuracy thus describe complementary facets of the probability density: the former reflects distribution’s “spread” (delocalization, “disorder”), while the latter measures its “narrowness” (localization, “order”).
This classical amplitude form of Eq. (20) is then naturally generalized into the domain of the quantum (complex) probability amplitudes, the wave functions of Schrödinger’s quantum mechanics. For example, for the one-electron state of Eq. (12), when \(p({{\varvec{r}}}) = \varphi ^{*}({{\varvec{r}}})\varphi ({{\varvec{r}}}) = {\vert }\varphi ({{\varvec{r}}}){\vert }^{2} = [R({{\varvec{r}}})]^{2}\), i.e., \(A({{\varvec{r}}}) = R({{\varvec{r}}})\), this generalized measure is given by the following MO functional related to the average kinetic energy \(T[\varphi ]\):
where from the spatial integration by parts,
This quantum kinetic energy also consists of the classical Fisher contribution, depending solely upon the electron probability distribution \(p\)(r),
and the non-classical, (phase/current)-related term,
Expressing the information functional of Eq. (21) in terms of the modulus and phase components of the argument MO state similarly gives:
Here, the two information densities-per-electron read:
The classical and non-classical densities-per-electron of these complementary measures of the information content are mutually related via the common-type dependence [9, 10]:
Thus, the square of the gradient of the local Shannon probe of the state quantum “indeterminicity” (disorder) generates the density of the corresponding Fisher measure of the state quantum “determinicity” (order). Notice, that the second of these relations determines the density \(S^{{ nclass}\cdot }({\varvec{r}})\) only up to its sign. Therefore, both positive and negative [see Eq. (18)] signs of this non-classical (phase-related) information density are admissible.
4 Comparing probability distributions
An important generalization of Shannon’s entropy concept, called the relative (cross) entropy, also known as the entropy deficiency, missing information or directed divergence, has been proposed by Kullback and Leibler [5, 6]. It measures the information “distance” between the two (normalized) probability distributions for the same set of events. For example, in the discrete probability scheme identified by events \({{\varvec{a}}} = \{a_{i}\}\) and their probabilities \({{\varvec{P}}}({{\varvec{a}}}) = \{P(a_{i})=p_{i}\} = {{\varvec{p}}}\), this discrimination information in \({{\varvec{p}}}\) with respect to the reference distribution \({{\varvec{P}}}({{\varvec{a}}}^{0}) = \{P(a_{i}^{0})=p_{i}^{0}\} = {{\varvec{p}}}^{0}\) reads:
This quantity provides a measure of the information resemblance between the two compared probability schemes. The more the two distributions differ from one another, the larger the information distance. For individual events the logarithm of probability ratio \( I_{i} = \log (p_{i}/p_{i}^{0})\), called the probability surprisal, provides a measure of the event information in \({{\varvec{p}}}\) relative to that in the reference distribution \({{\varvec{p}}}^{0}\). Notice that the equality in the preceding equation takes place only for the vanishing surprisal for all events, i.e., when the two probability distributions are identical.
Similar classical concepts of the information distance can be advanced within the Fisher measure. The directed-divergence between the continuous probability density \(p({{\varvec{r}}}) = {\vert }\varphi {\vert }^{2 }\) and the reference distribution \(p^{0}({{\varvec{r}}}) = {\vert }\varphi ^{0}{\vert }^{2}\), measuring the average probability-surprisal \(I_{p}({{\varvec{r}}})\),
has been generalized into its gradient analog [11,22]:
One can also introduce measures of the non-classical information distances, related to the phase/current degrees-of-freedom of the two quantum states \(\varphi \) and \(\varphi ^{0}\), which generate the associated (probability, phase, current) components, (\(p, \phi , {{\varvec{j}}}\)) and (\(p^{0}, \phi ^{0}, {{\varvec{j}}}^{0})\), respectively. The non-classical Shannon measure \(S[p, \phi ]\) of Eq. (18) then generates the following information distance measuring the average phase-surprisal \(I_{\phi }({{\varvec{r}}})\):
Two components of Eqs. (30) and (32) thus determine the following resultant entropy- deficiency between two complex wave functions:
In a search for the non-classical Fisher-information distance,
we use Eq. (28), which establishes a general relation between the complementary Shannon and Fisher information densities-per-electron. For comparing the two quantum states we thus propose
where we have used the gradient identity
Since the phase gradients are related to the corresponding “velocities”, which measure the corresponding currents-per-particle [see Eq. (15)],
the resulting non-classical contribution to the Fisher measure of the quantum information distance between the two electronic states [Eq. (34)],
represents the average value of the squared combination of currents (velocities) in the two states compared.
Together the two components of Eqs. (31) and (37) determine the resultant Fisher-information distance between the two complex wave functions:
The common amount of information in two dependent events \(a_{i}\) and \(b_{j}\), \(I(i:j)\), measuring the information about \(a_{i}\) provided by the occurrence of \(b_{j}\) or the information about \(b_{j}\) provided by the occurrence of \(a_{i}\), determines the mutual information in these two events,
where \(P(a_{i}\wedge b_{j}) \equiv \pi _{i,j}\) stands for the probability of the joint event, of simultaneously observing \(a_{i}\) and \(b_{j}\), while the quantity \(I(i{\vert }j) = -\log P(i{\vert }j)\) measures the conditional entropy in \(a_{i}\) given the occurrence of \(b_{j}\), or the self-information in the conditional event of observing \(a_{i}\) given \(b_{j}\). The mutual information \(I(i:j)\) may take on any real value, positive, negative, or zero: it vanishes, when both events are independent, i.e., when the occurrence of one event does not influence (or condition) the probability of the occurrence of the other event, and it is negative, when the occurrence of one event makes a non-occurrence of the other event more likely. It also follows from the preceding equation that the self-information of the joint event \(I(i \wedge j)=-\log \pi _{i,j}\) reads:
Thus, the information in the joint occurrence of two events \(a_{i}\) and \(b_{j}\) is the information in the occurrence of \(a_{i}\) plus that in the occurrence of \(b_{j}\) minus the mutual information. Clearly, for independent events, when \(\pi _{i,j}=\pi _{i,j}^{0}=p_{i}q_{j}, I(i:j) = 0\) and hence \(I(i \wedge j)=I(i)+I(j)\).
The mutual information of an event with itself defines its self-information: \(I(i:i) \equiv I(i) = \log [P(i{\vert } i)/p_{i}] = -\log p_{i}\), since for a single event \(P(i{\vert }i) = 1\). It vanishes for \(p_{i} = 1\), i.e., when there is no uncertainty about the occurrence of \(a_{i}\), so that the occurrence of this event removes no uncertainty, hence conveys no information. This quantity provides a measure of the uncertainty about the occurrence of the event itself, i.e., the information received when the event actually takes place.
Consider now two mutually dependent (discrete) probability vectors for different sets of events, \({{\varvec{P}}}({{\varvec{a}}}) = \{P(a_{i})=p_{i}\} \equiv {{\varvec{p}}}\) and \({{\varvec{P}}}({{\varvec{b}}}) = \{P(b_{j})=q_{j}\} \equiv {{\varvec{q}}}\) (see Fig. 1). One decomposes the joint probabilities of the simultaneous events \({{\varvec{a}}}\wedge {{\varvec{b}}} = \{a_{i} \wedge b_{j}\}\) in these two schemes, \(\mathbf{P}({{\varvec{a}}}\wedge {{\varvec{b}}}) = \{P(a_{i} \wedge b_{j})=\pi _{i,j}\} \equiv {\varvec{\uppi }}\), as products of the “marginal” probabilities of events in one set, say \({{\varvec{P}}}({{\varvec{a}}})\), and the corresponding conditional probabilities \(\mathbf{P}({{\varvec{b}}}\vert {{\varvec{a}}}) = \{P(j{\vert }i)\}\) of outcomes in the other set \({{\varvec{b}}}\), given that events \({{\varvec{a}}}\) have already occurred [see Eq. (39)]:
The relevant normalization conditions for such joint and conditional probabilities read:
The Shannon entropy of the product distribution \({\varvec{\uppi }}, S({\varvec{\uppi }}) = -\sum _{i}\sum _{j} \pi _{i,j}\log \pi _{i,j}\),
can be thus expressed as the sum of the average entropy in the marginal probability distribution, \(S({{\varvec{p}}})\), and the average conditional entropy in \({{\varvec{q}}}\) given \({{\varvec{p}}}\),
The latter represents the extra amount of the uncertainty/information about the occurrence of events \({{\varvec{b}}}\), given that the events \({{\varvec{a}}}\) are known to have occurred. In other words: the amount of information obtained as a result of simultaneously observing the events \({{\varvec{a}}}\) and \({{\varvec{b}}}\) equals to the amount of information in one set, say \({{\varvec{a}}}\), supplemented by the extra information provided by the occurrence of events in the other set \({{\varvec{b}}}\), when \({{\varvec{a}}}\) are known to have occurred already (see Fig. 1).
Diagram of the conditional-entropy and mutual-information quantities for two dependent probability distributions \({{\varvec{p}}}\) and \({{\varvec{q}}}\). Two circles enclose areas representing the entropies \(S({{\varvec{p}}})\) and \(S({{\varvec{q}}})\) of two separate probability vectors, while their common (overlap) area corresponds to the mutual information \(I({{\varvec{p}}}:{{\varvec{q}}})\) in these two distributions. The remaining part of each circle represents the corresponding conditional entropy, \(S({{\varvec{p}}}{\vert }{{\varvec{q}}})\) or \(S({{\varvec{q}}}{\vert }{{\varvec{p}}})\), measuring the residual uncertainty/information about events in one set of outcomes, when one has the full knowledge of the occurrence of events in the other set. The area enclosed by the circle envelope then represents the entropy of the “product” (joint) distribution: \(S({\varvec{\uppi }}) = S(\mathbf{P}({{\varvec{a}}}\wedge {{\varvec{b}}})) = S({{\varvec{p}}}) + S({{\varvec{q}}}) - I({{\varvec{p}}}:{{\varvec{q}}}) = S({{\varvec{p}}}) + S({{\varvec{q}}}{\vert }{{\varvec{p}}}) = S({{\varvec{q}}}) + S({{\varvec{p}}}{\vert }{{\varvec{q}}})\)
The classical Shannon entropy [Eq. (16)] can be thus interpreted as the mean value of self-informations in all individual events: \(S({{\varvec{p}}}) = \sum _{i}p_{i}I(i)\). One similarly defines the average mutual information in two probability distributions as the (\({\varvec{\uppi }}\)-weighted) mean value of the mutual information quantities for individual joint events (see also Fig. 1):
The equality holds only for independent distributions, when \(\pi _{i,j}=p_{i} q_{j}\equiv \pi _{i,j}^{0}\). Indeed, the amount of uncertainty in \({{\varvec{q}}}\) can only decrease, when \({{\varvec{p}}}\) has been known beforehand, \(S({{\varvec{q}}}) \ge S({{\varvec{q}}}{\vert }{{\varvec{p}}}) = S({{\varvec{q}}})-I({{\varvec{p}}}:{{\varvec{q}}})\), with equality being observed only when the two sets of events are independent, thus giving non-overlapping entropy circles in Fig. 1.
The average mutual information is an example of the entropy deficiency, measuring the missing information between the joint probabilities \(\mathbf{P}({{\varvec{a}}}\wedge {{\varvec{b}}}) = {\varvec{\uppi }}\) of the dependent events \({{\varvec{a}}}\) and \({{\varvec{b}}}\), and the joint probabilities \(\mathbf{P}^{ind.}({{\varvec{a}}}^{0}\wedge {{\varvec{b}}}^{0}) = {\varvec{\uppi }}^{0} = {{\varvec{p}}}^{\mathrm{T}}{{\varvec{q}}}\) for the independent events: \(I({{\varvec{p}}}:{{\varvec{q}}}) = \Delta S( {\varvec{\uppi }}{\vert } {\varvec{\uppi }}^{0})\). The average mutual information thus reflects a dependence between events defining the two probability schemes. A similar information-distance interpretation can be attributed to the average conditional entropy: \(S({{\varvec{p}}}{\vert }{{\varvec{q}}}) = S({{\varvec{p}}}) - \Delta S({\varvec{\uppi }}{\vert }{\varvec{\uppi }}^{0})\).
5 Communication channels
We continue this short IT overview with the entropy/information descriptors of a transmission of the electron-assignment “signals” in molecular communication systems [11–13]. The classical orbital networks [3, 6, 11–13, 18] propagate probabilities of electron assignments to basis functions of SCF MO calculations, while the quantum channels [13, 33] scatter wave functions, i.e., (complex) probability amplitudes, between such elementary states. The former loose memory of the phase aspect of this information propagation, which becomes crucial in the multi-stage (cascade, bridge) propagations [28]. In determining the underlying conditional probabilities of the output-orbital events, given the input-orbital events, or the scattering amplitudes of the emitting (input) states among the monitoring/receiving (output) states, one uses the (bond-projected) superposition principle (SP) of quantum mechanics [42] (see also next section).
We begin with some rudiments on the classical information systems. The basic elements of such a “device” are shown in Fig. 2. The signal emitted from \(n\) “inputs” \({{\varvec{a}}} = (a_{1}, a_{2}, {\ldots }, a_{n})\) of the channel source A is characterized by the a priori probability distribution \({{\varvec{P}}}({{\varvec{a}}}) = {{\varvec{p}}} = (p_{1}, p_{2}, {\ldots }, p_{n})\), which describes the way the channel is exploited. It can be received at \(m\) “outputs” \({{\varvec{b}}} = (b_{1}, b_{2}, {\ldots }, b_{m})\) of the system receiver B. The transmission of signals in such communication network is randomly disturbed thus exhibiting a typical communication noise. Indeed, the signal sent at the given input can in general be received with a non-zero probability at several outputs. This feature of communication systems is described by the conditional probabilities of the outputs-given-inputs, \(\mathbf{P}({{\varvec{b}}}{\vert }{{\varvec{a}}}) = \{P(b_{j}{\vert }a_{i})=P(a_{i}\wedge b_{j})/P(a_{i}) \equiv P(j {\vert } i)\}\), where \(\{P(a_{i}\wedge b_{j})\equiv \pi _{i,j}\} = {\varvec{\uppi }}\) stands for the probability of the joint occurrence of the specified pair of the input–output events. The latter define the simultaneous probability matrix \(\{P(a_{i}\wedge b_{j})\equiv \pi _{i,j}\} ={\varvec{\uppi }}\). The distribution of the output signal among the detection events \({{\varvec{b}}}\) is thus given by the a posteriori (output) probability distribution
The input probabilities reflect the way the channel is used (probed). The Shannon entropy \(S({{\varvec{p}}})\) of the source probabilities \({{\varvec{p}}}\) determines the channel a priori entropy. The average conditional entropy of the outputs given inputs \(S({{\varvec{q}}}{\vert }{{\varvec{p}}}) \equiv H(\mathbf{B}{\vert }\mathbf{A})\) is determined by the scattering probabilities \(\mathbf{P}({{\varvec{b}}}{\vert }{{\varvec{a}}}\)). It measures the average noise in the \({{\varvec{a}}}\rightarrow {{\varvec{b}}}\) transmission. The so called a posteriori entropy, of the input given output, \(H(\mathbf{A}{\vert }\mathbf{B})\equiv S({{\varvec{p}}}{\vert }{{\varvec{q}}})\), is similarly defined by the conditional probabilities of the \({{\varvec{b}}}\rightarrow {{\varvec{a}}}\) signals: \(\mathbf{P}({{\varvec{a}}}{\vert }{{\varvec{b}}}) = \{P(a_{i}{\vert }b_{j})=P(a_{i}\wedge b_{j})/P(b_{j})=P(i{\vert }j)\}\). It reflects the residual indeterminacy about the input signal, when the output signal has already been received. The average conditional entropy \(S({{\varvec{p}}}{\vert }{{\varvec{q}}})\) thus measures the indeterminacy of the source with respect to the receiver, while the conditional entropy \(S({{\varvec{q}}}{\vert }{{\varvec{p}}})\) reflects the uncertainty of the receiver relative to the source. An observation of the output signal thus provides on average the amount of information given by the difference between the a priori and a posteriori uncertainties, \(S({{\varvec{p}}}) - S({{\varvec{p}}}{\vert }{{\varvec{q}}}) = I({{\varvec{p}}}:{{\varvec{q}}})\), which defines the mutual information in the source and receiver. In other words, the mutual information measures the net amount of information transmitted through the communication channel, while the conditional entropy \(S({{\varvec{p}}}{\vert }{{\varvec{q}}})\) reflects a fraction of \(S({{\varvec{p}}})\) transformed into “noise” as a result of the input signal being scattered in the information channel. Accordingly, \(S({{\varvec{q}}}{\vert }{{\varvec{p}}})\) reflects the noise part of \(S({{\varvec{q}}}) = S({{\varvec{q}}}{\vert }{{\varvec{p}}}) + I({{\varvec{p}}}:{{\varvec{q}}})\) (see Fig. 1).
Schematic diagram of the communication system characterized by two probability vectors: \({{\varvec{P}}}({{\varvec{a}}}) = \{P(a_{i})\} = {{\varvec{p}}} = (p_{1}, {\ldots }, p_{n})\), of the channel “input” events \({{\varvec{a}}} = (a_{1}, {\ldots }, a_{n})\) in the system source A, and \({{\varvec{P}}}(\mathbf{b }) = \{P(b_{j})\} = {{\varvec{q}}} = (q_{1}, {\ldots }, q_{m})\), of the “output” events \({{\varvec{b}}} = (b_{1}, {\ldots }, b_{m})\) in the system receiver B. The transmission of signals in this communication channel is described by the (\(n\times m\))-matrix of the conditional probabilities \(\mathbf{P}({{\varvec{b}}}{\vert }{{\varvec{a}}}) = \{P(b_{j}{\vert }a_{i})\equiv P(j{\vert }i)\}\), of observing different “outputs” (columns, \(j = 1, 2, {\ldots }, m)\), given the specified “inputs” (rows, \(i = 1, 2, {\ldots }, n\)). For clarity, only a single scattering \(a_{i} \rightarrow b_{j}\) is shown in the diagram
In OCT the orbital channels [3, 6, 11–13] propagate probabilities of electron assignments to basis functions of SCF MO calculations, e.g., atomic orbitals (AO) \({\varvec{\chi }} = (\chi _{1}, \chi _{2}, {\ldots }, \chi _{m})\). The underlying conditional probabilities of the output AO events, given the input AO events, \(\mathbf{P}({\varvec{\chi }}'{\vert }{\varvec{\chi }}) = \{P(\chi _{j}{\vert }\chi _{i})\equiv P(j{\vert }i) \equiv P_{i\rightarrow j } \equiv A(j{\vert }i)^{2}\equiv (A_{i\rightarrow j})^{2}\}\), or the associated scattering amplitudes \(\mathbf{A}({\varvec{\chi }}'{\vert }{\varvec{\chi }}) = \{A(j{\vert }i) = A_{i\rightarrow j}\}\) of the emitting (input) states \({{\varvec{a}}} = {\vert }{\varvec{\chi }}\rangle = \{{\vert }\chi _{i}\rangle \}\) among the monitoring/receiving (output) states \({{\varvec{b}}} = {\vert }{\varvec{\chi }}'\rangle = \{{\vert }\chi _{j}\rangle \}\), results from the (bond-projected) SP of quantum mechanics [42]. The local description (LCT) similarly invokes the basis functions \(\{{\vert }{{\varvec{r}}}\rangle \}\) of the position representation, identified by the continuous labels of spatial coordinates determining the location \({{\varvec{r}}}\) of an electron. This complete basis set then determines both the input \({{\varvec{a}}} = \{{\vert }{{\varvec{r}}}\rangle \}\) and output \({{\varvec{b}}} = \{{\vert }{{\varvec{r}}}'\rangle \}\) events of the local molecular channel determined by the relevant kernel of conditional-probabilitities: \(P({{\varvec{r}}}'{\vert }{{\varvec{r}}})= P_{{{\varvec{r}}}\rightarrow {{\varvec{r}}}^{\prime }}= (A_{{{\varvec{r}}}\rightarrow {{\varvec{r}}}^{\prime }})^{2}\) [43].
In OCT the entropy/information indices of the covalent/ionic components of the system chemical bonds respectively represent the complementary descriptors of the average communication noise and amount of information flow in the molecular channel. One observes that the molecular input \({{\varvec{P}}}({{\varvec{a}}}) \equiv {{\varvec{p}}}\) generates the same distribution in the output of this network, \({{\varvec{q}}} = {{\varvec{p}}}\, \mathbf{P}({{\varvec{b}}}{\vert }{{\varvec{a}}}) = \{\sum _{i} p_{i }\,P(j{\vert }i)\equiv \sum _{i }P(i\wedge j)=p_{j}\} = {{\varvec{p}}}\), thus identifying \({{\varvec{p}}}\) as the stationary vector of AO-probabilities in the molecular ground state. This purely molecular communication channel is devoid of any reference (history) of the chemical bond formation and generates the average noise index of the IT bond-covalency measured by the average conditional-entropy of the system outputs-given-inputs: \(S({{\varvec{P}}}({{\varvec{b}}}){\vert }{{\varvec{P}}}({{\varvec{a}}})) = S({{\varvec{q}}}{\vert }{{\varvec{p}}}) \equiv S\).
The AO channel with the promolecular input signal, \({{\varvec{P}}}({{\varvec{a}}}_{0}) = {{\varvec{p}}}_{0}=\{p_{i}^{0}\}\), of AO in the system free constituent atoms, refers to the initial stage in the bond-formation process. It corresponds to the ground-state (fractional) occupations of the AO contributed by the system constituent atoms, before their mixing into MO. These input probabilities give rise to the average information flow index of the system IT bond-ionicity, given by the mutual-information in the channel promolecular inputs and molecular outputs:
This amount of information reflects the fraction of the initial (promolecular) information content \(S({{\varvec{p}}}_{0})\) which has not been dissipated as noise in the molecular communication system. In particlular, for the molecular input, when \({{\varvec{p}}}_{0}= {{\varvec{p}}}\) and hence the vanishing information distance \(\Delta S({{\varvec{p}}}{\vert }{{\varvec{p}}}_{0})\),
The sum of these two bond components, e.g.,
measures the absolute overall IT bond-multiplicity index, of all bonds in the molecular system under consideration, relative to the promolecular reference. For the molecular input this quantity preserves the Shannon entropy of the molecular input probabilities:
The relative index [43],
reflecting multiplicity changes due to the chemical bonds alone, is then interaction dependent. It correctly vanishes in the atomic dissociation limit of separated atoms, when \({{\varvec{p}}}_{0}\) and \({{\varvec{p}}}\) become identical. The entropy deficiency index \(S({{\varvec{p}}}{\vert }{{\varvec{p}}}_{0})\), reflecting the information distance between the molecular electron density, generated by the constituent bonded atoms, thus represents the overall IT difference-index of the system chemical bonds.
6 Superposition principle, conditional probabilities and non-additive quantities
Let us recall SP of quantum mechanics [42]:
Any combination \({\vert }\psi \rangle = \sum _{k} C_{k}{\vert }\psi _{k}\rangle \) of the admissible (orthonormal) quantum states \(\{{\vert }\psi _{k}\rangle \}\), where the set \(\{C_{k}=\langle \psi _{k}{\vert }\psi \rangle \}\) denotes generally complex expansion coefficients, also represents a possible quantum state of the system under consideration. The projections determining the expansion coefficients represent quantum amplitudes \(\{C_{k }=A(\psi _{k}{\vert }\psi ) = \langle \psi _{k}{\vert }\psi \rangle \}\) of the conditional probabilities
of observing \({\vert }\psi _{k}\rangle \) given \({\vert }\psi \rangle \). For the complete (variable) set \(\{{\vert }\psi _{k}\rangle \}\), when \(\sum _{k}{\vert }\psi _{k}\rangle \langle \psi _{k}{\vert } \equiv \sum _{k}\hat{\mathrm{P}}_k = 1\), these probabilities are normalized:
This axiom formally introduces the conditional probabilities between the specified quantum states, of observing the variable (monitoring) state \({\vert }\psi _{k}\rangle \) given the reference (parameter) state \({\vert }\psi \rangle \), which define the associated molecular communications. They are given by the expectation value in the variable state of the projection operator onto the reference state.
Let us now examine the time evolution of the representative conditional probability of observing \({\vert }\theta (t)\rangle \) given \({\vert }\psi (t)\rangle , P[\theta (t){\vert }\psi (t)] = \langle \theta (t)\vert \hat{\mathrm{P}}_{\psi }(t)\vert \theta (t)\rangle \). In the Schrödinger picture of quantum mechanics the dynamics of quantum states is governed by the system energy operator \(\hat{\mathrm{H}}\):
This Schrödinger equation then gives the following expression for the time derivative of the conditional probability \(P[\theta (t){\vert }\psi (t)]\) in question:
Therefore, the conditional probabilities between general quantum states, which determine the associated information channels, remain conserved in time and so do their entropic descriptors of the bond multiplicity and composition.
The amplitude \(A(\psi _{k}{\vert }\psi )\) preserves the relative phase of the two states involved, which is responsible for the quantum-mechanical interference. As an illustration consider the two (complex, orthonormal) basis states:
in the combined molecular state
Expressing the probability density \(P = {\vert }\psi {\vert }^{2}\) in terms of probabilities \(\{p_{k} = {\vert }\psi _{k}{\vert }^{2}= R_{k}^{2 }=p[\psi _{k}]\}\) and phases \(\{\phi _{k}\}\) of two individual states in this combination gives the familiar result:
It identifies the superposition term \(p_{\varvec{\psi }}^{nadd.} \), depending upon the relative phase \(\phi _{rel.} = \phi _{1 }-\phi _{2 }\) of two functions in the combined state, as the non-additive probability contribution,
expressed as the difference between the total probability in \(\psi \)-resolution,
and its additive contribution given by the weighted average of probability distributions of individual states,
In accordance with the SP, the probability “weights” in the preceding equation are provided by the squares of the combination coefficients, which define the relevant conditional probabilities \(P(\psi _{1}{\vert }\psi )=P(\psi _{2}{\vert }\psi ) = 1/2\):
The probability interference term
is responsible for the direct chemical bond, say between two hydrogens, when the two (orthogonalized) 1\(s\) AO’s of constituent atoms are mixed into the symmetric (doubly occupied) bonding MO. Clearly, for the real AO case, when \(\phi _{1 }=\phi _{2} = 0\), this contribution reduces into the geometric average of probability densities of the two components: \(p_{\varvec{\psi }}^{nadd.} =\sqrt{p_1 p_2 }\). It should be also observed that the overall probability \(p\) determines the resultant modulus factor \(R =\sqrt{p}\) of \(\psi =R \exp (\hbox {i}\varPhi )\), while its resultant phase follows from equation:
Of interest also is the related partitioning of the probability-current density in this combined state, into the corresponding additive and non-additive contributions [33]:
where bars denote the reduced quantities:
This interference contribution to the resultant flow of probability density again depends on the relative phases of the two states combined. For real member functions, for which the relative phase and currents identically vanish, the above additive and non-additive flows of the electron probability are both seen to identically vanish.
In a similar way one partitions other physical quantities, which generally depend on both \(p\) and \({{\varvec{ j}}}\) (or \(\varPhi )\). Consider, e.g., the quantum extension of the gradient measure of the information content in state \(\psi \) [Eq. (21)]:
where the classical Fisher functional \(I^{class.}[\psi ] = I[p]\) combines the contribution due to the probability distribution alone, while the non-classical functional \(I^{nclass.}[\psi ] = I[p, {{\varvec{j}}}] = I[p, \varPhi \)] carries the current(phase)-dependent information content.
Let us examine the superposition rule for the density \(f({{\varvec{r}}})\) of this quantum-generalized Fisher-information [32] in the combined state \(\psi \),
proportional to the squared modulus of the wave function gradient:
This information density defines the total local contribution in the adopted \({\varvec{\psi }}\)-resolution, \(f_{\varvec{\psi }} ^{total} \equiv f[\psi ]\), while the weighted sum of the information content of the two individual states determines its additive contribution:
The information density \(f_{k }\) in the complex member-state \(\psi _{k}\) similarly reads:
where \({{\varvec{j}}}_{k} \equiv {{\varvec{j}}}[\psi _{k}]\) denotes the probability-current density in \(\psi _{k}\):
The non-additive (interference) information density, determined by both the probability amplitudes and phases of the two combined states, now reads:
It again depends on the relative phase of two constituent states. This expression somewhat simplifies, when formulated in terms of the probability and current descriptors \(\{p_{k}, {{\varvec{j}}}_{k}\}\) of individual states. More specifically, eliminating \(\nabla \psi _{k}\) from \(\nabla p_{k}=\psi _{k}\nabla \psi _{k}^{*}+\psi _{k}^{*}\nabla \psi _{k}\) and Eq. (69),
gives:
This equation expresses the change in the quantum Fisher information density, relative to the reference level of the additive contribution of Eq. (67), which accompanies the quantum-mechanical superposition of two individual states in the combination of Eq. (56).
For the stationary member states, when the current-dependent contributions identically vanish, e.g., when combining two real AO into MO, this information contribution is seen to be solely determined by the product of the reduced gradients of the particle probability distributions in the combined state. It is then related to the non-additive kinetic energy in AO resolution [11–13, 44], which has been successfully employed as an efficient CG criterion for localizing chemical bonds in molecular systems [44]. The related quantity in MO resolution [45] generates the key concept of ELF [46–48].
7 Phase relations in two-orbital model
In order to examine the phase aspect of orbital superposition and orbital communications in a more detail we examine the 2-AO model of the preceding section, with each of the complex basis functions \({\varvec{\psi }}({{\varvec{r}}}) = [\psi _{1}({{\varvec{r}}}), \psi _{2}({{\varvec{r}}})]\) of the promolecular reference again contributing a single electron to this model two-electron system. These complex AO give rise to two MO: bonding,
and anti-bonding,
In a more compact, matrix notation, with \({\varvec{ \varphi }}({{\varvec{r}}}) = [\varphi _{b}({{\varvec{r}}}), \varphi _{a}({{\varvec{r}}})]\) grouping the orthonormal MO combinations, the preceding equations jointly read:
These MO now combine the complex AO,
where we again assume their spatial orthonormality:
Hence, MO-orthonormality condition implies the unitary character of the (complex) transformation matrix U:
The MO combinations can be similarly expressed in terms of their resultant moduli and phases:
The complementary conditional probabilities,
determining weights of AO in MO, also reflect the bond polarization, when two spin-paired electrons occupy \(\varphi _{b}\).
In terms of these resultant components the MO-orthonormality condition reads:
The two diagonal (normalization) requirements are seen to be automatically satisfied by the normalization of the complementary conditional probabilities of Eq. (79):
In order to satisfy the MO-orthogonality equation, e.g., \(\langle \varphi _{a}{\vert }\varphi _{b}\rangle = 0\), the resultant MO phases have to obey the off-diagonal constraint
This equation is automatically fullfilled for the vanishing modulus \(Z\) of this scalar product or its square
Hence, the MO-orthogonality constraint imposes the following requirement to be satisfied by phases \(\mathbf{f} = \{f_{k,s}\}\) of the complex LCAO MO coefficients U [Eq. (78)]:
In other words, the differences between phases of the expansion coefficients multiplying the two basis functions in the bonding and anti-bonding MO combinations, respectively, determine the opposite directions in the complex plane. The preceding equation can be also interpreted in terms of the opposite directions corresponding to differences between phases of the expansion coefficients in the same MO:
Yet another interpretation of this phase relation involves the cross-phase sums, \(\vartheta _{2,1}\equiv f_{2,b}+f_{1,a}\) and \(\vartheta _{1,2}\equiv f_{1,b}+f_{2,a}\),
For example, in the real AO case, for \({\varvec{\psi }} = {\varvec{ \chi }}\), the LCAO MO coefficients
correspond to the following modulus and phase parts of Eq. (78):
In accordance with Eqs. (84)–(86) they determine the opposite phase differences:
and sums:
8 Molecular communications
Let us now turn to the conditional probabilities between AO events in molecules. For simplicity we focus on the probability and amplitude channels in a single electron configuration; for the multi-configuration extension the reader is referred to refs. [33, 43]. An exploration of the chemical bond system in the given ground-state of a molecule indeed calls for the AO resolution determined by the basis functions \({\varvec{\chi }} = (\chi _{1}, \chi _{2}, {\ldots }, \chi _{m})\) of typical (HF or KS) SCF calculations. They express the bonding subspace of the singly occupied SMO,
which define the molecular ground-state \(\Psi (N)\) given by the Slater determinant consisting of \(N\)-lowest SMO:
Here \(\varphi _{k}({{\varvec{r}}})\) denotes the spatial function (MO) and \(\zeta _{k }= \{\alpha (\hbox {spin-}\textit{up}) \, \hbox {or} \, \beta (\hbox {spin-}\textit{down})\}\) stands for one of the two admissible spin states of an electron [see Eq. (9)].
In this simplest orbital approximation one thus takes into account only the physical (bond) subspace \({\varvec{\varphi }}\) of the configuration occupied MO, which defines the associated MO projector \(\hat{\mathrm{P}}_{\varvec{\varphi }} \equiv {\vert }{\varvec{\varphi }} \rangle \langle {\varvec{\varphi }}{\vert }\). It gives rise to the (idempotent) charge and bond-order (CBO) one-electron density matrix in AO representation,
where we have used the AO orthonormality, \(\langle {\varvec{\chi }}{\vert }{\varvec{\chi }}\rangle = \mathbf{I}_{m}\), and that of the occupied MO expanded in this basis, \(\langle {\varvec{\varphi }}|{\varvec{\chi }}\rangle \langle {\varvec{\chi }}{\vert }{\varvec{\chi }}\rangle \langle {\varvec{\chi }}{\vert }{\varvec{\varphi }}\rangle = \mathbf{C}^{\dagger }\mathbf{C} = \mathbf{I}_{N}\), which further implies
The molecular joint probabilities of the given pair of the input–output AO in the bond system determined by \({\varvec{\varphi }}\) are then proportional to the square of the corresponding CBO matrix element:
The conditional probabilities between AO, \(\mathbf{P}({\varvec{{\varvec{\chi }}}}'{\vert } {\varvec{{\varvec{\chi }}}}) = \{P(j {\vert }i)=P(i \wedge j)/p_{i}\}\),
reflect the electron delocalization in this MO system and identify the associated scattering amplitudes \(\mathbf{A}( {\varvec{\chi }}'\mathbf{{\vert }}{\varvec{\chi }}) = \{A(j\mathbf{{\vert }}i)=A_{i \rightarrow j}\}\):
These amplitudes for the ground-state probability propagation are thus related to the corresponding elements of the CBO matrix \({\varvec{\upgamma }}=\left\langle {\varvec{\chi }} \right| \hat{\mathrm{P}}_{\varvec{\varphi }} \left| {\varvec{\chi }} \right\rangle \), the AO representation of the ground-state occupied SMO projector \(\hat{\mathrm{P}}_{\varvec{\varphi }}\).
In the closed-shell state, when the occupied spatial MO accommodate two spin-paired electrons each, the ground state is generated by the \(N\)/2 lowest MO, \({\varvec{\varphi }}^{o} = (\varphi _{1}, \varphi _{2}, {\ldots }, \varphi _{N/2}) ={\varvec{\chi }}\mathbf{C}^{o}\),
and \(\hat{\mathrm{P}}_{\varvec{\varphi }} = {\vert } {\varvec{\varphi }}\rangle \langle {\varvec{\varphi }}{\vert } = 2{\vert } {\varvec{\varphi }}^{o}\rangle \langle {\varvec{\varphi }}^{o}\equiv 2\hat{\mathrm{P}}_{\varvec{\varphi }}^o\); hence, the SMO idempotency then implies \((\hat{\mathrm{P}}_{\varvec{\varphi }})^{2} = [2{\vert }{\varvec{\varphi }}^{o}\rangle \langle {\varvec{\varphi }}^{o}{\vert }]^{2} = 4{\vert } {\varvec{\varphi }}^{o}\rangle \langle {\varvec{\varphi }}^{o}{\vert } = 2\hat{\mathrm{P}}_{\varvec{\varphi }}\) and [see Eqs. (91) and (92)]
For such molecular states the representative conditional probability of the molecular AO channel reads [12, 13]:
Here, \(N_{i}^{o} = (\gamma _{i,i}^{o})^{-1}\) stands for the multiplicative constant required to satisfy the appropriate normalization condition:
where we have used the assumed closed-shell idempotency of Eq. (97). In Eq. (98) the \(i \rightarrow j\) probability scattering has been expressed as the expectation value in the input \(\hbox {AO}\,\chi _{{i}}\) of the communication operator to the specified output AO \(\chi _{j}, \hat{{\tilde{P}}}_j^o \equiv \hat{\mathrm{P}}_{\varvec{\varphi }}^o \hat{\mathrm{P}}_j \hat{{P}}_{\varvec{\varphi }}^o\).
It should be again stressed that the classical, probability-channel determined by the conditional probabilities of the output AO-events \({\varvec{\chi }}\)’ given the input AO-events \({\varvec{\chi }}\), \(\mathbf{P} ({\varvec{\chi }}'{\vert } {\varvec{\chi }}) = \{P(j {\vert }i)= P_{i\rightarrow j}\}\), which in short notation reads
losses memory about phases of the scattering amplitudes \(\{A_{i \rightarrow j}\}\), which are preserved in the associated amplitude-channel defined by the direct communications \(\mathbf{A}({\varvec{\chi }}'{\vert }{\varvec{\chi }}) = \{A(j{\vert }i)=A_{i\rightarrow j}\}\):
This observation also applies to the sequential (product) arrangements of several such (direct) channels, called “cascades”, for the indirect (bridge) communications between orbitals in molecules, since the modulus of the product of complex functions is given by the product of the moduli of its factors. For example, the single-AO intermediates \({\varvec{\chi }}\)” in the sequential three-orbital scatterings \({\varvec{\chi }} \rightarrow {\varvec{\chi }}''\rightarrow {\varvec{\chi }}\)’ define the following probability and amplitude cascades:
The associated (indirect) conditional probabilities between AO-events and their amplitudes are then given by products of the corresponding elementary two-orbital communications in each (direct) sub-channel:
Therefore, such bridge probabilities can be straightforwardly derived from the direct probability and amplitude channels. They satisfy the relevant bridge-normalization sum-rules over the final and intermediate output AO events:
This single-cascade development can be straightforwardly generalized to any bridge order. Consider the sequential \(t\)-cascade involving all basis functions at each propagation stage. Let us examine the resultant amplitudes, \(\mathbf{A}[( {\varvec{\chi }}'{\vert } {\varvec{\chi }}); t- {\varvec{\chi }}] = \{A_{i\rightarrow j}^{(t)}\}\), and probabilities, \(\mathbf{P}[({\varvec{\chi }}'{\vert } {\varvec{\chi }}); t\!-\!{\varvec{\chi }}] = \{{\vert }A _{i\rightarrow j}^{(t)}{\vert }^{2}\}\), of the multiple scatterings in the \(t\)-stage bridge involving sequential cascades via \(t\)-AO intermediates (orbital bridges) (\(k, l, {\ldots }, m, n)\), e.g., in the amplitude channel [31]:
Such \(t\)-cascade amplitudes \(\mathbf{A}[( {\varvec{\chi }}'{\vert }{\varvec{\chi }}); t-{\varvec{\chi }}] = \{A_{i\rightarrow j;k,l,\ldots ,m,n} \equiv A_{i\rightarrow j}^{(t)}\}\) are proportional to the corresponding matrix element of the (\(t+1\))-power of the (idempotent) projector onto the occupied SMO subspace,
where we have again used the idempotency property of the SMO projector \(\hat{\mathrm{P}}_{\varvec{\psi }}: (\hat{\mathrm{P}}_{\varvec{\psi }})^{n}=\hat{\mathrm{P}}_{\varvec{\psi }}\).
Hence, the amplitude \(A_{i\rightarrow j}^{(t)}\) for the complete consecutive \(t\)-cascade preserves the direct-scattering probabilities,
thus satisfying the important consistency requirement of the stationary molecular channel [30, 31]. It also obeys the relevant bridge-normalization sum-rules:
For the specified pair of the “terminal” AO, say \(\chi _{i}\in {\varvec{\chi }}\) and \(\chi _{j } \in {\varvec{\chi }}'\), one can similarly examine the indirect scatterings in the molecular bond system, via the incomplete cascades consisting of the remaining (“bridge”) functions \({\varvec{\chi }} ^{b} = \{{\varvec{\chi }}_{k\ne (i,j)}\}\), with the two terminal AO being then excluded from the set of admissible intermediate scatterers. The associated bridge-communications give rise to the indirect (through-bridge) components of bond multiplicities [28–32], which complement the familiar direct (through-space) chemical “bond-orders” [49–59] and provide a novel IT perspective on chemical interactions between more distant AIM, alternative to the fluctuational charge-shift mechanism [60].
9 Vertical equilibrium principles
The IT (entropic) representation in the theory of molecular electronic structure provides a thermodynamic-like outlook on molecular equilibria [16, 17]. A generally complex probability amplitudes in the molecular quantum mechanics, the system electronic wave functions, require generalized information measures of Sect. 3, which combine the classical and non-classical contributions, due to the particle probability and current (or phase) distributions, respectively. Let us briefly comment on the density-constrained (“vertical”) variational principles for these quantum information functionals [17], which closely resemble their familiar entropy and energy analogs in the ordinary thermodynamics [23]. By the Hohenberg–Kohn (HK) [35] theorem, the conserved values of the system ground-state energy or classical entropy in these searches, are exactly determined by the corresponding DFT functionals of the system ground-state electron density \(\rho _{0}({{\varvec{r}}}) = { Np}_{0}({{\varvec{r}}})\). It also fixes other classical measures of the state information content. Therefore, these “vertical” principles for determining molecular equilibria, for the fixed ground-state distribution of electrons, involve only displacements in the non-classical entropy/information complements, functionals of the system current/phase.
In Sect. 3 the non-classical information contributions for the constrained probability density \(p_{0}({{\varvec{r}}})\), in a trial state of a single particle [Eq. (12)], were shown to be given by the following functionals of the spatial phase function \(\phi ({{\varvec{r}}})\):
where \({{\varvec{j}}}_{0}[\phi ] \equiv {{\varvec{j}}}[p_{0},\phi ]\). The sign of the non-classical entropy term has been chosen to guarantee the maximum value \(S[p_{0},\phi =0]\) at the exact ground-state solution, when the spatial phase vanishes, for which the complementary non-classical Fisher information reaches its minimum value \(I[p_{0}, \phi = 0]=0\).
The combined classical and non-classical contributions determine the associated resultant entropy/information content of general (variational) quantum states:
The ground-state equilibrium of a molecule then alternatively results either from the entropy-constrained principle for the system minimum-energy, or from the energy-constrained searches for the maximum of the non-classical Shannon entropy or the minimum of the non-classical Fisher information [16, 17].
It should be realized that general (trial) states of such entropic rules generally imply non-vanishing contributions from both the classical (probability) and non-classical (phase-current) functionals of the entropy/information content. Only in the final, exact (stationary) ground-state, which exhibits purely time-dependent phase, the state information is measured by the corresponding classical measure, since then the space-dependent part of the wave-function phase, responsible for the current distribution, exactly vanishes.
As an illustration consider again a single particle moving in an external potential \(v({{\varvec{r}}})\) due to the fixed nuclei (Born–Oppenheimer approximation), described by the Hamiltonian
in the complex variational state \(\varphi ({{\varvec{r}}}) = R({{\varvec{r}}}) \exp [\hbox {i}\phi ({{\varvec{r}}})]\). In the non-degenerate ground state the lowest-energy amplitude eigenfunction of the Hamiltonian is then described solely by the modulus factor: \(\varphi _{0}=R_{0}\). It specifies the equilibrium probability distribution \(p_{0}=R_{0}^{2}\), while the exactly vanishing spatial phase \(\phi _{0} = 0\) implies the vanishing current density in this stationary molecular state: \({{\varvec{j}}}_{0}({{\varvec{r}}}) = (\hbar /m) p_{0 }\nabla \phi _{0} = {{\varvec{0}}}\).
Let us examine the modulus-constrained (vertical) search for the unknown phase function in the trial state \(\varphi ^{0}({{\varvec{r}}}) = R_{0}({{\varvec{r}}}) \exp [\mathrm{i}\phi ({{\varvec{r}}})]\), where \(R_{0}({{\varvec{r}}}) = [p_{0}({{\varvec{r}}})]^{1/2}\), for the conserved classical (phase-independent) entropy \(S^{class.}[\psi _{0}] = S[p_{0}]\) in the system exact ground-state, which also marks the vanishing spatial phase, \(\phi =\phi _{0}= 0\). The corresponding expression for the expectation value of the system energy in this probability-constrained state reads:
Its phase-minimum principle recovers the familiar (classical) DFT energy expression:
The optimum solution \(\phi _{0} = 0\) marks the maximum of the quantum entropy, \(S[p_{0}, \phi _{0}\)] = 0, and the minimum of the associated (density-constrained) non-classical Fisher information \(I[p_{0}, \phi _{0}] = 0\). This eigenstate solution indeed corresponds exclusively to the classical measures of the entropy/information content: \(S[\varphi _{0}] = S[p_{0}]\) and \(I[\varphi _{0}] = I[p_{0}]\).
This optimum solution of the maximum quantum entropy also implies the minimum of the associated (density-constrained) quantum Fisher information:
Therefore, the phase component, vital for identifying the trial (vertical) functions, identically vanishes for the exact phase \(\phi _{0}= 0\) of the ground state. Notice, that only then the classical DFT functionals of the system electron density can be used to predict the state average energy and the information content of this stationary electron distribution.
We have thus arrived at a remarkable parallelism with the ordinary thermodynamics [23]: the ground-state equilibrium results from the equivalent vertical (density-constrained) variational principles: either for the system minimum energy, at the constrained ground-state entropy \(S[p_{0}\)] or the classical information \(I[p_{0}\)], or—alternatively—for the extremum entropy/information, at the constrained ground-state energy \(E_{v}[p_{0}\)]. One has to use the quantum measures of the system information content, in order to distinguish the phase/current composition of the trial (vertical) states. The evolution of such entropic search is then properly described by the current shape of the phase function, which ultimately vanishes in the optimum ground-state solution.
Consider next a general case of a trial quantum state of \(N\) electrons, \(\Psi (N)\), corresponding to the fixed ground-state electron density \(\rho = \rho _{0} = Np_{0}\). The energy variational principle now involves a search for the optimum (normalized) wave function, which minimizes the expectation value of the electronic Hamiltonian
where \(\hat{\mathrm{F}}(N)\) combines the electron kinetic [\(\hat{\mathrm{T}}(N)\)] and repulsion [\(\hat{\mathrm{V}}_{ee} (N)\)] energy operators of \(N\) electrons. One recalls that the “entropic” interpretation has been also attributed previously [11, 13], to the density-constrained principles of the modern DFT, in searches performed for the specified electron density \(\rho \). For example, in Levy’s [36] constrained-search one defines the universal part of the density functional for the system electronic-energy, which admitts non \(-\)(\(v\)-representable) densities, by the following (vertical) variational principle,
here, one searches over wave functions which yield the given electron density \(\rho \), symbolically denoted by \(\Psi \!\!\rightarrow \!\!\rho \), and calculates the universal (\(v\)-independent) part \(F[\rho ]\) of the density functional for the system electronic energy,
as the lowest value (infimum) of the quantum expectation value of \(\hat{\mathrm{F}}(N)\). When this search is performed for the fixed ground-state density, \(\rho =\rho _{0}\), it also implies the fixed DFT value of the system electronic energy, by the first HK theorem [35]. This feature is thus reminiscent of the thermodynamic criterion for determining the equilibrium state formulated in the entropy representation. By analogy to the maximum-entropy principle for constant internal energy in the phenomenological thermodynamics, this DFT construction can be thus regarded as being also “entropic” in character [11].
It should be emphasized that the variational principle for determining the ground-state wave function, involving the constrained search for the minimum of the system energy, can be also interpreted as the DFT optimization over all admissible densities, in accordance with the second HK theorem [35]. It combines the external (“horizontal”) search, over trial electron densities, and the internal (vertical) search, over wave functions of \(N\) fermions that yield the current density of the external search:
Let us focus on the vertical (internal) optimization in the preceding equation. It corresponds to the fixed ground-state electron density, say, \(\rho =\rho _{0 }=\rho [v]\), identified in the (external) horizontal search. The internal, quantum-entropy rule thus involves the energy-constrained search over \(\Psi \rightarrow \rho _{0}\) for the optimum wave function \(\Psi [\rho _{0}\)] corresponding to the fixed, matching external potential \(v=v\rho _{0}]\) due to the “frozen” nuclei:
One observes the presence of Levy’s functional \(F[\rho _{0}\)] as the crucial (entropic) part of this extremun principle of the system physical information. Notice, that the external potential and electron-repulsion energies are fixed by the frozen-density constraint so that the optimum state also marks the infimum \(I[\rho _{0}] = I[\varphi _{0}\)] of the quantum Fisher measure of the information in the trial (vertical) wave functions, related to the system average kinetic energy \(T[\rho _{0}\)].
10 Conclusion
The quantum-generalized information measures and their vertical variation principles have been examined. This analysis of molecular equilibria has stressed the need for using the resultant information measures, which take into account both the classical and quantum contributions, due to the electronic probability and current (phase) distributions, respectively. The non-classical generalization of the gradient (Fisher) information introduces the information contribution due to the probability current. The proposed quantum-generalized Shannon entropy includes the additive contribution due to the average magnitude of the state phase. This extension has been accomplished by requesting that the relation between the classical Shannon and Fisher information densities-per-electron extends into their non-classical (quantum) analogs. A similar generalization of the information-distance (entropy-deficiency) concept for comparing spatial probability/current distributions has also been proposed in both the Shannon cross-entropy and Fisher missing-information representations.
These quantum-information terms complement the classical Fisher and Shannon measures, functionals of the particle probability distribution alone. The resultant quantum measures are thus capable to extract the full information content of the complex probability amplitudes (wave functions), due to both the probability and current distributions. Elsewhere, the associated continuity equations have been examined, the non-classical information sources, linked to the wave function phase or the probability-current densities, have been identified and the phase-current density has been introduced, which complements the familiar probability-current concept in quantum mechanics [10–13].
As in the ordinary thermodynamics, the equilibrium ground state of a molecule was shown to alternatively result either from the (entropy/information)-constrained principle for the system minimum energy, or from the energy-constrained search for the extremum of the information content: either the maximum of the non-classical Shannon entropy or the minimum of the quantum Fisher information. By the HK theorem the ground-state values of the density/probability functionals for the system energy and its entropy/information content uniquely identify the equilibrium distribution of electrons. Therefore, in vertical searches carried for this fixed electron density, the vanishing spatial phase and probability current in the non-degenerate ground-state, are both determined by the variational principles of the non-classical entropy/information contributions, for the fixed values of the corresponding classical terms. The spatial-phase aspect identifies the trial function in this density-constrained (vertical) searches, and it ultimately vanishes in the final non-degenerate ground-state solution.
The SP of quantum mechanics introduces the conditional probabilities between quantum states, which generate a network of molecular communications. The non-additive contributions to probability/current distributions and information densities have been identified and the phase relations in two-orbital model have been examined. The OCT of the chemical bond introduces the molecular information system transmitting “signals” of electron allocations to AO states, which define the set of elementary electronic events. The conditional probabilities between these basis functions, propagated via the network of the occupied molecular orbitals, determine the orbital communications in molecules, which are generated by the bond-projected SP. In the SCF MO theory their amplitudes are related to the corresponding elements of the CBO matrix. The standard conditional-entropy and mutual-information descriptors of this orbital network provide useful indices of the IT covalency and ionicity.
References
R.A. Fisher, Proc. Cambridge Phil. Soc. 22, 700 (1925)
B.R. Frieden, Physics from the Fisher Information - A Unification, 2nd edn. (Cambridge University Press, Cambridge, 2004)
C.E. Shannon, Bell System Tech. J. 27, 379, 623 (1948)
C.E. Shannon, W. Weaver, The Mathematical Theory of Communication (University of Illinois, Urbana, 1949)
S. Kullback, R.A. Leibler, Ann. Math. Stat. 22, 79 (1951)
S. Kullback, Information Theory and Statistics (Wiley, New York, 1959)
N. Abramson, Information Theory and Coding (McGraw-Hill, New York, 1963)
P.E. Pfeifer, Concepts of Probability Theory, 2nd edn. (Dover, New York, 1978)
R.F. Nalewajski, J. Math. Chem. 51, 297 (2013)
R.F. Nalewajski, Entropic concepts in electronic structure theory. Found. Chem. doi:10.1007/s10698-012-9168-7
R.F. Nalewajski, Information Theory of Molecular Systems (Elsevier, Amsterdam, 2006)
R.F. Nalewajski, Information Origins of the Chemical Bond (Nova, New York, 2010)
R.F. Nalewajski, Perspectives in Electronic Structure Theory (Springer, Heidelberg, 2012)
R.F. Nalewajski, in Frontiers in Modern Theoretical Chemistry: Concepts and Methods (Dedicated to B. M. Deb), ed. by P.K. Chattaraj, S.K. Ghosh (Taylor & Francis/CRC, London, 2013), pp. 143–180
R.F. Nalewajski, Struct. Bond. 149, 51 (2012)
R.F. Nalewajski, J. Math. Chem. 51, 369 (2013)
R.F. Nalewajski, Ann. Phys. (Leipzig) 525, 256 (2013)
R.F. Nalewajski, J. Phys. Chem. A 104, 11940 (2000)
R.F. Nalewajski, J. Phys. Chem A 107, 3792 (2003)
R.F. Nalewajski, Mol. Phys. 104, 255 (2006)
R.F. Nalewajski, Ann. Phys. Leipzig 13, 201 (2004)
R.F. Nalewajski, R.G. Parr, J. Phys. Chem A 105, 7391 (2001)
H.B. Callen, Thermodynamics: An Introduction to the Physical Theories of the Equilibrium Thermostatics and Irreversible Thermodynamics (Wiley, New York, 1960)
R.F. Nalewajski, Adv. Quant. Chem. 56, 217 (2009)
R.F. Nalewajski, D. Szczepanik, J. Mrozek, Adv. Quant. Chem. 61, 1 (2011)
R.F. Nalewajski, D. Szczepanik, J. Mrozek, J. Math. Chem. 50, 1437 (2012)
R.F. Nalewajski, J. Math. Chem. 47, 692, 808 (2010)
R.F. Nalewajski, J. Math. Chem. 49, 806 (2011)
R.F. Nalewajski, J. Math. Chem. 49, 371, 546 (2011)
R.F. Nalewajski, P. Gurdek, J. Math. Chem. 49, 1226 (2011)
R.F. Nalewajski, Int. J. Quantum Chem. 112, 2355 (2012)
R.F. Nalewajski, P. Gurdek, Struct. Chem. 23, 1383 (2012)
R.F. Nalewajski, Information theoretic approach to chemical bonds: quantum information measures, molecular equilibria and orbital communications,Quantum Matter (special issue Quantum Matter Chemistry, ed. by A. Herman), in press
W. Kohn, L.J. Sham, Phys. Rev. 140A, 1133 (1965)
P. Hohenberg, W. Kohn, Phys. Rev. 136B, 864 (1964)
M. Levy, Proc. Natl. Acad. Sci. USA 76, 6062 (1979)
W. Macke, Ann. Phys. Leipzig 17, 1 (1955)
T.L. Gilbert, Phys. Rev. B 12, 2111 (1975)
J.E. Harriman, Phys. Rev. A 24, 680 (1981)
G. Zumbach, K. Maschke, Phys. Rev. A 28, 544 (1983); Erratum. Phys. Rev. A 29, 1585 (1984)
C.F. von Weizsäcker, Z. Phys. 96, 431 (1935)
P.A.M. Dirac, The Principles of Quantum Mechanics, 4th edn. (Clarendon, Oxford, 1958)
R.F. Nalewajski, J. Math. Chem. 52, 42 (2014)
R.F. Nalewajski, P. de Silva, J. Mrozek, J. Mol. Struct: THEOCHEM 954, 57 (2010)
R.F. Nalewajski, A.M. Köster, S. Escalante, J. Phys. Chem. A 109, 10038 (2005)
A.D. Becke, K.E. Edgecombe, J. Chem. Phys. 92, 5397 (1990)
B. Silvi, A. Savin, Nature 371, 683 (1994)
A. Savin, R. Nesper, S. Wengert, T.F. Fässler, Angew. Chem. Int. Ed. Engl. 36, 1808 (1997)
K.A. Wiberg, Tetrahedron 24, 1083 (1968)
R.F. Nalewajski, A.M. Köster, K. Jug, Theoret. Chim. Acta (Berl.) 85, 463 (1993)
R.F. Nalewajski, J. Mrozek, Int. J. Quantum Chem. 51, 187 (1994)
R.F. Nalewajski, S.J. Formosinho, A.J.C. Varandas, J. Mrozek, Int. J. Quantum Chem. 52, 1153 (1994)
R.F. Nalewajski, J. Mrozek, G. Mazur, Can. J. Chem. 100, 1121 (1996)
R.F. Nalewajski, J. Mrozek, A. Michalak, Int. J. Quantum Chem. 61, 589 (1997)
J. Mrozek, R.F. Nalewajski, A. Michalak, Polish J. Chem. 72, 1779 (1998)
R.F. Nalewajski, Chem. Phys. Lett. 386, 265 (2004)
M.S. Gopinathan, K. Jug, Theor. Chim. Acta (Berl.) 63, 497, 511 (1983)
K. Jug, M.S. Gopinathan, in Theoretical Models of Chemical Bonding, vol. II, ed. by Z.B. Maksić (Springer, Heidelberg, 1990), p. 77
I. Mayer, Chem. Phys. Lett. 97, 270 (1983)
S. Shaik, D. Danovich, W. Wu, P.C. Hiberty, Nat. Chem. 1, 443 (2009)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Nalewajski, R.F. Quantum information descriptors and communications in molecules. J Math Chem 52, 1292–1323 (2014). https://doi.org/10.1007/s10910-014-0311-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10910-014-0311-7