1 Introduction

The thermal decomposition of alkyl esters to produce alkenes and carboxylic acids is a well-established process experimentally investigated a great number of times [1,2,3,4,5]. Detailed reviews that report on many studies involving the kinetics and mechanism of the decomposition of esters are available [4, 5].

Conjugated nitroalkenes (CNAs) have proved to be a valuable group of reactants in organic chemistry. Their strong electrophilic character makes them important precursors towards a wide variety of target molecules. They are useful compounds applied, e.g. in syntheses of many four-, five- and six-membered compounds in cycloaddition reactions [6,7,8,9,10,11]. Applications of nitroalkenes in organic synthesis are largely due to their ease of conversion into a variety of functionalities. Moreover, a considerable number of nitroalkenes exhibits remarkable biological activity [12,13,14,15].

There are many strategies for the preparation of CNAs. However, the most universal method is that based on the decomposition of nitroalkyl esters. The thermal decomposition of carboxylic esters to yield an alkene and a carboxylic acid has been studied since 1883 [16, 17]. Recently, we theoretically studied the thermal decomposition of nitroalkyl esters [18, 19]. Thus, for the thermal decomposition of nitroethyl benzoate (NEB) 1 yielding nitroethylene 2 and benzoic acid 3, we proposed [19] that this process could be characterised by a one-step two-stage mechanism [20] (see Scheme 1).

Scheme 1
scheme 1

General scheme of decomposition reaction of nitroethyl benzoate (NEB) 1. B3LYP/6-31G(d) relative energies with respect to NEB 1 are given in kcal·mol−1. Note that broken lines at TS within the breaking and forming regions do not refer to a conjugated cyclic pattern but only indicate the bonds that are going to break or form

Full size image

This decomposition reaction presents a high activation energy, 42.5 kcal mol−1, the reaction being endothermic by 16.3 kcal mol−1. The geometry of the transition state structure (TS) given in Fig. 1 shows that it presents a distorted six-membered rearrangement in which the length of the breaking O–C single bond is 1.750 Å, while the distances between the H atom and the C and O atoms are 1.569 and 1.095 Å, respectively [19].

Fig. 1
figure 1

B3LYP/6-31G(d) geometry of TS. Distances are given in angstroms, Å [19]

Full size image

Contemporary determination of the principles controlling a reaction mechanism is closely tied with the progress of quantum chemistry. One of the fundamental goals for understanding a given chemical rearrangement is to analyse the changes of quantum mechanical observables such as the electron density along the reaction pathway. This approach enables a comprehensive picture of the chemical reactivity in terms of how and when chemical events, e.g. bond rupture and formation processes, will take place. To this end, the Bonding Evolution Theory (BET) [21], which combines the topological analysis of the electron localisation function (ELF) [22] with the mathematical Catastrophe Theory (CT), was proposed [23,24,25]. BET has proved to be a useful quantum chemical tool for the study of reaction mechanisms [26,27,28,29].

Very recently, Domingo proposed the Molecular Electron Density Theory (MEDT) [30], in which changes in the electron density, but not molecular orbital (MO) interactions such as the Frontier Molecular Orbital (FMO) theory proposed [31], are responsible for the reactivity in organic chemistry. Note that the electron density obtained from the wavefunction is the unique physically observable. Within MEDT, besides an exhaustive exploration and characterisation of the reaction paths associated with the studied reaction, analysis of the CDFT reactivity indices [32, 33], as well as quantum chemical tools based on the topological analysis of the molecular electron density such as the ELF [22], the Quantum Theory of Atoms In Molecules (QTAIM) [34] and Non-Covalent Interactions (NCI) [35], are used in order to study the reactivity in organic chemistry.

It is stay accepted that decomposition reactions of alkyl carboxylates are essentially a pericyclic process [36]. Nonetheless, the last reports [37, 38] based on the analysis of the evolution of the electron density along a reaction involving a cyclic arrangement of nuclei, i.e. pseudocyclic reactions [39], reveal that the pericyclic mechanism does not exist as the bonding changes are not concerted [40]. In this work, as a continuation of the quantum chemical study about the decomposition reaction of nitroethyl carboxylates [18, 19], an MEDT study of the decomposition process of NEB 1 is performed in order to establish the molecular mechanism of this decomposition reaction and the nature of the electronic rearrangement along it.

2 Computational details

Calculations were performed using the Prometheus computer cluster in the CYFRONET regional computer centre in Cracow and the cluster of Domingo’s group. All calculations were carried out with the GAUSSIAN 09 package [41]. DFT calculations were performed using the B3LYP [42, 43] functional together with the 6-31G(d) basis set [44]. The stationary points were characterised by frequency calculations in order to verify the number of imaginary frequencies (zero for local minima and one for TSs). The IRC [45] paths, computed using the second order González-Schlegel integration method [46, 47], were traced in order to obtain the energy profiles connecting TS to the two associated minima of the proposed mechanism.

ELF studies were performed with the TopMod [48] programme using the corresponding gas phase B3LYP/6-31G(d) monodeterminantal wavefunctions. For the BET study, the corresponding gas phase reaction channel was followed by performing the topological analysis of the ELF for 855 nuclear configurations along the IRC path. ELF calculations were computed over a grid spacing of 0.1 a.u. for each structure, and ELF localisation domains were obtained for an ELF value of 0.75.

3 Results and discussion

The present theoretical study has been divided into three sections: i) in Sect. 3.1, an ELF topological analysis and a natural population analysis (NPA) of the reagent NEB 1 are performed in order to characterise its electronic structure; ii) in Sect. 3.2, a BET study of the decomposition reaction of NEB 1 is performed in order to characterise the molecular mechanism of this intramolecular process; and finally, iii) in Sect. 3.3, an MEDT study of the decomposition reaction of NEB 1 based, on the one hand, the BET study, and, on the other hand, the analysis of the energies related to the different bonding changes taking place along to the reaction, is given with the aim of providing an explanation of its activation energy.

3.1 ELF and NPA characterisation of the electronic structure of NEB 1

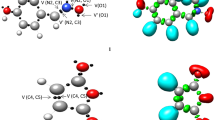
One appealing procedure that provides a straightforward connection between the electron density distribution and the chemical structure is the quantum chemical analysis of Becke and Edgecombe’s ELF [22]. Therefore, in order to characterise the electronic structure of NEB 1, a topological analysis of the ELF was first performed. ELF localisation domains and their attractor positions, together with the most representative valence basin populations, as well as the proposed ELF-based Lewis structure, together with the natural atomic charges, are shown in Fig. 2.

Fig. 2
figure 2

a ELF localisation domains of NEB 1, represented at an isosurface value of ELF = 0.75; b ELF basin attractor positions, together with the most representative valence basin populations; c the proposed ELF-based Lewis structures, together with the natural atomic charges, obtained through an NPA; and d the commonly used Lewis representation. Negative charges are coloured in red and positive charges are coloured in blue. ELF valence basin population and natural atomic charges are given in average number of electrons, e

Full size image

ELF topological analysis of NEB 1 shows the presence of three monosynaptic basins over the O1 and O3 oxygen atoms, V(O1), V′(O1) and V(O3), integrating total electron populations of 5.36e (O1) and 4.60e (O3), four disynaptic basins V(O1, C2), V(C2, O3), V(O3, C4) and V(C4, C5), integrating 2.39e, 1.61e, 1.39e and 1.95e, and one V(C5, H6) protonated basin with a population of 2.07e.

Within the ELF context, monosynaptic basins are associated with non-bonding regions, disynaptic basins are related to bonding regions and protonated basins correspond to bonding regions involving hydrogen atoms [49]. Thus, within the Lewis bonding model [50, 51], the V(O1), V′(O1) and V(O3) monosynaptic basins can be associated with O1 and O3 oxygen lone pairs, the V(O1, C2), V(C2, O3) and V(C5, C4) disynaptic basin with O1–C2, C2–C3 and C4–C5 single bonds, and the V(O3, C4) disynaptic and V(C5,H6) protonated basins with the O3–C4 and C5–H6 bonds that are going to be broken along the decomposition reaction of NEB 1 (see the proposed ELF-based Lewis structure in Fig. 2). Note, however, that the O1 and O3 oxygen “lone pairs” cannot actually be considered so. Interestingly, the V(O1, C2) population, which permits to categorise the O1–C2 bonding region as a single one, and the population of the O1 oxygen monosynaptic basins, ca. 5e, as well as the depopulated O3–C4 single bond, contrast with the common bonding pattern represented for NEB 1 (see the Lewis structures in Fig. 2). It is also worth mentioning that the latter feature may, at first glance, suggest a high feasibility for the rupture of the O3–C4 single bond.

Once the bonding pattern of NEB 1 was established, the charge distribution was analysed through an NPA [47, 48]. Natural atomic charges of the most relevant atoms are shown together with the proposed ELF-based Lewis structure given in Fig. 2. NPA of NEB 1 reveals that while the O1 and O3 oxygen atoms gather the higher negative charges of the six-membered framework involved in the reaction, − 0.61e (O1) and − 0.56e (O3), the C5 carbon is half as negatively charged, − 0.35e, and the C4 carbon only slightly, − 0.14e. On the other hand, while the carbonyl C2 carbon presents a relatively high positive charge, 0.82e, the H6 hydrogen is positively charged by 0.27e. Thus, while the O1, O3, C4 and C5 atoms gather negative charges, only the C2 carbon and the H6 hydrogen are positively charged.

Considering the set of resonance Lewis structures of NEB 1, neither the O3 oxygen nor the C4 or C5 carbons would never somehow gather negative charges. Consequently, the electronic structure of NEB 1 arising from both the topological analysis of the ELF and the NPA is quite different to that expected (see Fig. 2). Note that the charge distribution obtained through the NPA is the consequence of the asymmetric electron density delocalisation within a molecule resulting from the presence of different nuclei in the molecule, rather than the consequence of the resonance Lewis structures.

3.2 BET study of the decomposition reaction of NEB 1

When trying to achieve a better understanding of the mechanism of organic reactions, the so-called BET [21] has proven to be a very useful methodological tool. This quantum chemical methodology makes it possible to understand the bonding changes along a reaction path and, thus, to establish the nature of the electronic rearrangement associated with a given molecular mechanism [26,27,28,29].

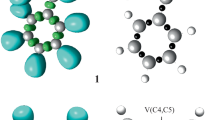
The populations, among other relevant parameters, of the most significant ELF valence basins (those associated with the bonding regions directly involved in the reaction) of the selected points of the IRC, Pi, defining the different topological phases are gathered in Table 1, while ELF localisation domains and their attractor positions for the points involved in the bond formation processes are shown in Fig. 3.

Table 1 ELF valence basin populations, distances of the breaking and forming bonds, relativea electronic energies of the IRC points, P0–P5, defining the six phases characterising the molecular mechanism of the decomposition of NEB 1. The stationary points 1, TS and MC are also included. Distances are given in angstroms, Å, electron populations in average number of electrons, e, and relative energies in kcal mol−1
Full size table
Fig. 3
figure 3

ELF localisation domains, represented at isosurface values of ELF = 0.75, together with their attractor positions the points of the IRC defining Phases I and II, involved in the rupture of the O3–C4 and C5–H6 bonds, and TS and Phase IV involved in the rupture of the C5–H6 bond and the formation of the O1–H6 bond along the decomposition reaction of NEB 1. The electron populations, in e, are given in brackets

Full size image

The long Phase I (see Fig. 4), 2.24 Å ≥ d(O1–H6) > 1.52 Å, 1.44 Å ≤ d(O3–C4) < 1.66 Å and 1.09 Å ≤ d(C5–H6) < 1.13 Å, begins at P0, which is the discontinue point of the IRC from TS towards the isolated reagent NEB 1. The ELF picture of P0 usually resembles that of the separated reagents. Thus, ELF topological analysis of P0 only reveals slight changes in the ELF valence basin electron populations of NEB 1 (see Table 1 and Fig. 2). Along this phase, the population of the V(O1, C2) disynaptic basin progressively decreases, while that of the V(C2, O3) and V(C4, C5) gradually increases, a behaviour maintained until the end of the reaction at MC. The V(C5, H6) protonated basin is also slightly depopulated. Note that along this phase, the O1 and H6 atoms remain non-bound.

Fig. 4
figure 4

Phases in which the IRC associated with the decomposition reaction of NEB 1 is topologically divided. The red point indicates the position of TS, black broken lines separate the phases defined by points Pi along the IRC, while blue, pink and green areas represent the different groups in which the reaction is mechanistically divided. Relative energies (∆E, in kcal mol−1) are given with respect to the more stable conformational isomer of NEB 1

Full size image

Phase II, 1.52 Å ≥ d(O1–H6) > 1.35 Å, 1.66 Å ≤ d(O3–C4) < 1.70 Å and 1.13 Å ≤ d(C5–H6) < 1.28 Å, begins at P1. At this point, the first most relevant topological change along the reaction path takes place; together with the disappearance of the V(O3, C4) disynaptic basin present in the previous phase by means of a fold F catastrophe, a new V′(O3) monosynaptic basin is created with an initial population of 1.04e, strongly increasing the non-bonding total electron density of the O3 oxygen to 5.79e. This significant topological change indicates that the rupture of the O3–C4 single bond begins at an O3–C4 distance of ca. 1.66 Å, resulting in the formation of a O3 pseudoradical centre. In this phase, the benzoate framework is formed.

Phase III, 1.35 Å ≥ d(O1–H6) > 1.08 Å, 1.70 Å ≤ d(O3–C4) < 1.76 Å and 1.28 Å ≤ d(C5–H6) < 1.60 Å, begins at P2. At this point, the second most relevant topological change along the reaction path occurs; the V(C5, H6) protonated basin present at the previous phase splits into two new V(C5) and V(H6) monosynaptic basins integrating 1.16e and 0.73e (see P1 and TS in Fig. 3). This significant topological change, associated with a cusp C catastrophe, indicates that the rupture of the C5–H6 bond takes place closely after the O3–C4 one, at a C5–H6 distance of ca. 1.28 Å, resulting in the formation of a C5 pseudoradical centre and a free pseudoradical H6 hydrogen. It should be emphasised that along this phase, the population of the two V(O1) and V′(O1) monosynaptic basins is redistributed between them in such a manner that at the end of this phase both basins end up with 1.30e and 4.15e. In this phase, the TS of the reaction, TS, d(O1–H6) = 1.095 Å, d(O3–C4) = 1.750 and d(C5–H6) = 1.569 Å, is found, presenting only slight variations in the ELF basin populations with respect to the topological features of P2 (see Table 1).

Along Phases I–III, the two V(O3, C4) disynaptic and V(C5, H6) protonated basins disappear, while the V(O1, C2) disynaptic basin is being depopulated and those related to the C2–C3 and C4–C5 bonding regions are being populated. Thus, the bonding changes taking place along Phases I–III, which are mainly associated with the rupture of the two O3–C4 and C5-H6 bonds, demand a high energy cost (EC) of ca. 37.1 kcal mol−1 (see Table 1).

Phase IV, 1.08 Å ≥ d(O1–H6) > 0.99 Å, 1.76 Å ≤ d(O3–C4) < 2.00 Å and 1.60 Å ≤ d(C5–H6) < 1.85 Å, begins at P3. At this point, the third most relevant topological change along the reaction path takes place; together with the strong depopulation of the V(O1) and V′(O1) monosynaptic basins by 1.16e, so that both merge into one new V(O1) monosynaptic basin integrating 4.36e, and the disappearance of the V(H6) monosynaptic basin, a new V(O1, H6) protonated basin is created with an initial population of 1.65e through the merger of two V(O1) and V(H6) monosynaptic basins (see P3 in Fig. 3). This topological change, associated with a cusp C catastrophe, reveals that the formation of the new O1-H6 single bond begins at an O1-H6 distance of ca. 1.08 by sharing part of the non-bonding electron density of the O1 oxygen with the pseudoradical H6 hydrogen. The V(C5) monosynaptic basin is still present at P3 with a population of 1.15e, but progressively decreases along Phase IV until 0.55e. As a consequence, the population of the adjacent V(C4, C5) disynaptic basin, integrating 2.51e at P3, increases in such a manner that the C4–C5 bonding region gradually acquires double bond character (see P3′s Lewis structure in Table 2).

Table 2 Sequential bonding changes along the decomposition reaction of NEB 1, showing the equivalence between the topological characterisation of the different phases and the chemical processes occurring along them. Distances are given in angstroms, Å, while the energies involved in each group, ∆E, are given in kcal mol−1
Full size table

Along Phase IV, a new V(O1,H6) protonated basin is created and further populated, while the other V(O1, C2), V(C2, O3) and V(C4, C5) disynaptic basins experience the same changes as in previous phases. The electron density of the V(C5) monosynaptic basin gradually decreases, being redistributed into the adjacent V(C4, C5) disynaptic basin provoking its population. Thus, the bonding changes taking place along Phase IV, which are mainly associated with the formation of the new O1–H6 bond, release a molecular relaxation energy of ca. 6.3 kcal mol−1 (see Table 1).

Phase V, 0.991 Å ≥ d(O1–H6) > 0.990 Å, 2.00 Å ≤ d(O3–C4) < 2.01 Å and 1.85 Å ≤ d(C5–H6) < 1.86 Å, begins at P4. At this point, established by a fold F catastrophe, while the V(C5) monosynaptic basin disappears, the V(C4, C5) disynaptic basin reaches 3.60e as a consequence of the redistribution of the population of the former basin into the latter. This high electron density permits to characterise the C4–C5 bonding region as a double bond at P4 (see P4′s Lewis structure in Table 2). On the other hand, the non-bonding electron density of the O3 oxygen atom is also redistributed between the two V(O3) and V′(O3) monosynaptic basins, integrating 3.15e and 2.21e.

Finally, the long Phase VI (see Fig. 4), 0.99 Å ≥ d(O1–H6) ≥ 0.98 Å, 2.01 Å ≤ d(O3–C4) ≤ 3.29 Å and 1.86 Å ≤ d(C5–H6) ≤ 2.83 Å, begins at P5 and ends at molecular complex MC, which is a minimum in the reaction path from TS towards the separated products, nitroethylene 2 and benzoic acid 3. At P5, the only notable topological change is the split of the single V(C4, C5) disynaptic basin present in the nitroethylene framework at the previous phase into two new V(C4, C5) and V′(C4, C5) disynaptic basins, integrating 1.68e and 1.92e, by means of a cusp C † catastrophe. This topological change is simply the consequence of an electron density reorganisation within the C4–C5 double bond region, as the total population has not varied.

Along Phases V and VI, the population of the disynaptic basins corresponding to the C4–C5 bonding region considerably increases, while the population variations of the other basins follow the same trend that along previous phases. Consequently, the bonding changes taking place along Phases V and VI, which are mainly associated with the formation of the C4–C5 double bond of nitroethylene 2 and the complete reorganisation to form the final structures of nitroethylene 2 and benzoic acid 3, release the maximum MRE along the reaction, ca. 19.9 kcal mol−1 (see Table 1).

At MC, d(O1–H6) = 0.967, d(O3–C4) = 3.288 Å and d(C5–H6) = 2.834 Å, only slight variations in the ELF basin populations with respect to those calculated at P5 are observed. After the increase of the population of the monosynaptic basins associated with the O3 oxygen due to the rupture of the O3–C4 single bond, they have been depopulated to 5.33e towards the V(C2, O3) disynaptic basin, which reaches 2.37e. Similarly, the monosynaptic basins associated with the O1 oxygen end up with 4.45e after their early population coming from the V(O1, C2) disynaptic basin and their next depopulation towards the new V(O1, H6) protonated basin, which integrates 1.69e.

From this BET study, the molecular mechanism of the decomposition reaction of NEB 1 can be summarised as follows (see Lewis structures in Table 2): i) this reaction is topologically characterised by six differentiated phases, emphasising the non-concerted nature of the bonding changes taking place along the reaction; ii) the reaction begins with the depopulation of the V(O3, C4) disynaptic and V(C5, H6) protonated basins, associated with the two O3–C4 and C5–H6 bonds that are going to be broken (Phases I–III), until they disappear (first the V(O3, C4) disynaptic basins and later the V(C5, H6) protonated one) giving rise to the formation of two V(C5) and V(H6) monosynaptic basins; iii) along Phases I–III, no bound six-membered cyclic structure exists. This fact, together with the non-concerted nature of the bonding changes, also allows ruling out the proposed pericyclic mechanism [52, 53] in which the bonding changes take place “in concert on a closed curve” assuming a bound cyclic structure; iv) as TS is found at the end of Phase III (see Fig. 4), the high activation energy associated with this decomposition reaction, 42.5 kcal mol−1 (see Table 1), can mainly be related to the disappearance of the mentioned V(O3, C4) and V(C5, H6) basins; v) TS consists of three different separated frameworks: the nitroethylene one, the benzoate one and a free pseudoradical hydrogen, precluding any conjugation and thus, any aromatic character of the TS [39]; vi) next, a new V(O1, H6) protonated basin, associated with an O1–H6 bond, is formed at Phase IV through the merger of two V(O1) and V(H6) monosynaptic basins at dO1-H6 = 1.08 Å, and further populated releasing 6.3 kcal mol−1; and finally, vii) the V(C5) monosynaptic basin disappears towards the V(C4, C5) disynaptic basin, whose population suddenly increases and causes the split into two V(C4, C5) and V′(C4, C5) disynaptic basins associated with the C4–C5 double bond of the nitroethylene framework.

3.3 MEDT study of the decomposition reaction of NEB 1

Within MEDT, the bonding changes are topologically and energetically analysed in order to understand the origin of the activation and the reaction energies associated with an organic reaction. In this section, the bonding changes arising from the BET study and their associated energy changes along the decomposition reaction of NEB 1 are summarised and described in a chemical fashion. Note that BET is a powerful tool to study the bonding changes along a reaction pathway, i.e. the molecular mechanisms, but neither the energies associated with the bonding changes nor energy differences between competitive reaction pathways are analysed within BET.

The sequential bonding changes resulting from the BET study of the decomposition reaction of NEB 1 are summarised in Table 2, together with a simplified representation of the molecular mechanism by ELF-based Lewis structures, while the phases and groups in which the corresponding IRC is topologically divided are represented in Fig. 4. Some appealing conclusions can be drawn from this MEDT study: i) the molecular mechanism of this reaction is topologically characterised by six differentiated phases which, in turn, can be reorganised in three Groups A–C associated with significant chemical events (see Table 2 and Fig. 4). This fact clearly allows ruling out the pericyclic mechanism [53] proposed for this reaction; ii) Group A, which comprises Phases I–III and demands a high EC of ca. 37.1 kcal mol−1, is associated with the rupture of the O3–C4 and C5–H6 bonds of NEB 1; iii) the rupture of the O3–C4 and C5–H6 bonds, at dO3-C4 = 1.66 Å and dC5-H6 = 1.28 Å, is only slightly asynchronous and could be considered a synchronous process (∆dO3-C4 = 0.03 Å and (∆dC5-H6 = 0.15 Å); iv) the rupture of these bonds leads to the formation of three O3, C5 and H6 pseudoradical centres; v) as TS is found at the end of Phase III, the high activation energy associated with this decomposition reaction in gas phase, 42.5 kcal mol−1, can mainly be related to the rupture of the O3–C4 (ca. 22.0 kcal mol−1) and C5–H6 (ca. 15.1 kcal mol−1) bonds of NEB 1, yielding two separated frameworks and a free hydrogen H6 atom stabilised by the C5 pseudoradical centre and the non-bonding O1 electron density; vi) the low electron population of the V(O3, C4) disynaptic basin together with the high EC demanded for the rupture of the first O3–C4 single bond suggests that this bond has a strong ionic character; vii) Group B, which comprises only Phase IV and releases an MRE of 6.3 kcal mol−1, is mainly associated with the formation of the new O1–H6 bond at a O1–H6 distance of ca. 1.1 Å by sharing part of the non-bonding electron density of the O1 oxygen with the free pseudoradical H6 hydrogen; and finally, viii) Group C, which comprises Phases V and VI and releases an MRE of 19.9 kcal mol−1, is mainly associated with the formation of the C4–C5 double bond at the nitroethylene framework and to the molecular electronic relaxation associated with the formation of nitroethylene 2 and benzoic acid 3.

4 Conclusions

The molecular mechanism of the decomposition reaction of NEB 1 yielding nitroethylene 2 and benzoic acid 3 has been studied within the MEDT using DFT methods at the B3LYP/6-31G(d) computational level. This decomposition reaction takes place through a one-step mechanism. BET analysis of this reaction provides a complete characterisation of the electron density changes along the reaction. The reaction begins by the synchronous rupture of the O3–C4 and C5–H6 single bonds of NEB 1. These changes, which demand an energy cost of 37.1 kcal mol−1, are responsible for the high activation energy associated with this decomposition reaction. Interestingly, while the rupture of the first O3–C4 single bond takes place heterolytically, the rupture of the C5–H6 takes place homolytically, leading to the formation of a pseudoradical hydrogen atom. Formation of the C4–C5 double bond present in nitroethylene 2 takes place at the end of the reaction. In spite of the fact that this process releases an MRE of 19.9 kcal mol−1, it is not sufficient to overcome the energy demanded for the rupture of the O3–C4 and C5–H6 bonds, and consequently, the overall process is endothermic.

The six differentiated phases in which the IRC associated with this decomposition reaction is divided clearly point out the non-concerted nature of the bonding changes. This behaviour, together with the flux of the electron density on going from the reagent NEB 1 towards TS1 (see Fig. 5), makes it possible to reject a pericyclic mechanism. These reactions in which the six associated atomic centres are assembled in a more or less distortioned six-membered cyclic rearrangement at the TS but not necessarily bound have recently been categorised as pseudocyclic reactions. Consequently, the decomposition reaction of NEB 1 can be considered a non-concerted one-step pseudocyclic reaction.

Fig. 5
figure 5

Main bonding changes on going to TS. The rupture of the C–O bond takes place heterolytically (red double-headed arrow), while the rupture of the C–H bond takes place homolytically (two blue single-headed arrows)

Full size image