1 Introduction

Quinones belong to the class of π-electron chemical compounds in which two units of CH are replaced by two carbonyl groups that have to be located in a way that does not lead to ionic canonical structures or in other words to form “a fully conjugated cyclic dione structure” [1]. In most cases, location of carbonyl group is either in the ortho- or in the para-type positions. Derivatives of quinones are common constituents of biologically important molecules as ubiquinone, which is important for aerobic respiration [2], or phylloquinone known as vitamin K [3]. In protic solvents, quinones are easily reducible to hydroquinones, whereas in aprotic solvents, they are electrochemically reduced to radical anions [4, 5]. A very important structural property of quinones is that the two carbonyl groups attached to a benzenoid ring system cause a very strong localization of the π-electron structure, i.e., decrease in aromaticity. In the case of ortho-benzoquinone, many aromaticity indices such as HOMA [6, 7], MCI [8, 9] or FLU [10] indicated antiaromatic properties of the ring [11] in contrast to benzene ring known as the archetypic aromatic π-electron system [12–15]. Moreover, the HOMA [6, 7] values for the ring with the two CO groups are −1.353 and −1.277 for 1,2- and 2,3-naphthoquinone [16], respectively, indicating antiaromaticity, whereas HOMA for the ring in naphthalene amounts to 0.811 [17].

Since the localization effect of the quinoid fragment is well known, the question may be posed: how far the localization impact of the ortho-quinoid fragment may affect further rings in 1,2- and 2,3-quinone derivatives of acenes? Then, the systems of this study are 1,2- (Scheme 1) and 2,3-quinone (Scheme 2) derivatives of linear benzenoids (Scheme 3). It is worth noting that a previous study on the aromaticity of pentalenoquinones already indicated that the relative position of the two C=O fragments has a large influence on the aromaticity of these pentalenoquinones [18].

Scheme 1
scheme 1

1,2-quinone derivatives of linear benzenoids

Full size image
Scheme 2
scheme 2

2,3-quinone derivatives of linear benzenoids

Full size image
Scheme 3
scheme 3

Linear benzenoids

Full size image

2 Computational methods

2.1 Geometry optimizations

The full geometry optimization of the set of systems shown in Schemes 1, 2 and 3 was performed using B3LYP hybrid functional [19–21] in conjunction with the 6-311+G(d) basis set [22, 23]. For equilibrium structures, a frequency analysis was performed in order to check whether all geometries corresponded to true ground state stationary points. Gaussian 09 [24] software package was used for this part of calculations. For open-shell systems, unrestricted UB3LYP/6-311+G(d) calculations with broken symmetry (using guess = mix option) were also performed. It appeared that for 2,3-anthraquinone and its larger analogues (tetra-, penta-, and hexa-ones), the lowest energy state corresponds to the diradical singlet state. Stability of their wavefunctions constructed from Kohn–Sham orbitals was also checked. All wavefunctions were found to be stable.

Accurate calculations of large open-shell systems are difficult and expensive; therefore, DFT methods are commonly used. The good performance of the UB3LYP method is confirmed by recent papers [25–30]. On the basis of previous results [31], spin contamination corrections were not included.

2.2 Stability analysis

The difference between electronic energies of 1,2-(E 1,2) and 2,3-(E 2,3) quinone derivatives of linear benzenoids allows to compare their relative stability:

$$ \Delta E = E_{1,2} {-}E_{2,3} $$
(1)

The same analysis can be done through comparison of stabilization energies ΔE 1,2 and ΔE 2,3, which can be estimated for the reaction:

$$ {\text{Linear benzenoid }}\left( {E_{\text{B}} } \right) \, + {\text{ O}}_{2} \left( {E_{{{\text{O}}_{2} }} } \right) \, = {\text{ quinone derivative }} + {\text{ H}}_{2} \left( {E_{{{\text{H}}_{2} }} } \right) $$
(2)

Therefore, the stabilization energies are expressed as follows:

$$ \Delta E_{1,2} = E_{1,2} + E_{{{\text{H}}_{2} }} {-} \, \left( {E_{\text{B}} + E_{{{\text{O}}_{2} }} } \right) $$
(3)
$$ \Delta E_{2,3} = E_{2,3} + E_{{{\text{H}}_{2} }} {-} \, \left( {E_{\text{B}} + E_{{{\text{O}}_{2} }} } \right) $$
(4)

It should be mentioned that in order to have the consistent model of reaction (2), we used in this scheme the singlet state energy of O2 molecule, having in mind the fact that the triplet state is the most stable form of that species.

2.3 Energy decomposition analysis

The Amsterdam Density Functional (ADF) program [32–34] was used to carry out energy decomposition analysis (EDA) in the framework of Kohn–Sham molecular orbital (MO) theory in single-point energy calculations using the B3LYP/6-311+G(d) geometries. All ADF calculations were carried out using the B3LYP functional [19–21] with the TZ2P basis set.

Each molecule of quinone (for both 1,2- and 2,3-series) can be divided into two fragments,·C4n-2H2n–CH·· (2-methtriyl-aryl, n = 1–6) and ··CH–CO–CO· (1,3,3-tridehydro-2-oxopropanal) in their quadruplet state, equivalent for both isomers. As an example, naphthoquinone is presented in Scheme 4. The energy of such reaction is equal to the total bonding energy, ΔE BE, computed as the energy difference between the mentioned molecule and the sum of the energies of the relaxed fragments. ΔE BE is composed of two components: (1) the preparation energy, also known as deformation energy, ΔE def, and (2) the interaction energy, ΔE int. The former component is always positive because it describes the amount of energy required to deform the fragments from their relaxed geometry to the one they acquire in the final molecule. The latter term is focused on the interaction between the deformed fragments, i.e., the fragments in the geometry they adopt in the studied molecule. ΔE int may be then divided in the framework of the Kohn–Sham MO model by using a quantitative EDA [35–40] into electrostatic interaction (ΔV elstat), Pauli repulsive orbital interactions (ΔE Pauli), and attractive orbital interactions (ΔE oi):

$$ \Delta E_{\text{int}} = \Delta V_{\text{elstat}} + \Delta E_{\text{Pauli}} + \Delta E_{\text{oi}} $$
(5)

Moreover, using the extended transition state (ETS) scheme [37, 38], the ΔE oi term can be divided into the contributions of orbitals with different symmetry. For planar systems, like the ones under analysis in the present work, the σ/π separation is possible:

Scheme 4
scheme 4

EDA fragment analysis of a 1,2-naphthoquinone and b 2,3-naphthoquinone

Full size image
$$ \Delta E_{\text{oi}} = \Delta E_{\sigma } + \Delta E_{\pi } $$
(6)

General theoretical background on the bond energy decomposition scheme used here (Morokuma–Ziegler) can be found in the papers by Bickelhaupt and Baerends [39, 41]. Finally, in the EDA of the bonding energy, open-shell fragments were treated with the spin-unrestricted formalism, but for technical reasons, spin polarization cannot be included. This error causes the studied interaction to become in the order of a few kcal/mol stronger. To facilitate a straightforward comparison, the EDA results were scaled to match exactly the regular bond energies. This scaling by a factor in the range 0.91–0.93 in all model systems does not affect trends.

At this point, it must be mentioned that it has been technically not possible to undertake the EDA calculations for singlet open-shell systems. Application of EDA to singlet open-shell systems leads always to singlet closed-shell results. Therefore, to estimate the results of the EDA for singlet open-shell systems, i.e., 2,3-quinones with 3 ≤ n ≤ 6, we decomposed the bonding energy of singlet closed-shell 2,3-quinones and applied some corrections. In particular, we assumed that ΔV elstat and ΔE Pauli energies for open- and closed-shell singlet species are the same, and only the orbital interaction (ΔE oi) term is corrected. For this purpose, the energy difference between values for the whole system at singlet open-shell and closed-shell computations is taken into account (added to the ΔE oi term). ΔE σ and ΔE π were also corrected by using the ratio ΔE σ(open)/ΔE oi(open) = ΔE σ(closed)/ΔE oi(closed) and ΔE π(open)/ΔE oi(open) = ΔE π(closed)/ΔE oi(closed), where corrected ΔE oi is used (for such correction ΔE σ + ΔE π = ΔE oi).

2.4 π-Electron delocalization analysis

Two types of aromaticity parameters have been used as quantitative measures of π-electron delocalization: (1) structural and (2) electronic based indices.

First, HOMA [6, 7], the geometry-based aromaticity index, may serve as a convenient, reliable [42], and easily accessible quantitative measure of π-electron delocalization [43] of the system (e.g., in the ring). The formula can be written as:

$$ {\text{HOMA}} = 1 - \frac{1}{n}\sum\limits_{j = 1}^{n} {\alpha_{\text{j}} \left( {R_{{{\text{opt,}}\,{\text{j}}}} - } \right.\left. {R_{\text{j}} } \right)^{2} } $$
(7)

where n is the number of bonds taken into the summation; α j is a normalization constant (for CC and CO bonds α CC = 257.7 and α CO = 157.38) fixed to give HOMA = 0 for a model non-aromatic system and HOMA = 1 for a system with all bonds equal to the optimal value R opt,j, assumed to be realized for fully aromatic systems (for CC and CO bonds R opt,CC = 1.388 and R opt,CO = 1.265 Å), whereas R j denotes bond lengths taken into calculation.

Second, electronic aromaticity criteria using the atomic partition provided by the quantum theory of atoms in molecules (QTAIM) [44] have been applied: the aromatic fluctuation index (FLU) [10] and the multicenter index (MCI) [8, 9].

FLU measures the amount of electron sharing between contiguous atoms. It is defined as:

$$ {\text{FLU}}({\rm A}) = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left[ {\left( {\frac{{V(A_{\text{i}} )}}{{V(A_{{{\text{i}} - 1}} )}}} \right)^{\alpha } \left( {\frac{{\delta \left( {A_{\text{i}} ,A_{{{\text{i}} - 1}} } \right) - \delta_{\text{ref}} \left( {A_{\text{i}} ,A_{{{\text{i}} - 1}} } \right)}}{{\delta_{\text{ref}} \left( {A_{\text{i}} ,A_{{{\text{i}} - 1}} } \right)}}} \right)} \right]^{2} } $$
(8)

where A 0 ≡ A N (N being the number of atoms in the ring) and V(A i) is the atomic valence given by:

$$ V(A_{\text{i}} ) = \sum\limits_{{A_{\text{j}} \ne A_{\text{i}} }} {\delta (A_{\text{i}} ,A_{\text{j}} )} $$
(9)

and α is a simple function to make sure that the first term in Eq. (8) is always greater or equal to 1, so it takes the values:

$$ \alpha = \left\{ {\begin{array}{*{20}l} 1 & {V(A_{\text{i}} ) > V(A_{{{\text{i}} - 1}} )} \\ { - 1} & {V(A_{\text{i}} ) \le V(A_{{{\text{i}} - 1}} )} \\ \end{array} } \right. $$
(10)

The δ ref(C,C) = 1.389 e, calculated from benzene at the B3LYP/6-311++G(d,p) level, was used in the calculations. FLU is close to 0 in aromatic species and differs from it in non-aromatic ones.

MCI is derived from the I ring index that was defined by Giambiagi et al. [45] as:

$$ I_{\text{ring}} (A) = 2^{\text{N}} \sum\nolimits_{{i_{1} ,i_{2} ,i_{3} \ldots ,i_{\text{N}} }}^{\text{OCC}} {S_{{i_{1} i_{2} }} } (A_{1} )S_{{i_{2} i_{3} }} (A_{2} ) \ldots S_{{i_{\text{N}} i_{1} }} (A_{\text{N}} ) $$
(11)

where S ij(A k) is the overlap between MOs i and j within the domain of atom k. In this formula, it is considered that the ring is formed by atoms in the string {A} = {A 1 , A 2 , … A N }. Extension of this I ring index of Giambiagi by Bultinck and coworkers resulted in the so-called MCI index

$$ {\text{MCI}}(A) = \frac{1}{2N}\sum\nolimits_{\text{P(A)}} {I_{ring} (A) = \frac{1}{2N}} \sum\nolimits_{P(A)} {\sum\nolimits_{{i_{1} ,i_{2} ,i_{3} \ldots ,i_{N} }}^{OCC} {S_{{i_{1} i_{2} }} } (A_{1} )S_{{i_{2} i_{3} }} (A_{2} ) \ldots S_{{i_{N} i_{1} }} (A_{N} )} $$
(12)

where P(A) stands for the N! permutations of the elements in the string {A}. The MCI index has been successfully applied to a broad number of situations, from simple organic compounds to complex all metal clusters with multiple aromaticity [8, 46–56]. For planar species, S ij(A k) = 0 for i ∈ σ and j ∈ π orbital symmetries; thus, MCI can be exactly split into σ- and π-contributions, namely MCIσ and MCIπ, respectively. When computed in an aromatic ring, the more positive the MCI, the more aromatic the ring.

FLU, I ring, and MCI indices have been obtained with the ESI-3D program [10, 57].

2.5 Hardness

The hardness of a chemical system, η, is a measure of the resistance of a chemical species to change its electronic configuration. It is defined as:

$$ \eta = \left( {\frac{{\partial^{2} {E}}}{{\partial {{N}}^{2} }}} \right)_{{\nu \left( {\vec{r}} \right)}} , $$
(13)

where N is the number of electrons of the system, and \( \nu \left( {\vec{r}} \right) \) is the potential acting on an electron at \( \vec{r} \) due to the nuclear attraction plus such other external forces as may be present. A three points finite difference approximation for the derivative leads to the following working definition when considering the Koopmans’ approximation: [58]

$$ \eta = \varepsilon_{\text{LUMO}} {-}\varepsilon_{\text{HOMO}} , $$
(14)

where ε LUMO and ε HOMO are the energies of the LUMO and the HOMO orbitals.

3 Results and discussion

It was recently shown that the lowest energy state of higher polyacenes can correspond to diradical singlet state instead of the closed-shell singlet state [59–61]. Similar results are also observed for some studied quinones. Diradical singlet state of 2,3-anthraquinone and its larger analogues (n ≥ 3, n being the number of the rings), obtained using the unrestricted broken symmetry UB3LYP/6-311+G(d) method, is found to be more stable than the closed-shell singlet state; the energy differences amount to 5.2, 15.9, 12.1, and 10.2 kcal/mol for 2,3-anthra-, tetra-, penta-, and hexaquinones, respectively. This is similar to what is found for acenes [61], although in these latter cases, the closed-shell species are more stable until n < 5 or 6. The change in the electronic ground state can also be understood using the Clar’s π-sextet model [62]. This model, known also as Clar’s rule, offers a qualitative picture of the aromatic character of a particular ring in a polycyclic benzenoid hydrocarbon molecule. Its implementation allows to classify rings according to their π-electron structure into aromatic sextets, empty rings, migrating rings, and those with localized double bonds. Clar’s rule has been validated experimentally and successfully applied in many cases, for review see [63]. As can be seen in Scheme 5, by changing from closed-shell (no π-sextets) to open-shell singlet state, a π-bond is lost and this is partially or totally compensated by the formation of a migrating π-sextet and some 1,4 interaction (Dewar-type resonance structure). It should be noted that Clar structure shown in Scheme 5b is reinforced by all applied aromaticity indices (see Table S1 in Supporting Information). Summarizing, in 2,3-quinones for n > 2, the diradical singlet situation is favored, as in the case of the acenes [25, 59, 61, 63] and in other polycyclic aromatic hydrocarbons [26–30, 64–69] and graphene nanoflakes [70, 71].

Scheme 5
scheme 5

Clar structures for the a closed-shell and b open-shell singlet states of 2,3-anthraquinone

Full size image

Therefore, for 2,3-isomers, only the results of the ground states (singlet closed shell for n ≤ 2 and singlet open shell for n ≥ 3) are presented below.

It is well known that structural data are one of the most important sources of information about molecules [72]. Therefore, before discussing the title question, let us look at the structural parameters of 1,2- and 2,3-quinone derivatives.

Ortho-quinoid groups are very important structural fragments in both series of quinones. In the case of 1,2-isomers (see Scheme 1), due to the lack of symmetry, the CO bonds may differ in lengths, whereas this is not the case for 2,3-isomers (Scheme 2). In 1,2-quinones, both CO elongate with increase in the number of rings (Fig. 1). Moreover, for quinones with n ≥ 2, C1O is always shorter than C2O. This difference can be rationalized by the use of the so-called Hammett–Streitwieser position constants [73], which describe the basicity of a given position for interactions with proton [74]. Their values for positions 1 and 2 in naphthalene are 0.35 and 0.25, respectively, indicating a greater basicity in position 1 and hence shorter C1O bonds. Similar data are also for positions 1 and 2 in anthracene (0.41 and 0.36, respectively).

Fig. 1
figure 1

Scatter plots of C=O bond lengths, R C=O, (in Å) versus the number of the rings (n) in (a) 1,2- and (b) 2,3-quinone derivatives

Full size image

Much more interesting is a scatter plot for 2,3-isomers presented in Fig. 1b. Even though both CO bonds have the same length, we observe important changes in their bond lengths for these particular derivatives. In this case, the range of the CO bond length variability amounts to 0.019 Å, whereas in the case of 1,2-derivatives, differences are <0.003 Å. Moreover, the shape of the presented relationships can be described by two linear equations: (1) with positive slope (0.0075) for the three shortest quinones and (2) with a negative slope (−0.0006) for the three longest isomers (the correlations coefficients amount to 0.960 and −0.995, respectively). The slope in the first case is almost 10 times greater than the observed for the second one and for 1,2-isomers. In other words, in 2,3-quinones with n ≤ 3, the CO bond lengthening is more sensitive to the enlargement of the molecule by an extra ring. Thus, we observe a clear different behavior between 1,2- and 2,3-quinones, with the change in trend for this latter found between n < 3 and n ≥ 3, which coincides with the change in the nature of the ground state referred above.

Structural data also allow to study π-electron delocalization; hence, the HOMA index is now the next tool used to investigate the differences between 1,2- and 2,3-quinone isomers of polycyclic acenes. Figure 2 presents the plots of the aromaticity index HOMAperimeter versus the number of the ring (n) for the two isomers of quinones; for comparison, data of linear benzenoid are also included. HOMAperimeter was calculated taking into account only bonds along the perimeter of the molecules thereby to describe the aromaticity of the whole molecule. Obtained values show that all quinone derivatives may be divided into two groups: (1) antiaromatic and (2) aromatic. In both cases, enlarging of the system results in increasing aromaticity (for the first group antiaromaticity decreases). It should be mentioned that the observed variability is similar for 1,2- and 2,3-quinone derivatives, although 1,2-anthraquinone is antiaromatic or non-aromatic, whereas its 2,3-analogue is slightly aromatic. Furthermore, the change from antiaromatic to aromatic character in 2,3-quinones takes place from n = 2 to n = 3, a behavior that coincides with the change in the nature of the ground state referred above (see Scheme 5). Additionally, obtained HOMAperimeter values indicate slightly greater aromaticity of 2,3- derivatives than 1,2-ones for molecules with n ≥ 3. In contrast with the aromaticity of the quinones measured with HOMAperimeter, the aromaticity of polyacenes decreases from 0.99 to 0.79 from benzene to hexacene, respectively.

Fig. 2
figure 2

HOMAperimeter values for polyacenes, 1,2-, and 2,3-quinone derivatives. Arabic numerals denote number of rings in the molecule

Full size image

HOMA values of particular rings in studied systems are presented in Fig. 3. If we first look at the ring containing the quinoid fragment (ring I in Schemes 1 and 2), we find that for 1,2-isomers the longer the quinone derivative, the lower its antiaromaticity (Fig. 3a). In the case of 2,3-derivatives, such trend is observed only for the four shortest quinones, whereas for the remaining molecules, the HOMA is almost constant (Fig. 3b). It should be noticed that antiaromaticity changes of the ring I correlate well with the observed CO bond length variations for both isomers. Thus, again, we can consider this case as two trends: for n < 3 (decrease in antiaromaticity) and n ≥ 3 (almost constant); with the lowest antiaromaticity corresponding to 2,3-tetraquinone. Interestingly, for n = 2, ring II is aromatic for 1,2-naphthoquinone, and it is non-aromatic for 2,3-naphthoquinone. This is the expected result from the Clar π-sextet rule as ring II of 1,2-naphthoquinone, unlike the 2,3-isomer, contains the π-sextet. In 2,3-quinones, for n ≥ 3, rings II and successive are aromatic as expected from the fact that a migrating π-sextet is generated in the diradicals (see Scheme 5). Finally, polyacenes present a monotonic decrease in aromaticity of ring I from benzene to hexacene (Fig. 3c).

Fig. 3
figure 3

HOMA values of particular rings in studied systems: a 1,2-quinones, b 2,3-quinones, and c linear benzenoids. Arabic numerals denote number of rings in the molecule, and Roman ones represent the labels of individual rings, n, in the molecule (see Schemes 1, 2, 3)

Full size image

For the remaining rings, the shapes of HOMA values in polyacenes and 1,2-quinone derivatives are quite similar, obviously not taking into consideration the ring I of quinones. Aromaticity of the middle ring is the largest in comparison with other rings of the molecule, and the elongation of the system causes a decrease in the aromaticity of all rings. In the case of 2,3-isomers, the most aromatic is the terminal ring of the molecule, although it is non-aromatic in 2,3-naphthoquinone (HOMA is close to 0.0).

Similar conclusions can be drawn from electronic aromaticity criteria FLU and MCI (see Figs S1 and S2) that support the above discussed conclusions drawn from geometry-based aromaticity values.

3.1 Which quinone isomer 1,2- or 2,3- is more stable?

Energy differences between the electronic and bonding energies of 1,2-quinone derivatives (Scheme 1) and their 2,3-counterparts (Scheme 2) lead to negative values (Eq. 1, see Fig. 4). In other words, 1,2-derivatives of quinone are always more stable than their corresponding 2,3-isomers. However, some strange peculiarity appears there again. As shown in Fig. 4, the variability of energy differences ΔE (Eq. 1) for both electronic and bonding energies is not monotonic, the largest differences being found for anthraquinone isomers. However, we found a monotonic decrease in absolute value of the energy differences starting from n = 3 (n values corresponding to 2,3-quinones with an open-shell singlet ground state).

Fig. 4
figure 4

Dependence of the difference in electronic energies (ΔE, Eq. 1, Gaussian results) and total bonding energies (ΔE BE, Eq. 1, ADF results) between 1,2- and 2,3-derivatives on the number of rings, n, in the molecule

Full size image

Since polyacenes are mother compounds for both kinds of quinones (Scheme 3), it is reasonable to compare the stabilization energies of these latter estimated on the basis of the reaction in Eq. 2. The obtained results (see Fig. 5) are striking. The stabilization energies of the quinone isomers (Eqs. 3, 4) plotted against the number of rings (n) have completely different shapes. For 1,2-isomers with 1 ≤ n ≤ 6, the observed changes in ΔE 1,2 are monotonic (their stability increases with increasing n), whereas for 2,3-isomers, the energy differences ΔE 2,3 pass through a maximum (less negative values) for n = 2 and for n ≥ 3 follow the same trend of decreasing when n increases (Fig. 5). Thus, assuming the quinoid fragment fused to the polyacene molecule as a perturbation of polyacene electron structure, we observe that the resulting changes depend on the type of isomer.

Fig. 5
figure 5

Dependence of the stabilization energy for 1,2- and 2,3- quinone derivatives, ΔE 1,2 and ΔE 2,3 (Eqs. 3, 4), on the number of rings, n, in the molecule

Full size image

3.2 Why 1,2-quinones are more stable than their 2,3-isomers?

To obtain a deeper insight into the origin of the relative stabilities of 1,2- and 2,3-quinones, an energy decomposition analysis was performed following the reaction presented in Scheme 4 with the corresponding fragments. It should be noted that both isomers can be constructed from two identical fragments, both in their quadruplet state in order to form the corresponding broken one single and one double bonds. However, to undertake the EDA analysis for singlet open-shell systems, i.e., 2,3-quinones with 3 ≤ n ≤ 6, appropriate corrections have to be applied for technical reasons (see Computational methods). Total bonding energies (ΔE BE) and all their components for both isomers are presented in Figs. 6, 7 and 8. Additionally, obtained results of the EDA analysis are gathered in Table S2 (see Supplementary Material).

Fig. 6
figure 6

Results of EDA analysis: a total bonding energy, ΔE BE and b deformation energy, ΔE def, for 1,2- and 2,3- quinone derivatives with enlargement of system by a consecutive ring, n

Full size image
Fig. 7
figure 7

Results of EDA analysis: a Pauli repulsive orbital interactions, ΔE Pauli, b electrostatic interactions, ΔV elstat, c orbital interactions, ΔE oi, and d total interaction energy, ΔE int for 1,2- and 2,3-quinone derivatives with enlargement of the system by a consecutive ring, n

Full size image
Fig. 8
figure 8

Components of attractive orbital interactions energy: a ΔE σ and b ΔE π for 1,2- and 2,3- quinone derivatives with enlargement of the system by a consecutive ring, n

Full size image

First, 1,2-quinone derivatives show quite constant ΔE BE values (see Fig. 6). Their bonding energy range of variability is equal 7.8 kcal/mol (for 2 ≤ n ≤ 6 amounts to 2.6 kcal/mol, see Table S2), and for systems with n > 1, stronger bonding is observed than for ortho-benzoquinone. On the other hand, the 2,3- ones show not only a weaker bonding, with the weakest value for isomer with n = 3, but also a larger variability of ΔE BE values (19.6 kcal/mol, Table S2). A look at the deformation energy term, ΔE def, shows that the previous differences in bonding energy cannot be justified with this component, since it varies in a small range (12.2–14.4 and 12.6–15.7 kcal/mol for 1,2- and 2,3-derivatives, respectively). With the exception of benzoquinone, the trend observed for the deformation energy is somewhat expected. First, there is an increase in deformation energy with the increase in size. This is expected if one takes into account that the larger the number of rings of the system, the more deformation is accumulated (each ring is a little bit deformed and contributes to the total deformation). This trend is lost when going from n = 2 to n = 3 in 2,3-quinones, but this is again not surprising given the fact that when going from 2,3-naphthoquinone to 2,3-anthraquinone, there is a change in the electronic state and, therefore, deformation energy in 2,3-naphthoquinone is not comparable to that of 2,3-anthraquinone. Then, we must find the corresponding explanation with the interaction energy term and its particular components (Eq. 5) depicted in Fig. 7.

The similarity of the trends between ΔE BE and ΔE int allows us to conclude that this latter term is responsible for the observed ΔE BE changes. Then, the relatively constant value of ΔE int in the 1,2-derivatives is also kept for the corresponding three components ΔE Pauli, ΔV elstat, and ΔE oi that show differences of only 8.3, 2.8, and 3.7 kcal/mol, respectively (see Table S2 in the Supplementary Material). On the other hand, for the 2,3-derivatives, the observed trend of ΔE int can be mainly attributed to the ΔE oi component, since changes in both repulsive ΔE Pauli and attractive ΔV elstat terms compensate each other. It is important to notice the much larger variability of these components for 2,3-isomers, amounting to 19.6, 9.8, and particularly 24.8 kcal/mol for ΔE Pauli, ΔV elstat, and ΔE oi, respectively.

More importantly, if we now decompose ΔE oi into ΔE σ and ΔE π contributions (Fig. 8), we can definitely affirm that the different behavior observed in 1,2- and 2,3-isomers can be mainly justified through this latter π-contribution, which causes the crucial variability with the change of the number of rings and gives the trend of ΔE BE observed in Fig. 6. Although the ΔE σ component provides most of the final ΔE oi term, the observed trend is basically due to the ΔE π contribution. Next, we will try to find the reason for such different behavior of this π-component between these isomers under analysis.

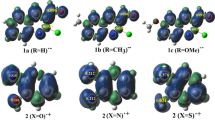
For this purpose, the overlaps 〈SOMOπ|SOMOπ〉 between the π single occupied molecular orbitals (SOMOπ) of each fragment have been calculated (Fig. 9). Let us remind that we consider each fragment at its quadruplet state, so we have two unpaired σ electrons and one unpaired electron on a π-orbital to form two σ- and one π-bonds in the final either 1,2- or 1,3-quinone derivatives. As it can be observed, the lowest overlap is found for 2,3-tetraquinone, thus justifying the above observed behavior concerning ΔE π.

Fig. 9
figure 9

Dependence of 〈SOMOπ|SOMOπ〉 overlaps between the orbitals with the unpaired π-electron of each fragment on the number of rings, n, of quinone derivatives. The red point denotes data for ortho-benzoquinone

Full size image

The higher 〈SOMOπ|SOMOπ〉 overlaps are easily understood from the inspection of the SOMOπ shapes of the ·C4n−2H2n–CH·· and ··CH–CO–CO· fragments depicted in Fig. 10 (SOMOπ of all ·C4n−2H2n–CH·· fragments are shown in Table S3). As can be seen, the π-interaction between these two fragments is more favorable when the ·C4n−2H2n–CH·· and ··CH–CO–CO· fragments interact to yield 1,2-quinones because the largest lobes of the two SOMOπ located in the CH moieties overlap in this particular 1,2-arrangement. The difference in overlap with the two dispositions is less for n = 2 and increases for n ≥ 3, following the same trend as the calculated 〈SOMOπ|SOMOπ〉 overlaps.

Fig. 10
figure 10

Graphical presentation of SOMOπ orbitals of the a ··CH–CO–CO·, b ·C6H4–CH··, and c ·C10H6–CH·· fragments

Full size image

Differences in shapes are also significant for σ-orbitals. The shapes of SOMOσ1 (Table S4) and SOMOσ2 (Table S5) are clearly different for 1,2- and 2,3-quinones. The corresponding orbital overlaps of these latter isomers are larger, in line with the stronger attractive σ-orbital interactions observed (see Fig. 8a). The graphical presentation of SOMOπ, SOMOσ1, and SOMOσ2 orbitals for the fragment with the C=O groups is given in Table S6, but as expected, their shapes are very similar for both quinone isomers.

Interrelations of σ- and π-electron energies for both types of derivatives are presented in Fig. 11. These relationships suggest a much more important contribution of π-electron structure as responsible for changes in σ-energy for the 2,3-quinone molecules than for 1,2-ones. Additionally, in the former case, a decrease in ΔE π is partially compensated by strengthening of σ-interactions. Moreover, it should be noted that ΔE σ describes changes of two σ-bonds, whereas ΔE π concerns only one bond. Therefore, at least for 2,3-derivatives, σ-type interactions can also be significant.

Fig. 11
figure 11

Relationship between ΔE σ and ΔE π for 1,2- and 2,3-quinone derivatives, data for ortho-benzoquinone are denoted by red point

Full size image

At this point, it would be worth comparing previous 1,2-naphthoquinone and 2,3-naphthoquinone isomers (Scheme 4) with phenanthrene and anthracene (Scheme 6). We can see that the two sets of isomers have a common fragment (the left one), although the other ones do not differ so much, as, in the sense that the two O atoms are changed by two HC=CH groups that are part of an aromatic six-membered ring. The corresponding EDA results for these systems (for phenanthrene and anthracene similar results were reported in Ref. [75]) are summarized in Table 1.

Scheme 6
scheme 6

Scheme of the fragmentation of phenanthrene (a) and anthracene (b)

Full size image
Table 1 Comparison of the EDA analysis for 1,2- and 2,3-naphthoquinone (Scheme 4) and their benzenoid analogues (Scheme 6) [75]. Energies in kcal/mol
Full size table

As in the case of quinone derivatives, 1,2-benzenoid analogue (phenanthrene) was found to be more stable than 2,3-one (anthracene). Again, we can observe that the main component which explains the stability differences in the two sets of isomers comes from the π-orbital interaction component (ΔE π), with a much higher variability in quinone derivatives than between anthracene and phenanthrene.

Finally, an important quantity related to stability of a given system is the hardness [58], η, defined by Eq. (14). Hardness is a measure of the resistance of chemical species to change its electronic configuration. As can be seen in Fig. 12, the HOMO–LUMO gaps of 1,2-systems are larger than for 2,3-ones, in line with greater stability of 1,2-derivatives (see Fig. 4) as well as the changes observed for kinked and straight phenanthrene and anthracene by some of us [75]. It is worth to note that for 1,2-quinones, the maximum is observed for 1,2-naphthoquinone, whereas in the case of 2,3-derivatives, HOMO–LUMO gap decreases monotonically with enlarging of the molecule. Dependences of HOMO and LUMO orbital energies on the number of rings for studied quinone derivatives are presented in Fig. S3. Energy of the HOMO increases (the value is less negative) in a regular way with increasing the number of rings for both isomers. LUMO energies of 1,2-quinones are higher than for 2,3-ones, according to greater stability of the former derivatives.

Fig. 12
figure 12

Hardness, η, (in eV) for 1,2- and 2,3-quinone derivatives with enlargement of the system by a consecutive ring, n

Full size image

4 Conclusions

As a whole, 1,2-quinone derivatives of linear benzenoids are more stable than their 2,3-quinone isomers. For these latter, from 2,3-anthraquinone to longer analogues, the diradical singlet state is the ground state structure. By means of the energy decomposition analysis (EDA), we showed that the larger stability of 1,2-quinones is due to stronger bonding that comes from stronger orbital interactions, in which π-contribution plays a main role. Better π-orbital interactions are a result of a more favorable overlap between the SOMOπ of the ·C4n−2H2n–CH·· and ··CH–CO–CO· fragments in the 1,2-arrangement. Interestingly, the influence of the π-orbital interactions on the relative stability between 1,2- and 2,3-naphthaquinones is larger than that observed between phenanthrene and anthracene. In both cases, the kinked isomers are favored due to better π-interactions.

Furthermore, 1,2-quinone derivatives present a monotonic change of the different analyzed properties: either structural (C=O bond lengths), aromatic (HOMA, FLU, MCI), or energetic criteria. At difference, 2,3-quinone isomers break this monotonic trend from 2,3-naphthoquinone to 2,3-anthroquinone in all the different measures. Again, through an EDA carried out with two equivalent fragments to form any of the two isomers, we can conclude that the orbital interactions in the π-system are the responsible for such difference.

Concerning the aromaticity analysis, for both isomers, the ring containing the quinoid fragment is antiaromatic, while electronic delocalization of the remaining rings is distributed differently. For 1,2-isomers, the aromaticity of the middle ring is the highest, whereas in the case of 2,3-isomers, the most aromatic is the terminal ring. Elongation of the system causes the decrease in the aromaticity of all rings in both cases.