Skip to main content
SpringerLink
Log in

Computer simulation of quantum dynamics in a classical spin environment

  • Regular Article
  • Published:
Theoretical Chemistry Accounts Aims and scope Submit manuscript

Abstract

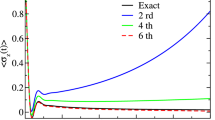
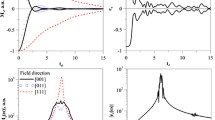
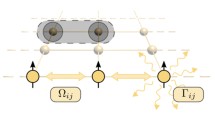
In this paper, a formalism for studying the dynamics of quantum systems coupled to classical spin environments is reviewed. The theory is based on generalized antisymmetric brackets and naturally predicts open-path off-diagonal geometric phases in the evolution of the density matrix. It is shown that such geometric phases must also be considered in the quantum–classical Liouville equation for a classical bath with canonical phase space coordinates; this occurs whenever the adiabatics basis is complex (as in the case of a magnetic field coupled to the quantum subsystem). When the quantum subsystem is weakly coupled to the spin environment, non-adiabatic transitions can be neglected and one can construct an effective non-Markovian computer simulation scheme for open quantum system dynamics in classical spin environments. In order to tackle this case, integration algorithms based on the symmetric Trotter factorization of the classical-like spin propagator are derived. Such algorithms are applied to a model comprising a quantum two-level system coupled to a single classical spin in an external magnetic field. Starting from an excited state, the population difference and the coherences of this two-state model are simulated in time while the dynamics of the classical spin is monitored in detail. It is the author’s opinion that the numerical evidence provided in this paper is a first step toward developing the simulation of quantum dynamics in classical spin environments into an effective tool. In turn, the ability to simulate such a dynamics can have a positive impact on various fields, among which, for example, nanoscience.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Kapral R, Sergi A (2005) Dynamics of condensed phase proton and electron transfer processes, vol. 1, ch. 92. In: Rieth M, Schommers W (eds) Handbook of theoretical and computational nanotechnology. American Scientific Publishers, Valencia, CA

    Google Scholar 

  2. Likharev KK (1996) Dynamics of Josephson junctions and circuits. CRC Press, Amsterdam

    Google Scholar 

  3. Hayashi T, Fujisawa T, Cheong HD, Jeong YH, Hirayama Y (2003) Coherent manipulation of electronic states in a double quantum dot. Phys Rev Lett 91:226804

    Article  CAS  Google Scholar 

  4. Petta JR, Johnson AC, Marcus CM, Hanson MP, Gossard AC (2004) Manipulation of a single charge in a double quantum dot. Phys Rev Lett 93:186802

    Article  CAS  Google Scholar 

  5. Petta JR, Johnson AC, Taylor JM, Laird EA, Yacoby A, Lukin MD, Marcus CM, Hanson MP, Gossard AC (2005) Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309:2180–2184

    Article  CAS  Google Scholar 

  6. Leggett AJ, Chakravarty S, Dorsey AT, Fisher MPA, Garg A, Zwerger W (1987) Dynamics of the dissipative two-state system. Rev Mod Phys 59:1–85

    Article  CAS  Google Scholar 

  7. Prokof’ev NV, Stamp PCE (2000) Theory of the spin bath. Rep Prog Phys 63:669–726

    Article  Google Scholar 

  8. Breuer H-P, Petruccione F (2002) The theory of open quantum systems. Oxford University Press, Oxford

    Google Scholar 

  9. Ottinger HC (2005) Beyond equilibrium thermodynamics. Wiley, Hoboken

    Book  Google Scholar 

  10. Ottinger HC (2000) Derivation of a two-generator framework of nonequilibrium thermodynamics for quantum system. Phys Rev E 62:4720

    Article  CAS  Google Scholar 

  11. Ottinger HC (2010) Nonlinear thermodynamic quantum master equation: properties and examples. Phys Rev A 82:052119

    Article  Google Scholar 

  12. Ottinger HC (2011) Euro Phys. Lett. 94:10006

    Article  Google Scholar 

  13. Ottinger HC (2012) Stochastic process behind nonlinear thermodynamic quantum master equation. I. Mean-field construction. Phys Rev A 86:032101

    Google Scholar 

  14. Flakowski J, Schweizer M, Ottinger HC (2012) Stochastic process behind nonlinear thermodynamic quantum master equation. II. Simulation. Phys Rev A 86:032102

    Article  Google Scholar 

  15. Sergi A (2013) Communication: quantum dynamics in classical spin baths. J Chem Phys 139:031101

    Article  Google Scholar 

  16. Anderson A (1995) Quantum backreaction on “classical” variables. Phys Rev Lett 74:621–625

    Article  CAS  Google Scholar 

  17. Prezhdo O, Kisil VV (1997) Mixing quantum and classical mechanics. Phys Rev A 56:162–176

    Article  CAS  Google Scholar 

  18. Zhang WY, Balescu R (1988) Statistical mechanics of a spin polarized plasma. J Plasma Phys 40:199–213

    Article  Google Scholar 

  19. Balescu R, Zhang WY (1988) Kinetic equation, spin hydrodynamics and collisional depolarization rate in a spin-polarized plasma. J Plasma Phys 40:215–234

    Article  Google Scholar 

  20. Osborn TA, Kondrat’eva MF, Tabisz GC, McQuarrie BR (1999) Mixed Weyl symbol calculus and spectral line shape theory. J Phys A 32:4149–4169

    Article  Google Scholar 

  21. Gerasimenko VI (1982) Dynamical equations of quantum–classical systems. Teoret Mat Fiz 50:77–87

    Google Scholar 

  22. Boucher W, Traschen J (1988) Semiclassical physics and quantum fluctuations. Phys Rev D 37:3522–3532

    Article  CAS  Google Scholar 

  23. Martens CC, Fang J-Y (1996) Semiclassical limit molecular dynamics on multiple electronic surfaces. J Chem Phys 106:4918–4930

    Article  Google Scholar 

  24. Kapral R, Ciccotti G (1999) Mixed quantum–classical dynamics. J Chem Phys 110:8919–8929

    Article  CAS  Google Scholar 

  25. Horenko I, Salzmann C, Schmidt B, Schutte C (2002) Quantum–classical Liouville approach to molecular dynamics: surface hopping gaussian phase-space packets. J Chem Phys 117:11075–11088

    Article  CAS  Google Scholar 

  26. Shi Q, Geva E (2004) A derivation of the mixed quantum–classical liouville equation from the influence functional formalism. J Chem Phys 121:3393–3404

    Article  CAS  Google Scholar 

  27. Sergi A, Sinayskiy I, Petruccione F (2009) Numerical and analytical approach to the quantum dynamics of two coupled spins in bosonic baths. Phys Rev A 80:012108

    Article  Google Scholar 

  28. Allen MP, Tildesley DJ (2009) Computer simulation of liquids. Oxford University Press, Oxford

    Google Scholar 

  29. Frenkel D, Smit B (2002) Understanding molecular simulation. Academic Press, London

    Google Scholar 

  30. Sergi A (2005) Non-Hamiltonian commutators in quantum mechanics. Phys Rev E 72:066125

    Article  Google Scholar 

  31. Sergi A (2007) Deterministic constant-temperature dynamics for dissipative quantum systems. J Phys A: Math Theor 40:F347–F354

    Article  Google Scholar 

  32. Sergi A (2006) Statistical mechanics of quantum–classical systems with holonomic constraints. J Chem Phys 124:024110

    Article  Google Scholar 

  33. Sergi A, Ferrario M (2001) Non-Hamiltonian equations of motion with a conserved energy. Phys Rev E 64:056125

    Article  CAS  Google Scholar 

  34. Sergi A (2003) Non-Hamiltonian equilibrium statistical mechanics. Phys Rev E 67:021101

    Article  Google Scholar 

  35. Sergi A, Giaquinta PV (2007) On the geometry and entropy of non-Hamiltonian phase space. J Stat Mech Theory Exp 02:P02013

    Google Scholar 

  36. Sergi A (2004) Generalized bracket formulation of constrained dynamics in phase space. Phys Rev E 69:021109

    Article  Google Scholar 

  37. Sergi A (2005) Phase space flows for non-Hamiltonian systems with constraints. Phys Rev E 72:031104

    Article  Google Scholar 

  38. de Polavieja GG, Sjöqvist E (1998) Extending the quantal adiabatic theorem: geometry of noncyclic motion. Am J Phys 66:431–438

    Article  Google Scholar 

  39. Mead CA, Truhlar DG (1979) On the determination of born-oppenheimer nuclear motion wave functions including complications due to conical intersections and identical nuclei. J Chem Phys 70:2284–2296

    Article  CAS  Google Scholar 

  40. Berry MV (1984) Quantal phase factors accompanying adiabatic changes. Proc R Soc Lond Ser A 392:45–57

    Article  Google Scholar 

  41. Shapere A, Wilczek F (eds) (1989) Geometric phases in physics. World Scientific, Singapore

    Google Scholar 

  42. Mead CA (1992) The geometric phase in molecular systems. Rev Mod Phys 64:51–85

    Article  CAS  Google Scholar 

  43. Kuratsuji H, Iida S (1985) Effective action for adiabatic process. Prog Theor Phys 74:439–445

    Article  Google Scholar 

  44. Tuckerman M, Martyna GJ, Berne BJ (1992) Reversible multiple time scale molecular dynamics. J Chem Phys 97:1990–2001

    Article  CAS  Google Scholar 

  45. Martyna GJ, Tuckerman M, Tobias DJ, Klein ML (1996) Explicit reversible integrators for extended systems dynamics. Mol Phys 87:1117–1157

    Article  CAS  Google Scholar 

  46. Sergi A, Ferrario M, Costa D (1999) Reversible integrators for basic extended system molecular dynamics. Mol Phys 97:825–832

    Article  CAS  Google Scholar 

  47. Ezra GS (2006) Reversible measure-preserving integrators for non-Hamiltonian systems. J Chem Phys 125:034104

    Article  Google Scholar 

  48. Sergi A, Ezra GS (2010) Bulgac-Kusnezov-Nose-Hoover thermostats. Phys Rev E 81:036705

    Article  Google Scholar 

  49. Sergi A, Ezra GS, Bulgac–Kusnezov–Nosé-Hoover thermostats for spins, unpublished

  50. Nielsen S, Kapral R, Ciccotti G (2001) Statistical mechanics of quantum–classical systems. J Chem Phys 115:5805–5815

    Article  CAS  Google Scholar 

  51. Sergi A, Giaquinta PV (2007) On computational strategies in molecular dynamics simulation. Phys Essays 20:629–640

    Article  Google Scholar 

  52. Pati AK (1998) Adiabatic berry phase and Hannay angle for open paths. Ann Phys 270:178–197

    Article  CAS  Google Scholar 

  53. Filipp S, Sjöqvist E (2003) Off-diagonal generalization of the mixed-state geometric phase. Phys Rev A 68:042112

    Article  Google Scholar 

  54. Englman R, Yahalom A, Baer M (2000) The open path phase for degenerate and non-degenerate systems and its relation to the wave function and its modulus. Eur Phys J D 8:1–7

    Article  CAS  Google Scholar 

  55. Manini N, Pistolesi F (2000) Off-diagonal geometric phases. Phys Rev Lett 85:3067–3071

    Article  CAS  Google Scholar 

  56. Frank J, Huang W (1997) Leimkuhler geometric integrators for classical spin systems. J Comput Phys 133:160–172

    Article  Google Scholar 

  57. Krech M, Bunker A, Landau DP (1998) Fast spin dynamics algorithms for classical spin systems. Comput Phys Commun 111:1–13

    Article  CAS  Google Scholar 

  58. Steinigeweg R, Schmidt H-J (2006) Symplectic integrators for classical spin systems comput. Phys Commun 174:853–861

    Article  CAS  Google Scholar 

  59. Yoshida H (1990) Construction of higher order symplectic integrators. Phys Lett A 150:262–268

    Article  Google Scholar 

Download references

Acknowledgments

The author is grateful to G. S. Ezra for many discussions, encouragement and support received in the past few years.

Author information

Authors and Affiliations

  1. School of Chemistry and Physics, University of KwaZulu-Natal, Private Bag X01, Scottsville, Pietermaritzburg, 3209, South Africa

    Alessandro Sergi

  2. National Institute of Theoretical Physics (NITheP), Durban, KwaZulu-Natal, South Africa

    Alessandro Sergi

Authors
  1. Alessandro Sergi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alessandro Sergi.

Additional information

Dedicated to Professor Greg Ezra and published as part of the special collection of articles celebrating his 60th birthday.

This work is based upon research supported by the National Research Foundation of South Africa.

Appendices

Appendix 1: Integration algorithm on the (1, 1) surface

In pseudo-code form, the algorithm provided by \(U_{(1,1)}^1(\tau )\) is:

$$\begin{aligned} U_{1,(1,1)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left\{ \frac{3}{2}C_1C_3\frac{\tau }{4} +[C_2+C_1S_x]^{\frac{3}{2}} \right\} ^{\frac{2}{3}}\\ \quad-\frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(142)
$$\begin{aligned} U_{2,(1,1)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ S_x \rightarrow S_x - \frac{\tau }{2} S_y \left( S_z-c_2b\right) \right. , \end{aligned}$$
(143)
$$\begin{aligned} U_{1,(1,1)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left\{ \frac{3}{2}C_1C_3\frac{\tau }{4} +[C_2+C_1S_x]^{\frac{3}{2}} \right\} ^{\frac{2}{3}}\\ \quad- \frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(144)
$$\begin{aligned} U_{(1,1)}^{S_y}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y +\frac{\tau }{2} \left[ \frac{\mu S_x(b+\mu S_z)-\mu (\Omega +S_x)S_z}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad + S_x\left. \left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(145)
$$\begin{aligned} U_{(1,1)}^{S_z}(\tau ):\left\{ \begin{array}{l} S_z \rightarrow \frac{B_2}{B_1} - \frac{1}{B_1}\left[ \left( B_2 - B_1S_z\right) ^{\frac{3}{2}}\right. \\ \quad-\left. \frac{3 B_1 B_3\tau }{2}\right] ^{\frac{2}{3}}, \end{array} \right. \end{aligned}$$
(146)
$$\begin{aligned} U_{(1,1)}^{S_y}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y +\frac{\tau }{2} \left[ \frac{\mu S_x(b+\mu S_z)-\mu (\Omega +S_x)S_z}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad +\left. S_x\left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(147)
$$\begin{aligned} U_{2,(1,1)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ S_x \rightarrow S_x - \frac{\tau }{2} S_y \left( S_z-c_2b\right) \right. ,\end{aligned}$$
(148)
$$\begin{aligned} U_{1,(1,1)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left\{ \frac{3}{2}C_1C_3\frac{\tau }{4} +[C_2+C_1S_x]^{\frac{3}{2}} \right\} ^{\frac{2}{3}}\\ \quad -\frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(149)
$$\begin{aligned} U_{1,(1,1)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow\frac{1}{C_1}\left\{ \frac{3}{2}C_1C_3\frac{\tau }{4} +[C_2+C_1S_x]^{\frac{3}{2}} \right\} ^{\frac{2}{3}}\\ \quad -\frac{C_2}{C_1}. \end{array} \right. \end{aligned}$$
(150)

The algorithm provided by \(U_{(1,1)}^2(\tau )\) is:

$$\begin{aligned} U_{(1,1)}^{S_z}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_z \rightarrow \frac{B_2}{B_1}\\ \quad - \frac{1}{B_1}\left\{ \left[ B_2 - B_1S_z\right] ^{\frac{3}{2}} -\frac{3 B_1 B_3\tau }{4}\right\} ^{\frac{2}{3}}, \end{array} \right. \end{aligned}$$
(151)
$$\begin{aligned} U_{1,(1,1)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left\{ \frac{3}{2}C_1C_3\frac{\tau }{4} +[C_2+C_1S_x]^{\frac{3}{2}}\right\} ^{\frac{2}{3}}\\ \quad -\frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(152)
$$\begin{aligned} U_{2,(1,1)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ S_x \rightarrow S_x - \frac{\tau }{2} S_y \left( S_z-c_2b\right) \right. ,\end{aligned}$$
(153)
$$\begin{aligned} U_{1,(1,1)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left\{ \frac{3}{2}C_1C_3\frac{\tau }{4} +[C_2+C_1S_x]^{\frac{3}{2}}\right\} ^{\frac{2}{3}}\\ \quad -\frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(154)
$$\begin{aligned} U_{(1,1)}^{S_y}(\tau ):\left\{ \begin{array}{l} S_y \rightarrow S_y +\tau \left[ \frac{\mu S_x(b+\mu S_z)-\mu (\Omega +S_x)S_z}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad + \left. S_x\left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(155)
$$\begin{aligned} U_{1,(1,1)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow\frac{1}{C_1}\left\{ \frac{3}{2}C_1C_3\frac{\tau }{4} +[C_2+C_1S_x]^{\frac{3}{2}} \right\} ^{\frac{2}{3}}\\ \quad-{}\frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(156)
$$\begin{aligned} U_{2,(1,1)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ S_x \rightarrow S_x - \frac{\tau }{2} S_y \left( S_z-c_2b\right) \right. , \end{aligned}$$
(157)
$$\begin{aligned} U_{1,(1,1)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left\{ \frac{3}{2}C_1C_3\frac{\tau }{4} +[C_2+C_1S_x]^{\frac{3}{2}} \right\} ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(158)
$$\begin{aligned} U_{(1,1)}^{S_z}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_z \rightarrow \frac{B_2}{B_1} \\ \quad- \frac{1}{B_1}\left\{ \left[ B_2 - B_1S_z\right] ^{\frac{3}{2}} -\frac{3 B_1 B_3\tau }{4}\right\} ^{\frac{2}{3}}. \end{array} \right. \end{aligned}$$
(159)

The algorithm provided by \(U_{(1,1)}^3(\tau )\) is:

$$\begin{aligned} U_{(1,1)}^{S_y}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y +\frac{\tau }{4} \left[ \frac{\mu S_x(b+\mu S_z)-\mu (\Omega +S_x)S_z}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad +\left. S_x\left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(160)
$$\begin{aligned} U_{(1,1)}^{S_z}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_z \rightarrow \frac{B_2}{B_1} \\ \quad- \frac{1}{B_1}\left[ \left( B_2 - B_1S_z\right) ^{\frac{3}{2}} -\frac{3 B_1 B_3\tau }{4}\right] ^{\frac{2}{3}}, \end{array} \right. \end{aligned}$$
(161)
$$\begin{aligned} U_{(1,1)}^{S_y}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y +\frac{\tau }{4} \left[ \frac{\mu S_x(b+\mu S_z)-\mu (\Omega +S_x)S_z}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad+\left. S_x\left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(162)
$$\begin{aligned} U_{1,(1,1)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left\{ \frac{3}{2}C_1C_3\frac{\tau }{2} +[C_2+C_1S_x]^{\frac{3}{2}} \right\} ^{\frac{2}{3}}\\ \quad -\frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(163)
$$\begin{aligned} U_{2,(1,1)}^{S_x}(\tau ):\left\{ S_x \rightarrow S_x - \tau S_y\left( S_z-c_2b\right) \right. ,\end{aligned}$$
(164)
$$\begin{aligned} U_{1,(1,1)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{ll} S_x \rightarrow \frac{1}{C_1}\left\{ \frac{3}{2}C_1C_3\frac{\tau }{2} +[C_2+C_1S_x]^{\frac{3}{2}} \right\} ^{\frac{2}{3}}\\ \quad -\frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(165)
$$\begin{aligned} U_{(1,1)}^{S_y}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y +\frac{\tau }{4} \left[ \frac{\mu S_x(b+\mu S_z) -\mu (\Omega +S_x)S_z}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad + \left. S_x\left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(166)
$$\begin{aligned} U_{(1,1)}^{S_z}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_z \rightarrow \frac{B_2}{B_1} \\ \quad - \frac{1}{B_1}\left[ \left( B_2 - B_1S_z\right) ^{\frac{3}{2}} -\frac{3 B_1 B_3\tau }{4}\right] ^{\frac{2}{3}}, \end{array} \right. \end{aligned}$$
(167)
$$\begin{aligned} U_{(1,1)}^{S_y}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y +\frac{\tau }{4} \left[ \frac{\mu S_x(b+\mu S_z)-\mu (\Omega +S_x)S_z}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad + \left. S_x\left( S_z-c_2b\right) \right] . \end{array} \right. \end{aligned}$$
(168)

Appendix 2: Integration algorithm on the (2, 2) surface

The algorithm provided by \(U_{(2,2)}^1(\tau )\) is

$$\begin{aligned} U_{1,(2,2)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left[ -\frac{3}{2}C_1C_3\frac{\tau }{4} +\left( C_2+C_1S_x\right) ^{\frac{3}{2}} \right] ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(169)
$$\begin{aligned} U_{2,(2,2)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ S_x \rightarrow S_x -\frac{\tau }{2} S_y \left( S_z-c_2b\right) \right. ,\end{aligned}$$
(170)
$$\begin{aligned} U_{1,(2,2)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left[ -\frac{3}{2}C_1C_3\frac{\tau }{4} +\left( C_2+C_1S_x\right) ^{\frac{3}{2}} \right] ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(171)
$$\begin{aligned} U_{(2,2)}^{S_y}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y + \frac{\tau }{2}\left[ \frac{\mu (\Omega +S_x)S_z-\mu S_x(b+\mu S_z)}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad + \left. S_x\left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(172)
$$\begin{aligned} U_{(2,2)}^{S_z}(\tau ):\left\{ \begin{array}{l} S_z \rightarrow \frac{B_2}{B_1} \\ \quad - \frac{1}{B_1}\left[ \left( B_2-B_1S_z\right) ^{\frac{3}{2}} + \frac{3}{2} B_1B_3 \tau \right] ^{\frac{2}{3}}, \end{array} \right. \end{aligned}$$
(173)
$$\begin{aligned} U_{(2,2)}^{S_y}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y + \frac{\tau }{2}\left[ \frac{\mu (\Omega +S_x)S_z-\mu S_x(b+\mu S_z)}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad + \left. S_x\left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(174)
$$\begin{aligned} U_{1,(2,2)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left[ -\frac{3}{2}C_1C_3\frac{\tau }{4} +\left( C_2+C_1S_x\right) ^{\frac{3}{2}}\right] ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(175)
$$\begin{aligned} U_{2,(2,2)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ S_x \rightarrow S_x -\frac{\tau }{2} S_y\left( S_z-c_2b\right) \right. ,\end{aligned}$$
(176)
$$\begin{aligned} U_{1,(2,2)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left[ -\frac{3}{2}C_1C_3\frac{\tau }{4} +\left( C_2+C_1S_x\right) ^{\frac{3}{2}} \right] ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}. \end{array} \right. \end{aligned}$$
(177)

The algorithm provided by \(U_{(2,2)}^2(\tau )\) is

$$\begin{aligned} U_{(2,2)}^{S_z}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_z \rightarrow \frac{B_2}{B_1} \\ \quad - \frac{1}{B_1}\left[ \left( B_2-B_1S_z\right) ^{\frac{3}{2}} + \frac{3}{2} B_1B_3 \frac{\tau }{2}\right] ^{\frac{2}{3}}, \end{array} \right. \end{aligned}$$
(178)
$$\begin{aligned} U_{1,(2,2)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left[ -\frac{3}{2}C_1C_3\frac{\tau }{4} +\left( C_2+C_1S_x\right) ^{\frac{3}{2}} \right] ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}, \end{array} \right. , \end{aligned}$$
(179)
$$\begin{aligned} U_{2,(2,2)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ S_x \rightarrow S_x -\frac{\tau }{2} S_y \left( S_z-c_2b\right) \right. ,\end{aligned}$$
(180)
$$\begin{aligned} U_{1,(2,2)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left[ -\frac{3}{2}C_1C_3\frac{\tau }{4} +\left( C_2+C_1S_x\right) ^{\frac{3}{2}} \right] ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(181)
$$\begin{aligned} U_{(2,2)}^{S_y}(\tau ):\left\{ \begin{array}{l} S_y \rightarrow S_y + \tau \left[ \frac{\mu (\Omega +S_x)S_z-\mu S_x(b+\mu S_z)}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad + \left. S_x\left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(182)
$$\begin{aligned} U_{1,(2,2)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left[ -\frac{3}{2}C_1C_3\frac{\tau }{4} +\left( C_2+C_1S_x\right) ^{\frac{3}{2}} \right] ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(183)
$$\begin{aligned} U_{2,(2,2)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ S_x \rightarrow S_x -\frac{\tau }{2} S_y\left( S_z-c_2b\right) \right. ,\end{aligned}$$
(184)
$$\begin{aligned} U_{1,(2,2)}^{S_x}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left[ -\frac{3}{2}C_1C_3\frac{\tau }{4} +\left( C_2+C_1S_x\right) ^{\frac{3}{2}} \right] ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(185)
$$\begin{aligned} U_{(2,2)}^{S_z}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_z \rightarrow \frac{B_2}{B_1} \\ \quad - \frac{1}{B_1}\left[ \left( B_2-B_1S_z\right) ^{3/2} + \frac{3}{2} B_1B_3 \frac{\tau }{2}\right] ^{2/3}. \end{array} \right. \end{aligned}$$
(186)

The algorithm provided by \(U_{(2,2)}^3(\tau )\) is

$$\begin{aligned} U_{(2,2)}^{S_y}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y + \frac{\tau }{4}\left[ \frac{\mu (\Omega +S_x)S_z-\mu S_x(b+\mu S_z)}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad + \left. S_x\left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(187)
$$\begin{aligned} U_{(2,2)}^{S_z}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_z \rightarrow \frac{B_2}{B_1} \\ \quad - \frac{1}{B_1}\left[ \left( B_2-B_1S_z\right) ^{\frac{3}{2}} + \frac{3}{2} B_1B_3 \frac{\tau }{2}\right] ^{\frac{2}{3}}, \end{array} \right. \end{aligned}$$
(188)
$$\begin{aligned} U_{(2,2)}^{S_y}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y + \frac{\tau }{4}\left[ \frac{\mu (\Omega +S_x)S_z-\mu S_x(b+\mu S_z)}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad + \left. S_x \left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(189)
$$\begin{aligned} U_{1,(2,2)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left[ -\frac{3}{2}C_1C_3\frac{\tau }{2} +\left( C_2+C_1S_x\right) ^{\frac{3}{2}}\right] ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(190)
$$\begin{aligned} U_{2,(2,2)}^{S_x}(\tau ):\left\{ S_x \rightarrow S_x -\tau S_y\left( S_z-c_2b\right) \right. ,\end{aligned}$$
(191)
$$\begin{aligned} U_{1,(2,2)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_x \rightarrow \frac{1}{C_1}\left[ -\frac{3}{2}C_1C_3\frac{\tau }{2} +\left( C_2+C_1S_x\right) ^{\frac{3}{2}} \right] ^{\frac{2}{3}}\\ \quad - \frac{C_2}{C_1}, \end{array} \right. \end{aligned}$$
(192)
$$\begin{aligned} U_{(2,2)}^{S_y}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y + \frac{\tau }{4}\left[ \frac{\mu (\Omega +S_x)S_z-\mu S_x(b+\mu S_z)}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}}\right. \\ \quad + \left. S_x\left( S_z-c_2b\right) \right] , \end{array} \right. \end{aligned}$$
(193)
$$\begin{aligned} U_{(2,2)}^{S_z}\left( \frac{\tau }{2}\right):\left\{ \begin{array}{l} S_z \rightarrow \frac{B_2}{B_1}\\ \quad - \frac{1}{B_1}\left[ \left( B_2-B_1S_z\right) ^{\frac{3}{2}} + \frac{3}{2} B_1B_3 \frac{\tau }{2}\right] ^{\frac{2}{3}}, \end{array} \right. \end{aligned}$$
(194)
$$\begin{aligned} U_{(2,2)}^{S_y}\left( \frac{\tau }{4}\right):\left\{ \begin{array}{l} S_y \rightarrow S_y + \frac{\tau }{4}\left[ \frac{\mu (\Omega +S_x)S_z-\mu S_x(b+\mu S_z)}{\sqrt{C^2+2\mu (\Omega S_x - c_1 b S_z)}} \right. \\ \quad + \left. S_x\left( S_z-c_2b\right) \right] . \end{array} \right. \end{aligned}$$
(195)

Appendix 3: Integration algorithm on the \((1,2)\) surface

The algorithm provided by \(U_{(1,2)}^1(\tau )\) is

$$\begin{aligned} U_{(1,2)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ S_x \rightarrow S_x - \frac{\tau }{2}S_y\left( S_z-c_2b\right) \right. ,\end{aligned}$$
(196)
$$\begin{aligned} U_{(1,2)}^{S_y}(\tau ):\left\{ S_y \rightarrow S_y +\tau S_x\left( S_z-c_2b\right) \right. , \end{aligned}$$
(197)
$$\begin{aligned} U_{(1,2)}^{S_x}\left( \frac{\tau }{2}\right):\left\{ S_x \rightarrow S_x - \frac{\tau }{2}S_y\left( S_z-c_2b\right) \right. . \end{aligned}$$
(198)

The algorithm provided by \(U_{(1,2)}^2(\tau )\) is

$$\begin{aligned} U_{(1,2)}^{S_y}\left( \frac{\tau }{2}\right):\left\{ S_y \rightarrow S_y +\frac{\tau }{2} S_x\left( S_z-c_2b\right) \right. ,\end{aligned}$$
(199)
$$\begin{aligned} U_{(1,2)}^{S_x}(\tau ):\left\{ S_x \rightarrow S_x - \tau S_y\left( S_z-c_2b\right) \right. ,\end{aligned}$$
(200)
$$\begin{aligned} U_{(1,2)}^{S_y}\left( \frac{\tau }{2}\right):\left\{ S_y \rightarrow S_y +\frac{\tau }{2} S_x\left( S_z-c_2b\right) \right. . \end{aligned}$$
(201)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sergi, A. Computer simulation of quantum dynamics in a classical spin environment. Theor Chem Acc 133, 1495 (2014). https://doi.org/10.1007/s00214-014-1495-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00214-014-1495-4

Keywords

Search

Navigation