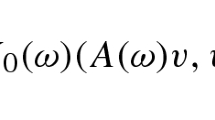1 Introduction

The main objective of this paper is to combine two successful strategies from the literature: the first being operator splitting schemes for evolution equations on general, infinite dimensional frameworks and the second being stochastic optimization methods. Operator splitting schemes are an established tool in the field of numerical analysis of evolution equations and have a wide range of applications. Stochastic optimization methods have proven to be efficient at solving large-scale optimization problems, where it is infeasible to evaluate full gradients. They can drastically decrease the computational cost in e.g. machine learning settings. The link between these two seemingly disparate areas is that an iterative method applied to an optimization problem can also be seen as a time-stepping method applied to a gradient flow connected to the optimization problem. In particular, stochastic optimization methods can then be interpreted as randomized operator splitting schemes for such gradient flows. In this context, we introduce a general randomized splitting method that can be applied directly to evolution equations, and provide a rigorous convergence analysis.

Abstract evolution equations of the type

$$\begin{aligned} {\left\{ \begin{array}{ll} u'(t) + A(t)u(t) = f(t), \quad t \in (0,T],\\ u(0) = u_0 \end{array}\right. } \end{aligned}$$

are an important building block for modeling processes in physics, biology and social sciences. Standard examples which appear in a variety of applications are fluid flow problems, where we model how a flow evolves on a given domain over time, compare [1, 26] and [37, Section 1.3]. The operator A(t) can denote, for example, a non-linear diffusion operator such as the p-Laplacian or a porous medium operator.

Deterministic operator splitting schemes as discussed in more detail in [16] are a powerful tool for this type of equation. An example is given by a domain decomposition scheme, where we split the domain into sub-domains. Instead of solving one expensive problem on the entire domain, we deal with cheaper problems on the sub-domains. This is particularly useful in modern computer architectures, as the sub-problems may often be solved in parallel.

Moreover, evolution equations are tightly connected to unconstrained optimization problems, because the solution of \(\min _u F(u)\) is a stationary point of the gradient flow \(u'(t) = -\nabla F(u(t))\). The latter is an evolution equation on an infinite time horizon with \(A = -\nabla F\) and \(f = 0\). In the large-scale case, such optimization problems benefit from stochastic optimization schemes. The most basic such method, the stochastic gradient descent, was first introduced already in [32], but since then it has been extended and generalized in many directions. See, e.g., the review article [3] and the references therein.

Via the gradient flow interpretation, we can see these optimization methods as time-stepping schemes where a randomly chosen sub-problem is considered in each time step. In essence, it is therefore a randomized operator splitting scheme. The difference between the works mentioned above and ours is that we apply these stochastic optimization techniques to solve the evolution equation itself rather than just finding its stationary state.

We consider nonlinear evolution equations in an abstract framework similar to [7, 10, 11] where operators of a monotone type have been studied. Deterministic splitting schemes for such equations has been considered in e.g. [14, 15, 17, 29]. A particular kind of splitting schemes which is most closely related to our work, domain decomposition methods, have been studied in [6, 7, 13, 30, 31]. In this paper, we extend this framework of deterministic splitting schemes to a setting of randomized methods.

Outside of the context of optimization, other kinds of randomized methods have already proved themselves to be useful for solving evolution equations. Starting in [34, 35] explicit schemes for ordinary differential equations have been randomized. This approach has been further extended in [2, 4, 18, 22, 24]. In [8], it has been extended both to implicit methods and to partial differential equations and in [23] to finite element approximations. While these works considered certain randomizations in their schemes, they are conceptually different from our approach. Their main idea is to approximate any appearing integrals through

$$\begin{aligned} \int _{t_{n-1}}^{t_n} f(t) \,\textrm{d}t \approx f(\xi _n) \quad \text {and} \quad \int _{t_{n-1}}^{t_n} A(t)v \,\textrm{d}t \approx A(\xi _n) v, \end{aligned}$$

where \(\xi _n\) is a random variable that takes on values in \([t_{n-1}, t_n]\). This ansatz coincides with a Monte Carlo integration idea. In this paper, we use a different approach where we decompose the operator in a randomized fashion. More precisely, we approximate data

$$\begin{aligned} f = \frac{1}{s}\sum _{\ell = 1}^{s} f_{\ell } \quad \text {and} \quad A = \frac{1}{s}\sum _{\ell = 1}^{s} A_{\ell } \end{aligned}$$

by

$$\begin{aligned} f_B = \frac{1}{|B |}\sum _{\ell \in B} f_{\ell } \quad \text {and} \quad A_B = \frac{1}{|B |}\sum _{\ell \in B} A_{\ell } \end{aligned}$$

where the batch \(B \subset \{1,\dots ,s\}\) is chosen randomly. The stochastic approximations \(f_B\) and \(A_B\) of the original data f and A are cheaper to evaluate in applications. This is less related to Monte Carlo integration and more similar to stochastic optimization methods, compare [3, 9]. Similar ideas have been considered in [19, 20, 28], where a random batch method for interacting particle systems has been studied. Moreover, very recently and during the preparation of this work, a similar approach has also been applied to the optimal control of linear time invariant (LTI) dynamical systems in [38]. While the convergence rate provided there is essentially the same as what we establish in our main result Theorem 5.2, our setting is more general and allows for nonlinear operators on infinite dimensional spaces rather than finite dimensional matrices. We also consider the error of the time stepping method that is used to approximate the solution to \(u'(t) + A_B(t)u(t) = f_B(t)\), while the error bounds in [38] assume that this evolution equation is solved exactly.

This paper is organized as follows. In Sect. 2, we begin by explaining our abstract framework. This includes both the precise assumptions that we make and the definition of our time-stepping scheme. We give a more concrete application of the abstract framework in Sect. 3. With the setting fixed, we first prove in Sect. 4 that the scheme and its solution are indeed well-defined. We prove the convergence of the scheme in expectation in Sect. 5. These theoretical convergence results are illustrated by numerical experiments with two-dimensional linear and quasilinear nonlinear and linear diffusion problem in Sect. 6. Finally, we collect some more technical auxiliary results in Appendix A.

2 Setting

In the following, we introduce a theoretical framework for the randomized operator splitting. This setting is similar to the one in [7].

Assumption 2.1

Let \((H,( \cdot , \cdot )_{H},\Vert \cdot \Vert _H)\) be a real, separable Hilbert space and let \((V, \Vert \cdot \Vert _V)\) be a real, separable, reflexive Banach space, which is continuously and densely embedded into H. Moreover, there exists a semi-norm \(|\cdot |_V\) on V and a \(C_V \in (0,\infty )\) such that \(|\cdot |_V \le C_V \Vert \cdot \Vert _V\).

Denoting the dual space of V by \(V^*\) and identifying the Hilbert space H with its dual space, the spaces from Assumption 2.1 form a Gelfand triple and fulfill, in particular,

$$\begin{aligned} V \overset{d}{\hookrightarrow }\ H \cong H^* \overset{d}{\hookrightarrow }\ V^*. \end{aligned}$$

Assumption 2.2

Let the spaces H and V be given as stated in Assumption 2.1. Furthermore, for \(T \in (0,\infty )\) as well as \(p \in [2,\infty )\), let \(\{A(t)\}_{t \in [0,T]}\) be a family of operators \(A(t) :V \rightarrow V^*\) that satisfy the following conditions:

  1. (i)

    The mapping \(Av :[0,T] \rightarrow V^*\) given by \(t \mapsto A(t)v\) is continuous almost everywhere in (0, T) for all \(v \in V\).

  2. (ii)

    The operator \(A(t) :V \rightarrow V^*\), \(t \in [0,T]\), is radially continuous, i.e., the mapping \(s \mapsto \langle A(t)(v+s w), w \rangle _{V^*\times V}\) is continuous on [0, 1] for all \(v,w \in V\).

  3. (iii)

    There exists \(\kappa _A \in [0,\infty )\) and \(\eta _A \in [0,\infty )\), which do not depend on t, such that the operator \(A(t) + \kappa _A I :V \rightarrow V^*\), \(t \in [0,T]\), fulfills the monotonicity-type condition

    $$\begin{aligned} \langle A(t)v - A(t)w, v - w \rangle _{V^*\times V} + \kappa _A \Vert v - w\Vert _H^2 \ge \eta _A |v - w |_V^p \end{aligned}$$

    for all \(v,w \in V\).

  4. (iv)

    The operator \(A(t) :V \rightarrow V^*\), \(t \in [0,T]\), is uniformly bounded such that there exists \(\beta _A \in [0,\infty )\), which does not depend on t, with

    $$\begin{aligned} \Vert A(t) v \Vert _{V^*} \le \beta _A \big (1 + \Vert v\Vert _V^{p-1}\big ) \end{aligned}$$

    for all \(v \in V\).

Assumption 2.3

The function f is an element of the Bochner space \(L^2(0,T;H)\), and the initial value \(u_0 \in H\), where H is the Hilbert space from Assumption 2.1.

Remark 1

We note that Assumption 2.2  (iii) implies that the operator \(A(t) + \kappa _A I :V \rightarrow V^*\), \(t \in [0,T]\), fulfills a uniform semi-coercivity condition. That is, there exist constants \(\mu _A, \lambda _A \in [0,\infty )\), which do not depend on t, such that

$$\begin{aligned} \langle A(t) v, v \rangle _{V^*\times V}+ \kappa _A \Vert v\Vert _H^2 + \lambda _A \ge \mu _A |v |_V^p \end{aligned}$$

for all \(v \in V\). This follows by taking \(w = 0\) in (iii), since then

$$\begin{aligned} \langle A(t)v, v \rangle _{V^*\times V} + \kappa _A \Vert v\Vert _H^2 \ge \langle A(t)0, v \rangle _{V^*\times V} + \eta _A |v |_V^p, \end{aligned}$$

and by the Cauchy-Schwarz inequality and the weighted Young’s inequality (Lemma A.2),

$$\begin{aligned} \langle A(t)0, v \rangle _{V^*\times V} \ge -\Vert A(t)0\Vert _{V^*}\Vert v\Vert _V \ge -\Bigg ( \frac{\Vert A(t)0\Vert _{V^*}^q}{\varepsilon ^{\frac{q}{p}} q } + \varepsilon \Vert v\Vert _V^p \Bigg ) \end{aligned}$$

with \(\frac{1}{p} + \frac{1}{q} = 1\) and \(\varepsilon > 0\). Since \(|v |_V \le C_V\Vert v\Vert _V\), we can absorb the second term and take \(\lambda _A = \varepsilon ^{-\frac{q}{p}} q^{-1} \Vert A(t)0\Vert _{V^*}^q\) and \(\mu _A = \eta _A - \varepsilon \) after choosing an \(\varepsilon \) such that \(\mu _A \ge 0\). This also shows that the constants \(\lambda _A\) and \(\mu _A\) are not unique. We can, e.g., increase the coercivity constant at the cost of a larger constant term \(\lambda _A\). Both these terms enter into our error bounds, which can thus be tuned slightly.

In the case that \(A(t)0 = 0\), the constant term disappears and we have \(\mu _A = \eta _A\). If \(A(t)0 \ne 0\), one could recover this situation by the transformation \((A, f) \rightarrow (\tilde{A}, \tilde{f})\) with \(\tilde{A}(t)u = A(t)u - A(t)0\), \(\tilde{f}(t) = f(t) - A(t)0\). But in the case that \(A(t)0 \in V^* {\setminus } H\) this can cause issues since we require that \(f(t) \in H\). Moreover, it might lead to difficulties in solving the nonlinear equations of the form \((I - h_n\tilde{A}(t_n)) u^{n} = u^{n-1} + h_n\tilde{f}(t_n)\). We therefore do not apply such a transformation in this paper.

Assumptions 2.1–2.3, are requirements on the problem that we want to solve. The following Assumptions 2.4–2.5 are needed to state the approximation scheme for the given problem.

Assumption 2.4

Let \((\Omega , \mathcal {F}, \mathcal {P})\) be a complete probability space and let \(\{\xi _n\}_{n \in \mathbb {N}}\) be a family of mutually independent random variables. Further, let the filtration \(\{\mathcal {F}_n\}_{n \in \mathbb {N}}\) be given by

$$\begin{aligned}&\mathcal {F}_0 := \sigma \big (\mathcal {N} \in \mathcal {F}: \mathcal {P}(\mathcal {N}) = 0 \big )\\&\mathcal {F}_n := \sigma \big (\sigma \big (\xi _i : i \in \{1,\dots ,n\}\big ) \cup \mathcal {F}_0 \big ), \quad n \in \mathbb {N}, \end{aligned}$$

where \(\sigma \) denotes the generated \(\sigma \)-algebra.

In the following, we denote the expectation with respect to the probability distribution of \(\xi \) for a random variable X in the Bochner space \(L^1(\Omega ; H)\) by \(\mathbb {E}_{\xi }[X]\). Moreover, we abbreviate the total expectation by

$$\begin{aligned} \mathbb {E}_n [X] = \mathbb {E}_{\xi _1}[\mathbb {E}_{\xi _2}[ \dots \mathbb {E}_{\xi _n}[X] \dots ]]. \end{aligned}$$

We denote the space of Hölder continuous functions on [0, T] with Hölder coefficient \(\gamma \in (0,1)\) and values in H by \(C^{\gamma }([0,T];H)\). For notational convenience we include the case \(\gamma = 1\) and denote the space of Lipschitz continuous functions by \(C^{1}([0,T];H)\).

Assumption 2.5

Let Assumptions 2.1–2.4 be fulfilled. Assume that for almost every \(\omega \in \Omega \) there exists a real Banach space \(V_{\xi (\omega )}\) such that \(V {\mathop {\hookrightarrow }\limits ^{d}} V_{\xi (\omega )} {\mathop {\hookrightarrow }\limits ^{d}} H\), \(\bigcap _{\omega \in \Omega } V_{\xi (\omega )} = V\) and there exists a semi-norm \(|\cdot |_{V_{\xi (\omega )}}\) on \(V_{\xi (\omega )}\) and a \(C_{V_{\xi (\omega )}} \in (0,\infty )\) such that \(|\cdot |\le C_{V_{\xi (\omega )}} \Vert \cdot \Vert _{V_{\xi (\omega )}}\). Moreover, the mapping from \(\omega \mapsto V_{\xi (\omega )}\) is measurable in the sense that for every \(v \in H\) the set \(\{ \omega \in \Omega : v \in V_{\xi (\omega )}\}\) is an element of the complete generated \(\sigma \)-algebra

$$\begin{aligned} \mathcal {F}_{\xi } := \sigma \big (\sigma (\xi ) \cup \sigma \big (\mathcal {N} \in \mathcal {F}: \mathcal {P}(\mathcal {N}) = 0 \big ) \big ). \end{aligned}$$

Further, let the family of operators \(\{A_{\xi (\omega )}(t)\}_{\omega \in \Omega , t \in [0,T]}\) be such that for almost every \(\omega \in \Omega \), \(\{A_{\xi (\omega )}(t)\}_{t \in [0,T]}\) fulfills Assumption 2.2 with the spaces \(V_{\xi (\omega )}\), H and \(V_{\xi (\omega )}^*\) and corresponding constants \(\kappa _{\xi (\omega )}\), \(\eta _{\xi (\omega )}\), \(\beta _{\xi (\omega )}\). These give rise to the semi-coercivity constants \(\mu _{\xi (\omega )}\) and \(\lambda _{\xi (\omega )}\) as in Remark 1. Moreover, the mapping \(A_{\xi }(t) v :\Omega \rightarrow V^*\) is \(\mathcal {F}_{\xi }\)-measurable and the equality \(\mathbb {E}_{\xi } [ A_{\xi }(t) v ] = A(t) v\) is fulfilled in \(V^*\) for \(v \in V\). The mappings \(\kappa _{\xi }, \eta _{\xi }, \mu _{\xi }, \beta _{\xi }, \lambda _{\xi } :\Omega \rightarrow [0,\infty )\) are measurable and there exist \(\kappa , \lambda \in [0,\infty )\) which fulfill \(\kappa _{\xi } \le \kappa \) almost surely and \(\mathbb {E}_{\xi } \big [\lambda _{\xi } \big ] \le \lambda \).

Further, let the family \(\{f_{\xi (\omega )}\}_{\omega \in \Omega }\) be given such that \(f_{\xi (\omega )} \in L^2(0,T; H)\). Moreover, the mapping \(f_{\xi }(t) :\Omega \rightarrow H\) is \(\mathcal {F}_{\xi }\)-measurable and \(\mathbb {E}_{\xi } [ f_{\xi }(t) ] = f(t)\) is fulfilled in H for almost all \(t \in (0,T)\).

Under the setting explained in the above assumptions, we consider the initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u'(t) + A(t)u(t) = f(t)\quad &{}\text {in } V^*, \quad t \in (0,T],\\ u(0) = u_0 &{}\text {in } H. \end{array}\right. } \end{aligned}$$
(1)

For a non-uniform temporal grid \(0 = t_0<t_1< \dots < t_N = T\), a step size \(h_n = t_n - t_{n-1}\), \(h = \max _{n \in \{1,\dots ,N\}} h_n\), and a family of random variables \(\{f^n\}_{n \in \{1,\dots ,N\}}\) such that \(f^n:\Omega \rightarrow H\) is \(\mathcal {F}_{\xi _n}\)-measurable, we consider the scheme

$$\begin{aligned} {\left\{ \begin{array}{ll} U^n - U^{n-1} + h_n A_{\xi _n}(t_n) U^n = h_n f^n \quad &{}\text {in } V_{\xi _n}^*, \quad n \in \{1,\dots ,N\},\\ U^0 = u_0 &{}\text {in } H. \end{array}\right. } \end{aligned}$$
(2)

Note that \(U^n :\Omega \rightarrow H\) is a random variable and therefore some statements involving it below only hold almost surely. Whenever there is no risk of misinterpretation, we omit writing almost surely for the sake of brevity.

When proving that the scheme is well-defined and establishing an a priori bound, it is sufficient to assume that \(\{f_{\xi _n}\}_{n \in \{1,\dots ,N\}}\) are integrable with respect to the temporal parameter. In that case, we can choose for example

$$\begin{aligned} f^n = \frac{1}{h_n} \int _{t_{n-1}}^{t_n} f_{\xi _n}(t) \,\textrm{d}t \quad \text {in } H \text { almost surely.} \end{aligned}$$
(3)

When considering our error bounds, we assume more regularity for the functions \(\{f_{\xi _n}\}_{n \in \{1,\dots ,N\}}\) and demand continuity with respect to the temporal parameter. In this case, we may also use

$$\begin{aligned} f^n = f_{\xi _n}(t_n) \quad \text {in } H \text { almost surely.} \end{aligned}$$
(4)

We will focus on this second choice for the error bounds in Sect. 5.

3 Application: Domain decomposition

One main application that is allowed by our abstract framework is a domain decomposition scheme for a nonlinear fluid flow problem. Domain decomposition schemes are well-known for deterministic operator splittings. However, to the best of our knowledge, it has not been studied in the context of a randomized operator splitting scheme.

3.1 Deterministic domain decomposition

To exemplify our abstract Eq. (1), we consider a (nonlinear) parabolic differential equation. In the following, let \(\mathcal {D}\subset \mathbb {R}^d\), \(d \in \mathbb {N}\), be a bounded domain with a Lipschitz boundary \(\partial \mathcal {D}\). For \(p \in [2, \infty )\), we consider the parabolic p-Laplacian with homogeneous Dirichlet boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t u(t,x) - \nabla \cdot (\alpha (t) |\nabla u(t,x) |^{p-2}\nabla u(t,x)) =\tilde{f}(t,x), &{}(t,x) \in (0,T) \times \mathcal {D},\\ u(t,x) = 0,&{}(t,x) \in (0,T) \times \partial \mathcal {D},\\ u(0,x) = u_0(x), &{}x \in \mathcal {D}, \end{array}\right. } \end{aligned}$$
(5)

for \(\alpha :[0,T] \rightarrow \mathbb {R}\) and \(u_0 :\mathcal {D}\rightarrow \mathbb {R}\). The notation \(\tilde{f}\) is used to differentiate between the function \(\tilde{f} :(0,T) \times \mathcal {D}\rightarrow \mathbb {R}\) and the abstract function f on (0, T) that it gives rise to through \([f(t)](x) = \tilde{f}(t,x)\). We consider a domain decomposition scheme similar to [13] for \(p = 2\) and to [6, 7] for \(p \in [2,\infty )\). For the sake of completeness, we recapitulate the setting here also with a different boundary condition.

For \(s \in \mathbb {N}\), let \(\{ \mathcal {D}_{\ell } \}_{\ell =1}^{s}\) be a family of overlapping subsets of \(\mathcal {D}\). Let each subset have a Lipschitz boundary and let the union of them fulfill \(\bigcup _{\ell =1}^s \mathcal {D}_{\ell } = \mathcal {D}\). On the sub-domains \(\{ \mathcal {D}_{\ell } \}_{\ell =1}^{s}\), let the partition of unity \(\{\chi _{\ell } \}_{\ell =1}^{s}\subset W^{1,\infty }(\mathcal {D})\) be given such that the following criteria are fulfilled

$$\begin{aligned} \chi _{\ell } (x)>0\text { for all }x\in \mathcal {D}_{\ell }, \quad \chi _{\ell } (x) = 0\text { for all }x\in \mathcal {D}{\setminus }\mathcal {D}_{\ell }, \quad \sum _{\ell =1}^{s} \chi _{\ell }= 1 \end{aligned}$$

for \(\ell \in \{1,\dots ,s\}\). With the help of the functions \(\{\chi _{\ell }\}_{\ell \in \{1,\dots ,s\}}\), it is now possible to introduce suitable functional spaces \(\{V_{\ell }\}_{\ell \in \{1,\dots ,s\}}\). We use the weighted Lebesgue space \(L^p(\mathcal {D}_{\ell },\chi _{\ell })^d\) that consists of all measurable functions \(v = (v_1,\dots ,v_d) :\mathcal {D}_{\ell } \rightarrow \mathbb {R}^d\) such that

$$\begin{aligned} \Vert (v_1,\ldots ,v_{d})\Vert _{L^p(\mathcal {D}_{\ell },\chi _{\ell })^d} = \Big (\int _{\mathcal {D}_{\ell }}\chi _{\ell } |(v_1,\ldots ,v_{d})|^p \,\textrm{d}x\Big )^{\frac{1}{p}} \end{aligned}$$

is finite. In the following, let the pivot space \(\left( H, ( \cdot , \cdot )_{H}, \Vert \cdot \Vert _H \right) \) be the space \(L^2(\mathcal {D})\) of square integrable functions on \(\mathcal {D}\) with the usual norm and inner product. The spaces V and \(V_{\ell }\), \(\ell \in \{1,\dots ,s\}\), are given by

$$\begin{aligned} V = \text {clos}_{\Vert \cdot \Vert _{V}} \big (C_0^{\infty }(\mathcal {D})\big ) = W_0^{1,p}(\mathcal {D}) \quad \text {and} \quad V_{\ell } = \text {clos}_{\Vert \cdot \Vert _{V_{\ell }}} \big (C_0^{\infty }(\mathcal {D})\big ), \end{aligned}$$

with respect to the norms

$$\begin{aligned} \Vert \cdot \Vert _{V} = \Vert \cdot \Vert _H + \Vert \nabla \cdot \Vert _{L^p(\mathcal {D})^d} \quad \text {and}\quad \Vert \cdot \Vert _{V_{\ell }} = \Vert \cdot \Vert _H + \Vert \nabla \cdot \Vert _{L^p(\mathcal {D}_{\ell },\chi _{\ell })^d} \end{aligned}$$
(6)

and semi-norms

$$\begin{aligned} |\cdot |_{V} = \Vert \nabla \cdot \Vert _{L^p(\mathcal {D})^d} \quad \text {and}\quad |\cdot |_{V_{\ell }} = \Vert \nabla \cdot \Vert _{L^p(\mathcal {D}_{\ell },\chi _{\ell })^d}. \end{aligned}$$

Note that a bootstrap argument involving the Sobolev embedding theorem shows that the norm given in (6) is equivalent to the standard norm in the space. We can now introduce the operators \(A(t) :V \rightarrow V^*\), \(A_{\ell }(t) :V_{\ell } \rightarrow V^*_{\ell }\), \(\ell \in \{ 1,\dots ,s\}\), \(t\in [0,T]\), given by

$$\begin{aligned} \langle A(t) u, v \rangle _{V^*\times V}&= \int _{\mathcal {D}} \alpha (t) |\nabla u |^{p-2} \nabla u \cdot \nabla v \,\textrm{d}x,\quad u,v\in V, \\ \langle A_{\ell }(t) u,v \rangle _{V_{\ell }^{*}\times V_{\ell }}&= \int _{\mathcal {D}_{\ell }} \chi _{\ell } \alpha (t) |\nabla u |^{p-2} \nabla u \cdot \nabla v \,\textrm{d}x, \quad u,v\in V_{\ell }. \end{aligned}$$

Similarly, we define the right-hand sides \(f_{\ell } :[0,T] \rightarrow H\), \(\ell \in \{1,\dots ,s\}\), where \(f_{\ell }(t) = \chi _{\ell } f(t)\) in H for almost every \(t \in (0,T)\).

Lemma 3.1

Let the parameters of Eq. (5) be given such that \(\alpha \in C([0,T];\mathbb {R})\), \(u_0 \in L^2(\mathcal {D})\) and \(\tilde{f} \in L^2((0,T) \times \mathcal {D})\). Then the setting described above fulfills Assumptions 2.1–2.3.

Let the partition of unity \(\{\chi _{\ell } \}_{\ell =1}^{s}\subset W^{1,\infty }(\mathcal {D})\) fulfill that for every function \(\chi _{\ell }\) there exists \(\varepsilon _0 \in (0,\infty )\) such that \(\mathcal {D}_{\ell }^{\varepsilon } = \{ x\in \mathcal {D}_{\ell }: \chi _{\ell }(x) \ge \varepsilon \}\) is a Lipschitz domain for all \(\varepsilon \in (0,\varepsilon _0)\). Then V and \(V_{\ell }\), \(\ell \in \{1,\dots ,s\}\), are reflexive Banach spaces and \(V = \bigcap _{\ell = 1}^s V_{\ell }\). Further, the family of operators \(\{A_{\ell }(t)\}_{t \in [0,T]}\), \(\ell \in \{1,\dots ,s\}\) fulfills Assumption 2.2 with the spaces \(V_{\ell }\), H and \(V_{\ell }^*\). Moreover, \(\sum _{\ell = 1}^{s} A_{\ell }(t) v = A(t) v\) is fulfilled in \(V^*\) for \(v \in V\) for almost every \(t \in (0,T)\) and corresponding constants \(\kappa _A = \kappa _{\ell } = \lambda _A = \lambda _{\ell } = 0\), \(\mu _A = \mu _{\ell } = \eta _A = \eta _{\ell } = 1\).

Finally, the family \(\{f_{\ell }\}_{\ell \in \{1,\dots ,s\}}\) fulfills \(f_{\ell } \in L^2(0,T; H)\) and \(\sum _{\ell = 1}^{s} f_{\ell }(t) = f(t)\) in H for almost all \(t \in (0,T)\).

Proof

The space \(H = L^2(\mathcal {D})\) is a real, separable Hilbert space, while \(V = W_0^{1,p}(\mathcal {D})\) is a real, separable Banach space that is densely embedded into H. Thus, they fulfill Assumption 2.1. Analogously to [6, Lemma 3], the spaces V and \(V_{\ell }\), \(\ell \in \{1,\dots ,s\}\), are reflexive Banach spaces and since \(C_0^{\infty }(\mathcal {D})\) is dense in H and \(C_0^{\infty }(\mathcal {D}) \subseteq V \subset V_{\ell }\) it follows that V and \(V_{\ell }\) are dense in H. It remains to prove that \(\bigcap _{\ell = 1}^s V_{\ell } = V\) is fulfilled. First, we notice that \(\Vert w\Vert _{L^p( \mathcal {D}_{\ell },\chi _{\ell })^d} \le \Vert w\Vert _{L^p(\mathcal {D})^d}\) for every \(w \in L^p(\mathcal {D})^d\). Thus, it follows that \(V \subseteq V_{\ell }\) for every \(\ell \in \{1,\dots ,s\}\) and in particular \(V \subseteq \bigcap _{\ell = 1}^s V_{\ell }\). The other inclusion \(\bigcap _{\ell = 1}^s V_{\ell } \subseteq V\) requires more attention. For \(\varepsilon \in (0,\infty )\), we introduce the set \(\mathcal {D}_{\ell }^{\varepsilon } = \{ x \in \mathcal {D}: \chi _{\ell }(x) \ge \varepsilon \}\). By assumption the sets \(\mathcal {D}_{\ell }^{\varepsilon }\) have Lipschitz boundary for \(\varepsilon \) small enough. We consider the spaces of restricted functions

$$\begin{aligned} C_0^{\infty }(\mathcal {D})\vert _{\mathcal {D}_{\ell }^{\varepsilon }} = \{ u \in C^{\infty }(\mathcal {D}_{\ell }^{\varepsilon }) : u\vert _{\partial \mathcal {D}_{\ell }^{\varepsilon } \cap \partial \mathcal {D}} = 0\} \quad \text {and} \quad V_{\ell }^{\varepsilon } = \{ u\vert _{\mathcal {D}_{\ell }^{\varepsilon }} : u \in V_{\ell } \}. \end{aligned}$$

If a weight function \(\chi _{\ell }\) fulfills \(0< \varepsilon< \chi _{\ell } \le 1 <\infty \) on the whole domain \(\mathcal {D}\), it follows that the weighted Lebesgue space \(L^p(\mathcal {D}_{\ell }^{\varepsilon },\chi _{\ell })^d\) coincides with the space \(L^p(\mathcal {D}_{\ell }^{\varepsilon })^d\) (see, e.g., [25, Chapter 3]). Thus, we obtain \(V_{\ell }^{\varepsilon }= W^{1,p}(\mathcal {D}_{\ell }^{\varepsilon })\). The continuity of the trace operator (see, e.g., [27, Theorem 15.23]), implies that

$$\begin{aligned} \overline{C_0^{\infty }(\mathcal {D})\vert _{\mathcal {D}_{\ell }^{\varepsilon }} }^{\Vert \cdot \Vert _{V_{\ell } }} = \{ u \in W^{1,p}(\mathcal {D}_{\ell }^{\varepsilon }) : u\vert _{\partial \mathcal {D}_{\ell }^{\varepsilon } \cap \partial \mathcal {D}} = 0\}. \end{aligned}$$

This shows that \(u \in V_{\ell }\) is zero on \(\partial \mathcal {D}_{\ell }^{\varepsilon } \cap \partial \mathcal {D}\) for every \(\varepsilon \in (0,\infty )\) small enough. As \(\varepsilon \) can be chosen arbitrarily small, it follows that \(u \in V_{\ell }\) fulfills \(v\vert _{\partial \mathcal {D}\cap \partial \mathcal {D}_{\ell }} = 0\). In combination with [6, Lemma 1], we obtain that \(\bigcap _{\ell = 1}^{s} V_{\ell } = W^{1,p}_0(\mathcal {D}) = V\).

Similar to the argumentation of [6, Lemma 4], it follows that the families of operators \(\{A(t)\}_{t \in [0,T]}\) and \(\{A_{\ell }(t)\}_{t \in [0,T]}\), \(\ell \in \{1,\dots ,s\}\), fulfills Assumption 2.2 with respect to the corresponding spaces with \(\kappa _A = \kappa _{\ell } = \lambda _A = \lambda _{\ell } = 0\), \(\mu _A = \mu _{\ell } = \eta _A = \eta _{\ell } = 1\).

Assumption 2.3 is fulfilled as \(\tilde{f} \in L^2((0,T) \times \mathcal {D})\) means that the abstract function f belongs to \(L^2(0,T;L^2(\mathcal {D}))\). Thus, as \(\chi _{\ell } \in W^{1,\infty }(\mathcal {D})\), it follows that \(f_{\ell } = \chi _{\ell } f \in L^2(0,T;H)\) and \(\sum _{\ell = 1}^{s} f_{\ell }(t) = f(t)\) in H for almost every \(t \in (0,T)\). \(\square \)

3.2 Randomized scheme

For a randomized splitting in combination with a domain decomposition, different approaches can be applied. One possibility is to choose a random support of the weight functions \(\{\chi _{\ell }\}_{\ell \in \{1,\dots ,s\}}\). This could possibly be done efficiently using priority queue techniques similar to those in [36]. In this paper, we instead fix the weight functions, but choose a random part of the operator in every time step. For the operator \(A(t) = \sum _{\ell = 1}^{s} A_{\ell }(t)\) and a right hand side \(f(t) = \sum _{\ell = 1}^{s} f_{\ell }(t)\), we introduce a random variable \(\xi :\Omega \rightarrow 2^{\{1, \dots , s\}}\) such that \([A_{\xi }(t)](\omega ) = \sum _{\ell \in \xi (\omega )} A_{\ell }(t) / \tau _{\ell }\) and \([f_{\xi }(t)](\omega ) = \sum _{\ell \in \xi (\omega )} f_{\ell }(t) / \tau _{\ell }\) with

$$\begin{aligned} \tau _{\ell } = \sum _{ B \in 2^{\{1, \dots , s\}} : \ \ell \in B} \mathcal {P}(\Omega _{\xi = B}) \quad \text {with} \quad \Omega _{\xi = B} = \{ \omega \in \Omega : \xi (\omega ) = B\}. \end{aligned}$$

The value \(\tau _{\ell }\) is the proper scaling factor which ensures that \(\mathbb {E}_{\xi } [A_{\xi }(t)] = A(t)\) and \(\mathbb {E}_{\xi } [f_{\xi }(t)] = f(t)\). We tacitly assume that \(\tau _{\ell } > 0\), because otherwise we would be in a situation where at least one \(A_{\ell }(t)\) is never chosen. Such a strategy would obviously not work. We set \(V_{\xi (\omega )} = \bigcap _{\ell \in \xi (\omega )} V_{\ell }\).

Lemma 3.2

Let \(\{\xi _n\}_{n \in \{1,\dots ,N\}}\) fulfill Assumption 2.4 such that \(\xi _n :\Omega \rightarrow 2^{\{1,\dots ,s\}}\) and \(\xi _n^{-1}(B) \in \mathcal {F}_{\xi _n}\) for all \(B \subset 2^{\{1,\dots ,s\}}\) and \(n \in \{1,\dots ,N\}\). Under the setting above, Assumption 2.5 is fulfilled.

Proof

In the following proof, we drop the index n to keep the notation simpler. The embedding and norm properties are fulfilled as verified in the previous lemma. It remains to verify the measurability condition. We need to verify that for every \(v \in H\), the set \(\{\omega \in \Omega : v \in V_{\xi (\omega )}\} \in \mathcal {F}_{\xi } = \sigma \big ( \sigma (\xi ) \cup \sigma (\mathcal {N} \in \mathcal {F}: \mathcal {P}(\mathcal {N}) = 0)\big )\). For fixed \(v \in H\), we set \(B_v = \{\ell \in \{1,\dots , s\}: v \in V_{\ell }\} \in 2^{\{1,\dots ,s\}}\). Then it follows that

$$\begin{aligned} \{\omega \in \Omega : v \in V_{\xi (\omega )}\} = \big \{ \omega \in \Omega : \xi (\omega ) \in 2^{B_v} \big \} = \xi ^{-1}\big (2^{B_v}\big ) \in \mathcal {F}_{\xi }. \end{aligned}$$

Moreover, we need to verify that the mapping \(\omega \mapsto A_{\xi (\omega )}(t)v\) is measurable for every \(v \in H\). This can be seen from the decomposition \(A_{\xi }(t)v = S_{A(t)v} \circ \xi \) where \(S_{A(t)v} :2^{\{1,\dots ,s\}} \rightarrow V^*\) is given through \(S_{A(t)v} (B) = \sum _{\ell \in B} A_{\ell }(t)v\). As \(\xi ^{-1}(B) \in \mathcal {F}_{\xi }\) for all \(B \subset 2^{\{1,\dots ,s\}}\) and \(S_{A(t)v}^{-1}(X) \subset 2^{\{1,\dots ,s\}}\) for any open set \(X \subset V^*\), the mapping \(\omega \mapsto A_{\xi (\omega )}(t)v\) is measurable. Analogously, it can be proved that the mapping \(\omega \mapsto f_{\xi (\omega )}(t)\) is measurable. In Lemma 3.1, we already verified that an operator \(A_{\xi (w)}\) fulfills the conditions from Assumption 2.2. Thus, it only remains to prove the expectation property from Assumption 2.5. This is fulfilled as

$$\begin{aligned} \mathbb {E}_{\xi } [A_{\xi }(t) v]&= \sum _{B \in 2^{\{1,\dots ,s\}}} \mathcal {P}(\Omega _{\xi = B})\sum _{\ell \in B} \frac{1}{\tau _{\ell }} A_{\ell }(t) v \\&= \sum _{\ell = 1}^{s} \frac{1}{\tau _{\ell }} A_{\ell }(t) v \sum _{B \in 2^{\{1,\dots ,s\}} : \ \ell \in B }{ \mathcal {P}(\Omega _{\xi = B}) } = \sum _{\ell = 1}^{s} A_{\ell }(t) v = A(t) v \quad \text {in } V^* \end{aligned}$$

holds true for \(v \in V\) and for almost every \(t \in [0,T]\). The same algebraic manipulation in H instead of \(V^*\) shows that \(\mathbb {E}_{\xi } [f_{\xi }(t)] = f(t)\). \(\square \)

4 Solution is well-defined

In the coming section, we show that our scheme (2) is well-defined. This includes that first of all the scheme possesses a unique solution. We consider a purely deterministic Eq. (1). However, as the numerical scheme is randomized, the solution \(U^n\) of (2) is a mapping of the type \(U^n :\Omega \rightarrow H\). Thus, we also need to make sure that it is a measurable function. These facts are verified in Lemma 4.1. Moreover, we provide an integrability result in the form of an a priori bound in Lemma 4.2.

Lemma 4.1

Let Assumptions 2.1–2.5 be fulfilled. Further, let the random variables \(f^n :\Omega \rightarrow H\) be given such that they are \(\mathcal {F}_{\xi _n}\)-measurable for every \(n \in \{1,\dots , N\}\). Then for \(\kappa h_n \le \kappa h < 1\) there exists a unique \(\mathcal {F}_n\)-measurable function \(U^n :\Omega \rightarrow H\) such that \(U^n(\omega ) \in V_{\xi _n(\omega )}\) and (2) is fulfilled for every \(n \in \{1,\dots ,N\}\).

Proof

For \(\omega \in \Omega \), we find that the operator \(I + h_n A_{\xi _n(\omega ) }(t_n) :V_{\xi _n(\omega )}\rightarrow V_{\xi _n(\omega )}^*\) is monotone, radially continuous and coercive. Thus, it is surjective, compare [33, Theorem 2.18]. Moreover, for \(U_1, U_2 \in V_{\xi _n(\omega )}\) with \(\big (I + h_n A_{\xi _n(\omega ) }(t_n) \big )U_1 = \big (I + h_n A_{\xi _n(\omega ) }(t_n) \big )U_2\), it follows that

$$\begin{aligned} 0&= \left\langle \big (I + h_n A_{\xi _n(\omega ) }(t_n) \big )U_1 - \big (I + h_n A_{\xi _n(\omega ) }(t_n) \big )U_2, U_1 - U_2 \right\rangle _{V_{\xi _n(\omega )}^* \times V_{\xi _n(\omega )}}\\&\ge \big (1 - h_n \kappa \big ) \Vert U_1 - U_2 \Vert _H^2. \end{aligned}$$

Thus, it follows that \(\Vert U_1 - U_2 \Vert _H = 0\) and \(I + h_n A_{\xi _n(\omega ) }(t_n) \) is injective for \(\kappa h_n < 1\) and, in particular, bijective.

It remains to verify that \(U^n :\Omega \rightarrow H\) is well-defined. We define the auxiliary function \(g :\Omega \times H \rightarrow V^*\) such that

$$\begin{aligned} (\omega , U) \mapsto {\left\{ \begin{array}{ll} h_n f^n (\omega ) + U^{n-1} - \big (I + h_n A_{\xi _n(\omega ) }(t_n) \big ) U, &{}U \in V_{\xi _n(\omega )}\\ e, &{}U \in H {\setminus } V_{\xi _n(\omega )}, \end{array}\right. } \end{aligned}$$

where \(e \in V^*\) with \(\Vert e\Vert _{V^*} = 1\). In the following, we want to apply Lemma A.3 to the function g to prove that \(U^n\) is measurable. Applying [33, Lemma 2.16], it follows that for fixed \(\omega \in \Omega \), the function \(v \mapsto \langle g(\omega , v), w \rangle _{V^*\times V}\) is continuous for all \(v, w \in V_{\xi _n(\omega )}\). It remains to verify that for fixed \(v \in H\) and \(w \in V\), the function \(\omega \mapsto \langle g(\omega , v), w \rangle _{V^*\times V}\) is measurable. Let B be an open set in \(V^*\). It then follows that

$$\begin{aligned}&\big (g(\cdot , v) \big )^{-1} (B) \\&\quad = \{ \omega \in \Omega : g(\omega , v) \in B \}\\&\quad = \{ \omega \in \Omega : v \in V_{\xi _n(\omega )}, h_n f^n (\omega ) + U^{n-1} - \big (I + h_n A_{\xi _n(\omega ) }(t_n) \big ) v \in B \}\\&\quad \quad \cup \{ \omega \in \Omega : v \in H {\setminus } V_{\xi _n(\omega )}, e \in B \} \\&\quad = \big (\{ \omega \in \Omega : v \in V_{\xi _n(\omega )}\} \cap \{ \omega \in \Omega : h_n f^n (\omega ) + U^{n-1} - \big (I + h_n A_{\xi _n(\omega ) }(t_n) \big ) v \in B \} \big )\\&\quad \quad \cup \big (\{ \omega \in \Omega : v \in H {\setminus } V_{\xi _n(\omega )}\} \cap \{ \omega \in \Omega : e \in B \}\big )\\&\quad =: (T_1 \cap T_2) \cup T_3. \end{aligned}$$

As the function \(\omega \mapsto h_n f^n (\omega ) + U^{n-1} - \big (I + h_n A_{\xi _n(\omega ) }(t_n) \big )v\) is measurable, it follows that \(T_2 \subset \Omega \) is measurable. The sets \(T_1\) and \(T_3\) are measurable by assumption. Thus, it follows that \(\omega \mapsto g(\omega , v)\) and therefore \(\omega \mapsto \langle g(\omega , v), w \rangle _{V^*\times V}\) is measurable.

As argued above for every \(\omega \in \Omega \), there exists a unique element \(U^n(\omega )\) such that \(g(\omega , U^n(\omega )) = 0\). Thus, we can now apply Lemma A.3 to prove that \(U^n :\Omega \rightarrow H\) is \(\mathcal {F}_n\)-measurable. \(\square \)

Lemma 4.2

Let Assumptions 2.1–2.5 be fulfilled. Further, let the random variables \(f^n :\Omega \rightarrow H\) be given such that they are \(\mathcal {F}_{\xi _n}\)-measurable and \(\mathbb {E}_{\xi _n} \big [ \Vert f^n \Vert _{H}^2 \big ] < \infty \) for every \(n \in \{1,\dots , N\}\). Then for \(2\kappa h_n \le 2\kappa h < 1\) the solution \(\{U^n\}_{n \in \{1,\dots ,N\}}\) of (2) fulfills the a priori bound

$$\begin{aligned}&\mathbb {E}_n \big [\Vert U^n\Vert _H^2\big ] + \sum _{i=1}^{n}\mathbb {E}_i \big [ \Vert U^i - U^{i-1}\Vert _H^2 \big ] + 2 \sum _{i=1}^{n} h_i \mathbb {E}_i \big [ \mu _{\xi _i}|U^i|_{V_{\xi _i}}^2\big ]\\&\quad \le C \Big ( 2\Vert u_0\Vert ^2 + 4 T \lambda + 5 C T \sum _{i=1}^{N} h_i \mathbb {E}_{\xi _i} \big [ \Vert f^i \Vert _{H}^2 \big ] \Big ), \end{aligned}$$

where \(C = \frac{1}{1- 2\,h \kappa } \exp \big (\frac{2\kappa T}{1- 2\,h \kappa }\big )\) for all \(n \in \{1,\dots ,N\}\).

The proof of this lemma is very similar to the proof of our main result Theorem 5.1 and therefore omitted. The main necessary modification is to directly test (2) with \(U^n\) and use the semi-coercivity from Remark 1.

5 Stability and convergence in expectation

With the previous sections in mind, we can now turn our attention to the main results of this paper. We provide error bounds for the scheme (2) measured in expectation. First, we give a stability result in Theorem 5.1. The aim of this bound is to show how two solutions of the same scheme with respect to different right-hand sides and initial values differ. This stability result can then be used to prove the desired error bounds in Theorem 5.2 by using well-chosen data that agrees with the exact solution at the grid points. Note that in contrast to other works (e.g. [10, 11]), we measure \(f(t) - A(t)u(t)\) in the H-norm. This can be interpreted as a stricter regularity assumption. The advantage is that certain error terms disappear in expectation, compare the second bound in Lemma A.4.

Theorem 5.1

Let Assumptions 2.1–2.5 be fulfilled. Further, let the random variable \(f^n :\Omega \rightarrow H\) be given such that it is \(\mathcal {F}_{\xi _n}\)-measurable and \(\mathbb {E}_{\xi _n} \big [ \Vert f^n \Vert _H^2 \big ] < \infty \) for every \(n \in \{1,\dots , N\}\). Let \(\{U^n\}_{n \in \{1,\dots ,N\}}\) be the solution of (2) and let \(\{V^n\}_{n \in \{1,\dots ,N\}}\) be the solution of

$$\begin{aligned} {\left\{ \begin{array}{ll} V^n - V^{n-1} + h_n A_{\xi _n}(t_n) V^n = h_n g^n \quad &{}\text {in } V_{\xi _n}^*, \quad n \in \{1,\dots ,N\}, \\ V^0 = v_0 \quad &{}\text {in } H, \end{array}\right. } \end{aligned}$$
(7)

for \(v_0 \in H\) and \(g^n :\Omega \rightarrow H\) such that it is \(\mathcal {F}_{\xi _n}\)-measurable and \(\mathbb {E}_{\xi _n} \big [ \Vert g^n\Vert _H^2 \big ] < \infty \) for every \(n \in \{1,\dots , N\}\). Then for \(2\kappa h_n \le 2\kappa h < 1\), it follows that

$$\begin{aligned}&\mathbb {E}_n \big [ \Vert U^n - V^n\Vert _H^2\big ] + \frac{1}{2} \sum _{i=1}^{n} \mathbb {E}_i \big [\Vert U^i - V^i - (U^{i-1} -V^{i-1})\Vert _H^2 \big ]\\&\quad \quad + 2 \sum _{i=1}^{n} h_i \mathbb {E}_i \big [ \eta _{\xi _i}|U^i - V^i |_{V_{\xi _i}}^p\big ] \\&\quad \le 2 C \Vert u_0 -v_0\Vert ^2 + 4 C \sum _{i=1}^{N} h_i^2 \mathbb {E}_i \big [ \Vert f^i - g^i\Vert _H^2\big ] + 5 C^2 T \sum _{i=1}^{N} h_i \big \Vert \mathbb {E}_{\xi _i} \big [ f^i - g^i \big ] \big \Vert _H^2 \end{aligned}$$

for \(C = \frac{1}{1 - 2\,h \kappa } \exp \big (\frac{2\kappa T}{1 - 2 \kappa T}\big )\) and \(n \in \{1,\dots ,N\}\).

Proof

We start by subtracting (7) from (2) and testing with \(U^i - V^i\) to get

$$\begin{aligned}&\big ((U^i - V^i) - (U^{i-1} - V^{i-1}),U^i - V^i\big )_{}\nonumber \\&\quad + h_n \langle A_{\xi _i}(t_i) U^i - A_{\xi _i}(t_i) V^i, U^i - V^i \rangle _{V_{\xi _i}^*\times V_{\xi _i}} = h_n ( f^i - g^i , U^i - V^i )_{}.\quad \end{aligned}$$
(8)

For the first term of this equality, we use the identity \(( a - b , a )_{} = \frac{1}{2} (\Vert a\Vert ^2 - \Vert b\Vert ^2 + \Vert a-b\Vert ^2 )\) for \(a, b \in H\) to find that

$$\begin{aligned}&\big ((U^i - V^i) - (U^{i-1} - V^{i-1}),U^i - V^i\big )_{}\\&\quad = \frac{1}{2} \big ( \Vert U^i - V^i\Vert _H^2 - \Vert U^{i-1} - V^{i-1}\Vert _H^2 + \Vert U^i - V^i - (U^{i-1} - V^{i-1})\Vert _H^2 \big ). \end{aligned}$$

Due to the monotonicity condition from Assumption 2.2 (iii), we obtain

$$\begin{aligned} \langle A_{\xi _i}(t_i) U^i - A_{\xi _i}(t_i) V^i, U^i - V^i \rangle _{V_{\xi _i}^*\times V_{\xi _i}} + \kappa _{\xi _i}\Vert U^i - V^i \Vert _H^2 \ge \eta _{\xi _i}|U^i - V^i |_{V_{\xi _i}}^p. \end{aligned}$$

It remains to find a bound for the right-hand side of (8). Applying Cauchy-Schwarz’s inequality and the weighted Young’s inequality for products (Lemma A.2 with \(\varepsilon = 1\)), it follows that

$$\begin{aligned}&h_i \big (f^i - g^i,U^i - V^i\big )_{}\\&\quad = h_i \big (f^i - g^i,U^{i-1} - V^{i-1}\big )_{} + h_i \big (f^i - g^i,U^i - V^i - (U^{i-1} - V^{i-1})\big )_{}\\&\quad \le h_i \big (f^i - g^i,U^{i-1} - V^{i-1}\big )_{} + h_i \Vert f^i - g^i\Vert _H \Vert U^i - V^i - (U^{i-1} - V^{i-1})\Vert _H\\&\quad \le h_i \big (f^i - g^i,U^{i-1} - V^{i-1}\big )_{} + h_i^2 \Vert f^i - g^i\Vert _H^2 + \frac{1}{4} \Vert U^i - V^i - (U^{i-1} - V^{i-1})\Vert _H^2. \end{aligned}$$

Combining the previous statements, we find

$$\begin{aligned} 0&= ( U^i - V^i - (U^{i-1} - V^{i-1}) , U^i - V^i )_{}\\&\quad + h_i \langle A_{\xi _i}(t_i) U^i - A_{\xi _i}(t_i) V^i , U^i - V^i \rangle _{V_{\xi _i}^*\times V_{\xi _i}} - h_i \big (f^i - g^i,U^i - V^i\big )_{}\\&\ge \frac{1}{2} \big ( \Vert U^i - V^i\Vert _H^2 - \Vert U^{i-1} - V^{i-1}\Vert _H^2 + \Vert U^i - V^i - (U^{i-1} - V^{i-1})\Vert _H^2 \big )\\&\quad - h_i \kappa _{\xi _i}\Vert U^i - V^i \Vert _H^2 + h_i \eta _{\xi _i}|U^i - V^i |_{V_{\xi _i}}^p\\&\quad -h_i \big (f^i - g^i,U^{i-1} - V^{i-1}\big )_{} - h_i^2 \Vert f^i - g^i\Vert _H^2 - \frac{1}{4} \Vert U^i - V^i - (U^{i-1} - V^{i-1})\Vert _H^2. \end{aligned}$$

After rearranging the terms and multiplying both sides of the inequality with the factor 2, we obtain the following bound

$$\begin{aligned}&\Vert U^i - V^i\Vert _H^2 - \Vert U^{i-1} - V^{i-1}\Vert _H^2 + \frac{1}{2}\Vert U^i - V^i - (U^{i-1} -V^{i-1})\Vert _H^2\\&\qquad + 2 h_i \eta _{\xi _i}|U^i - V^i |_{V_{\xi _i}}^p\\&\quad \le 2 h_i \kappa _{\xi _i}\Vert U^i - V^i \Vert _H^2 + 2 h_i \big (f^i - g^i,U^{i-1} - V^{i-1}\big )_{} + 2 h_i^2 \Vert f^i - g^i\Vert _H^2. \end{aligned}$$

By first taking the \(\mathbb {E}_{\xi _i}\)-expectation of this inequality and then applying also the \(\mathbb {E}_{i-1}\)-expectation, we find that

$$\begin{aligned}&\mathbb {E}_i \big [ \Vert U^i - V^i\Vert _H^2\big ] - \mathbb {E}_{i-1}\big [ \Vert U^{i-1} - V^{i-1}\Vert _H^2\big ] + \frac{1}{2} \mathbb {E}_i \big [\Vert U^i - V^i - (U^{i-1} - V^{i-1})\Vert _H^2 \big ]\\&\qquad + 2 h_i \mathbb {E}_i \big [ \eta _{\xi _i}|U^i - V^i |_{V_{\xi _i}}^p\big ] \\&\quad \le 2 h_i \mathbb {E}_i \big [ \kappa _{\xi _i}\Vert U^i - V^i \Vert _H^2 \big ] + 2 h_i \mathbb {E}_{i-1}\big [ \big (\mathbb {E}_{\xi _i} \big [f^i - g^i \big ],U^{i-1} - V^{i-1}\big )_{}\big ]\\&\qquad + 2 h_i^2 \mathbb {E}_{\xi _i} \big [ \Vert f^i - g^i\Vert _H^2\big ]. \end{aligned}$$

After combining the previous two inequalities and summing up from \(i = 1\) to \(n \in \{1,\dots ,N\}\), we obtain

$$\begin{aligned} \begin{aligned}&\mathbb {E}_n \big [\Vert U^n - V^n\Vert _H^2\big ] + \frac{1}{2}\sum _{i=1}^{n} \mathbb {E}_i \big [ \Vert U^i - V^i - (U^{i-1} - V^{i-1})\Vert _H^2 \big ]\\&\qquad + 2 \sum _{i=1}^{n} h_i \mathbb {E}_i \big [ \eta _{\xi _i}|U^i - V^i |_{V_{\xi _i}}^p\big ]\\&\quad \le \Vert u_0 - v_0\Vert _H^2 + 2 \kappa \sum _{i=1}^{n} h_i \mathbb {E}_i \big [ \Vert U^i - V^i \Vert _H^2\big ] \\&\qquad + 2 \sum _{i=1}^{n} h_i \mathbb {E}_{i-1}\big [ \big (\mathbb {E}_{\xi _i} \big [f^i - g^i \big ],U^{i-1} - V^{i-1}\big )_{}\big ] + 2 \sum _{i=1}^{N} h_i^2 \mathbb {E}_{\xi _i} \big [ \Vert f^i - g^i\Vert _H^2\big ], \end{aligned} \end{aligned}$$
(9)

where we only made the right-hand side bigger by summing to the final value N. In the following, denote \(i_{\max } \in \{1,\dots ,N\}\) such that \(\max _{i \in \{1,\dots ,N\}} \mathbb {E}_i \big [\Vert U^i - V^i \Vert _H^2 \big ] = \mathbb {E}_{i_{\max }} \big [\Vert U^{i_{\max }} - V^{i_{\max }}\Vert _H^2 \big ]\). By Lemma A.3, it follows that \(U^{i-1} - V^{i-1}\) is \(\mathcal {F}_{i-1}\)-measurable and thus independent of the \(\mathcal {F}_{\xi _i}\)-measurable random variable \(f^i - g^i\). Therefore, we find that

$$\begin{aligned}&2 \sum _{i=1}^{n} h_i \mathbb {E}_{i-1}\big [ \big (\mathbb {E}_{\xi _i} \big [f^i - g^i \big ],U^{i-1}- V^{i-1}\big )_{}\big ]\\&\quad \le 2 \sum _{i=1}^{n} h_i \big \Vert \mathbb {E}_{\xi _i} \big [ f^i - g^i \big ] \big \Vert _H\mathbb {E}_{i-1} \big [ \Vert U^{i-1} - V^{i-1}\Vert _H \big ] \\&\quad \le 2 \big (\mathbb {E}_{i_{\max }} \big [\Vert U^{i_{\max }} - V^{i_{\max }}\Vert _H^2 \big ]\big )^{\frac{1}{2}} \sum _{i=1}^{N} h_i \big \Vert \mathbb {E}_{\xi _i} \big [ f^i - g^i \big ] \big \Vert _H. \end{aligned}$$

To keep the presentation compact, we abbreviate

$$\begin{aligned} B_1 = \sum _{i=1}^{N} h_i^2 \mathbb {E}_i \big [ \Vert f^i - g^i\Vert _H^2\big ] \quad \text {and} \quad B_2 = \sum _{i=1}^{N} h_i \big \Vert \mathbb {E}_{\xi _i} \big [ f^i - g^i \big ] \big \Vert _H. \end{aligned}$$

Setting

$$\begin{aligned} x_n&= \mathbb {E}_n \big [\Vert U^n - V^n\Vert _H^2\big ] + \frac{1}{2}\sum _{i=1}^{n} \mathbb {E}_i \big [ \Vert U^i - V^i -(U^{i-1} - V^{i-1})\Vert _H^2 \big ]\\&\quad + 2 \sum _{i=1}^{n} h_i \mathbb {E}_i \big [ \eta _{\xi _i}|U^i - V^i |_{V_{\xi _i}}^p\big ], \end{aligned}$$

we have \(2\kappa \sum _{i=1}^{n}{ h_i \mathbb {E}_i \big [ \Vert U^i - V^i \Vert _{H}^2\big ]} \le 2\kappa \sum _{i=1}^{n}{ h_i x_i}\). We can now apply Grönwall’s inequality (Lemma A.1) to (9). It follows that

$$\begin{aligned} x_n \le C \Big (\Vert u_0 - v_0\Vert ^2 + 2 B_1 + 2 \big (\mathbb {E}_{i_{\max }} \big [\Vert U^{i_{\max }} - V^{i_{\max }} \Vert _H^2 \big ]\big )^{\frac{1}{2}} B_2 \Big ), \end{aligned}$$
(10)

for \(C = \frac{1}{1- 2\,h \kappa } \exp \big (\frac{2\kappa T}{1- 2\,h \kappa }\big )\). As this inequality holds for every \(n \in \{1,\dots ,N\}\), it is also fulfilled for \(i_{\max }\). Thus, it follows that

$$\begin{aligned}&\mathbb {E}_{i_{\max }} \big [\Vert U^{i_{\max }} - V^{i_{\max }}\Vert _H^2\big ]\\&\quad \le C \big (\Vert u_0 -v_0\Vert ^2 + 2 B_1+ 2 \big (\mathbb {E}_{i_{\max }} \big [\Vert U^{i_{\max }} - V^{i_{\max }}\Vert _H^2 \big ]\big )^{\frac{1}{2}} B_2\big ). \end{aligned}$$

We can now use that \(x^2 \le 2ax + b^2\) implies that \(x \le 2a +b\) for \(a,b,x \in [0,\infty )\) and find

$$\begin{aligned} \big (\mathbb {E}_{i_{\max }} \big [\Vert U^{i_{\max }}- V^{i_{\max }}\Vert _H^2\big ]\big )^{\frac{1}{2}} \le C^{\frac{1}{2}} \big (\Vert u_0 -v_0\Vert ^2 + 2 B_1\big )^{\frac{1}{2}} + 2 C B_2. \end{aligned}$$

Inserting this bound in (10) and applying Young’s inequality (Lemma A.2 for \(\varepsilon = 1\)), we then obtain

$$\begin{aligned}&\mathbb {E}_n \big [\Vert U^n -V^n\Vert _H^2\big ] + \frac{1}{2}\sum _{i=1}^{n}\mathbb {E}_i \big [ \Vert U^i - V^i -(U^{i-1} - V^{i-1})\Vert _H^2 \big ]\\&\qquad + 2 \sum _{i=1}^{n} h_i \mathbb {E}_i \big [ \eta _{\xi _i}|U^i - V^i |_{V_{\xi _i}}^2\big ]\\&\quad \le C \Big (\Vert u_0 -v_0\Vert ^2 + 2 B_1 + 2 C^{\frac{1}{2}} \big (\Vert u_0 - v_0\Vert ^2 + 2 B_1\big )^{\frac{1}{2}} B_2+ 4 C B_2^2 \Big )\\&\quad \le C \Big (\Vert u_0 -v_0\Vert ^2 + 2 B_1 + \big (\Vert u_0 - v_0\Vert ^2 + 2 B_1\big ) + C B_2^2 + 4 C B_2^2 \Big )\\&\quad = 2 C \big (\Vert u_0 -v_0\Vert ^2 + 2 B_1\big ) + 5 C^2 B_2^2. \end{aligned}$$

It only remains to insert

$$\begin{aligned} B_2^2 = \Big ( \sum _{i=1}^{N} h_i \big \Vert \mathbb {E}_{\xi _i} \big [ f^i - g^i \big ] \big \Vert _H \Big )^2 \le T \sum _{i=1}^{N} h_i \big \Vert \mathbb {E}_{\xi _i} \big [ f^i - g^i \big ] \big \Vert _H^2, \end{aligned}$$

to finish the proof. \(\square \)

Theorem 5.2

Let Assumptions 2.1–2.5 be fulfilled. Further, let \(f_{\xi _n} \in C([0,T]; H)\) almost surely and \(f^n = f_{\xi _n}(t_n) \in L^2(\Omega ;H)\) for all \(n \in \{1,\dots ,N\}\). Let \(\{U^n\}_{n \in \{1,\dots ,N\}}\) be the solution of (2) and u be the solution of (1) that fulfills \(u' \in C^{\gamma } ([0,T]; H)\), \(\gamma \in (0,1]\). Moreover, let \(A_{\xi _n}(t_n) u(t_n) \in L^2(\Omega ; H)\) be fulfilled.

Then for \(2\kappa h_n \le 2\kappa h < 1\) and \(e^n = U^n - u(t_n)\), it follows that

$$\begin{aligned}&\mathbb {E}_n \big [\Vert e^n\Vert _H^2\big ] + \frac{1}{2}\sum _{i=1}^{n}\mathbb {E}_i \big [ \Vert e^i - e^{i-1}\Vert _H^2 \big ]+ 2 \sum _{i=1}^{n} h_i \mathbb {E}_i \big [ \eta _{\xi _i}|e^i |_{V_{\xi _i}}^p\big ]\\&\quad \le 8 h C \sum _{i = 1}^{N} h_i \mathbb {E}_{\xi _i} \big [ \big \Vert f_{\xi _i}(t_i) - A_{\xi _i}(t_i) u(t_i)- (f(t_i) - A(t_i) u(t_i)) \big \Vert _H^2 \big ] \\&\qquad + 4 h^{1 + 2 \gamma } C |u' |_{C^{\gamma }([0,T];H)}^2 T + 5 h^{2\gamma } C^2 |u' |_{C^{\gamma }([0,T];H)}^{2} T^2, \end{aligned}$$

where \(C = \frac{1}{1- 2\,h \kappa } \exp \big (\frac{2\kappa T}{1- 2\,h \kappa }\big )\) for all \(n \in \{1,\dots ,N\}\).

Proof

We use \(\{V^n\}_{n \in \{1,\dots ,N\}}\) given by

$$\begin{aligned} {\left\{ \begin{array}{ll} V^n - V^{n-1} + h_n A_{\xi _n}(t_n) V^n = h_n g^n \quad &{}\text {in } V_{\xi _n}^*, \quad n \in \{1,\dots ,N\}, \\ V^0 = u_0 \quad &{}\text {in } H, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} g^n = \frac{1}{h_n} \big ( u(t_n) - u(t_{n-1})\big ) + A_{\xi _n}(t_n) u(t_n) \in L^2(\Omega ; H). \end{aligned}$$

With this particular choice of \(g^n\), we can now show that \(V^n = u(t_n)\) for every \(n \in \{1.\dots ,N\}\). Given the initial value \(u_0\), the solution \(V^1\) is then given by

$$\begin{aligned} V^1&= u_0 + h_1 g^1 - h_1 A_{\xi _1}(t_1) V^1\\&= u_0 + \big ( u(t_1) - u(t_{0})\big ) + h_1 A_{\xi _1}(t_1) u(t_1) - h_1 A_{\xi _1}(t_1) V^1\\&= u(t_1) + h_1 A_{\xi _1}(t_1) u(t_1) - h_1 A_{\xi _1}(t_1) V^1. \end{aligned}$$

Therefore, it follows that

$$\begin{aligned} (I + h_1 A_{\xi _1}(t_1) ) V^1 = (I + h_1 A_{\xi _1}(t_1) ) u(t_1) \quad \text {in } V_{\xi _1}^*. \end{aligned}$$

Since \(I + h_1 A_{\xi _1}(t_1)\) is injective, we find \(V^1 = u(t_1)\) in \(V_{\xi _1}\). Recursively, it follows that \(V^n = u(t_n)\) in \(V_{\xi _n}\) for all other \(n \in \{1,\dots , N\}\). Together with the stability estimate from Theorem 5.1 we find for \(e^n = U^n - V^n = U^n - u(t_n)\) that

$$\begin{aligned} \mathbb {E}_n \big [\Vert e^n\Vert _H^2\big ] + \frac{1}{2}\sum _{i=1}^{n}\mathbb {E}_i \big [ \Vert e^i - e^{i-1}\Vert _H^2 \big ] + 2 \sum _{i=1}^{n} h_i \mathbb {E}_i \big [ \eta _{\xi _i}|e^i |_{V_{\xi _i}}^2\big ] \le 4 C B_1 + 5 C^2 B_2^2, \end{aligned}$$

where

$$\begin{aligned} B_1&= \sum _{i=1}^{N} h_i^2 \mathbb {E}_i \big [ \Vert f^i - g^i\Vert _H^2\big ], \quad B_2 = \sum _{i=1}^{N} h_i \big \Vert \mathbb {E}_{\xi _i} \big [ f^i - g^i \big ] \big \Vert _H,\\ C&= \frac{1}{1 - 2 h \kappa } \exp \Big (\frac{2\kappa T}{1 - 2 \kappa T}\Big ). \end{aligned}$$

Applying Lemma A.4 for \(u' \in C^{\gamma }([0,T];H)\), it follows that

$$\begin{aligned} B_1&\le h \sum _{i=1}^{N} h_i \mathbb {E}_{\xi _i} \Big [ \Big \Vert f_{\xi _i}(t_i) - A_{\xi _i}(t_i) u(t_i) - \frac{1}{h_i} \int _{t_{i-1}}^{t_i} \big (f(t) - A(t) u(t)\big ) \,\textrm{d}t\Big \Vert _H^2 \Big ] \\&\le 2 h \sum _{i = 1}^{N} h_i \mathbb {E}_{\xi _i} \big [ \big \Vert f_{\xi _i}(t_i) - A_{\xi _i}(t_i) u(t_i)- (f(t_i) - A(t_i) u(t_i)) \big \Vert _H^2 \big ] \\&\qquad + 2 h^{1 + 2 \gamma } |u' |_{C^{\gamma }([0,T];H)}^2 T \end{aligned}$$

and

$$\begin{aligned} B_2^2&\le T \sum _{i=1}^{N} h_i \Big \Vert \mathbb {E}_{\xi _i} \Big [ f_{\xi _i}(t_i) - A_{\xi _i}(t_i) u(t_i) - \frac{1}{h_i} \int _{t_{i-1}}^{t_i} \big (f(t) - A(t) u(t)\big )\,\textrm{d}t \Big ] \Big \Vert _H^2\\&\le h^{2\gamma } |u' |_{C^{\gamma }([0,T];H)}^{2} T^2. \end{aligned}$$

Altogether, we obtain

$$\begin{aligned}&\mathbb {E}_n \big [\Vert e^n\Vert _H^2\big ] + \frac{1}{2}\sum _{i=1}^{n}\mathbb {E}_i \big [ \Vert e^i - e^{i-1}\Vert _H^2 \big ] + 2 \sum _{i=1}^{n} h_i \mathbb {E}_i \big [ \eta _{\xi _i}|e^i|_{V_{\xi _i}}^2\big ]\\&\quad \le 8 h C \sum _{i = 1}^{N} h_i \mathbb {E}_{\xi _i} \big [ \big \Vert f_{\xi _i}(t_i) - A_{\xi _i}(t_i) u(t_i)- (f(t_i) - A(t_i) u(t_i)) \big \Vert _H^2 \big ] \\&\qquad + 4 h^{1 + 2 \gamma } C |u' |_{C^{\gamma }([0,T];H)}^2 T + 5 h^{2\gamma } C^2 |u' |_{C^{\gamma }([0,T];H)}^{2} T^2. \end{aligned}$$

\(\square \)

Remark 2

The main results can all be modified to a slightly different setting, where the right-hand side f(t) takes values in \(V^*\) and where the family \(\{\xi _n\}_{n \in \mathbb {N}}\) of random variables does not have to be mutually independent. In return, this setting requires slightly stronger assumptions on the operator A(t). First, we assume additionally that there exists a constant \(c_V \in (0,\infty )\) such that \(\Vert \cdot \Vert _V \le c_V \big ( \Vert \cdot \Vert _H + |\cdot |_V\big )\) is fulfilled. To generalize the a priori bound from Lemma 4.2 and the stability results from Theorem 5.1, we need to assume that \(\mu _A\) from Assumption 2.2 (v) and \(\eta _A\) from Assumption 2.2 (iii) are strictly positive, respectively. Moreover, if there exist \(\gamma \in (0,1]\) and \(C \in [0,\infty )\) such that

$$\begin{aligned} \sum _{i = 1}^{N} h_i \mathbb {E}_i \big [ \big \Vert f_{\xi _i}(t_i) - A_{\xi _i}(t_i) u(t_i) - (f(t_i) - A(t_i) u(t_i)) \big \Vert _{V_{\xi _i}^*}^2\big ] \le C h^{2 \gamma } \end{aligned}$$

is fulfilled and \(u' \in C^{\gamma }([0,T];H)\), we obtain similar error bounds. We omit the proofs, which are very similar to the ones presented above.

6 Numerical experiments

To illustrate the theoretical convergence results for the randomized scheme in practice, we apply it to Eq. (5) as discussed in Sect. 3. This boundary, initial-value problem fits our setting as already explained there. We also consider what happens when we replace the nonlinear diffusion term with linear diffusion, and a smoother exact solution.

In both cases, we consider the problem on the spatial domain \(\mathcal {D}= [-1,1] \times [-1,1]\) which we split into rectangular sub-domains \(\mathcal {D}_{\ell }\), \(\ell \in \{1,\ldots , s\}\), with \(M_x\) rectangles along the x-axis and \(M_y\) rectangles along the y-axis. We choose \(\mathcal {D}_{\ell }\) such that they have an overlap of 0.2 on all internal sides. This means that, for example, with \(M_x = M_y = 3\), we have \(s = M_x M_y = 9\) sub-domains with, e.g., \(\mathcal {D}_{1} = [-1, -0.267] \times [-1, -0.267]\), \(\mathcal {D}_{2} = [-0.467, 0.467] \times [-1, -0.267]\) and \(\mathcal {D}_{5} = [-0.467, 0.467] \times [-0.467, 0.467]\). Note that they are not uniform in size, because the sub-domains adjacent to the outer edge of \(\mathcal {D}\) have no overlap on one or two sides.

We have to choose a strategy for which sub-problems to select in each time step, i.e. specify the probabilities \(\mathcal {P}(\Omega _{\xi = B})\) for \(B \subset 2^{\{1,\dots ,s\}}\). We consider two strategies. In the first, we simply use \(\mathcal {P}(\Omega _{\xi = \{\ell \}}) = 1/s\). Thus every sub-domain is equally probable to be chosen. As a minor variation, we instead select a set of k sub-domains by drawing with replacement according to the uniform probabilities.

In the second strategy, we make use of a predictor. In addition to the stochastic approximation, we compute a deterministic approximation \(Z^n\) using the backward Euler method, but on a coarser spatial mesh. The idea is that while this approximation is less accurate, it should be significantly cheaper to compute and still resemble the true solution. In the \(n^{\text {th}}\) time step, we compute \(\Psi _n = |Z^{n-1} |+ |Z^n |+ |\tilde{f}(t_n, \cdot ) |> 10^{-3}\). This function is either 0 or 1 and indicates where in the domain something is actually happening. For each sub-domain, we then check whether it is “sufficiently active” or not by evaluating \(\Vert \Psi _n \chi _l\Vert \ge \rho \Vert \Psi _n\Vert \) for a parameter \(\rho \in (0,1)\). We select the set of those sub-domains which pass the test with probability \(1-\rho \) and the set of all the other sub-domains with probability \(\rho \).

We note that the errors for the first strategy are noticeably larger than those of the second strategy. In the following, we will use fewer sub-domains for the first strategy for that reason. More precisely, we use \(M_x = 3\) and \(M_y = 1\) for first strategy and \(M_x = 3\) and \(M_y = 3\) for the second strategy. Furthermore, we can observe that the second strategy works better with more sub-domains, since it essentially adaptively groups them into only two larger sub-domains; the active set and the inactive set. Increasing the number of sub-domains increases the fidelity such that the choice of whether each sub-domain is active or not becomes easier, albeit at a higher computational cost. If the spatial discretization is using finite elements, the limit case would be when every element is its own subdomain. This is what is considered in [36] for a deterministic scheme, where it is, indeed, observed that the overhead costs can be prohibitive even when using very efficient data structures.

We only report errors here, since this is the focus of the paper. A natural next step would be to investigate also the computation times and the efficiency of the schemes compared to deterministic schemes. Since the randomized methods need to solve equation systems of smaller size, they are expected to outperform the deterministic schemes. However, this depends on many factors, such as the problem size, the number of subdomains, the behaviour of the exact solution and the random strategy used. Further, for such a comparison to be useful, it has to be performed with equally optimized and parallelized code for both the randomized and deterministic cases. Such advanced software engineering is out of the scope of this article. Nevertheless, when applying our non-parallelized and not fully optimized code to the linear diffusion problem using the first strategy, we observed a factor 2 speed-up that was independent of the number of time steps.

6.1 A nonlinear example

In our first experiment, we use the problem parameters \(T = 1\), \(p = 4\) and \(\alpha (t) \equiv 1\). Further, we choose the source term \(\tilde{f}\) such that the exact solution is given by \(u(t, x, y) = \tilde{u}(x - r \cos (2\pi t), y - r \sin (2\pi t))\) with \(r = 1/2\),

$$\begin{aligned} \tilde{u}( x, y) = \Bigl [0.03 - \frac{10^{3/8}}{4} (x^2 + y^2)^{\frac{4}{3}} \Bigr ]_+^{\frac{3}{4}} \end{aligned}$$

and \([\cdot ]_+ = \max \{\cdot , 0\}\). This describes a localized pulse that starts centered at (0.5, 0) and which then rotates around the origin at the constant distance r. The shape of the pulse is inspired by the closed-form Barenblatt solution to \(\partial _t u = \nabla \cdot (|\nabla u(t,x) |^{p-2}\nabla u)\), see e.g. [21]. At \(t = 0\), this solution is a Dirac delta, which then expands into a cone-shaped peak for \(t>0\). Our pulse is this solution frozen at the time \(t = 0.001\). We note that due to the sharp interface where the pulse meets the x-y-plane and to the sharp peak, u is of low regularity.

We discretize the problem in space using central finite differences, such that the approximation of the p-Laplacian is 2nd-order accurate. We use 100 computational nodes in each spatial dimension, for a total of \(10\, 000\) degrees of freedom. Thus, the temporal error dominates the spatial error when considering the full error in the following. For the temporal discretization, we use the scheme (2), along with one of the two strategies outlined above. For the first strategy, we try \(k = 1\) and \(k = 2\). For the second, we evaluate the different parameters \(\rho = 0.01, 0.05, 0.1, 0.2\). We compute approximations for the different (constant) time steps \(h_n = 2^{-5}, 2^{-6}, \ldots , 2^{-13}\) and estimate their corresponding errors at the final time by running the method with 50 random iterations and averaging. That is, we approximate

$$\begin{aligned} \mathbb {E}_N \big [\Vert e^N\Vert _H^2\big ] \approx \frac{1}{50} \sum _{j=1}^{50}{ \Vert U_j^N - U_{\text {ref}}\Vert _H^2}, \end{aligned}$$

where \(U_j^N\) is the numerical approximation on the j-th path and \(U_{\text {ref}}\) is the exact solution \(u(t_N, \cdot , \cdot )\) evaluated at the spatial grid.

Figure 1 shows the resulting relative errors vs. the time steps, with the first strategy in the upper plot and the second strategy in the lower. We observe that both strategies result in errors that decrease as \(\mathcal {O}(h^{1/2})\), in line with Theorem 5.2.

Fig. 1
figure 1

The relative errors \(\big (\mathbb {E}_N\big [ \Vert U^N - U_{\text {ref}}\Vert ^2 \big ] \big )^{1/2} / \; \Vert U_{\text {ref}}\Vert \) for the nonlinear setting described in Sect. 6.1. The upper plot uses the first randomized strategy and the lower plot uses the second strategy. We observe that the errors decay as \(\mathcal {O}(h^{1/2})\), in line with Theorem 5.2, irrespective of the choice of \(\rho \) or k. A smaller \(\rho \) or larger k decreases the error, but of course also incurs a higher computational cost

Full size image

6.2 A linear example

As a second experiment, we consider a linear version of the previous problem. We use the same parameters as in the previous section, except that we set \(p = 2\) and \(\alpha (t) = 0.1\), and that the rotating pulse is now Gaussian rather than a sharp peak. More precisely, the exact solution is given by

$$\begin{aligned} u(t, x, y) = e^{-100 (x - r \cos (2\pi t))^2 - 100 (y - r \sin (2\pi t))^2}. \end{aligned}$$

The resulting errors are shown in Fig. 2. Again, we note that the first, uniform, strategy converges as \(\mathcal {O}(h^{1/2})\), in line with Theorem 5.2. The second strategy with \(\rho = 0.01\) performs significantly better and the error behaves like \(\mathcal {O}(h)\) in the first part of the plot. This is essentially the same behaviour as if we would apply backward Euler to the full problem, but the method only updates the approximation on the most relevant sub-domains and is therefore cheaper to evaluate. This improved convergence order is possible due to the extra smoothness present in this linear problem. In the error bound of Theorem 5.2, the first term becomes small due to the used strategy, and because the solution is smooth the remaining terms are of size \(h^3\) and \(h^2\), respectively.

Increasing the parameter \(\rho \) means that we disregard more of the information from the predictor, and as seen in Fig. 2 this causes the convergence order to decrease towards 1/2. On the other hand, setting \(\rho = 0\) means that we always choose all the sub-domains and thereby do more computations than if we would simply solve the full problem directly. The parameter \(\rho \) is therefore a design parameter, and further research is required on how to choose it optimally for specific problem classes. Regardless of the choice, however, we still have \(\mathcal {O}(h^{1/2})\)-convergence.

Fig. 2
figure 2

The relative errors \(\big (\mathbb {E}_N\big [ \Vert U^N - U_{\text {ref}}\Vert ^2 \big ] \big )^{1/2} / \; \Vert U_{\text {ref}}\Vert \) for the linear setting described in Sect. 6.2. The upper plot uses the first randomized strategy and the lower plot uses the second strategy. We observe that the errors for the first strategy decay as \(\mathcal {O}(h^{1/2})\), similarly to the nonlinear case. For the second strategy, large \(\rho \) also leads to convergence of order 1/2, while sufficiently small \(\rho \) leads to faster convergence of order 1

Full size image