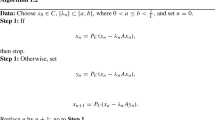1 Introduction

Many models in mechanics, optimal control, and other areas can be formulated in terms of variational problems seeking the minimiser of

figure a

Our focus in the present work is on the numerical discretisation of (\({\mathcal {P}}\)) in the case of non-autonomous integrands \(\phi :\Omega \times {\mathbb {R}}^{m\times n} \rightarrow {\mathbb {R}}\), \(m,n \in {\mathbb {N}}\), that are Carathèodory, convex in the second component, and satisfy the non-standard growth conditions with \(1< p_-< p_+ < \infty \) and

$$\begin{aligned} -c_0 +c_1 {|{\xi }|}^{p_-}\le \phi (x,\xi )\le c_2{|{\xi }|}^{p_+} +c_0. \end{aligned}$$
(1)

We will assume throughout this paper that \(\Omega \subset {\mathbb {R}}^n\) is a bounded polygonal domain (to allow for discretisation), \(W :=\lbrace v \in W^{1,p_-}(\Omega ;{\mathbb {R}}^m) :v|_{\partial \Omega } = \psi |_{\partial \Omega }\rbrace \) with boundary data \(\psi \in W^{1,p_+}(\Omega ;{\mathbb {R}}^m)\), and right-hand side \(f\in L^{p_-'}(\Omega ;{\mathbb {R}}^m)\). Under these natural restrictions, Tonelli’s theorem states well-posedness of (\({\mathcal {P}}\)). In the context of nonlinear elasticity such problems were studied in [1, 2].

A naive approach to discretise (\({\mathcal {P}}\)) is the minimisation of the energy \({\mathcal {F}}\) over some discrete subspace \(W_h \subset W\). However, non-standard growth conditions \(p_-< p_+\) may lead to the Lavrentiev gap phenomenon [33, 40, 41], that is, it may occur with \(H :=W \cap W^{1,\infty }(\Omega ;{\mathbb {R}}^m)\) that

$$\begin{aligned} \min _{v \in W} {\mathcal {F}}(v) < \inf _{w \in H} {\mathcal {F}}(w). \end{aligned}$$
(2)

Since conforming discretisations generally satisfy \(W_h \subset H\), the strict inequality in (2) implies the failure of this scheme. Indeed, the approximated energy \(\min _{W_h} {\mathcal {F}}\) converges to the so-called H-minimum \(\inf _{H} {\mathcal {F}}\) as the underlying triangulation is refined [14].

Several numerical schemes have been suggested to overcome the Lavrentiev gap, see for example [6, 7, 14, 25, 31, 32]. These methods require a regularisation/penalisation leading to convergence only in a dual limit. The careful balancing of the regularisation parameter with refinement of the underlying triangulation is a challenging task that can be avoided, in some important situations, by the use of non-conforming finite element methods where \(W_h \not \subset W\) [34, 35]. This non-conforming approach leads to a numerical scheme that converges to the W-minimum \(\min _W {\mathcal {F}}\) for autonomous and convex integrands \(\phi (x,\xi )=\phi (\xi )\).

In the present work we show how to adapt the numerical scheme as well as the convergence analysis for the much larger class of variational problems (\({\mathcal {P}}\)) with non-autonomous integrands. The main result in Theorem 1 states the convergence of the approximated minimiser and energy to a W-minimiser \(u\in \text {argmin}_W {\mathcal {F}}\) and the W-minimum \(\min _{W} {\mathcal {F}}\), provided a specialised numerical quadrature rule is employed and under mild additional restrictions on the integrand (cf. (A1)–(A3) or (B) on p. 4). These assumptions are valid for a wide class of variational problems that exhibit a Lavrentiev gap, including important models such as the double-phase potential [5, 10, 13, 21, 24, 42], the variable exponent Laplacian [27, 41, 42], and the weighted p-energy [28]. The problems cited above do not exhaust the full range of present research in numerical analysis for problems with non-standard growth (for example, a posteriori estimates for variational problems with nonstandard power functionals [36]).

1.1 Outline

Section 2.1 introduces the numerical scheme that utilises Crouzeix-Raviart functions and a one-point quadrature rule. Section 2.2 provides two sets (A) and (B) of assumptions. The set (A) contains, compared to the set (B), a weaker assumption on the quadrature and stronger assumptions on the integrand. The convergence proof of the numerical scheme follows in Sect. 2.3. The proof is quite direct under the assumption in (B). The relaxed assumption on the quadrature in (A) requires a more involved analysis, which is performed in Sect. 2.4. This proof exploits ideas of Zhikov [39], in particular it relies on the dual variational problem and the concept of relaxation (18) allowing us to pass to more regular problems. We summarise examples for energies that lead to a Lavrentiev gap in Sect. 3. Numerical experiments, displayed in Sect. 4, apply our numerical scheme to these energies. In addition, the numerical experiments underline the importance of a suitable quadrature and further investigate singularities and the Lavrentiev gap for energies with multiple saddle points. We summarise required known results and calculations in the appendix.

2 Convergent numerical scheme

This section introduces the numerical scheme (Sect. 2.1) and proves its convergence (Sect. 2.3–2.4) under suitable assumptions on the integrand and quadrature (Sect. 2.2).

2.1 Discretisation

Let \(({\mathcal {T}}_h)_{h>0}\) be a (not necessarily shape-regular and nested) sequence of regular triangulations of the domain \(\Omega \) into simplices with diameters \(\text {diam}(T) < h\) for all \(T\in {\mathcal {T}}_h\). Let \({\mathcal {E}}_h\) denote the set of facets (\((d-1)\)-subsimplices) of all cells \(T\in {\mathcal {T}}_h\). The Crouzeix–Raviart space reads

$$\begin{aligned} \text {CR}^1({\mathcal {T}}_h)&:=\big \{ v_h\in L^\infty (\Omega ;{\mathbb {R}}^m) :v_h|_T \text { is affine for all }T\in {\mathcal {T}}_h\text { and}\\&\qquad \qquad \qquad \text {continuous in the midpoints }\text {mid}(e)\text { for all }e\in {\mathcal {E}}_h\big \}. \end{aligned}$$

Recall the boundary data \(\psi \in W^{1,p_+}(\Omega ;{\mathbb {R}}^m)\) from the definition of the space W in (\({\mathcal {P}}\)) and let \({\mathcal {E}}_h(\partial \Omega )\) denote the set of all facets \(e\in {\mathcal {E}}_h\) on the boundary \(\partial \Omega \). We define the space

$$\begin{aligned} W^{\text {nc}}_h:=\left\{ v_h\in \text {CR}^1({\mathcal {T}}_h):v_h(\text {mid}(e)) = \frac{1}{|e|} \int _e \psi \,\mathrm {d}s\text { for all }e \in {\mathcal {E}}_h(\partial \Omega )\right\} . \end{aligned}$$

Notice that the Crouzeix-Raviart space is non-conforming in the sense that \(W^{\text {nc}}_h\not \subset W\). In particular, the gradient is only defined in the sense of distributions. However, it is possible to apply the gradient element-wise, that is, we set the broken gradient

$$\begin{aligned} (\nabla _h v)|_T :=\nabla v|_T \qquad \text {for all }v \in W^{\text {nc}}_h+ W\text { and }T\in {\mathcal {T}}. \end{aligned}$$

Numerical schemes for problems with Lavrentiev gap appear to be very sensitive with respect to quadrature errors (cf. Sect. 4.3). We will carefully analyse conditions under which the following simple one-point quadrature rule yields a convergent scheme: Given points \(x_T \in T,\) \(T \in {\mathcal {T}}_h\), we approximate \(\phi \) by the mesh-dependent integrand

$$\begin{aligned} \phi _h(x,\cdot ) :=\phi (x_T,\cdot )\quad \text {for all } x \in T\in {\mathcal {T}}_h. \end{aligned}$$

This integrand is piece-wise constant in the first component and defines for all \(v \in W + W^{\text {nc}}_h\) and \(h>0\) the functional

$$\begin{aligned} {\mathcal {F}}_h(v) :=\int _\Omega \phi _h(x,\nabla _h v) - f \cdot v\,\mathrm {d}x = \sum _{T\in {\mathcal {T}}_h} \int _T \phi (x_T,\nabla v) - f \cdot v\,\mathrm {d}x. \end{aligned}$$

The resulting numerical scheme seeks a minimiser

figure b

The existence of a discrete solution follows from the growth condition (1) and the direct method in calculus of variations.

2.2 Main result

To state the convergence of the numerical scheme in (\({\mathcal {P}}_h^\text {nc}\)), we introduce two alternative sets of assumptions on the integrand and the quadrature points \(x_T \in T\in {\mathcal {T}}_h\).

  • (Quadrature) There exists a constant \(c \in (0,1]\) such that we have for all \(T \in {\mathcal {T}}_h\), \(\xi \in {\mathbb {R}}^{m \times n}\), and \(h>0\)

    figure c

    Moreover, we assume the point-wise convergence \(\phi _h(x,\xi ) \rightarrow \phi (x,\xi )\) as \(h\rightarrow 0\) for almost all \(x\in \Omega \) and all \(\xi \in {\mathbb {R}}^{m\times n}\).

  • (\(\Delta _2\)-condition) There exist constants \(C,C_0 \in {\mathbb {R}}_{\ge 0}\) such that we have for almost all \(x\in \Omega \) and all \(\xi \in {\mathbb {R}}^{m\times n}\)

    $$\begin{aligned} \phi (x, 2\xi )&\le C\, \phi (x,\pm \xi ) +C_0. \end{aligned}$$
    (A2)

  • (\(\nabla _2\)-condition) If the constant c in (A1) is smaller than 1, there are constants \(K,K_0 \in {\mathbb {R}}_{\ge 0}\) such that we have for almost all \(x\in \Omega \) and all \(\xi \in {\mathbb {R}}^{m\times n}\)

    $$\begin{aligned} K\, \phi (x,2 \xi )&\le \phi (x, \pm K \xi )+K_0. \end{aligned}$$
    (A3)

Notice that the \(\nabla _2\)-condition is equivalent to the \(\Delta _2\)-condition for the convex conjugate \(\phi ^*\), see Proposition A3. The numerical experiment in Sect. 4.3 shows that an assumption on the quadrature is necessary. The assumption in (A1) seems to be rather general, but might be relaxed if one uses additional information of specific energies. The relaxed assumption in (A1) comes with the price of a more involved convergence analysis. In particular, we investigate the dual problem, which requires the additional assumptions in (A2) and (A3).

We can circumvent this instructive but involved analysis by the following more restrictive assumption on the quadrature.

  • There exists a constant \(c_\phi <\infty \) such that, for all \(h>0\) and \(\xi \in {\mathbb {R}}^{m\times n}\) with \(c_\phi <|\xi |\),

    $$\begin{aligned} \phi _h(x,\xi ) \le \phi (x,\xi )\qquad \text {for almost all }x\in \Omega . \end{aligned}$$
    (B)

    Moreover, we suppose the point-wise convergence \(\phi _h(x,\xi ) \rightarrow \phi (x,\xi )\) as \(h\rightarrow 0\) for almost all \(x\in \Omega \) and all \(\xi \in {\mathbb {R}}^{m\times n}\).

The following main result of this paper states convergence of the numerical scheme under the assumptions in (A1)–(A3) or the assumption in (B). Its proof is postponed to the following two subsections.

Theorem 1

(Convergence) Suppose the integrand \(\phi \) satisfies the two-sided growth conditions (1) and (A1)–(A3) or (B). Then the energies converge to the minimal energy, that is, we have

$$\begin{aligned} \lim _{h \rightarrow 0}{\mathcal {F}}_h(u_h) = {\mathcal {F}}(u) = \min _{v\in W} {\mathcal {F}}(v). \end{aligned}$$
(3)

Moreover, there exists a subsequence \((h_j)_{j\in {\mathbb {N}}}\) with \(h_j \rightarrow 0\) such that

$$\begin{aligned} u_{h_j}&\rightarrow u&\text {strongly in }L^{p_-}(\Omega ;{\mathbb {R}}^m), \end{aligned}$$
(4)
$$\begin{aligned} \nabla _{h_j} u_{h_j}&\rightharpoonup \nabla u&\text {weakly in }L^{p_-}(\Omega ;{\mathbb {R}}^{m\times n}). \end{aligned}$$
(5)

If the minimiser \(u\in W\) is unique, the entire sequence converges. If the integrand is strictly convex, then the convergence is strong.

Remark 2

(Alternative schemes) It should be possible to extend the following arguments and therefore also our main result to numerical schemes that share certain similarities with the Crouzeix-Raviart FEM. In particular, the result should extend to the (lowest-order) unstabilized HHO scheme in [16] and to DG schemes with an averaged penalty term as in [29], provided the penalties are scaled properly, cf. [8].

2.3 Proof of convergence

The proof of Theorem 1 requires three preliminary results. The first one is an asymptotic lower bound for the computed energy. Its proof utilises the point-wise convergence in (A1) or (B), that is,

$$\begin{aligned} \lim _{h\rightarrow 0} \phi _h(x,\xi ) = \phi (x,\xi )\qquad \text {for all } \xi \in {\mathbb {R}}^{m\times n} \text { and almost all }x \in \Omega . \end{aligned}$$
(6)

A further tool is the conjugate functional (see for example [22]), which involves the convex conjugate (with \(\phi _0 :=\phi \))

$$\begin{aligned} \phi _h^*(\cdot ,\xi ) :=\sup _{t \in {\mathbb {R}}^{m\times n}} \lbrace \xi :t - \phi _h(\cdot ,t) \rbrace \qquad \text {for all } \xi \in {\mathbb {R}}^{m\times n}\text { and } h\ge 0. \end{aligned}$$
(7)

The growth condition (1) and properties of the convex conjugate in Lemma A1 yield for all \(h\ge 0\), all \(\xi \in {\mathbb {R}}^{m\times n}\), and almost all \(x\in \Omega \) the growth

$$\begin{aligned} -c_0+ c_2^{1-p_+'} |\xi |^{p_+'} \le \phi _h^*(x,\xi ) \le c_1^{1-p_-'}|\xi |^{p_-'} + c_0. \end{aligned}$$
(8)

Lemma 3

(Lower bound) Let \((\vartheta _h)_{h>0} \subset L^1(\Omega ;{\mathbb {R}}^{m\times n})\) be a weakly convergent sequence \(\vartheta _h\rightharpoonup \vartheta \) in \(L^1(\Omega ;{\mathbb {R}}^{m\times n})\) as \(h \rightarrow 0\). Then we have

$$\begin{aligned} \int _\Omega \phi (x, \vartheta ) \,\mathrm {d}x \le \liminf _{h\rightarrow 0} \int _\Omega \phi _h(x, \vartheta _h)\,\mathrm {d}x. \end{aligned}$$

Proof

Let \((\vartheta _h)_{h>0} \subset L^1(\Omega ;{\mathbb {R}}^{m\times n})\) be a weakly convergent sequence \(\vartheta _h\rightharpoonup \vartheta \) in \(L^1(\Omega ;{\mathbb {R}}^{m\times n})\) as \(h\rightarrow 0\). Young’s inequality yields for all \(z\in L^\infty (\Omega ;{\mathbb {R}}^{m\times n})\) and \(h\ge 0\) that

$$\begin{aligned} \int _\Omega z: \vartheta _h\, \mathrm {d}x-\int _\Omega \phi _h^*(x,z)\, \mathrm {d}x \le \int _\Omega \phi _h(x,\vartheta _h)\, \mathrm {d}x. \end{aligned}$$
(9)

Lemma A5 states that the point-wise convergence (6) implies point-wise convergence of the conjugates, that is, we have

$$\begin{aligned} \lim _{h\rightarrow 0} \phi ^*_h(x,\xi ) = \phi ^*(x,\xi )\qquad \text {for all } \xi \in {\mathbb {R}}^{m\times n} \text { and almost all }x \in \Omega . \end{aligned}$$

This point-wise convergence and the upper growth condition (8) for \(\phi _h^*\) allow for the application of Lebesgue’s theorem, which yields

$$\begin{aligned} \lim _{h\rightarrow 0} \int _\Omega \phi _h^*(x,z) \, \mathrm {d}x= \int _\Omega \phi ^*(x,z) \, \mathrm {d}x. \end{aligned}$$
(10)

Taking the limit in (9), using the weak convergence in \(L^1(\Omega ;{\mathbb {R}}^{m\times n})\), and applying the identity in (10) result in

$$\begin{aligned} \sup _{z\in L^\infty (\Omega ;{\mathbb {R}}^{m\times n})} \int _\Omega z:\vartheta \, \mathrm {d}x-\int _\Omega \phi ^*(x,z)\, \mathrm {d}x&\le \liminf _{h\rightarrow 0} \int _\Omega \phi _h(x,\vartheta _h)\, \mathrm {d}x. \end{aligned}$$

The lemma follows from an application of the conjugate functional theorem [22,  Chap. IX, Prop. 2.1], which says

$$\begin{aligned}&\sup _{z\in L^\infty (\Omega ;{\mathbb {R}}^{m\times n})} \int _\Omega z:\vartheta \, \mathrm {d}x-\int _\Omega \phi ^*(x,z)\, \mathrm {d}x = \int _\Omega \phi (x, \vartheta )\, \mathrm {d}x. \end{aligned}$$

\(\square \)

In order to apply the previous lemma, we have to show that the gradients \((\nabla _h u_h)_{h>0}\) of the discrete minimiser have a weakly convergent subsequence. This property follows from the following more general result.

Lemma 4

(Convergent subsequence) Let \(v_h\in W^{\text {nc}}_h\) be uniformly bounded in the sense that

$$\begin{aligned} \sup _{h>0}\, \Vert \nabla _hv_h\Vert _{L^{p_-}(\Omega )} < \infty . \end{aligned}$$

Then there exists a sequence \((h_j)_{j\in {\mathbb {N}}}\) with \(h_j \searrow 0\) and a function \(v\in W\) with

$$\begin{aligned} \begin{aligned} v_{h_j}&\rightarrow v&\text {strongly in }L^{p_-}(\Omega ;{\mathbb {R}}^m), \\ \nabla _{h_j} v_{h_j}&\rightharpoonup \nabla v&\text {weakly in } L^{p_-}(\Omega ;{\mathbb {R}}^{m \times n}). \end{aligned} \end{aligned}$$

Proof

Applying the result of [35,  Thm. 4.3] implies the statement but with \(\nabla v_{h_j} \rightharpoonup \nabla v\) weakly in \(L^1(\Omega ;{\mathbb {R}}^{m \times n})\). The uniform \(L^{p-}(\Omega ;{\mathbb {R}}^{m \times n})\) bound on \(\nabla v_{h_j}\) immediately implies that in fact \(\nabla v_{h_j} \rightharpoonup \nabla v\) weakly in \(L^{p-}(\Omega ;{\mathbb {R}}^{m \times n})\) as stated. The strong convergence of \(v_{h_j}\) in \(L^{p-}(\Omega ;{\mathbb {R}}^{m})\) then follows by the compactness of the embedding of broken Sobolev spaces [8]. \(\square \)

The final auxiliary result is an asymptotic upper bound for the minimal energy \({\mathcal {F}}_h(u_h) = \min _{W^{\text {nc}}_h} {\mathcal {F}}_h\).

Lemma 5

(Upper bound) Suppose (A1)– (A3) or (B), then we have

$$\begin{aligned} \limsup _{h\rightarrow 0} {\mathcal {F}}_h(u_h) \le \min _{W} {\mathcal {F}} = {\mathcal {F}}(u). \end{aligned}$$

Proof

Step 1 (Upper bound for \({\mathcal {F}}_h({\mathcal {I}}_hv)\)). Let \(v\in W\) be arbitrary and set its non-conforming interpolation \({\mathcal {I}}_hv \in W^{\text {nc}}_h\) by

$$\begin{aligned} {\mathcal {I}}_hv(\text {mid}(e)) :=\frac{1}{|e|} \int _e v \,\mathrm {d}s\qquad \text {for all facets }e\in {\mathcal {E}}_h. \end{aligned}$$

An integration by parts reveals for all \(T\in {\mathcal {T}}_h\) that

$$\begin{aligned} \nabla ({\mathcal {I}}_hv)|_T = \frac{1}{|T|} \int _T \nabla v\, \mathrm {d}x. \end{aligned}$$
(11)

Since \(\phi _h|_T\) with \(T\in {\mathcal {T}}_h\) is constant in the first component and convex in its second, Jensen’s inequality and (11) yield

$$\begin{aligned} \int _T \phi _h(x,\nabla {\mathcal {I}}_hv)\,\mathrm {d}x \le \int _T \phi _h(x, \nabla v)\,\mathrm {d}x. \end{aligned}$$

This estimate and the inequality \(\Vert v - {\mathcal {I}}_hv \Vert _{L^{p_-}(T)} \le C_\text {apx}\, \text {diam}(T) \, \Vert \nabla v\Vert _{L^{p_-}(T)}\) with \(C_\text {apx} = 1 + 2/n\) for all \(T\in {\mathcal {T}}_h\) [34,  Lem. 2] show

$$\begin{aligned} {\mathcal {F}}_h({\mathcal {I}}_hv)&= \sum _{T\in {\mathcal {T}}_h} \int _T \phi _h(x,\nabla {\mathcal {I}}_hv) - f\cdot {\mathcal {I}}_hv\,\mathrm {d}x \nonumber \\&\le C_\text {apx}\, h\, \Vert f \Vert _{L^{p_-'}(\Omega )} \,\Vert \nabla v\Vert _{L^{p_-}(\Omega )} + \sum _{T\in {\mathcal {T}}_h} \int _T \phi _h(x,\nabla v) - f\cdot v\,\mathrm {d}x. \end{aligned}$$
(12)

Step 2 (Proof with (B)). Suppose the assumption in (B) holds true with threshold \(c_\phi <\infty \). Then the sum in the upper bound (12) satisfies

$$\begin{aligned}&\sum _{T\in {\mathcal {T}}_h} \int _T \phi (x_T,\nabla v) - f\cdot v \,\mathrm {d}x \\&\quad = \sum _{T\in {\mathcal {T}}_h} \int _{T \cap \lbrace |\nabla v| \le c_\phi \rbrace } \phi (x_T,\nabla v) \,\mathrm {d}x +\int _{T \cap \lbrace c_\phi < |\nabla v|\rbrace } \phi (x_T,\nabla v) \,\mathrm {d}x - \int _T f\cdot v \,\mathrm {d}x\\&\quad \le {\mathcal {F}}(v) + \sum _{T\in {\mathcal {T}}_h} \int _{T \cap \lbrace |\nabla v| \le c_\phi \rbrace } \phi (x_T,\nabla v) - \phi (x,\nabla v) \,\mathrm {d}x. \end{aligned}$$

The growth condition (1) results for almost all \(x\in T \cap \lbrace |\nabla u| \le c_\phi \rbrace \) with \(T\in {\mathcal {T}}_h\) in the upper bound

$$\begin{aligned} |\phi (x_T,\nabla v(x))| \le c_2{|{\nabla v(x)}|}^{p_+}+c_0 \le c_2c_\phi ^{p_+}+c_0. \end{aligned}$$

Hence, Lebesgue’s dominated convergence theorem shows

$$\begin{aligned} \sum _{T\in {\mathcal {T}}_h} \int _{T \cap \lbrace |\nabla u| \le c_\phi \rbrace } \phi (x_T,\nabla v) - \phi (x,\nabla v) \,\mathrm {d}x \rightarrow 0 \qquad \text {as }h\rightarrow 0. \end{aligned}$$

This concludes the proof under the assumption in (B).

Step 2’ (Proof with (A1)–(A3)). The inequality in (12) reads

$$\begin{aligned} {\mathcal {F}}_h({\mathcal {I}}_hv)&\le {\mathcal {F}}_h(v) + C_\text {apx}\, h\, \Vert f \Vert _{L^{p_-'}(\Omega )} \,\Vert \nabla v\Vert _{L^{p_-}(\Omega )}. \end{aligned}$$

Taking the limit \(h\rightarrow 0\) yields

$$\begin{aligned} \limsup _{h\rightarrow 0} \min _{W^{\text {nc}}_h} {\mathcal {F}}_h \le \limsup _{h\rightarrow 0} \min _{W} {\mathcal {F}}_h. \end{aligned}$$

Thus, the lemma follows from the claim

$$\begin{aligned} \limsup _{h\rightarrow 0} \inf _{W} {\mathcal {F}}_h \le \min _W {\mathcal {F}}. \end{aligned}$$
(13)

The proof of the claim in (13) is rather involved and, thus, postponed to the following Sect. 2.4. \(\square \)

After these three preliminary results we can prove this paper’s main result.

Proof of Theorem 1

Lemma 5 and the growth condition (1) lead for all sufficiently small \(h>0\) to the upper bound

$$\begin{aligned}&\sum _{T\in {\mathcal {T}}_h} \Vert \nabla u_h\Vert _{L^{p_-}(T)}^{p_-} - c_0|T| - C_\text {apx}\, h\,\Vert f \Vert _{L^{p_-'}(T)} \Vert \nabla u_h\Vert _{L^{p_-}(T)}\\&\quad \le \sum _{T\in {\mathcal {T}}_h} \int _T \phi (x_T,\nabla u_h)\,\mathrm {d}x - C_\text {apx}\, h\,\Vert f \Vert _{L^{p_-'}(T)} \Vert \nabla u_h\Vert _{L^{p_-}(T)}\\&\quad \le {\mathcal {F}}_h(u_h) \le {\mathcal {F}}(u) + 1. \end{aligned}$$

In particular, we have for all sufficiently small \(h>0\) a uniform upper bound \( \Vert \nabla _h u_h\Vert _{L^{p_-}(\Omega )}\le C < \infty . \) Hence Lemma 4 yields the existence of a subsequence \((u_{h_j})_{j\in {\mathbb {N}}}\) and a function \(v\in W\) with

$$\begin{aligned} u_{h_j} \rightarrow v \text { strongly in }L^{p_-}(\Omega ;{\mathbb {R}}^m),\quad \nabla _{h_j} u_{h_j} \rightharpoonup \nabla v\text { weakly in }L^{p_-}(\Omega ;{\mathbb {R}}^{m\times n}). \end{aligned}$$

An application of Lemma 3 and 5 shows that

$$\begin{aligned} {\mathcal {F}}(v) \le \liminf _{j\rightarrow \infty } {\mathcal {F}}_{h_j}(u_{h_j}) \le \limsup _{h\rightarrow 0} {\mathcal {F}}_h(u_h) \le {\mathcal {F}}(u) = \min _{w\in W} {\mathcal {F}}(w) < \infty . \end{aligned}$$

In particular, \(v = u\) minimises the functional \({\mathcal {F}}\) over the set \(W\). This shows (4) and (5). Since the arguments apply to any subsequence, the entire sequence \(({\mathcal {F}}_h(u_h))_{h>0}\) converges to \({\mathcal {F}}(u) = \min _{W}{\mathcal {F}} = \lim _{h\rightarrow 0}{\mathcal {F}}_h(u_h)\). This shows (3).

If, in addition, the minimiser \(u\in W\) is unique, the same argument proves the convergence of the entire sequence \(u_{h}\rightarrow u\text { strongly in }L^{p_-}(\Omega ;{\mathbb {R}}^m)\) and \(\nabla _hu_{h} \rightharpoonup \nabla u\text { weakly in }L^{p_-}(\Omega ;{\mathbb {R}}^{m\times n})\) as \(h\rightarrow 0\). If the integrand is strictly convex in the second component then the strong convergence follows from [38]. \(\square \)

2.4 Proof of lemma 5

We verify the claim in (13) under the assumptions in (A1)–(A3), which we assume throughout this subsection. Our proof relies on techniques from [39]. Among others, we exploit the dual formulation of the minimisation problem for all \(h\ge 0\)

figure d

In order to include boundary data and right-hand side, we shift the functional \({\mathcal {F}}_h\) as follows. The surjectivity of the divergence operator [9] yields the existence of a function \(F \in L^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})\) with \(\text {div}\, F = f\). We set \(\phi _0 :=\phi \) and define for all \(h\ge 0\) and \(\xi \in {\mathbb {R}}^{m\times n}\) the (shifted) integrand

$$\begin{aligned} \Phi _h(\cdot ,\xi ) :=\phi _h(\cdot ,\xi ) + F : \xi . \end{aligned}$$

Recall the boundary data \(\psi \in W^{1,p_+}(\Omega ;{\mathbb {R}}^m)\) and define the energy

$$\begin{aligned} \hat{{\mathcal {F}}}_h(v) :=\int _\Omega \Phi _h(x,\nabla v + \nabla \psi ) \, \mathrm {d}x\qquad \text {for all }v \in W^{1,1}(\Omega ;{\mathbb {R}}^m). \end{aligned}$$

An integration by parts (with outer unit normal vector \(\nu \)) shows for all \(v \in W_0^{1,p_-}(\Omega ;{\mathbb {R}}^m)\) with homogeneous Dirichlet boundary data the identity

$$\begin{aligned} \hat{{\mathcal {F}}}_h( v) - \int _{\partial \Omega } \psi \cdot F\nu \, \mathrm {d}s= {\mathcal {F}}_h( v + \psi ). \end{aligned}$$

In particular, we have for all \(h\ge 0\) the equivalence of (\({\mathcal {P}}_h\)) and the problem

$$\begin{aligned} \min _{v\in W_0^{1,p_-}(\Omega ;{\mathbb {R}}^m)} \hat{{\mathcal {F}}}_h( v) - \int _{\partial \Omega } \psi \cdot F\nu \, \mathrm {d}s. \end{aligned}$$

The dual problem involves the convex conjugate \(\Phi _h^*\), which reads

$$\begin{aligned} \begin{aligned} \Phi _h^*(\cdot ,\zeta )&:=\sup _{\xi \in {\mathbb {R}}^{m\times n}} \lbrace \zeta :\xi - \Phi _h(\cdot ,\xi )\rbrace = \sup _{\xi \in {\mathbb {R}}^{m\times n}} \lbrace (\zeta -F) : \xi - \phi _h(\cdot ,\xi )\rbrace \\&= \phi _h^*(\cdot ,\zeta - F)\qquad \qquad \qquad \text {for all }\zeta \in {\mathbb {R}}^{m\times n}\text { and }h\ge 0. \end{aligned} \end{aligned}$$
(14)

Lemma 6

(Properties of \(\Phi ^*_h\)) Let \(h\ge 0\).

  1. (1)

    There exist positive constants \({\overline{c}}_1,{\overline{c}}_2<\infty \) and a function \({\overline{c}}_0\in L^1(\Omega )\) such that the integrand \(\Phi ^*_h\) satisfies for almost all \(x\in \Omega \) and all \(\xi \in {\mathbb {R}}^{m\times n}\) the two sided growth condition

    $$\begin{aligned} -{\overline{c}}_0(x) +{\overline{c}}_2{|{\xi }|}^{p_+'}\le \Phi ^*_h(x,\xi )\le {\overline{c}}_1{|{\xi }|}^{p_-'} + {\overline{c}}_0(x). \end{aligned}$$
    (15)
  2. (2)

    With an h-independent constant \(C< \infty \) it holds for almost all \(x\in \Omega \) and all \(\xi \in {\mathbb {R}}^{m\times n}\) that

    $$\begin{aligned} \Phi ^*(x,\xi ) - 1 \le C\, \Phi ^*_h(x,\xi ). \end{aligned}$$
    (16)
  3. (3)

    Let \((\tau _h)_{h>0}\subset L^1(\Omega ;{\mathbb {R}}^{m\times n})\) be a weakly convergent sequence \(\tau _h \rightharpoonup \tau \) in \(L^1(\Omega ;{\mathbb {R}}^{m\times n})\). Then we have

    $$\begin{aligned} \int _{\Omega } \Phi ^*(x,\tau )\, \mathrm {d}x\le \liminf _{h\rightarrow 0} \int _\Omega \Phi ^*_h(x,\tau _h)\, \mathrm {d}x. \end{aligned}$$

Proof of 1

Let \(\xi \in {\mathbb {R}}^{m\times n}\) and \(h\ge 0\). The growth condition in (8) shows

$$\begin{aligned} \phi _h^*(\cdot ,\xi ) \le (-c_0 + c_1|\xi |^{p_-})^* = c_0 + c_1^{1-p_{-}'} {|{\xi }|}^{p_-'}. \end{aligned}$$

This bound and the identity in (14) lead almost everywhere in \(\Omega \) to

$$\begin{aligned} \Phi _h^*(\cdot ,\xi )&= \phi _h^*(\cdot ,\xi - F) \le c_0 + c_1^{1-p_{-}'} {|{\xi - F}|}^{p_-'} \\&\le c_0 +2^{p_-'-1}c_1^{1-p_{-}'}( {|{F}|}^{p_-'} + {|{\xi }|}^{p_-'}). \end{aligned}$$

The lower bound in (15) follows similarly.

Proof of 2. Let \(\xi \in {\mathbb {R}}^{m\times n}\). By the properties of the convex conjugate (see Lemma A1) and the assumption in (A1) we have

$$\begin{aligned} \phi ^*(\cdot ,\xi ) \le c\, \phi _h^*(\cdot ,\xi /c) + 1\qquad \text {almost everywhere in }\Omega . \end{aligned}$$

If \(c=1\), this yields \(\phi ^*(\cdot ,\xi ) \le C \phi _h^*(\cdot ,\xi ) + 1\) with constant \(C = 1\). If \(c<1\), we use the \(\nabla _2\)-condition (A3) (which yields the \(\Delta _2\)-condition for \(\phi ^*_h\), see Proposition A3) to conclude \(\phi ^*(\cdot ,\xi ) \le C \phi _h^*(\cdot ,\xi ) + 1\) with some constant \(C < \infty \). This and the identity in (14) yield (16).

Proof of 3. The proof repeats the steps from the proof of Lemma 3. \(\square \)

We continue with the definition of the dual problem by setting the spaces \(X :=L^{p_-}(\Omega ;{\mathbb {R}}^{m\times n})\) and \( V :=\lbrace \nabla v :v\in W_0^{1,p_-}(\Omega ;{\mathbb {R}}^m)\rbrace \subset X. \) The orthogonal complement of V reads

$$\begin{aligned} V^\perp&:=\left\{ \tau \in X^* :\int _\Omega \tau :\nabla v\, \mathrm {d}x= 0 \text { for all } v\in W^{1,p_-}_0(\Omega ;{\mathbb {R}}^m) \right\} \\&= \left\{ \tau \in L^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n}):\text {div}\, \tau = 0 \right\} =:L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n}). \end{aligned}$$

By [22,  Chap. IX, Prop. 2.1] we have for all \(h\ge 0\) and \(\tau \in L^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})\)

$$\begin{aligned} \sup _{\xi \in L^{p_-}(\Omega ;{\mathbb {R}}^{m \times n})} \int _\Omega \xi : \tau \, \mathrm {d}x- \int _\Omega \Phi _h(x,\xi ) \, \mathrm {d}x= \int _\Omega \Phi _h^*(x,\tau ) \, \mathrm {d}x. \end{aligned}$$

This identity and an integration by parts lead to the dual functional

$$\begin{aligned} \begin{aligned} {\mathcal {G}}_h(\tau )&= \hat{{\mathcal {F}}}_h^*(\tau ) :=\sup _{\xi \in X} \int _\Omega \tau : \xi \, \mathrm {d}x- \int _\Omega \Phi _h(x,\xi + \nabla \psi ) \, \mathrm {d}x\\&= \sup _{\vartheta \in X} \int _\Omega \tau : \vartheta \, \mathrm {d}x- \int _\Omega \Phi _h(x,\vartheta ) \, \mathrm {d}x- \int _\Omega \tau : \nabla \psi \, \mathrm {d}x\\&= \int _\Omega \Phi _h^*(x,\tau ) \, \mathrm {d}x- \int _\Omega \tau : \nabla \psi \, \mathrm {d}x\qquad \text {for all }\tau \in L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n}). \end{aligned} \end{aligned}$$
(17)

Lemma 7

(Equivalent problems) It holds for all \(h\ge 0\) that

$$\begin{aligned} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_h = - \min _{W_0^{1,p_-}(\Omega ;{\mathbb {R}}^m)} \hat{{\mathcal {F}}}_h = - \int _{\partial \Omega } \psi \cdot F\nu \, \mathrm {d}s- \min _W {\mathcal {F}}_h. \end{aligned}$$

Proof

The first identity follows from the classical convex optimisation theorem (see for example [22,  Chap. III, Thm. 4.1]). The second identity results from the design of the (shifted) functional \(\hat{{\mathcal {F}}}_h\). \(\square \)

An advantage of the dual problem is that we can use the growth condition in (15) to apply Lebesgue’s theorem, as done in the following lemma. The lemma involves the dual functional

$$\begin{aligned} {\mathcal {G}}(\tau ) :={\mathcal {G}}_0(\tau ) = \int _\Omega \Phi ^*(x,\tau )\, \mathrm {d}x- \int _\Omega \tau :\nabla \psi \, \mathrm {d}x\quad \text {for all }\tau \in L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n}). \end{aligned}$$

Lemma 8

(Point-wise convergence) We have

$$\begin{aligned} \lim _{h\rightarrow 0} {\mathcal {G}}_h(\tau ) = {\mathcal {G}}(\tau )\qquad \text {for all }\tau \in L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n}). \end{aligned}$$

Proof

Let \(\tau \in L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})\). Due to the growth condition in (15) and the convergence result in Lemma A5 (which can be applied due to the assumption in (A1)) we can apply Lebesgue’s dominated convergence theorem to conclude \(\int _\Omega \Phi ^*(x,\tau ) - \Phi ^*_h(x,\tau )\, \mathrm {d}x\rightarrow 0\) as \(h\rightarrow 0\). \(\square \)

A consequence of the point-wise convergence result is the following lemma.

Lemma 9

(Upper bound for \({\mathcal {G}}_h\)) We have

$$\begin{aligned} \limsup _{h\rightarrow 0} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_h \le \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}. \end{aligned}$$

Proof

Point-wise convergence (Lemma 8) yields for all \(\tau \in L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})\)

$$\begin{aligned}&\limsup _{h\rightarrow 0} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_h \le \limsup _{h\rightarrow 0}\, {\mathcal {G}}_h(\tau ) = {\mathcal {G}}(\tau ). \end{aligned}$$

\(\square \)

The following relaxation leads to an equivalent characterisation of the dual problem. We set for all \(h\ge 0\) and \(\tau \in L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\) the relaxed energy

$$\begin{aligned} \overline{{\mathcal {G}}}_h(\tau ) :=\inf _{\begin{array}{c} (\tau _k)_{k=1}^\infty \subset L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})\\ \lim _{k\rightarrow \infty } \Vert \tau _k - \tau \Vert _{L^{p_+'}(\Omega )} = 0 \end{array}} \liminf _{k\rightarrow \infty } {\mathcal {G}}_h(\tau _k). \end{aligned}$$
(18)

We denote by \(\text {dom}\) the effective domain of a functional, for example

$$\begin{aligned} \text {dom}\,\overline{{\mathcal {G}}}_h = \lbrace \tau \in L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n}):\overline{{\mathcal {G}}}_h(\tau ) < \infty \rbrace \qquad \text {with }h\ge 0. \end{aligned}$$

Lemma 10

(Properties of the relaxed energy functional \(\overline{{\mathcal {G}}}_h\)) Let \(h\ge 0\).

  1. (1)

    It holds that

    $$\begin{aligned} {\mathcal {G}}_h(\tau )&= \overline{{\mathcal {G}}}_h(\tau )&\text {for all }\tau \in L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n}),\\ {\mathcal {G}}_h(\chi )&\le \overline{{\mathcal {G}}}_h(\chi )&\text {for all }\chi \in L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n}). \end{aligned}$$
  2. (2)

    The minimum of \(\overline{{\mathcal {G}}}_h\) over \(L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\) is attained and we have

    $$\begin{aligned} \min _{L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})} \overline{{\mathcal {G}}}_h = \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_h. \end{aligned}$$
  3. (3)

    It holds that

    $$\begin{aligned} \text {dom}\,\overline{{\mathcal {G}}}_h \subset \text {dom}\,\overline{{\mathcal {G}}}. \end{aligned}$$
  4. (4)

    For all \(\tau \in \text {dom}\,\overline{{\mathcal {G}}}_h\) we have

    $$\begin{aligned} \overline{{\mathcal {G}}}_h(\tau ) = {\mathcal {G}}_h(\tau ). \end{aligned}$$
  5. (5)

    The relaxed functional \(\overline{{\mathcal {G}}}_h\) is convex and weakly lower semi-continuous, that is, for all weakly convergent sequences \(\tau _n \rightharpoonup \tau \) in \(L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\)

    $$\begin{aligned} \overline{{\mathcal {G}}}_h(\tau ) \le \liminf _{n\rightarrow \infty } \overline{{\mathcal {G}}}_h(\tau _n). \end{aligned}$$

Proof of 1

Lemma 6(3) and the fact that strong convergence implies weak convergence show the inequality

$$\begin{aligned} {\mathcal {G}}_h(\chi ) \le \overline{{\mathcal {G}}}_h(\chi ) \qquad \text {for all }\chi \in L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n}). \end{aligned}$$

Equality follows for \(\tau \in L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})\) by setting the constant sequence \(\tau _k :=\tau \) for all \(k\in {\mathbb {N}}\).

Proof of 2. Since \(\overline{{\mathcal {G}}}_h\) satisfies the same growth conditions as \({\mathcal {G}}_h\) (cf. (15)), Tonelli’s theorem leads to the existence of a minimiser of \(\overline{{\mathcal {G}}}_h\) in \(L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\). Since we have the identity \({\mathcal {G}}_h = \overline{{\mathcal {G}}}_h\) for all \(\tau \in L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})\), it holds that

$$\begin{aligned} \min _{L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})} \overline{{\mathcal {G}}}_h \le \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_h. \end{aligned}$$

On the other hand, for any sequence \((\tau _k)_{k=1}^\infty \subset L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})\) we have

$$\begin{aligned} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_h \le \liminf _{k\rightarrow \infty } {\mathcal {G}}_h(\tau _k). \end{aligned}$$

Applying this observation to the definition of \(\overline{{\mathcal {G}}}_h\) shows

$$\begin{aligned} \min _{L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})} \overline{{\mathcal {G}}}_h \ge \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_h. \end{aligned}$$

Proof of 3. The inclusion follows from the estimate in (16).

Proof of 4. We set for all \(\tau \in L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\) the functional

$$\begin{aligned} {\mathcal {G}}_h^0(\tau )&:=\int _\Omega \Phi ^*_h(x,\tau )\, \mathrm {d}x= \int _\Omega \phi ^*_h(x,\tau -F)\, \mathrm {d}x. \end{aligned}$$

Let \(x\in \Omega \) and \(\xi \in {\mathbb {R}}^{m\times n}\). By definition we have \( \Phi _h(x,2\xi )=\phi _h(x,2\xi )+F(x):2\xi . \) Recall the constants \(C,C_0\) in the \(\Delta _2\)-condition (A2). Young’s inequality shows for the second addend

$$\begin{aligned} F(x):2\xi&\le (C+1)\, F(x):\xi + 2/(C+1)\,F(x): \xi \\&\le (C+1)\, F(x):\xi + \phi _h(x,\xi ) + \phi _h^*(x,2/(C+1)\, F(x)). \end{aligned}$$

Set the function \(C_1 :=C_0 + \phi _h^*(\cdot ,2/(C+1)\, F) \in L^1(\Omega )\). Then the previous inequality and the \(\Delta _2\)-condition (A2) result in the \(\Delta _2\)-condition for \(\Phi _h\)

$$\begin{aligned} \Phi _h(x,2\xi ) \le C \phi _h(x,\xi ) + C_0 + F(x):2\xi \le (C+1)\, \Phi _h(x,\xi )\, + C_1(x). \end{aligned}$$

Hence, Proposition A6 yields \( \overline{{\mathcal {G}}}^0_h={\mathcal {G}}^0_h\) on \(\text {dom}\,\overline{{\mathcal {G}}}^0_h. \) The definition of the energy \({\mathcal {G}}_h\) in (17), the definition of its relaxation \(\overline{{\mathcal {G}}}_h\) in (18), and the regularity of the boundary data \(\psi \in W^{1,p_+}(\Omega ;{\mathbb {R}}^{m})\) lead to \(\text {dom}\,\overline{{\mathcal {G}}}_h = \text {dom}\,\overline{{\mathcal {G}}}^0_h\) and

$$\begin{aligned} \overline{{\mathcal {G}}}_h(\tau ) = \overline{{\mathcal {G}}}_h^0(\tau ) - \int _\Omega \nabla \psi :\tau \, \mathrm {d}x\qquad \text {for all } \tau \in L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n}). \end{aligned}$$

Combining these observations concludes the proof.

Proof of 5. The convexity of \(\overline{{\mathcal {G}}}_h\) follows from the convexity of \({\mathcal {G}}_h\). Moreover, [11,  Prop. 1.3.1] yields the lower semi-continuity of the relaxation functional \(\overline{{\mathcal {G}}}_h\) with respect to strong convergence in \(L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\). The weak lower semi-continuity follows from the lower semi-continuity and convexity of \(\overline{{\mathcal {G}}}_h\), see [17,  Cor. 3.22] or [22,  Chap. I, Cor. 2.2]. \(\square \)

The beneficial properties of \(\overline{{\mathcal {G}}}_h\) allow us to prove the following result.

Lemma 11

(Equality) We have

$$\begin{aligned} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})}{\mathcal {G}} =\lim _{h\rightarrow 0} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_h. \end{aligned}$$
(19)

Proof

Let \((h_j)_{j=1}^\infty \subset {\mathbb {R}}_{>0}\) be a sequence with \(h_j \searrow 0\) as \(j\rightarrow \infty \). We denote for all \(j\in {\mathbb {N}}\) by \(\sigma _{j} \in L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\) a minimiser of \(\overline{{\mathcal {G}}}_{h_j}\). By the growth conditions (15) the sequence \((\sigma _{j})_{j=1}^\infty \subset L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\) is uniformly bounded in \(L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\). Thus, there exists a function \(\sigma \in L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\) and a weakly convergent subsequence (which we do not relabel) \(\sigma _{j} \rightharpoonup \sigma \) in \(L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})\) as \(j\rightarrow \infty \). By Lemma 10(3) we have \(\sigma _j \in \text {dom}\,\overline{{\mathcal {G}}}_{h_j}\subset \text {dom}\,\overline{{\mathcal {G}}}\). Lemma 10(5), the identity in (16), the fact that \(\sigma _j\) is a minimiser, and the upper growth condition in (15) show

$$\begin{aligned} \overline{{\mathcal {G}}}(\sigma )\le \liminf _{j\rightarrow \infty }\overline{{\mathcal {G}}}(\sigma _j) \le \liminf _{j\rightarrow \infty } C\,\overline{{\mathcal {G}}}_{h_j}(\sigma _j) + |\Omega | < \infty . \end{aligned}$$

Hence, \(\sigma \in \text {dom}\,\overline{{\mathcal {G}}}\) and so Lemma 10(4) yields \({\mathcal {G}}(\sigma ) = \overline{{\mathcal {G}}}(\sigma )\). Lemma 63, \(\sigma _j\) being a minimiser of \(\overline{{\mathcal {G}}}_{h_j}\), and Lemma 8 result in

$$\begin{aligned} \begin{aligned} \overline{{\mathcal {G}}}(\sigma )&= {\mathcal {G}}(\sigma ) \le \liminf _{j\rightarrow \infty } {\mathcal {G}}_{h_j}(\sigma _{j}) \le \liminf _{j\rightarrow \infty } {\mathcal {G}}_{h_j}(\tau )= {\mathcal {G}}(\tau ) \end{aligned} \end{aligned}$$
(20)

for all \( \tau \in L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})\). This inequality and Lemma 10(2) yield

$$\begin{aligned} \min _{L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})} \overline{{\mathcal {G}}} \le \overline{\mathcal G}(\sigma ) \le \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}} = \min _{L_{\text {div}}^{p_+'}(\Omega ;{\mathbb {R}}^{m\times n})} \overline{{\mathcal {G}}}. \end{aligned}$$

Combining this inequality with (20) shows

$$\begin{aligned} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}} = \overline{{\mathcal {G}}}(\sigma ) \le \liminf _{j\rightarrow 0} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_{h_j}. \end{aligned}$$

Since this result is true for subsequences of any sequence \(h_j\searrow 0\), we have

$$\begin{aligned} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})}{\mathcal {G}} \le \liminf _{h\rightarrow 0} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_h. \end{aligned}$$

This and the upper bound in Lemma 9 lead to the identity in (19). \(\square \)

After these preliminary results we can complete the proof Lemma 5.

Proof of the claim in (13)

The duality of the primal and dual problems (Lemma 7) and the equality in (19) lead to

$$\begin{aligned} \limsup _{h \rightarrow 0} {\mathcal {F}}_h(u_h)&\le \limsup _{h \rightarrow 0} \min _{W} {\mathcal {F}}_h = - \int _{\partial \Omega } \psi \cdot F\nu \, \mathrm {d}s- \liminf _{h \rightarrow 0} \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}_h \\&=-\int _{\partial \Omega } \psi \cdot F\nu \, \mathrm {d}s- \inf _{L_{\text {div}}^{p_-'}(\Omega ;{\mathbb {R}}^{m\times n})} {\mathcal {G}}= \min _{W} {\mathcal {F}}. \end{aligned}$$

This concludes the proof of Lemma 5 under (A1)–(A3). \(\square \)

3 Examples on lavrentiev gap

First examples of energies \({\mathcal {F}}\) with non-standard growth (1) that experience a Lavrentiev gap go back to Zhikov [41]. A key idea in these examples is the construction of a function \(u\in W\) which satisfies for any sequence \((u_n)_{n\in {\mathbb {N}}} \subset H\) with \(u_n \rightarrow u\) in \(W^{1,p_-}(\Omega ;{\mathbb {R}}^m)\)

$$\begin{aligned} {\mathcal {F}}(u_n) \rightarrow \infty \qquad \text {as } n\rightarrow \infty . \end{aligned}$$

In the following examples we have \(m=1\), \(n=2\), and \(\Omega = (-1,1)^2\). For all \(x=(x_1,x_2) \in \Omega \) the function u reads \(u=(1-x_1^2-x_2^2)\, u_0(x)\) with

figure e

Scaling the boundary data leads for sufficiently large scaling parameters \(\lambda \) to the Lavrentiev gap phenomenon [5,  Sec. 3.3]. Since the singularity of the function u is concentrated in the origin, examples of this type are called “one saddle point” or “checker board” setup.

In the following we summarise known examples for non-autonomous problems caused by a single saddle point. In all these examples we have the boundary data \(\psi = \lambda u_0\) with \(\lambda >0\), the right-hand side \(f \equiv 0\), and the following integrands for all \(x=(x_1,x_2) \in \Omega \) and \(\xi \in {\mathbb {R}}^2\).

  1. (1)

    Piece-wise constant variable exponent (Zhikov [41]). Let \(1<p_-<2<p_+<\infty \), then the integrand reads \(\phi (x,\xi ):={|{\xi }|}^{p(x)}/p(x)\) with

    figure f
  2. (2)

    Continuous variable exponent (Zhikov [42], Hästo [27]). As in the previous example we have the \(p(\cdot )\)-Laplacian \(\phi (x,\xi ) :={|{\xi }|}^{p(x)}/p(x)\) but with power (with linear interpolation in the dashed regions)

    figure g
  3. (3)

    Double phase potential (Zhikov [42], Esposito–Leonetti–Mingione [21]). This example involves the integrand \(\phi (x,\xi )=1/p_-\, {|{\xi }|}^{p_-}+a(x)/p_+\,{|{\xi }|}^{p_+}\) with powers \(1<p_-<2<2+\alpha<p_+<\infty \), where the constant \(\alpha \ge 0\) enters the weight

    figure h
  4. (4)

    Borderline case of double phase potential (Balci–Surnachev [10]). This example involves constants \(\beta >1\), \(\gamma >1\) and the weight function a from the previous example with \(\alpha = 0\). The integrand reads

    $$\begin{aligned} \phi (x,\xi )=\log ^{-\beta }(e+{|{\xi }|}) {|{\xi }|}^2+a(x)\log ^{\gamma }(e+{|{\xi }|}) {|{\xi }|}^2. \end{aligned}$$

Further examples involve fractal contact sets [5] or matrix-valued integrands [23]. The latter example was already treated numerically in [35].

4 Experiments

In this section we investigate the Lavrentiev gap phenomenon numerically. We approximate the W-solution by the non-conforming scheme introduced in Sect. 2 and the H-solution by a conforming scheme with exact (or at least more accurate) quadrature. The convergence of the latter scheme with exact quadrature to the H-minimiser has been shown in [14]. We denote the solutions to the non-conforming scheme by \(u_\text {nc}\in \text {CR}^1({\mathcal {T}}_h)\) and to the conforming scheme by \(u_\text {c}\in {\mathcal {L}}^1_1({\mathcal {T}})\), where \({\mathcal {L}}^1_1({\mathcal {T}})\) denotes the Lagrange space of continuous and piece-wise affine functions. The corresponding energies read \({\mathcal {F}}_h(u_\text {nc})\) and \({\mathcal {F}}(u_\text {c})\). Our computations utilise an adaptive mesh refinement strategy driven by the residual-based error indicator introduced in [34] for the non-conforming scheme. If not mentioned specifically, we solve the non-linear systems with a Newton scheme.

4.1 Model problems

In this subsection we apply our numerical scheme to the minimisation problems introduced in Sect. 3. These problems experience a Lavrentiev gap for all sufficiently large parameters \(\lambda > \lambda _0\) in the boundary data \(\psi = \lambda u_0\) with some unknown threshold \(\lambda _0\ge 0\). We use our numerical method to explore this threshold. This visualises the performance of our scheme and provides some insights for further analytical investigation.

4.1.1 Experiment 1 (piece-wise constant variable exponent)

In our computations for the first example in Sect. 3 we set the exponents \(p_- = 3/2\) and \(p_+=3\). Our initial triangulation resolves the domains for \(p_-\) and \(p_+\), which allows for an exact quadrature with piece-wise constant exponents. In particular, (A1)–(A3) as well as (B) are obviously satisfied. For the boundary data \(\psi = \lambda u_0\) with \(\lambda =1\) the exact solution reads \(u(x_1,x_2) = x_2\) for all \((x_1,x_2) \in \Omega \). The convergence history plots, displayed on the left-hand side of Fig. 1, indicate that there is no Lavrentiev gap for \(\lambda \le 1\) and that there is a gap for \(\lambda >1\). Moreover, the convergence history plot suggests the speed of convergence \(\min _W {\mathcal {F}} - {\mathcal {F}}(u_\text {nc}) = {\mathcal {O}}(\text {ndof}^{-1})\) and \({\mathcal {F}}(u_\text {c}) - \min _H {\mathcal {F}} = {\mathcal {O}}(\text {ndof}^{-1})\).

Fig. 1
figure 1

Convergence history plot of the distances \({\mathcal {F}}(u_\text {c})-{\mathcal {F}}(u_\text {nc})\) of the conforming and non-conforming solutions in Experiment 1 (left) and Experiment 3 (right), where the dashed lines --- indicate the rate \({\mathcal {O}}(\text {ndof}^{-1})\)

Full size image
Fig. 2
figure 2

Computed energies of W- and H-solution (left) and the distance \({\mathcal {F}}(u_\text {c}) - {\mathcal {F}}_h(u_\text {nc})\) of the conforming and non-conforming solutions for various scalings \(\lambda \) (right) in Experiment 2

Full size image

4.1.2 Experiment 2 (continuous variable exponent)

In this subsection we investigate the second example in Sect. 3. We set the exponents \(p_- = 3/2\) and \(p_+=3\). The initial triangulation resolves the domains for \(p_-\) and \(p_+\) and we use a minimum quadrature rule, that is, we choose the point \(x_T\in T\in {\mathcal {T}}\) in (A1) as the minimiser \(x_T = \text {argmin}_T p\). Hence, (A1)–(A3) is satisfied. Figure 2 displays the approximated energies \({\mathcal {F}}_h(u_\text {nc})\) of the W-solution and \({\mathcal {F}}(u_\text {c})\) of the H-solution as well as the differences \({\mathcal {F}}(u_\text {c}) - {\mathcal {F}}_h(u_\text {nc})\) of the approximated energies for various scaling parameters \(\lambda \).

Pre-asymptotically these differences converge with the constant rate \(\text {ndof}^{-1/2}\). After that pre-asymptotic regime, the speed of convergence slows down for \(\lambda \ge 3\), indicating a failure of convergence. This failure suggests a Lavrentiev gap for \(\lambda \ge 3\).

The rate of convergence \(\text {ndof}^{-1/2}\) (for \(\lambda = 2\) and pre-asymptotically for \(\lambda \ge 3\)) is smaller than the rate \(\text {ndof}^{-1}\) in the previous experiment. This reduced rate is caused by the minimum quadrature rule; the loss of midpoint symmetry reduces the order of accuracy. Numerical experiments indicate that the energy \({\mathcal {F}}(u_\text {nc})\) does, in contrast to the energy \({\mathcal {F}}_h(u_\text {nc})\), not converge to the W-minimiser. However, computing the minimum \(\min _{\text {CR}^1({\mathcal {T}}_h)} {\mathcal {F}}\) over the non-conforming space with a more accurate quadrature rule leads to faster convergence of the approximated energy to the W-minimiser.

4.1.3 Experiment 3 (double phase potential)

In this experiment we approximate the minimisers of the energy in the third example in Sect. 3 with parameters \(\alpha = 0\) as well as \(p_- = 3/2\) and \(p_+=3\). The initial triangulation resolves the weight function a, allowing for an exact quadrature with piece-wise constant weights. Thus, (A1)–(A3) hold true. The right-hand side in Fig. 1 displays the convergence history plot of the energies \({\mathcal {F}}(u_\text {c}) - {\mathcal {F}}(u_\text {nc})\). The plot indicates a Lavrentiev gap for \(\lambda \ge 0.4\).

Fig. 3
figure 3

Energies of W-solution and H-solution (top left), the distances \({\mathcal {F}}(u_\text {c}) - {\mathcal {F}}(u_\text {nc})\) of the conforming and non-conforming solutions for various scalings \(\lambda \) (top right), and the H-minimiser \(u_\text {c}\) (bottom left) as well as the W-minimiser \(u_\text {nc}\) (bottom right) for \(\lambda = 1\)

Full size image

4.1.4 Experiment 4 (borderline case of double phase potential)

In this experiment we investigate the fourth example of Sect. 3 with parameters \(\beta = \gamma = 2\). As in the previous experiments we use an initial triangulation that resolves the weight function a, allowing for exact quadrature and (A1)–(A3). Since the Newton scheme struggles with the computation of the discrete minimiser, we utilise a fixed point iteration similar to the one introduced in [18] without regularisation. The paper [10] proves that the W-minimum grows asymptotically slightly slower than the H-minimum with respect to the scaling of the boundary data \(\psi = \lambda u_0\), leading to a gap for all sufficiently large parameters \(\lambda \). Our numerical experiments, displayed in Fig. 3, indicate a gap for all \(\lambda >0\). Moreover, the W- and H-solution differ significantly.

Fig. 4
figure 4

Convergence of computed energies with adaptive (solid line) and uniformly (dashed line) refined meshes to reference value from Experiment 1

Full size image

4.2 Multiple saddle points

4.3 Bad quadrature/geometric regularisation

This experiment investigates the importance of an appropriate quadrature rule. Therefore, we perturb the quadrature in Experiment 1. Our initial triangulation resolves the piece-wise constant exponent \(p(\cdot )\). Thus, it has a node in the origin \(0\in \Omega \). Let \(\omega (0) \subset {\mathcal {T}}\) denote the nodal patch with respect to this node, that is, the set of all triangles \(T\in {\mathcal {T}}\) with \(0\in T\). Our perturbed piece-wise constant exponents read

$$\begin{aligned} p_\text {max}|_T = {\left\{ \begin{array}{ll} p_+ &{}\text {for } T\in \omega (0),\\ p&{}\text {for } T\in {\mathcal {T}} \setminus \omega (0) \end{array}\right. }\quad \text {and}\quad p_\text {min}|_T = {\left\{ \begin{array}{ll} p_- &{}\text {for } T\in \omega (0),\\ p&{}\text {for } T\in {\mathcal {T}} \setminus \omega (0). \end{array}\right. } \end{aligned}$$

Notice that these approximations converge to the exact exponent p as the mesh is refined. We minimise the functionals

$$\begin{aligned} {\mathcal {F}}_\text {max} = \int _\Omega \frac{1}{p_\text {max}(x)}|\nabla _h \cdot |^{p_\text {max}(x)}\,\mathrm {d}x,\quad {\mathcal {F}}_\text {min} = \int _\Omega \frac{1}{p_\text {min}(x)}|\nabla _h \cdot |^{p_\text {min}(x)}\,\mathrm {d}x \end{aligned}$$
Fig. 5
figure 5

Variable exponent p (top left), the distances \({\mathcal {F}}(u_\text {c}) - {\mathcal {F}}(u_\text {nc})\) of the conforming and non-conforming solutions for various scalings \(\lambda \) (top right), and the H-minimiser \(u_\text {c}\) (bottom left) as well as the W-minimiser \(u_{\text {nc}}\) (bottom right) for \(\lambda = 5\)

Full size image

over the Lagrange and Crouzeix-Raviart space with boundary data \(\psi = \lambda u_0\) and \(\lambda = 5\). The corresponding solutions read \(u_\text {c}^\text {max} \in {\mathcal {L}}^1_1({\mathcal {T}})\) and \(u_\text {nc}^\text {max} \in \text {CR}^1({\mathcal {T}}_h)\) as well as \(u_\text {c}^\text {min} \in {\mathcal {L}}^1_1({\mathcal {T}})\) and \(u_\text {nc}^\text {min} \in \text {CR}^1({\mathcal {T}}_h)\). Figure 4 compares the resulting energies with a reference solution computed in Experiment 1 on the finest triangulation. It indicates that the minimisation of the energy \({\mathcal {F}}_\text {max}\) over the conforming and non-conforming space leads to the H-minimiser; the minimisation of the energy \({\mathcal {F}}_\text {min}\) over the conforming and non-conforming space leads to the W-minimiser. This shows that the conforming scheme requires exact or at least some suitable quadrature to converge to the H-minimiser. Moreover, our computations indicate that it might be possible to design a conforming scheme that converges to the W-minimiser by introducing a regularisation near singularities. However, the adaptive scheme experiences difficulties after \(\text {ndof} = \dim \text {CR}^1({\mathcal {T}}_h)\) exceeds \(10^4\). Thus, its convergence to the exact W-minimiser is unclear.

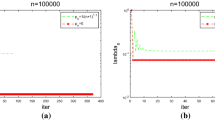
The last example explores the Lavrentiev gap phenomenon for a problem with three saddle points. More precisely, we compute the W- and H-minimiser of the variable exponent \(p(\cdot )\)-Laplacian \(\int _\Omega |\nabla _h\cdot |^{p(x)}/p(x)\, \mathrm {d}x\) on the domain \(\Omega = (-1,5)\times (-1,1)\) with boundary data \(\psi (x_1,x_2) = \lambda x_2\) for all \((x_1,x_2) \in {\overline{\Omega }}\) and parameters \(\lambda >0\). The piece-wise constant exponent (visualised in Fig. 5) attains the values \(p_- = 3/2\) and \(p_+ = 3\) and reads for all \((x_1,x_2)\in \Omega \)

$$\begin{aligned} p(x_1,x_2) = {\left\{ \begin{array}{ll} p_-&{}\text {for } |x_1|< |x_2|\text { and }x_1<1,\\ p_-&{}\text {for } |x_1-2|< |x_2|\text { and }1\le x_1<3,\\ p_-&{}\text {for } |x_1-4| < |x_2|\text { and }3\le x_1,\\ p_+&{}\text {else}. \end{array}\right. } \end{aligned}$$

For \(\lambda = 1\) the exact minimiser reads \(u(x_1,x_2) = x_2\) for all \((x_1,x_2) \in \Omega \). The initial triangulation resolves the exponent p. Thus, we can apply an exact quadrature with piece-wise constant exponents satisfying (A1)–(A3). Figure 5 displays a convergence history plot of the energies for various \(\lambda \) as well as a plot of the H- and W-minimiser for \(\lambda = 5\). As in Experiment 1, it seems that there is a gap for \(\lambda >1\). The W-minimiser seems to jump for \(\lambda >1\) in all three saddle points.

5 Conclusion

In this paper we have successfully adapted the Crouziex–Raviart finite element scheme to approximate variational problems with non-autonomous integrands even in the presence of the Lavrentiev gap phenomenon. We have identified assumptions on which convergence is guaranteed, and have demonstrated numerically on a wide range of test cases that the scheme is practical and can reliably predict the existence (or non-existence) of Lavrentiev gaps. The examples we considered here are of primary interest to the theoretical study of regularity of solutions to variational problems. Indeed we hope that our numerical scheme could be employed more generally towards refining and extending the analytical results based on which we chose our examples.

More generally, however, our results provide strong new evidence for the advantages of non-conforming methods in the numerical solution of difficult variational problems. On that theme, we note that a long-standing open problem is the extension of our convergence results to poly-convex or even quasi-convex integrands. Further investigation might involve the use of problem dependent strategies, as for example done in [4, 19, 20] for conforming and in [3, 12, 15, 26] for non-conforming schemes for problems without Lavrentiev gap, to conclude rates of convergence and to relax some assumptions like the growth condition (1) for specific problems.