Abstract
The classical serendipity and mixed finite element spaces suffer from poor approximation on nondegenerate, convex quadrilaterals. In this paper, we develop families of direct serendipity and direct mixed finite element spaces, which achieve optimal approximation properties and have minimal local dimension. The set of local shape functions for either the serendipity or mixed elements contains the full set of scalar or vector polynomials of degree r, respectively, defined directly on each element (i.e., not mapped from a reference element). Because there are not enough degrees of freedom for global \(H^1\) or \(H(\text {div})\) conformity, exactly two supplemental shape functions must be added to each element when \(r\ge 2\), and only one when \(r=1\). The specific choice of supplemental functions gives rise to different families of direct elements. These new spaces are related through a de Rham complex. For index \(r\ge 1\), the new families of serendipity spaces \({\mathscr {DS}}_{r+1}\) are the precursors under the curl operator of our direct mixed finite element spaces, which can be constructed to have reduced or full \(H(\text {div})\) approximation properties. One choice of direct serendipity supplements gives the precursor of the recently introduced Arbogast–Correa spaces (SIAM J Numer Anal 54:3332–3356, 2016. https://doi.org/10.1137/15M1013705). Other fully direct serendipity supplements can be defined without the use of mappings from reference elements, and these give rise in turn to fully direct mixed spaces. Our development is constructive, so we are able to give global bases for our spaces. Numerical results are presented to illustrate their properties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Serendipity finite elements \({{{\mathscr {S}}}}_r({\hat{E}})\) can be defined on a rectangle \({\hat{E}}\) [19, 23, 46]. Over a rectangular mesh, they merge together to form \(H^1\) conforming spaces of scalar functions. These finite elements have the distinction of having a minimal number of degrees of freedom (DoFs) for the given order of approximation \(r+1\) in \(L^2\). Similarly, the Brezzi-Douglas-Marini mixed finite elements BDM\(_r({\hat{E}})\) [20] are defined so that they merge together on a rectangular mesh into \(H(\text {div})=\big \{{{\mathbf {v}}}\in (L^2)^2:\nabla \cdot {{\mathbf {v}}}\in L^2\big \}\) conforming spaces of vector functions. These finite elements also have a minimal number of DoFs for the same order of approximation.
Both of these elements appear in the periodic table of the finite elements as given by Arnold and Logg [13] (where they are denoted \({{{\mathscr {S}}}}_r\varLambda ^0\) and \({{{\mathscr {S}}}}_r\varLambda ^1\), respectively). They should be studied together, since they are related by a de Rham complex [5, 11, 12]

which implies that \(\text {BDM}_r({\hat{E}})=\text {curl}\,{{{\mathscr {S}}}}_{r+1}({\hat{E}})\oplus {{\mathbf {x}}}{\mathbb {P}}_{r-1}({\hat{E}})\), where \({\mathbb {P}}_{r-1}(\hat{E})\) are polynomials of degree \(r-1\).
In this paper, we define new families of (we call them direct) serendipity and mixed finite elements on a general nondegenerate, convex quadrilateral E. These new finite elements generalize the complex (1), and they maintain \(H^1\) or \(H(\text {div})\) conformity, provide optimal order approximation properties, and possess a minimal number of DoFs.
1.1 Existing finite elements
The serendipity finite elements on rectangles \({{{\mathscr {S}}}}_r({\hat{E}})\), especially the 8-node biquadratic (\(r=2\)) and the 12-node bicubic (\(r=3\)) elements, have been well studied for many years. They appear in almost any introductory reference on finite elements, e.g., [19, 23, 46], and they are provided by software packages both in academia [27] and industry [35]. Compared with the full tensor product Lagrange finite elements \({\mathbb {P}}_{r,r}({\hat{E}})\), serendipity finite elements use fewer degrees of freedom, and they are usually more efficient in terms of the number of local computations performed. It was not until recently, however, that a general definition of the serendipity finite element spaces of arbitrary order on rectangles in any space dimension was given by Arnold and Awanou [6, 7] (see also [32]).
The serendipity finite element spaces work very well on computational meshes of rectangular elements, but it is well known that their performance is degraded on quadrilaterals when the space is mapped from a rectangle, when \(r\ge 2\). This is not the case for tensor product Lagrange finite elements [8, 36, 38]. To be more precise, mapped serendipity elements of index r do not approximate to optimal order \(r+1\) on E, but the image of the full space of tensor product polynomials \({\mathbb {P}}_{r,r}({\hat{E}})\) maintains accuracy on E. We note that Rand, Gillette, and Bajaj [40] recently introduced a new family of Serendipity finite elements based on generalized barycentric coordinates of index \(r=2\) that is accurate to order three on any convex, planar polygon. A generalization to any order of approximation was given by Floater and Lai [31], but on quadrilaterals, they require \(\dim {\mathbb {P}}_r+r\) shape functions, which is more than the minimal required when \(r>2\).
There are many families of mixed finite elements on rectangles, beginning with those of Raviart and Thomas [41] and generalized by Nédélec [39]. These and the BDM\(_r\) finite elements are extended to quadrilaterals using the Piola transform [41, 48]. For most spaces, this creates a consistency error and consequent loss of approximation of the divergence [1, 9, 16, 21, 48].
The construction of mixed finite elements on quadrilaterals that maintain optimal order accuracy is considered in many papers. Most address only low order cases (see, e.g., [15, 17, 22, 26, 37, 43, 44]). The exceptions we are aware of are the families of finite elements of Arnold, Boffi, and Falk (ABF\(_r\)(E)) [9], Siqueira, Devloo, and Gomes [45], and Arbogast and Correa (AC\(_r(E)\) and AC\(_r^{\text {red}}(E)\), written in this paper as AC\(_r^r(E)\) and AC\(_r^{r-1}(E)\), respectively) [1]. The ABF elements are defined for rectangles and extended to quadrilaterals in the usual way (i.e., by mapping via the Piola transformation). They rectify the problem of poor divergence approximation by including more degrees of freedom in the space, so that approximation properties are maintained after Piola mapping. The spaces of [45] also involve the Piola map, but in a unique way. They also add shape functions to their space to obtain accuracy. The AC elements use a different strategy. These elements are defined by using vector polynomials directly on the element (i.e., without being mapped) and supplemented by two vector shape functions defined on a reference square and mapped via Piola. The AC spaces have minimal local dimension with respect to the requirement of global \(H(\text {div})\) conformity and optimal order of approximation.
1.2 New finite elements
In this paper, we introduce new families of direct serendipity and mixed finite elements that have optimal approximation properties of all orders \(r=(0,)1,2,\ldots \) and maintain minimal local dimension. They are direct in the sense that the shape functions contain a full set of polynomials of degree r defined directly on the element, as in the AC spaces. Because there are not enough degrees of freedom to achieve \(H^1\) or \(H(\text {div})\) conformity over meshes of quadrilaterals, supplemental functions need to be added to each element. These supplemental functions can be defined in many ways as we will see, and each choice gives rise to a different family of direct finite elements. These families are novel, and each finite element of a given index r in the family is a novel finite element, except possibly for the low order elements (\(r\le 2\)) of some specific families, since as we noted above, many low order finite elements are known to exist.
The families of direct serendipity elements have the same number of degrees of freedom as the corresponding classical serendipity element, and they take the form
Each family is defined by the choice of the two supplemental functions (or one, if \(r=1\)) spanning \({\mathbb {S}}_r^{\mathscr {DS}}(E)\). We give a very general, but explicit, construction for these supplements. They can be defined directly on E, or they can be defined on \({\hat{E}}\) and mapped to E. In fact, we will construct a nodal basis over E, and these nodal basis functions can be merged together to give an \(H^1\) conforming global basis. When \(r = 1\) we obtain new elements akin to barycentric coordinates (i.e., they are linear on edges and sum to one, but they are not necessarily positive everywhere).
There are two classes of families of direct mixed elements, which correspond to reduced and full \(H(\text {div})\)-approximation. For index r, a vector function is approximated to order \(r+1\) accuracy, but the divergence of the vector is approximated to order \(r-1\) or r for reduced and full \(H(\text {div})\)-approximation, respectively. Each class of direct mixed elements has the same optimal number of degrees of freedom as the AC elements of that class. They take a form similar to (2), which is
for the reduced and full \(H(\text {div})\)-approximation spaces, respectively, where \({\tilde{{\mathbb {P}}}}_r\) are homogeneous polynomials of degree r. Again, each family is defined by the choice of the two supplemental functions spanning \({\mathbb {S}}_r^{{\mathbf {V}}}(E)\). When \(r=0\), we also construct \({{\mathbf {V}}}_0^0(E)={\mathbb {P}}_0^2(E)\oplus {{\mathbf {x}}}{\mathbb {P}}_0(E)\oplus {\mathbb {S}}_0^{{\mathbf {V}}}(E)\) with a single supplement.
The serendipity and mixed families are related by de Rham theory:
We define one family of direct serendipity elements that is the precursor of the reduced and full AC spaces. We also define many fully direct serendipity elements that use no mappings to define \({\mathbb {S}}_r^{{\mathscr {DS}}}(E)\), which in turn generate new reduced and full direct \(H(\text {div})\) approximation mixed spaces that use no mappings whatsoever.
1.3 Outline of the paper
We set some basic notation in the next section. We construct new families of direct serendipity elements in Sect. 3 for any index \(r\ge 2\), and in Sect. 4 for index \(r=1\). Our development is constructive, and results in a local nodal basis. These serendipity spaces do not involve mappings from a reference element. In Sect. 5, we define direct serendipity spaces based on supplements that are mapped from a reference element (when \(r\ge 1\)). We discuss the stability and approximation properties of the new direct serendipity elements in Sect. 6.
In Sect. 7, we turn our attention to the construction of direct mixed finite elements through a de Rham complex. We recover the spaces AC\(_r^{r-1}(E)\) and AC\(_r^r(E)\) before defining new direct mixed finite element spaces, which do not require mappings from a reference element. Implementation is discussed, either using the hybrid method, or using an \(H(\text {div})\)-conforming global basis, which is constructed. We discuss the stability and approximation properties of the new mixed elements in Sect. 8. Some numerical results illustrating the performance of our new direct serendipity and mixed finite elements appear in Sect. 9. Finally, a summary of our results and conclusions are given in the last section of the paper. Moreover, a second de Rham complex involving the gradient and curl operators provides new \(H(\text {curl})=\big \{{{\mathbf {v}}}\in (L^2)^2:\text {curl}\,{{\mathbf {v}}}\in L^2\big \}\) elements as well.
2 Some notation
Let \({\mathbb {P}}_r(\omega )\) denote the space of polynomials of degree up to r on \(\omega \subset {\mathbb {R}}^d\), where \(d=0\) (a point), 1, or 2. Recall that
Let \({\tilde{{\mathbb {P}}}}_r(\omega )\) denote the space of homogeneous polynomials of degree r on \(\omega \). Then
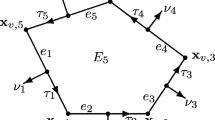
Let the element \(E\subset {\mathbb {R}}^2\) be a closed, nondegenerate, convex quadrilateral. By nondegenerate, we mean that E does not degenerate to a triangle, line segment, or point. We choose to identify the edges and vertices of E adjacently in the counterclockwise direction, as depicted in Fig. 1. Let the edges of E be denoted \(e_i\), \(i=1,2,3,4\), and the vertices be \({{\mathbf {x}}}_{v,1}=e_1\cap e_2\), \({{\mathbf {x}}}_{v,2}=e_2\cap e_3\), \({{\mathbf {x}}}_{v,3}=e_3\cap e_4\), and \({{\mathbf {x}}}_{v,4}=e_1\cap e_4\). Let \(\nu _i\) denote the unit outer normal to edge \(e_i\), and let \(\tau _i\) denote the unit tangent vector of \(e_i\) oriented in the counterclockwise direction, for \(i=1,2,3,4\). Let the reference element \({\hat{E}}\) be \([-1,1]^2\). Define the bilinear and bijective map \({{\mathbf {F}}}_{\!E}:{\hat{E}}\rightarrow E\) that maps the vertices of \({\hat{E}}\) to those of E, oriented with \((-1,-1)\) being mapped to \({{\mathbf {x}}}_{v,1}\).
We define the linear polynomial \(\lambda _i({{\mathbf {x}}})\) giving the distance of \({{\mathbf {x}}}\in {\mathbb {R}}^2\) to edge \(e_i\) opposite the normal direction. It is
where \({{\mathbf {x}}}_i^*\in e_i\) is any point on the edge. If \({{\mathbf {x}}}\) is in the interior of E, these functions are strictly positive, and each vanishes on the edge which defines it.
We denote by \(F_{\!E}^0\) the pullback map associated with \({{\mathbf {F}}}_{\!E}^{-1}\); that is, \(F_{\!E}^0\) is the map taking a function \({\hat{\phi }}\) defined on \({\hat{E}}\) to a function \(\phi \) defined on E by the rule
where \({{\mathbf {x}}}={{\mathbf {F}}}_{\!E}({\hat{{{\mathbf {x}}}}})\). We denote by \({{\mathbf {F}}}_{\!E}^1\) the Piola map taking a vector function \({\hat{\pmb \psi }}\) defined on \({\hat{E}}\) to a vector function \(\pmb \psi \) defined on E by the rule
where \(DF_{\!E}({\hat{{{\mathbf {x}}}}})\) is the Jacobian matrix of \({{\mathbf {F}}}_{\!E}\) and \(J_E\) is its absolute determinant.
Recall Ciarlet’s definition [23] of a finite element.
Definition 1
(Ciarlet 1978) Let
- 1.:
-
\(E\subset {\mathbb {R}}^d\) be a bounded closed set with nonempty interior and a Lipschitz continuous boundary,
- 2.:
-
\({{{\mathscr {P}}}}\) be a finite-dimensional space of functions on E, and
- 3.:
-
\({{{\mathscr {N}}}}= \{ N_1, N_2,\ldots , N_{\dim {{{\mathscr {P}}}}} \}\) be a basis for \({{{\mathscr {P}}}}'\).
Then \((E, {{{\mathscr {P}}}}, {{{\mathscr {N}}}})\) is called a finite element.
Our task is to define the shape functions \({{{\mathscr {P}}}}\) and the degrees of freedom (DoFs) \({{{\mathscr {N}}}}\). The DoFs give a basis for \({{{\mathscr {P}}}}'\) provided that we have unisolvence of the shape functions (i.e., for \(\phi \in {{{\mathscr {P}}}}\), \(N_j(\phi )=0\) for all j implies that \(\phi =0\)). To achieve optimal approximation properties, we will require that \({{{\mathscr {P}}}}\supset {\mathbb {P}}_r(E)\) for each index r. That is, the polynomials will be directly included within the function space, and hence we call our new finite elements direct serendipity and direct mixed finite elements.
Let \(\varOmega \subset {\mathbb {R}}^2\) be a connected, polygonal domain with a Lipschitz boundary (i.e., \(\varOmega \) has no slits), and let \({{{\mathscr {T}}}}_h\) be a conforming finite element partition or mesh of \(\varOmega \) into nondegenerate, convex quadrilaterals of maximal diameter \(h>0\). The DoFs must be defined so that the shape functions on adjoining elements merge together. For serendipity spaces, we want the global space to reside in \(H^1(\varOmega )\), so the elements must merge continuously across each edge e. For mixed spaces, the vector variable must lie in \(H(\text {div};\varOmega )\), which means that the normal components (fluxes) of the vectors on an edge e in adjacent elements must be continuous.
3 Direct serendipity elements when \(r\ge 2\)
We present our definition of direct serendipity elements when \(r\ge 2\) in this section. The case \(r=1\) requires special treatment, and will be given below in Sect. 4.
Our dual objectives are that \({\mathbb {P}}_r(E)\subset {\mathscr {DS}}_r(E)\) and that shape functions on adjoining elements merge continuously, i.e., so the space over \(\varOmega \) satisfies \({\mathscr {DS}}_r(\varOmega )\subset H^1(\varOmega )\). These objectives require us to consider the lower dimensional geometric objects within E (as in [6]). The minimal number of DoFs associated to each lower dimensional object must correspond to the dimension of the polynomials of degree r that restrict to that object. These numbers are given in Table 1. A quadrilateral has 4 vertices, 4 edges, and one cell of dimension 0, 1, and 2, respectively. Each vertex requires \(\dim {\mathbb {P}}_r({\mathbb {R}}^0)=1\) DoF, the interior of each edge requires \(\dim {\mathbb {P}}_{r-2}({\mathbb {R}})=r-1\) DoFs (not counting the two vertices), and the interior of each cell requires \(\dim {\mathbb {P}}_{r-4}({\mathbb {R}}^2)=\left( \begin{matrix}r-2\\ 2\end{matrix}\right) =\frac{1}{2}(r-2)(r-3)\) DoFs (not counting the edge and vertex DoFs). There are cell DoFs only if \(r\ge 4\), but the formula works for \(r\ge 2\). The total number of DoFs is then
and so to define \({\mathscr {DS}}_r(E)\), we will supplement \({\mathbb {P}}_r(E)\subset {\mathscr {DS}}_r(E)\) with the span of two linearly independent functions, \(\phi _{s,1}({{\mathbf {x}}})\) and \(\phi _{s,2}({{\mathbf {x}}})\). We have many choices for the supplemental functions, the span of which is denoted \({\mathbb {S}}_r^{\mathscr {DS}}(E)=\text {span}\{\phi _{s,1},\phi _{s,2}\}\). Each choice gives rise to a distinct family of direct serendipity elements of index \(r\ge 2\); that is, the shape functions (\({{{\mathscr {P}}}}\) in Definition 1) are
We define the DoFs (\({{{\mathscr {N}}}}\) in Definition 1) as a set of nodal functionals \(N_i\) defined at a nodal point \({{\mathbf {x}}}^{\text {node}}_j\), i.e.,
As depicted in Fig. 2, for vertex DoFs, the nodal points are exactly the vertices \({{\mathbf {x}}}_{v,1}\), \({{\mathbf {x}}}_{v,2}\), \({{\mathbf {x}}}_{v,3}\), and \({{\mathbf {x}}}_{v,4}\) of E. We have choices for the location of the rest of the nodal points. For edge DoFs, we simply choose nodal points so that they, plus the two vertices, are equally distributed on each edge. There are \(r-1\) nodal points on the interior of each edge, which can be denoted \({{\mathbf {x}}}_{e,ij}\), \(j=1,\ldots ,r-1\), for nodal points that lie on edge \(e_i\), \(i=1,2,3,4\), ordered in the counterclockwise direction. The interior cell DoFs can be set, for example, on points of a triangle T strictly inside E, where the set of nodal points is the same as the nodes of the Lagrange element of order \(r-4\) on the triangle T. We denote the interior nodal points as \({{\mathbf {x}}}_{E,i}\), \(i=1,\ldots ,\frac{1}{2}(r-2)(r-3)\). The total number of nodal points is indeed \(D_r\).
We will define a basis for the shape functions \({{{\mathscr {P}}}}\) dual to \({{{\mathscr {N}}}}\), which will give unisolvence and a properly defined finite element. Such shape functions are called nodal basis functions. For a nodal point \({{\mathbf {x}}}^{\text {node}}_j\), they have the property that \(N_j(\varphi _{i})=\varphi _{i}({{\mathbf {x}}}^{\text {node}}_j) = \delta _{ij}\), the Kronecker delta. But first, we define the supplemental functions.
3.1 Supplemental functions
As stated above, we define distinct families of direct serendipity finite elements depending on a choice of two supplemental functions. These will be defined by a choice of four functions, two of which are linear polynomials, denoted \(\lambda _{24}({{\mathbf {x}}})\) and \(\lambda _{13}({{\mathbf {x}}})\). The other two functions should be continuous on E (and so bounded), and they are denoted \(R_{13}({{\mathbf {x}}})\) and \(R_{24}({{\mathbf {x}}})\). The supplemental functions are then
and the supplemental space is defined as
When \(r=2\), \(\lambda _{24}\) and \(\lambda _{13}\) are not needed.
The linear function \(\lambda _{24}\) is defined by its zero set line \({{{\mathscr {L}}}}_{24}\). As shown in Fig. 3, let \({{{\mathscr {L}}}}_1\) and \({{{\mathscr {L}}}}_3\) be the infinite lines containing the edges \(e_1\) and \(e_3\), respectively. We require that \({{{\mathscr {L}}}}_{24}\) is chosen to intersect both \({{{\mathscr {L}}}}_1\) and \({{{\mathscr {L}}}}_3\). Moreover, when \(e_1\) and \(e_3\) are not parallel, \({{{\mathscr {L}}}}_1\) and \({{{\mathscr {L}}}}_3\) intersect in a point \({{\mathbf {x}}}_{13}={{{\mathscr {L}}}}_1\cap {{{\mathscr {L}}}}_3\), and we also require that \({{\mathbf {x}}}_{13}\notin {{{\mathscr {L}}}}_{24}\) (i.e., so that \(\lambda _{24}({{\mathbf {x}}}_{13})\ne 0\)). In a similar way, \({{{\mathscr {L}}}}_{13}\), the zero set line of \(\lambda _{13}\), is chosen to intersect the lines \({{{\mathscr {L}}}}_2\) and \({{{\mathscr {L}}}}_4\) extending \(e_2\) and \(e_4\), respectively, and when they are not parallel, \({{{\mathscr {L}}}}_{13}\) must avoid the intersection point \({{\mathbf {x}}}_{24}={{{\mathscr {L}}}}_2\cap {{{\mathscr {L}}}}_4\). Let \(\nu _{24}\) and \(\nu _{13}\) denote a unit normal to \({{{\mathscr {L}}}}_{24}\) and \({{{\mathscr {L}}}}_{13}\), and let \({{\mathbf {x}}}_{24}^*\) and \({{\mathbf {x}}}_{13}^*\) denote any point on these lines, respectively. Then we define
This definition is very general, but it is sufficient to provide a well defined finite element; however, accuracy considerations require a more restrictive definition, such as that given in Lemma 1 (where \({{{\mathscr {L}}}}_{24}\) should intersect \(e_2\) and \(e_4\), and \({{{\mathscr {L}}}}_{13}\) should intersect \(e_1\) and \(e_3\)). We remark that a simple choice is to take
although the normalization is not strictly necessary. Later in (97) we will need the tangent vectors \(\tau _{24}\) and \(\tau _{13}\), defined counterclockwise from the normals \(\nu _{24}\) and \(\nu _{13}\), respectively.
The continuous functions \(R_{13}\) and \(R_{24}\) are defined to satisfy the properties
They are \(\pm 1\) on opposite edges, but arbitrary on the other two edges. A smoothness requirement will be added later in Lemma 1. A simple choice is to take the rational functions
(note that the denominators do not vanish on E). One could also use the bilinear map \({{\mathbf {F}}}_{\!E}:{\hat{E}}\rightarrow E\) and \(F_{\!E}^0\) discussed in Sect. 2, where \({\hat{E}}=[-1,1]^2\), to define
Theorem 1
Let E be a nondegenerate, convex quadrilateral. Suppose that \(\lambda _{13}\) and \(\lambda _{24}\) are linear functions with zero lines that intersect, for \(\lambda _{13}\), the lines containing \(e_1\) and \(e_3\), and for \(\lambda _{24}\), the lines containing \(e_2\) and \(e_4\), but avoiding the intersection points if they exist. Suppose also that the bounded functions \(R_{13}\) and \(R_{24}\) are continuous and satisfy (17). Then for \(r\ge 2\),
with nodal DoFs defined by (12), is a well defined finite element. Moreover, \({\mathscr {DS}}_r(E)\) has the minimal possible dimension (10) needed for \(H^1\) conformity, and so it is a direct serendipity finite element.
It remains only to prove that the DoFs are unisolvent (i.e., that \({{{\mathscr {N}}}}\) is a basis for the dual space). We will do this by constructing explicitly a nodal basis, which could be used in practical implementations if one wished to do so.
Remark 1
If E is a rectangle, the classic serendipity spaces arise from our construction using a specific set of choices. For simplicity, assume \(E={\hat{E}}=[-1,1]^2\) is the square oriented with \(e_1\subset \{(-1,{\hat{y}}):{\hat{y}}\in {\mathbb {R}}\}\) being on the left (every other rectangle is affine equivalent to \({\hat{E}}\)). To recover the classic serendipity space \({{{\mathscr {S}}}}_r(E)\), take in \({\mathscr {DS}}_r(E)\) \(\lambda _{13}={\hat{y}}+c_{13}\) and \(\lambda _{24}={\hat{x}}+c_{24}\) for some constants \(c_{13}\) and \(c_{24}\), and take \(R_{13}={\hat{x}}\) and \(R_{24}={\hat{y}}\), which is the simple choice (18). All other choices give new serendipity finite elements on the square, to the best of our knowledge. However, since these are defined in a nonsymmetric way, they are probably of little interest.
3.2 Proof of Theorem 1: construction of nodal basis functions
We define
so that \(R_i\) is 1 on edge \(e_i\), 0 on the opposite edge, and arbitrary on the other two edges. Note that
3.2.1 Interior cell nodal basis functions
For the entire cell E, we have interior shape functions only when \(r\ge 4\) (recall Table 1). These shape functions are
and they vanish on all four edges (i.e., at all edge and vertex nodes). Let \(\{\phi _{E,i}\}\subset {\mathbb {P}}_{r-4}\) be a nodal basis for the cell nodes \(\{{{\mathbf {x}}}_{E,i}\}\), where \(i=1,\ldots ,\dim {\mathbb {P}}_{r-4}\). That is, \(\phi _{E,i}({{\mathbf {x}}}_{E,j}) = \delta _{ij}\). Our interior cell nodal basis functions are then
3.2.2 Edge nodal basis functions
We construct \(\varphi _{e,11}({{\mathbf {x}}})\), which is 1 at \({{\mathbf {x}}}_{e,11}\) and vanishes at all other nodal points. The construction of the other edge nodal basis functions is similar.
For some \(p\in {\mathbb {P}}_{r-3}(E)\) (take \(p=0\) if \(r=2\)), we let
This function vanishes on all edges but \(e_1\). Let
We want q to vanish at the nodes \({{\mathbf {x}}}_{e,1i}\) for \(i=2,\ldots ,r-1\); that is, we want p to satisfy the conditions
(note that \(\lambda _{3}({{\mathbf {x}}}_{e,1i})\ne 0\)). These \(r-2\) conditions uniquely define p along the edge \(e_1\), i.e., they define \({\tilde{p}}\in {\mathbb {P}}_{r-3}(e_1)\) as a function of \(t={{\mathbf {x}}}\cdot \tau _1\). The coefficients can be found using Newton’s divided difference interpolation formulas for the points \(t_i={{\mathbf {x}}}_{e,1i}\cdot \tau _1\) (\(i=2,\ldots ,r-1\)) and values given on the right hand side of (25). For example, the low order cases are
We define \(p({{\mathbf {x}}})\) by extending \({\tilde{p}}(t)\) to E constantly along perpendicular lines, i.e.,
Our construction will succeed provided \(q({{\mathbf {x}}}_{e,11})\ne 0\). So suppose to the contrary that \(q({{\mathbf {x}}}_{e,11})=0\). We restrict \({{\mathbf {x}}}\) to \({{{\mathscr {L}}}}_1\) (the line extending \(e_1\), as in Fig. 3) and let \(t={{\mathbf {x}}}\cdot \tau _1\). Conversely, given t, there is a unique \({{\mathbf {x}}}\in {{{\mathscr {L}}}}_1\) such that \({{\mathbf {x}}}\cdot \tau _1=t\). Let \({\tilde{\lambda }}_3(t)=\lambda _3({{\mathbf {x}}})\) on \({{{\mathscr {L}}}}_1\), and similarly \({\tilde{\lambda }}_{24}(t)=\lambda _{24}({{\mathbf {x}}})\). These functions are linear in t. Since \(R_1({{\mathbf {x}}})=1\) on \(e_1\), \(q({{\mathbf {x}}})\) restricted to \(e_1\) is the polynomial \({\tilde{q}}\in {\mathbb {P}}_{r-2}(e_1)\) defined by
We have assumed that \({\tilde{q}}(t_1)=0\), so \({\tilde{q}}(t_i)=q(x_{e,1i}) =0\) for all \(i=1,\ldots ,r-1\). That is, \({\tilde{q}}(t)\) is a polynomial of degree \(r-2\) vanishing at \(r-1\) points, and so it vanishes identically. We have two cases to consider. First, suppose that the lines through \(e_1\) and \(e_3\) intersect at \({{\mathbf {x}}}_{13}\) (see Fig. 3). Now
is a contradiction, since \(\lambda _3({{\mathbf {x}}}_{13}) = 0\) and \(\lambda _{24}({{\mathbf {x}}}_{13})\ne 0\) by our choice of this linear function. Second, suppose that the lines through \(e_1\) and \(e_3\) are parallel. Then \(\lambda _3|_{e_1}=\alpha >0\) is a strictly positive constant, and so
This is clearly a contradiction, since the zero line of \(\lambda _{24}\) is transverse to \(e_3\) (again by our choice) leading us to conclude that \({\tilde{\lambda }}_{24}^{r-2}\) must have strict degree \(r-2\).
We have concluded that \(q({{\mathbf {x}}}_{e,11})\ne 0\), and so also \(\phi _{e,11}({{\mathbf {x}}}_{e,11})\ne 0\). We complete the construction by defining
The nodal basis functions \(\{\varphi _{e,ij}:i=1,2,3,4,\ j=1,\ldots ,r-1\}\) for the other edge nodes are defined similarly.
3.2.3 Vertex nodal basis functions
For the vertices, \(r\ge 2\), so we can define the shape functions
wherein we interpret indices modulo 4. These four functions vanish at all of the edge nodes, and \(\phi _{v,i}({{\mathbf {x}}}_{v,j})=0\) if \(i\ne j\) and is positive otherwise. The nodal basis functions are then
This completes the construction of the \(D_r=\dim {\mathbb {P}}_r(E)+2\) (recall (10)) nodal basis functions for \({\mathscr {DS}}_r(E)\). This also completes the proof of Theorem 1.
3.3 Implementation as an \(H^1\)-Conforming Space
On the mesh \({{{\mathscr {T}}}}_h\) of \(\varOmega \), the global direct serendipity finite element space of index r is
Because our elements are polynomials of degree r on the edges, they merge together continuously, provided that their edge and vertex DoFs match on element boundaries.
We constructed a local nodal basis for \({\mathscr {DS}}_r(E)\), \(r\ge 2\); that is, one for which every basis function vanishes at all but one nodal point, and it equals to one at this point. These local basis functions (after extension by zero outside the element), merge together continuously to give a global nodal basis for \({\mathscr {DS}}_r={\mathscr {DS}}_r(\varOmega )\subset H^1(\varOmega )\). In this way we construct global nodal basis functions, each equal to one at a nodal point and zero at all the other nodal points (so far for \(r\ge 2\), but also for \(r=1\), after the construction of the next section is complete).
4 Direct serendipity elements when \(r=1\)
It is shown in [8] that when \(d=2\), the convergence of the linear serendipity finite element space (\(r=1\)) does not degenerate on quadrilaterals. The parametric serendipity element \({{{\mathscr {S}}}}_1(E)\) is the tensor product space of bilinear functions \({\mathbb {P}}_{1,1}({\hat{E}})\) on \({\hat{E}}\) mapped to E by \(F_{\!E}^0\), and, in fact,
has the form of a direct serendipity space with only one supplemental function.
Theorem 2
Let E be a nondegenerate, convex quadrilateral. The space \({\mathscr {DS}}_1(E)\) is a well defined direct serendipity finite element of index \(r=1\) if and only if
for some supplemental function R that reduces to a linear function on each edge of E and satisfies
As just noted, the mapped function
gives the usual parametric serendipity space, and it is linear on each edge of E and satisfies (34).
Proof
We first show that (33) with any such R will give a well defined serendipity finite element \({\mathscr {DS}}_1(E)\) by showing that it has a nodal basis. The nodal basis is constructed by first defining the linear functions with zero lines corresponding to the diagonals of the element E. Let \(\nu _{d,1}\) be either unit normal to the first diagonal joining \({{\mathbf {x}}}_{v,1}\) with \({{\mathbf {x}}}_{v,3}\), and let \(\nu _{d,2}\) be either unit normal for the second diagonal joining \({{\mathbf {x}}}_{v,2}\) with \({{\mathbf {x}}}_{v,4}\). Then let
The nodal basis functions are
Note that there is no division by zero, so these functions are well defined, and that they are in \({\mathscr {DS}}_1(E)={\mathbb {P}}_1\oplus \text {span}\{R\}\), as required.
For the direct implication of the theorem, every well defined direct serendipity space \({\mathscr {DS}}_1(E)\) has a nodal basis of dimension four (recall Table 1) and contains \({\mathbb {P}}_1(E)\). Since \(R=\varphi _{v,1}({{\mathbf {x}}})-\varphi _{v,2}({{\mathbf {x}}})+\varphi _{v,3}({{\mathbf {x}}})-\varphi _{v,4}({{\mathbf {x}}})\) is in the space and cannot be in \({\mathbb {P}}_1(E)\), we conclude that \({\mathscr {DS}}_1(E)\) has the form (33). \(\square \)
One way to define R is to use generalized barycentric coordinates (GBCs) [29, 30, 33, 40]. There are many types of GBCs, including Wachspress, mean value, Sibson, and harmonic coordinates. The functions \(\varphi _i({{\mathbf {x}}}):E\rightarrow {\mathbb {R}}\), \(i=1,2,3,4\), are GBCs if they satisfy the two properties:
-
1.
(non-negativity) \(\varphi _i\ge 0\) on E;
-
2.
(linear completeness) for any linear function \(L:E\rightarrow {\mathbb {R}}\),
$$\begin{aligned} L({{\mathbf {x}}}) = \sum _{i=1}^4L({{\mathbf {x}}}_{v,i})\varphi _i({{\mathbf {x}}}). \end{aligned}$$
These four functions are linearly independent, they are linear on each edge e of \(\partial E\), their span includes \({\mathbb {P}}_1(E)\), and they form a nodal basis with respect to the vertices, i.e., \(\varphi _i({{\mathbf {x}}}_{v,j})=\delta _{ij}\) for all i, j [30, 33]. So by their definition, their span is a direct serendipity finite element, and moreover they constitute the nodal basis.
However, we do not require the non-negativity property. Functions satisfying linear completeness for \(L\in {\tilde{{\mathbb {P}}}}_1(E)\) are called homogeneous coordinates, and they were completely characterized in [30] in terms of areas of triangles. After normalization, these give direct serendipity finite elements. In the technical sense of their characterization (which requires the choice of four functions), no one can find new spaces. However, our new characterization of the spaces (33) can be used to give an alternate construction that is based on simple linear functions.
Our idea is to construct R inside \({\mathscr {DS}}_2(E)\) so that R satisfies (34). There are many ways to define \(DS_2(E)\), so we get many R’s, a different one for each choice of the space \(DS_2(E)\). Let \(\varphi _{e,i1}^{(2)}({{\mathbf {x}}})\) be the edge nodal basis function for the node \({{\mathbf {x}}}_{e,i1}^{(2)}\) in \({\mathscr {DS}}_2(E)\), \(i=1,2,3,4\). It is quadratic on each edge. Let
which is quadratic as well, and then define
Then
Restricted to the edges, R is nominally quadratic, but it reduces to a linear polynomial on each edge, since R is 1 at one vertex, \(-1\) at the other, and vanishes at the midpoint, i.e., at \({{\mathbf {x}}}_{e,i1}^{(2)}\) for all i.
5 Serendipity supplements based on mapping from a reference element
There are other ways to define serendipity finite elements. In this section, we define the supplemental space on the reference element \({\hat{E}}\) and map it to E using the bilinear map. When \(r=1\), we obtain \({{{\mathscr {S}}}}_1(E)\) defined in (32) using \({\mathbb {S}}_1(E)=\text {span}\{R^{\text {mapped}}\}\), where (35) defines \(R^{\text {mapped}}=F_{\!E}^0({\hat{x}}_1{\hat{x}}_2)\). When \(r\ge 2\), \({\mathbb {S}}_r(E)=\text {span}\{\phi _{s,1}^{\text {mapped}},\phi _{s,2}^{\text {mapped}}\}\), where
This construction gives us direct serendipity elements with mapped supplements. For \(r\ge 2\), we must show unisolvence with this supplemental space. As before, we show this property by constructing a nodal basis.
Since the supplements are not used in the construction of interior cell nodal basis functions, the definition (23) continues to be valid. Moreover, once the edge nodal basis functions are defined, the vertex nodal functions are defined by (30). Thus, we need only construct the edge nodal basis functions. As in Sect. 3.2.2, we discuss only the nodal basis function \(\varphi _{e,11}({{\mathbf {x}}})\) at nodal point \({{\mathbf {x}}}_{e,11}\), since the other edge nodal basis functions are constructed similarly.
Easily, with \({{\mathbf {x}}}={{\mathbf {F}}}_{\!E}({\hat{{{\mathbf {x}}}}})\),
wherein we defined \(R_{13}({{\mathbf {x}}})=F_{\!E}^0({\hat{x}}_1)\) as in (19) and
which is a nonlinear function. However, because \({{\mathbf {F}}}_{\!E}\) is a bilinear map, on the edges \(e_1\) and \(e_3\), \(\lambda _{13}^*\) is linear and \(F_{\!E}^0(1-{\hat{x}}_2^2)\) is quadratic (but these may be different linear and quadratic functions on the two edges).
The function \(\lambda _{24}^*\) has the zero set being the line joining the center of \(e_1\) to the center of \(e_3\). Let \({{\mathbf {x}}}_{24}^*\) be any point on this line and \(\nu _{24}\) denote a unit normal to the line. Define the linear function
which mimics \(\lambda _{24}^*\) in the sense that both are linear on \(e_1\) and \(e_3\), and they have the same zero set. Then there are constants \(a_i\ne 0\) of the same sign such that
In fact, \(a_1=1/\lambda _{24}({{\mathbf {x}}}_{v,4})\) and \(a_3=1/\lambda _{24}({{\mathbf {x}}}_{v,3})\), since \(\lambda _{24}^*\) is 1 at these two corners.
The function \(F_{\!E}^0(1-{\hat{x}}_2^2)\) is quadratic and vanishes at the ends of \(e_1\) and \(e_3\), so
for constants \(b_i>0\), defined by considering the center points of \(e_1\) and \(e_3\).
For some \(p\in {\mathbb {P}}_{r-3}(E)\), we define
This function vanishes on \(e_2\) and \(e_4\). It also vanishes on \(e_3\), since there \(R_{13}=1\), and so
Restricted to \(e_1\), we have \(R_{13}=-1\) and
Since \((b_3a_3^{r-2}/b_1 + a_1^{r-2})\ne 0\), this is formally the same as (24) on \(e_1\), up to some constants. Thus the construction in Sect. 3.2.2 can be used here to complete the definitions of the edge nodal basis functions. We conclude that the direct serendipity element with mapped supplements, i.e.,
is a well defined finite element.
6 Approximation properties of \({\mathscr {DS}}_r\)
In this section, we develop the stability and convergence theory for our new direct serendipity finite elements. For the most part, we work over the entire domain \(\varOmega \), with the assumption that \(\text {diam}(\varOmega )=1\) for simplicity. To obtain global approximation properties, we need to assume that the mesh is uniformly shape regular [34, pp. 104–105], which means the following.
Definition 2
For any \(E\in {{{\mathscr {T}}}}_h\), denote by \(T_i\), \(i=1,2,3,4\), the sub-triangle of E with vertices being three of the four vertices of E. Define the parameters
A collection of meshes \(\{{{{\mathscr {T}}}}_h\}_{h>0}\) is uniformly shape regular if there exists \(\sigma _*>0\) such that the ratio \(\displaystyle {\rho _E}/{h_E}\ge \sigma _*>0\) for all \(E\in {{{\mathscr {T}}}}_h\), where \(\sigma _*\), the shape regularity parameter, is independent of \({{{\mathscr {T}}}}_h\) and \(h>0\).
A shape regular mesh has a bound on the number of quadrilaterals that can share a single vertex.
In Sects. 3 and 4 , we constructed local and global nodal bases for \({\mathscr {DS}}_r(E)\) and \({\mathscr {DS}}_r={\mathscr {DS}}_r(\varOmega )\) for \(r\ge 1\); that is, one for which every basis function vanishes at all but one nodal point, and it equals to one at this point. In this section, we denote the set of global nodal basis functions as \(\{\varphi _1,\ldots ,\varphi _{N_r}\}\), corresponding to global nodal points \(\{a_1,\ldots ,a_{N_r}\}\), respectively, where \(N_r=\dim {\mathscr {DS}}_r\).
6.1 An interpolation operator mapping onto \({\mathscr {DS}}_r\)
We first construct an interpolation operator mapping onto \({\mathscr {DS}}_r\) following Scott and Zhang [42]. For each node \(a_i\) in the interior of some element \(E\in {{{\mathscr {T}}}}_h\), we set \(K_i\) to be (the closed set) E, and we call such a node an interior node. For each node \(a_i\) in the interior of edge e of \({{{\mathscr {T}}}}_h\) (i.e., not at the vertices), we set \(K_i=e\) (a closed set). These nodes are called edge nodes. For each node \(a_i\) being a vertex of \({{{\mathscr {T}}}}_h\), we choose \(K_i\) to be any fixed edge e containing \(a_i\), with the restriction that if \(a_i\in \partial \varOmega \), then \(e\subset \partial \varOmega \). Note that e is chosen from among multiple edges. These nodes are called vertex nodes.
We define a special \(L^2\)-dual nodal basis \(\{\psi _1,\ldots ,\psi _{N_r}\}\) as follows. For each node \(a_i\), we denote the total number of nodes in \(K_i\) as \(n_i\), and then denote these nodes in \(K_i\) as \(\{a_{i,j}: j=1,\ldots ,n_i\}\), where \(a_{i,1}=a_i\), which correspond to the global nodal basis functions \(S_i=\{\varphi _{i,j}: j=1,\ldots ,n_i\}\). Restricted to \(K_i\), we have an \(L^2(K_i)\)-dual nodal basis \(\{\psi _{i,j}: j=1,\ldots ,n_i\}\subset \text {span}\,S_i\) satisfying
where we use a slight abuse of notation in that dx should be \(d\sigma \) for edge and vertex nodes. Finally, for the node \(a_i\), we take \(\psi _i=\psi _{i,1}\). (As described, this construction is highly redundant. Since it is used only for theoretical purposes, we do not explore its efficient implementation.)
For any node \(a_i\) giving rise to \(K_i\) and \(\psi _i\),
This is easily seen as follows. If \(a_i\) is an interior node, then this expression is exactly (52) (since the latter expression holds for all nodes on E). If \(a_i\) is an edge or vertex node, then when \(a_j\) is also an edge or vertex node, (53) is (52), and when \(a_j\) is an interior node, \(\varphi _j\) vanishes on the edges of \({{{\mathscr {T}}}}_h\) (and thus on \(K_i\)).
We can now define an interpolation operator \({{{\mathscr {I}}}}_h^r:W_p^l(\varOmega )\rightarrow {\mathscr {DS}}_r\) by
where \(1\le p \le \infty \) and \(l>1/p\) (but \(l\ge 1\) if \(p=1\)). By the trace theorem, the nodal values \(\displaystyle \int _{K_i}\psi _i({{\mathbf {y}}})\,v({{\mathbf {y}}})\,dy\) are well defined for any \(v\in W_p^l(\varOmega )\), even when \(K_i\) is an edge. Note that \({{{\mathscr {I}}}}_h^r\) depends on our choice of \(K_i\), but we suppress this fact in the notation for simplicity. Because (53) holds, this operator is a projection on \({\mathscr {DS}}_r\).
6.2 Boundedness of the interpolation operator \({{{\mathscr {I}}}}_h^r\)
To obtain approximation properties, the interpolation \({{{\mathscr {I}}}}_h^r\) needs to be a bounded operator. Scott and Zhang’s proof of this fact in their situation [42] does not hold directly for our construction, since we need to use non-affine mappings from the reference element to the actual elements, and we use non polynomial shape functions. We give a proof of boundedness based on a continuous dependence argument.
On an element \(E\in {{{\mathscr {T}}}}_h\), it is clear that the linear functions \(\lambda _i\) defined in (7) depend only on \({{\mathbf {x}}}\) and the vertices of E, and that this dependence is continuous. For simplicity of discussion, we use the simple choices given in (16) and (18) and consider only the direct serendipity finite elements based on this choice. We will remove this restriction at the end of the section. However, for these simple choices, it is clear that these four functions used to define the serendipity finite elements are continuously differentiable functions of \({{\mathbf {x}}}\) and the vertices of E.
For the element \(E\in {{{\mathscr {T}}}}_h\), we show it on the right in its translated and rotated local coordinates, and its corresponding local reference element \({\tilde{E}}=E/H={{\mathbf {F}}}_{\!{\tilde{E}}}({\hat{E}})\) in the center. The interior nodal points are mapped from the reference element \({\hat{E}}\), shown on the left
We need to fix the domain to the reference element \({\hat{E}}=[-1,1]^2\). For any \(E\in {{{\mathscr {T}}}}_h\), let \(H=H_E\) be the maximal edge length of E. (By shape regularity, \(H_E\) is comparable to \(h_E\), the diameter of E.) Since our finite element construction is invariant under translation and rotation, for any \(E\in {{{\mathscr {T}}}}_h\) we can assume that \({{\mathbf {x}}}_{v,1}=(0,0)\) and \({{\mathbf {x}}}_{v,2}=(H,0)\), as depicted in Fig. 4. Furthermore, we can scale E by 1/H to define a local reference element \({\tilde{E}}=E/H\) with vertices (0, 0), (1, 0), \((v_1,v_2)\), and \((v_3,v_4)\). We can view E as the image of the bilinear map \({{\mathbf {F}}}_{\!E}=H{{\mathbf {F}}}_{\!{\tilde{E}}}\) defined in Sect. 2, which is a continuous function of \({\hat{{{\mathbf {x}}}}}\in {\hat{E}}\) and the vertices of E (since E is nondegenerate). Boundedness of this mapping is well-known for shape regular meshes. To be more precise, let \({\mathbf {F}}_{K_i}={\mathbf {F}}_E|_{K_i}\) when \(K_i=E\) or \(K_i\) is an edge of some E. By the uniform shape regularity of the mesh, for some constant C independent of \(K_i\) [23, Theorem 4.3.3],
These are the properties of the mapping needed in the argument of Scott and Zhang [42]. Further, since the bilinear mappings \({{\mathbf {F}}}_E\) are defined on nondegenerate quadrilaterals, \({{\mathbf {F}}}_E\) and \({{\mathbf {F}}}_E^{-1}\) are smooth, and similar bounds hold for higher order derivatives. In particular, higher order derivatives of \({{\mathbf {F}}}_{{\tilde{E}}}\) and \({{\mathbf {F}}}_{{\tilde{E}}}^{-1}\) are uniformly bounded.
The edge nodal points have been placed uniformly on each edge. We need to fix a place for the interior nodal points, so that their positions vary continuously with the location of the vertices. Recall that the interior nodal points correspond to Lagrange nodal points for \({\mathbb {P}}_{r-4}\). We can fix these on a triangle with vertices at, say, \((-1/3,-1/3)\), \((1/3,-1/3)\), and \((-1/3,1/3)\) inside \({\hat{E}}=[-1,1]^2\), and map these to \({\tilde{E}}\) and E, as depicted in Fig. 4. This is done only for the proof. In the end, we have a global space of functions \({\mathscr {DS}}_r(\varOmega )\) defined independently of the location of the nodal points, so this change in their position is not important to the construction.
For any \(E\in {{{\mathscr {T}}}}_h\), let \(\varphi _j^{{\tilde{E}}}\), \(j=1,\ldots ,\dim {\mathscr {DS}}_r(E)\), be the local nodal basis functions constructed on \({\tilde{E}}\). Each depends only on \(\xi =({\hat{{{\mathbf {x}}}}},v_1,v_2,v_3,v_4)\), where \({\tilde{{{\mathbf {x}}}}}={{\mathbf {F}}}_{\!{\tilde{E}}}({\hat{{{\mathbf {x}}}}})\in {\tilde{E}}\), and each \(\varphi _j^{{\tilde{E}}}\) varies continuously with respect to these variables. The set of admissible \(\xi \) is bounded, since no side of \({\tilde{E}}\) has length greater than 1. Moreover, the shape regularity constraints are given by (albeit complicated) continuous functions of \((v_1,v_2,v_3,v_4)\) involving maximal inscribed circles being required to lie in the closed interval \([\sigma _*,\infty )\). Therefore the set of admissible \(\xi \) is a closed, and hence compact, set. We conclude that each \(\varphi _j^{{\tilde{E}}}\) and its derivatives are bounded uniformly with respect to the shape of \({\tilde{E}}\). That is, there exists a constant \(C=C(\sigma _*, m, q)\) independent of \(\xi \) such that
where \(\sigma _*\) is the shape regularity parameter. Since locally \(\varphi _j^{\tilde{E}}({{\mathbf {x}}}/H)=\varphi _j^E({{\mathbf {x}}})\), we also have a bound for the global nodal basis functions, namely,
We also need to show that the dual basis functions are bounded such that for any node \(a_i\),
which is a result analogous to [42, Lemma 3.1]. Here, \(h_{K_i}=h_{E_i}\), where \(K_i\subset E_i\) (for both possible \(E_i\) when \(K_i\) is an edge). Let \(\psi _j^{{\tilde{E}}}\), \(j=1,\ldots ,\dim {\mathscr {DS}}_r(E)\), be the dual nodal basis functions defined for nodes in \({\tilde{E}}\) as defined in Sect. 6.1. These are also continuous functions of \(\xi \) (and possibly the corresponding values of \(\xi \) for its neighboring elements, due to the treatment of vertex nodes). By a similar continuity and compactness argument, we conclude that \(\psi _j^{{\tilde{E}}}\) is bounded uniformly with respect to the shape of \({\tilde{E}}\) and its neighbors. When \(a_i\) is an interior node, \({\tilde{K}}_i={\tilde{E}}\), so
Since \(\varphi _k^{{\tilde{E}}}({{\mathbf {x}}}/H)=\varphi _k^E({{\mathbf {x}}})\), we conclude that \(\psi _j^{{\tilde{E}}}({{\mathbf {x}}}/H)\,H^{-2}=\psi _j({{\mathbf {x}}})\) and so (59) holds. When \(a_i\) is an edge or vertex node, \({\tilde{K}}_i\) and \(K_i\) are edges which are affinely related to the reference interval \([-1,1]\). Moreover, the functions in question, when restricted to the edge, are polynomials. Thus Scott and Zhang’s argument holds directly, and so (59) holds in general. This and (57) lead to the conclusion that the interpolation operator is bounded.
We can extend the proof to more general \(\lambda _{24}\) and \(\lambda _{13}\). These linear functions are defined by their zero lines, which are defined by two points each. However, we have a restriction that for \(\lambda _{24}\), say, the zero set line \({{{\mathscr {L}}}}_{24}\) must intersect both \({{{\mathscr {L}}}}_1\) and \({{{\mathscr {L}}}}_3\), but not at their intersection when they are not parallel. This choice of four points (two for each of \(\lambda _{24}\) and \(\lambda _{13}\)) could be added as parameters to the variable \(\xi \). However, then the restriction implies that \(\xi \) does not vary over a compact set. So we must restrict the choice of these four points. We make a simple (and practical) requirement that the zero set line \({{{\mathscr {L}}}}_{24}\) intersects \(e_1\) and \(e_3\), and \({{{\mathscr {L}}}}_{13}\) intersects \(e_2\) and \(e_4\). We actually choose four points (which are added into \(\xi \)), one on each fixed and closed edge of \({\hat{E}}\), and map them through \({{\mathbf {F}}}_E\) to define \(\lambda _{24}\) and \(\lambda _{13}\). In this way, \(\lambda _{24}\) and \(\lambda _{13}\) are defined as continuous functions of \(\xi \), and \(\xi \) varies over a compact set, and the argument above continues to hold.
We can generalize the possible \(R_{13}\) and \(R_{24}\) that can be used as well. Of course they must satisfy the requirement (17), but they must also be uniformly differentiable functions of \(\xi \). Such is the case for the mapped choice \(R_{13}^{\text {mapped}}\) and \(R_{24}^{\text {mapped}}\) of (19). Using standard scaling arguments, we have shown the following lemma, analogous to [42, Theorem 3.1].
Lemma 1
Let \(v \in W^l_p(\varOmega )\), with \(1\le p\le \infty \) and \(\ell >1/p\) (or \(\ell \ge 1\) if \(p=1\)). Let \({{{\mathscr {T}}}}_h\) be uniformly shape regular (Definition 2) with shape regularity parameter \(\sigma _*\). For every \(E\in {{{\mathscr {T}}}}_h\), suppose that the basis functions of \({\mathscr {DS}}_{r}(E)\) are constructed using \(\lambda _{24}\) and \(\lambda _{13}\) such that the zero set \({{{\mathscr {L}}}}_{24}\) intersects \(e_1\) and \(e_3\), and \({{{\mathscr {L}}}}_{13}\) intersects \(e_2\) and \(e_4\). Moreover, assume that \({R}_{13}\) and \({R}_{24}\) are uniformly differentiable functions of the vertices of E up to order m. Then for \(r\ge 1\), \(E\in {{{\mathscr {T}}}}_h\), \(1 \le q \le \infty \), and any nonnegative integer m,
where \(E^* = \bigcup _{F\in {{{\mathscr {T}}}}_h,\,{F}\cap {E}\ne \emptyset }{F}\) and \(|\cdot |_{W_p^{k}}\) is the seminorm of k-th order derivatives.
We remark that the mapped supplements (43) vary continuously with the element shape, and so satisfy the lemma above.
6.3 Approximation properties of the \({\mathscr {DS}}_r\) spaces
We use the Bramble-Hilbert lemma [18] in the form developed by Dupont and Scott in [28] (see also [19]). A domain \(\omega \) is star-shaped with respect to a ball \(B_r\) of radius r if for all \(x\in \omega \), the closed convex hull of \(\{x\}\cup B_r\) is a subset of \(\omega \). Let \(r_{\max }=\sup \{r:\omega \) is star-shaped with respect to \(B_r\}\) and \(h=\text {diam}(\omega )\), and define the chunkiness parameter of \(\omega \) by \(h/r_{\max }\). Then the Bramble-Hilbert Lemma, i.e., that
has a constant C that depends continuously on the chunkiness parameter. On the local reference element \(\omega ={\tilde{E}}\) (actually its interior), the chunkiness parameter varies continuously in a compact set due to the shape regularity assumption, so the constant C has an upper bound independent of the vertices of \({\tilde{E}}\).
Combining Lemma 1 and the Bramble-Hilbert lemma (61), we derive our theorem for local and global error estimation using \(E^*\) defined just after (60).
Theorem 3
With the assumptions of Lemma 1, there exists a constant \(C=C(r, \sigma _*)>0\) such that for all functions \(v \in W^{\ell }_p(E^*)\), with \(1\le p\le \infty \) and \(\ell >1/p\) (or \(\ell \ge 1\) if \(p=1\)),
Moreover, there exists a constant \(C=C(r, \sigma _*)>0\), independent of \(h=\max _{E\in {{{\mathscr {T}}}}_h}h_E\), such that for all functions \(v\in W^{\ell }_p(\varOmega )\),
7 Construction of direct mixed finite elements using a de Rham complex
The de Rham complex of interest here is

where the curl (or rot) of a scalar function \(\phi ({{\mathbf {x}}})=\phi (x_1,x_2)\) is \(\text {curl}\,\phi = \bigg (\dfrac{\partial \phi }{\partial x_2},-\dfrac{\partial \phi }{\partial x_1}\bigg )\). From left to right, the image of one linear map is the kernel of the next. On rectangular elements, it is known [6, 7] that the serendipity space \({{{\mathscr {S}}}}_{r+1}\) is the precursor of the Brezzi-Douglas-Marini space BDM\(_r\) [20] for \(r\ge 1\); that is, on the reference square \({\hat{E}}\), (1) holds.
7.1 Reduced and full AC spaces
We have the following extension of (1) to quadrilateral elements E. The direct serendipity spaces \({\mathscr {DS}}_r^{\text {mapped}}\) (49) using the mapped supplements (43) is the precursor of the reduced \(H(\text {div})\)-approximating Arbogast–Correa space AC\(_r^{r-1}\) [1], \(r\ge 1\), defined on meshes of convex quadrilaterals:

Moreover, the full \(H(\text {div})\)-approximating space AC\(_r^r\), for \(r\ge 0\), satisfies

This observation is clear once one realizes three sets of facts. First, the direct serendipity elements based on (43) have the structure
Second, the AC elements have the structure
where \({{\mathbf {F}}}_{\!E}^1\) is the Piola mapping (9) from \({\hat{E}}\) to E. Finally, we have the fairly well-known Helmholtz-like decomposition (see, e.g., [1])
the relation between the \(\text {curl}\) operator and the bilinear and Piola maps
and the fact that the \(\text {div}\) operator takes \({{\mathbf {x}}}{\mathbb {P}}_{s}\) one-to-one and onto \({\mathbb {P}}_{s}\) for any \(s\ge 0\).
Now we see from (73) that, when \(r\ge 1\),
and so
is in the kernel of the operator \(\text {div}\). Finally, (72) says that
These spaces satisfy the exact sequence properties of the de Rham complex (65)–(66). For \(r=0\), it is easy to check that \({{{\mathscr {S}}}}_1(E)={\mathscr {DS}}_1(E)\) (see (32)) precedes the element AC\(_0^0\)(E) in the de Rham sequence (66).
7.2 Direct mixed finite elements when \(r\ge 1\)
According to [1], a reduced or full \(H(\text {div})\)-approximating mixed finite element space defined directly on a quadrilateral E of minimal local dimension takes the form (\({{{\mathscr {P}}}}\) in Definition 1)
where, in that paper, the choice of \({\mathbb {S}}_r^{{\mathbf {V}}}(E)\) is given by taking (71). However, it is noted that other supplemental functions could be used [1, near (3.15)]. Their normal components must lie in \({\mathbb {P}}_r(e_i)\) on each edge \(e_i\) and, if they are mapped by the Piola transform, they must contain a nontrivial component of the DoFs of \(\text {curl}\,{\hat{x}}_1^{r+1}{\hat{x}}_2\) and \(\text {curl}\,{\hat{x}}_1{\hat{x}}_2^{r+1}\). For \(r\ge 1\), the supplemental space \({\mathbb {S}}_r^{{\mathbf {V}}}(E)\) must be of dimension two and linearly independent of \({\mathbb {P}}_r^2(E)\), so that
As given in [1], the DoFs (\({{{\mathscr {N}}}}\) in Definition 1) for \(\pmb \psi \in {{\mathbf {V}}}_r^{s}(E)\), \(s=r-1,r\), are given (after fixing a basis for the test functions) by
where \(d\sigma \) is the one dimensional surface measure and the \(H^1(E)\) and \(H(\text {div};E)\) bubble functions, for \(r\ge 3\), are
Note that the number of DoFs agrees with the dimension of the space (79).
Unlike the construction given in [1], which only considered mixed finite elements, we use here the de Rham theory to construct a mixed finite element space \({{\mathbf {V}}}_r^s\) based on a well defined direct serendipity space. For \(r\ge 1\), we have de Rham complexes for both reduced and full direct \(H(\text {div})\)-approximating mixed elements:

for any variant of our new direct serendipity spaces. We define spaces of vector functions according to these de Rham complexes, using the fact that the \(\text {div}\) operator takes \({{\mathbf {x}}}{\mathbb {P}}_{k}\) one-to-one and onto \({\mathbb {P}}_{k}\). These spaces are
and they have the form (77)–(78), provided we define
Theorem 4
Let E be a nondegenerate, convex quadrilateral and \({\mathscr {DS}}_{r+1}(E)={\mathbb {P}}_{r+1}(E)\oplus {\mathbb {S}}_{r+1}^{{\mathscr {DS}}}(E)\) be a well defined direct serendipity finite element for \(r\ge 1\). Then the mixed spaces
with DoFs defined by (80)–(82) are well defined finite elements. Moreover, for \(s=r-1,r\), \({{\mathbf {V}}}_r^s(E)\) has the minimal possible dimension (79) needed for \(H(\text {div})\) conformity and the property that \(\text {div}\,{{\mathbf {V}}}_r^s(E) = {\mathbb {P}}_s(E)\).
Proof
It remains only to show that in fact these spaces are unisolvent for the DoFs (80)–(82); that is, that these spaces are well defined mixed finite elements. So suppose that \(\pmb \psi \in {{\mathbf {V}}}_r^{s}(E)\), \(s=r-1,r\), and has vanishing DoFs. By construction,
where \(\phi \in {\mathscr {DS}}_{r+1}(E)\) and \(\pmb \psi _d\in {{\mathbf {x}}}{\mathbb {P}}_s\). The DoFs (81), with (80), imply that for \(q\in {\mathbb {P}}_s(E)\),
Since \(\nabla \cdot \pmb \psi _d\in {\mathbb {P}}_s(E)\), we conclude that \(\nabla \cdot \pmb \psi _d=0\), and further that \(\pmb \psi _d=0\).
We next observe the well known fact that tangential derivatives of functions along the edges of E map by the \(\text {curl}\) operator to normal components; that is, if we define the (counterclockwise) unit tangential vector
then for \(\phi \in {\mathscr {DS}}_{r+1}(E)\),
Therefore, the DoFs (80) imply that for any edge \(e_i\) and \(p\in {\mathbb {P}}_r(e_i)\),
and we conclude that \(\nabla \phi \cdot \tau =0\) on \(\partial E\), and so \(\phi =c\) is constant on \(\partial E\). Now \(\phi -c\in {\mathscr {DS}}_{r+1}(E)\) vanishes on \(\partial E\), so we conclude that \(\phi -c\in {\mathbb {B}}_{r+1}(E)\). The DoF (82) with \({{\mathbf {v}}}=\text {curl}(\phi -c)=\text {curl}\,\phi \) implies that \(\text {curl}\,\phi =0\). Thus \(\pmb \psi =0\), and the proof of unisolvence is complete. \(\square \)
We can use any of our direct serendipity spaces to define direct mixed finite elements \({{\mathbf {V}}}_r^{r-1}(E)\) or \({{\mathbf {V}}}_r^{r}(E)\). As we saw earlier, if we use \({\mathscr {DS}}_{r+1}^{\text {mapped}}(E)\), we recover the known finite elements AC\(_r^{r-1}(E)\) and AC\(_r^r(E)\). However, the direct serendipity spaces of Sect. 3 give new (direct) mixed finite elements.
7.3 Direct mixed finite elements when \(r=0\)
When \(r=0\), there are no reduced \(H(\text {div})\) approximation finite element spaces. The full \(H(\text {div})\) approximation direct elements have dimension 4, and they take the form
where R was defined in Sect. 4 above as \(F_{\!E}^0({\hat{x}}_1{\hat{x}}_2)\) or in (42) using the special construction in \({\mathscr {DS}}_2(E)\). The former is the space AC\(_0^0\) [1], and the later appears to be a new mixed finite element satisfying
7.4 Implementation using the hybrid mixed method
The mixed space of vector functions \({{\mathbf {V}}}_r^s\) over \(\varOmega \) is defined by merging continuously the normal fluxes across each edge e of the mesh \({{{\mathscr {T}}}}_h\). That is, for \(r\ge 0\), \(s=r-1,r\), \(s\ge 0\),
This space is normally paired with a space approximating scalar functions. When, say, solving a second order elliptic partial differential equation in mixed form, the vector functions \({{\mathbf {V}}}_r^s\) are paired with the scalar functions
These scalar spaces are the divergences of the corresponding vector function spaces.
However, in practical implementation, the hybrid form of the mixed method is often used [10]. In that case, the elements \({{\mathbf {V}}}_r^{s}(E)\) are simply concatenated, and no globally merged basis is required. The Lagrange multiplier space, used to enforce the normal flux continuity through an additional equation, is simply
To represent the vector functions in \({{\mathbf {V}}}_r^s\) as we presented them, it would appear that we need to apply the curl operator extensively. However, this is not the case, since the vector polynomials in these spaces are clear, so we need only apply the curl operator to the supplemental functions. Even then, taking a curl can be avoided in some cases. As we saw earlier, \(\text {curl}\,{\mathbb {S}}_{r+1}^{{\mathscr {DS}},\text {mapped}}(E)\) gives the supplements for the known finite elements AC\(_r^s(E)\), \(s=r-1,r\), which are computed in (71) using the Piola transform rather than the curl operator.
For example, suppose we use the direct serendipity elements from Sect. 3 (so \(r\ge 1\)), with supplements defined by (14). We note that
where \(j=1,2,3,4\) or \(j=(24),(13)\). The only difficult curls required are \(\text {curl}\,R_{13}\) and \(\text {curl}\,R_{24}\). However, if the simple choice (18) is taken, then
The supplemental vector functions are then
7.5 Implementation as an \(H(\text {div})\)-conforming mixed space
The \(H(\text {div})\) spaces \({{\mathbf {V}}}_r^{r-1}\) and \({{\mathbf {V}}}_r^{r}\) defined in (94) can be given a global basis with the normal components of the shape functions merged continuously on each edge of the mesh \({{{\mathscr {T}}}}_h\). We present a method that uses the nodal basis functions of the serendipity space of index \(r+1\) preceding \({{\mathbf {V}}}_r^{r-1}\) or \({{\mathbf {V}}}_r^{r}\) in the de Rham complex.
Since the \(H(\text {div})\) bubble functions \({\mathbb {B}}_r^{{{\mathbf {V}}}}\) (83) have no normal flux, they can be handled easily. For each \(E\in {{{\mathscr {T}}}}_h\), when \(r\ge 3\) one can define the global basis functions
using the interior cell nodal basis functions (23) with a superscript as a reminder that the index of the direct serendipity space is \(r+1\). The shape functions arising from the edge nodal basis functions, like (28), also present no particular difficulty. For each edge e of the mesh shared by elements \(E_{k}\) and \(E_{\ell }\) (with e being locally edge \(i_1\) and \(i_2\), respectively), when \(r\ge 1\) one can define
These global basis functions are in \(H(\text {div})\) because the serendipity elements are continuous, so the tangential derivatives (i.e., the flux—see (91)) agree across e. Moreover, the average normal flux vanishes on each edge.
The most delicate global basis functions to construct are those for which the average normal flux is a constant on each edge e of the mesh. For each \(r\ge 0\), these are given primarily, but not completely, by taking curls of the serendipity vertex nodal basis functions (30). However, each of these functions has normal flux on two edges, and there are only three linearly independent functions per element (since the kernel of curl consists of the constant functions). For each element E having e as an edge, we need to consider the vector functions \({\mathbb {P}}_0^2(E)\oplus {{\mathbf {x}}}{\mathbb {P}}_0(E)\) with these curls. The proper construction requires some work on each element E of the mesh. We begin the construction by defining \(\phi _{v,i}^*\in {\mathscr {DS}}_{r+1}(E)\) such that \(\phi _{v,i}^*({{\mathbf {x}}}_{v,k})=\delta _{ik}\) and its restriction to each edge of E is a linear function. To be precise,
Then define \(\pmb \psi ^*_{v,i}=\text {curl}\,\phi ^*_{v,i}\), for which
We also define \(\pmb \psi ^{**}_{v,i}({{\mathbf {x}}}) = {{\mathbf {x}}}-{{\mathbf {x}}}_{v,i+2}\in {{\mathbf {x}}}{\mathbb {P}}_0(E)\oplus {\mathbb {P}}_0^2(E)\), for which
Finally, for each edge e of the mesh which is edge i of element E, we define
which has flux 1 on \(e_i\) and 0 on all other edges. These can be merged across edges to define global basis functions in \(H(\text {div})\), which have constant divergence on each element. (In fact, one could define \(\pmb \psi _{e,0}\) using the same expression with i replaced by \(i-1\). By alternation of the choice for different edges of E, only two of the \(\phi ^*_{v,i}\) need be constructed in practice.)
Finally, when \(s\ge 1\) we define the global basis functions associated to the nonconstant divergences. These functions are local to each element \(E\in {{{\mathscr {T}}}}_h\). Working on E, we begin with the functions \({{\mathbf {x}}}{\mathbb {P}}_s^*(E)\), where \({\mathbb {P}}_s^*(E)=\sum _{k=1}^s{\tilde{{\mathbb {P}}}}_k(E)\subset {\mathbb {P}}_s(E)\). Take \(p_i({{\mathbf {x}}})\) in a basis for \({\mathbb {P}}_s^*(E)\), so \(i=1,\ldots ,\tfrac{1}{2}(s+2)(s+1)-1\). We must remove the normal flux on \(\partial E\) from \({{\mathbf {x}}}p_i({{\mathbf {x}}})\). We do this using (99) and (100) by defining
and setting the coefficients \(\alpha _{j,k}\) on each edge \(e_j\) so that
where \(c_j={{\mathbf {x}}}\cdot \nu _j|_{e_j}\) is a constant. The coefficients can be found in a number of ways, including a straightforward application of linear algebra requiring the solution of four small \((r+1)\times (r+1)\) linear systems. An alternative can be given once one realizes that on edge \(e_j\), for \(k\ge 1\),
is the derivative of a Lagrange basis polynomial \({\mathfrak {L}}_k(t)\), where \({{\mathbf {x}}}(t)=(1-t){{\mathbf {x}}}_{v,j-1}+t\,{{\mathbf {x}}}_{v,j}\) for \(t\in [0,1]\). Thus
and the coefficients can be read off by substituting in the Lagrange points \(t_\ell =\ell /(r+1)\) for \(\ell =1,\ldots ,r+1\). The global basis is now fully defined.
8 Stability and approximation properties for \({{\mathbf {V}}}_r^s\)
In this section, we develop the stability and convergence theory for our new direct mixed finite elements. Again, we assume that \(\text {diam}(\varOmega )=1\) for simplicity.
As was done by Raviart and Thomas [41] for their mixed spaces, we can define a projection operator \(\pi :H(\text {div};\varOmega )\cap (L^{2+\epsilon }(\varOmega ))^2\rightarrow {{\mathbf {V}}}_r^s\), \(s=r-1,r\), where \(\epsilon >0\). The operator \(\pi \) is pieced together from locally defined operators \(\pi _E\). Following [1], we define \(\pi _E{{\mathbf {v}}}\) in terms of the DoFs (80)–(82). The operator \(\pi \) satisfies the commuting diagram property [25], which is to say that
where \({{{\mathscr {P}}}}_{W_s}\) is the \(L^2\)-orthogonal projection operator onto \(W_s=\nabla \cdot {{\mathbf {V}}}_r^s\).
To show that certain important properties of \(\pi _E\) do not depend on the vertices of E except for scale, we work over the scaled element \({\tilde{E}}\), which was introduced in Sect. 6.2. We need to fix a basis for the DoFs (80)–(82), so let \({\tilde{p}}_j({\tilde{t}}) = {\tilde{t}}^j\) and \({\tilde{p}}_{j,k}({\tilde{{{\mathbf {x}}}}}) = {\tilde{x}}_1^j {\tilde{x}}_2^k\) where j, k are integers. For any \({\tilde{{{\mathbf {v}}}}}\in H^1({\tilde{E}})\), we define the linear functional \(N_\beta ^{{\tilde{E}}}({\tilde{{{\mathbf {v}}}}})\) with index \(\beta \) as follows:
Denote the set of all possible indices of \(\beta \) as \({\mathscr {B}}\). By a continuity and compactness argument, similar to that given in Sect. 6.2, there exists a constant \(C>0\), independent of the vertices of \({\tilde{E}}\), such that \(\forall \beta \in {\mathscr {B}}\),
where \(\Vert \cdot \Vert _{j,\omega }\) is the norm of \(W_2^j(\omega )=H^j(\omega )\). By unisolvence, there exists a basis \(\{\pmb \phi _{\beta }^{{\tilde{E}}}, \beta \in {\mathscr {B}}\}\) for \({{\mathbf {V}}}^s_r({\tilde{E}})\), such that
Then \(\pi _{{\tilde{E}}}\) can be defined as
Note that \(\pmb \phi _{\beta }^{{\tilde{E}}}\) varies continuously with respect to vertices of \({\tilde{E}}\), and so there exists a constant \(C>0\), such that
Combining (105) and (107), there exists a constant \(C>0\), independent of the vertices of \({\tilde{E}}\), such that
By the boundedness of \(\pi _{{\tilde{E}}}\) in \(H^1\), the Bramble-Hilbert Lemma (61), and usual scaling arguments, there exists a polynomial \({\tilde{{{\mathbf {p}}}}} \in {\mathbb {P}}^2_{k-1}({\tilde{E}})\) for \(1\le k \le r+1\) such that
where the constants do not depend on the vertices of \({\tilde{E}}\). The \(L^2\)-orthogonal projection \({{{\mathscr {P}}}}_{W_s}\) gives optimal approximation, and so also \(\nabla \cdot ({{\mathbf {u}}}-\pi {{\mathbf {u}}})=\nabla \cdot {{\mathbf {u}}}-{{{\mathscr {P}}}}_{W_s}\nabla \cdot {{\mathbf {u}}}\) is optimally approximated. We have shown the following.
Lemma 2
With the assumptions of Lemma 1, there is a constant \(C>0\), independent of \({{{\mathscr {T}}}}_h\) and \(h>0\), such that
where \(s=r-1\ge 0\) and \(s=r\ge 1\) for reduced and full \(H(\text {div})\)-approximation, respectively. Moreover, the discrete inf-sup condition
holds for some \(\gamma >0\) independent of \({{{\mathscr {T}}}}_h\) and \(h>0\).
9 Numerical results
We test our finite elements on the Dirichlet problem
where the second order tensor \({{\mathbf {a}}}({{\mathbf {x}}})\) is uniformly positive definite and bounded, and \(f\in L^2(\varOmega )\). The problem can be written in the weak form: Find \(p\in H_0^1(\varOmega )\) such that
where \((\cdot ,\cdot )\) is the \(L^2(\varOmega )\) inner product. Setting
we also have the mixed weak form: Find \({{\mathbf {u}}}\in H(\text {div};\varOmega )\) and \(p\in L^2(\varOmega )\) such that
These weak forms give rise to finite element approximations. In view of Theorem 3 and Lemma 2, it is well known that the following theorem holds [19, 21].
Theorem 5
With the assumptions of Lemma 1, there exists a constant \(C>0\), independent of \({{{\mathscr {T}}}}_h\) and \(h>0\), such that
where \(p_h\in {\mathscr {DS}}_r(\varOmega )\cap H_0^1(\varOmega )\) approximates (115). Moreover, with \(s=r-1,r\),
where \(({{\mathbf {u}}}_h,p_h)\in {{\mathbf {V}}}_r^s\times W_s\) approximates (117)–(118).
We consider the test problem (113)–(114) defined on the unit square \(\varOmega = [0,1]^2\) with the coefficient \({{\mathbf {a}}}\) being the \(2\times 2\) identity matrix, i.e., we solve the Poisson equation. We use the method of manufactured solutions, taking the exact solution to be \(u(x,y) = \sin (\pi x)\sin (\pi y)\) and the source term is \(f(x,y) = 2\pi ^2\sin (\pi x)\sin (\pi y)\).
Solutions are computed on three different sequences of meshes. The first sequence, \({{{\mathscr {T}}}}_h^1\), is a uniform mesh of \(n^2\) square elements (two sets of parallel edges per element). The second sequence, \({{{\mathscr {T}}}}_h^2\), is a mesh of \(n^2\) trapezoids of base h and one pair of parallel edges of size 0.75h and 1.25h, as proposed in [8]. The third sequence, \({{{\mathscr {T}}}}_h^3\), is chosen so as to have no pair of edges parallel. The first \(4\times 4\) meshes for each sequence are shown in Fig. 5. Finer meshes are constructed by repeating the same pattern over the domain.
Our computer program uses the deal.II library [14]. The integrals must be approximated using quadrature rules, since we have nonpolynomial basis functions. In general, one can use a rule based on squares mapped to the quadrilateral, or one can cut each quadrilateral into two triangles and use a rule suitable for triangles. To accurately approximate the bilinear form, the order of the quadrature rule should be at least 2r. Construction of the finite element basis requires some computation, as described in Sects. 3 and 7. If one uses parallel computing, the time cost for these routines can be scaled nearly perfectly in parallel, since they basically involve only local computations. Moreover, in a time dependent problem, the basis needs to be computed only once. We find that reducing the global number of degrees of freedom in a serendipity space versus a tensor product space, even at the expense of a slightly more expensive basis construction, is worthwhile [2, 47].
9.1 Direct serendipity spaces
We present convergence studies for the fully direct serendipity spaces \({\mathscr {DS}}_r\) using the elements defined in (11) and (14), i.e., the ones that use no mappings. We compare with the two spaces of elements given by mapping the local serendipity spaces \({{{\mathscr {S}}}}_r({\hat{E}})\) and the tensor product spaces \({\mathbb {P}}_{r,r}({\hat{E}})\) to the mesh elements (the latter are simply called the \({\mathbb {P}}_{r,r}\) spaces).
We take the simple choice (16) for \(\lambda _{24}\) and \(\lambda _{13}\). We do not quite use the simple choice (18) for \(R_{13}\) and \(R_{24}\). Instead, we let \(\nu _H=(\nu _2-\nu _4)/|\nu _2-\nu _4|\) and \(\nu _V=(\nu _1-\nu _3)/|\nu _1-\nu _3|\), define \(a_i=\sqrt{1-(\nu _H\cdot \nu _i)^2}\) (\(i=1,3\)) and \(b_i=\sqrt{1-(\nu _V\cdot \nu _i)^2}\) (\(i=2,4\)), and then set
These functions are constant on each opposite pair of edges, but not \(\pm 1\) (this makes no difference to the development presented above).
For an \(n\times n\) mesh, the total number of degrees of freedom for \({\mathbb {P}}_{r,r}\) is \((nr+1)^2 = {{{\mathscr {O}}}}(r^2n^2)\), and for \({{{\mathscr {S}}}}_r\) and \({\mathscr {DS}}_r\) it is
Therefore, the total number of degrees of freedom for a serendipity space is asymptotically about half the size of that for a tensor product space of the same order.
9.1.1 Convergence order versus maximal element diameter h
We report the \(L^2\) and \(H^1\)-seminorm errors and convergence orders for \(r=2,3,4,5\) as h decreases (i.e., as n increases) on mesh sequence \({{{\mathscr {T}}}}_h^1\) in Tables 2 and 3. The direct serendipity space \({\mathscr {DS}}_r\) and the regular serendipity space \({{{\mathscr {S}}}}_r\) coincide on the square mesh \({{{\mathscr {T}}}}_h^1\). All three spaces show an \((r+1)\)-th order convergence in the \(L^2\)-norm and an r-th order convergence in the \(H^1\)-seminorm, as we should expect from theory (see Theorem 5). Our results are fully consistent with the recently reported results in [24] for the standard serendipity elements on rectangles.
Tables 4 and 5 show the errors and orders of convergence for the trapezoidal mesh sequence \({{{\mathscr {T}}}}_h^2\). The tensor product spaces \({\mathbb {P}}_{r,r}\) and \({\mathscr {DS}}_r\) achieve the expected optimal convergence rates: \((r+1)\)-th order in the \(L^2\) norm and r-th order in the \(H^1\)-seminorm. The regular serendipity spaces \({{{\mathscr {S}}}}_r\) have worse than optimal convergence rates in both norms (as was also observed in [8]). The errors and convergence rates for \({\mathbb {P}}_{r,r}\), \({\mathscr {DS}}_r\), and \({{{\mathscr {S}}}}_r\) on mesh sequence \({{{\mathscr {T}}}}_h^3\) are similar to those on \({{{\mathscr {T}}}}_h^2\), so we omit showing them.
Finally, we present the errors and convergence rates for the serendipity spaces \({\mathscr {DS}}_r^{\text {mapped}}\) using elements defined in (49), which have supplements mapped from the reference element. The results for \(r=2,3,4,5\) on mesh \({{{\mathscr {T}}}}_h^2\) are shown in Table 6. One can see optimal convergence rates and errors that compare favorably with those of the fully direct spaces in Tables 4 and 5, although the latter are perhaps slightly better.
In all cases, for a fixed value of n, the errors for \({\mathbb {P}}_{r,r}\) are smaller than that for \({\mathscr {DS}}_r\). One might have expected to see such a result, since \({\mathbb {P}}_{r,r}\) has many more degrees of freedom at its disposal to better approximate the solution. However, the serendipity spaces are advantageous in terms of memory usage and time to solution (see [24]), so if one is given a single fixed mesh for solving the problem, it is more efficient to use the serendipity spaces. It is not uncommon in engineering applications to be given a fixed mesh, such as in petroleum engineering applications where the mesh is determined by the subsurface geology and geostatistical issues.
9.1.2 Convergence order versus the number of DoFs
If the mesh is not viewed as being fixed but can be varied as one wishes, it would be more appropriate to compare the errors with respect to the number of unknowns (i.e., the total number of DoFs). This is done in Fig. 6 for square meshes, where we plot the log (base 10) of the error versus the log of the square root of the number of DoFs, which is a surrogate for h. One can see that the serendipity space is more efficient for \(r=2\), the two spaces are about equally efficient for \(r=3\), and the tensor product space is more efficient for \(r\ge 4\). This behavior was also observed on rectangular meshes in [24] for the standard serendipity spaces. Similar results are seen in Fig. 7 for the trapezoidal meshes \({{{\mathscr {T}}}}_h^2\).
This phenomenon can be explained as follows. Suppose that the solution u is analytic, so that locally on an element E, we may view it as an infinite dimensional polynomial. The \({\mathscr {DS}}_r(E)\) finite elements are able to match only the monomials in u up to order r (see [28]). However, the \({\mathbb {P}}_{r,r}(E)\) finite elements are able to match many more monomials, up to the highest degree monomial \(x^ry^r\). When \(r=2\), \({\mathbb {P}}_{r,r}(E)\) can only match the three extra monomials \(x^2y\), \(xy^2\), and \(x^2y^2\), and no improvement in accuracy over \({\mathscr {DS}}_r(E)\) was seen in our examples. However, as r increases, \({\mathbb {P}}_{r,r}(E)\) can match on the order of \(\tfrac{1}{2}r^2\) more monomials than \({\mathscr {DS}}_r(E)\), and some improvement in accuracy was seen.
True solution \(u(x,y) = x^5y^k\). Log scale \(L^2\)-norm and \(H^1\)-seminorm errors versus the number of DoFs for tensor product \({\mathbb {P}}_{4,4}\) (blue and yellow dotted lines, squares) and \({\mathscr {DS}}_4\) (red and purple solid lines, circles) on trapezoidal meshes \({{{\mathscr {T}}}}_h^2\) (color figure online)
To test this explanation, we changed the manufactured true solution to be a single monomial \(u(x,y) = x^5y^k\), with \(k=0,1,2,3,4,5\), and tested the case \(r=4\). Simple polynomials should better approximate the case \(k=0\), while tensor product approximations should handle the “diagonal” case \(k=5\) better. This is indeed the case, as shown in Fig. 8. The more advantageous choice of finite element changes from \({\mathscr {DS}}_r\) to \({\mathbb {P}}_{r,r}\) as k increases, with fairly equivalent results seen for \(k=2\).
The next series of tests considers the manufactured true solution \(u(x,y)=\log (x+ky+1)\), which is analytic with all orders of monomials in its Taylor expansion. As k increases, the relative strength of the “diagonal” monomials decrease, and so we should expect that \({\mathscr {DS}}_r\) performs better. This is the case, as shown in Fig. 9, where we test \(r=2,3,4,5\), \(k=1,2,4\), and use a mesh generated by a random perturbation of the vertices of a rectangular mesh. We see that \({\mathbb {P}}_{r,r}\) is more efficient when \(k=1\), \({\mathscr {DS}}_r\) is more efficient when \(k=4\), and they are fairly equivalent when \(k=2\). Similar results are seen if one uses the trapezoidal mesh \({{{\mathscr {T}}}}_h^2\), and other analytic functions such as square root, exponential, and trigonometric functions.
True solution \(u(x,y) = \big [1 + 0.1\sin \big (\pi \cos (\pi x)\cos (3\pi y/2)\big )\big ](1-x)\), akin to the pressure in a linear flood shown on the left. Log scale \(L^2\)-norm (center) and \(H^1\)-seminorm (right) errors versus the number of DoFs for tensor product \({\mathbb {P}}_{r,r}\) and \({\mathscr {DS}}_r\) on trapezoidal meshes \({{{\mathscr {T}}}}_h^2\), \(r=2,3,4,5\)
The previous test motivates us to consider a typical groundwater or petroleum engineering problem related to a linear flood. In such a problem, a pressure difference is imposed from left to right. In a homogeneous medium, the pressure field would vary linearly, but in a heterogeneous porous medium, the pressure is perturbed from a clean linear variation. To simulate such a flood, we imposed the manufactured true solution \(u(x,y)=\big [1 + 0.1\sin \big (\pi \cos (\pi x)\cos (3\pi y/2)\big )\big ](1-x)\). The convergence of the error versus the number of DoFs is shown in Fig. 10. In this test, \({\mathscr {DS}}_r\) outperforms \({\mathbb {P}}_{r,r}\) for all \(r=2,3,4,5\).
We conclude that if one is given a fixed number of DoFs (rather than a fixed mesh), it is difficult to predict whether it is more efficient in terms of accuracy to use \({\mathbb {P}}_{r,r}\) or \({\mathscr {DS}}_r\). However, the \({\mathbb {P}}_{r,r}\) elements do not lead to mixed finite elements with the appropriate order of convergence [1, 8]. So even though there are cases where one might prefer to use \({\mathbb {P}}_{r,r}\), it is nevertheless critical to understand the \({\mathscr {DS}}_r\) finite elements, since they are needed to define the direct mixed finite elements in the de Rham sequence (84). We give numerical examples of these spaces next.
9.2 Fully direct mixed finite elements on quadrilaterals
We verify the convergence rates for the new fully direct mixed finite elements \({{\mathbf {V}}}_r^s\times W_s\) derived in Sect. 7.2. These are implemented without the use of any mapping from the reference element. We take the simple choices (16) and (18), although the choice (123) provides similar results. We apply the hybrid form of the mixed finite element method (Sect. 7.4). The errors and the orders of convergence when \(r=1,2\) on mesh \({{{\mathscr {T}}}}_h^2\) are presented in Table 7. Again, results are similar on \({{{\mathscr {T}}}}_h^3\) meshes. As the theory predicts, the scalar p, the vector \({{\mathbf {u}}}\), and the divergence \(\nabla \cdot {{\mathbf {u}}}\) obtain order of approximation \(s+1\), \(r+1\), and \(s+1\), respectively, for the reduced (\(s=r-1\)) and full (\(s=r\)) \(H(\text {div})\)-approximation spaces.
Our numerical test agrees with that taken in [1], where results for the full and reduced AC spaces and the mapped BDM spaces appear. Results for our fully direct mixed spaces agree very closely with the results for the AC spaces, and these far exceed the performance of the mapped BDM spaces.
10 Summary and conclusions
We defined finite elements on a nondegenerate, convex quadrilateral E of minimal local dimension (i.e., with a minimal number of DoFs) using a different construction technique than what has been used by other authors. Our approach allows us to define entire families of finite elements, one for each index of approximation r. Moreover, the choices made in the construction give rise to different families of finite elements. To the best of our knowledge, they are all novel, except in three instances. The classic serendipity spaces on rectangles are recovered by our techniques as noted in Remark 1 (and then also the mixed elements that these give rise to, i.e., to the BDM family of mixed elements on rectangles). The two families of AC mixed finite elements are known [1], and these can be recovered by our construction as discussed in Sect. 7.1. It is also possible that for certain families, and then only for low order finite elements (with \(r\le 2\)), that our construction leads to known finite elements. It is difficult to determine what choices we would need to make in the construction of our families of finite elements that would reproduce these known elements, and we did not attempt to do that here.
We defined a wide variety of direct serendipity elements on a nondegenerate, convex quadrilateral E and proved their convergence properties (Theorems 1, 2, and 3 ). They have the form
The supplemental space \({\mathbb {S}}_r^{\mathscr {DS}}(E)\) has dimension 2 when \(r\ge 2\) and 1 when \(r=1\). It can be defined by a choice of four functions. Referring to Fig. 1, the linear functions \(\lambda _{24}\) and \(\lambda _{13}\) are arbitrary except that the zero line of \(\lambda _{24}\) should intersect the edges \(e_2\) and \(e_4\), and \(\lambda _{13}\) should intersect the edges \(e_1\) and \(e_3\). The (most likely nonlinear) functions \(R_{13}\) and \(R_{24}\) should be continuously differentiable and reduce to \(-1\) (or any negative constants) on \(e_1\) and \(e_2\), respectively, and 1 (or any positive constants) on \(e_3\) and \(e_4\), respectively. For example, one can take the simple choices
The case \(r=1\) is special, but when \(r\ge 2\), the fully direct supplemental space is then
A supplemental space can also be defined using the bilinear map between \({\hat{E}}=[-1,1]^2\) and E as
We defined a wide variety of direct mixed elements on E and proved their convergence properties (Theorem 4 and Lemma 2). The de Rham theory is useful in this regard, and the elements take the form
for reduced and full \(H(\text {div})\)-approximation spaces, respectively, where
If (127) is used, one obtains the AC spaces [1] (these are are not fully direct since the supplemental functions are mapped from the reference element). Otherwise, the choices we make in the construction lead to different families of finite elements, and they are the first families of fully direct mixed spaces with a minimal number of DoFs to be defined on quadrilaterals.
The direct serendipity and mixed elements can be merged to create \(H^1(\varOmega )\) and \(H(\text {div};\varOmega )\) conforming spaces, respectively, on a mesh \({{{\mathscr {T}}}}_h\) of nondegenerate, convex quadrilaterals. If the meshes are shape regular as \(h\rightarrow 0\) and the four functions in (125) are chosen to be continuously differentiable with respect to the vertices of the element, then the spaces have both optimal approximation properties and minimal local dimension.
Numerical results were presented to illustrate their performance. All of the spaces attained the theoretical optimal convergence rates. On a fixed mesh, the direct serendipity spaces are more efficient in terms of accuracy than finite elements based on mapping tensor product polynomials to quadrilaterals. When comparing the total number of DoFs versus accuracy, it is not clear whether the finer mesh direct serendipity or coarser mesh tensor product spaces will be more efficient. In any case, the direct serendipity spaces are needed to define the direct mixed elements.
As a final result, we make a simple observation. The de Rham complex (64) in \({\mathbb {R}}^2\) is sometimes described as

where the curl of a vector function \(\pmb \psi =\big (\psi _1,\psi _2\big )\) is the scalar \(\text {curl}\,\pmb \psi ({{\mathbf {x}}}) = \dfrac{\partial \psi _1}{\partial x_2} - \dfrac{\partial \psi _2}{\partial x_1}\). This form of the complex is just a rotation of (64). It gives us reduced and full direct \(H(\text {curl})\)-approximating elements
where
These spaces can be arranged to form an exact sequence that discretizes the de Rham complex, namely

for any variant of our new direct serendipity spaces. We can merge these elements globally by matching tangential components across the edges.
We close by mentioning two open problems relating to this work. First, we plan in future work to extend the ideas presented in this paper to define families of direct serendipity and mixed finite elements on convex polygons [4]. We expect that a similar construction can be given, although the number of supplemental functions will depend on the number of sides N of the polygon \(E_N\) and the index r. Our construction of serendipity elements for \(N=4\) was to define them for \(r\ge 2\) and then define the elements for \(r=1\) using the \(r=2\) elements. We expect that a similar development can be used for polygons.
A second open problem is to determine how to construct general families of direct finite elements on cuboidal hexahedra (and perhaps even on convex polytopes), perhaps by generalizing the work [3] on mixed elements. The cubical case shows that the supplemental functions of the serendipity elements are used to separate DoFs on both faces and edges. This mixing of concerns makes the construction on hexahedra a bit more involved. Moreover, for \(H^1\) conformity, the traces of the elements on the faces cannot reduce to just polynomials. If the scalar serendipity spaces can be defined, one cannot discover the mixed finite elements immediately. The relevant de Rham sequence is

and its discrete analogue is the exact sequence

where the space of vector-valued functions \({{\mathbf {X}}}\) must be determined.
References
Arbogast, T., Correa, M.R.: Two families of H(div) mixed finite elements on quadrilaterals of minimal dimension. SIAM J. Numer. Anal. 54, 3332–3356 (2016). https://doi.org/10.1137/15M1013705
Arbogast, T., Tao, Z.: Direct serendipity finite elements on convex quadrilaterals. Tech. Rep. ICES REPORT 17-28, Institute for Computational Engineering and Sciences, Univ. of Texas at Austin, October (2017)
Arbogast, T., Tao, Z.: Construction of H(div)-conforming mixed finite elements on cuboidal hexahedra. Numer. Math. 142, 1–32 (2019). https://doi.org/10.1007/s00211-018-0998-7
Arbogast, T., Wang, C.: Direct serendipity and mixed finite elements on convex polygons (in preparation) (2022)
Arnold, D.N.: Spaces of finite element differential forms. In: Analysis and Numerics of Partial Differential Equations, pp. 117–140. Springer (2013)
Arnold, D.N., Awanou, G.: The serendipity family of finite elements. Found. Comput. Math. 11, 337–344 (2011)
Arnold, D.N., Awanou, G.: Finite element differential forms on cubical meshes. Math. Comp. 83, 1551–1570 (2014)
Arnold, D.N., Boffi, D., Falk, R.S.: Approximation by quadrilateral finite elements. Math. Comp. 71, 909–922 (2002)
Arnold, D.N., Boffi, D., Falk, R.S.: Quadrilateral H(div) finite elements. SIAM. J. Numer. Anal. 42, 2429–2451 (2005)
Arnold, D.N., Brezzi, F.: Mixed and nonconforming finite element methods: Implementation, postprocessing and error estimates. RAIRO Modél. Math. Anal. Numér. 19, 7–32 (1985)
Arnold, D.N., Falk, R.S., Winther, R.: Finite element exterior calculus, homological techniques, and applications. Acta Numer. 15, 1–155 (2006)
Arnold, D.N., Falk, R.S., Winther, R.: Finite element exterior calculus: from Hodge theory to numerical stability. Bull. Am. Math. Soc. (N.S.) 47, 281–354 (2010)
Arnold, D.N., Logg, A.: Periodic table of the finite elements. SIAM News 47 (2014)
Bangerth, W., Davydov, D., Heister, T., Heltai, L., Kanschat, G., Kronbichler, M., Maier, M., Turcksin, B., Wells, D.: The deal.II library, version 8.4. J. Numer. Math. 24, 135–141 (2016)
Bochev, P.B., Ridzal, D.: Rehabilitation of the lowest-order Raviart-Thomas element on quadrilateral grids. SIAM J. Numer. Anal. 47, 487–507 (2008)
Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications, No. 44 in Springer Series in Computational Mathematics. Springer, Heidelberg (2013)
Boffi, D., Kikuchi, F., Schöberl, J.: Edge element computation of Maxwell’s eigenvalues on general quadrilateral meshes. Math. Models Methods Appl. Sci. M3AS 16, 265–273 (2006)
Bramble, J.H., Hilbert, S.R.: Estimation of linear functionals on Sobolev spaces with applications to Fourier transforms and spline interpolation. SIAM J. Numer. Anal. 7, 112–124 (1970)
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods. Springer, New York (1994)
Brezzi, F., Douglas, J., Jr., Marini, L.D.: Two families of mixed elements for second order elliptic problems. Numer. Math. 47, 217–235 (1985)
Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods. Springer, New York (1991)
Chen, W., Wang, Y.: Minimal degree H(curl) and H(div) conforming finite elements on polytopal meshes. Math. Comp. 86, 2053–2087 (2017)
Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. North-Holland, Amsterdam (1978)
Crum, J., Cheng, C., Ham, D.A., Mitchell, L., Kirby, R.C., Levine, J.A., Gillette, A.: Bringing trimmed serendipity methods to computational practice in firedrake. Tech. Rep. arXiv:2104.12986 [math.NA] (2021)
Douglas, J., Jr., Roberts, J.E.: Global estimates for mixed methods for second order elliptic equations. Math. Comp. 44, 39–52 (1985)
Duan, H.-Y., Liang, G.-P.: Nonconforming elements in least-squares mixed finite element methods. Math. Comp. 73, 1–18 (2004)
Dupont, T., Hoffman, J., Johnson, C., Kirby, R.C., Larson, M.G., Logg, A., Scott, L.R.: The fenics project. Tech. Rep. 2003-21, Chalmers Finite Element Center, Chalmers University of Technology, Goteborg, Sweden (2003)
Dupont, T., Scott, L.R.: Polynomial approximation of functions in Sobolev space. Math. Comp. 34, 441–463 (1980)
Floater, M.S.: Generalized barycentric coordinates and applications. Acta Numer. 161–214 (2015)
Floater, M.S., Hormann, K., Kós, G.: A general construction of barycentric coordinates over convex polygons. Adv. Comput. Math. 24, 311–331 (2006)
Floater, M.S., Lai, M.-J.: Polygonal spline spaces and the numerical solution of the Poisson equation. SIAM J. Numer. Anal. 54, 797–824 (2016)
Gillette, A., Kloefkorn, T.: Trimmed serendipity finite element differential forms. Math. Comp. 88, 583–606 (2019)
Gillette, A., Rand, A., Bajaj, C.: Error estimates for generalized barycentric interpolation. Adv. Comput. Math. 37, 417–439 (2012)
Girault, V., Raviart, P.A.: Finite Element Methods for Navier–Stokes Equations: Theory and Algorithms. Springer, Berlin (1986)
Hibbitt, I.: Karlsson& Sorensen, ABAQUS/Standard User’s Manual (2001)
Kaliakin, V.N.: Introduction to Approximate Solution Techniques, Numerical Modeling, and Finite Element Methods. CRC Press, Boca Raton (2001)
Kwak, D.Y., Pyo, H.C.: Mixed finite element methods for general quadrilateral grids. Appl. Math. Comput. 217, 6556–6565 (2011)
Lee, N.-S., Bathe, K.-J.: Effects of element distortions on the performance of isoparametric elements. Intl. J. Numer. Meth. Eng. 36, 3553–3576 (1993)
Nédélec, J.C.: Mixed finite elements in \({ R}^3\). Numer. Math. 35, 315–341 (1980)
Rand, A., Gillette, A., Bajaj, C.: Quadratic serendipity finite elements on polygons using generalized barycentric coordinates. Math. Comp. 83, 2691–2716 (2014)
Raviart, R.A., Thomas, J.M.: A mixed finite element method for 2nd order elliptic problems. In: Galligani, I., Magenes, E. (eds.) Mathematical Aspects of Finite Element Methods, no. 606 in Lecture Notes in Mathematics, pp. 292–315. Springer, New York (1977)
Scott, L.R., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comp. 54, 483–493 (1990)
Shen, J.: Mixed Finite Element Methods: Analysis and Computational Aspects. Ph.D. thesis, University of Wyoming (1992)
Shen, J.: Mixed finite element methods on distorted rectangular grids. Tech. Rep. ISC-94-13-MATH, Institute for Scientific Computation, Texas A&M University, College Station, Texas (1994)
Siqueira, D., Devloo, P.R.B., Gomes, S.M.: A new procedure for the construction of hierarchical high order hdiv and hcurl finite element spaces. J. Comput. Appl. Math. 240, 204–214 (2013)
Strang, G., Fix, G.J.: An Analysis of the Finite Element Method. Series in Automatic Computation, Prentice-Hall, Englewood Cliffs (1973)
Tao, Z.: Numerical Analysis of Multiphase flows in Porous Media on Non-Rectangular Geometry. Ph.D. thesis, University of Texas at Austin (2017)
Thomas, J.M.: Sur l’analyse numerique des methodes d’elements finis hybrides et mixtes. Ph.D. thesis, Sciences Mathematiques, à l’Universite Pierre et Marie Curie (1977)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the U.S. National Science Foundation under Grants DMS-1418752, DMS-1720349, and DMS-2111159.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arbogast, T., Tao, Z. & Wang, C. Direct serendipity and mixed finite elements on convex quadrilaterals. Numer. Math. 150, 929–974 (2022). https://doi.org/10.1007/s00211-022-01274-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-022-01274-3