Direct serendipity and mixed finite elements on convex polygons

Abstract

We construct new families of direct serendipity and direct mixed finite elements on general planar, strictly convex polygons that are H¹ and H(div) conforming, respectively, and possess optimal order of accuracy for any order. They have a minimal number of degrees of freedom subject to the conformity and accuracy constraints. The name arises because the shape functions are defined directly on the physical elements, i.e., without using a mapping from a reference element. The finite element shape functions are defined to be the full spaces of scalar or vector polynomials plus a space of supplemental functions. The direct serendipity elements are the precursors of the direct mixed elements in a de Rham complex. The convergence properties of the finite elements are shown under a regularity assumption on the shapes of the polygons in the mesh, as well as some mild restrictions on the choices one can make in the construction of the supplemental functions. Numerical experiments on various meshes exhibit the performance of these new families of finite elements.

1 Introduction

Serendipity finite elements defined on a rectangle $\hat {E}$, denoted as $\mathcal {S}_{r}(\hat {E})$, r ≥ 1, are well known to be H¹-conforming and approximate to order r + 1 with a minimal number of degrees of freedom (DoFs). The finite elements $\mathcal {S}_{r+1}(\hat E)$ are related to Brezzi-Douglas-Marini [1] mixed finite elements $\textrm {BDM}_{r}(\hat {E})$, r ≥ 1, through a de Rham complex [2]. $\textrm {BDM}_{r}(\hat {E})$ is H(div)-conforming and has optimal order approximation properties with a minimal number of DoFs. Arnold and Awanou [3, 4] have given a definition, construction, and geometric decomposition of $\mathcal { S}_{r}(\hat {E})$ and $\textrm {BDM}_{r}(\hat {E})$ of any approximation order on cubical meshes in any dimension. However, the elements lose optimal order accuracy when mapped to a quadrilateral E.

Recently, the current authors and Z. Tao [5] constructed serendipity spaces directly on quadrilaterals of any approximation order r + 1 ≥ 2 without using a mapping from a reference element. The resulting new family of spaces were called direct serendipity finite elements and denoted $\mathcal {D}\mathcal {S}_{r}(E)$, r ≥ 1. The de Rham complex then yields a strategy to construct H(div) conforming direct mixed finite elements, denoted $\mathbf {V}_{r}^{r-1}(E)$ and ${\mathbf {V}_{r}^{r}}(E)$, giving optimal order reduced and full H(div)-approximation with a minimal number of DoFs. The direct serendipity finite elements take the form

$$ {\mathcal{D}\mathcal{S}}_{r}(E) = \mathbb P_{r}(E)\oplus\mathbb S_{r}^{{\mathcal{D}\mathcal{S}}}(E), $$

(1)

where $\mathbb P_{r}(E)$ is the space of polynomials on E up to degree r, and $\mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E)$ consists of supplemental functions. The direct mixed elements take a similar form. In this paper, we construct a new family of direct serendipity and direct mixed finite elements for a general planar, strictly convex polygon, discuss their approximation properties, and test their performance by numerical experiments.

Other approaches to construct serendipity and mixed finite elements with a minimal number of degrees of freedom have appeared in the literature. In [6], Rand, Gillette, and Bajaj used products of linear generalized barycentric coordinates to construct serendipity finite elements on quadrilaterals. Based on this work, Sukumar [7] constructed quadratic maximum-entropy serendipity shape functions. These two works only have elements with quadratic order of accuracy, and it appears to be technically difficult to develop higher order accurate serendipity finite elements in this way. However, their construction works for general polygonal elements, including non-convex ones. For mixed spaces, Chen and Wang [8] constructed minimal degree H(curl) and H(div) conforming finite elements of linear accuracy based on generalized barycentric coordinates and the Whitney forms. Floater and Lai [9] generalized this idea to construct finite element spaces for a general order of accuracy r. However, their construction asks for more DoFs than the minimum, since $\frac {1}{2}(r-1)(r-2)$ interior DoFs are always required for any polygon. Another methodology, the serendipity virtual element method, was introduced in [10] to deal with general polygonal elements, including non-convex and very distorted elements. The method works for any order of accuracy r, but it uses even more interior DoFs, $\frac {1}{2}r(r-1)$.

In the rest of this paper, we generalize the construction in [5] to a general strictly convex polygon E_N with N vertices. Our construction does not extend to non strictly convex polygons. We begin by introducing some notation in Section 2. In Section 3 we define higher order direct serendipity elements (r ≥ N − 2) and show their unisolvence and conformity by the construction of nodal basis functions. In Section 4, lower order direct serendipity elements (r < N − 2) are constructed within a higher order direct serendipity space. We discuss the approximation properties and convergence rates of the space $\mathcal {D}\mathcal {S}_{r}$ over the whole domain Ω in Section 5. In Sections 6 and 7, we construct direct mixed finite elements from the direct serendipity elements and the de Rham complex, and then discuss the convergence theory. In Section 8, we provide some numerical results that test the performance of our direct spaces on various meshes. Finally, the results are summarized in Section 9.

2 Some notation

Let $\mathbb P_{r}(\omega )$ denote the space of polynomials of degree up to r on $\omega \subset \mathbb {R}^{d}$, where d = 0 (a point), 1, or 2. Recall that

$$ \dim\mathbb P_{r}(\mathbb{R}^{d}) = \left( \begin{array}{cccc}r+d\\d \end{array}\right) = \frac{(r+d)!}{r! d!}. $$

(2)

Let $\tilde {\mathbb {P}}_{r}(\omega )$ denote the space of homogeneous polynomials of degree r on ω. Then

$$ \dim\tilde{\mathbb{P}}_{r}(\mathbb{R}^{d}) = \left( \begin{array}{cccc}r+d-1\\d-1 \end{array}\right) = \frac{(r+d-1)!}{r! (d-1)!},\quad d\ge1. $$

(3)

When r < 0, we interpret $\mathbb P_{r}$ as the empty set with dimension zero.

Let the element $E=E_{N}\subset \mathbb {R}^{2}$ be a closed, nondegenerate, strictly convex polygon with N ≥ 3 edges. By nondegenerate, we mean that E_N does not degenerate to any polygon with fewer edges, a line segment, or a point. We choose to identify the edges and vertices of E_N adjacently in the counterclockwise direction, as depicted in Fig. 1 (throughout the paper, we interpret indices modulo N). Let the edges of E_N be denoted e_i, i = 1,2,…,N, and the vertices be x_v,i = e_i ∩ e_i+ 1. Let ν_i denote the unit outer normal to edge e_i, and let τ_i denote the unit tangent vector of e_i oriented in the counterclockwise direction, for i = 1,2,…,N.

Fig. 1

A pentagon E₅, with edges e_i, outer unit normals ν_i, tangents τ_i, and vertices x_v,i

Let the overall domain ${\Omega }\subset \mathbb {R}^{2}$ be a connected, polygonal open set with a Lipschitz boundary (i.e., Ω has no slits). Let $\mathcal {T}_{h}$ be a conforming finite element partition or mesh of $\bar {\Omega }$ into elements (closed, nondegenerate, convex polygons) of maximal diameter h > 0. These elements need not have the same number of edges.

For any two distinct points y₁ and y₂, let ${\mathscr{L}}{[\mathbf {y}_{1},\mathbf {y}_{2}]}$ be the line passing through y₁ and y₂, and take ν[y₁,y₂] to be the unit vector normal to this line interpreted as going from y₁ to y₂ in the clockwise direction (i.e., pointing to the right). Then we define a linear polynomial giving the signed distance of x to ${\mathscr{L}}{[\mathbf {y}_{1},\mathbf {y}_{2}]}$ as

$$ \lambda{[\mathbf{y}_{1},\mathbf{y}_{2}]}(\mathbf{x})= -(\mathbf{x}-\mathbf{y}_{2})\cdot\nu{[\mathbf{y}_{1},\mathbf{y}_{2}]}. $$

(4)

To simplify the notation for linear functions that will be used throughout the paper, let ${\mathscr{L}}_{i}={\mathscr{L}}[\mathbf {x}_{v,i-1},\mathbf {x}_{v,i}]$ be the line containing edge e_i and let λ_i(x) give the distance of $\mathbf {x}\in \mathbb {R}^{2}$ to edge e_i opposite the normal direction, i.e.,

$$ \lambda_{i}(\mathbf{x}) = \lambda[\mathbf{x}_{v,i-1},\mathbf{x}_{v,i}](\mathbf{x})= - (\mathbf{x}-\mathbf{x}_{v,i})\cdot\nu_{i}, \quad i=1,2,\ldots,N. $$

(5)

These functions are strictly positive in the interior of E_N, and each vanishes on the edge which defines it.

Recall Ciarlet’s definition [11] of a finite element.

Definition 2.1 (Ciarlet 1978)

Let

• 1. $E\subset \mathbb {R}^{d}$ be a bounded closed set with nonempty interior and a Lipschitz continuous boundary,

• 2. $\mathcal {P}$ be a finite-dimensional space of functions on E, and

• 3. $\mathcal {N} = \{ N_{1}, N_{2},\ldots , N_{\dim \mathcal {P}} \}$ be a basis for $\mathcal {P}^{\prime }$.

Then $(E, \mathcal {P}, \mathcal {N})$ is called a finite element.

3 Direct serendipity elements when r ≥ N − 2

We construct direct serendipity elements for r ≥ N − 2 in this section. The construction for 1 ≤ r < N − 2 is different, and it is discussed in Section 4.

To obtain both that $\mathbb P_{r}(E)\subset {\mathcal {D}\mathcal {S}}_{r}(E)$ and that the shape functions on adjoining elements can be merged together continuously, we consider the lower dimensional geometric objects within E. As shown in Table 1, the minimal number of DoFs associated to each lower dimensional object must correspond to the dimension of the polynomials that restrict to that object. A polygon with N sides has N vertices, N edges, and one cell of dimension 0, 1, and 2, respectively. Each vertex requires $\dim \mathbb P_{r}(\mathbb {R}^{0})=1$ DoF, each edge requires $\dim \mathbb P_{r-2}(\mathbb {R})=r-1$ DoFs (interior to the edge), and each cell requires $\dim \mathbb P_{r-N}(\mathbb {R}^{2})=\left (\begin {array}{cccc}r-N+2\\2 \end {array}\right )=\frac 12(r-N+2)(r-N+1)$ DoFs (interior to the cell). There are cell DoFs only if r ≥ N, but the formula works for r ≥ N − 2. The total number of DoFs is then D_N,r, where

$$ D_{N,r} = N + N(r-1) + \frac12(r-N+2)(r-N+1) = \dim\mathbb P_{r}(E) + \frac12N(N-3), $$

(6)

and so to define ${\mathcal {D}\mathcal {S}}_{r}(E)$, we will supplement $\mathbb P_{r}(E)\subset {\mathcal {D}\mathcal {S}}_{r}(E)$ with the span of $\frac 12N(N-3)$ linearly independent functions. The quantity $\frac 12N(N-3)$ can be interpreted as the number of pairs of edges that are not adjacent.

Table 1 Geometric decomposition and number of degrees of freedom (DoFs) associated to each geometric object of a polygon E_N for a serendipity element of index r ≥ N − 2 ≥ 1

3.1 Shape functions

To define the supplemental basis functions, we have two series of choices for each i,j such that 1 ≤ i < j ≤ N and 2 ≤ j − i ≤ N − 2 (i.e., i and j are nonadjacent). First, as shown in Fig. 2, one must choose two distinct points $\mathbf {x}^{i,j}_{1}\in {\mathscr{L}}_{i}$ and $\mathbf {x}^{i,j}_{2}\in {\mathscr{L}}_{j}$ that avoid the intersection point $\mathbf {x}_{i,j}={\mathscr{L}}_{i}\cap {\mathscr{L}}_{j}$, if it exists. Then let

$$ \lambda_{i,j}(\mathbf{x}) = \lambda[\mathbf{x}^{i,j}_{1}, \mathbf{x}^{i,j}_{2}](\mathbf{x}) = -(\mathbf{x} - \mathbf{x}^{i,j}_{2})\cdot\nu_{i,j}, \quad\nu_{i,j}=\nu[\mathbf{x}^{i,j}_{1}, \mathbf{x}^{i,j}_{2}], $$

(7)

be the linear function associated to the line ${\mathscr{L}}_{i,j}={\mathscr{L}}[\mathbf {x}^{i,j}_{1},\mathbf {x}^{i,j}_{2}]$. Simple choices are to take the midpoints of the edges, or

$$ \lambda_{i,j}^{\text{simple}} = \frac{\lambda{[\mathbf{x}_{v,j},\mathbf{x}_{v,i-1}]} - \lambda{[\mathbf{x}_{v,i},\mathbf{x}_{v,j-1}]}} {\|\nu{[\mathbf{x}_{v,j},\mathbf{x}_{v,i-1}]} - \nu{[\mathbf{x}_{v,i},\mathbf{x}_{v,j-1}]}\|}, $$

(8)

although the normalization is not strictly necessary.

Fig. 2

Illustration on E₅ of the zero line ${\mathscr{L}}_{1,4}$ of $\lambda _{1,4}(\mathbf {x})=-(\mathbf {x}-\mathbf {x}_{2}^{1,4})\cdot \nu _{1,4}$ and the intersection point $\mathbf {x}_{1,4}={\mathscr{L}}_{1}\cap {\mathscr{L}}_{4}$, if it exists

Second, one must choose the functions R_i,j to satisfy the properties

$$ R_{i,j}(\mathbf{x})\vert_{e_{i}} = -1,\quad R_{i,j}(\mathbf{x})\vert_{e_{j}} = 1. $$

(9)

These are ± 1 on e_i and e_j, but arbitrary on the other edges. For example, take the simple rational functions

$$ R_{i,j}(\mathbf{x}) = R_{i,j}^{\text{simple}}(\mathbf{x}) = \frac{\lambda_{i}(\mathbf{x}) - \lambda_{j}(\mathbf{x})}{\lambda_{i}(\mathbf{x}) + \lambda_{j}(\mathbf{x})} $$

(10)

(note that the denominators do not vanish on E_N, since e_i and e_j are not adjacent).

The supplemental basis functions are then constructed as

$$ \phi_{s,i,j} = \Big({\prod}_{k\neq i,j}\lambda_{k}\Big)\lambda_{i,j}^{r-N+2}R_{i,j}, $$

(11)

and the supplemental space is defined to be

$$ \begin{array}{@{}rcl@{}} \mathbb S_{r}^{{\mathcal{D}\mathcal{S}}}(E_{N}) &=& \mathbb S_{r}^{{\mathcal{D}\mathcal{S}}}(E_{N};\lambda_{i,j},R_{i,j})\\ &=& \text{span}\big\{\phi_{s,i,j} : 1\le i<j\le N,\ 2\le j-i\le N-2\big\}. \end{array} $$

(12)

The λ_i,j’s are not needed when r = N − 2, and $\mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E_{N})$ is empty when N = 3. The full space $\mathcal {P}$ in Definition 2.1 is

$$ {\mathcal{D}\mathcal{S}}_{r}(E_{N}) = \mathbb P_{r}(E_{N})\oplus\mathbb S_{r}^{{\mathcal{D}\mathcal{S}}}(E_{N}). $$

(13)

Each of our earlier choices gives rise to a distinct family of direct serendipity elements of index r ≥ N − 2 ≥ 1.

3.2 Degrees of freedom

DoFs could be defined in various ways. DoFs based on orthogonal polynomials are generally more numerically stable. However, to ease the exposition and proof of unisolvence, we simply use DoF functionals given by evaluation at (nodal) points.

As depicted in Fig. 3, for vertex DoFs, the nodal points are exactly the vertices x_v,i, of E_N, where i = 1,2,…,N. For edge DoFs, we simply fix nodal points so that they, plus the two vertices, are equally distributed on each edge. There are r − 1 nodal points on the interior of each edge, which can be denoted x_e,i,j, j = 1,2,…,r − 1, for nodal points that lie on edge e_i, i = 1,2,…,N, ordered in the counterclockwise direction. The interior cell DoFs can be set, for example, on points of a triangle T strictly inside E, where the set of nodal points is the same as the nodes of the Lagrange element of order r − N on the triangle T. We denote the interior nodal points as x_E,i, $i=1,2,\ldots ,\frac 12(r-N+2)(r-N+1)$.

Fig. 3

The nodal points for the DoFs of a direct serendipity finite element E₅, for small r

The total number of nodal points is indeed D_N,r. If $\{x_{1}^{\text {nodal}},x_{2}^{\text {nodal}},\ldots ,x_{D_{N,r}}^{\text {nodal}}\}$ is the set of all nodal points, then the set of DOFs ($\mathcal {N}$ in Definition 2.1) is

$$ \mathcal{N} = \{N_{i} : N_{i}(\phi) = \phi(\mathbf{x}^{\text{node}}_{i})\text{ for all }\phi(\mathbf{x}),\ i=1,2,\ldots,D_{N,r}\}. $$

(14)

3.3 Unisolvence and conformity of the finite element

In this section we will show that we have a properly defined finite element.

Theorem 3.1

The finite element ${\mathcal {D}\mathcal {S}}_{r}(E_{N}) = \mathbb P_{r}(E_{N})\oplus \mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E_{N})$, for $\mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E_{N})$ given by (12), with nodal DoFs (14) is well defined (i.e., unisolvent) when r ≥ N − 2. Moreover, a nodal basis is given by the functions defined below in (20), (23), and (26).

To prove the theorem, we will explicitly construct a basis of shape functions φ_i for $\mathcal {P}$ dual to $\mathcal {N}$. Such shape functions are called nodal basis functions. For a nodal point $\mathbf {x}^{\text {node}}_{j}$, they have the property that $N_{j}(\varphi _{i})=\varphi _{i}(\mathbf {x}^{\text {node}}_{j}) = \delta _{ij}$, the Kronecker delta. The unisolvence property (i.e., that $\mathcal {N}$ is a basis for the dual space) is then immediate. Moreover, it follows from the construction that we obtain global H¹ conforming elements by just matching vertex and edge DoFs on the boundaries of the elements; that is, local basis functions merge together continuously to give a global nodal basis for ${\mathcal {D}\mathcal {S}}_{r}={\mathcal {D}\mathcal {S}}_{r}({\Omega })\subset H^{1}({\Omega })$. Our construction directly extends that given in [5] for the case N = 4.

Before beginning the construction, it is convenient to define

$$ \mathcal{R}_{i,j}(\mathbf{x}) = \tfrac12\big(1 - R_{i,j}(\mathbf{x})\big),\quad \mathcal{R}_{j,i}(\mathbf{x}) = \tfrac12\big(1 + R_{i,j}(\mathbf{x})\big), $$

(15)

so that $\mathcal {R}_{k,\ell }$ is 1 on edge e_k, 0 on e_ℓ, and arbitrary on the other edges. Let us now set λ_j,i = λ_i,j when i < j, and define, for any 1 ≤ k,ℓ ≤ N, 2 ≤|k − ℓ|≤ N − 2,

$$ \phi_{k,\ell}(\mathbf{x}) = \Big({\prod}_{m\neq k,\ell}\lambda_{m}\Big)\lambda_{k,\ell}^{r-N+2}\mathcal{R}_{k,\ell} \quad\in{\mathcal{D}\mathcal{S}}_{r}(E_{N}). $$

(16)

These lie in $\mathbb P_{r}(E)\oplus \mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E)$ and satisfy

$$ \phi_{k,\ell}(\mathbf{x})=\begin{cases} \ \ \ \ \ \ \ \ \ \ \ \quad \quad 0, &\mathbf{x} \in e_{m},\ m \ne k, \\ \displaystyle\Big({\prod}_{m\neq k,\ell}\lambda_{m}\Big)\lambda_{k,\ell}^{r-N+2}\in \mathbb P_{r}(e_{k}), &\mathbf{x}\in e_{k}. \end{cases} $$

(17)

Moreover,

$$ {\mathcal{D}\mathcal{S}}_{r}(E_{N}) = \mathbb P_{r}(E_{N}) + \text{span}\{\phi_{k,\ell}:1 \le k,\ell \le N,\ 2\le \vert k-\ell\vert \le N-2\}. $$

(18)

3.3.1 Interior cell nodal basis functions

For the element E_N, we have interior shape functions only when r ≥ N (recall Table 1). These shape functions are

$$ \lambda_{1}\lambda_{2}\cdots\lambda_{N}\mathbb P_{r-N}, $$

(19)

and they vanish on all the edges (i.e., at all edge and vertex nodes). Let $\{\phi _{E,i}\}\subset \mathbb P_{r-N}$ be a nodal basis for the cell nodes {x_E,i}, where $i=1,2,\ldots ,\dim \mathbb P_{r-N}$. That is, ϕ_E,i(x_E,j) = δ_ij. Our interior cell nodal basis functions are then

$$ \varphi_{E,i}(\mathbf{x}) = \frac{\lambda_{1}(\mathbf{x})\lambda_{2}(\mathbf{x})\cdots\lambda_{N}(\mathbf{x})\phi_{E,i}(\mathbf{x})} {\lambda_{1}(\mathbf{x}_{E,i})\lambda_{2}(\mathbf{x}_{E,i})\cdots\lambda_{N}(\mathbf{x}_{E,i})}, \quad i=1,2,\ldots,\dim\mathbb P_{r-N}. $$

(20)

3.3.2 Edge nodal basis functions

For ${\mathcal {D}\mathcal {S}}_{r}(E_{N})$, there are r − 1 edge nodes on each edge. To simplify the notation, we construct φ_e,1,1(x), which is 1 at x_e,1,1 and vanishes at all other nodal points. The construction of the other edge nodal basis functions is similar.

For some $\tilde p\in \mathbb P_{r-N+1}(e_{1})$ (take $\tilde p = 0$ when r = N − 2) and for some coefficients β_j, let

$$ \phi_{e,1,1}(\mathbf{x}) = \Big({\prod}_{m\ne 1}\lambda_{m}(\mathbf{x})\Big)p(\mathbf{x}) + {\sum}_{j\ne N,1,2}\beta_{j}\phi_{1,j}(\mathbf{x}) \quad\in{\mathcal{D}\mathcal{S}}_{r}(E_{N}), $$

(21)

where $p(\mathbf {x}) = \tilde p((\mathbf {x}-\mathbf {x}_{v,N})\cdot \tau _{1})$ extends $\tilde p$ to E_N constantly in the normal direction to ${\mathscr{L}}_{1}$. This function vanishes on all edges but e₁.

Denote

$$ t_{e,1,n}=(\mathbf{x}_{e,1,n}-\mathbf{x}_{v,N})\cdot\tau_{1} \quad\text{and}\quad \tilde p(t)={\sum}_{\ell=0}^{r-N+1}\alpha_{\ell} t^{\ell}. $$

We require that ϕ_e,1,1(x_e,1,n) = δ_1,n for n = 1,2,…,r − 1, so the r − 1 coefficients {α_ℓ,β_j} solve the square linear system

$$ \begin{array}{@{}rcl@{}} && \frac{\phi_{e,1,1}(\mathbf{x}_{e,1,n})}{(\lambda_{N}\lambda_{2})(\mathbf{x}_{e,1,n})} = \Big(\!{\prod}_{m\ne N,1,2}\lambda_{m}(\mathbf{x}_{e,1,n})\Big){\sum}_{\ell=0}^{r-N+1}\alpha_{\ell} t_{e,1,n}^{\ell}\\ &&\quad + {\sum}_{j\ne N,1,2}\beta_{j}\Big(\!{\prod}_{m\ne N,1,2,j}\lambda_{m}(\mathbf{x}_{e,1,n})\Big)\lambda_{1,j}^{r-N+2}(\mathbf{x}_{e,1,n}) = \frac{\delta_{1,n}}{(\lambda_{N}\lambda_{2})(\mathbf{x}_{e,1,n})}. \end{array} $$

(22)

Assume for the moment that the function ϕ_e,1,1 is well defined on E_N. It takes the value 1 at x_e,1,1 and vanishes at all the other vertex and edge nodes, so we define

$$ \varphi_{e,1,1}(\mathbf{x}) = \phi_{e,1,1}(\mathbf{x}) - {\sum}_{k=1}^{\dim\mathbb P_{r-N}(E)}\phi_{e,1,1}(\mathbf{x}_{E,k}) \varphi_{E,k}(\mathbf{x}). $$

(23)

The nodal basis functions {φ_e,i,j : i = 1,2,…,N, j = 1,2,…,r − 1} for the other edge nodes are defined similarly. In Fig. 4, we show an edge nodal basis function for a pentagon. The next Lemma justifies that ϕ_e,1,1 is well defined on E_N.

Fig. 4

Plots of the r = 3 basis function for the edge node at $(\frac {1}{3},0)$ of a pentagon

Lemma 3.1

There exists a unique set of coefficients α_ℓ, ℓ = 0,1,…,r − N + 1, and β_j, j = 3,4,…,N − 1, solving the (r − 1) × (r − 1) linear system (22).

Proof

For $t\in \mathbb {R}$, let x(t) = x_v,N + tτ₁ and define $\tilde q(t)\in \mathbb P_{r-2}(e_{1})$ by

$$ \begin{array}{@{}rcl@{}} \tilde q(t) = \frac{\phi_{e,1,1}(\mathbf{x}(t))}{(\lambda_{N}\lambda_{2})(\mathbf{x}(t))} &=& \Big(\!{\prod}_{m\ne N,1,2}\!\!\lambda_{m}(\mathbf{x}(t))\Big) \tilde p(t)\\ &&+ {\sum}_{j\ne N,1,2}\beta_{j}\Big(\!{\prod}_{m\ne N,1,2,j}\!\!\lambda_{m}(\mathbf{x}(t))\Big)\lambda_{1,j}^{r-N+2}(\mathbf{x}(t)). \end{array} $$

(24)

We must show that the linear system has a unique solution, which is equivalent to showing that $\tilde q(t_{e,1,n}) =0$ for all n = 1,2,…,r − 1, then all α_ℓ = 0 and β_j = 0 (j≠N,1,2). Now $\tilde q(t)$ is a polynomial of degree r − 2, and it vanishes at r − 1 points, so it vanishes identically.

Suppose that the lines through e₁ and e_j intersect at $\mathbf {x}_{1,j}={\mathscr{L}}_{1}\cap {\mathscr{L}}_{j}$ for some j≠N,1,2. Since λ_j(x_1,j) = 0, $\tilde q((\mathbf {x}_{1,j}-\mathbf {x}_{v,N})\cdot \tau _{1})$ reduces to

$$ 0 = \tilde q((\mathbf{x}_{1,j}-\mathbf{x}_{v,N})\cdot\tau_{1}) = \beta_{j}\Big(\!{\prod}_{m\ne N,1,2,j}\lambda_{m}(\mathbf{x}_{1,j})\Big)\lambda_{1,j}^{r-N+2}(\mathbf{x}_{1,j}). $$

But λ_m(x_1,j)≠ 0 for all m≠ 1,j and λ_1,j(x_1,j)≠ 0 by our choice of this linear function, so we conclude that β_j = 0.

We have two cases to consider. First, if no edge is parallel to e₁ (so the intersection points x_1,j exist for all j≠N,1,2), then all the β_j vanish. Second, suppose that the lines through e₁ and e_j are parallel for some j≠N,1,2. No other edges can also be parallel, so we conclude β_k = 0 for all k≠j. Moreover, $\lambda _{j}\vert _{e_{1}}=c>0$ is a strictly positive constant, and so

$$ 0 = \tilde q(t) = \Big(\!{\prod}_{m\ne N,1,2,j}\!\!\lambda_{m}(\mathbf{x}(t))\Big) \Big({\sum}_{\ell=0}^{r-N+1}\!c \alpha_{\ell} t^{\ell}+\beta_{j}\lambda_{1,j}^{r-N+2}(\mathbf{x}(t))\Big), $$

or

$$ \beta_{j}\lambda_{1,j}^{r-N+2}(\mathbf{x}(t)) = - {\sum}_{\ell=0}^{r-N+1}\!c \alpha_{\ell} t^{\ell} \in \mathbb P_{r-N+1}(e_{1}). $$

The zero line of λ_1,j is transverse to e₁ (again by our choice of this linear function), leading us to conclude that $\lambda _{1,j}^{r-N+2}$ must have strict degree r − N + 2. Therefore, again, all the β_j = 0.

We have reduced $\tilde q(t)=0$ to a positive function times $\tilde p(t)$, so we must conclude that $\tilde p(t)=0$. That is, all the α_ℓ = 0, and the proof is complete. □

3.3.3 Vertex nodal basis functions

For the vertices, since r ≥ N − 2, we can define for each i = 1,2,…,N the shape functions

$$ \phi_{v,i}(\mathbf{x}) = {\prod}_{j\ne i,i+1}\lambda_{j}(\mathbf{x}) - {\sum}_{k=i}^{i+1}{\sum}_{\ell=1}^{r-1}\Big({\prod}_{j\ne i,i+1}\lambda_{j}(\mathbf{x}_{e,k,\ell})\Big) \varphi_{e,k,\ell}(\mathbf{x}), $$

(25)

wherein we interpret indices modulo N. These N functions vanish at all of the edge nodes, and ϕ_v,i(x_v,j) = 0 if i≠j and is positive otherwise. The nodal basis functions are then

$$ \varphi_{v,i}(\mathbf{x}) = \frac{\phi_{v,i}(\mathbf{x}) - {\sum}_{k=1}^{\dim\mathbb P_{r-N}(E)}\phi_{v,i}(\mathbf{x}_{E,k}) \varphi_{E,k}(\mathbf{x})}{\phi_{v,i}(\mathbf{x}_{v,i})}, \quad i=1,2,\ldots,N. $$

(26)

A vertex nodal basis function for a pentagon is shown in Fig. 5. This completes the construction of the $D_{N,r}=\dim \mathbb P_{r}(E_{N})+\frac 12N(N-3)$ nodal basis functions for $\mathcal {D}\mathcal {S}_{r}(E_{N})$. It also completes the proof of Theorem 3.1.

Fig. 5

Plots of the r = 3 basis function for the vertex node at (1,0) of a pentagon

4 Direct serendipity elements when 1 ≤ r < N − 2

There are vertex and possibly edge nodes, but no interior nodes, when 1 ≤ r < N. The total number of DoFs needed for E_N is then simply

$$ D_{N,r} = N + N(r-1) = Nr \ge \dim\mathbb P_{r}(E_{N}). $$

(27)

Our strategy is to define the space as a subset of a higher order direct serendipity space; that is, for some index s such that r < s < N, we define

$$ {\mathcal{D}\mathcal{S}}_{r}^{(s)}(E_{N}) = \big\{\varphi\in{\mathcal{D}\mathcal{S}}_{s}(E_{N}) : \varphi\vert_{e}\in\mathbb P_{r}(e)\text{ for all edges \textit{e} of }E_{N}\big\}. $$

(28)

Theorem 4.1

The finite element (28) with nodal DoFs (14) is well defined (i.e., unisolvent) when r < N − 2 and r < s < N. Moreover,

$$ {\mathcal{D}\mathcal{S}}_{r}^{(s)}(E_{N}) = \mathbb P_{r}(E_{N})\oplus\mathbb S_{r}^{{\mathcal{D}\mathcal{S}}}(E_{N}) $$

(29)

for some supplemental space of functions $\mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E_{N})$, and a nodal basis is given by the functions listed in (33) and defined as in (31) and (32).

As a practical matter, one should take s = N − 2. It is obvious that $\mathbb P_{r}(E_{N})\subset {\mathcal {D}\mathcal {S}}_{r}^{(s)}(E_{N})$, since $\mathbb P_{r}(E_{N})\subset \mathbb P_{s}(E_{N})\subset {\mathcal {D}\mathcal {S}}_{s}(E_{N})$ restricts to ∂E_N as required. That is, ${\mathcal {D}\mathcal {S}}_{r}^{(s)}(E_{N})$ has the form (29). We prove the rest of the theorem in the next section by constructing a nodal basis.

4.1 Construction of the nodal basis functions when r < N − 2

We construct nodal basis functions for ${\mathcal {D}\mathcal {S}}_{r}(E_{N})$ from ${\mathcal {D}\mathcal {S}}_{s}(E_{N})$ for any r < s < N. To make the notation clear as to which order (r or s) a quantity refers to, we will use a superscript within parentheses. For example, edge node x_e,1,1 will be referred to as $\mathbf {x}_{e,1,1}^{(r)}$ if it is the node in ${\mathcal {D}\mathcal {S}}_{r}(E)$, and $\mathbf {x}_{e,1,1}^{(s)}$ if it is the node in ${\mathcal {D}\mathcal {S}}_{s}(E)$ (these two nodes are not at the same position).

We first note that for each j = 0,1,…,r, there exists a unique $\tilde p^{(r)}_{j}(t)\in \mathbb P_{r}([0,1])$ interpolating r + 1 points as

$$ \tilde p^{(r)}_{j}(k/r) = \delta_{j,k},\quad \forall k=0,1,\ldots,r. $$

(30)

A basis function for edge node $\mathbf {x}_{e,i,j}^{(r)}$, i = 1,2,…,N and j = 1,2,…,r − 1, is then

$$ \varphi^{(r,s)}_{e,i,j}(\mathbf{x}) = {\sum}_{k=1}^{s-1}\tilde p^{(r)}_{j}(k/s) \varphi^{(s)}_{e,i,k}(\mathbf{x})\in{\mathcal{D}\mathcal{S}}_{s}(E_{N}), $$

(31)

which vanishes on all the edges except for e_i. Restricted to e_i, it is nominally a polynomial of degree s. However, it agrees with $\tilde p^{(r)}_{j}$ at s + 1 > r + 1 points, so it is in fact a polynomial of degree r on e_i. In consequence, $\varphi ^{(r,s)}_{e,i,j}\in {\mathcal {D}\mathcal {S}}_{r}^{(s)}(E_{N})$, and it vanishes at all nodes of ${\mathcal {D}\mathcal {S}}_{r}^{(s)}(E)$ except $\mathbf {x}_{e,i,j}^{(r)}$, where it is one (i.e., it is a nodal basis function).

For a vertex node $\mathbf {x}_{v,i}=\mathbf {x}_{v,i}^{(r)}=\mathbf {x}_{v,i}^{(s)}$, we define

$$ \begin{array}{@{}rcl@{}} \varphi^{(r,s)}_{v,i}(\mathbf{x}) &=& \varphi^{(s)}_{v,i}(\mathbf{x}) + {\sum}_{j=1}^{s-1}\tilde p^{(r)}_{r}(j/s) \varphi^{(s)}_{e,i,j}(\mathbf{x}) + {\sum}_{j=1}^{s-1}\tilde p^{(r)}_{0}(j/s) \varphi^{(s)}_{e,i+1,j}(\mathbf{x})\\ &\in&{\mathcal{D}\mathcal{S}}_{s}(E_{N}), \end{array} $$

(32)

which vanishes on all the edges except e_i and e_i+ 1. As before, we conclude that it is a polynomial of degree r on edges e_i and e_i+ 1, and so $\varphi ^{(r,s)}_{v,i}(\mathbf {x})\in {\mathcal {D}\mathcal {S}}_{r}^{(s)}(E_{N})$. Moreover, it is the nodal basis function for x_v,i, since it vanishes at all edge nodes $\mathbf {x}_{e,k,j}^{(r)}$ of e_k, k = i,i + 1, and $\varphi ^{(r,s)}_{v,i}(\mathbf {x}_{v,i})=1$.

Finally, since there are no interior cell DoFs, we conclude that

$$ \begin{array}{@{}rcl@{}} {\mathcal{D}\mathcal{S}}_{r}^{(s)}(E_{N}) & = & \text{span}\big\{\{\varphi^{(r,s)}_{v,i}: i=1,2,\ldots,N\}\\ &&\qquad\qquad\cup \{\varphi^{(r,s)}_{e,i,j}: i=1,2,\ldots,N,\ j = 1,2,\ldots,r-1 \}\big\}, \end{array} $$

(33)

which indeed has dimension Nr. This completes the proof of Theorem 4.1.

4.2 A second construction identifying the supplemental function space

From either the definition (28) or from the nodal basis (33), it is difficult to determine the supplemental space $\mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E_{N})$ in (29). In this section, we give an explicit construction $\mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E_{N})$. In practice, the supplemental space is not needed to implement ${\mathcal {D}\mathcal {S}}_{r}(E_{N})$ (one would simply use (33)); however, as we will see later, it could be used to implement mixed finite elements.

It will be convenient in this section to use a notation that unifies edge and vertex nodes. For each edge index i = 1,2,…,N and j = 0,1,…,r, let

$$ \mathbf{x}_{n,i,j} = \begin{cases} \mathbf{x}_{v,i-1}&\text{if }j=0\text{ (interpret} i-1\ \text{as}\ N\ \text{when} i=1),\\ \mathbf{x}_{v,i}&\text{if }j=r,\\ \mathbf{x}_{e,i,j}&\text{if }j=1,2,\ldots,r-1. \end{cases} $$

(34)

We caution that the vertices are represented twice in this indexing convention. Let the full set of nodal points be denoted

$$ \begin{array}{@{}rcl@{}} \mathcal{A} &=& \{\mathbf{x}_{v,i}, \mathbf{x}_{e,i,j} : i=1,2,\ldots,N,\ j=1,2,\ldots,r-1\}\\ &=& \{\mathbf{x}_{n,i,j}:i=1,2,\ldots,N,\ j=1,2,\ldots,r\}. \end{array} $$

We will divide this set into two disjoint subsets $\mathcal {A}_{\mathbb P}$ and $\mathcal {A}_{\mathbb S}=\mathcal {A}\setminus \mathcal {A}_{\mathbb P}$.

The subset of nodes $\mathcal {A}_{\mathbb P}$ is chosen iteratively as follows, and as depicted in Fig. 6. For each k = r + 1,…,2,1 in descending order, first select a distinct edge e_i(k) with index i(k) ∈{1,2,…,N}. At this stage, there are at least N − r + k − 1 > 0 edges left to choose from, since N − r > 2 and k ≥ 1. Second, select k distinct nodes x_{n,i(k),j(ℓ)} on this chosen edge, with the indices j(ℓ) ∈{0,1,…,r} and ℓ = 1,2,…,k. The only restriction is that one may not choose a vertex node that lies on any of the previously chosen edges. Since there are 2 vertex nodes and r − 1 edge nodes, one can always meet this restriction. As a simple example, one can choose edges i(k) = k and take only edge nodes, except for x_v,r and x_v,r+ 1 on e_r+ 1 and x_v,r− 1 on e_r.

Fig. 6

A choice of nodes $\mathcal {A}_{\mathbb P}$ and $\mathcal {A}_{\mathbb S}$ for N = 6, r = 3. And the dashed lines show the choices of zero lines for the construction of ϕ_{n,i(2),j(ℓ)}, ℓ = 1,2

The total number of nodes in $\mathcal {A}_{\mathbb P}$ is

$$ {\sum}_{k=1}^{r+1}k = \frac12(r+2)(r+1) = \dim\mathbb P_{r}(E_{N}). $$

(35)

The total number of unselected nodes $\mathcal {A}_{\mathbb S}=\mathcal {A}\setminus \mathcal {A}_{\mathbb P}$ is the same as the dimension of $\mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E_{N})$. For each node $\mathbf {x}_{n,i,j}\in \mathcal {A}_{\mathbb S}$, we construct $\varphi _{n,i,j}=\varphi _{n,i,j}^{(r,s)}$, the supplemental function associated to x_n,i,j as in the previous section. The supplemental space is then

$$ \mathbb S_{r}^{{\mathcal{D}\mathcal{S}}}(E_{N}) = \text{span}\{\varphi_{n,i,j} : \mathbf{x}_{n,i,j}\in\mathcal{A}_{\mathbb S}\}\subset{\mathcal{D}\mathcal{S}}_{r}^{(s)}(E_{N}), $$

(36)

and it has the correct dimension. These basis functions are nodal, by construction.

To verify that (36) is indeed the supplemental space, we finish the construction of the nodal basis (i.e., for nodal points in $\mathcal {A}_{\mathbb P}$) by including additional functions only from $\mathbb P_{r}(E_{N})$. We do this iteratively for each k = 1,2,…,r + 1 in ascending order as follows. For k = 1, we construct the nodal basis function for x_n,i(1),j(1) by first defining

$$ \phi_{n,i(1),j(1)}(\mathbf{x}) = {\prod}_{m=2}^{r+1}\frac{\lambda_{i(m)}(\mathbf{x})}{\lambda_{i(m)}(\mathbf{x}_{n,i(1),j(1)})}\ \in\mathbb P_{r}, $$

(37)

which vanishes at all the nodes of $\mathcal {A}_{\mathbb P}$ except x_n,i(1),j(1), where it is one. By the choice of edges, the denominator does not vanish. Then

$$ \varphi_{n,i(1),j(1)}(\mathbf{x}) = \phi_{n,i(1),j(1)}(\mathbf{x}) - {\sum}_{\mathbf{x}_{n,i,j}\in\mathcal{A}_{\mathbb S}}\phi_{n,i(1),j(1)}(\mathbf{x}_{n,i,j}) \varphi_{n,i,j}(\mathbf{x}), $$

(38)

and this is indeed our nodal basis function for the node x_n,i(1),j(1).

For k = 2, we need to construct the nodal basis functions for the two points on the edge e_i(2). Note that we have one more point compared to the previous step, but we also have one fewer edge to deal with, since we now have φ_n,i(1),j(1). Therefore we can construct for each ℓ = 1,2,

$$ \begin{array}{@{}rcl@{}} &&\phi_{n,i(2),j(\ell)}(\mathbf{x})\\ & =& \frac{\lambda[\mathbf{x}_{n,i(1),j(1)},\mathbf{x}_{n,i(2),j(\ell^{*})}](\mathbf{x})}{\lambda[\mathbf{x}_{n,i(1),j(1)},\mathbf{x}_{n,i(2),j(\ell^{*})}](\mathbf{x}_{n,i(2),j(\ell)})} {\prod}_{m=3}^{r+1}\frac{\lambda_{i(m)}(\mathbf{x})}{\lambda_{i(m)}(\mathbf{x}_{n,i(2),j(\ell)})}\ \in\mathbb P_{r}, \end{array} $$

where ℓ^∗ = 2,1 is the other index. For each ℓ = 1,2, the function vanishes at all the nodes of $\mathcal {A}_{\mathbb P}$ except x_{n,i(2),j(ℓ)}, where it is one. Then let

$$ \begin{array}{@{}rcl@{}} \varphi_{n,i(2),j(\ell)}(\mathbf{x}) = \phi_{n,i(2),j(\ell)}(\mathbf{x}) - \!{\sum}_{\mathbf{x}_{n,i,j}\in\mathcal{A}_{\mathbb S}}\!\phi_{n,i(2),j(\ell)}(\mathbf{x}_{n,i,j}) \varphi_{n,i,j}(\mathbf{x}), \end{array} $$

which give our two desired nodal basis functions on e_i(2).

Perhaps the general construction is clear. For k = 1,2,…,r + 1, first define for each ℓ = 1,2,…,k,

$$ \begin{array}{@{}rcl@{}} &&\phi_{n,i(k),j(\ell)}(\mathbf{x})\\ &=& {\prod}_{m=1,m\ne\ell}^{k}\frac{\lambda[\mathbf{x}_{n,i(1),j(1)},\mathbf{x}_{n,i(k),j(m)}](\mathbf{x})} {\lambda[\mathbf{x}_{n,i(1),j(1)},\mathbf{x}_{n,i(k),j(m)}](\mathbf{x}_{n,i(k),j(\ell)})} {\prod}_{m=k+1}^{r+1}\frac{\lambda_{i(m)}(\mathbf{x})}{\lambda_{i(m)}(\mathbf{x}_{n,i(k),j(\ell)})}\\ &&\in\mathbb P_{r}, \end{array} $$

and then set

$$ \begin{array}{@{}rcl@{}} \varphi_{n,i(k),j(\ell)}(\mathbf{x}) &=& \phi_{n,i(k),j(\ell)}(\mathbf{x}) - \!{\sum}_{\mathbf{x}_{n,i,j}\in\mathcal{A}_{\mathbb S}}\!\phi_{n,i(k),j(\ell)}(\mathbf{x}_{n,i,j}) \varphi_{n,i,j}(\mathbf{x})\\ && - {\sum}_{m=2}^{k-1}{\sum}_{l=1}^{m}\phi_{n,i(k),j(\ell)}(\mathbf{x}_{n,i(m),j(l)}) \varphi_{n,i(m),j(l)}(\mathbf{x}). \end{array} $$

This completes the identification of ${\mathcal {D}\mathcal {S}}_{r}^{(s)}(E_{N})$ as $\mathbb P_{r}(E_{N})\oplus \mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E_{N})$ for the supplemental space defined by (36).

5 Approximation properties of ${\mathcal {D}\mathcal {S}}_{r}$

To obtain global approximation properties, we need to assume that the mesh is uniformly shape regular in some sense. We take the definition due to Girault and Raviart [12, pp. 104–105].

Definition 5.1

For any $E_{N}\in \mathcal {T}_{h}$, denote by T_i, i = 1,2,…,N(N − 1)(N − 2)/6, the sub-triangle of E_N with vertices being three of the N vertices of E_N. Define the parameters

$$ \begin{array}{@{}rcl@{}} h_{E_{N}} &=& \text{diameter of }E_{N}, \end{array} $$

(39)

$$ \begin{array}{@{}rcl@{}} \rho_{E_{N}} &=& 2 \min_{1\leq i\leq N(N-1)(N-2)/6}\{ \text{diameter of largest circle inscribed in }T_{i} \}. \end{array} $$

(40)

A collection of meshes $\{\mathcal {T}_{h}\}_{h>0}$ is uniformly shape regular if there exists a shape regularity parameterσ_∗ > 0, independent of $\mathcal { T}_{h}$ and h > 0, such that the ratio

$$ \frac{\rho_{E_{N}}}{h_{E_{N}}} \geq \sigma_{*}>0\quad\text{for all }E_{N}\in\mathcal{T}_{h}. $$

(41)

A shape regular mesh has the property that every element can take on vertices only in a compact set of possible values (up to translation and rotation). It also has a bound on the number of elements that can share a single vertex. We need the following hypothesis on the construction of the finite elements.

Assumption 5.1

For every $E_{N}\in \mathcal {T}_{h}$, suppose that the basis functions of ${\mathcal {D}\mathcal {S}}_{r}(E_{N})$ are constructed using λ_i,j such that the zero set ${\mathscr{L}}_{i,j}$ intersects e_i and e_j. Moreover, assume that R_i,j are uniformly differentiable functions of the vertices of E_N up to order m ≤ r + 1.

Theorem 5.1

Let $\mathcal {T}_{h}$ be uniformly shape regular with shape regularity parameter σ_∗ and let Assumption 5.1 hold. Let $1\le p\le \infty$ and ℓ > 1/p (or ℓ ≥ 1 if p = 1). Then for r ≥ 1, there exists a constant C = C(r,σ_∗) > 0, independent of $h=\max \limits _{E_{N}\in \mathcal {T}_{h}}h_{E_{N}}$, such that for all functions v ∈ W^ℓ,p(Ω),

$$ \inf_{v_{h}\in{\mathcal{D}\mathcal{S}}_{r}({\Omega})}\|v - v_{h}\|_{W^{m,p}({\Omega})} \leq C h^{\ell-m} \|v\|_{W^{\ell,p}({\Omega})}, \quad 0\leq m \leq \ell \leq r+1. $$

(42)

The proof follows closely that given in [5] for the quadrilateral case and so is omitted here except for discussion of one important issue. The proof uses a continuous dependence argument, relying on the fact that the set of vertices lies in a compact set as well as Assumption 5.1, which ensures that the construction of the finite elements on E_N depends continuously on its vertices. The issue that arises when dealing with polygons is settling on a suitable reference configuration, from which the true element of the mesh is a continuous and compact perturbation.

The main argument is illustrated in Fig. 7 for a pentagonal element $E_{N}=E_{5}\in \mathcal {T}_{h}$ for which, after translation and rotation, x_v,1 = (0,0) and x_v,2 = (H,0). The reference domain is a regular polygon (equilateral and equiangular) $\hat E_{N}$ with two fixed vertices $\hat {\mathbf {x}}_{v,1}=(0,0)$ and $\hat {\mathbf {x}}_{v,2}=(1,0)$. We need a bijective and smooth map $\mathbf {F}_{\!\tilde E_{N}}:\hat E_{N}\to \tilde E_{N}=E_{N}/H$ with (ℓ,0) being mapped to (ℓ,0), ℓ = 0,1. In the case of a quadrilateral, one uses a bilinear map. For a polygon, it is probably clear to the reader that such a map $\mathbf {F}_{\!\tilde E_{N}}:\hat E_{N}\to \tilde E_{N}$ exists. To be rigorous, however, we construct $\mathbf {F}_{\!\tilde E_{N}}$ using smooth barycentric coordinates $\{\hat \varphi _{v,i}:i=1,\ldots ,N\}$ on E_N [13]. The map is then

$$ \mathbf{F}_{\!\tilde E_{N}}(\hat{\mathbf{x}}) = {\sum}_{i=1}^{N} \frac1H \mathbf{x}_{v,i} \hat\varphi_{v,i}(\hat{\mathbf{x}}). $$

(43)

Fig. 7

An element $E_{5}\in \mathcal {T}_{h}$ is shown on the right-hand side in its translated and rotated local coordinates. It is the image of a regular reference polygon $\hat E_{5}$ on the left-hand side. The map is decomposed into one that changes the geometry but not the size $\mathbf {F}_{\!\tilde E}:\hat E_{5}\to \tilde E_{5}$, and a scaling map $\tilde {\mathbf {x}}\mapsto H\tilde {\mathbf {x}}$

6 The de Rham complex and mixed finite elements

The de Rham complex of interest here is

$$ \mathbb{R} \lhook\joinrel\longrightarrow H^{1} \overset{\text{curl} }{\protect\relbar\protect\joinrel\protect\relbar\protect\joinrel\protect\relbar\protect\joinrel\rightarrow} H(\text{div}) \overset{\text{div} }{\protect\relbar\protect\joinrel\protect\relbar\protect\joinrel\protect\relbar\protect\joinrel\rightarrow} L^{2} \longrightarrow 0, $$

(44)

where the curl (or rot) of a scalar function ϕ(x) = ϕ(x₁,x₂) is $\text {curl} \phi = \bigg (\frac {\partial \phi }{\partial x_{2}},-\frac {\partial \phi }{\partial x_{1}}\bigg )$. From left to right, the image of one linear map is the kernel of the next.

6.1 Direct mixed finite elements on polygons

For r = 0 and s = 0, as well as for each r = 1,2… and s = r − 1,r, there are important discrete analogues of the de Rham complex involving the direct serendipity spaces and mixed finite element spaces, denoted ${\mathbf {V}_{r}^{s}}(E_{N})$, namely

$$ \mathbb{R} \lhook\joinrel\longrightarrow {\mathcal{D}\mathcal{S}}_{r+1}(E_{N}) \overset{\text{curl} }{\protect\relbar\protect\joinrel\protect\relbar\protect\joinrel\protect\relbar\protect\joinrel\rightarrow} {\mathbf{V}_{r}^{s}}(E_{N}) \overset{\text{div} }{\protect\relbar\protect\joinrel\protect\relbar\protect\joinrel\protect\relbar\protect\joinrel\rightarrow} \mathbb P_{s}(E_{N}) \longrightarrow 0. $$

(45)

On triangular and rectangular elements when r ≥ 1, it is known that the classic serendipity space $\mathcal {S}_{r+1}$ (in place of ${\mathcal {D}\mathcal {S}}_{r+1}$ above) is the precursor of the Brezzi-Douglas-Marini mixed finite element space BDM_r [1, 3, 4] (in place of $\mathbf {V}_{r}^{r-1}$ above). It is also known that on quadrilateral elements, the direct serendipity space is the precursor of the direct mixed spaces [5]. The families of mixed finite elements on E_N, N > 4, are new.

To dissect the properties of these new elements, we note two facts. First, the divergence operator takes $\mathbf {x}\mathbb P_{s}$ one-to-one and onto $\mathbb P_{s}$. Second, the well-known Helmholtz-like decomposition holds [14]

$$ {\mathbb P_{r}^{2}} = \text{curl} \mathbb P_{r+1}\oplus\mathbf{x}\mathbb P_{r-1}. $$

(46)

From (45), we have a reduced (s = r − 1 ≥ 0) and full (s = r) H(div)-approximating mixed finite element space ($\mathcal {P}$ in Definition 2.1) defined directly on a polygon E_N with minimal number of DoFs of the form

$$ \begin{array}{@{}rcl@{}} \mathbf{V}_{r}^{r-1}(E_{N}) &=& \text{curl} {\mathcal{D}\mathcal{S}}_{r+1}(E_{N})\oplus\mathbf{x}\mathbb P_{r-1}\\ &=& \text{curl} \mathbb P_{r+1}(E_{N})\oplus\mathbf{x}\mathbb P_{r-1}\oplus\text{curl} \mathbb S_{r+1}^{{\mathcal{D}\mathcal{S}}}(E_{N})\\ &=& {\mathbb P_{r}^{2}}(E_{N})\oplus\mathbb S_{r}^{\mathbf{V}}(E_{N}), \end{array} $$

(47)

$$ \begin{array}{@{}rcl@{}} {\mathbf{V}_{r}^{r}}(E_{N}) &=& \text{curl} {\mathcal{D}\mathcal{S}}_{r+1}(E_{N})\oplus\mathbf{x}\mathbb P_{r}\\ &=& \text{curl} \mathbb P_{r+1}(E_{N})\oplus\mathbf{x}\mathbb P_{r}\oplus\text{curl} \mathbb S_{r+1}^{{\mathcal{D}\mathcal{S}}}(E_{N})\\ &=& {\mathbb P_{r}^{2}}(E_{N})\oplus\mathbf{x}\tilde{\mathbb{P}}_{r}\oplus\mathbb S_{r}^{\mathbf{V}}(E_{N}), \end{array} $$

(48)

with the following definition of the supplemental (vector valued) functions

$$ \mathbb S_{r}^{\mathbf{V}}(E_{N}) = \text{curl} \mathbb S_{r+1}^{{\mathcal{D}\mathcal{S}}}(E_{N}). $$

(49)

Similar to [5, 14], the DoFs ($\mathcal {N}$ in Definition 2.1) for ${\mathbf {v}\in \mathbf {V}_{r}^{s}}(E_{N})$, s = r − 1,r, are given (after fixing a basis for the test functions) by

$$ \begin{array}{@{}rcl@{}} &&{\int}_{e_{i}}\mathbf{v}\cdot\nu_{i} p d\sigma,\quad\quad\forall p\in\mathbb P_{r}(e_{i}),\ i=1,2,\ldots,N, \end{array} $$

(50)

$$ \begin{array}{@{}rcl@{}} &&{\int}_{E_{N}}\mathbf{v}\cdot\nabla q dx,\quad\quad\forall q\in\mathbb P_{s}(E_{N}),\ q\text{ not constant}, \end{array} $$

(51)

$$ \begin{array}{@{}rcl@{}} &&{\int}_{E_{N}}\mathbf{v}\cdot\pmb\psi dx,\quad\quad\forall \pmb\psi\in\mathbb B_{r}^{\mathbf{V}}(E_{N}),\text{ if }r\ge N-1, \end{array} $$

(52)

where dσ is the one dimensional surface measure and the H¹(E_N) and H(div;E_N) bubble functions, for r ≥ N − 1, are

$$ \mathbb B_{r+1}(E_{N}) = \lambda_{1}\lambda_{2}\ldots\lambda_{N}\mathbb P_{r-N+1}(E_{N}) \ \text{and}\ \mathbb B_{r}^{\mathbf{V}}(E_{N}) = \text{curl} \mathbb B_{r+1}(E_{N}). $$

(53)

We remark that the edge DoFs (50) determine the normal components (flux) of our vector functions, the divergence DoFs (51) determine the divergence of our vector functions (with the previous edge DoFs), and the curl DoFs (52) control the curl of our vector functions.

Theorem 6.1

The finite element ${\mathbf {V}_{r}^{s}}(E_{N})$ defined by (47)–(48), (49) for r = 1,2… and s = r − 1,r (but s ≥ 0) with DoFs (50)–(52), (53) is well defined (i.e., unisolvent). Moreover, it has the minimal number of DoFs needed of a space of index r that is H(div) conforming and has independent divergence approximation to order s.

Proof

The minimal number of DoFs needed are expressed by (50)–(52), since (50) is required for H(div) conformity of order r and (51) is required for independent divergence approximation to order s. Moreover, (52) is required to control polynomials of degree r which have no divergence nor edge normal flux.

The total number of degrees of freedom is

$$ D_{N,r}^{\mathbf{V}} = \begin{cases} N\dim\mathbb P_{r}(e) + (\dim\mathbb P_{s}(E_{N}) - 1)\\ \qquad\qquad+ \dim\mathbb P_{r-N+1}(E_{N}), &\text{if }r\ge N-1,\\ N\dim\mathbb P_{r}(e) + (\dim\mathbb P_{s}(E_{N}) - 1), &\text{if }r<N-1, \end{cases} $$

(54)

and the local dimensions of the spaces are

$$ {\dim\mathbf{V}_{r}^{s}}(E_{N}) = (\dim{\mathcal{D}\mathcal{S}}_{r+1}-1) + \dim(\mathbf{x}\mathbb P_{s}). $$

(55)

By (6) and (27), these numbers agree. In fact,

$$ D_{N,r}^{\mathbf{V}} = \begin{cases} N(r+1) - 1 + \frac12(s+2)(s+1)\\ \qquad+ \frac12(r-N+3)(r-N+2), & r\ge N-1,\\ N(r+1) - 1 + \frac12(s+2)(s+1), & r< N-1. \end{cases} $$

(56)

The remainder of the proof, to show that these spaces are unisolvent (i.e., a vector function in ${\mathbf {V}^{s}_{r}}{(E_{N})}$ with vanishing DoFs is zero everywhere), is essentially the same as that given in [5] for direct mixed spaces on quadrilaterals. □

6.2 Implementation of the mixed method

The mixed space of vector functions ${\mathbf {V}_{r}^{s}}$ over Ω is defined by merging continuously the normal fluxes across each edge e of the mesh $\mathcal {T}_{h}$. That is, for r ≥ 0, s = r − 1,r, s ≥ 0,

$$ {\mathbf{V}_{r}^{s}} = \big\{\mathbf{v}\in H(\text{div};{\Omega}) : \mathbf{v}\big\vert_{E_{N}}{\in\mathbf{V}_{r}^{s}}(E_{N})\text{ for all }E_{N}\in\mathcal{T}_{h}\big\}. $$

(57)

Associated to this space is the scalar space of its divergences, namely,

$$ W_{s} = \text{div} {\mathbf{V}_{r}^{s}} = \big\{w\in L^{2}({\Omega}) : w\big\vert_{E_{N}}\in\mathbb P_{s}(E_{N})\text{ for all }E_{N}\in\mathcal{T}_{h}\big\}. $$

(58)

It is used, for example, when solving a second order elliptic partial differential equation in mixed form.

6.2.1 Implementation using the hybrid mixed method

The hybrid form of the mixed method is often used [15] so that no globally merged basis is required. A Lagrange multiplier space is used to enforce the normal flux continuity through an additional equation, using the space

$$ {\Lambda}_{r} = \big\{\lambda\in L^{2}\big(\cup_{E_{N}\in\mathcal{T}_{h}}\partial E_{N}\big) : \lambda\big\vert_{e}\in\mathbb P_{r}(e)\text{ for each edge }e\text{ of }\mathcal{ T}_{h}\big\}. $$

(59)

The vector functions in ${\mathbf {V}_{r}^{s}}(E_{N})$ can be represented by any of the equivalent forms in (47)–(48). First, since ${\mathbf {V}_{r}^{s}}(E_{N})=\text {curl} {\mathcal {D}\mathcal {S}}_{r+1}(E_{N})\oplus \mathbf {x}\mathbb P_{s}$, we can construct the full space ${\mathcal {D}\mathcal {S}}_{r+1}(E_{N})$ as discussed in Sections 3 and 4.1, apply the curl operator, and add in $\mathbf {x}\mathbb P_{s}(E_{N})$. But we can also use the fact that $\mathbf {V}_{r}^{r-1}(E_{N})={\mathbb P_{r}^{2}}(E_{N})\oplus \mathbb S_{r}^{\mathbf {V}}(E_{N})$ and ${\mathbf {V}_{r}^{r}}(E_{N})={\mathbb P_{r}^{2}}(E_{N})\oplus \mathbf {x}\tilde {\mathbb {P}}_{r}\oplus \mathbb S_{r}^{\mathbf {V}}(E_{N})$, and simply add to the polynomials the supplemental space $\mathbb S_{r}^{\mathbf {V}}(E_{N})=\text {curl} \mathbb S_{r+1}^{{\mathcal {D}\mathcal {S}}}(E_{N})$. To construct $\mathbb S_{r+1}^{{\mathcal {D}\mathcal {S}}}(E_{N})$, one uses (11)–(12) when r is large, and otherwise requires the construction given in Section 4.2.

6.2.2 Implementation as an H(div)-conforming mixed space

If an explicit basis for the H(div)-conforming space (57) of vector-valued functions is required, one can proceed as follows. The construction is an extension of the N = 4 case given in [5]. We use the fact that the tangential derivative of a function along an edge e_i of an element E_N maps by the curl operator to a normal derivative, i.e., for $\phi \in {\mathcal {D}\mathcal {S}}_{r+1}(E_{N})$,

$$ \nabla\phi\cdot\tau_{i}\big\vert_{e_{i}} = \text{curl} \phi\cdot\nu_{i}\big\vert_{e_{i}}, \quad\text{with } \tau_{i}=(-\nu_{i,2},\nu_{i,1})\text { on }e_{i}. $$

(60)

Since the serendipity spaces are globally continuous, the tangential derivatives will agree across e_i, which implies that the global basis functions arising from ${\mathcal {D}\mathcal {S}}_{r+1}({\Omega })$ will be in H(div;Ω).

We construct H(div)-conforming vector basis functions in four sets, related to the edge DoFs (50) with nonconstant test functions, the edge DoFs (50) with constant test functions, the divergence DoFs (51), and the curl DoFs (52).

Basis functions from curls of interior cell basis functions of ${\mathcal {D}\mathcal {S}}_{r+1}(E_{N})$

The interior cell basis functions of ${\mathcal {D}\mathcal {S}}_{r+1}(E_{N})$ are $\{\varphi _{E,i}^{(r+1)},\ i=1,2,\ldots ,\dim \mathbb P_{r+1-N}\}$ as given by (20) (the superscript is a reminder that the index of the direct serendipity space is r + 1). However, any basis for (19), i.e., the bubble space $\mathbb B_{r+1}(E_{N})$ defined in (53), suffices. Denote it as $\{\phi _{E_{N},i}^{(r+1)},\ i=1,2,\ldots ,\dim \mathbb P_{r+1-N}\}$. Then for each $E_{N}\in \mathcal {T}_{h}$, the global basis functions for ${\mathbf {V}_{r}^{s}}$ are

$$ \pmb\psi_{b,E_{N},i} = \begin{cases}\text{curl} \phi_{E_{N},i}^{(r+1)},\\ \qquad i=1,\ldots,\tfrac12(r+3-N)(r+2-N), &\text{on }E_{N},\\ 0,&\text{otherwise}. \end{cases} $$

(61)

These exist only when r ≥ N − 1, and they are in fact the H(div) bubble functions $\mathbb B_{r}^{\mathbf {V}}$ appearing in (53). They have no normal flux and no divergence. They are associated to the curl DoFs (52).

Basis functions from curls of interior edge basis functions of ${\mathcal {D}\mathcal {S}}_{r+1}(E_{N})$

The interior edge basis functions of ${\mathcal {D}\mathcal {S}}_{r+1}(E_{N})$ are $\{\varphi _{e,i,j}^{(r+1)},\ i=1,2,\ldots ,N,\ j=1,2,\ldots ,r\}$ as given by (23) or (31) when r < N − 2. For r ≥ N − 2, one could use the simpler set $\{\phi _{e,i,j}^{(r+1)}/\phi _{e,i,j}^{(r+1)}(\mathbf {x}_{e,i,j})\}$ given in (21) which ignores the internal cell DoFs, and we proceed with this choice (the case r < N − 2 is entirely similar). Consider an edge e of the mesh shared by elements E_k and E_ℓ with k < ℓ and e locally denoted as edge i₁ and i₂, respectively. The global basis functions for ${\mathbf {V}_{r}^{s}}$ are, for r ≥ 1 and j = 1,…,r,

$$ \pmb\psi_{e,j}(\mathbf{x}) = \begin{cases} \text{curl} \phi_{e,i_{1},j}^{(r+1)}(\mathbf{x})/\phi_{e,i_{1},j}^{(r+1)}(\mathbf{x}_{e,i_{1},j}),&\mathbf{x}\in E_{k},\\ \text{curl} \phi_{e,i_{2},r-j+1}^{(r+1)}(\mathbf{x})/\phi_{e,i_{2},r-j+1}^{(r+1)}(\mathbf{x}_{e,i_{2},r-j+1}),&\mathbf{x}\in E_{\ell},\\ 0,&\mathbf{x}\notin E_{k}\cup E_{\ell}. \end{cases} $$

(62)

These functions have vanishing divergence but nonvanishing normal flux; however, the average normal flux vanishes. They are associated to the edge DoFs (50) with nonconstant test functions.

Basis functions from curls of vertex basis functions of ${\mathcal {D}\mathcal {S}}_{r+1}(E_{N})$

We will now construct basis functions that have constant normal flux on a single edge of the mesh. These cannot have vanishing divergence. We will use the vertex basis functions of ${\mathcal {D}\mathcal {S}}_{r+1}(E_{N})$, which are $\{\varphi _{v,i}^{(r+1)},\ i=1,2,\ldots ,N\}$ as given in (26) or (32). Again, when r ≥ N − 2 we can instead simply use $\{\phi _{v,i}^{(r+1)}/\phi _{v,i}^{(r+1)}(\mathbf {x}_{v,i})\}$ given in (25), and we proceed with the discussion using this case. The construction is complicated by the fact that the curls of these functions have nonvanishing normal flux on all the edges of the mesh emanating from the vertex in question.

We work on the element E_N, and we first modify the serendipity vertex basis functions so that their restrictions to each edge e of E_N is a linear function, i.e., we define for all i

$$ \begin{array}{@{}rcl@{}} \phi^{*}_{v,i}(\mathbf{x}) &=& \frac{\phi^{(r+1)}_{v,i}(\mathbf{x})}{\phi^{(r+1)}_{v,i}(\mathbf{x}_{v,i})}\\ &&+ {\sum}_{j=1}^{r} \bigg[ \frac{j}{r+1}\frac{\phi^{(r+1)}_{e,i,j}(\mathbf{x})}{\phi^{(r+1)}_{e,i,j}(\mathbf{x}_{e,i,j})} + \Big(1 - \frac{j}{r+1}\Big) \frac{\phi^{(r+1)}_{e,i+1,j}(\mathbf{x})}{\phi^{(r+1)}_{e,i+1,j}(\mathbf{x}_{e,i+1,j})}\bigg], \end{array} $$

again using indices modulo N. Then define $\pmb \psi ^{*}_{v,i}=\text {curl} \phi ^{*}_{v,i}$, for which

$$ \pmb\psi^{*}_{v,i}(\mathbf{x})\cdot\nu_{j}\big\vert_{e_{j}} = \nabla\phi^{*}_{v,i}(\mathbf{x})\cdot\tau_{j}\big\vert_{e_{j}} = \begin{cases} 1/\vert e_{i}\vert,&j=i,\\ -1/\vert e_{i+1}\vert,&j=i+1,\\ 0,&\text{otherwise}. \end{cases} $$

We also use the vector $\pmb \psi ^{**}_{v,i}(\mathbf {x}) = \mathbf {x}-\mathbf {x}_{v,i+1}\in \mathbf {x}\mathbb P_{0}(E_{N}){\oplus \mathbb P_{0}^{2}}(E_{N}){\subset \mathbf {V}_{r}^{s}}(E_{N})$, which is in our space and satisfies

$$ \pmb\psi^{**}_{v,i}(\mathbf{x})\cdot\nu_{j}\big\vert_{e_{j}} = \begin{cases} 0,&j=i+1,i+2, \\ (\mathbf{x}_{v,j}-\mathbf{x}_{v,i+1})\cdot\nu_{j},&\text{otherwise}, \end{cases} $$

which is nonnegative on every edge e_j.

For any edge e_i of element E_N, we define a vector function with flux only on e_i by canceling the fluxes of $\pmb \psi ^{**}_{v,i}$ on all the other edges using some of the $\pmb \psi ^{*}_{v,k}$. Precisely, we define for edge e = e_i of element E_N

$$ \begin{array}{*{20}l} \pmb\psi_{e,0}\big\vert_{E_{N}} = \frac{1}{c_{i,i+N}}\Bigg(\pmb\psi^{**}_{v,i}-{\sum}_{j=i+3}^{i+N-1}c_{i,j} \vert e_{j}\vert \pmb\psi^{*}_{v,j}\Bigg), \\ c_{i,i+2} = 0,\quad c_{i,j} = (\mathbf{x}_{v,j}\!-\mathbf{x}_{v,i+1})\cdot\nu_{j} + \frac{\vert e_{j-1}\vert}{\vert e_{j}\vert} c_{i,j-1} > 0,\quad j = i+3,\ldots,i+N, \end{array} $$

(63)

which has normal flux 1 on e_i and 0 on all the other edges. These can be merged across edges to define H(div)-conforming global basis functions, which have constant divergence on each element. Note that the choice of vertex index x_v,i+ 1 in $\pmb \psi ^{**}_{v,i}$ is only for convenience in presenting the construction. We might have chosen it to be any other vertex except x_v,i− 1 and x_v,i. The basis functions here are associated to the edge DoFs (50) with constant test functions.

Basis functions with nonvanishing and nonconstant divergence

Finally, when s ≥ 1 we define the global basis functions associated to the nonconstant divergences. They are local to each element $E_{N}\in \mathcal {T}_{h}$. Working on E_N, we begin with the functions $\mathbf {x}\mathbb P_{s}^{*}(E_{N})$, where $\mathbb P_{s}^{*}(E_{N})={\sum }_{k=1}^{s}\tilde {\mathbb {P}}_{k}(E_{N})\subset \mathbb P_{s}(E_{N})$. Take p_i(x) in a basis for $\mathbb {P}_{s}^{*}(E_{N})$, so $i=1,\ldots ,\tfrac 12(s+2)(s+1)-1$. We must remove the normal flux on ∂E_N from xp_i(x). We do this using (62) and (63) by defining

$$ \pmb\psi_{d,E_{N},i}(\mathbf{x}) = \begin{cases}\displaystyle \mathbf{x} p_{i}(\mathbf{x}) - {\sum}_{j=1}^{N}{\sum}_{k=0}^{r}\alpha_{j,k} \pmb\psi_{e_{j},k}(\mathbf{x}),&\text{on }E_{N},\\ 0,&\text{otherwise}, \end{cases} $$

(64)

and setting the coefficients α_j,k on each edge e_j so that

$$ 0 =c_{j} p_{i}(\mathbf{x}) - {\sum}_{k=0}^{r}\alpha_{j,k} \pmb\psi_{e_{j},k}(\mathbf{x})\cdot\nu_{j}\big\vert_{e_{j}}, $$

(65)

where $c_{j}=\mathbf {x}\cdot \nu _{j}\vert _{e_{j}}$ is a constant. The coefficients can be found once one realizes that on edge e_j, $\varphi _{e,j,k}^{(r+1)}(x)\big \vert _{e_{j}}=\mathfrak {L}_{k}(t)$, a Lagrange basis polynomial, where x(t) = (1 − t)x_v,j− 1 + tx_v,j for t ∈ [0,1]. Therefore, for k ≥ 1,

$$ \pmb\psi_{e_{j},k}(\mathbf{x})\cdot\nu_{j}\big\vert_{e_{j}} = \text{curl} \varphi_{e,j,k}^{(r+1)}(x)\cdot\nu_{j}\big\vert_{e_{j}} = \nabla\varphi_{e,j,k}^{(r+1)}(x)\cdot\tau_{j}\big\vert_{e_{j}} = \frac{\mathfrak{L}_{k}^{\prime}(t)}{\vert\mathbf{x}_{v,j} - \mathbf{x}_{v,j-1}\vert}, $$

and

$$ 0 = c_{j} {{\int}_{0}^{t}}p_{i}(\mathbf{x}(s)) ds - \alpha_{j,0} t - {\sum}_{k=1}^{r}\frac{\alpha_{j,k} \mathfrak{L}_{k}(t)}{\vert\mathbf{x}_{v,j} - \mathbf{x}_{v,j-1}\vert}. $$

(66)

The coefficients can be read off by substituting in the Lagrange points t_ℓ = ℓ/(r + 1) for ℓ = 1,…,r + 1. These basis functions are associated to the divergence DoFs (51) with nonconstant local divergence.

The global basis is now fully defined.

7 Approximation properties for ${\mathbf {V}_{r}^{s}}$

In this section, we state the approximation theory for our new direct mixed finite elements. A discussion and detailed proof for the N = 4 case has been given in [5]. The proof for polygons is very similar, and so omitted here.

We can define a projection operator $\pi :H(\text {div};{\Omega })\cap (L^{2+\epsilon }({\Omega }))^{2}{\to \mathbf {V}_{r}^{s}}$, s = r − 1,r, where 𝜖 > 0, by piecing together locally defined operators π_E. For suitable v, π_Ev is defined in terms of the DoFs (50)–(52). The operator π satisfies the commuting diagram property [16], which is to say that

$$ \mathcal{P}_{W_{s}}\nabla\cdot\mathbf{v}=\nabla\cdot\pi\mathbf{v}, $$

(67)

where $\mathcal {P}_{W_{s}}$ is the L²-orthogonal projection operator onto $W_{s}={\nabla \cdot \mathbf {V}_{r}^{s}}$. The following lemma holds.

Theorem 7.1

Let $\mathcal {T}_{h}$ be uniformly shape regular with shape regularity parameter σ_∗ and let Assumption 5.1 hold. Then for ${\mathbf {V}_{r}^{s}}$ there is a constant C = C(r,σ^∗) > 0, independent of h > 0, such that

$$ \begin{array}{@{}rcl@{}} \|\mathbf{v}-\pi\mathbf{v}\|_{L^{2}({\Omega})} &\le& C \|\mathbf{v}\|_{H^{k}({\Omega})} h^{k},\quad\quad k=1,\ldots,r+1, \end{array} $$

(68)

$$ \begin{array}{@{}rcl@{}} \|p-\mathcal{P}_{W_{s}}p\|_{L^{2}({\Omega})} &\le& C \|p\|_{H^{k}({\Omega})} h^{k},\quad\quad k=0,1,\ldots,s+1, \end{array} $$

(69)

$$ \begin{array}{@{}rcl@{}} \|\nabla\cdot(\mathbf{v}-\pi\mathbf{v})\|_{L^{2}({\Omega})} &\le& C \|\nabla\cdot\mathbf{v}\|_{H^{k}({\Omega})} h^{k},\quad\quad k=0,1,\ldots,s+1, \end{array} $$

(70)

where s = r − 1 ≥ 0 and s = r ≥ 1 for reduced and full H(div)-approximation, respectively. Moreover, the discrete inf-sup condition

$$ \sup_{\mathbf{v}_{h}{\in\mathbf{V}_{r}^{s}}}\frac{(w_{h},\nabla\cdot\mathbf{v}_{h})}{\|\mathbf{v}_{h}\|_{H(\text{div})}} \ge \gamma \|w_{h}\|_{L^{2}({\Omega})},\quad\forall w_{h}\in W_{s}, $$

(71)

holds for some γ = γ(r,σ^∗) > 0 independent of h > 0.

8 Numerical results

We test our finite elements on Poisson’s equation

$$ \begin{array}{@{}rcl@{}} -\nabla\cdot(\nabla p) &=& f \quad\text{in }{\Omega}, \end{array} $$

(72)

$$ \begin{array}{@{}rcl@{}} p &=& 0 \quad\text{on }\partial{\Omega}, \end{array} $$

(73)

where f ∈ L²(Ω). The problem can be written in the weak form: Find $p\in {H_{0}^{1}}({\Omega })$ such that

$$ (\nabla p,\nabla q) = (f,q), \quad\forall q\in {H_{0}^{1}}({\Omega}), $$

(74)

where (⋅,⋅) is the L²(Ω) inner product. Setting

$$ \mathbf{u} = -\nabla p, $$

(75)

we have the mixed weak form: Find u ∈ H(div;Ω) and p ∈ L²(Ω) such that

$$ \begin{array}{@{}rcl@{}} &&(\mathbf{u},\mathbf{v}) - (p,\nabla\cdot\mathbf{v}) =0, \quad\forall\mathbf{v}\in H(\text{div};{\Omega}), \end{array} $$

(76)

$$ \begin{array}{@{}rcl@{}} &&(\nabla\cdot\mathbf{u},w) = (f,w), \quad\forall w\in L^{2}({\Omega}). \end{array} $$

(77)

These weak forms give rise to finite element approximations. In view of Theorems 5.1 and 7.1, it is well known that the following theorem holds [17, 18].

Theorem 8.1

Let $\mathcal {T}_{h}$ be uniformly shape regular with shape regularity parameter σ_∗ and let Assumption 5.1 hold. There exists a constant C > 0, depending on r and σ_∗ but otherwise independent of $\mathcal {T}_{h}$ and h > 0, such that

$$ \|p-p_{h}\|_{H^{m}({\Omega})}\leq C h^{s+1-m} \vert p\vert_{H^{s+1}({\Omega})},\quad s=0,1,\ldots,r,\quad m=0,1, $$

(78)

where $p_{h}\in {\mathcal {D}\mathcal {S}}_{r}({\Omega })\cap {H_{0}^{1}}({\Omega })$ approximates (74) for r ≥ 1. Moreover,

$$ \begin{array}{@{}rcl@{}} \|\mathbf{u}-\mathbf{u}_{h}\|_{L^{2}({\Omega})} &\le& C\|\mathbf{u}\|_{H^{k}({\Omega})}h^{k},\quad\quad k=1,\ldots,r+1, \end{array} $$

(79)

$$ \begin{array}{@{}rcl@{}} \|p-p_{h}\|_{L^{2}({\Omega})} &\le& C\|\mathbf{u}\|_{H^{k}({\Omega})}h^{k},\quad\quad k=1,\ldots,s+1, \end{array} $$

(80)

$$ \begin{array}{@{}rcl@{}} \|\nabla\cdot(\mathbf{u}-\mathbf{u}_{h})\|_{L^{2}({\Omega})} &\le& C\|\nabla\cdot\mathbf{u}\|_{H^{k}({\Omega})}h^{k},~~ k=0,1,\ldots,s+1, \end{array} $$

(81)

where $(\mathbf {u}_{h},p_{h}){\in \mathbf {V}_{r}^{s}}\times W_{s}$ approximates (76)–(77), for r ≥ 0 and 0 ≤ s = r,r − 1.

We consider the test problem (72)–(73) defined on the unit square Ω = [0,1]². The exact solution is $u(x_{1},x_{2}) = \sin \limits (\pi x_{1})\sin \limits (\pi x_{2})$ and the source term is $f(\mathbf {x}) = 2\pi ^{2}\sin \limits (\pi x_{1})\sin \limits (\pi x_{2})$.

Solutions are computed on two different sequences of meshes, each has n² elements and is a Voronoi diagram mesh generated using the software package PolyMesher [19]. The first set of meshes, ${\mathcal {T}_{h}^{1}}$, is a simple mesh composed of polygons generated from regularly spaced seeds. The seeds are initially uniformly spaced and then alternatively perturbed up or down in the y-direction by one-quarter of the regular spacing. The number of vertices of each element is N = 4, 5, or 6. The second sequence, ${\mathcal {T}_{h}^{2}}$, is generated by PolyMesher using n² random initial seeds and up to 10,000 iterations to smooth the mesh. We illustrate these patterns by showing the n = 6 and n = 18 cases in Fig. 8.

Fig. 8

Meshes with 6 × 6 and 18 × 18 elements

We give results on each mesh sequence for n = 6, 10, 14, 18, and 22. The maximum, minimum, and average shape regularity parameters are shown in Table 2. Sequence ${\mathcal {T}_{h}^{1}}$ has a fixed maximum and minimum shape regularity parameter; moreover, the average shape regularity parameter decreases and converges to a constant as the number of elements increases. However, since the meshes of ${\mathcal {T}_{h}^{2}}$ are generated randomly, we can see in Fig. 8 that there is no fixed pattern in the shape of the elements, and so the shape regularity parameter varies as well. The n = 18 and 22 meshes seem to be less regular than the other ${\mathcal {T}_{h}^{2}}$ meshes, so to improve the regularity, we removed some of the small edges, creating the “modified ${\mathcal {T}_{h}^{2}}$” mesh sequence, as described later in Section 8.1.2.

Table 2 Maximum, minimum, and average shape regularity parameters for each mesh

8.1 Direct serendipity spaces

We present in this section convergence studies for the direct serendipity spaces ${\mathcal {D}\mathcal {S}}_{r}$.

8.1.1 Shape regular meshes of mostly hexagons, ${\mathcal {T}_{h}^{1}}$

Table 3 shows the errors and orders of convergence for the mesh sequence ${\mathcal {T}_{h}^{1}}$ consisting of quadrilaterals, pentagons, and hexagons. The convergence rates are consistent with the theory.

Table 3 Errors and convergence rates for ${\mathcal {D}\mathcal {S}}_{r}$ on ${\mathcal {T}^{1}_{h}}$ meshes

We observed (in results not reported here) that for the same number of elements, the error on a mesh from ${\mathcal {T}_{h}^{1}}$ is smaller compared to a mesh of trapezoids. As n increases, the ${\mathcal {T}_{h}^{1}}$ meshes are refined in a fixed pattern, giving a higher percentage of elements that are hexagons in the interior of the mesh. This observation suggests that elements with more edges might tend to give better approximations.

To test this hypothesis, we graphed the L² error on each element in Fig. 9 at level n = 10 and 18 with r = 5. The error is indeed concentrated around the boundary, where the quadrilateral and pentagonal elements concentrate. However, the solution $u(x_{1},x_{2}) = \sin \limits (\pi x_{1})\sin \limits (\pi x_{2})$ on [0,1]² has a single hump over the domain, so the solution is steepest near the boundary and thus harder to approximate there.

Fig. 9

The L² error on each element for mesh sequence ${\mathcal {T}^{1}_{h}}$ at level n = 10 and n = 18 with approximation index r = 5

We performed two additional tests, with the L² error on each element shown in Fig. 10. For the first additional test, we solved the same problem on the domain [0,2] × [− 1,1] using a mesh given by reflecting the original n = 18 mesh with respect to x = 1, and then reflecting this with respect to y = 0. This test shows that when the original boundary elements are moved to the interior of the domain, we still observe the same larger error. For the second additional test, we solved the problem on the unit square domain with the original mesh, but we set the exact solution to be $u(x_{1},x_{2}) = \sin \limits (2\pi x_{1})\sin \limits (2\pi x_{2})$, which has four humps. From the figure, we see that the solution is better approximated in the interior where hexagons are used versus the approximation near the boundary.

Fig. 10

The L² error on each element for the two additional tests based on mesh sequence ${\mathcal {T}^{1}_{h}}$ at level n = 18 with approximation index r = 5

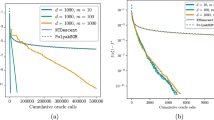
To further verify that hexagons are better at approximation, we performed experiments for index r = 2,3,4,5 at levels n = 6,10,14,18,22 on seven different meshes, each emphasizing a fixed number of edges N for the elements. The first mesh consists of isosceles right triangles, and we distort it with random noise to get the second mesh. The third mesh consists of squares, the fourth mesh is a mesh of identical trapezoids, and the fifth mesh consists of quadrilaterals obtained by randomly distorting the vertices of a square mesh. The sixth mesh is ${\mathcal {T}_{h}^{1}}$ (mostly hexagons), and we distort it with some randomness to get the seventh mesh. To simplify the presentation, we only show results for r = 5 in Fig. 11, since the others are similar. We plot the log of error versus half the log of the number of degrees of freedom for each mesh sequence. We see that for the same number of degrees of freedom, hexagonal elements give the best results, followed by quadrilaterals, with triangular elements giving the worst performance.

Fig. 11

Log of the L²-norm and H¹-seminorm errors versus half the log of the number of DoFs on seven different mesh sequences with n = 6,10,14,18,22 and r = 5

8.1.2 Not so shape regular meshes of mostly hexagons, ${\mathcal {T}_{h}^{2}}$

Table 4 presents the errors and orders of convergence for the mesh sequence ${\mathcal {T}_{h}^{2}}$ generated by n² random initial seeds. We see that the convergence rates are generally correct, but they are not steady due to the randomness inherent in the mesh refinement process. Of particular concern are the rates for n = 18,22, especially as r increases. We attribute this behavior to the poor shape regularity of these two random meshes (recall Table 2).

Table 4 Errors and convergence rates for ${\mathcal {D}\mathcal {S}}_{r}$ on ${\mathcal {T}^{2}_{h}}$ meshes

An examination of the spatial distribution of the error for n = 18, as shown on the left in Fig. 12, suggests that the error is exceptionally large near one corner. The n = 18 mesh has two edges that are relatively very short containing the vertices (0.108,0.050) and (0.890,0.057), and the n = 22 mesh has five short edges. We created the modified ${\mathcal {T}^{2}_{h}}$ meshes by removing one vertex of each short edge. As can be seen in Table 2, the shape regularity parameters of the elements of the modified mesh are more uniform. The right plot in Fig. 12 shows that the error is reduced without the offending edges. The overall error and convergence results for the modified mesh are presented in Table 5, and they are closer to the expected rates.

Fig. 12

The L² error on each element of the domain [0,1]² for ${\mathcal {T}^{2}_{h}}$ with level n = 18 and approximation index r = 5 before and after modifying the mesh. The two small edges were taken out of the mesh by removing vertices located at (0.108,0.050) and (0.890,0.057)

Table 5 Errors and convergence rates for ${\mathcal {D}\mathcal {S}}_{r}$ on modified ${\mathcal {T}^{2}_{h}}$ meshes

8.2 Direct mixed spaces

We now consider the direct mixed finite elements ${\mathbf {V}_{r}^{s}}\times W_{s}$ derived in Section 6.2. These are implemented both in hybrid form (Section 6.2.1) and as H(div)-conforming elements (Section 6.2.2), which, of course, provide the same results.

The L² and H¹-seminorm errors and convergence orders for the mesh sequence ${\mathcal {T}_{h}^{1}}$ with r = (0, )1,2,3 appear in Tables 6–7. The theory predicts that the scalar p, the vector u, and the divergence ∇⋅u should attain the order of approximation s + 1, r + 1, and s + 1, respectively, for the reduced (s = r − 1) and full (s = r) H(div)-approximation spaces. We see rates of convergence that are close to the theoretical ones. Moreover, the errors for ${\mathcal {T}_{h}^{1}}$ are a bit smaller than what we see for meshes of trapezoids, due to having many elements with more than four edges.

Table 6 Errors and convergence rates in L² for reduced H(div)-approximation direct mixed finite elements on ${\mathcal {T}_{h}^{1}}$ meshes

Table 7 Errors and convergence rates in L² for full H(div)-approximation direct mixed finite elements on ${\mathcal {T}_{h}^{1}}$ meshes

The errors and orders of convergence of the modified ${\mathcal {T}_{h}^{2}}$ mesh sequence are given in Tables 8–9. We see the expected results.

Table 8 Errors and convergence rates in L² for reduced H(div)-approximation direct mixed finite elements on modified ${\mathcal {T}_{h}^{2}}$ meshes

Table 9 Errors and convergence rates in L² for full H(div)-approximation direct mixed finite elements on modified ${\mathcal {T}_{h}^{2}}$ meshes

9 Summary and conclusions

We defined direct serendipity finite elements on general closed, nondegenerate, and convex polygons E_N with N vertices for any index of approximation r. A direct serendipity element has its function space of the form of polynomials plus supplemental functions, i.e.,

$$ {\mathcal{D}\mathcal{S}}_{r}(E_{N}) = \mathbb P_{r}(E_{N})\oplus\mathbb S_{r}^{{\mathcal{D}\mathcal{S}}}(E_{N}),\quad r\geq1, $$

(82)

with the supplemental space $\mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E_{N})$ being of minimal local dimension subject to the requirement of global H¹-conformity. For higher order finite element spaces with r ≥ N − 2, the supplemental space $\mathbb S_{r}^{{\mathcal {D}\mathcal {S}}}(E_{N})$ has dimension $\frac {1}{2}N(N-3)$, which is the number of pairs of nonadjacent edges. This fact inspires our construction (12), for which different choices of λ_i,j and R_i,j give rise to different spaces. Each index i,j represents a pair of nonadjacent edges e_i and e_j of E_N. Simple choices for λ_i,j and R_i,j can be made, as given in (8) and (10). The lower order direct serendipity finite element spaces with r < N − 2, are given as the subset of functions in ${\mathcal {D}\mathcal {S}}_{N-2}(E_{N})$ that restrict to polynomials of degree r on ∂E_N. Taking nodal DoFs, we constructed nodal bases for the direct serendipity spaces.

By the de Rham theory, each direct serendipity element ${\mathcal {D}\mathcal {S}}_{r+1}(E_{N})$ gives rise to both a reduced and a full H(div)-approximation direct mixed finite element

$$ \begin{array}{@{}rcl@{}} \mathbf{V}_{r}^{r-1}(E_{N}) &=& \text{curl} {\mathcal{D}\mathcal{S}}_{r+1}(E_{N})\oplus\mathbf{x}\mathbb P_{r-1}(E_{N})\\ &=& {\mathbb P_{r}^{2}}(E_{N})\oplus\mathbb S_{r}^{\mathbf{V}}(E_{N}),\quad r\ge1, \end{array} $$

(83)

$$ \begin{array}{@{}rcl@{}} {\mathbf{V}_{r}^{r}}(E) &=& \text{curl} {\mathcal{D}\mathcal{S}}_{r+1}(E_{N})\oplus\mathbf{x}\mathbb P_{r}(E_{N})\\ &=& {\mathbb P_{r}^{2}}(E_{N})\oplus\mathbf{x}\tilde{\mathbb{P}}_{r}(E_{N})\oplus\mathbb S_{r}^{\mathbf{V}}(E_{N}),\quad r\ge0, \end{array} $$

(84)

respectively, where $\mathbb S_{r}^{\mathbf {V}}(E) = \text {curl} \mathbb S_{r+1}^{{\mathcal {D}\mathcal {S}}}(E_{N})$ has minimal local dimension subject to the requirement of global H(div)-conformity. These mixed elements can be implemented globally in the hybrid form of the mixed method without the need of a global basis. However, we also provided an explicit conforming global basis that we constructed locally on each E_N using the basis of ${\mathcal {D}\mathcal {S}}_{r+1}(E_{N})$.

The convergence theory handled the polygonal geometry through a continuous dependence argument over a compact set of perturbations. Assuming that the meshes are shape regular as h → 0 (Definition 5.1) and that the functions λ_i,j and R_i,j in (12) are chosen to be continuously differentiable with respect to the vertices of the element (i.e., Assumption 5.1), we obtained optimal approximation rates for the elements in Theorems 5.1 and 7.1.

We presented and discussed numerical results from finite element numerical solutions of Poisson’s equation. The convergence rates were consistent with the theory, Theorem 8.1, and provided confirmation of the optimal order of accuracy of the finite element approximations. We found that mesh shape regularity was quite important in terms of the observed error. In particular, we found that short edges, which lead to a poor (i.e., small) shape regularity parameter, could also result in a poor approximation in that region of the mesh. Removing such edges greatly improved the approximation and convergence rates. We also observed that meshes that emphasize elements with many edges per element outperform meshes with fewer edges per element. This observation, as well as the need for flexible meshing in some applications, can be considered justification for using polygonal elements.